A spatially explicit Bayesian framework for cognitive schooling behaviours

Abstract

Social aggregations such as schools, swarms, flocks and herds occur across a broad diversity of animal species, strongly impacting ecological and evolutionary dynamics of these species and their predators, prey and competitors. The mechanisms through which individual-level responses to neighbours generate group-level characteristics have been extensively investigated both experimentally and using mathematical models. Models of social groups typically adopt a ‘zone’ approach, in which individuals’ movement responses to neighbours are functions of instantaneous relative position. Empirical studies have demonstrated that most social animals such as fish exhibit well-developed spatial memory and other advanced cognitive capabilities. However, most models of social grouping do not explicitly include spatial memory, largely because a tractable framework for modelling acquisition of and response to historical spatial information has been lacking. Using fish schooling as a focal example, this study presents a framework for including cognitive responses to spatial memory in models of social aggregation. The framework utilizes Bayesian estimation parameters that are continuously distributed in time and space as proxies for animals’ spatial memory. The result is a hybrid Lagrangian–Eulerian model in which the effects of cognitive state and behavioural responses to historical spatial data on individual-, group- and population-level distributions of social animals can be explicitly investigated.

1. Introduction

Schools, flocks, herds, swarms and other social aggregations are widespread among diverse types of animals, and play key roles in predator–prey dynamics, competition, migration, reproduction, disease transmission, colonization of new habitats and other ecological functions. Social aggregation behaviour is particularly interesting as an evolutionary phenomenon because the long-term costs and benefits of a particular behaviour are mediated through numerous interactions with neighbours, whose characteristics (including behaviour) may vary substantially at the group and population levels [1]. Coordinated social behaviours are also of substantial interest in control theory, where biomimetic algorithms have been used to implement cooperative control of teams of autonomous vehicles [2].

Social aggregation behaviour has long been a focus of empirical work, including ‘microscopic’ studies quantifying individual-level movements within and around groups through motion analysis, and ‘macroscopic’ studies measuring higher-level characteristics such as group size distributions, fidelity of individuals to groups, fidelity of groups to spatial positions or movement routes, etc. Behavioural observations of social animals in the context of social interaction, foraging and migration have established that many, probably most, of these animals exhibit high-level cognitive functions (see Brown et al. [3] for a comprehensive review of cognition in fish). Cognitive capacities commonly include learning from fellow group members and retention of spatial memory about the time and location of past events [4]. Further, evidence suggests that the level of cognitive capabilities varies with the apparent utility of those capabilities, suggesting both that learning from conspecifics and spatial memory play important roles in shaping behaviour, and that maintaining these capabilities is costly.

In parallel with empirical work, a large body of mathematical theory aimed broadly at mechanistically linking alternative microscopic social interaction algorithms with their emergent macroscopic consequences has been developed [5]. At the individual level, most theoretical models of social movement algorithms assume some form of ‘zone’ model, in which responses to neighbours are a function of relative position. For example, common elements of such models include repulsion zones in which neighbours that are too close elicit avoidance responses, attraction zones in which distant neighbours elicit approach responses and alignment zones in which neighbours elicit directional conformance to enhance polarization within neighbourhoods.

In most existing zone models, individuals respond to instantaneous positions of neighbours. Historical effects of past events are present in these models, but only implicitly. For example, historical effects in zone models can be encoded in incremental responses to neighbours, so that individuals respond gradually or partially to unfolding neighbour distributions. Historical effects are also evident in multiple stable group states, and in hysteresis in group structure [6]. However, these implicit manifestations of historical effects may or may not be accurate reflections of empirically observed cognitive capabilities such as spatial memory. Their accuracy is difficult to assess because few theoretical tools exist to tractably model cognitive responses to spatial memory in the context of social movement algorithms.

In this study, I develop a framework for modelling social aggregation— specifically, fish schooling—as an explicit cognitive response to spatial memory. The framework uses Bayesian estimation to approximate fishes’ spatial memory. Hence, it can be interpreted as a general and simplified approach towards mimicking animals’ encoding and updating of spatio-temporal data, or as a set of more specific quantitative hypotheses about how neural processing derives statistical estimates from ambiguous data. Bayesian estimation has been previously applied to the study of animal aggregation, for example in development of discrimination rules for assessing acoustic signatures of fish schools [7]. Mann et al. [8] used Bayesian discrimination to optimally select social behaviour algorithms, including algorithms with memory, showing that direction changes in glass shrimp are influenced by past encounters with neighbours. Perez-Escudero & de Polavieja [9] used Bayesian estimation as a model for cognition in the context of social site selection in sticklebacks, showing that historical selections by conspecifics influence subsequent decision-making. Here, I adapt this approach by assuming that schooling individuals assess spatial characteristics of the local population using Bayesian estimation. I model individuals’ spatial memory by assuming that Bayesian parameters are scalar fields—that is, distributed continuously in time and space—and derive a quantitative approach to determining the spatio-temporal evolution of those fields (rationale and results of this derivation are presented in the main text of this study, with additional mathematical details in the electronic supplemental material). I develop a simple individual-based simulation in which typical zone-type social behavioural algorithms are implemented, but with explicit cognitive responses to spatial memory rather than solely to instantaneous neighbour positions. The results suggest that the timescale of spatial memory has potentially pronounced impacts on individual-, group- and population-level distributions of social animals.

2. Development of a modelling framework

The modelling framework presented in this study follows from three primary assumptions, which, as suggested by empirical observations, may be biologically defensible for many grouping animals:

• — Social animals have awareness of their own and neighbours’ positions and velocities in fixed spatial coordinates. That is, individuals retain information about neighbours that is georeferenced [4], not solely in relation to their own position and velocity as assumed in most zone models. For example, this assumption implies that an individual that is initially approaching a stationary group but then reverses direction is aware that it has moved and not the group.

• — Social animals have memory, and can base social movement and other behavioural decisions on a combination of current conditions and past events. This assumption expresses the biological consensus that most social organisms have some form of functional memory [9,10], though in some cases memory may be mediated through physiology or morphology rather than being exclusively neuronal.

• — Spatial scales associated with strong neighbour–neighbour interactions are much smaller than limiting distances for neighbour detection. In explicit terms, if L_d is a characteristic spatial scale of the minimal region containing the neighbours with which an individual interacts most strongly, and L_D is the maximum distance over which that individual can detect and assess neighbours, the assumption is that L_d ≪ L_D. In the context of existing social modelling literature, this assumption is essentially that behavioural zones associated with the strongest repulsion, attraction and alignment responses to neighbours lie well within the maximum distance at which neighbours can be detected [11]. Empirically, this assumption appears valid, for example, in most situations where all or part of a group can be seen from a distance much greater than typical intra-group separation distances. This arguably includes most laboratory and field observations of social animal groups.

Several implications follow directly from these three assumptions. One is that any spatial position within an individual's neighbourhood has been observable to that individual for a substantial preceding time. More explicitly, for an individual with movement speed v, the period over which a location within its neighbourhood has been within its detection distance is minimally

and if movement is not persistently straight may be much longer. Another implication is that, as a focal animal moves, it can associate successive georeferenced observations of a given location within its detection distance into a temporal sequence that potentially contains much more information about population characteristics at that location than does any single instantaneous observation.

2.1. Space and timescales of social grouping

Useful starting points for modelling cognitive schooling are the characteristic space and timescales at which distributions of individuals and groups vary. The characteristic timescale over which properties such as population density within a neighbourhood can change significantly is roughly τ_d = L_d/v. τ_d is effectively a neighbourhood renewal timescale, because it represents the time interval over which individuals within that neighbourhood can be substantially removed, replaced or augmented. That is, over time intervals ≪τ_d, little change can occur in neighbourhood density, while over time intervals ≫τ_d, a significant change is likely. Additionally, many animal groups are characterized by inter-individual spacing and direction that are strongly correlated over distances that are much larger than L_d. Labelling the length scale of these correlations as L_g, it follows that the timescale over which density and direction are strongly correlated as a group passes over a given location is approximately τ_g = L_g/v, where typically τ_g≫τ_d. Group edges, variations in direction and other group-level spatial features represent limits to spatial correlations. Hence, if most individuals are most of the time within L_D of these features (e.g. if most group members are within sight of an edge), an implication is that typically L_g≪L_D.

The timescales τ_g and τ_d are significant to an individual estimating the statistical characteristics of nearby neighbourhoods using georeferenced, temporally sequenced information. Successive observations of quantities like neighbourhood density taken at intervals ≪τ_d are not independent, and thus do not effectively constrain statistical estimation. The observation interval that maximizes statistical information is therefore ≈ τ_d. On the other hand, the quantities being estimated are relatively constant over intervals < τ_g, but fluctuate over longer timescales. Hence, observations from times ≫τ_g in the past are likely uninformative about current conditions, and should be discounted or discarded.

As noted, georeferenced observations of a given location are limited by detection distance to ≈ τ_obs. By the earlier-mentioned arguments, we expect that L_D≫L_g≫L_d, so that correlation time rather than detectability constrains estimation within individuals’ local neighbourhoods. A further consequence of the relative magnitudes of these length scales is that individuals approaching a given neighbourhood from different directions likely have very similar estimates. If so, approximating those estimates as common assessments shared by all individuals, rather than as individual-specific, may be a computationally useful simplification that introduces acceptable errors.

2.2. Estimates of neighbourhood density

Subject to the earlier-mentioned constraints, I assume that a prototypical individual (say, the jth) counts other individuals within a neighbourhood centred at position x_j at equal, discrete intervals δt ≈ τ_d. After a sampling period of n δt, the fish has made n observations, m₁,m₂, …,m_n, where m_i is the number of neighbours at the ith observation. I assume m_i is a stochastic variable that locally has a statistical distribution for which a Bayesian conjugate prior can be derived [12], and use a simple Bayesian updating scheme to approximate the jth individual's cognitive assessment of its neighbour observations. As a simple concrete example, here I assume that m is locally Poisson-distributed with parameter ρ_j. The conjugate prior then takes the form of a gamma distribution with shape parameter α > 0 and inverse scale parameter β > 0,

2.1

Equation (2.1) represents the probability distribution of Poisson parameters prior to a set of observations. Intuitively, β can be interpreted as the total number of observations, and α as the total number of neighbours observed, so that ρ = α/β. By the rationale presented in the electronic supplementary material, I model the posterior parameters subsequent to the ith observation with the updating rules

2.2

for estimation of the parameters in (2.1) for the probability distribution of local density estimates. In (2.2), the exponential terms represent temporal discounting on a timescale T. The limit T → 0 represents the no-memory case, as implemented in most zone models, while the limit T → ∞ represents estimation of statistically stationary data, as in standard Bayesian estimation. The rationale in §2.1 suggests T ≈ τ_g is a favourable choice of T for schooling fish.

2.3. Estimates of neighbourhood direction

Additionally, I assume that individual j can observe the movement direction of other individuals within a neighbourhood centred at x_j. I assume movement directions follow a distribution with a conjugate prior, and again use a Bayesian updating scheme to approximate individuals’ cognitive assessments. As a simple example, here I assume that movement directions within a neighbourhood are described by a von Mises distribution,

2.3

In (2.3), M represents the probability of randomly drawing a direction θ given a mean direction λ and concentration parameter κ. Large values of κ imply that neighbours’ movement directions are tightly clustered around λ; κ → 0 implies movements approach a uniform angular distribution.

The conjugate prior for the joint distribution of λ and κ [13] is

2.4

where I₀ is the modified Bessel function of the first kind, order 0 (see electronic supplementary material for additional details). Intuitively, λ₀ represents an estimated preferred direction, while R₀ represents a concentration—i.e. a directional certainty—in the λ₀ direction. After directions θ_k, k = 1,2, …,m_i are observed in the ith neighbour count, the updated parameters R_i and λ_i are given by

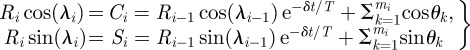2.5

2.4. Spatial redistribution of cognitive variables

As suggested already, α_i , β_i , C_i , S_i , R_i and λ_i can all be assessed at any point in space and time, and hence are scalar fields that vary continuously over the model domain. These fields represent cognitive variables that do not necessarily obey physically meaningful conservation laws. Nonetheless, a socially interacting animal with a current cognitive assessment applicable to a given neighbourhood may anticipate that the location to which that assessment most accurately applies may change over time, and conversely that the assessment most applicable to a given location at some future time may currently apply to a different location. In the current mathematical context, the fields α_i, β_i, C_i, S_i, R_i and λ_i can undergo spatial redistribution. A simple but useful form for this spatial redistribution of cognitive assessment is a system of advection–diffusion equations,

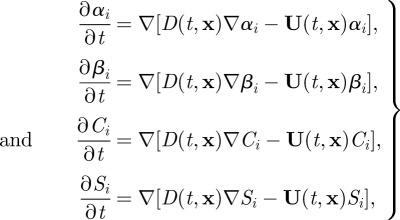2.6

to apply during the interval between the ith and i + 1st observations, with R_i, λ_i to be correspondingly updated according to (2.5). Note that the quantitative values of the advection–diffusion coefficients U and D are to this point undefined elements of individuals’ cognitive responses to spatial data, but that they are likely to vary in space and time according to local values of α_i, β_i, C_i, S_i, R_i and λ_i. Hence, (2.6) represents a coupled set of nonlinear partial differential equations.

3. A simplified simulation of cognitive schooling

To illustrate how the Bayesian framework for cognitive schooling outlined in §2 can be used to model social aggregation, and the potential impacts of spatial memory on individual-, group- and population-level distributions, I modified one of the simplest zone-type behaviours from the literature by assuming individuals respond to cognitive memory variables as well as to instantaneous neighbour positions. The model assumes that individuals have a neighbourhood within which they seek to maintain a target number of neighbours; when the actual number of neighbours is greater or less than this target, individuals increment their direction as appropriate towards the left or right (figure 1), depending on which side has more neighbours [14,15]. Additionally, individuals increment their directions to align with the prevailing direction in their neighbourhood. The simulation is stochastic, in that neighbour density and direction are inferred from the Bayesian field parameters via random draws from the distributions (2.1) and (2.3). Additional details are given in the electronic supplemental materials and cited references.

Figure 1.

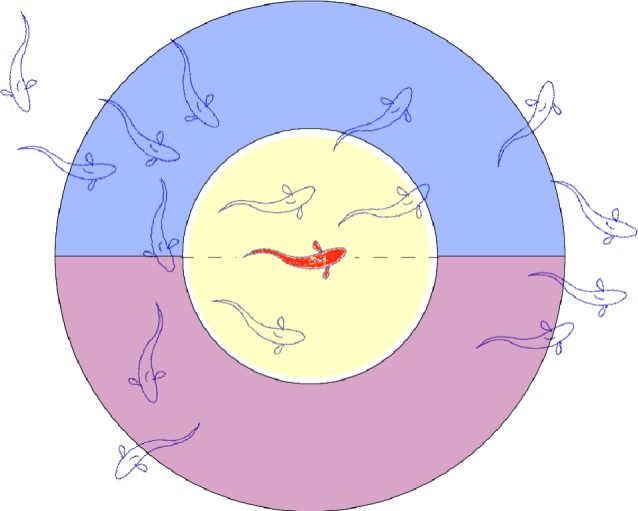
Schematic of the zone model used in the cognitive schooling simulation. Variable fields associated with spatial memory (α_i, β_i, C_i, S_i, R_i and λ_i ) as implemented in this simulation are defined for two different neighbourhood sizes. The yellow circle indicates a ‘nearest neighbour’ response zone, in which a focal individual assesses local density within a radius r_NN. Having assessed whether the nearest neighbourhood density differs from the target density, the appropriate turning direction is determined with reference to a larger ‘detection distance’ neighbourhood of radius r_D, indicated jointly by the yellow circle and the red and blue semicircles. The geometrical parameters r_NN and r_D correspond, respectively, to the spatial scales of strong neighbour interactions, L_d, and maximum detection distance, L_D. For simulations in this study, r_NN = 2.1 and r_D = 6.1. For example, for the focal (red) fish in the schematic, the number of near neighbours is 3, the number of detectable neighbours in the left semicircle is 7 and the number of detectable neighbours in the right semicircle is 3. Hence, an individual with a target density less than three near neighbours would turn incrementally to the right, while an individual with a target density more than three near neighbours would turn incrementally to the left.

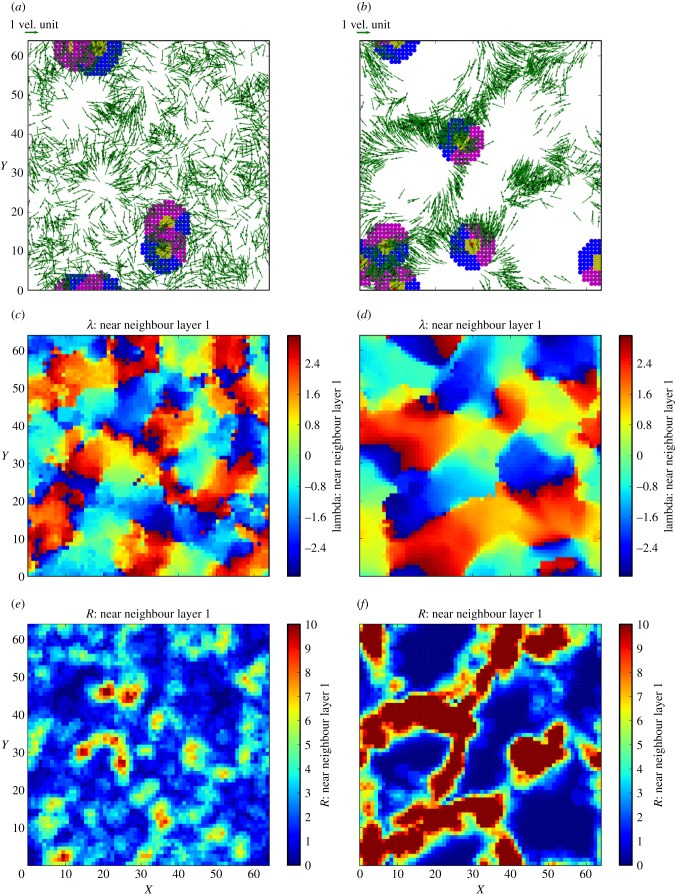
To illustrate large-scale effects of spatial memory, snapshots of individual positions and velocity vectors are presented in figure 2 for short memory (T = 0.25) and long memory (T = 8) simulations, in which parameters are otherwise the same. Comparison of the two snapshots, in which an increase in T mediates a transition from weak to strong schooling, clearly demonstrates that spatial memory potentially augments the ability to maintain size, polarity and density within groups of social animals. Spatial plots of estimated preferred direction (λ) and directional certainty (R) provide an insight into the mechanisms underlying this transition: estimated direction is coherent over much larger spatial scales, and directional certainty substantially elevated, in the long spatial memory case.

Figure 2.

Effects of increasing memory parameter, T, on spatial dynamics in the simulation of cognitive schooling. (a,c,e) reflect short memory (T = 0.25); (b,d,f) reflect long memory (T = 8). (a,b) Positions and velocity vectors of 2048 individuals at t = 256 in a periodic 64 × 64 domain. For five random individuals, neighbourhoods are shown with colours corresponding to figure 1. With other parameters held constant, increased memory timescale T strongly augments schooling characteristics such as group size and polarity. Spatial scales of estimated preferred direction (λ) show coherence over larger spatial scales for larger T (c,d). Increased memory also strongly increases both magnitude and spatial coherence of directional certainty, R (e,f).

Transitions in population-level grouping as a function of the memory parameter T are further illustrated by time-series plots of spatial means and coefficients of variation for estimated population density (ρ) and directional certainty, R (figure 3). Population density estimates converge from random uniform initial conditions over a timescale T (which they must, given the constant number of individuals in the simulation), but coefficients of variation of estimated populations increase gradually as spatial distributions develop towards statistical stationarity over timescales ≫T. Interestingly, while directional certainty (and its coefficient of variation) increase monotonically with T, the bottom panel in figure 3 shows that the coefficient of variation for population density has a maximum (parameters other than T held constant). This maximum may indicate a transition at which spatial memory becomes important (near T = 1), reflecting competing mechanisms: increases in T strengthen the overall school structure (as in figure 2) but also increase the temporal and spatial ‘spread’ of population estimates, moderating their variation.

Figure 3.

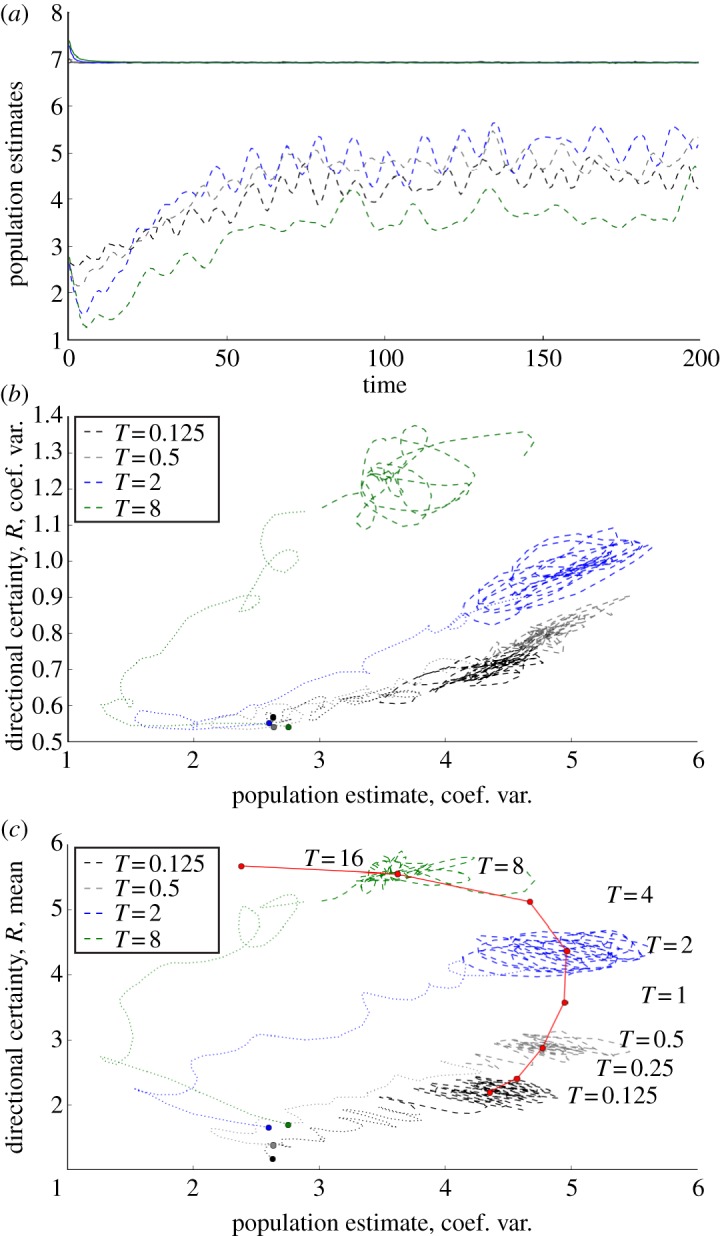
Variation in cognitive variable fields as functions of memory timescale parameter, T. In all plots, T = 0.125, 0.5, 2, 8 are represented by black, grey, blue and green lines, respectively. (a) Time series of spatially averaged estimated population density (ρ) within the ‘nearest neighbourhood’ (i.e. within r_NN = 2.1) of each position in the domain (solid lines). As expected, estimates of population average converge approximately on a timescale T. However, coefficients of variation (dashed lines) show long transients, reflecting extended approaches to statistical stationarity in group density and extent. (b) Spatially averaged ‘directional certainty’ R (solid lines) and its coefficient of variation (dashed lines) also show extended transients. The strong increases of directional certainty with T reflect the increased information available to animals with longer memories. (c) Plots of estimated population density (ρ) coefficient of variation against spatially averaged directional certainty (R). In this panel, initial transients (t ≤ 48) are shown as dotted lines and longer timescale dynamics (48 ≤ t ≤ 200) as dashed lines. Initial conditions are shown as filled circles. Trends in the ρ–R relationship are further illustrated by red circles, representing time averages of mean ρ and coefficient of variation of R over the interval 48 ≤ t ≤ 200. The curve connecting these circles suggests that a maximum variation of population density occurs at T ≈ 1, suggesting a possible transition between ‘short’ and ‘long’ memory timescale dynamics.

4. Discussion

The likely availability to many social animals of georeferenced historical information about neighbours’ positions and movements broadens the range of behaviour types potentially underlying important animal grouping phenomena in nature, and suggests novel algorithms for coordinated control of robotic platforms. Social behaviours that involve complex, coordinated decision-making based on memory and relatively sophisticated spatial processing can be reasonably thought of as ‘cognitive’ schooling, flocking, etc., to emphasize the centrality of cognitive processing rather than physical constraints on detection and movement in shaping animal groups. In foraging contexts, taxis-, kinesis and Lévy-type behaviours derived from biased random walks have long been used to model the roles of sophisticated movement strategies in circumventing constraints on locomotion and long-range detection of resources [16–18]. Many of these random walk foraging behaviours depend explicitly or implicitly on some form of memory- or time-integration of signals. The results of this study reinforce the expectation from empirical observations of social animals, that cognitive decision-making based on spatial memory substantially augments formation and regulation of coordinated groups. Implications include that social aggregations will form and persist in situations where zone models and other memory-less approaches suggest they can not occur, and that aggregation features strongly reflect historical grouping dynamics that often differ substantially from prevailing conditions.

The main contribution of this study is the scaling rationale and conceptual framework for spatially explicit modelling of social behaviours involving georeferenced spatial memory and cognition in their aggregation behaviour. Here, the focus was on schooling in fish, but models of other social groups would in many cases share the key characteristics on which the present modelling framework depends. Bayesian statistics have been previously used to model socially mediated decision-making relevant to spatial movement but not in a spatially explicit context [9]. This study extends these approaches by modelling spatial information as distributed Bayesian parameters that encode animals’ cognitive states in an efficient and tractable way. By treating spatial information explicitly, this modelling framework raises (but does not, in the short run, answer) questions about how to empirically quantify animals’ spatial memories and cognitive behavioural responses to those memories. Here, the focus has been on developing and demonstrating an abstract approach—methods to quantitatively estimate behavioural rules and parameters from microscopic and macroscopic data on animal groups are not considered in this study, but are a necessary next step if the framework is to be useful.

The assumptions underlying the model concern the functional definition of an individual's neighbourhood. As a concrete example, consider predation risk to an individual as a function of other individuals in its neighbourhood. If predators select and attack prey at a distance of approximately L_pred, predation risk to a focal individual likely depends most strongly on the presence of neighbours within a neighbourhood of approximately L_pred in extent. Hence, in this case, L_d ≈ L_pred is a reasonable functional definition of neighbourhood extent. With this as an explicit independent metric for L_d, the key assumption in the model development is that L_D≫L_d, where L_D is the maximum distance over which other individuals can be detected. If this assumption is met, the implication is that individuals with cognitive responses to spatial memory may be at a significant advantage in assessing the present and future state of local populations. Even for very simple grouping algorithms, such as that illustrated in figures 1–3, these cognitive responses can qualitatively and quantitatively augment schooling dynamics.

The proposed modelling framework, in which spatial memory is represented as continuous Bayesian parameter fields but cognitive responses are specified at the individual level, intrinsically has a dual Lagrangian–Eulerian character. While implementation of this approach involves some computational bookkeeping, the duality also opens possibilities that may be advantageous. In the context of coordination of large robotic teams, Eulerian scalar fields representing directionality, density and uncertainty offer both a human-accessible summary of system state and means to coherently manipulate large sets of Lagrangian agents. Required computations, though more involved than for many simple social aggregation models, intrinsically scale with the number of individuals rather than the square of that number, as in many everyone-sees-everyone social models. In the simulations presented here, Lagrangian and Eulerian models were advanced on the same timesteps, but that approach could be perhaps be made more efficient by emphasizing Eulerian timestepping using equation-free modelling methods [19], or by approximating the dual Lagrangian–Eulerian model with a stochastic partial differential equation analogue. For parameters applicable to some social animal groups, it is likely that the model equations presented in this study can be approximated with much simpler forms, and analytical solutions may be possible for these simpler but still memory-encoding models.