Collective navigation of cargo-carrying swarms

Abstract

Much effort has been devoted to the study of swarming and collective navigation of micro-organisms, insects, fish, birds and other organisms, as well as multi-agent simulations and to the study of real robots. It is well known that insect swarms can carry cargo. The studies here are motivated by a less well-known phenomenon: cargo transport by bacteria swarms. We begin with a concise review of how bacteria swarms carry natural, micrometre-scale objects larger than the bacteria (e.g. fungal spores) as well as man-made beads and capsules (for drug delivery). A comparison of the trajectories of virtual beads in simulations (using different putative coupling between the virtual beads and the bacteria) with the observed trajectories of transported fungal spores implies the existence of adaptable coupling. Motivated by these observations, we devised new, multi-agent-based studies of cargo transport by agent swarms. As a first step, we extended previous modelling of collective navigation of simple bacteria-inspired agents in complex terrain, using three putative models of agent–cargo coupling. We found that cargo-carrying swarms can navigate efficiently in a complex landscape. We further investigated how the stability, elasticity and other features of agent–cargo bonds influence the collective motion and the transport of the cargo, and found sharp phase shifts and dual successful strategies for cargo delivery. Further understanding of such mechanisms may provide valuable clues to understand cargo-transport by smart swarms of other organisms as well as by man-made swarming robots.

1. Introduction

Collective navigation (also referred to as swarming intelligence) has been observed in many organisms. Examples include swarming of locust [1], fish [2] and bacteria [3–5] as well as the collective flight of birds [6] and trail organization in ants [7]. Such collective behaviours, bringing new functionality and computational ability to the group, have been shown to result from simple interactions [8–20]. Models that reduce the complicated natural systems to sets of simple rules have been used to study the effect of different interactions and computations on the macroscopic group behaviour. The ‘self-propelling particles’ model [21], in which the motion of each individual is determined by the mean orientation of its local neighbourhood, shows phases of coherent motion and clustering, depending on the density of agents and the effect of noise. More interaction rules such as collision avoidance and attraction, preferential movement directions, and influences from the environment such as chemotaxis have also been investigated in [22–29].

A swarm of organisms moving collectively has the advantage of simultaneously sensing the environment at different locations and under different noise perturbations. Through interactions, organisms can transmit and receive information and, as a consequence, enhance each other's capabilities and those of the group as a whole. Micro-organisms are especially sensitive to noise due to stochastic variations in their internal mechanisms, sensory system and the external environment. Consensus decision-making can cause such statistical noise to be smoothed out and thus provide an advantage compared with the capabilities of an individual microbe [30–32].

The studies here are motivated by the realization that some bacteria can exhibit remarkable collective behaviours ranging from the formation of complex colonies to advanced collective navigation [33]. To do so, bacteria use a wealth of communication mechanisms, from physical interactions to the exchange of chemical messages and even to the exchange of genetic information. These modes of communication enable bacteria to regulate task distribution with cell differentiation (cells with diverse capabilities) for elevated adaptability [34,35]. Our studies are, in particular, motivated by the bacterial ability to transport natural cargo (e.g. the Paenibacillus vortex transport of fungal spores over very long distances—tens of centimetres [36]), as well as man-made beads of different sizes. This has been explored within artificial systems such as structured, micro-fabricated environments, where fixed arrays of flagellated bacteria have been shown to transport beads up to 5 µm in diameter. Gliding bacteria have been shown to move a micrometre-scale rotor [37,38]. In addition, it was previously shown that swimming bacteria can carry nanoparticles in a way that is relevant to drug delivery to mammalian cells [39]. Microbeads have also been covalently linked to motile algae, which can be used as light-directed, ‘microoxen’ to transport their cargo rapidly up to 20 cm within microfluidic channels [40]. These artificial cargo systems have uses within the micro-engineering world, where there is interest in using micro-organisms to fabricate, or be part of, miniaturized devices [41]. The discovery that cargo items can be other micro-organisms opens up questions of ecology relating to the dispersal of bacteria or fungi, and adds interest in that the cargo organism may play a proactive part in its own transport.

Motivated by the earlier-mentioned observations, as well as additional observations of micrometre-scale objects carried by bacteria (beads, nanoparticles or components of miniaturized devices), we build upon the previous modelling of collective navigation of bacteria-inspired agents in complex terrain to include collective cargo transport by agent swarms. We note that previous models of cargo-carrying swarms focused on stochastic modelling of chemotactic ensembles pushing a bead by propulsion [42]. Here, we use agent-based modelling and simulations to study the transport of cargo by bacteria-inspired agents. We inspected three models for collective cargo transport and investigated the effect of the characteristics of the agent–cargo connections on the collective motion of the swarm and the cargo, particularly on their navigation efficiency in a complex terrain. We expanded one of the investigated models to include large cargo-carrying swarms in a lubricating fluid. The model captured some of the biological observations such as the effect of lubrication on the navigation of larger swarms and parallel transport of multiple cargoes.

2. Collective transport of cargo by swarming bacteria

We use the collective swarming of the P. vortex social bacteria to introduce the phenomenon of cargo transport by bacteria swarms. For that purpose, we present a concise summary of our previous findings with some additional analysis of the microscopic dynamics of the swarming cells.

2.1. Swarming intelligence in Paenibacillus vortex bacteria

The P. vortex self-lubricating bacteria exhibit advanced motility used by flagella (swimming and swarming) and possibly also twitching by pili (based on genome sequencing [43]). In conjunction with cell–cell attractive and repulsive chemotactic signalling and physical links, P. vortex can move on versatile terrain [33,43]. When grown on hard surfaces, P. vortex bacteria generate specialized pioneering parties that are pushed forward by repulsive chemotactic signals sent from the cells at the back. These parties of dense bacteria vortices pave the way for the colony to expand. Vortex formation is social behaviour that requires multiple cell organization. Swarming cells are coupled by rapidly forming, reversible and non-rigid connections to form a loose raft, connected via flagella [33,36]. The vortices then serve as building blocks for new colonies with flexible modular organization (figure 1).

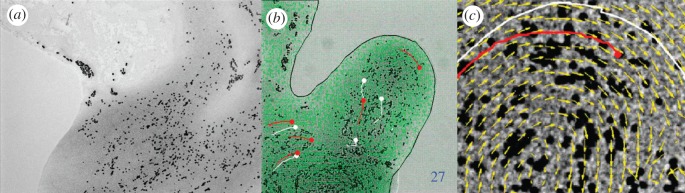
Figure 1.

Bacterial colony as a community of cooperating swarming cells. The pictures show a swarm generated during growth on plates. (a) An example of a complex colony developed by the social Paenibacillus vortex bacteria strain when grown (from point inoculation at the centre) on 7.5 g l^–1 peptone and 2.25% (w/v) agar for 6 days. The grey shades indicate the cell density—darker for higher density. The vortices—the dark dots in (a)—contain thousands of bacteria that rotate around a common centre while they move forward as a foraging unit. Vortices are pushed forward by repulsive signals sent from the mother colony. (b) A closer look at the vortices at magnification 500×. (c) magnification 1200×. (d) Scanning electron microscopy (SEM) image of vortex. Scale bars: (a) 10 mm, (b) 3 mm, (c) 15 µm, (d) 5 µm.

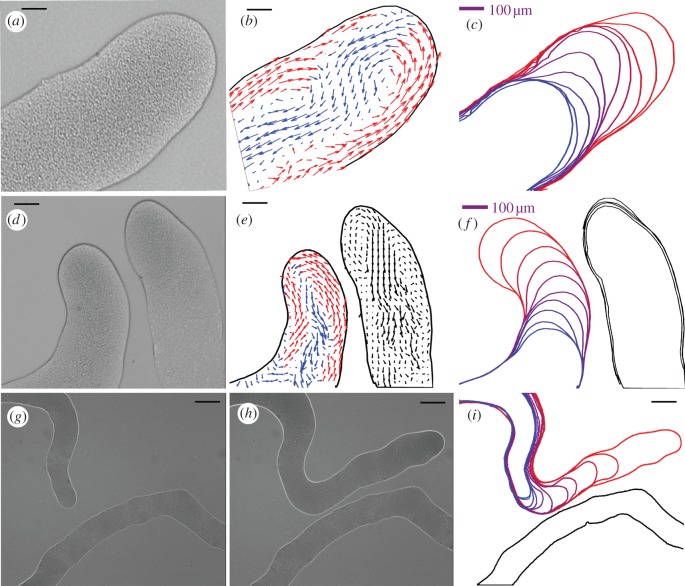
When grown on soft surfaces, these bacteria can form foraging, snake-like swarms that act as arms sent out in search for food, hundreds of bacteria wide [33]. The swarms can expand very efficiently by making use of self-regulated complex internal movements of the individual bacteria (figure 2a). These swarms exhibit advanced collective navigation—they can collectively change direction when food is sensed or another nearby swarm is detected; the swarms avoid crossing each other's trail (figure 2d,g,h), presumably as a result of chemorepellent signals used during colony formation [44–48].

Figure 2.

Interactions between swarms. (a) An example of snake-like swarm of P. vortex. The figure shows a swarm generated during growth on reduced strength Mueller Hinton medium gelled with 1.5% w/v Eiken agar (RMHA). An optical microscopic picture of the swarm. The small dots are the individual cells. (b) Velocity field of the bacteria swarming calculated as explained in the text. At each point, the average velocity of several neighbouring cells is calculated. The red arrows indicate a flow towards the tip of the swarm, and the blue arrows indicate a backward flow. The size of the arrows corresponds to the magnitude of the computed flow. (c) The envelope of the swarm at successive times illustrating the vortex movement. (d) Close view of repulsion between two swarms. Parts (e,f) are similar to (b,c). (g) A global view of repulsion between two swarms. Parts (h,i) are similar to (b,c). Note the slow down in the swarm movement when another swarm is detected and the increase in speed after the change in the swarm direction. Scale bars, (g,h,i) 140 µm.

The mutual swarm–swarm repellent is likely to have an important colony-level function, as it ensures that the individual swarms will spread over the terrain, leading to a more efficient coverage and therefore a higher chance to find food sources. Upon detection of food sources at a distance, the bacteria use collective navigation (chemotaxis), and the swarm turns towards the source. In figure 3a–c, we show an example of a change in direction of a moving swarm upon detection of signals from sources added at a distance. The swarms can even split and reunite when scattered patches of nutrients are detected (figure 3d–f). The results suggest not only the collective change in propagation of the swarm, but also a very sophisticated optimization strategy that the bacteria have developed to ensure their survival [33].

Figure 3.

An Illustration of the ‘swarming intelligence’ of the P. vortex bacteria when searching for food. The pictures (in negative shades—bright areas correspond to high bacterial density) are snapshots from video clips at 50× magnification. Growth on 0.3% w/v Muller–Hinton agar. (a–c) Navigation towards a single source as is explained in the text. Time lapse between the first and third picture is 50 s. (d–f) Navigation in the presence of several signals. Time lapse between first and third picture is 44 s. For more details, see Ingham & Ben-Jacob [33]. Scale bars, (a–f) 200 µm.

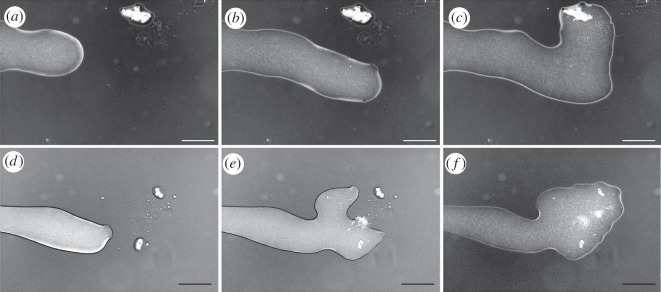
2.2. Transport of man-made beads

It was shown that swarming P. vortex bacteria can efficiently transport microbeads of different sizes (1–20 µm diameter) both by the snake-like swarms and by rotating vortices (figure 4). Microbeads were not transported by monolayers of P. vortex; transport required multi-layered masses of thousands of cells. Even when beads were transported over several centimetres, the pattern of beads was often conserved. This suggests that the architecture of the swarm is relatively stable; the beads are not moving, to a great extent, relative to each other. Therefore, P. vortex has a notable ability to transport objects larger than its size. Previous studies on microbial transport have either covalently attached non-living cargo objects to individual motile cells or used layers of bacteria confined in micro-fabricated chambers or other arrays of immobile organisms with active flagella to move beads [38,39,49]. However, it was shown that none of these methods are necessary for cargo transport by P. vortex. Unmodified, swarming bacteria can pick up and retain cargo objects without covalent attachment and move them over tens of centimetres.

Figure 4.

Transport of micrometre-scale polystyrene beads by P. vortex. (a) Moving, rotating P. vortex colony cultured on RMHA (1.5% w/v) carrying a cargo of 1 µm diameter fluorescent microspheres. View by digital interference contrast microscopy. Arrows show the direction of the rotation of the colony. T indicates a trail of bacteria and lubricant. Moving microspheres are primarily located in the cell masses while those at the periphery of the trail are no longer in motion. (b) Same as (a), with microspheres visualized by fluorescence microscopy. (c) Vortex of P. vortex carrying 3 µm diameter beads. The arrow is pointing at the bead. (d) A swarm of P. vortex carrying 20 µm diameter beads.

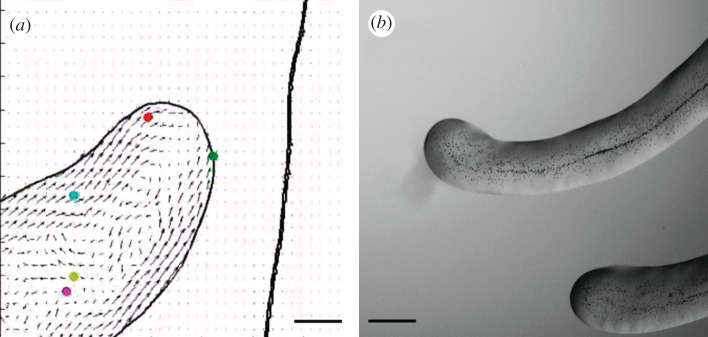
2.3. Tracking and modelling of virtual cargo

We performed video tracking and image analysis of cargo-carrying swarms to extract time-developing velocity maps (figure 5, see electronic supplementary material). By using virtual beads, which follow the direction and speed of the bacterial mass, we analysed the effect of different coupling parameters between the bacteria and the virtual cargo. As we show in the next section in more detail, virtual beads (virtual cargo) were placed within the velocity map near real cargo to check the similarity between the trajectories. From the initial position, virtual beads followed the local direction of the velocity field at each frame. The trajectory and velocity of each virtual bead was compared with that of the nearest cargo.

Figure 5.

Transport of man-made beads and virtual beads. (a) A snapshot from video tracking of P. vortex with simulated virtual beads as explained in the text (colourful dots). (b) Two swarms carrying man-made beads (black spots). Scale bars: (a) 200 µm, (b) 150 µm.

2.4. Transport of biological cargo

In transport of man-made (artificial) objects, P. vortex bacteria probably use mechanisms developed for transport of biological cargo. Recently, it was shown that swarming P. vortex is able to transport its own spores (of about 0.5 µm in diameter) when added to swarming bacteria. Given that sporulation takes time and resources, and the rapidity by which P. vortex can swarm into unfavourable environments, it may be a survival advantage to carry preformed spores rather than to generate new ones in a crisis. Spore transport may act as a ‘bet hedging’ strategy against the failure of adventurous swarms to find a favourable niche.

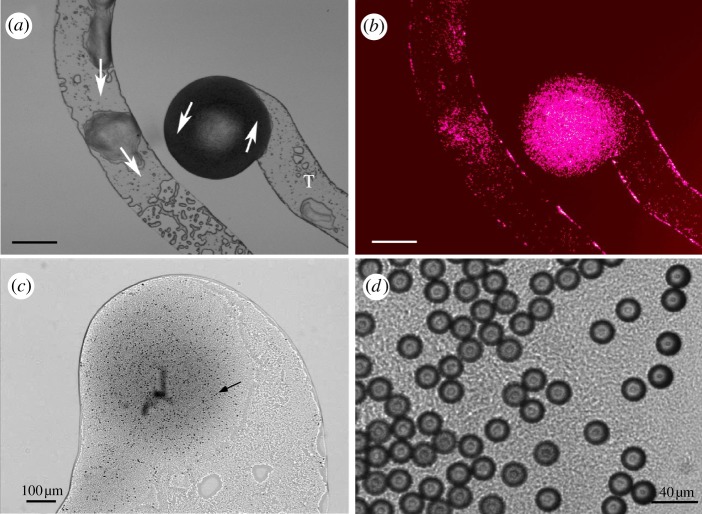
More surprising are the recent observations showing that P. vortex swarms can transport the non-motile fungus Aspergillus fumigatus conidia (non-motile asexual fungal spores), and even clusters of conidia (of about 25 µm diameter), over very long distances of at least 30 cm and at rates of up to 10.8 mm h⁻¹ (figure 6) [36]. This notable ability of P. vortex to transport biological objects larger than itself might explain the organism's limited ability to transport 20 µm diameter beads.

Figure 6.

Conidia transport by P. vortex. (a) Conidia of Aspergillus fumigates are moved on a large surface of P. vortex cells. (b) Paenibacillus vortex swarm transporting conidia (red) with virtual beads (white). The continuous black line indicates the edge of the swarm. (c) A close-up view of conidia transport in a swarm with the velocity map and trajectory of conidia (red) and trajectory of simulated virtual beads (white). Black dots are the conidia. Arrows indicate the motion direction. For details, see Ingham et al. [36]. Scale bars: (a,b) 200 µm, (c) 10 µm.

Conidia transport is beneficial for both participants; while fungi enjoys rapid local dispersal and translocation from environments where they cannot germinate to regions where germination and outgrowth are possible, bacteria use the germinated mycelia of fungi to cross bridge air gaps that it cannot cross unaided.

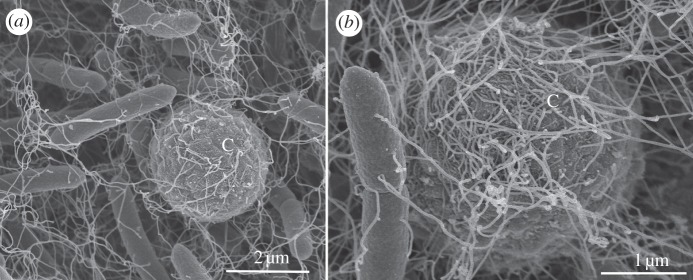
In agreement with previous observations of bead movement, SEM imaging of the transferred conidia showed that the conidia were incorporated within the rafting mass of moving and interconnected bacteria, with the flagella of P. vortex both linking adjacent bacteria and entrapping the conidia (figure 7). This sample was prepared using a liquid glutaraldehyde-based fixation using osmium trioxide treatment to preserve the structure of the flagella. An alternative procedure involving a non-intrusive, vapour-based fixation [50] gave a similar view of the bacterial–conidial interaction, suggesting that the result was not substantially distorted by sample preparation artefacts. Each conidium was captured by 6–30 flagella, typically derived from two to nine bacteria. In the bacteria–conidia interactions, flagella are making contacts with the surface of the A. fumigatus conidia. Another interesting phenomenon is the decrease in transport efficiency of germinated conidia, which might be explained either by signal transduction between dragging bacteria and pulled conidia, or by size limitation of the cargo or by changes in the surface properties (e.g. hydrophobicity) of the conidia.

Figure 7.

Imaging of transport by SEM. (a) Conidium of A. fumigates during transport by a P. vortex swarm imaged 3 h after inoculation. C indicates the conidium. (b) A close-up view of a second conidium—round structure in the middle, wrapped with multiple flagella. Conidia (a,b) were imaged at locations 2–4 cm from the inoculation point.

3. Collective transport of cargo by bacteria-inspired agents

In this section, we investigate the collective navigation of bacteria-inspired chemotactic agents with orientation interactions. More specifically, each agent measures the local gradient direction and biases its motion according to the sensed direction and the interactions with the other agents.

3.1. Collective navigation of bacteria-inspired agents in complex terrains

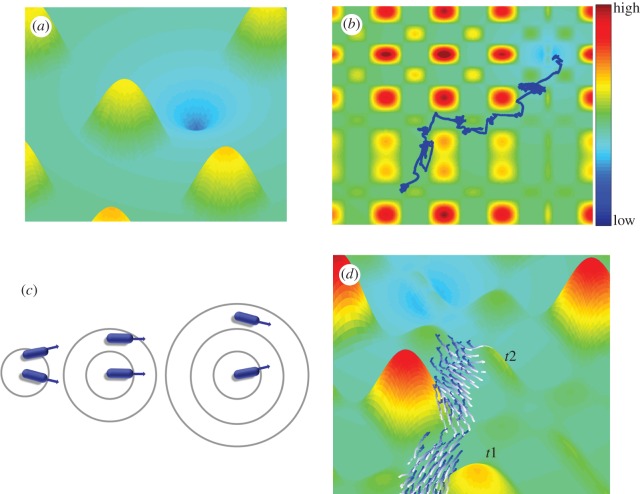
We study the navigation efficiency (the time it takes the swarm to reach the target) of swarms carrying cargo in a complex terrain. The navigation efficiency in our model is proportional to the distance travelled between the source and the target because the agents' velocity is kept constant. The agents are moving in a two-dimensional terrain (the height on the z-axis represents the food concentration; low height corresponds to a high food level) of a locally changing map on top of a global valley containing local minima, maxima and saddle points (figure 8a, see electronic supplementary material). The resulting navigation problem is challenging for swarms with short memory and limited computational abilities.

Figure 8.

Model of interacting bacteria-inspired agents. (a) An overview of the terrain. (b) An individual agent moves towards the target in a biased random walk composed of a string of forward excursions and tumbles. The tumble is a change in direction taken from a Gaussian distribution whose variance is a function of the chemical concentration. When the chemical gradient is small, the variance is large, and vice versa. (c) Agents repel from close agents, align with intermediate agents and attract to further agents. (d) A frame from a simulation of bacteria-inspired interacting agents moving collectively towards the target in a complex terrain. The figure shows snapshots from two different time steps (t1 and t2) illustrating the motion of the group towards the target. High/low indicate the terrain height, corresponding to opposite low/high levels of food concentration. Simulation parameters are N = 50, (RR,RO,RA) = (1,3,0.3), σ = 0, τ = 0.5, w = 0.5.

The movement of an individual agent is inspired by (but different than) chemotaxis [51–55] in swarming bacteria [56,57]; an agent moves forward in equal-sized excursions followed by a tumble, a change in direction taken from a Gaussian distribution whose variance is large when the change in height is small and vice versa (figure 8b). This means that an agent will change its direction by a smaller angle (probabilistically) when the height decreases, causing a bias of its motion towards lower terrains. To avoid confusion, we note that in comparing the agent navigation towards low terrain with bacteria navigation towards food sources, low height corresponds to higher food concentration and vice versa. During a forward excursion, an agent will avoid collisions with nearby agents by repulsion, orient its movement direction with intermediate agents and attract to further agents (figure 8c). During a reorientation, it will select a new direction according to the chemical gradient (height). For more details, see electronic supplementary material.

In a previous model [58], the effects of performance-adaptable interactions were studied. Here, we model bacteria-inspired interacting agents with static interactions, in order to simplify and separate the effect of the cargo on the collective navigation from the cargo effect on the adaptable interactions.

3.2. Collective cargo transport by smart agents

We inspected the effect of three features of the agent–cargo bonds: stability, elasticity and drag. The stability of the bonds determines their formation and breakage. The elasticity of the bonds determines how they are affected by the agents and the cargo. The drag of the bonds is determined according to the dependence of the force applied by the bond on the bond's end points. The different bond characteristics suggest different mechanisms of cargo transport—for example, mutual attraction with constant force, mutual attraction with a force that depends on the distance between the end points, like a spring, and a force that depends on the propulsion of the agents.

We inspected three putative mechanisms of the interactions between a swarm and its cargo: rope-like, coil-like and elastic stick. In all three cases, the cargo–agent connections are dynamic; they are formed instantly inside the radius of connection, R_c, and break outside of that radius, giving the set of agents that are connected to the cargo, 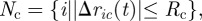where Δr_ic(t) = r_i(t) − r_c(t), and r_c(t) is the location of the cargo. Bonds can be elastic or rigid. Bonds, in one extreme, extend, contract and change their orientation freely. In another extreme, once a bond is formed, the bond's length and orientation throughout the motion are maintained. In nature, the elasticity of the cargo-cell connections is determined by the materials from which they are made and by the environment. The elasticity of bonds in the presented models is intermediate between these two extremes. The force applied by the bonds can depend on the distance between the end points, the bond's length or on the propulsion of one end point, the agent. We investigated how the characteristics of the bonds affect the swarm motion by studying three different models of agent–cargo bonds.

3.2.1. Rope model

Agent–cargo bonds were modelled as free ropes (figure 9). Free ropes elongate and shorten instantly, and the force that they apply on the end points is constant, independent of their length and of the end point propulsion. The direction of motion of the cargo changes according to the sum of the forces applied on it by the pulling agents. The magnitude of the force applied on the cargo by agent i is denoted by F_ic(t) = k, where k is the pulling constant. Note that all the agents apply the same force on the cargo and that there is a drag, the force an agent applies on the cargo equals the force the cargo applies on the agent.

Figure 9.

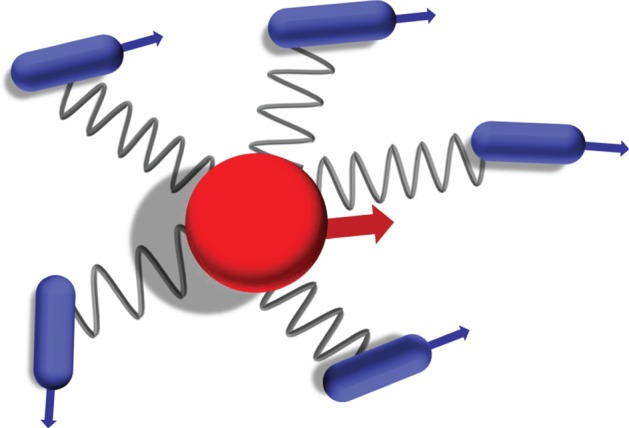
An illustration of cargo–cell bonds. The connections between the cargo and the agents are modelled as coils, with mutual attraction. Cargo is marked in red and agents in blue. The arrows represent the velocity directions of the cells and cargo, respectively.

The velocity of the cargo, v _c(t + Δt), is given by

3.1

where 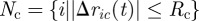is a set of all the agents connected to the cargo at time t, b_ic(t) = Δr_ic(t)/|Δr_ic(t)| is the direction of the pulling bond from agent i to the cargo (pointing at the agent), and w = 0.5 accounts for persistence (1 − w accounts for friction). Notice that w, as well as the force, depends on Δt. See the electronic supplementary material for analysis of the discretization process of the equations.

The force is mutual; so, in a similar manner, the cargo pulls on the agents towards its current location. During a forward excursion, the final direction of an agent equals a linear combination of the direction resulting from the group interactions and the agent's previous direction with the force applied by the cargo:

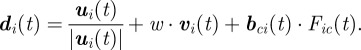3.2

We note that u_i(t) is the direction resulting from the group interactions of agent i (see the electronic supplementary material). During a tumble, a new angle is selected and then the force is applied in a similar manner. The magnitude of the velocity of an agent is constant.

3.2.2. Coil model

Agent–cargo bonds were modelled as coils that apply a force that is proportional to the displacement of the coil. The magnitude of the force applied on the cargo by agent i is given by

3.3

where k and c_eq are the force constant of the spring and its equilibrium length accordingly. The velocity of the cargo is given in (3.1), and the direction of an agent is given in (3.2).

3.2.3. Elastic stick model

Agent–cargo bonds were modelled as elastic sticks that apply a force inversely proportional to the length of the bonds and to the angle between the agent's velocity direction and the bond's direction. Notice that the elastic stick can either push or pull the cargo, depending on the agent's velocity direction. The cargo's velocity equals the sum of the forces applied on it by its neighbouring agents.

The magnitude of the force applied on the cargo by agent i, F_ic(t), is given by

3.4

where k is the force constant of the elastic stick. Note that the force is inversely proportional to the distance with a cutoff at 1 and that it is proportional to the matrix multiplication of b_ic(t) and v_i(t). The velocity of the cargo is thus given by

3.5

The cargo applies an opposite force to the agents, thus, the final direction of the agent during a forward excursion is a linear combination of all the directions: group interactions, previous direction and the opposite force,

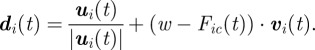3.6

During a tumble, the force is added to the new direction.

3.3. The cargo effect on the collective navigation

To study the effect of the interactions between the agents and the cargo on their collective navigation, we simulated the navigation of swarms composed of N = 50 on a complex terrain. The simulation started with the agents' locations, 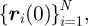uniformly distributed around the starting position within a sufficiently small circle such that the group was cohesive. The cargo was located in the middle of the circle. The agents' velocities were uniformly distributed over all directions. The velocity of the cargo was zero. We defined the path length to reach the target to be the time it took half of the agents in the group to reach the target (the median path length); this corresponds to the navigation time multiplied by |v| = 1. The group alignment was given by

3.7

The group alignment is the average alignment between individual agents over the trajectory. Notice that the group alignment is in the range [0,1].

We found complex collective behaviours that were generated owing to the agent interactions with the collectively transported cargo. Note that because many agents interact with the cargo, the inclusion of the cargo introduces additional nonlinear and non-trivial effective agent–agent interactions. Groups may fracture, split into subgroups with one delivering the cargo, become more cohesive and aligned or become more cohesive but less aligned. All these different delivering methods were created in the three simple models of cargo-carrying swarms (see figure 10, electronic supplementary material, for examples).

Figure 10.

Simulation snapshots. Frames from simulations of the rope: (a) step 380; (b) step 500, coil; (c) step 1000; (d) step 1260, and elastic stick; (e) step 520; (f) step 800. Frames show groups transporting cargo towards the target or splitting into two subgroups with one transporting the cargo. Simulation parameters are as in figure 8, R_c = 4,c_eq = 1 and k = 0.1, k = 0.05, k = 0.1 for the rope, coil and elastic stick model, respectively. The cargo is marked by the red circle. The agent–cargo bonds are marked by red lines. The agents are marked by the blue to white worms indicating their current (blue) to past (white) locations.

Successful delivery of cargo by the swarms was achieved in the rope and coil models. By successful delivery of the cargo, we mean a case where at some point in time, both the cargo and the swarm are located very close to the target, and this point in time is lower than the simulation length (10 000 time steps).

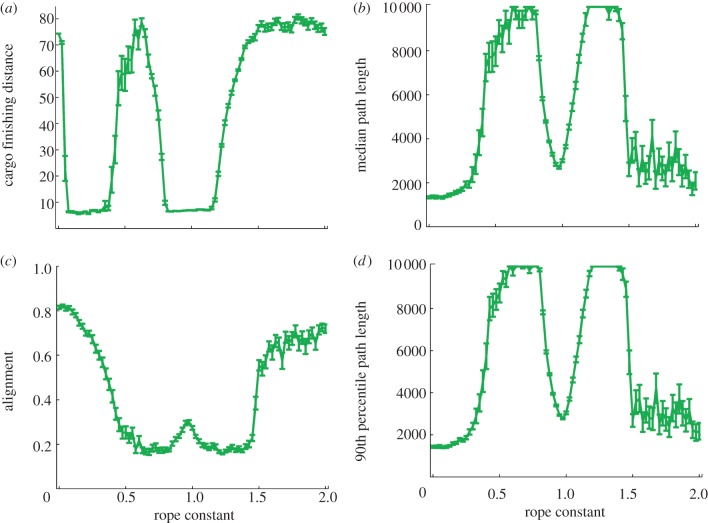
Swarms with rope-like agent–cargo bonds had two distinct successful phases (figure 11) where the switch into these phases was sharp. In the first, for 0.1 ≤ k ≤ 0.3 and intermediate R_c (figure 11a), swarms transported the cargo to the target with almost no effect on the navigation efficiency (figure 11b,d), compared with the behaviour of interacting swarms in the absence of cargo given by k = 0. Cargo-carrying groups were much less aligned, owing to fracture (figure 11c). Notice that decreasing R_c moves the behaviour out of the successful phase (see electronic supplementary material). In the second successful phase, swarms transported the cargo to the target, but it took almost twice the time (figure 11b,d). This phase corresponded with slow-moving cohesive unaligned groups. For high k values, groups dropped the cargo owing to irregularities and noise that arise from an increasing velocity of the cargo while the agents' velocities remain constant. The sharp transitions between collective behaviour states due to changes in the characteristics of the agent–cargo bonds arise from the nonlinearity of the interactions, because the cargo mediates another form of effective interactions between the agents.

Figure 11.

Rope-like agent–cargo bonds can create cohesive groups that deliver the cargo. (a) The distance of the cargo from the target at the end of the simulation as a function of the rope constant, k, is shaped like two wells. The first well corresponds with splitting groups where a subgroup delivers the cargo. The second well corresponds with slow collective motion of the group transporting the cargo. (b) The path length increases with k for small values due to the effect of the cargo and decreases for high values since the cargo is dropped due to irregularities in the magnitude of its velocity. The well corresponds with slow cohesive non-aligned motion. Comparison to a model of interacting swarms in the absence of cargo is given by k = 0. (c) Group alignment decreases quickly with k for small values due to the effect of the cargo and increases quickly for higher values since the cargo is dropped. The small hill is due to the collective motion of non-aligned groups. (d) The 90th percentile path length is similar to the median path length. Simulation parameters are as in figure 8, R_c = 4, statistics collected over 50 runs of the simulation.

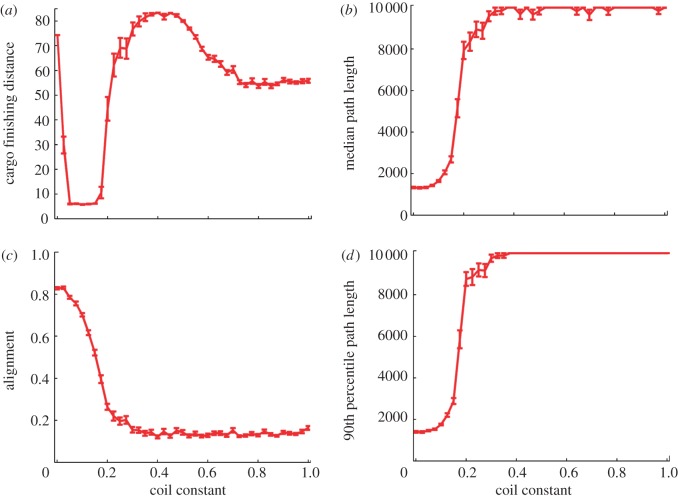
Groups with coil-like agent–cargo bonds had one successful phase where groups collectively transported the cargo to the target (figure 12a). For high values of k, cohesive unaligned (figure 12c) groups (as in the rope model) carried the cargo closer to the target (figure 12a) but took a longer time (figure 12b,d). A sharp switch out of the successful phase occurred for an increase in k (figure 12) and for a decrease or increase in R_c (see the electronic supplementary material).

Figure 12.

Coil-like agent–cargo bonds can create cohesive groups that deliver the cargo. (a) The distance of the cargo from the target at the end of the simulation as a function of the coil constant, k. For higher values, the decrease is due to slow non-aligned cohesive motion centred around the cargo. (b) The path length increases with k. (c) Group alignment decreases quickly with k. (d) The 90th percentile path length is similar to the median path length. Simulation parameters are as in figure 8, R_c = 4, c_eq = 1, statistics collected over 50 runs of the simulation.

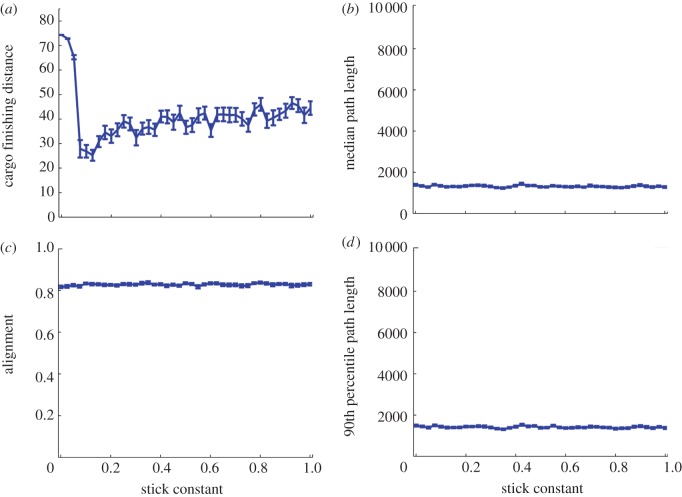
The elastic stick model showed the minimal effect of the cargo on the navigation effectiveness and on the group behaviour, but the ‘payoff’ was a high probability of failure by dropping the cargo before reaching the target (figure 13). We would like to note that from a biological (‘bacteria’) perspective, it might be more beneficial to transport the cargo with adaptable attachment: the idea is that the bacteria retain the ‘option’ to drop the cargo in the case it generates too much stress (e.g. limits the navigation efficiency or the cargo is parasitic organisms). For example, in the case of conidia transport, it was shown that when the transported conidia reach favourable environments, they slow down the swarming bacteria, which in turn drop the conidia [36].

Figure 13.

Stick-like agent–cargo bonds create cohesive and aligned groups that fail to deliver the cargo to the target. (a) The distance of the cargo from the target at the end of the simulation as a function of the stick constant. (b) The path length is independent of k. (c) Group alignment is independent of k. (d) The 90th percentile path length is the same as the median path length. Simulation parameters are as in figure 8, R_c = 4, statistics collected over 50 runs of the simulation.

3.4. Large cargo-carrying swarms in a lubricating fluid

We expanded the above coil model to include the effect of a lubricating fluid (known to be secreted by many swarming bacteria to facilitate their motility) as well as the transport of multiple cargo. The lubricating fluid is modelled by a discrete dual phase field, resulting in an expanding edge. The edge blocks the motion of approaching agents, and their velocity direction is then chosen randomly. The edge expands according to the locations of the agents. At each time step, the set of points that transform their phase is given by 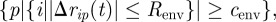where Δr_ip(t) = r_i(t) − p. In other words, this is the set of points that are close enough to a sufficintly large number of agents. Notice that the edge expands; thus the points cannot transform their phase back. We simulated the navigation of cargo-carrying swarms within the lubricant representing envelop. The swarms were composed of N = 150 agents and transported three objects. Initially, the cargo objects were placed randomly in a circle around the starting position, among the agents. The cargo objects repel from each other, modelling hard core repulsion; so the velocity of cargo object c is given by

3.8

where b_cd(t) = Δr_cd(t)/|Δr_cd(t)|.

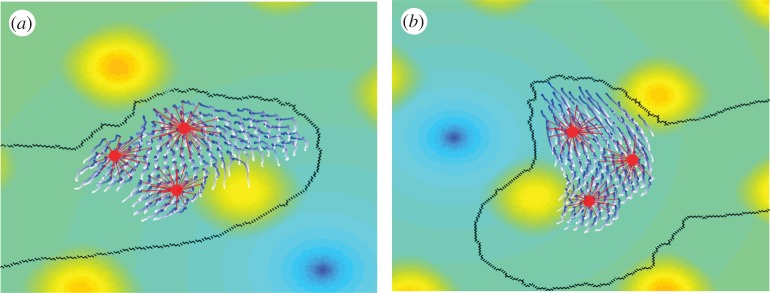
The results show that the agents constrained in an expanding edge with elastic stick agent–cargo bonds can transport multi-piece cargo to the target (figure 14).

Figure 14.

Simulation snapshots from the extended model. Frames from a simulation of the extended model: (a) step 380, (b) step 500. Frames show agents in an expanding edge delivering three cargo pieces to the target. Simulation parameters are as in figure 8, R_c = 4, k = 0.1, R_env = 2, c_env = 2.

4. Looking ahead

This work has been motivated by the recently discovered phenomenon in which biological cargo can be collectively transported over long distances by swarms of social bacteria. We were specifically guided by the example of mutually facilitated dispersal between the non-motile fungus Aspergillus fumigatus and the swarming soil bacterium P. vortex: The bacteria can rescue the fungi from hostile locations, and be benefited by using the fungal mycelia as natural bridges to cross air gaps. These observations led us to the development of a new class of computer models to study cargo-carrying, bacteria-inspired agents.

We expanded a previous model of bacteria-inspired agents to include the transport of cargo. We found that cargo-carrying swarms can navigate efficiently according to a global gradient in a complex terrain. We further investigated how the stability, elasticity and other features of agent–cargo bonds influence the collective motion and the transport of the cargo and found sharp phase shifts and dual successful strategies for cargo delivery. We presented three models for the agent–cargo bonds and investigated the collective navigation and cargo delivery of swarms in a complex terrain. We found that chemotactic swarms can deliver cargo using simple rules of interaction and simple computations. In one model (rope model), we found two distinct parameter regimes that result in successful transport, one where groups split and one subgroup delivers the cargo, and the second where the group remains cohesive and progresses slowly with the cargo towards the target. Succesful transport was also achieved in the coil model under a small parameter regime. In the elastic stick model, groups navigated efficiently, but had a large probability of dropping the cargo. As a step towards modelling the experimental system, we presented an extended model to capture the effect of the lubricating fluid (modelled by inclusion of an engulfing envelop) and the ability to transport several objects.

In the multi-agent simulations study, we focused on a small group of bacteria-inspired agents carrying one cargo object and moving in a complex terrain (representing a complex concentration field that bacteria are likely to encounter in natural environments). In this first modelling approach, we did not include the dynamics of bond formation and breakage [59]. In addition, the models did not include variability between the agents. Variability is a frequent feature in biological systems (e.g. genetically identical bacteria can still vary in their phenotypic properties) and may have a strong effect on the collective behaviour of groups.

We investigated the resulting collective behaviour from different agent–cargo bonds and compared with the experimental system in order to gain an understanding of the characteristics of these structures. A minimal disruption mechanism, as given by the elastic stick model, may be a survival advantage in times of depletion. On the other hand, mechanisms such as the rope and coil models are advantageous because they guarantee that the cargo will be delivered. As we mentioned earlier, in many circumstances, it might be more beneficial to transport the cargo with regulated attachment efficacy so that the cargo will be dropped in case of too much stress or if the cargo is of parasitic organisms. In the case of conidia transport by P. vortex, previous findings [36] show that the cargo does get dropped and that moderate cargo loads do not affect the swarming speed of groups, suggesting a model similar to the elastic stick.

Back to the cargo transport by bacteria, the cargo, either beads or fungal spores, was carried by multiple coordinated and well-organized rafts of structured microbes. Flagella and pili from several cells are used to wrap the cargo that was dragged, powered by the cell movement. Because the flagella attachment is reversible and possibly coordinated by signalling, it is reasonable to assume that the connections can elongate and shorten quickly as well as disconnect and recreated upon the movement and distancing of the microbes. Assessment of the experimental observations of the conidia transport in light of the results of the simple multi-agent models imply the existence of some signal transduction between the swarming bacteria and their biological cargo enabling the observed adaptable transport. Studying cargo transport in bacteria may lead to greater understanding of cargo transport in other organisms or to the discovery of mechanisms for robotic transport. To do so will require extension of the models presented here to include additional biological features and, in particular, cargo–agent co-regulation of the bond dynamics.