Abstract
Fish schooling is a phenomenon of long-lasting interest in ethology and ecology, widely spread across taxa and ecological contexts, and has attracted much interest from statistical physics and theoretical biology as a case of self-organized behaviour. One topic of intense interest is the search of specific behavioural mechanisms at stake at the individual level and from which the school properties emerges. This is fundamental for understanding how selective pressure acting at the individual level promotes adaptive properties of schools and in trying to disambiguate functional properties from non-adaptive epiphenomena. Decades of studies on collective motion by means of individual-based modelling have allowed a qualitative understanding of the self-organization processes leading to collective properties at school level, and provided an insight into the behavioural mechanisms that result in coordinated motion. Here, we emphasize a set of paradigmatic modelling assumptions whose validity remains unclear, both from a behavioural point of view and in terms of quantitative agreement between model outcome and empirical data. We advocate for a specific and biologically oriented re-examination of these assumptions through experimental-based behavioural analysis and modelling.
Keywords: fish schools, self-organization, collective behaviour, animal groups, coordination, individual-based model
1. Introduction
Collective motion is a widespread phenomenon in biological systems, from the captivating beauty of starlings performing aerial displays over their roost at dusk, to the march of cells during wound healing. Such phenomena span all ranges of size, scale and number of constituent group members, spread among almost all environments. The striking similarities in observed patterns, and the finding that under certain conditions very different microscopic mechanisms can lead to the same behaviour at the collective level, have paved the way for the theoretical modelling of collective motion and its high-level properties [1,2]. These studies have revealed the power of self-organization in creating new forms and facilitating functions as a result of individual interactions. Yet, despite this endeavour and a growing interest in collective behaviour, very little is known about the actual mechanisms at work in many biological systems, making previous research, which has largely been based on general a priori modelling hypotheses, often inconclusive regarding the mechanisms and the nature (epiphenomenal [3] or functional) of natural collective processes. Advocating for an experiment-based modelling of individual behaviour leading to collective motion, we will focus here on fish schooling. After reviewing the extensive literature addressing the question of the functions and behavioural mechanisms involved in the formation and maintenance of fish schools, we examine the different types of fish school models that have been introduced, and we discuss aspects of these works that give rise to their experimental flaws and success. We then discuss some key behavioural unknowns that one is facing when trying to construct realistic models, advocating for specific data collection and experimental analysis aimed at their resolution.
2. Multi-scale approaches of schooling behaviour
We must first make clear what the term ‘schooling’ refers to. Following Radakov [4], we consider that social aggregations of fish are fundamentally polyfunctional and adaptive, highly integrated and conditioned by an ecological context and its necessities [5]. It follows that the repertoire of collective behaviours exhibited in vitro may not fully reflect the complexity and diversity of this dynamical behaviour in the full context of environmental contingencies. Owing to the constant transitions of global behaviour occurring in nature for a given population [5], we must clearly separate the broad social phenomenon from its most obvious manifestations (figure 1). In a modelling and/or experimental context, schooling typically refers to the coordinated swimming of fish, independently of the factors that trigger the synchronicity. This phenomenological definition is oriented by our aim of an accurate and experiment-based understanding of individual behavioural mechanisms involved in synchronized swimming.
Figure 1.
Collective motion patterns in fish schools. Individuals’ interactions give rise to a variety of dynamical structures that can be (a) poorly or (b) highly (Copyright © agasfer, www.flickr.com, with permission) polarized (Copyright © breic, www.flickr.com, with permission). Other configurations of fish schooling include milling (c) (Copyright © Tammy Peluso) and bait ball (d) structures (Copyright © Barry Fackler with permission).
Schooling is widely spread among fish living in oceans and freshwaters. It has been estimated that 50 per cent of fish species school as juveniles, and that approximately 25 per cent of species school throughout their life [6]. Understanding schooling also has important practical implications; a large component of commercially exploited species school, and improvements of fisheries stock assessment accuracy and fishing techniques rely on understanding schooling behaviour. As a matter of fact schooling is relevant to many research fields in biology, including ecology, ethology, ichthyology, evolutionary biology and neurosciences, but also in statistical physics and computational sciences.
Since the observations of Parr [7], a large number of studies have been carried out to characterize schooling phenomena, addressing the question of which schooling patterns are exhibited in natural or experimental conditions, and why. Species that exhibit schooling tendencies are found and studied over a wide range of natural environments, for example pelagic fish of the Baltic Sea and Atlantic Ocean [4], coral-reef fish in the Californian Gulf [5] and many freshwater fish. Field observations have primarily been conducted by means of aerial observations [4, ch. 2]. These have been supplemented by increasingly accurate sonar techniques allowing to access the size, form and density of actual schools: for instance, the multi-beam sonar of Fréon et al. [8] and the emergent ocean acoustic waveguide remote-sensing technique allows instantaneous sampling of fish density over huge areas, revealing large-scale collective behaviour, i.e. diurnal aggregation and migration of herrings during spawning season (see Makris et al. [9] and Jagannathan [10] for a review). A recent work by Handegard et al. [11] used a high-frequency sonar imaging technique with a 2 cm spatial resolution and 24 m2 span to track the motion of both schooling prey and group-hunting predators in a natural marine environment, demonstrating the importance of collective behaviour to the strategies used by both predators and prey. In large clupeid schools, for example, acoustic imaging suggests groups to be highly heterogeneous with vacuoles and nuclei, and irregular frontiers [8,12]. The degree to which such density variations can be explained by individual behavioural rules as opposed to environmental factors such as the influence of the recording vessel, oxygen consumption within such large groups [13] and flow features of the aquatic environment are not yet understood. The amoeboid shape, along with elongated form of the school and limited vertical extension, seems to be shared characteristics of pelagic fish, but the measured mean density greatly varies between species [14].
Quantitative experimental approaches of fish schooling have been conducted prior to such technological advancements. The seminal works of Breder [15], Shaw & Sachs [16] and Radakov [4] have emphasized the mechanisms of information transfer among individuals within schools, suggesting this is a general, and likely valuable, adaptation arising from social aggregation. Radakov [4] described the coordinated movement of fish in a school of Atherinomorus as ‘waves of agitation’ that could reflect against obstacles and attenuate and ‘streams of agitation’ where the directional information of one frightened fish is either amplified by social interactions to propagate to the whole school, or dies out. Another series of experiments on various fish species swimming in school in a flow channel (Pitcher and colleagues on cods, pollocks, herrings and minnows [17–19], following the method of Cullen et al. [20]) unveiled the structural properties, in a statistical sense, of the school by means of video-recording and analysis of the extracted three-dimensional positions, opening the way to modelling studies. The fact that most of these authors focused on structural similarities across taxa and situations should not occlude the fact that the mechanisms at work in creating such structures are deeply linked to an adaptive specific behaviour and an ecological context.
When trying to get functional (‘ultimate’) explanations for schooling behaviour, schooling appears to be intrinsically adaptive and polyfunctional (see Krause & Ruxton [21], for a review). In some cases, it can improve foraging activity (mechanisms reviewed in Pitcher [22, ch. 12]) such as when information can be obtained from the foraging behaviour of others to improve an individual's own exploitation of a patchy resource (when the benefits of increased acquisition outweigh the costs of increased competition among group members) [23], or as a consequence of an evolved coordinated hunting technique (e.g. in tunas and spotted seatrout [11]). It can as well be a cost for the member, e.g. under the assumption of homogeneous food distribution leading to competition among the school, in balance with passive or active anti-predator benefits [22]. In relation to anti-predator benefits, increasing group size has been shown experimentally to lower predator per capita encounter rate, and thus risk [24–27], at least until a certain group size beyond which per capita risk can be constant [11]. Furthermore, upon encounter, active predator avoidance can be achieved in a prey school via a palette of synchronized escape manoeuvres (fountain effect, herd, vacuole; see Pitcher & Wyche [28] and Handegard et al. [11]). The efficiency of these collective responses may lie in the inability for a predator to focus its attack on a single fish (see Krakauer [29] for a neural network model supporting this confusion effect). We note that such escape manoeuvres can all result from collectives that use the same, simple, behavioural interactions, as opposed to relying on grouping individuals that change interaction types [30]. Predator vigilance at the school level is also thought to result from an increased chance of one or some group members to detect cryptic predators (the so-called many eyes effect [31]) and mechanisms allowing fast information transfer across the school (the so-called Trafalgar effect [25]). Counterbalancing these benefits, predators may also prefer attacking large groups of fish or detect them more easily, as evidenced in recent experimental work [32,33].
Schooling has also been thought to confer hydrodynamic benefits if individuals adopt positions such that they exploit the shedding of vortex sheets from those ahead [34]. An elongated diamond-shape pattern and a phase opposition of neighbours’ tail movements in a column are the school features theoretically found to optimize energy recovery from vortices produced by other group members, and fish trying to increase their efficiency would thus behave so as to adopt this configuration. This hypothesis can be tested by measuring the energy consumption when swimming. Tail beat frequency, which has been demonstrated to be positively correlated with oxygen consumption for solitary fish [35], is used as a proxy of the effort of the fish. Recent experiments on schools of roach [36] and seabass [35] found a significant reduction in tail beat frequency of the trailing fish compared with those of the front. However, because of the indirect nature of the measurement, there is still no conclusive proof of an energetic saving when swimming in school, and it is worth mentioning that many previous studies were confounded by the fact that fish in large groups tended to be less stressed, and thus may be expected to use less oxygen. Furthermore, if gaining a hydrodynamic advantage on large fast-cruising clupeids schools that need to migrate between their spawning and feeding sites is obvious, it may not stand for smaller river fish that also exhibit schooling, a view supported by experimental studies by Hanke & Lauder [37]. All these examples illustrate more broadly how difficult it is to establish a direct link between function and behaviour.
The proximate causes of fish schooling, i.e. the actual behavioural rules followed by individuals of a given species, are still poorly understood, although they could be crucial in understanding the evolution of collective motion and the associated functional benefits described earlier. A lack of quantitative data on fish schooling, and the fact that multiple sets of behavioural rules may yield practically identical global behaviour [38], raises a serious obstacle for the identification of such rules. With the growing interest in methodologies to infer interaction rules, and in experiment-based modelling, paths are being paved to allow deeper investigations of the rules that underlie schooling behaviour in a variety of contexts, such as in open, or more complex, environments [39–42]. While they cannot capture the full diversity of behaviours likely seen under natural conditions, laboratory experiments on schooling have the advantage of being highly controlled, allowing experimentalists to isolate key features of the social behaviour in schools [43]. Thus, they may be used effectively to determine specific behaviours, and they will bring us closer to an understanding of the mechanisms of the evolutionary convergence among organisms that exhibit apparently similar collective motion.
3. Insights from fish school models
3.1. From individual to collective behaviour
As the description of schooling has progressed in terms of its functions and interplay with ecological constraints, and in terms of experimental characterization of emerging patterns, the interest in developing a framework to bridge the gap between individual and collective behaviour becomes clear. A major improvement of our understanding of collective motion in fish has thus been reached through the effort on modelling fish school behaviour using agent-based models, which has permitted researchers to set hypothetical individual rules and test through numerical simulations the resulting behaviour at the school level. The first successful attempts of such models [44–48], sometimes coming from unexpected fields such as computer animation [49], demonstrated that despite some methodological flaws (few fishes leading to a dominant border effect [43]; poor exploration of initial conditions, as pointed out later [50]), simple individual behavioural rules often referred to as ‘traffic rules’, with appropriately tuned parameters, were able to reproduce the collective behaviour of a fish school with its main features (cohesion, polarity, shape and structure).
Schooling was thus classified among the growing collection of self-organized biological phenomena [1]. An intensification of the modelling and simulation effort over the last decades yield an important collection of models and studies, shedding some light on the complex interplay between the individual and school levels, and subsequent methodological and conceptual issues [51].
We will first present the most common ingredients implemented in individual-based models of collective motion and then categorize the existing models by the mean of their mathematical proximity. Through this categorization, the diversity of problems tackled by modelling studies is evoked.
3.2. A typology of individual based models for fish schooling
An agent-based model of collective motion starts with the mathematical definition at the individual level of the swimming abilities of the fish, at least implicitly, and the behavioural algorithms that define its interactions with the other individuals. Although they vary much in mathematical complexity and formalism, most are composed of three behavioural rules based on the main properties observed at the school level: collision avoidance, directional orientation (and thus synchronization of direction of travel) and finally cohesion. The repulsion rule facilitates collision avoidance and typically is given the highest priority, as inspired by observation on animal groups [41] as well as modelling [52]. The tendency to match behaviour of nearby neighbours, which is also termed allelomimetic behaviour [53], is typically expressed in an explicit rule of alignment for an individual trying to match the speed and direction of its neighbours. Recent experimental evidence has suggested that it might not be an explicit behavioural rule [41,42], but rather that coordinated motion might be achieved using social repulsion and attraction only (as supported by theoretical models [54–56]). Finally, an attraction rule mimics a tendency to group with conspecifics in order to produce aggregation, a prerequisite of school existence.
Moreover, these rules are often completed by a stochastic component to account for the individual intrinsic behavioural stochasticity (as Kuhlia mugil [40]). This noise corresponds to the intrinsic errors made when acquiring information on neighbours, changes in the motivational state of the fish or local (uncorrelated among individuals) sources of environmental noise. In the same spirit, swimming rules have to be supplemented by a stochastic component accounting for the variations in swimming abilities of the individuals as well as the fine scale or complex interactions with the water we will not take into account (wake turbulence [34], induced flows [57]) as long as the retroaction between medium and individual is estimated negligible [58].
3.3. Synchronous self-propelled particles models
We arbitrarily put together under this designation all modelling efforts oriented towards the understanding of fish schooling where the individuals' speed is kept constant or drawn into a probability distribution [44,45] reproducing experimental data [59] and does not change as a consequence of interactions with neighbours. An individual fish therefore moves in straight line between successive time steps, with speed c0 and bearing di(t) (directional unit vector). At each time step, a preferred direction di(t + 1) for the individual is computed according to the direction dj(t) and relative position rij(t) = rj(t)–ri(t) of the other fish in a defined neighbourhood Ni(t) with n(t) neighbours. This update can be expressed by the following general equations:
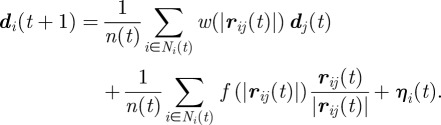 |
The preferred direction di(t + 1) is then normalized to a unit vector. The new position of the particle is updated as follows:
The first right-hand term of the preferred direction equation corresponds to the alignment rule, with a fish tending to match the average (simple or weighted) direction of its neighbours. The second right-hand term ensures repulsion and attraction, and it takes respectively negative or positive values when the neighbours are too close or too far away. The last term ηi(t) is a stochastic component (for the origins and consequences of stochasticity in this context, see [60,61]). The coefficients w(r) and f(r) are used to define the relative range and weight of attraction and repulsion/alignment (A/R/A). Some models include behavioural zones of some extent where a specific rule is applied ([44,47,60,62], on boïds [49]); some adopt functional forms for the attraction/repulsion coefficient [63,64]. Other biologically relevant ingredients are usually added such as a blind sensory zone [65], body size and form [66], or fish individual characteristics drawn from field-observed distribution [44,45], so that the behaviour of particles is closer to that of real fish.
It is important to notice that the definition of neighbourhood on which each term is calculated is a crucial point to consider because of its consequences on the behavioural output. Three main definitions can be found in the literature that lead to very different behaviours at large scale: first, the metric neighbourhood [64,67], where all individuals are taken into account within a surrounding area of a defined range. Second, the topological neighbourhood that remains invariant with respect to density changes, as first discussed by Ballerini et al. [68] in connection to data gathered on starling flocks. This topological neighbourhood has proved to lead to robust cohesion of the school under predation [68], and it may be achieved either by considering a fixed number of neighbours according to their proximity (K nearest neighbours) [68,69] or by using the first shell of a Voronoi tessellation [40,70]. This geometrical tessellation defines a zone of danger [71] for each member of the school, i.e. a zone where a hypothetical predator is closer to this member than any of its neighbours. The selfish herd hypothesis assumes that a predator would most likely attack the closest fish, thus making the interest of any fish to reduce the area of its zone of danger. The first shell of a Voronoi tessellation contains the neighbours of a focal fish with which their respective zones of danger share a border. By monitoring these neighbours, an individual could evaluate its vulnerability. From a functional point of view, the behavioural mechanisms should be selected so as to minimize the zone of danger in the case of a predator attack [72]. The third notable approach of neighbourhood is derived from visual processing considerations. It corresponds to a dynamical selection of the neighbourhood [73] based on selective attention to motion.
To make a connection between individual behaviour and schooling patterns, numerous synthetic studies have been carried out, systematically varying individual parameters and measuring their influence on observables at the local level (nearest-neighbour distance, preferred positions of neighbours), group level (polarity, group momentum, shape, structure) and population levels (group-size distribution) [74]. The outcome of various hierarchies between the A/R/A rules has been studied on the motion of small groups of fish [63,75] and on the equilibrium structure (i.e. under no influence of randomness) at the collective level [76]. A crucial point is the presence of sharp transitions in collective behaviour that were observed for little parameter changes. For example, a slight change in the radius of orientation (if near the critical point) yielded drastic changes at the school level in terms of polarization and structure, such as transition between schooling, milling and swarming, as shown in Couzin et al. [62].
This algorithmic simplicity at the individual level, witnessed by a limited number of parameters, and yet, the presence of a diversity of patterns at collective levels (swarming, milling, synchronized swimming), provides the opportunity to conceptualize general emergent properties through mathematical modelling [77]. The complexity can be reduced to an explanatory and predictive ideal mechanism, under logical or mathematical form, referred as a self-organization principle [1,78], bringing some amount of generality into collections of case studies. Nevertheless, the goal of such models is not to capture the precise behaviour of an individual fish but rather to identify the minimal general components required for schooling.
3.4. Asynchronous self-propelled particles models
A typical feature of models of collective motion is a competition between a stochastic component and a tendency to order, although it is important to note that stochastic effects may also facilitate the instatement of collective motion [79]. However, there is a different way to implement stochasticity, which has been recently investigated by Bode et al. [80]. Instead of updating in synchronous way the position and velocity of all agents and add to the set of rules a random component, the agent updates are made through a deterministic set of rules in a random order. Interestingly, this asynchronous update yields a topological-like behaviour [81], very similar to what has been deduced from analyses on starling flocks [68].
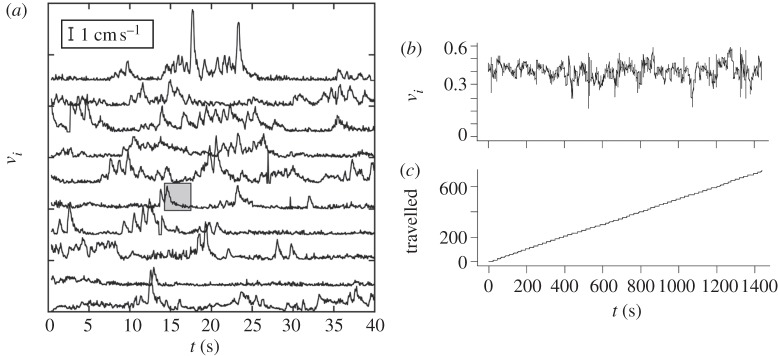
Even though this behaviour is reminiscent of the schools of Paracheirodon innesi (C. Becco & N. Vandewalle 2009, Experimental study of collective behaviours in fish swarms, unpublished data), where the continuous motion of the school is composed of the sum of individual bouts and pauses with no apparent synchronicity (figure 2a), Bode et al. emphasize that there is no direct link between the updating frequency and the actual locomotors events. Yet, this new approach has an interesting ability to match experimental data [80]: a simple variation of update frequency can reproduce the speed distributions observed in groups of three spine sticklebacks under various level of agitation as they are frightened, hungry or steady.
Figure 2.
Different species of fish use different modes of swimming, ranging from a nearly constant speed to bouts and pauses in motion. (a) Time evolution of individual speeds |vi| for 1 ≤ i ≤ N in a school of Paracheirodon Innesi. Each speed is displayed with a vertical shift in order to show the activity of each fish in the school. Speed scale is given in the upper left corner. Most of the time, fish have a nearly zero speed before suddenly exhibiting high accelerations followed by a speed decrease (legend from (C. Becco & N. Vandewalle 2009, Experimental study of collective behaviours in fish swarms, unpublished data)). (b) Time series of the speed of an individual in a group of four Kuhlia mugil. (c) The cumulative sum yields a linear relationship over the experiment's duration, opening the way for a constant speed modelling.
3.5. Social forces models
Besides their success in linking functional properties at the school level to behavioural mechanisms at the individual scale and some experimental success [82,83], it is unlikely that the self-propelled particles framework, as we defined it, has the ability to lead to models accurately reproducing experimental data of species, notably in explaining the experimental speed distributions and consequently the mechanisms responsible for speed synchronization. In particular, a series of simulation studies have shown that the mean speed of an individual could be considered as an emergent property as well [51,69,74]. In self-propelled particles models, fixed speed implies a direct proportionality between polarization and mean speed of the school. Viscido et al. [74] performed experiments on groups of four and eight fish over periods of 10 min, exhibiting large deviations to this property.
The social forces framework considers a school as Newtonian particles submitted to ‘social forces’ (attraction and repulsion [63], orientation, random force accounting for intrinsic stochasticity and complexity of animal behaviour [61,84]) and physical forces. The inclusion of explicit physical forces into individual rules of motion is one of the main motivations for these models. Indeed, the introduction of drag is found to have a drastic effect on collective behaviour [74]. While it widens the modelling horizon and allows some analytical work [61,84], this framework increases the number of potentially arbitrary factors that have to be implemented in the model.
Hopefully, it comes along with a number of tools developed for particle physics: methods such as Force-Matching [39] (also adaptable to self-propelled particles models) or Force Mapping, further discussed in §3.6, allowing to find best-fitted social forces relatively to a set of data. A recent experimental work [82] brought an evidence of frontal preference in the influential neighbours of an assembly of Surf Scoters swimming against the drift currents. A social force model with A/R/A rules supplemented with weak frontal preference (an early modelling hypothesis [48]) has shown a good agreement between observed and predicted structure (radial distribution, angular preferred position). However, even if the model was able to reproduce the observation data quite well, it has been calibrated with the best set of free parameters that optimized the simulated patterns towards the observed collective properties (namely the authors made their model fit at the collective scale). In such a case, it is well known that several models can be fitted to a dataset at the collective scale, simply because the search for the best match is unconstrained and can be performed for each model, so that the collective level underdetermines the individual level.
3.6. Statistical physics of collective motion
An intense interdisciplinary work exists over individual-based modelling, particularly with statistical physics, following the seminal work of Vicsek [60]. The reader interested in the treatment of the problem by statistical physicists is referred to the reviews of Giardina [85] and Vicsek [86]. Tools initially developed for the study of out of equilibrium physical or chemical systems are adapted to the problem of living organisms. These methods aim at investigating possibly universal features of collective motion over diffusion, long-range order or presence of high-order and high-density regions at the onset of collective motion [87], named travelling bands. They may be analytical, through translations of agent-based models to Eulerian descriptions (in terms of continuous velocity and density fields), either phenomenologically [88] or analytically derived [89]. This approach aims at the understanding of the general mechanisms by which local rules lead to large-scale synchronization, those mechanisms being thought to be rather independent of the detailed nature of the systems' components. This idea of independence of the large-scale behaviour relative to fine behavioural details is inspired by the existence and similarities of collective motion phenomenon in very different species and even in non-living systems. We think that for being crucial in the understanding of the ubiquity of collective motion phenomena in biological systems, this statistical physics approach does not aim to address the behavioural mechanisms that govern the dynamics of these phenomena. Collective motion in biological systems is rather seen in analogy with an out-of-equilibrium phase transition from a disordered phase where no global order is found to an ordered phase in which the system (i.e. the school) is highly polarized [60]. This critical change in global behaviour is obtained by varying the value of a behavioural parameter such as noise [60,90], blind angle size [65], speed [91], alignment tendency [62] or a ‘strategy parameter’ [92], which weighs a behavioural compromise between aligning with neighbours and reacting to their direction changes. The validity of this view finds some support in the experimental work of Becco et al. [93] that showed that such transition from disorder to order can be obtained by increasing the density of Tilapia fish in a shallow water arena. Increasing density, in the Vicsek model, is equivalent to decreasing the noise, as the directional information transfer during fish ‘collisions’ is favoured by density. Interestingly, in an equivalent experimental set-up on another species, Gautrais et al. [40] found the inverse effect of density on global order, the school being unable to form beyond a certain density, underlining that at the intermediate level of size and number of an experimental set-up, the school can be dominated by fine behavioural details and yield a much different global behaviour than its large-scale statistically predicted one. Another rapid transition from disordered to highly synchronized behaviour at a critical density has been found in large population of spawning herrings by Makris et al. [9].
3.7. Self-organization and functional properties
Nevertheless, modelling is crucial to understand how does biological functions emerge from interactions between individual components. Among biological functions of long-lasting interest [4,94] is the transmission of information among the school, studied and heuristically defined with self-propelled particles and social force systems [86]. In these modelling frameworks, transmission of information can be defined, for example, in the terms of time needed for a particle to propagate its influence through a given fraction of the population [92], and thus its optimality (i.e. the maximization of its measured value) associated with a set of individual parameters. These works also allow some insights on how collective sensing [23] and decision-making [95] can be achieved in the schooling phenomenon. Striking is the demonstration of the possibility of a purely collective memory, the school being able to encode in its structure the memory of its previous state, a hysteresis being observed when slowly going from disorder to order and back acting on the behavioural parameters of the individuals [62].
Also successfully explained by a modelling approach is the mechanism of self-sorting of individuals in a school [62]. Costs and benefits of being part of a school vary as a function of the individual position within the school, a hungry individual being more likely to take a risk, but more successfully forage, on the edge [22]. In a large school or when its horizon is crowded, the fish cannot direct itself to its area of interest, ignorant of their own position within the school. Couzin et al. [62] demonstrated that by changing behaviour, with respect to neighbours, individuals can regulate (probabilistically) their relative position within the school. The anti-predator benefit of the confusion effect is also optimized for an individual being locally non-conspicuous, and this may be achieved by local interactions in the school as shown in Kunz & Hemelrijk [66] and Ioannou et al. [28]. To sum up, a change in an individual strategy can lead, via self-organization, to a change in its position within the group or in the local composition of the group, even if no information about the shape of the group is accessible to that fish, in particular if its visual horizon is crowded or if the school is extending beyond its visual range.
4. Open issues for the investigation of cognitive and behavioural mechanisms involved in schooling
With several models exhibiting similar global-collective patterns provided they are appropriately tuned (see the discussion on this particular issue in Gautrais et al. [40] and Weitz et al. [38]), conclusions on the specific mechanisms ensuring those different functions in various species are still out of reach. A way to reconcile data with models and ensure that one does not predetermine the behavioural rules to get a desired schooling behaviour is to proceed with a bottom-up approach on each species. This method is illustrated by a recent experimental work that leads to a model reproducing quantitatively the behaviour of fish both at individual and collective levels, based on a fish kinematic with interesting long-time diffusive properties [40,96]. The idea is to build a model incrementally from scratch, validating at each step the modelling choices through a specific experimental design. In the past, the very same methodological framework has been successfully applied to characterize and model individuals' interactions that govern collective behaviour in pre-social and social insects [97–99].
In this approach, we believe that there exist some key behavioural components that have to be carefully evaluated. A first important component is the kinematic that characterizes the motion of a single fish. Depending on its intrinsic features, it may or may not facilitate the inference of social interactions at stake in the school. Then, the type of information (i.e. the stimuli) gathered by an individual to control its movement is also crucial, especially when the perception or the behavioural reactions of a fish change in different environmental conditions. Assuming that these stimuli can be somewhat decomposed into a sum of pair interactions, one has then to consider which neighbours a fish is going to interact with. If this assumption is wrong, one has to identify the kind of information processing a fish is doing, namely how the stimuli are combined and what are the resulting consequences on the motion of the fish. Finally, a last issue concerns the impact of endogenous physiological and behavioural changes on data collection and analysis.
4.1. Characterizing the spontaneous motion of fish
Schooling phenomena occur in species that have evolved widely different swimming abilities and behaviours. Constrained by biomechanics, the elected swimming mode (see Sfakiotakis et al. [57] for a review) can lead to a continuous motion, as for most pelagic fish (see fig. 2b,c from K. mugil [100] or cod, saith and herring [19]), or to discontinuous burst-slide swimming (fig. 2a, from C. Becco & N. Vandewalle 2009, Experimental study of collective behaviours in fish swarms, unpublished data): the fish propels itself intermittently and then slides until viscosity stops the motion. In the latter case, individual swimming speed is highly variable, in particular for small river fish such as zebrafish (Danio rerio) or firehead tetra (see fig. 2a Hemmigrammus bleheri from C. Becco & N. Vandewalle 2009, Experimental study of collective behaviours in fish swarms, unpublished data). Most importantly, speed variability acts on the same timescales as the individual updates of its direction of motion. In addition to the theoretical result that synchronicity in ‘swimming bursts’ deeply influences the global schooling behaviour [80], the integration of individual swimming abilities in a model may be a crucial point for its relevance at the intermediate-size.
Numerous agent-based modelling studies already constrain the motion of individuals to realistic values, tuning parameters such as the maximum speed, the maximum turning speed, and the update frequency in self-propelled particles models or introducing a maximum acceleration and a drag force in social forces models. There exists some evidence in the literature showing that manoeuvrability constraints are key behavioural factors that determine the ability to perform schooling behaviour. The introduction of drag in a social force model [74] yielding an asymptotical limit speed for the fish, i.e. manoeuvrability constraints, has a dramatic impact on individual trajectories, in particular the path curvature, and also on poupulation-level properties, as it leads to increasing group sizes. Similarly, in a self-propelled particles model [50], varying the maximum turning rate is a means of selecting the accessible states of the system. The spontaneous motion, i.e. the limit case of a non-interacting fish defined as a constant speed random walk with correlated successive orientations in Gautrais et al. [100] and as a Langevin process for the social force model with drag in Viscido et al. [74], generates different large-scale diffusive properties [96].
Furthermore, when trying to characterize from experimental data the interactions between individuals in a fish school, one must start with a ‘null-model’ that adequately characterizes the motion of an isolated individual (see Katz et al. [41] in which the analysis of fish interactions is performed under an implicit social force assumption).
4.2. Inferring interactions between individuals
Recently, several studies have explored ways to infer social interactions directly from experimental data rather than trying to test a priori rules with the satisfying properties at the collective level. The force-map technique [41] and the non-parametric inference technique [42] have been used to estimate from experiments with two fish the effective turning and speeding forces experienced by an individual, once the relevant variables on which they may depend have been chosen. In the force-map approach, the implicit assumption considers that fish are particles on which social and physical forces act. Those effective forces capture the ‘coarse grain’ regularities of actual interactions, and thus constitute a powerful tool. But the explained fraction of the variance is low, and its origin remains largely unexplained—in particular, the intrinsic variability of individual behaviour, and the coupling between arbitrarily chosen variables. To be more than a powerful visualization tool, this approach has to demonstrate its ability to lead to a model that would reproduce in turn the experimental data. A partial answer is given by the work done by Lukeman et al. [82], that quantitatively reproduces at the collective level the behaviour of surf scoters, thanks to a self-propelled particles model with an additional frontal preference hypothesis. However, without an agreement of the model at the individual level, it is difficult to evaluate to which extent the extracted behavioural algorithm corresponds to the actual behaviour—in this case, the value of the frontal preference hypothesis.
A different approach is a bottom-up modelling introduced by Gautrais et al., which has been applied to investigate the schooling behaviour in groups of barred flagtails (K. mugil) [40]. Once the spontaneous motion of an isolated fish has been modelled and its parameters quantified, a dynamical framework is defined within which the interactions of that fish with the physical environment and neighbouring fish are included. The influence of the tank wall is estimated directly from experimental data. Series of two-fish experiments are then used to suggest interactions and their functional form, in that case attraction and alignment only, and to quantify the parameters of these functions with inversion techniques. The validation of the model is based on the agreement of model predictions with experiments on several observables and with different group sizes. This step-by-step procedure ensures that the model properly reproduces the observed data, uncovering the behavioural rules at work in school maintenance for the experimental situation. This approach therefore needs to be extended to other experimental conditions. It is important to increase the local density of fish to investigate the short-range mechanism of repulsion, which is found unnecessary to explain school dynamics and collision avoidance in the experimental set-up. Conversely, experiments intended to investigate school formation, where inter-individual distance converges towards a statistical equilibrium that is much smaller than the initial value, are much needed to characterize and model the attraction among fish.
4.3. Acquiring and updating information on neighbours
The main sensory channels involved in schooling are vision [101] and the lateral line used to detect movement and vibration in the surrounding water [102,103] (see von der Emde et al. [104] for physiological and ecological considerations). Both channels have different properties: they act respectively at long and short range, vision operates in both the near and far field, whereas the lateral lines are limited to the near fields; and they also depend on the physical context (light, opacity, water flows). And both seem equally crucial [105], as a lateral line-disabled fish will not be able to school [103] and a blind fish will not be able to join its school if he loses its wake [102].
More important than the physiological processes involved in the acquisition of information is the kind of information a fish acquires and how it maps these estimates to motor control programmes. The assumption that a fish acts on the basis of discrete and absolute information such as the position and speed of some neighbours may be reconsidered with regard to recent works. We can think of a more continuous and global kind of information such as that driving the motion of pedestrian crowds [106]. This is found to direct a pedestrian towards the locally less crowded area estimated with the angular density measure, which is by itself a continuous and local variable. Lemasson et al. [73] have introduced an A/R/A model with neurobiological mechanisms of processing and integrating the information. This model goes well beyond the usual modelling hypothesis that mainly consists of a direct calculation using the absolute positions and velocities of neighbours. The angular position, speed and direction of neighbours' images on the retina of focal fish are integrated to weigh and trigger its behavioural reactions. The model implements selective information processing, using key properties of image detection and motion forecasting to select the set of neighbours eliciting each of the three behavioural reactions: attraction, alignment and repulsion. However, we are far away from deriving behavioural mechanisms from the present understanding of the actual cognitive and sensorimotor processes at work in each schooling species. Nonetheless, the insight gained on what information is actually perceived by an individual should allow us to make more realistic hypotheses even if the complexity is increased.
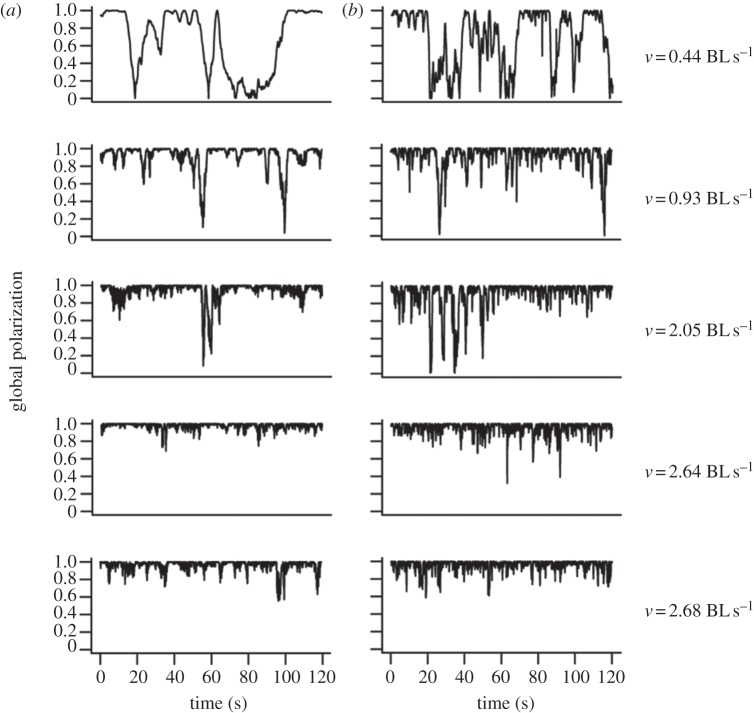
Together with the issue of which type of information is used is the coupling between the motion of the individual and the perceptual capabilities of fish. In the Lemasson's model [73], the matching response is defined proportional to the speed of individual fish, the displacement of an object on the retina of the individual being proportional to the speed of this object. From an ecological point of view, half the species of fish move intermittently [107], and among the benefits gained from this type of locomotion may stand an increased sensitivity to the surrounding while resting. Pauses on the move allow a stabilization of the visual field and an increase in the signal-to-noise ratio from the lateral lines [108]. It is worth mentioning that the dynamic correlation between cruising individual speed and school structure, already noted by Aoki [59], has been experimentally captured by the bottom-up modelling approach of Gautrais et al. [40] through a dependency on swimming speed of the main coefficients controlling interactions between fish, namely the weights of positional and directional information, that may have a physiological origin. As shown in figure 3, increasing swimming speed leads to an increase in group polarization.
Figure 3.
(a) Time series of the alignment between two fish (left) for each experiment and (b) corresponding model simulations (right), ordered by increasing fish speed. Speed is expressed in fish body lengths per second. The speed and polarization interrelation is captured through speed dependency of the model's coefficient (text and figure from [40]).
4.4. Determining which neighbours a fish is interacting with
From the STARFLAG project [109,110] that mapped the three-dimensional structure of free-flying starling flocks emerged strong experimental evidence for topological-like interactions [68]. Each bird seems to pay attention to approximately seven nearest neighbours [68], suggesting how cohesiveness can be maintained in groups that exhibit such density variability. The neighbourhoods defined a priori in a modelling study can be justified by physical sensory arguments (e.g. range of vision through diffusive medium, rapid attenuation of pressure waves) or by neurobiological arguments as in the selective attention model [73]. But considering the tremendous effects of the chosen neighbourhood on the outputs of the simulations in terms of cohesiveness, structure and dynamics of a school, the ultimate test should be a confrontation with experiments, i.e. with the behaviour of actual species. In a bottom-up modelling approach, provided that the interactions among fish have been correctly described, it is theoretically possible to quantitatively discriminate various neighbourhood choices through simulation and data collection across various scales (figure 4). But so far these effects are hard to observe in experiments because of the geometrical constraints due to the finite-sized arena [40].
Figure 4.
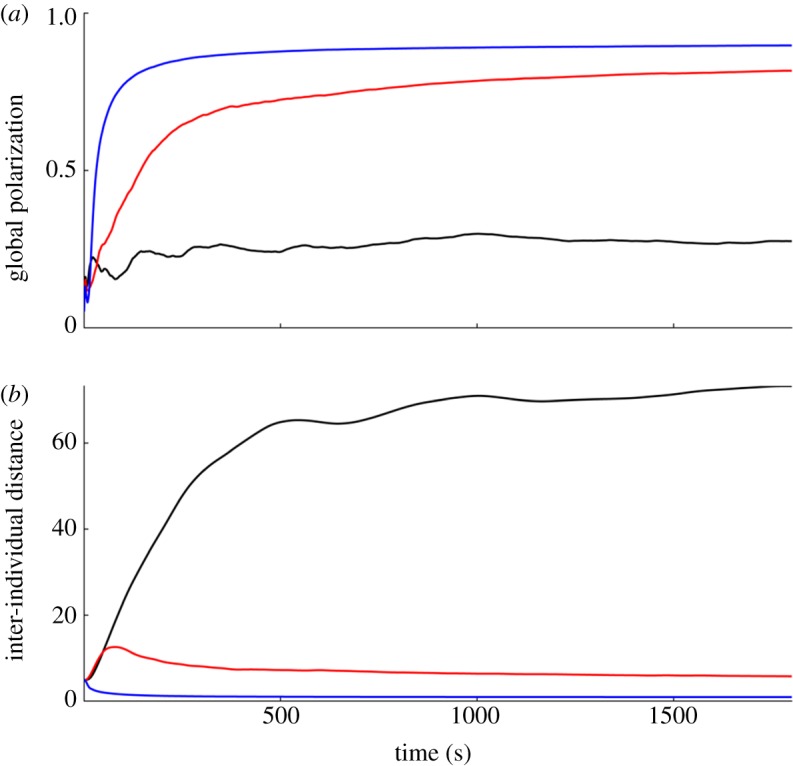
Impact of various neighbourhoods on group polarization and inter-individual distances in a simulated fish-school model. Simulations are from Gautrais et al. model [40] with a speed of 0.54 body length per second and parameters fitted from data on groups of 10 fish. We simulated a school of 100 fish for half an hour in a 100 m diameter arena. Initial orientations of fish are randomly chosen and their initial positions are randomly distributed within a circle of 30 m diameter in the centre of the arena. (a) Global polarization of the school for various definition of the neighbourhood. Blue line denotes all fish are considered within a 4 m range. Red line denotes only the fish that belongs to the first shell in a Voronoi tessellation are considered. Black line denotes only the seven nearest neighbours are considered. (b) Mean inter-individual distance between fish. The drop in global polarization and the large inter-individual distances observed when the seven nearest neighbours are considered are due to the split of the school.
The quantitative observation of a free-swimming school being uneasily achieved, we might consider designing experimental and analytical techniques, allowing us to discriminate between competing hypotheses. The necessity of an adequate experimental design relative to an analysis tool is stressed by the recent development of Bayesian inference methods [111]. In these conditions, a Bayesian methodology is shown to have the ability to validate a model against experimental data that covers sufficiently different configurations, i.e. experimentally sampling a transitory rather than static evolution. Reproducible experiments have to be designed in order to study such transitory phases. One could think of provoking the dispersion of a school with a device simulating an attack, allowing us to record the transitory phase of grouping from an initial dispersed condition. A recent work by Herbert-Read et al. [42] using a classical experimental set-up has shown that the social force most representative of the data was essentially acting on a single nearest neighbour, constituting evidence for a single nearest-neighbour interaction for this species. In their methodology, the inferred social force is fitted into an artificial neural network using the maximum-likelihood method, and thus not explicitly parametrized. As such, it does not provide a straightforward way to formulate a model.
4.5. Determining which ways are used by the individual to integrate information
An individual may take into account information from various neighbours to control its next move. It may be expressed in a modelling framework as a combination of pair interactions, e.g. by summing [69] or averaging [50]. The limited cognitive abilities at work nonetheless make suspect some utterly complex calculations over a large number of influential individuals. Recent experimental work by Katz et al. [41] suggests that integration of information cannot be seen as additive social forces, and rather points towards synergetic or averaging combination of respectively speeding and turning forces. While modelling the motion of another species, school motion was best fitted when averaging the influences, the overall intensity roughly equalling the intensity of random influences.
In pedestrians, it has been shown that simple heuristics applied by an individual to the whole sensorial environment may match both requirements of low cognitive complexity and high efficiency at the collective level [106]. In that case, individuals are found to direct their motion towards the less-crowded angular direction. This rule is equivalent to finding the minimum of a local density landscape; a pedestrian, through visual information processing, may easily find an approximate solution but the rule is intrinsically hard to describe as a combination of pair interaction. We may remain aware that the reaction behaviour can be based upon a global stimulus that cannot be decomposed further, thus making the leap from pair interactions to whole-school interactions reciprocally hard to achieve formally. A similar heuristic rule leading to a global herding has also been used in a model [72] illustrating how the selfish herd hypothesis [71] could work efficiently. In this so-called local crowded horizon mechanism, each individual evaluates the density of the herd along all directions and direct its motion towards the angular direction in which the crowd density is the highest. Doing so, each individual considers the presence of all neighbours weighted by a ‘visual function’ that decreases according to the distance. This approach could be refined by taking into account only the influence of visible neighbours, through integrating the shape characteristics of school members, thus making the definition of the local crowded horizon compatible with what the fish can actually perceive.
4.6. Determining group size effects and their influence on the reactional state of fish
Adaptive properties at the collective level emerge from the behaviours of the interacting individuals that react to biological cues such as predators, food resources or to physical cues (such as light intensity, temperature) that can be controlled in a laboratory experiment. These stimuli may elicit punctually a stereotyped response (such as C-start elicited by water flows similar to a predator suction [108]) but may also affect the internal state of the individual, leading to mid-term changes in behaviour. Several studies tried to capture this behavioural switch, with some success either with data analysis only [112] or in a self-propelled particles framework. Tien et al. [113] evidenced a neutral zone and a fall in nearest-neighbour distance when frightening schools of fish swimming in a pond. Another study by Hoare et al. [83] exhibited the link between group size selection and internal state eliciting an anti-predator response, hunger, and compared it with a control steady state. In these examples, the effect on behaviour of a change in the internal state of fish is captured through the modification of the behavioural parameters of the model. As a matter of fact, the accurate modelling of fish behaviour allows measuring behavioural switches as variations of the behavioural parameter of the model. This has been shown for instance by Gautrais et al. [40], who detected a change in behavioural parameters with increasing density, leading to a disordered swimming once a critical density has been reached. It is worth noting that in that particular case, the individuals may change their behaviour relative to the density [91]. This additional coupling, namely the influence of the school as a whole on the behaviour of its constituent individuals, is a topic that we may carefully consider in future investigations.
To limit the impact of the behavioural variations due to non-physical factors such as habituation or any variation in the internal state of fish, it is prudent to get an estimation of the behavioural variability in the long term. A series of experiments led by Miller & Gerlai [114] on zebrafish explored quantitatively the effect of habituation on fish behaviour with the experimental arenas (no effect) as well as the effect of food presence (lowered density) and exposure to aerial model predator (no habituation, punctual effect).
5. Conclusions
In trying to understand why fish school evolutionary biologists have identified several emergent functional ‘supra-organismic’ properties that may benefit the individuals that belong to a school. But an accurate knowledge of behavioural mechanisms and interactions involved in schooling is also important to understand how these properties emerge. Decades of modelling studies and an increasing data collection aimed to understand the connection between individual interactions and school properties. Numerous modelling frameworks have been developed, and shed light on the potential mechanisms driving school formation, maintenance and patterns of motion. Most of these models represent idealized a priori behavioural algorithms that make their theoretical study easier. In searching for the actual behavioural mechanisms at work in fish, one could make a simple comparison of large-scale data with simulation output. However, it is hard to find biologically relevant individual mechanisms with such a top-down approach because of the strong coupling between individual behaviour and external cues, be they ecological or physical, the internal state of fish and finally the output of the school itself.
We have emphasized a set of major and unknown behavioural components that are likely to play a crucial role in schooling. As all these elements are coupled with each other, we suggest long-term incremental modelling work in direct confrontation with experimental data that may result into their characterization. The first component is the motion of a single fish, poorly considered up to now because of its lack of generality. It has to be carefully characterized and modelled so as to uncouple its consequences on school behaviour from those that result from interactions among fish. These interactions are a second important component already investigated through new methods of data analysis that prove their ability in questioning the validity of a priori model assumptions for specific fish behaviour. Third, the nature of the stimuli used by an individual to control its trajectory is also crucial, as their perception may also depend on the fish motion and the environmental conditions. Fourth, the neighbours considered by a fish and from which stimuli are integrated into a behavioural response. Several hypotheses, namely metric, topologic or dynamic neighbourhood, have emerged from simulation studies that now require some experimental validation. Then, there is the question of the integration of the influence of a discrete number of neighbours. This is a rather complex cognitive hypothesis that is in competition with much simpler heuristics based on visual processing. Finally, a last issue concerns the impact of endogenous factors such as physiological and behavioural changes that may strongly impact data collection and analysis.
The knowledge gained on such behavioural components is relative to a species. But we may hope that, after deciphering several behavioural mechanisms across different taxa, we will be able to identify several classes of fish school models.
Acknowledgements
We are grateful to Hugues Chaté for his critical and constructive comments on the manuscript. U.L. was supported by a doctoral fellowship from the scientific council of the University Paul Sabatier. This study was supported by grants from the Centre National de la Recherche Scientifique and University Paul Sabatier (project Dynabanc). I.D.C. acknowledges support from Office of Naval Research award (N00014-09-1-1074), NSF award (PHY-0848755) and Army Research Office grant (W911NG-11-1-0385).
References
- 1.Camazine S., Deneubourg J.-L., Franks N., Sneyd J., Theraulaz G., Bonabeau E. 2001. Self-organization in biological systems. Princeton, NJ: Princeton University Press [Google Scholar]
- 2.Ben-Jacob E., Cohen I., Levine H. 2000. Cooperative self-organization of microorganisms. Adv. Phys. 49, 395–554 10.1080/000187300405228 (doi:10.1080/000187300405228) [DOI] [Google Scholar]
- 3.Parrish J. K., Edelstein-Keshet L. 1999. Complexity, pattern, and evolutionary trade-offs in animal aggregation. Science 284, 99–101 10.1126/science.284.5411.99 (doi:10.1126/science.284.5411.99) [DOI] [PubMed] [Google Scholar]
- 4.Radakov D. V. 1973. Schooling in the ecology of fish. New York, NY: John Wiley [Google Scholar]
- 5.Hobson E. S. 1973. Diel feeding migrations in tropical reef fishes. Helgoland Mar. Res. 24, 361–370 [Google Scholar]
- 6.Shaw E. 1978. Schooling fishes: the school, a truly egalitarian form of organization in which all members of the group are alike in influence, offers substantial benefits to its participants. Am. Sci. 66, 166–175 [Google Scholar]
- 7.Parr A. E. 1927. A contribution to the theoretical analysis of the schooling behaviour of fishes. Bull. Bingham Oceanogr. Collection 1, 1–32 [Google Scholar]
- 8.Fréon P., Gerlotto F., Soria M. 1992. Changes in school structure according to external stimuli: description and influence on acoustic assessment. Fish. Res. 15, 45–66 10.1016/0165-7836(92)90004-D (doi:10.1016/0165-7836(92)90004-D) [DOI] [Google Scholar]
- 9.Makris N. C., Ratilal P., Jagannathan S., Gong Z., Andrews M., Bertsatos I., Rune Godø O., Nero R. W., Jech J. M. 2009. Critical population density triggers rapid formation of vast oceanic fish shoals. Science 323, 1734–1737 10.1126/science.1169441 (doi:10.1126/science.1169441) [DOI] [PubMed] [Google Scholar]
- 10.Jagannathan S., et al. 2009. Ocean acoustic waveguide remote sensing (OAWRS) of marine ecosystems. Mar. Ecol. Prog. Ser. 395, 137–160 10.3354/meps08266 (doi:10.3354/meps08266) [DOI] [Google Scholar]
- 11.Handegard N. O., Leblanc S., Boswell K., Tjostheim D., Couzin I. D. 2012. The dynamics of coordinated group hunting and collective information-transfer among schooling prey. Curr. Biol. 22, 1213–1217 10.1016/j.cub.2012.04.050 (doi:10.1016/j.cub.2012.04.050) [DOI] [PubMed] [Google Scholar]
- 12.Paramo J., Gerlotto F., Oyarzun C. 2010. Three dimensional structure and morphology of pelagic fish schools. J. Appl. Ichthyol. 26, 853–860 10.1111/j.1439-0426.2010.01509.x (doi:10.1111/j.1439-0426.2010.01509.x) [DOI] [Google Scholar]
- 13.McFarland W. N., Moss S. A. 1967. Internal behavior in fish schools. Science 156, 260–262 10.1126/science.156.3772.360 (doi:10.1126/science.156.3772.360) [DOI] [PubMed] [Google Scholar]
- 14.Simmonds E. J., MacLennan D. 2005. Fisheries acoustics: theory and practice. Oxford, UK: Blackwell Science Ltd [Google Scholar]
- 15.Breder C. M., Jr 1959. Studies on social groupings in fishes. Bull. Am. Museum Nat. Hist. 117, 397–481 [Google Scholar]
- 16.Shaw E., Sachs B. D. 1967. Development of the optomotor response in the schooling fish, Menidia menidia. J. Comp. Physiol. Psychol. 63, 385–388 10.1037/h0024636 (doi:10.1037/h0024636) [DOI] [PubMed] [Google Scholar]
- 17.Pitcher T. J., Partridge B. L. 1979. Fish school density and volume. Mar. Biol. 54, 383–394 10.1007/BF00395444 (doi:10.1007/BF00395444) [DOI] [Google Scholar]
- 18.Partridge B. L., Pitcher T., Cullen J. M., Wilson J. 1980. The three-dimensional structure of fish schools. Behav. Ecol. Sociobiol. 6, 277–288 10.1007/BF00292770 (doi:10.1007/BF00292770) [DOI] [Google Scholar]
- 19.Partridge B. L., Pitcher T. J. 1981. Internal dynamics and the interrelations of fish in schools. J. Comp. Physiol. 164, 313–325 10.1007/BF00612563 (doi:10.1007/BF00612563) [DOI] [Google Scholar]
- 20.Cullen J. M., Shaw E., Baldwin H. A. 1965. Methods for measuring the three-dimensional structure of fish schools. Anim. Behav. 13, 534–543 10.1016/0003-3472(65)90117-X (doi:10.1016/0003-3472(65)90117-X) [DOI] [PubMed] [Google Scholar]
- 21.Krause J., Ruxton G. D. 2002. Living in groups. Oxford, UK: Oxford University Press [Google Scholar]
- 22.Pitcher T. J. 1993. Behaviour of teleost fishes. London, UK: Chapman & Hall [Google Scholar]
- 23.Grünbaum D. 1998. Schooling as a strategy for taxis in a noisy environment. Evol. Ecol. 12, 503–522 10.1023/A:1006574607845 (doi:10.1023/A:1006574607845) [DOI] [Google Scholar]
- 24.Neill S. R. J., St, Cullen J. M. 1974. Experiments on whether schooling by their prey affects the hunting behaviour of cephalopods and fish predators. J. Zool. 172, 549–569 10.1111/j.1469-7998.1974.tb04385.x (doi:10.1111/j.1469-7998.1974.tb04385.x) [DOI] [Google Scholar]
- 25.Treherne J. E., Foster W. A. 1981. Group transmission of predator avoidance behaviour in a marine insect: the Trafalgar effect. Anim. Behav. 29, 911–917 10.1016/S0003-3472(81)80028-0 (doi:10.1016/S0003-3472(81)80028-0) [DOI] [Google Scholar]
- 26.Turner G. F., Pitcher T. J. 1986. Attack abatement: a model for group protection by combined avoidance and dilution. Am. Nat. 128, 228–240 10.1086/284556 (doi:10.1086/284556) [DOI] [Google Scholar]
- 27.Wrona F. J., Jamieson Dixon R. W. 1991. Group size and predation risk: a field analysis of encounter and dilution effects. Am. Nat. 137, 186–201 10.1086/285153 (doi:10.1086/285153) [DOI] [Google Scholar]
- 28.Pitcher T. J., Wyche C. J. 1983. Predator avoidance behaviour of sand-eel schools: why schools seldom split. In Predators and prey in fishes (eds D. L. G. Noakes, B. G. Linquist, G. S. Helfman & J. A. Ward), pp. 193–204. The Hague: Dr. W. Junk. [Google Scholar]
- 29.Krakauer D. C. 1995. Groups confuse predators by exploiting perceptual bottlenecks: a connectionist model of the confusion effect. Behav. Ecol. Sociobiol. 36, 421–429 10.1007/BF00177338 (doi:10.1007/BF00177338) [DOI] [Google Scholar]
- 30.Couzin I. D., Krause J. 2003. Self-organization and collective behavior in vertebrates. Adv. Stud. Behav. 32, 1–75 10.1016/S0065-3454(03)01001-5 (doi:10.1016/S0065-3454(03)01001-5) [DOI] [Google Scholar]
- 31.Powell G. V. N. 1974. Experimental analysis of the social value of flocking by starlings (Sturnus vulgaris) in relation to predation and foraging. Anim. Behav. 22, 501–505 10.1016/S0003-3472(74)80049-7 (doi:10.1016/S0003-3472(74)80049-7) [DOI] [Google Scholar]
- 32.Botham M. S., Kerfoot C. J., Louca V., Krause J. 2005. Predator choice in the field; grouping guppies, Poecilia reticulate, receive more attacks. Behav. Ecol. Sociobiol. 59, 181–184 10.1007/s00265-005-0018-7 (doi:10.1007/s00265-005-0018-7) [DOI] [Google Scholar]
- 33.Ioannou C. C., Krause J. 2007. Searching for prey: the effects of group size and number. Anim. Behav. 75, 1383–1388 10.1016/j.anbehav.2007.09.012 (doi:10.1016/j.anbehav.2007.09.012) [DOI] [Google Scholar]
- 34.Weihs D. 1973. Hydromechanics of fish schooling. Nature 241, 290–291 10.1038/241290a0 (doi:10.1038/241290a0) [DOI] [Google Scholar]
- 35.Herskin J., Steffensen J. F. 1998. Energy savings in sea bass swimming in a school: measurements of tail beat frequency and oxygen consumption at different swimming speeds. J. Fish. Biol. 53, 366–376 10.1111/j.1095-8649.1998.tb00986.x (doi:10.1111/j.1095-8649.1998.tb00986.x) [DOI] [Google Scholar]
- 36.Svendsen J. C., Vendsen J. S., Bildsoe M., Steffensen J. F. 2003. Intra-school positional preference and reduced tail beat frequency in trailing positions in schooling roach under experimental conditions. J. Fish. Biol. 62, 834–846 10.1046/j.1095-8649.2003.00068.x (doi:10.1046/j.1095-8649.2003.00068.x) [DOI] [Google Scholar]
- 37.Hanke W., Lauder G. V. 2006. Fish schooling: 3D kinematics and hydrodynamics. Integr. Comp. Biol. 46(Suppl. 1), E54 [Google Scholar]
- 38.Weitz S., Blanco S., Fournier R., Gautrais J., Jost C., Theraulaz G. 2012. Modelling collective animal behavior with a cognitive perspective: a methodological framework. PLoS ONE 7, e38588. 10.1371/journal.pone.0038588 (doi:10.1371/journal.pone.0038588) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Eriksson A., Nilsson Jacobi M., Nystrom J., Tunstrom K. 2010. Determining interaction rules in animal swarms. Behav. Ecol. 21, 1106–1111 10.1093/beheco/arq118 (doi:10.1093/beheco/arq118) [DOI] [Google Scholar]
- 40.Gautrais J., Ginelli F., Fournier R., Blanco S., Soria M., Chaté H., Theraulaz G. 2012. Deciphering interactions in moving animal groups. PLoS Comput. Biol. 8, e1002678. 10.1371/journal.pcbi.1002678 (doi:10.1371/journal.pcbi.1002678) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Katz Y., Tunstrom K., Ioannou C. C., Huepe C., Couzin I. D. 2011. Inferring the structure and dynamics of interactions in schooling fish. Proc. Natl Acad. Sci. USA 108, 18 720–18 725 10.1073/pnas.1107583108 (doi:10.1073/pnas.1107583108) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Herbert-Read J. E., Perna A., Mann R. P., Schaerf T. M., Sumpter D. J. T., Ward A. J. W. 2011. Inferring the rules of interaction of shoaling fish. Proc. Natl Acad. Sci. USA 108, 18 726–18 731 10.1073/pnas.1109355108 (doi:10.1073/pnas.1109355108) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Parrish J. K., Viscido S. V., Grünbaum D. 2002. Self-organized fish schools: an examination of emergent properties. Biol. Bull. 202, 296–305 10.2307/1543482 (doi:10.2307/1543482) [DOI] [PubMed] [Google Scholar]
- 44.Aoki I. 1982. A simulation study on the schooling mechanism in fish. Bull. J. Soc. Sci. Fish 48, 1081–1088 10.2331/suisan.48.1081 (doi:10.2331/suisan.48.1081) [DOI] [Google Scholar]
- 45.Aoki I. 1984. Internal dynamics of fish schools in relation to inter-fish distance. Bull. J. Soc. Sci. Fish 50, 751–758 10.2331/suisan.50.751 (doi:10.2331/suisan.50.751) [DOI] [Google Scholar]
- 46.Okubo A. 1986. Dynamical aspects of animal grouping: swarms, schools, flocks, and herds. Adv. Biophys. 22, 1–94 10.1016/0065-227X(86)90003-1 (doi:10.1016/0065-227X(86)90003-1) [DOI] [PubMed] [Google Scholar]
- 47.Huth A., Wissel C. 1992. The simulation of the movement of fish schools. J. Theor. Biol. 156, 365–385 10.1016/S0022-5193(05)80681-2 (doi:10.1016/S0022-5193(05)80681-2) [DOI] [Google Scholar]
- 48.Huth A., Wissel C. 1994. The simulation of fish schools in comparison with experimental data. Ecol. Model. 75–76, 135–146 10.1016/0304-3800(94)90013-2 (doi:10.1016/0304-3800(94)90013-2) [DOI] [Google Scholar]
- 49.Reynolds C. W. 1987. Flocks, herds, and schools: a distributed behavioral model. Comput. Graph 21, 25–35 10.1145/37402.37406 (doi:10.1145/37402.37406) [DOI] [Google Scholar]
- 50.Gautrais J., Jost C., Theraulaz G. 2008. Key behavioural factors in a self-organised fish school model. Ann. Zool. Fennici 45, 415–428 [Google Scholar]
- 51.Viscido S., Parrish J., Grünbaum D. 2004. Individual behavior and emergent properties of fish schools: a comparison of observation and theory. Mar. Ecol. Prog. Ser. 273, 239–249 10.3354/meps273239 (doi:10.3354/meps273239) [DOI] [Google Scholar]
- 52.Gueron S., Levin S. A., Rubenstein D. I. 1996. The dynamics of herds: from individuals to aggregations. J. Theor. Biol. 182, 85–98 10.1006/jtbi.1996.0144 (doi:10.1006/jtbi.1996.0144) [DOI] [Google Scholar]
- 53.Deneubourg J. L., Goss S. 1989. Collective patterns and decision-making. Ethol. Ecol. Evol. 1, 295–311 10.1080/08927014.1989.9525500 (doi:10.1080/08927014.1989.9525500) [DOI] [Google Scholar]
- 54.Strömbom D. 2011. Collective motion from local attraction. J. Theor. Biol. 283, 145–151 10.1016/j.jtbi.2011.05.019 (doi:10.1016/j.jtbi.2011.05.019) [DOI] [PubMed] [Google Scholar]
- 55.Romanczuk P., Couzin I. D., Schimansky-Geier L. 2009. Collective motion due to individual escape and pursuit response. Phys. Rev. Lett. 102, 010602. 10.1103/PhysRevLett.102.010602 (doi:10.1103/PhysRevLett.102.010602) [DOI] [PubMed] [Google Scholar]
- 56.D'Orsogna M. R., Chuang Y. L., Bertozzi A. L., Chayes L. S. 2006. Self-propelled particles with soft-core interactions: patterns, stability, and collapse. Phys. Rev. Lett. 96, 104302. 10.1103/PhysRevLett.96.104302 (doi:10.1103/PhysRevLett.96.104302) [DOI] [PubMed] [Google Scholar]
- 57.Sfakiotakis M., Lane D. M., Davies J. B. C. 1999. Review of fish swimming modes for aquatic locomotion. IEEE J. Oceanic Eng. 24, 237–252 10.1109/48.757275 (doi:10.1109/48.757275) [DOI] [Google Scholar]
- 58.Flierl G., Grünbaum D., Levin S. A., Olson D. 1999. From individuals to aggregations: the interplay between behavior and physics. J. Theor. Biol. 196, 397–454 10.1006/jtbi.1998.0842 (doi:10.1006/jtbi.1998.0842) [DOI] [PubMed] [Google Scholar]
- 59.Aoki I. 1980. An analysis of the schooling behavior of fish: internal organization and communication process. Bull. Ocean Res. Inst. 12, 1–65 [Google Scholar]
- 60.Vicsek T., Czirók A., Ben-Jacob E., Cohen I., Shochet O. 1995. Novel type of phase transition in a system of self-driven particles. Phys. Rev. Lett. 75, 1226–1229 10.1103/PhysRevLett.75.1226 (doi:10.1103/PhysRevLett.75.1226) [DOI] [PubMed] [Google Scholar]
- 61.Niwa H. S. 1994. Self-organizing dynamic model of fish schooling. J. Theor. Biol. 171, 123–136 10.1006/jtbi.1994.1218 (doi:10.1006/jtbi.1994.1218) [DOI] [Google Scholar]
- 62.Couzin I. D., Krause J., James R., Ruxton G. D., Franks N. R. 2002. Collective memory and spatial sorting in animal groups. J. Theor. Biol. 218, 1–11 10.1006/jtbi.2002.3065 (doi:10.1006/jtbi.2002.3065) [DOI] [PubMed] [Google Scholar]
- 63.Warburton K., Lazarus J. 1991. Tendency-distance models of social cohesion in animal groups. J. Theor. Biol. 150, 473–488 10.1016/S0022-5193(05)80441-2 (doi:10.1016/S0022-5193(05)80441-2) [DOI] [PubMed] [Google Scholar]
- 64.Grégoire G., Chaté H., Tu Y. 2003. Moving and staying together without a leader. Physica D Nonlinear Phenomena 181, 157–170 10.1016/S0167-2789(03)00102-7 (doi:10.1016/S0167-2789(03)00102-7) [DOI] [Google Scholar]
- 65.Newman J. P., Sayama H. 2008. Effect of sensory blind zones on milling behavior in a dynamic self-propelled particle model. Phys. Rev. E 78, 011913. 10.1103/PhysRevE.78.011913 (doi:10.1103/PhysRevE.78.011913) [DOI] [PubMed] [Google Scholar]
- 66.Kunz H., Hemelrijk C. K. 2003. Artificial fish schools: collective effects of school size, body size, and body form. Artif. Life 9, 237–253 10.1162/106454603322392451 (doi:10.1162/106454603322392451) [DOI] [PubMed] [Google Scholar]
- 67.Chaté H., Ginelli F., Raynaud F. 2008. Collective motion of self-propelled particles interacting without cohesion. Phys. Rev. E 77, 046113. 10.1103/PhysRevE.77.046113 (doi:10.1103/PhysRevE.77.046113) [DOI] [PubMed] [Google Scholar]
- 68.Ballerini M., et al. 2008. Interaction ruling animal collective behavior depends on topological rather than metric distance: evidence from a field study. Proc. Natl Acad. Sci. USA 105, 1232–1237 10.1073/pnas.0711437105 (doi:10.1073/pnas.0711437105) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Viscido S. V., Parrish J. K., Grünbaum D. 2005. The effect of population size and number of influential neighbors on the emergent properties of fish schools. Ecol. Model. 183, 347–363 10.1016/j.ecolmodel.2004.08.019 (doi:10.1016/j.ecolmodel.2004.08.019) [DOI] [Google Scholar]
- 70.Ginelli F., Chaté H. 2010. Relevance of metric-free interactions in flocking phenomena. Phys. Rev. Lett. 105, 168103. 10.1103/PhysRevLett.105.168103 (doi:10.1103/PhysRevLett.105.168103) [DOI] [PubMed] [Google Scholar]
- 71.Hamilton W. D. 1971. Geometry for the selfish herd. J. Theor. Biol. 31, 295–311 10.1016/0022-5193(71)90189-5 (doi:10.1016/0022-5193(71)90189-5) [DOI] [PubMed] [Google Scholar]
- 72.Viscido S. V., Miller M., Wethey D. S. 2002. The dilemma of the selfish herd: the search for a realistic movement rule. J. Theor. Biol. 217, 183–194 10.1006/jtbi.2002.3025 (doi:10.1006/jtbi.2002.3025) [DOI] [PubMed] [Google Scholar]
- 73.Lemasson B. H., Anderson J. J., Goodwin R. A. 2009. Collective motion in animal groups from a neurobiological perspective: the adaptive benefits of dynamic sensory loads and selective attention. J. Theor. Biol. 261, 501–510 10.1016/j.jtbi.2009.08.013 (doi:10.1016/j.jtbi.2009.08.013) [DOI] [PubMed] [Google Scholar]
- 74.Viscido S. V., Parrish J. K., Grünbaum D. 2007. Factors influencing the structure and maintenance of fish schools. Ecol. Model. 206, 153–165 10.1016/j.ecolmodel.2007.03.042 (doi:10.1016/j.ecolmodel.2007.03.042) [DOI] [Google Scholar]
- 75.Parrish J. K., Hamner W. M. 1997. Animal groups in three dimensions. Cambridge, UK: Cambridge University Press [Google Scholar]
- 76.Mirabet V., Auger P., Lett C. 2007. Spatial structures in simulations of animal grouping. Ecol. Model. 201, 468–476 10.1016/j.ecolmodel.2006.10.018 (doi:10.1016/j.ecolmodel.2006.10.018) [DOI] [Google Scholar]
- 77.Sumpter D. J. T. 2006. The principles of collective animal behaviour. Phil. Trans. R. Soc. B 361, 5–22 10.1098/rstb.2005.1733 (doi:10.1098/rstb.2005.1733) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 78.Ward A. J., Herbert-Read J. E., Sumpter D. J. T., Krause J. 2011. Fast and accurate decisions through collective vigilance in fish shoals. Proc. Natl Acad. Sci. USA 108, 2312–2315 10.1073/pnas.1007102108 (doi:10.1073/pnas.1007102108) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 79.Yates C. A., Erbana R., Escuderoc C., Couzind I. D., Buhle J., Kevrekidisf I. G., Mainia P. K., Sumpter D. J. T. 2009. Inherent noise can facilitate coherence in collective swarm motion. Proc. Natl Acad. Sci. USA 106, 5464–5469 10.1073/pnas.0811195106 (doi:10.1073/pnas.0811195106) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 80.Bode N. W., Faria J. J., Franks D. W., Krause J., Wood A. J. 2010. How perceived threat increases synchronization in collectively moving animal groups. Proc. R. Soc. B 277, 3065–3070 10.1098/rspb.2010.0855 (doi:10.1098/rspb.2010.0855) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 81.Bode N. W., Franks D. W., Wood A. J. 2011. Limited interactions in flocks: relating model simulations to empirical data. J. R. Soc. Interface 8, 301–304 10.1098/rsif.2010.0397 (doi:10.1098/rsif.2010.0397) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 82.Lukeman R., Li Y.-X., Edelstein-Keshet L. 2010. Inferring individual rules from collective behavior. Proc. Natl Acad. Sci. USA 107, 12 576–12 580 10.1073/pnas.1001763107 (doi:10.1073/pnas.1001763107) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 83.Hoare D. J., Couzin I. D., Godin J. G. J., Krause J. 2004. Context-dependent group size choice in fish. Anim. Behav. 67, 155–164 10.1016/j.anbehav.2003.04.004 (doi:10.1016/j.anbehav.2003.04.004) [DOI] [Google Scholar]
- 84.Niwa H. S. 1996. Newtonian dynamical approach to fish schooling. J. Theor. Biol. 181, 47–63 10.1006/jtbi.1996.0114 (doi:10.1006/jtbi.1996.0114) [DOI] [Google Scholar]
- 85.Giardina I. 2008. Collective behavior in animal groups: theoretical models and empirical studies. HFSP J. 2, 205–219 10.2976/1.2961038 (doi:10.2976/1.2961038) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 86.Vicsek T., Zafeiris A. 2012. Collective motion. Phys. Rep. 517, 71–140 10.1016/j.physrep.2012.03.004 (doi:10.1016/j.physrep.2012.03.004) [DOI] [Google Scholar]
- 87.Grégoire G., Chaté H. 2004. Onset of collective and cohesive motion. Phys. Rev. Lett. 92, 025702. 10.1103/PhysRevLett.92.025702 (doi:10.1103/PhysRevLett.92.025702) [DOI] [PubMed] [Google Scholar]
- 88.Toner J., Tu Y. 1998. Flocks, herds, and schools: a quantitative theory of flocking. Phys. Rev. E 58, 4828–4859 10.1103/PhysRevE.58.4828 (doi:10.1103/PhysRevE.58.4828) [DOI] [Google Scholar]
- 89.Bertin E., Droz M., Gregoire G. 2003. Boltzmann and hydrodynamic description for self-propelled particles. Phys. Rev. E 74, 022101. 10.1103/PhysRevE.74.022101 (doi:10.1103/PhysRevE.74.022101) [DOI] [PubMed] [Google Scholar]
- 90.Czirok A., Stanley H. E., Vicsek T. 1997. Spontaneously ordered motion of self-propelled particles. J. Phys. A 30, 1375–1385 10.1088/0305-4470/30/5/009 (doi:10.1088/0305-4470/30/5/009) [DOI] [Google Scholar]
- 91.Mishra S., Tunstrom K., Couzin I. D., Huepe C. 2012. Collective dynamics of self-propelled particles with variable speed. Phys. Rev. E 86, 011901. 10.1103/PhysRevE.86.011901 (doi:10.1103/PhysRevE.86.011901) [DOI] [PubMed] [Google Scholar]
- 92.Szabo P., Nagy M., Vicsek M. 2008. Turning with the others: novel transitions in an SPP model with coupling of accelerations. Phys. Rev. E 79, 021908. 10.1103/PhysRevE.79.021908 (doi:10.1103/PhysRevE.79.021908) [DOI] [PubMed] [Google Scholar]
- 93.Becco Ch., Vanderwalle N., Delcourt J., Poncin P. 2006. Experimental evidences of a structural and dynamical transition in fish school. Physica A 367, 487–493 10.1016/j.physa.2005.11.041 (doi:10.1016/j.physa.2005.11.041) [DOI] [Google Scholar]
- 94.Sumpter D. J. T., Buhl J., Biro D., Couzin I. D. 2008. Information transfer in moving animal groups. Theory Biosci. 127, 177–186 10.1007/s12064-008-0040-1 (doi:10.1007/s12064-008-0040-1) [DOI] [PubMed] [Google Scholar]
- 95.Couzin I. D., Krause J., Franks N. R., Levin S. A. 2005. Effective leadership and decision-making in animal groups on the move. Nature 433, 513–516 10.1038/nature03236 (doi:10.1038/nature03236) [DOI] [PubMed] [Google Scholar]
- 96.Degond P., Motsch S. 2008. Large scale dynamics of the persistent turning walker model of fish behavior. J. Stat. Phys. 131, 989–1021 10.1007/s10955-008-9529-8 (doi:10.1007/s10955-008-9529-8) [DOI] [Google Scholar]
- 97.Jeanson R., Blanco S., Fournier R., Deneubourg J. L., Fourcassie V., Theraulaz G. 2003. A model of animal movements in a bounded space. J. Theor. Biol. 225, 443–451 10.1016/S0022-5193(03)00277-7 (doi:10.1016/S0022-5193(03)00277-7) [DOI] [PubMed] [Google Scholar]
- 98.Jeanson R., Rivault C., Deneubourg J. L., Blanco S., Fournier R., Jost C., Theraulaz G. 2005. Self-organized aggregation in cockroaches. Anim. Behav. 69, 169–180 10.1016/j.anbehav.2004.02.009 (doi:10.1016/j.anbehav.2004.02.009) [DOI] [Google Scholar]
- 99.Theraulaz G., et al. 2002. Spatial patterns in ant colonies. Proc. Natl Acad. Sci. USA 99, 9645–9649 10.1073/pnas.152302199 (doi:10.1073/pnas.152302199) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 100.Gautrais J., Jost C., Soria M., Campo A., Motsch S., Fournier R., Blanco S., Theraulaz G. 2009. Analyzing fish movement as a persistent turning walker. J. Math. Biol. 58, 429–445 10.1007/s00285-008-0198-7 (doi:10.1007/s00285-008-0198-7) [DOI] [PubMed] [Google Scholar]
- 101.Hemmings C. C. 1966. Olfaction and vision in fish schooling. J. Exp. Biol. 45, 449–464 [Google Scholar]
- 102.Pitcher T. J., Partridge B. L., Wardle C. S. 1976. A blind fish can school. Science 194, 963–965 10.1126/science.982056 (doi:10.1126/science.982056) [DOI] [PubMed] [Google Scholar]
- 103.Faucher K., Parmentier E., Becco C., Vandewalle N., Vandewalle P. 2010. Fish lateral system is required for accurate control of shoaling behaviour. Anim. Behav. 79, 679–687 10.1016/j.anbehav.2009.12.020 (doi:10.1016/j.anbehav.2009.12.020) [DOI] [Google Scholar]
- 104.von der Emde G., Mogdans J., Kapoor B. G. 2004. The senses of fish: adaptations for the reception of natural stimuli. Boston, MA: Kluwer [Google Scholar]
- 105.Partridge B. L., Pitcher T. J. 1980. The sensory basis of fish schools: relative roles of lateral line and vision. J. Comp. Physiol. A 135, 315–325 10.1007/BF00657647 (doi:10.1007/BF00657647) [DOI] [Google Scholar]
- 106.Moussaïd M., Helbing D., Theraulaz G. 2011. How simple rules determine pedestrian behavior and crowd disasters. Proc. Natl Acad. Sci. USA 108, 6884–6888 10.1073/pnas.1016507108 (doi:10.1073/pnas.1016507108) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 107.Kramer D. L., McLaughlin R. L. 2001. The behavioral ecology of intermittent locomotion. Am. Zool. 41, 137–153 10.1668/0003-1569(2001)041[0137:TBEOIL]2.0.CO;2 (doi:10.1668/0003-1569(2001)041[0137:TBEOIL]2.0.CO;2) [DOI] [Google Scholar]
- 108.Feitl K. E., Ngo V., McHenry M. J. 2010. Are fish less responsive to a flow stimulus when swimming?. J. Exp. Biol. 213, 3131–3137 10.1242/jeb.045518 (doi:10.1242/jeb.045518) [DOI] [PubMed] [Google Scholar]
- 109.Cavagna A., Giardina I., Orlandi A., Parisi G., Procaccini A., Viale M., Zdravkovic V. 2008. The STARFLAG handbook on collective animal behaviour. I. Empirical methods. Anim. Behav. 76, 217–236 10.1016/j.anbehav.2008.02.002 (doi:10.1016/j.anbehav.2008.02.002) [DOI] [Google Scholar]
- 110.Cavagna A., Giardina I., Orlandi A., Parisi G., Procaccini A. 2008. The STARFLAG handbook on collective animal behaviour. II. Three-dimensional analysis. Anim. Behav. 76, 237–248 10.1016/j.anbehav.2008.02.003 (doi:10.1016/j.anbehav.2008.02.003) [DOI] [Google Scholar]
- 111.Mann R. P. 2011. Bayesian inference for identifying interaction rules in moving animal groups. PLoS ONE 6, e22827. 10.1371/journal.pone.0022827 (doi:10.1371/journal.pone.0022827) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 112.Grünbaum D., Viscido S., Parrish J. K. 2005. Extracting interactive control algorithms from group dynamics of schooling fish. Lect. Notes Control Inf. 309, 103–117 [Google Scholar]
- 113.Tien J. H., Levin S. A., Rubenstein D. I. 2004. Dynamics of fish shoals: identifying key decision rules. Evol. Ecol. Res. 6, 555–565 [Google Scholar]
- 114.Miller N., Gerlai R. 2007. Quantification of shoaling behaviour in zebrafish (Danio rerio). Behav. Brain Res. 184, 157–166 10.1016/j.bbr.2007.07.007 (doi:10.1016/j.bbr.2007.07.007) [DOI] [PubMed] [Google Scholar]