Gametic phase disequilibrium, often referred to as linkage disequilibrium (LD), describes the non-independence of alleles at different loci on the same chromosome. There are various measures of LD proposed in the literature (Hedrick, 1987; Devlin and Risch, 1995) for the purposes of inferring population evolutionary history and mapping genes (Slatkin, 2008). In a recent paper in this journal, Mangin et al. (2012) proposed a new LD measure 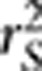 aiming to correct the bias due to population structure by taking into account of the population structure matrix. In this letter, we point out that
aiming to correct the bias due to population structure by taking into account of the population structure matrix. In this letter, we point out that 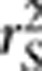 is essentially the square of the partial correlation coefficient between two loci given the population structure, which was not explicitly explained in the paper. We also distinguish between the partial correlation and the conditional correlation, as the latter was ambiguously used in the paper. We further extend the result on the relationship between
is essentially the square of the partial correlation coefficient between two loci given the population structure, which was not explicitly explained in the paper. We also distinguish between the partial correlation and the conditional correlation, as the latter was ambiguously used in the paper. We further extend the result on the relationship between 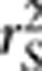 and power of association tests to generalized linear models and discuss the potential use of
and power of association tests to generalized linear models and discuss the potential use of 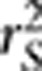 in human genetic mapping.
in human genetic mapping.
A natural way to measure LD is by the correlation coefficient. Consider two diallelic loci A and B, with alleles A1 and A2 at locus A and alleles B1 and B2 at locus B. Denote by pi, where i∈{A1, A2, B1, B2}, allele frequencies, and by pj, where j∈{A1B1, A1B2, A2B1, A2B2}, haplotype frequencies. The widely used LD measure 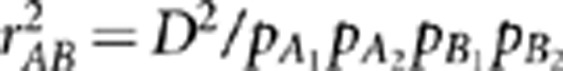 , where
, where 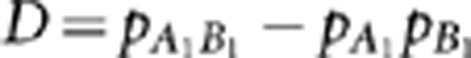 , is the square of Pearson's correlation coefficient that measures the linear dependence between the two loci (Hill and Robertson, 1968). Suppose in a sample there exists population structure that can distort the correlation between the two loci. One way to measure LD controlling for confounding effects is by the partial correlation coefficient. Denote by YA and YB the random variables of genotypes at loci A and B, respectively, and by S a vector of variables on the population structure. Regress YA and YB on S by the linear regression models YA=SβA+ɛA and YB=SβB+ɛB, respectively, where βA and βB are regression coefficients, and ɛA and ɛB are residuals. The partial correlation rAB.S between YA and YB controlling for S is then defined as Pearson's correlation between the residual variables ɛA and ɛB (Yule, 1907). Alternatively, the partial correlation rAB.S can be calculated as a negative off-diagonal element of the inverse correlation matrix (Whittaker, 1990), which is exactly the square root of formula (1) in Mangin et al. (2012). Therefore, the new LD measure they proposed is the square of the partial correlation coefficient—
, is the square of Pearson's correlation coefficient that measures the linear dependence between the two loci (Hill and Robertson, 1968). Suppose in a sample there exists population structure that can distort the correlation between the two loci. One way to measure LD controlling for confounding effects is by the partial correlation coefficient. Denote by YA and YB the random variables of genotypes at loci A and B, respectively, and by S a vector of variables on the population structure. Regress YA and YB on S by the linear regression models YA=SβA+ɛA and YB=SβB+ɛB, respectively, where βA and βB are regression coefficients, and ɛA and ɛB are residuals. The partial correlation rAB.S between YA and YB controlling for S is then defined as Pearson's correlation between the residual variables ɛA and ɛB (Yule, 1907). Alternatively, the partial correlation rAB.S can be calculated as a negative off-diagonal element of the inverse correlation matrix (Whittaker, 1990), which is exactly the square root of formula (1) in Mangin et al. (2012). Therefore, the new LD measure they proposed is the square of the partial correlation coefficient—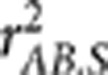 —between two loci controlling for the population structure, which is a direct extension of the original measure
—between two loci controlling for the population structure, which is a direct extension of the original measure 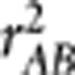 that is used in the absence of population stratification.
that is used in the absence of population stratification.
As the formula of partial covariance was referred to as the one for ‘conditional covariance' in the paper (p 286), it is worth pointing out that these two are equivalent only in special situations, such as when variables follow a multivariate normal distribution. The partial correlation rAB.S in general is not equal to the conditional correlation rAB|S. The former by definition is independent of S, whereas the latter is not necessarily free of S. Even if rAB|S is free of S, there exists the inequality 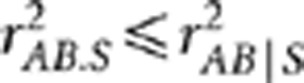 , where the equality holds when both the conditional variances and covariance of YA and YB given S are free of S (Lawrance, 1976). Below we performed a simulation study to show their subtle difference in case of rAB|S being independent of S. Simulation settings I, III and V mimicked those by Mangin et al. (2012) (Table 1), except for replacing
, where the equality holds when both the conditional variances and covariance of YA and YB given S are free of S (Lawrance, 1976). Below we performed a simulation study to show their subtle difference in case of rAB|S being independent of S. Simulation settings I, III and V mimicked those by Mangin et al. (2012) (Table 1), except for replacing 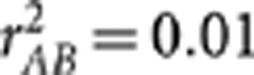 by 0.1; in settings II, IV and VI, the allele frequencies in the second population were also changed. In these six settings, the two loci were in the same degree of LD in the two populations but with different minor allele frequencies. In each population 1000 haplotypes were simulated and randomly assigned into 500 pairs. The genotypes were then scored in an additive fashion. The crude sample correlation coefficient
by 0.1; in settings II, IV and VI, the allele frequencies in the second population were also changed. In these six settings, the two loci were in the same degree of LD in the two populations but with different minor allele frequencies. In each population 1000 haplotypes were simulated and randomly assigned into 500 pairs. The genotypes were then scored in an additive fashion. The crude sample correlation coefficient 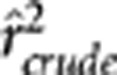 , the partial correlation coefficient
, the partial correlation coefficient 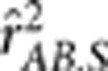 and the conditional correlation coefficient
and the conditional correlation coefficient 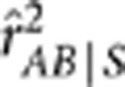 were estimated based on the genotypic scores. Ten thousand replicates were simulated, and the mean and standard error of the estimates were recorded in Table 1. In all settings,
were estimated based on the genotypic scores. Ten thousand replicates were simulated, and the mean and standard error of the estimates were recorded in Table 1. In all settings, 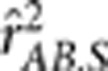 was smaller than
was smaller than 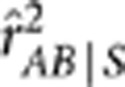 , but the difference between them was small. Theoretically, in settings I, III and V they should be equal because the minor allele and the major allele at each diallelic locus were simply flipped between the two populations, and thus both the conditional variances and covariance of YA and YB given S are free of S; the small differences (∼10−4) were due to sampling errors. In settings II, IV and VI, the differences between them (∼10−3) were one order of magnitude greater than that in settings I, III and V.
, but the difference between them was small. Theoretically, in settings I, III and V they should be equal because the minor allele and the major allele at each diallelic locus were simply flipped between the two populations, and thus both the conditional variances and covariance of YA and YB given S are free of S; the small differences (∼10−4) were due to sampling errors. In settings II, IV and VI, the differences between them (∼10−3) were one order of magnitude greater than that in settings I, III and V.
Table 1. Mean (and its s.e.a) of correlation coefficient estimates of a mixture of two populationsb.
| I | II | III | IV | V | VI | |
|---|---|---|---|---|---|---|
| Population 1 | ||||||
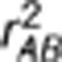
|
0.10 | 0.10 | 0.25 | 0.25 | 0.50 | 0.50 |
| pA1 | 0.90 | 0.90 | 0.90 | 0.80 | 0.90 | 0.70 |
| pB1 | 0.90 | 0.55 | 0.90 | 0.55 | 0.90 | 0.55 |
| Population 2 | ||||||
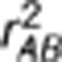
|
0.10 | 0.10 | 0.25 | 0.25 | 0.50 | 0.50 |
| pA1 | 0.10 | 0.70 | 0.10 | 0.65 | 0.10 | 0.60 |
| pB1 | 0.10 | 0.70 | 0.10 | 0.65 | 0.10 | 0.60 |
| Mixed Population | ||||||
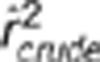
|
0.7227 (0.0188) | 0.0438 (0.0131) | 0.7925 (0.0160) | 0.1980 (0.0247) | 0.8757 (0.0125) | 0.4716 (0.0281) |
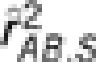
|
0.1012 (0.0247) | 0.0969 (0.0177) | 0.2508 (0.0366) | 0.2484 (0.0251) | 0.5007 (0.0412) | 0.4995 (0.0265) |
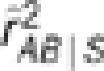
|
0.1014 (0.0247) | 0.1030 (0.0186) | 0.2511 (0.0366) | 0.2515 (0.0253) | 0.5011 (0.0412) | 0.5005 (0.0264) |
Based on 10 000 replicates.
Five hundred diploid subjects from each population.
Measuring LD between loci by 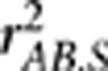 in the case of population stratification is in the same spirit as measuring correlation between covariate-adjusted phenotypes and genotypes in genetic association studies (Price et al., 2006; Xing et al., 2011). Suppose an allele at locus A is the causal variant for a trait. Mangin et al. (2012) derived in a linear regression setting that the power to detect association between the trait and locus A would be reduced by a factor of
in the case of population stratification is in the same spirit as measuring correlation between covariate-adjusted phenotypes and genotypes in genetic association studies (Price et al., 2006; Xing et al., 2011). Suppose an allele at locus A is the causal variant for a trait. Mangin et al. (2012) derived in a linear regression setting that the power to detect association between the trait and locus A would be reduced by a factor of 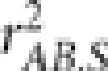 when locus B was examined instead. As a matter of fact, this conclusion holds in general when modeling phenotype–genotype association by a generalized linear model, as ɛB can be viewed as a surrogate variable for ɛA, and it is well known the asymptotic relative efficiency of a test using ɛB versus using ɛA equals the square of their correlation coefficient (Lagakos, 1988; Tosteson and Tsiatis, 1988).
when locus B was examined instead. As a matter of fact, this conclusion holds in general when modeling phenotype–genotype association by a generalized linear model, as ɛB can be viewed as a surrogate variable for ɛA, and it is well known the asymptotic relative efficiency of a test using ɛB versus using ɛA equals the square of their correlation coefficient (Lagakos, 1988; Tosteson and Tsiatis, 1988).
Characterizing LD structure is instructive in designing genetic association studies, which is a major goal of the International HapMap Consortium (2005) and the 1000 Genomes Project Consortium (2010). These projects focus on genetically homogeneous populations to document population-specific parameters. However, in reality, a study sample can be genetically heterogeneous with substructure even though the recruiting criterion requires a specific ethnic group. Imagine the diversity of African Americans in a metropolitan area. Considering that a lot of genome-wide association studies have been carried out, it will be valuable to use these available genome-wide genotypes to document ethnic- and geographic-specific 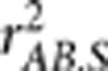 for the purpose of facilitating future genetic studies conducted in the same population.
for the purpose of facilitating future genetic studies conducted in the same population.
Finally, we also want to point out that the other LD measure 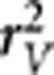 proposed by Mangin et al. (2012) for the purpose of correcting the bias due to relatedness is the square of the correlation coefficient of two loci modeled by a linear regression—the coefficient of determination—using generalized least squares given the kinship matrix instead of using ordinary least squares and assuming independence between subjects as when calculating the usual correlation coefficient.
proposed by Mangin et al. (2012) for the purpose of correcting the bias due to relatedness is the square of the correlation coefficient of two loci modeled by a linear regression—the coefficient of determination—using generalized least squares given the kinship matrix instead of using ordinary least squares and assuming independence between subjects as when calculating the usual correlation coefficient.
Acknowledgments
We thank Dr Robert Elston for critically reading, commenting and editing the paper. This study is supported by the American Heart Association Scientist Development Grant 10SDG4220051 to CX.
The authors declare no conflict of interest.
References
- 1000 Genomes Project Consortium A map of human genome variation from population-scale sequencing. Nature. 2010;467:1061–1073. doi: 10.1038/nature09534. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Devlin B, Risch N. A comparison of linkage disequilibrium measures for fine-scale mapping. Genomics. 1995;29:311–322. doi: 10.1006/geno.1995.9003. [DOI] [PubMed] [Google Scholar]
- Hedrick PW. Gametic disequilibrium measures: proceed with caution. Genetics. 1987;117:331–341. doi: 10.1093/genetics/117.2.331. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hill WG, Robertson A. Linkage disequilibrium in finite populations. Theor Appl Genet. 1968;38:226–231. doi: 10.1007/BF01245622. [DOI] [PubMed] [Google Scholar]
- International HapMap Consortium A haplotype map of the human genome. Nature. 2005;437:1299–1320. doi: 10.1038/nature04226. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lagakos SW. Effects of mismodelling and mismeasuring explanatory variables on tests of their association with a response variable. Stat Med. 1988;7:257–274. doi: 10.1002/sim.4780070126. [DOI] [PubMed] [Google Scholar]
- Lawrance AJ. On conditional and partial correlation. Am Stat. 1976;30:146–149. [Google Scholar]
- Mangin B, Siberchicot A, Nicolas S, Doligez A, This P, Cierco-Ayrolles C. Novel measures of linkage disequilibrium that correct the bias due to population structure and relatedness. Heredity. 2012;108:285–291. doi: 10.1038/hdy.2011.73. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Price AL, Patterson NJ, Plenge RM, Weinblatt ME, Shadick NA, Reich D. Principal components analysis corrects for stratification in genome-wide association studies. Nat Genet. 2006;38:904–909. doi: 10.1038/ng1847. [DOI] [PubMed] [Google Scholar]
- Slatkin M. Linkage disequilibrium--understanding the evolutionary past and mapping the medical future. Nat Rev Genet. 2008;9:477–485. doi: 10.1038/nrg2361. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tosteson TD, Tsiatis AA. The asymptotic relative efficiency of score tests in a generalized linear model with surrogate covariates. Biometrika. 1988;75:507–514. [Google Scholar]
- Whittaker J.1990Graphical Models in Applied Multivariate Statistics1st ednNew York John Wiley and Sons [Google Scholar]
- Xing G, Lin CY, Xing C. A comparison of approaches to control for confounding factors by regression models. Hum Hered. 2011;72:194–205. doi: 10.1159/000332743. [DOI] [PubMed] [Google Scholar]
- Yule GU. On the theory of correlation for any number of variables treated by a new system of notation. Proc Roy Soc A. 1907;79:182–193. [Google Scholar]


