The pollen dispersal kernel and mating system of an insect-pollinated tropical palm, Oenocarpus bataua

Abstract

Pollen dispersal shapes the local genetic structure of plant populations and determines the opportunity for local selection and genetic drift, but has been well studied in few animal-pollinated plants in tropical rainforests. Here, we characterise pollen movement for an insect-pollinated Neotropical canopy palm, Oenocarpus bataua, and relate these data to adult mating system and population genetic structure. The study covers a 130-ha parcel in which all adult trees (n=185) were mapped and genotyped at 12 microsatellite loci, allowing us to positively identify the source tree for 90% of pollination events (n=287 of 318 events). Mating system analysis showed O. bataua was effectively outcrossed (t_m=1.02) with little biparental inbreeding (t_m−t_s=−0.005) and an average of 5.4 effective pollen donors (N_ep) per female. Dispersal distances were relatively large for an insect-pollinated species (mean=303 m, max=1263 m), and far exceeded nearest-neighbour distances. Dispersal kernel modelling indicated a thin-tailed Weibull distribution offered the best fit to the genetic data, which contrasts with the fat-tailed kernels typically reported for pollen dispersal in trees. Preliminary analyses suggest that our findings may be explained, at least in part, by a relatively diffuse spatial and temporal distribution of flowering trees. Comparison with previously reported estimates of seed movement for O. bataua suggests that pollen and seed dispersal distances may be similar. These findings add to the growing body of information on dispersal in insect-pollinated trees, but underscore the need for continued research on tropical systems in general, and palms in particular.

Introduction

Pollination biology is a key determinant of short-term micro-evolutionary processes in plants. Pollen movement, along with seed dispersal, drives the distribution of genetic diversity in plant populations and is important for generating within- and between-population genetic structure. Wright (1943) recognised that restricted dispersal could lead to population sub-division as an outcome of restricted propagule movement, and introduced the concept of neighbourhood size (N_e) to describe the effective number of randomly mating individuals in a population area. Neighbourhood size has become a common metric of the scale and effectiveness of dispersal, and determining how pollination biology affects N_e is a fundamental goal in plant ecology and genetics (Crawford, 1984).

The average and maximum distances pollen travels between the pollen source and maternal tree are often used as an index of neighbourhood size by plant biologists (Levin and Kerster, 1971). The focus on distance per se in pollination biology can be related to the early observation that pollen dispersal kernels (that is, the probability density function of propagule dispersal distances from individual plants) typically follow a leptokurtic distribution, characterised by a very steep rate of decline near the origin with a long tail of relatively rare long-distance events (Levin and Kerster, 1974). This strongly leptokurtic pollen dispersal kernel, typical of wind-dispersed, temperate zone tree species such as pines and oaks (Oddou-Muratorio et al., 2005; Robledo-Arnuncio and Gil, 2005), is numerically dominated by short-distance pollination events involving near neighbours, which limits N_e. In such cases, longer distance dispersal events contribute disproportionately to mean neighbourhood size and the effective number of sires. As a consequence, researchers have placed heavy emphasis on the ‘tail' of leptokurtic distributions (whether fat- or thin-tailed) and hence on dispersal distance per se as a metric of N_e (Austerlitz et al., 2004).

As the number of studies on plant pollination has expanded, however, the extent to which this relationship between dispersal distance and N_e can be applied across systems has been questioned (Ashley, 2010). Indeed, there is a growing appreciation that the relationship between species' dispersal distance and number of sires, may vary considerably, which is likely to have important consequences for gene movement and, ultimately, the distribution of genetic diversity within and between plant populations (Loveless and Hamrick, 1984). For this reason, accurately characterising a broader diversity of pollen dispersal kernels and identifying the ecological factors, such as pollinator behaviour, wind patterns or flowering synchrony, that may underlie variation in kernel shapes is likely to advance our understanding of contemporary gene flow dynamics in plant systems.

Pollen flow in plants has now been examined in a range of species using a suite of approaches based on parent-offspring genotype data (reviewed in Austerlitz et al. (2004); Smouse and Sork (2004); Burczyk and Koralewski (2005)). By identifying and genotyping all potential pollen sources within a sufficiently large study area, direct paternity assignment can be used to categorically identify the male parent of individual seeds, and thus provides insight into how individual traits of contributing males or ecological context may affect the relationship between dispersal distance and N_e. Paternal diversity measures (probability of paternal identity, (PPI) Smouse and Robledo-Arnuncio, 2005) enable us to measure the degree of sharing of pollen donors amongst individual female trees and to estimate effective number of sires. Further, spatially-explicit mating models are available to infer the individual dispersal kernel, which provides important information on the shape of the dispersal tail (Burczyk et al., 2002; Oddou-Muratorio et al., 2005). The combination of these approaches provides a powerful lens with which to examine realised pollination dynamics, with the potential to address the ecological factors contributing to the relationship between dispersal distance and numbers of contributing males and, ultimately, N_e.

In the current study, we characterise effective pollen dispersal in an insect-pollinated neotropical canopy palm tree species, Oenocarpus bataua. Palms are an ecologically, taxonomically, economically and numerically important component of tropical forests around the globe (Henderson et al., 1995). They are a conspicuous food source for frugivorous vertebrates and consequently seed dispersal dynamics have received attention, yet surprisingly little is known about pollination dynamics in this group. Our specific objectives were to: (1) document the mating patterns of O. bataua; (2) use direct parentage to identify pollen sources and characterise the pollen dispersal kernel for O. bataua, including calculating the effective number of pollen sires contributing to seed crops; (3) assess patterns of fine-scale spatial and population genetic structure in light of these findings; and (4) to conduct preliminary analyses relating observed patterns of pollen movement to ecological correlates such as density or phenology. In doing so, our broader goal is to contribute to a much-needed and slowly growing body of work characterising pollen dispersal dynamics among insect-pollinated tropical trees in general, and palms in particular.

Materials and methods

Study species and location

The canopy palm O. bataua is widely distributed throughout Neotropical rainforest on both sides of the Andes cordillera in South America (Henderson et al., 1995). It is a long-lived, slow-growing monoecious species that produces inflorescences of thousands of small inconspicuous flowers. The species exhibits thermogenic nocturnal anthesis, and pollination is by several species of Coleoptera and bees, with no evidence for vertebrate or wind pollination (Nunez-Avellaneda and Rojas-Robles, 2008). Duration of anthesis is 28–32 days, beginning with a masculine phase (13–15 days; a single male flower is active 12–24 h and is estimated to contain>100 000 pollen grains), followed by a 7–9 day period of inactivity, and finally a female phase of 5–7 days (Nunez-Avellaneda and Rojas-Robles, 2008). This protandrous system of flower development is likely to favour cross-fertilisation in this species. Multiple inflorescences sometimes occur on the same individual, providing a potential mechanism for self-fertilisation, however, in these cases inflorescences have been asynchronous such that male and female flowers have not been observed on the same individual at the same time, even across multiple inflorescences (Nunez-Avellaneda and Rojas-Robles, 2008). Fertilised flowers develop large-seeded, lipid-rich fruits (up to 2000 fruits per infructesence) that are consumed by a range of large-bodied vertebrates, including primates and humans (Henderson et al., 1995). At the population level, the species exhibits a supra-annual pattern of reproduction, in that the majority of individuals synchronously reproduce at intervals of 2 or more years; however, at our study site there is always a small proportion of individuals in flower or fruit at any one point in time (J Karubian, unpublished data; see also Rojas-Robles and Stiles (2009)).

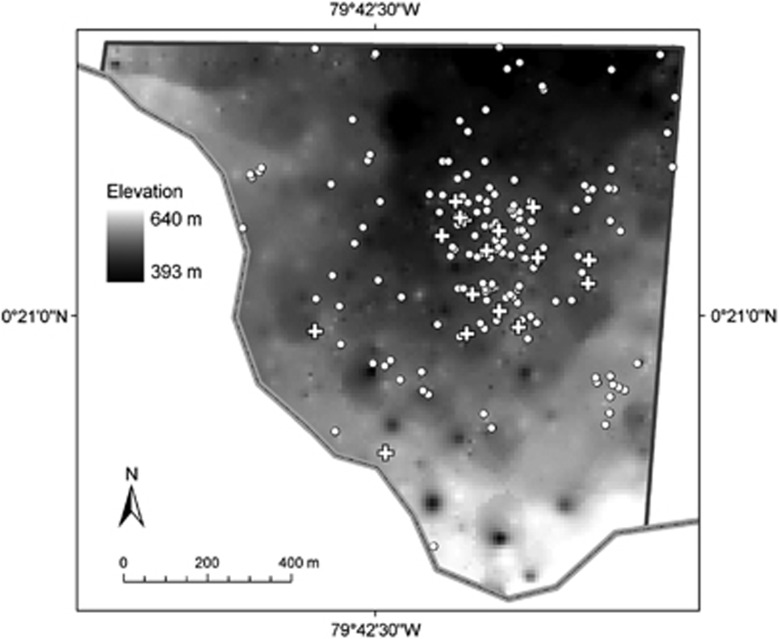
Our study was conducted at the Bilsa Biological Station (hereafter BBS; 79″45′W, 0″22′N; 330–730 m elevation), a 3500-ha reserve of humid Chocó rainforest in northwest Ecuador. We extended the 30 ha mapped parcel described in Karubian et al. (2010) to 130 ha for this study to better capture dispersal distances (Figure 1). This study plot was bounded on the eastern side by a ‘hard edge' of pasture and on the south-western side by the highest ridge in the area, which has a small dirt road running along it. Forest quality declines within ∼100 m of the road on both sides of the ridge, which may act as a barrier to dispersal to the Southwest, and the hard edge to the East may also act as a barrier to dispersal reducing the amount of long-distance pollen movement into the study area from these directions. The remainder of the study parcel contains a mix of selectively logged and primary contiguous forest, which extends beyond the parcel boundaries to the North and which presents no obvious boundaries to dispersal. All adult O. bataua trees (individuals which exhibited evidence of at least one reproductive event, as determined by remnant bracts where inflorescences had been present, n=188) within the study plot were identified and mapped using a GPS with ±7 m accuracy (Garmin, Atchison, KS, USA). Two GPS readings were taken and the mean coordinates were used to describe the location of adults.

Figure 1.

Elevational map of 130 ha study plot at Bilsa Biological Station, northwest Ecuador, showing location of all adult O. bataua trees (circles) and trees from which seeds were collected for pollen dispersal analysis in May 2008 (crosses).

Sample collection

Mature fruits were collected from infructesences of adult O. bataua individuals (n=16 adults) in BBS in May–June 2008 (Figure 1); these trees are referred to as ‘maternal' trees hereafter. We sampled all individuals with mature fruits during the field collection phase of the study within a 30-ha study area we had established at that time (see Karubian et al., 2010). Groups of seeds from maternal trees were maintained in separate bags and leaf tissue from each maternal tree was also collected to confirm the maternal genetic contribution to the seeds. Seeds were treated by removing the outer fleshy covering and placed into individual pots (labelled by maternal tree and fruit number) for germination in an outdoor nursery at BBS. The same soil mixture was used for all seeds, and germination success was high (98%). Leaf tissue was collected from the emergent seedlings (n=19–20 seedlings per adult), stored in paper envelopes and kept dry until DNA extraction. Either leaf, root or trunk material was collected from the remainder of candidate parents in the study plot.

Genetic analyses

Genomic DNA was extracted from seedling and adult leaf, root or trunk tissue using the Qiagen 96 Plant kit (Qiagen, Valencia, CA, USA) following the manufacturer's instructions. We amplified seedling (n=318) and adult DNA samples for 12 microsatellite loci identified by Montufar et al. (2007) (Table 1), with the exception of three adult trees for which we could not obtain useable DNA (n=185 of 188 adult trees genotyped). For the following loci we redesigned either the forward or reverse primers to enable multiplex pooling of PCR products: Ob10R (new): 5′-CAGCTTCCAAGATACCGAAT-3′ Ob11R (new): 5′-TAGTAGCATTTGCCGAACTG-3′ Ob12F (new): 5′-CTCTTCGACGTAAAACCATC-3′ Ob23R (new): 5′-GAGTCCCGTCATGGTAACTG-3′. In each case the matching F or R primer remained unchanged from that published by Montufar et al. (2007). DNA was amplified in two PCR multiplex reactions containing six loci each. Reactions were performed in 15 μl volumes using the Qiagen Multiplex PCR Kit (Qiagen) with 7.5 μl 2 × Multiplex PCR Mastermix, 1.5 μl 2 μℳ Primer Mix, 0.6 μl 10 × bovine serum albumin (BSA), dH₂O and 1.5 μl DNA. Polymerase chain reactions were performed on an Eppendorf ProS thermal cycler using cycling conditions outlined in the Qiagen Multiplex PCR Kit, with an annealing temperature of 55°C. The two PCR multiplexes were then pooled and run on an ABI 3100 capillary sequencer. Product sizes were scored relative to an internal size standard (LIZ500, Applied Biosystems, Foster City, CA, USA) using automated allele calling procedures in Genemapper (Applied Biosystems) software. Approximately 5% of samples were PCR amplified and genotyped twice to calculate genotyping error rates.

Table 1. Descriptive population genetic statistics calculated from adult O. bataua trees (n=185) at Bilsa Biological Station, Ecuador, genotyped at 12 microsatellite loci, and mean values of adults and offspring (n=357 progeny collected from 18 adults).

Locus	N	Na	Ne	Ho	He	F	PID	PEX	Errora (%)	HWE
Ob06	184	4	2.4	0.60	0.59	−0.031	0.232	0.175	0	NS
Ob07	185	7	4.7	0.84	0.79	−0.071	0.075	0.413	0	NS
Ob11	185	4	2.6	0.52	0.61	0.142	0.231	0.190	0	*
Ob12	182	9	1.8	0.47	0.44	−0.066	0.326	0.112	0	NS
Ob22	185	11	7.1	0.90	0.86	−0.051	0.034	0.563	2.08	NS
Ob23	184	6	1.8	0.42	0.43	0.012	0.365	0.096	0	NS
Ob03	185	8	4.7	0.79	0.79	0.000	0.071	0.423	0	NS
Ob10	184	7	5.3	0.84	0.81	−0.031	0.059	0.460	0	NS
Ob19	185	8	5.4	0.83	0.81	−0.016	0.058	0.463	0	NS
Ob04	185	5	2.2	0.58	0.54	−0.076	0.261	0.151	0	NS
Ob16	185	3	2.1	0.55	0.53	−0.022	0.274	0.143	2	NS
Ob02b	181	12	7.7	0.87	0.87	0.003	0.030	0.586	4.55	NS
Mean adults	184	6.5	3.6	0.67	0.66	−0.019	PIDC 2.8E−10	PEXC 0.983	0.72	NS
Mean offspring	318	6.6	3.5	0.67	0.66	−0.012	—	—	0.72	NS

Abbreviations: F, Inbreeding coefficient; H_e, expected heterozygosity; H_o, observed heterozygosity; HWE, Hardy–Weinberg equilibrium; N, no. of individuals genotyped; N_a, no. of alleles; N_e, no. of effective alleles; NS, non-significant; P_ID, probability of identity; P_EX, probability of parentage exclusion (one parent known); P_IDC, combined probability of identity, P_EXC, combined probability of parentage exclusion; Error, genotyping error rate (%); NS, *P<0.05).

^aError rates were calculated across the entire data set, including adults and offspring.

^bOb02 excluded from mean values.

Data analysis

Mating system analysis

Mating system parameters (multilocus outcrossing rate t_m, biparental inbreeding t_m−t_s, and correlated paternity r_p) were estimated from progeny arrays using a model of mixed mating as implemented in the software MLTR v3.2 (Ritland, 2002). Parameter estimates were calculated using known maternal parents and the Newton–Raphson estimation procedure implemented in MLTR (Ritland, 2002). Population allele frequencies were obtained from maternal trees and candidate parents from the study plot (n=185 genotyped adults). Parameter estimates were bootstrapped 1000 times, resampling from maternal families, to obtain standard errors. Mating system parameters were estimated for individual families (n=16 families) and at the population level.

Paternity analysis and PPI

We used the programme Cℰℛ𝒱𝒰𝒮 v 3.0.3 (Marshall et al., 1998) to categorically assign paternity to offspring from known maternal trees. As O. bataua is monoecious, it is possible for an individual to be both a seed donor and to contribute paternity to the offspring of other maternal trees. Parentage analysis was conducted on the 318 offspring from 16 maternal O. bataua trees within our plot with 185 candidate parents. Critical (Δ) values for parentage assignment were estimated using a simulation with the following conditions: 10 000 offspring genotypes, 185 candidate fathers, assuming 90% of candidate fathers were sampled and with a genotyping error rate of 0.01. To add an extra level of stringency, we manually checked our initial paternity assignments, and for assignments where two or more mismatches between parent and offspring genotypes were present (n=18), we checked adult and offspring genotypes and allowed the assignment if the called alleles were out by one repeat unit to allow for some allele binning error (n=14). Pollen dispersal distance was calculated for seeds based on the position of the maternal tree and putative pollen parent within the plot. The effective pollination neighbourhood area (A_ep) was calculated for each maternal tree from the variance of pollen flow distance (σ²), assuming a circular area around each maternal tree (A_ep=2πσ², Levin, 1988).

Also using the paternity assignments for individual maternal trees estimated above, we calculated the PPI following Smouse and Robledo-Arnuncio (2005). This approach involves calculation of two estimators: r_gg, which provides an estimate of the degree of pollen source overlap within a single maternal tree (and which can be converted to N_ep=1/r_gg, the number of effective sires) and r_ij, which estimates the overlap between pairs of maternal trees. We present mean and s.d. of values of r_gg and r_ij for the maternal trees included in the paternity analysis above. We quantified the genetic differentiation of pollen pools sampled by different females using T𝒲𝒪𝒢ℰ𝒩ℰℛ analysis in Gℰ𝒩AℒE𝒳 (Smouse and Sork, 2004; Peakall and Smouse, 2006) to estimate Φ_FT, which is analogous to estimating population differentiation using F_ST. Finally, using the observed patterns of paternity (number of sires and relative fertility) for each progeny array we used maximum-likelihood methods to estimate N_d, the minimum effective pollen donor pool size per female as calculated in Nason et al. (1996).

Pollen dispersal kernel

We estimated the pollen dispersal kernel (the probability of pollen travelling from its origin (0,0) to fertilise seed at position (x,y)) for O. bataua progeny arrays using the spatially-explicit Nℰℐ𝒢ℋℬ𝒪𝒰ℛℋ𝒪𝒪𝒟 model of Burczyk et al. (2002) implemented in the software NM+ (Chybicki and Burczyk, 2010). The Nℰℐ𝒢ℋℬ𝒪𝒰ℛℋ𝒪𝒪𝒟 model uses a maximum-likelihood fractional paternity assignment approach whereby for each sampled seed, paternity may result from (1) a paternal tree located outside the study plot due to pollen immigration (with probability m_p) or (2) by a paternal tree located within the study plot (with probability (1−m_p)). In the latter case offspring may be the result of self-pollination with probability s. We matched initial settings of these parameters in the programme NM+ to those estimated for our study plot using categorical paternity assignment above and included null allele frequencies as calculated in Cℰℛ𝒱𝒰𝒮. The neighbourhood parameter was set to ‘infinite' to include all sampled adults in our study plot as the neighbourhood size (Chybicki and Burczyk, 2010). Pollen dispersal was modelled using two-parameter exponential-power and Weibull dispersal kernels (Chybicki and Burczyk, 2010) with estimates given of a and b (the scale and shape parameters, respectively) from which the average distance of pollen dispersal (d_p) is estimated. The shape parameter b describes the shape of the dispersal kernel tail, with b<1 indicating fat-tailed dispersal (that is, the long-range decay of probability is slow) and b>1 indicates dispersal is thin-tailed, with a rapid decrease of the dispersal function, implying few long-distance dispersal events (Austerlitz et al., 2004). For both the exponential-power and Weibull families of curves, b=2 approximates a normal distribution (Chybicki and Burczyk, 2010).

Ecological correlates

We conducted a preliminary assessment of two ecological factors that may potentially impact pollen dispersal in our system: (1) the local density of conspecific adult trees surrounding our sampled maternal trees, regardless of their reproductive status; and, (2) Euclidian distances between (a) maternal trees and all adult conspecifics in the study plot and (b) reproductive (flowering) conspecific adults in any given month. We calculated local density of adult O. bataua trees surrounding the n=16 maternal trees used in this study as a simple count of the number of adults within a circle of 75 m diameter centred on each maternal tree; this diameter size was selected because it gave an approximately normal distribution of local density estimates. We then used correlation analyses to test for relationships between local adult O. bataua density with paternal diversity and average distance of realised pollen dispersal for each maternal tree. We did not have access to real-time phenology data when the pollination events we analysed genetically took place (in 2006–07). Instead, we calculated the frequency distribution of distances between trees with active inflorescences within the study plot at monthly intervals between May 2010 and February 2011 (n=124–164 trees surveyed per interval; Karubian, unpublished data). We then used these data to qualitatively assess similarities between the distribution of realised pollination distances and distances between all adult O. bataua trees, and all concurrently flowering O. bataua trees. As O. bataua is non-uniformly distributed across our study plot (Figure 1) we used the Clark–Evans nearest-neighbour (NN) statistic (R) (Clark and Evans, 1954) to assess the spatial pattern of these distributions, that is, whether trees were clumped (R<1), uniformly (R=1) or randomly (R>1) distributed.

Adult population structure

We described the genetic structure of the population of adult O. bataua trees within our study plot using descriptive population genetic statistics (number of alleles, heterozygosity, inbreeding and tests for Hardy–Weinberg equilibrium) calculated in Gℰ𝒩AℒE𝒳 v6.3 (Peakall and Smouse, 2006). To test for spatial genetic structure among adults in the study plot we performed spatial autocorrelation analysis in the programme S𝒫𝒜𝒢ℰ𝒟ℐ v1.2 (Hardy and Vekemans, 2002) using the kinship coefficient of Loiselle et al. (1995) and distance classes with equal numbers of pairwise comparisons. Spatial locations were permuted 10 000 times to obtain error estimates of the null hypothesis (F_ij=0) and error estimates of the observed kinship values among adult trees were calculated by jackknifing over loci 1000 times. The strength of the spatial genetic structure was assessed using the Sp statistic of Vekemans and Hardy (2004), calculated as−b_Flog/(1−F₁) where b_Flog is the mean slope of the regression of kinship coefficients on log₁₀ distance and F₁ is the mean kinship coefficient of the first distance class.

Results

Marker quality and genotyping success

We successfully obtained genotypes for 185 of 188 adult O. bataua trees located within our 130 ha plot, and for 318 offspring collected from 16 maternal trees. Relatively high failure rate and genotyping error at locus Ob02 (Table 1) led us to exclude this locus from mating system and parentage analysis, though it was retained for other analyses as appropriate. Paternity exclusion rates using the remaining 11 loci were high (combined P_excl=0.983, Table 1), however, Cℰℛ𝒱𝒰𝒮 identified two of the 11 loci as having significant excess of homozygotes indicative of null alleles. Null allele frequencies at these loci were low (Ob10=0.023; Ob19=0.029) and were explicitly taken into account in our pollen dispersal analyses.

Mating system

Overall, O. bataua was highly outbred with individual outcrossing rates (t_m) ranging from 0.95 to 1.0 (mean t_m=1.02±0.08) (Table 2). In addition, little biparental inbreeding was detected in the population (t_m−t_s=0.009). There was a moderate degree of correlated paternity within progeny arrays (r_p=0.198), indicating ∼20% of offspring were full-sibs (Table 2). Family level estimates of mating system parameters are in Supplementary Table S1.

Table 2. Population-level estimates of mating system and pollen diversity statistics for O. bataua.

Mating system analysis
Multilocus outcrossing rate (tm)	1.02±s.e. 0.08
Biparental inbreeding (tm−ts)	0.01±s.e. 0.08
Correlated paternity (rp)	0.20±s.e. 0.03
Paternity analysis
Mean no. of progeny tested per maternal tree	20
Mean no. of progeny assigned paternity per maternal tree	18
Total no. of pollen donors identified	98
Mean no. of pollen donors per maternal tree	9.8
Mean/median/maximum pollination distance	303/269/1283 m
Mean effective pollination neighbourhood (Aep) area/diameter	18.5 ha/485 m
Mean minimum pollen donor pool size per female (Nd)	16.5
Probability of paternal identity (PPI)
Mean correlation of paternal identities within maternal trees (rgg)	0.184±s.d. 0.166
Mean no. effective pollen donors (Nep)	5.4

Methods section contains details on each analysis.

Pollen dispersal, paternal diversity and dispersal kernel estimation

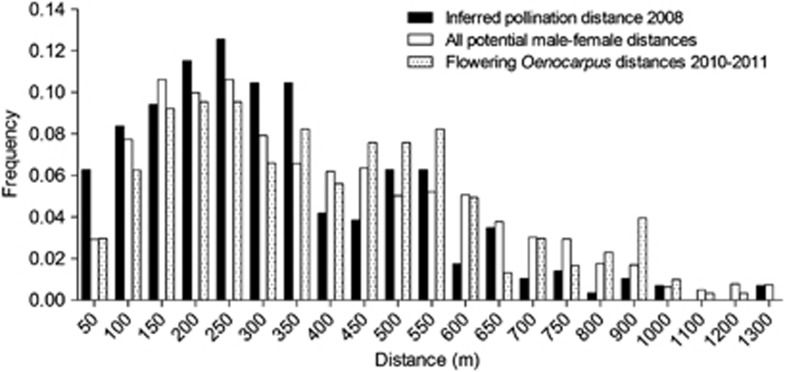
Using categorical paternity assignment in Cℰℛ𝒱𝒰𝒮 we initially assigned a paternal parent from within our study plot to most offspring (92%) with at least 80% confidence. Using our more stringent criteria (see Methods), we accepted paternity assignments for 287 of the 318 offspring sampled (90%) with >80% confidence to adult trees located within our 130 ha plot. Overall, effective pollination distances within the study site showed an approximately bell-shaped distribution with the mean distance of pollen dispersal 303±s.d. 206 m (Figure 2). The mean distance to nearest pollen donor and median and maximum pollen dispersal distances were 113 m, 269 m and 1263 m, respectively. For comparison, the mean distance to NN for the maternal trees sampled was 28±s.d. 32 m, and the mean, median and maximum pairwise distances between maternal trees and all other adult O. bataua individuals within our study parcel were 317±s.d. 219, 271 and 1269 m, respectively. The effective pollination neighbourhood ranged from A_ep=3.3–65.5 ha between maternal trees (Supplementary Table S1), with the mean A_ep=18.5 ha equivalent to a circle of diameter 485 m centred on a maternal tree.

Figure 2.

Frequency distribution of observed pollination distances for seeds sampled in 2008 (black bars), inter-tree distances of all adult trees relative to the sampled maternal trees (white bars) and distances between flowering trees observed in the 2010–11 flowering season (hatched bars) for the palm species O. bataua in northwest Ecuador. Mean nearest-neighbour distance for each data set was 113, 28 and 62 m, respectively.

We found that 98 trees contributed paternity to offspring of the 16 maternal trees tested. Male reproductive success was highly skewed towards a small number of individuals; for example, only 7 of 98 pollen donors contributed more than 10 offspring, with many individuals contributing single offspring (Supplementary Figure S1). Overall, paternity analysis revealed an average of 9.8 fathers contributing to each progeny array (Table 2). The paternal matching rates (PPI) within progeny arrays from individual maternal trees ranged from r_gg=0.026−0.614 (mean=0.184±s.d. 0.166), which translates to an estimate of an average N_ep=5.4 per female (range: 1.6–38.5; Table 2). This estimate is similar to that calculated from the correlated paternity statistic from MLTR by N_ep=1/r_p=5.05. There was low overlap in paternal identity between maternal trees (mean r_ij=0.012±s.d. 0.031) suggesting that individual maternal trees are sampling from distinct pollen pools. Indeed, T𝒲𝒪𝒢ℰ𝒩ℰℛ analysis showed there was significant, but moderate, genetic differentiation amongst pollen pools sampled by individual maternal trees (Φ_FT=0.096, P<0.001). Using maximum-likelihood methods we estimated the average minimum effective pollen donor pool size was 16.5 (range=4–41) pollen donors per female (Table 2).

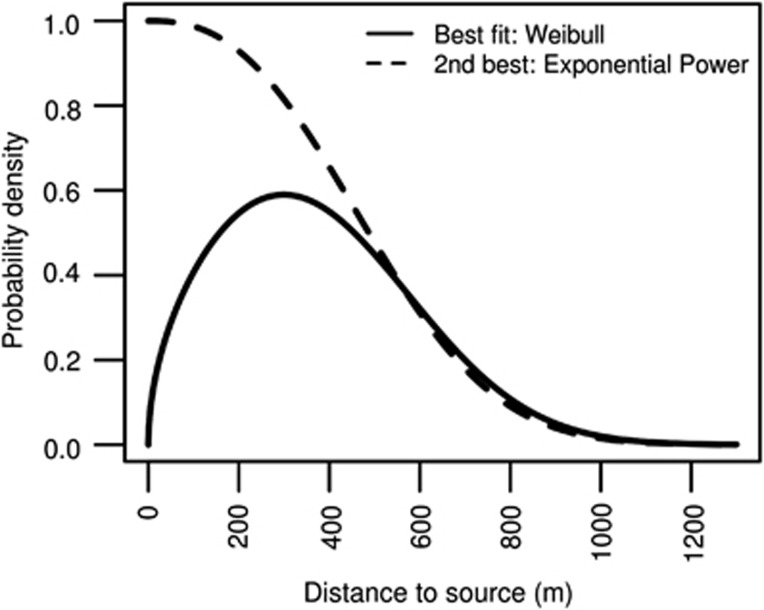
Pollen dispersal kernel modelling using fractional paternity assignment in the Nℰℐ𝒢ℋℬ𝒪𝒰ℛℋ𝒪𝒪𝒟 model indicated the dispersal kernel of O. bataua was thin-tailed (b>1) (Figure 3, Table 3). When all mating system and dispersal parameters were jointly estimated, the Weibull dispersal kernel had the highest model likelihood, though not greatly different to the exponential-power model, and both models indicated a higher rate of pollen immigration than expected from our categorical paternity analysis (m_p=0.38 vs 0.1, respectively; Table 3). This analysis estimated the mean distance of dispersal from source trees to be 604±168 m under a Weibull distribution, and 444±68 m under an exponential distribution (Table 3).

Figure 3.

Best fit two-parameter dispersal kernels for O. bataua progeny arrays. Scale and shape parameters estimated using the Nℰℐ𝒢ℋℬ𝒪𝒰ℛℋ𝒪𝒪𝒟 model (Burczyk et al., 2002). Additional mating model parameters are in Table 3.

Table 3. Selfing rate (s), pollen immigration rate (m _p), mean distance of pollen dispersal (d _p), dispersal kernel scale (a) and shape parameters (b) and model log likelihoods (LogL) estimated from O. bataua progeny arrays using the Nℰℐ𝒢ℋℬ𝒪𝒰ℛℋ𝒪𝒪𝒟 model (Burczyk et al., 2002).

Model	s	mp	dp	a	b	LogL
Exponential-power	0.0037 (0.004)	0.383 (0.03)	444.0 (67.7)	564.04	2.512 (0.950)	−5601.553
Weibull	0.0038 (0.004)	0.383 (0.03)	604.64 (168.9)	679.55	1.781 (0.147)	−5600.586

Dispersal models were seeded using initial parameters derived from categorical paternity analysis, that is, m_p=0.1 (90% of offspring were assigned paternity within our study plot), d_p=303 m, s=0.0). Standard error of parameter estimates in parentheses.

Correlation of paternal diversity and pollination distance with ecological factors

Local tree density (number of conspecifics within 75 m diameter circle around focal tree) had little effect on the number of fathers detected per family via parentage analysis (r²=0.022, P=0.583) or the correlation of paternal identity within seed crops (PPI) (r²=0.017, P=0.625). However, there was a strong, negative correlation between mean pollination distance and local tree density (r²=0.378, P=0.011). Mean pollination distance per family showed little relationship with either the number of fathers detected via parentage analysis (r²=0.005, P=0.788) or PPI (r²=0.016, P=0.637), though overall there was a low but significant negative correlation of number of seeds sired and inter-mate distance (r²=0.022, P=0.012).

The distribution of pollination distances matched closely with the distribution of pairwise distances between concurrently flowering O. bataua trees, and also with the distribution of pairwise distances between maternal trees and all O. bataua adult trees in our study plot, with only a very slight bias towards short-distance matings (Figure 2). The mean distance between flowering trees in 2010–2011 was 366±226 m, and the median and maximum distances were 334 and 1170 m, respectively, congruent with the observed pollination patterns from the 2008 seed cohort. NN analysis showed that, while the distribution of adult trees in the plot was clumped (mean NN=28±32 m, R=0.67), flowering trees and pollinating trees were a randomly distributed sub-set of these (flowering trees, mean NN=62±57 m, R=1.27; pollinating trees, mean NN=113±90 m, R=1.96; Supplementary Table S2).

Population genetic structure of adults

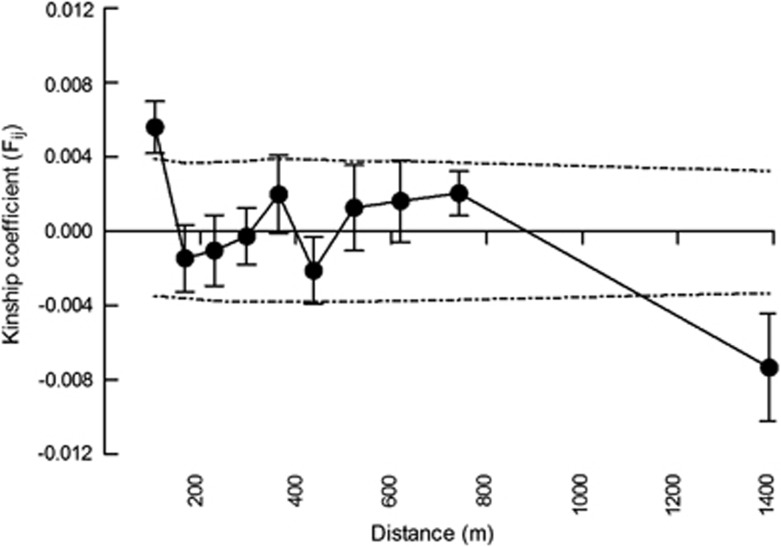
Consistent with the mating system and pollen dispersal results, there was little evidence for inbreeding in the adult O. bataua population at BBS, with observed and expected heterozygosity equivalent (H_O=0.67±0.05, H_E=0.66±s.e. 0.05) and mean F_IS=−0.019±0.018 (Table 1). Similarly, genetic diversity of offspring from the sampled maternal trees showed little deviation in population genetic parameters from the adult population (H_E=0.67±0.04) and showed no evidence of inbreeding (F_IS=−0.012±0.02). High levels of gene flow meant that there was little genetic structure among adults overall (Sp=0.0022), with only weak correlation between adult genotypes in the first distance class (mean distance=67 m, Figure 4) in spatial autocorrelation analysis.

Figure 4.

Spatial autocorrelation analysis of adult O. bataua from Bilsa Biological Station, northwest Ecuador. Mean kinship coefficient (F_ij)±s.e. plotted against distance. Dashed lines are the upper and lower 95% confidence intervals around the null hypothesis (F_ij=0) determined by permutation testing.

Discussion

Gene flow via the movement of both pollen and seed contributes to the genetic structure of plant populations and defines effective neighbourhood size. Here, we have provided insight into the patterns of movement of pollen for the widespread Neotropical insect-pollinated palm O. bataua in contiguous Chocó rainforest of northwest Ecuador. We find that O. bataua is highly outbred and that pollen dispersal is widespread across our study plot. Overall, the mean distance of pollen movement in successful matings was 303 m, which exceeded the mean nearest-neighbour distances within the study plot by an order of magnitude, and which translates into a relatively large effective neighbourhood size (18.5 ha) per maternal tree. Also, individual maternal trees received pollen from a diversity of males (average 9.8 males identified by paternity analysis per female; number of effective males N_ep=5.4), with little overlap in paternal identity between maternal trees. In keeping with these findings, we expect that extensive pollen gene flow, in combination with high levels of seed dispersal (Karubian et al., 2010), contribute to the lack of spatial genetic structure detected among adult O. bataua trees at any but the shortest distance classes we measured.

In contrast to the highly leptokurtic distributions reported for many other species, particularly wind-pollinated species (Austerlitz et al., 2004; Robledo-Arnuncio and Gil, 2005), the distribution of inter-mate distances within our study plot was approximately bell-shaped, with relatively few short-distance matings. Similarly, the dispersal kernel we generated for O. bataua using the spatially-explicit Nℰℐ𝒢ℋℬ𝒪𝒰ℛℋ𝒪𝒪𝒟 model was best described by a Weibull distribution with high probability of dispersal at intermediate distances, and a very rapid decline in dispersal probability with increasing distance. The preponderance of intermediate distance pollination events and overall pollen movement we observed is qualitatively similar to that documented in recent studies (for example, Bittencourt and Sebbenn (2007); de Lacerda et al. (2008); Jha and Dick (2010); Zhou and Chen (2010); Fuchs and Hamrick (2011)), suggesting a non-leptokurtic pattern of realized pollination events may not be uncommon, especially amongst tropical species.

Dispersal kernel modelling estimates the frequency distribution of dispersal distances of propagules from an individual source tree (Oddou-Muratorio et al., 2005), in contrast to the population-level patterns of pollen receipt detected via paternity analysis. While we found qualitatively similar dispersal curves with each analysis type, dispersal kernel modelling using the Nℰℐ𝒢ℋℬ𝒪𝒰ℛℋ𝒪𝒪𝒟 approach (Burczyk et al., 2002; Chybicki and Burczyk, 2010) estimated a greater rate of pollen immigration into our study plot than detected by paternity analysis (38% vs 10%, respectively). The discrepancy likely arises due to the differences of each analytical approach; estimating dispersal kernel parameters requires genetic data to be fit to an underlying model of dispersal (for example, exponential-power, Weibull), which typically assume a long tail of dispersal, whereas paternity analysis is assumption- and model-free. However, the hard edge that bounds the forest parcel on one side and the soft edge to a second side may have reduced the amount of pollen immigration into our site, potentially leading to an under-estimation of long-distance pollen gene flow in this species using parentage methods.

The shape of the tail of the dispersal kernel (that is, whether thin- or fat-tailed) impacts the ultimate distribution of genetic diversity within and between populations. Most empirical studies to date report that pollen dispersal kernels are fat-tailed in tree species (Dick et al., 2003; Austerlitz et al., 2004; Oddou-Muratorio et al., 2005; Klein et al., 2006). Here, we find that the dispersal distribution in O. bataua was thin-tailed (b>1). While a 10% pollen immigration rate is likely to be biologically meaningful, the thin-tailed shape of the O. bataua distribution does imply that that long-distance dispersal is less frequent in this species than in those species exhibiting fat-tailed distributions. This has important consequences for colonisation dynamics including the genetic composition of newly established populations. For example, Klein et al. (2006) have shown that thin-tailed dispersal kernels result in a colonisation wave of constant speed, composed of propagules sourced from the closest trees and that the number and diversity of sources remains relatively constant as colonisation advances. This finding may indicate that O. bataua may be more susceptible to genetic bottlenecks during re-colonisation following disturbance than other tree species with fat-tailed dispersal kernels, though dispersal dynamics are likely to change in fragmented or disturbed landscapes relative to the contiguous conditions studied here (for example, Dick et al. (2003)).

The genetic structure of plant populations is determined not only by the spatial scale of gene dispersal but also by the degree of genetic mixing achieved by dispersal processes. At the level of the individual tree, we found no evidence that the diversity of pollen sources was strongly affected by mean pollen dispersal distance. This challenges the assumption that pollen dispersal distance can be used as a proxy of pollen sire diversity among progeny arrays. Indeed, at the population level little empirical evidence exists on the relationship between dispersal distances and N_ep (Ashley, 2010). Previous studies have stated that the larger the paternal pool, the higher will be the fitness of the maternal plant (Levin, 1988). Thus, additional work relating N_ep and diversity of pollen sources to pollination distance and the shape of the dispersal kernel is needed to better understand how pollination dynamics affect microevolutionary processes such as the genetic composition of recruits and plant fitness.

High rates of direct paternity assignment, such as those obtained in the current study, allow us to assess relationships between individual and/or ecological traits with observed patterns of pollen movement. What ecological factors may drive the patterns we have observed here? In the absence of a genetic self-incompatibility system in O. bataua acting to limit near-neighbour matings, we tentatively suggest that the temporal and spatial distribution of flowering adults, in combination with a mobile pollinator, may be useful in explaining the observed pollen dispersal kernel in O. bataua. In particular, our phenology data from 2010–11 suggests that O. bataua, like many other tropical species, may flower at relatively low densities and that flowering individuals may be randomly distributed across the landscape (see also Rojas-Robles and Stiles (2009)). We consider it likely that similar (unrecorded) phenological conditions occurred in 2006–07 when the samples we analysed were fertilised, and that the resulting low effective density of flowering trees may underlie the patterns of pollen dispersal we documented, particularly the lack of near-neighbour matings, the relatively long dispersal distances, and the peak in pollination events at 200–300 m that matches closely the peak in neighbour distances among the entire study population, and also among flowering individuals. We propose that this pattern may be relatively common among tropical versus temperate insect-pollinated trees, as less synchrony in flowering times is expected in the Tropics (but see Tani et al. (2009)). More work in this and other systems, including measuring the effective density of flowering trees at the time of fertilisation events, would shed light on the patterns of causality in this proposed relationship.

Pollen dispersal distances have only been characterised in a few palm species; our estimates of dispersal distances are greater than those documented for Iriartea deltoidea (median 102–247 m depending on cohort; Sezen et al., 2007) and Astrocaryum mexicanum (range 13–23 m; Eguiarte et al., 1993). Dispersal between populations 22 km apart has been documented in Euterpe edulis, presumed to be pollen- rather than seed-mediated (Gaiotto et al., 2003). In our study, mean pollination distances were greater in more isolated trees, underscoring the high mobility of beetle pollinators, whose long-distance movements may be facilitated by a heat reward provided by O. bataua (Nunez-Avellaneda and Rojas-Robles, 2008). Given the ecological and economic importance of palms (Henderson et al., 1995), there is a clear need for basic descriptive work on this group. In addition to characterising dispersal syndromes for a greater taxonomic and ecological range of species in contiguous habitat types, there is a particular need to address the consequences of palm trees left as remnant trees in areas otherwise cleared for cattle or agriculture, an exceedingly common situation throughout the Tropics (Henderson et al., 1995).

Both pollen and seed dispersal contribute to the spatial genetic structure of populations, but the relative contribution of each process to overall gene dispersal remains unclear for many species (Sezen et al., 2007). Previous studies of seed dispersal in this system used direct parentage analysis to estimate mean seed dispersal distances of ∼300 m by the long-wattled umbrellabird (Cephalopterus penduliger) into a central display area (lek), as well as for unknown dispersal agents into random plots outside the lek (Karubian et al., 2010). A second study combining radio tracking and gut retention trials estimated slightly lower seed dispersal distances for male and female Umbrellabirds (257 and 218 m, respectively; Karubian et al., 2012). These values suggest approximately equivalent dispersal distances for seed versus pollen in this system, similar to that found in I. deltoidea (Sezen et al., 2007). By comparing the estimates of maternal and paternal diversity (N_em/N_ep from PMI (Karubian et al., 2010) and PPI analyses from the current study, respectively) we also find that genetic mixing achieved via pollen dispersal is similar to that of seed dispersal into random plots outside Umbrellabird leks in BBS (N_ep=5.4 vs N_em=5.3 in progeny arrays and seedling plots, respectively). However, mixing generated by male Umbrellabird seed dispersal into lek sites is substantially greater (N_em=27.0). As such, it may be that lekking behaviour by male Umbrellabirds has the greatest effect on the localised genetic structure of O. bataua at BBS, though more work is needed to resolve this question. In particular, simultaneously estimating male and female contributions to dispersed seedlings (made possible by the fact that the woody seed remains attached to established O. bataua seedlings for several months) would enable us to ultimately disentangle the effects of pollen and seed movement on realised gene dispersal and genetic mixing (Grivet et al., 2009).

Taken together, the mating system and patterns of pollen and seed dispersal of O. bataua ensure a system of high genetic mixing, at least at local scales in relatively intact populations such as the one found in BBS. Indeed, there was little deviation from random mating (as measured by F_is) in either adult or offspring samples in this study and very weak spatial genetic structure in the adult population (S_p=0.002), with only a small positive correlation of genotypes at distances <100 m. Given the high levels of anthropogenic disturbance throughout the Neotropics, a priority for future studies is to address how activities such as habitat fragmentation and local extirpation of dispersal agents in less pristine habitats may perturb dispersal mutualisms, and what the impact on genetic diversity and spatial structure of O. bataua may be.

Data Archiving

Data have been deposited at Drya; doi:10.5061/dryad.pb128.

The authors declare no conflict of interest.