Skip to main content
PMC home page
Heredity logoLink to Heredity
. 2012 Sep 19;109(6):361–371. doi: 10.1038/hdy.2012.51

Detecting the footprints of divergent selection in oaks with linked markers

P G Goicoechea 1,*, R J Petit 2,3, A Kremer 2,3
PMCID: PMC3499841  PMID: 22990311

Abstract

Genome scans are increasingly used to study ecological speciation, providing a useful genome-wide perspective on divergent selection in the presence of gene flow. Here, we compare current approaches to detect footprints of divergent selection in closely related species. We analyzed 192 individuals from two interfertile European temperate oak species using 30 nuclear microsatellites from eight linkage groups. These markers present little intraspecific differentiation and can be used in combination to assign individual genotypes to species. We first show that different outlier detection tests give somewhat different results, possibly due to model constraints. Second, using linkage information for these markers, we further characterize the signature of divergent selection in the presence of gene flow. In particular, we show that recombination estimates for regions with outlier markers are lower than those for a control region, in line with a prediction from ecological speciation theory. Most importantly, we show that analyses at the haplotype level can distinguish between truly divergent (bi-directional) selection and positive selection in one of the two species, offering a new and improved method for characterizing the speciation process.

Keywords: divergent selection, divergence hitchhiking, outlier detection, linkage disequilibrium, score tests, Quercus

Introduction

Divergent selection, defined as selection acting in contrasting directions in different groups of individuals (Schluter, 2000), has been a topic of great interest in recent years because of its central role in studies of ecological speciation. Although work in this area initially focused on the responses of individual genes to divergent selection, there has been a gradual shift towards a genomic approach (Nosil and Feder, 2012), with a growing number of studies using genome/multilocus scans to analyze this process in relation to ecological speciation (Nosil et al., 2009; Apple et al., 2010; Galindo et al., 2010; and references therein). Such scans rely on single-locus outlier detection methods, which are based on population genetics theory (Lewontin and Krakauer, 1973; Bowcock et al., 1991; Beaumont and Nichols, 1996; Schlötterer, 2002; Beaumont and Balding, 2004). Positive selection reduces neutral diversity at linked neutral sites via hitchhiking effects (Maynard-Smith and Haigh, 1974), creating a selective sweep. Other phenomena associated with selective sweeps include changes in linkage disequilibrium (LD) patterns (Kim and Nielsen, 2004; McVean, 2007) and in the site frequency spectrum (Braverman et al., 1995; Nordborg et al., 2005).

Recently, Via and West (2008) and Via (2009) described a new type of hitchhiking that differs from hitchhiking after a selective sweep. This between-population process (Via, 2012) is exclusive to organisms evolving under divergent selection and has therefore been named ‘divergence hitchhiking'. In contrast to what happens following a selective sweep in a large panmictic population, where LD created by the sweep is rapidly eroded, LD tends to be more persistent around genes that are responding to divergent selection among populations due to a reduction in the rate of effective gene flow and recombination (Via, 2009). Eventually, as speciation progresses, divergent selection in the presence of gene flow produces a genetic mosaic of divergent and non-divergent genomic regions (Nosil et al., 2007; Smadja et al., 2008; Via, 2012). Divergence hitchhiking should also operate under other modes of divergent selection, such as when intrinsic (non-environmental) factors drive selection, which should produce distinctive selection footprints (Bierne, 2010). Therefore, there is a need to evaluate suitable approaches to better characterize the molecular signatures of these processes.

Attempts to use outlier detection tests to infer divergent selection have highlighted the lack of available information on several related subjects, such as the actual causes of selection, the potential impact of background differentiation on outlier detection and the likelihood of false positives (Nosil et al., 2009; Michel et al., 2010). Despite these issues, a growing number of researchers have attempted to infer the occurrence of ecological speciation by identifying outlier markers related to changes in environmental variables (Murray and Hare, 2006; Savolainen et al., 2006; Joost et al., 2007) or by identifying cases where the same outliers occur in replicated pairs of populations (Bonin et al., 2006; Egan et al., 2008; Poncet et al., 2010). To date, none of these studies have considered linkage information. However, haplotype tests based on LD mapping have proven to be more powerful (that is, require smaller sample sizes) than standard single-locus methods in association studies (Bader, 2001; Liu et al., 2008) and candidate gene studies (Clark, 2004). Haplotype tests should also be more robust than single-marker tests because evolutionary forces tend to increase the variability of single markers and the simultaneous analysis of multiple markers in the form of haplotypes should thus yield comparatively simpler patterns (Akey et al., 2001). Moreover, advanced statistical methods for inferring haplotypes from genotypic data have now been developed (Stephens et al., 2001; Excoffier et al, 2003; Stephens and Donnelly, 2003) and divergence hitchhiking is expected to produce LD extending across relatively large chromosomal regions (Via, 2012). This suggests that it may be possible to analyze divergence hitchhiking regions by scanning the genomes of ecologically important non-model species with linked markers.

Oaks represent a particularly good model system to study divergent selection in the presence of gene flow because the reproductive barriers in this genus seem to depend on the ecological contexts (Muller, 1952; Lepais et al., 2009; Zeng et al., 2010). Two of the most extensively studied oak species are the sessile Quercus petraea and the pedunculate Q. robur (Petit et al., 2004). They are commonly found in sympatry across Europe and Asia, in mixed forests, where hybridization occurs spontaneously (Streiff et al., 1999; Lepais et al., 2009; Lepais and Gerber, 2011). However, there are persistent strong differences between the two species with respect to certain ecologically important traits, such as leaf and fruit morphology (Kremer et al., 2002), water-use efficiency (Ponton et al., 2002; Parelle et al., 2007) and the amount of volatile compounds in their wood (Prida et al., 2007). Scotti-Saintagne et al. (2004) used a genetic mapping approach to demonstrate the existence of several ‘islands' of strongly differentiated loci surrounded by regions of low differentiation, which is consistent with the expected spatial clustering of outlier markers due to ecological speciation (Via, 2009). Later, Muir and Schlötterer (2005) identified one outlier marker in two such islands using a different outlier detection test.

In the study presented herein, we further investigate the signatures of divergent selection in these oak species. The study was conducted in three stages. First, we used five outlier detection methods based on different underlying assumptions to search for selection signals at individual loci. Second, we used a limited number of loosely linked markers to explore the haplotypic structures around outlier loci from several linkage groups. Clear differences were observed between the haplotypic structures of the selected regions and those of a control region consisting of three markers with average differentiation. Finally, we show that haplotypic methods, in contrast to outlier methods, are capable of distinguishing between truly divergent (bi-directional) selection and directional selection in one species only.

Materials and methods

A total of 192 trees from the two European temperate oak species (Q. petraea (Matt.) Liebl. and Q. robur L.) were sampled from 10 populations located in eight European countries. Their geographical coordinates, the type of stand involved (mono-specific or mixed-species stands), the morphological classification of the sampled trees and the number of trees and simple sequence repeats (SSRs) analyzed within each population are provided in Table 1. Half of the studied data set has been used in a previous investigation (Scotti-Saintagne et al., 2004). In this work, we increased the number of trees in all mixed stands and added three new stands. For these new samples, we analyzed only a subset of 18 SSRs that displayed significant between-species differentiation (based on FST) in the first survey.

Table 1. Characteristics of the sampled populations.

Stand (name) Latitude/longitude Type Species (morph) Nb trees SSRs
P1 (Petit Charnie) 48.083/−0.167 Mixed Q. petraea 8 30
        4 18
      Q. robur 8 30
        4 18
P3 (De Meinweg) 51.179/6.14 Mixed Q. petraea 12 18
      Q. robur 12 18
P4 (Arlaban) 42.967/−2.55 Mixed Q. petraea 8 30
        4 18
      Q. robur 8 30
        4 18
P4b (Montejo) 41.117/−3.500 Mixeda Q. petraea 8 30
P5 (Dalkeith) 55.903/−3.055 Mixed Q. petraea 8 30
        4 18
      Q. robur 8 30
        4 18
P6 (Sigmundsherberg) 48.680/15.750 Mixed Q. robur 8 18
P7 (Roudsea Wood) 54.218/−3.018 Mixed Q. petraea 8 30
        4 18
      Q. robur 8 30
        4 18
P9 (Gysinge) 60.468/17.310 Q. robur Q. robur 8 30
P10 (Büren) 47.105/7.383 Mixed Q. petraea 8 30
        4 18
      Q. robur 8 30
        4 18
P12 (Rantzau) 54.250/10.520 Mixed Q. petraea 12 18
      Q. robur 12 18
Open in a new tab

Abbreviation: SSRs, simple sequence repeats.

a

Q. petraea–Q. pyrenaica mixed stand.

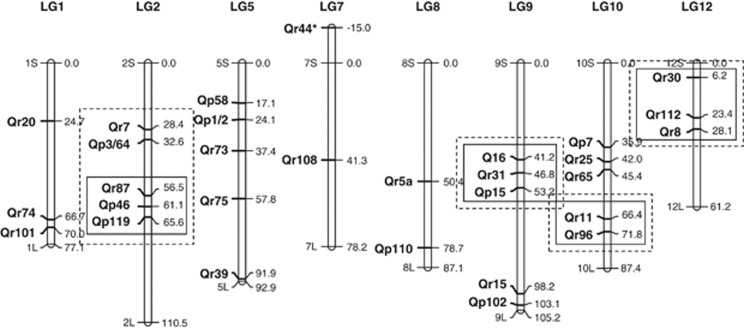
Leaf morphology was used to guide sampling in mixed forests. In particular, morphologically intermediate individuals were avoided because they could increase the proportion of admixed trees in the sample (see below). The SSRs used in this study were designed by Dow et al. (1995), Steinkellner et al. (1997) and Kampfer et al. (1998). We selected 30 SSRs that had been mapped on a Q. robur-controlled cross (Barreneche et al., 1998; Scotti-Saintagne et al., 2004). Their linkage map positions are shown in Figure 1. Protocols for DNA isolation and PCR amplification were slightly modified from those described by Mariette et al. (2002). Forward primers were 5′ labeled with either the IRD700 or the IRD800 chromophore (Eurofins MWG Operon, Ebersberg, Germany) and alleles were visualized on a LI-COR sequencer (LI-COR Biosciences, Lincoln, NE, USA). The absolute sizes of the alleles were determined by direct comparison with a 10-bp ladder (LI-COR Biosciences) run in triplicate on each gel. Stutter bands and the Iℳ𝒜𝒢ℰJ (Abramoff et al., 2004) software package were used to match the different alleles within each gel.

Figure 1.

Figure 1

Open in a new tab

Oak linkage groups showing the location of the 30 SSRs used in this study (after Scotti-Saintagne et al., 2004). Map positions are indicated to the right of each LG. The boxes indicate the markers used for haplotype inferences and recombination estimates (continuous line) and for haplotype score tests (dashed line).

Population structure

We inferred the genetic structure in our sample using S𝒯ℛ𝒰𝒞𝒯𝒰ℛℰ v.2.1 (Pritchard et al., 2000; Falush et al., 2003). Inferences were based on a linkage model with correlated allele frequencies, using a unique drift rate from the ancestral population(s) (see Supplementary File 1 for the results obtained with another model and for an admixture test). We ran five independent chain replicates of 106 iterations following a burn-in period of 105 iterations, for a fixed number of populations (K=1–5). Previous analyses on a subset of the data had already demonstrated that when using this model, the probabilities obtained decreased steadily after K=3 (data not shown). Model convergence was checked using S𝒯ℛ𝒰𝒞𝒯𝒰ℛℰ likelihood and summary statistics plots. We used the post-hoc criterion described by Evanno et al. (2005) to determine the most likely number of clusters. The full search algorithm of Cℒ𝒰ℳ𝒫𝒫 v.1 (Jakobsson and Rosenberg, 2006) was used to handle the across-chains variation in the proportion of intra-individual mixed ancestry. The resulting final configuration was used to plot the ancestry coefficients with Dℐ𝒮𝒯ℛ𝒰𝒞𝒯 v.1.1 (Rosenberg, 2004).

Genetic diversity and differentiation

The data set for ‘pure' species (see Supplementary File 1) was used to estimate the genetic diversity and interspecific differentiation for the 30 SSRs. Observed (Ho) and expected heterozygosities (He) and allelic richness (AR) were calculated using the methods described by Nei (1973) and El Mousadik and Petit (1996), respectively. We measured interspecific differentiation using FST (Weir and Cockerham, 1984) and D (Jost, 2008), another differentiation parameter that uses a multiplicative partitioning of diversity based on the effective number of alleles. Unbiased estimates of these parameters were calculated with F𝒮𝒯𝒜𝒯 (Goudet, 2001) and Sℳ𝒪𝒢𝒟 (Crawford, 2010). The significance of each FST estimate was evaluated using 16 000 permutations. Similarly, 1000 bootstrapped samples were used to calculate the variance of D and its 95% confidence intervals. These results are shown in Supplementary File 2.

Outlier tests

Only data on purebred individuals were retained for these analyses. We used five outlier tests with different underlying assumptions. The first two tests are based on the F𝒟ℐ𝒮𝒯2 method of Beaumont and Nichols (1996), which uses coalescent simulations under either the infinite allele model (IAM, Kimura and Crow, 1964) or the stepwise mutation model (SMM, Ohta and Kimura, 1973) to characterize genetic differentiation (FST) for a given heterozygosity level. The third test, B𝒜𝒴ℰ𝒮ℱ𝒮𝒯 (Beaumont and Balding, 2004), relies on a Bayesian analysis to characterize differences in migration rates among individual markers. The last two methods, ln RV and ln RH (Schlötterer, 2002; Kauer et al., 2003), use the observed data to fit standardized normal distributions whose tails contain the outliers. Further details concerning these analyses are presented in Supplementary File 3.

Linkage disequilibrium

LD estimates were used to search for further selection signals in our data, as an increase in LD between markers is commonly used to infer selection (Hudson et al., 1994; Kohn et al., 2000). Genotypic LD within species was investigated using F𝒮𝒯𝒜𝒯 (Goudet, 2001), based on data from purebred individuals. Significance tests were conducted using the log-likelihood ratio G-statistic (Goudet et al., 1996), with 16 000 permutations. Deviations from Hardy–Weinberg equilibrium (H–W equilibrium) were tested for on a per locus basis by randomizing alleles among individuals within samples to determine the departure of FIS from zero.

Obtaining reliable genotypic LD estimates from multiallelic markers, such as SSRs, requires very large sample sizes given the large number of genotypes involved. This difficulty can be eliminated by analyzing haplotypic LD, for which smaller sample sizes are needed. We therefore estimated haplotypic LD in all segments harboring positive selection outliers (linkage group 2 (LG2), LG10 and LG12) and in one control LG without outliers (LG9). Following haplotype reconstructions (see below), we used Aℛℒℰ𝒬𝒰ℐ𝒩 v.3.5 (Excoffier and Lischer, 2010) to perform LD analysis while accounting for haplotype information. The exact test of Guo and Thompson (1992) was used to detect deviations from H–W equilibrium using 5 × 105 dememorization steps and a final chain of 107 steps. The significance of the observed LD was estimated using an extension of Fisher's exact test on contingency tables (Raymond and Rousset, 1995). In this test, Markov chains were run for 107 steps that were preceded by 9 × 105 dememorization steps. Results concerning both genotypic and haplotypic LD estimates are shown in Supplementary File 6.

Inferring haplotypes

We first inferred haplotypes and then performed haplotype-based analyses and studied haplotype sharing among individuals and between species. Haplotypes were inferred using two methods that explicitly allow for recombination: Pℋ𝒜𝒮ℰ v.2.1 (Stephens et al., 2001; Stephens and Donnelly, 2003) and the ELB algorithm (Excoffier et al., 2003). Four linkage groups were studied: the three LGs that contain at least one marker that appeared to be under positive selection (LG2 (Qp119, Qp46 and Qr87), LG10 (Qr11 and Qr96) and LG12 (Qr8, Qr112 and Qr30)) and one control region in which we found no outliers (LG9 (Q16, Qr31 and Qp15)). Note that Q16 and Qp15 had low/moderate allelic richness, which facilitated the detection of shared haplotypes in spite of the lower number of genotyped trees at Q16 and Qr31. Other segments with non-outliers situated at appropriate distances could not be used as additional control regions owing to the large number of alleles at the corresponding loci (that is, Qr72 and Qr101 or Qp7, Qr25 and Qr65). Haplotype reconstruction was conducted for markers from each LG using the full data set after excluding trees with missing data. Details on the inferences made using the ELB algorithm are presented in Supplementary File 5.

Pℋ𝒜𝒮ℰ haplotype inferences for each linkage group were based on five independent Bayesian chains with lengths of 5 × 108, chains were sampled every 500 iterations after a burn-in period of 2.5 × 105 iterations. The relative positions of each marker within the linkage groups (Figure 1) were transformed into base pairs using the assumption that 1 cM is roughly equal to 108 bp. This is the default value for humans (Pℋ𝒜𝒮ℰ documentation) and was used by Koopman et al. (2007) in their analyses of gene flow and introgression in apple trees, whose genomes are about the same size as those of oaks. We also tested a larger recombination probability obtained by computing the ratio of the size of the oak genome (Zoldo et al., 1988) to the full linkage length (c=(0.94 pg × 0.975 Gb pg−1)/1200 cM]. The IAM was used to model mutations at loci Qp46 and Qr31 (because they contain a large number of alleles that differ by only 1 bp), whereas the SMM was used to model mutations at all other markers. Both models were allowed to occasionally deviate from the most stringent assumptions by using δ values of 0.01 and 0.99 (where δ=0 and δ=1 correspond to the pure IAM and SMM models, respectively). Our assumptions concerning the variation in the recombination rate are consistent with the general model of Li and Stephens (2003).

We also used Pℋ𝒜𝒮ℰ to estimate the population genetics recombination parameter (ρ=4Nc), where c is the recombination probability per base pair and N is the effective population size, using inferred haplotypes as a starting point (Li and Stephens, 2003; Crawford et al., 2004). We compared the recombination estimates for the three LGs containing markers putatively under positive selection (LG2, LG10 and LG12) to that for the control LG without any apparent outliers (LG9). We used the -X100 option and modified the number of burn-in iterations, the thinning intervals and the final chain lengths to increase the accuracy of the estimates (see Supplementary File 4 for details). Recombination rates were estimated using the default number of individuals (100) in all cases save that of LG9 (84). To test the calculations' sensitivity to the recombination priors, we first used the default priors for the population genetics recombination parameter (μ=0.0004) and for the difference allowed between the estimate and the prior (f=106), both of which are appropriate for humans (Pℋ𝒜𝒮ℰ documentation). We then used two ‘oaks priors' (μ=0.04, f=104) that are expected to be more informative on the basis of experimental results (see Jaramillo-Correa et al. (2010), for a ρ estimate in tree populations). In all cases, we tested the convergence of the Bayesian chains (Supplementary File 4) before reporting the medians.

Haplotype score tests

We used haplotype score tests (Schaid et al., 2002) to search for significant associations between haplotypes and species. The score tests are an extension of the trend in proportions tests (Armitage, 1955), which are commonly used to compare haplotypic frequencies between cases and controls in association studies (Devlin and Roeder, 1999). One important advantage of using score tests is that they can incorporate the posterior haplotype probabilities, which are included as covariates. This makes them appropriate for analyzing inferred haplotypes (Schaid et al., 2002). On the other hand, the tests assume that all individuals are unrelated (Sinnwell and Schaid, 2009), which could make them sensitive to the genetic structure in our data (but see below). After excluding missing data, we used the full data set to analyze the five markers in the LG2 (region Qp119–Qr7), the three markers in the LG12 (region Qr8—Qr30), the two markers in the LG10 (region Qr11–Qr96) and the three markers in the LG9 (region Q16–Qp15).

These analyses were performed using the ‘haplo.stats' library (Sinnwell and Schaid, 2009) in the R environment (R Development Core Team, 2010). We obtained 100 maximum likelihood estimates of haplotype probabilities for each species with the modified EM algorithm (Excoffier and Slatkin, 1995; Schaid et al., 2002) and the solution with the largest likelihood was retained. Score statistics for the associations between the haplotypes and the binary trait ‘species', together with P-values, were obtained using the ‘haplo.score' function with the additive haplotype effects model. We used two thresholds for minimum haplotype counts (10 and 5) to avoid introducing bias in the global score due to rare haplotypes. The data set for LG9 was comparatively small and so a threshold of 3 was used in this case. The contributions of consecutive two-marker haplotypes from LG2, LG12 and LG9 were compared with the function ‘haplo.score.slide', which uses a sliding-window approach.

Results

The structure of the genetic data

We identified two clusters in our sample (Supplementary Figure S1-1a) using the post-hoc criterion of Evanno et al. (2005). Furthermore, the plot of intra-individual ancestries showed that the genetic groups closely reflected the trees' morphological classification (Supplementary Figure S1-1b). The ancestry of most of the studied trees derived almost exclusively from just one of the genetic groups (qi<0.15 or qi>0.85). These trees were considered to be ‘purebreds'. However, a significant number of the trees (13.5%), most of which came from the two British populations, had more balanced levels of shared ancestry (0.15<qi<0.85). Simulations including a prior based on morphological classification (see Supplementary File 1 and Supplementary Figure S1-3) provided statistical support for the hypothesis that this shared ancestry was due to admixture.

Heterozygosity and differentiation

The two oak species were found to have similar levels of genetic diversity and allelic richness (Supplementary File 2). The mean heterozygosity values for Q. petraea and Q. robur were 0.874 and 0.875, respectively, whereas the corresponding mean allelic richness values were 23.0 and 24.8. A total of 19 SSRs had interspecific FST values differing significantly from zero after the Holm–Bonferroni correction. All LGs studied contained at least one marker with a significant FST value. The estimated values for the differentiation parameter D (Jost, 2008) were much larger than those for FST. All of the confidence intervals for D excluded zero, indicating significant interspecific differentiation for all 30 markers.

Outlier tests

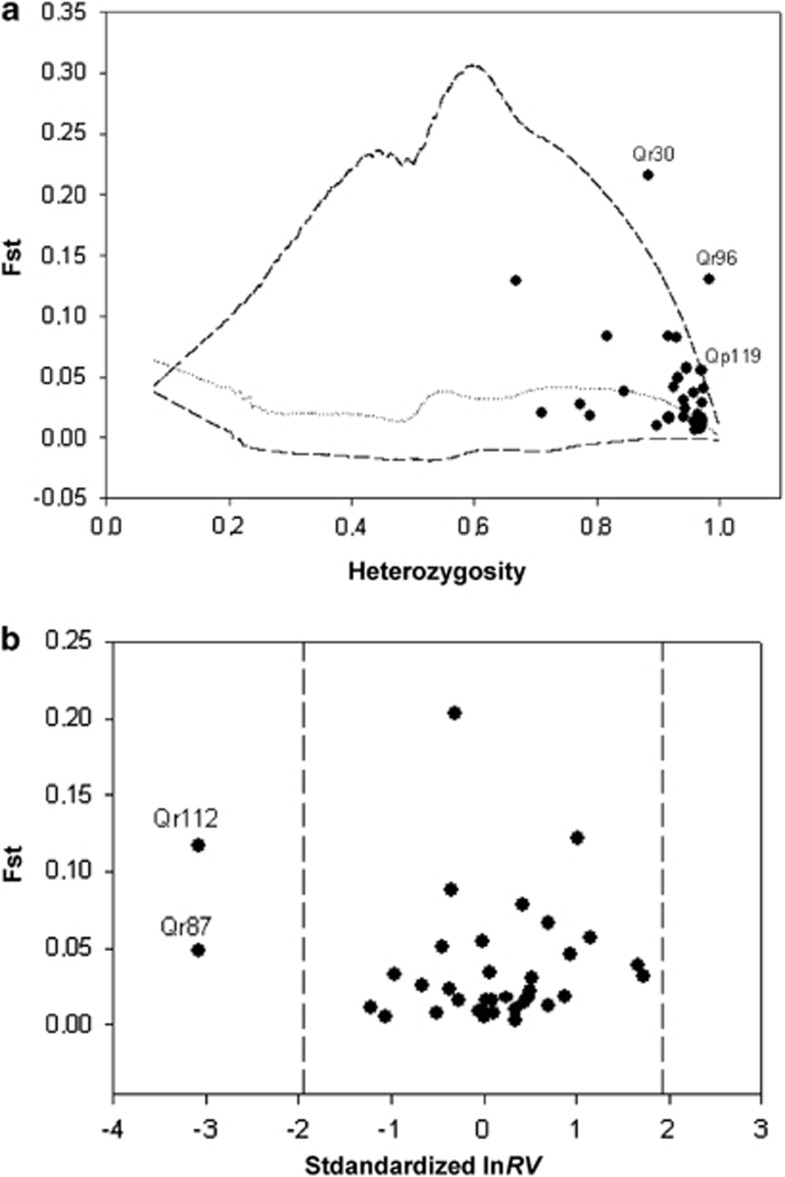
The various methods used to search for outlier loci yielded complex results. In particular, none of the markers was identified as an outlier by every test applied. Two tests (F𝒟ℐ𝒮𝒯2, using the SMM, and ln RV) were sufficient to discover all five candidate loci for positive selection (Figure 2); the other tests either provided redundant information or identified candidate loci for balancing selection (Supplementary Table S3-1).

Figure 2.

Figure 2

Open in a new tab

Detection of differentiation outlier markers using two outlier detection methods: F𝒟ℐ𝒮𝒯2 (using the SMM for coalescent simulations) and ln RV. In the first chart, (a) the observed heterozygosity is plotted against the differentiation values. The 95% envelope (dashed lines) and the median (dotted line) obtained from the coalescent simulations are also plotted. In the second chart, (b) the standardized ln RV estimates are plotted against the differentiation values. Dashed lines indicate the limits of the 95% confidence interval (−1.96, +1.96).

At least part of the observed heterogeneity in the selection signal is likely to be due to differences in the models underpinning the different tests, as shown in Supplementary Figure S3-2. Markers for which the heterozygosity was much lower in one species than in the other (for example, Qr30, Qr96 or even Qp119) were outliers in tests based on FST–heterozygosity comparisons. Markers that had fewer alleles at the distribution tails in one species (Qr87, Qr112) were outliers in the ln RV test statistic. The Bayesian test, which is the only one that models migration, detected one marker with reduced heterozygosity (Qr96) and one marker with reduced variation in the number of repeats (Qr112).

Genotypic linkage disequilibrium

Only two markers located 5 cM apart in LG2 (Qp46 and Qr87) showed significant LD in both species (Supplementary File 6, Supplementary Table S6-1). One of the involved loci (Qr87) was identified as a significant outlier based on the ln RV test statistic.

Haplotype sharing among individuals and between species

We used three criteria to evaluate the confidence in the haplotypes inferred using Pℋ𝒜𝒮ℰ: (1) the coincidence of the haplotypes obtained from five independent Bayesian chains, (2) the goodness of fit between the inferred haplotypes and an approximate coalescent with recombination (Supplementary File 4) and (3) the probabilities assigned by Pℋ𝒜𝒮ℰ to the inferred haplotypes (Supplementary Figure S4-1). Furthermore, we found that the two reconstruction methods (Pℋ𝒜𝒮ℰ and the ELB algorithm) infer similar haplotypes and similar haplotypic LD patterns. As a result, the following discussion focuses exclusively on the haplotype sharing and haplotypic LD results obtained using Pℋ𝒜𝒮ℰ. See Supplementary File 4 and Supplementary Tables S6-2,3 for results obtained using the ELB algorithm.

Despite the low number of shared haplotypes and their low frequencies (Supplementary Table S4-1), almost two-thirds of the trees carried at least one shared haplotype. As expected, shared haplotypes were slightly easier to reconstruct (that is, had higher probabilities) than unique haplotypes (Supplementary Figure S4-1, left panel). The medians of the probability values for all the inferred haplotypes were rather large for all LGs harboring putatively selected loci (LG2: 0.80; LG10: 0.96; and LG12: 0.76). For LG9, three-marker haplotypes were reconstructed with lower confidence (median value=0.69), this was probably partly due to the lower sample size and partly because of a lower LD in this case (see below). Comparisons between the two species showed that Q. petraea haplotypes were reconstructed with higher confidence than Q. robur haplotypes in LG2 and LG12, whereas the opposite pattern was found for LG10 (Supplementary Figure S4-1, right panel). We attribute this to heterozygosity differences at the corresponding loci (see Supplementary File 2).

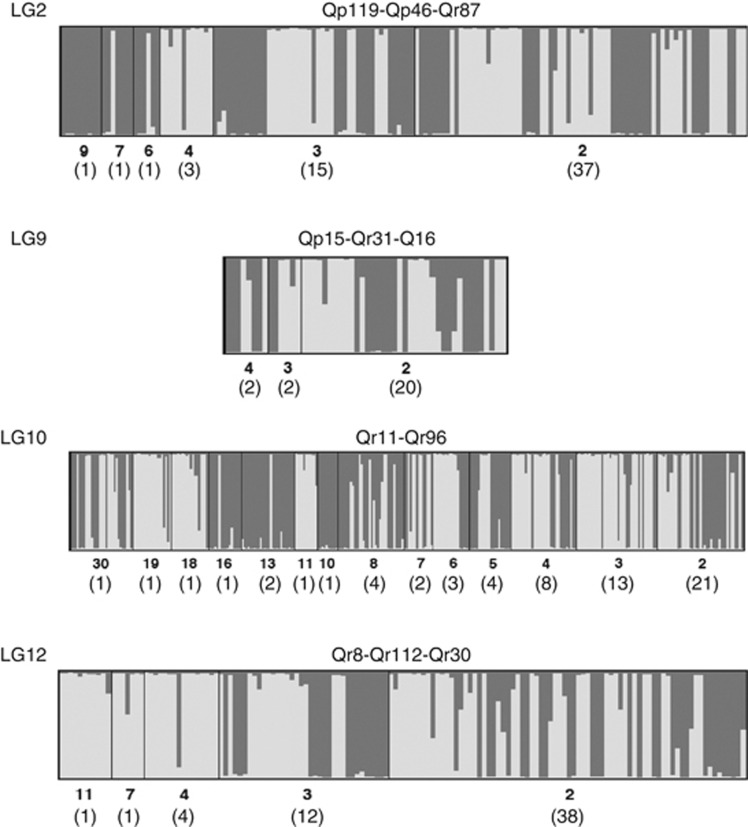
High-frequency haplotypes were species-specific in LG2, LG10 and LG12, whereas in LG9 they were shared across species (Figure 3). Note that in LG10, the most frequent haplotype was shared between the two species but other frequent haplotypes were species-specific.

Figure 3.

Figure 3

Open in a new tab

Intra vs interspecific haplotype sharing around chromosome fragments that are probably under selection (LG2, LG10 and LG12) and in the control segment with no selection signals (LG9). Inferred haplotypes are represented by vertical bars (light and dark grays for Q. petraea and Q. robur, respectively). Haplotype frequencies (in order of decreasing frequency from left to right) and the number of different haplotypes with such frequencies (in brackets) are indicated below the plots.

Recombination estimates

Coalescent modeling was used to estimate background recombination rates using haplotypic data as the starting point. Only Bayesian chains that used the ‘oak priors' and the small recombination probability reached convergence (Supplementary File 5). Therefore, we report only estimates obtained with these priors (Table 2). The rate of recombination within LG10, which includes a segment that is putatively under positive selection, was more than ten times lower than that within control segments from LG9. Bayesian chains reached convergence for recombination estimates in LG12, but longer chains were needed to ensure accurate point estimates (Supplementary File 5). Despite this, the results obtained suggest that the background recombination rate for this region is 15 times lower than that for the control, and that the rate for the Qr112–Qr30 region, which was also inferred to be under directional selection, is even lower.

Table 2. Population genetics recombination estimates ( ρ , background recombination) in segments Qp119–Qp46–Qr87 (LG2), Qp15–Qr31–Q16 (LG9), Qr11–Qr96 (LG10) and Qr8–Qr112–Qr30 (LG12).

ρ   r1a r2a
‘Oak priors' (μ=0.04, f=10 000)
 LG2b NA NA NA
 LG9 0.0337 0.99 0.99
 LG10 0.0022 0.73 NA
 LG12 0.0014 0.94 0.69
Open in a new tab

Abbreviations: LG, linkage group; NA, not available.

a

Recombination within each of the two-marker segments (r1–r2) is given as a function of the background recombination.

b

Bayesian chains failed to converge.

LD using haplotype inferences

Considering only markers in H–W equilibrium, we found significant LD at LG2 in both species (Supplementary Table S6-2). Several allele pairs showed large contributions to the disequilibrium (Table 3). The only other region in Q. petraea with markers at H–W equilibrium is the Qr112–Qr30 segment. The global LD test was not significant for this region (Supplementary Table S6-2), as would be expected for such a large segment. Two other regions in Q. robur were at H–W equilibrium (Qr11–Qr96 and Qr8–Qr112). The global LD in the first of these regions was not significant, although one haplotype was not at equilibrium. The last segment showed significant global LD and an excess of several high-frequency haplotypes (Table 3 and Supplementary Table S6-2).

Table 3. LD analyses using haplotypes inferred by Phase.

Markers Q. petraea
 Q. robur
  Haps a Obs b Exp b D′ij c Prob d Haps a Obs b Exp b D′ij c Prob d
Qp119-Qp46 13-219 6 2.8 0.20 0.026 10-202 15 14.7 0.01 0.907
  18-199 6 3.3 0.16 0.086 10-194 8 4.3 0.38 0.024
  13-205 4 1.3 0.35 0.009 10-205 5 3.7 0.16 0.388
  22-191 4 1.4 0.39 0.016 10-208 5 2.5 0.46 0.045
  36-191 4 0.9 0.76 0.000 10-193 4 2.5 0.28 0.222
  18-191 0 3.6 −1.00 0.024 17-202 4 2.8 0.16 0.394
            10-191 0 4.0 −1.00 0.013
            10-199 0 2.8 −1.00 0.041
                     
Qp46-Qr87 199-19 18 4.0 0.70 0.000 202-17 22 11.9 0.34 0.000
  191-22 15 5.4 0.44 0.000 202-26 15 5.1 0.79 0.000
  186-20 9 2.5 0.48 0.000 194-23 9 1.7 0.59 0.000
  219-23 8 1.9 0.47 0.000 198-27 4 0.3 0.65 0.000
  219-22 7 3.8 0.21 0.050 205-24 4 0.9 0.28 0.000
  195-20 6 1.7 0.46 0.000 216-23 4 0.9 0.51 0.000
  191-21 4 3.6 0.02 0.803 202-23 2 5.9 −0.66 0.042
  191-19 0 4.3 −1.00 0.012 191-17 0 3.2 −1.00 0.032
  199-22 0 5.0 −1.00 0.006 194-17 0 3.5 −1.00 0.025
            202-24 0 3.4 −1.00 0.024
                     
Qr11-Qr96e 6-07 16 9.9 0.29 0.009 12-03 16 15.4 0.10 0.746
  12-09 12 10.1 0.11 0.397 7-03 14 14.0 0.01 0.981
  12-03 12 9.3 0.16 0.232 15-03 13 11.2 0.38 0.294
  6-09 9 9.0 0.00 0.991 16-03 11 14.7 −0.25 0.064
  12-08 6 4.7 0.16 0.421 17-03 10 10.5 −0.04 0.784
  6-08 6 4.2 0.21 0.255 18-03 7 7.7 −0.09 0.647
  6-05 4 4.2 −0.04 0.918 8-03 6 4.2 1.00 0.101
  7-07 4 1.2 0.58 0.003 14-03 5 5.6 −0.10 0.647
  12-07 2 11.1 −0.82 0.000 26-03 5 3.5 1.00 0.135
  6-03 3 8.3 −0.64 0.014 27-03 5 3.5 1.00 0.135
            11-03 4 4.9 −0.18 0.458
            19-03 4 4.9 −0.18 0.458
            17-10 4 1.0 0.30 0.001
                     
Qr8-Qr112e 30-13 17 16.4 0.10 0.760 18-13 9 3.7 1.00 0.000
  18-13 14 13.4 0.12 0.745 39-13 9 4.5 0.69 0.005
  31-13 8 6.0 1.00 0.090 31-13 6 4.1 0.32 0.214
  39-13 8 6.7 0.56 0.311 41-13 6 6.2 −0.03 0.918
  19-13 6 4.5 1.00 0.145 42-18 6 1.6 0.59 0.000
  29-13 6 5.2 0.44 0.491 43-13 5 4.1 0.15 0.562
  36-13 6 6.7 −0.11 0.569          
  38-13 5 4.5 0.34 0.618          
  33-13 3 5.2 −0.43 0.047          
  40-13 3 5.2 −0.43 0.047          
                     
Qr112-Qr30f 13-07 48 53.0 −0.26 0.057 18-22 10 3.4 0.422 0.000
  14-07 17 10.2 0.63 0.001 13-15 9 5.8 0.392 0.067
  13-35 8 7.5 0.21 0.687 13-13 9 5.8 0.392 0.067
  13-32 6 4.5 1.00 0.145 13-14 5 4.1 0.149 0.562
  13-26 6 4.5 1.00 0.145 13-22 5 7.8 −0.362 0.159
  13-13 4 3.7 0.21 0.780 16-11 4 0.8 0.448 0.000
  13-27 4 4.5 −0.11 0.646 17-27 4 0.9 0.507 0.000
  12-07 4 5.8 −0.31 0.268          
Open in a new tab
a

Haplotypes in highest disequilibrium are in bold characters.

b

Only haplotypes with highest observerd (or expected) frequencies are shown.

c

Standardized disequilibrium estimates.

d

Chi-square probabilities (exact P-values).

e

Biased estimates in Q. petraea due to single marker Hardy–Weinberg disequilibrium.

f

Biased estimates in Q. robur due to single marker Hardy–Weinberg disequilibrium.

In the case of LG10 in Q. petraea, Qr96 displayed only weak deviation from H–W equilibrium frequencies, whereas Qr11 was in H–W equilibrium. Significant global LD and an excess of several high-frequency haplotypes were inferred in this region, assuming that the analyses are robust to weak departures from H–W equilibrium (Table 3 and Supplementary Table S6-2).

Haplotype score tests for association

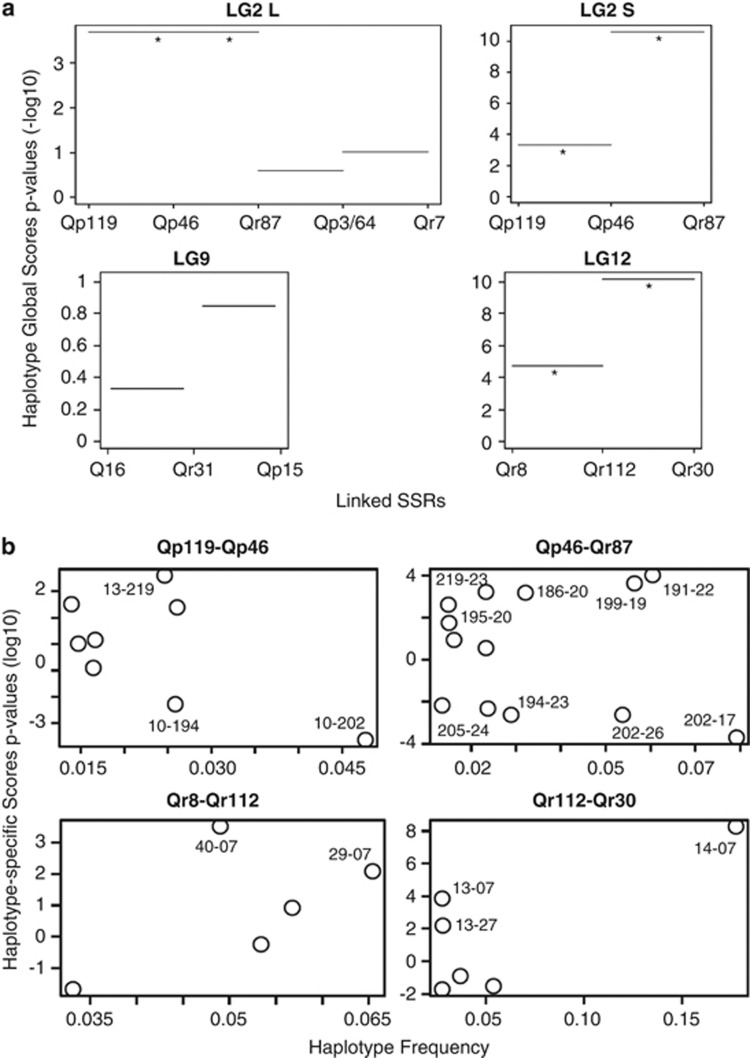
Global score tests for association between full-length haplotypes and species were significant in LG2, LG10 and LG12, but non-significant in LG9 (data not shown). The sliding-window approach (Figure 4a) showed that the tests were significant for the LG2-S region (Qp119–Qp46–Qr87), with the strongest association found for the Qp46–Qr87 segment. The two-marker haplotypes from LG12 were also significantly associated with species, this association was strongest for the Qr112–Qr30 segment. However, the tests were non-significant for the two segments from LG9.

Figure 4.

Figure 4

Open in a new tab

Haplotype score tests. (a) Global haplotype score P-values, on a logarithmic scale, are represented by horizontal bars for contiguous two-marker haplotypes. Significant scores are indicated by asterisks. (b) Logarithmic haplotype-specific scores P-values (represented by circles) are plotted against the haplotype frequencies. Significant scores are labeled with the corresponding haplotype codes. Positive scores indicate association with Q. petraea and negative scores with Q. robur.

In contrast to global scores, haplotype-specific scores can be used to determine whether the associations between haplotypes and traits are present in both species or only in one (Figure 4b). The two LG2 segments contain haplotypes that are significantly associated with both species (positive scores for Q. petraea and negative scores for Q. robur), whereas LG12 haplotypes are significantly associated with Q. petraea only (positive scores). LG10 had haplotypes associated with both species (not shown). We did not estimate haplotype-specific scores for LG9 because the global and the sliding-window tests were non-significant in this case.

Discussion

We have used haplotypic tests and recombination estimates to characterize regions surrounding differentiation outliers in oaks. Our results provide stronger evidence for directional selection than was obtained in previous studies that used multilocus data sets to search for selection signals without considering LD information, because LD between markers is expected to increase around gene(s) responding to selection (Kim and Nielsen, 2004). The number of markers used in this methodological study was substantially smaller than those typically used in current genome scans, which could create doubts about haplotype reconstructions. However, genetic distances among markers used in the haplotype reconstructions were around 5 cM. Although these distances might be close to the upper limits for haplotype reconstruction, the haplotype probabilities obtained (which depend on the homozygosity of the data) were quite high. This was probably due in part to our decision to reconstruct haplotypes in segments showing strong selection signals and which thus exhibit reduced heterozygosity. Note that the reduced population recombination rates observed in such segments probably mean that the genetic distances obtained in the controlled crosses progenies were overestimated in relation to the effective recombination rate observed in natural populations. Overall, the clear detection of LD signals, reduced rates of recombination and strong associations with particular species achieved with these haplotypic analyses makes them very promising for the analysis of divergence hitchhiking.

As noted before, outlier detection methods appear to be partly redundant and partly complementary. This suggests the need to use several outlier methods to detect selection signals corresponding to different evolutionary scenarios (Przeworski, 2002; Przeworski et al., 2005; Kim, 2006). For instance, the method based on the loss of rare alleles (ln RV) can probably detect older selection footprints than methods based on heterozygosity differences (F𝒟ℐ𝒮𝒯2, B𝒜𝒴ℰ𝒮F𝒮𝒯, ln RH), because heterozygosity recovers faster than allelic richness following a bottleneck (Nei et al., 1975). On the other hand, multiple testing increases the risk of false positives (Narum and Hess, 2011). Therefore, we performed three types of tests to further characterize the regions surrounding differentiation outliers: a search for frequent haplotypes with extended LD, a comparison of population genetics recombination estimates in regions that are potentially under selection and in control regions, and score tests for association between frequent haplotypes and species status.

The first of these analyses is essentially a simple long-range LD test. These tests have been used extensively in fine-scale LD mapping and association studies (McPeek and Strahs, 1999; Sabeti et al., 2002; Butty et al., 2007; Curtis et al., 2008), investigations of genome-wide epistatic interactions (Zhang and Liu, 2007) and in gene flow and introgression studies (Koopman et al., 2007). A direct comparison of LD among segments with and without outliers was not possible due to large Hardy–Weinberg disequilibrium at two of the three linked loci in the control region. Nevertheless, our recombination estimates indicate that the LD should be lower in the control region than in regions of similar length containing outlier loci. One limitation of our analyses is the potential bias in LD estimates due to uncertainties in haplotype reconstructions. However, the agreement between the two haplotype reconstruction methods, the large probabilities for the two-marker haplotypes inferred using reconstructions based on the coalescent and the uniqueness of most low-probability haplotypes should considerably reduce this risk. On the other hand, LD could be increased by several biological and historical factors besides divergent selection, including admixture (Gaut and Long, 2003). However, we do not believe that the sampling of different populations from each species presents a problem in our study because: first, high-frequency haplotypes were not exclusive to one population (data not shown), and second, the two temperate European oaks exhibit little differentiation among populations (Zanetto et al., 1993).

The second test estimates the population genetics recombination parameter (ρ), which is expected to decrease under divergence hitchhiking (Via, 2009). We are not aware of any previous use of this parameter in such a context, but it seems to be a very promising tool for detecting reduced rates of recombination around the genes that are responding to divergent selection. Although there seems to be a need for further fine-tuning before this approach can be generalized, our estimates indicate that regions around putatively selected genes do indeed exhibit reduced effective recombination relative to control regions.

The third approach used score tests to identify associations between frequent haplotypes and species. Score tests have been widely used for haplotype association studies in humans (North et al., 2006; Li and Schaid, 2009). In principle, these tests could be sensitive to existing interspecific genetic structure. However, the association score tests were in good agreement with both the haplotypic LD estimates (LG2, LG10) and the outlier tests (LG12). Moreover, the differences revealed by the sliding-window analyses of LG2 suggest that these tests have enough sensitivity to differentiate between putatively selected and neutral regions located in the same linkage group. However, it remains to be determined whether H–W disequilibrium could affect the conclusions obtained with these tests (Schaid et al., 2002).

Advantages of haplotypic approaches for studying divergent selection

As noted previously, the search for ecological speciation footprints is one of the main causes for the increase in the number of studies dealing with divergent selection and outlier tests. Ascertaining the actual environmental causes leading to divergent selection is one of the major challenges in such studies. This has been partly solved with the application of several indirect methods, such as co-location with QTLs (Rogers and Bernatchez, 2005) or the search of parallel outliers in replicate pairs of populations (Bonin et al., 2006). However, these methods do not solve another problem arising from allele frequencies-based outlier methods, that is, whether outliers are caused by directional or divergent (bi-directional) selection. One major advantage of haplotypic LD and score tests is that they can detect selective pressures affecting either both species in question or only one of them (Figure 5). Conversely, allele frequencies-based differentiation outlier methods can only detect selection in the species with the lower heterozygosity (F𝒟ℐ𝒮𝒯2, ln RH), variance in number of repeats (ln RV) or migration rate (B𝒜𝒴ℰ𝒮F𝒮𝒯). Our results based on haplotype reconstruction point to simultaneous divergent (that is, bi-directional) selection in at least two out of the three linkage groups harboring outlier markers, suggesting that both oak species are evolving according to their own trajectories, rather than there being a situation in which only one of the two species is actively diverging from the other. Such insights into the selection type (that is, divergent vs directional) can only be obtained by the use of haplotype-based methods. If used more broadly, these methods could greatly improve the characterization of divergent selection in nature.

Figure 5.

Figure 5

Open in a new tab

Comparison among selection signals detected by single-locus methods (differentiation outliers tests, circles) and methods that account for haplotypic information (LD, arrows; Score Tests, rectangles). The symbol patterns indicate whether selection signals were detected in both species (hatched) or in only one of them (empty, Q. petraea; filled, Q. robur). Approximate distances (cM) between markers are given to the left of the linkage groups.

Overall, our results indicate that haplotypic approaches may be uniquely powerful in studies of divergent selection. As such, they should now be adapted and scaled-up to analyze larger data sets (for example, Galindo et al., 2010; Baxter et al., 2011; Hohenlohe et al., 2011). Higher marker density will improve the probabilities of the inferred haplotypes, thereby further increasing the confidence in haplotypic analyses.

Data archiving

Full genotypes and metadata, together with Supplementary Information files, are stored at the Dryad repository (provisional 10.5061/dryad.099s2).

Acknowledgments

This study was conducted with the financial support from the Commission of the European Communities, via the ‘Quality of life and Management of Living resources' research Program (Project OAKFLOW QLK5-2000-00960). RJP was supported by the LINKTREE project from the Eranet Biodiversa programme (ANR-08-BDVA-006). We are indebted to project partners who provided samples (J Buiteveld, K Burg, J Cottrell, L Gil, F Gugerli, A König, M Lascoux, A Lowe), to EM Gillet and F Raspail for compiling updated versions of G𝒮ℰ𝒟 and Pℰℛℳ𝒰𝒯, and to SC González-Martínez and P Garnier-Géré for critical reading and helpful discussions. Three anonymous referees are also acknowledged for criticism that improved the manuscript. PGG is thankful to the Pierroton group for their warm welcome during a half-sabbatical year that triggered the ideas developed in this study. PGG, RJP and AK are supported by the EU network of excellence EVOLTREE.

The authors declare no conflict of interest.

Footnotes

Supplementary Information accompanies the paper on Heredity website (http://www.nature.com/hdy)

Supplementary Material

Supplementary File 1
Click here for additional data file. (333KB, doc)
Supplementary File 2
Click here for additional data file. (68.5KB, doc)
Supplementary File 3
Click here for additional data file. (347KB, doc)
Supplementary File 4
Click here for additional data file. (744KB, doc)
Supplementary File 5
Click here for additional data file. (429KB, doc)
Supplementary File 6
Click here for additional data file. (464.5KB, doc)

References

  1. Abramoff MD, Magelhae PJ, Ram SJ. Image processing with ImageJ. Biophoton Int. 2004;11:36–42. [Google Scholar]
  2. Akey J, Lin J, Xiong M. Haplotypes vs single marker linkage disequilibrium tests: what do we gain. Eur J Hum Genet. 2001;9:291–300. doi: 10.1038/sj.ejhg.5200619. [DOI] [PubMed] [Google Scholar]
  3. Apple JL, Grace T, Joern A, Amand PS, Wisely SM. Comparative genome scan detects host-related divergent selection in the grasshoper Hesperotettix viridis. Mol Ecol. 2010;19:4012–4028. doi: 10.1111/j.1365-294X.2010.04792.x. [DOI] [PubMed] [Google Scholar]
  4. Armitage P. Tests for linear trends in proportions and frequencies. Biometrics. 1955;11:375–386. [Google Scholar]
  5. Bader JS. The relative power of SNPs and haplotypes as genetic markers for association tests. Pharmacogenomics. 2001;2:11–24. doi: 10.1517/14622416.2.1.11. [DOI] [PubMed] [Google Scholar]
  6. Barreneche T, Bodénès C, Lexer C, Trontin JF, Fluch S, Streiff R, et al. A genetic linkage map of Quercus robur L (pedunculate oak) based on RAPD, SCAR, microsatellite, minisatellite, isozyme and 5S rDNA markers. Theor Appl Genet. 1998;97:1090–1103. [Google Scholar]
  7. Baxter SW, Davey JW, Johnston JS, Shelton AM, Heckel DG, Jiggins CD, et al. Linkage mapping and comparative genomics using next-generation RAD sequencing of a non-model organism. PLoS ONE. 2011;6:e19315. doi: 10.1371/journal.pone.0019315. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Beaumont MA, Balding DJ. Identifying adaptive genetic divergence among populations from genome scans. Mol Ecol. 2004;13:969–980. doi: 10.1111/j.1365-294x.2004.02125.x. [DOI] [PubMed] [Google Scholar]
  9. Beaumont MA, Nichols RA. Evaluating loci for use in the genetic analysis of population structure. Proc R Soc Lond B Biol Sci. 1996;263:1619–1626. [Google Scholar]
  10. Bierne N. The distinctive footprints of local hitchhiking in a varied environment and global hitchhiking in a subdivided population. Evolution. 2010;64:3254–3272. doi: 10.1111/j.1558-5646.2010.01050.x. [DOI] [PubMed] [Google Scholar]
  11. Bonin A, Taberlet P, Miaud C, Pompanon F. Explorative genome scan to detect candidate loci for adaptation along a gradient of altitude in the common frog (Rana temporaria) Mol Biol Evol. 2006;23:773–783. doi: 10.1093/molbev/msj087. [DOI] [PubMed] [Google Scholar]
  12. Bowcock AM, Kidd JR, Mountain JL, Herbert JM, Carotenuto L, Kidd KK, et al. Drift, admixture and selection in human evolution: a study with DNA polymorphisms. Proc Natl Acad Sci USA. 1991;88:839–843. doi: 10.1073/pnas.88.3.839. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Braverman JM, Hudson RR, Kaplan NL, Langley CH, Stephan W. The hitchhiking effect on the site frequency spectrum of DNA polymorphisms. Genetics. 1995;140:783–796. doi: 10.1093/genetics/140.2.783. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Butty V, Roy M, Sabeti P, Besse W, Benoist C, Mathis D. Signatures of strong population differentiation shape extended haplotypes across the human CD28, CTLA4, and ICOS costimulatory genes. Proc Natl Acad Sci USA. 2007;104:570–575. doi: 10.1073/pnas.0610124104. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Clark AG. The role of haplotypes in candidate gene studies. Genet Epidemiol. 2004;27:321–333. doi: 10.1002/gepi.20025. [DOI] [PubMed] [Google Scholar]
  16. Crawford D, Bhangale T, Li N, Hellenthal G, Rieder M, Nickerson D, et al. Evidence for substantial fine-scale variation in recombination rates across the human genome. Nat Genet. 2004;36:700–706. doi: 10.1038/ng1376. [DOI] [PubMed] [Google Scholar]
  17. Crawford NG. SMOGD: a software for the measurement of genetic diversity. Mol Ecol Res. 2010;10:556–557. doi: 10.1111/j.1755-0998.2009.02801.x. [DOI] [PubMed] [Google Scholar]
  18. Curtis D, Vine AE, Knight J. Study of regions of extended homozygosity provides a powerful method to explore haplotype structure of human populations. Ann Hum Genet. 2008;72:261–278. doi: 10.1111/j.1469-1809.2007.00411.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Devlin B, Roeder K. Genomic control for association studies. Biometrics. 1999;55:997–1004. doi: 10.1111/j.0006-341x.1999.00997.x. [DOI] [PubMed] [Google Scholar]
  20. Dow BD, Ashley MV, Howe HF. Characterization of highly variable (GA/CT)n microsatellites in the bur oak, Quercus macrocarpa. Theor Appl Genet. 1995;91:137–141. doi: 10.1007/BF00220870. [DOI] [PubMed] [Google Scholar]
  21. Egan SP, Nosil P, Funk DJ. Selection and genomic differentiation during ecological speciation: isolating the contributions of hos-association via a comparative genome scan of Neochlamisus bebbianae leaf beetles. Evolution. 2008;62:1162–1181. doi: 10.1111/j.1558-5646.2008.00352.x. [DOI] [PubMed] [Google Scholar]
  22. El Mousadik A, Petit RJ. High level of genetic differentiation for allelic richness among populations of the argan tree (Argania spinosa L. Skeels) endemic of Morocco. Theor Appl Genet. 1996;92:832–839. doi: 10.1007/BF00221895. [DOI] [PubMed] [Google Scholar]
  23. Evanno G, Regnaut S, Goudet J. Detecting the number of clusters of individuals using the software structure: a simulation study. Mol Ecol. 2005;14:2611–2620. doi: 10.1111/j.1365-294X.2005.02553.x. [DOI] [PubMed] [Google Scholar]
  24. Excoffier L, Laval G, Balding D. Gametic phase estimation over large genomic regions using and adaptive window approach. Hum Genomics. 2003;1:7–19. doi: 10.1186/1479-7364-1-1-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Excoffier L, Lischer HEL. Arlequin suite ver. 3.5: a new series of programs to perform population genetic analysis under Linux and Windows. Mol Ecol Res. 2010;10:564–567. doi: 10.1111/j.1755-0998.2010.02847.x. [DOI] [PubMed] [Google Scholar]
  26. Excoffier L, Slatkin M. Maximum-likelihood estimation of molecular haplotype frequencies in a diploid population. Mol Biol Evol. 1995;12:921–927. doi: 10.1093/oxfordjournals.molbev.a040269. [DOI] [PubMed] [Google Scholar]
  27. Falush D, Stephens M, Pritchard JK. Inference of population structure using multilocus genotype data: linked loci and correlated allele frequencies. Genetics. 2003;164:1567–1587. doi: 10.1093/genetics/164.4.1567. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Galindo J, Grahame JW, Butlin RK. An EST based genome scan using 454 sequencing in the marine snail Littorina saxatiles. J Evol Biol. 2010;23:2004–2016. doi: 10.1111/j.1420-9101.2010.02071.x. [DOI] [PubMed] [Google Scholar]
  29. Gaut BS, Long AD. The lowdown on linkage disequilibrium. Plant Cell. 2003;15:1502–1506. doi: 10.1105/tpc.150730. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Goudet J.2001Fstat, a program to estimate and test gene diversities and fixation indices (v. 2.9.3)Available from http://www2.unil.ch/popgen/softwares/fstat.htm . Updated from Goudet (1995).
  31. Goudet J, Raymond M, de Meeüs T, Rousset F. Testing differentiation in diploid populations. Genetics. 1996;144:1933–1940. doi: 10.1093/genetics/144.4.1933. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Guo S, Thompson E. Performing the exact test of Hardy-Weinberg proportion for multiple alleles. Biometrics. 1992;48:361–372. [PubMed] [Google Scholar]
  33. Hohenlohe PA, Amish SJ, Catchen JM, Allendorf FW, Luikart G. Next-generation RAD sequencing identifies thousand of SNPs for assessing hybridization between rainbow and wastslope cutthroat trout. Mol Ecol Res. 2011;11:117–122. doi: 10.1111/j.1755-0998.2010.02967.x. [DOI] [PubMed] [Google Scholar]
  34. Hudson RR, Bailey K, Skarecky D, Kwiatowski J, Ayala FJ. Evidence for positive selection in the superoxide dismutase (Sod) region of Drosophila melanogaster. Genetics. 1994;136:1329–1340. doi: 10.1093/genetics/136.4.1329. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Jakobsson M, Rosenberg NA. CLUMPP: a cluster matching and permutation program for dealing with label switching and multimodality in analysis of population structure. Bioinformatics. 2006;23:1801–1806. doi: 10.1093/bioinformatics/btm233. [DOI] [PubMed] [Google Scholar]
  36. Jaramillo-Correa JP, Verdú M, González-Martínez SC. The contribution of recombination to heterozygosity differs among plant evolutionary lineages and life-forms. BMC Evol Biol. 2010;10:22. doi: 10.1186/1471-2148-10-22. [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Joost S, Bonin A, Bruford MW, Després L, Conord C, Erhardt G, et al. A Spatial Analysis Method (SAM) to detect candidate loci for selection: towards a landscape genomics approach to adaptation. Mol Ecol. 2007;16:3955–3969. doi: 10.1111/j.1365-294X.2007.03442.x. [DOI] [PubMed] [Google Scholar]
  38. Jost L. G𝒮𝒯 and its relatives do not measure differentiation. Mol Ecol. 2008;17:4015–4026. doi: 10.1111/j.1365-294x.2008.03887.x. [DOI] [PubMed] [Google Scholar]
  39. Kampfer S, Lexer C, Glössl J, Steinkellner H. Characterization of (GA)n microsatellite loci from Quercus robur. Hereditas. 1998;129:183–186. [Google Scholar]
  40. Kauer M, Dieringer D, Schlötterer C. A microsatellite variability screen for positive selection associated with the ‘out of Africa' habitat expansion of Drosophila melanogaster. Genetics. 2003;165:1137–1148. doi: 10.1093/genetics/165.3.1137. [DOI] [PMC free article] [PubMed] [Google Scholar]
  41. Kim Y. Allele frequency distribution after recurrent selective sweeps. Genetics. 2006;172:1967–1978. doi: 10.1534/genetics.105.048447. [DOI] [PMC free article] [PubMed] [Google Scholar]
  42. Kim Y, Nielsen R. Linkage disequilibrium as a signature of selective sweeps. Genetics. 2004;167:1512–1524. doi: 10.1534/genetics.103.025387. [DOI] [PMC free article] [PubMed] [Google Scholar]
  43. Kimura M, Crow JF. The number of alleles that can be maintained in a finite population. Genetics. 1964;49:725–738. doi: 10.1093/genetics/49.4.725. [DOI] [PMC free article] [PubMed] [Google Scholar]
  44. Kohn M, Pelz HJ, Wayne RK. Natural selection mapping of the warfarin-resistance gene. Proc Natl Acad Sci USA. 2000;97:7911–7915. doi: 10.1073/pnas.97.14.7911. [DOI] [PMC free article] [PubMed] [Google Scholar]
  45. Koopman WJM, Li S, Coart E, Van de Weg E, Vosman B, Roldán-Ruiz I, et al. Linked vs. unlinked markers: multilocus microsatellite haplotype-sharing as a tool to estimate gene flow and introgression. Mol Ecol. 2007;16:243–256. doi: 10.1111/j.1365-294X.2006.03137.x. [DOI] [PubMed] [Google Scholar]
  46. Kremer A, Dupouey JL, Deans JD, Cottrell J, Csaikl U, Finkeldey R, et al. Leaf morphological differentiation between Quercus robur and Quercus petraea is stable across western European mixed oak stands. Ann For Sci. 2002;59:777–787. [Google Scholar]
  47. Lepais O, Gerber S. Reproductive patterns shape introgression dynamics and species succession within the European white oaks complex. Evolution. 2011;65:156–170. doi: 10.1111/j.1558-5646.2010.01101.x. [DOI] [PubMed] [Google Scholar]
  48. Lepais O, Petit RJ, Guichoux E, Lavabre JE, Alberto F, Kremer A, et al. Species relative abundance and direction of introgression in oaks. Mol Ecol. 2009;18:2228–2242. doi: 10.1111/j.1365-294X.2009.04137.x. [DOI] [PubMed] [Google Scholar]
  49. Lewontin RC, Krakauer J. Distribution of gene frequency as a test of the theory of the selective neutrality of polymorphisms. Genetics. 1973;74:175–195. doi: 10.1093/genetics/74.1.175. [DOI] [PMC free article] [PubMed] [Google Scholar]
  50. Li N, Stephens M. Modeling linkage disequilibrium and identifying recombination hotspots using single-nucleotide polymorphism data. Genetics. 2003;165:2213–2233. doi: 10.1093/genetics/165.4.2213. [DOI] [PMC free article] [PubMed] [Google Scholar]
  51. Li WY, Schaid DJ. Power comparison between similarity-based multilocus association methods, logistic regression and score tests for haplotypes. Genet Epidemiol. 2009;33:183–197. doi: 10.1002/gepi.20364. [DOI] [PMC free article] [PubMed] [Google Scholar]
  52. Liu N, Zhang K, Zhao H. Haplotype-association analysis. Adv Genet. 2008;60:335–405. doi: 10.1016/S0065-2660(07)00414-2. [DOI] [PubMed] [Google Scholar]
  53. Mariette S, Cottrell J, Csaikl UM, Goicoechea PG, König A, Lowe AJ, et al. Comparison of levels of diversity detected with AFLP and microsatellite markers within and among mixed Q. petraea (Matt.) Liebl. and Q. robur L. stands. Silvae Genet. 2002;51:72–79. [Google Scholar]
  54. Maynard-Smith JM, Haigh J. The hitch-hiking effect of a favourable gene. Genet Res. 1974;23:23–35. [PubMed] [Google Scholar]
  55. McPeek MS, Strahs A. Assessment of linkage disequilibrium by the decay of haplotype sharing, with application to fine-scale genetic mapping. Am J Hum Genet. 1999;65:858–875. doi: 10.1086/302537. [DOI] [PMC free article] [PubMed] [Google Scholar]
  56. McVean G. The structure of linkage disequilibrium around a selective sweep. Genetics. 2007;175:1395–1406. doi: 10.1534/genetics.106.062828. [DOI] [PMC free article] [PubMed] [Google Scholar]
  57. Michel AP, Sim S, Powell THQ, Taylor MS, Nosil P, Feder JL. Widespread genomic divergence during sympatric speciation. Proc Natl Acad Sci USA. 2010;107:9724–9729. doi: 10.1073/pnas.1000939107. [DOI] [PMC free article] [PubMed] [Google Scholar]
  58. Muir G, Schlötterer C. Evidence for shared ancestral polymorphism rather than recurrent gene flow at microsatellite loci differentiating two hybridizing oaks (Quercus spp.) Mol Ecol. 2005;14:549–561. doi: 10.1111/j.1365-294X.2004.02418.x. [DOI] [PubMed] [Google Scholar]
  59. Muller CH. Ecological control of hybridization in Quercus: a factor in the mechanism of evolution. Evolution. 1952;6:147–161. [Google Scholar]
  60. Murray MC, Hare MP. A genomic scan for divergent selection in a secondary contact zone between Atlantic and Gulf of Mexico oysters, Crassostrea virginica. Mol Ecol. 2006;15:4229–4242. doi: 10.1111/j.1365-294X.2006.03060.x. [DOI] [PubMed] [Google Scholar]
  61. Narum S, Hess JE. Comparison of FST outlier tests for SNP loci under selection. Mol Ecol Res. 2011;11:184–194. doi: 10.1111/j.1755-0998.2011.02987.x. [DOI] [PubMed] [Google Scholar]
  62. Nei M. Analysis of gene diversity in subdivided populations. Proc Natl Acad Sci USA. 1973;70:3321–3323. doi: 10.1073/pnas.70.12.3321. [DOI] [PMC free article] [PubMed] [Google Scholar]
  63. Nei M, Maruyama T, Chakraborty R. The bottleneck effect and genetic variability in populations. Evolution. 1975;29:1–10. doi: 10.1111/j.1558-5646.1975.tb00807.x. [DOI] [PubMed] [Google Scholar]
  64. Nordborg M, Hu TT, Ishino Y, Jhaveri J, Toomajian C, Zheng H, et al. The pattern of polymorphism in Arabidopsis thaliana. PLoS Biol. 2005;3:1289–1299. doi: 10.1371/journal.pbio.0030196. [DOI] [PMC free article] [PubMed] [Google Scholar]
  65. North BV, Sham PC, Knight J, Martin ER, Curtis D. Investigation of the ability of haplotype association and logistic regression to identify associated susceptibility loci. Ann Hum Genet. 2006;70:893–906. doi: 10.1111/j.1469-1809.2006.00301.x. [DOI] [PubMed] [Google Scholar]
  66. Nosil P, Egan SP, Funk DJ. Heterogeneous genomic differentiation between walking-stick ecotypes: ‘isolation by adaptation' and multiple roles for divergent selection. Evolution. 2007;62:316–336. doi: 10.1111/j.1558-5646.2007.00299.x. [DOI] [PubMed] [Google Scholar]
  67. Nosil P, Feder JL. Genomic divergence during speciation: causes and consequences. Philos Trans R Soc Lond B Biol Sci. 2012;367:332–342. doi: 10.1098/rstb.2011.0263. [DOI] [PMC free article] [PubMed] [Google Scholar]
  68. Nosil P, Funk DJ, Ortiz-Barrientos D. Divergent selection and heterogeneous genomic divergence. Mol Ecol. 2009;18:375–402. doi: 10.1111/j.1365-294X.2008.03946.x. [DOI] [PubMed] [Google Scholar]
  69. Ohta T, Kimura M. A model of mutation appropriate to estimate the number of electrophoretically detectable alleles in a finite population. Genet Res. 1973;22:201–204. doi: 10.1017/s0016672300012994. [DOI] [PubMed] [Google Scholar]
  70. Parelle J, Brendel O, Jolivet Y, Dreyer E. Intra- and interspecific diversity in the response to waterlogging of two co-ocurring white oak species (Quercus robur and Q. petraea) Tree Physiol. 2007;27:1027–1034. doi: 10.1093/treephys/27.7.1027. [DOI] [PubMed] [Google Scholar]
  71. Petit RJ, Bodénès C, Ducousso A, Roussel G, Kremer A. Hybridization as a mechanism of invasion in oaks. New Phytol. 2004;161:151–164. [Google Scholar]
  72. Poncet BN, Herrmann D, Gugerli F, Taberlet P, Holderegger R, Gielly L, et al. Tracking genes of ecological relevance using a genome scan in two independent regional population samples of Arabis alpine. Mol Ecol. 2010;19:2896–2907. doi: 10.1111/j.1365-294X.2010.04696.x. [DOI] [PubMed] [Google Scholar]
  73. Ponton S, Dupouey JL, Bréda N, Dreyer E. Comparison of water-use efficiency of seedlings from two sympatric oak species: genotype x environment interactions. Tree Physiol. 2002;22:413–422. doi: 10.1093/treephys/22.6.413. [DOI] [PubMed] [Google Scholar]
  74. Prida A, Ducousso A, Puech J-L, Petit RJ, Nepveu G. Variation in wood volatile compounds in a mixed oak stand: strong species and spatial differentiation in whisky-lactone content. Ann For Sci. 2007;64:313–320. [Google Scholar]
  75. Pritchard JK, Stephens M, Donnelly P. Inference of population structure using multilocus genotype data. Genetics. 2000;155:945–959. doi: 10.1093/genetics/155.2.945. [DOI] [PMC free article] [PubMed] [Google Scholar]
  76. Przeworski M. The signature of positive selection at randomly chosen loci. Genetics. 2002;160:1179–1189. doi: 10.1093/genetics/160.3.1179. [DOI] [PMC free article] [PubMed] [Google Scholar]
  77. Przeworski M, Coop G, Wall JD. The signature of positive selection on standing genetic variation. Evolution. 2005;59:2312–2323. [PubMed] [Google Scholar]
  78. R Development Core Team 2010R: A Language and Environment for Statistical Computing R Foundation for Statistical Computing: Vienna, Austria; ISBN 3-900051-07-0,. . http://www.R-project.org . [Google Scholar]
  79. Raymond M, Rousset F. An exact test for population differentiation. Evolution. 1995;49:1280–1283. doi: 10.1111/j.1558-5646.1995.tb04456.x. [DOI] [PubMed] [Google Scholar]
  80. Rogers SM, Bernatchez L. Integrating QTL mapping and genome scans towards the characterization of candidate loci under parallel selection in the lake whitefish (Coregonus clupeaformis) Mol Ecol. 2005;14:351–361. doi: 10.1111/j.1365-294X.2004.02396.x. [DOI] [PubMed] [Google Scholar]
  81. Rosenberg NA. Distruct: a program for the graphical display of population structure. Mol Ecol Notes. 2004;4:137–138. [Google Scholar]
  82. Sabeti PC, Reich DE, Higgins JM, Haninah Z, Levine P, Richter DJ, et al. Detecting recent positive selection in the human genome from haplotype structure. Nature. 2002;419:832–837. doi: 10.1038/nature01140. [DOI] [PubMed] [Google Scholar]
  83. Savolainen V, Anstett M-C, Lexer C, Hutton I, Clarkson JJ, Norup MV, et al. Sympatric speciation in palms in an oceanic island. Nature. 2006;441:2010–2013. doi: 10.1038/nature04566. [DOI] [PubMed] [Google Scholar]
  84. Schaid DJ, Rowland CM, Tines DE, Jacobson RM, Poland GA. Score tests for association between traits and haplotypes when linkage phase is ambiguous. Am J Hum Genet. 2002;70:425–434. doi: 10.1086/338688. [DOI] [PMC free article] [PubMed] [Google Scholar]
  85. Schlötterer C. A microsatellite-based multilocus screen for the identification of local selective sweeps. Genetics. 2002;160:753–763. doi: 10.1093/genetics/160.2.753. [DOI] [PMC free article] [PubMed] [Google Scholar]
  86. Schluter D. The Ecology of Adaptive Radiation. Oxford University Press, Oxford, UK; 2000. [Google Scholar]
  87. Scotti-Saintagne C, Mariette S, Porth I, Goicoechea PG, Barreneche T, Bodénès C, et al. Genome scanning for interspecific differentiation between two closely related oak species [Quercus robur L and Q. petraea (Matt.) Liebl.] Genetics. 2004;168:1615–1626. doi: 10.1534/genetics.104.026849. [DOI] [PMC free article] [PubMed] [Google Scholar]
  88. Sinnwell JP, Schaid DJ.2009haplo.stats: Statistical analysis of haplotypes with traits and covariates when linkage phase is ambiguousR package version 1.44. . http://mayoresearch.mayo.edu/mayo/research/schaid_lab/software.cfm .
  89. Smadja G, Galindo J, Butlin R. Hitching a lift on the road to speciation. Mol Ecol. 2008;17:4177–4180. doi: 10.1111/j.1365-294x.2008.03917.x. [DOI] [PubMed] [Google Scholar]
  90. Steinkellner H, Fluch S, Turetschek E, Lexer C, Streiff R, Kremer A, et al. Identification and characterization of (GA/CT)n microsatellite loci from Quercus petraea. Plant Mol Biol. 1997;33:1093–1096. doi: 10.1023/a:1005736722794. [DOI] [PubMed] [Google Scholar]
  91. Stephens M, Donnelly P. A comparison of Bayesian methods for haplotype reconstruction. Am J Hum Genet. 2003;73:1162–1169. doi: 10.1086/379378. [DOI] [PMC free article] [PubMed] [Google Scholar]
  92. Stephens M, Smith NJ, Donnelly P. A new statistical method for haplotype reconstruction from population data. Am J Hum Genet. 2001;68:978–989. doi: 10.1086/319501. [DOI] [PMC free article] [PubMed] [Google Scholar]
  93. Streiff R, Ducousso A, Lexer C, Steinkellner H, Glössl J, Kremer A. Pollen dispersal inferred from paternity analysis in a mixed oak stand of Quercus robur L and Quercus petraea (Matt.) Liebl. Mol Ecol. 1999;8:831–841. [Google Scholar]
  94. Via S. Natural selection in action during speciation. Proc Natl Acad Sci USA. 2009;106 (suppl. 1:9939–9946. doi: 10.1073/pnas.0901397106. [DOI] [PMC free article] [PubMed] [Google Scholar]
  95. Via S. Divergence hitchhiking and the spread of genomic isolation during ecological speciation with gene flow. Philos Trans R Soc Lond B Biol Sci. 2012;367:451–460. doi: 10.1098/rstb.2011.0260. [DOI] [PMC free article] [PubMed] [Google Scholar]
  96. Via S, West J. The genetic mosaic suggests a new role for hitchhiking in ecological speciation. Mol Ecol. 2008;17:4334–4345. doi: 10.1111/j.1365-294X.2008.03921.x. [DOI] [PubMed] [Google Scholar]
  97. Weir BS, Cockerham CC. Estimating F-statistics for the analysis of population structure. Evolution. 1984;38:1358–1370. doi: 10.1111/j.1558-5646.1984.tb05657.x. [DOI] [PubMed] [Google Scholar]
  98. Zanetto A, Kremer A, Labbé T. Differences of genetic variation based on isozymes of primary and secondary metabolism in Quercus petraea. Ann For Sci. 1993;50:245–252. [Google Scholar]
  99. Zeng YF, Liao WJ, Petit RJ, Zhang D-Y. Exploring species limits in two closely related Chinese oaks. PLoS One. 2010;5:e15529. doi: 10.1371/journal.pone.0015529. [DOI] [PMC free article] [PubMed] [Google Scholar]
  100. Zhang Y, Liu JS. Bayesian inference of epistatic interactions in case-control studies. Nat Genet. 2007;39:1167–1173. doi: 10.1038/ng2110. [DOI] [PubMed] [Google Scholar]
  101. Zoldo V, Pape D, Brown SC, Panaud O, Iljak-Yakovlev S. Genome size and base composition of several Quercus species: inter- and intra-population variation. Genome. 1988;41:162–168. [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary File 1
Click here for additional data file. (333KB, doc)
Supplementary File 2
Click here for additional data file. (68.5KB, doc)
Supplementary File 3
Click here for additional data file. (347KB, doc)
Supplementary File 4
Click here for additional data file. (744KB, doc)
Supplementary File 5
Click here for additional data file. (429KB, doc)
Supplementary File 6
Click here for additional data file. (464.5KB, doc)

Articles from Heredity are provided here courtesy of Nature Publishing Group

RESOURCES