Genome scanning for detecting adaptive genes along environmental gradients in the Japanese conifer, Cryptomeria japonica

Abstract

Local adaptation is important in evolutionary processes and speciation. We used multiple tests to identify several candidate genes that may be involved in local adaptation from 1026 loci in 14 natural populations of Cryptomeria japonica, the most economically important forestry tree in Japan. We also studied the relationships between genotypes and environmental variables to obtain information on the selective pressures acting on individual populations. Outlier loci were mapped onto a linkage map, and the positions of loci associated with specific environmental variables are considered. The outlier loci were not randomly distributed on the linkage map; linkage group 11 was identified as a genomic island of divergence. Three loci in this region were also associated with environmental variables such as mean annual temperature, daily maximum temperature, maximum snow depth, and so on. Outlier loci identified with high significance levels will be essential for conservation purposes and for future work on molecular breeding.

Introduction

Local adaptation is important in evolutionary processes and speciation (Hoffmann and Willi, 2008; Stapley et al., 2010). It occurs over relatively long periods of time in plant populations with long generation times, such as forest tree species. The process of local adaptation involves the genetic divergence of specific loci in populations inhabiting different environments. Once identified, these loci can be used for conservational purposes, for future forestation, and to study the mechanisms by which trees adapt to specific environments. Forest tree species have not been as extensively domesticated as crop species, and natural populations are still abundant. By identifying and studying adaptive genes in these natural populations, it is possible to gain new insights into the adaptive mechanisms that allow them to flourish in the wild (Neale and Savolainen, 2004; González-Martínez et al., 2006; Neale, 2007; Savolainen and Pyhäjärvi, 2007; Savolainen et al., 2007; Neale and Ingvarsson, 2008; Grattapaglia et al., 2009). This is facilitated by certain properties of forest tree species: they typically have relatively low genetic differentiation between populations on average, are widely distributed in different environments and have relatively large population sizes. Consequently, the selective pressures acting on a population in a given environment tend to result in adaptation by selecting for a relatively small number of genotype changes at a few specific loci (Howe et al., 2003; Holliday et al., 2010; Pelgas et al., 2011).

Genome scanning is an effective and useful method for detecting genetic differentiation and candidate genes associated with specific phenotypes or environmental variables in forest tree species (Eveno et al., 2008; Namroud et al., 2008; Eckert et al., 2010; Holliday et al., 2010; Neale and Kremer, 2011; Prunier et al., 2011). Recently developed multiple genotyping methods have greatly reduced the cost of single-nucleotide polymorphism (SNP) genotyping. Thus, multiple-marker-based neutrality tests are frequently used for detecting functional DNA variations. The most widely used ‘outlier tests' are multiple-population tests such as the F_ST-based test (Beaumont and Nichols, 1996), the coalescent-based simulation approach (Vitalis et al., 2001) and the lnRv test based on the Gaussian null distribution (Kauer et al., 2003). The Bayesian method implemented in BayeScan has the advantage that it estimates population-specific F_ST coefficients, thereby accounting for different demographic histories and different amounts of genetic drift between populations (Foll and Gaggiotti, 2008). When identifying outlier loci, it is generally necessary to use multiple tests in order to minimize the false-positive rate; however, false positives remain common even when using multiple methods and multitest correction (Pérez-Figueroa et al., 2010). It is therefore important to validate the detected outlier loci in multiple ways to determine whether or not they genuinely are adaptive. Luikart et al. (2003) suggested several ways to confirm outlier behavior and selection, including considering their genomic location, quantitative trait locus mapping and testing for genotyping errors.

Cryptomeria japonica is an allogamous coniferous species that relies on wind-mediated pollen and seed dispersal. Modern natural forests of the species are distributed across various different environments in the Japanese Archipelago, from Aomori Prefecture (40° 42′ N) to Yakushima Island (30° 15′ N) (Hayashi, 1960). However, its distribution is discontinuous and scattered across small, restricted areas as a result of its extensive exploitation over the last thousand years (Ohba, 1993). The geographical variation between natural forests of C. japonica has been investigated, focusing on both morphological traits (needle length, needle curvature and other features; Murai, 1947) and diterpene components (Yasue et al., 1987). The results of these studies suggest that there are two main lines: ura-sugi (C. japonica var. radicans, found near the Sea of Japan) and omote-sugi (C. japonica, located near the Pacific Ocean). The ura-sugi variety has slender branchlets with soft leaves, while the omote-sugi variety has rough branchlets with hard leaves (Yamazaki, 1995). A previous study focusing on 148 cleaved amplified polymorphic sequence loci revealed genetic differentiation between the two varieties, and four outlier loci were identified as potential local adaptation genes (Tsumura et al., 2007) that may be associated with the genetic differentiation between the varieties.

In the study reported herein, we identified potential local adaptation genes at 1026 loci using two tests and also studied the relationships between specific SNPs and environmental variables such as climate data to investigate the selective pressures acting on the studied populations. The linkage map positions of outlier loci that were associated with specific environmental variables are also discussed.

Materials and methods

Investigated populations

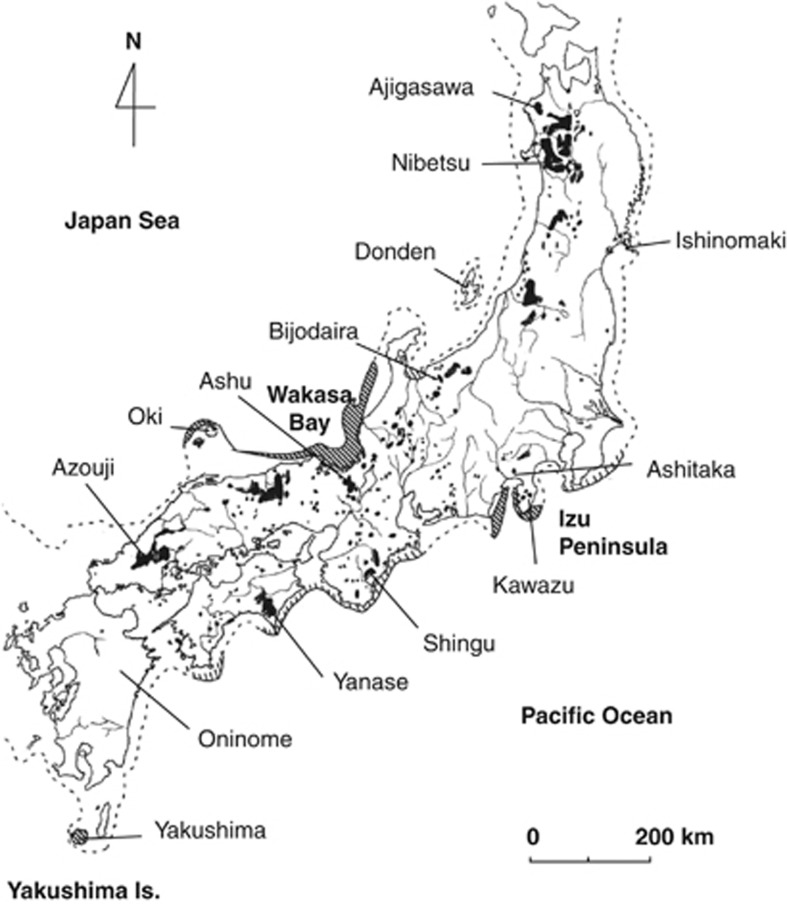
We examined 14 populations in this study with 186 individuals in total (the average number of individuals per population was 13.29): seven from the Japan Sea side of Japan and seven from the Pacific Ocean side (Table 1). All trees sampled were growing in national forests that were candidates for in situ gene-conservation programs. The locations of the sampled populations covered most of the natural distribution of C. japonica (Figure 1, Tsumura et al., 2007).

Table 1. Locations and environment variables for 14 investigated natural populations in C. japonica.

Population	Abbreviation	Latitude	Longitude	Altitude (m)	Number of individuals	Mean annual temperature (°C)	Mean daily maximum temperature (°C)	Mean daily minimum temperature (°C)	Annual precipitation (mm)	Annual sunshine hours (h)	Amount of global solar radiation (MJ m−2)	Deepest snow (cm)
Ajigasawa	AJG	40.44.53	140.12.54	110	14	9.7	13.7	5.9	1312.3	1711.5	12.3	70
Nibetsu	NBT	39.48.22	140.15.36	320	15	11.3	15.2	7.6	1701.2	1593.7	11.8	37
Ishinomaki	ISN	38.19.43	141.29.31	190	13	11.1	14.3	8.5	1276.3	1972.4	13.1	7
Donden	DND	38.08.23	138.23.00	730	14	9.9	13.0	6.8	2184.0	1658.7	12.7	99
Bijodaira	BJD	36.34.55	137.27.55	1000	16	7.8	11.6	3.7	2884.4	1552.2	12.9	171
Ashitaka	AST	35.12.30	138.49.90	1000	17	8.2	11.4	4.3	2886.1	1857.7	14.0	37
Kawazu	KWZ	34.49.53	139.00.00	650	8	15.9	19.1	12.9	2921.6	1830.1	12.5	1
Ashu	ASH	35.18.28	135.46.26	700	18	9.3	13.8	5.4	2379.4	1523.4	12.4	55
Oki	OKI	36.16.60	133.19.45	360	9	11.9	15.7	8.3	1873.9	1782.5	13.2	29
Azouji	AZJ	34.46.70	132.06.12	360	16	12.0	17.3	7.1	2220.4	1635.9	12.8	43
Shingu	SNG	33.49.24	135.45.36	170	16	14.2	20.0	9.3	2870.5	1834.0	12.8	2
Yanase	YNS	33.35.40	134.05.80	500	8	12.9	18.1	8.8	3739.7	2004.6	14.2	2
Oninome	ONN	32.42.06	131.31.43	960	6	10.2	15.1	5.9	2762.2	1884.7	14.0	2
Yakushima	YKU	30.18.17	130.34.17	1100	16	13.3	15.6	11.1	4119.7	1559.8	13.6	0

Figure 1.

Natural distribution of C. japonica in Japan (shaded areas; from Hayashi, 1960) and the locations of the 14 natural populations surveyed in this study. The dotted line indicates the coastline ca. 18 000 years ago. Areas shaded in bold or within thin diagonal lines show established refugia (Izu Peninsula, Wakasa Bay, Oki Island and Yakushima Island) and probable refugia, respectively, at that time (Tsukada, 1986).

SNP genotyping

We selected one SNP each from 1536 unique expressed sequence tag contigs in C. japonica. This assumes implicitly that SNPs within different expressed sequence tag contigs are independent (that is, unlinked). The identification of SNPs was carried out previously and was accomplished through the resequencing of 5170 unique expressed sequence tag contigs in a discovery panel of four C. japonica individuals collected from a range-wide sample of trees (Uchiyama et al., 2012). Multiplexed genotyping of SNP markers for natural populations was carried out using Illumina's 1536-plex GoldenGate array (Illumina Inc., San Diego, CA, USA) according to the protocol recommended by the manufacturer. A total of 0.5–1.0 μg of genomic DNA per sample (at a rate of 100–200 ng μl⁻¹) was used in each GoldenGate assay. Only SNPs with Illumina design scores above 0.6 were used. When multiple SNPs were available within the same sequence, a single highly polymorphic SNP was selected as the target for that sequence. The GoldenGate assay uses highly multiplexed allele-specific extension methods and universal PCR amplification reactions. The PCR products, which were fluorescently labeled by using the 5′-labeled primers P1 (Cy3) and P2 (Cy5), were hybridized to capture probes on the beads in the array. The ratio of the fluorescent signals from two allele-specific ligation products was used to determine the genotype. Signal intensities were quantified and matched to specific alleles, using the Genome Studio v2010.2 software package in Illumina BeadArray Reader (Illumina Inc.). The quality of the GoldenGate genotype scores for individual SNPs was assessed based on their GenTrain cluster and GenCall genotype scores in GenomeStudio (Illumina Inc.). A minimum GenCall50 (GC₅₀) score of 0.25 was chosen as the threshold for inclusion of SNP loci in the final data set, and genotypic clusters were edited manually when necessary. In the present study, this threshold corresponded to SNPs with accurate scoring for at least 95% of the individuals, with most successful SNPs scored for over 99% of the individuals analyzed.

Genetic structure

To evaluate the within-population variation, we used the proportion of polymorphic loci (Pl) at the 95% probability level, the unbiased heterozygosity (H_e), (Nei, 1977) and allelic richness (R_s) calculated from the allele frequencies of all loci analyzed. Allelic richness was measured by the method of El Mousadik and Petit (1996) with a reference sample size of 6. The fixation indices, F_IS=1−H_e/H_o, for polymorphic loci and their averages over all loci were determined to compare the observed genotype frequencies with expectations based on the Hardy–Weinberg equilibrium (Wright, 1922; Nei, 1977; Nei and Chesser, 1983). Deviations from such expectations were analyzed using Fisher's exact test. Coefficients of gene differentiation, F_ST, among populations, were calculated to determine how gene diversity was partitioned at each level (Wright, 1978). These analyses were done using the FSTAT software package (Goudet, 2000) and GenAlEx (Peakall and Smouse, 2006). To detect population structure and infer the most appropriate number of subpopulations (K) for interpreting the data without prior information on the number of locations at which the populations were sampled, we used the F-model of Bayesian clustering approach proposed by Pritchard et al. (2000). For this analysis, we excluded 184 loci with high linkage disequilibrium (LD) values (χ² test, significant at 99% level after Bonferroni correction), 141 outlier loci that were detected by Fdist2 analysis and a locus that was distorted from the Hardy–Weinberg equilibrium. Ten independent runs with K values ranging from 1 to 10 were performed using 2 × 10⁶ MCMC (Marcov chain Monte Carlo) sampling after a burn-in period of 50 000 iterations. The posterior probability was then calculated for each value of K using the estimated log likelihood of K to identify the optimal K value. The optimal number of K was defined as the one at which the log likelihood of the data, ln P(X|K) (Pritchard et al., 2000) or ΔK, the rate of change of ln P(X|K) between successive K values (Evanno et al., 2005), was maximal. To examine the genetic differentiation between two groups representing the two varieties, C. japonica and C. japonica var. radicance, we performed a hierarchical analysis of molecular variance (Excoffier et al., 1992) in which the significance levels for variance components were tested using permutations.

Methods for detecting candidate loci for divergence

The following methods were used to detect signs of natural selection and to tentatively identify the environmental parameters associated with the corresponding selective pressures acting on C. japonica populations. We also compared the distributions of the F_ST values over all loci to their expected distributions under the assumption of neutrality. Beaumont and Nichols (1996) have shown that the distribution of F_ST as a function of heterozygosity in the context of an island model is quite robust, that is, insensitive to variations in factors such as population structure, demographic structure and mutation level. We therefore used this method to identify markers deviating from the null hypothesis of neutral evolution. All calculations for identifying potential non-neutral genes in the studied populations were performed using the Fdist2 (Beaumont and Nichols, 1996) and Arlequin programs (Excoffier and Lischer, 2010). Arlequin program allows us the hierarchical analysis using two genetic lines such as ura-sugi and omote-sugi varieties. In the analysis using Fdist2, we identified the outlier loci using not only all 14 populations but also each variety populations such as seven ura-sugi populations and seven omote-sugi populations.

An alternative method for identifying candidate loci is BayeScan, which uses a Bayesian method to directly estimate a posterior probability for each locus and a reversible-jump MCMC approach to selection (Foll and Gaggiotti, 2008). The main advantage of BayeScan is that it estimates population-specific F_ST coefficients and therefore accommodates differences in demographic history and the extent of genetic drift between populations. This method is an extension of that proposed by Beaumont and Balding (2004), and it is based on a logistic regression model that decomposes genetic variation into population- and locus-specific effects. Preliminary tests were conducted using a burn-in of 10 000 iterations, a thinning interval of 50 and a sample size of 10 000 (Foll and Gaggiotti, 2008). Four independent runs were performed for each of the two data sets to account for the consistency of the detected outliers. The loci were ranked according to their estimated posterior probability and all loci with a value over 0.990 were retained as outliers. This corresponds to a log₁₀ Bayes factor of more than 2, making it possible to be confident in the validity of the model.

The gathering of environmental data for each population and the identification of correlations with the genetic data

Environmental information on the area of origin of each population, including longitude, latitude, altitude, mean annual temperature, mean annual precipitation, annual sunshine hours, amount of global solar radiation and maximum snow depth over 30 years (1971–2000) was obtained from the Japan Meteorological Agency (2002), in the form of detailed 1-km mesh data. We used information from the 1-km mesh data to estimate the mean annual temperature, precipitation and snowfall, and so on, for each site using the program in Mesh climatic data of Japan of the Japan Meteorological Agency (2002).

To calculate correlations between SNP allele frequencies and climate variables, we used the Bayesian linear model method of Coop et al. (2010), which controls for population history by incorporating a covariance matrix of populations and that accounts for differences in sample size among populations. Using the full set of SNPs, we estimated a covariance matrix of allele frequencies across populations. This covariance matrix was used as the basis of the null model for the transformed allele frequencies at each SNP to be tested. For each tested SNP, the method generates a Bayes factor as a measure of the support for the alternative model relative to the null model, in which the transformed population allele frequency distribution is dependent on population structure alone. The significance threshold for ranked Bayes factors was set to 2.0, and the environmental variables considered were latitude, longitude and ten climate variables. All climate variables were standardized before analysis. In this analysis, we included the geographical information such as latitude and longitude to find out the false positives because they are sometimes correlated with some environmental variables.

Putative functions for the detected outlier loci were identified by performing BLASTx searches of the NCBI database using Blast2GO (Conesa et al., 2005, Supplementary Table 1).

Mapping the outlier loci on the linkage map, and LD

The YI pedigree used to determine the positions of the outlier loci of C. japonica had previously been used to construct a linkage map, in which a total of 438 markers were assigned to 11 large linkage groups (LGs) and some small or nonintegrated LGs, giving a total map length of 1372.2 cM (Tani et al., 2003). The mapped population was genotyped using Illumina's 1536-plex GoldenGate array, as discussed above. All linkage analyses and map estimations were performed using the JoinMap v3.0 software package (Van Ooijen and Voorrips, 2001). During map construction, markers were assigned to tentative LGs by comparing the linkages formed at logarithm of odds thresholds ranging from 3.0 to 9.0, increasing in increments of 1.0. Finally, the markers were ordered at a logarithm of odds threshold of 8.0. Map distances were calculated using the Kosambi mapping function (Kosambi, 1944).

Coefficients of LD were calculated as described by Weir (1996), using squared allele–frequency correlations (r²) for pairs of loci on the basis of genotype data from the investigated populations. The differences from equilibrium were verified by the χ² tests (Weir, 1996). These analyses were performed using the GDA software package (Lewis and Zaykin, 2002).

Assuming a random distribution of markers, if the genome were divided into N intervals, the number of markers per interval would follow a Poisson distribution. To determine whether outlier loci were randomly distributed, every LG was divided into 15, 20, 25 and 50-cM intervals. We used the χ² test to compare the actual distribution of outlier loci to that expected for a Poisson distribution, as described by Kang et al. (2010).

Results

SNP genotyping

Of the 1536 SNPs, 1031 (67.1%) yielded data that met our quality thresholds according to the GoldenGate genotyping system (Uchiyama et al., 2012). The median GC₅₀ score across all usable SNPs was 0.81, with an average call rate of 98.6%. A minimum GenCall50 (GC50) score of 0.30 was chosen for inclusion of SNP loci in the final data set and genotypic clusters were edited manually as needed. Of those 1031 SNPs, 5 were monomorphic and were therefore discarded. The remaining 1026 SNPs were used in subsequent analyses.

Genetic structure

The Pl values for the SNPs ranged from 0.786 to 0.951 with an average of 0.901. The R_s values also varied, from 1.569 to 1.794 with an average of 1.721, and the H_e values ranged from 0.292 to 0.320 with an average of 0.311 (Table 2). In contrast to findings from previous studies, these parameters do not reveal any clear geographical trends (Takahashi et al., 2005; Tsumura et al., 2007). The average F_IS value for all loci was not significantly different from expectations under the Hardy–Weinberg equilibrium except for one locus, SNPg04215.

Table 2. Genetic diveristy of 14 investigated populations in C. japonica based on 1023 SNPs.

Population a	Number of investigated individuals	Ho	Unbiased He	Pl	RS	FIS
AJG	14	0.304	0.304	0.890	1.739	0.000
NBT	15	0.305	0.314	0.925	1.766	0.029
ISN	14	0.312	0.318	0.916	1.738	0.020
DND	16	0.309	0.312	0.930	1.776	0.008
BJD	18	0.314	0.314	0.951	1.794	−0.001
AST	9	0.311	0.311	0.865	1.684	−0.001
KWZ	16	0.311	0.314	0.928	1.731	0.012
ASH	13	0.311	0.318	0.942	1.768	0.025
OKI	17	0.301	0.308	0.919	1.764	0.022
AZJ	8	0.312	0.309	0.850	1.657	−0.009
SNG	16	0.306	0.313	0.940	1.767	0.023
YNS	8	0.312	0.320	0.875	1.602	0.026
ONN	6	0.298	0.304	0.786	1.569	0.021
YKU	16	0.284	0.292	0.900	1.736	0.027
Mean	13.3	0.306	0.311	0.901	1.721	0.015

Abbreviation: SNPs, single-nucleotide polymorphisms.

^aSee Table 1.

The overall genetic differentiation among populations at the 1026 loci was low (F_ST=0.0391). We also conducted an analysis of molecular variance to determine the variation within and among groups (the two varieties) and populations, and to test the significance of the among-population variation. The variation among populations was 7.72% and was highly significant (P<0.001), while the proportions of variance among varieties and among populations within varieties were 2.74% and 4.98%, respectively.

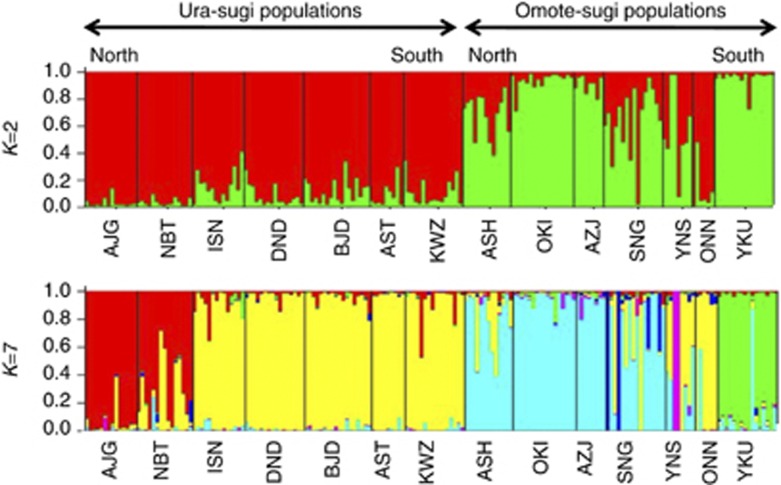
Bayesian clustering of the information from the 743 loci after excluding the outlier loci demonstrated that the models with K=2 and K=7 both provided satisfactory explanations of the observed data, as judged by the delta K and the highest log-likelihood values, respectively (Supplementary Figure 1). Both of the bar plots for K=2 and K=7 revealed clear differences between populations of the two varieties with the exception of the Oninome population (Figure 2). In addition, the bar plot for K=7 separated the populations for each variety. The ura-sugi variety populations were divided into two groups, with the first consisting of two northern populations and the second containing all the others. Conversely, the omote-sugi populations were divided into three major groups. The first comprised four northern populations, the southernmost population from Yakushima and two others. The two other omote-sugi population groups carried a higher proportion of ura-sugi-type alleles.

Figure 2.

Genetic relationships among the 14 populations surveyed using STRUCTURE (Pritchard et al., 2000) based on 1023 SNPs. The model with K=2 and K=7 showed the delta K value and the highest log-likelihood value, respectively.

Outlier loci

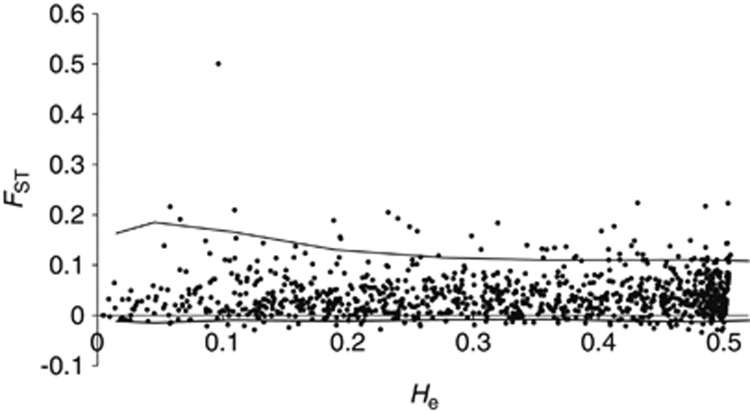
Using the F_ST-based method (Fdist2), we identified 63 loci lying outside the 99% confidence interval (upper), and an additional 40 loci that were also outside (below) the CI (Figure 3). The method of considering the hierarchical structure, such as ura-sugi and omote-sugi varieties, using Arlequin was identified for yet another 34 loci (Table 3). BLASTx searches identified putative functions for 41 of these loci (65% Table 3).

Figure 3.

Distribution of F_ST values as a function of the within-population heterozygosity (H_e) based on 1026 loci in C. japonica. The envelope of values (99% confidential interval) corresponds to neutral expectations in the infinite-allele model constructed according to the method of Beaumont and Nichols (1996).

Table 3. Outlier loci detected by Fdist2 (P<0.99), Arlequin (P<0.99) and BayeScan (Bayes factor >2) analyses, and their linkage group and putative function by BLASTx search (E-value cutoff ⩽1 × 10⁻³).

Locus	Fdist2					Arlequin FST	BayeScan			Linkage group	Putative function
	All populations			Omote	Ura	P value	All populations	Omote	Ura
	He	FST	P				P
SNPg03850	0.4314	0.2237	0.0000	*	*	0.0010	0.0000		*	—	No hit
SNPg04215	0.0965	0.5006	0.0000	*		0.0000	0.0062			7	Endo-1,4-beta-glucanase
SNPg01385	0.5036	0.2231	0.0000			0.0004	0.0000			—	No hit
SNPg04024	0.4856	0.2173	0.0000	*		0.0004	0.0000			11	MYBPA1 protein
SNPg01330	0.2321	0.2050	0.0000	*		0.0002	0.0000			11	Adenosine 3′-phospho 5′-phosphosulfate transporter
SNPg04607	0.2399	0.1927	0.0000		*	0.0017	0.0016			—	No hit
SNPg04808	0.3198	0.1837	0.0001	*		0.0026				3	Leucine-rich repeat receptor protein kinase EXS precursor
SNPg02882	0.4127	0.1772	0.0001				0.0032			2	Putrescine aminopropyltransferase-related protein
SNPg05302	0.4025	0.1679	0.0001		*					—	Dead box ATP-dependent RNA helicase
SNPg02447	0.2492	0.1766	0.0002		*		0.0060			—	Amidophosphoribosyltransferase
SNPg00860	0.2554	0.1675	0.0004			0.0030	0.0022			6	No hit
SNPg00921	0.2987	0.1582	0.0005	*				*		—	GDSL-motif lipase hydrolase family protein
SNPg04111	0.4737	0.1490	0.0005	*						2	No hit
SNPg03578	0.4289	0.1486	0.0005	*						—	2-Hydroxyacid dehydrongenase
SNPg04480	0.1938	0.1560	0.0010	*		0.0008	0.0022			11	Glucan endo-1,3-beta-glucosidase precursor
SNPg01805	0.4264	0.1386	0.0012			0.0022				11	Glucan endo-1,3-beta-glucosidase precursor
SNPg03910	0.1887	0.1887	0.0012	*		0.0012				3	Endo-1,4-beta-glucanase
SNPg02822	0.1943	0.1525	0.0013			0.0011	0.0002			11	Methyltransferase-like protein 13-like
SNPg03082	0.4573	0.1376	0.0013			0.0008	0.0100			2	No hit
SNPg03744	0.5032	0.1437	0.0014			0.0074	0.0034			—	No hit
SNPg03195	0.5025	0.1429	0.0015			0.0019	0.0016			—	Protein-binding protein
SNPg01042	0.3742	0.1366	0.0019			0.0038	0.0028			10	Harpin-induced protein-like
SNPg03273	0.3429	0.1397	0.0019		*					11	Putative TIR/NBS/LRR disease resistance protein
SNPg01079	0.5026	0.1117	0.0022		*		0.0098		*	—	No hit
SNPg04166	0.3650	0.1342	0.0023	*			0.0082			—	No hit
SNPg00581	0.4857	0.1353	0.0025							9	No hit
SNPg04244	0.4947	0.1104	0.0025							2	Major facilitator protein
SNPg02884	0.3551	0.1324	0.0026							—	LPXTG-motif cell wall anchor domain protein
SNPg04589	0.4082	0.1313	0.0028							2	Extracellular ligand-gated ion channel
SNPg00517	0.3589	0.1310	0.0029		*					—	lon protease homolog peroxisomal-like
SNPg04896	0.4868	0.1085	0.0029							2	TIR-NBS class disease resistance protein
SNPg02875	0.3063	0.1311	0.0036							8	No hit
SNPg00066	0.0580	0.2161	0.0036	*		0.0021				2	VTC2-like protein
SNPg03555	0.5042	0.1058	0.0037							10	Strictosidine synthase family protein
SNPg05041	0.4941	0.1051	0.0039							—	No hit
SNPg01589	0.4926	0.1047	0.0040							—	S-receptor kinase
SNPg05257	0.2724	0.1186	0.0040		*					4	20-s Proteasome subunit paf1
SNPg01300	0.4314	0.1225	0.0041	*						—	Light-regulated zinc finger protein 1
SNPg01839	0.1095	0.2095	0.0043	*	*	0.0009				—	No hit
SNPg02637	0.4356	0.1210	0.0046			0.0014	0.0062			—	p-Aminobenzoate synthase
SNPg02373	0.4827	0.1109	0.0047							5	Unknown
SNPg05351	0.4849	0.1108	0.0047							5	No hit
SNPg00531	0.1106	0.1537	0.0048				0.0026			3	Chaperone protein DnaJ chloroplast
SNPg02059	0.2579	0.1161	0.0048		*					—	Aldo keto reductase
SNPg04667	0.4172	0.1104	0.0049							1	No hit
SNPg05574	0.4359	0.1101	0.0050			0.0077				10	No hit
SNPg04724	0.4084	0.1100	0.0050		*					8	Hexokinase 1
SNPg02675	0.4385	0.1100	0.0050							3	Glycoside hydrolase, family 17
SNPg01003	0.1929	0.1151	0.0052							7	Late embryogenesis-abundant hydroxyproline-rich glycoprotein
SNPg03769	0.4170	0.1220	0.0055			0.0019				7	Brassinosteroid insensitive 1-associated receptor kinase 1precursor
SNPg02786	0.3866	0.1085	0.0056							5	2-Hydroxyacid dehydrongenase
SNPg01044	0.4640	0.1174	0.0060							7	Lactoylglutathione lyase
SNPg03110	0.4545	0.1067	0.0064							10	No hit
SNPg00114	0.5056	0.1203	0.0066							2	No hit
SNPg02495	0.0659	0.1912	0.0070	*		0.0051				2	Early-responsive to dehydration 7
SNPg00236	0.2515	0.1106	0.0070							—	F-box and wd40 domain protein
SNPg02706	0.3823	0.1176	0.0076			0.0078				8	ATP-dependent RNA helicase DHX8
SNPg03565	0.4769	0.1133	0.0081			0.0080				—	Histone h4
SNPg01835	0.5041	0.1153	0.0091							10	No hit
SNPg00660	0.4872	0.1147	0.0094							8	Nitrite reductase
SNPg01833	0.3560	0.1142	0.0096		*					1	No hit
SNPg05180	0.3810	0.1141	0.0097							1	F-box-like protein
SNPg03808	0.4746	0.1106	0.0098							6	ARC6h-like protein
SNPg00006						0.0004				—	Pinus taeda anonymous locus umn_2311_01 genomic sequence
SNPg04004					*	0.0009				—	No hit
SNPg01566					*	0.0010				3	No hit
SNPg04934						0.0012				5	Ankyrin partial
SNPg01953						0.0014				6	PREDICTED: uncharacterized protein LOC100253581
SNPg05269						0.0019				7	No hit
SNPg04802						0.0020				9	Galactose oxidase-like
SNPg01166						0.0022				4	P. taeda anonymous locus 0_6264_01 genomic sequence
SNPg03800						0.0027				—	LRR-kinase protein
SNPg03964						0.0030				11	GCK domain-containing protein
SNPg02633						0.0031				9	Leucine-rich repeat transmembrane protein kinase
SNPg04798					*	0.0032				—	No hit
SNPg03049						0.0038				—	Pentatricopeptide repeat-containing
SNPg04439						0.0039				4	No hit
SNPg01041					*	0.0041				7	Cell number regulator 1
SNPg00017					*	0.0044				—	No hit
SNPg02303						0.0045				—	No hit
SNPg00923					*	0.0050				—	Acidic endochitinase-like
SNPg01152						0.0055				8	Transmembrane receptors ATP-binding protein
SNPg01574						0.0055				9	UDP-glycosyltransferase
SNPg03804						0.0057				7	No hit
SNPg00315						0.0060				—	Predicted protein (Micromonas sp. RCC299)
SNPg00024						0.0064				—	Pyruvate kinase
SNPg05588						0.0065				4	Vesicle-associated protein 4-2-like
SNPg05020						0.0067				—	No hit
SNPg02220					*	0.0072				6	DNA-binding protein
SNPg00438						0.0073				—	No hit
SNPg02428						0.0080				3	Maternal effect embryo arrest 12 protein
SNPg00094						0.0082				—	No hit
SNPg01108						0.0082				3	Unknown
SNPg00054						0.0091				—	PI-PLC × domain-containing protein at5g67130-like
SNPg00531						0.0093				—	Chaperone protein DnaJ
SNPg02256						0.0096				11	Microtubule-associated protein map65-1a
SNPg03226						0.0096				11	Vps51 Vps67 family (components of vesicular transport) protein
SNPg00161					*					—	Pseudo-response receiver
SNPg01491				*		0.0084				1	Glycoside hydrolase family 47 protein
SNPg02982					*					—	Glycosylphosphatidylinositol anchor biosynthesis protein 11
SNPg04411					*					2	Resistance gene region between conserved kinase-2 and p-loop domains
SNPg05191							0.0052			2	E3 ubiquitin-protein ligase ring1-like
SNPg00033				*						3	Yippee-like protein
SNPg00140				*	*					3	Nramp transporter
SNPg02378					*					3	No hit
SNPg00718					*					5	No hit
SNPg01667					*					—	FAD/NAD(P)-binding oxidoreductase family protein
SNPg02442					*					5	Condensation domain-containing protein
SNPg05366				*						5	Phenylalanine ammonia lyase
SNPg00892				*						—	Nucleotide-sugar transporter family protein
SNPg01169				*						7	EREBP transcription factor
SNPg02235				*						1	No hit
SNPg02348					*					7	No hit
SNPg02489				*						10	Unknown
SNPg04760				*						10	No hit
SNPg02148					*				*	11	Transmembrane protein 45B-like
SNPg02671					*					11	No hit
SNPg03025				*						11	Lysyl-tRNA synthetase
SNPg01727					*					—	FAD NAD-binding oxidoreductase family protein
SNPg01899					*					—	Unknown
SNPg03715				*						—	No hit
SNPg04159					*					—	opc-8:0 ligase1
SNPg04392				*						—	Leucine-rich repeat-containing protein
SNPg04510				*						—	No hit
SNPg04924				*						—	No hit
SNPg05020				*						—	No hit
SNPg05148				*						—	Ilectin receptor-like kinase

Abbreviation: SNP, single-nucleotide polymorphism.

Statistically siginificant level. *<0.01.

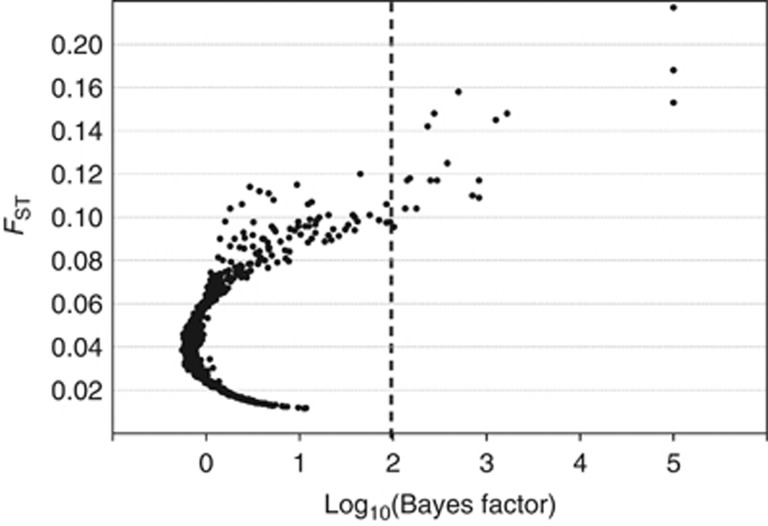
Using the Bayesian method implemented in BayeScan, we identified 52 loci as outliers with a log₁₀ Bayes factor above 1, all of which were also detected by the F_ST-based method except for SNPg05191. Of these outlier loci, 20 had log₁₀ Bayes factor values above 2 (Figure 4); 19 of these 20 were also identified as outliers by the F_ST-based method (Table 3). Five of the 20 loci had log₁₀ Bayes factors above 3, corresponding to a posterior probability of locus effects above 0.999; four had a log₁₀ Bayes factor of 5, corresponding to a posterior probability of 1.000. BLASTx searches identified putative functions for 11 of the 20 loci with log₁₀ Bayes factors above 2 (55% Table 3).

Figure 4.

Plot of F_ST values and Bayes factors (log₁₀) for 1026 loci obtained using the BayeScan outlier test. Dashed lines indicate the Bayes factor threshold of 2 (log₁₀) that provides ‘decisive' evidence for selection corresponding to a posterior probability of 0.99.

Using within-variety F_ST analysis, 54 outlier loci were identified. All but three of the identified outlier loci were detected only in either omote-sugi or ura-sugi variety populations; the three exceptions were SNPg03850, SNPg01839 and SNPg00140 (Table 3). The 25 outlier loci were also detected when all populations were included in the analysis. Using the Bayesian method, only four loci were identified in either the omote-sugi or ura-sugi populations, two of which were present in all populations.

Relationships between specific loci and environmental variables

Eighteen loci were associated with environmental variables (Table 4). The environmental variable with the greatest number of associations was the daily maximum temperature, which was related to six loci; the maximum snow depth and latitude were associated with five and three, respectively. All environmental variables were associated with at least one locus. The 12 out of 18 loci found to be related to an environmental variable were also identified as outliers in either the Fdist2, Arlequin or BayeScan analyses. BLASTx searches identified putative functions for 10 of the 18 environment-associated loci.

Table 4. Significant associations between loci and environmnental variables (P<0.01), and their linkage group and the putative function by BLAST search.

	Environmental variable										Fdist2 a	BayeScan *	Arlequin *	Linkage group	Putative function
	Longitude	Latitude	Altitude	Mean annual temperature	Daily maximum temperature	Daily minimum temperature	Annual precipitation	Annual sunshine hours	Amount of global solar radiation	Maximum snow depth
SNPg00563						**					*		*	3	No hit
SNPg00660	**								**		**			8	Nitrite reductase
SNPg01042					**						**	**	**	10	Harpin-induced protein-like
SNPg01330		**		**	***						**	**	***	11	Adenosine 3-phospho 5-phosphosulfate
SNPg01385		**		**	***	**					**	***	***	—	No hit
SNPg01589		**								**	**	***	*	6	S-receptor kinase
SNPg01835						**					**	*	*	10	No hit
SNPg02192									**					—	Calcium-dependent protein
SNPg02235			**								**			7	No hit
SNPg02446									**					5	No hit
SNPg02685					**									11	Hydroxyproline-rich glycoprotein family protein-like
SNPg02929	**											*		—	No hit
SNPg03082		**				**					**	**	***	2	No hit
SNPg03259							**							4	Subtilisin-like protease
SNPg04024					**			**		**	***	***	***	11	MYBPA1 protein
SNPg04308					**									—	Uncharacterized protein
SNPg04607										**	***	**	**	—	No hit
SNPg05593		**					**							—	O-acyltransferase wsd1-like

Abbreviation: SNP, single-nucleotide polymorphism.

^aStatistically siginificant level. *<0.05, **<0.01 and ***<0.001.

Distribution of outlying loci on the linkage map, and LD

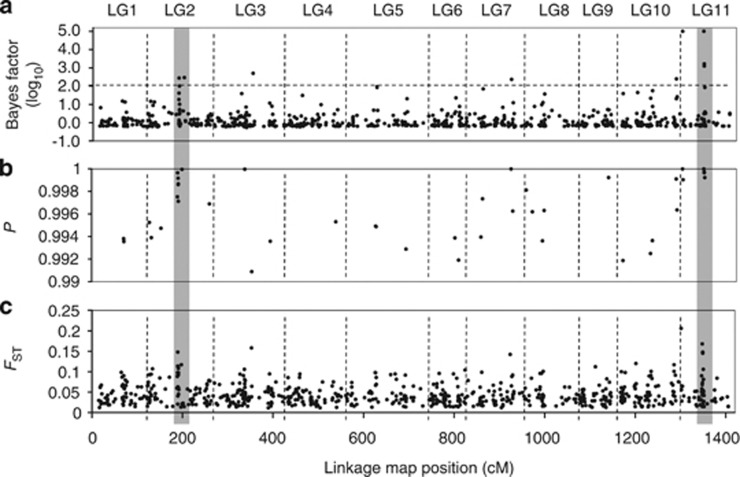
In total, 100 loci were identified as outlier loci or loci associated with environmental variables for all populations. Sixty-four of these loci were successfully mapped on the C. japonica linkage map, and their distribution was studied (Figure 5, Moriguchi et al., 2012). The numbers of mapped outlier loci in each LG varied substantially. For example, LG 4 contained only three loci, while LG2 contained 11. The observed distribution of loci deviated significantly from the Poisson distribution for all marker intervals considered (15, 20, 25 and 50 cM) and was therefore not random (P<0.001). Eight of the 14 loci that were detected by all of the Fdist2, Arlequin and BayeScan methods were mapped on the linkage map; 4 on LG11, and one on each of LG2, LG6, LG7 and LG10. The outlier loci thus formed clumps on specific LGs, particularly LG2 and LG11 (Figure 5). The outlier distribution was related to the F_ST distribution; regions with high F_ST values had high numbers of outlier loci.

Figure 5.

The distribution of markers identified as being potentially involved in local adaptation across the genome of C. japonica. The figure shows plots of marker position (based on 1255 mapped SNPs or the other DNA markers; Moriguchi et al., 2012) in cumulative centiMorgans (cM) versus (a) Bayes factor (log₁₀), as determined by BayeScan analysis, (b) the probability that the locus is an outlier as judged by the F_ST-based test (Beaumont and Nichols, 1996) and (c) F-statistic value, F_ST. Vertical dashed lines demarcate the 11 LGs. The two gray zones indicate candidate regions associated with local adaptation.

LD was detected for only five of the 2145 possible combinations of the 66 loci. Three pairs of loci were closely linked to one another on LG2, LG5 and LG11, respectively, two of which corresponded to the clumped regions of outlier loci discussed above. Locus SNPg04215 was mapped to LG7 but exhibited high LD (more than r²=0.270) with SNPg00066 and SNPg02495 on LG2.

Discussion

Genetic structure

The genetic differentiation between the studied C. japonica populations was low (F_ST=0.0391). Hierarchical analysis indicated that genetic variation among varieties and populations accounted for 2.74% and 4.98% of the total variation, respectively. These results are similar to those from our previous study (Tsumura et al., 2007). While there was little genetic differentiation between variety groups, what differentiation there was pertained to genes related for local adaptation. A K value of 7 yielded the highest log-likelihood value in the structure analysis and provided a much clearer picture of the species' genetic structure than had been obtained in our previous study (Tsumura et al., 2007). Although the extent of the genetic differentiation between varieties was relatively modest, they were clearly distinguished from one another in the structure analysis excluding ONN population in omote-sugi populations. This population might be established immigration from Chugoku populations such as Azouji and others after extinction of natural forest in Kyushu Island (Takahara, 1998). We therefore examined outlier loci both for all populations and within populations of individual varieties after excluding ONN population from omote-sugi variety populations. However, the obtained result is not largely different in case of inclusion of ONN population.

Detection of outlier loci

The number of outlier loci identified with Fdist2 and Arlequin was roughly three times greater than the number identified with BayeScan for all populations, even when using the same significance threshold (0.99) in both cases and considering the hierarchical structure. Fdist2 may be more prone to detecting false positives than other methods (Pérez-Figueroa et al., 2010), but all of the loci identified by BayeScan were also detected by Fdist2 with the exception of six loci (Table 3). This illustrates the necessity of performing multiple tests to detect outlier loci. It may be that BayeScan is more efficient than Fdist2 at identifying true positives. Pérez-Figueroa et al. (2010) conducted a simulation to compare the efficiency of three different programs (DFDIST, DETSELD and BayeScan) for detecting loci under directional selection using dominant markers. They concluded that BayeScan is more efficient than the alternatives because it automatically optimizes the values of its parameters (Pérez-Figueroa et al., 2010). However, some false positives are inevitable even when multitest corrections and multiple methods are used.

Tests for detecting outlier loci that deviate from neutral expectations are unable to identify false positives (type I errors). We therefore conducted all Fdist2, Alrequin and BayeScan tests, imposing a 99% P lower limit for the identification of genes under selective pressure; the expected number of false positives was thus 1026 × 0.01=10.26. As 14 outlier loci were identified by both tests, it appears that at least some are unlikely to be false positives (owing to type I errors). The 14 loci identified by all Fdist2, Alrequin and BayeScan are thus strong candidates as genes involved in adaptation to local environments.

1.4% of the 1026 loci investigated were identified as candidate loci. This proportion of candidate loci is similar to that found in a previous study (2.7%) in which 148 cleaved amplified polymorphic sequence loci were examined (Tsumura et al., 2007). Eckert et al. (2010) identified 22 candidate loci (BF log₁₀>2.0) associated with climate variables from 1730 loci in 682 loblolly pine tree samples covering the full range of the species. Prunier et al. (2011) also identified 10 candidate loci above 99% confidence interval in black spruce. The proportion of detected loci (1.3% and 1.7%, respectively) associated to the climate variables was very similar with our results. The average F_ST value of the 14 candidate loci was 0.1943 (the values for individual candidate loci ranged from 0.1210 to 0.5006), which is substantially higher than the average F_ST value for all loci (0.0391). This means that different populations have substantially different allelic compositions at these 14 loci, presumably because of the different selective pressures acting upon them.

When we examined the status of outlier loci within groups representing the two varieties, two-thirds of the loci detected in all populations were not identified as outliers in either variety group by Fdist2. With BayeScan, only three of the loci detected in all populations were identified as outliers in one of the variety groups or the other. These genes might be important in the two varieties' adaptation to their different environments. In Japan, the coast of the Japan Sea experiences heavy snowfall but the Pacific Ocean side is quite dry in the winter. The ura-sugi variety is found on the Japan Sea side and has short needles with narrow angles, which are thought to confer selective advantages in areas with heavy snowfall in the winter. The outlier genes were detected in all populations and also in each variety group, and are therefore likely to be important in local adaptation.

Relationships with environmental variables

Correlation analyses were performed for several environmental variables, bearing in mind the possibility that multiple loci might be associated with any one of these variables. Some of the environmental variables were correlated with one another—specifically, the latitude and the longitude (r=0.81), and the latitude and the annual precipitation (r=−0.86). This reflects the fact that the Japanese archipelago extends in a rough line from the southwest to the northeast and the environmental gradient examined in this study mirrors that of the archipelago; the natural C. japonica forest has a wide-ranging distribution, from 30°N, 130°E to 40°N, 140°E (Table 1, Figure 1). There is heavy snowfall on the Japan Sea side in the winter season but the Pacific Ocean side is quite dry in the winter, and the annual precipitation is much higher in the southern part of Japan than elsewhere in the country. There are thus significant differences in the environmental factors affecting the different regions examined in this work, especially in terms of the annual precipitation and the maximum depth of fallen snow (Table 1). There is a cline of environmental variables such as precipitation, temperature and snowfall along the Japanese archipelago from the northeast to southwest. The formation of the Japanese archipelago began around 17 million years ago, with the earliest incarnation of the Japan Sea forming around 7 million years ago (Taira, 2001). Ever since then, there have been significant climatic differences between the Japan Sea side and Pacific Ocean sides of Japan. A C. anglica fossil dated to the later phase of the Miocene has been found in Japan, and is a likely ancestor of C. japonica. Moreover, C. japonica fossils have been found that date back to the Pleiocene, and so post-date the formation of the Japanese archipelago (Uemura, 1981). C. japonica has thus adapted climatic differences over extended periods of time while expanding its distribution, in the face of global climate changes including several glacial and interglacial periods.

Eight of the 14 candidate genes identified by all Fdist2, Arlequin and BayeScan were associated with at least one of the latitude, the mean annual temperature, the daily minimum or maximum temperature, the maximum snow depth and the annual sunshine hours (Table 3). Three of them were associated with two or more environmental variables that correlated with one another, suggesting that the genes might have responded to the same selection pressures.

Putative functions for four of these eight candidate genes were revealed by BLASTx searches. For example, SNPg04024 is a putative MYBPA1 protein and would thus activate the promoters of several of the general flavonoid pathway genes (Bogs et al., 2007). This kind of function is important for defense against diseases and predators, and for the survival of the individual and/or population. Individuals with genotypes that confer advantages in their specific environments would be selected for, changing the allele frequency at the candidate loci in that population. However, it is important to properly account for hitchhiking effects when making suggestions of this kind, because it is possible that the genes identified may simply be closely linked to the true adaptive gene.

In addition to the location and climate data, other environmental variables such as soil type and the species composition of the forest will also have important effects on selection. Phenotypic differences of the two varieties such as needle, branchlets and wood characteristics that are the result of selection will also be important for association study.

Such information should be collected and used in future association analyses.

The clumpy distribution of the outlier loci, and LD

Significant deviations from the Poisson distribution of outlier loci were observed for all marker intervals (P<0.001), indicating that the 64 mapped outlier loci and loci associated with environmental variables were not randomly distributed on the linkage map; instead, they tended to cluster, especially on LG2 and LG11 (Figure 5), in a manner reminiscent of the ‘genomic islands of divergence' discussed by Nosil et al. (2009). These two genomic regions, which are likely to have a major role in local adaptation, cover around 1.7 cM on LG2 and about 2.1 cM on LG11, corresponding to about 10.2 and 12.6 Mb, respectively, in this species. Three of the outlier loci in the LG11 region (SNPg01330, SNPg02685 and SNPg04024) were associated with some environment variables. Two of the loci in the LG11 region had Bayes factors above 3 (log₁₀), which is generally interpreted as a ‘decisive' level of significance. The SNPg04024 locus has a Bayes factor of 5, giving a posterior probability of 1. We are thus convinced that the LG11 region is affected by directional selection along the environmental gradient, presumably by factors such as mean annual temperature, daily maximum temperature, hours of sunshine and/or maximum snow depth. Scotti-Saintagne et al. (2004) identified some important regions of their genomes associated with adaptation using both methods of outlier detection and quantitative trait locus mapping.

Surprisingly, the LD among the loci in each of the region is also high, affecting one pair in each of LG2 and LG11. Although LD in forest trees decays rapidly within several thousand basepairs (Neale and Savolainen, 2004), Eckert et al. (2010) have observed high LD in the loblolly pine, affecting the set of five SNPs located on LG 8. The LD of forest trees has to date only been estimated in coding regions; it is possible that the LD values of non-coding regions might be higher than those for coding regions, as is the case in angiosperms (Gaut et al., 2007; Moritsuka et al., 2012). The SNPg04215 locus on LG7 exhibited substantial LD with two loci on LG2, which is unusual; the high LD might reflect the effects of directional selection, resulting in the same selection pressure. Evolutionary mechanisms such as co-adaptation of gene complexes might be affected by this LD (Dobzhansky, 1970).

The outlier loci detected in the other regions with high significance levels are also strong candidates for involvement in local adaptation. It will be necessary to confirm whether these loci correspond to genuine adaptive genes, to compare the sequences of the full-length regions containing these genes in populations from different environments, and to determine the LD associated with these loci. The identification of outlier loci with high significance levels is essential for conservation efforts and will be required for future work on molecular breeding.

Data Archiving

Data have been deposited at Dryad: doi:10.5061/dryad.gt178.

The authors declare no conflict of interest.