Skip to main content
NCBI home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2013 Mar 1.
Published in final edited form as: Biomech Model Mechanobiol. 2011 Jul 12;11(3-4):493–503. doi: 10.1007/s10237-011-0328-9

Human Annulus Fibrosus Material Properties from Biaxial Testing and Constitutive Modeling are Altered with Degeneration

Grace D O’Connell 1, Sounok Sen 1, Dawn M Elliott 1
PMCID: PMC3500512  NIHMSID: NIHMS412989  PMID: 21748426

Abstract

The annulus fibrosus (AF) of the intervertebral disc undergoes large and multidirectional stresses and strains. Uniaxial tensile tests are limited for measuring AF material properties, because freely contracting edges can prevent fiber stretch and are not representative of in situ boundary conditions. The objectives of this study were to measure human AF biaxial tensile mechanics and to apply and validate a constitutive model to determine material properties. Biaxial tensile tests were performed on samples oriented along the circumferential-axial and the radial-axial directions. Data were fit to a structurally-motivated anisotropic hyperelastic model composed of isotropic extrafibrillar matrix, nonlinear fibers, and fiber-matrix interactions (FMI) normal to the fibers. The validated model was used to simulate shear and uniaxial tensile behavior, to investigate AF structure-function, and to quantify the effect of degeneration. The biaxial stress-strain response was described well by the model (R2>0.9). The model showed that the parameters for fiber nonlinearity and the normal FMI correlated with degeneration, resulting in an elongated toe region and lower stiffness with degeneration. The model simulations in shear and uniaxial tension successfully matched previously published circumferential direction Young’s modulus, provided an explanation for the low values in previously published axial direction Young’s modulus, and was able to simulate shear mechanics. The normal FMI were important contributors to stress and changed with degeneration, therefore, their microstructural and compositional source should be investigated. Finally, the biaxial mechanical data and constitutive model can be incorporated into a disc finite element model to provide improved quantification of disc mechanics.

Keywords: biaxial tension, annulus fibrosus, continuum modeling, intervertebral disc, degeneration

Introduction

The annulus fibrosus (AF) of the intervertebral disc is composed of a proteoglycan-rich matrix containing collagen fibers that are aligned at 28–44° above and below the horizontal plane in adjacent lamellae (Cassidy, Hiltner et al. 1989). It is this cross-ply fiber-reinforced structure that enables the AF to support and distribute the large and multidirectional stresses and strains experienced by the disc.

Human AF tissue properties are highly anisotropic and nonlinear in uniaxial tension, compression, and shear (Galante 1967; Acaroglu, Iatridis et al. 1995; Iatridis, Setton et al. 1998; Iatridis, Kumar et al. 1999), with a high tensile modulus in the circumferential direction. The degenerative changes in AF tensile mechanical properties have been modest (Acaroglu, Iatridis et al. 1995; Guerin and Elliott 2006; O’Connell, Guerin et al. 2009); however, when a constitutive model was applied to uniaxial tensile data, the material parameters representing the extrafibrillar matrix and the shear fiber-matrix interactions increased with degeneration (O’Connell, Guerin et al. 2009). The findings of that study suggests that there are microstructural changes within the tissue that were not detected by tissue testing alone. That study used samples tested only the radial and the circumferential direction – the axial direction tensile response gave spurious results due to lack of fiber stretch with the freely contracting edges of the uniaxial test (Adams and Green 1993; Elliott and Setton 2001; Guerin and Elliott 2007; O’Connell, Guerin et al. 2009). Using uniaxial tensile tests to quantify AF material properties is limited because the disc’s in situ geometry and loading is not consistent with testing boundary conditions of freely contracting edges and large aspect ratios.

Biaxial tensile testing has been widely applied to evaluate skin and cardiovascular tissue mechanics (Tong and Fung 1976; Sacks and Chuong 1993; Kang, Humphrey et al. 1996; Sun, Sacks et al. 2005; Guo, Humphrey et al. 2007; Choi, Lee et al. 2008), and has had some application in the AF (Bass, Ashford et al. 2004; Bruehlmann, Hulme et al. 2004; Gregory and Callaghan 2011). Bruelmann et al. designed their study to evaluate inter- and intra-lamellar strains in the bovine AF and did not measure forces or calculate material properties (Bruehlmann, Hulme et al. 2004). Bass et al. applied biaxial tensile loads to human AF and calculated material properties with a constitutive model, but the circumferential direction strain was fixed, therefore, loading did not span physiological tensile loads (Bass, Ashford et al. 2004). Gregory and Callaghan observed a higher linear-region modulus for the porcine AF in biaxial testing than uniaxial testing (Gregory and Callaghan 2011), a phenomenon that can be explained by the boundary constraints using elasticity theory. To date, the effect of degeneration on the biaxial mechanical properties of human AF is not known and will be quantified in this study.

Material properties cannot be directly calculated from biaxial experiments, but must be determined using a constitutive model (Sacks and Sun 2003). The AF has been modeled using a fiber-induced anisotropic hyperelastic material originally developed by Spencer (Spencer 1972). These models describe the micro-structural components (i.e. fibers and the extrafibrillar matrix) using the principle invariants of the Green deformation tensor and structural tensors representing the collagen fiber populations. (e.g., (Wu and Yao 1976; Klisch and Lotz 1999; Elliott and Setton 2000; Eberlein, Holzapfel et al. 2001; Wagner and Lotz 2004; Peng, Guo et al. 2006; O’Connell, Guerin et al. 2009)). Moreover, some models study the AF structure-function relationships by including contributions due to interactions between the isotropic extrafibrillar matrix and collagen fibers through fiber-matrix interactions terms (Elliott and Setton 2001; Peng, Guo et al. 2006; Wagner, Reiser et al. 2006; Guerin and Elliott 2007; O’Connell, Guerin et al. 2009). In this manner, continuum models are useful to interpret and elucidate experimental measurements and can be used to investigate functional effects of micro-structural changes with degeneration. Finally, robust AF constitutive models may be incorporated into structural finite element models to overcome limitations associated with using truss elements to describe the fiber contributions (Acaroglu, Iatridis et al. 1995; Eberlein, Holzapfel et al. 2001; Schroeder, Huyghe et al. 2010; Jacobs, Cortes et al. 2011).

Therefore, the objectives of this study were to measure human AF biaxial tensile mechanics and to apply and validate a constitutive model to determine material properties related to the matrix, fibers, and fiber-matrix interactions. The model was then used to simulate the AF shear and uniaxial tensile behavior, to investigate AF structure-function, and to quantify the effect of degeneration.

Methods and Materials

Biaxial Testing

Thirteen human spine sections were obtained from an IRB approved tissue source (NDRI, Philadelphia, Pennsylvania; age = 25 – 80 years). A series of T1ρ-weighted images were acquired to determine the T1ρ relaxation time of the nucleus pulposus (T1ρ relaxation time = 46 – 146 msec). The T1ρ relaxation time has recently been used to investigate correlations of disc mechanics with degeneration because the continuous scale of the T1ρ relaxation time (versus integer-based grading) provides a more powerful statistical tool, and is strongly correlated with the proteoglycan content of the nucleus pulposus (Auerbach, Johannessen et al. 2006; Johannessen, Auerbach et al. 2006; Nguyen, Johannessen et al. 2008; O’Connell, Vresilovic et al. 2011; Borthakur, Maurer et al. 2011 In Press; O’Connell, Malhotra et al. 2011 In Press). Following imaging, the intervertebral discs from the L3–L4 and/or the L4–L5 levels were dissected from the vertebral bodies and samples were prepared from the anterior AF of tissue that did not contain annular fissures (n = 16). Two 10 mm square samples were prepared from each disc, one oriented along the circumferential (circ)-axial directions and along the radial-axial directions (Figure 1A). Samples were dissected from semi-frozen discs and sectioned on a freezing-stage microtome to ensure uniform thickness with planar surfaces. The sample size was limited by the disc height; therefore, severely degenerate samples from collapsed discs were not included.

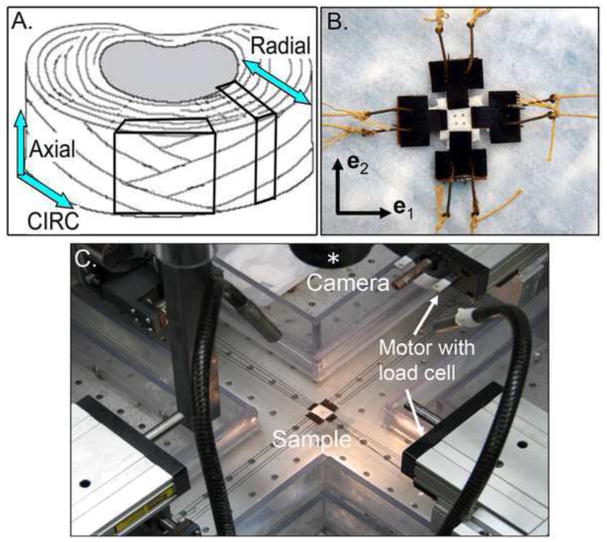
Figure 1.

Figure 1

Open in a new tab

A) Orientation of samples dissected from the outer AF and B) a representative sample prepared for biaxial testing. C) Biaxial testing device with four motors and two load cells (one in each direction). The sample is located in the center of the device and a camera (lens is denoted by the asterisk) is used to acquire images during loading.

Samples were prepared for mechanical testing by gluing ‘T’ shaped waterproof sandpaper at the ends with cyanoacrylate (Loctite 454) as the bonding agent (Figure 1B). The final dimensions were measured as the length between the sandpaper ends and were used to calculate the cross sectional area in the reference configuration. The circ-axial samples had final dimensions of 7.1 ± 0.8 x 7.0 ± 0.8 x 2.1 ± 0.3 mm (circ width x axial width x thickness), and the final dimensions for the radial-axial samples were 7.0 ± 1.1 x 6.6 ± 0.8 x 1.8 ± 0.2 mm (radial width x axial width x thickness). Hooks were placed through the sandpaper and attached to Kevlar thread (Figure 1B), which interfaced with the pulleys on a custom-built biaxial testing device (Figure 1C) that was designed based on an established biaxial testing system (Sacks 1999). Each pulley was attached to a motor that was controlled by a custom-written Labview program. Four motors (404100XR, Parker Hannifin, Rohnert Park, CA) were used to apply tensile loads on all four sides of the sample, and two load cells (Model# 41, Honeywell, Columbus, OH) were attached to perpendicular sides (i.e., the e1 and the e2 direction) (Figure 1C). Four brass beads (diameter = 0.5 mm) were glued on the surface of the center 1/3 region for strain analysis and control during testing (Figure 1B). The strain in the center region was assumed to be homogeneous, which is supported by finite element analysis (Sun, Sacks et al. 2005). Images were acquired with a high-resolution camera (1392 × 1040 pixel; camera: A102f, Basler Vision Technologies, Exton, PA; lens: Navitar TV zoom 7000, Rochester, NY; asterisk in Figure 1C) to track the location of the four brass beads. The sample reference configuration was selected as the first image acquired during the biaxial loading (i.e. the first image after preconditioning). The fiber angle was measured manually using the first acquired image (ImageJ 1.40g, NIH).

Two-dimensional Lagrangian strains (E) were calculated using a finite element analysis (Equation 1), where λ is the principal stretch ratio and κ is the in-plane shear calculated from the quadrilateral finite element shape represented by the four beads (Sacks and Sun 2003).

E11=12(λ12+κ22-1)E22=12(λ22+κ12-1)E12=12(λ1κ1+λ2κ2) (1)

The stress was calculated as the force in the reference condition divided by the cross sectional area (width x thickness). All mechanical testing was performed in a phosphate buffered saline bath at room temperature.

The sample was preloaded for 10 minutes at 0.5 N in the circumferential and axial directions and at 0.25 N in the radial direction. A 10 cycle precondition was applied from 0–2% strain at rate of 1%/s in each direction. These preload and precondition parameters were selected based on the parameters used for AF uniaxial tensile testing (Guerin and Elliott 2007; O’Connell, Guerin et al. 2009). A range of strain ratios was then applied with a 90-minute unloaded recovery between tests. For each strain ratio, the sample was stretched at a quasi-static rate of 0.01%/s along the primary direction (i.e., the direction with the larger applied strain). The circ-axial samples were tested with five strain ratios: fixing the axial direction at zero strain (axial-fixed), circ:axial strain ratios of 2:1, 1:1 (equibiaxial), 1:2, and fixing the circumferential direction at zero strain (circ-fixed). The maximum stress in either loading direction was limited to 1.5 MPa to prevent tissue damage.

Preliminary studies confirmed that the circ-axial sample fully recovered following a 90-minute unloaded recovery; allowing for several strain ratios to be applied to each sample. To confirm that the sample was not damaged during loading, the axial-fixed loading condition was repeated at the end of the experiment, and the toe- and linear-region modulus was compared to the first axial-fixed test. No significant differences were observed in the behavior of the two axial-fixed tests (Wilcoxon p > 0.1). In contrast, the radial-axial samples were tested in only one strain ratio that consisted of holding the axial direction fixed at zero strain. Preliminary studies demonstrated that the radial direction did not recover in this orientation so additional strain ratios could not be performed.

Constitutive Modeling

A structurally motivated anisotropic hyperelastic model for finite deformations was formulated based upon the work of Spencer (Spencer 1972), where the AF was modeled by summing strain energy functions describing the matrix (Wm), the fibers (Wf), and the fiber-matrix interactions (FMI) normal to the fibers (W∞), as previously described (Guerin and Elliott 2007; O’Connell, Guerin et al. 2009). Briefly, strain energy functions were formulated using the integrity basis of invariants (Ii, i =1–7, Equation 2) formed from the right Cauchy-Green deformation tensor C and the unit fiber direction vectors a and b,

I1=trCI4=a·C·aI6=b·C·bI2=1/2[(trC)2-trC2]I5=a·C2·aI7=b·C2·b (2)

The invariants involving fiber stretch (I4 – I7) were restricted to be greater than or equal to 1.0, requiring the collagen fibers to buckle in compression (Eberlein, Holzapfel et al. 2001; Nerurkar, Mauck et al. 2008; Ateshian, Rajan et al. 2009). The individual strain energy equations (Wi) were required to be positive definite, Wi ≥ 0. The ci (ci, i=1–6) in the following equations represent the material properties. The formulation of each term was previously described in detail, so are presented in their final form below (Guerin and Elliott 2007; O’Connell, Guerin et al. 2009):

Wm=c1(I1-3)+c2(I2-3)+c3(J-1)2-2(c1+2c2)lnJ (3a)
Wf=∑α=4,6c42c5(ec5(Iα-1)2-1) (3b)
W⊥=c6[(1/2I12-I1-I2+1/2)+1/2(1/2(I42+I62)-(I5+I7)+1)] (3c)

The parameters c1-c4 and c6 have units of MPa and c5 is unitless. The first Piola-Kirchhoff stress (P) was determined by differentiating the strain energy equation with respect to the deformation tensor to obtain the full constitutive law as: P=2F•dWdC, which is defined as the force per unit area in the reference configuration.

Model-fit, Sensitivity Analysis and Validation

The material properties (ci, i=1–6) were determined using a custom algorithm in MatLab (lsqcurvefit, MatLab Inc.) as previously described (Guerin and Elliott 2007; O’Connell, Guerin et al. 2009). The model-fit was performed using disc-matched stress-strain datasets from the radial-axial experiments, circ-axial experiments and the directly measured fiber angle (a, b). First, the radial-axial data was fit to the stress-stretch response derived from the extrafibrillar matrix strain energy equation, Wm, to determine c133 c2 and c3. Once the matrix parameters were determined, the circ-axial stress-stretch data from the 1:2 and 2:1 (circ:axial strain ratio) experiments were simultaneously fit to the stress equation derived from the full strain energy equation (W = Wm + Wf + W∞) to determine c433 c5, and c6. As in previous biaxial tensile testing, the out-of-plane tissue contraction was not measured; therefore, the out-of-plane Poisson’s ratio of 1.2 was selected. This value was selected to be higher than the Poisson’s ratio measured in uniaxial tension in the radial direction because of the increased boundary constraints in biaxial tensile testing (Bass, Ashford et al. 2004). The out-of-plane Poisson’s ratio was used to calculate the out-of-plane strain used in the deformation tensor C. A parametric study was performed for the out-of-plane Poisson’s ratio ranging from 0.5 to 2.5, showing little effect on the biaxial stress-strain response (see Supplemental Figure 1A).

The material properties are reported as the median and interquartile range, as the values did not represent a normal Gaussian distribution. A correlation coefficient (R2) value was calculated to provide a measure of association of the model-fit to the experimental data. A Bland-Altman analysis (B-A), which calculates the bias and standard deviation of residuals, was used to provide a measure of agreement between the model-fit and experimental data (Aspden 2005).

A sensitivity analysis was performed on the constitutive model that was determined to provide the best fit to the biaxial data by varying each model parameter by the mean ± 2X the standard deviation and evaluating the linear-region modulus from the stress-strain response in the circumferential direction under the 2:1 strain configuration. The modulus was calculated using the bilinear algorithm, as previously described (Guerin and Elliott 2006). If the linear-region modulus deviated from the linear-region modulus calculated using the average model parameters by more than 10%, the model was considered to be sensitive to the parameter.

Only the 1:2 and 2:1 strain ratios were used to determine the material properties, reserving the other strain ratios for model-validation. The sample-specific model parameters (c1-c6) were used to simulate the stress-stretch response in the axial-fixed, equibiaxial and circ-fixed configuration. The Bland-Altman analysis was applied to compare the stress-stretch data from the model and the experiment for each strain configuration. An acceptable difference between the model and experimental data was selected as less than 0.1 MPa.

Application of Model to Structure-Function Mechanisms, Degeneration, and Simulations

The stress contribution of the matrix, fibers, and their interactions was determined to evaluate their relative role to the AF structure-function relationship. The stress contribution was calculated at the linear region of the circumferential and axial direction using the stress-stretch data from the 2:1 experiment. The linear region stress was defined at the mid-point between the transition strain and the final applied strain, where the transition strain is the intersection of discrete linear curve fits to the toe and linear region, as previously described (Guerin and Elliott 2007; O’Connell, Guerin et al. 2009). A Wilcoxon test was performed to compare the stress contribution between the circumferential and axial directions.

The effect of degeneration on each material parameter was evaluated by using a Spearman’s correlation between the model parameters (ci) and the measured T1ρ relaxation time. Significance was set at p ≤ 0.05 and a trend was defined as 0.05 < p ≤ 0.10. To evaluate the effect of degeneration on the global behavior of the outer anterior AF, the circumferential stress-strain response in equibiaxial loading was calculated using the material properties for nondegenerated (at T1ρ =150 msec) and degenerate (at T1ρ = 50 msec) AF. This was done using the median for parameters that did not correlate with degeneration (c1-c4) and the value from the correlation line for parameters that did correlate with degeneration (c5 and c6).

Finally, the model was used to simulate the stress-strain response in uniaxial tension along the circumferential direction and simple shear in the circ-axial direction using a custom written algorithm in MatLab (MatLab, Inc.). The effect of the out-of-plane Poisson’s ratio on uniaxial tensile modulus was evaluated by varying the Poisson’s ratio from 0.5 to 2.5, showing large effects (Supplemental Figure 1B). Based on these results, we chose to use the directly measured Poisson’s ratio of 2.06 from uniaxial tensile experiments (O’Connell, Guerin et al. 2009), to calculate the out-of-plane strain and a traction-free boundary condition was applied. The simulated stress-stretch response was used to calculate the stress contribution for the matrix, fibers and normal FMIs, as well as the linear-region Young’s modulus and shear modulus.

Results

Model-fit and Validation

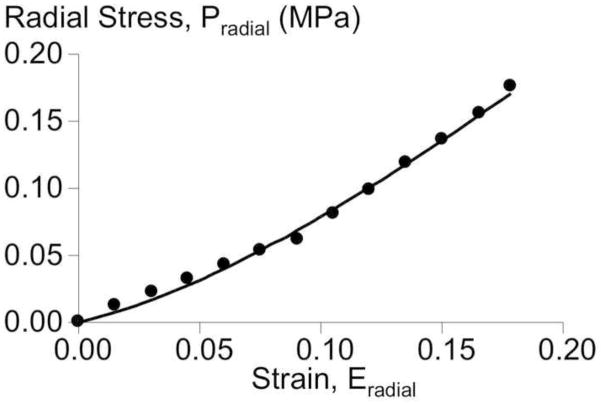
In the radial-axial test orientation, the radial stress-strain response was nonlinear, but only at relatively large strains, greater than 0.10 (Figure 2). The radial stress-strain response was described well by the compressible Mooney-Rivlin model, with a high R2 and low Bland-Altman bias (R2 = 0.996, B-A bias and standard deviation = −0.0001 ± 0.0027 MPa, Figure 2). The median (interquartile) values for the matrix material parameters were c1 = 0.84 (0.62, 1.48) MPa, c2 = −0.72 (−1.42, −0.57) MPa, and c3 = 0.94 (0.00, 2.23) MPa.

Figure 2.

Figure 2

Open in a new tab

A representative radial stress-strain response for a radial-axial sample, where the axial direction was fixed. Experimental data (circles) and model-fit (solid line) are shown.

In the circ-axial test orientation, the stress-strain response was nonlinear in both directions for all strain ratios (Figure 3). In addition, the elastic modulus increased and the stress limit was reached at lower strains as the constraint on the perpendicular side was increased (Figure 3). The circumferential and axial stress-strain response in the 1:2 and 1:2 strain ratios was described well by using the disc-matched matrix properties (c1-c3) and fitting for the material properties (c4-c6), with R2 greater than 0.9 (Table 1, Figure 4). The model fit very well to the stress-stretch data in the circumferential direction, whether or not the normal FMI term was included (Table 1; Figure 4A). However, in the axial direction, the model fit well if the normal FMI were included (R2 = 0.93) but did not fit well when they were not included (R2 = 0.65; Table 1; Figure 4B). Based on these results, the full model with all strain energy terms (extrafibrillar matrix, fibers, and normal FMIs) was used for model-validation and applications.

Figure 3.

Figure 3

Open in a new tab

Stress-strain response in the A) circumferential and B) axial direction for all applied strain ratios (1:0 (axial-fixed), 1:2, 1:1, 2:1, 0:1 (circ-fixed)).

Table 1.

Model-fit in the circumferential and axial directions. The material properties are provided for the fibers and the normal FMI for the M+F and the M+F+N models. Statistical analysis was only performed on the M+F+N model.

Circumferential-Axial Directions
Model-fit Model Parameters
R2-Circ R2-Axial Bias (MPa) Resid SD (MPa) c4 (MPa) c5 c6 (MPa)
M + F 0.90 0.65 −0.0292 0.1083 3.58 (2.23, 4.20) 63.9 (18.2, 93.6) N/A
M + F + N 0.92 0.93 −0.0030 0.0573 2.05 (1.55, 3.14) 99.6* (37.7, 133.2) 2.64‡ (1.12, 4.25)
Open in a new tab
*

denotes a significant correlation with degeneration and

‡

denotes a trend.

Figure 4.

Figure 4

Open in a new tab

A representative stress-strain response for circ-axial sample under the 1:2 strain configuration loading. Experimental data (circles) and model-fit (solid line) are shown for the (A) circumferential and (B) axial directions. The curve fits represent the model with normal FMI terms (M+F+N) and without the interactions terms (M+F).

Sensitivity Analysis and Validation

A sensitivity analysis was performed for each model parameter by varying each parameter by the mean ± 2 standard deviations and evaluating the biaxial mechanical properties for the 2:1 strain configuration in the circumferential and axial directions. The axial direction stress-stretch behavior was not sensitive to changes in the matrix parameter, c2, the fiber parameters, c4 and c5, and the normal FMI parameter, c6 (see supplemental data available online - Supplemental Figure 2). In contrast, the circumferential direction stress-stretch behavior was only sensitive to the fiber parameters.

The model was validated using the disc-specific material properties and comparing the measured stress-strain response at the 1:1, 0:1, and 1:0 strain ratios with the model predicted response. Under equibiaxial loading (1:1), the predicted stress in the circumferential and axial directions deviated from the experimentally measured stress by −0.01 ± 0.07 MPa (average ± standard deviation), which was less than 2% of the maximum stress. The predicted stress response in the axial-fixed and circ-fixed strain ratios deviated from the experimental stress by −0.11 ± 0.18 MPa and −0.04 ± 0.09 MPa, respectively, approximately 10% of the maximum stress.

Application of Model to Structure-Function Mechanisms, Degeneration and Simulations

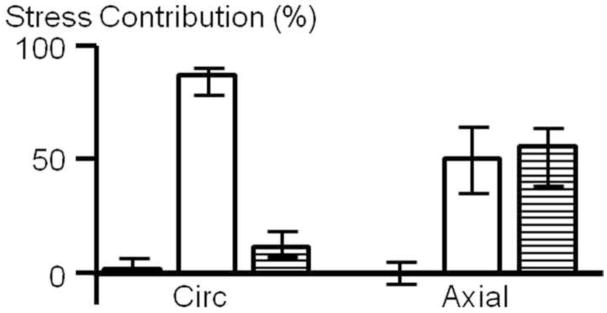
To consider AF structure-function mechanisms, the relative contribution of the matrix, fibers, and FMI to the total stress was determined in the circumferential and axial direction. The stress contribution of the individual components was significantly different between the circumferential and axial direction (Figure 5). The matrix contributed little to the total stress in both the circumferential (4.1%) and axial (2.5%) directions. In the circumferential direction, the fiber stretch was responsible for the greatest proportion of stress (82.7%), followed by the normal FMI term (14.0%). In contrast, in the axial direction, the stress contribution of the fibers (42.5%) and the normal FMIs (55.0%) was similar.

Figure 5.

Figure 5

Open in a new tab

Percent of stress contribution of the extrafibrillar matrix (black), fibers (white) and normal FMI (striped) in the circumferential and axial directions (shown for the 2:1 strain configuration). The stress contribution of each component was significantly different between the circumferential and axial directions (p < 0.05).

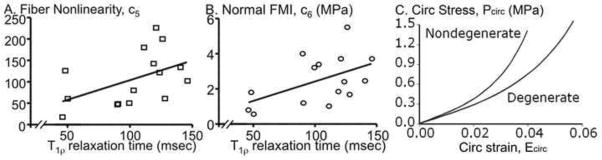
To evaluate whether the material properties were altered with degeneration, a Spearman’s correlation was performed between the material properties (ci) and the T1ρ relaxation time, which is a continuous measure of disc degeneration (Johannessen, Auerbach et al. 2006; Nguyen, Johannessen et al. 2008). The matrix parameters (c1–3) and the fiber stiffness (c4) were not correlated with degeneration (p ≥ 0.2). The fiber nonlinearity property (c5) was moderately correlated with T1ρ time, where the fiber nonlinearity decreased with degeneration (lower T1ρ relaxation time; p = 0.04, r = 0.55; Figure 6A). There was a trend for the normal FMI property (c6) to have a moderate correlation with degeneration (p = 0.08, r = 0.47; Figure 6B). To visualize the effect of degeneration, the circumferential stress-strain response in equibiaxial loading was simulated using median material parameters for c1-c4 and values for c5 and c6 that were calculated from the regression line at T1ρ = 150 msec for a nondegenerate and T1ρ = 50 msec for a degenerated disc. The degenerated AF had an elongated toe-region and a decreased elastic modulus (Figure 6C).

Figure 6.

Figure 6

Open in a new tab

Correlations between T1r relaxation time and material parameters were only significant for the (A) fiber nonlinearity, c5 = 0.92* T1r + 12.8 (r=0.55, p = 0.04), and a trend for the (B) normal FMI, c6 = 0.02* T1r + 0.12 (r=0.47, p =0.08). (C) Mean equibiaxial stress-strain response in the circumferential direction. The material properties for a nondegenerate and degenerated sample was determined by the correlation line at T1r = 150 ms and 50 ms, respectively.

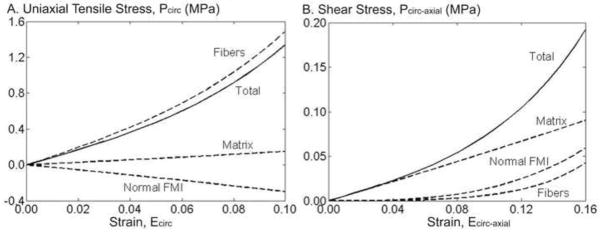
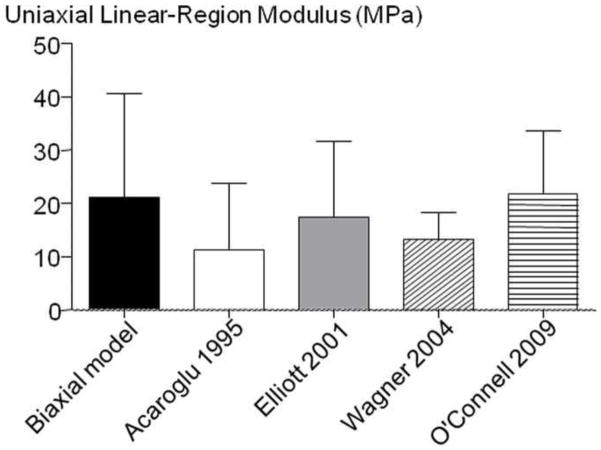
As most available AF properties are for uniaxial tension in the circumferential direction, the model parameters were used to simulate this stress-strain response (Figure 7A). The linear-region Young’s modulus was determined as the slope of the stress-strain response at the midpoint between the transition strain and the maximum strain (0.10). The predicted Young’s modulus was 21.0 ± 19.6 MPa and the transition strain between the toe- and linear-region was 0.058 ± 0.008, both of which were within one standard deviation of previously reported values (Figure 8 – shown for Young’s modulus) (Acaroglu, Iatridis et al. 1995; Elliott and Setton 2001; Wagner, Reiser et al. 2006; Guerin and Elliott 2007). However, in the toe-region, the model predicted a Young’s modulus (7.33 ± 5.50 MPa) that was larger than previously reported (2.5 – 3.4 MPa) (Elliott and Setton 2001; O’Connell, Guerin et al. 2009). The structure-function relationship in uniaxial tension was evaluated by calculating the relative stress contribution of each subcomponent, as described above for biaxial loading. The stress-strain response in circumferential uniaxial tension was dominated by the fibers, the matrix had negligible contribution and the stress from the normal FMIs was negative (Figure 7A).

Figure 7.

Figure 7

Open in a new tab

Model prediction of (A) uniaxial tension and (B) simple shear along the circumferential direction. The solid line represents the total stress-strain response in uniaxial and shear, the subcomponents are shown as dashed lines (fibers, matrix, and normal FMIs).

Figure 8.

Figure 8

Open in a new tab

Average and standard deviation of the linear-region Young’s modulus predicted by the model (Biaxial model) and previous studies (Acaroglu 1995, Elliott 2001, Wagner 2004, O’Connell 2009).

Finally, the model was used to simulate the AF response under simple shear, applied along the circumferential direction. The shear response was nonlinear (Figure 7B). The shear modulus in the toe-region was 2.29 ± 1.75 MPa, in the linear-region was 9.64 ± 14.33 MPa, and the transition strain was 0.11 ± 0.03. Evaluation of the structure-function relationship demonstrated that the shear stress was dominated by the matrix (Figure 7B), which is in contrast to tensile loading where the matrix contribution was negligible. At higher shear strains (> 0.10), the fiber and the normal FMI contribution increased to approximately 20% of the total shear stress (Figure 7B).

Discussion

Biaxial tensile loading was applied to human AF tissue and a structurally motivated nonlinear, anisotropic, hyperelastic constitutive model was applied to the biaxial stress-strain response and validated with data that was not used in curve fitting. The stress-strain response was nonlinear and comparable to previous biaxial experiments, where applying a transverse strain increases the apparent modulus and decreases the transition strain between the toe- and linear-region (Figure 3) (Humphrey, Strumpf et al. 1990; Sacks and Chuong 1993; Sacks 1999; Bass, Ashford et al. 2004; Gregory and Callaghan 2011). The constitutive model was successfully validated using the biaxial data and the predicted response was within 10% of the experimental stress. In addition, the model predicted a tensile Young’s modulus of 21 MPa in the circumferential direction, which was well within the range of directly measured (12–24 MPa) (Acaroglu, Iatridis et al. 1995; Elliott and Setton 2001; Wagner, Reiser et al. 2006; Guerin and Elliott 2007). Successful validation of independent loading configurations has not previously been shown for AF constitutive models, demonstrating the power of combining biaxial tension with the model formulation used here to establish a robust AF constitutive formulation.

The modulus calculated from biaxial data in the circumferential direction was similar that reported in uniaxial tension (Figure 8); however, this was not the case in the axial direction. For uniaxial tension in the axial direction, stresses only reach 0.05 MPa under an applied strain of 30–40% and the linear-region Young’s modulus was 0.4 MPa (Guerin and Elliott 2007; O’Connell, Guerin et al. 2009). In contrast, in this biaxial tension study, the axial direction stresses were an order of magnitude higher than uniaxial tension (on the same order of magnitude as the circumferential direction, Figure 3), and the linear region Young’s modulus was 12.5 MPa in the circ-fixed strain configuration. This discrepancy is a limitation in the uniaxial tensile testing of the AF, not the biaxial test or the constitutive model. In the unconstrained configuration required for AF uniaxial tension, the fibers are not stretched, but are compressed due to Poisson’s ratio effects of the freely contracting edges. In situ, the AF fibers insert into the vertebral body and are constrained; therefore, the fibers stretch in a manner similar to the biaxial tensile loading. This difference clearly shows the advantage of biaxial tension over uniaxial tension for studying a fiber-reinforced tissue like the annulus fibrosus.

Degeneration

Disc structural mechanics change dramatically with degeneration, however, mechanical changes in the AF have been quite moderate and difficult to detect (Adams and Green 1993; Fujita, Duncan et al. 1997; Haughton, Lim et al. 1999; Fujita, Wagner et al. 2000; Elliott and Setton 2001; Guerin and Elliott 2006; Guerin and Elliott 2007; O’Connell, Guerin et al. 2009). Several factors may have contributed to the modest alterations observed with degeneration, including grouping the continuous degradation process into subgroups of degeneration, exclusion of severely degenerated discs with a narrowed disc height, or a lack of specificity to microstructural changes when testing macro-structural properties. Using a continuous quantitative measure of degeneration, the structurally based constitutive model applied in this study showed that the parameters for fiber nonlinearity (c5) and the normal FMI (c6) correlated with degeneration (Figure 6). These changes resulted in overall degenerative effects of an elongated toe region and lower stresses for a given strain (Figure 6C), which is consistent with an increased range of motion in degenerated discs (Nachemson, Schultz et al. 1979; Keller, Spengler et al. 1987; Brown, Pollintine et al. 2008; O’Connell, Vresilovic et al. 2011). Although the microstructural and compositional contributors to degenerated AF mechanics are currently unknown, the model results suggest that future studies should specifically investigate microstructural contributors to fiber nonlinearity and normal FMI mechanics. Perhaps focusing on degradation of collagen fibers, the elastin network, proteoglycans, or collagen crosslinking.

Simulations of Uniaxial Tension and Shear

The simulation of circumferential uniaxial tension was commensurate to previously published data (Figure 8). The uniaxial tensile response in the circumferential direction was dominated by the fibers, with the normal FMI being relatively small and compressive (Figure 7A). In a previous study, the normal FMI were restricted to tension-only, which resulted in this term having no contribution to the overall stress (O’Connell, Guerin et al. 2009). The compressive normal FMI in this simulation suggests that as the fibers rotate in the direction of loading, they move closer to one another, resulting in a negative term.

Shear is an important component of physiological disc loading, particularly in torsion (Schmidt, Heuer et al. 2009), and may contribute to AF tears (Vernon-Roberts, Fazzalari et al. 1997). The model simulation predicted a shear modulus of 2.3 MPa, consistent with, although higher, than the directly measured 0.4 to 0.6 MPa shear moduli (Fujita, Wagner et al. 2000; Jacobs, Smith et al. 2011 In Press). The simulation showed that the matrix supported the entire shear stress at low strains. As the strain increased, the fibers and FMI began to contribute, but not to the same degree as the matrix (Figure 7B). This is consistent with experimental data, where a tensile preload increases the role of fiber stretch in shear, significantly increased the shear modulus (Jacobs, Smith et al. 2011 In Press). The model simulation in shear was less accurate than it was in uniaxial tension. It is possible that the lamellae behave as individual fiber populations with a shear interaction term between the lamellae (Nerurkar, Mauck et al. 2011). Therefore, the model predictions in shear may be improved by describing the individual lamellae with a shear interaction term, rather than as a continuum of fiber populations. The discrepancies between the model and experimental data may also be due to the difficult nature of the experimental shear experiments, which are highly dependent on boundary conditions and test protocols (Iatridis, Kumar et al. 1999; Fujita, Wagner et al. 2000; Jacobs, Smith et al. 2011 In Press).

Structure-Function Mechanisms

An advantage of structurally based models is that it provides a platform to study the relation between the structure-function mechanisms to the mechanical role of the tissue components. In this study we focused on the contribution of the extrafibrillar matrix, fibers, and fiber-matrix interactions normal to the fibers. We observed that the normal FMI had a significant role in the axial direction, where they contributed to 55% of the total stress, while they contributed less than 15% in the circumferential direction (Figure 5). The importance of including the normal FMI term in the model was apparent by the poor model-fit to the axial direction data when they were excluded, compared to when they were included (Figure 4C). As mentioned above, with respect to degeneration, the physical mechanism for normal FMI remains unknown, but is an important topic for future micro-mechanical studies.

In previous studies the shear FMI, interactions parallel to the fibers, were important contributors in circumferential uniaxial tensile loading (Guerin and Elliott 2007; O’Connell, Guerin et al. 2009). The shear FMI is a nonlinear function related to fiber rotation. In uniaxial tensile testing, fibers re-orient by up to 10° in uniaxial tension (Guerin and Elliott 2006). In biaxial testing, however, the fiber rotation is minimal (0 to 2°, data not shown) resulting in negligible shear FMI and undefined material parameters. Therefore, shear FMI were not included in this study. A model that includes both normal and shear FMI would need to be simultaneously fit to both biaxial and circumferential uniaxial tensile datasets so that strains in both conditions are encountered in the experiment. Inclusion of shear FMI may improve the simulation of planar shear loading.

Limitations, Future Work, and Conclusions

There are some limitations to the current study. The out-of-plane strain was not directly measured (similar to most uniaxial and biaxial studies). Therefore, in the model curve-fit a Poisson’s ratio was assumed to provide out-of-plane strains that were combined with the traction-free boundary condition. For the circ-axial samples the out-of-plane strain is in the radial direction the contribution to the total stress likely to be minimal. Similarly, the radial-axial samples were only used to calculate the matrix parameters, which were small in magnitude. Therefore, the assumed Poisson’s ratio likely had minimal effect. Nonetheless, direct measurement of out-of-plane strain is recommended for future studies. A second limitation is that the radial tensile parameters were defined to be isotropic extrafibrillar matrix, neglecting potential contribution of interlamellar structures such as elastin or minor collagens. The interlamellar AF structure is poorly understood. Since the matrix contribution was so small in tension, this assumption had little impact. However, this assumption may have contributed to the predicted shear modulus, dominated by the matrix properties (Figure 7B), being higher than measured shear moduli (Jacobs, Smith et al. 2011 In Press). Ongoing studies are measuring the extrafibrillar matrix tensile properties in confined compression with osmotic loading to isolate the matrix from any fiber contribution (Cortes, Gerasimowicz et al. 2011). Finally, we gripped the sample with a clamping method rather than using hooks, because hooks pulled out of our radial direction samples at low stresses. Based on finite element analyses, the clamps may have induced stress concentrations near the grips, increasing the measured loads and somewhat overestimated the stresses in the center of the sample (Sun, Sacks et al. 2005). However, both hooks and clamps provide uniform stress at the center of the sample (Jacobs N.T., Cortes D.H. et al. 2011). Ongoing finite element modeling studies will quantify the correction factor due such to biaxial test boundary conditions.

In this study, biaxial tensile loading and a structurally motivated nonlinear, anisotropic, hyperelastic constitutive model was applied and validated to human AF tissue. Successful validation to independent loading configurations has not previously been shown for AF models, demonstrating the power of combining biaxial tension with the model formulation used here, to establish a robust AF constitutive formulation. The model, in combination with a continuous quantitative measure of disc degeneration, showed that the parameters for fiber nonlinearity and the normal FMI correlated with degeneration, resulting in an elongated toe region and lower stiffness with degeneration. Biaxial tension data successfully matched previously published uniaxial circumferential Young’s modulus, provided an explanation for the low values in previously published axial direction Young’s modulus, and was reasonably able to simulate shear mechanics. The normal FMI were important contributors to stress and changed with degeneration, therefore their microstructural and compositional source should be investigated. Finally, this new tissue mechanical data and constitutive model can be incorporated into disc finite element models to provide improved fidelity to AF mechanics.

Supplementary Material

1

References

  1. Acaroglu ER, Iatridis JC, et al. Degeneration and aging affect the tensile behavior of human lumbar anulus fibrosus. Spine. 1995;20(24):2690–701. doi: 10.1097/00007632-199512150-00010. [DOI] [PubMed] [Google Scholar]
  2. Adams MA, Green TP. Tensile properties of the annulus fibrosus. I. The contribution of fibre-matrix interactions to tensile stiffness and strength. Eur Spine J. 1993;2(4):203–8. doi: 10.1007/BF00299447. [DOI] [PubMed] [Google Scholar]
  3. Aspden RM. Agreement Between Two Experimental Measures or Between Experiment and Theory. J Biomech. 2005;38(10):2136–7. doi: 10.1016/j.jbiomech.2005.05.009. [DOI] [PubMed] [Google Scholar]
  4. Ateshian GA, Rajan V, et al. Modeling the matrix of articular cartilage using a continuous fiber angular distribution predicts many observed phenomena. J Biomech Eng. 2009;131(6):061003. doi: 10.1115/1.3118773. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Auerbach JD, Johannessen W, et al. In vivo quantification of human lumbar disc degeneration using T(1rho)-weighted magnetic resonance imaging. Eur Spine J. 2006;15(Suppl 3):S338–44. doi: 10.1007/s00586-006-0083-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Bass EC, Ashford FA, et al. Biaxial testing of human annulus fibrosus and its implications for a constitutive formulation. Ann Biomed Eng. 2004;32(9):1231–42. doi: 10.1114/b:abme.0000039357.70905.94. [DOI] [PubMed] [Google Scholar]
  7. Borthakur A, Maurer PM, et al. MRI and discography pressure as novel biomarkers for disc degeneration and low back pain. Spine. 2011 doi: 10.1097/BRS.0b013e31820287bf. In Press. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Brown KR, Pollintine P, et al. Biomechanical implications of degenerative joint disease in the apophyseal joints of human thoracic and lumbar vertebrae. Am J Phys Anthropol. 2008;136(3):318–26. doi: 10.1002/ajpa.20814. [DOI] [PubMed] [Google Scholar]
  9. Bruehlmann SB, Hulme PA, et al. In situ intercellular mechanics of the bovine outer annulus fibrosus subjected to biaxial strains. J Biomech. 2004;37(2):223–31. doi: 10.1016/s0021-9290(03)00244-6. [DOI] [PubMed] [Google Scholar]
  10. Cassidy JJ, Hiltner A, et al. Hierarchical structure of the intervertebral disc. Connective Tissue Research. 1989;23:75–88. doi: 10.3109/03008208909103905. [DOI] [PubMed] [Google Scholar]
  11. Choi G, Lee SH, et al. Percutaneous endoscopic approach for highly migrated intracanal disc herniations by foraminoplastic technique using rigid working channel endoscope. Spine. 2008;33(15):E508–15. doi: 10.1097/BRS.0b013e31817bfa1a. [DOI] [PubMed] [Google Scholar]
  12. Cortes DH, Gerasimowicz KM, et al. Transactions of the Orthopaedic Research Society. Long Beach, CA: 2011. Material properties of the extrafibrillar matrix of annulus fibrosus in tension and compression. [Google Scholar]
  13. Eberlein R, Holzapfel GA, et al. An Anisotropic Model for Annulus Tissue and Enhanced Finite Element Analysis of Intact Lumbar Disc Bodies. Computer Methods in Biomechanics and Biomedical Engineering. 2001;4:209–229. [Google Scholar]
  14. Elliott DM, Setton LA. A linear material model for fiber-induced anisotropy of the anulus fibrosus. J Biomech Eng. 2000;122(2):173–9. doi: 10.1115/1.429639. [DOI] [PubMed] [Google Scholar]
  15. Elliott DM, Setton LA. Anisotropic and inhomogeneous tensile behavior of the human anulus fibrosus: experimental measurement and material model predictions. J Biomech Eng. 2001;123(3):256–63. doi: 10.1115/1.1374202. [DOI] [PubMed] [Google Scholar]
  16. Fujita Y, Duncan NA, et al. Radial tensile properties of the lumbar annulus fibrosus are site and degeneration dependent. J Orthop Res. 1997;15(6):814–9. doi: 10.1002/jor.1100150605. [DOI] [PubMed] [Google Scholar]
  17. Fujita Y, Wagner DR, et al. Anisotropic shear behavior of the annulus fibrosus: effect of harvest site and tissue prestrain. Med Eng Phys. 2000;22(5):349–57. doi: 10.1016/s1350-4533(00)00053-9. [DOI] [PubMed] [Google Scholar]
  18. Galante JO. Tensile properties of the human lumbar annulus fibrosus. Acta Orthop Scand. 1967;100(Suppl):1–91. doi: 10.3109/ort.1967.38.suppl-100.01. [DOI] [PubMed] [Google Scholar]
  19. Gregory DE, Callaghan JP. A comparison of uniaxial and biaxial mechanical properties of the annulus fibrosus: a porcine model. J Biomech Eng. 2011;133(2):024503. doi: 10.1115/1.4003327. [DOI] [PubMed] [Google Scholar]
  20. Guerin HA, Elliott DM. Degeneration affects the fiber reorientation of human annulus fibrosus under tensile load. J Biomech. 2006;39(8):1410–8. doi: 10.1016/j.jbiomech.2005.04.007. [DOI] [PubMed] [Google Scholar]
  21. Guerin HL, Elliott DM. Quantifying the contributions of structure to annulus fibrosus mechanical function using a nonlinear, anisotropic, hyperelastic model. J Orthop Res. 2007;25(4):508–16. doi: 10.1002/jor.20324. [DOI] [PubMed] [Google Scholar]
  22. Guo H, Humphrey JD, et al. Effects of biaxial stretch on arteriolar function in vitro. Am J Physiol Heart Circ Physiol. 2007;292(5):H2378–86. doi: 10.1152/ajpheart.00810.2006. [DOI] [PubMed] [Google Scholar]
  23. Haughton VM, Lim TH, et al. Intervertebral disk appearance correlated with stiffness of lumbar spinal motion segments. AJNR Am J Neuroradiol. 1999;20(6):1161–5. [PMC free article] [PubMed] [Google Scholar]
  24. Humphrey JD, Strumpf RK, et al. Biaxial mechanical behavior of excised ventricular epicardium. Am J Physiol. 1990;259(1 Pt 2):H101–8. doi: 10.1152/ajpheart.1990.259.1.H101. [DOI] [PubMed] [Google Scholar]
  25. Iatridis JC, Kumar S, et al. Shear mechanical properties of human lumbar annulus fibrosus. J Orthop Res. 1999;17(5):732–7. doi: 10.1002/jor.1100170517. [DOI] [PubMed] [Google Scholar]
  26. Iatridis JC, Setton LA, et al. Degeneration affects the anisotropic and nonlinear behaviors of human anulus fibrosus in compression. J Biomech. 1998;31(6):535–44. doi: 10.1016/s0021-9290(98)00046-3. [DOI] [PubMed] [Google Scholar]
  27. Jacobs NT, Cortes DH, et al. Effect of Boundary Conditions on Stress-Strain Uniformity in Biaxial Tension of Annulus Fibrosus. Orthopaedic Research Society; Long Beach, CA: 2011. [Google Scholar]
  28. Jacobs NT, Cortes DH, et al. Transactions of the Orthopaedic Research Society. Long Beach, CA: 2011. Effect of boundary conditions on stress-strain uniformity in biaxial tension of annulus fibrosus. [Google Scholar]
  29. Jacobs NT, Smith LJ, et al. Effect of orientation and targeted extracellular matrix degradation on annulus fibrosus shear mechanical properties. JMBBM. 2011 doi: 10.1016/j.jmbbm.2011.03.016. In Press. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Johannessen W, Auerbach JD, et al. Assessment of human disc degeneration and proteoglycan content using T1rho-weighted magnetic resonance imaging. Spine. 2006;31(11):1253–7. doi: 10.1097/01.brs.0000217708.54880.51. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Kang T, Humphrey JD, et al. Comparison of biaxial mechanical properties of excised endocardium and epicardium. Am J Physiol. 1996;270(6 Pt 2):H2169–76. doi: 10.1152/ajpheart.1996.270.6.H2169. [DOI] [PubMed] [Google Scholar]
  32. Keller TS, Spengler DM, et al. Mechanical behavior of the human lumbar spine. I. Creep analysis during static compressive loading. J Orthop Res. 1987;5(4):467–78. doi: 10.1002/jor.1100050402. [DOI] [PubMed] [Google Scholar]
  33. Klisch SM, Lotz JC. Application of a fiber-reinforced continuum theory to multiple deformations of the annulus fibrosus. J Biomech. 1999;32(10):1027–36. doi: 10.1016/s0021-9290(99)00108-6. [DOI] [PubMed] [Google Scholar]
  34. Nachemson AL, Schultz AB, et al. Mechanical properties of human lumbar spine motion segments. Influence of age, sex, disc level, and degeneration. Spine (Phila Pa 1976) 1979;4(1):1–8. doi: 10.1097/00007632-197901000-00001. [DOI] [PubMed] [Google Scholar]
  35. Nerurkar NL, Mauck RL, et al. ISSLS prize winner: Integrating theoretical and experimental methods for functional tissue engineering of the annulus fibrosus. Spine. 2008;33(25):2691–701. doi: 10.1097/BRS.0b013e31818e61f7. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Nerurkar NL, Mauck RL, et al. Modeling interlamellar interactions in angle-ply biologic laminates for annulus fibrosus tissue engineering. Biomech Model Mechaniobiol. 2011 doi: 10.1007/s10237-011-0288-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Nguyen AM, Johannessen W, et al. Noninvasive quantification of human nucleus pulposus pressure with use of T1rho-weighted magnetic resonance imaging. J Bone Joint Surg Am. 2008;90(4):796–802. doi: 10.2106/JBJS.G.00667. [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. O’Connell GD, Guerin HL, et al. Thoretical and Uniaxial Experimental Evaluation of Human Annulus Fibrosus Degeneration. J Biomech Eng. 2009 doi: 10.1115/1.3212104. [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. O’Connell GD, Malhotra NR, et al. The Effect of Discectomy and the Dependence on Degeneration of Human Intervertebral Disc Strain in Axial Compression. Spine. 2011 doi: 10.1097/BRS.0b013e318216752f. In Press. [DOI] [PMC free article] [PubMed] [Google Scholar]
  40. O’Connell GD, Vresilovic E, et al. Human Intervertebral Disc Internal Strain In Compression Loading: The Effect of Disc Region, Loading Position, and Degeneration. J Orthop Res. 2011;29(4):547–55. doi: 10.1002/jor.21232. [DOI] [PMC free article] [PubMed] [Google Scholar]
  41. Peng XQ, Guo ZY, et al. An Anisotropic Hyperelastic Constitutive Model with Fiber-Matrix Shear Interaction for the Human Annulus Fibrosus. J Appl Mech. 2006;73:815–824. [Google Scholar]
  42. Sacks MS. A method for planar biaxial mechanical testing that includes in-plane shear. J Biomech Eng. 1999;121(5):551–5. doi: 10.1115/1.2835086. [DOI] [PubMed] [Google Scholar]
  43. Sacks MS, Chuong CJ. Biaxial mechanical properties of passive right ventricular free wall myocardium. J Biomech Eng. 1993;115(2):202–5. doi: 10.1115/1.2894122. [DOI] [PubMed] [Google Scholar]
  44. Sacks MS, Sun W. Multiaxial mechanical behavior of biological materials. Annu Rev Biomed Eng. 2003;5:251–84. doi: 10.1146/annurev.bioeng.5.011303.120714. [DOI] [PubMed] [Google Scholar]
  45. Schmidt H, Heuer F, et al. Dependency of disc degeneration on shear and tensile strains between annular fiber layers for complex loads. Med Eng Phys. 2009;31(6):642–9. doi: 10.1016/j.medengphy.2008.12.004. [DOI] [PubMed] [Google Scholar]
  46. Schroeder Y, Huyghe JM, et al. A biochemical/biophysical 3D FE intervertebral disc model. Biomech Model Mechanobiol. 2010;9(5):641–50. doi: 10.1007/s10237-010-0203-0. [DOI] [PubMed] [Google Scholar]
  47. Spencer AJM. Deformations of Fibre-reinforced Materials. Oxford, London: University Press; 1972. [Google Scholar]
  48. Sun W, Sacks MS, et al. Effects of boundary conditions on the estimation of the planar biaxial mechanical properties of soft tissues. J Biomech Eng. 2005;127(4):709–15. doi: 10.1115/1.1933931. [DOI] [PubMed] [Google Scholar]
  49. Tong P, Fung YC. The stress-strain relationship for the skin. J Biomech. 1976;9(10):649–57. doi: 10.1016/0021-9290(76)90107-x. [DOI] [PubMed] [Google Scholar]
  50. Vernon-Roberts B, Fazzalari NL, et al. Pathogenesis of tears of the anulus investigated by multiple-level transaxial analysis of the T12-L1 disc. Spine. 1997;22(22):2641–6. doi: 10.1097/00007632-199711150-00012. [DOI] [PubMed] [Google Scholar]
  51. Wagner DR, Lotz JC. Theoretical model and experimental results for the nonlinear elastic behavior of human annulus fibrosus. J Orthop Res. 2004;22(4):901–9. doi: 10.1016/j.orthres.2003.12.012. [DOI] [PubMed] [Google Scholar]
  52. Wagner DR, Reiser KM, et al. Glycation increases human annulus fibrosus stiffness in both experimental measurements and theoretical predictions. J Biomech. 2006;39(6):1021–9. doi: 10.1016/j.jbiomech.2005.02.013. [DOI] [PubMed] [Google Scholar]
  53. Wu HC, Yao RF. Mechanical behavior of the human annulus fibrosus. J Biomech. 1976;9(1):1–7. doi: 10.1016/0021-9290(76)90132-9. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

1
NIHMS412989-supplement-1.doc (2.8MB, doc)

RESOURCES