Quantifying and correcting for the winner's curse in quantitative-trait association studies

Abstract

Quantitative traits (QT) are an important focus of human genetic studies both because of interest in the traits themselves, and because of their role as risk factors for many human diseases. For large-scale QT association studies including genome-wide association studies (GWAS), investigators usually focus on genetic loci showing significant evidence for SNP-QT association, and genetic effect size tends to be overestimated as a consequence of the winner’s curse. In this paper, we study the impact of the winner’s curse on QT association studies in which the genetic effect size is parameterized as the slope in a linear regression model. We demonstrate by analytical calculation that the overestimation in the regression slope estimate decreases as power increases. To reduce the ascertainment bias, we propose a three-parameter maximum likelihood method and then simplify this to a one-parameter method by excluding nuisance parameters. We show that both methods reduce the bias when power to detect association is low or moderate, and that the one-parameter model generally results in smaller variance in the estimate.

Introduction

For complex disease genetics research in humans, remarkable progress has been made recently with a number of genome-wide case-control association studies published. In parallel, there have been increasing efforts to investigate the association between genotype and disease-related QT at population level [www.genome.gov/gwastudies]. One rationale behind QT studies is that, because the traits examined are in many cases risk factors for disease, identified quantitative trait loci (QTL) may also be disease predisposing loci.

A commonly used method to detect the SNP-QT association is to regress the observed trait values on a score based on the individual’s SNP genotype. The slope of the linear regression is a measure of the strength of the genetic effect. As in disease case-control association studies, for QT association studies, investigators usually focus on genetic loci showing significant evidence for SNP-QT association. As a consequence of the winner’s curse [Lohmueller et al., 2003], the effect size estimator tends to overestimate the true genetic effect size. Several investigators have studied the winner’s curse effect in the context of QT linkage analysis [Göring et al., 2001; Siegmund, 2002; Allison et al., 2003; Sun and Bull, 2005; Wu et al., 2006] or disease association analysis [Zöllner and Pritchard, 2007; Garner, 2007; Yu et al., 2007; Zhong and Prentice, 2008; Ghosh et al., 2008; Xiao and Boehnke, 2009].

In this paper, we study the winner’s curse effect in the context of QT association studies. We quantify analytically the impact of the winner's curse on the estimate of the genetic effect size parameterized as the linear regression slope as a function of sample size, allele frequency, and statistical significance level. We then describe an ascertainment-corrected maximum likelihood method similar to that we and others derived for case-control disease association studies [Zöllner and Pritchard, 2007; Xiao and Boehnke, 2009] to correct for this bias. We describe both a fully parameterized model in which we estimate the intercept, slope, and error of the linear regression model, and a simplified model which focuses only on the regression equation slope parameter resulting in a one-parameter model. We also consider a mean square error (MSE) weighted estimator [Zhong and Prentice 2008] calculated as the weighted average of the uncorrected and corrected estimators using MSE as the weight. We compare the performance (bias, standard error, MSE) of these ascertainment-corrected maximum likelihood estimators (MLEs) and that of the naïve, uncorrected estimators.

As for case-control studies [Zöllner and Pritchard, 2007; Xiao and Boehnke, 2009], we find that (1) the factors that result in overestimation of the regression slope can be summarized by study power alone, independent of sample size and allele frequency, and that overestimation decreases as power increases; (2) compared to the uncorrected estimator of the regression slope, the ascertainment-corrected estimators based on the one- and three-parameter models result in reduced absolute bias when study power is low or moderate, and have comparable absolute bias when power is high; (3) the MSE of the ascertainment-corrected MLE of the regression slope based on the one-parameter model is generally smaller than that for the three-parameter model; and is also smaller than the uncorrected estimator when power is low or moderate; and (4) the MSE weighted estimator generally improves the ascertainment correction compared to the three- and one-parameter-model based ascertainment-corrected MLEs. We recommend the use of the MSE-weighted version of the one-parameter-based ascertainment-corrected maximum likelihood method for estimation of genetic effect size in large-scale quantitative trait association studies.

Methods

I. Models and Assumptions

We assume N independent samples genotyped at an autosomal quantitative trait locus (QTL) with alleles A and a. Let p be the frequency for the minor allele a. For individual i, let y_i be the trait value and X_i be the genotype score, depending on the genetic model we assume. For example, X_i = 0 for AA, 1 for Aa, and 2 for aa if we assume an additive model or X_i = 0 for AA or Aa, and 1 for aa for a recessive allele a.

To test for SNP-QT association, we assume the linear regression model: y_i = β₀ + β₁X_i + ε_i, where {ε_i} are independently and identically distributed as normal with mean 0 and variance σ². For simplicity in what follows, we assume an additive genetic model and no other covariates in the linear regression model, although these assumptions are easily relaxed.

In a QT association study, we focus on the slope β₁ in the linear regression model as a measure of the genetic effect size, and calculate the regression-based t-test statistic $T=\frac{\left|{\widehat{\beta }}_1\right|}{SE({\widehat{\beta }}_1)}$ for the null hypothesis of no association H₀: β₁ = 0. Here, β̂₁ and SE(β̂₁) are the estimated regression slope and its standard error (SE) obtained from the linear regression. We claim the association significant at significance level α when T > t_α/2,N–2, based on the t distribution with N-2 degrees of freedom.

II. Uncorrected (naïve) estimators

In practice, investigators often estimate the effect size of the QTL, parameterized as the linear regression slope β₁, using the same data used for the initial association test. We call this uncorrected estimator of β₁ "naïve" because it ignores the possible bias associated with focusing only on genetic markers with statistically significant association results.

To assess the impact of the winner's curse, we calculate the expected value of this uncorrected estimator β̂_1,un conditional on obtaining significant evidence for association:

$$E({\widehat{\beta }}_{1,un}|T>t_{\alpha /2,N-2})=E({\widehat{\beta }}_{1,un}|\frac{|{\widehat{\beta }}_{1,un}|}{SE({\widehat{\beta }}_{1,un})}>t_{\alpha /2,N-2})$$ (1)

To simplify this calculation, we approximate (1) by assuming $SE({\widehat{\beta }}_{1,un})\approx \raisebox{1ex}{$\sigma $}\!\left/ \!\raisebox{-1ex}{$\sqrt{S_{xx}}$}\right.$:

$$\begin{array}{l}E({\widehat{\beta }}_{1,un}|T>t_{\alpha /2,N-2})\approx E({\widehat{\beta }}_{1,un}|\frac{\left|{\widehat{\beta }}_{1,un}\right|}{\raisebox{1ex}{$\sigma $}\!\left/ \!\raisebox{-1ex}{$\sqrt{S_{xx}}$}\right.}>t_{\alpha /2,N-2})\\ ={\displaystyle \underset{-\infty }{\overset{-a}{\int }}z\times f(z;{\beta }_1,\raisebox{1ex}{${\sigma }^2$}\!\left/ \!\raisebox{-1ex}{$S_{xx}$}\right.|z>a)dz}+{\displaystyle \underset{a}{\overset{+\infty }{\int }}z\times f(z;{\beta }_1,\raisebox{1ex}{${\sigma }^2$}\!\left/ \!\raisebox{-1ex}{$S_{xx}$}\right.|z>a)dz}\\ =\frac{{\beta }_1-{\displaystyle \underset{-a}{\overset{a}{\int }}z\times f(z;{\beta }_1,\raisebox{1ex}{${\sigma }^2$}\!\left/ \!\raisebox{-1ex}{$S_{xx}$}\right.)dz}}{P(T>t_{\alpha /2,N-2})}\end{array}$$ (2)

where f(z; β₁, σ²)is the density function of normal distribution with mean β₁ and variance σ², $a=\raisebox{1ex}{$t_{\alpha /2,N-2}\sigma $}\!\left/ \!\raisebox{-1ex}{$\sqrt{S_{xx}}$}\right.$, and $S_{xx}={{\displaystyle \sum _{i=1}^N(X_i-\overline{X})}}^2$. Note that the denominator of (2) is the power of the study, which equals 1 minus the cumulative distribution function (CDF) of the non-central t distribution with N – 2 degrees of freedom and non-centrality parameter $\frac{{\beta }_1\sqrt{S_{xx}}}{\sigma }$. From (2), we calculate the bias of the estimator as E(β̂_1,un|T > t_α/2,N–2) − β₁, and the proportional bias as $\frac{E({\widehat{\beta }}_{1,un}|T>t_{\alpha /2,N-2})-{\beta }_1}{{\beta }_1}$.

We also quantify the winner’s curse effect in the estimator of the coefficient of determination $R^2=\frac{S{S}_{reg}}{S{S}_{reg}+S{S}_{res}}$, where SS_reg and SS_res are the regression and residual sums of squares, respectively. By dividing both the numerator and denominator by SS_res, $R^2=\frac{F}{F+N-2}$, where $F=\frac{S{S}_{reg}/1}{S{S}_{res}/(N-2)}$ is the F test statistic for H₀: β₁ = 0. When there are no other covariates in the model, F = T². We calculate the expected difference in estimates of R² when taking into account or ignoring this ascertainment as:

$$E\left(R^2|T>t_{\alpha /2,N-2}\right)-E\left(R^2\right)=E\left(\frac{F}{F+N-2}|F>F_{\alpha ,1,N-2}\right)-E\left(\frac{F}{F+N-2}\right)=\frac{{\displaystyle \underset{F_{\alpha ,1,N-2}}{\overset{+\infty }{\int }}\frac{x}{x+N-2}}g(x)dx}{P(F>F_{\alpha ,1,N-2})}-{\displaystyle \underset{0}{\overset{+\infty }{\int }}\frac{x}{x+N-2}}g(x)dx$$ (3)

Here g(x) is the density of the F distribution with 1 and N 2 degrees of freedom, and F_{α,1, N–2} is the corresponding quantile at significance level α. Notice that, were R² a constant, the expected difference in (3) would be its bias in estimation owing to the winner's curse. Consequently, we define the estimated “proportional bias” of R² as $\frac{E\left(R^2|T>t_{\alpha /2,N-2}\right)-E\left(R^2\right)}{E\left(R^2\right)}$.

III. Ascertainment-corrected MLEs

Three-parameter model

The naïve estimator ignores the fact that we typically are interested in estimates of the regression slope β₁ only if we have strong evidence for SNP-QT association. To address this, we propose an ascertainment-corrected maximum likelihood method that conditions on obtaining evidence for association. To this end, we calculate the conditional likelihood function

$$L({\beta }_0,{\beta }_1,\sigma |y,X,T>t_{\alpha /2,N-2})={\displaystyle \prod _{i}f(y_i;{\beta }_0+{\beta }_1{x}_i,{\sigma }^2|T>t_{\alpha /2,N-2})=\frac{1\{T>t_{\alpha /2,N-2}\}}{P(T>t_{\alpha /2,N-2})}{\displaystyle \prod _{i}f(y_i;{\beta }_0+{\beta }_1{x}_i,{\sigma }^2)}}$$ (4)

where the indicator function 1{T > t_{α/2, N–2}} equals 1 if T > t_{α/2, N–2} and 0 otherwise, and f(y_i; µ, σ²) is the normal density function with mean µ and variance σ².

We maximize the likelihood (4) as a function of β₀, β₁, and σ to obtain the ascertainment-corrected MLEs β̂_0,as, β̂_1,as and σ̂_as by using the Nelder-Mead [1965] simplex method. We calculate the empirical standard errors of these estimates based on 1000 simulation replicates.

One-parameter model

Since our primary interest is to estimate the slope β₁, the intercept β₀ and variance σ² are nuisance parameters. We propose a one-parameter model to obtain a corrected estimator for β₁ only. Here, we assume the uncorrected estimator β̂_1,un is consistent and asymptotically normal since $\frac{v\widehat{a}r({\widehat{\beta }}_{1,un})}{\text{var}({\widehat{\beta }}_{1,un})}~1$ holds for a typical GWAS sample size. We confirmed this assumption by simulation (results not shown). In this case, we calculate the conditional likelihood for β₁ as:

$$L({\beta }_1|{\widehat{\beta }}_{1,un},T>t_{\alpha /2,N-2})=f({\widehat{\beta }}_{1,un};{\beta }_1,v\widehat{a}r({\widehat{\beta }}_{1,un})|T>t_{\alpha /2,N-2})\approx \frac{1\{T>t_{\alpha /2,N-2}\}f({\widehat{\beta }}_{1,un};{\beta }_1,v\widehat{a}r({\widehat{\beta }}_{1,un}))}{P(T>t_{\alpha /2,N-2}|{\beta }_1)}$$ (5)

We maximize the likelihood (5) as a function of β₁ to obtain the ascertainment-corrected MLE β̃_1,as by using the Nelder-Mead simplex method, and calculate the empirical standard error of this estimator based on 1000 simulation replicates.

IV. MSE-Weighted MLEs

Following Zhong and Prentice [2008], we also consider a weighted estimator β̂_1,w, calculated as the weighted average of the uncorrected and corrected estimators as β̂_1,w = K̂ β̂_1,un + (1–K̂) β̂_1,cor. The weight $\widehat{K}=\frac{{\widehat{\sigma }}_{un}^2}{{\widehat{\sigma }}_{un}^2+{\left({\widehat{\beta }}_{1,un}-{\widehat{\beta }}_{1,cor}\right)}^2}$, where the denominator is the estimated mean square error (MSE), and the corrected estimator β̂_1,cor is the MLE based on either the three- or one-parameter-model. Zhong and Prentice [2008] showed that in the case-control setting, this weighted estimator generally results in a smaller bias compared to the naïve and ascertainment-corrected estimators.

Simulations

We simulated the trait value y_i (i = 1, …, N) from the normal distribution with mean β₀+ β₁X_i and variance σ² given the true parameter values (β₀, β₁, and σ) and the genotype score X_i simulated based on the QTL genotype frequencies assuming HWE. We calculated the test statistic $T=\frac{\left|{\widehat{\beta }}_1\right|}{SE({\widehat{\beta }}_1)}$ based on the simulated data, where β̂₁ and SE(β̂₁) were the estimated regression slope and its standard error (SE) obtained from the linear regression without correction. We kept the simulated trait values only if T > t_{α/2, N-2}.

Results

I. Uncorrected Estimators

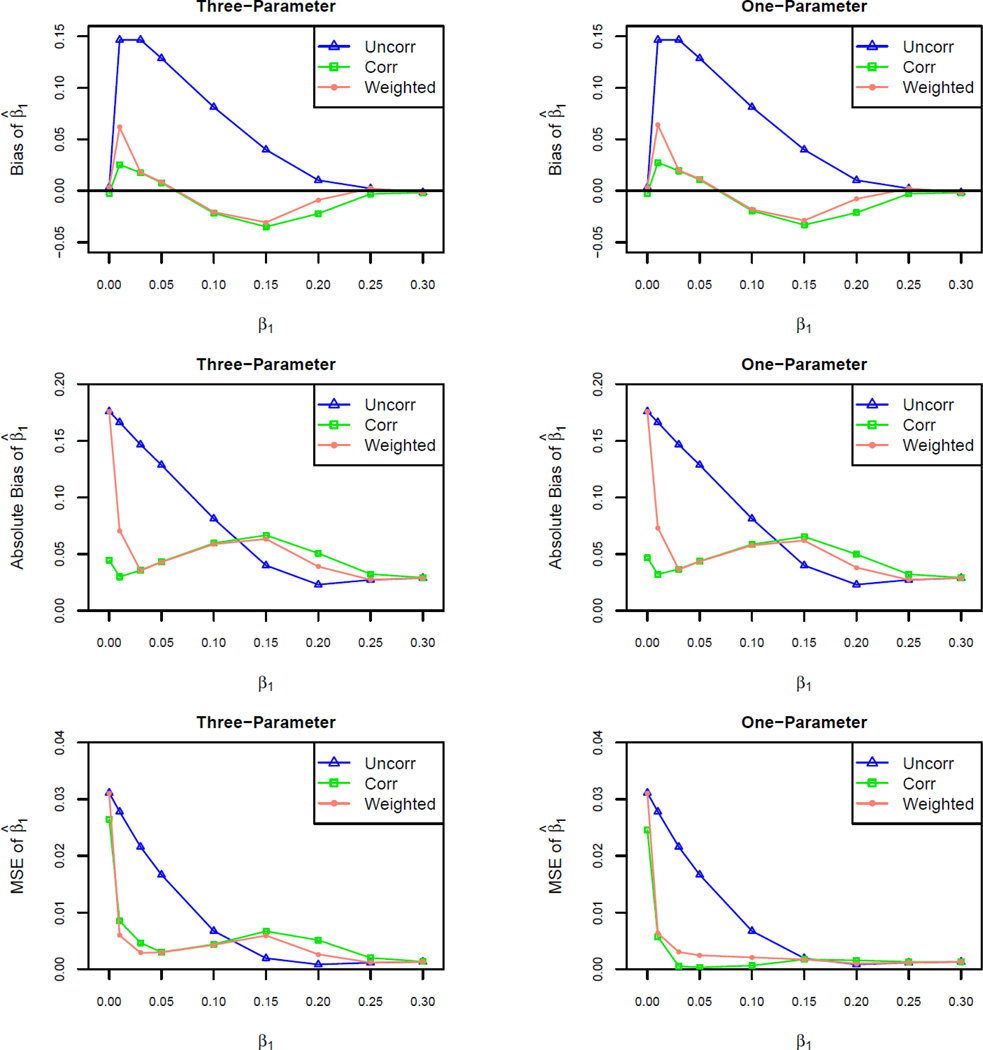
For a SNP showing significant evidence for QT association, there is a clear upward bias in the uncorrected estimator β̂_1,unof the genetic effect size β₁ (Figure 1). This bias is particularly severe when power is low owing to small sample size N and/or small genetic effect size β₁ (Figure 2). As power increases, bias decreases. Under the null hypothesis (β₁ = 0), β₁ is equally likely to be over- or under-estimated so that the bias is zero while the absolute bias and the mean square error (MSE) are large owing to large variance. Due to symmetry, here and for the rest of the figures, we provide results only for β₁ ≥ 0. For example, given a SNP-QT association study with N = 2000 samples, minor allele frequency (MAF) p = .3, and testing at significance level of α = 10⁻⁶ under an additive genetic model, if the true value for β₁ is 0.1 (power = 5%), the expected value of the uncorrected estimator of β₁ is .178, resulting in an absolute bias of .078 and a proportional bias of 78%. In this case, a follow-up study designed to have 80% power at significance level α = .05 would include 595 samples, but have actual power of only 35%.

Figure 1.

Bias, absolute bias, and mean square error (MSE) of the uncorrected, corrected, and MSE-weighted estimators for β₁ from three- and one-parameter models with sample size N = 2000 and allele frequency p = .3 under an additive genetic model. Significance level α = 10⁻⁶.

Figure 2.

Proportional bias of the uncorrected (black), corrected (dark blue), and MSE-weighted (orange) estimators for β₁ from three- and one-parameter models. Significance levels A) α = 10⁻⁶ and B) α = 10⁻⁸. Results are presented for β₁ ≥ 0 under an additive genetic model.

As for case-control studies [Zöllner and Pritchard, 2007; Xiao and Boehnke, 2009], we found that for a fixed significance level α, the proportional bias in the uncorrected estimator of β₁ is solely a function of power, whatever the sample size, allele frequency, and genetic model (Figure 2). Given fixed power, different significance levels result in different proportional bias in the naïve estimator of β₁. As expected, proportional bias decreases as power increases, since the conditioning event becomes increasingly likely as power increases. At significance level α = 10⁻⁶, the uncorrected estimator of β₁ gives a proportional bias of 50% when power is 10% but is nearly unbiased when power is 95% (Figure 2A).

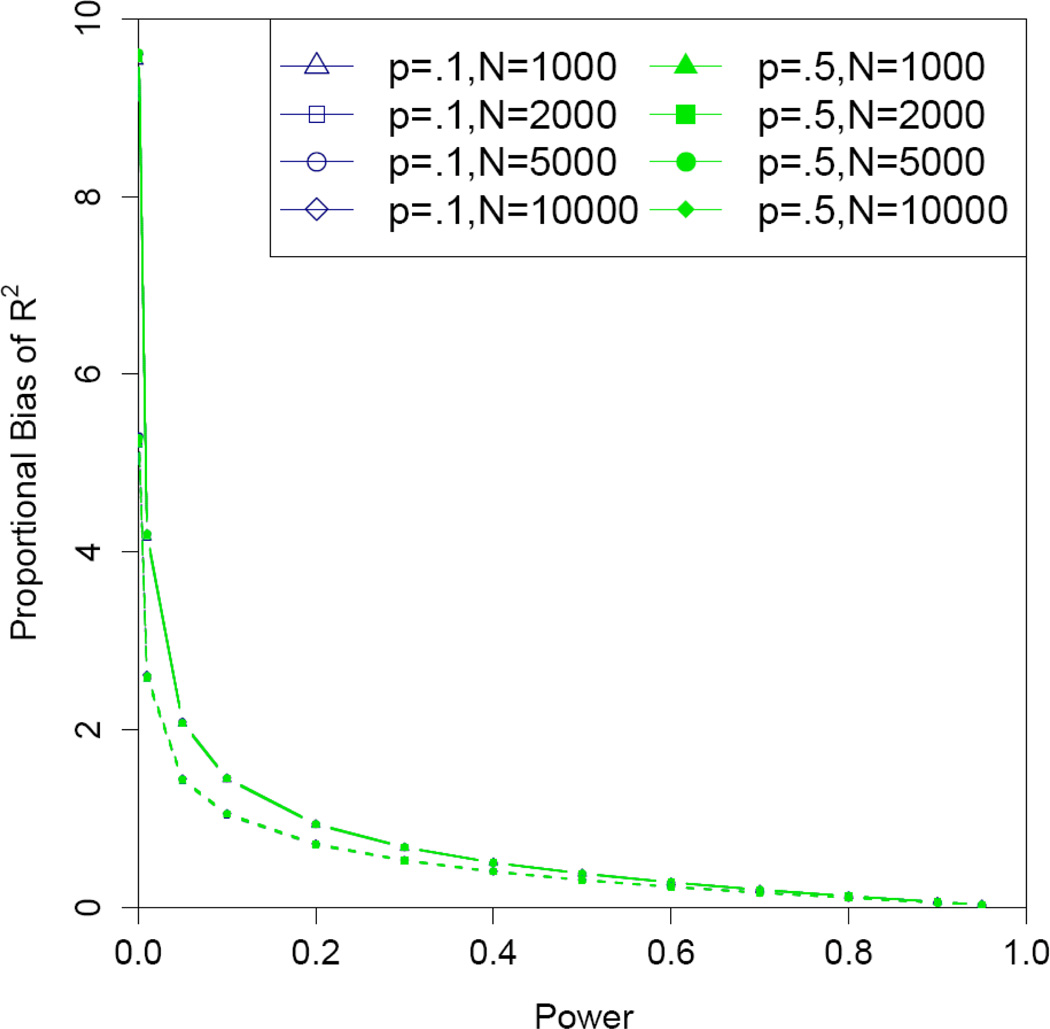
Interestingly, we found that, at a fixed significance level, the estimated “proportional bias” in the uncorrected estimator of the coefficient of determination R² is solely a function of the power as well (Figure 3), independent of sample size and allele frequency.

Figure 3.

Estimated proportional bias of the coefficient of determination R² versus power for the uncorrected estimator under an additive genetic additive model. Significance levels α = 10⁻⁴ (solid) and α = 10⁻⁶ (dashed).

II. Corrected ML and MSE-Weighted Estimators

We found that both three- and one-parameter model-based ascertainment-corrected MLEs for the genetic effect size β₁ are less biased than the uncorrected estimator when power is low or moderate (< 60%) (Figure 2). For example, given N = 2000 samples, allele frequency p = .3, and testing at significance level of α = 10⁻⁶ under an additive model, if the true value for β₁ is 0.1 (power = 5%), the proportional bias of the corrected MLE of δ from the three- and one-parameter models are both about −20%, compared to +78% before correction. However, both corrected estimators tend to underestimate the true effect size. As expected, the bias and absolute bias of the MSE-weighted estimator are intermediate between those of the uncorrected and corrected estimators (Figure 1). In this case, a follow-up study designed to have 80% power based on the ascertainment-corrected estimator at significance level α = .05 would include 2480 samples and have actual power 89%, whereas 1880 samples actually would be sufficient to achieve 80% power.

The three-parameter and one-parameter estimators have very similar performance in bias reduction (Figure 1 and 2). However, the standard error of the MLE from one-parameter model is smaller compared to that of three-parameter model, and also the uncorrected estimator (Figure 1). As with bias and absolute bias, the variance of the MSE-weighted estimator is intermediate between that of the uncorrected and corrected estimators (Figure 1).

In the typical range of power for GWAS, we found that the MSE weighted estimator generally results in smaller bias compared to the uncorrected estimator or to the corrected estimators based on either the one- or three- parameter model (Figure 2). The improvement of the ascertainment correction is substantial when power is high. For example, at significance level α = 10⁻⁶, when study power is 80%, the proportional bias is 10% for the uncorrected estimator of β₁, and −18% for the ascertainment corrected estimators from both one- and three-parameter models, but only −5% for the weighted estimator.

Discussion

Similar to disease-marker case-control association studies, in QT association studies, the genetic effect size for associated markers tends to be overestimated as a consequence of the winner's curse. This is true because the association test statistic is correlated with the estimator of the genetic effect, and since investigators focus primarily on markers that show statistically significant evidence of association. In this paper, we parameterized the genetic effect size as the slope in a QT-genotype score linear regression, as is typical for QT association studies. We quantified the bias of the naïve estimator that ignore this ascertainment, and showed that the proportional bias in the estimators decreases as power increases. Interestingly, at fixed significance level, the proportional biases of the regression slope and the coefficient of determination are functions solely of power, independent of allele frequency or sample size.

To correct for this ascertainment bias, we proposed a three-parameter maximum likelihood model, and then simplified this to a one-parameter model rid of nuisance parameters. The ascertainment-corrected MLEs for the regression slope obtained from both models are generally less biased than the uncorrected estimators unless study power is moderate to high (>60%). However, both models tend to overcorrect. Since the uncorrected estimator is generally biased upward and the corrected estimators downward, following Zhong and Prentice [2008], we also considered the estimator β̂_1,w which takes a weighted average of the uncorrected and corrected estimators using the estimated MSE as the weight. Our simulations suggest that this MSE weighted estimator generally results in smaller bias compared to the uncorrected or ascertainment-corrected estimators based on either the one- or three-parameter model. This weighted estimator has little impact when power is low, but improves the ascertainment correction substantially when power is high.

Although the three- and one-parameter model based estimators of the effect size β₁ have very similar performance in bias reduction, the standard error of the MLE from one-parameter model is smaller than that of three-parameter model. This is likely primarily owing to optimizing the likelihood function over a one- versus three-parameter space. In addition, our one-parameter model makes an explicit normality assumption on the slope estimator.

Perhaps an even more important advantage of the one-parameter model is that it works only on the regression slope estimate obtained from linear regression without ascertainment correction, and so does not require individual-level QT and SNP genotype data. Thus, the one-parameter model can be used for large scale meta-analysis in which only summary data are available.

We assumed normally distributed QT data in our likelihood-based ascertainment-correction methods. To assess the robustness of our conclusions to failure of this assumption, we carried out additional simulations in which the QT was distributed as Cauchy (t distribution with one degree of freedom). There was no meaningful change in our results. Further, in practice, most QT GWAS use a transformation (for example, the inverse normal transformation) on the raw trait data to meet (approximately) the normality assumption, making this less of a concern.

In this study, we provide a less biased estimator of the effect size in QT association study, which allows for a more appropriate design for follow-up studies in sample size calculation based on this less biased estimator compared to the naïve estimator. We focused on one-stage designed QT association study, but it is easy to extend this approach to multi-stage designs. Similarly, we only presented results under an additive model with no covariates, but it is straightforward to generalize the approach to other genetic models by simply reparameterizing the genotype score or including covariates in the model.

In summary, we have presented analytic calculations to quantify the impact of the winner's curse in QT association studies, and demonstrate substantial overestimation of the genetic effect parameterized as the regression slope when study power is not high (< 60%). To correct for this ascertainment bias, we propose a fully parameterized maximum likelihood model and also a simplified likelihood model with nuisance parameters excluded. We demonstrate that the ascertainment-corrected estimators from both these models result in reduced absolute bias compared to the uncorrected estimator when study power is not high, and similar absolute bias when power is high. We show that the variance of the one-parameter-model based estimator is generally smaller than that of the three-parameter model. We also consider a MSE-weighted estimator and show that it generally results in smaller bias compared to the unweighted estimators based on either the one- or the three-parameter model. We recommend the use of the MSE-weighted version of the one-parameter maximum likelihood method for estimation of genetic effect size in QT association studies.