Tailored fibro-porous structure of electrospun polyurethane membranes, their size-dependent properties and trans-membrane glucose diffusion

Abstract

The aim of this study was to develop polyurethane (PU) based fibro-porous membranes and to investigate the size-effect of hierarchical porous structure on permeability and surface properties of the developed electrospun membranes. Non-woven Selectophore™ PU membranes having tailored fibre diameters, pore sizes, and thickness were spun using electrospinning, and their chemical, physical and glucose permeability properties were characterised. Solvents, solution concentration, applied voltage, flow rate and distance to collector, each were systematically investigated, and electrospinning conditions for tailoring fibre diameters were identified. Membranes having average fibre diameters – 347, 738 and 1102 nm were characterized, revealing average pore sizes of 800, 870 and 1060 nm and pore volumes of 44, 63 and 68% respectively. Hydrophobicity increased with increasing fibre diameter and porosity. Effective diffusion coefficients for glucose transport across the electrospun membranes varied as a function of thickness and porosity, indicating high flux rates for mass transport. Electrospun PU membranes having significantly high pore volumes, extensively interconnected porosity and tailorable properties compared to conventional solvent cast membranes can find applications as coatings for sensors requiring analyte exchange.

1. INTRODUCTION

Electrospinning is a fibre spinning technology wherein fibres having diameters from 2 nm to 10s of μm are spun under the influence of electric field [1, 2]. The advantage of electrospinning is that submicron fibre diameters can be achieved, which is not feasible with conventional dry or wet spinning methods. Under the influence of electric field, a flowing dielectric liquid stretches as it emerges from a needle or a hole in a flat end (spinneret) to form a cone, commonly referred to as Taylor cone, from the tip of which tiny droplets lift off (electrospraying) and if the applied voltage is sufficiently large, the droplets lifting off coalesce to form (usually one) thin jet of liquid (electrospinning) [2–4]. The formation of the Taylor cone and the thin jet of liquid are also dependent on the viscosity and the electrical resistivity of the polymer solution [2–4]. Provided the solvent containing the polymer evaporates fast enough, the thin jet forms the fibre. The continuous electrospun fibre is collected on a grounded collector, whose configuration can be varied to obtain different fibre sizes, orientation and the resulting electrospun 3D structures [2].

Electrospun membranes, having unique non-woven fibro-porous structure, offer small pores sizes, large pore volumes, and good mechanical stability per unit weight, leading to their wide-spread use as nano-filtration membranes for air and water purification [5, 6]. As filtration membranes, they were shown to support high flux rates for air, moisture and fluid permeability, which is essential for light-weight garments, wound dressings as well as high-pressure air and water filtration systems [6]. More recently, electrospun biomaterials have been of particular interest for biomaterials and tissue engineering due to their remarkable similarity to nano-fibrous natural extracellular matrix (ECM) [7–9]. They have been tested as scaffolds for tissue engineering of blood vessel, skin, bone, cartilage, skeletal muscle, neural and many other soft tissues [7–9]. Their larger surface area per unit volume also prompted development as electrodes for sensing applications and carriers for drug delivery [7, 10].

However, to our knowledge, they have not been reported as mass-transport limiting or anti-fouling membranes for implantable biosensors that require analyte exchange. Biocompatible membrane technologies are of major importance in medical applications. Coatings for biosensor and other medical devices are among a number of applications of lifesaving diagnosis, monitoring and therapeutic devices. The coatings are often required to operate in complex biological fluids such as blood or plasma. Selective transport of targeted analyte molecules, sieving of large biomolecules, biocompatibility – preventing biofouling and fibrous encapsulation and robust mechanical properties are essential for making interference free and long-term sensing especially when implanted in the body.

Solvent cast polyurethanes have been widely used as mass-transport limiting membranes for implantable biosensors due to their excellent hydrolytic stability and good biocompatibility [6, 11]. However, their permeability to solute (e.g. glucose) transport is susceptible to huge variations (within and between the manufacture batches) due to their unpredictable pore geometries and pore size distributions [12, 13]. The hypothesis for our overall research was that the highly interconnected porous structure of PU electrospun coatings would provide highly controllable permeability for solute transport, as well as bio-mimicking 3-D fibro-porous structure of the natural extracellular matrix for implantable biosensors.

However, before the membranes can be applied on sensors, it was first essential to determine the electrospinning parameters for obtaining the fibres of desired diameters and membrane structure. Hence, in this study, we systematically evaluated the different parameters namely, solvents, solution concentration, applied voltage, flow rate and distance to collector for electrospinning the commercial Selectophore™ PU. Different combinations of parameters were identified to electrospin different PU fibre membranes (on a flat plate collector) having average fibre diameters specifically in the range between 100 and 1500 nm. Following optimization, a set of PU membranes having average fibre diameters of 347, 738 and 1102 nm were chosen for extensive characterization of membrane properties. These set of membranes were primarily intended for application as mass-transport limiting membranes for implantable glucose biosensors. Hence, in this paper, we further report the characterization of their properties using FTIR (qualitative chemical stability), SEM (morphology, fibre diameter, and membrane thickness), bubble point and gravimetry (porosity), contact angle (hydrophilicity) and glucose diffusion across the membranes’ cross-section (permeability to analyte/solute).

2. MATERIALS AND METHODS

Selectophore™ PU [a medical-grade aliphatic poly(ether-urethane)], Tetrahydrofunan (THF), N,N-Dimethylformamide (DMF), bovine serum albumin (BSA), glutaraldehyde grade I (50%) (GTA), glucose oxidase (GOD) (EC 1.1.3.4, Type X-S, Aspergillus niger, 157,500U/g, Sigma), ATACS 5104/4013 epoxy adhesive, Brij 30, D-(+)-glucose and 0.01M phosphate buffered saline (PBS) tablets were purchased from Sigma–Aldrich–Fluka. Teflon-coated platinum–iridium (9:1 in weight, Ø 0.125mm) and silver wires (Ø 0.125mm) were obtained from World Precision Instruments, Inc. (Sarasota, FL).

2.1. Electrospinning Selectophore™ PU

A typical vertical setup consisting of a high voltage power supply (EL30R1.5, Glassman High Voltage Inc., Hampshire, UK), a syringe pump (Fusion 100), a PTFE tubing (Ø 1/16’) connecting a 10 ml plastic syringe (BD) to a 22G stainless steel needle (BD, flat-tip, FISHMAN, UK) spinneret, and a 16×16 cm² grounded steel plate collector was used for electrospinning PU (Supplementary Figure 1). Solvents (THF and DMF mixed in weight ratios of 100:0, 70:30, 50:50, 30:70 and 0:100), solution concentration (8, 10 and 12 wt%), flow rate (0.1 to 1.2 ml/h), applied electric potential (11 to 25 kV) and distance between spinneret and collector (18 to 24 cm), were varied to optimize the parameters for electrospinning PU at ambient conditions (23±3.32°C room temperature and 35 to 47% relative humidity). Electrospinning time was varied from 1 to 120 min to obtain membranes of different thicknesses. The membranes were dried at room temperature and stored in a power assisted vacuum desiccator until further use.

2.2. Infrared Spectroscopy

An ATR-FTIR spectrophotometer (PerkinElmer Inc.) was used to investigate any qualitative changes to the polymer structure due to electrospinning, and also to qualitatively monitor any residual solvents in the electrospun membranes. Each spectrum, acquired in transmittance mode, was an average of 128 scans at a resolution of 4 cm⁻¹.

2.3. Morphology

The quality of electrospun membranes being prepared was first screened visually under an optical microscope (LEICA S60) to ascertain the uniformity of the fibre being formed. Thereafter, morphology of small samples of the different electrospun membranes were sputter coated for 30 sec with gold using an AGAR high-resolution sputter-coater and observed under SEM (Zeiss Supra 35VP field emission SEM (FESEM) in SE mode).

2.4. Fibre Diameter and Membrane Thickness

The fibre diameters were measured on SEM images using a software programme for length measurements developed in-house using Matlab. For each measurement, the software first requires a line to be drawn at one edge along the length of the fibre followed by a second line perpendicular to the first line drawn across to the other edge of the fibre to obtain the actual and the accurate measurement for fibre diameter. The accuracy of these measurements was cross-confirmed with Image J image analysis software. For the measurement of fibre diameter, a total of 160 measurements were made on 8 different SEM images, each representing a non-overlapping random field of view for each electrospun membrane configuration. To measure thickness, the membranes were snap-frozen using liquid nitrogen, followed by cutting using a scalpel and images of their cross-sections obtained using SEM. The above-mentioned software was used for measuring membrane thickness. Membrane thicknesses were also measured using a digital micrometer.

2.5. Pore Size and Porosity

The pore size for the different membranes was measured using extrusion porosimetry (also called bubble point measurement) as reported earlier [14]. Membranes electrospun for 2 h were used for bubble point measurements. The pressure needed to blow air through a liquid filled membrane was used to determine the bubble point. The range of pore sizes (radius a ) were calculated using the Young-Laplace equation [14] (Eq. 1):

$$a=\frac{2{\gamma }_{\text{st}}cos\theta }{\Delta \text{P}}$$ (Eq. 1)

• where ΔP is the differential pressure,

• γ^st the surface tension of the wetting liquid and

• θ the wetting angle. For a completely wetted membrane with all pores filled with the wetting liquid, cos θ is 1 [14]. This is valid if the walls of the pores are assumed to be straight with a sharp edge, as there would be a film of the wetting liquid presenting on the pore wall. In any cases, for instance in our study, a contact angle ( θ ) of 20° was used giving a value of 0.94 (cos 20°).

The porosity of the membranes was determined using gravimetry. The dimensions of the membranes were measured using micrometer (No. 293-832 Mitutoyo, Japan) and ruler to obtain thickness and surface area. The weight of the sample was measured using a high sensitivity balance (Fisher Scientific, resolution 0.01 mg). The resulting data was fitted in equations 2 and 3 to obtain the apparent density (ρ_app) and porosity (ε) of the membranes.

$${\rho }_{\text{app}}=\frac{\text{m}}{\text{d}\times \text{A}}$$ (Eq. 2)

$$\epsilon =1-\frac{{\rho }_{\mathit{app}}}{{\rho }_b}$$ (Eq. 3)

where m = the mass of the membrane (g), d = the thickness of the membrane (cm), A= the area of nanofibrous mat (cm²), ρ_b = the bulk density of materials (g/cm³). The bulk density for Selectophore™ PU as reported by the manufacturer was 1.04 g/cm³ [15].

2.7 Contact angle measurements

The contact angles for a drop of distilled water on electrospun membranes were measured using a contact angle instrument (OCA15+, Data-physics, Germany) at room temperature. A single drop of 1μL DI water was dropped on the surface of a flat 10 × 10 mm membrane using a syringe perpendicular and image captured in <1s after the water droplet became stable on the surface. This process was repeated four times on each membrane. The contact angles were then measured using the instrument’s SCA20 software.

2.8 Diffusion test

The effects of fibre diameter, thickness and porosity of electrospun PU membranes on their permeability to glucose were tested using a biodialyser (singled-sided biodialyser system with magnet, 1 ml, Sigma-Aldrich) in a beaker as a two-component diffusion chamber. The biodialyser has an integrated magnet, 1 ml sample well and a threaded cap ring to mount a membrane on top of the sample well exposing a 113.14 mm² membrane area for diffusion. Membranes for diffusion test were prepared using a ring-shaped aluminium template having an inner circle of 12 mm diameter cut out and an outer diameter of 22 cm. Following electrospinning, the membranes on the template ring were harvested and soaked in PBS (pH 7.4) at 37 °C for seven days to ensure equilibrium swelling of the membranes. For diffusion test, the donor solution chamber (A) of the biodialyser was filled with 1 ml of glucose solution in PBS and the wet membrane was mounted and secured with the treaded cap ring. The assembly was immersed in 49 ml of receiving PBS without glucose (chamber B) and rotated slowly (~250rpm) at a fixed rate and temperature in order to minimise boundary layer effects (diffusion resistance at the interface between the liquid and membrane) [16, 17]. Pre-calibrated amperometric glucose sensors made in-house were immersed in the receiving PBS to continuously log the changes in glucose concentration (as described in section 2.9). The donor chamber solution concentration was chosen such that the eventual equilibrium glucose concentration of receiver solution reaches 30 mM. The experiment was run overnight to ensure equilibrium was reached. The sensor response current was converted to concentration vs time (flux) curve. The effective diffusion coefficient was determined from the time dependent glucose concentration assuming that a quasi-steady-state concentration condition within the membrane. Based on the assumptions, combining the diffusion equation with Fick’s law and mass balance conditions between the two chambers A and B given equation (4): [18, 19].

$$\begin{array}{l}\frac{C_B-C_A}{C_{B0}-C_{A0}}=e^{-\frac{t}{\tau }}\text{with}\\ =\frac{d}{D_{\mathit{eff}}S}\frac{V_A{V}_B}{(V_A+V_B)},\end{array}$$ (Eq. 4)

where C_A, C_B and V_A and V_B are the concentration and the volume of chambers A and B, l is the membrane thickness, S is the membrane area, and D_eff is the effective diffusion constant in the membrane. The mean relaxation time τ for each membranes with different thickness was calculated by linear regression of ln(C_B-C_A)/C_B0-C_A0) vs t from experimentally measured values of tracer concentration of chamber B at different times, and then D_eff could be calculated from the mean relaxation time τ.

2.9 Glucose biosensor

A miniature coil-type implantable glucose biosensor, routinely used in our laboratory, [12, 20] was used to continuously monitor the diffusion of glucose across the electrospun PU membranes (section 2.8). The amperometric sensor is a two electrode system based on Pt-Ir working and silver/silver chloride (Ag/AgCl) reference electrodes. The working electrode consisted of a Pt-Ir coil reinforced with cotton, which was coated with an inner glucose oxidase enzyme layer and an outer epoxy-polyurethane mass-transport limiting membrane. The sensor response currents were logged using Apollo 4000 Amperometric Analyzer (World Precision Instruments Inc., Sarasota, FL) at 0.7 V versus Ag/AgCl reference electrode and correlated with changes in glucose concentrations as reported earlier [12, 20].

2.10 Statistical analysis

Statistical analyses were done using statistical software (SPSS v.15). One-way analysis of variance (ANOVA), using Tukey’s test for post hoc evaluation was used to identify statistical differences of P<0.05.

3 RESULTS AND DISCUSSION

3.1 Optimization of electrospinning parameters

Each of the parameters: solvents, flow rate, applied potential, distance from spinneret to collector and solution concentration was individually varied while keeping all the other parameters constant to study each of their influence on fibre structure and diameter.

3.1.1 Solvents

For assessing the solvent effects on electrospun PU fibre structure, 20 kV applied voltage, 1 ml/h flow rate, 22 cm distance to collector and 10 wt% solution concentration were used, while varying the solvent composition, having THF and DMF at ratios of 100:0, 70:30, 50:50, 30:70 and 0:100 (w/w). The morphology and fibre diameter distribution histograms for the electrospun membranes as a function of solvent composition are presented in Fig 1. When PU was electrospun with its solution in 100% THF, hollow elongated spheroid shaped beads of 2 to 10 μm diameter formed (Fig 1A) and the spinneret needle tip often got blocked during the electrospinning process. This was mainly due to the rapid evaporation of THF, which has a low boiling point, viscosity and surface tension (Table 1). Although much less prominent, the hollow spheroid shaped beads still formed when a 70:30 ratio THF:DMF solvent mixture was used (Fig 1B). With increasing DMF in the mixed solvent to 50:50 (1:1) and 30:70 THF to DMF solvent ratios, the bead formation was eliminated (Fig 1C & D). However when PU was electrospun in 100% DMF spindle shaped beads formed (Fig 1E). Overall, the fibre diameter measurements (Fig 1F to J, Table 2) in conjunction with morphology (Fig 1A to E) revealed an increase in fibre diameter with a corresponding narrower fibre diameter distribution until 50:50 THF:DMF and vice versa, clearly indicate the effect of the polarity and evaporation rate of solvents on the electrospinning of PU. It is clear that synergetic effects of the high dielectric constant, dipole moment, boiling point and surface tension of DMF (Table 1) are attributed to increase the surface tension, decrease the volatility of the mixed solvent, increase conductivity of the blend-solvent solutions, and thus improve the mass throughput of the solutions from the spinneret, preventing bead formation and clogging of spinneret, in agreement with other reports in the literature [21]. Beyond the optimal conductivity the higher charge density in the electrospinning jet causes bending instability and increases jet path and stretching, resulting in a reduction in fibre diameter. However, when PU was electrospun in pure DMF, although not phase-separated and hollow, spindle shaped beads formed (Fig 1E). Such morphology was also reported in other studies [22–24], attributed to the higher surface tension but relatively lower viscosity of PU solution in 100% DMF. As a result, for optimization of rest of the parameters THF:DMF solvent ratio was fixed at 1:1.

Figure 1.

Morphology and fibre diameter distribution histograms for the electrospun membranes as a function of solvent composition - ratios of THF: DMF at 100:0 (A, F), 70: 30 (B, G), 50:50 (C, H), 30:70 (D, I), 0:100 (E, J). PU solution concentration of 10 % (w/w), 20kV applied voltage, flow rate of 1 ml/h and 22 cm distance to collector, were kept constant.

Table 1.

Solvents used in this study and their properties [49].

Solvent	Boiling Point (°C)	Surface Tension (mN/m)	Dielectric Constant	Dipole Moment	Viscosity ( Pa.s)
THF	66	26.4	7.5	1.63	5.5 × 10−4
DMF	153	37.1	38.3	3.82	9.2 × 10−4

Table 2.

Systematic evaluation of effects of the electrospinning parameters namely, solvents, flow rate, applied voltage, distance to collector and solution concentration on the fibre diameter of Selectophore™ PU (M_w ~100,000).

Solvents(%) wt/wt		Flow Rate (ml/h)	Applied Voltage (kV)	Distance from Spinneret to Collector (cm)	Solution Concentration (%, wt/wt)	Fibre Diameter
THF	DMF
100	0	1	20	22	10	486±231*
70	30	1	20	22	10	735±362*
50	50	1	20	22	10	738±131
30	70	1	20	22	10	538±208
0	100	1	20	22	10	517±340*
50	50	0.1	20	22	10	445±109
50	50	0.2	20	22	10	624±117
50	50	0.6	20	22	10	670±122
50	50	1.0	20	22	10	738±131
50	50	1.2	20	22	10	695±129
50	50	1.0	15	22	10	1120±247
50	50	1.0	20	22	10	738±131
50	50	1.0	25	22	10	551±111
50	50	1.0	20	12	10	1011±161
50	50	1.0	20	17	10	845±115
50	50	1.0	20	22	10	712±90
50	50	1.0	20	27	10	737±111
50	50	1.0	20	32	10	885±128
50	50	1.0	20	22	8	423±92*
50	50	1.0	20	22	10	738±131
50	50	1.0	20	22	12	936±197

^*indicates bead formation.

3.1.2 Solution Flow Rate

Flow rate was varied from 0.1 to 2 ml/h, while maintaining solution concentration at 10%, voltage at 20 kV and distance to collector at 22 cm. For flow rates from 0.1 to 1.2 ml/h, no bead formation was observed. The size of the Taylor cone increased with increasing flow rate. But, when the flow rate reached 2 ml/h, the size of droplet was too big to suspend at the tip of the needle resulting in the free fall of droplets on the collector. As listed in Table 2, the average fibre diameter increased up to a flow rate of 1 ml/h and thereafter it appeared to decrease. However, for flow rates <1 ml/h, at the set applied voltage of 20 kV, the electrospinning jet emerging from the Taylor cone was not stable and continuous across the electrospinning duration, indicating 1 ml/h as the optimum flow rate for the fixed parameters. The increase in fibre diameters with increasing flow rate up to 1 ml/h can be attributed to the increasing volume of polymer solution in the Taylor cone. However, the increase peaked and started to decrease with further increase in flow rate. The decrease is apparent from the fact that for the increasing volume of polymer solution in the Taylor cone in conjunction with increasing the flow rate, a corresponding increase in surface charge (induced by increasing the applied voltage) is essential to stretch the Taylor cone, stabilize the jet and reduce the fibre diameter [25].

3.1.3 Applied Voltage between Spinneret and Flat-Plate Collector

In contrast to the flow rate, an increase in applied voltage resulted in a significant decrease in average fibre diameters (Table 2). The membranes were electrospun with 10% PU solution, 1 ml/h flow rate and 22 cm distance to collector. At voltages below 11 kV, no jet emerged from Taylor Cone and the PU solution dripped. Further, with increasing applied voltage the Taylor Cone receded closer to spinneret tip. Also at 25kV, occasionally, secondary jets formed during electrospinning. The different jets repelled each other causing thinner fibres depositing on a larger area on the collector. It is worthwhile to note that higher voltages resulted in a more uniform and narrow fibre diameter distributions (Table 2). The effect of applied voltage on the diameter and structure of fibres has been a debatable issue. This study as well as other reports in the literature suggested a decrease in fibre diameter with an increase in applied voltage [26, 27]. This could be due to the higher surface charge and the lower volume of polymer solution available in the receding Taylor cone with increasing applied voltage. In contrast, some studies report increasing applied voltage to cause no change or even an increase in fibre diameter [28–32]. The divergent observations on the effects of applied voltage on fibre characteristics are thought to be influenced by the polymer properties and choice of solvents, further supporting the need for polymer specific process optimization for electrospinning.

3.1.4 Distance between the spinneret tip and collector

Distance between the spinneret tip and collector influences the flight time for the electrospinning jet and the electric field strength. To obtain independent fibres, the electrospinning jet must be allowed enough time for most of the solvent to evaporate. Short distances between the spinneret and collector cause stronger electric fields, which in turn accelerate the jet. As a result, there may not be sufficient time for solvent to evaporate before the fibre hits the collector [33]. Provided there is sufficient electrostatic field strength, increasing the distance between the spinneret and needle causes stretching of fibres, reducing the fibre diameter. However, beyond an optimum distance, the strength of the electrostatic field decreases, thus lowering the stretching effect and increase in fibre diameter [31]. As summarised in Table 2, increasing the distance from 17 up to 22 cm leads to a decrease in the average fibre diameter and thereafter the reverse trend was observed. Thus for the set parameters of 10% solution, 21 kV applied voltage and 1ml/h flow rate, an optimum distance of 22 cm between spinneret and collector was identified. At this condition, an evenly distributed nano-web with the lowest average fibre diameter was achieved.

3.1.5 Solution Concentration

For a given molecular weight of a polymer and solvent chosen, its solution concentration is the primary factor affecting its viscosity and therefore its electrospinnability. For electrospinning PU, 3 concentrations, namely 8%, 10% and 12% were tested, while having 1:1 for THF:DMF solvent ratio, 20 kV applied voltage, 1 ml/h flow rate and 22 cm distance to collector constant (Table 2). The morphology and fibre diameter distribution histograms are presented in Fig 1C&H and Fig 2. Bead formation was observed for an 8% PU solution in 1:1 THF:DMF (Fig 2A), indicating a less viscous solution. At 10 and 12 % PU solution concentrations, the viscosity was sufficient to prevent bead formation (Fig 1C & 2C). A trend of an increase in the average fibre diameter having wider distribution with increasing concentration was observed as illustrated in Fig 2. It has been proven that higher viscosity allows ionic charge distribution among the polymer chains and solvent molecules such that the polymer solution is stretched to form uniform fibres [34]. The increasing viscosity with increasing concentration is said to prevent the charged jet from splaying and splitting, thus reducing the jet’s path and bending instability [35] resulting in increasing fibre diameter. The lower splaying, in turn, also causes the fibres to be deposited in a smaller area on the collector. Srivastava et al. explain the increasing fibre diameter with increasing polymer solution concentration to be induced by the faster evaporation of low solvent content and the greater viscoelastic forces acting against the columbic forces of the charges results in the less stretching of fibres and thus the formation of thicker fibres [24]. The results achieved in this work further reiterate that the polymer solution concentration and the choice of solvents play a critical role on the resultant structure and diameter of the resultant electrospun fibres.

Figure 2.

SEM images of the PU electrospun fibrous webs and their fibre diameter distribution with different concentration at 8wt% (A,D), 10wt% (B,E), 12wt% (C,F) , constant THF:DMF solvent ratio of 50:50, voltage of 20kV, DTC of 22cm, and flow rate of 1.0ml/h

3.1.6 Optimized parameters

To generate finer fibres, 8wt% PU solutions in three different solvent mixture of THF to DMF ratios of 3:1, 1:1 and 2:3 (w/w) were tested. For the 8% PU solution in 3:1 THF:DMF solvent mixture, the external electrostatic strength was varied by applied voltages between 9 and 27 kV. The flow rate was also varied to suit the applied voltage such that the electrospinning jet forms, while maintaining the distance to collector constant at 22 cm. Irrespective of the changes in the applied voltage and flow rates, 8% PU solution in 3:1 THF:DMF solvent mixture always resulted in bead formation, and no jet formed below 10kV. Similarly, for 8% PU in 1:1 THF:DMF solvent mixture, irrespective of the applied voltage and flow rate, beads formed and their density increased with increasing applied voltage, with the exception of 27kV, where beads began to join to form thick fibres. Finally, an 8% PU solution in 2:3 (40:60) THF to DMF produced beadless and uniform fibres.

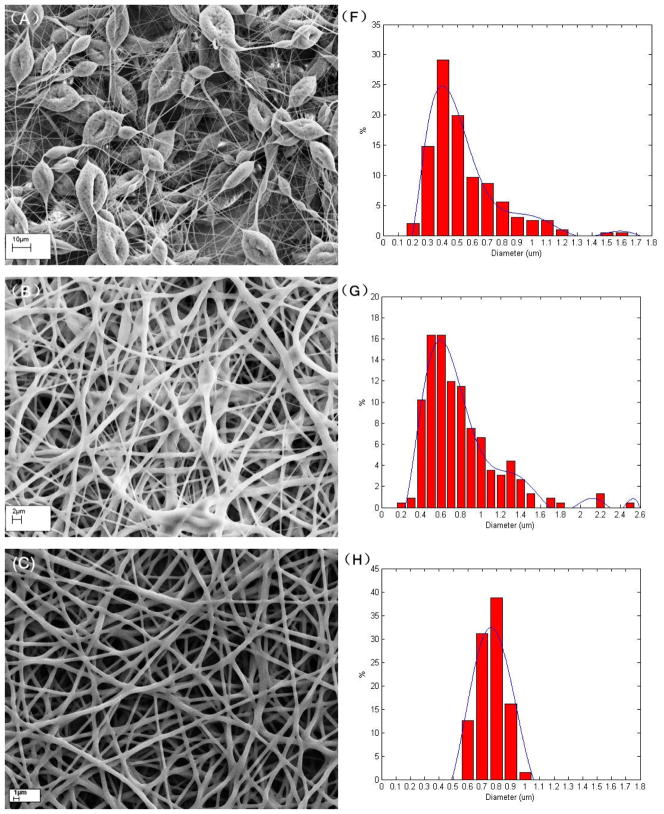
Based on the extensive electrospinning process optimization experiments presented above, it is evident that electrospinning can be used to generate membranes with desired fibre diameters. The typical influence of the different solution and processing parameters on the structure of the electrospun fibres and their membranes was further reiterated by our study results and more importantly, the solvent compositions, solution concentrations, flow rates, applied voltages, and distances to collector were identified for preparing electrospun PU membranes having desired fibre diameters. Towards the goals of achieving membranes with different fibre diameters and interconnected porous structures, three membrane configurations (Table 3 and Fig 3) having average fibre diameters of 347.4nm, 738.4nm and 1102.3nm, designated as 8PU, 10PU and 12PU membranes respectively, were shortlisted to study the effect of the different diameters on morphology, porosity, mechanical, surface hydrophilicity and solute diffusion properties.

Table 3.

Electrospinning parameters for the three shortlisted membrane configurations

Designation	PU Solution Concentration (wt %)	Solvent THF:DMF (%) (wt:wt)	Voltage (kV)	Feed Rate (ml/h)	Distance to Collector (cm)	Fibre
8PU	8	40:60	21	0.6	22	347±87
10PU	10	50:50	20	1.0	22	738±131
12PU	12	50:50	20	1.2	22	1102±210

Figure 3.

Morphology of the membranes A) 8PU, B) 10PU, and C) 12PU and D) their respective fibre diameters. The average fibre diameter for each membrane configuration is statistically different from the other two membranes.

3.2 Characterization of electrospun PU membranes

3.2.1 Chemical structure and residual solvent evaluation using FTIR Spectroscopy

Qualitative investigation of changes to chemical structure of PU and any residual solvents in the electrospun membranes was done using ATR-FTIR spectroscopy. Solvents, a solvent cast PU film and as-supplied PU were tested as controls. The FTIR spectra (Fig 4) of electrospun PU membranes had the characteristic absorption peaks at 3324, 2855, 1715, 1530, 1232, 1111 and 779 cm⁻¹ which are assigned to ν (N-H), ν (C-H), ν (C=O), ν (C=C), ν (C-C), ν (C-O) and ν (C-H) respectively on substituted hexane ring respectively [36, 37]. The spectra of solvent cast PU, as-supplied PU Pellet and electrospun PU membranes all had similar absorption peaks with the exception of the absorption peak at about 1111 cm⁻¹ concerning the C-O-C stretching vibration, which shifted slightly to a higher wave number after electrospinning, suggestive of formation of local packing or orientation of related soft chain segments in the confinement of micro-/nano-fibrous structure during electrospinning. Otherwise, the high applied voltages during electrospinning did not affect chemical structure of PU. Furthermore, the strong absorption peaks characteristic for DMF, C N at 1657 cm⁻¹, and THF, C-F at 1065 cm⁻¹, were not observed in the spectra for solvent cast films or electrospun PU membranes, indicating no residual solvents following the drying cycles in vacuum desiccator.

Figure 4.

ATR-FTIR spectra for DMF, THF, as-supplied PU pellets, solvent cast PU film and electrospun PU membrane.

3.2.2 Thickness versus electrospinning time

Thickness is an essential parameter that influences the permeability and transport properties of a membrane. For the chosen three membrane configurations, namely 8PU, 10PU and 12PU, membrane thicknesses increased linearly with increasing electrospinning time for 12PU (R² of 0.9931) and 10PU (R² of 0.9893) respectively, while that for 8PU was not as linear (R² of 0.9166) (Fig 5). The increase in membrane thickness as a function of increasing PU solution concentration was as expected. However, the relatively smaller slope for increase in membrane thickness for 8PU as a function of increasing electrospinning time (Fig 5) can be attributed to fusion fibres with neighbouring stacking layers (Fig 3A) potentially due to incomplete evaporation of solvents during electrospinning.

Figure 5.

Thickness of the electrospun membranes: A) 8PU, B) 10PU, and C) 12PU as a function of electrospinning time.

3.2.3 Pore Size and Porosity

The membranes 8PU, 10PU and 12PU were prepared using a 2h electrospinning time to obtain membranes thick enough to meet the safety requirement for the bubble point measuring apparatus. Figure 6 shows the pore size distribution of the three electrospun membrane configurations measured using bubble point measurements. 8PU, 10PU and 12PU having fibre diameters of about 347, 738 and 1102 nm respectively were determined to have radii for majority of their pores and corresponding distribution (%) at about 800 nm (68%), 870 nm (36%) and 1060 nm (29%) respectively from Fig.6. The results revealed an increase of the average pore size with increasing fibre diameter. The pore size distribution was very narrow for 8PU compared to wide distributions for 10PU and 12PU membranes. The reducing percentage of the majority of pores having uniform size is indicative of wider pore size distributions with increasing fibre diameters.

Figure 6.

Pore size distributions for the electrospun membranes 8PU, 10PU and 12PU, as determined by bubble extrusion porosimetry.

The results for fibre packing density and pore volume determined by gravimetry shown in Table 4 also reiterate the increasing porosity as a function of fibre diameter. Gravimetry method revealed a decreasing fibre packing density and an increasing pore volume with increasing fibre diameter. The fibre packing density (*) is significantly higher and pore volume (^#) significantly lower for 8PU when compared to 10PU and 12PU membranes. The pore volumes were about 44%, 63% and 68% respectively for 8PU, 10PU and 12PU, which is much higher than conventional porous membranes that usually have up to 34% pore volumes having lesser pore interconnectivity [13]. In addition, if the pores size distribution is narrow and porosity in sub-micron dimension, they could function as size or molecular weight cut-off membranes. Having significantly smaller fibre diameters (~347 nm), pore size (~800 nm) and pore size distribution (68% between 700 and 900 μm), and about 44% pore volume (Fig 6 and Table 4), 8PU is anticipated to allow high flux/flow of solvents or solutes across, while acting as a mass-transport limiting membrane.

Table 4.

Fibre packing density and pore volume estimations for electrospun PU membranes based on gravimetry, calculated using equations 2.2 and 2.3. The electrospinning time for the membranes was 2h, and n=3 per test membrane.

Sample Designation	Thickness (μm)	Fibre Diameter (μm)	Fibre Packing Density (g/cm³)	Pore Volume (%)
8PU	28.4±5.4	0.347±0.087	0.580±0.028*	44.19±2.54#
10PU	86.0±12.9	0.738±0.131	0.408±0.013	62.87±1.18
12PU	180.6±42.2	1.102±0.210	0.381±0.020	65.40±1.85

The fibre packing density (*) is significantly higher and pore volume (^#) significantly lower for 8PU when compared to 10PU and 12PU membranes.

3.2.4 Surface Contact Angle Measurement

The hydrophobic and hydrophilic natures of membranes have an important role in biosensor applications through their effects on the diffusion of analytes, protein adsorption and foreign body reactions. The surface wetting analysis using contact angle measurements demonstrated an increase in hydrophobicity as a function of increasing fibre diameters and porosity for electrospun PU membranes. Fig 7 illustrates the typical morphology of a 1μl droplet of DI water on the different PU membranes and their corresponding contact angles. The solvent cast non-porous PU film showed the smallest contact angle of about 86°, while the electrospun PU membranes, 8PU, 10PU and 12PU had 104.3°, 116.1° and 122.5° respectively. The static contact angle measured is determined by the surface chemistry and the surface roughness of the membrane. Cassie-Baxter model (Cassie’s law) for two component composite smooth surface [38–40] describes the contact angle θ on a solid surface changes to θ* if the liquid is suspended on the tops of microstructures of porous surface:

$$\mathit{cos}{\theta }^{\ast }=(\mathit{cos}+1)-1$$ (Eq. 5)

Figure 7.

Contact angle measurements: (A) the morphology of water droplet (1μL) on solvent cast PU film and the three electrospun PU membrane variables; and (B) contact angles as a function of fibre diameter. Contact angles (θ) less than 90° are indicative of hydrophilic surface and greater than 90° indicative of a relatively hydrophobic surface. A zero contact angle represents rapid and complete wetting.

Where: ϕ is the area fraction of the solid that touches the liquid. Based on Cassie-Baxter model, the areas fraction of the actual contact surface for the membrane, 8PU, 10PU and 12PU, was estimated to be 30.9%, 1.5% and 0.04% respectively from the measurement results of apparent contact angle above using Eq.5. Clearly the actual contact area reduced substantially with increasing fibre diameter, having only 0.04% area touching the liquid in 12PU. Increased pore size and porosity of the 12PU membrane with larger fibre diameter are envisaged to almost full of air pocket phase (the contact angle of water in air =180°) at the surface of the membrane, enhancing the hydrophobic nature of PU. Similar observations were also reported earlier [39, 41]. The bigger pores on the electrospun membrane surface are said to entrap more air causing the surface to be more hydrophobic [42–44]. Liu et al. also suggest that the smaller the pore in the material, the higher their capillary effect contributing to faster water absorption, thus decreasing the contact angle with decreasing pore sizes [45]. This reiterates that the actual contact surface area is the controllable parameter for changing the surface wetting nature. The results indicate that the hydrophilicity-hydrophobicity balance for a particular polymer can be adjusted to some extent using straightforward electrospinning technology towards generating biocompatible surfaces.

3.2.5 Glucose Diffusion Test

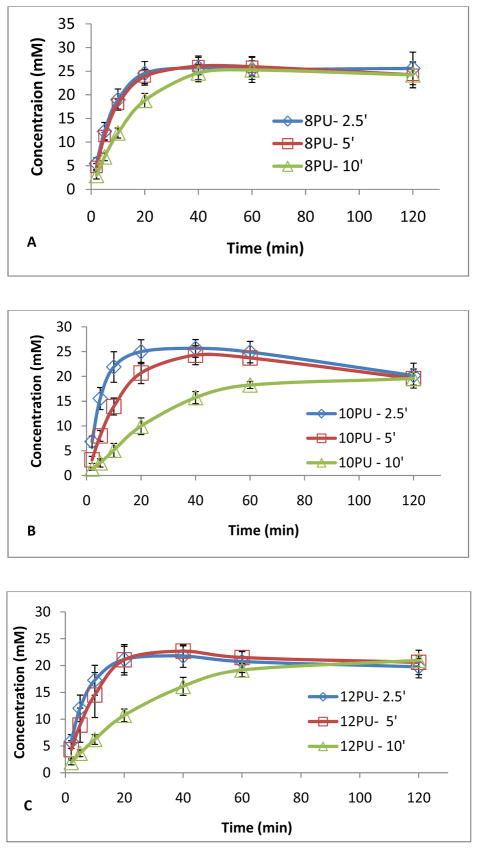
Considering the intended application as coatings for glucose biosensors (model sensors), it was important that the designed coatings cause minimal decrease in sensitivity, which we hypothesized can be achieved by increasing the flux of trans-membrane transport of glucose. Hence, we first screened the different electrospun membrane configurations, optimized in this study, for their permeability to glucose using rotating biodialysers as a function of membrane thickness and porosity. Three different electrospinning times namely 2.5, 5 and 10 min were used to obtain 8PU, 10PU and 12PU membranes having fine differences in thickness (Table 4). The original glucose diffusion profiles had 10 data points recorded per second. To minimize the enormity of the data for statistical analysis, we extracted readings for the time points 2, 5, 10, 20, and 40 min for each of the membranes. The resulting glucose diffusion profiles for the different membranes as a function of time are shown in Fig 8A–C.

Figure 8.

Glucose diffusion across A) 8PU, B) 10PU and C) 12PU membranes, and D) the trends of the average relaxation time and effective diffusion coefficient calculated from the diffusion measurement as a function of time, and thickness (electrospinning times of 2.5, 5 and 10 min). Data is represented as Mean ± SE (standard error) of mean, n=5.

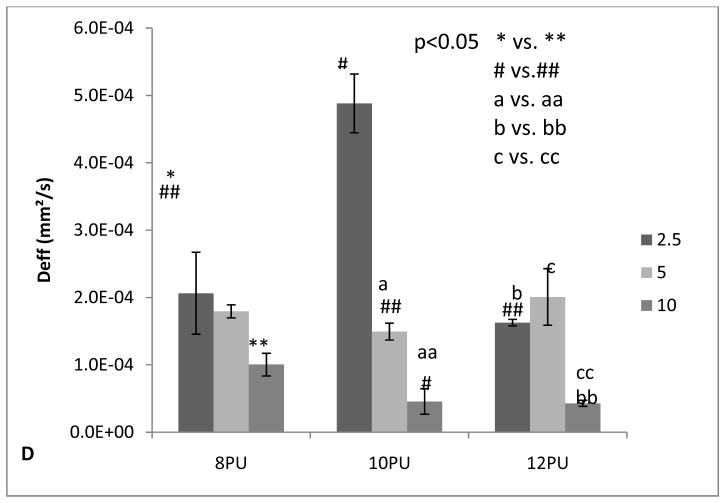
Based on the two-chamber diffusion model described in Section 2.8, the mean relaxation times, τ, for each type of membranes were determined by best fitting using Eq. 4, and their corresponding effective diffusion coefficients were calculated by inputting thickness and area of the membranes. The results are listed in Table 5, which are mean values from 5 membranes tested for each type of the membranes. The values of the effective diffusion coefficient for the fibrous membranes fall within a wide range from ( 0.429 ± 0.45)×10⁻⁵ to 4.88 ± 0.44)×10⁻⁴ mm²/s as a function of membrane thickness and membrane structure. The highest D_eff, (4.88 ± 0.44)×10⁻⁴ mm²/s observed for 10PU2.5’ is close to the glucose diffusion coefficient in water (D=6.73×10⁻⁴ mm²/s) [46] indicating a high flux rate mass transport through the membranes. Such behaviour can be attributed to the highly interconnected porous network structure having about 44 to 69 % pore volume of the fibro-porous electrospun membranes (Table 4), which is significantly different to conventional porous membranes that have pore volume up to 34%, without compromising on mechanical properties [13]. Moreover, the effective diffusion coefficient of the membrane can be tailored by producing finer nano-fibous nanoporous structure similar to various types of nano-membranes reported such as the nanoporous polyethylene membrane (0.18×10⁻⁴ mm²/s) and a 20 nm asymmetric alumina membrane from Whatman (1.39×10⁻⁴ mm²/s) [47].

Table 5.

The thickness of electrospun membranes used for diffusion tests and their corresponding average relaxation time and effective diffusion coefficient as a function of electrospinning time.

Sample-Electrospinning time (min)	Mean of thickness (μm)	Average relaxation time, τ (min)	Effective diffusion coefficient, Deff (mm²/s)
Water$	-	-	(6.73)E-04
8PU-2.5	15.3	12.31±2.84	(2.06±0.61)E-04
8PU-5	15.6	14.16±0.78	(1.79±0.10)E-04
8PU-10	16.0	26.38±4.38	(1.00±0.17)E-04
10PU-2.5	17.5	5.88±0.55	(4.88+0.44)E-04
10PU-5	19.0	20.79±1.71	(1.49±0.13)E-04
10PU-10	21.9	86.19±28.97	(4.56±1.90)E-05
12PU-2.5	18.9	19±0.56	(1.63±0.05)E-04
12PU-5	21.5	17.95±4.02	(2.01±0.41)E-04
12PU-10	26.4	100.92±10.52	(4.29±0.45)E-05

n=5.

^$[46].

As a function of membrane thickness (electrospinning time), a increasing trend of the average relaxation time (τ) and reduction of effective diffusion coefficients (D_eff) confirms a decrease in the rate of diffusion of glucose across each of the three membrane configurations 8PU, 10PU and 12PU with increasing electrospinning time from 2.5, 5 to 10 min (Fig 8A–D and Table 5). Particularly in the cases of 10PU and 12PU, the increase of τ and reduction of D_eff tends to be more drastic compared with 8PU, which is consistent with the steeper increase in thickness of the membrane causing increased diffusion distance throughout the thicker membrane produced (Fig 5). Membrane configurations in terms of fibre diameter, porosity, pore size and pore size distribution also influence the diffusion kinetics of the membranes. The trend of effective diffusion coefficient in correlation to the membrane configuration is not that straightforward (Fig 8D). Maxwell model predicts an increase of effective diffusion coefficient with increasing porosity of the membrane based on a simplified periodically spaced porous structure [48]. Given the relatively close thickness of three membranes electrospun for 2.5 min (Table 5), D_eff = (4.88 ± 0.44)×10⁻⁴ mm²/s for 10PU2.5 with higher porosity and pore size more than doubles compared with D_eff = (2.06 ± 0.61)×10⁻⁴ mm²/s for 8PU2.5, but D_eff = (1.63 ± 0.06)×10⁻⁴ mm²/s for 12PU2.5 with the largest porosity and pore size is unexpectedly lower. Such variations in magnitudes at each time point between the groups, 8PU, 10PU and 12PU, can be attributed to subtle variations in their thicknesses and fibro-porous structure resulting from the differences in electrospinning parameters and ambient conditions during electrospinning on static flat plate collector.

In summary, diffusion tests confirmed the controllable high flux rates associated with electrospun membranes with extensive pore interconnectivity. The effective diffusion coefficient can be tailored in a wide range of values by changing the membrane structures though controlling electrospinning conditions demonstrated in the case of 8PU and 10 PU with finer fibre diameter and uniform porous structure. The membrane with controlled structure and diffusion performance can be consistently produced by applying simple, controllable and efficient electrospinning technique, compared with other processes for fabrication of nanoporous membranes.

4. CONCLUSION

In this work, parameters for electrospinning micro- and sub-micro-scaled elastic Selectrophore™ PU fibres were extensively and systematically investigated and sets of parameters for spinning PU membranes having desired fibre diameters were identified. Three membrane configurations designated as 8PU, 10PU and 12PU having average fibre diameters 347, 738 and 1102 nm respectively were chosen and tested for membrane properties. Electrospinning process did not affect the chemical structure of PU except for a slight shift in the peak for the –C–O–C– in the PU backbone indicating a change in conformation of the PU in the electrospun membrane. Pore sizes and volume increased with increasing fibre diameters. Thickness of the 12PU and 10PU membranes spun on a flat-plate collector increased linearly with increasing electrospinning time. But that of 8PU was not as linear, potentially due to the fusing of neighbouring fibres resulting for slower drying of the relatively higher DMF content in the feed PU solution. Increasing fibre diameters and their corresponding larger pore sizes resulted in increased surface hydrophobicity of electrospun PU membranes. The large pore volumes in the electrospun PU membranes resulted in higher glucose flux rates, which can be further tuned by varying the fibre diameters and membrane thicknesses. The thinner the membranes, the closer were their trans-membrane glucose diffusion coefficients to that of glucose in water without any membranes. The fibre-size-dependent properties of electrospun PU membranes, especially their high and tuneable flux rates for trans-membrane glucose diffusion is anticipated to find them applications as coatings for sensors and other biomedical devices requiring analyte exchange. Further studies elucidating the methods for coating miniature glucose biosensors with electrospun PU membrane configurations reported in this paper, the coatings’ efficacy as mass-transport limiting and biocompatible membranes, and their pre-clinical biocompatibility and functional efficacy will feature in future papers.

Highlights.

• Precise control of fibre diameter and porous structure of electrospun biomedical PU membrane

• The size-effect of hierarchical porous structure on permeability and surface properties of electrospun PU membranes

• PU membranes with tailored glucose diffusion coefficient provide a mass transport limiting function for biosensors