Pooled testing procedures for screening high volume clinical specimens in heterogeneous populations

Abstract

Pooled testing is a procedure commonly used to reduce the cost of screening a large number of individuals for infectious diseases. In its simplest form, pooled testing works by compositing a set of individual specimens (e.g., blood or urine) into a common pool. If the pool tests negative, all individuals within it are diagnosed as negative. If the pool tests positive, retesting is needed to decode the positive individuals from the negative individuals. Traditionally, pooled testing has assumed that each individual has the same probability of being positive. However, this assumption is often unrealistic, especially when known risk factors can be used to measure distinct probabilities of positivity for each individual. In this paper, we investigate new pooled testing algorithms that exploit the heterogeneity among individual probabilities and subsequently reduce the total number of tests needed, while maintaining accuracy levels similar to standard algorithms that do not account for heterogeneity. We apply these algorithms to data from the Infertility Prevention Project, a nationally implemented program supported by the Centers for Disease Control and Prevention.

1. Introduction

Pooled testing, also known as group testing, is a procedure where individual specimens (e.g., urine or blood) are combined into a pooled specimen to test for a binary response (e.g., positive or negative HIV status). In the most widely used form of pooled testing known as “Dorfman testing” [1], pools that test negative have all individuals within them declared negative. Pools that test positive indicate that at least one individual within each pool is positive, and individual retesting of each specimen is subsequently used to decode the positives from the negatives. The strong appeal of pooled testing is that it can significantly reduce the number of tests and associated costs when the prevalence for a disease is small. This has led to the application of pooled testing in a wide variety of infectious disease screening settings, such as blood donation screening by the American Red Cross [2, 3], chlamydia and gonorrhea opportunistic testing in medical clinics [4], influenza surveillance through blood donations [5], and West Nile virus surveillance in mosquitoes [6].

Pooled testing is gaining acceptance for chlamydia and gonorrhea screening as part of the Infertility Prevention Project (IPP). The nationally implemented IPP is supported by the Centers for Disease Control and Prevention, and its purpose is to assess and reduce the presence of these infections in the United States. A few of the participating state public health laboratories, such as the State Hygienic Laboratory at the University of Iowa, use Dorfman testing to screen tens of thousands of specimens per year. However, given the pervasive edict of “make do with less” under which most public health laboratories now must operate, it is important to determine if other pooled testing procedures could result in larger reductions in the number of tests expended. This is especially of interest given that newly developed pooled testing procedures [7, 8, 9, 10 ] can now take advantage of risk factors (e.g., gender, behavior, and clinician observations) for individuals to more efficiently find positive individuals within heterogeneous screening populations. The purpose of our paper is to present the first general comparison of standard pooled testing procedures to those that account for heterogeneity in the screening population. This is done by using a database of previously diagnosed individuals tested at the Nebraska Public Health Laboratory (NPHL) and by implementing a computer simulation designed to emulate the pooled testing process. Because individual testing currently is used by the NPHL, their data provide a unique opportunity to make comparisons among a number of pooled testing procedures and to compare with individual testing.

An outline of our paper is as follows. Sections 2 and 3 review the standard and the newly developed procedures, respectively. We will use the term “informative” to denote these newly developed pooled testing procedures because they account for the extra information available within a heterogeneous population. In a similar manner, we will use the term “non-informative” to denote the standard pooled testing procedures which do not account for heterogeneity. Section 4 compares these procedures using the IPP data application and simulation. Section 5 summarizes and discusses the broad impacts of this research (e.g., applications to settings other than the IPP).

2. Non-informative procedures

While Dorfman testing is the easiest to apply, it usually leads to the largest number of tests needed among all pooled testing procedures. We next describe three non-informative procedures that generally result in a smaller number of tests. Section 4 investigates when these procedures are better than Dorfman testing and which are better among each other.

Rather than testing all members of a positive pool individually, a positive pool can be split into two or more sub-pools. If any sub-pool tests positive, further splitting or individual testing can be performed on it. A specific form of pool splitting is halving, which was popularized by Litvak et al. [11]. For this procedure, each split creates two new equally sized sub-pools (or as close to equal as possible). Because a large number of halving steps can be time consuming, most applications involve only 3 (3H) or 4 (4H) steps. For example, 3-step halving splits a positive initial pool of size 8 into two sub-pools of size 4. Individual testing is performed on any sub-pool that tests positive. A further application of 4-step halving splits a positive sub-pool of size 4 into two more sub-pools of size 2 before individual testing.

Another alternative to immediate individual testing for a positive pool was given by Sterrett [12]. This procedure tries to exploit the fact that there is most likely a very small number of positives within properly sized pools (often, there is only one positive per pool). For an initial pool that tests positive, Sterrett’s procedure retests individuals at random one-by-one until the first positive individual is found. Once the first positive is found, individuals that have not been retested are re-pooled and tested again. Retesting ends if this new pool tests negative. One-by-one retesting continues if this new pool tests positive, and the same algorithmic process continues until all individuals are declared positive or negative.

Matrix (M) or array testing, originally proposed by Phatarfod and Sudbury [13], is a pooled testing procedure often used with high throughput screening. Unlike halving and Sterrett’s procedures, where individuals are assigned to one initial pool, individuals are assigned to two separate pools. This is done by constructing a matrix-like grid of specimens and pooling individuals within rows and within columns. Specimens lying at the intersections of positive rows and positive columns are tested individually to decode the positives from the negatives. Specimens lying outside of these intersections are declared negative, except in the case of a row testing positive without any positive columns and vice versa. These exceptions can occur due to testing error, and individual testing is performed on all individuals within these pools to determine diagnoses [14].

3. Informative procedures

Informative procedures rely on the basic idea that individuals have different risks of being positive. These risks can be measured in a number of ways. Commonly, a training data set of individual diagnoses and corresponding risk factors are used to estimate a binary regression model. This model can be applied to the current individuals being screened in order to estimate their risk probability of having a disease. These probabilities are then used in one or more of the following ways:

1. To select pool sizes,

2. To organize the initial testing in a way that minimizes the number of positive pools, and

3. To determine the order in which individuals are retested within a positive pool.

Because these procedures use additional information in the testing protocol, they are known as informative retesting procedures. We review the proposed implementations of informative retesting next.

Due to the wide application of Dorfman testing, McMahan et al. [8] proposes two procedures that take advantage of this large user base. First, threshold optimal Dorfman (TOD) uses a probability threshold to categorize individuals as “high” or “low” risk. For example, a threshold level of 0.2 categorizes individuals with estimated probabilities above this level as high risk and individuals below this level as low risk. In application, this threshold can be chosen beforehand or chosen automatically by an algorithmic process (see [8] for details). High risk individuals are tested individually, and low risk individuals are ordered by their risk probabilities and are screened using Dorfman testing with pools of equal size (or as close to equal size as possible). The pool size chosen for the low risk individuals is the size that minimizes the estimated expected number of tests. Second, pool-specific optimal Dorfman (PSOD) begins by ordering individuals by their estimated risk probabilities. Under the constraint that the ordered individuals are placed into successive pools, optimal pool sizes are found by minimizing the estimated expected number of tests through a greedy optimization algorithm. Again, individuals within positive pools are retested individually. In practice, both TOD and PSOD are applied to “blocks” of individuals. For example, if a laboratory has 100 specimens to test at the beginning of the day, TOD and PSOD will find the pooling configuration for these individuals only.

Halving can also take advantage of varying risk probabilities. Black et al. [9] proposed ordered halving where sub-pools are formed by maximizing one sub-pool’s probability of being positive and maximizing the other sub-pool’s probability of being negative. The purpose is to increase the chance that all positives will be pooled together throughout the retesting process; this enables other sub-pools to test negative at earlier steps. Sub-pool configurations are found by first ordering individuals by their estimated risk probabilities. Individuals below the median are assigned to one sub-pool and individuals above the median are assigned to the other sub-pool. Also, as with non-informative halving, only 3-step (3H.order) and 4-step (4H.order) implementations are recommended for practicality reasons.

An informative version of Sterrett’s procedure is given by Bilder et al. [7]. Instead of retesting individuals in positive pools at random, individuals are chosen by their estimated risk probabilities – the highest is chosen first, the second highest is chosen second, and so on – until the first positive individual is found. When the algorithmic process is repeated after each positive individual is found, this is called full informative Sterrett (FIS). Simpler approaches are also proposed by Bilder et al. [7] that limit the number of steps. After the first positive is found and the remaining individuals are re-pooled, one-stage informative Sterrett (1SIS) performs individual testing if the new pool tests positive. In a similar manner, two-stage informative Sterrett (2SIS) performs individual testing if the second new pool tests positive.

Informative retesting for matrix testing involves placing specimens into a matrix configuration that attempts to minimize the number of rows and columns that test positive. By doing so, this potentially reduces the number of retests needed. McMahan et al. [10] propose two square matrix layouts. First, the spiral layout (M.spiral) places the individual with the largest risk probability in the (1,1) cell of the matrix (upper left corner). Individuals with the second, third, and fourth largest probabilities are put into the (2,1), (2,2), and (1,2) cells, respectively, which creates a “spiraling” around the first cell. This spiraling continues until all cells of the matrix are filled. Second, the gradient (M.gradient) layout orders individuals by their estimated risk probabilities and places them into successive columns. For example, column 1 contains the ordered individuals with the largest risk probabilities, column 2 contains the ordered individuals with the next largest risk probabilities, and so on, until all columns are filled.

4. Infertility Prevention Project

As we mentioned in Section 1, the IPP is implemented in all 50 states. While there are small differences in how testing is performed across states (e.g., differences in assays used, availability of certain covariates, etc.), our investigation for Nebraska alone can have a large impact on how millions of individuals are screened each year throughout the IPP. Furthermore, because pooled testing is frequently implemented in other high volume clinical specimen settings, we discuss in Section 5 how the results in this paper may impact other applications.

Individuals tested in Nebraska submit either urine or swab specimens at health care clinics across the state, and these specimens are all tested at the NPHL in Omaha. Each individual provides information on their age, race, gender, symptoms, and risk history (multiple partners, new partner in the last 90 days, contact with someone who has a sexually transmitted disease). Clinical observations reported on each individual include cervical friability, pelvic inflammatory disease, cervicitis, and urethritis statuses. Each specimen is tested individually at the NPHL using the BD ProbeTec ET CT/GC Amplified DNA Assay, and the reported sensitivity (S_e) and specificity (S_p) values for this assay are given in Table 1 . Based on these values and the overall disease prevalences, we also include in the table the positive predictive value (PPV) and negative predictive value (NPV) that correspond to simulations to be discussed in this section.

Table 1.

Assay accuracy at the NPHL. The column header shows the disease (C = chlamydia, G = gonorrhea), gender (F = female, M = male), and specimen (S = swab, U = urine) combination.

	CFS	CMS	CFU	CMU	GFS	GMS	GFU	GMU
Se	0.928	0.925	0.805	0.930	0.966	0.985	0.849	0.970
Sp	0.960	0.950	0.960	0.950	0.980	0.960	0.980	0.960
PPV	0.633	0.775	0.637	0.621	0.389	0.648	0.419	0.344
NPV	0.995	0.986	0.983	0.994	1.000	0.999	0.997	0.999

To begin our pooled testing evaluation, a training data set is constructed using the 23,146 individuals screened during 2008. The diagnoses within the training data are assumed to be without error because we need to assess classification errors from pooled testing. First-order logistic regression models are fit to these data to estimate the probability of positivity, where separate models are used for each disease/gender/specimen combination (8 models in all). Covariates in these models consist of the self-reported information and clinical observations available on each individual. Our test data set consists of 27,521 individuals screened in 2009. We use the estimated models from the training data to estimate the risk probabilities for individuals in the test data. The Web-based Supporting Materials display histograms and box plots of these estimated probabilities.

Within a disease/gender/specimen combination, individuals are assigned to initial pools with a maximum size of 20. This value was chosen as a compromise between what has been used elsewhere for chlamydia and gonorrhea screening and the larger pool sizes occurring in other applications. For example, pool sizes of ten or less are common in chlamydia and gonorrhea screening (see references given in the review paper of [15]). Also, the American Red Cross [2] uses pools of size 16 for HIV screening, but we have seen pools of up to size 90 used for HIV screening elsewhere [16]. For TOD and PSOD, initial pool sizes are determined algorithmically using blocks of size 64. For the other procedures, the “optimal” pool size chosen minimizes the estimated expected number of tests for the training data. These optimal pool sizes are listed in the Web-based Supporting Materials. The test data individuals are assigned to pools chronologically when a pooled testing procedure does not order them otherwise.

To simulate how pooled testing is performed and to obtain a measurement of overall testing error, all pool and individual test responses are generated from a Bernoulli distribution with probability parameter S_e or S_p, depending on their 2009 status (which we assume is obtained without error). For example, suppose a pool of size 5 has individuals that were all declared negative in 2009. Our simulation would generate the pooled test response 0 (negative) with probability S_p and the pooled test response 1 (positive) with a probability of 1 − S_p. Similarly, if there was at least one positive in the pool, our simulation would generate the pooled test response 0 (negative) with probability 1 − S_e and the pooled test response 1 (positive) with a probability of S_e. We use 500 separate simulation runs to account for variability, and we report averages across these simulation runs next.

Figure 1 plots the percentage reduction in the number of tests relative to individual testing. The Web-based Supporting Materials provide tables for the number of tests and a plot similar to Figure 1 that makes direct comparisons with Dorfman testing. Overall prevalences of chlamydia and gonorrhea are given in Figure 1 to help provide context when interpreting these results. Not surprisingly, smaller prevalences lead to larger reductions in tests, and Dorfman testing has the smallest reduction in all but one case. FIS has the largest reduction in four of the eight disease/gender/specimen combinations, but 2SIS is usually very similar to FIS (including beating FIS twice). For two of the eight combinations, 4-step ordered halving has the largest reduction in tests, where the maximum pool size is used for both instances. This suggests that a larger pool size may have reduced the number of tests by an even larger amount. Larger pool sizes could potentially result in fewer tests being needed for other procedures too, especially for gonorrhea screening. For example, the gradient layout results in the largest test reduction of −79.6% for gonorrhea/male/urine when using a pool size of 20.

Figure 1.

Percentage change in the number of tests relative to individual testing. Abbreviations for the pooled testing procedures are given in Sections 2 and 3 when they are introduced. Table 1 gives the key for the disease/gender/specimen abbreviations.

Informative retesting almost always reduces the number of tests when compared to their non-informative counterparts. Note that we did not include a comparison with the non-informative Sterrett procedure because individuals are retested at random. Within classes of informative retesting procedures, we typically see the following patterns (“<” means smaller number of tests):

1. Dorfman – PSOD< TOD, except for gonorrhea/male/urine

2. Halving – 4-step< 3-step

3. Sterrett – FIS< 2SIS < 1SIS, although 2SIS sometimes results in fewer tests than FIS

4. Matrix – Gradient< spiral; non-informative matrix testing sometimes results in fewer tests than spiral.

The Dorfman-based procedures most often result in the highest number of tests in comparison to other classes of procedures. Overall, the Sterrett-based procedures appear to have the smallest number of tests (or close to the smallest number of tests) in most cases. We will discuss choosing among the informative retesting procedures in Section 5.

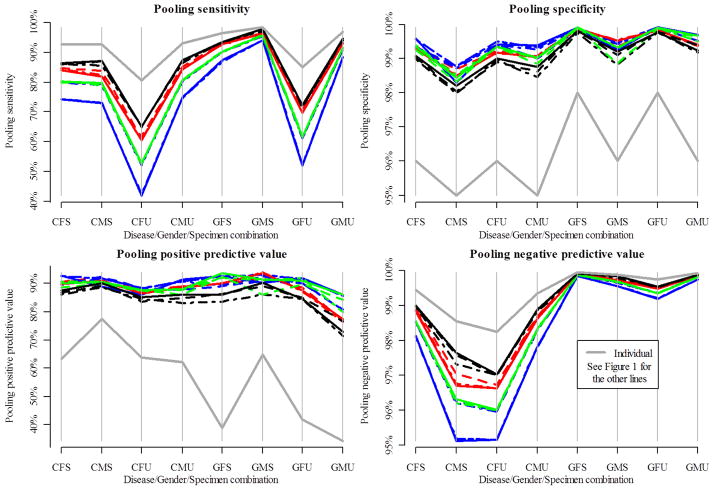
Measures of accuracy are given in Figure 2 and the Web-based Supporting Materials. The pooling sensitivity (specificity) is the probability that an individual is diagnosed as positive (negative) through using pooled testing, given that they are truly positive (negative). The pooling positive (negative) predictive value is the probability that an individual is truly positive, given that they were diagnosed as positive (negative) through using pooled testing. The dark gray lines in Figure 2 provide references for individual testing accuracy as given in Table 1 . We see from Figure 2 that pooled testing results in smaller pooling sensitivity and pooling negative predictive values than individual testing. This happens because pooled testing makes negative classifications only after one negative test for a pool. However, pooled testing also results in larger pooling specificity and pooling positive predictive values than individual testing. This happens because pooled testing makes positive classifications only after multiple positive tests occur.

Figure 2.

Measures of accuracy for chlamydia and gonorrhea screening. Note that each plot has a different y-axis scale. Table 1 gives the key for the disease/gender/specimen abbreviations.

Larger step procedures (e.g., 4-step halving) tend to be more extreme with respect to the accuracy measures than smaller step procedures (e.g., Dorfman-based procedures). This is more evident when the assay sensitivity is lower as with testing female urine specimens. Interestingly, while the Sterrett-based procedures potentially could have a large number of steps, their accuracy levels are generally comparable with the other procedures. This may result from the Sterrett-based procedures quickly finding the few positives within a positive pool. The gradient and spiral matrix layouts and the ordered halving procedures have accuracy levels similar to their non-informative counterparts. This suggests that these informative retesting procedures do not result in a loss of accuracy. PSOD and usually TOD tend to have slightly higher accuracy than Dorfman testing.

No computer simulation can completely replicate what happens in actual application. In the interest of full disclosure, we now describe the assumptions and simplifications that were needed for this study. First, the logistics of implementing pooled testing are not of primary interest here. A “cost” component (in terms of time and money) could have been included in our comparisons; however, this would have involved additional assumptions and would have led to differences across laboratories. We chose not to include cost, which essentially means that our comparisons are made with an equal cost for each test. Second, the assay used by the NPHL actually screens for chlamydia and gonorrhea simultaneously. We are not aware of any pooled testing research that investigates how to take advantage of a single assay testing for multiple diseases at the same time. The end result for our study here is that more tests are reported than would be needed in application. Third, there are a few assumptions made about the accuracy of the assay itself. We assume that the S_e and S_p levels are constant for all pool sizes. This is reasonable for properly calibrated tests. Also, we assume that there are no dilution effects and no inhibitors that may prevent a positive response from being realized beyond what is already quantified by the assay sensitivity and specificity.

5. Conclusions

In this paper, we have presented the first comprehensive evaluation of non-informative and informative procedures for pooled testing applied to a heterogeneous population. We have shown that alternatives to Dorfman testing usually result in a large reduction in testing loads. Also, we have shown that informative retesting can reduce testing loads further when compared to their corresponding non-informative counterparts. With respect to accuracy, pooled testing improves upon the overall pooling specificity and pooling positive predictive value when compared to individual testing. However, pooling sensitivity and pooling negative predictive values can be much lower when the assay sensitivity is low. Dorfman testing and its informative versions generally provide the largest pooling sensitivity and pooling negative predictive values in the low assay sensitivity settings. The accuracy levels for pooled testing greatly improve with more sensitive assays.

This paper has focused on applications for the IPP; however, there are many other places where pooled testing is used in heterogeneous populations. For example, the American Red Cross screens millions of blood donations per year for hepatitis B, hepatitis C, and HIV using Dorfman testing with pools of size 16 [2, 3 ]. Each blood donor fills out a questionnaire, which includes questions on age, gender, location, and first time donor status, that could be used to implement informative retesting. High volume clinical specimen screening also occurs at state veterinary diagnostic laboratories. For example, the Nebraska Veterinary Diagnostic Laboratory uses pooled testing with trichomonas screening for bulls. In this application, a specimen that contains something unusual (e.g., pus) triggers individual testing, which is somewhat analogous to TOD discussed in Section 3 . Other potential covariates that could be used in this application include whether or not an animal displays symptoms or the herd’s geographical proximity to other herds known to harbor the disease. Lastly, pharmaceutical drug discovery experiments look for active compounds in large chemical libraries that include hundred of thousands of members. These experiments are sometimes performed using pooled testing [17, 18 ]. The chemical structures of the compounds could be used to describe heterogeneity in the library and could be exploited for informative retesting purposes.

There is not one pooled testing procedure that is best (in terms of number of tests and accuracy) all of the time. Prevalence levels, assay accuracy, availability of risk factor information, and risk probability distributions all play roles in determining which procedure is best. Furthermore, ease of application is an important consideration in any laboratory setting to prevent human error. Whenever risk factor information is available and can be used to estimate individual risk probabilities, we recommend using an informative retesting procedure. Even simple procedures, like TOD, can provide a noticeable reduction in the number of tests when compared to Dorfman testing. When high throughput screening is available so that pooling can be automated, more complex procedures, such as gradient matrix testing, are recommended.

A general strategy to assess how well pooled testing would work in a particular application is to find the expected number of tests using the formulas provided by the references cited in Sections 2 and 3. Some of these references provide R programs to facilitate this process. For example, the website http://www.chrisbilder.com/grouptesting contains R programs for the Dorfman, Sterrett, and matrix-based procedures. Once expected values are calculated, sensible judgments can be made regarding which procedure leads to the smallest expected number of tests in a specific setting. Additional computations can also be made to examine accuracy.

This work leads to a number of different possibilities for future research. First, while the reduced accuracy levels for some measures are disappointing, there may be ways to overcome this problem. Often, this reduction is due to a “quick” classification of negative individuals through their first negative pooled test. Confirmatory testing could be included in any retesting protocol in an attempt to avoid false negative diagnoses. In addition, some form of informative retesting could be implemented among these individuals to more quickly find possible false negatives. Second, there has been no research investigating the role that model quality has in making informative retesting effective. One might expect that using a poor fitting model would result in the informative procedures performing much like their non-informative counterparts. However, this may not be true, because many informative procedures use risk probability estimates only to order individuals (such as with ordered halving). Other procedures, like PSOD, rely on point estimates more heavily, so their performance may be less robust to a poor model.