Microarchitecture and Bone Quality in the Human Calcaneus; Local Variations of Fabric Anisotropy

Abstract

The local variability of microarchitecture of human trabecular calcaneus bone is investigated using high resolution microCT scanning. The fabric tensor is employed as the measure of the microarchitecture of the pore structure of a porous medium. It is hypothesized that a fabric tensor-dependent poroelastic ultrasound approach will more effectively predict the data variance than will porosity alone. The specific aims of the present study are i) to quantify the morphology and local anisotropy of the calcaneus microarchitecture with respect to anatomical directions, ii) to determine the interdependence, or lack thereof, of microarchitecture parameters, fabric, and volumetric bone mineral density (vBMD), and iii) to determine the relative ability of vBMD and fabric measurements in evaluating the variance in ultrasound wave velocity measurements along orthogonal directions in the human calcaneus. Our results show that the microarchitecture in the analyzed regions of human calcanei is anisotropic, with a preferred alignment along the posterior-anterior direction. Strong correlation was found between most scalar architectural parameters and vBMD. However, no statistical correlation was found between vBMD and the fabric components, the measures of the pore microstructure orientation. Therefore, among the parameters usually considered for cancellous bone (i.e., classic histomorphometric parameters such as porosity, trabecular thickness, number and separation), only fabric components explain the data variance that cannot be explained by vBMD, a global mass measurement, which lacks the sensitivity and selectivity to distinguish osteoporotic from healthy subjects because it is insensitive to directional changes in bone architecture. This study demonstrates that a multi-directional, fabric-dependent poroelastic ultrasound approach has the capability of characterizing anisotropic bone properties (bone quality) beyond bone mass, and could help to better understand anisotropic changes in bone architecture using ultrasound.

INTRODUCTION

The ability of bone to adapt its local tissue mass and architecture to its mechanical environment is known as Wolff’s law. Consistent with this observation is the fact that the elastic properties of an adapted bone fit the mechanical environment forces acting on that bone⁽¹⁾. “The characterization of the geometry of the local architectural structure of a porous material by porosity alone is not sufficient due to the directional variation of pore orientation”⁽²⁾. Even though the important role microarchitecture plays in bone mechanics was understood a long time ago, the current gold standard to diagnose bone loss and osteoporosis remains the areal Bone Mineral Density - aBMD^(3–4). The aBMD is a measure of the mass density in the tissue and thus is highly correlated to bone mass when measured in the spine, wrist and femoral neck^{(3, 5–6)}. However, a significant number of women diagnosed with osteoporosis based on aBMD measurement do not suffer fractures, whereas many women with normal aBMD do^(7–12). These studies have demonstrated that aBMD measurements lack both sensitivity and selectivity to effectively identify patients at risk of fracture, supporting the argument that other factors (i.e. bone architecture) are required to better assess bone loss and osteoporosis.

A recent paradigm shift occurred in the orthopedic community, and it is now well accepted that the ability of bone to fulfill its mechanical function and resist low trauma fractures depends not only on the aBMD but also on tissue composition and architecture^(13–28). Accordingly, development of non-invasive approaches to assess bone quality beyond quantity is required^(29–34). Ultrasound wave propagation is an attractive approach to assess anisotropic mechanical properties and diagnose osteoporosis^{(33, 35–36)} because it is non-ionizing, inexpensive and non-invasive. More importantly, ultrasound wave propagation is sensitive to bone mass density, tissue composition and bone microarchitecture^{(35, 37–39)}. However, the relationship between bone microarchitecture and wave propagation in anisotropic porous media is complex and not fully understood. The role of anisotropic architecture on the mechanical properties of trabecular bone was introduced by Cowin⁽²⁾ using a fabric tensor F. The fabric tensor F is a quantitative stereological measure of the degree of structural anisotropy and the mechanical principal orientations of cancellous bone⁽²⁾. More recently, Cowin and Cardoso^(40–41) introduced the fabric tensor in the wave propagation equations to calculate the velocity of longitudinal and shear waves in anisotropic porous media.

The goal of this study is to characterize local variations of trabecular microstructure in the human calcaneus and to determine the effect of such architectural properties on the anisotropic ultrasound wave velocities along multiple directions in human calcanei. The hypothesis of this study is that classic histomorphometric parameters (porosity, trabecular thickness, number and separation) are all correlated to the porosity in the human calcaneus, but that the fabric tensor is highly correlated to the directional variance of the microarchitecture. Microarchitecture orientation has an influence of ultrasound wave propagation; therefore, the combination of porosity (ϕ) with fabric tensor (F) should be a better predictor of the ultrasound wave velocity in anisotropic bone than porosity alone. To test this hypothesis, we report in this work our efforts i) to quantify the morphology and local anisotropy of the calcaneus microarchitecture with respect to anatomical directions using high resolution microCT (µCT), ii) to determine the ultrasound wave velocity along multiple anatomical directions in human calcanei using 3D finite differences time domain (FDTD) numerical simulations, and iii) to determine the ability of the fabric tensor to describe the variance in ultrasound wave velocity measurements along orthogonal directions in human calcanei.

MATERIALS AND METHODS

Sample preparation

Sixteen human calcanei were obtained from the National Disease Research Interchange (NDIR; Philadelphia, PA) resource center. Bone donors were female, 60 to 74 years old, who died of cardio/pulmonary failure, drug/alcohol abuse, cancer or natural causes. Calcanei were harvested within 24h postmortem, and immediately fixed in 10% formaldehyde. Upon arrival at our laboratory, calcanei were carefully cleaned free of soft tissues and immersed in formaldehyde at 20°C for one more day and stored at 4°C.

MicroCT image acquisition

Calcanei were thawed until reaching room temperature prior to scanning with an 1172 SkyScan high resolution µCT system (SkyScan, Belgium). X-ray projections were acquired at a nominal isotropic voxel size resolution of 13.47µm using a 0.5 mm aluminum filter to eliminate beam hardening artifacts. X-ray projections were generated every 0.2 degrees of rotation, obtaining 900 consecutive projections. To produce high-contrast, low-noise images the projections were averaged 4 times, and a median filter was used to prevent speckle noise formation. Due to the large size of specimens, 4 consecutive vertical connected scans were needed to scan each bone; each of these scans consumed approximately 11 hours. Hydroxyapatite rods (HA, 2 mm diameter, 0.25 and 0.75 gHA/cm³) were scanned using the same protocol to calibrate images for tissue mineral density (TMD).

Image processing

Approximately 4500 images per sample were reconstructed from X-ray projections using the back-projection reconstruction algorithm in NRecon software (Skyscan, V1.6.1.1, SkyScan). Hounsfield unit (HU) and tissue mineral density calibration procedures were performed in CTAn software (CT Analyzer, v.1.6.1, SkyScan, Belgium). Four volumes of interest (VOIs) were selected from regions that contained water, air, 0.25 or 0.75 gHA/cm³. The mean grayscale index value from water and air was used to calibrate images in HU, and the mean grayscale index values from the 0.25 and 0.75gHA/cm³ mineral rods were used to generate a calibration curve between the grayscale color in each pixel and the corresponding mineral density in gHA/cm³. After image density calibration, the separation (image segmentation) between mineralized and soft tissues in each scan was performed using a mean global thresholding procedure. The threshold value was determined by analyzing the images using an edge detection algorithm (ImageJ v 1.37, National Institutes of Health). The tissue mineral density threshold obtained through this edge detection procedure was 0.40 gHA/cm³.

Anatomical realignment of images and VOI description

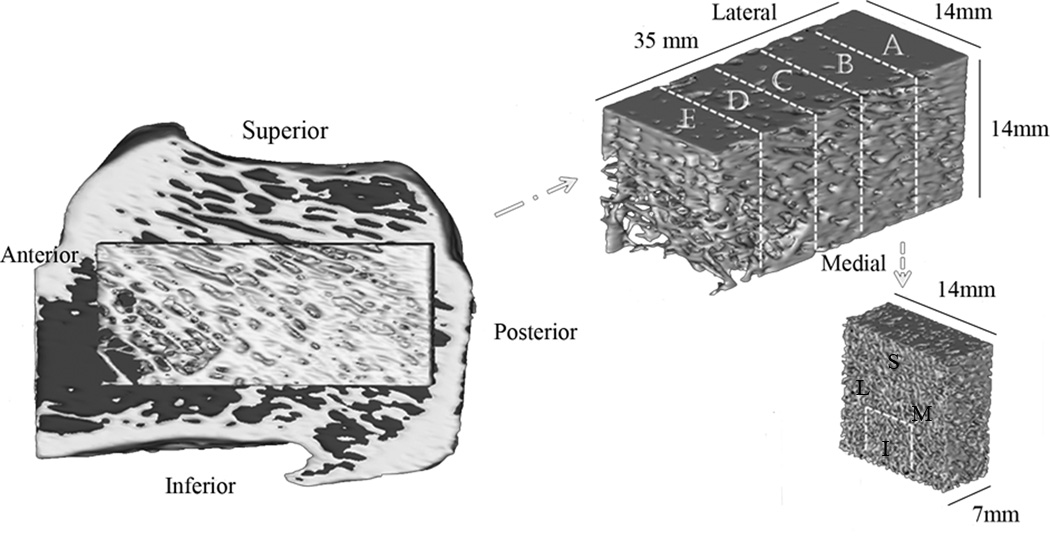
An anatomical Cartesian coordinate system with axes defined along the ML (medial-lateral), PA (posterior-anterior) and SI (superior-inferior) directions was introduced to investigate the relationship between directional measurements of bone microarchitecture and bone anatomy. The stack of µCT images was realigned with respect to the anatomical coordinate system by rotating the dataset around the ML, PA and SI directions of each calcaneus using DataViewer software (Ver.1.4.3, SkyScan, Belgium). To quantitatively measure the local microarchitecture of calcanei, volumes of interest (VOIs) were obtained from each calcaneus dataset as follows. A 14×14×35 mm³ parallelepiped-shaped sample was selected 5mm away from the posterior end of each sample. The parallelepiped was divided into five 14×14×7 mm³ layers (denoted as layer A, B, C, D, and E) from the posterior to the anterior location of the sample (Figure 1). Four 7×7×7 mm³ cubic volume of interests (VOIs) were obtained from each layer based on their anatomical location within each layer as medial, lateral, inferior or superior (named as region M, L, I, and S). Therefore, each VOI was designated by two uppercase Latin letters; the first letter refers to the layer (A, B, C, D, and E) and the second one refers to the anatomical region (M, L, I, and S) within the layer. For instance, the volume of interest A–L is located in the lateral position of layer A (Figure 1). It is important to notice that the analyzed regions of interest in this study do not cover the whole cancellous tissue of the calcaneus, only the cancellous tissue within the parallelepiped-shaped volume in Figure 1.

Figure 1.

The 3D image in the left is a section of the whole calcaneus from HR-CT images. The anterior (left), posterior (right), superior (top) and inferior (bottom) aspects of the whole bone were used to align all the samples in the same orientation. At the center of the whole sample, a parallelepiped 14 mm × 14 mm × 35 mm region is shown in yellow, which was divided into five equal 7 mm × 7 mm × 14 mm layers (A, B, C, D, and E), and each layer into four 7mm diameter spherical volumes of interest with respect to their anatomical location (medial, lateral, superior, inferior).

Global measurements of microarchitecture

For each VOI, global architectural parameters were measured, including the porosity (ϕ), trabecular number (Tb.N), trabecular thickness (Tb.Th), and trabecular spacing (Tb.Sp). Since images were calibrated for mineral density, volumetric bone mineral density (vBMD) and TMD were obtained using built-in algorithms in CTAn software employing the guidelines for assessment of bone microarchitecture using µCT⁽⁴²⁾. vBMD was quantified before segmentation of images which includes both mineralized tissue and marrow, but TMD was obtained after segmentation, comprising the mineralized tissue only. The partial volume effect on TMD measurements was investigated in a separate set of samples. Six cylindrical samples (5mm diameter, 10mm height) were cut from the anterior region of 6 calcanei, scanned at 3.4µm and 13.5µm, and their TMD was measured. Both scans were processed in the same manner and calibrated using the same mineral density hydroxyapatite standards.

Fabric tensor

The fabric tensor serves as a measure of the degree of structural anisotropy of the porous medium^{(1–2, 40)}. Use of the fabric tensor is restricted to materials with orthotropic or higher symmetry⁽²⁾. The eigenvectors of F are the principal axes of material symmetry of the porous solid medium and the eigenvalues of F provide a measure of the distribution of porous volume fraction in the direction of the principal axes of material symmetry. Human cancellous bone is considered as an orthotropic porous medium^(43–44). If the three eigenvalues of the fabric tensor, F₁, F₂, and F₃, are distinct, F₁ ≠ F₂ ≠ F₃, the fabric is orthotropic; if two are equal, F₁ = F₂ ≠ F₃, the fabric is transversely isotropic; and if all three are equal, F₁ = F₂ = F₃, the fabric is isotropic. As with any symmetric positive definite second order tensor in 3D, the fabric tensor may be represented as an ellipsoid. The ellipsoid is one with three unequal axes for an orthotropic fabric, one unique axis for a transversely isotropic fabric (forming an ellipsoid of revolution about the unique axis) and the ellipsoid becomes a sphere in the case of an isotropic fabric. The fabric tensor is a good measure of the pore structure anisotropy in cancellous bone tissue⁽¹⁵⁾, as well as the mechanical and fabric main directions that coincide in cancellous bone⁽⁴⁵⁾.

Directional measurements of microarchitecture

The directional variation of pore orientation can be calculated using the mean intercept length (MIL), the volume orientation (VO), and the star volume distribution (SVD) methods^{(43, 46–48)}. In this study, directional measurements of microarchitecture were calculated via the measurement of MIL tensor M⁽¹⁾ using CTAn software. Then, values of the fabric tensor F eigenvalues F₁, F₂ and F₃, were obtained by taking the inverse square root of the eigenvalues of MIL tensor M⁽⁴³⁾. Fabric components were normalized by dividing each one by the sum F₁+F₂+ F₃. The three eigenvectors of F represent the principal axes of material symmetry, which also correspond to the principal orientations of trabeculae. The components of the fabric eigenvectors are expressed relative to the anatomical coordinate axis; their vector components are the directional cosines of eigenvectors in the anatomical coordinate system⁽¹⁾. The degree of anisotropy (DA) was measured as the ratio of the largest to the smallest directional component of MIL tensor.

Numerical simulations of wave propagation

Finite-difference time-domain (FDTD) numerical simulations^(49–53) were used to determine the velocity of ultrasound waves propagating along the three anatomical directions (medial-lateral, anterior-posterior, and inferior-superior) on the 7×7×7mm³ cubic VOIs from µCT images using Wave3000 FDTD software (Ver2.0, CyberLogic, Inc., New York, NY). A preliminary study was performed to determine the effect of the voxel size on the wave velocities obtained from FDTD numerical simulations. FDTD simulations were done on µCT images at the original voxel size of 13.47×13.47×13.47µm³, and after the voxel size was increased three times to a voxel size of 40.41×40.41×40.41 µm³. FDTD wave velocities were identical for both resolutions; therefore, all subsequent FDTD simulations were performed after increasing 3 times the voxel size of original images, which considerably reduced the computational time. Images were then binarized into bone and marrow, and using MATLAB (Ver. R2010b, Mathworks, Natick, MA), VOIs were located in the center of a virtual 45×45×45mm³ cube container with material properties similar to marrow fluid. The material properties of the fluid representing the mixture of blood and marrow were defined as follow: mass density = 1055 kg/m³; Lame constants λ = 2634 MPa; and μ = 0 MPa; V_L = 1580.09 m/s; and damping factor η = 0.1 Pa-s. For bone, human cortical properties were used: mass density = 1850 kg/m³; λ = 9306 MPa; μ = 3127 MPa; V_L = 2900 m/s; η = 40 Pa-s. The ultrasound source produced a 500 kHz – 5µs sine exponential pulse (damping factor α = 0.5m⁻¹) propagating through transmission. The distance between the source and the sample was 20mm, and two 6mm diameter receivers were located exactly at the front and back face of the sample, so that the time of flight (TOF) of the wave propagating through the sample was easily computed. Infinite boundary conditions were set at the limits of the cube container to avoid wave reflections. The numerical simulation was performed using a grid voxel size of 150×150×150µm³ with a Δt = 0.0192µs, that required a total simulation time duration of 25µs. The resolution wavelength was 3.2 mm approximately, which is larger than the size of the pores (Tb.Sp.) and the trabecular thickness (Tb.Th.). Speed of sound (SOS) was determined by dividing the sample size by the time difference between the peaks of the waves measured at the front and back interfaces of the sample.

Anisotropic poroelastic ultrasound (PEUS) wave propagation model

The role of porous media microarchitecture was recently introduced in the anisotropic poroelasticity theory of wave propagation⁽⁴⁰⁾. Key to the development of such a theory was the incorporation of the fabric tensor into the governing equations for wave motion in the linear theory of anisotropic poroelastic materials^{(2, 17)}. This new approach resulted in a poroelastic Christoffel equation for anisotropic poroelastic media with six roots. Four of those six roots are nonzero, and correspond to the four wave modes of propagation in each direction in porous media, two of which are longitudinal and two are shear wave modes. Analytical expressions were given in Cowin and Cardoso⁽⁴⁰⁾ for the velocity and attenuation of each wave mode for the case in which the direction of wave propagation coincides with the normal to a plane of symmetry of the anisotropic medium. Later, that study was extended to the propagation of waves along an arbitrary direction in orthotropic porous media⁽⁴¹⁾. Global changes in velocity of wave propagation are functions of the porosity and material properties of the solid and fluid constituents (i.e. density and elastic constants of tissue matrix and marrow), while directional changes of ultrasound wave velocity are a function of the porous media microarchitecture as quantified by the fabric tensor. For the present study, the longitudinal fast wave velocity was computed using equations in Cardoso and Cowin⁽⁴¹⁾ along three anatomical directions in all four M, L, I, and S regions of layer C, using the measurements of porosity and fabric from each VOI. Densities of solid and fluid constituents were considered the same as the ones used for FDTD numerical simulations.

Statistical analysis

Three-hundred twenty VOIs obtained from 16 human calcanei were analyzed using the Prism5 statistics software package (GraphPad Software Inc.). Repeated measures ANOVA with a significance level of p < 0.05 and Bonferroni's multiple comparison test was performed to identify differences in global and directional architectural parameters (vBMD, TMD, Porosity, Tb.N, Tb.Th, Tb.Sp, F and DA) among different layers (A to E) and anatomical locations (M, L, I, S), as well as after averaging the results by layer or by anatomical location. Raw data was reported and shown in figures as mean ± standard deviation. To analyze the correlation among microstructural parameters, Pearson’s correlation coefficient was calculated and p < 0.05 was set as the significance level.

RESULTS

Histomorphometry measurements

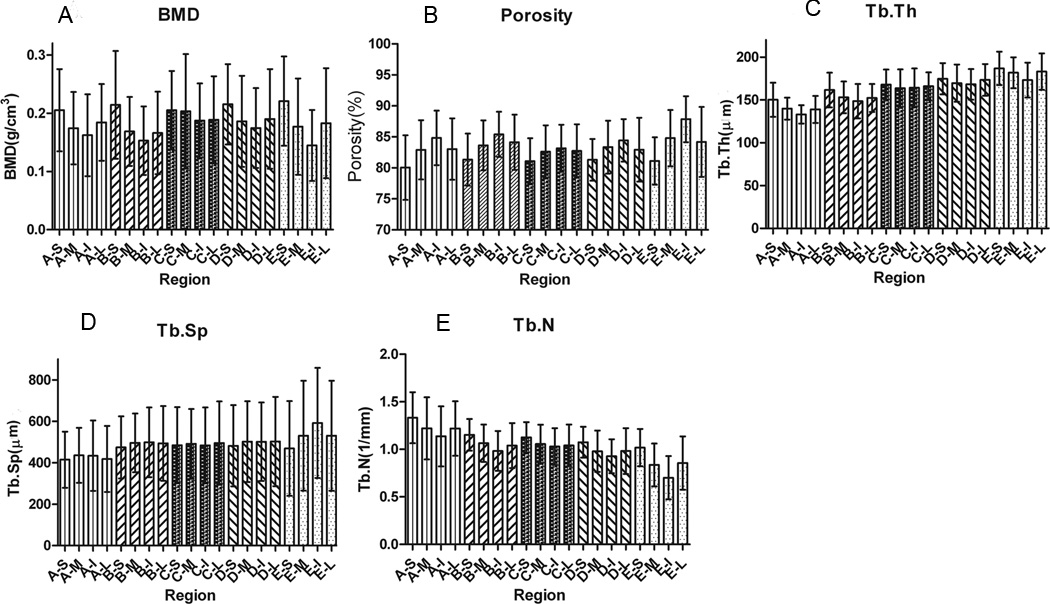
The local variability of several histomorphometric parameters is illustrated in Figure 2. The average vBMD on all VOIs was found to be 0.185±0.073g/cm³. The maximal difference observed among VOIs was 0.076 g/cm³, which was found between E–S and E–I regions (Figure 2A). A pattern of change on vBMD can be observed on each layer: the vBMD is the largest in the superior region and the smallest in the inferior region within each layer, but the vBMD is practically equal in the medial and lateral regions. Overall, the highest vBMD is observed in the superior region of layer E, which is the closest to the anterior aspect of the bone, and the lowest vBMD is observed in the inferior region of the same layer E. However, the vBMD values were not significantly different statistically, except when comparing the E–I region with B–S, D–S, and E–S.

Figure 2.

Local variation of vBMD (A), porosity (B), Tb.Th (C), Tb.Sp (D) and Th.N (E) averaged by VOI (20 regions of interest for 16 human calcanei)

The average tissue mineral density measured at 13.5µm resolution among all 320 VOI's was 0.872±0.063 gHA/cm³. However, TMD measurements at 13.5µm resolution could be affected by partial volume associated to the voxel size. The comparison of TMD measured on a subset of samples (n=6) at two different resolutions indicates that the TMD at the 13.5µm resolution (0.926±0.035 gHA/cm³) is underestimated by 11.5% when compared to the TMD from the same samples at the 3.4µm resolution (1.047±0.046 gHA/cm³). There is indeed an influence of partial volume effect on TMD measurements carried out at 13.5µm resolution. This is a limitation of the TMD data acquired at 13.5µm; therefore, local variations of TMD are not reported here. However, to the best of author's knowledge, this is the first report of TMD in the human calcaneus at 13.5µm and 3.4µm resolutions, and could serve as a reference value to compare future TMD measurements at this skeletal site.

The analysis of porosity of the individual VOIs revealed an average porosity of 83.2±4.3% and a maximum porosity difference among regions of 7.8%. A similar pattern of porosity was found for all layers, which is opposite to the trend shown for vBMD. The inferior regions show higher porosity than the corresponding superior regions (Figure 2C), and the same porosity was found on the medial and lateral regions of all layers. However, there is no statistical difference in porosity among most of the VOIs. The regions A–S and E–I have the lowest and highest porosity values and exhibited statistically significant differences when compared to a few other regions.

The average Tb.Th value for all analyzed regions was found 162±18µm. Similarly to vBMD, the Tb.Th was found the largest in the superior regions and smallest in the inferior regions in each layer (Figure 2D). The Tb.Th values in the medial and lateral regions in each layer are practically equal. The maximum mean difference of Tb.Th among regions was 53µm; this difference was located between region E–S with the highest Tb.Th value and region A–I with the lowest Tb.Th value. There were no statistically significant differences when comparing the four M, L, I, and S regions within each layer. However, when analyzing the layers, a statistically significant increase in Tb.Th was noticed from the posterior to the anterior location. The mean distance between trabeculae (Tb.Sp) exhibited no pattern of change within layers or M, L, I, and S regions (Figure 2E). The average of Tb.Sp values for all regions was 487±190µm. The maximum mean difference of Tb.Sp values among regions is 177µm; this was found between region A–S located close to the anterior and inferior boundaries and E–I located close to the posterior and superior boundaries. There is no significant difference in Tb.Sp for all regions except between E–I and all regions in layer A.

The number of trabeculae per unit length is reported by VOI in Figure 2F. The average of Tb.N for all regions was 1.039±0.225mm⁻¹. The maximum mean difference in Tb.N among regions was 0.631mm⁻¹, this is between region A-S with the highest Tb.N value and E–I with the lowest Tb.N value.

Data was also analyzed after averaging the values by layer or by anatomical region. When data was pooled by layer, no trend was found in vBMD, porosity, and Tb.Sp. A small trend was found on Tb.Th and Tb.N, in which the first increase from layer A toward layer E, and the opposite occurs for Tb. N, which decreases when going from the posterior to the anterior region. This slight trend was however not statistically significant. When data was pooled by M, L, I, and S anatomical region, a small difference between superior and inferior regions was noticeable on all morphometric parameters, but again no statistically significant difference was found (data not shown).

Fabric components

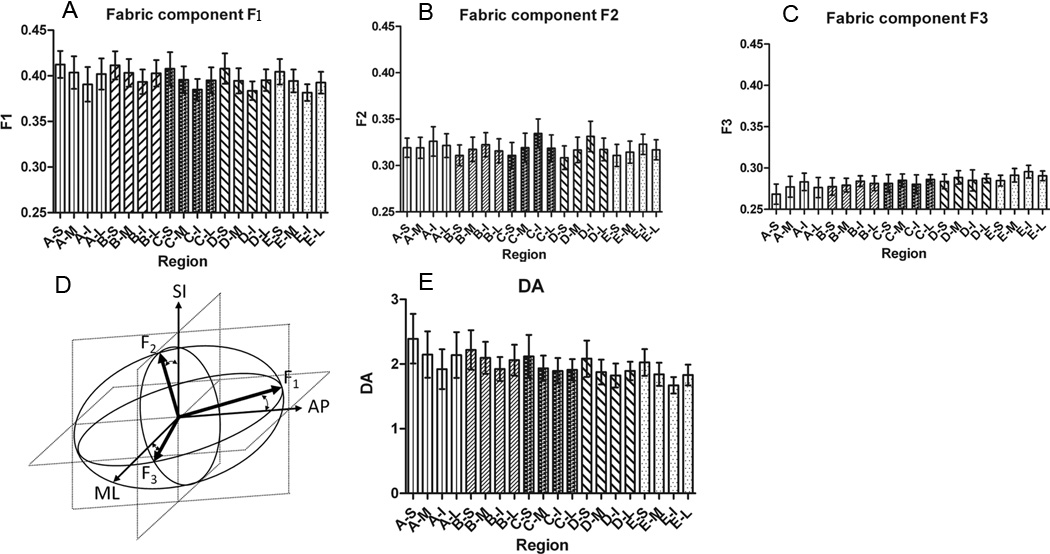
Values of F₁, F₂ and F₃ components of the fabric tensor for all VOIs are illustrated in Figure 3A, 3B and 3C respectively. The first panel of this figure shows a similar pattern in F₁, a pattern in which the M and L regions are similar, but the superior region has the smallest value and the inferior region has the largest value in each layer. There is no statistically significant difference in F₁ components in different layers in the same medial, lateral, inferior, or superior anatomical regions. In other words, when moving from the posterior to the anterior region of bone, no changes in the value of F₁ were found. The same pattern was found for F₂ and F₃ among each layer (A to E), in which the medial and lateral regions are similar, and in contrast to F₁, the superior region has the largest value and the inferior region has the smallest value.

Figure 3.

Local variation of fabric components F₁, F₂, and F₃ (A, B & C) in respect to anatomical location (20 regions of interest for 16 human calcanei), illustration of fabric tensor ellipsoid at the region A–S (D), and Local variation of DA (E).

The mean values of F₁, F₂ and F₃ for all regions were found to be 0.398±0.016, 0.319±0.014, and 0.286±0.011 respectively, which are all statistically different (Table 1). These three unequal mean fabric values show that the cancellous bone in the calcaneus is orthotropic. Thus the fabric tensor can be illustrated as an ellipsoid with three different fabric eigenvalues in the three different axes as is shown for the region A–S in Figure 3D. F₁ as the largest value of F_i (i=1, 2, 3) was found in the anterior-posterior direction, which indeed corresponds to the main trabecular orientation. Surprisingly, the magnitude of F₁ was highly similar on all VOIs, and the direction (as given by eigenvectors) almost the same. Larger variability on eigenvalue magnitude and eigenvector direction across the VOIs was found for the other two principal directions of fabric (i.e. F₂ and F₃).

Table 1.

Descriptive statistics of fabric eigenvalues (F₁, F₂, and F₃ components) eigenvectors (primary, secondary and tertiary directions) representing the trabecular magnitude based on 320 volumes of interest from 16 human calcanei.

	F1	F2	F3
Mean value	0.398	0.319	0.283
Standard deviation	0.016	0.014	0.011
Max. mean difference	0.031	0.026	0.027

Trabecular principal orientations

The angles between the fabric eigenvectors and the anatomical coordinate axis were calculated and their averages are summarized in Table 2. From Table 2 one can see that the direction cosines of the average normalized primary trabecular direction in the anatomical ML, AP, SI coordinate system are: (−0.05, 0.84, −0.50), the mean ± SD angle between the average primary trabecular direction and the corresponding anatomical coordinate axis was found to be 93±1°, 31±4° and 120±4°, respectively. There is no significant difference between the first components of the primary trabecular direction (medial-lateral axis), but there was a change observed in the second and third components of the primary direction (Table 2). The average normalized eigenvectors 2 and 3 are the secondary and tertiary directions respectively. The results show that the consistency observed for the primary direction was not seen on the secondary and tertiary directions.

Table 2.

Descriptive statistics of fabric eigenvectors (primary, secondary and tertiary directions) representing the orientation based on 320 volumes of interest from 16 human calcanei.

	primary direction	secondary direction	tertiary direction
Mean Eigenvalue	(−0.05, 0.84, −0.51)	(0.15,0.51,0.82)	(0.98,−0.01,−0.09)
Mean angles between the eigenvalues and the anatomical directions	(93°,30°,120°)	(81°,59°,34°)	(10°,90°,95°)
Standard deviation	(1°,4°,4°)	(11°,5°,6°)	(7°,5°,10°)

Degree of anisotropy (DA)

The assessment of the degree of anisotropy for all VOIs indicates that there is the same pattern of change of the DA in each layer (Figure 3E) as seen for F₁. Specifically, the DA is the largest in the superior regions and smallest in inferior regions in each layer. Also, the DA in medial and lateral regions in each layer are practically equal. The average DA for all regions is 1.99±0.29.

Statistical correlation among microarchitectural parameters

The correlation between vBMD, ϕ, Tb.N, Tb.Th, Tb.Sp, F₁, F₂, F₃ and DA is summarized in Table 3. It was found that global descriptors of microarchitecture, such as vBMD, ϕ, Tb.N, Tb.Th, and Tb.Sp are strongly related among themselves. It is significant to note that the directional parameters such as F₁, F₂, F₃ and DA are also statistically correlated among themselves. However, there is no correlation between vBMD and fabric component measurements, confirming that fabric is a measurement of architecture independent of vBMD. Moreover, some fabric component measurements (F₁, F₂, F₃) are weakly correlated to some of the other global descriptors of microarchitecture (ϕ, Tb.N, Tb.Th, and Tb.Sp). This result could be due to the geometry dependency of both fabric and microarchitecture, but the directionality in global descriptors of microarchitecture is obscured in the scalar character of these descriptors whereas directionality exists in the tensorial character of fabric component measurements.

Table 3.

Correlation coefficient (R²) and p value among architectural parameters, F₁, F₂, F₃, DA, ϕ, vBMD, TMD, Tb.Th, Tb.Sp, and Tb.N measured on 320 VOIs from 16 human calcanei.

	F1	F2	F3	DA	ϕ	vBMD	Tb.N	Tb.Th	Tb.Sp
F1	1	−0.76	−0.52	0.87	0	−0.03	0.026	0.15	0.19
p		0	0	0	0.957	0.569	0.636	0.008	0.001
F2		1	−0.15	−0.36	−0.11	0.07	−0.21	0.072	−0.24
p			0.007	0	0.041	0.208	0	0.196	0
F3			1	−0.86	0.15	−0.04	0.24	−0.32	0.02
p				0	0.009	0.429	0	0	0.701
DA				1	−0.07	0.02	−0.11	0.27	0.09
p					0.182	0.772	0.048	0	0.108
ϕ					1	−0.67	−0.35	−0.65	0.48
p						0	0	0	0
vBMD						1	0.42	0.68	−0.8
p							0	0	0
Tb.N							1	−0.14	−0.11
p								0.009	0.043
Tb.Th								1	−0.7
p									0
Tb.Sp									1

Effect of fabric on ultrasound wave propagation measurements

The fast wave velocity was computed along the three anatomical directions (AP, ML, SI) of the VOIs in the C layer of bones using the poroelastic ultrasound wave propagation theory^(40–41) considering two different approaches: i) an approach neglecting fabric anisotropy in which the fabric is considered to be isotropic (F₁ = F₂ = F₃ = 1/3), and ii) an approach with fabric anisotropy, in which the fabric components are taken from the present study on each VOI. The frequency employed in the simulations was 500KHz, and the velocity of the wave propagation is within the range of [1600–1900m/s]. As a result, the wavelengths of the waves in the medium are in the range of [3.2 – 3.8mm] which is smaller than the size of the analyzed samples and much larger than the pore size (trabecular spacing) of the porous media. The fast wave velocities from FDTD numerical simulations were compared to fast wave velocities from the approach without fabric anisotropy in Figure 4A. Figure 4A shows that for a single value of FDTD velocity, and neglecting anisotropy, there is a large variability in the poroelastic model predicted velocities. Global measurements of architecture (i.e. vBMD, porosity, Tb.Th, Tb.Sp, Tb.N) were found to be moderate/good predictors of the wave velocities (R²=0.74 and p<0.0001) for anisotropic cancellous bone. However, the approach taking into account the anisotropy of fabric improved the prediction (R²=0.88 and p<0.0001) of the fast wave velocities (Figure 4B) when compared to the density-based approach without fabric anisotropy. This improvement in wave velocity predictability occurred because the poroelastic model includes both global (porosity or vBMD) and directional (fabric) measures of bone microarchitecture.

Figure 4.

FDTD ultrasound wave velocities as a function of vBMD (A) and fabric tensor-dependent poroelastic ultrasound approach (B).

DISCUSSION

Bone morphometric parameters such as vBMD, Tb.N, Tb.Th, and F₁ component exhibit a similar pattern in each layer characterized by a small local variability that depends on the anatomical location of the region of interest. Smaller values for these parameters are located in the inferior region, slightly larger values are found in the medial and lateral regions, and the largest values are always located in the superior region. The opposite trend was observed for the porosity, Tb.Sp, F₂, F₃, and DA. In particular, there is no vBMD change across the regions of interest except at the E–I region, being characterized by the highest porosity and lowest vBMD. In general, most changes observed in vBMD, porosity, Tb.N, Tb.Th and Tb.Sp are small and statistically not significant. Mean values of bone morphometric parameters found in this study are in close agreement with previous reports in the human calcaneus ^(54–59) as may be seen from Table 4. Differences in BMD measurements with other studies can be observed because clinical BMD measurements are aBMD (g/cm²) ^(60–61) for the whole calcaneus or after dividing the aBMD by the width of the heel^(62–63). However, the vBMD in Chaffai et al.,⁽⁶⁴⁾ and in the present study was measured in a region of interest within the calcaneus and reported per unit volume (g/cm³). The vBMD observed in our samples seem to correspond to osteoporotic bones; nevertheless, since the vBMD value reported in this study was not measured with a DEXA machine, no formal identification between normal, osteopenic, or osteoporotic bone was possible in our samples.

Table 4.

Comparisons of morphology indices, BMD, TMD, ϕ, Tb.N, Tb.Th, Tb.Sp, and DA reported in the human calcaneus, reported as mean±SD.

	BMD g/cm3, * g/cm2	TMD gHA/cm3	ϕ (%)	Tb.Th (µm)	Tb.Sp (µm)	Tb.N (mm−1)	DA
Eckstein et al.(54)	-	-	86.0±4.9	~150	~700	-	~1.75
Hildebrand et al.(55)	-	-	88±3.5	129±18	679±107	1.46±0.20	1.75±0.15
Nicholson et al.(56)	-	-	88	127	684	1.00	1.747
Cortet et al.(57)	-	-	85	119	740	1.29	-
Ulrich et al.(58)	-	-	88.35±3.33	127±17	684±109	1.45±0.20	1.74±0.15
Diederichs et al.(59)	-	-	86±5	140±20	720±130	1.28±0.19	-
Mittra et al.(60)	*0.407±0.160	-	86±5	-	-	-	-
Cheng et al.(62)	*0.709±0.122	-	-	-	-	-	-
Salminen et al.(63)	*0.430±0.090	-	-	-	-	-	-
Majumbdar et al.(61)	*0.132±0.045	-	74±13	170±50	540±200	1.46±0.34	1.94±0.13
Chaffai et al.(64)	0.200±0.072	-	92.8±3.5	72±18	830±230	1.17±0.28	1.56±0.14
Present Study	0.185±0.073	+0.873±0.064 §0.926±0.035 #1.047±0.046	83.2±4.31	162 ±18	487±190	1.04±0.23	1.99±0.29

*areal BMD expressed in g/cm^{2 +}TMD measured from 320 VOI's at 13.5m, and ^§TMD from cylindrical samples (n=6) at 13.5m as well as ^#TMD measured at 3.4µm resolution.

The fabric components are the only architectural parameters with variability within each VOI. In most cases, F₁ almost doubles the value of F₃, and the main direction of F₁ is preferentially aligned to the orientation of trabeculae along the AP direction. Since the three distinct components of the fabric tensor for each region of interest are unequal, we concluded that the cancellous tissue of the calcaneus bone is neither isotropic nor transversely isotropic. As proposed in other studies^(43–44) the cancellous tissue of the calcaneus bone may be considered to be orthotropic. The fact that the fabric eigenvalues were distinct and the three associated fabric eigenvectors were found to be perpendicular in this study means that the cancellous bone investigated was orthotropic. This alignment of the architecture could be due to the external forces applied to bone by ground in the posterior side and by the talus in the anterior side. However, when each of the fabric components is analyzed separately across the different layers and anatomical regions, there is a remarkable consistency in their magnitude and direction. In calculating the principal axis of symmetry in the regions of interest, there is more consistency and less standard deviation in the primary direction of the trabeculae compared to those in the secondary and tertiary directions. A small increase in data variance of the primary orientation of the trabeculae was observed in moving from the inferior towards the superior regions. Also, in regions with large porosity values, the DA and F₁ are smaller, and in lower porosity regions, the DA and F₁ are larger.

Ultrasound wave velocities along three orthogonal directions of the sample were measured in this study. Thus, three different wave velocities were associated with a single value of vBMD for each VOI. In this study, the wavelengths [3.2–3.8mm] generated in bone at 500KHz are smaller than the size of the analyzed samples (7mm) by a factor 2 approximately, which could have an effect on FDTD measured velocities. Importantly, a strong correlation was found between all scalar architectural parameters (porosity, Tb.N, Tb.Th, and Tb.Sp) and vBMD, but no statistical correlation was found between vBMD and the fabric tensor components. This result is in agreement with the low correlation between aBMD and MIL components reported by Newitt et al.,⁽⁶⁵⁾ at the ultradistal wrist, and at the calcaneum by Mittra et al.,⁽⁶⁰⁾. Therefore, only fabric components seem to explain data variance on acoustic anisotropy that cannot be explained by vBMD. This acoustic anisotropy is strongly related to the bone microstructure orientation of trabeculae. Therefore, the correlation between FDTD velocity and poroelastic ultrasound wave velocity is improved when the directional information is considered by the fabric-dependent poroelastic model^(40–41). Previous studies showed that the fabric tensor improves the prediction of the stiffness tensor^{(53, 66)}. While in the present study, all three fabric tensor components were found independent of vBMD, analysis of directional measurements of microarchitecture in the calcaneus reported in Mittra et al⁽⁶⁰⁾ indicates that two MIL components were strongly correlated to BMD. A possible explanation for the differences between these two studies could be i) the scanning resolution, which was approximately 3³=27 times smaller voxels in our study due to the fact that our work was done at a later date with more recent equipment, and ii) the difficulty in keeping the orientation of the two MIL axes that lie on the transverse plane of the circular cylindrical sample consistent during µCT scanning for all samples. In this last case, the value of two MIL components could be averaged out, losing the directional information they contain, and the one MIL component that was found independent of BMD could possibly be the one along the axis of the cylindrical sample and therefore consistent with our result.

Many studies have focused on finding a combination of microarchitectural parameters to best predict functional measurements of bone mechanical properties (i.e. mechanical or ultrasound-derived elasticity and ultimate strength). While it is reasonable to consider that trabecular thickness, number and spacing should indicate the quality of the architecture, these parameters usually fail to significantly improve prediction of bone elastic properties when compared to BMD alone. This could be explained by the fact that most parameters provided by µCT are correlated among them, and they all reflect global changes in mass quantity. We believe that a most appropriate strategy to develop a bone quality assessment approach lies in looking for measurements of microarchitecture that are independent of vBMD, and more importantly, that are direction-dependent, such as the fabric tensor. Directional modulation of mass density by fabric^(40–41) could be defined as an independent measurement of bone quality, helping to better understand changes in bone architecture and to improve the sensitivity and selectivity to distinguish osteoporotic from healthy subjects beyond vBMD.