A Framework for the Comparison of Maximum Pseudo Likelihood and Maximum Likelihood Estimation of Exponential Family Random Graph Models

Abstract

The statistical modeling of social network data is difficult due to the complex dependence structure of the tie variables. Statistical exponential families of distributions provide a flexible way to model such dependence. They enable the statistical characteristics of the network to be encapsulated within an exponential family random graph (ERG) model. For a long time, however, likelihood-based estimation was only feasible for ERG models assuming dyad independence. For more realistic and complex models inference has been based on the pseudo-likelihood. Recent advances in computational methods have made likelihood-based inference practical, and comparison of the different estimators possible.

In this paper, we present methodology to enable estimators of ERG model parameters to be compared. We use this methodology to compare the bias, standard errors, coverage rates and efficiency of maximum likelihood and maximum pseudo-likelihood estimators. We also propose an improved pseudo-likelihood estimation method aimed at reducing bias. The comparison is performed using simulated social network data based on two versions of an empirically realistic network model, the first representing Lazega’s law firm data and the second a modified version with increased transitivity. The framework considers estimation of both the natural and the mean-value parameters.

The results clearly show the superiority of the likelihood-based estimators over those based on pseudo-likelihood, with the bias-reduced pseudo-likelihood out-performing the general pseudo-likelihood. The use of the mean value parameterization provides insight into the differences between the estimators and when these differences will matter in practice.

1 Introduction

Likelihood-based estimation of exponential family random graph (ERG) models is complicated because the likelihood function is difficult to compute for models and networks of reasonable size (e.g., networks with 30 or more actors and models of dyad dependence). Until recently inference for ERG models has been almost exclusively based on a local alternative to the likelihood function referred to as the pseudo-likelihood (Strauss and Ikeda, 1990). This was originally motivated by (and developed for) spatial models by Besag (1975), and extended as an alternative to maximum likelihood estimation for networks (Frank and Strauss, 1986; Strauss and Ikeda, 1990; Frank, 1991) (see also Wasserman and Pattison, 1996; Wasserman and Robins, 2005; Besag, 2000). The computational tractability of the pseudo-likelihood function seemed to make it a tempting alternative to the full likelihood function.

In recent years much progress has been made in likelihood-based inference for ERG models by the application of Markov Chain Monte Carlo (MCMC) algorithms (Geyer and Thompson, 1992; Crouch et al., 1998; Corander et al., 1998, 2002; Handcock, 2002; Snijders, 2002; Hunter and Handcock, 2006). At the same time we have gained a far better understanding of the problem of degeneracy (Snijders, 2002; Handcock, 2003; Snijders et al., 2006; Robins et al., 2007), leading to the development of several software packages for fitting ERG models (Handcock et al., 2003; Boer et al., 2003; Wang et al., 2008).

Since ERG models are within the exponential family class, the properties of their maximum likelihood estimator (MLE) have been studied, although little is available on their application to network models. Not much is known about the behavior of the maximum pseudo-likelihood estimator (MPLE), and how it compares to that of the MLE. Corander et al. (1998) investigate maximum likelihood estimation of a specific type of exponential family random graph model (with the numbers of two-stars and triangles as sufficient statistics) and compare them to the MPLE in two ways. First, they consider small graphs with fixed sufficient statistics and compare the actual MLE (determined by full enumeration), an approximated MLE, and the MPLE, and conclude that the MPLE appears to be biased. They also consider graphs with fixed edge counts generated by a model with known clustering parameter. They estimate this known parameter using the MLE and the MPLE and conclude that outside the unstable region of the MLE, the MPLE is more biased than the MLE with this difference being smaller for larger networks (40–100 nodes). Wasserman and Robins (2005) argue that the MPLE is intrinsically highly dependent on the observed network and, consequently, may result in substantial bias in the parameter estimates for certain networks. In a comparison of the MPLE and the MLE in 20 networks, Robins et al. (2007) find that the MPLE are similar to the MLE for networks with a relatively low dependence structure but can be very different for network data with more dependency.

Lubbers and Snijders (2007) investigated the behavior of the MPLE and the MLE in several specifications of the ERG model. Their work is not a simulation study but can be characterized as a meta analysis of a large number of same gender social networks of adolescents. Although Lubbers and Snijders (2007) conclude that the results obtained are not seriously affected by the estimation method, the behavior of the MPLE and the MLE were quite divergent in many cases. The MPLE algorithm did not always converge, possibly due to infinite estimates, and produced inaccurate standard errors.

Approaches to avoid the problem of ERG model degeneracy and associated estimation problems include the use of new network statistics (Snijders et al., 2006; Hunter and Handcock, 2006) in the ERG model specification. Handcock (2003) proposed mean value parameterization as an alternative to the common natural parameterization to enhance the understanding of the degeneracy problem.

Because the pseudo-likelihood can be expected to misrepresent at least part of the dependence structure of the social network expressed in the likelihood, it is generally assumed that inference based on the pseudo-likelihood is problematic. However, the maximum likelihood-based methods are not privileged in this setting as the asymptotic arguments that bolster them do not apply. The underestimation of standard errors based on the pseudo-likelihood has been a concern (cf. Wasserman and Robins, 2005). Moreover, the MPLE has the undesirable property of sometimes resulting in infinite estimates (manifested by reported estimates that have numerically large magnitude). Handcock (2003) shows that, under certain conditions, if the MPLE is finite, it is also unique. Corander et al. (1998) however, found considerable variability and bias in the MPLE of the effects of the number of 2-stars and the number of triangles in relatively small undirected networks with a fixed number of edges. They also showed that the bias and mean-squared error of the MLE are associated with the size of the parameter values, as is typical for parameter configurations where model degeneracy may become a problem.

For dyad independence models the likelihood and pseudo-likelihood functions coincide (if the pseudo-likelihood function is defined at the dyad-level). The common assumption then is that the estimates will diverge as the dependence among the dyads increases. It may also be expected that differences between the estimators will be smaller for actor (or dyadic) covariate effects than for structural network effects, such as the number of transitive triads, representing the dependency in the network. Moreover, if the dependence in the network is relatively low, the MPLE may be a reasonable estimate. In analyses of social network data with many possible (actor) covariates, the easily and quickly obtained MPLE may provide a good starting point for further analyses with selected covariates.

The two main goals of the paper are to present a framework to evaluate estimators of ERG model parameters, and to present a case-study comparing traditionally important estimators in this context.

The framework allows researchers to evaluate the properties of estimators for the network models most relevant to their specific applications. It also allows different estimators to be compared against each other.

The case-study has the goal of deepening our understanding of the relative performance of the MLE and the two pseudo-likelihoods estimators for fitting exponential family random graph models to social network data. We do this by presenting a detailed study in one specific case, and thereby illustrating a framework for comparison which could be used in future studies. The novelty of this approach is that it combines the realism of a complex model known to represent a real-world data set with the systematic investigation of a simulation study. Unlike an empirical study, this approach allows us to compare properties of the estimators in a setting where the true values generating the data are known. Unlike a simulation study, it allows us to treat a known realistic model. As part of our detailed study, we include a systematic comparison of the natural parameter estimates as well as the mean value parameter estimates. The mean value parameterization is helpful in comparing and understanding the differences between the MLE and the pseudo-likelihood methods in terms of the observed network statistics.

We also address three secondary goals. First, we propose and analyze the properties of a modified MPLE designed to reduce bias in generalized linear models (Firth, 1993). Although Firth’s approach is motivated heuristically here, we find it produces smaller bias than the MPLE, resulting in greater efficiency with respect to the MLE, especially in the mean value parameterization.

Second, we deepen our comparison of the estimators by repeating the primary study on a model with increased transitivity. The comparison of the two versions provides insight into the relationship between the degree of transitivity and the relative performance of the estimators. Note that our focus on transitivity is motivated by the particular form of dependence evident in our empirical data. Other applications may require different statistics to capture the dependence adequately.

Finally, we provide high-level software tools to implement the framework in the paper. The software is based on the statnet (Handcock et al., 2003) suite of packages in the R statistical language (R Development Core Team, 2007). We provide the code for the case-study as part of the supplementary materials.

2 Exponential Family Random Graph Models

Let the random matrix Y represent the adjacency matrix of an unvalued network on n individuals. We assume that the diagonal elements of Y are 0 –that self-partnerships are disallowed. Suppose that 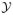denotes the set of all possible networks on the given n individuals. The multivariate distribution of Y can be parameterized in the form:

$$P_{\eta ,\mathcal{Y}}(Y=y)=\frac{exp\left[{\eta }^{T}Z(y)\right]}{c(\eta ,\mathcal{Y})}y\in \mathcal{Y}$$ (1)

where η ∈ ℝ^q is the model parameter and Z: 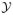→ ℝ^q are statistics based on the adjacency matrix (Frank and Strauss, 1986; Wasserman and Pattison, 1996; Handcock, 2002).

This model is an exponential family of distributions with natural parameter η and sufficient statistics Z(Y). There is an extensive literature on descriptive statistics for networks (Wasserman and Faust, 1994; Borgatti et al., 1999). These statistics are often crafted to capture features of the network (e.g., centrality, mutuality and betweenness) of primary substantive interest to the researcher. In many situations the researcher has specified a set of statistics based on substantive theoretical considerations. The above model then has the property of maximizing the entropy within the family of all distributions with given expectation of Z(Y) (Barndorff-Nielsen, 1978). Paired with the flexibility of the choice of Z this property provides some justification for the model (1) that will vary from application to application. The choice of Z, however, is by no means arbitrary, because the thus assumed dependence structure of the network is related to the possible outcomes of Y under the model. The Markov assumption made by Frank and Strauss (1986), where dyads which do not share an individual are conditionally independent, is elegant but often too simple. The more elaborate dependence of Robins and Pattison (2005) and Snijders et al. (2006) and the recent developments in MCMC estimation (Snijders, 2002; Snijders et al., 2006) have revealed the importance of choosing appropriate statistics to represent network dependency structure.

The denominator c(η, 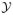) is the normalizing function that ensures the distribution sums to one: $c(\eta ,\mathcal{Y})={\displaystyle \sum _{y\in \mathcal{Y}}}exp\left[{\eta }^{T}Z(y)\right]$. This factor varies with both η and the support 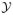and is the primary barrier to simulation and inference under this modeling scheme.

ERG models have usually been expressed in their natural parameterization η. Here we also consider the alternative mean value parameterization for the model based on the 1 – 1 mapping: μ: ℝ^q → C defined by

$$\mu (\eta )={\mathbb{E}}_{\eta }[Z(Y)]$$ (2)

where C is the relative interior of the convex hull of the sample space of Z(Y). The mapping is strictly increasing in the sense that

$${({\eta }_a-{\eta }_b)}^T(\mu ({\eta }_a)-\mu ({\eta }_b))\ge 0$$ (3)

with equality only if P_ηa, 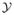(Y = y) = P_ηb, 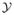(Y = y) ∀y. It is also injective in the sense that

$$\mu ({\eta }_a)=\mu ({\eta }_b)\to P_{{\eta }_a,\mathcal{Y}}(Y=y)=P_{{\eta }_b,\mathcal{Y}}(Y=y)\forall y.$$ (4)

For each natural parameter for the model (1) there is a unique mean-value parameter corresponding to that model (and vice versa). In practical terms the value μ( η) can be computed by the average of Z(Y) for graphs Y simulated from the model with natural parameter η. The inverse mapping η(μ) can be solved by numerically inverting the process (Geyer and Thompson, 1992).

In the mean value parameterization, the natural parameter η is replaced by parameter μ(η), which corresponds to the expected value of the sufficient statistic Z(Y ) under the model with natural parameter η (Barndorff-Nielsen, 1978).

One advantage of the mean value parameterization is that from the researcher’s perspective it is actually more “natural” than the η parameterization because it is defined on the scale of network statistics. This means that the MLE parameter estimates coincide with the value of the observed corresponding network statistics. Thus, a certain model specification can be evaluated immediately by its capacity to reproduce the observed network statistics. See Handcock (2003) for details.

2.1 Illustration for the Erdős-Rényi Model

In this subsection the difference between the natural and mean value parameterizations is illustrated for the Bernoulli distribution, as used in the simple homogeneous ERG model with independent arcs.

A directed Erdős-Rényi network is generated by an ERG model for n actors with one model term capturing the density D of arcs,

$$P_{\eta ,\mathcal{Y}}(Y=y)=\frac{exp(\eta D(y))}{c(\eta ,\mathcal{Y})}$$

with $D(y)=\frac{1}{N}{\sum }_{i\ne j}{y}_{ij}$. and N = n(n − 1), the number of possible ties in the social network. It is also referred to as the homogeneous Bernoulli model.

In this case, the normalizing constant is

$$c(\eta ,\mathcal{Y})=\sum _{s=0}^N\left(\begin{array}{c}N\\ s\end{array}\right)exp(\eta s/N)={(1+exp(\eta /N))}^N$$

The mean value parameterization for the model is:

$$\mu \equiv \mu (\eta )=E_n(D(y))=\frac{exp(\eta )}{1+exp(\eta )},$$

representing the probability that a tie exists from a given actor to another given actor. It follows that

$$\eta =log(\frac{\mu }{1-\mu }),$$

is the (common) log-odds that a given directed pair have a tie. So, for the Erdős-Rényi model, we find that the natural parameter η is a simple function of the mean value parameter, and vice versa.

The gradient or rate of change in η as a function of μ is [μ(1 − μ)]⁻¹, which is unbounded as the probability approaches 0 or 1. The rate of change in μ as function of η is equal to exp(η)/(1 + exp(η))² which can be re-expressed as μ(1 − μ), the variance of the number of arcs under the binomial distribution with constant tie probability μ. Thus, the rate of change in the mean value parameterization is bounded between zero and one-quarter and is a (quadratic) function of the network density.

Although it is only in special cases that such a clear relation between the natural and mean value parameterization exists, it can be helpful in understanding the differences between them.

For any given model, both parameterizations can be considered simultaneously. The issues raised by each are similar to those raised by the choice of parameterization for log-linear analysis: log-linear versus marginal parameterizations. See Agresti (2002), section 11.2.5 for details.

It is worth emphasizing that the relationship between natural and mean value parameterizations is a function of the model itself, not the estimation procedure. Therefore, the same mapping applies to all three estimation procedures considered in this paper.

2.2 Inference for Exponential Family Random Graph Models

As we have specified the full joint distribution of the network through (1), it is natural to conduct inference within the likelihood framework (Besag, 1975; Geyer and Thompson, 1992). Differentiating the loglikelihood function:

$$\ell (\eta ;y)\equiv log[P_{\eta ,\mathcal{Y}}(Y=y)]={\eta }^{T}Z(y)-log[c(\eta ,\mathcal{Y})]$$ (5)

shows that the maximum likelihood estimate η̂ satisfies

$$Z(y_{\text{obs}})={\mathbb{E}}_{\widehat{\eta }}Z(Y),$$ (6)

where Z(y_obs) is the observed network statistic. This also indicates that the maximum likelihood estimate of the mean-value parameter μ̂ ≡ μ( η̂) satisfies

$$\widehat{\mu }=Z(y_{\text{obs}}),$$ (7)

a result familiar from the binomial and normal distributions.

As can be seen from (5), direct calculation of the log-likelihood by enumerating 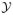is infeasible for all but the smallest networks. As an alternative, we can approximate the likelihood equations (6) by replacing the expectations by (weighted) averages over a sample of networks generated from a known distribution (typically the MLE or an approximation to it). This procedure is described in Geyer and Thompson (1992). To generate the sample we use a MCMC algorithm (Geyer and Thompson, 1992; Snijders, 2002; Handcock, 2002).

Computationally, inference under the mean value parameterization is similar to inference under the natural parameterization. While the point estimator is trivial (see (7)), obtaining high quality measures of uncertainty of the estimator appears to require a MCMC procedure. Explicitly, from (7),

$${\mathbb{V}}_{\eta }[\widehat{\mu }]={\mathbb{V}}_{\eta }[Z(Y)],$$ (8)

so the covariance of μ̂ can be estimated by a (weighted) variance over a sample of networks generated from a known distribution (typically, the MLE). This requires the MLE of the natural parameter to be known. Hence the same MCMC sample used to estimate η̂ via the Geyer-Thompson procedure can be used to estimate the covariance of μ̂. The two procedures are closely related and of about the same computational complexity. This relationship is familiar for the binomial distribution (thought of as an exponential family) where the natural parameter is the log-odds of a success, the mean-value parameter is the expected number of successes, the mean-value MLE is the observed number of successes and the variance of the mean-value MLE can be estimated by plugging in the mean-value MLE for the mean-value parameter in the known formula of the variance of the observed data.

Until recently inference for the model (1) has been almost exclusively based on a local alternative to the likelihood function referred to as the pseudo-likelihood (Besag, 1975; Strauss and Ikeda, 1990). Consider the conditional formulation of the model (1):

$$\text{logit}[P_{\eta ,\mathcal{Y}}(Y_{ij}=1\mid Y_{ij}^c=y_{ij}^c)]={\eta }^T\delta (y_{ij}^c)y\in \mathcal{Y}$$ (9)

where $\delta (y_{ij}^c)=Z(y_{ij}^{+})-Z(y_{ij}^{-})$, the change in Z (y) when y_ij changes from 0 to 1 while the remainder of the network remains $y_{ij}^c$ (See Strauss and Ikeda, 1990). The pseudo-likelihood for the model (1) is:

$${\ell }_P(\eta ;y)\equiv {\eta }^T\sum _{ij}\delta (y_{ij}^c)y_{ij}-\sum _{ij}log\left[1+exp({\eta }^T\delta (y_{ij}^c))\right].$$ (10)

This form is algebraically identical to the likelihood for a logistic regression model where each unique element of the adjacency matrix, y_ij, is treated as an independent observation with the corresponding row of the design matrix given by $\delta (y_{ij}^c)$. Then the MLE for this logistic regression model is identical to the MPLE for the corresponding ERG model, a fact that is exploited in computation. Therefore, algorithms to compute the MPLE for ERG models are typically deterministic while the algorithms to compute their MLEs are typically stochastic. In addition, algorithms to compute the MLE can be unstable if the model is near degenerate. This can lead to computational failure. Practitioners are attracted to the speed and determinism of the MPLE and the statistical superiority of the MLE needs to be justified.

In the simplest class of ERG models, in which each edge is assumed independent of every other edge, the likelihood for the ERG model, given in (1) reduces to the form given by (10), and the MLE and the MPLE are identical. In more complicated and realistic models involving dependence between edges, however, this dependence is ignored in the MPLE approximation. For this reason, estimates and standard errors derived from the MPLE are suspect. Although its statistical properties for social networks are poorly understood, the MPLE has been in common usage. While the more sophisticated packages currently use the MLE (Handcock et al., 2003; Boer et al., 2003; Wang et al., 2008) the MPLE has had strong historical usage and continues to be advocated (Saul and Filkov, 2007).

In addition, we propose an alternative pseudo-likelihood estimator. This method was originally proposed by Firth (1993) as a general approach to reducing the asymptotic bias of maximum likelihood estimates by penalizing the likelihood function. The penalized pseudo-likelihood for the model (1) is then defined as:

$${\ell }_{BP}(\eta ;y)\equiv {\ell }_P(\eta ;y)+\frac{1}{2}log\mid I(\eta )\mid$$ (11)

where I(η) denotes the expected Fisher information matrix for the formal logistic model underlying the pseudo-likelihood evaluated at η. We refer to the estimator that maximizes ℓ_BP (η; y_obs) as the maximum bias-corrected pseudo-likelihood estimator (MBLE). Heinze and Schemper (2002) showed that Firth’s method is particularly useful in rare-events logistic regression where infinite parameter estimates may result because of so called (quasi-) separation, the situation where successes and failures are perfectly separated by one covariate or by a linear combination of covariates. Handcock (2003) identifies a similar phenomenon in ERG models. He finds computational degeneracy resulting from observed sample statistics near the boundary of the convex hull. We propose the MBLE here in hopes that its performance advantage near the boundary of the sample space in logistic regression will be retained in the ERG model setting. We note that this motivation for the MBLE is heuristic and any bias-correction properties need to be empirically ascertained.

3 Study design

3.1 Framework and Goals

We aim to consider many characteristics of the procedures in depth for a specific model, rather than directly compare the point estimates over many data sets. While the latter approach has value, as demonstrated by Lubbers and Snijders (2007), fixing on a model used to represent a realistic data set enables the study to focus on the many characteristics of the procedures themselves (rather than just their point estimates). This limits the generalizability of this study in terms of range of models, but increases the generalizability in terms of the range of characteristics of the procedures.

The general structure of the simulation study is as follows:

• Begin with the MLE model fit of interest for a given network.

• Simulate networks from this model fit.

• Fit the model to each sampled network using each method under comparison.

• Evaluate the performance of each estimation procedure in recovering the known true parameter values, along with appropriate measures of uncertainty.

The main interest of this simulation study is to compare the performance of the maximum likelihood (MLE), maximum pseudo-likelihood (MPLE), and maximum pseudo-likelihood with Firth’s bias-correction penalty (MBLE) estimators. There are two key features of this comparison: the accuracy of point estimation, and the accuracy of estimators of uncertainty.

The accuracy of point estimation is compared using relative efficiency, computed as the ratio of mean squared errors. Because the true parameters of the generating model are known for both parameterizations, the computation of mean squared errors is straight forward. The MLE is then treated as the reference and the relative efficiency of a pseudo-likelihood estimate is computed as the ratio of its mean squared error to that of the MLE. This is done separately for each parameter, and under both parameterizations.

For each estimator, a standard error estimate is derived from the estimated curvature of the corresponding log-likelihood or log-pseudo-likelihood ((5), (10), and (11)). We refer to these as “perceived” standard errors because these are the values formally derived as the standard approximations to the true standard errors from asymptotic arguments that have not been justified for these models. These are the values typically provided by standard software (Handcock et al., 2003; Boer et al., 2003; Wang et al., 2008). Similarly, perceived confidence intervals are computed using the perceived standard error estimates and assuming a t-distribution with 35 × 36 × 0.5 − 7 = 623 degrees of freedom. In the natural parameter space, these intervals correspond to the standard Wald-based significance tests for each parameter. Throughout we will specify a nominal coverage of 95%.

The accuracy of estimators of uncertainty is assessed by comparing the actual coverage rates of perceived confidence intervals to their nominal coverage.

3.2 Technical Considerations

The sampling distributions of the estimators include infinite values if the graph space 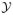includes networks on the boundary of the convex hull C. Hence we focus on the sampling distributions conditional on the observed network being on the interior of the convex hull. In this case the bias and MSE of the natural parameter estimates are finite (Barndorff-Nielsen, 1978). The conditional sampling distributions are chosen to reflect the fact that practitioners faced with infinite parameter estimates will treat the inference distinctly from analysis with finite estimates: the de facto practice effectively focuses on the conditional sample space.

The mean value parameters are a function of the natural parameters. Their values are estimated by simulating networks from the natural parameter estimates and computing the mean sufficient statistics over those samples. For the MLE this is just the known parameter value. The bias of each procedure is the difference between the mean parameter estimate over samples and the true parameter values from which the networks were sampled. Similarly, the standard deviation of each procedure is simply the standard deviation of the parameter values over all samples. The mean squared error, used to compute relative efficiency, is the mean of the squared difference between the parameter estimates and the true parameters.

Based on the geometry of the likelihood of the exponential family models, the covariance of the mean value parameter estimates can also be computed as the inverse of the covariance of the natural parameters estimates (Barndorff-Nielsen, 1978). The perceived confidence intervals are then computed assuming a t-distribution with 623 degrees of freedom. The bias and MSE of mean-value parameter estimates are always finite, but for comparability we use the sampling distribution conditional on the observed network being on the interior of the convex hull. (The results are robust to this choice).

3.3 Case Study Original Model

The Lazega (2001) undirected collaboration network of 36 law firm partners is used as the basis for the study. The first step is to consider a well fitting model for the data. We focus on one with seven parameters. Typical for the ERG model are the structural parameters, related to network statistics, here the number of edges (essentially the density) and the geometrically weighted edgewise shared partner statistic (denoted by GWESP), a measure of the transitivity structure in the network. Two nodal attributes are used: seniority (ranknumber/36) and practice (corporate or litigation). Three dyadic homophily attributes are used: practice, gender (3 of the 36 lawyers are female) and office (3 different locations of different size). This is Model 2 in Hunter and Handcock (2006). The model has been slightly reparameterized by replacing the alternating k-triangle term with the GWESP statistic. The scale parameter for the GWESP term was fixed at its MLE (0.7781), (see Hunter and Handcock, 2006, for details). A summary of the MLE parameters used is given in the first numerical column of Table 1. Note that we are taking these parameters as “truth” and considering networks produced by this model.

Table 1.

Natural and mean value model parameters for Original model for Lazega data, and for model with increased transitivity.

Parameter	Natural Parameterization		Mean Value Parameterization
	Original	Increased Transitivity	Original	Increased Transitivity
Structural
edges	−6.506	−6.962	115.00	115.00
GWESP	0.897	1.210	190.31	203.79
Nodal
seniority	0.853	0.779	130.19	130.19
practice	0.410	0.346	129.00	129.00
Homophily
practice	0.759	0.756	72.00	72.00
gender	0.702	0.662	99.00	99.00
office	1.145	1.081	85.00	85.00

3.4 Procedure

In the second step 1000 networks are simulated from this choice of the parameters. For these networks, the MLE, the MPLE and the MBLE are obtained using statnet (Handcock et al., 2003), both for the natural parameterization and for the mean value parameterization (see Handcock, 2003). One sampled network has observed statistics residing on the edge of the convex hull of the sample space. This network is computationally degenerate in the sense of Handcock (2003). For such networks the natural parameter MLEs and MPLEs are known to be infinite and, as noted above, their values were not included in the numerical summaries.

To investigate the change in relative performance with higher transitivity, another set of networks with higher transitivity is considered. Transitivity is conceptualized in terms of the observed GWESP statistic, as compared to its expected value in the dyad independent graph with a GWESP natural parameter of 0. The original network has GWESP statistic 190.3. The MLE of the mean-value parameter for GWESP for the model with the natural parameter of GWESP fixed at zero is 136.4. (This can be computed simply by fitting the model to the network omitting the GWESP and computing the mean GWESP for networks generated from that model). Thus the observed network has increased transitivity by 53.9 units of GWESP above what is expected for a random network with the same mean-values for the other terms. From this perspective, increasing transitivity by 100×α percent can be represented by a model with mean value GWESP parameter 190.3+α53.9 with the mean value parameters of the other terms unchanged. The natural and mean value parameters corresponding to this increased transitivity model are also displayed in Table 1.

Increasing the transitivity in the network also increases the problem of degeneracy. Doubling the transitivity (α = 1), and even adding half of the transitivity (α = .5) both result in degenerate models with an unacceptable proportion of probability mass on very high density and very low density graphs. Therefore, the higher transitivity model considered adds one quarter of the transitivity in the original (α = .25). An additional 1000 networks are sampled from this model, and fit with each of the three methods considered. In this case, two sampled networks were computationally degenerate and were not included in the numerical summaries due to infinite MLEs and MPLEs.

4 Results

4.1 Relative Efficiency of Estimators

The relative efficiency of each set of estimators is presented in Table 2. For each parameter, the MLE is treated as the reference category, and the efficiency is calculated as the ratio of mean-squared errors. Relative efficiencies are computed separately for each parameter and estimation method, in both the natural and mean value parameterizations.

Table 2.

Relative efficiency of the MPLE, and the MBLE with respect to the MLE

	Natural Parameterization						Mean Value Parameterization
	Original			Increased Transitivity			Original			Increased Transitivity
Parameter	MLE	MPLE	MBLE	MLE	MPLE	MBLE	MLE	MPLE	MBLE	MLE	MPLE	MBLE
Structural
edges	1	0.80	0.94	1	0.66	0.80	1	0.21	0.29	1	0.15	0.20
GWESP	1	0.64	0.68	1	0.50	0.55	1	0.28	0.37	1	0.19	0.24
Nodal
seniority	1	0.87	0.92	1	0.78	0.83	1	0.22	0.30	1	0.17	0.22
practice	1	0.91	0.96	1	0.72	0.77	1	0.19	0.27	1	0.12	0.16
Homophily
practice	1	0.91	0.96	1	0.94	1.01	1	0.23	0.32	1	0.15	0.19
gender	1	0.81	0.91	1	0.78	0.86	1	0.23	0.31	1	0.17	0.22
office	1	0.92	1.00	1	0.79	0.87	1	0.23	0.32	1	0.15	0.20

The MLE is substantially more efficient than the MPLE or the MBLE.

For nearly every term in either parameterizations and both models, the MLE has lower mean squared error than the MPLE or the MBLE. (In the only three exceptions to this pattern, the MLE and MBLE have nearly identical mean-squared error.) Furthermore, the MBLE out-performs the MPLE for every parameter estimate of both models in both parameterizations. The best pseudo-likelihood relative performance is exhibited by the MBLE in the natural parameterization of the original model, with relative efficiencies above 0.9 for all terms except the GWESP term. In the natural parameterization, the relative performance of the pseudo-likelihood methods is weakest for the GWESP term, with relative efficiencies of 0.64 and 0.68 for the MPLE and the MBLE in the original model, and 0.50 and 0.55 in the increased transitivity model. The natural parameterization pseudo-likelihood relative performance is also weaker in the increased transitivity model for the edges and nodal effect terms, although there is no consistent pattern of performance across models for the homophily terms.

In the mean value parameterization, the relative efficiency of the pseudo-likelihood methods is far less than in the natural parameterization. The best pseudo-likelihood performance here is again attained by the MBLE, which continues to out-perform the MPLE, and in the original model, which is again fitted by pseudo-likelihood with greater relative efficiency than the increased transitivity model. In this case, the best efficiency is only 37%, this time for the GWESP term. The other relative efficiencies for the MBLE of the mean value parameterization of the original model hoover around 30%. The MPLE fares worse with relative efficiencies closer to 20%. In the increased transitivity model, the MBLE drops to around 20%, while the MPLE drops below 20%.

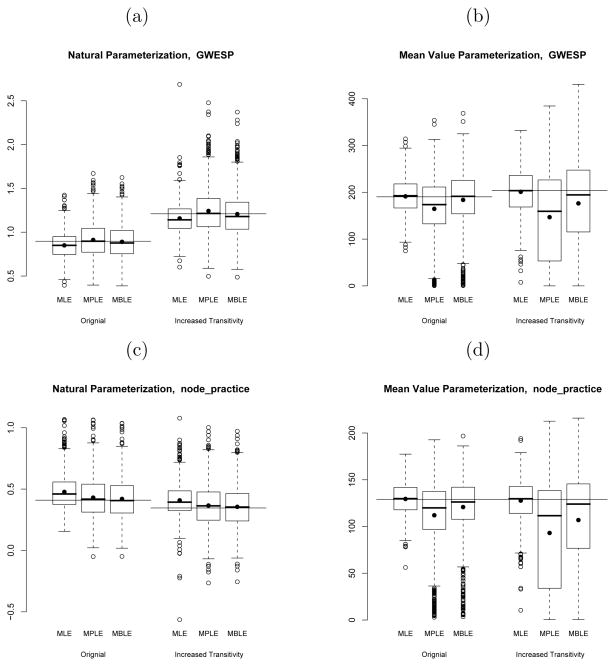
These results are illuminated by additional information on the distributions of estimators. We provide this information in boxplots of the estimators for several key model parameters (see Figure 1). These are arranged for ease of comparison as follows:

Fig. 1.

Boxplots of the distribution of the MLE, the MPLE and the MBLE of the geometrically weighted edgewise shared partner statistic (GWESP), differential activity by practice statistic (node practice), and homophily on practice statistic (homoph practice) under the natural and mean value parameterization for 1000 samples of the original Lazega network and 1000 samples of the Lazega network with increased transitivity

• For each parameter, natural parameter estimates are shown on the left sub-figure, and mean-value parameters on the right sub-figure.

• Each box is labeled according to the estimation method: MLE, MPLE, or MBLE.

• In each subfigure, the three distributions corresponding to the original model are presented together, followed by the three distributions corresponding to the model with increased transitivity.

• The horizontal line through each section represents the true parameter value. Note that these values are different for the natural parameters of the original and increased transitivity models, as well as for the mean value parameter of the GWESP term.

• The boxplots give the quartiles and tails of each estimator distribution. The dots correspond to the means of those distributions.

For reasons of space, boxplots are only included for three of the model parameters: GWESP, differential activity by practice, and homophily on practice. These are chosen to represent the three main classes of parameters in the model: structural, nodal, and homophily. The results for other model parameters are similar to the examples presented from their respective classes.

The ML estimators display the largest bias among the natural parameter estimates, but with much smaller variance, as exemplified in particular by Figures 1(a) and 1(c). The exception to this pattern is displayed in the plot 1(e) for the term representing homophily on practice. In this case, the variance of the MLE is comparable to that of the MBLE, while the MLE still retains more bias, resulting in slightly greater efficiency of the MBLE.

Although it is difficult to discern from these plots, the MBLE exhibits less bias than the MPLE for most parameters. The MBLE also generally exhibits slightly lower variance than the MPLE, resulting in the superior overall efficiency of the MBLE.

The MLE is biased in the natural parameter space because by construction it is unbiased in the space of mean value parameters. Figures 1(b), 1(d), 1(f) demonstrate that with negligible bias and substantially smaller variance, the MLE clearly out-performs the pseudo-likelihood methods in the mean value parameter space.

There is a pronounced left skew to the mean value parameter estimates for the pseudo-likelihood methods. The bivariate scatter plots in Figure 2 suggest that it is this set of samples with very low mean value parameter estimates that account for much of the bias, and therefore efficiency loss of the pseudo-likelihood methods. The MBLE performs better than the MPLE because its estimates are less skewed than those of the MPLE.

Fig. 2.

Comparison of error in mean value parameter estimates for edges in original (top) and increased transitivity (bottom) models.

4.2 Coverage Rates of Nominal 95% Confidence Intervals

Table 3 presents the observed coverage rates of nominal 95% confidence intervals based on the perceived standard errors and t-approximation.

Table 3.

Coverage rates of nominal 95% confidence intervals for the MLE, the MPLE, and the MBLE of model parameters for original and increased transitivity models. Nominal confidence intervals are based on the estimated curvature of the model and the t distribution approximation.

	Natural Parameterization						Mean Value Parameterization
	Original			Increased Transitivity			Original			Increased Transitivity
Parameter	MLE	MPLE	MBLE	MLE	MPLE	MBLE	MLE	MPLE	MBLE	MLE	MPLE	MBLE
Structural
edges	94.9	97.5	98.0	96.4	98.2	98.2	93.1	44.9	49.4	85.5	23.8	28.5
GWESP	92.7	74.6	74.1	94.2	78.8	77.6	91.4	56.7	62.7	85.9	31.3	36.6
Nodal
seniority	94.4	97.8	98.0	95.4	98.4	98.7	91.6	45.5	49.0	84.4	22.8	27.6
practice	94.0	98.1	98.6	95.5	98.4	98.8	93.2	51.0	57.9	89.9	35.9	39.3
Homophily
practice	94.8	98.1	98.1	94.6	97.9	98.0	92.6	52.0	57.1	89.7	31.1	37.3
gender	95.8	98.7	98.8	95.3	98.1	98.8	92.0	46.5	51.6	84.8	22.7	28.5
office	94.2	98.1	98.4	95.1	98.2	98.4	92.5	50.2	54.4	87.8	27.0	32.3

In the natural parameterization, the perceived confidence intervals perform well for the MLE, with coverage rates quite close to the nominal 95% for both the original and increased transitivity models. Both pseudo-likelihood methods perform less well, with coverage rates which are too high for all parameters except the GWESP term, whose coverage percentage is too small. The GWESP coverage rates are less than 75% and 79%, for the nominal 95% intervals for the original and increased transitivity models respectively. The coverage rates for the other terms are all 97.5% or above, again for nominal 95% intervals. Both the MPLE and the MBLE have higher natural parameter coverage rates for the model with increased dependence, which is detrimental to the performance of the already-too-high coverage rates for most terms, and slightly improves the performance of the too high coverage rates for the GWESP term. This suggests that the pseudo-likelihood-based standard error estimates for the structural transitivity term are underestimated while they are overestimated for the nodal and dyadic attribute terms.

In the mean value parameterization, again, the coverage rates for the MLE are far closer to the nominal 95% than either of the pseudo-likelihood methods. In this parameterization, all the coverage rates are low. The MLEs of the original parameters achieve the best performance, with coverage rates as high as 93.2% for the nodal effect of practice, and dipping only as low as 91.4% for the GWESP term. In the increased transitivity model, the MLE coverage rates are substantially lower, ranging from 89.9% for the nodal practice term to 84.4% for the nodal seniority term.

Although these rates are quite low, the mean-value parameterization coverage-rate performance of the MLE is remarkably superior to that of the pseudo-likelihood methods. The highest coverage rate recovered by these methods is 62.7%, for the MBLE estimate of the GWESP parameter in the original model, for a nominal 95% interval. The MBLE coverage rates are all higher than, and therefore out-perform those of the MPLE, with coverage ranging from 49.0% to 62.7% for the original model, and 28.5% to 39.3% for the increased transitivity model, as compared to the original model range of 44.9% to 56.7% and increased transitivity model range 22.7% to 35.9% for the MPLE. Comparison of the standard deviations of the sampling distributions to the perceived standard errors reveals that the latter are far too small for the pseudo-likelihood methods, at around one-third of the sampling standard deviations.

5 Discussion

We have presented a framework to assess estimators for ERG models. This framework has the following key features:

• The use of the mean-value parametrization space as an alternate metric space to assess model fit.

• The adaptation of a simulation study to the specific circumstances of interest to the researcher: e.g. network size, composition, dependency structure.

• It assesses the efficiency of point estimation via mean-squared error in the different parameter spaces.

• It assesses the performance of measures of uncertainty and hypothesis testing via actual and nominal interval coverage rates.

• It provides methodology to modify the dependence structure of a model in a known way, for example, changing one aspect while holding the other aspects fixed.

• It enables the assessment of performance of estimators to be to alternative specifications of the underlying model.

The second contribution is a case study comparing the quality of maximum likelihood and two maximum pseudo-likelihood estimators. This supports the superior performance of maximum likelihood estimation over maximum pseudo-likelihood estimation on a number of measures, for structural and covariate effects.

In a dyad independent model, such as the one in this study with the GWESP parameter removed, the MLE and the MPLE would be identical, while the MBLE would be a slight modification of these to reduce the bias of the natural parameter estimates. In the full dyad dependent model considered here, the MLE is able to appropriately accommodate the dependence induced by the transitivity term, while the MPLE and the MBLE can only approximate the transitivity pattern. Therefore, it is not surprising that in the natural parameterization, the MLE out-performs the pseudo-likelihood methods to the greatest degree in the estimation of the GWESP parameter, in terms of both efficiency and coverage rates. The inferior performance of the MPLE and the MBLE natural parameters for the nodal and dyadic attribute terms results from the dependence between the GWESP estimates and the estimates for other model terms. Greater variability in the GWESP results in greater variability in other parameters. This uncertainty also leads to inflated variance estimates for the other parameters, contributing to inflated coverage rates of nominal confidence intervals. Meanwhile, the GWESP perceived standard errors are underestimated, resulting in too low coverage rates. Therefore, the notion that inference based on the pseudo-likelihood is problematic are supported. In this case, pseudo-likelihood based tests for the structural parameters tend to be liberal, and for the nodal and dyadic attributes conservative. A similar pattern appears to hold for the Lubbers and Snijders (2007) study (see their Figure 2).

As a transformation of the full set of natural parameters, the mean value parameterization is even more conducive to uncertainty in the natural parameter for the transitivity term decreasing performance on all terms. In addition, the MLE is constructed to be unbiased in the mean value parameters. Together, these two effects contribute to the drastically superior performance of the MLE on the mean value scale. The pseudo-likelihood methods show about three times the mean squared error of the MLE, and the perceived coverage rates of nominal 95% confidence intervals hover around 50%. In the model with increased transitivity, these effects are even stronger, with relative efficiency below .25 and coverage rates below 40%.

The MBLE is constructed to correct for the bias of the MPLE on the natural parameter scale. It does, in fact, show the smallest bias for the natural parameter estimates. In the case of the practice homophily term, this correction is helpful enough to give the MBLE a mean squared error at least as good as that of the MLE.

Although the main focus of this case study is the comparison of the MLE to the pseudo-likelihood methods, it is worth noting that the MBLE consistently out-performs the MPLE in these analyses. The original intent of the method was to reduce the bias of the natural parameter estimates, and it is successful here. However the MBLE also reduces the bias of the mean value parameter estimates relative to the MPLE. Intuitively this is because of the large bias in the mean value parameterizations of the MPLE, and the impact of the penalty term jointly on all parameters.

As an illustration, in Figure 2 the MLE, the MPLE and the MBLE mean values for the edges are plotted (in deviation from the number of edges in the original network), for the networks sampled using the parameter estimates obtained for the original network (top two panels) and for the sampled networks with increased transitivity (the two panels at the bottom). Given that the MLE is unbiased (apart from sampling error), the top left panel demonstrates that although the MPLE and MLE are close for many sampled networks, the MPLE underestimates the edge parameter for many other networks, and that it has a larger variance than the MLE with a far less symmetric distribution. The line in the panel indicates the 75% density region, around the line of equality. The remaining points seem to clutter at the bottom of the panel, indicating that the MPLE may result in networks with (extremely) low edges, for non-extreme MLE values. From the top right panel, where the MPLE is plotted against the MBLE, it is clear that the bias correction of the MBLE corrects for some, but not all, of this underestimation. Most of the correction occurs for networks with (extremely) low edge MPLE. The degree of underestimation and of correction are greater in the increased transitivity model, shown in the bottom two panels. The density lines in the left panel show a substantively larger cluttering of extremely low MPLE edge parameters. Plots for the MBLE vs. the MLE (not shown) are very similar to those for the MPLE vs. the MLE.

The case study results are slightly conservative in favor of the MPLE and the MBLE as the MLE results include the additional computational uncertainty of the MCMC algorithm to estimate the MLE. In the case of the bias of mean value parameter MLEs, which are known to be 0, computational biases are intentionally left in place to represent the performance of the estimators as they might be used in practice. The one deviation from this principle is the exclusion of three “degenerate” sample networks (with observed sufficient statistics at the edges of their possible range), one from the original model and two from the increased transitivity model, from the final analysis.

It is worthwhile noting that computational complexity provides another potential difference between pseudo and maximum likelihood estimation. In fact, this is one reason the MPLE has been used for so long. Recent advances in computing power and in algorithms has made the MLE a feasible alternative for most applications (Geyer and Thompson, 1992; Snijders, 2002; Hunter and Handcock, 2006). More details about computing time and other computational aspects can be found in the Appendix.

To further investigate differences in the effect of the estimation method on structural and covariate parameters, it would have been good to study a simple triangle model (as Corander et al., 1998, 2002). Unfortunately, this model is degenerate for the Lazega data, providing further evidence that the triangle model may often be too crude to be useful in realistic settings. Corander et al. (1998, 2002) avoid the problem of degeneracy by considering only graphs with a fixed number of edges. The GWESP term has a similar motivation and fits well on the same data. In future research using this framework, a similar comparison could be based on any other measure of dependence.

We have used standard error estimates from the inverse of the Hessian to compute confidence intervals and coverage rates. We take this approach because these standard error estimates are often used to compute Wald-type confidence intervals and for testing purposes. It is important to remember, however, that we have no asymptotic justification for this approach for models with structural transitivity. It might well be the case that this approach leads to worse results in networks with increased transitivity, as was found in underestimated perceived standard errors for all mean value parameters. Lack of normality could be another (partial) explanation, in view of the deteriorated coverage rates.

Note that exact testing is an alternative to the Wald approximation (Besag, 2000). To determine an exact p–value for a coefficient, for example, simulate from the model conditional on the observed values of the statistics in the model and omitting the target statistic. The p–value is then based on the quantile of the observed target statistic among those from the sampled networks. While this approach is feasible, it is usually prohibitively expensive computationally.

Summarizing the main findings of our case study, we can make three practical recommendations, in addition to the overall conclusion that it is always better to use the MLE than the MBLE or the MPLE. First, if the MLE is not feasible, the MBLE is to be preferred over the MPLE. Second, if one’s main interest is in investigating nodal and dyadic attribute effects, the MBLE/MPLE can be useful as a first selection criterion, especially in the natural parameterization, where the bias is reasonably low. The MPLE performs worst for structural effects representing the transitivity in the network. Third, it can be worthwhile to also consider the mean value parameterization to obtain more insight into directly observable and interpretable network characteristics and statistics.

In view of the specificity of the models investigated in the case study, we realize that these conclusions will have limited generalizability. Therefore, as a final recommendation, we encourage further comparison of maximum likelihood estimation to (bias-corrected) pseudo-likelihood estimation in other applications. To this purpose, we have made available the code used to implement the framework in this study. See the Appendix for further technical details.

A Computational Details

All computations were done using the statnet (Handcock et al., 2003) suite of packages in the R statistical language (R Development Core Team, 2007). The statnet packages are free and open-source and are available from the Comprehensive R Archive Network (CRAN) website http://www.R-project.org. In addition, more information about the statnet packages is available on the web at http://statnetproject.org. All estimates are based on the ergm function, with various optional arguments. The arguments used are listed in Table A.1, and their function is described. Unless otherwise noted, the program used the ergm defaults for the options. Much of this description can be found in the internal documentation of Handcock et al. (2003). For details on this computations see Handcock et al. (2008); Hunter et al. (2008); Morris et al. (2008); Butts (2008) and Goodreau et al. (2008).

Table A.1.

Arguments to the statnet function ergm used to compute the MLE.

Argument	First Round	Second Round	Third Round
theta0	.9 truth + .1 MPLE	prior fit	prior fit
interval	2000	3000	3000
burnin	500000	500000	500000
MCMCsamplesize	5000	10000	5000
maxit	2	2	4
steplength	.7	.7	.5

The estimation of the MLE in either the natural or mean-value parameterization relies heavily on the generation of sampled networks from a model specified by a given set of natural parameters. We do this via MCMC using a Metropolis-Hastings algorithm to produce a Markov Chain of networks starting from the observed network (Hunter et al., 2008). We now provide details of the parameters of the algorithm used. The theta0 argument specifies the starting parameter values. Hunter and Handcock (2006) discuss the important role played by starting parameter values in fitting complex ERG models. The ergm default is to use the MPLE fit to begin the MLE fit. This approach was used for the samples from the original model. The increased transitivity samples, however, were more difficult to fit, so the MPLE estimate proved to be too far from the MLE to lead consistently to converged estimates over large numbers of sampled networks. Two modifications were introduced to address this problem. First, the initial parameter estimates were computed by adding 90% of the MPLE estimate to 10% of the model parameters from the original model. This had the effect of providing some correction in cases where the MPLE estimates were very far from the MLE. Second, the model fit was accomplished using two ergm calls. The first was less precise and with smaller sample size, and aimed at producing a rough initial set of parameter estimates closer to the MLE than its original values. The second ergm call was started at the estimate produced by the first, and involved a larger sample size in the interest of producing a more precise final set of parameter estimates. Note that these sophistications robustify the estimation of the MLE for the purposes of automation over the 1000 networks, but do not effect the ultimate MLE itself. Based on the results of this study we will use the MBLE estimate as the default in ergm.

The interval argument determines the number of Markov Chain steps between successive samples. The burnin argument determines the number of initial samples discarded to avoid any possible bias of the original network. And the MCMCsamplesize argument determines the total number of samples taken.

Once the sample is completed, the curvature of the MCMC approximation to the log-likelihood is evaluated and an MCMC-MLE estimate is produced. This estimate was obtained, however, based on a sample from parameter values potentially quite far from the true MLE, so it was potentially inefficient. With a new, improved MLE estimate in hand, it is possible to produce an additional sample based on this estimate to greatly refine the estimate. The ergm argument maxit does just this: it specifies the number of times an estimate should be produced, with each successive estimate based on a sample from the previous estimate.

The final argument steplength modifies the Newton-Raphson optimization of the Monte Carlo approximation to the log-likelihood to account for the uncertainty in the approximation to the actual log-likelihood. The value is between 0 and 1 and indicates how much of the step toward the estimated optimum is taken at each iteration.

Sample networks were fit with two or more successive calls to ergm, with arguments listed in the first column of arguments in Table A.1. The first two rounds of model-fitting were used for all models. Then, a check for convergence was performed: if the mean value parameter estimate for the edges term had error greater than 5 edges, the fit was deemed not sufficiently converged and the third round of model-fitting was repeated until the mean value edges term was accurate within 5 edges.