Structural Adaptation of Normal and Tumour Vascular Networks

Abstract

Vascular networks are dynamic structures, adapting to changing conditions by structural remodelling of vessel diameters and by growth of new vessels and regression of existing vessels. The vast number of blood vessels in the circulatory system, more than 10⁹, implies that vessels’ arrangement and structure are not under individual genetic control but emerge as a result of generic responses of each segment to the various stimuli that it experiences. To obtain insight into the types of response that are needed, a network-oriented approach has been used, in which theoretical models are used to simulate structural adaptation in vascular networks, and the results are compared with experimental observations. With regard to the structural control of vessel diameters, this approach shows that responses to both haemodynamic and metabolic stimuli are needed for the formation of functionally adequate and efficient network structures. Furthermore, information transfer in both upstream and downstream directions is essential for balancing flows between long and short flow pathways. Otherwise, functional shunting occurs, that is, short pathways become enlarged and flow bypasses longer pathways. Information transfer in the upstream direction is achieved by conducted responses communicated along vessel walls. Simulations of structural adaptation in tumour microvascular networks indicate that impaired vascular communication, resulting in functional shunting, may be an important factor causing the dysfunctional microcirculation and local hypoxia typically observed in tumours. Anti-angiogenic treatment of tumours may restore vascular communication and thereby improve or normalize flow distribution in tumour vasculature.

The structure of the circulatory system is subject to continuous change during growth and maturation and in response to exercise, wound healing and diseases [1,2]. These structural adaptations may involve alterations in the dimensions and wall composition of individual vessel segments (remodelling), the growth of new segments (angiogenesis) and the loss of existing segments (pruning). Structural change of vascular networks is important in many normal and pathological processes. A capillary network of adequate density is required to meet the needs of the tissue for oxygen and other substances. Thus, angiogenesis is fundamental to tissue development and wound healing, and the generation of a vascular supply to the implanted tissue is a major challenge in tissue engineering. The diameter and wall thickness of conduit vessels strongly affect perfusion of the regions that they supply and are also subject to dynamic control. For example, the response of a tissue to a blockage of a feeding vessel is dependent on the presence of collateral flow pathways and their ability to enlarge and perfuse the affected region, while in the development of hypertension, inward remodelling accompanied by wall thickening is a typical structural feature. Finally, the vascular supply of tumours is an important target for therapeutic approaches.

The locations of the major arteries and veins are determined during development and are generally consistent among individuals. However, this is not the case in the microcirculation. When the large total number of blood vessels in the microcirculation (in the range 10⁹–10¹⁰ in human beings) and the dynamic and stochastic characteristics of its structure are considered, it becomes obvious that the locations and properties of all microvessels cannot be under individual genetic control. Instead, the structure of the microcirculation must be considered an emergent property, resulting from the behaviours of numerous interconnected segments, which behave according to a generic set of responses to the several stimuli that they experience. This set of responses by vessel segments will be referred to as ‘rules’ in the following discussion. They are themselves the result of the intrinsic behaviours of the endothelial and smooth muscle cells forming the vessel walls. These rules are dependent on genetic information and its expression in a given species and tissue. Knowledge of vascular cell responses may provide clues to the rules of vessel behaviour. Conversely, improved understanding of the vessel-level rules may suggest hitherto unrecognized aspects of vascular cell behaviour.

Direct experimental approaches have provided much information about structural remodelling of blood vessels. Ex vivo perfusion systems allow manipulation of haemodynamic conditions and observation of resulting structural changes over periods of hours to days [3–5]. In vivo animal models can be used to observe structural responses to surgical alterations in flow conditions over periods of days to weeks [6–10]. Such experimental approaches have been used to investigate the responses of individual vessels (generally arteries) to mechanical stimuli, including fluid shear stress acting on the endothelial cell layer and circumferential and axial stresses acting on the wall, and to metabolic and pharmacological stimuli. However, not all aspects of structural adaptation can be readily explored using such techniques. Direct observation of structural changes is difficult in the very small vessels of the microcirculation. Moreover, the network arrangement of the microcirculation leads to many interactions among vessel segments. Any experimental manipulation produces multiple effects, making it difficult to analyse the resulting changes in network structure and function in terms of cause and effect, especially on a quantitative level.

In this MiniReview, an alternative ‘network-oriented’ approach is emphasized. This approach relies upon a combination of theoretical and experimental approaches. Theoretical models are developed to simulate structural adaptation and to predict the properties of mature networks, based on given sets of assumptions about the ‘rules’ of adaptation. By comparing the results with experimentally observed network structures, information about the ‘rules’ can be deduced. This approach can be applied in normal tissues and in pathological situations such as tumour microcirculation.

Theoretical approaches have been used by a number of groups to investigate structural adaptation of blood vessels. Hacking et al. [11] showed that a response to wall shear stress alone is not sufficient to control vessel diameters in a network. Quick et al. [12] investigated the consequences of adaptive responses to pressure and wall shear stress in small conductance vessels. Exploring the relationship between acute and long-term control of vascular diameters, Jacobsen et al. [13] developed a theory for arteriolar remodelling based on maintenance of smooth muscle cell activation. More detailed models of arterial remodelling, considering the deposition and turnover of various structural components, have been developed by Valentin and Humphrey [14]. In general, these studies consider either individual segments or networks with simplified or idealized structures. In the following MiniReview, we focus on an approach based on realistic, heterogeneous network structures.

Simulation of Structural Adaptation in Microvascular Networks

In the network-oriented approach to studying diameter adaptation [15,16], the vessel network is represented as a set of interconnected cylindrical segments, each with a defined length and luminal diameter. The luminal diameter D of each segment is assumed to vary with time t according to a differential equation of the form

$$\frac{1}{D}\frac{\mathrm{d}D}{\mathrm{d}t}=S_{\mathrm{tot}}$$ (1)

where S_tot represents the combined effect of multiple stimuli acting on the segment, including haemodynamic and biochemical factors. These stimuli are indicated schematically in fig. 1 and discussed in more detail later. The system of equations is solved approximately using discrete time steps.

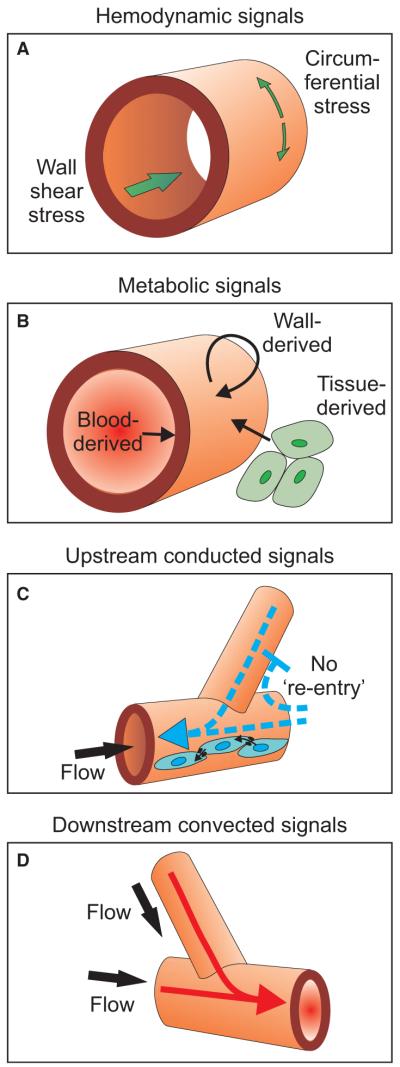
Fig. 1.

Schematic diagram showing haemodynamic forces and other factors acting on vessel walls. (A) Haemodynamic signals include wall shear stress acting on endothelial cells because of blood flow and circumferential stress generated in the wall as a result of intravascular pressure. (B) Metabolic signals may be generated by the blood, the wall and the surrounding parenchymal cells, and may act on all components of the wall. (C) Upstream propagation of signals occurs via conducted responses propagated along the vascular walls. Cell-to-cell coupling by gap junctions mediates this process. The blunt-headed arrow represents the no-re-entry phenomenon (see text for explanation.) (D) Convective transport of vasoactive metabolites provides a mechanism for downstream propagation of signals.

To estimate the haemodynamic stimuli (fig. 1A), it is necessary to compute the distribution of blood flow in the network at each time step. The network is analysed as a set of interconnected hydrodynamic resistances, with prescribed blood pressures or flow rates at the boundary nodes. The hydrodynamic resistance R of a segment is defined using Poiseuille’s law

$$R=\frac{\Delta P}{Q}=\frac{128L{\mu }_{\mathrm{app}}}{\pi D^4}$$ (2)

where ΔP is the pressure drop, Q is the flow rate, L is the length and μ_app is the apparent viscosity, which in itself is a function of segment diameter and haematocrit [17]. From this calculation, the blood pressure within each segment can be deduced. The wall shear stress is given by

$${\tau }_w=\frac{32{\mu }_{\mathrm{app}}Q}{\pi D^3}$$ (3)

In the models reviewed here, blood vessels’ structural adaptation to metabolic conditions is represented in terms of responses to the oxygen level within the vessels. The oxygen level is computed using a simplified approach in which a fixed rate of oxygen demand per vessel length is assumed, given by the overall oxygen demand of the tissue region divided by the total length of the segments that supply it [15].

Early theories of structural adaptation assumed that the diameter of each segment is controlled so as to achieve a target level of the wall shear stress [18,19]. Such behaviour can be represented using Equation 1 if a term dependent on the difference between the actual wall shear stress and the target level is included in S_tot, such that a wall shear stress above the target level causes a structural increase in diameter. According to Equation 3, the maintenance of a target wall shear stress results in a cubic dependence of flow rate on vessel diameter. This is consistent with an optimality principle known as Murray’s law [20] and with experimental observations of networks of arterioles [21]. However, analyses of microvascular networks in the rat mesentery [22] showed a systematic increase in wall shear stress with intravascular pressure from the venules to the arterioles. Such behaviour was incorporated in the model by assuming a pressure-dependent set point for wall shear stress. This implies that venous vessels are larger than corresponding arterial vessels carrying the same blood flow. Another consequence is that the pressure drop is much larger in the arterioles than in the venules, and capillary pressure is much lower than arterial pressure.

The further logical steps in the development of the model [15,16] are indicated in fig. 2. Analysis of the model under the assumption that diameters respond only to the haemodynamic signals of pressure and wall shear stress shows that parallel flow pathways are unstable (fig. 2A) [19]. Furthermore, this assumption neglects the obvious need for network structure to respond to metabolic needs. Introduction of a signal dependent on local oxygen level (fig. 1B) provides a metabolic response and can be shown to stabilize parallel pathways (fig. 2B).

Fig. 2.

Schematic diagram to illustrate effects of responses to haemodynamic and metabolic stimuli on structural adaptation of diameters in microvascular networks. In each case, small arrows represent flow direction from arteriole (red) to venule (blue). Diameter changes are exaggerated for clarity. (A) Response to pressure leads to arteriovenous asymmetry: venule diameters are larger than corresponding arteriolar diameters. The response to wall shear stress has the effect of destabilizing parallel flow pathways. Whichever pathway experiences the larger wall shear stress increases in diameter, taking a larger share of the flow and thereby further increasing its wall shear stress. The other branch shrinks to zero diameter if no other stimuli are included. (B) As in (A), but including an additional local metabolic signal, such that a low-flow channel receives a growth stimulus. Inclusion of metabolic signal stabilizes parallel pathways. (C) Configuration with unequal pathway lengths. Pressure response acts as in (A). If shear and local metabolic signals are included, the short flow pathway tends to increase in diameter and take most of the flow. The long pathway receives inadequate flow. (D) As in (C), but including upstream conducted metabolic response. The long flow pathway receives a large conducted signal and increases in diameter, leading to a flow distribution that is distributed more appropriately according to tissue needs.

In real microvascular networks, feeding and draining vessels are frequently adjacent, and this implies a large variation in the length of flow pathways (fig. 2C). The pressure gradient is high in short flow pathways, which tends to cause high levels of shear stress and enlargement of the short pathways, leading to formation of functional shunts. To overcome this tendency, the upstream portion of the long pathway must somehow receive a stimulus to grow to a diameter larger than that of the short pathway. Both vessels are subject to essentially the same metabolic environment, and therefore such behaviour cannot be accounted for by responses to purely local stimuli. Therefore, it is necessary to assume that information about the number and/or metabolic needs of dependent vessels is transmitted both upstream and downstream to their parent feeding and draining vessels (fig. 2D).

The finding that upstream and downstream transmission of information is necessary to suppress the formation of functional shunts was reached by the use of network-oriented approach. It would not be readily apparent from consideration of the behaviour of individual segments. Being reached from theoretical arguments, this finding does not prescribe the biological mechanisms of information transfer. For downstream transmission of information, a readily available mechanism is the convective transport of one or more metabolic signals (fig. 1D). One candidate is the release of ATP by red blood cells at a rate dependent on oxyhaemoglobin saturation [23]. However, theoretical arguments imply that other wall-derived or tissue-derived signals must also contribute [24]. Convective mechanisms are unlikely to provide upstream information transfer. The most likely mechanism involves conducted responses along vessel walls, whose endothelial and smooth muscle cells communicate with each other via gap junctions [25,26] (fig. 1C). In a gap junction, a pair of coupled hemichannels embedded in the external membranes of two adjacent cells forms a continuous pathway for movement of ions and molecules from one cell to the other. Summation of signals travelling upstream from two daughter arterioles and converging in the parent arteriole has been demonstrated [27]. This suggests that the conducted response reaching a given arteriole represents an integration of vasoactive stimuli arriving from downstream vessels and that a vessel supplying longer or more numerous distal vessels would tend to receive a larger conducted response than a vessel supplying fewer, shorter distal vessels. Evidence that conducted responses may be involved in the structural remodelling of blood vessels has recently been shown by experiments using connexin knockout mice [28].

A further implication of this analysis is that when an upstream conducted response reaches a vascular bifurcation, it does not affect other vessels that flow into the same bifurcation (fig. 1C). According to the preceding arguments, such ‘re-entry’ would lead to functional shunting [29]. Experimental evidence for suppression of re-entry is provided by observations of skeletal muscle, in which local muscle stimulation caused dilation of upstream arteriolar segments but did not increase flow in neighbouring capillaries in non-stimulated regions fed by the same arterioles [30]. This ‘no re-entry’ phenomenon suggests that mechanisms exist for rectification of conducted responses at bifurcations. Recent studies have shown that heterotypic gap junctions may exhibit asymmetric voltage-sensitive gating characteristics [31]. Furthermore, some gap junction proteins have been shown to be localized to regions near vessel bifurcations [32]. Thus, while the biophysical basis for suppression of re-entry is not known, a number of observations support the possibility of non-linear, spatially selective processes associated with conducted responses in vascular walls.

The characteristics of a normal microvascular network are illustrated in fig. 3A, which shows an experimentally observed region of a microvascular network in a rat mesentery. Two short flow pathways that connect the main feeding and draining vessels are indicated. These vessels have very small diameters, and so they drain only a very small fraction of the flow that is delivered by the major vessels. According to the aforementioned arguments, these vessels receive a low level of conducted response because they feed much shorter flow pathways than the major branches and so receive much smaller conducted responses. A detailed theoretical model for structural adaptation, including all the effects mentioned to this point, predicts vessel diameters and flow rates that are in good quantitative agreement with measured diameters [15].

Fig. 3.

Comparison of network structures in normal and tumour tissues. Computer-generated visualizations of network structures. Vessels are colour-coded according to generation number, defined as the number of vessel bifurcations between the main feeding arteriole and the given vessel (red colours, Art) or between the main draining venule(s) and the given vessel (blue colours, Ven). Black arrows indicate flow direction in main arterioles and venules. (A) Region of rat mesentery. *Two short flow pathways from the main arteriole to the main venule. On these pathways, diameters are relatively small, and flow is a very small fraction of that in the main feeding arteriole. (B) Region of tumour resulting from human squamous cell carcinoma (FaDu) cells injected in a dorsal skin fold window chamber implanted in a nude mouse. Asterisks indicate a short flow pathway from the main arteriole to the main venule. On this pathway, diameters are 15–18 μm, and flow is approximately 50% of that in the main feeding arteriole. Experimental methods used to observe network structures were described previously [43].

The structural adaptation of blood vessels involves changes not only in luminal diameter but also in wall mass and wall thickness, thus giving rise to a number of different modes of remodelling [33]. Structural adaptation of vessel diameter and wall mass has been analysed using a network-oriented approach by Pries et al. [34].

Structural Adaptation in Tumour Vascular Networks

The growth of a solid tumour depends on the presence of a vascular system to deliver nutrients to the cancer cells. As a consequence, tumour angiogenesis has been a focus of attention for decades [35]. Relative to normal tissues, tumour microvasculature typically shows several aberrant features, including heterogeneous vessel spacing, leaky dilated vessels with irregular diameters and a relatively large fraction of hypoxic tissue [36]. The occurrence of hypoxic regions reduces the effectiveness of radiation treatment, whose action is strongly dependent on oxygen level [37] and some types of chemotherapy [38]. Exposure to hypoxia may cause selective survival of more malignant or drug-resistant tumour cell sub-populations [39]. Most chemotherapeutic agents are delivered by the blood, and the irregular structure of tumour vasculature results in non-uniform drug delivery [40]. Hypoxia also contributes to up-regulation of transcription factors, such as HIF-1, which in turn activates a number of cell survival pathways that contribute to tumour progression [41]. Therefore, improved understanding of the mechanisms controlling the structure of tumour vasculature could provide a basis for new or improved treatment strategies.

The initial strategy of inhibiting angiogenesis to restrict tumour growth [35] showed promising results in animals but did not yield long-term survival benefits in human patients. However, an anti-angiogenic drug led to a significant increase in survival time in some patients when given in combination with chemotherapy [42]. This finding might be considered paradoxical, because inhibiting the growth of microvasculature might be expected to restrict the delivery of drugs to tissue. Jain [36] hypothesized that drug delivery to the tumour was in fact improved by anti-angiogenic therapy, because of an effect that he termed ‘normalization’ of the vasculature. However, the mechanism underlying this ‘normalization’ was not clearly identified.

The network-oriented approach as already described was applied to the analysis of structural adaptation in a tumour vascular network [43]. Growing tumours are observed to migrate towards and co-opt blood vessels from the surrounding tissues [44], which then grow and proliferate under the action of tumour-generated growth factors. Therefore, we considered that the diameter adaptation model for normal tissues, as described previously, might also apply to tumour networks, but with altered values of the parameters describing structural responses to the various stimuli. Observations were made of the vasculature in a tumour generated by human squamous carcinoma cells injected in a window chamber on a dorsal skin fold in a mouse. After 10 days, a fluorescent agent was introduced into the circulation and the vasculature was observed by confocal microscopy, allowing reconstruction of the three-dimensional network structure in a region of the tumour. A computer visualization of the reconstructed network is shown in fig. 3B. This network was used for simulations of structural adaptation according to the model already described.

Two dimensionless parameters were introduced to characterize structural and functional properties of networks, ‘diameter mismatch’ and ‘oxygen deficit’. As mentioned earlier, blood flow rate is proportional to the cube of diameter in a network satisfying Murray’s law. At bifurcations, the flow of the parent vessel must equal the sum of the flows in the daughter vessels, which implies that that the sum of the cubes of the daughter segment diameters equals the cube of the mother daughter diameter in such a network. The diameter mismatch was defined as the deviation from this relationship. Although Murray’s law is not satisfied in entire networks, as already pointed out, it is approximately satisfied among vessels of a given type [21]. Therefore, this criterion can be applied when comparing segments that meet at a single bifurcation. Oxygen deficit was defined as the amount of tissue not receiving oxygen divided by the total tissue volume, as estimated using the simplified model of oxygen transport described in the previous section.

Both the diameter mismatch and the oxygen deficit were found to be elevated in the tumour network relative to normal (mesenteric) networks when measured vessel diameters were used. The two network structures were then subjected to simulated structural adaptation of vessel diameters. Two modes of adaptation were considered: normal adaptation, in which the parameters of the model were chosen so that the values of diameter mismatch and oxygen deficit in the adapted mesentery network matched those obtained from measured diameters; and tumour adaptation, in which a corresponding procedure was carried out for the tumour network. When the fitted model parameters were compared, the most striking difference was that the parameter k_c, representing the influence of the upstream conducted response, was much lower for the tumour network than for the normal network. Other significant differences between the deduced tumour and normal parameters were that the shrinking tendency was reduced for the tumour, representing a tendency of tumour vessels to grow to larger diameters than corresponding normal vessels and that the randomization of shrinking tendency was higher, representing a tendency to higher dispersion in vessel diameters in tumours.

These results may be interpreted as follows [29,43]. In the tumour vasculature, the regular structure consisting of endothelial cells, basement membrane and smooth muscle layers is frequently disrupted [45,46]. This may lead to disturbance of gap junction connections between vascular cells and interfere with conducted responses. Furthermore, the high levels of vascular endothelial growth factor (VEGF) present in tumours may also disrupt gap junction communication [47]. As discussed earlier, conducted responses play an important role in the avoidance of functional shunting. In tumours, flow increases in short pathways at the expense of longer pathways, leading to functional shunting of blood flow, inefficient flow distribution, and the formation of hypoxic areas even in tumours with relatively high levels of vascularity and perfusion. The higher levels of growth factors in tumours are also consistent with the reduced shrinking tendency, while the heterogeneity of the tumour environment is consistent with the higher randomization of shrinking tendency.

These findings provide a potential mechanistic explanation for the ‘normalization’ of tumour vasculature that is believed to result from anti-VEGF therapy [36]. Inhibition of the interaction between VEGF and its receptors in tumour vasculature may partially restore communication among endothelial cells by reversing the effects described earlier. This would be expected to reduce the occurrence of functional shunts, making perfusion more uniform and enhancing the delivery of chemotherapeutic drugs. It is possible that a reduction in the randomness of growth also contributes to the improvement in perfusion resulting from anti-VEGF therapy. However, the apparent reduced growth tendency of vessels resulting from such therapy would have the effect of reducing perfusion, thereby counteracting the improvement in perfusion associated with ‘normalization’. The ability of structural adaptation mechanisms to achieve appropriate flow distribution among multiple flow pathways appears to be of key importance in this phenomenon.

Discussion

Blood vessels are subject to continuous remodelling in response to several stimuli including wall shear stress, intravascular pressure, metabolic signals and conducted responses. A network-oriented approach to the analysis of structural adaptation can be used to deduce ‘rules’ governing these responses. In particular, this approach reveals the importance of upstream conducted responses for the control of flow distribution between short and long pathways in heterogeneous network structures. If conducted responses are not sufficiently effective, networks can form functional shunts, leading to inefficient distribution of blood flow and regions of hypoxia. Reduced influence of conducted responses may underlie some of the aberrant properties of tumour microcirculation. Anti-angiogenic treatments, for example targeting VEGF receptors, may exert their normalizing effect by restoring conducted responses.

In recent decades, growth and remodelling of the vascular system have been subject to intense experimental investigation using a wide range of molecular, cellular, organ culture and in vivo approaches. A wealth of information has been obtained about the properties of many components of the system. However, the functional behaviour of the vasculature depends upon the complex interactions among these components and on their ability to self-organize and adapt to changing conditions. The network-oriented approach described here, based on a combination of experimental data and theoretical simulations, serves as a complement to other approaches aimed at understanding normal vascular structure and function and developing therapeutic approaches that target the vasculature.