Probing exchange kinetics and atomic resolution dynamics in high-molecular-weight complexes using dark-state exchange saturation transfer NMR spectroscopy

Abstract

We present the protocol for the measurement and analysis of dark-state exchange saturation transfer (DEST), a novel solution NMR method for characterizing, at atomic resolution, the interaction between an NMR-‘visible’ free species and an NMR-‘invisible’ species transiently bound to a very high-molecular-weight (>1 MDa) macromolecular entity. The reduced rate of reorientational motion in the bound state that precludes characterization by traditional NMR methods permits the observation of DEST. ¹⁵N-DEST profiles are measured on a sample comprising the dark state in exchange with an NMR-visible species; in addition, the difference (ΔR₂) in ¹⁵N transverse relaxation rates between this sample and a control sample comprising only the NMR-visible species is also obtained. The ¹⁵N-DEST and ΔR₂ data for all residues are then fitted simultaneously to the McConnell equations for various exchange models describing the residue-specific dynamics in the bound state(s) and the interconversion rate constants. Although the length of the experiments depends strongly on sample conditions, approximately 1 week of NMR spectrometer time was sufficient for full characterization of samples of amyloid-β (Aβ) at concentrations of ~100 μM.

INTRODUCTION

The ability to characterize the dynamics, as well as the structure, of increasingly large biological macromolecules in solution using recent NMR methods has expanded our mechanistic understanding of biomolecular function at the atomic level¹. Although several methods for high-resolution structural and dynamic characterization of proteins, nucleic acids and their complexes exist, none are able to observe, with atomic resolution, the dynamic equilibrium between a form observable by traditional solution NMR techniques and very-high-molecular-weight complexes formed by interactions with membranes, supramolecular structures, large aggregates and solid surfaces. We have recently developed a novel solution NMR method known as DEST to obtain interaction kinetics and residue-by-residue dynamic information in the ‘dark’ or NMR-invisible bound state². Here we describe the protocol for planning, measuring and analyzing DEST experiments. This protocol can be used to characterize the interaction kinetics and molecular motions of bound states in a number of potentially interesting biological systems, including interactions of proteins or peptides with large complexes such as the ribosome, proteasome or chaperones, or with membranes and membrane-bound proteins.

DEST NMR

When a molecule binds to a high (≥1 MDa)-molecular-weight entity, the reduced rate of molecular tumbling leads to a marked increase in nuclear spin transverse relaxation rates, R₂ (i.e., line-width), precluding observation by standard solution NMR techniques³. The large difference in R₂ between the free and bound forms, however, enables the observation of DEST². The key to the DEST experiment is as follows. A weak radiofrequency (RF) field applied far off resonance leaves resonances of the free form essentially unperturbed. The bound state resonances, however, are selectively saturated, as the small component of transverse magnetization created by an RF field, even far off resonance (up to 30 kHz in our system), is efficiently relaxed by the large R₂ in the bound state. In other words, even though the bound resonances are broadened beyond detection, they can be perturbed and partially saturated. Saturation of the bound resonances is transferred back to the resonances of the free species by chemical exchange and subsequently measured as attenuation of the easily observable resonances of the NMR-visible species. The attenuation as a function of RF offset is dependent on the R₂ in the bound state, enabling dynamics in the bound state to be probed on a residue-by-residue basis. The difference in apparent ¹⁵N-R₂ of the sample containing a dark state and a reference sample containing only the NMR-visible state, ΔR₂, is also measured. The maximum ΔR₂ value provides an estimate of the pseudo–first-order association rate constant $k_{\text{on}}^{\text{app}}$ (ref. 3). By fitting the observed ¹⁵N-DEST profiles and ¹⁵N-ΔR₂ data for all residues simultaneously, the residue-specific R₂ values in the dark state and the kinetic parameters connecting the visible and dark states can be extracted. Although fitting to observed ¹⁵N-DEST profiles without ¹⁵N-ΔR₂ data is possible for simple (two-state) models, it is not recommended, as two-state models can reproduce experimental profiles of more complicated systems if the kinetic rates are not constrained by additional data. Similarly, the use of at least two different applied RF fields improves the ability to discriminate between potential models and solutions producing otherwise equivalent fits (in general, two RF fields are sufficient).

¹⁵N-DEST spectroscopy probes exchange processes on timescales ranging from ~10 ms to ~1 s. The on-rate can be modulated by increasing or decreasing the total concentration of the dark species, as the pseudo–first-order rate constant for the conversion of the free species to the dark state is directly proportional to the concentration of the dark species. DEST is complementary to paramagnetic relaxation enhancement⁴ and relaxation dispersion spectroscopy⁵ that can be used to probe exchange reactions involving sparsely-populated states on timescales less than 250–500 μs and from ~50 μs to 10 ms, respectively, as well as pulsed H/D exchange experiments that probe the formation of stable contacts on a time-scale of minutes to days^6,7. Note that the observation of paramagnetic relaxation enhancement and relaxation dispersion profiles relies on differences in the length of paramagnetic center-proton vectors and chemical shifts, respectively, whereas DEST is dependent on large differences in transverse relaxation rates between the exchanging species. The transferred nuclear Overhauser effect (NOE)⁸ that relies on exchange between free and bound species to derive structural restraints on a bound ligand is also complementary to DEST, which provides position-specific dynamical information. Unlike other NMR saturation methods such as saturation transfer difference experiments⁹, DEST is a quantitative technique because it uses heteronuclear (e.g., ¹⁵N) saturation pulses, avoiding the complications of rapid dipolar-coupled magnetization transfers (i.e., spin diffusion) observed for ¹H saturation examples, even for samples with sparse protonation¹⁰.

Summary of the ¹⁵N-DEST and ΔR₂ experiments and analysis

In short, the protocol involves the measurement of ¹⁵N-DEST profiles on a sample in which a dark NMR-invisible state is populated, as well as of the ¹⁵N-R₂ values for both the sample of interest and a matched reference sample containing only the NMR-visible state. To facilitate the application of DEST, we introduce DESTfit, a new computer program for the analysis and design of DEST experiments, which is freely available online (http://spin.niddk.nih.gov/clore/Software/software.html).

Experimental design

The protocol for a successful DEST experiment for samples labeled with ¹⁵N at backbone amide positions is applicable under a broad range of conditions that meet the following requirements.

First, a soluble species that gives rise to an observable ¹H-¹⁵N heteronuclear single-quantum coherence (HSQC) spectrum should be in slow exchange on the chemical shift timescale with a bound species of very high molecular weight. Typically, the requirement of slow exchange is clearly met when the reference sample, containing only the NMR-visible species, and the sample including a dark NMR-invisible state give rise to resonances with identical chemical shifts but substantial differences in ¹⁵N-R₂ values (i.e., a measurable ΔR₂). The observation of measurable ΔR₂, >1 s⁻¹ in our experience, is a useful indicator that DEST experiments will be successful. It is noteworthy that these increases in R₂ for systems in slow exchange do not arise from exchange effects on an intermediate chemical shift timescale³. Unlike the case of intermediate exchange, ΔR₂ is independent of both magnetic field and nucleus; thus, for any backbone amide group, ΔR₂ values at 900 and 500 MHz, for example, will be the same, as will ΔR₂ values for ¹⁵N and ¹H_N nuclei of the same residue. The equivalence of ΔR₂ across measurement conditions indicates that the only mechanism for the observed line broadening is the binding of an NMR-visible species to a very-high-molecular-weight species with very fast transverse relaxation rates, and hence, near-instantaneous transverse relaxation. The maximum observed increase in apparent R₂ of the resonances of the unbound species reflects the apparent first-order rate constant $k_{\text{on}}^{\text{app}}$ for the conversion of the NMR-visible species to the NMR-invisible species (Fig. 1).

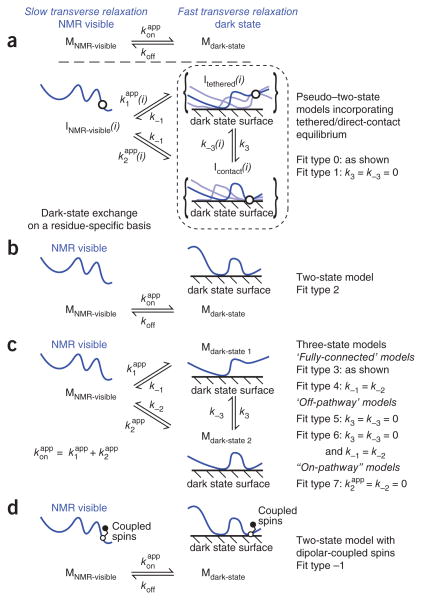
Figure 1.

Summary of the kinetic models available in the DESTfit program. (a) Pseudo–two-state models in which the equilibrium between the NMR-visible and dark states is described by a single $k_{\text{on}}^{\text{app}}$ and k_off, connecting the free (M_NMR-visible) and dark (M_dark-state) states of the exchanging species, whereas the dark state is partitioned into residue-specific equilibria of ensembles of tethered (I_tethered) and direct-contact (I_contact) states for residue i, such that the concentration of I_NMR-visible = M_NMR-visible for all i (i.e., M refers to the entire molecule, whereas I provides a description on a residue basis). (b) A two-state model, described by a single $k_{\text{on}}^{\text{app}}$ and k_off. (c) Three-state models in which two thermodynamically distinct dark states are populated, including fully connected (Fit types 3 and 4), ‘off-pathway’ (Fit types 5 and 6) and ‘on-pathway’ (Fit type 7) models. (d) A two-state model incorporating the effect of dipolar coupling between spins of different chemical shifts, most useful for analysis of ¹H DEST data.

Second, $k_{\text{on}}^{\text{app}}$ and the dissociation rate constant k_off for the return to the NMR-visible state must be on the order of, or faster than, the longitudinal relaxation rate, R₁, of the DEST nuclei (backbone ¹⁵N in this instance, typically < 2 s⁻¹). This rate requirement arises because DEST must occur while magnetization is stored longitudinally (i.e., as ¹⁵N_z magnetization) during the saturation time, which therefore limits the maximum DEST saturation/exchange time. $k_{\text{on}}^{\text{app}}$ must also be < 100 s⁻¹, as the precise measurement of larger ¹⁵N-R₂ values is difficult. The requirement that 1/k_off be on the order of, or shorter than, the saturation time arises because saturation of the species visiting the dark state is observed as attenuation of NMR-visible state resonances upon chemical exchange. R₁ also places a lower limit on $k_{\text{on}}^{\text{app}}$, as the intensive nuclei enhanced by polarization transfer (INEPT) magnetization transfers used to create initial ¹⁵N_z magnetization are inefficient in the dark state. Therefore, ¹⁵N_z is typically only created in the NMR-visible species and must be transferred to the dark state by chemical exchange for subsequent saturation.

Third, the dark state must be reasonably populated (i.e., ≥0.5%) to observe DEST. In the case of Aβ40 and Aβ42, ~5% of the exchanging peptide population was in the bound state at any time, which was sufficient for observable DEST to build up through an extended saturation period of ~1 s (ref. 2). The extent to which kinetic and dynamic parameters of the system affect the ability to observe measurable DEST can be simulated in DESTfit by inputting estimated values in the appropriate fitting parameter file and selecting the option to predict DEST from model parameters rather than fitting model parameters to experimental data.

The current protocol allows the determination of R₂ at back-bone ¹⁵N nuclei positions in one or more dark states, $R_2^{\text{dark}}$, as well as the determination of the kinetic rates connecting visible and dark states on a protein- or residue-specific level (see Table 1 for descriptions of the available kinetic models). For a protein that is disordered in the NMR-visible state, residue-specific $R_2^{\text{dark}}$ or equilibrium constants connecting tethered and direct-contact states, K₃ (Table 1), can be used to determine residue-specific behavior in the dark state. In a globular protein, however, $R_2^{\text{dark}}$ rates are expected to be similar through the folded regions, and hence $R_2^{\text{dark}}$ may not correlate with residues mediating binding. However, the ordering or folding upon binding of disordered regions or loops will be detected. We are currently developing extensions of the DEST methodology to side chain groups that will allow unambiguous determination of binding site residues and specific side chain degrees of freedom that become ordered in the dark state.

TABLE 1.

Kinetic models available in DESTfit software.

Fit type	Description
0	Pseudo–two-state model with dark states comprising tethered and direct-contact ensembles connected by a global rate constant, k3, connecting tethered and direct-contact states
1	Pseudo–two-state model with dark states comprising tethered and direct-contact ensembles in which there is no kinetic connection between tethered and direct-contact states (i.e., k3 = 0 s−1)
2	Two-state model (one NMR-visible state and one dark state)
3	Three-state model (one NMR-visible and two dark states) in which all states are fully kinetically connected
4	Three-state model (one NMR-visible and two dark states) in which all states are fully kinetically connected and the dissociation rate constants from dark states to the visible state are constrained to be equal
5	Three-state model (one NMR-visible and two dark states) in which dark states are kinetically separated from each other (i.e., dark states are ‘off-pathway’)
6	Three-state model (one NMR-visible and two dark states) in which dark states are kinetically separated from each other (i.e., dark states are ‘off-pathway’) and dissociation rate constants from dark states to the visible state are constrained to be equal
7	Three-state model (one NMR-visible and two dark states) in which dark state 2 is kinetically separated from the NMR-visible state (i.e., dark state 1 is an obligatory intermediate ‘on-pathway’ to dark state 2)
−1	Two-state model in which spin-spin coupling in NMR-visible and dark states is incorporated for cases where the isolated spin approximation is not valid, as in the case for DEST experiments using 1H-saturation in fully protonated systems3

Controls

The observation of off-resonance saturation in the experimental DEST profiles is necessary for the success of this protocol. Once DEST is measured for the sample containing the dark state, the experimental DEST profiles can be compared with simulations in which the NMR-visible state is not in exchange with a dark state (by setting $k_{\text{on}}^{\text{app}}$ to 0) to ensure that the observed width of the DEST profiles cannot be explained by the NMR-visible state itself. In addition, a control DEST experiment can be measured on the reference sample containing only the NMR-visible state and compared with that measured on the sample containing the dark state to confirm that any off-resonance saturation observed for the dark-state sample is in fact due to the presence of the dark state.

MATERIALS

REAGENTS

• Sample for NMR analysis (see REAGENT SETUP and Step 1 of the PROCEDURE)

• Deuterated solvent

EQUIPMENT

• NMR spectrometer (a ¹H Larmor frequency of 500 MHz or higher and a cryogenically cooled probe are highly recommended to improve sensitivity and reduce experiment time)

• vance spectrometer running TopSpin 2.1 software (Bruker)

• Varian spectrometer (Agilent Technologies)

• Linux- or OS X–based computer system for data processing and analysis

• nmrPipe and nmrDraw data processing and analysis suites (http://spin.niddk.nih.gov/NMRPipe/)

• MATLAB (The Mathworks) software including Statistics Toolbox and Optimization Toolbox, or installation of free MATLAB Compiler Runtime (MCR) libraries distributed along with DESTfit

• DESTfit software for the analysis of DEST data (http://spin.niddk.nih.gov/clore/Software/software.html)

• ¹H-¹⁵N chemical shift assignment table

• ¹⁵N-R₁ values for each backbone amide position; although uniform, estimated values can be used as the DEST experiment is designed to be insensitive to the value of R₁ across the entire range expected for biomolecules

REAGENT SETUP

NMR sample

The sample contains the molecule(s) of interest with ¹⁵N isotope labeling, which gives rise to well-resolved cross-peaks in a 2D ¹H-¹⁵N HSQC spectrum. Standard sample conditions for collection of ¹H-¹⁵N HSQC experiments apply to this experiment and are detailed elsewhere¹¹ (i.e., an ¹⁵N-labeled sample dissolved in 90–95% H₂O with 5–10% D₂O for the deuterium lock signal). NMR samples should contain 2–10% (vol/vol) deuterated solvent (e.g., ²H₂O) for the NMR lock. Although this protocol is optimized for observing backbone amide positions of peptide and protein samples, it should be possible to adapt the method to other macromolecules, including nucleic acids.

EQUIPMENT SETUP

NMR spectrometer

The NMR spectrometer must able to collect sufficiently well-resolved ¹H-¹⁵N 2D NMR spectra with sufficient sensitivity, the exact parameters for which are highly sample specific.

NMR pulse sequences

The DEST pulse sequence² provided with DESTfit is designed for a Bruker Avance spectrometer running the TopSpin 2.1 software or higher, but it is easily modified for use on any Bruker or Varian spectrometer. Standard pulse sequences for the measurement of ¹⁵N-R₂ are also required¹¹.

PROCEDURE

Sample preparation

• 1|Prepare two NMR samples: a reference sample containing the protein or peptide of interest entirely in the NMR-visible state, and a sample containing the same protein populating both the NMR-visible state and potential dark states. In the case of the Aβ peptides, the two samples (unstirred and at 4 °C) were obtained by simply using two different concentrations of peptide: at low concentration (≤50 μM), Aβ is entirely monomeric and remains stable for several weeks, whereas at higher concentrations (>150 μM), the sample equilibrates over a period of about 1 week to establish a stable pseudoequilibrium that persists for several weeks and in which the peptide is partitioned between monomer and protofibrils (ranging in mass from 1.8 to 85 MDa)². In other systems involving two components, such as an NMR-visible species exchanging on the surface of a large supramolecular complex (>1 MDa), the sample containing both visible and dark states is obtained by simply adding the supramolecular complex. The exact concentration of the high-molecular-weight species required will depend on the exchange characteristics and equilibrium properties of the system and can only be determined empirically; i.e., the concentration of the high-molecular-weight species required is the concentration at which observable ΔR₂ values can be accurately measured on the resonances of the NMR-visible species, but the ΔR₂ values cannot be so large as to broaden the resonances of the visible species to a level beyond which the signal-to-noise ratio is too low to permit accurate ΔR₂ or DEST measurements. Typically, accurate DEST data require the ¹⁵N-R₂ values of the visible species in the sample containing the dark state to be not larger than about 20 s⁻¹.

NMR data collection and processing: experiments measuring ΔR₂

• 2|As for any NMR experiment, insert the reference sample into the magnet and tune, match and shim the instrument to the sample of interest.
• 3|Collect ¹H-¹⁵N HSQC and NMR data for the measurement of the transverse relaxation rate constants for backbone ¹⁵N nuclei (¹⁵N-R₂ data) for the reference sample.

  ▲ CRITICAL STEP Data should be collected with a sufficient signal-to-noise ratio such that R₂ can be precisely determined, typically with uncertainties of < 5%; this takes ~12 h, depending on sensitivity and sample concentration.

• 4|Repeat Step 2 for the sample containing the dark state.
• 5|Perform Step 3 for the sample containing the dark state.
• 6|Visualize the overlay of the ¹H-¹⁵N HSQC spectrum of the sample of interest with the reference sample to determine that there are no major chemical shift differences between the spectra, thereby ensuring that sample conditions are identical except for the presence of a dark state.
• 7|Process NMR data using nmrPipe to extract ¹⁵N-R₂ and error estimates at each residue position in both samples.
• 8|Calculate ΔR₂, the difference between ¹⁵N-R₂ in the sample of interest and the reference sample, at each residue position.

  ▲ CRITICAL STEP ΔR₂ must be determined precisely, typically with an uncertainty in ΔR₂ of < 5%, for quantitative interpretation of small ΔR₂ (~1 s⁻¹). DEST is unlikely to be observed if ΔR₂ is not substantially greater than 0.2 s⁻¹

  ? TROUBLESHOOTING

NMR data collection and processing: experiments measuring DEST

• 9|Set up DEST saturation parameters for the ¹⁵N-DEST pulse program (Box 1).
• 10|Run the first increment of an interleaved DEST experiment on the sample and reference, process 1D data and overlay 1D spectra as a function of RF offset to confirm the presence of measurable saturation transfer for at least some resonances of the sample containing the dark state at offsets where the reference sample shows no saturation transfer.

  ▲ CRITICAL STEP It is recommended that DEST be apparent in the first increment to confirm that parameters will lead to DEST before collecting a long, interleaved 2D DEST experiment.

  ? TROUBLESHOOTING

• 11|Collect a 2D ¹⁵N-DEST experiment.
• 12|To determine the attenuation due to DEST at each backbone ¹⁵N position as a function of saturation offset, process the ¹⁵N-DEST experiment using the nmrPipe processing scripts provided with DESTfit.

Box 1. Choosing experimental parameters for ¹⁵N-DEST.

In addition to standard NMR acquisition parameters, the DEST experiment has the following parameters that control the DEST saturation period specified in the DEST pulse sequence:

• Mixing time: limited to ~3 × ¹⁵N-R₁ (depending on the sensitivity and sample concentration). Set by adjusting the number of times the program executes the 100-ms saturation loops, balancing sufficient a signal-to-noise ratio with sufficient mixing time for DEST buildup. Default: 900 ms. In cases in which $k_{\text{on}}^{\text{app}}$ and k_off are both on the order of R₁, a comparison of best-fit parameters at a series of mixing times may also provide an additional metric of the consistency of the solutions. In all cases, a mixing time of 1/R₁ is an appropriate starting value.

• Saturation RF field strength: set the power level of the continuous-wave saturation field so that the dark state is observably saturated but the reference sample is not saturated when far from resonance (> 2 kHz, depending on saturation field). Suggested RF field strengths: 350 and 150 Hz. Calculate the power level for DEST saturation, p_DEST, by

  $$p_{\text{DEST}}=p_{\text{ref}}+20·{log}_{10}\left(\frac{1}{4t_{\text{ref}}^{\pi /2_f}}\right)·{(-1)}^n$$ (1)

  where p_ref is the power level (dB) for the reference 90° pulse of known length, $t_{\text{ref}}^{\pi /2}$ is the length of the reference 90° pulse (s), f is the desired saturation field strength (Hz) and n is 0 for instruments in which higher dB values indicate lower power levels (as in the case of Bruker Biospin instruments), and n is 1 when lower dB indicates lower power levels (as in the case of Varian instruments).

• Saturation offsets: set in the pulse program so that the attenuation due to DEST is negligible compared with the reference experiment (no saturation) at the largest offsets but clearly apparent as offsets decrease. Default: 15 offsets ranging from 35 to − 35 kHz, for each of the two fields.

Preparation of input data

• 13|Create a copy of the DESTfit directory to use as a template.
• 14|Set up the input files in the inputs/ directory with appropriate file names and contents specifying the model of interest (Tables 2 and 3), using the template files provided.

  ▲ CRITICAL STEP The choice of initial values of the fitting parameters and parameter ranges is important. Example parameters are provided in the parameter file, and the final column in the file is set to 0 to let the parameter vary or to 1 to fix the parameter to the provided initial value (Table 3).

• 15|Install MCR libraries using the following commands:

TABLE 2.

Sample input file names, description and data format.

File name	Description	Format of data columns
dest.txt	DEST data	Residue number, Frequency of resonance in DEST dimension (15N for 15N-DEST) measured from 0 p.p.m. (Hz), Peak intensities as a function of frequency (N data points where N is the number of experiments including reference experiments)
frequencies.txt	Saturation offset of DEST saturation pulse	Offset from carrier frequency (Hz) for each data point in dest.txt in the same order, including a value of 0 for reference experiments
satfields.txt	DEST saturation field intensity as a function of offset	Saturation field (Hz) for each data point in dest.txt in the same order, with 0 used to specify reference experiments
R2.txt	Transverse relaxation rate in the NMR-visible state	Residue number, R2 (s−1)
R1.txt	Longitudinal relaxation rate in the NMR-visible state (Note: as these values do not affect the result within the entire range of R1 for biomolecules, estimated values can be used)	Residue number, R1 (s−1)
deltaR2.txt	Difference in R2 between dark state and reference sample	Residue number, ΔR2 (s−1), s.d. (s−1)
DESTconstants.txt	Various experimental parameters	Fit type (integer from 0 to 7 and - 1, see fit descriptions Table 1) B0field expressed as 1H Larmor frequency (MHz) Carrier frequency in DEST experiment (p.p.m.) DEST experiment sweep-width (Hz) DEST nucleus (3 for 15N, 2 for 13C, 1 for 1H) Relative weighting factor for ΔR2 values in fit optimization (e.g., 0.5) Length of DEST saturation pulse (s) Make plots (1 for yes, 0 for no) Save plots to file (1 for yes, 0 for no) Optimize parameters (1 for yes, 0 for no; i.e., if 0 just simulate with the initial parameter value and generate output) Optimize dark-state resonance offset chemical shift (CS; 0 for no, same CS as light state, 1 for yes, use a single residue-specific dark-state offset for all dark states, 2 use a separate residue-specific CS for each of two dark state) Values of R1 of dark states (0 to assume R1 in the dark state is uniform rate of 0.5 s−1, 1 to use position-specific R1 for dark states equal to user provided R1 in the NMR-visible state)
params1.txt	Various kinetic and relaxation parameters for McConnell model fitting	See Table 3
normalize.txt	Scaling factor to manually normalize data points	Residue number, number by which to multiply auto-normalized DEST data to achieve desired normalization
folded.txt	Correction for aliased resonance positions	Residue number, integer number of times resonance position provided in dest.txt column 2 is aliased (positive integer for aliased downfield, negative for aliased upfield; where aliased downfield indicates that actual resonance position is downfield of spectral window)
darkoff.txt	Dark state CS, initial guess	CS (p.p.m.) for each data point in dest.txt in the same order, if the option to optimize CSs in the dark state is specified in DESTconstants.txt
darkoff2.txt	Dark state 2 CS, initial guess	CS (p.p.m.) for each data point in dest.txt in the same order, if the option to optimize CSs of two dark states independently is specified in DESTconstants.txt

TABLE 3.

Fitting parameters format and examples for each fit type.

Fit type	Parameter list (in prescribed order) and description	Example param[X].txt entries (initial value, lower bound, upper bound, fix parameter)
0	Fraction of the exchanging species in NMR-visible state	0.95, 0.01, 1.0, 0
	$k_{\text{on}}^{\text{app}}({\text{s}}^{-1})$, sum of on-rates to the dark states usually set to the maximum observed ΔR2	3.15, 1.2, 3.15, 0
	k3 (s−1), rate constant from tethered to direct-contact state	0.1, 1e-6, 1e6, 0
	$R_2^{\text{contact}}({\text{s}}^{-1})$, R2 in direct-contact dark state	19e3, 500, 1e7, 0
	$R_2^{\text{tethered}}({\text{s}}^{-1})$, residue-specific R2 in tethered state	200, 20, 1e7, 0
	K3, residue-specific equilibrium constant equal to [direct-contact] / [tethered]	1, 1e-9, 1e9, 0
1	Fraction of the exchanging species in NMR-visible state	0.95, 0.01, 1.0, 0
	$k_{\text{on}}^{\text{app}}({\text{s}}^{-1})$, sum of on-rates to the dark states usually set to the maximum observed ΔR2	3.15, 1.2, 3.15, 0
	$R_2^{\text{contact}}({\text{s}}^{-1})$, R2 in direct-contact dark state	19e3, 500, 1e7, 0
	$R_2^{\text{tethered}}({\text{s}}^{-1})$, residue-specific R2 in tethered state	200, 20, 1e7, 0
	K3, residue-specific equilibrium constant equal to [direct-contact] / [tethered]	1, 1e-9, 1e9, 0
2	Fraction of the exchanging species in NMR-visible state	0.95, 0.01, 1.0, 0
	$k_{\text{on}}^{\text{app}}({\text{s}}^{-1})$, on-rate to the dark states usually set to the maximum observed ΔR2	3.15, 1.2, 3.15, 0
	$k_{\text{2}}^{\text{dark}}({\text{s}}^{-1})$, residue-specific R2 in dark state	200, 20, 1e7, 0
3	Fraction of the exchanging species in NMR-visible state	0.90, 0.01, 0.99, 0
	$k_{\text{on}}^{\text{app}}({\text{s}}^{-1})$, sum of on-rates to the dark states usually set to the maximum observed ΔR2	3.15, 1.2, 3.15, 0
	Fraction of the exchanging species in dark state 1	0.1, 0.01, 0.3, 0
	k3 (s−1), rate constant from dark state 1 to dark state 2	0.1, 1e-6, 1e6, 0
	k−1 (s−1), rate constant from dark state 1 to visible state (‘off-rate’)	0.1, 1e-6, 1e6, 0
	$R_2^{\text{dark}(1)}({\text{s}}^{-1})$, residue-specific R2 in dark state 1	200, 20, 1000, 0
	$R_2^{\text{dark}(2)}({\text{s}}^{-1})$, residue-specific R2 in dark state 2	5000, 1000, 1e9, 0
4	Fraction of the exchanging species in NMR-visible state	0.90, 0.01, 0.99, 0
	$k_{\text{on}}^{\text{app}}({\text{s}}^{-1})$, sum of on-rates to the dark states usually set to the maximum observed ΔR2	3.15, 1.2, 3.15, 0
	Fraction of the exchanging species in dark state 1	0.1, 0.01, 0.3, 0
	k3 (s−1), rate constant from dark state 1 to dark state 2	0.1, 1e-6, 1e6, 0
	$R_2^{\text{dark}(1)}({\text{s}}^{-1})$, residue-specific R2 in dark state 1	200, 20, 1000, 0
	$R_2^{\text{dark}(2)}({\text{s}}^{-1})$, residue-specific R2 in dark state 2	5000, 1000, 1e9, 0
5	Fraction of the exchanging species in NMR-visible state	0.90, 0.01, 0.99, 0
	$k_{\text{on}}^{\text{app}}({\text{s}}^{-1})$, sum of on-rates to the dark states usually set to the maximum observed ΔR2	3.15, 1.2, 3.15, 0
	Fraction of the exchanging species in dark state 1	0.1, 0.01, 0.3, 0
	k−1 (s−1), rate constant from dark state 1 to visible state (‘off-rate’)	0.1, 1e-6, 1e6, 0
	$R_2^{\text{dark}(1)}({\text{s}}^{-1})$, residue-specific R2 in dark state 1	200, 20, 1000, 0
	$R_2^{\text{dark}(2)}({\text{s}}^{-1})$, residue-specific R2 in dark state 2	5000, 1000, 1e9, 0
6	Fraction of the exchanging species in NMR-visible state	0.90, 0.01, 0.99, 0
	$k_{\text{on}}^{\text{app}}({\text{s}}^{-1})$, sum of on-rates to the dark states usually set to the maximum observed ΔR2	3.15, 1.2, 3.15, 0
	Fraction of the exchanging species in dark state 1	0.1, 0.01, 0.3, 0
	$R_2^{\text{dark}(1)}({\text{s}}^{-1})$, residue-specific R2 in dark state 1	200, 20, 1000, 0
	$R_2^{\text{dark}(2)}({\text{s}}^{-1})$, residue-specific R2 in dark state 2	5000, 1000, 1e9, 0
7	Fraction of the exchanging species in NMR-visible state	0.90, 0.01, 0.99, 0
	$k_{\text{on}}^{\text{app}}({\text{s}}^{-1})$, sum of on-rates to the dark states usually set to the maximum observed ΔR2	3.15, 1.2, 3.15, 0
	Fraction of the exchanging species in dark state 1	0.1, 0.01, 0.3, 0
	k3 (s−1), rate constant from dark state 1 to dark state 2	0.1, 1e–6, 1e6, 0
	$R_2^{\text{dark}(1)}({\text{s}}^{-1})$, residue-specific R2 in dark state 1	200, 20, 1000, 0
	$R_2^{\text{dark}(2)}({\text{s}}^{-1})$, residue-specific R2 in dark state 2	5000, 1000, 1e9, 0
−1	Fraction of population in large R2 (direct-contact) states when bound	0.01, 0.01, 1.0, 0
	$k_{\text{on}}^{\text{app}}({\text{s}}^{-1})$, on-rate to the dark state usually set to the maximum observed ΔR2	3.15, 1.2, 3.15, 0
	Offset (Hz) of dipolar-coupled spin from observed spin	2400, 0, 2500, 1
	koff (s−1), off-rate from the dark state	70, 1e–6, 1e6, 0
	$R_2^{\text{large}}({\text{s}}^{-1})$, R2 in direct-contact population fraction	20000, 50, 1e9, 0
	$R_2^{\text{small}}({\text{s}}^{-1})$, R2 in mobile or tethered population fraction	10, 5, 50, 0

 cd MCRinstallers
 ./MCRInstaller_LINUX64.bin for Linux computer systems or
open MCRInstaller_OSX.dmg for OS X computer systems

Simultaneous fitting of model to DEST profiles and ΔR₂ data

• 1|6Run the appropriate binary program from the main DESTfit directory, and specify the MATLAB directory in which the MCR libraries are found.

For Linux:

 ./run_DESTfit_LINUX64.sh ~/MATLAB_Compiler_Runtime/v715/

For OS X:

 ./run_DESTfit_OSX.sh
/Applications/MATLAB/MATLAB_Compiler_Runtime/v714/

• ! CAUTION The argument specifying the path to the MCR libraries may vary depending on the location specified upon installation (Step 14).

  ? TROUBLESHOOTING

Extracting data from completed fit

• 17|Examine the graphical output for goodness of fit to the DEST profiles and ΔR₂ data.

  ? TROUBLESHOOTING

• 18|Examine the text file output for fitted parameters (Table 4).

  ? TROUBLESHOOTING

  Troubleshooting advice can be found in Table 5.

TABLE 4.

Output file names and description of contents.

File name	Description
fitout_glblparams.txt	Best-fit global parameters and s.d. (σ) for each parameter equal to 68% confidence interval
fitted_R2dark1.txt, fitted_R2dark2.txt	Residue-specific R2 and σ (R2) (s−1) of the dark state(s). Both are computed for fit type 3–7, and only the R2 in the single dark state is computed for fit type 1
fitted_R2tethered.txt	Residue-specific R2 for tethered state. Computed for fit type 0 and 1
fitted_K3.txt	Residue-specific equilibrium constant K3 = [direct-contact]/[tethered]. Computed for fit type 0 or 1
plotres_[X].png	Plot of the DEST data as a function of saturation pulse offset frequency for residue [X], in .png image file format
plotvarnum_[Y].png	Plot of residue-specific parameter [Y] as a function of residue. Varnum 1 and 2 correspond to $R_2^{\text{tethered}}$ and K3, respectively, for fit types 0 and 1, and to R2 in dark states 1 and 2, $R_2^{\text{dark}(1)}$ and $R_2^{\text{dark}(2)}$, respectively, for fit types 2 to 7
plot_deltaR2.png	Plot of ΔR2 experimental versus that computed from best-fit model, in .png image file format
exptDEST_res[X].txt	Experimental input DEST data for residue [X], formatted for ease of plotting. Format: saturation offset, relative peak intensity as a function of offset and saturation field (Hz)
fitDEST_res[X].txt	Best-fit model DEST data for residue [X], formatted for ease of plotting. Format: saturation offset, relative peak intensity as a function of offset and saturation field (Hz)

TABLE 5.

Troubleshooting table.

Step	Problem	Possible reason	Solution
8	Δ R2 equal to 0 at all residue positions; DEST is unlikely to be observed if Δ R2 is not substantially greater than 0.2 s−1	Insufficient population of dark state	Modify sample conditions or concentrations to increase the conversion rate from the NMR-visible to the dark species. This can often be accomplished by increasing the concentration of the dark state
	Negative values of Δ R2 are computed or R2 is not repeatable	Imperfect reference and dark-state sample condition matching. Small changes in pH (on the order of 0.2 pH units) near physiological pH of 7 can change the rate of 1HN exchange with 1H from bulk water on the order of 1 s−1 or greater	Option 1: the reference sample should be changed (i.e., pH adjusted) such that the sample conditions match. Resonance positions of 1H-15N correlations of histidine residues can be used as sensitive internal reporters of the relative pH of the two samples, and titrating the pH of the reference sample to precisely overlay with the 1H-15N correlation spectrum is a useful way to ensure sample consistency. If pH adjustment after sample creation is not possible, several reference samples with slightly different sample pH can be screened for the best overlay and/or used for R2 measurement. Option 2: pulse sequences that remove the contribution of water exchange to the measured relaxation rates12 can be used in place of standard 15N-R2 measurements; or lower the sample temperature
10	No DEST (off-resonance) saturation is observed	Saturation power is too weak	Increase the saturation power (Box 1)
		$R_2^{\text{dark}}$ is too small to give rise to DEST	Increase $R_2^{\text{dark}}$ by decreasing temperature or increasing the size of the dark state
16	Warning concerning local minima of optimization	It is difficult to guarantee a global optimum solution in an extremely large parameter space search	Convergence may be confirmed by independent fitting with different initial parameters, leading to the same solutions
17	Poor fit to DEST and/or ΔR2 data	Model is inappropriate for the system of interest	Change the fit type of the model (e.g., change from fit type 2, two-state model, to fit type 3 or 1, three-state or tethered/ bound models, respectively)

TIMING

Experiment measurement time may be as long as 3–5 d. Setup and collection of the DEST experiment (Steps 9–11) can be done in parallel with processing of ¹⁵N-R₂ experiments and calculation of ΔR₂ (Steps 7 and 8). The preparation of input files (Steps 13 and 14) can be done in parallel with the collection of the DEST experiment (Step 11).

Step 3: ~12 h, depending on the sensitivity and sample concentration (data should be collected with sufficient signal to noise such that R₂ can be precisely determined, typically with uncertainties of <5%)

Step 5: ~12 h, depending on the sensitivity and sample concentration

ANTICIPATED RESULTS

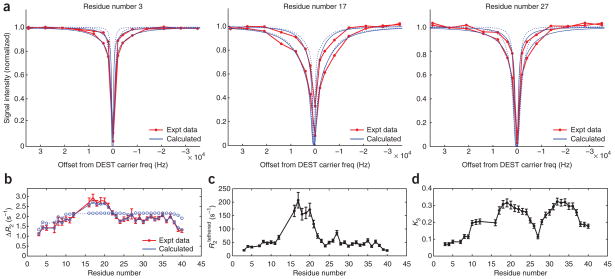
The parameters for the selected model that best fit all the experimental data will be displayed on the screen. The experimental ¹⁵N-DEST profiles and ΔR₂ data are plotted against the values predicted using the selected model and fitted parameters (Fig. 2). The match between the experimental (red) and simulated (blue) data should be examined to determine whether the model fitting was qualitatively successful. If the selected model and free parameters are appropriate for the experimental data, DEST profiles and ΔR₂ values predicted from the best-fit model should closely approximate the experimental observations. The best-fit residue-specific parameters R₂ in the dark state(s) and K₃ (for fit types 0 and 1) and their uncertainties are also displayed graphically (Fig. 2). The output directory contains files tabulating the displayed best-fit parameters, as well as the simulated and experimental data for plotting in external programs and the displayed figures in .png image format (Table 4).

Figure 2.

Screenshots of figures output by the DESTfit software. (a) Comparison of experimental (red) and calculated (blue) ¹⁵N-DEST profiles observed for Aβ40 at 260 μM for residues E3 (left), L17 (center) and N27 (right). (b) Comparison of experimental (red) and simulated (blue) ΔR₂ for Aβ40 at 260 μM relative to Aβ40 at 50 μM. (c,d) Best-fit residue-specific $R_2^{\text{tethered}}$ (c) and K₃ (d), in which the error bars represent confidence intervals for one s.d. Calculated experimental DEST and ΔR₂ profiles for the best-fit pseudo–two-state model with dark states comprising tethered and direct-contact ensembles, fit type 1 (blue solid lines) show significantly better agreement with experimental values compared with those for the best-fit simple two-state model, fit type 2 (blue dotted lines). Expt data, experimental data; freq, frequency.

The described protocol was applied to ΔR₂ and DEST data recorded on samples of Aβ40 and Aβ42 to observe the dynamics of the peptide bound to protofibrils that spontaneously form under quiescent conditions². The match between the experimental and best-fit parameters obtained using DESTfit for model type 1 is excellent for both ΔR₂ and ¹⁵N-DEST for 260 μM Aβ40 (Fig. 2, solid lines). Parameter fitting using two-state (fit type 2) or three-state models (fit types 3–7) does not adequately fit the DEST and ΔR₂ data (two-state model: Fig. 2, dashed lines), indicating the necessity of the selection of a different model (i.e., fit type) to account for the observed behavior². The best-fit global parameters, $R_2^{\text{contact}}=16,200{\text{s}}^{-1}\pm 700{\text{s}}^{-1}$ and k_off = 48 s⁻¹ ± 3 s⁻¹, measure the slow dynamics of any residue in the dark state in direct contact with the protofibril surface and the dissociation rate constant from the dark state, respectively. Compared with the iterative fitting procedure originally used for the analysis of Aβ DEST data², DESTfit makes use of advanced features of MATLAB optimization routines for problems with large numbers of parameters but a sparse finite-difference Jacobian in order to significantly improve fit speed and convergence. As a result, there may be small differences in the absolute values of the fitted parameters from those reported previously², but these differences are insignificant. The residue-specific parameters $R_2^{\text{tethered}}$ and K₃ (Fig. 2) measure the average dynamics in the tethered portion of the dark state at each residue and the equilibrium constant between tethered and direct-contact states at each residue position, respectively. Together, these results provide direct observation of the otherwise invisible protofibril-bound state of Aβ. Larger values of K₃ indicate a higher fraction of time spent in direct contact with the high-molecular-weight species, as observed for the hydrophobic regions of Aβ40 and Aβ42 (ref. 2). Because $R_2^{\text{tethered}}$ increases as the average number of residues separating the residue of interest from the surface of the high-molecular-weight species decreases, the residue-specific $R_2^{\text{tethered}}$ can provide a measure of the average tethering length. By using this protocol, the residue-specific dynamic and kinetic parameters of dark states of other systems of biological interest will be accessible, thereby providing atomic-resolution characterization of the otherwise unobservable dark state.