Acoustic Radiation Force Impulse Imaging of Mechanical Stiffness Propagation in Myocardial Tissue

Abstract

Acoustic radiation force impulse (ARFI) imaging has been shown to be capable of imaging local myocardial stiffness changes throughout the cardiac cycle. Expanding on these results, the authors present experiments using cardiac ARFI imaging to visualize and quantify the propagation of mechanical stiffness during ventricular systole. In vivo ARFI images of the left ventricular free wall of two exposed canine hearts were acquired. Images were formed while the heart was externally paced by one of two electrodes positioned on the epicardial surface and either side of the imaging plane. Two-line M-mode ARFI images were acquired at a sampling frequency of 120 Hz while the heart was paced from an external stimulating electrode. Two-dimensional ARFI images were also acquired, and an average propagation velocity across the lateral field of view was calculated. Directions and speeds of myocardial stiffness propagation were measured and compared with the propagations derived from the local electrocardiogram (ECG), strain, and tissue velocity measurements estimated during systole. In all ARFI images, the direction of myocardial stiffness propagation was seen to be away from the stimulating electrode and occurred with similar velocity magnitudes in either direction. When compared with the local epicardial ECG, the mechanical stiffness waves were observed to travel in the same direction as the propagating electrical wave and with similar propagation velocities. In a comparison between ARFI, strain, and tissue velocity imaging, the three methods also yielded similar propagation velocities.

A major determinant of cardiac function is the precise coordination of the electrical conduction pathways and the resultant contraction of the heart.^1–3 Cardiac arrhythmias arise when there is improper electrical conductance within the heart, resulting in asynchronous or other abnormal cardiac function. Although much information about these arrhythmias can be gleaned by analyzing the global electrocardiogram (ECG), localizing the specific aberrant pathways that cause various arrhythmias is achieved primarily by determining the electrical propagation pathways within the heart. Current clinical methods that determine local electrical propagation involve the introduction of invasive intracardiac catheters and electrodes to measure the endocardial ECG directly. As a result, many groups have investigated indirect alternatives for measuring electrical propagation within the heart by tracking mechanical changes that follow from the action potential and therefore propagate along the same electrical paths.

The feasibility of indirectly measuring myocardial electrical propagation via mechanical motion tracking has been most directly demonstrated by attaching and tracking visual markers onto the heart.^4,5 Several imaging techniques have been investigated for their potential to noninvasively perform similar analyses. Faris et al.⁶ used tagged magnetic resonance imaging (MRI) to calculate circumferential strains in three dimensions within canine hearts and observed a mechanical wave occurring approximately 25 ms after the electrical activation propagation. Pernot et al.⁷ applied ultrasonic motion-tracking algorithms to observe a mechanical wave that propagated through the interventricular septum at systole within murine hearts and measured a mechanical propagation velocity that was comparable to velocities measured for electrical propagation. This method has since been successful in detecting irregular mechanical propagation in ischemic canine hearts.⁸ Rappaport et al.⁹ also used ultrasound to measure tissue motion within a two-dimensional (2-D) imaging plane in ovine hearts and demonstrated that the mechanical activation and propagation reflected its electrical homologue. All three methods estimated mechanical propagation velocities between 0.5 and 1.0 m/s, the typical range of measured electrical conductance velocities.¹⁰

These methods show promise as noninvasive alternatives for measuring mechanical analogues of electrical propagation; however, motion within the heart is dependent on various myocardial properties, including load, heart rate, and chamber volumes. Consequently, the subtleties of local displacements are difficult to observe in the presence of gross cardiac motion. Also, infarcted or hibernating tissues, which experience reduced contraction and compromised electrical conduction, are passively displaced by activity of adjacent tissues or changes in chamber pressure.^11,12 Therefore, identifying a propagating mechanical wave from tissue motion can be problematic.

Another mechanical property that could be used to track propagation within the heart is myocardial stiffness. Although several cellular mechanisms contribute to myocardial stiffness, the formation of actin-myosin cross-bridges has been shown to be a significant determinant in the increase of myocardial stiffness during contraction, with the greater number of cross-bridges resulting in increased stiffness.¹³ Therefore, as the electrical action potential stimulates cross-bridge formation, we expect myocardial stiffness to follow the electrical propagation paths.

Current clinical gold standards for myocardial stiffness measure a corollary value known as elastance. Rather than measuring the stress-strain relation, elastance is measured through parametric analysis of the pressure-volume (PV) relation. Several methods have been developed that use myocardial elastance as a measure for myocardial contractility and function as well as a determinant for cardiac disorders, including systolic and diastolic heart failure.^14,15 In addition, changes in myocardial elastance and stiffness have been correlated with the presence of infarcted, ischemic, and ablated tissue.¹⁶

Acoustic radiation force impulse (ARFI) imaging has been shown to provide insight into the local stiffness properties in various soft tissues.^17–23 ARFI imaging uses high-intensity acoustic pulses to apply acoustic radiation force to absorbing or reflecting targets within soft tissue and tracks the mechanical response of the tissue to gain insight into its elasticity. This phenomenon is caused by a transfer of momentum from the acoustic wave to the propagation medium. The radiation force (N/cm³) generated by a propagating acoustic wave is given by

$$F\left(\overrightarrow{r},t\right)=\frac{2\alpha I\left(\overrightarrow{r},t\right)}{c},$$ (1)

Where I(r⃗, t) is the local time-averaged acoustic intensity (W/cm²), α is the attenuation coefficient (Np/cm), and c is the speed of sound (m/s).^24,25 Within regions of interest where I(r⃗, t), α, and c are relatively constant, the radiation force, and therefore stress, can also be considered uniform. As the material’s elastic modulus and deflection under a given load are inversely related, the inverse of displacement can be interpreted as stiffness in the presence of uniform stress.

Investigations into cardiac ARFI imaging have demonstrated it to be capable of visualizing changes in local myocardial stiffnesses throughout the cardiac cycle, with rapid increases in left ventricular stiffness coincident with the QRS complex and ventricular systole.^26,27 We hypothesize that ARFI imaging can also measure myocardial stiffness propagation within the heart and present studies performed within an externally paced left ventricle that investigate this hypothesis.

Methods

Imaging Methods

A Siemens SONOLINE Antares ultrasound scanner (Siemens Healthcare, Ultrasound Business Unit, Mountain View, California) was used with a VF10-5 linear array for all experimentation. All B-mode and ARFI imaging sequences were acquired using the Siemens Ultrasonic Research Interface to record in-phase (I) and quadrature (Q) signals from the received echoes.²⁸ Each image was formed at a center frequency of 6.67 MHz and an axial focus of 1.5 cm. The ARFI-excitation pulse was also transmitted using a 6.67-MHz center frequency and a transmit F/# of 1.5. Conventional B-mode images were formed across a 38-mm lateral field of view and with a line density of 6.7 lines per millimeter. The imaging field of view was selected so that mechanical propagation could be repeatedly observed within the ultrasound images. Both B-mode and ARFI imaging acquisitions used 4:1 parallel-receive beamforming to shorten acquisition times.^26,29,30

All images of the heart were formed epicardially with an open-chest preparation. A vacuum apparatus, placed directly on the heart, was used to help the transducer better maintain a single imaging plane through the heart during a heartbeat.^31,32 The vacuum apparatus also helped maintain acoustic coupling (through an 8-mm-thick gel pad) with the myocardium. Displacements were estimated using a phase-shift estimation algorithm on the acquired I/Q data.³³ To correct for phase wrapping errors, displacement discontinuities through time greater than half of a wavelength within the data were shifted a full wavelength in the opposite direction. Physiological motion artifacts were removed from all ARFI images using an interpolation-based quadratic motion filter.²⁶

ARFI-induced displacement plots were made by taking the motion-filtered displacements measured 0.67 ms after cessation of the radiation force pulse at each lateral location. Time-delay estimates between these ARFI-induced displacement curves at various lateral locations were calculated using the normalized cross-correlation method.³⁴ A direction and velocity of propagation of myocardial stiffness across the field of view were then calculated based on the time-delay estimates and their lateral spacings.

M-mode ARFI imaging

Two-line M-mode ARFI images, as described by Hsu et al.,³² were acquired at a sampling rate of 120 Hz to observe stiffness changes within the heart for approximately one second (≈2 heartbeats). The lateral spacing of the two M-mode lines was 0.95 cm. The lateral spacing of the M-mode lines was selected to ensure sufficient distance to observe a measurable time delay between the two locations while maintaining a sufficiently large transmit aperture to generate each ARFI excitation. Traditional M-mode imaging was also simultaneously performed at each ARFI imaging lateral location at a sampling rate of 480 Hz. Incremental axial displacements were calculated from these M-mode lines with the same phase-shift estimation algorithm used to estimate displacements within the ARFI images.

From these data, midmyocardial axial tissue velocities and normalized axial strains were estimated. Axial tissue velocities were estimated by multiplying the incremental axial displacements measured within a 0.2-cm axial kernel at an imaging depth of 2.1 cm by the M-mode pulse repetition frequency. As the vacuum apparatus holding the transducer was placed directly on the heart, the observed motion of the myocardium differed from most other myocardial strain images in the previous literature, which almost exclusively use noninvasive (e.g., transthoracic) imaging. Therefore, midmyocardial normalized axial strains were calculated by tracking the axial positions of two points within the myocardium: one at the epicardial surface and the other at the midmyocardium. The difference in incremental axial displacements at these tracked points, divided by the axial distance between the two points, and integrated through time was taken to be the midmyocardial strain.³⁵ Linear drift was removed by fitting a line through the strains measured at the times of application of the pacing stimulus and subtracting it from the entire plot. Normalized strains were then calculated by dividing each individual strain plot by its largest measured strain magnitude.

ECG-gated 2-D ARFI imaging

ECG-gated 2-D ARFI images were also acquired in this study.³² As the hearts were externally paced for these experiments, the sequences were triggered off the pacing electrode stimulus rather than the global ECG. ARFI-induced displacements were measured at each lateral location at an ARFI imaging frame rate of 65 Hz. In total, 25 ARFI imaging frames were acquired within a single cardiac cycle. The 2-D ARFI image spanned a 22-mm lateral field of view with a line density of 3.3 lines per millimeter.

Physiological motion filter

An interpolation-based quadratic motion filter was used to separate ARFI-induced displacements from natural cardiac motion.³² The ARFI imaging sequences used preexcitation tracking so that displacement estimates made before transmission of the radiation force pulse could also be used in the physiological motion filter. For the two-line M-mode ARFI imaging sequences, an end-time threshold of 2.80 ms was used, leaving 0.33 ms of displacement data after this end-time threshold for the motion filter. In addition, 0.33 ms of displacement data immediately preceding the ARFI excitation were also used in the motion filter. In total, these tracking times corresponded to four preexcitation and four postexcitation displacement estimates. The ECG-gated 2-D ARFI images were motion filtered using two preexcitation displacement estimates within a 0.66-ms tracking interval and four postexcitation displacement estimates within a 1.32-ms tracking interval and after a 3.1-ms end-time threshold.

Experimental Methods

Local ECGs were recorded on the epicardial surface of the heart with an electrophysiology (EP) plaque whose aperture was selected to approximately match the ARFI imaging field of view and spanned a 3 × 3-cm surface with 112 electrodes. With the plaque held in place by hand, local electrocardiograms were recorded at each electrode at a sampling frequency of 3 kHz and bandpass filtered with cutoff frequencies of 0.5 Hz and 1000 Hz. Electrical propagation was measured by tracking the peak negative voltage measured at each point. Averaging through multiple consecutive heartbeats, the direction and lateral propagation velocities across the plaque were determined using a least squares linear regression of the times of these negative peaks and locations of each electrode. The velocity component of this regression was taken as the electrical propagation velocity.

Experimental Procedure

Two canine subjects, each weighing approximately 30 kg and with heart rates between 80 and 110 beats per minute (bpm), were imaged for these experiments as approved by the Institutional Animal Care and Use Committee at Duke University and conforming to the Research Animal Use Guidelines of the American Heart Association. A left thoracotomy was performed to expose the heart, and the pericardium was cut away. The transducer was inserted into a vacuum apparatus and centered over the left ventricular free wall, along the long axis of the heart. The transducer was positioned such that the left side of the image was toward the base of the heart.

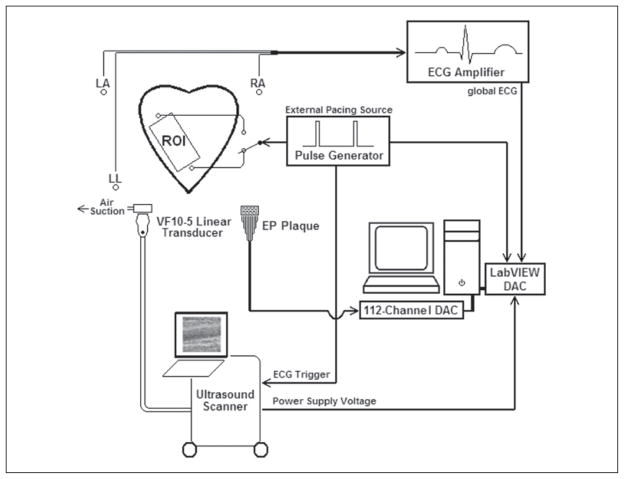
For both subjects, two stimulating electrodes were sutured onto the epicardium such that they were positioned laterally on either side of the transducer and in line with the imaging plane. The heart was paced externally by one electrode at rates slightly above (approximately +10%) the normal sinus rhythm of the animal. As a result, depending on which electrode was used to pace the heart, an electrical action potential could be made to propagate across the field of view from either base to apex (left to right) or apex to base (right to left). Throughout these experiments, the pacing site was alternated between the two electrodes while allowing the heart sufficient time to adjust to the pacing location before acquiring data. A diagram of the experimental setup is shown in Figure 1.

Figure 1.

Graphical representation of the experimental setup. An exposed and externally paced canine heart is imaged with a transducer/vacuum apparatus placed over a region of interest (ROI) directly on the left ventricular free wall. Electrocardiogram (ECG)–gated B-mode and acoustic radiation force impulse images, the voltage from the power supply of the ultrasound scanner, global ECG, and stimulating pulse waveforms were simultaneously recorded via data acquisition cards (DACs) and temporally registered. The procedure was performed while pacing on either side of the transducer. The transducer/vacuum apparatus was then removed and replaced with a 112-electrode electrophysiology (EP) plaque. The procedure was then repeated while recording local epicardial potentials over the same ROI.

As a control, passive, zero-amplitude excitation, two-line M-mode ARFI images of the left ventricular free wall were acquired for both subjects. These ARFI images were acquired while pacing from either electrode. Average absolute residual displacements, measured 0.67 ms after cessation of the radiation force pulse, were estimated across multiple heartbeats to examine the effectiveness of the physiological motion filter. The residual displacement plots were also inspected for indications of electromechanical propagation between the two lateral locations.

Active two-line M-mode ARFI images that included 45-μs excitation pulses were acquired for the first canine subject while pacing the heart from either stimulating electrode. An average time delay between the two M-mode tissue displacement curves was estimated through the cardiac cycle with the normalized cross-correlation method.³⁴ The time delay between the displacement curves was used to calculate a direction and velocity of propagation of myocardial stiffness.

A comparison between myocardial stiffness propagation and electrical action potential propagation was performed. Two-dimensional ARFI images were formed while the heart of the second canine subject was paced from the basal electrode. Time delays in lateral myocardial stiffening during systole were measured within a 2-D ARFI imaging field of view using the lateral location most proximal to the pacing source as the reference (zero-delay) curve. Least squares regression was used to determine a direction and average velocity of lateral stiffness propagation across the field of view. Next, the transducer/vacuum apparatus was removed and replaced with the EP plaque. The local epicardial electrocardiograms were recorded within a comparable field of view across multiple consecutive heartbeats. The propagation of the electrical action potential was determined, and a lateral propagation velocity and direction were calculated. These values were compared with the ARFI imaging-assessed direction and velocity of myocardial stiffness propagation. The process was repeated while pacing from the apical electrode.

To examine the relationship between stiffness and other metrics that have been used to determine myocardial electromechanical propagation, two-line M-mode ARFI images were formed while the heart of the second canine subject was paced from the apical electrode. Midmyocardial ARFI-induced displacements, normalized strains, and tissue velocities were calculated from this sequence. Propagation velocities were calculated by estimating the systolic time delays between the two lateral locations from each of these measurements. Systole was defined as the period between the excitation of the stimulating electrodes and the moment when the ARFI-induced displacements reached their minimum. The transducer/vacuum apparatus was removed and replaced with the EP plaque. A linear least squares regression was used to calculate electrical propagation velocities, and those values were compared with the three mechanical propagation velocities.

Results

For each experiment of this study, three or four image acquisitions of each data type were performed. As the purpose of this study was to demonstrate a potential application of ARFI imaging, the entirety of the results from every acquisition is not presented. Instead, the ARFI imaging data presented most clearly reflect the general trends observed within the full data sets.

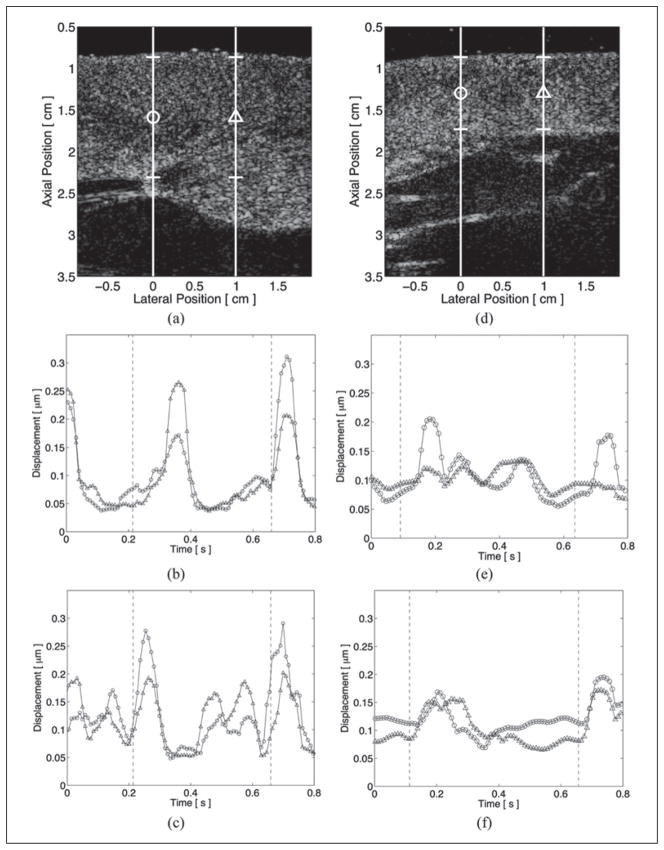
As passive ARFI imaging sequences provide no external excitation to the tissue, displacements measured within these images are results of cardiac motion only and, after motion filtering, reflect the expected levels of cardiac motion artifact within subsequent ARFI images. Average absolute residual displacements through the entire thickness of the left ventricular free wall of the two animal subjects from passive ARFI imaging acquisitions are shown in Figure 2. Figure 2a–c corresponds to the first animal, and Figure 2d–f corresponds to the second animal. Lateral positions and regions of interest are marked by their respective shapes within the matched B-mode images in Figure 2a, d. Residual displacement plots obtained while pacing from the basal electrode are shown in Figure 2b, e. Residual displacement plots obtained while pacing from the apical electrode are shown in Figure 2c, f. The application of the pacing stimulus is marked in each ARFI-induced displacement plot by dashed vertical lines. From these four plots, the motion filter used in these experiments can be observed to reduce physiological motion artifacts to below 0.35 μm through the entire cardiac cycle. Physiological motion artifacts were greatest shortly after application of the pacing stimulus and corresponded to myocardial contraction and periods of increased cardiac motion. However, no direction of propagation can be observed within any of these residual displacement plots, as no clear delay is present between the two lateral locations.

Figure 2.

Average absolute residual displacements through multiple heartbeats from passive, two-line M-mode acoustic radiation force impulse images within the left ventricular free walls of two animal subjects. The corresponding B-mode images (a and d) show the lateral locations marked by their respective shapes and the regions of interest. When pacing from either the basal (b and e) or apical (c and f) electrode, displacement artifacts are below 0.35 μm through the entire cardiac cycle. The times of application of the stimulating electrodes are marked in each plot by the dashed vertical lines.

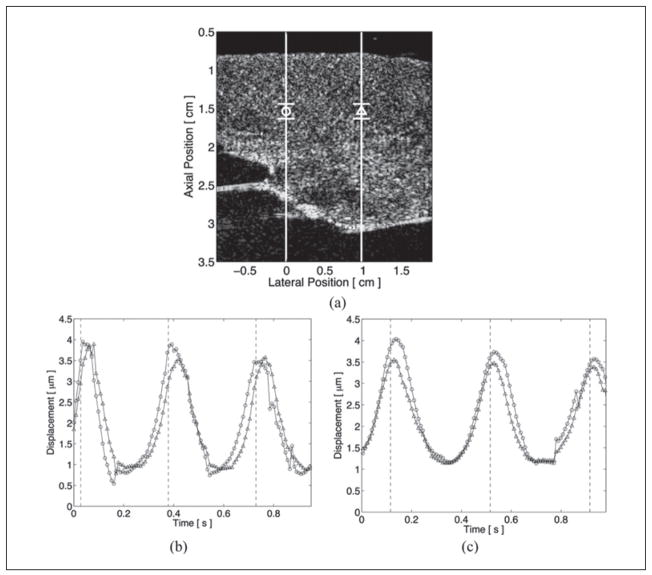
The propagation of myocardial stiffness can be seen with ARFI imaging, as demonstrated in Figure 3. Lateral locations and relative depths of the displacement plots within the M-mode ARFI images are marked by vertical lines and their respective shapes in the corresponding B-mode image in Figure 3a. The motion-filtered displacement plots of the active two-line M-mode ARFI imaging acquisitions are shown in Figure 3b, c. Application times of the pacing stimulus are marked by the dashed vertical lines within each displacement plot. As the ARFI imaging sequences included high-intensity excitation pulses, these displacement plots contain both tissue displacements responding to the application of radiation force as well as physiological cardiac motion artifacts comparable to those previously measured in Figure 2c, e. Both plots show myocardial stiffening and relaxation occurring earlier for the M-mode line proximal to the excitation source. When pacing near the base (Figure 3b), the M-mode line on the left side of the image can be observed to lead the M-mode line on the right. When pacing near the apex (Figure 3c), the reverse trend can be seen as the M-mode line on the right side of the image now leads the left. Using the normalized cross-correlation method, the average time delay between the M-mode ARFI lines through systole for the two complete cardiac cycles was estimated to be 11.3 ± 2.5 ms when paced from the base and −10.7 ± 4.4 ms when paced from the apex. These delays corresponded to average propagation velocities between the M-mode lines of 0.84 m/s and −0.88 m/s, respectively.

Figure 3.

Matched B-mode and active two-line M-mode acoustic radiation force impulse (ARFI) images of an externally paced left ventricle. The lateral locations and regions of interest are marked with their respective shapes within the B-mode image (a). Pacing electrodes were positioned on either side of the lateral field of view. The times when the myocardium was stimulated by the pacing electrodes are marked by the dashed vertical lines within the ARFI-induced displacement plots. When pacing from the left (b), myocardial stiffening at the left lateral location (circle plot) leads the right (triangle plot). When pacing from the right (c), the reverse trend is seen, and myocardial stiffening at the right lateral location now leads the left.

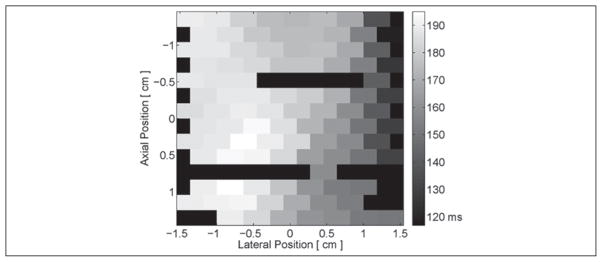
A time-to-peak negative epicardial voltage image, recorded by the 112-electrode EP plaque, is shown in Figure 4. This image has been masked at pixels with no discernible action potential. These inactive locations were the result of improper contact between the plaque and the myocardial surface as well as poor connections between the plaque and the recording system. With the pacing source positioned to the right of the image, peak negative voltages can be seen to occur later in time as the distance from each electrode to the pacing source increases. As the plaque was elevationally centered on the pacing source, this electrical propagation was predominantly in the lateral dimension (right to left) with only a slight bottom-to-top propagation. An acceleration of this wave as it propagated away from the pacing source can also be seen within this image as differences in the time of peak negative voltage on the left side of the image were less than on the right side of the image.

Figure 4.

Sample time (milliseconds after application of the pacing stimulus) to peak negative epicardial voltage along a section of canine left ventricular free wall. With the pacing electrode located near the apex and to the right of the image, a general trend of increasing time delays to peak negative voltage from right to left is present. Black-colored pixels within the image indicate electrodes where an action potential could not be measured.

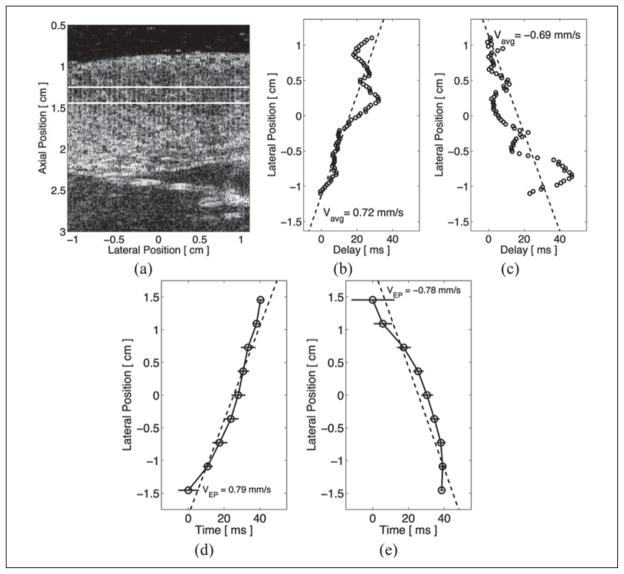
Estimated time delays between ARFI-induced displacement curves within 2-D ARFI imaging acquisitions are shown in Figure 5. The matched B-mode image is shown in Figure 5a with the region of interest marked between the two horizontal lines. Time delays were estimated while pacing externally from either the basal (Figure 5b) or the apical (Figure 5c) electrode. In each case, the lateral location most proximal to the pacing electrode was used as the reference (zero delay) line. As observing stiffness propagation and measuring propagation velocities were of interest, the independent and dependent axes are switched in these time-delay plots. Both plots show increasing delays as the lateral locations moved farther away from the selected stimulating electrode, reflecting the propagation of mechanical stiffness across the field of view and away from the pacing electrode. Linear least squares regressions of the ARFI imaging-based data estimated average lateral propagation velocities across the field of view to be 0.72 m/s (R² = 0.69) for right-traveling propagation and −0.69 m/s (R² = 0.65) for left-traveling propagation. The corresponding epicardial electrical propagation velocities for each stimulating electrode were measured to be 0.79 m/s (R² = 0.91) and −0.78 m/s (R² = 0.83).

Figure 5.

Matched B-mode and time delays between acoustic radiation force impulse (ARFI)–induced tissue displacement curves and times to peak negative epicardial voltages when paced by an external source. The ARFI imaging region of interest is marked by the two horizontal lines within the matched B-mode image (a). The lateral location most proximal to the selected pacing source was defined as the reference line and zero delay. When pacing from either the left (b) or the right (c) side of the image, time delays between the other lateral locations and that reference line were estimated using the normalized cross-correlation method. Time delays to peak negative voltages are shown when observing electrical propagation while pacing from the left (d) or the right (e) side of the image. Using a least squares linear approximation (dashed lines), the average propagation velocities of the left- and right-traveling stiffness propagation were measured to be −0.69 m/s and 0.72 m/s, respectively. The corresponding electrical lateral propagation velocities were measured to be −0.78 m/s and 0.79 m/s, respectively.

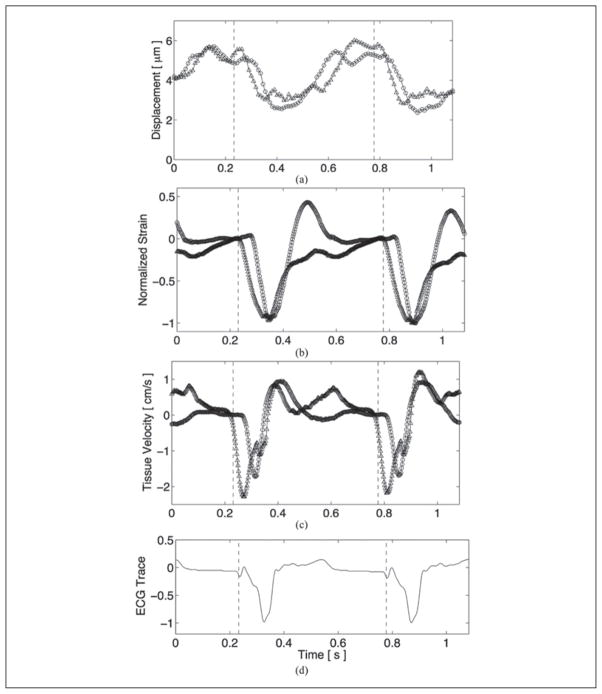
A comparison of electromechanical propagation between ARFI, strain, and tissue velocity imaging, while pacing from the apical electrode, is shown with the matched global ECG in Figure 6. Electromechanical propagation at systole is evident for all three cases, as the M-mode line proximal to the pacing site (triangle plot) leads the distal M-mode line (circle plot). Using the normalized cross-correlation method, average systolic propagation velocities measured with ARFI, strain, and tissue velocity imaging, with standard deviations reflecting the variability within the calculated time delays at different times during systole, were 0.75 ± 0.13 m/s, 0.78 ± 0.04 m/s, and 0.71 ± 0.12 m/s, respectively. The corresponding average lateral electrical propagation velocity on the epicardium was measured with the EP plaque to be slightly faster, at 0.86 ± 0.23 m/s.

Figure 6.

Electromechanical propagation comparison between acoustic radiation force impulse (a), normalized strain (b), and tissue velocity (c) imaging with the matched global electrocardiogram (d). The points of application of the pacing electrode are marked by the dashed vertical lines in each plot. For all three cases, the M-mode line proximal to the pacing source (triangle plot) leads the distal M-mode line (circle plot) at systole.

Discussion

With the inclusion of preexcitation tracking lines, the interpolation-based motion filters effectively reduced average physiological cardiac motion artifacts to below 0.35 μm through the thickness of the myocardium at all points of the cardiac cycle. With diastolic ARFI-induced tissue displacements above 3.5 μm in all subsequent acquisitions, motion artifacts were sufficiently low to make accurate time-delay estimates and calculate propagation velocities with ARFI imaging. Motion artifacts were also reduced by the vacuum apparatus, which steadied the transducer atop the regions of interest and reduced out-of-beam motion and the resultant signal decorrelation.

In all ARFI-induced displacement plots presented in this article, a rapid decrease in ARFI-induced displacements during systole and an increase in displacement during diastole can be observed. However, intersubject variability in the shape of the ARFI-induced displacement plots is also present. Some of this is can be attributed to the fact that, although the left ventricle was always imaged, transducer positioning between subjects was only approximately maintained. In addition, as maintaining contact between the transducer and the heart was a major priority, the pressure applied by the transducer on the heart to accomplish this requirement varied between subjects. Therefore, a variable external load on the heart was present, possibly causing these intersubject disparities in how the hearts contracted and in the shape of the ARFI-induced displacement waveforms.

Two-line M-mode ARFI imaging methods estimated similar propagation velocity magnitudes between the two lateral locations when paced from either side of the transducer. In addition, both observed propagation directions corresponded to stiffness propagation that was traveling away from the pacing source, as expected. In all M-mode ARFI-induced displacement plots, a short delay (approximately 30 ms) can be observed between the application of the electrical stimulus and the point where the ARFI-induced displacements dropped sharply and indicated the onset of myocardial stiffening. This delay can be attributed to a lag between electrical activation and mechanical contraction as well as an approximately 1-cm separation between the pacing electrode and the positions of the M-mode lines and the time associated with the action potential propagating from the pacing source into the field of view.

The 2-D ARFI images produced similar results to the two-line M-mode acquisitions, as the ARFI-induced displacement curves at lateral locations proximal to the pacing electrode led those measured at distal locations. In addition, the magnitudes of the average propagation velocities within each 2-D image were comparable to each other. The two-line M-mode ARFI imaging sequences estimated greater propagation velocities, although all values were between the predicted range of electrical conductance propagation.¹⁰ One likely explanation for this difference is the fact that electrical propagation is dependent on the underlying myocardial fiber orientation and conduction pathways. As a result, a degree of variability within the measured propagation velocities between experiments and subjects is expected, and an exact reproduction of results among subjects is unrealistic. To fully characterize this phenomenon and assess its potential clinical significance, however, a future investigation including more subjects is needed.

As demonstrated in Figure 5, the matched average epicardial electrical propagation velocities calculated within the same field of views agreed with average stiffness propagation velocities in both direction and magnitude. The percent differences in velocity magnitudes between these two methods for the left- and right-traveling action potentials, using the local electrical propagation velocities as the gold standard, were calculated to be −8.9% and −11.5%, respectively. This agreement suggests that stiffness propagation followed electrical propagation. In both directions, however, propagation velocities estimated from ARFI imaging were slower than those measured from the epicardial action potential. A probable cause for this discrepancy is that the M-mode ARFI-induced displacement plots reflect midmyocardial lateral stiffness propagation, whereas the electrodes of the surface plaque measured epicardial lateral electrical propagation. As a result, with the complex geometry and structure of the heart, stiffness propagation measured through the midmyocardial band may not reflect propagation at the superficial but approximately parallel surface of the epicardium. In addition, as propagation velocities were measured only in a single (lateral) dimension, any misalignment between the transducer and epicardial plaque would result in differences between these two measurements.

The time-delay profiles in Figure 5 suggest that a constant velocity approximation does not adequately model the observed propagations. ARFI imaging-derived delays can be observed to oscillate about an average stiffness propagation velocity, while the epicardial ECG appears to accelerate as the action potential propagates away from the pacing source. This discrepancy could have been caused by many factors, including motion artifacts or imprecise temporal gating and registration of the 2-D ARFI imaging sequences. Nevertheless, although higher order differences exist between these two methods, the results indicate that myocardial stiffness propagation approximately follows the measured electrical propagation within the heart.

When comparing ARFI, strain, and tissue velocity imaging, all three methods indicate that electromechanical propagation is most easily observed during systole and myocardial contraction. As seen in the previous 2-D ARFI imaging/electrical propagation comparison, the electrical propagation velocity was estimated to be higher than any of the electromechanical measurements, although still within one standard deviation of the data. Transducer-plaque misregistration and variant propagation paths through the thickness of the myocardium may be the source of this discrepancy. Such nonuniform activation electrical propagation has been observed in previous studies.³⁶ Conversely, as all three electromechanical measurements (ARFI-induced displacements, normalized strains, and tissue velocities) were made within a single region of interest and during a single acquisition, the average propagation velocities could be expected to be more similar and accordingly were all within 0.1 m/s of each other.

The two-line M-mode ARFI-induced displacement plots in Figure 3 from the first subject display stiffness curves with one lateral location leading the other throughout the entire cardiac cycle. This is not the case with any of the mechanical plots in Figure 6 in diastole, defined as the period between the T-wave and the application of the next pacing stimulus. No clear indication of a diastolic mechanical wave propagating away from the pacing electrode was present. All three methods suggested some degree of reversal in propagation, while the strain and tissue velocity plots also had dissimilar mechanical activity between the two lateral locations. Consequently, diastolic delay and propagation velocity estimation were not performed. These results likely can be attributed to the passive nature of diastolic relaxation. As no subsequent action potential actively stimulates repolarization, the cellular mechanisms of diastolic repolarization occur in a less spatially coordinated manner.³⁷ As a result, myocardial relaxation may not follow the same propagation paths as during contraction.

As previously mentioned, all ARFI-induced displacement plots contained a short time delay after application of the stimulating pulse to the onset of myocardial stiffening and contraction. This delay is believed to be associated with the time necessary for the electrical signal to propagate from the stimulating electrode into the field of view. However, the same delay was not observed in these experiments within the other electromechanical plots, as strains and tissue velocities at the M-mode line proximal to the pacing source begin to fall nearly coincident with the stimulating pulse. This apparent lack of delay could be a consequence of both strain and tissue velocity imaging being motion-based algorithms. As such, these measurements are derived from observing changes in myocardial fiber lengths and thicknesses as the muscle contracts and relaxes. However, as no one myocardial fiber can move independently of another, an action potential may induce additional motion that is uncoupled from the propagation of the electrical action potential and can therefore propagate at velocities determined by the mechanical properties of the tissue. Additional experiments are necessary to examine this phenomenon before definitive conclusions can be made.

ARFI imaging may experience a similar effect in the presence of bulk changes in myocardial elasticity—both actively from changes in stiffness of the surrounding myocardium and passively from changes in external sources that influence myocardial stiffness, such as chamber pressures. The observation of the temporal delay between the application of the stimulating pulse and the onset of myocardial stiffening within each ARFI-induced displacement plot presented within this article suggests that these bulk changes in myocardial elasticity are more subtle, and therefore ARFI imaging may be better suited to make high-spatial-resolution images of electromechanical propagation. However, further optimization or more sophisticated strain and tissue velocity estimates may be able to account for these neighboring effects and improve spatial resolution.

The research herein presented propagation velocities only in the lateral dimension. To obtain additional information and increase the applicability of ARFI imaging, 2-D or full three-dimensional (3-D) stiffness propagation maps are preferred. Although not performed in this study, axial stiffness tracking may be achievable by selecting an appropriate ARFI-excitation F/# so that the depth of field can span the entire thickness of the tissue. Elevational stiffness tracking can be achieved with 3-D ARFI imaging. Preliminary research into 3-D ARFI imaging has been performed with promising results.³⁸ However, frame and sampling rates must be considered when forming ARFI images with sufficient temporal resolution necessary to predict electromechanical propagation.

An important factor in the visualization of stiffness propagation is maintaining a specific region of myocardium within the field of view. As a result, this experiment was performed on an exposed chest with a vacuum apparatus stabilizing the transducer over a fixed section of myocardium. If attempting to visualize stiffness propagation less invasively, more sophisticated motion-tracking techniques and filters would be necessary. In addition to this requirement, due to the regular challenges of transthoracic cardiac imaging in general—such as the limited number of viewing angles and relatively great depth of the heart—transthoracic ARFI imaging of stiffness propagation is problematic. However, an intracardiac approach may be a more successful, as the imaging transducer could be placed in close proximity over a region of myocardium and maintain a fixed view of that region of myocardium. Given the invasive nature of an intracardiac implementation, it may also be possible to concurrently (along with ARFI imaging) measure electrical activity with a conventional electrode-based approach and decouple the electrical component from the mechanical component in the resulting electromechanical response. Such an approach would offer keen insight into the mechanical nature of cardiac pathologies and could present new diagnostic opportunities.

Conclusion

ARFI imaging was able to determine a direction and velocity of the propagation of mechanical stiffness through the myocardium. The measured velocities of myocardial stiffness propagation are comparable to typical values of measured electrical conductance velocities. The measured epicardial electrophysiological wave propagation matched the direction of propagation of the stiffness wave. The velocities of mechanical stiffness propagation also closely matched those measured using strain and tissue velocity methods. These results indicate that ARFI imaging is capable of measuring myocardial stiffness propagation during systole.