Abstract
The extracellular space (ECS) consists of the narrow channels between brain cells together with their geometrical configuration and contents. Despite being only 20–60 nm in width, the ECS typically occupies 20% of the brain volume. Numerous experiments over the last 50 years have established that molecules moving through the ECS obey the laws of diffusion but with an effective diffusion coefficient reduced by a factor of about 2.6 compared to free diffusion. This review considers the origins of the diffusion barrier arising from the ECS and its properties. The paper presents a brief overview of software for implementing two point-source paradigms for measurements of localized diffusion properties: the real-time iontophoresis or pressure method for small ions and the integrative optical imaging method for macromolecules. Selected results are presented. This is followed by a discussion of the application of the MCell Monte Carlo simulation program to determining the importance of geometrical constraints, especially dead-space microdomains, and the possible role of interaction with the extracellular matrix. It is concluded that we can predict the impediment to diffusion of many molecules of practical importance and also use studies of the diffusion of selected molecular probes to reveal the barrier properties of the ECS.
1 Extracellular Space
The vast numbers of cells that compose the brain fall into two classes: neurons and glia. Neurons process information and signal to each other predominantly by fast electrical signals whereas the glial cells are more enigmatic in function but may be broadly described as supporting the neurons. The two types of cells occur in similar numbers and have complex shapes. They are closely packed but, crucially, every cell is separated from its neighbor by a small gap and the multiply connected space comprising all these gaps is known as the extracellular space (ECS; Fig. 1A). One may think of each cell as being enveloped in an ‘atmosphere’ of ECS and, indeed, the totality of the ECS has been likened to the water phase of a soap film.
Figure 1.
ECS geometry. Panel A shows electron micrograph of a region of rat cortex with several nerve fibers, together with other neuronal and glia extensions, surrounding a dendritic profile containing mitochondria. The ECS has been outlined in red but the true width is likely underestimated because of shrinkage during the fixation and processing of the tissue. Note that some fibers form bundles; this may produce anisotropic diffusion in some brain regions. Scale bar approximately 1 μm. Micrograph courtesy of Dr. C. B. Jaeger. Panel B shows simplified schematic of a small region of ECS between a group of neurons (green) and glia (red). The ECS may harbor dead-space microdomains in the form of local expansions, or voids (V), or invaginations (I) of cellular elements or glial wrapping around cells.
The ECS is vital to the function of brain cells. It provides a reservoir of ions, most importantly, Na+, K+, Ca2+ and Cl− that are essential to maintain neuronal electrical activity. It allows metabolic substrates and products to move to and from the network of blood vessels that permeate the brain and it also allows other substances, acting as chemical signals, to travel between cells. It is this aspect of the ECS, as a conduit for the movement of molecules, which will be the focus of this brief review. Not only may the ECS be viewed as a passage way, it may also be seen as a barrier to molecular movement. From an applied perspective, the ECS is a crucial route for the delivery of drugs to brain cells – in cancer chemotherapy for example – and this provides further impetus for study.
There have been two reviews of diffusion in the ECS that are much more extensive than that provided here. The review by Nicholson (14) was written for a physics audience and the more recent and comprehensive paper by Syková and Nicholson (27) contains an outline of theory with more physiological data and extensive references. A shorter review (16) has been popular as an introduction to the topic. Because of these prior reviews only a few illustrative references will be cited here.
1.1 Definitions and equations
Together the ECS and the cells may be viewed as a two-phase porous medium; the ECS is the highly connected phase whereas individual cells are isolated from each other. Substances are confined to move in the ECS because cell membranes are either impermeable or only permeable to certain molecules. The medium within the ECS is mainly water with the addition of approximately 150 mM of NaCl and many other ions and substances present at much smaller concentrations. The average width of the ECS is estimated to be between 20–60 nm (34), nevertheless the ECS typically occupies 20% of the brain. This is formally represented by the volume fraction, α, defined as
| (1) |
where the subscripts on V denote the respective volume of ECS and the volume of the whole tissue both measured in a small region of brain that is sometimes referred to as a Representative Elementary Volume (REV). Volume fraction is written as a decimal and in an unhindered or ‘free’ medium, such as an aqueous solution or very dilute gel, α = 1. In other disciplines, volume fraction may be called ‘porosity’. If the average volume of a cell or cellular element is VC and the associated cell surface area is SC then, regarding the cell surface as having a layer of ECS of thickness d, so that 2d is the average width of the ECS, it follows that the average volume-to-surface ratio for the cellular element, P, is given by
| (2) |
Later in this review we will make the gross simplification that the brain is composed of cubical cells, each with a side of length 2a, so P = a/3 then, if α = 0.2 and the ECS width is taken as 2d = 60 nm, we obtain from the approximation in Eq (2) that 2a = 0.72 μm as the side of a ‘typical’ cell (a precise calculation based on cubic geometry would yield 2a = 0.78 μm because the diagonal space where edges of cubes are adjacent is widened by a factor of ).
Substances released into the ECS move predominately by diffusion. Using volume averaging techniques appropriate for porous media (14, 15) the classical diffusion equation can be derived:
| (3) |
Here C is concentration in the ECS, Q is the strength of a source of released substance and f(C) is a term representing loss of diffusing material by a variety of processes and kinetics. Note that neuroscientists usually define the concentration C with respect to the ECS while others may favor defining concentration with respect to the whole tissue; these two concentrations differ by the factor α. The reason that neuroscientists prefer their definition is because the receptors on the surfaces of cells sense the local concentration in the ECS so this is the physiologically relevant variable.
A crucial parameter appearing in Eq (3) is the effective diffusion coefficient, D*, measured in the brain. We assume that D* is constant within a brain region where the anatomical structure is homogeneous (e.g. neocortex). This conclusion is supported by experimental measurements which essentially perform a random sampling. Note that over very small distances of a few micrometers there will be local fluctuation in D* but all our equations assume volume averaging over an appropriate REV so local fluctuations are removed (15).
Because of the hindrance imposed by various factors, D* < D where D is the diffusion coefficient measured in a ‘free’ medium (ideally water but in a neuroscience context, a dilute salt solution). Hindrance to diffusion is captured in the dimensionless tortuosity parameter, λ, where
| (4) |
In certain tissues (e.g. corpus callosum or molecular layer of the cerebellum) diffusion is inherently anisotropic and both D* and λ become tensors rather than scalars. In some situations there may be an additional term in Eq (3) representing the contribution of bulk flow (hydrodynamic flow) that will take the form of a scalar product of the flow velocity vector v and concentration gradient ∇C. The requirement for this term is still debated and, in any event, bulk flow will have little influence on short-term and near-distance diffusion and is neglected in this review. Bulk flow does play a role when drugs are infused into brain tissue under pressure, a technique often called convection enhanced delivery (CED) (2).
1.2 Relevant solutions to diffusion equation
Here we describe some solutions to Eq (3) that are of practical importance in research on diffusion in brain tissue. In the following discussion the extracellular concentration, C, is understood to vary smoothly over space, despite the presence of vast numbers of boundaries and local discontinuities (Fig. 1B) because volume averaging arguments have shown this to be justified (15).
Probably the simplest case where the diffusion equation has been applied in the brain is when a radiolabeled substance at concentration C0 has been perfused over a surface for a long period and the subsequent radioactivity at time t counted in small blocks of tissue to provide C as a function of distance x from the perfused surface (5). Then Eq (3) becomes one-dimensional with no source or loss terms and (ref. 4, Eq 2.45)
| (5) |
here and elsewhere ‘erfc’ is the complementary error function.
Typically, radiolabeled sucrose (D = 7.0 × 10−6 cm2s−1 at 37 °C; Section 2.5) is used because it remains in the ECS. Measurement times are typically t ~ 1 hour and x is measured in mm or cm. Curve fitting extracts λ while α can be determined by measuring the radioactivity per unit volume of tissue adjacent to the perfused surface. This method of measuring diffusion was used extensively by Rall, Fenstermacher, Patlak and others in the 1960’s and 1970’s (see ref. 14 for references) but is not in common use anymore. Equation (5) remains useful, however, for estimating how a drug might penetrate the brain when perfused into a ventricle (brain cavity).
Today, diffusion measurements in brain tissue usually involve a ‘point-source paradigm’ where a probe substance is released from a pseudo point-source, typically a micropipette with a tip diameter of 2–5 μm, and the ensuing concentration distribution sampled at a single location as a function of time or at a sequence of times as a function of distance. To obtain the basic point-source solution to Eq (3) the tissue is assumed homogeneous and the source Q is regarded as a Dirac delta function in both space and time, i.e. instantaneous release of a substance at the origin of a Cartesian coordinate system. To give generality to the solution we can take the medium as being anisotropic and assume that measurements are made in the principal axes defined by the diffusion or tortuosity tensor and that these axes coincide with the Cartesian coordinates. It is also useful to include a term for loss of the diffusing substance and usually it is adequate to represent this by a first order process, f (C) α = k′C, then the solution to Eq (3) is (27):
| (6) |
where . In an isotropic medium, λx = λy = λz = λ and .
In many instances it is desirable to release the substance at a point-source in space but deliver it as a pulse of finite duration tp, then by convolution in time of the solution with a delta function source, Eq (6), one obtains for 0 ≤ t ≤ tp
| (7) |
and the concentration after the pulse ends, t > tp, is simply given by
| (8) |
1.3 Barrier properties
Extensive experimental data (see Section 2.4) show that a typical value for λ in the nervous system is about 1.6, which implies that D* is some 2.6 times smaller than D. This is true only for molecules or ions that are much smaller than the typical width of the ECS; for macromolecules λ is increased, in part because of more frequent interaction with the walls of the narrow channels through the ECS (34). Furthermore, the space accessible to the traveling molecule is restricted to about 20% of the whole tissue volume (i. e. α = 0.2). Thus all molecules that diffuse through the ECS are substantially hindered and the ECS acts as a barrier between the source of the molecules and the target. The properties of this barrier may change when the brain experiences trauma or during growth and development (27). There may even be much finer, local, control of λ and α that our present techniques cannot resolve.
What is the origin of the hindrance to diffusion in brain tissue? There are two main contributions to tortuosity: geometry and extracellular matrix. In discussing geometry it needs to be recognized that the ECS is a well-connected region in the sense that, between any two locations a few tens of micrometers apart, there are multiple paths through the ECS. Thus hindrance does not arise from an approach to a percolation threshold, rather, the geometry impedes diffusion by introducing delays into the diffusion process (7, 8,), either by the necessity for diffusing molecules to travel around cellular boundaries or because they encounter dead-spaces.
It is obvious that the first geometrical effect will come into play when molecules are forced to take a more circuitous route between two points, increasing the travel time and resulting in a reduced D* and larger λ. There is a second type of geometrical entity that can produce a further increase in tortuosity, namely ‘dead-space microdomains’. These may be introduced by invaginations (‘I’, Fig. 1B) in cell membranes so the cells are no longer convex, through the ECS enlarging locally to create ‘voids’ (‘V’, Fig. 1B) or by partial enclosure of neurons by glia cells (Fig. 1B) to form a local dead-end. The common feature of all theses dead-spaces is that when particles enter these regions they lose a certain amount of time inside before emerging and continuing on through the highly connected ECS. The concept of a dead-space affecting diffusion is well established in other disciplines: for example dead-end pores were analyzed by Goodknight et al. (6) while the influences of local changes in size of the connected space were explored by Siegel and Langer (24) and in our own study (3). This topic will be discussed in more detail in Section 3.2.
The extracellular matrix is largely composed of long-chain molecules many of which carry fixed negative charges on the predominant molecular species that include chondroitin sulfate, heparan sulfate and hyaluronan (33, 36). The matrix can assert a viscous drag on diffusing molecules and the negative charges may interact with mobile positively charged ions or molecules or interact more specifically with the mobile molecules. More will be said about the matrix in Section 3.3.
1.4 Role of experiments and modeling
Experiments with small radiolabeled tracers some 50 years ago established the approximate values of λ and α that we use today (14). To obtain parameter values, these early experiments relied on a careful fitting of solutions to the diffusion equation with the experimental data and the success of the analysis not only provided parameter values but also confirmed that the diffusion equation was applicable to such a complex medium as the brain. This symbiosis of experiment and theory continued with the introduction by Nicholson and Phillips (15) of the real-time iontophoresis (RTI), and the closely related real-time pressure (RTP) injection, methods that embody the point-source paradigm for diffusion analysis in the brain; these have now been used in more than 50 experimental studies (27). While very successful in measuring basic structural parameters, the RTI and RTP methods have mainly employed the cation tetramethylammonium (TMA+) and are not suitable for studying the diffusion of larger molecules. To overcome this restriction, the integrative optical imaging (IOI) method was introduced by Nicholson & Tao (17). The RTI, RTP and IOI methods will be detailed in Section 2.
As more and better data accumulated, there has been increasing impetus for more sophisticated modeling to test hypotheses about the factors responsible for the measured values. Several models emerged, which are briefly surveyed by Syková & Nicholson (27). Here we will focus on the Monte Carlo simulation approach (Section 3). As studies of diffusion in the brain have progressed, a gradual paradigm shift has occurred. Initially, especially with the radiotracer techniques, the focus was on how particular molecules moved through the brain, their effective diffusion coefficients, the ‘distribution space’ (molecules that permeate and accumulate in cells may have an apparent α > 1) and the loss characteristics. These sorts of data are valuable for describing drug delivery. Later, the emphasis shifted somewhat to using molecules that were predominantly confined to the ECS and whose diffusion behavior could enable them to probe the structural constraints provided by their local environment. Previously the ECS had been largely inaccessible to study because the size of the channels is not accurately preserved for electron microscopy (34) but the use of diffusion as a tool for structural analysis has led to an increased understanding of the microenvironment of the ECS.
2 Experimental measurement techniques
This section briefly outlines the two point-source paradigms in current use and describes the custom software that is available to control the experiments, acquire the data and fit the data with the appropriate solutions of the diffusion equations. All the software is now written in Matlab (Mathworks, Natick, MA, U.S.A).
2.1 Real-time pressure (RTP) and real-time iontophoresis (RTI) methods
The real-time pressure (RTP) and real-time iontophoresis (RTI) methods both use two micropipettes, one to release the diffusing substance and the other to measure the concentration at a point (Fig. 2). In both techniques the source micropipette is filled with a solution of the substance of interest but the ejection methods differ. For RTP, a brief pulse of nitrogen gas (~ 0.1 s) is applied via a sealed tube inserted in the back of the micropipette and this approximates a delta function in time and causes a brief release of the substance of interest from the tip of the micropipette. The subsequent spread of molecules in the ECS then follows Eq (6). The source term is given by Q = UCf, where U is the volume ejected and Cf is the concentration of the ejected substance. For RTI, a silver wire coated with AgCl is sealed into the back of the micropipette and a pulse of current, of appropriate polarity, applied for 10–60 s, causing iontophoretic release of a suitable substance, which must be charged. Because of the finite pulse duration, Eqs (7) and (8) now describe the diffusion process. The source is Q = Int/zF where I is the applied current, nt is the transport number of that source micropipette (i.e. the fraction of the applied current that ejects the substance of interest), z is the substance valency and F is Faraday’s electrochemical equivalent.
Figure 2.
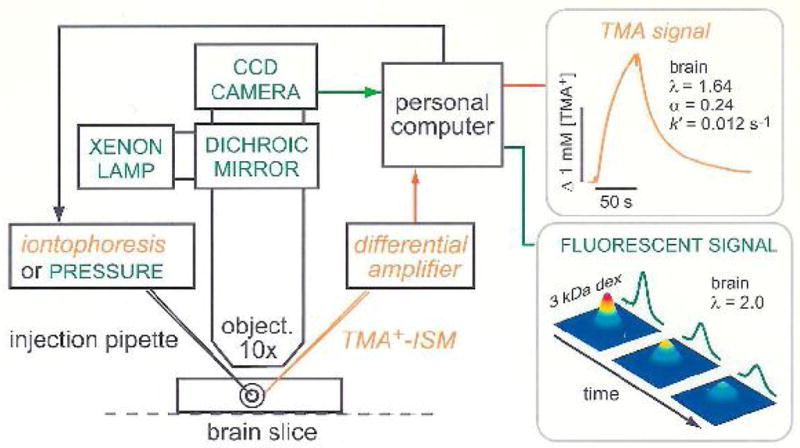
Setup for diffusion measurements using the real-time iontophoretic or pressure (RTI/RTP) methods and integrative optical imaging (IOI) method. A brain slice or dilute agarose gel is placed in a chamber that is perfused with oxygenated physiological saline solution on the stage of a compound microscope. For RTI/RTP, an extracellular probe ion, most commonly TMA+, is released from a glass micropipette and detected with an ion-selective microelectrode (TMA+-ISM), positioned about 100 μm away. The resulting diffusion curves (concentration versus time) are amplified, digitized and stored on a computer enabling an appropriate diffusion equation to be fitted to the data. In dilute agarose gel, the free diffusion coefficient, D, and transport number, nt, are measured. In the brain slice, the effective diffusion coefficient, D*, volume fraction, α and loss factor, k′, are measured. For IOI, a fluorescent molecule, here dextran (3000 Mr, i.e. 3 kDa) labeled with a fluorescent dye, is briefly pressure injected and a time-series of images captured using a CCD-equipped camera. An appropriate diffusion equation is fitted to the intensity profiles measured along selected image axes enabling D or D*, to be extracted in agarose gel or brain slice, respectively. Also note that the methods are not confined to brain slices but also may be used in vivo (modified from ref. 10).
For both RPI and RTI methods, a sensing micropipette is located 50 – 150 μm away from the source; this sensor usually is an ion-selective microelectrode (ISM), which is a special type of micropipette that can measure the concentration of an appropriate ion (13). Other electrochemical microsensors are occasionally used, such as carbon fiber microelectrodes in conjunction with voltammetry (21). The use of ISMs dictates that both the RTP and RTI methods employ ions, the most useful one for probing the ECS being TMA+ although this ion has some limitations (12). Details of ISM construction and use with the RTP and RTI techniques are have been described (11, 13); effective sensors only exist for a few ions (see refs. 13 and 15). When feasible, the RTI method is preferred to the RTP because, with suitable calibration, nt can be determined and this enables the source strength to be specified and consequently α can be measured. When the RTP method is employed, the ejected volume U may vary and so α cannot be determined. On the other hand, the RTP method works with substances that cannot be reliably delivered by iontophoresis (see ref. 9). Both methods yield measurements of λ because that is determined from the time-course of the diffusion curves, not the amplitude.
These methods may be used either with brain slices or with an anesthetized in vivo animal. Fig. 2 illustrates a brain slice where the source and sensing micropipettes are introduced with two independent micromanipulators under microscopic visualization; when using in vivo preparations the two micropipettes are usually glued together (27). The associated timing electronics for iontophoresis or pressure injection, and devices for buffering and conditioning the signal from the ISM are all standard commercial items. The equipment is controlled by an D/A converter and the signals digitized with an A/D converter connected to a PC (see ref. 11 for technical details).
2.2 Software for RTP/RTI
We have developed two programs for the RTP/RTI techniques, the first, called Wanda, is for data acquisition and the second, called Walter, is used for data analysis. Wanda writes a binary file for each diffusion curve and Walter reads and processes these files. This makes the programs independent, so that data acquired by other means may be analyzed by Walter.
2.2.1 Wanda – The data acquisition program for RTP/RTI
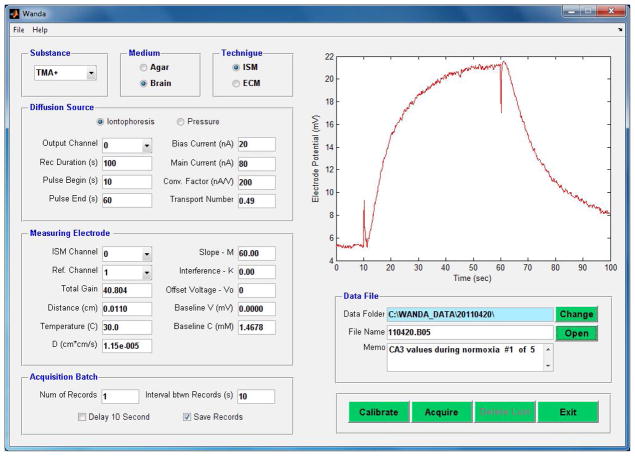
The Wanda program controls the release of ions from a pressure ejection or iontophoresis source and records the time course of ionic concentration measured by the ISM along with the parameters that define the experiment. The software has a long history; the first program for the RTI technique, called VOLTORO, performed both the functions of data acquisition and data analysis and was written in 1980’s by Dr. Charles Nicholson using the Pascal programming language and subsequently went through several iterations, computers and operating systems and is still used in some laboratories. The current version of Wanda was developed by Dr. Lian Tao and completely re-written in Matlab to run in Microsoft Windows. The major feature of the current incarnation is that it has a graphical user interface (GUI), which has been developed using the GUIDE environment of Matlab (Fig. 3). For data acquisition, Wanda employs the Matlab Data Acquisition Toolbox to control a National Instruments (Austin, Texas, USA) A/D and D/A converter.
Figure 3.
Graphical User Interface (GUI) for the Wanda software. This program is responsible for instrument control and data acquisition under the RTI/RTP paradigm. See text for further details.
Figure 3 shows the Wanda main screen, which contains most of the display and control objects of the program. The objects on the main screen have been grouped into several panels, with each panel controlling one aspect of the program.
The top three panels define the Substance, e.g. TMA+, the Medium, specifying whether the experiment is being carried out in dilute agarose gel to represent a ‘free’ medium or in brain tissue and the Technique panel specifying whether the experiment employs an ISM or ECM (Electrochemical Microsensor e.g. a carbon fiber microelectrode used in conjunction with fast-scan cyclic voltammetry).
The Diffusion Source panel allows choice of an iontophoresis (RTI) or a pressure (RTP) source. For RTI, the panel controls the strength and duration of the main current pulse and a constant bias current that maintains the concentration of TMA+ or other ion in the tip of the iontophoresis microelectrode. The transport number (nt) is also entered after being determined from measurements on the source micropipette in agarose. When a pressure source is chosen, the panel is populated with another set of appropriate parameters.
The Measuring Electrode panel specifies the A/D configuration and the distance between the diffusion source and the sensing microelectrode together with the temperature at which the experiment is carried out and D for the diffusing substance; these are important parameters for subsequent calculation of λ.
The Acquisition Batch and Data File panels define how records are taken and stored. A set of command buttons at the bottom right of the GUI controls the experiment. Finally, the acquired data is displayed as a voltage in real time in the large panel in the upper right of the GUI. In Fig. 3 a typical record from the hippocampus CA3 region of the brain is shown. The source and ISM are separated by 110 μm and the voltage on the ISM rises during the 50 s long iontophoretic pulse and then falls at its cessation. The start and finish of the pulse are indicated by fast voltage transients that are artifacts generated by the electronic switch of the current source and the ultra high impedance of the ISM (typically > 1GΩ).
2.2.2 Walter – The data analysis program for RTI
Walter is a command-line driven program that accepts the voltage data and parameters acquired by Wanda, converts the voltage to a concentration, and applies non-linear curve fitting to extract α, λ and k′ from the diffusion curve. The present version was written in Matlab by Dr. Nicholson. The overall design philosophy of Walter is to allow all the records in a given experiment to be read in and displayed together so that anomalies may be easily seen. Selected records then can be analyzed by either fitting Eq (6) if the RTP method is used or Eqs (7) or (8) for RTI. The fitting makes use of the Nelder-Mead non-linear simplex algorithm (available in Matlab). This is a relatively simple and very robust fitting algorithm. To guard against getting stuck in a local minimum, a set of randomized starting points are generated and the best fits selected from the resulting ensemble. Original and fitted curves are displayed in various ways and all the incoming data as well as the fitting parameters for all the analyzed records may be output to an Excel spreadsheet. The spreadsheet can be used for further statistical analyses or as a means of transferring to a specialized plotting program, or as a new input to Walter. In other words, all the data and analysis captured in an experiment may be stored in a spreadsheet if desired.
2.3 Integrative optical imaging (IOI)
The RTP and RTI methods use specialized point sensors that can only be constructed for a very limited set of substances, mostly small ions. To extend the point-source paradigm to a wider range of substances, especially macromolecules that are likely to form a significant component of the chemical traffic in the ECS, we introduced the integrative optical imaging (IOI) method (17). This method can be used to measure the diffusion of almost any molecule, as long as a fluorescent label can be attached to it. For example, the IOI technique has been used to study the synthetic drug-carrier PHPMA (20) with sizes up to 106 Mr and the physiologically significant substance, epidermal growth factor (EGF; ref. 32). Recently, the IOI method has been used with quantum dot nanocrystals to explore the size of the actual spaces between brain cells (34).
The IOI technique is quite simple: fluorescent molecules are released from a micropipette just as in the RTP method but now the 3D cloud of diffusing molecules is visualized using epi-fluorescence microscopy (Fig. 2) and a sequence of 2D images registered with a cooled CCD camera. Each image is essentially an integral of the projected cloud of molecules weighted by the defocused point-spread function of the microscope objective. The justification and derivation of the theoretical expression has been given (17, 29), and here we only restate the derived expression for image intensity on the image plane of the camera
| (9) |
where x′ and y′ denote the coordinates on the image plane. The constant M is the magnification of the optical system. The variable γ is a function of the effective diffusion coefficient and time: . The amplitude term E(γ) is a complicated function of γ but independent of x′ and y′, so the image intensity at any given time is simply a 2D Gaussian function of x′ and y′. Consequently γ, and hence D*, may be extracted by suitable curve fitting of Eq (9) at each of a sequence of times ti.
The equipment necessary to carry out the IOI method is again readily available from commercial sources. An upright epi-fluorescence microscope with a large fixed stage is used and either brain slices or an in vivo rat or mouse may be accommodated. A cooled CCD camera is mounted on the microscope and both camera and microscope are controlled by a PC (see ref. 11 for details). One limitation of the IOI method is that imaging can only be done effectively down to a depth of ~ 400 μm (i.e. the microscope is focused on a plane not more than 200 μm below the slice or brain surface).
2.4 Software for the IOI method
Two programs are used for the IOI technique, the first, called Devida, is for data acquisition and the second, called Ida, performs data analysis. They follow a similar philosophy to Wanda and Walter in that Devida has a comprehensive GUI and writes output files that are then read and analyzed by Ida, which again is a command-line program.
2.4.1 Devida – The data acquisition program for IOI
This program controls the release of fluorescent molecules from a pressure ejection source into agarose gel or brain tissue. Then the program records a sequence of images of the diffusing molecules with a Photometrics CCD-based camera (Photometrics, Tucson, Arizona, USA) mounted on a fluorescence microscope. The timing sequences for the camera are controlled by a programmable multi-channel pulse generator under the control of the Devida program.
The first program developed for IOI, called DIF, was developed in the early 1990s by Dr. Tao. The program was written in the Microsoft C language. In the early 2000’s, Dr. Nicholson completely re-wrote DIF as two programs in Matlab. The programs were named Devida and Ida, and used for data acquisition and data analysis, respectively. For the actual data acquisition and camera control, Devida was run simultaneously with a third-party program, V++ (Digital Optics, Auckland, New Zealand). In the last decade, all the IOI data were acquired and analyzed with these two programs.
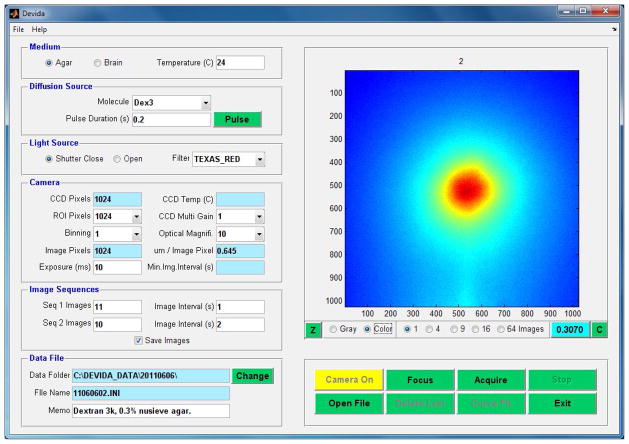
The current version of the Devida program has been re-written in Matlab by Dr. Tao, and it runs under the Microsoft Windows operating system and, like Wanda, it has a GUI. For data acquisition, the new Devida employs the PVCAM (Photometrics Virtual Camera Access Method) library, which eliminates the need for a third-party program. By using Matlab and PVCAM, Devida can be used in other labs with different Photometrics cameras.
Fig. 4 shows the Devida main screen, which contains all the display and control objects of the program. In a similar way to the Wanda GUI, the objects on the main screen have been grouped into several panels, with each panel controlling one aspect of the program. Thus the Medium panel specifies whether the experiment is carried out in agarose gel or brain tissue, as well as the temperature of the medium. The Diffusion Source panel selects the molecule in use from a drop-down list and specifies the duration of the pressure pulse applied to the micropipette to eject the molecule. The Light Source panel controls the behavior of the protective shutter on the light source. This is normally closed when measurements are not being made to reduce photo-bleaching of the fluorescent molecule. This panel also selects the fluorescent filter cube in the microscope to match the excitation and emitting wavelengths of the fluorescent molecule in use. The Camera panel specifies all the operating parameters of the Photometrics CCD camera. The Image Sequences panel allows two time sequences to be defined for image capture: a fast initial sequence and a subsequent slower one. This enables both the early and late behavior of the diffusing cloud to be captured while reducing the image storage requirements. The Data File panel handles the location and labeling of the data files. Data are written as two files, the first is a plain text file that captures all the setup parameters from the GUI, along with other fixed parameters specific to a given camera and microscope. The second is a binary file containing the raw image data for the sequences specified. The unlabeled image display panel (the largest panel at the top right) shows the real-time images during focusing and data acquisition or displays images retrieved from data files. The image intensities, representing concentration of the diffusing molecule, may be displayed in pseudo-color or monochrome. This panel also has objects that control image display and for focusing the microscope.
Figure 4.
Graphical User Interface (GUI) for the Devida software. This program is responsible for microscope and associated instrument control and image acquisition under the IOI paradigm. See text for further details.
2.4.2 Ida – The data analysis program for IOI
The Ida program was written by Dr. Nicholson and is again similar in function to Walter i.e. it is a command-line driven program, written in Matlab, that uses curve-fitting to extract D* and consequently λ from the data acquired by Devida. Because of the complicated amplitude term in Eq (9), as well as the fact that the exact amount of substance injected is not known, and the integrative nature of the method, α cannot be determined from an IOI experiment. It is assumed that there is no loss of the large molecules typically used with the IOI method and that none enter cells or are otherwise immobilized.
Ida enables the entire sequence of images to be displayed, subtracts an initial control image to remove any background features and determines the center of each injection. Curve fitting is again accomplished using the Nelder-Mead simplex algorithm. Curves are fitted along the x- and y-axes and along two other equally spaced axes. In an anisotropic medium, images will be elliptical and the effective diffusion coefficients are determined along the major and minor axes (see ref. 35). The fitting results, along with all relevant parameters, can again be output to an Excel spreadsheet; however the original data cannot be contained in the spreadsheet because of the size of the image files.
2.5 Brief survey of diffusion parameter values
This part will discuss a few representative results obtained with three experimental techniques: radiotracers, the RTI/RTP methods and IOI. A more comprehensive survey is provided by Syková & Nicholson (27); that review also discusses some other methods that have been used to measure ECS diffusion parameters. The rest of this section refers to the data presented in Table 1.
Table 1.
Selected values of α and γ obtained with radiolabel, RTI, RTP and IOI methods.
| Molecule | Mr | dH | D | °C | Species | Region | α | λ | Method | Ref |
|---|---|---|---|---|---|---|---|---|---|---|
| sucrose | 342 | 1.0 | 7.0 | 37 | rabbit | caudate | 0.21 | 1.60 | radio | 5 |
| methotrexate | 508 | 1.3 | 5.3 | 37 | monkey | caudate | 0.28 | 2.43 | radio | 5 |
| TMA+ | 74 | < 1.0 | 11.1 | 37 | rat | cortex | 0.18 – 0.22 | 1.54 – 1.65 | RTI | 27 |
| TMA+ | 74 | < 1.0 | 11.1 | 37 | mouse | cortex | 0.23 | 1.67 | RTI | 1 |
| TMA+ | 74 | < 1.0 | 9.82 | 21–23 | turtle | cb. ml | 0.31 | 1.44, 1.95, 1.58 | RTI | 22 |
| α-NS− | 174 | < 1.0 | 7.60 | 37 | rat | cb. ml | 0.18 | 1.54 | RTI | 15 |
| Ca2+ | 40 | < 1.0 | 9.4 | 34 | rat | cortex | n/a | 2.05 | RTP | 9 |
| AF488 | 547 | 1.2 | 5.19 | 34 | rat | cortex | n/a | 1.54 | IOI | 9 |
| Dex3 | 3000 | 3 | 2.2 | 37 | rat | cortex | n/a | 2.04 | IOI | 34 |
| Dex70 | 70,000 | 14 | 0.47 | 37 | rat | cortex | n/a | 2.69 | IOI | 34 |
| EGF | 6600 | 3.7 | 1.7 | 34 | rat | cortex | n/a | 1.79 | IOI | 32 |
| BSA | 66,000 | 7.4 | 0.83 | 34 | rat | cortex | n/a | 2.26 | IOI | 30 |
| lactoferrin | 80,000 | 9.3 | 0.71 | 37 | rat | cortex | n/a | 3.50 | IOI | 33 |
Molecule: TMA+, tetramethylammonium; α-NS−, α-naphthalenesulfonate; AF488, Alexa Fluor 488 hydrazide (Molecular Probes, Invitrogen, Carlsbad, California, USA); Dex3, dextran 3000 Mr; Dex70, dextran 70,000 Mr; EGF, epidermal growth factor; BSA, bovine serum albumin.
Mr. Relative molecular weight.
dH. Hydrodynamic diameter (units: nm). Estimated from Stokes-Einstein equation.
D. Free diffusion coefficient (units: × 106 cm2 s−1).
°C. Temperature at which D was measured (units: degrees Celsius).
Species. Animal species in which measurements were made.
Region: Brain region where measurements were made: caudate, caudate nucleus; cortex, various areas of neocortex; cb. ml. cerebellum, molecular layer.
α. Volume fraction of ECS (units: non-dimensional).
λ. Tortuosity of ECS (units: non-dimensional).
Method. Diffusion method employed: radio, radiolabel; RTI, real-time iontophoresis; RTP, real-time pressure; IOI, integrative optical imaging.
Ref. Reference.
Radiolabeled sucrose provided very representative values of α and λ when used in the rabbit caudate nucleus. In contrast, measurements with the anti-cancer drug, methotrexate, indicated a larger than normal ‘distribution space’ suggesting that a significant amount of the substance was entering cells and the kinetics of this process may have contributed to the large value of λ.
The results with the monovalent cation TMA+ using RTI indicate ‘normal’ α and λ in the rat and mouse cortex that are comparable with the results obtained with the uncharged sucrose in rabbit caudate nucleus. The TMA+ results in turtle cerebellar molecular layer show distinct anisotropy (later confirmed with IOI, see ref. 35) accompanied by a larger than normal α-value. The early result using α–naphthalenesulfonate (α-NS−) failed to reveal anisotropy in rat cerebellar molecular layer, possibly for technical reasons, but did show that anions could be used as probes of diffusion properties.
The divalent cation Ca2+ does not release well by iontophoresis from a glass micropipette so the RTP method was used (consequently no estimate of α was available); the value of λ obtained in the cortex with this ion was much higher than normal and application of an enzyme that removed part of the extracellular matrix revealed that the increased hindrance was caused largely by interaction with the matrix (9; see Section 3.4).
The use of the IOI technique has provided tortuosity data on a wide ranging set of molecules. The smallest, AF488, a dye molecule, gave a similar λ-value to that obtained with TMA+ but substantially larger molecules gave tortuosities that increased with size. Dextrans are randomly coiled polymers with a roughly spherical shape. They are polydisperse (so Mr is only approximate) that are capable of deformation whereas EGF, BSA and lactoferrin are rigid proteins. For a given Mr, the loosely coiled dextrans are larger than the proteins but have similar tortuosities possibly because their deformability aids passage through the ECS. This conjecture is supported by extensive data on PHPMA polymer diffusion (20). Lactoferrin interacts with the heparan sulfate component of the extracellular matrix and, like the finding with Ca2+, this may account for some of the increased tortuosity (33).
3 Modeling the ECS with MCell
In this section we illustrate how Monte Carlo modeling, using the MCell (‘Monte Carlo Simulation of Cellular Microphysiology’) program, may be applied to further understand the properties of the ECS. MCell (25; www.mcell.psc.edu; www.mcell.cnl.salk.edu) has been developed at the University of Pittsburg and at the Salk Institute in California and is a highly optimized Monte Carlo program designed for studying diffusion of molecules in sub-cellular and extracellular microenvironments. The original impetus for the development of MCell came from a need to model the diffusion of acetylcholine molecules in the complex synaptic cleft of the neuromuscular junction, after the molecules had been released from synaptic vesicles, and their subsequent reaction with postsynaptic receptors (26). In the initial work, realistic geometry on the micrometer scale was captured by digitizing serial electron micrographs.
The MCell program works at a more coarse-grained level than a typical molecular dynamics simulation but is sufficiently detailed to capture cellular physiology and may be said to represent mesoscale modeling. In addition to the usual Monte Carlo capacity to handle complex geometry, MCell incorporates sophisticated reaction kinetics between molecules and is sufficiently optimized that useful simulations may be carried out on a high-end personal computer. All these features make MCell an appropriate tool to model diffusion and interaction with complex ECS geometries and with the interstitial matrix. These features enable MCell to be employed to test different hypotheses raised by experimental observations and to assess the consistency of experimental data.
All applications of MCell go through four steps: modeling, simulation, visualization and analysis. Modeling uses a script written in the Model Description Language (MDL). This defines and instantiates the parameters of that describe the problem, comprising number of molecules, their release sites, diffusion coefficients, reactions, and geometry, including behavior of molecules at each surface. Simulation takes place when the MCell program runs the MDL script on a Linux-based machine. The MDL file also defines output options at specified intervals that generate files that may be read by the visualization program DReAMM (‘Design, Render, and Animate MCell Models’; www.mcell.psc.edu/DReAMM). DReAMM has been developed at the University of Pittsburg using the open source program OpenDX (Visualization Data Explorer software originally written by IBM) and has an extensive GUI that displays MCell outputs in flexible and sophisticated 3D graphics and even can make movies. The final analysis phase is carried out with our own custom software that computes D* and λ from the binary output files.
Comparing the Monte Carlo paradigm of MCell to numerical methods of solving explicit partial differential equations (PDE’s) indicates the following relative merits. The major advantage of MCell is its ability to handle very complex geometries with thousands of different surface elements and boundary conditions. A second advantage is the capacity to employ realistic reaction schemes without concern about stability or convergence. In contrast, numerical solutions of PDE’s score well in multiphysics situations where, for example, it is required to combine hydrodynamic flow or electric fields with diffusion. When dealing with reactions, the use of PDE’s also enables the use of arbitrary concentrations whereas the concentration available at any location in MCell is dependent on the number of particles in use. Even when exploring the implications of geometry, MCell requires a minimum number of particles to reduce the error to acceptable levels and the use of many particles may cause the calculations to be excessively prolonged. Another factor in running MCell is that periodic boundary conditions are not implemented, requiring that the geometry be extended so that particles remain within it; this may exceed the storage capacity of the PC. Often these issues can be alleviated by using analysis to transform the original problem or by making use of inherent symmetry in the geometry. Users of both MCell and numerical methods have to be mindful in choosing an appropriate time-step to ensure an accurate solution. Finally, for diffusion problems, MCell is an intuitive method of solution that is more readily grasped and visualized than typical numerical methods.
3.1 Determination of D* from MCell simulation
Using MCell, the effective diffusion coefficient, D*, for molecules moving in the ECS of a structured medium, after the molecules have been released from a point-source at the origin, may be calculated in at least two ways. In the first approach, employed by Tao and Nicholson (31) and Tao et al. (28), particles are counted at time t in a sequence of concentric sampling boxes centered on the source-point. In an isotropic medium, for a cube-shaped sampling box of side 2A, integration of Eq (6), leads to the expression:
| (10) |
Here ‘erf’ is the error function, N0 is the initial number of molecules and N(A,t) is the number in the sampling box. Using appropriate curve fitting, D* may be estimated at a sequence of times.
The sampling box method is less useful in an anisotropic medium and here a second approach is used. Starting with the standard definition of the diffusion coefficient in terms of the mean square distances of an ensemble of particles with coordinates x, y, z and r2 = x2 + y2 + z2, the required diffusion coefficients may be calculated:
| (11) |
where are the principal values of the diffusion tensor and D* is the mean value. The components of the tortuosity tensor are calculated immediately from Eq (4). The analysis described in Eq (11) is realized by using a custom program, Amco, written by Dr. Nicholson and running in Matlab or Octave, to analyze the binary output files generated by MCell.
3.2 ECS modeled from an ensemble of packed cubes
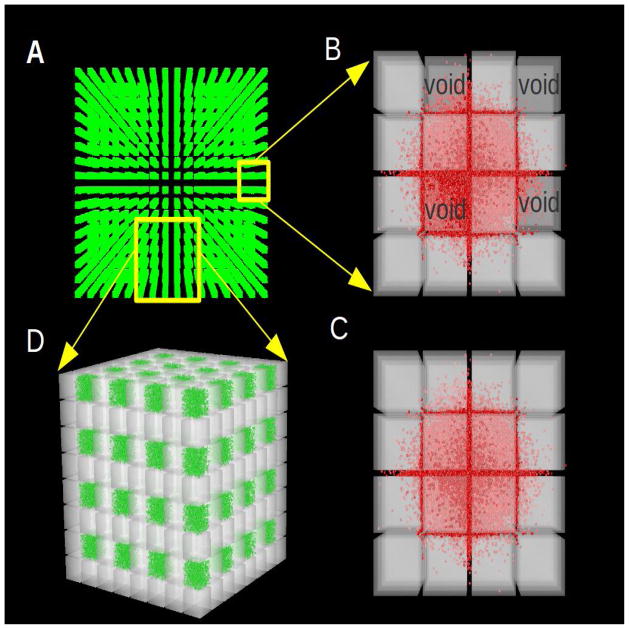
The simplest way of representing the geometry of brain cells together with their atmosphere of ECS is to assume that cells are all similar in shape and size and pack together in a 3D environment with a uniform spacing between them. Cubes, truncated octahedral, a combination of three different types of solids (a small rhombicuboctahedron, a cube and two tetrahedra) and random convex polyhedra have been used and all give similar results (7, 31), so here we confine ourselves to cubes (Fig. 5). We use a sufficient number of cubes to ensure that the molecules remain in the geometry during the time of the simulation and the molecules spread sufficiently far to allow the estimated D* to attain a constant value.
Figure 5.
Visualization, using DReAMM software, of ensembles of cubes and associated ECS employed in MCell simulations. Panel A shows a perspective view from the top of just the 4,096 voids in an entire 32×32×32 cubes and void geometry (equivalent to 32,768 cubes). As described in the text, every eighth cube has been replaced by a void (here visualized as extracellular matrix, colored green, see also Fig. 7). To aid visualization, the remaining cubes are not shown but they fill most of the gaps between the voids. Many simulations used 64×64×64 cubes with voids (equivalent to 262,144 cubes). Panel B shows an enlarged view of a stack of just 4×4×4 cubes with all cubes present showing the location of the voids. The stack is taken from the larger ensemble with ECS conforming to α = 0.2, which is a typical value found in experiments. A total of 10,000 molecules (shown in red) are shown at at t = 0.1 ms after release diffusing from a point-source in the center through the spaces between the cubes and also within the voids. Using flat projection, a view of the entire ensemble from the top is obtained showing that diffusing molecules have explored the vicinity of several cubes by this time. Using the DReAMM program the cube surfaces are displayed in transparent gray in order to visualize the molecules that are moving in the lower layers of the geometry. Note that the exaggerated size of the red molecules is used as an aid to visualization and is not a feature of the simulation (in MCell, molecules are regarded as point structures). Panel C shows the same diffusion paradigm as detailed for Panel B in a geometry with uniformly distributed cubes and no voids. Panel D shows a larger region of the geometry, with 8×8×8 cubes with voids, seen from a perspective that emphasizes the 3D structure. As in panel A, to aid visualization, each void is filled with extracellular matrix (shown in green). There are 1300 matrix molecules in each void, giving a concentration of 10 μM and they forms the basis for reaction simulations depicted in Fig. 7.
For the cube problem and related geometries, Tao & Nicholson (31) established that there is a simple relationship between α and D*, and hence between α and λ
| (12) |
It follows from this relationship that the value of λ attributable to ‘pure geometry’, λg, cannot exceed 1.225 (i.e. when α → 0) and for the typical α = 0.2 found in the brain, λg = 1.18. It may be noted that Eq (12) is directly related to the expression derived by Maxwell for the effective conductivity of a conductive medium containing a sparse distribution of insulated spheres (see ref. 31 for more discussion).
Using Eq (12) as a starting point we built the geometry from cubes with side 2a = 0.6 μm and separation 2d = 0.0462 μm to give a value for α of 0.2 (see Eq (2)). We used ensembles of 32 × 32 × 32 cubes or 64 × 64 × 64 cubes (Fig. 5A). Fig. 5C shows the distribution of 10,000 molecules at a time of 0.1 ms after release from a source point in an ensemble of cubes. The molecule here was chosen to be Ca2+ (D = 7.4 × 10−6 cm2.s−1 at a temperature of 23 °C, ref. 9) and the simulation did indeed yield a value of λ = 1.19 which compares well with the value of 1.18 predicted by Eq (12).
As noted earlier, in the real brain, λ ~ 1.6 while both Eq (12) and simulation yield a much smaller value, so factors other than ‘pure geometry’ must be in play. One class of candidates is dead-spaces: regions where diffusing particles become trapped for a period of time. Previous MCell models (7, 10, 28), backed by experimental data have shown that invaginations of cellular membranes (cavities), local expansions of the ECS (voids) and possibly glial wrapping, increase λ substantially beyond that predicted by Eq (12) (Fig. 1B). A semi-empirical equation for the tortuosity value in a medium containing dead-spaces was formulated by Tao et al. (28):
| (13) |
where α is the total volume fraction, αc is the volume fraction of the dead-spaces and β is an empirical ‘exit factor’ that informally captures the probability that molecules leave the dead-space. Mostly, 2 < β < 3 (see Table 1 in ref. 28).
For this review we have illustrated the effect of introducing dead-spaces by a new way of creating voids in the ECS; we simply removed one cube in every eight from the ensemble (Figs. 5B, 5D). To calculate αc, we define α0 as the volume fraction in the absence of dead-spaces, here that would be the case when all cubes were present, then
| (14) |
Following Tao and Nicholson (31) we define l to be the side of a cube so l = 2a, and L to be the side of the ‘bounding frame’ of the cube, which means that the new volume includes the ECS associated with the cube, then L = 2(a + d). It follows from Eq (1) that α0 = 1 − (l3/L3). The volume fraction α when M cubes are removed (0 ≤ M ≤ 8) is
| (15) |
Consequently
| (16) |
Then, setting M = 1 (one cube removed) and substituting for αc in Eq (13)
| (17) |
It also follows that the minimum value of α is 1/8, which occurs when α0 = 0.
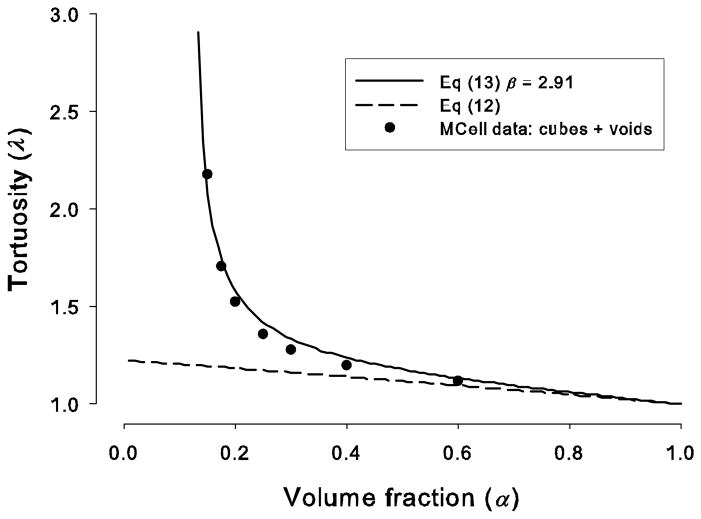
Figure 6 shows that the tortuosity in media with voids is much higher than in the uniform media. This is not just an effect of moving the cubes closer to achieve the same volume fraction, because from Eq (12) the maximum value that can be obtained from this maneuver is 1.225. Rather, the increased value of λ may be attributed to the hold-up of molecules in the voids (seen in Fig. 5B) combined with the difficulty of escaping into the narrow interstitial spaces. We expect that the tortuosity in the media with voids should conform to Eq (13) and Eq (17) and Fig. 6 shows the resulting plot with β =2.91, which represented the best fit to the simulation data.
Figure 6.
Tortuosity of ECS versus volume fraction with and without voids. The solid line represents the plot of Eq (13) with a value β = 2.91, obtained by a non-linear curve fit to the MCell simulation data (filled circles) for a geometry with cubes and voids. Each cube was had side 2a = 0.6 μm and 64×64×64 cubes were used. The spacing between cubes was adjusted so that the total volume fraction corresponded to the depicted values. Note that the minimum possible volume fraction was α = 0.128 and this occurred when the spaces between cubes approached zero and then α was determined only by the missing cube. The dashed line corresponds to the case where no void is present, i.e. Eq (12) with the geometry made up of a uniform distribution of cubes.
3.3 Representation of molecular interaction with extracellular matrix through reactions
The extracellular matrix interacts with diffusing molecules through several potential mechanisms: viscosity or high density of polymeric molecules in the ECS which exert steric hindrance (18), electrostatic interaction between negatively charged components of the matrix and positively charged mobile molecules (19), and specific binding interactions (steric attraction) (23). Our laboratory has recently published experimental evidence showing that lactoferrin interacts with the matrix component heparan sulfate (33) and in a separate study we showed that Ca2+ interacts with another matrix component, chondroitin sulfate (9). The transport process itself continues to obey the diffusion equation suggesting that interactions with matrix may be represented by a fast-equilibrium reaction scheme (ref. 4, Chapter 14). Here we focus on the Ca2+ interaction, which manifests itself as a reduced effective diffusion coefficient (i.e. increased tortuosity) compared to that obtained with the monovalent cation TMA+.
The formal development of this argument is as follows. Let C represent concentration of Ca2+ in ECS, B, concentration of binding sites of the matrix and S, concentration of complex formed between Ca2+ and matrix, then the binding and unbinding processes may be described by a second-order (bimolecular) reaction scheme as:
| (18a) |
| (18b) |
where kf [M−1 s−1] is the forward rate constant for complex formation and kb [s−1] the backward rate constant for complex dissociation. Assuming that, locally, the reaction process is much faster than the diffusion process and there is equilibrium between the mobile and complexed molecules, the Law of Mass Action states that
| (19) |
Making the additional assumption that B ≫ C, so that B may be regarded as constant, then the second-order reaction scheme will be reduced to a first-order
| (20) |
with the dimensionless parameter R = kfB/kb = B/KD where KD = kb/kf [M] is the equilibrium dissociation constant.
Following Crank (ref. 4, Chapter 14), the diffusion equation with a loss term representing the reaction process is given by:
| (21) |
substituting for S in Eq (21) using Eq (20) results in
| (22) |
and the basic diffusion equation is recovered so D*/(1+R) can be defined as the new effective diffusion coefficient. Note that D* is the effective diffusion coefficient arising from geometry. This gives a final tortuosity as the product of the tortuosity arising purely from geometry (which may include dead-spaces), λg, multiplied by the tortuosity arising from interaction with the matrix, λm:
| (23) |
Figure 7 shows four successive snapshots representing Ca2+ (C; red molecules) diffusing from a point source and interacting with ‘matrix’ molecules (B; green molecules) positioned in the voids that were the topic of the previous calculations discussed in Section 3.2 (see also Fig. 5). A population of the complex (S; blue molecules) is progressively generated through the diffusion-reaction process in the ECS. Note that Fig. 7 represents a view looking down through the stack of translucent cellular cubes so the diffusing red molecules appear with reduced intensity in the planes between cells in the lower levels of the stack.
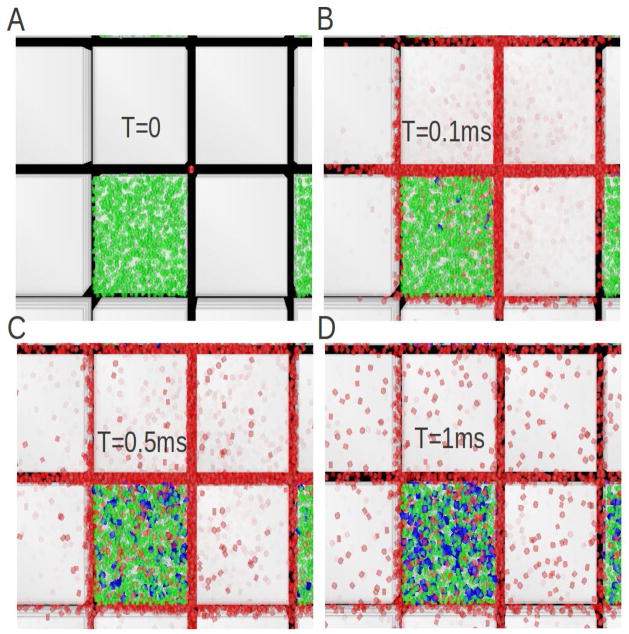
Figure 7.
Visualization of molecules interacting with matrix in voids. Green molecules represent the matrix, the diffusing molecules are red the molecular complex between the matrix and diffusing molecules is represented in blue. A total of 10,000 molecules were released from a point source (red dot in the middle of panel A) at the center of a geometry comprising 32×32×32 cubes with every eighth cube removed to form voids. The matrix was concentrated the in voids at a value of 10 μM and volume fraction was 0.28 (excluding the voids) and 0.37 (including the voids). Forward and backward rate constants for binding and unbinding of diffusing molecules to the matrix were set (somewhat arbitrarily) to kf = 5.6×108 M−1.s−1 and kb = 2.2×103 s−1; when combined with the matrix concentration averaged over the whole ECS this gave an R-value of 0.6 (see Eq 20). The free diffusion coefficient was D = 7.4×10−6 cm2 s−1, which is the value for Ca2+ at 23 °C. Panels show a small region of the ensemble of cubes, looking down through the semi transparent surfaces. They show molecules diffusing from the source point at t = 0 (Panel A) and then exploring their microenvironment at successive times, t = 0.1 ms (Panel B), t = 0.5 ms (Panel C) and t = 1 ms (Panel D). As time passes an increasing amount of complex (blue) is formed. Visualization with DReAMM.
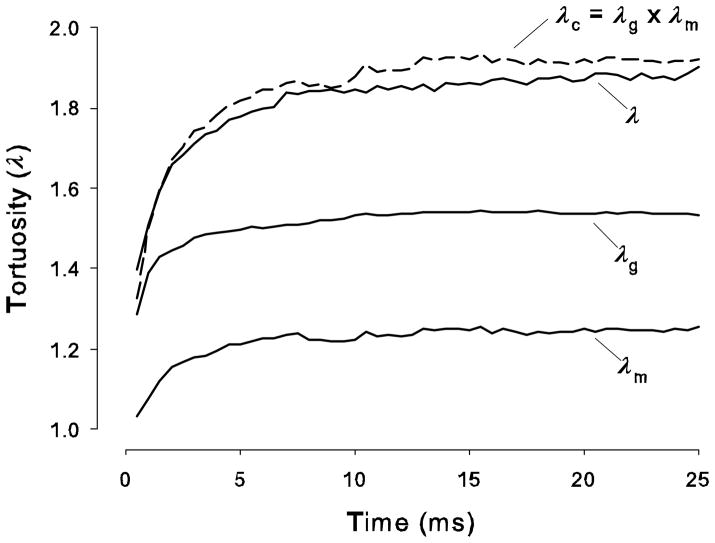
Equation (23) has been tested. Figure 8 shows three curves, each represents a MCell simulation after release of 5000 Ca2+ molecules from origin where the tortuosity has been calculated using Eq (11). The plot labeled ‘λg’ represents the result in a medium with cubes and voids (i.e. one cube in eight removed) as a function of time. The plot labeled ‘λm’ shows the result a medium containing only matrix at a uniform concentration of 2.34 μM (i.e. no geometry present). The plot labeled ‘λ’ represents tortuosity calculated in a medium with both cubes and voids but with the addition of a quantity of matrix in the voids such that the matrix concentration averaged over the whole ECS is also 2.34 μM Note that other simulations where the matrix is uniformly distributed in both the voids and connecting space of the ECS at the same concentration give similar results. Finally, ‘λc’ represents the product of the λg and λm curves. It is seen that λ and λc are close in value (the λ-curve is still rising slowly and by 50 ms it will coincide with λc) thus verifying the validity of Eq (23). It should be noted that the theory is only valid when λ reaches a steady-state value because classic diffusion theory assumes that D* is time-independent. It is clear from these simulations, which are based on representative dimensions for the cells and ECS in brain tissue, that a steady-state is reached in < 50 ms. Experimental measurements are typically taken at much longer times scales so the constancy of D* under the point source paradigm is assured.
Figure 8.
Multiplicative properties of tortuosities. Curve labeled ‘λg’ represents tortuosity computed, using Eq (11), from an MCell simulation in a medium with cubes and voids (i.e. one cube in eight removed) as a function of time after release of 5000 Ca2+ molecules from origin. Curve labeled ‘λm’ represent a similar tortuosity calculation in a medium containing only matrix at a concentration of 2.34 μM (i.e. no geometry present). Curve labeled ‘λ’ represents tortuosity calculated in a medium with cubes and voids but with a quantity of matrix in the voids such that the matrix concentration averaged over the whole ECS is also 2.34 μM. Finally, ‘λc’ represents the product of the λg and λm curves. It is seen that λ and λc are close in value. Parameters: kf, kb and D as for Fig. 7; α = 0.2.
4 Conclusions
At first sight an electron micrograph of brain tissue suggests that the intricate pathways that form the ECS are unlikely to permit any recognizable form of diffusion to take place. Yet 50 years of careful biophysical research, much of it with the RTI and IOI methods, has revealed that many different types of molecule do diffuse through the ECS according to the basic laws laid down by Adolf Fick in 1855 (and it may be remembered that Fick was a physician himself). Experiments show that most small molecules that do not interact specifically with cells or the contents of the ECS have an effective diffusion coefficient that is reduced from the free value by a factor of about 2.6 and move in a space that occupies 20% of the brain volume. One suspects that these values are not accidental but are constrained by the signaling and energetic requirements of the brain.
It remains necessary to account for the magnitude of the hindrance. Monte Carlo modeling has been useful here and has shown that something more than simple geometrical factors must be involved. To date the most likely candidates are dead-space microdomains and interaction with the extracellular matrix. The first mechanism can account for the known data and would affect all molecules but the anatomical substrates have yet to be identified completely. Matrix interaction is known to occur for some molecules but not all and is the most plausible candidate when abnormally large tortuosities are encountered with small ions or molecules. Macromolecules are inherently more hindered in their passage through the ECS and the hindrance increases with size, suggesting that both viscous drag and interaction with the channel boundaries of the ECS are coming into play.
Diffusion studies, both experimental and theoretical have provided two types of information. The first tells us how a particular molecule is likely to distribute in the brain. This is useful for discussing some types of signaling between cells and for the important practical application of drug delivery. The second type of information is the main topic of this brief review: the study of diffusion can reveal properties of the ECS that, because of its narrow width and fragile nature, cannot be revealed by more direct means. Because the spaces between cells are below the resolution of light microcopy they cannot be visualized in living tissue whereas fixed tissue, viewed in electron micrographs, often suffers from distortion of the ECS. This leaves diffusion analysis as the only effective means of studying the ECS at the present time.
Acknowledgments
We thank Dr. Sabina Hrabĕtová for her comments. The work was supported by NIH/NINDS Grant NS 28642.
References
- 1.Andĕrová M, Kubinová Š, Mazel T, Chvátal A, Eliasson C, Pekny M, Syková E. Effect of elevated K+, hypotonic stress, and cortical spreading depression on astrocyte swelling in GFAP-deficient mice. Glia. 2001;35(3):189–203. doi: 10.1002/glia.1084. [DOI] [PubMed] [Google Scholar]
- 2.Bobo RH, Laske DW, Akbasak A, Morrison PF, Dedrick RL, Oldfield EH. Convection-enhanced delivery of macromolecules in the brain. Proc Natl Acad Sci USA. 1994;91(6):2076–2080. doi: 10.1073/pnas.91.6.2076. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Chen KC, Nicholson C. Changes in brain cell shape create residual extracellular space volume and explain tortuosity behavior during osmotic challenge. Proc Natl Acad Sci USA. 2000;97(15):8306–8311. doi: 10.1073/pnas.150338197. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Crank J. The Mathematics of Diffusion. 2. Clarendon Press; Oxford: 1975. [Google Scholar]
- 5.Fenstermacher JD, Kaye T. Drug “diffusion” within the brain. Ann NY Acad Sci. 1988;531:29–39. doi: 10.1111/j.1749-6632.1988.tb31809.x. [DOI] [PubMed] [Google Scholar]
- 6.Goodknight RC, Klikoff WA, Fatt I. Non-steady-state fluid flow and diffusion in porous media containing dead-end pore volume. J Phys Chem. 1960;64:1162–1168. [Google Scholar]
- 7.Hrabe J, Hrabĕtová S, Segeth K. A model of effective diffusion and tortuosity in the extracellular space of the brain. Biophys J. 2004;87(3):1606–1617. doi: 10.1529/biophysj.103.039495. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Hrabĕtová S, Hrabe J, Nicholson C. Dead-space microdomains hinder extracellular diffusion in rat neocortex during ischemia. J Neurosci. 2003;23(23):8351–8359. doi: 10.1523/JNEUROSCI.23-23-08351.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Hrabĕtová S, Masri D, Tao L, Xiao F, Nicholson C. Calcium diffusion enhanced after cleavage of negatively charged components of brain extracellular matrix by chondroitinase ABC. J Physiol. 2009;587(Pt 16):4029–4049. doi: 10.1113/jphysiol.2009.170092. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Hrabĕtová S, Nicholson C. Contribution of dead-space microdomains to tortuosity of brain extracellular space. Neurochem Int. 2004;45(4):467–477. doi: 10.1016/j.neuint.2003.11.011. [DOI] [PubMed] [Google Scholar]
- 11.Hrabĕtová S, Nicholson C. Biophysical properties of brain extracellular space explored with ion-selective microelectrodes, integrative optical imaging and related techniques. In: Michael AC, Borland LM, editors. Electrochemical Methods for Neuroscience. CRC Press, Taylor Francis Group; Boca Raton: 2007. pp. 167–204. [PubMed] [Google Scholar]
- 12.Kaur G, Hrabĕtová S, Guilfoyle DN, Nicholson C, Hrabe J. Characterizing molecular probes for diffusion measurements in the brain. J Neurosci Meth. 2008;171(2):218–225. doi: 10.1016/j.jneumeth.2008.03.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Nicholson C. Ion-selective microelectrodes and diffusion measurements as tools to explore the brain cell microenvironment. J Neurosci Meth. 1993;48(3):199–213. doi: 10.1016/0165-0270(93)90092-6. [DOI] [PubMed] [Google Scholar]
- 14.Nicholson C. Diffusion and related transport properties in brain tissue. Rep Prog Phys. 2001;64:815–884. [Google Scholar]
- 15.Nicholson C, Phillips JM. Ion diffusion modified by tortuosity and volume fraction in the extracellular microenvironment of the rat cerebellum. J Physiol. 1981;321:225–257. doi: 10.1113/jphysiol.1981.sp013981. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Nicholson C, Syková E. Extracellular space structure revealed by diffusion analysis. Trends Neurosci. 1998;21(5):207–215. doi: 10.1016/s0166-2236(98)01261-2. [DOI] [PubMed] [Google Scholar]
- 17.Nicholson C, Tao L. Hindered diffusion of high molecular weight compounds in brain extracellular microenvironment measured with integrative optical imaging. Biophys J. 1993;65(6):2277–2290. doi: 10.1016/S0006-3495(93)81324-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Ogston AG, Preston BN, Wells JD. On the transport of compact particles through solutions of chain-polymers. Proc Roy Soc London A. 1973;333:297–316. [Google Scholar]
- 19.Parker KH, Winlove CP, Maroudas A. The theoretical distributions and diffusivities of small ions in chondroitin sulphate and hyaluronate. Biophy Chem. 1988;32(2–3):271–282. doi: 10.1016/0301-4622(88)87013-3. [DOI] [PubMed] [Google Scholar]
- 20.Prokopová-Kubinová Š, Vargová L, Tao L, Ulbrich K, Šubr V, Syková E, Nicholson C. Poly[N-(2-hydroxypropyl)methacrylamide] polymers diffuse in brain extracellular space with same tortuosity as small molecules. Biophys J. 2001;80(1):542–548. doi: 10.1016/S0006-3495(01)76036-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Rice ME, Nicholson C. Measurement of nanomolar dopamine diffusion using low-noise perfluorinated ionomer coated carbon fiber microelectrodes and high-speed cyclic voltammetry. Anal Chem. 1989;61:1805–1810. doi: 10.1021/ac00192a005. [DOI] [PubMed] [Google Scholar]
- 22.Rice ME, Okada YC, Nicholson C. Anisotropic and heterogeneous diffusion in the turtle cerebellum: Implications for volume transmission. J Neurophysiol. 1993;70(5):2035–2044. doi: 10.1152/jn.1993.70.5.2035. [DOI] [PubMed] [Google Scholar]
- 23.Rodriguez-Carvajal MA, Imberty A, Perez S. Conformational behavior of chondroitin and chondroitin sulfate in relation to their physical properties as inferred by molecular modeling. Biopolymers. 2003;69(1):15–28. doi: 10.1002/bip.10304. [DOI] [PubMed] [Google Scholar]
- 24.Siegel RA, Langer RL. A new Monte Carlo approach to diffusion in constricted porous geometries. J Colloid Interface Sci. 1986;109(2):426–440. [Google Scholar]
- 25.Stiles JR, Bartol TM. Monte Carlo methods for simulating realistic synaptic microphysiology using MCell. In: De Schutter E, editor. Computational Neuroscience: Realistic Modeling for Experimentalists. CRC Press; London: 2001. pp. 87–127. [Google Scholar]
- 26.Stiles JR, Van Helden D, Bartol TM, Jr, Salpeter EE, Salpeter MM. Miniature endplate current rise times <100 ms from improved dual recordings can be modeled with passive acetylcholine diffusion from a synaptic vesicle. Proc Natl Acad Sci USA. 1996;93(12):5747–5752. doi: 10.1073/pnas.93.12.5747. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Syková E, Nicholson C. Diffusion in brain extracellular space. Physiol Rev. 2008;88(4):1277–1340. doi: 10.1152/physrev.00027.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Tao A, Tao L, Nicholson C. Cell cavities increase tortuosity in brain extracellular space. J Theoret Biol. 2005;234(4):525–536. doi: 10.1016/j.jtbi.2004.12.009. [DOI] [PubMed] [Google Scholar]
- 29.Tao L, Nicholson C. The three-dimensional point spread functions of a microscope objective in image and object space. J Micros - Oxford. 1995;178(Part 3):267–271. doi: 10.1111/j.1365-2818.1995.tb03604.x. [DOI] [PubMed] [Google Scholar]
- 30.Tao L, Nicholson C. Diffusion of albumins in rat cortical slices and relevance to volume transmission. Neurosci. 1996;75(3):839–847. doi: 10.1016/0306-4522(96)00303-x. [DOI] [PubMed] [Google Scholar]
- 31.Tao L, Nicholson C. Maximum geometrical hindrance to diffusion in brain extracellular space surrounding uniformly spaced convex cells. J Theoret Biol. 2004;229(1):59–68. doi: 10.1016/j.jtbi.2004.03.003. [DOI] [PubMed] [Google Scholar]
- 32.Thorne RG, Hrabĕtová S, Nicholson C. Diffusion of epidermal growth factor in rat brain extracellular space measured by integrative optical imaging. J Neurophysiol. 2004;92(6):3471–3481. doi: 10.1152/jn.00352.2004. [DOI] [PubMed] [Google Scholar]
- 33.Thorne RG, Lakkaraju A, Rodriguez-Boulan E, Nicholson C. In vivo diffusion of lactoferrin in brain extracellular space is regulated by interactions with heparan sulfate. Proc Natl Acad Sci USA. 2008;105(24):8416–8421. doi: 10.1073/pnas.0711345105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Thorne RG, Nicholson C. In vivo diffusion analysis with quantum dots and dextrans predicts the width of brain extracellular space. Proc Natl Acad Sci USA. 2006;103(14):5567–5572. doi: 10.1073/pnas.0509425103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Xiao F, Nicholson C, Hrabe J, Hrabĕtová S. Diffusion of flexible random-coil dextran polymers measured in anisotropic brain extracellular space by integrative optical imaging. Biophys J. 2008;95(3):1382–1392. doi: 10.1529/biophysj.107.124743. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Yamaguchi Y. Lecitans: organizers of the brain extracellular matrix. Cell Mol Life Sci. 2000;57:276–289. doi: 10.1007/PL00000690. [DOI] [PMC free article] [PubMed] [Google Scholar]