A fully implicit finite element method for bidomain models of cardiac electromechanics

Abstract

We propose a novel, monolithic, and unconditionally stable finite element algorithm for the bidomain-based approach to cardiac electromechanics. We introduce the transmembrane potential, the extracellular potential, and the displacement field as independent variables, and extend the common two-field bidomain formulation of electrophysiology to a three-field formulation of electromechanics. The intrinsic coupling arises from both excitation-induced contraction of cardiac cells and the deformation-induced generation of intra-cellular currents. The coupled reaction-diffusion equations of the electrical problem and the momentum balance of the mechanical problem are recast into their weak forms through a conventional isoparametric Galerkin approach. As a novel aspect, we propose a monolithic approach to solve the governing equations of excitation-contraction coupling in a fully coupled, implicit sense. We demonstrate the consistent linearization of the resulting set of non-linear residual equations. To assess the algorithmic performance, we illustrate characteristic features by means of representative three-dimensional initial-boundary value problems. The proposed algorithm may open new avenues to patient specific therapy design by circumventing stability and convergence issues inherent to conventional staggered solution schemes.

1. Introduction

The past two decades have seen tremendous progress in the computational modeling of the heart [23, 24]. Efficient computational tools for the assistance of patient specific treatment of cardiac disorders is of great scientific and socio-economical interest [3]. We have come to appreciate that these tools can provide access to regionally varying quantities such as wall strains or stresses, which are virtually impossible to measure in the beating heart [30, 58]. Although tremendous effort has been devoted to understand the coupled electrical and mechanical response of the heart, most existing algorithms solve the electrical and mechanical fields in a decoupled way, typically by using different discretization techniques in time and space for the individual fields [27]. Historically, the biochemical response has been modeled by biophysicists [12, 21, 36], the electrical response by electrical engineers [2, 7], the mechanical response by mechanical engineers [8, 20], and the clinical response by clinicians [5, 25]. The lack of cross-talk between the individual disciplines has hampered the creation of a unified, robust and stable, fully coupled multiscale-multifield solution strategy.

The bidomain equations represent a homogenization of the in-tracellular and extracellular medium [33, 59]. The coupled bidomain equations of electrophysiology have been traditionally solved through staggered solution schemes. The solution of the parabolic and elliptic part of the the bidomain equations via operator splitting follows a common recipe: In the first step, the elliptic part is solved for a constant transmembrane potential φ. In the second step, the parabolic part is solved for a constant external potential φ_e [56, 61, 63]. Apparently, the operator splitting simplifies the coupled nonsymmetric set of equations with symmetric and smaller subsystems at the expense of computation time and stability [15, 48]. The strong coupling due to steep excitation wavefront causes significant stability issues and renders the staggered algorithms computationally inefficient and expensive. This fact motivated the intense study of the monodomain equation, which is obtained through the proportionality assumption between the conduction tensors of the intra- and extracellular domains of the bidomain model. This assumption reduces the coupled bidomain equations to a single parabolic reaction-diffusion equation, which a priori satisfies the elliptic part of the bidomain model. It should be mentioned that the simplified monodomain model of electrophysiology is incapable of modeling the externally applied shock-induced polarization due to nonproportional conductances between the intra- and extracellular spaces and typically mispredicts the velocity of the front depolarization wave [44]. This limits use of the monodomain model in defibrillation simulations. An alternative remedy for the solution of the bido-main equations is the improvement of the solution algorithms. To this end, semi-implicit integration methods where the local and global field variables are updated through explicit and semi-implicit methods [26], predictor-corrector type time stepping algorithms [61, 63, 54] and three-step operator splitting techniques are employed in order to improve the stability and accuracy of solution algorithms [62]. Various preconditioning strategies, e.g. symmetric successive over relaxation [41], block Jacobi [14, 61], block triangular monodomain [15], multigrid [40, 41, 56, 48] and multilevel (hybrid) Schwarz methods have been devised for the linearized set of equations resulting from operator splitting algorithms [35, 49, 50, 51]. A hybridomain model, which is adapted based on a posteriori error estimator to either bi- or monodomain, is introduced in order to improve the comptutational efficiency of the semi-implicit integration [34].

Various anisotropic continuum based models [22, 37] and finite element formulations [16] are developed for the passive mechanical response of the heart. The three-dimensional structure of the heart can be constructed from segmented MRI data [43, 45] and the myofiber orientation in the heart can be obtained by anisotropic least square filtering followed by fiber and sheet tracking techniques applied to the Diffusion Tensor Magnetic Resonance Imaging data of the excised human heart [46]. Operator splitting schemes based on monodomain electrophysiology have been proposed for the electromechanical excitation-contraction problem in [39, 47, 60, 38]. These approaches combine a finite difference method to integrate the excitation equations, with a Galerkin finite element method to solve the equations governing tissue mechanics.

Current state-of-the-art electrophysiological and passive mechanical models enable researchers to explore arrhythmogenesis at the organ level. In order to enable the use of these models for patient-specific therapy design, we still lack efficient numerical methods. At this point, it is noteworthy to say that the above mentioned procedures do not heal the inherent instability issues associated with both decoupled semi-explicit solution strategies and nonconsistent linearization of the variational formulation. Recently, we have proposed a unified, unconditionally stable, finite element formulation based on a Galerkin-type variational formulation for the monodomain electrophysiology [17], bidomain electrophysiology [9] and monodomain based two-field electromechanics [18]. The unconditional stability and the quadratic convergence of the formulations results from the fully implicit backward Euler scheme employed for the integration of the global and local field variables and the consistent linearization of the residual terms obtained from the weak form.

In this follow up work, we extend the monolithic schemes proposed for the bidomain electrophysiology [9] and the two-field electromechanics [18] to three-field excitation contraction coupling [10]. The proposed structure is inherently modular and can be easily generalized to the three-field electro-chemistry [64], the four-field photo-electro-chemistry [1], or the four-field chemo-electro-mechanics of the heart. Unlike existing discretization schemes, which are most powerful on regular grids [6], the proposed finite element based discretization can be applied to arbitrary geometries with arbitrary initial and boundary conditions. It is easily applicable to medical-image based patient-specific geometries [29, 42, 66]. The resulting algorithm provides an unconditionally stable and geometrically flexible framework, which opens possibilities for the analysis of defibrillation phenomena and their impact on the electromechanical behavior of heart tissue. We demonstrate the performance of the proposed approach through a coupled electromechanical analysis of spiral wave initiation in a slice of cardiac tissue and excitation contraction of a three-dimensional generic biventricular heart model. The computational cost of the model in comparison to monolithic monodomain electromechanics formulation is commented.

This manuscript is organized as follows: In Section 2, we introduce the governing equations of cardiac electromechanics consisting of the bidomain model of electrophysiology and the quasi-static linear momentum balance. Section 3 is devoted to the derivation of the weak forms of the field equations, their consistent linearization, and their spatio-temporal discretization. Therein, we apply the finite element method in space and a backward Euler type finite difference scheme in time. In Section 4, we specify the constitutive equations for the underlying source and flux terms, and derive the corresponding consistent algorithmic tangent moduli. Section 5 is concerned with numerical examples demonstrating the distinctive performance of the proposed approach. We conclude the manuscript with closing remarks in Section 6.

2. Governing equations of the cardiac electromechanics

This section introduces the field equations and corresponding state variables of the coupled boundary value problem of cardiac electromechanics.

2.1. Geometric mappings and the field variables

A body B is a three-dimensional manifold consisting of material points ∈ B. The motion of the body is defined by a one-parameter function of time via bijective mappings

$$\mathit{\chi }(\mathcal{P},t)=\{\begin{array}{l}B\to \mathcal{B}(\mathcal{P},t)\in {\mathbb{R}}^3\times {\mathbb{R}}_{+}\hfill \\ \mathcal{P}\mapsto \mathit{x}={\mathit{\chi }}_t(\mathcal{P})=\mathit{\chi }(\mathcal{P},t).\hfill \end{array}$$ (1)

The point x = ( , t) denotes the configuration of the particle 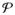at time t ∈ 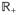. Let the configuration of the material points at a reference time t₀ be denoted by X = 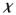( 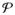, t₀) ∈ 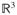and 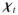( 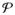) = 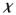( 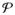, t) denote the placement map for a frozen time frame t. Then, the deformation map ${\mathit{\varphi }}_t{\mathit{\chi }}_t\circ {\mathit{\chi }}_0^{-1}(\mathit{X})$ with

$${\mathit{\varphi }}_t(\mathit{X})=\{\begin{array}{l}{\mathcal{B}}_0\to \mathcal{B}\in {\mathbb{R}}^3\hfill \\ \mathit{X}\mapsto \mathit{x}=\mathit{\varphi }(\mathit{X},t)\hfill \end{array}$$ (2)

maps the reference configuration X ∈ 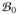of a material point onto the spatial counterpart x ∈ 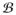. The deformation gradient

$$\mathit{F}:T_X{\mathcal{B}}_0\to T_x\mathcal{B};\mathit{F}:={\nabla }_X{\mathit{\varphi }}_t(\mathit{X})$$ (3)

maps the unit tangent of the reference or the Lagrangean configuration onto its counterpart in the current or the Eulerian configuration. The gradient operators ∇_X [•] and ∇_x[•] denote the spatial derivative with respect to the reference X and current x coordinates, respectively. Moreover, the Jacobian J:= det F > 0 characterizes the volume map of infinitesimal reference volume elements onto the associated spatial volume elements. Furthermore, the reference 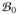and the spatial 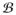manifolds are locally furnished with the covariant reference G and current g metric tensors in the neighborhoods 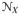of X and 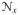of x, respectively. These metric tensors are required for the mapping between the co- and contravariant objects in the Lagrangean and Eulerian manifolds [31]. In order to impose the quasi-incompressible nature of the biological tissues, the deformation gradient F is decomposed into volumetric F_vol:= J^1/31 and unimodular F̄: = J^−1/3 F parts

$$\mathit{F}={\mathit{F}}_{\mathit{vol}}\overline{\mathit{F}}.$$ (4)

The ventricular myocardium is represented as a continuum with a hierarchical architecture consisting of discrete interconnected sheets of unidirectionally aligned muscle fibers [4, 11]. We consider the orthotropic nature of cardiac tissue with two spatially varying preferred directions which characterize the local orientation of myofibers and sheets forming the myocardium [22]. We introduce the Lagrangean unit vectors f₀ and s₀ such that |f₀|_G = 1 and |s₀|_G = 1. Under the action of ϕ_t, the Eulerian counterparts are obtained through the isochoric tangent maps as

$$\mathit{f}=\overline{\mathit{F}}{\mathit{f}}_0\text{and}\mathit{s}=\overline{\mathit{F}}{\mathit{s}}_0,$$ (5)

respectively.

2.2. Field equations of cardiac electromechanics

The electromechanical state of the heart is governed by three primary field (state) variables

$$\text{State}:=\{\mathit{\varphi }(\mathit{X},t),\mathrm{\Phi }(\mathit{X},t),{\mathrm{\Phi }}_e(\mathit{X},t))\},$$ (6)

namely the deformation map ϕ_t, the extracellular potential Φ_e and the transmembrane potential or the so-called action potential Φ:= Φ_i − Φ_e, which is defined as the difference between the intracellular potential Φ_i and the extracellular potential Φ_e. The spatio-temporal evolution of the state variables is described by three field equations. The electrophysiology of cardiac tissue is governed by the bidomain equations, which are based on the homogenized geometrical description of the diffusion-reaction equations of the extra- and intracellular media interacting through voltage-gated ion channels and ion exchangers [33, 59]. Contrary to the monodomain model, where the transmembrane potential is the only field variable related to the electrophysiology, the intra- and extracellular potentials are treated as independent field variables in the bidomain model.

2.3. Bidomain equations of cardiac electrophysiology

The electrophysiology of a material point X of cardiac tissue at time t is defined as State(X, t):= {Φ_i(X, t), Φ_e(X, t)}. In the absence of externally applied current, the total current flux 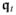of the body is preserved, leading to the following conservation law on the boundary of the subdomain ∂ ∈

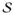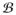
$${\int }_{\partial \mathcal{S}}{\mathfrak{q}}_t·\mathfrak{n}dA=0;{\mathfrak{q}}_t={\mathfrak{q}}_i+{\mathfrak{q}}_e,$$ (7)

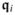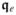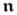where , and are the intra- and extracellular current flux vectors and the surface normal vector, respectively. Transformation of the surface integral to a volume integral via the Gauss theorem and the application of the localization theorem yield the local or strong form of (7)

$$\text{div}{\mathfrak{q}}_t=0.$$ (8)

The constitutive relations between the current fluxes and the potentials of the intra- and extracellular media follow the Ohm’s law

$${\mathfrak{q}}_i=-{\widehat{\mathfrak{D}}}_i·{\nabla }_x{\mathrm{\Phi }}_i;{\mathfrak{q}}_e=-{\widehat{\mathfrak{D}}}_e·{\nabla }_x{\mathrm{\Phi }}_e.$$ (9)

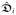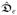Here, and are the intra- and extracellular conductance tensors, respectively. Moreover, we define the transmembrane current i_T as the sum of the ionic and capacitive currents from the intracellular space into the extracellular space such that

$$i_T=\zeta \left({\mathcal{C}}_m\stackrel{.}{\mathrm{\Phi }}+{\mathcal{J}}_{\mathit{ion}}(\mathrm{\Phi },r)\right)\text{with}\mathrm{\Phi }={\mathrm{\Phi }}_i-{\mathrm{\Phi }}_e.$$ (10)

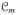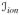Here, ζ denotes the membrane surface to volume ratio in a periodic representative unit of cardiac tissue. and are the membrane capacitance per unit area and the current density flowing through the membrane ion channels, see Figure 1. The notation [•]:= D[•]/Dt is employed for the material time derivative throughout the manuscript. The transmembrane current i_T acts as a source term from the intracellular medium to the extracellular medium, which can be accounted for in the current conservation equations of each subspace as follows

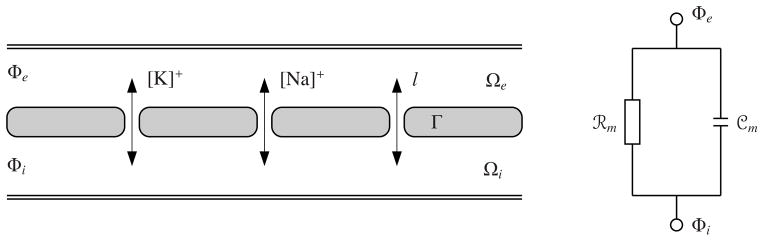
Figure 1.

One-dimensional representaion of myocardium and approximation of the cell membrane by resistor-capacitor circuit. The circuit consists of a nonlinear resistor 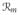dependent on the ionic concentrations (sodium [Na]⁺, potassium [K]⁺ and leakage currents) of intra- and extracellular domains and a capacitor .

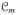$$\text{div}{\mathfrak{q}}_i=-i_T;\text{div}{\mathfrak{q}}_e=i_T.$$ (11)

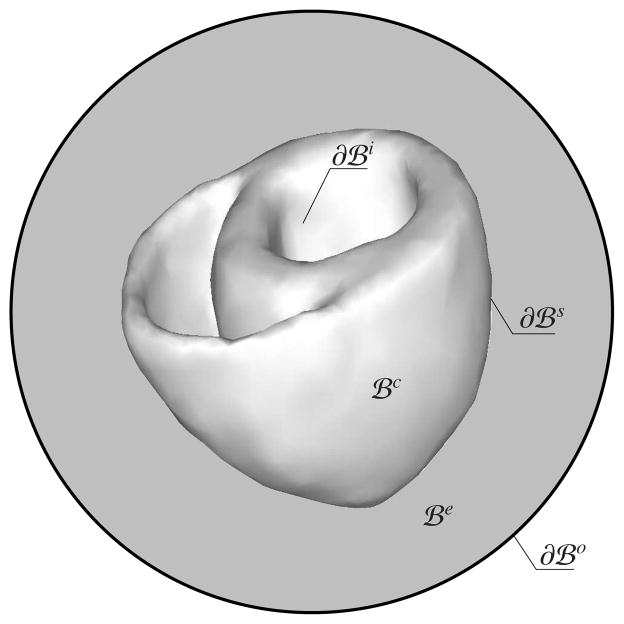
Equations (8) and (11) constitute the strong form of the coupled bidomain model of cardiac electrophysiology. The summation of (11)₁ and (11)₂ defines the conservation of total current, rendering one of two equations redundant. Due to electrophysiological differences between the heart tissue and the surrounding medium, we can distinguish between the two domains, the cardiac domain 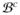and the extracardiac domain 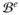, such that the total domain of interest is 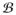= 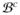∪ 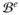. The boundary of the cardiac domain, ∂ 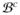= ∂ 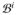∪ ∂ 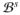, consists of the endocardium ∂ 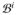, the boundary of the inner walls, and the epicardium ∂ 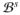, the boundary of the outer walls, such that ∂ 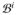∩ ∂ 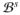= ∅, see Figure 2. Similarly, the boundary of the extracardiac domain, ∂ 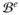= ∂ 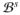∪ ∂ 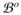, consists of the epicardium ∂ 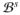and the outer boundary ∂ 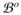, such that ∂ 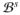∩ ∂ 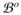= ∅. We can further decompose each boundary into Dirichlet and Neumann-type boundaries, such that $\partial {\mathcal{B}}^a=\partial {\mathcal{B}}_{\phi }^a\cup \partial {\mathcal{B}}_q^a$ and $\partial {\mathcal{B}}_{\phi }^a\cap \partial {\mathcal{B}}_q^a=\varnothing$, where a:= {c, e}. In the absence of an extracardiac domain, the epicardium is identical with the boundary of the extracardiac domain, ∂ 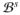= ∂ 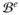. We can then rewrite the Neumann boundary conditions at the interface ∂ 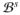as follows

Figure 2.

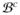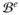Illustration of the cardiac and extracardiac domains and and the endocardium ∂ 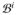, the epicardium ∂ 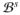, and outer boundary ∂ .

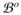$${\mathfrak{q}}_t·\mathfrak{n}={\mathfrak{q}}_0·\mathfrak{n}\text{on}\partial {\mathcal{B}}_q^s.$$ (12)

The extracardiac medium is represented by a single potential term Φ₀ and the corresponding flux vector 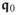= − 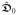∇Φ₀, 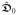denoting the extracardiac conductance. It possesses no transmembrane currents, and the set of transient diffusion equation takes the simple form

$$\text{div}{\mathfrak{q}}_0=0\text{in}{\mathcal{B}}^e.$$ (13)

Equation (12) states that the total current 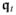can be discretized continuously in the intra- and extracardiac medium leading to the following boundary conditions:

$${\mathrm{\Phi }}_0={\overline{\mathrm{\Phi }}}_0\text{on}\partial {\mathcal{B}}_{\phi }^e\text{and}{\mathfrak{q}}_0·\mathfrak{n}=i_{\mathit{app}}\text{on}\partial {\mathcal{B}}_q^e,$$ (14)

where i_app denotes the applied current at the boundary. The second set of equations stem from (11) and is bounded to the myocardium introducing the boundary conditions

$${\mathrm{\Phi }}_{i,e}={\overline{\mathrm{\Phi }}}_{i,e}\text{on}\partial {\mathcal{B}}_{\phi }\text{and}{\mathfrak{q}}_{i,e}·\mathfrak{n}={\overline{\mathfrak{q}}}_{i,e}\text{on}\partial {\mathcal{B}}_q,$$ (15)

such that ∂ 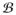= ∂ 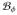∪ ∂ and ∂ ∩ ∂ = ∅. The bidomain equations (11)₁ and (8) are recast into a more coherent form

$$\stackrel{.}{\mathrm{\Phi }}=\text{div}({\mathfrak{D}}_i·\nabla \mathrm{\Phi })+\text{div}({\mathfrak{D}}_i·\nabla {\mathrm{\Phi }}_e)+f^{\mathrm{\Phi }}(\mathrm{\Phi },r),$$ (16)

$$0=-\text{div}({\mathfrak{D}}_i·\nabla \mathrm{\Phi })-\text{div}(\mathfrak{D}·\nabla {\mathrm{\Phi }}_e)$$ (17)

in along with the normalized conductances

$$\mathfrak{D}:=\frac{1}{\zeta {\mathcal{C}}_m}({\widehat{\mathfrak{D}}}_i+{\widehat{\mathfrak{D}}}_e)\text{and}{\mathfrak{D}}_i:=\frac{1}{\zeta {\mathcal{C}}_m}{\widehat{\mathfrak{D}}}_i.$$ (18)

The bidomain equations are derived for a rigid unit volume of cardiac tissue where the gradient operators with respect to material and spatial setting are identical such that ∇ = ∇_x = ∇_X. For the extension of the bidomain equations to the finite deformation setting, two assumptions are made: The electrical fluxes of Kirchhoff type are assumed to be linearly depending on the positive spatial gradient of the respective potentials

$${\mathfrak{q}}_a:={\mathfrak{D}}_a·{\nabla }_x{\mathrm{\Phi }}_a\text{where}a=\{i,e\}.$$ (19)

Moreover, the Equations (16, 17) are assumed to be valid in the spatial setting, e.g. divergence operator is taken to be div(•) = ∇_x · (•) and for unit volume of the deformed configuration.

Modification of the bidomain equations according to the assumptions made above and normalizing the flux terms with the volume change J, we end up with the modified set of equations describing the cardiac electrophysiology of a deforming medium

$$\stackrel{.}{\mathrm{\Phi }}=J\text{div}(J^{-1}{\mathcal{D}}_i·{\nabla }_x\mathrm{\Phi })+J^{-1}\text{div}(J^{-1}{\mathfrak{D}}_i·{\nabla }_x{\mathrm{\Phi }}_e)+{\mathcal{F}}^{\phi },$$ (20)

$$0=J\text{div}\left(J^{-1}{\mathfrak{D}}_i·{\nabla }_x\mathrm{\Phi }\right)+J\text{div}\left(J^{-1}\mathfrak{D}·{\nabla }_x{\mathrm{\Phi }}_e\right)$$ (21)

for a unit undeformed volume in 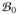. Equation (20) is a parabolic partial differential equation and equation (21) defines an elliptic partial differential equation. is the Fitzhugh-Nagumo type generic function defining the excitation induced ionic currents through the cell membrane from the intracellular to the extracellular domain.

2.4. Cardiac mechanics

The balance of linear momentum

$$J\text{div}[J^{-1}\widehat{\mathit{\tau }}]+\mathit{b}=\mathbf{0}\text{in}\mathcal{B}$$ (22)

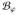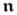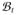states the quasi-static mechanical equilibrium in terms of the Kirchhoff stress tensor τ̂ and a given body force b. The balance of linear momentum (22) is subjected to essential boundary conditions ϕ = ϕ̄ on ∂ and natural boundary conditions t̄ = J⁻¹τ · on ∂ such that ∂ 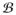= ∂ 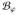∪ ∂ 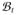and ∂ 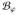∩ ∂ 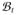= ∅. The momentum balance depends on the transmembrane potential Φ through the functional dependence of the Kirchhoff stress tensor.

2.5. Constitutive equations

The solution of the coupled initial boundary value problem requires the definition of the constitutive relations which characterize the Kirchhoff stress tensor τ̂, the potential flux vectors and the current source 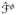appearing in Equations (20–22). The Kirchhoff stress tensor τ̂ can be decomposed into the passive τ̂^pas and active τ̂^act parts

$$\widehat{\mathit{\tau }}={\widehat{\mathit{\tau }}}^{\text{pas}}(\mathit{g};\mathit{F})+{\widehat{\mathit{\tau }}}^{\text{act}}(\mathit{g};\mathit{F},\mathrm{\Phi }),$$ (23)

see [38, 47]. The passive part τ̂^pas is solely governed by mechanical deformation, while the active part τ̂^act is generated by the excitation-induced contraction of the myocytes during the course of depolarization. Since the formulation is laid out in the Eulerian setting, we need to explicitly include the current metric g among the arguments of the constitutive functions. Since the parabolic and the elliptic parts of the bidomain equations are altered in order to replace the intracellular potential Φ_i with the transmembrane potential Φ, the following potential flux vectors are defined

$${\mathfrak{q}}_i={\mathfrak{D}}_i·{\nabla }_x(\mathrm{\Phi });{\mathfrak{q}}_{ie}={\mathfrak{D}}_i·{\nabla }_x({\mathrm{\Phi }}_e);{\mathfrak{q}}_e=\mathfrak{D}·{\nabla }_x({\mathrm{\Phi }}_e)$$ (24)

through the deformation-dependent anisotropic spatial conduction tensors 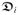(g; F, f₀) and 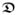(g; F, f₀) governing the conduction speed of the non-planar depolarization fronts of the intra- and extracellular media in three-dimensional anisotropic cardiac tissue. In the monodomain model of cardiac electro-physiology, based on the assumption of coaxiality of the intra-and extracellular conductances, a unique effective monodomain conductance reads . The elliptic part of the bidomain equations can also be omitted by the coaxiality assumption [9]. The last constitutive relation characterizes the electrical source term of the Fitzhugh-Nagumo-type excitation equation (20)

$${\widehat{\mathcal{F}}}^{\phi }={\widehat{\mathcal{F}}}_{\text{e}}^{\phi }(\mathrm{\Phi },r)+{\widehat{\mathcal{F}}}_{\text{m}}^{\phi }(\mathit{g};\mathit{F},{\mathit{f}}_0,\mathrm{\Phi }).$$ (25)

It is additively decomposed into the excitation-induced purely electrical part ${\widehat{\mathcal{F}}}_{\text{e}}^{\phi }(\mathrm{\Phi },r)$ and the stretch-induced mechano-electrical part ${\widehat{\mathcal{F}}}_{\text{m}}^{\phi }(\mathit{g};\mathit{F},{\mathit{f}}_0,\mathrm{\Phi })$. The former describes the effective current generation due to the inward and outward flow of ions across the cell membrane. This ionic flow is triggered by a perturbation of the resting potential of a cardiac cell beyond some physical threshold upon the arrival of the depolarization front. The latter accounts for the opening of ion channels under the action of deformation [28, 38]. Apart from the primary field variables, the recovery variable r appears among the arguments of ${\widehat{\mathcal{F}}}_{\text{e}}^{\phi }$ in (25). It characterizes the repolarization response of the action potential. The evolution of the recovery variable r determines the shape and the duration of the action potential inherent to each cardiac cell and may change throughout the heart. Its evolution is commonly modeled by a local ordinary differential equation

$$\stackrel{.}{r}={\widehat{f}}^r(\mathrm{\Phi },r).$$ (26)

From an algorithmic point of view, the local nature of the evolution equation (26) allows us to treat the recovery variable as an internal variable. This is one of the key features of the proposed formulation that preserves the modular global structure of the field equations as set out in our recent works [17, 18]. Furthermore, as mentioned in Section 1, cardiac tissue possesses an anisotropic and inhomogeneous micro-structure. This undoubtedly necessitates the explicit incorporation of a position-dependent orientation of myocytes, possibly in terms of structural tensors, in the argument list of the constitutive functions for τ̂, D̂ and ${\widehat{\mathcal{F}}}_m^{\phi }$. At this stage, however, we have suppressed this dependency for the sake of conciseness by leaving details out until Section 4 where we introduce the active and passive response of the cardiac tissue.

Having the field equations and the functional forms of the constitutive equations at hand, we are now in a position to construct a unified finite element framework for the monolithic numerical solution of the strongly coupled problem of three-field cardiac electromechanics.

3. The finite element formulation

In this section, we present a monolithic set of equations derived from a Galerkin type finite element formulation. To this end, we construct the weak forms of the Equations (20–22) and consistently linearize them along the three independent field variables, namely the deformation map ϕ (X, t), the transmembrane potential Φ(X, t) and the extracellular potential Φ_e(X, t). An identical temporal as well as spatial discretization scheme will be employed for the mechanical and electrical fields. All field variables are discretized with isoparametric shape functions to transform the continuous integral equations of the nonlinear weighted residuals and their linearizations to a set of coupled, discrete algebraic equations. This set of algebraic equations is then solved monolithically via a Newton-type iterative solution scheme for the nodal degrees of freedom.

3.1. Weak formulation

A conventional Galerkin procedure is applied to construct the weak forms of the governing field equations (20–22). For this purpose, the residual equations are multiplied by the weight functions δϕ, δΦ, and δΦ_e, which satisfy the essential boundary conditions, δϕ = 0 on ∂ 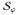, δΦ = 0 on ∂ 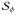, and δΦ_e = 0 on ∂ 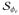and belong to the Hilbert space $H_0^1(\mathcal{B})$ consisting of functions which, along with their weak partial derivatives, are square integrable in the domain 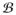. The weighted residual equations are then integrated over the solid volume. The conventional procedures, integration by parts along with the Gauss theorem, lead to the following weighted residual expressions for the balance of linear momentum

$$G^{\varphi }=G_{int}^{\varphi }(\delta \mathit{\varphi },\mathit{\varphi },\mathrm{\Phi })-G_{\text{ext}}^{\varphi }(\delta \mathit{\varphi })=0,$$ (27)

the parabolic part of the bidomain equations

$$G^{\phi }=G_{int}^{\phi }(\delta \mathrm{\Phi },\mathit{\varphi },\mathrm{\Phi },{\mathrm{\Phi }}_e)-G_{\text{ext}}^{\phi }(\delta \mathrm{\Phi },\mathit{\varphi },\mathrm{\Phi },{\mathrm{\Phi }}_e)=0,$$ (28)

and the elliptic part of the bidomain equations

$$G^{{\phi }_e}=G_{int}^{{\phi }_e}(\delta {\mathrm{\Phi }}_e,\mathit{\varphi },\mathrm{\Phi },{\mathrm{\Phi }}_e)-G_{\text{ext}}^{{\phi }_e}(\delta {\mathrm{\Phi }}_e,\mathit{\varphi },\mathrm{\Phi },{\mathrm{\Phi }}_e)=0.$$ (29)

The explicit forms of the individual terms in (27) are defined as

$$\begin{array}{l}{G}_{int}^{\varphi }:={\int }_{\mathcal{B}}{\nabla }_x(\delta \mathit{\varphi }):\widehat{\mathit{\tau }}dV,\\ G_{\text{ext}}^{\varphi }:={\int }_{\mathcal{B}}\delta \mathit{\varphi }·\mathit{b}dV+{\int }_{\partial {\mathcal{S}}_t}\delta \mathit{\varphi }·\overline{\mathit{t}}dA,\end{array}$$ (30)

where the body force b and the surface traction t̄ are assumed to be given. The weak residual expressions $G_{int}^{\phi }$ and $G_{\text{ext}}^{\phi }$ in (28) stem from the parabolic part of the bidomain equations (20) and read

$$\begin{array}{l}{G}_{int}^{\phi }:={\int }_{\mathcal{B}}\left(\delta \mathrm{\Phi }\stackrel{.}{\mathrm{\Phi }}+{\nabla }_x(\delta \mathrm{\Phi })·({\widehat{\mathfrak{q}}}_i+{\widehat{\mathfrak{q}}}_{ie})\right)dV,\\ G_{\text{ext}}^{\phi }:={\int }_{\mathcal{B}}\delta \mathrm{\Phi }{\widehat{\mathcal{F}}}^{\phi }dV+{\int }_{\partial {\mathcal{S}}_q}\delta \mathrm{\Phi }\overline{\mathfrak{q}}dA\end{array}$$ (31)

along with the definitions

$${\widehat{\mathfrak{q}}}_i={\mathfrak{D}}_i·{\nabla }_x\mathrm{\Phi },{\widehat{\mathfrak{q}}}_{ie}={\mathfrak{D}}_i·{\nabla }_x{\mathrm{\Phi }}_e,{\widehat{\mathfrak{q}}}_e=\mathfrak{D}·{\nabla }_x{\mathrm{\Phi }}_e.$$ (32)

Likewise, the residual expressions $G_{int}^{{\phi }_e}$ and $G_{\text{ext}}^{{\phi }_e}$ in (29) of the elliptic part of the bidomain equations (21) are given by

$$\begin{array}{l}{G}_{\text{int}}^{{\phi }_e}:={\int }_{\mathcal{B}}{\nabla }_x(\delta {\mathrm{\Phi }}_e)·({\widehat{\mathfrak{q}}}_i+{\widehat{\mathfrak{q}}}_e)dV,\\ G_{\text{ext}}^{{\phi }_e}:={\int }_{\partial \mathcal{B}}\delta {\mathrm{\Phi }}_e{\overline{\mathfrak{q}}}_{t}dA.\end{array}$$ (33)

The surface flux terms $\overline{\mathfrak{q}}=({\widehat{\mathfrak{q}}}_i+{\widehat{\mathfrak{q}}}_{ie})·\mathfrak{n}$ and ${\overline{\mathfrak{q}}}_t=({\widehat{\mathfrak{q}}}_i+{\widehat{\mathfrak{q}}}_e)·\mathfrak{n}$ are the prescribed natural boundary conditions. In contrast to the mechanical external term in (30)₂, $G_{\text{ext}}^{\phi }$ depends explicitly upon the field variables through the non-linear source term .

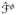3.2. Consistent linearization

The weighted residual equations (30, 31, 33) are nonlinear functionals of the primary variables due to the geometric and constitutive terms. The solution of these equations thus requires a consistent linearization with respect to the field variables about ϕ = ϕ̃, Φ = Φ̃ and Φ_e = Φ̃_e

$$\begin{array}{l}\text{Lin}{G}^{\varphi }{\mid }_{\stackrel{\sim }{\mathit{\varphi }},\stackrel{\sim }{\mathrm{\Phi }}}:=G^{\varphi }(\delta \mathit{\varphi },\stackrel{\sim }{\mathit{\varphi }},\stackrel{\sim }{\mathrm{\Phi }})+\mathrm{\Delta }{G}^{\varphi }(\delta \mathit{\varphi },\stackrel{\sim }{\mathit{\varphi }},\stackrel{\sim }{\mathrm{\Phi }};\mathrm{\Delta }\mathit{\varphi },\mathrm{\Delta }\mathrm{\Phi })=0,\\ \text{Lin}{G}^{\phi }{\mid }_{\stackrel{\sim }{\mathit{\varphi }},\stackrel{\sim }{\mathrm{\Phi }},{\stackrel{\sim }{\mathrm{\Phi }}}_e}:=G^{\phi }(\delta \mathrm{\Phi },\stackrel{\sim }{\mathit{\varphi }},\stackrel{\sim }{\mathrm{\Phi }},{\stackrel{\sim }{\mathrm{\Phi }}}_e)+\mathrm{\Delta }{G}^{\phi }(\delta \mathrm{\Phi },\stackrel{\sim }{\mathit{\varphi }},\stackrel{\sim }{\mathrm{\Phi }},{\stackrel{\sim }{\mathrm{\Phi }}}_e;\mathrm{\Delta }\mathit{\varphi },\mathrm{\Delta }\mathrm{\Phi },\mathrm{\Delta }{\mathrm{\Phi }}_e)=0,\\ \text{Lin}{G}^{{\phi }_e}{\mid }_{\stackrel{\sim }{\mathit{\varphi }},\stackrel{\sim }{\mathrm{\Phi }},{\mathrm{\Phi }}_e}:=G^{{\phi }_e}(\delta {\mathrm{\Phi }}_e,\stackrel{\sim }{\mathit{\varphi }},\stackrel{\sim }{\mathrm{\Phi }},{\stackrel{\sim }{\mathrm{\Phi }}}_e)+\mathrm{\Delta }{G}^{{\phi }_e}(\delta {\mathrm{\Phi }}_e,\stackrel{\sim }{\mathit{\varphi }},\stackrel{\sim }{\mathrm{\Phi }},{\stackrel{\sim }{\mathrm{\Phi }}}_e;\mathrm{\Delta }\mathit{\varphi },\mathrm{\Delta }\mathrm{\Phi },\mathrm{\Delta }{\mathrm{\Phi }}_e)=0.\end{array}$$ (34)

The incremental terms ΔG^ϕ and ΔG^φ, which can be obtained through the Gâteaux derivative, may be expressed in the following decomposed forms

$$\mathrm{\Delta }{G}^{\gamma }=\mathrm{\Delta }{G}_{int}^{\gamma }-\mathrm{\Delta }{G}_{\text{ext}}^{\gamma }\text{for}\gamma =\varphi ,\phi ,{\phi }_e,$$ (35)

based on the definitions in (20–22). We then start with the elaboration of the increment $\mathrm{\Delta }{G}_{int}^{\varphi }$ according to (30)₁

$$\mathrm{\Delta }{G}_{int}^{\varphi }={\int }_{\mathcal{B}}\mathrm{\Delta }({\nabla }_x(\delta \mathit{\varphi })):\widehat{\mathit{\tau }}+{\nabla }_x(\delta \mathit{\varphi }):\mathrm{\Delta }\widehat{\mathit{\tau }}dV.$$ (36)

Linearization of the non-linear terms in (36) yields

$$\begin{array}{l}\mathrm{\Delta }({\nabla }_x(\delta \mathit{\varphi }))=-{\nabla }_x(\delta \mathit{\varphi }){\nabla }_x(\mathrm{\Delta }\mathit{\varphi });\\ \mathrm{\Delta }\widehat{\mathit{\tau }}={\mathbf{\pounds }}_{\mathrm{\Delta }\mathit{\varphi }}\widehat{\mathit{\tau }}+{\nabla }_x(\mathrm{\Delta }\mathit{\varphi })\widehat{\mathit{\tau }}+\widehat{\mathit{\tau }}{\nabla }_x^T(\mathrm{\Delta }\mathit{\varphi })+{\mathfrak{C}}^{\varphi \phi }\mathrm{\Delta }\mathrm{\Phi },\end{array}$$ (37)

where £_Δϕ τ̂ denotes the objective Lie derivative along the increment Δ_ϕ and can be expressed as

$$\begin{array}{l}{\mathbf{\pounds }}_{\mathrm{\Delta }\mathit{\varphi }}\widehat{\mathit{\tau }}={\mathbb{C}}^{\varphi \varphi }:\frac{1}{2}{\mathbf{\pounds }}_{\mathrm{\Delta }\mathit{\varphi }}\mathit{g}={\mathbb{C}}^{\varphi \varphi }:(\mathit{g}{\nabla }_x(\mathrm{\Delta }\mathit{\varphi }));\\ {\mathbf{\pounds }}_{\mathrm{\Delta }\mathit{\varphi }}\mathit{g}=\mathit{g}{\nabla }_x(\mathrm{\Delta }\mathit{\varphi })+{\nabla }_x^T(\mathrm{\Delta }\mathit{\varphi })\mathit{g}.\end{array}$$ (38)

The fourth-order spatial tangent moduli 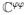in (38) and the sensitivity of the Kirchhoff stresses to the action potential ℭ^ϕφ introduced in (37)₂ are defined as

$${\mathbb{C}}^{\varphi \varphi }:=2{\partial }_{\mathit{g}}\widehat{\mathit{\tau }}(\mathit{g};\mathit{F},\mathrm{\Phi })\text{and}{\mathfrak{C}}^{\varphi \phi }:={\partial }_{\mathrm{\Phi }}\widehat{\mathit{\tau }}(\mathit{g};\mathit{F},\mathrm{\Phi }),$$ (39)

respectively. Incorporation of (37, 38) into (36) results in the following expression

$$\mathrm{\Delta }{G}_{int}^{\varphi }={\int }_{\mathcal{B}}{\nabla }_x(\delta \mathit{\varphi }):{\mathbb{C}}^{\varphi \varphi }:(\mathit{g}{\nabla }_x(\mathrm{\Delta }\mathit{\varphi }))dV+{\int }_{\mathcal{B}}{\nabla }_x(\delta \mathit{\varphi }):({\nabla }_x(\mathrm{\Delta }\mathit{\varphi })\widehat{\mathit{\tau }})dV+{\int }_{\mathcal{B}}{\nabla }_x(\delta \mathit{\varphi }):{\mathfrak{C}}^{\varphi \phi }\mathrm{\Delta }\mathrm{\Phi }dV.$$ (40)

The terms in (40) demonstrate the inherent nonlinearities arising from the mechanical material response, the geometry, and the coupled electromechanical stress response. Since the body force b and the traction boundary conditions t̄ in (30)₂ are prescribed, we have $\mathrm{\Delta }{G}_{\text{ext}}^{\varphi }=0$ yielding the identity $\mathrm{\Delta }{G}^{\varphi }\equiv \mathrm{\Delta }{G}_{\text{int}}^{\varphi }$. Recalling the explicit algorithmic form of $G_{\text{int}}^{\phi }$ from (31)₁, the increment $\mathrm{\Delta }{G}_{\text{int}}^{\phi }$ can be expressed as

$$\mathrm{\Delta }{G}_{\text{int}}^{\phi }={\int }_{\mathcal{B}}\delta \mathrm{\Phi }\frac{\mathrm{\Delta }\mathrm{\Phi }}{\mathrm{\Delta }t}+\mathrm{\Delta }({\nabla }_x\delta \mathrm{\Phi })·({\widehat{\mathfrak{q}}}_i+{\widehat{\mathfrak{q}}}_{ie})dV+{\int }_{\mathcal{B}}{\nabla }_x(\delta \mathrm{\Phi })·\mathrm{\Delta }({\widehat{\mathfrak{q}}}_i+{\widehat{\mathfrak{q}}}_{ie})dV.$$ (41)

Analogous to (37)₁, linearization of ∇_x(δΦ) leads to

$$\mathrm{\Delta }({\nabla }_x(\delta \mathrm{\Phi }))=-{\nabla }_x(\delta \mathrm{\Phi }){\nabla }_x(\mathrm{\Delta }\mathit{\varphi }).$$ (42)

Furthermore, based on the functional definition of the spatial potential fluxes, 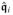, 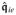and 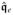, we obtain

$$\begin{array}{l}\mathrm{\Delta }{\widehat{\mathfrak{q}}}_i={\mathbf{\pounds }}_{\mathrm{\Delta }\mathit{\varphi }}{\widehat{\mathfrak{q}}}_i+{\nabla }_x(\mathrm{\Delta }\mathit{\varphi })·{\widehat{\mathfrak{q}}}_i+{\mathfrak{D}}_i·{\nabla }_x(\mathrm{\Delta }\mathrm{\Phi }),\\ \mathrm{\Delta }{\widehat{\mathfrak{q}}}_{ie}={\mathbf{\pounds }}_{\mathrm{\Delta }\mathit{\varphi }}{\widehat{\mathfrak{q}}}_{ie}+{\nabla }_x(\mathrm{\Delta }\mathit{\varphi })·{\widehat{\mathfrak{q}}}_{ie}+{\mathfrak{D}}_i·{\nabla }_x(\mathrm{\Delta }{\mathrm{\Phi }}_e),\\ \mathrm{\Delta }{\widehat{\mathfrak{q}}}_e={\mathbf{\pounds }}_{\mathrm{\Delta }\mathit{\varphi }}{\widehat{\mathfrak{q}}}_e+{\nabla }_x(\mathrm{\Delta }\mathit{\varphi })·{\widehat{\mathfrak{q}}}_e+\mathfrak{D}·{\nabla }_x(\mathrm{\Delta }{\mathrm{\Phi }}_e),\end{array}$$ (43)

where £_Δϕ 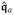denotes the objective Lie derivative of the potential flux 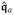along the increment Δϕ

$${\mathbf{\pounds }}_{\mathrm{\Delta }\mathit{\varphi }}{\widehat{\mathfrak{q}}}_a={\mathfrak{C}}_a:\frac{1}{2}{\mathbf{\pounds }}_{\mathrm{\Delta }\mathit{\varphi }}\mathit{g}={\mathfrak{C}}_a:(\mathit{g}{\nabla }_x(\mathrm{\Delta }\mathit{\varphi }))$$ (44)

for a ={i, ie, e}. In Equations (43–44), the second-order deformation-dependent conduction tensors

$${\mathfrak{D}}_i:={\mathfrak{D}}_i(\mathit{g};\mathit{F},{\mathit{f}}_0),\mathfrak{D}:=\mathfrak{D}(\mathit{g};\mathit{F},{\mathit{f}}_0)$$ (45)

and the third-order mixed moduli

$${\mathfrak{C}}_a:=2{\partial }_{\mathit{g}}{\widehat{\mathfrak{q}}}_a(\mathit{g};\mathit{F},\mathrm{\Phi })\text{for}a=\{i,ie,e\}$$ (46)

are introduced, respectively. Substituting the results (42–43) and (44) into (41), we obtain the following explicit expression for the increment

$$\mathrm{\Delta }{G}_{int}^{\phi }{\int }_{\mathcal{B}}\delta \mathrm{\Phi }\frac{\mathrm{\Delta }\mathrm{\Phi }}{\mathrm{\Delta }t}dV+{\int }_{\mathcal{B}}{\nabla }_x(\delta \mathrm{\Phi })·{\mathfrak{D}}_i·({\nabla }_x(\mathrm{\Delta }\mathrm{\Phi })+{\nabla }_x(\mathrm{\Delta }{\mathrm{\Phi }}_e))dV+{\int }_{\mathcal{B}}{\nabla }_x(\delta \mathrm{\Phi })·{\mathfrak{C}}^{\phi \varphi }:(\mathit{g}{\nabla }_x(\mathrm{\Delta }\mathit{\varphi }))dV,$$ (47)

where ℭ^φϕ = ℭ_i + ℭ_ie. The external term $G_{\text{ext}}^{\phi }$ in (28) depends non-linearly on the field variables through the source term 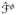defined in (25). For a given q̄ on ∂ 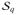, we then obtain the following incremental form

$$\mathrm{\Delta }{G}_{\text{ext}}^{\phi }:={\int }_{\mathcal{B}}\delta \mathrm{\Phi }\mathrm{\Delta }{\widehat{\mathcal{F}}}^{\phi }dV$$ (48)

where

$$\mathrm{\Delta }{\widehat{\mathcal{F}}}^{\phi }=\mathcal{H}:(\mathit{g}{\nabla }_x(\mathrm{\Delta }\mathit{\varphi }))+\mathcal{H}\mathrm{\Delta }\mathrm{\Phi }$$ (49)

is the linearization of the scalar-valued function 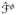. The tangent terms 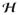and 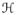in (48)₂ are defined as

$$\mathcal{H}:=2{\partial }_{\mathit{g}}{\widehat{\mathcal{F}}}^{\phi }(\mathit{g};\mathit{F},\mathrm{\Phi })\text{and}\mathcal{H}:={\partial }_{\mathrm{\Phi }}{\widehat{\mathcal{F}}}^{\phi }(\mathit{g};\mathit{F},\mathrm{\Phi }),$$ (50)

respectively. Based on the decomposed form introduced before, the scalar tangent term 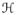can be expressed as

$$\mathcal{H}={\mathcal{H}}_{\text{e}}+{\mathcal{H}}_{\text{m}}\text{with}{\mathcal{H}}_{\text{e}}:={\partial }_{\mathrm{\Phi }}{\widehat{\mathcal{F}}}_{\text{e}}^{\phi },{\mathcal{H}}_{\text{m}}:={\partial }_{\mathrm{\Phi }}{\widehat{\mathcal{F}}}_{\text{m}}^{\phi }.$$ (51)

Inserting the result (49) into (48), we obtain the linearized external term

$$\mathrm{\Delta }{G}_{\text{ext}}^{\phi }={\int }_{\mathcal{B}}\delta \mathrm{\Phi }(\mathcal{H}:(\mathit{g}{\nabla }_x(\mathrm{\Delta }\mathit{\varphi }))+\mathcal{H}\mathrm{\Delta }\mathrm{\Phi })dV.$$ (52)

Considering the weak form of the elliptic part of the bidomain equations $G_{\text{int}}^{{\phi }_e}$ in (33), the increment $\mathrm{\Delta }{G}_{\text{int}}^{{\phi }_e}$ can be written as

$$\mathrm{\Delta }{G}_{\text{int}}^{{\phi }_e}={\int }_{\mathcal{B}}\mathrm{\Delta }({\nabla }_x\delta {\mathrm{\Phi }}_e)·({\widehat{\mathfrak{q}}}_i+{\widehat{\mathfrak{q}}}_e)+{\nabla }_x(\delta {\mathrm{\Phi }}_e)·\mathrm{\Delta }({\widehat{\mathfrak{q}}}_i+{\widehat{\mathfrak{q}}}_e)dV.$$ (53)

Substituting the results (42, 43) and (44) into (53), we finally obtain

$$\mathrm{\Delta }{G}_{\text{int}}^{{\phi }_e}={\int }_{\mathcal{B}}{\nabla }_x(\delta {\mathrm{\Phi }}_e)·({\mathfrak{D}}_i·{\nabla }_x(\mathrm{\Delta }\mathrm{\Phi })+\mathfrak{D}·{\nabla }_x(\mathrm{\Delta }{\mathrm{\Phi }}_e))dV+{\int }_{\mathcal{B}}{\nabla }_x(\delta {\mathrm{\Phi }}_e)·{\mathfrak{C}}^{{\phi }_e\varphi }:\mathit{g}{\nabla }_x(\mathrm{\Delta }\mathit{\varphi })dV,$$ (54)

where ℭ^φ_eϕ = ℭ_i + ℭ_e. The increment operator Δ [•] in Equation (42) applies to Φ_e in the same way as Φ. This completes the linearization within the continuous spatial setting. The increment $\mathrm{\Delta }{G}_{\text{ext}}^{{\phi }_e}$ vanishes, since the external term $G_{\text{ext}}^{{\phi }_e}$ in (29, 33) depends solely on the prescribed boundary flux term .

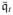3.3. Spatial discretization

In a final step, we perform the spatial discretization of the field variables to obtain algebraic counterparts of the residual expressions (30, 31, 33) and construct the element matrices from the linearized terms (40, 47, 54). To this end, we discretize the reference domain 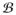into element subdomains 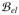such that $\mathcal{B}\approx {\cup }_{e=1}^{n_{el}}{\mathcal{B}}_{el}^h$ with n_el denoting the number of the subdomains 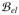in the body. We then interpolate the field variables and the associated weight functions on each element domain by introducing the discrete nodal values and 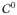-continuous shape functions

$$\begin{array}{ll}{\mathit{\varphi }}^h={\sum }_{i=1}^{{\text{n}}_{\text{en}}}{\mathcal{N}}^i{\widehat{\mathit{x}}}_i& \delta {\mathit{\varphi }}^h={\sum }_{i=1}^{{\text{n}}_{\text{en}}}{\mathcal{N}}^i\delta {\widehat{\mathit{x}}}_i,\\ {\mathrm{\Phi }}^h={\sum }_{j=1}^{{\text{n}}_{\text{en}}}{\mathcal{N}}^j{\widehat{\mathrm{\Phi }}}_j& \delta {\mathrm{\Phi }}^h={\sum }_{j=1}^{{\text{n}}_{\text{en}}}{\mathcal{N}}^j\delta {\widehat{\mathrm{\Phi }}}_j,\\ {\mathrm{\Phi }}_e^h={\sum }_{k=1}^{{\text{n}}_{\text{en}}}{\mathcal{N}}^k{\widehat{\mathrm{\Phi }}}_{ek}& \delta {\mathrm{\Phi }}_e^h={\sum }_{k=1}^{{\text{n}}_{\text{en}}}{\mathcal{N}}^k\delta {\widehat{\mathrm{\Phi }}}_{ek},\end{array}$$ (55)

where n_en refers to the number of nodes per element. Based on the discretization (55), the spatial gradient of the weight functions and of the incremental fields read

$$\begin{array}{ll}{\nabla }_x(\delta {\mathit{\varphi }}^h)={\sum }_{i=1}^{{\text{n}}_{\text{en}}}\delta {\widehat{\mathit{x}}}_i\otimes {\nabla }_x{\mathcal{N}}^i& {\nabla }_x\mathrm{\Delta }{\mathit{\varphi }}^h={\sum }_{i=1}^{{\text{n}}_{\text{en}}}\mathrm{\Delta }{\widehat{\mathit{x}}}_i\otimes {\nabla }_x{\mathcal{N}}^i\\ {\nabla }_x(\delta {\mathrm{\Phi }}^h)={\sum }_{j=1}^{{\text{n}}_{\text{en}}}\delta {\widehat{\phi }}_j\otimes {\nabla }_x{\mathcal{N}}^j& {\nabla }_x\mathrm{\Delta }{\mathrm{\Phi }}^h={\sum }_{j=1}^{{\text{n}}_{\text{en}}}\mathrm{\Delta }{\widehat{\mathrm{\Phi }}}_j\otimes {\nabla }_x{\mathcal{N}}^j\\ {\nabla }_x(\delta {\mathrm{\Phi }}_e^h)={\sum }_{k=1}^{{\text{n}}_{\text{en}}}\delta {\widehat{\mathrm{\Phi }}}_{ek}\otimes {\nabla }_x{\mathcal{N}}^k& {\nabla }_x\mathrm{\Delta }{\mathrm{\Phi }}_e^h={\sum }_{k=1}^{{\text{n}}_{\text{en}}}\mathrm{\Delta }{\widehat{\mathrm{\Phi }}}_{ek}\otimes {\nabla }_x{\mathcal{N}}^k.\end{array}$$ (56)

Incorporating the discretized representations (55, 56) in (27, 28, 29) along with (30, 31, 33), we obtain the discrete residual vectors

$$\begin{array}{l}{\mathbb{R}}^{\varphi }={\text{A}}_{e=1}^{{\text{n}}_{\text{el}}}{\int }_{{\mathcal{B}}_{el}^h}{\nabla }_x{\mathcal{N}}^i·\widehat{\tau }-{\mathcal{N}}^i\mathit{b}dV-{\int }_{\partial {\mathcal{S}}_t^e}{\mathcal{N}}^i·\overline{\mathit{t}}dA=\mathbf{0},\\ {\mathbb{R}}^{\phi }={\text{A}}_{e=1}^{{\text{n}}_{\text{el}}}{\int }_{{\mathcal{B}}_{el}^h}{\mathcal{N}}^i\frac{\mathrm{\Phi }-{\mathrm{\Phi }}_n}{\mathrm{\Delta }t}+{\nabla }_x{\mathcal{N}}^i·({\widehat{\mathfrak{q}}}_i+{\widehat{\mathfrak{q}}}_{ie})dV-{\int }_{{\mathcal{B}}_{el}^h}{\mathcal{N}}^i{\widehat{\mathcal{F}}}^{\phi }dV-{\int }_{\partial {\mathcal{B}}^{el}}{\mathcal{N}}^i\overline{\mathfrak{q}}dA=0,\\ {\mathbb{R}}^{{\phi }_e}={\text{A}}_{e=1}^{{\text{n}}_{\text{el}}}{\int }_{{\mathcal{B}}_{el}^h}{\nabla }_x{\mathcal{N}}^i·({\widehat{\mathfrak{q}}}_i+{\widehat{\mathfrak{q}}}_e)dV-{\int }_{\partial {\mathcal{B}}_{el}^h}{\mathcal{N}}^i{\overline{\mathfrak{q}}}_{t}dA=0\end{array}$$ (57)

where the operator A denotes the standard assembly of element contributions at the local element nodes i = 1,…,n_en over n_el subdomains. Following analogous steps, the discrete form of the linearized residual terms (34) can readily be obtained by substituting the discretized representations (55–56) in (40, 47, 52, 54). Alternatively, the linearization of the discrete residual expressions (57)_1–3 can be shown as follows

$$\text{Lin}\mathbb{R}=\mathbb{R}+\frac{\partial \mathbb{R}}{\partial \mathbb{U}}\mathrm{\Delta }\mathbb{U};\mathbb{R}=\left\{\begin{array}{l}{\mathbb{R}}^{\varphi }\hfill \\ {\mathbb{R}}^{\phi }\hfill \\ {\mathbb{R}}^{{\phi }_e}\hfill \end{array}\right\};\mathbb{U}=\left\{\begin{array}{l}{\widehat{\mathit{x}}}^h\hfill \\ {\widehat{\mathrm{\Phi }}}^h\hfill \\ {\widehat{\mathrm{\Phi }}}_e^h\hfill \end{array}\right\}.$$ (58)

The coupled element matrix is derived via incorporation of (55, 56) into (40, 47, 52, 54)

$$\mathbb{K}=\frac{\partial \mathbb{R}}{\partial \mathbb{U}}=\underset{e=1}{\overset{n_{el}}{\text{A}}}{\mathbb{K}}_{el};{\mathbb{K}}_{el}:=\left[\begin{array}{lll}{\mathbb{K}}^{\varphi \varphi }\hfill & {\mathbb{K}}^{\varphi \phi }\hfill & {\mathbb{K}}^{\varphi {\phi }_e}\hfill \\ {\mathbb{K}}^{\phi \varphi }\hfill & {\mathbb{K}}^{\phi \phi }\hfill & {\mathbb{K}}^{\phi {\phi }_e}\hfill \\ {\mathbb{K}}^{{\phi }_e\varphi }\hfill & {\mathbb{K}}^{{\phi }_e\phi }\hfill & {\mathbb{K}}^{{\phi }_e{\phi }_e},\hfill \end{array}\right]$$ (59)

where the components of element matrix 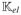are defined as

$$\begin{array}{l}{\mathbb{K}}^{\varphi \varphi }={\int }_{{\mathcal{B}}_{el}^h}{\nabla }_x^T{\mathcal{N}}^i·\mathbb{C}·{\nabla }_x{\mathcal{N}}^j+{\nabla }_x{\mathcal{N}}^i·\widehat{\tau }·{\nabla }_x{\mathcal{N}}^{j}dV,\\ {\mathbb{K}}^{\varphi \phi }={\int }_{{\mathcal{B}}_{el}^h}{\nabla }_x^T{\mathcal{N}}^i·{\mathfrak{C}}^{\varphi \phi }{\mathcal{N}}^{j}dV,\\ {\mathbb{K}}^{\varphi {\phi }_e}=\mathbf{0},\\ {\mathbb{K}}^{\phi \varphi }={\int }_{{\mathcal{B}}_{el}^h}{\nabla }_x{\mathcal{N}}^i·{\mathfrak{C}}^{\phi \varphi }·{\nabla }_x{\mathcal{N}}^{j}dV+{\int }_{{\mathcal{B}}_{el}^h}{\mathcal{N}}^i\mathcal{H}·{\nabla }_x{\mathcal{N}}^{j}dV\\ {\mathbb{K}}^{\phi \phi }={\int }_{{\mathcal{B}}_{el}^h}{\nabla }_x^T{\mathcal{N}}^i·{\mathfrak{D}}_i·{\nabla }_x{\mathcal{N}}^j+{\mathcal{N}}^i\left(\frac{1}{\mathrm{\Delta }t}-\mathcal{H}\right){\mathcal{N}}^{j}dV,\\ {\mathbb{K}}^{\phi {\phi }_e}={\int }_{{\mathcal{B}}_{el}^h}{\nabla }_x^T{\mathcal{N}}^i.{\mathfrak{D}}_i·{\nabla }_x{\mathcal{N}}^{j}dV,\\ {\mathbb{K}}^{{\phi }_e\varphi }={\int }_{{\mathcal{B}}_{el}^h}{\nabla }_x{\mathcal{N}}^i.{\mathfrak{C}}^{{\phi }_e\varphi }·{\nabla }_x{\mathcal{N}}^{j}dV,\\ {\mathbb{K}}^{{\phi }_e\phi }={\int }_{{\mathcal{B}}_{el}^h}{\nabla }_x^T{\mathcal{N}}^i.{\mathfrak{D}}_i·{\nabla }_x{\mathcal{N}}^{j}dV,\\ {\mathbb{K}}^{{\phi }_e{\phi }_e}={\int }_{{\mathcal{B}}_{el}^h}{\nabla }_x^T{\mathcal{N}}^i.\mathfrak{D}·{\nabla }_x{\mathcal{N}}^{j}dV.\end{array}$$ (60)

4. Constitutive equations

In this section, we specify the constitutive equations that are utilized in the representative numerical examples in Section 5. However, the generic coupled formulation described in Section 3 is independent of the particular choice of constitutive functions characterizing the physiology of cardiac tissue. We identify the explicit expressions for the Kirchhoff stress τ̂, the potential fluxes q̂_i, q̂_e, q̂_ie, and the current source , whose functional dependencies have already been briefly outlined in Section 2.5. These equations include not only the explicit functional evaluations, but also the accompanying ordinary differential equations governing the temporal evolution of the related internal variables. This, in turn, requires the construction of algorithmic procedures for the local update of these internal variables at the quadrature point level. We also illustrate the computation of the consistent tangent moduli, to ensure quadratic convergence of the underlying Newton iteration.

4.1. Active and passive stress response

Cardiac tissue possesses a highly anisotropic micro-structure that is chiefly made up of unevenly distributed myofibers. We characterize the orthotropic tissue microstructure in terms of two characteristic directions, the local orientation of the myofibers and the normal to the sheets forming the myocardium [16, 22]. We model cardiac tissue as hyperelastic material characterized in terms of a free energy function, such that the stresses are derived from the potential as conjugate pairs of the strain measures. To achieve an objective representation of the free energy function independent of the choice of reference frame and superimposed rigid body transformations, we introduce a set of invariants associated with the unimodular part of the right Cauchy-Green tensor C̄ and the two unit vectors f₀ and s₀ [55]

$$\begin{array}{ll}{\overline{I}}_1:=\text{tr}(\overline{\mathit{C}}),\hfill & {\overline{I}}_{4\text{f}}:=\overline{\mathit{C}}:({\mathit{f}}_0\otimes {\mathit{f}}_0),\hfill \\ {\overline{I}}_{4\text{s}}:=\overline{\mathit{C}}:({\mathit{s}}_0\otimes {\mathit{s}}_0),\hfill & {\overline{I}}_{8\text{fs}}:=\overline{\mathit{C}}:\text{sym}({\mathit{f}}_0\otimes {\mathit{s}}_0).\hfill \end{array}$$ (61)

In line with [13, 32, 53], the free energy function is additively decomposed into volumetric and isochoric parts

$$\mathrm{\Psi }=U(J)+\overline{\mathrm{\Psi }}({\overline{I}}_1,{\overline{I}}_{4\text{f}},{\overline{I}}_{4\text{s}},{\overline{I}}_{8\text{fs}}).$$ (62)

The volumetric part is used to enforce quasi-incompressiblity and the deviatoric part characterizes the orthotropic isochoric response in terms of Fung-type free energy functions according to [22]

$$\overline{\mathrm{\Psi }}=\frac{a}{2b}exp[b({\overline{I}}_1-3)]+\frac{a_{\text{fs}}}{2b_{\text{fs}}}\{exp[b_{\text{fs}}{\overline{I}}_{8\text{fs}}^2]-1\}+\sum _{i=\text{f},\text{s}}\frac{a_i}{2b_i}\{exp[b_i{({\overline{I}}_{4i}-1)}^2]-1\}.$$ (63)

The additive decomposition of the free energy (62) leads to the decomposed stress response through the Doyle-Ericksen formula

$$\mathit{\tau }={\mathit{\tau }}_{\text{vol}}+{\mathit{\tau }}_{\text{iso}}=\widehat{p}{\mathit{g}}^{♯}+\overline{\mathit{\tau }}:\mathbb{P}$$ (64)

in terms of the pressure p̂:= JU′(J), the Kirchhoff stress τ̄:= 2 ∂_g Ψ̄ and the contravariant metric tensor in the Eulerian manifold g^♯ = g⁻¹. The isochoric part of the Kirchhoff stress tensor τ_iso is obtained through the contraction of τ̄ with the isochoric projection tensor $\mathbb{P}:=\mathbb{I}-\frac{1}{3}{\mathit{g}}^{♯}\otimes {\mathit{g}}^{♯}$ where 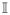:= −_g g^♯is the fourth-order identity tensor. The explicit form of τ̄ reads

$$\overline{\mathit{\tau }}=2{\overline{\mathrm{\Psi }}}_1\overline{\mathit{b}}+2{\overline{\mathrm{\Psi }}}_{4\text{f}}\mathit{f}\otimes \mathit{f}+2{\overline{\mathrm{\Psi }}}_{4\text{s}}\mathit{s}\otimes \mathit{s}+2{\overline{\mathrm{\Psi }}}_{8\text{fs}}\text{sym}(\mathit{f}\otimes \mathit{s}),$$ (65)

where the deformation-dependent scalar coefficients Ψ̄₁, Ψ̄_4f, Ψ̄_4s, and Ψ̄_8fs are defined as follows

$$\begin{array}{l}{\overline{\mathrm{\Psi }}}_1:={\partial }_{{\overline{I}}_1}\mathrm{\Psi }=\frac{a}{2}exp[b({\overline{I}}_1-3)],\\ {\overline{\mathrm{\Psi }}}_{4\text{f}}:={\partial }_{{\overline{I}}_{4\text{f}}}\mathrm{\Psi }=a_{\text{f}}({\overline{I}}_{4\text{f}}-1)exp[b_{\text{f}}{({\overline{I}}_{4\text{f}}-1)}^2],\\ {\overline{\mathrm{\Psi }}}_{4\text{s}}:={\partial }_{{\overline{I}}_{4\text{s}}}\mathrm{\Psi }=a_{\text{s}}({\overline{I}}_{4\text{s}}-1)exp[b_{\text{s}}{({\overline{I}}_{4\text{f}}-1)}^2],\\ {\overline{\mathrm{\Psi }}}_{8\text{fs}}:={\partial }_{{\overline{I}}_{8\text{fs}}}\mathrm{\Psi }=a_{\text{fs}}{\overline{I}}_{8\text{fs}}exp[b_{\text{fs}}{\overline{I}}_{8\text{fs}}^2].\end{array}$$ (66)

The active Kirchhoff stress τ̂^act is generated by the excitation-induced contraction of the cardiac muscle cells, this part of the stress tensor is approximated to be of purely anisotropic form

$${\widehat{\mathit{\tau }}}^{\text{act}}(\mathit{g};\mathrm{\Phi },\mathit{f})=\sigma (\mathrm{\Phi })\mathit{f}\otimes \mathit{f}.$$ (67)

The above equation implies that the direction of the active stress tensor is dictated by the deformed structural tensor f ⊗ f, while its magnitude is chiefly determined by the transmembrane potential-dependent active fiber tension σ(Φ). To model the twitch-like response of the fiber tension σ (Φ), we adopt an evolution equation [38]

$$\stackrel{.}{\sigma }=\epsilon (\mathrm{\Phi })[k_{\sigma }(\mathrm{\Phi }-{\mathrm{\Phi }}_r)-\sigma ],$$ (68)

in which the parameter k_σ controls the saturated value of σ for a given potential Φ and a given resting potential Φ_r, which is about −80 mV for cardiac cells. That is, σ̇ vanishes identically when σ admits the value σ_∞ = k_σ (Φ − Φ_r) for ε(Φ) ≠ 0. Contrary to its Heaviside form proposed in [38], we use the following smoothly varying form for the rate switch function [18]

$$\epsilon (\mathrm{\Phi })={\epsilon }_0+({\epsilon }_{\infty }-{\epsilon }_0)exp[-exp(-\xi (\mathrm{\Phi }-\mathrm{\Phi }))]$$ (69)

in terms of the parameters ε₀ and ε_∞ that characterize the two limiting values of the function for Φ < Φ̄ and Φ > Φ̄ about the phase shift Φ̄, respectively. The transition rate of ε from ε₀ to ε_∞ about Φ̄ is determined by the parameter ξ. To compute the current value of σ, we discretize the above equations in time using an implicit backward Euler scheme. The closed-form algorithmic expression for the active fiber tension reads

$$\sigma (\mathrm{\Phi })=\frac{1}{1+\mathrm{\Delta }t\epsilon (\mathrm{\Phi })}[{\sigma }_n+\mathrm{\Delta }t\epsilon (\mathrm{\Phi })k_{\sigma }(\mathrm{\Phi }-{\mathrm{\Phi }}_r)]$$ (70)

in terms of the current action potential Φ and the fiber tension σ_n of the previous time step t_n, which is stored as a history variable at each quadrature point of the finite element discretization. Next, we determine the algorithmic tangent moduli based on the definition (38)

$${\mathbb{C}}^{\varphi \varphi }={\mathbb{C}}^{\text{vol}}+{\mathbb{C}}^{\text{iso}}.$$ (71)

The volumetric part is given by the common expression

$${\mathbb{C}}^{\text{vol}}=(\widehat{p}+\widehat{\kappa }){\mathit{g}}^{♯}\otimes {\mathit{g}}^{♯}-2p\mathbb{I}$$ (72)

where κ̂:= J²U″(J) is the bulk modulus. The symmetric fourth identity tensor has the indicial representation ${\mathbb{I}}^{\mathit{ijkl}}:=\frac{1}{2}(g^{ik}{g}^{jl}+g^{il}{g}^{jk})$ in terms of the components of the contravariant metric g^♯. The isochoric part of the moduli has the following form

$${\mathbb{C}}^{\text{iso}}=\mathbb{P}:[\overline{\mathbb{C}}+\frac{2}{3}(\overline{\mathit{\tau }}:\mathit{g})\mathbb{I}-\frac{2}{3}(\mathbb{P}:\overline{\mathit{\tau }}\otimes {\mathit{g}}^{♯}+{\mathit{g}}^{♯}\otimes \overline{\mathit{\tau }})]:\mathbb{P}$$ (73)

where the unimodular tangent term 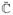is derived from the stress expression (65)

$$\overline{\mathbb{C}}=4{\overline{\mathrm{\Psi }}}_1^{\prime }(\overline{\mathit{b}}\otimes \overline{\mathit{b}})+4{\overline{\mathrm{\Psi }}}_{4\text{f}}^{\prime }\mathbb{F}+4{\overline{\mathrm{\Psi }}}_{4\text{s}}^{\prime }\mathbb{S}+4{\overline{\mathrm{\Psi }}}_{8\text{fs}}^{\prime }\text{sym}(\mathit{f}\otimes \mathit{s})\otimes \text{sym}(\mathit{f}\otimes \mathit{s})$$ (74)

in terms of the fourth order structural tensors

$$\mathbb{F}:=\mathit{f}\otimes \mathit{f}\otimes \mathit{f}\otimes \mathit{f}\text{and}\mathbb{S}:=\mathit{s}\otimes \mathit{s}\otimes \mathit{s}\otimes \mathit{s}.$$ (75)

Similarly, the sensitivity of the Kirchhoff stress tensor to the transmembrane potential then follows from (39)₂

$${\mathfrak{C}}^{\varphi \phi }={\sigma }^{\prime }(\mathrm{\Phi })\mathit{f}\otimes \mathit{f}\text{with}{\sigma }^{\prime }(\mathrm{\Phi }):={\partial }_{\mathrm{\Phi }}\sigma (\mathrm{\Phi }).$$ (76)

4.2. Spatial potential flux

We assume that the second-order conduction tensors 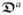in the intra- and extracellular domains a:= {i,e} can be additively decomposed

$${\mathfrak{D}}^a=d_{\left|\right|}^a\mathit{f}\otimes \mathit{f}+d_{\perp }^a({\mathit{g}}^{♯}-\mathit{f}\otimes \mathit{f})$$ (77)

into the conductance along the fiber direction $d_{\left|\right|}^a$ and the transverse conductance across the fiber direction $d_{\perp }^a$, which can be determined experimentally using microelectrode array recordings [7]. The third-order mixed moduli ℭ^a which is defined in (46) and enter the formulations in (47) and (54) follows from inseting (46) into (32)

$$\begin{array}{l}{\mathfrak{C}}_i=-2d_{\perp }^i{\nabla }_x\mathrm{\Phi }·\mathbb{I},\\ {\mathfrak{C}}_{ie}=-2d_{\perp }^i{\nabla }_x{\mathrm{\Phi }}_e·\mathbb{I},\\ {\mathfrak{C}}_e=-2(d_{\perp }^i+d_{\perp }^e){\nabla }_x{\mathrm{\Phi }}_e·\mathbb{I}.\end{array}$$ (78)

4.3. Current source

Last, we specify the constitutive equation for the electrical source term 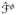. To set up the model equations and parameters in the non-dimensional space, we introduce the non-dimensional transmembrane potential φ and the non-dimensional time τ through the following conversion formulae

$$\mathrm{\Phi }={\beta }_{\phi }\phi -{\delta }_{\phi }\text{and}t={\beta }_t\tau .$$ (79)

The non-dimensional potential φ is related to the physical transmembrane potential Φ through the factor β_φ and the potential difference δ_φ, both in millivolt (mV). Likewise, the dimension-less time τ is converted to the physical time t by multiplying it with the factor β_t in millisecond (ms). We then obtain the following conversion expressions

$${\widehat{\mathcal{F}}}^{\phi }=\frac{{\beta }_{\phi }}{{\beta }_t}{\widehat{f}}^{\phi },\mathcal{H}=\frac{{\beta }_{\phi }}{{\beta }_t}\mathit{h}\text{and}\mathcal{H}=\frac{1}{{\beta }_t}h$$ (80)

for the normalized source term f̂^φ, and the non-dimensional counterparts h:= ∂_φ f̂^φ and h:= 2 ∂_g f̂^φ of the tangent terms defined in (50). The additive split of 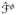, introduced in (25) Section 2.5, along with (80)₁ implies the equivalent decomposition of ${\widehat{f}}^{\phi }={\widehat{f}}_{\text{e}}^{\phi }+{\widehat{f}}_{\text{m}}^{\phi }$ into the purely electrical part ${\widehat{f}}_{\text{e}}^{\phi }$ and the stretch-induced mechano-electrical part ${\widehat{f}}_{\text{m}}^{\phi }$. This leads to the dimensionless counterpart of (51)

$$h=h_{\text{e}}+h_{\text{m}}\text{with}{h}_{\text{e}}:={\partial }_{\phi }{\widehat{f}}_{\text{e}}^{\phi },h_{\text{m}}:={\partial }_{\phi }{\widehat{f}}_{\text{m}}^{\phi }.$$ (81)

Throughout the subsequent treatments, the Aliev-Panfilov model [2] is used for the description of the source term ${\widehat{f}}_{\text{e}}^{\phi }$ and the evolution of the recovery variable r, following the algorithmic treatment introduced in [17, 18].

5. Representative numerical examples

In this section, we illustrate the performance of the fully coupled algorithm established in the previous sections. First, we examine an orthotropic block of tissue subjected to an initially smooth excitation wave, which turns into a reentrant spiral wave after a slight perturbation. Second, we analyze the excitation of a generic biventricular heart to illustrate the overall electro-physiological and electro-mechanical features of the excitation-contraction coupling in the heart. The convergence behaviour of the proposed algorithm will be discussed for each example. The stretch induced mechano-electric feedback is omitted throughout the subsequent treatments.

5.1. Excitation-induced contraction in spiral re-entry problem

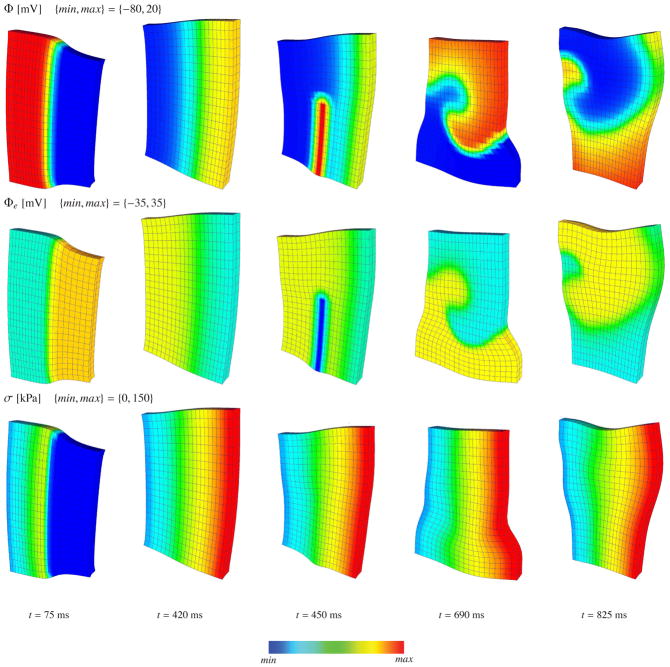
A three-dimensional 100 mm × 100 mm × 12 mm slice of an orthotropic cardiac tissue is discretized into 21 × 21 × 2 eight-node coupled brick elements as described in [17, 19]. The myofibers are aligned in the horizontal x-direction and the sheets are aligned in the vertical y-direction. The material properties of the myocardium are summarized in Table 1. The initial value of the transmembrane potential is set to its resting value of Φ(X, t₀) = −80 mV in the entire domain, except in the x = 0 plane where the transmembrane potential is set to Φ (X, t₀) = −40 mV to trigger an excitation wave front. The initial value of the extracellular potential is set to Φ_e(X, t₀) = 0 in the entire domain. The intra- and extracellular conductances are kept proportional to recover the special case of monodomain electromechanics. The nodes in the z = 0 plane are supported by uncoupled linear springs with stiffnesses of k_x = k_y = 10⁻³ N/mm and k_z = 10⁻¹ N/mm to provide a fairly unconstrained representation. Flux-free Neumann boundary conditions are applied to the parabolic and elliptic parts of the initial boundary value problem. We apply 150 fixed time increments of Δt = 3 ms followed by 1000 fixed time increments of Δt = 1 ms. Once the wave front has formed, it travels in the horizontal x–direction, depolarizing the tissue sample and causing contraction along the horizontal myocyte direction, see frame t = 75 ms in Figure 3. Then, the myocytes start to restitute their undeformed state as the block repolarizes, see frame t = 420 ms. To initiate a spiral wave, we follow the procedure suggested in [17]. We apply an additional current source of 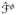← 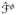+ 5β_φ/β_t between the interval t ∈ [440, 460] ms in the rectangular region bounded by the coordinates x ∈ [40,50] mm, y ∈ [0, 55] mm and z ∈ [0, 12]. The snapshots in Figure 3 for t > 460 ms demonstrate the initition, development and stable rotation of the reentrant spiral wave. In order to assess the computational efficiency of the proposed algorithm and its computational cost relative to the monodomain formulation in [18], we perform a successive mesh refinement with 11 ×11 ×2, 15 × 15 × 2 and 25 × 25 × 2 elements, respectively. Table 2 summarizes the norms of the global residual of the first five iterations for the 21 ×21 ×2 element discretization. Convergence is linear for the first few steps and then turns quadratic until the residual tolerance is reached. For the rest of the simulation the convergence remains quadratic throughout.

Table 1.

Material parameters for spiral re-entry problem.

Passive stress	a = 0.496 kPa, b = 7.21, af = 15.19 kPa, bf = 20.42, as = 3.28 kPa, bs = 11.18 afs = 0.66 kPa, bfs = 9.47
Active stress	kσ = 0.25 × 10−3 kPa mV−1, Φr = −80 mV
Switch function	ε0 = 0.1 mV−1, ε∞ = 1 mV−1, ξ = 1 mV−1 Φ̄ = 0 mV
Conduction	$\begin{array}{l}{d}_{\left|\right|}^i=1.6{\text{mm}}^2{\text{ms}}^{-1},d_{\perp }^i=1.5{\text{mm}}^2{\text{ms}}^{-1}\\ d_{\left|\right|}^e=1.6{\text{mm}}^2{\text{ms}}^{-1},d_{\perp }^e=1.5{\text{mm}}^2{\text{ms}}^{-1}\end{array}$
Excitation	α = 0.01 [−], b = 0.15 [−], c = 8 [−], γ = 0.002 [−], μ1 = 0.2 [−], μ2 = 0.3 [−]

Figure 3.

Initiation and rotation of a spiral re-entry in excitable and deformable cardiac tissue. The first, second and third row denote the transmembrane potential Φ, extracellular potential Φ_e and active fiber tension σ, respectively.

Table 2.

Quadratic convergence of global residual for spiral re-entry problem.

time [ms]	3	75	420	450	570	630	690	825
step 1	1.0000E+00	1.0000E+00	1.0000E+00	1.0000E+00	1.0000E+00	1.0000E+00	1.0000E+00	1.0000E+00
step 2	9.0110E−03	7.0588E−02	3.7917E−04	1.7091E−03	2.8000E−04	3.2632E−04	2.6667E−04	2.6471E−05
step 3	5.7143E−04	6.4706E−04	1.2083E−10	7.0909E−08	2.1000E−10	4.9474E−10	1.0000E−09	2.5000E−12
step 4	2.1978E−05	1.6471E−07	3.6250E−23	7.0909E−15	2.8000E−18	4.6842E−16	4.0556E−16	1.4118E−20
step 5	1.8681E−05	1.0588E−11	–	–	–	–	–	–
step n	2.5275E−15	2.9412E−19	–	–	–	–	–	–
nsteps	9	6	4	4	4	4	4	4

Table 3 illustrates the total computation times until t = 1450 ms for both the monodomain and the bidomain model for the different discretizations. All simulations are carried out on a single 3.40 GHz Intel Pentium(R) processor on 32bit Windows XP operating system with 3.24GB RAM. The total computation time includes the writing of the whole mesh database and nodal data information of the state variables into.VTK type files for the visualization toolkit after each time step. As the mesh size decreases or the number of elements increases, the computation times of the bidomain formulation converge to those of the monodomain formulation. This result indicates that the bidomain formulation generates almost no extra cost, especially at large scale simulations. This is mainly due to the weak coupling between the elliptic and and parabolic parts of the bidomain equations in the case of proportional intra- and extracellular conductances.

Table 3.

Computational times of mono- and bidomain-based spiral re-entry problem.

Mesh	Monodomain	Bidomain	Ratio
[−]	[s]	[s]	[−]
11 ×11 ×2	610.92	650.13	1.064
15 ×15 ×2	1782.81	1849.76	1.037
21 ×21 ×2	6092.41	6277.39	1.030
25 ×25 ×2	12239.79	12384.05	1.012

5.2. Excitation-contraction in generic biventricular heart

Next, we consider a three-dimensional generic biventricular heart, constructed from two truncated ellipsoids, see [52]. The dimensions and spatial discretization of the geometry are adopted from our previous contribution [18]. The heart is discretized with 13348 four-node coupled tetrahedral elements connected through 3059 nodes. The myofiber orientation is varied from +70° in the endocardium, the inner wall, to −70° in the epicardium, the outer wall, as described in [18]. The material parameters used for this model problem are given in Table 4. The displacement degrees of freedoms on the top base surface of the ventricles are fixed and flux-free boundary conditions are imposed on all surfaces. Excitation is initiated by assigning an elevated transmembrane potential of Φ₀ = −10 mV at the nodes located at the upper part of septum. The remainder of the heart is assigned the resting potential of Φ(X, t₀) = −80 mV. The initial value of the extracellular potential is set to Φ_e(X, t₀) = 0 for the entire domain. An adaptive time stepping algorithm is used [57, 64], with a starting time increment value Δt(t₀) = 5 ms bounded in Δt ∈ [0.01, 10] ms.

Table 4.

Material parameters for generic biventricular heart problem.

Passive stress	a = 0.496 kPa, b = 7.21, af = 15.19 kPa, bf = 20.42, as = 3.28 kPa, bs = 11.18 afs = 0.66 kPa, bfs = 9.47
Active stress	kσ = 0.1 × 10−5 kPa mV−1, Φr = −80 mV
Switch function	ε0 = 0.1 mV−1, ε∞ = 1 mV−1, ξ = 1 mV−1 Φ̄ = 0 mV
Conduction	$\begin{array}{l}{d}_{\left|\right|}^i=2.0{\text{mm}}^2{\text{ms}}^{-1},d_{\perp }^i=0.2{\text{mm}}^2{\text{ms}}^{-1}\\ d_{\left|\right|}^e=2.0{\text{mm}}^2{\text{ms}}^{-1},d_{\perp }^e=0.8{\text{mm}}^2{\text{ms}}^{-1}\end{array}$
Excitation	α = 0.01 [−], b = 0.15 [−], c = 8 [−], γ = 0.002 [−], μ1 = 0.2 [−], μ2 = 0.3 [−]

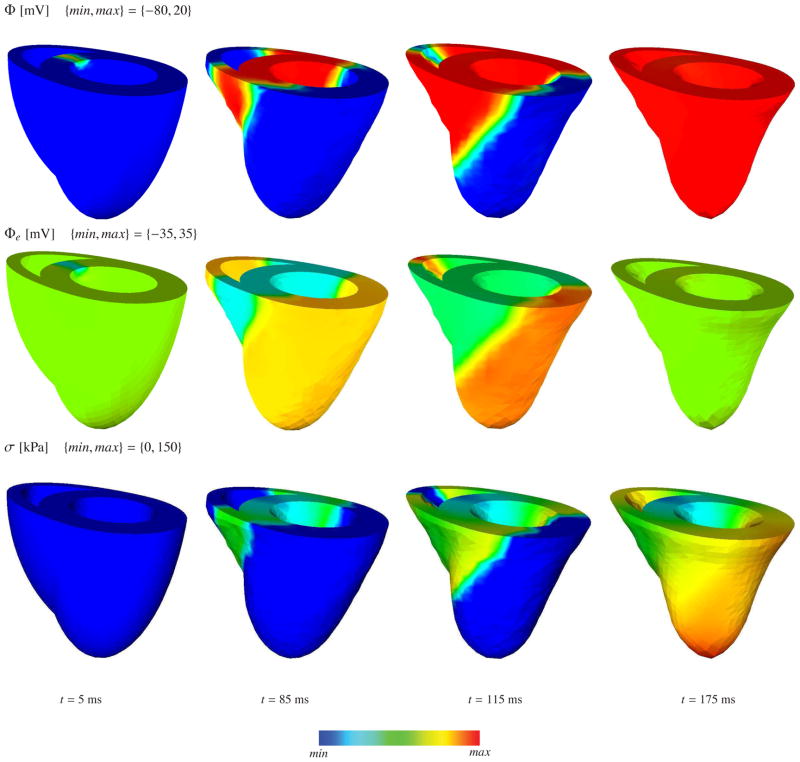
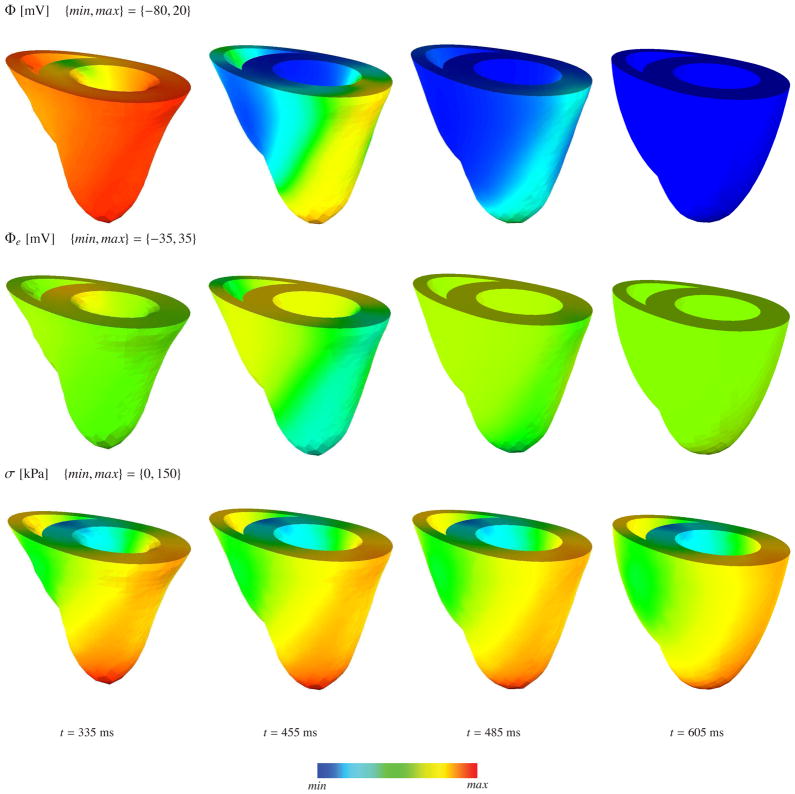
The deformed geometry of the generic heart and the color plots corresponding to the transmembrane potential, the extracellular potential and the active fiber tension in depolarization and repolarization phases are depicted in Figure 4 and Figure 5, respectively. The algorithm conceptually captures both the depolarization and the repolarization phases. Unfortunately, our relatively corse benchmark mesh cannot resolve the discontinuity at the apex accurately. The steep curvature at the apex induces a discontinuity in the conductances along the fiber direction, which artificially elongates the action potential duration and leads to an artificially slow reduction of the active fiber tension in the apex region. We have recently established a more accurate feature based Poisson interpolation, which resolves the apex discontinuity more accurately and avoids these spurious contractions [65]. The apex singularity will inherently disappear when we solve the underlying problem on real patient-specific geometries [64].

Figure 4.

Coupled excitation induced contraction of generic heart model at various stages of depolarization. The first, second and third row denote the transmembrane potential Φ, extracellular potential Φe and active fiber tension σ, respectively.

Figure 5.

Coupled excitation induced contraction of generic heart model at various stages of repolarization. The first, second and third row denote the transmembrane potential Φ, extracellular potential Φ_e and active fiber tension σ, respectively.

The convergence behaviour of the global Newton-Raphson iteration is depicted in Table 5 for various stages of depolarization and repolarization. The depolarization wave-front renders the problem stiff and smaller time increments are required. However, the repolarization phase of the problem is numerically easier to tackle because of the lack of steep potential gradients. Since the the intra- and extracellular conductances are not proportional, an equivalent monodomain conductance cannot be obtained for this particular problem. Assuming an effective monodomain conductance by means of geometric average of the conductances along the fiber and transverse directions, we have compared the computational costs of the bidomain and monodomain based electromechanics formulations. Since mono- and bidomain based simulations are not exactly equivalent though, we compare the computation time required for the depolarization wave to reach the bottom of the left ventricle. Table 6 shows the corresponding computation times for both simulations. The anisotropic distribution of the fiber directions and non-proportional conductances add additional complexity to the problem, which particularly affects the elliptic part of the bidomain equations. This is reflected by the additional 75% in computational cost in the excitation-contraction of generic heart problem.

Table 5.

Quadratic convergence of global residual for generic biventricular heart problem.

time [ms]	5	85	115	175	335	455	485	605
Δt [ms]	5.0	2.0	2.0	1.5	10.0	10.0	10.0	10.0
step 1	1.0000E+00	1.0000E+00	1.0000E+00	1.0000E+00	1.0000E+00	1.0000E+00	1.0000E+00	1.0000E+00
step 2	6.0000E−05	7.5000E−03	1.4211E−02	2.6154E−04	9.4737E−07	1.3044E−02	1.0571E−02	2.9730E−05
step 3	8.0909E−08	3.2500E−06	1.8421E−05	3.1538E−11	9.4737E−14	6.3043E−06	3.4286E−06	5.1351E−09
step 4	2.6364E−10	5.9167E−09	3.6842E−08	–	–	4.1304E−12	4.2857E−08	1.9730E−13
step 5	3.2727E−12	6.2500E−13	1.9474E−11	–	–	–	2.7143E−10	–
step 6	–	–	–	–	–	–	2.1714E−14	–
nsteps	5	5	5	3	3	4	6	4

Table 6.

Computational times of mono- and bidomain-based generic biventricular heart problem.

Monodomain	Bidomain	Ratio (B/M)
[s]	[s]	[−]
11648	20376	1.75

6. Discussion and outlook

We have proposed a fully coupled finite element method for cardiac electromechanics, which is inherently modular, unconditionally stable, computationally efficient, and robust. Modularity is obtained by defining constitutive equations independently for source and flux terms of all three fields. Unconditional stability is ensured by using the backward Euler method for the temporal discretization of the local recovery variable r and the transmembrane potential Φ. Efficiency is guaranteed by the Newton Raphson iteration in combination with a consistent algorithmic linearization of the underlying weak forms of the governing equations. Robustness is enhanced by the fully coupled, monolithic solution strategy.

In weakly coupled multifield problems, decoupling based on operator-splitting methods can improve computational efficiency by dividing a big non-symmetric problem into smaller symmetric subproblems. Depending on the degree of coupling, operator splitting might induce instabilities, which can be overcome by refining the time step size. In general, there is an inherent competition between saving computer time by solving smaller symmetric subsystems and losing computer time by smaller time step sizes relative to monolithic schemes.

For the particular problem of cardiac electromechanics, steep potential gradients and strong coupling between the electrical and mechanical fields could render operator splitting inefficient. As we have demonstrated here, the use of the classical Newton Raphson solution strategy, along with consistently linearized residuals, ensures the quadratic convergence of the iterative solver. Depending on the number of overall degrees of freedom, an consistently linearized implicit algorithm might be superior to decoupled solution strategies based on operator-splitting schemes. Specifically, in our setup, the proposed implicit approach allows us to use straightforward time-adaptive schemes, in which the time step size is adjusted based on the number of iteration steps. In addition, the proposed approach is highly modular and generic. It is independent from the particular choice of electrical and mechanical constitutive models, and can be implemented into basically any commercial nonlinear finite element environment.

We believe that, despite intense research, the use of finite element methods in cardiac electromechanics is still under-appreciated. With this manuscript, we hope to encourage future research along this direction. Discretizing all relevant fields with unique discretization schemes both in time and space, like we have proposed here, enables the use of generic finite element packages and commercially available solvers. These typically come with well-established tools like error estimators or readily available temporally and spatially adaptive schemes. Overall, robust and efficient solution algorithms in electromechanics have the potential to enable the design and refinement of treatment strategies for heart disease, the number one cause of death in the industrialized nations.

• Cardiac contraction is initiated by smoothly propagating excitation waves.

• Existing models solve this excitation-contraction coupling in a staggered sense.

• Here we propose a monolithic, fully implicit excitation-contraction algorithm.

• We represent excitation using the bidomain model of electrophysiology.

• Our model accurately predicts excitation and contraction in an idealized heart.