Statistical measures for workload capacity analysis

Abstract

A critical component of how we understand a mental process is given by measuring the effect of varying the workload. The capacity coefficient (Townsend & Nozawa, 1995; Townsend & Wenger, 2004) is a measure on response times for quantifying changes in performance due to workload. Despite its precise mathematical foundation, until now rigorous statistical tests have been lacking. In this paper, we demonstrate statistical properties of the components of the capacity measure and propose a significance test for comparing the capacity coefficient to a baseline measure or two capacity coefficients to each other.

Measures of changes in processing, for instance deterioration, associated with increases in workload have been fundamental to many advances in cognitive psychology. Due to their particular strength in distinguishing the dynamic properties of systems, response time based measures such as the capacity coefficient (Townsend & Nozawa, 1995; Townsend & Wenger, 2004) and the related Race Model Inequality (Miller, 1982) have been gaining employment in both basic and applied sectors of cognitive psychology. The purview of application of these measures includes areas as diverse as memory search (Rickard & Bajic, 2004), visual search (Krummenacher, Grubert, & Müller, 2010; Weidner & Muller, 2010), visual perception (Eidels, Townsend, & Algom, 2010; Scharf, Palmer, & Moore, 2011), auditory perception (Fiedler, Schröter, & Ulrich, 2011), flavor perception (Veldhuizen, Shepard, Wang, & Marks, 2010), multi-sensory integration (Hugenschmidt, Hayasaka, Peiffer, & Laurienti, 2010; Rach, Diederich, & Colonius, 2011) and threat detection (Richards, Hadwin, Benson, Wenger, & Donnelly, 2011).

While there have been a number of statistical tests proposed for the Race Model Inequality (Gondan, Riehl, & Blurton, 2012; Maris & Maris, 2003; Ulrich, Miller, & Schröter, 2007; Van Zandt, 2002), there has been a lack of analytical work on tests for the capacity coefficient. At this point, the only quantitative test available for the capacity coefficient is that proposed by Eidels, Donkin, Brown, and Heathcote (2010). This test is limited to testing an increase in workload from one to two sources of information. Furthermore, it relies on the assumption that the underlying channels can be modeled with the Linear Ballistic Accumulator (Brown & Heathcote, 2008). In this paper, we develop a more comprehensive statistical test for the capacity coefficient that is both nonparametric and can be applied with any number of sources of information.

The capacity coefficient, C(t), was originally invented to provide a precise measure of workload effects for first-terminating (i.e., minimum time; referred to as “OR” or disjunctive processing) processing efficiency (Townsend & Nozawa, 1995). It complements the survivor interaction contrast (SIC), a tool which assesses mental architecture and decisional stopping rule (Townsend & Nozawa, 1995). The capacity coefficient has been extended to measure efficiency in exhaustive (AND) processing situations (Townsend & Wenger, 2004). In fact, it is possible to extend the capacity coefficient to any Boolean decision rule (e.g., Blaha, 2010; Townsend & Eidels, 2011).

The logic of the capacity coefficient is relatively straightforward. We demonstrate this logic using a comparison between a single source of information and two sources for clarity; but the reasoning readily extends to more sources and the theory section applies to the general case. Consider the experiment depicted in Fig. 1, in which a participant responds ‘yes’ if a dot appears either slightly above the mid-line of the screen, slightly below, or both and responds ‘no’ otherwise (a simple detection task). Optimally, the participant would respond as soon as she detects any dot, whether or not both were present. We refer to this as ‘first-terminating’ processing, or simply ‘OR’ processing. Alternatively, participants may wait to respond until they have determined whether or not a dot is present both above and below the mid-line. This is ‘exhaustive’ or ‘AND’ processing. In this design, AND processing is sub-optimal, but in other designs, such as when the participant must only respond ‘yes’ when both dots are present, AND processing is necessary.

Fig. 1.

An illustration of the possible stimuli in Eidels et al. (submitted for publication). The actual stimuli had much lower contrast. We refer to the condition with both the upper and lower dots present as PP (for present–present). PA indicates only the upper dot is present (for present–absent). AP indicates only the lower dot is present and AA indicates neither dot is present. In the OR task, participants responded yes to PP, AP or PA. In the AND task, participants responded yes to PP only and no otherwise.

If information about the presence of either of the dots is processed independently and in parallel, then the probability that the OR process is not complete at time t is the product of the probabilities that each dot has not yet been detected.¹ Let F be the cumulative distribution function of the completion time, and the subscript X|Y indicate that the function corresponds to the completion time of process X under stimulus condition Y. Using this notation, the prediction of the independent, parallel, first-terminating process is given by,

$$1-F_{\mathit{\text{AB}}|\mathit{\text{AB}}}(t)=(1-F_{A|\mathit{\text{AB}}}(t))(1-F_{B|\mathit{\text{AB}}}(t)).$$ (1)

We make the further assumption that there is no change in the speed of detecting a particular dot due to changes in the number of other sources of information (unlimited capacity). Thus, we can drop the reference to the stimulus condition,

$$F_{A|\mathit{\text{AB}}}(t)=F_{A|A}(t)\equiv F_A(t),F_{B|\mathit{\text{AB}}}(t)=F_{B|B}(t)\equiv F_B(t)$$

$$1-F_{\mathit{\text{AB}}}(t)=(1-F_A(t))(1-F_B(t)).$$ (2)

We refer to a model with these collective assumptions – unlimited capacity, independent and parallel – as a UCIP model. This prediction of equality forms the basis of the capacity coefficient and plays the role of the null hypothesis in the statistical tests developed in this paper.

To derive the capacity coefficient prediction for the UCIP model, we need to put Eq. (2) in terms of cumulative hazard functions (cf. Chechile, 2003; Townsend & Ashby, 1983, pp. 248–254). We do this using the relationship H(t) = −ln(1 − F(t)), where $H(t)={\displaystyle {\int }_0^t}f(s)/(1-F(s))\mathit{\text{ ds}}$ is the cumulative hazard function.

$$1-F_{\mathit{\text{AB}}|\mathit{\text{AB}}}(t)=(1-F_A(t))(1-F_B(t))$$

$$\text{ln }(1-F_{\mathit{\text{AB}}|\mathit{\text{AB}}}(t))=\text{ln }((1-F_A(t))(1-F_B(t)))=\text{ln }(1-F_A(t))+\text{ln }(1-F_B(t))$$

$$H_{\mathit{\text{AB}}}(t)-H_A(t)+H_B(t).$$ (3)

The capacity coefficient for OR processing is defined by the ratio of the left and right hand side of Eq. (3),

$${\mathrm{C}}_{\text{OR}}(t)=\frac{H_{\mathit{\text{AB}}}(t)}{H_A(t)+H_B(t)}.$$ (4)

This definition gives an easy way to compare against the baseline UCIP model performance. From Eqs. (3) and (4), we see that UCIP performance implies C_OR(t) = 1.

The capacity coefficient for AND processing is defined in an analogous manner, with the cumulative reverse hazard function (cf. Chechile, 2011; Townsend & Eidels, 2011; Townsend & Wenger, 2004) in place of the cumulative hazard function. The cumulative reverse hazard function, denoted by K(t) is defined as,

$$K(t)\equiv -{\displaystyle {\int }_t^{\mathrm{\infty }}}\frac{f(s)}{F(s)}\mathit{\text{ds}}=\text{ln }(F(s)).$$ (5)

If the participant has detected both dots when both are present in an AND task, then he must have already detected each dot individually. If the dots are processed independently and in parallel, this means,

$$F_{\mathit{\text{AB}}|\mathit{\text{AB}}}(t)=F_{A|\mathit{\text{AB}}}A(t)F_{B|\mathit{\text{AB}}}(t).$$ (6)

With the additional assumption of unlimited capacity, we have,

$$F_{\mathit{\text{AB}}}(t)=F_A(t)F_B(t).$$ (7)

As above, we take the natural logarithm of both sides to obtain the prediction in terms of cumulative reverse hazard functions.

$$\text{ln }(F_{\mathit{\text{AB}}}(t))=\text{ln }(F_A(t)F_B(t))=\text{ln }(F_A(t))+\text{ln }(F_B(t))$$

$$K_{\mathit{\text{AB}}}(t)=K_A(t)+K_B(t).$$ (8)

With the cumulative reverse hazard function, relatively larger magnitude implies relatively worse performance. Thus, to maintain the interpretation of C(t) > 1 implying performance is better than UCIP, the capacity coefficient for AND processing is defined by,

$${\mathrm{C}}_{\text{AND}}(t)=\frac{K_A(t)+K_B(t)}{K_{\mathit{\text{AB}}}(t)}.$$ (9)

With the definitions of the OR and AND capacity coefficients in hand, we now turn to issues of statistical testing. We begin by adapting the statistical properties of estimates for the cumulative hazard and reverse cumulative hazard functions to estimates of UCIP performance. Then, based on those estimates, we derive a null-hypothesis-significance test for the capacity coefficients. We do not establish the statistical properties of the capacity coefficient itself, but rather the components. The statistical test is based on the sampling distribution of the difference of the predicted UCIP performance and the participant’s performance when all targets are present. The “difference” form leads to more analytically tractable results than a test based on the ratio form. Nonetheless, the logic of the test is the same, if the values are statistically significant (nonzero for the difference; not one for the ratio) then the UCIP model may be rejected.

1. Theory

The capacity coefficients are based on cumulative hazard functions and reverse cumulative hazard functions. Although it would be theoretically possible to use the machinery developed for the empirical cumulative distribution function to study the empirical cumulative hazard functions, using the identities mentioned above, H(t) = −log(1 − F(t)), K(t) = log(F(t)) (cf. Townsend & Wenger, 2004), we instead use a direct estimate of the cumulative hazard function, the Nelson–Aalen (NA) estimator (e.g., Aalen, Borgan, & Gjessing, 2008). This approach greatly simplifies the mathematics because many of the properties of the estimates follow from the basic theory of martingales. There is no particular advantage of one approach over the other in terms of their statistical qualities (Aalen et al., 2008).

1.1. The cumulative hazard function

Let Y(t) be the number of responses that have not occurred as of immediately before t and let T_j be the jth element of the ordered set of response times RT and let n be the number of response times. Then the NA estimator of the cumulative hazard function is given by,

$$Ĥ(t)\equiv {\displaystyle \sum _{T_j\le t}}\frac{1}{Y(T_j)}.$$ (10)

Intuitively, this estimator results from estimating f(t) by 1/n whenever there is a response and zero otherwise; and estimating 1 − F(t) by the number of response times larger than t divided by n. This gives an estimate of h(t) = f(t)/(1 − F(ts)) ≈ (1/n)/(Y(t)/n) = 1/Y(t) whenever there is a response and zero otherwise. Integrating across s ∈ [0, t] leads to the sum in Eq. (10) to estimate ${\displaystyle {\int }_0^t}h(s)\mathit{\text{ ds}}$.

Aalen et al. (2008) demonstrate that this is an unbiased estimator of the true cumulative hazard function and derive the variance of the estimator based on a multiplicative intensity model. We outline the argument here, then extend the results to an estimator for redundant target UCIP model performance using data from single target trials.

We begin by representing the response times by a counting process.² At time t, we define the counting process N(t) as the number of responses that have occurred by time t. The intensity process of N(t), denoted λ(t), is the probability that a response occurs in an infinitesimal interval, conditioned on the responses before t, divided by the length of that interval. For notational convenience, we also introduce the function J(t),

$$J(t)=\{\begin{array}{cc}1\hfill & \text{if }Y(t)>0\hfill \\ 0\hfill & \text{if }Y(t)=0.\hfill \end{array}$$ (11)

If we introduce the martingale, $M(t)=N(t)-{\displaystyle {\int }_0^t}\lambda (s)\mathit{\text{ ds}}$, then we can write the increments of the counting process as,

$$\mathit{\text{dN}}(t)=\lambda (t)\mathit{\text{dt}}+\mathit{\text{dM}}(t).$$ (12)

Under the multiplicative intensity model, the intensity process of N(t) can be rewritten by λ(t) = h(t)Y(t), where Y(t) is a process representing the total number of responses that have not occurred by time t and h(t) is the hazard function. This model arises from treating the response to each trial as an individual process. Each response has its own hazard rate h_i(t) and an indicator process Y_i(t) which is 1 if the response has not occurred by time t and 0 otherwise. If the hazard rate is the same for each response that will be included in the estimate, then the counting process N(t) follows the multiplicative intensity model with h(t) = h_i(t) and $Y(t)={\displaystyle {\sum }_i^n}{Y}_i(t)$.

Rewriting Eq. (12) using the multiplicative intensity model gives,

$$\mathit{\text{dN}}(t)=h(t)Y(t)\mathit{\text{dt}}+\mathit{\text{dM}}(t).$$

If we multiply by J(t)/Y(t), and let J(t)/Y(t) = 0 when Y(t) = 0, then,

$$\frac{J(t)}{Y(t)}\mathit{\text{dN}}(t)=J(t)h(t)\mathit{\text{dt}}+\frac{J(t)}{Y(t)}\mathit{\text{dM}}(t).$$

By integrating, we have,

$${\displaystyle {\int }_0^t}\frac{J(s)}{Y(s)}\mathit{\text{dN}}(s)={\displaystyle {\int }_0^t}J(s)h(s)\mathit{\text{ds}}+{\displaystyle {\int }_0^t}\frac{J(s)}{Y(s)}\mathit{\text{dM}}(s).$$

The integral on the left is the NA estimator given in Eq. (10), using integral notation. The first term on the right is our function of interest, the cumulative hazard function (up until t_max, when all responses have occurred) which we denote H*(t). The last term is an integral with respect to a zero mean martingale, which is in turn a zero mean martingale. Hence,

$$\mathrm{E}(Ĥ(t)-H^{*}(t))=0.$$

Thus, the NA estimator is an unbiased estimate of the true cumulative hazard function, until t_max.

For statistical tests involving Ĥ(t), we will also need to estimate its variance. To do so, we use the fact that the variance of a zero mean martingale is equal to the expected value of its optional variation process.³ Because the integral ${\displaystyle {\int }_0^t}\frac{J(s)}{Y(s)}\mathit{\text{dM}}(s)$ with respect to a zero mean martingale, the optional variation process is given by,

$$[Ĥ(t)-H^{*}(t)]={\displaystyle {\int }_0^t}\frac{J(s)}{Y^2(s)}\mathit{\text{dN}}(s).$$

Thus,

$$\text{Var }(Ĥ(t)-H^{*}(t))=\mathrm{E}({\displaystyle {\int }_0^t}\frac{J(s)}{Y^2(s)}\mathit{\text{dN}}(s)).$$

Therefore, an estimator of the variance of Ĥ(t) − H*(t) is given by,

$${\mathrm{\sigma ̂}}_H^2(t)\equiv {\displaystyle {\int }_0^t}\frac{J(s)}{Y^2(s)}\mathit{\text{dN}}(s)={\displaystyle \sum _{t\le T_j}}\frac{1}{Y^2(T_j)}.$$

The asymptotic behavior of the NA estimator is also well known. Ĥ(t) is a uniformly consistent estimator of H(t) and $\sqrt{n}\left(Ĥ(t)-H(t)\right)$ converges in distribution to a zero mean Gaussian martingale (Aalen et al., 2008; Andersen, Borgan, & Keiding, 1993).

1.2. The cumulative reverse hazard function

To estimate the capacity coefficient for AND processing, we must also adapt the NA estimator to the cumulative reverse hazard function. Based on the NA estimator of the cumulative hazard function, we define the following estimator,

$$\mathrm{K̂}(t)\equiv -{\displaystyle \sum _{T_j\ge t}}\frac{1}{G(T_j)}.$$ (13)

Here G(s) is an estimate of the cumulative distribution function given by the number of responses that have occurred up to and including s. Intuitively, this corresponds to estimating $-{\displaystyle {\int }_t^{\mathrm{\infty }}}f(t)/F(t)\mathit{\text{ dt}}$ by setting f(t) = 1/n whenever there is an observed response and using G(t) to estimate F(t), dovetailing nicely with the NA estimator of the cumulative hazard function. Each of the properties mentioned above for the NA estimator of the cumulative hazard (unbiasedness, consistency and a Gaussian limit distribution) also hold for the estimator of the cumulative reverse hazard.

Similar to J(t) for the cumulative hazard estimate, we need to track whether or not the estimate of the denominator of Eq. (13) is zero,

$$Q(t)=\{\begin{array}{cc}1\hfill & \text{if }G(t)>0\hfill \\ 0\hfill & \text{if }G(t)=0\hfill \end{array}$$ (14)

$$K^{*}(t)\equiv -{\displaystyle {\int }_t^{t_{\text{max}}}}Q(s)k(s)\mathit{\text{ds}}.$$ (15)

Theorem 1. K̂(t) is an unbiased estimator of K*(t).

Theorem 2. An unbiased estimate of the variance of K̂(t) is given by,

$${\mathrm{\sigma ̂}}_K^2(t)\equiv {\displaystyle \sum _{T_j\ge t}}\frac{1}{G^2(T_j)}.$$ (16)

Theorem 3. K̂(t) is a uniformly consistent estimator of K(t).

Theorem 4. $\sqrt{n}\left(\mathrm{K̂}(t)-K(t)\right)$ converges in distribution to a zero mean Gaussian process as the number of response times used in the estimate increases.

1.3. Estimating UCIP performance

Having established estimators for the cumulative hazard function and cumulative reverse hazard function, we now need an estimate of the performance of the UCIP model based on the single target response times. On an OR task, the UCIP model cumulative hazard function is simply the sum of the cumulative hazard functions of each of the single target conditions (cf. Eq. (3)). In this model, the probability that a response has not occurred by time t, 1−F_UCIP(t), is the probability that none of the sub-processes have finished by time t, 1 − F_i(t). Hence,

$$1-F_{\text{UCIP}}(t)={\displaystyle \prod _{i=1}^k}(1-F_i(t))$$

$$\text{log }(1-F_{\text{UCIP}}(t))=\text{log }\left({\displaystyle \prod _{i=1}^k}(1-F_i(t))\right)$$

$$H_{\text{UCIP}}(t)={\displaystyle \sum _{i=1}^k}\text{log }(1-F_i(t))={\displaystyle \sum _{i=1}^k}{H}_i(t).$$ (17)

Based on this, a reasonable estimator for the cumulative hazard function of the race model is the sum of NA estimators of the cumulative hazard function for each single target condition,

$${Ĥ}_{\text{UCIP}}(t)\equiv {\displaystyle \sum _{i=1}^k}{Ĥ}_i(t).$$ (18)

To find the mean and variance of this estimator, we return to the multiplicative intensity model representation of the sub-processes stated above. We use the * notation as above,

$$H_{\text{UCIP}}^{*}(t)={\displaystyle \sum _{i=1}^k}{\displaystyle {\int }_0^t}{h}_i(s)J_i(s)\mathit{\text{ ds}}.$$ (19)

We will also need to distinguish among the ordered response times for each single target condition. We use T_ij to indicate the jth element in the ordered set of response times from condition i.

Theorem 5. Ĥ_UCIP(t) is an unbiased estimator of $H_{\text{UCIP}}^{*}(t)$.

Theorem 6. An unbiased estimate of the variance of Ĥ_UCIP(t) is given by,

$${\mathrm{\sigma ̂}}^2(t)={\displaystyle \sum _{i=1}^k}{\displaystyle \sum _{T_{\mathit{\text{ij}}}\le t}}\frac{1}{Y_i^2(T_{\mathit{\text{ij}}})}.$$ (20)

Theorem 7. Ĥ_UCIP(t) is a uniformly consistent estimator of H_UCIP(t).

Theorem 8. Let $n={\displaystyle {\sum }_{i=1}^k}{n}_i$ where n_i is the number of response times used to estimate the cumulative hazard function of the completion time of the ith channel. Then, $\sqrt{n}\left({Ĥ}_{\text{UCIP}}-H_{\text{UCIP}}\right)$ converges in distribution to a zero mean Gaussian process as the number of response times used in the estimate increases.

Assuming a UCIP process on an AND task, the probability that a response has occurred by time t, F_UCIP(t), is the probability that all of the sub-processes have finished by time t, F_i(t). Hence,

$$F_{\text{UCIP}}(t)={\displaystyle \prod _{i=1}^k}{F}_i(t)$$

$$\text{log }(F_{\text{UCIP}}(t))=\text{log }\left({\displaystyle \prod _{i=1}^k}{F}_i(t)\right)$$

$$K_{\text{UCIP}}(t)={\displaystyle \sum _{i=1}^k}\text{log }(F_i(t))={\displaystyle \sum _{i=1}^k}{K}_i(t).$$ (21)

Thus, to estimate the cumulative reverse hazard function of the UCIP model on an AND task, we use the sum of NA estimators of the cumulative reverse hazard function for each single target condition,

$${\mathrm{K̂}}_{\text{UCIP}}(t)\equiv {\displaystyle \sum _{i=1}^k}{\mathrm{K̂}}_i(t).$$ (22)

The estimators of the UCIP cumulative reverse hazard functions retain the statistical properties of the NA estimator of the individual cumulative reverse hazard function: Because we are using a sum of estimators, the consistency, unbiasedness and Gaussian limit properties all hold for the UCIP AND estimator just as they do for the UCIP OR estimator.

Theorem 9. K̂_UCIP(t) is an unbiased estimator of $K_{\text{UCIP}}^{*}(t)$.

Theorem 10. An unbiased estimate of the variance of K̂_UCIP(t) is given by,

$${\mathrm{\sigma ̂}}^2(t)\equiv {\displaystyle \sum _{i=1}^k}{\displaystyle \sum _{T_{\mathit{\text{ij}}}\ge t}}\frac{1}{G_i^2(T_{\mathit{\text{ij}}})}.$$ (23)

Theorem 11. K̂_UCIP is a uniformly consistent estimator of K_UCIP.

Theorem 12. Let $n={\displaystyle {\sum }_{i=1}^k}{n}_i$ where n_i is the number of response times used to estimate the cumulative hazard function of the completion time of the ith channel. Then, $\sqrt{n}\left({\mathrm{K̂}}_{\text{UCIP}}-K_{\text{UCIP}}\right)$ converges in distribution to a zero mean Gaussian process as the number of response times used in the estimate increases.

1.3.1. Handling ties

In theory the underlying response time distributions are continuous and thus there is no chance of two exactly equal response times. In practice, measurement devices and truncation limit the possible observed response times to a discrete set. This means repeated values are possible. Aalen et al. (2008) suggest two ways of dealing with these repeated values. One method is to add a zero mean, small-variance random-value to the tied response times. Alternatively, one could use the number of responses at a particular time in the numerator of Eqs. (10) and (13). If we let d(t) be the number of responses that occur exactly at time t, this leads to the estimators,

$$Ĥ(t)\equiv {\displaystyle \sum _{T_j\le t}}\frac{d(T_j)}{Y(T_j)}$$ (24)

$$\mathrm{K̂}(t)\equiv {\displaystyle \sum _{T_j\le t}}\frac{d(T_j)}{G(T_j)}.$$ (25)

1.4. Hypothesis testing

Having established an estimator of UCIP performance, we now turn to hypothesis testing. Here, we focus on a test with UCIP performance as the null hypothesis. In the following, we will use the subscript r to refer to the condition when all sources indicate a target (i.e., the redundant target condition in an OR task or the target condition on an AND task). We begin with the difference between the participant’s performance when all sources indicate a target and the estimated UCIP performance,

$${Ĥ}_{\mathrm{r}}(t)-{Ĥ}_{\text{UCIP}}(t)={\displaystyle \sum _{T_j^{(r)}\le t}}\frac{1}{Y_{\mathrm{r}}(T_j^{(r)})}-{\displaystyle \sum _{i=1}^k}{\displaystyle \sum _{T_{\mathit{\text{ij}}}\le t}}\frac{1}{Y_i(T_{\mathit{\text{ij}}})}$$ (26)

$${\mathrm{K̂}}_{\mathrm{r}}(t)-{\mathrm{K̂}}_{\text{UCIP}}(t)={\displaystyle \sum _{T_j^{(r)}\ge t}}\frac{1}{G_{\mathrm{r}}(T_j^{(r)})}-{\displaystyle \sum _{i=1}^k}{\displaystyle \sum _{T_{\mathit{\text{ij}}}\ge t}}\frac{1}{G_i(T_{\mathit{\text{ij}}})}.$$ (27)

Following the same line of reasoning given for the unbiasedness of the cumulative hazard function estimators, the expected difference is zero under the null hypothesis that H_r(t) = H_UCIP(t). Furthermore, the point-wise variance of the function is the sum of the point-wise variances of each individual function,

$${\displaystyle \sum _{T_j^{(r)}\le t}}\frac{1}{{Y_{\mathrm{r}}}^2(T_j^{(r)})}+{\displaystyle \sum _{i=1}^k}{\displaystyle \sum _{T_{\mathit{\text{ij}}}\le t}}\frac{1}{Y_i^2(T_{\mathit{\text{ij}}})}$$ (28)

$${\displaystyle \sum _{T_j^{(r)}\ge t}}\frac{1}{{G_{\mathrm{r}}}^2(T_j^{(r)})}+{\displaystyle \sum _{i=1}^k}{\displaystyle \sum _{T_{\mathit{\text{ij}}}\ge t}}\frac{1}{G_i^2(T_{\mathit{\text{ij}}})}.$$ (29)

The difference functions converge in distribution to a Gaussian process. Hence, at any t, under the null hypothesis, the difference will be normally distributed. We can then divide by the estimated variance at that time so the limit distribution is a standard normal.

In general, we may want to weight the difference between the two functions, e.g., use smaller weights for times where the estimates are less reliable. Let L(t) be a predictable weight process that is zero whenever any of Y_i or Y_r is zero (G_i or G_r is zero for AND), then we define our general test statistics as,

$${\mathrm{Z}}_{\text{OR}}={\displaystyle \sum _{T_j^{(r)}\le t}}\frac{L(T_j)}{Y_{\mathrm{r}}(T_j^{(r)})}-{\displaystyle \sum _{i=1}^k}{\displaystyle \sum _{T_{\mathit{\text{ij}}}\le t}}\frac{L(T_j)}{Y_i(T_{\mathit{\text{ij}}})}$$ (30)

$${\mathrm{Z}}_{\text{AND}}={\displaystyle \sum _{T_j^{(r)}\ge t}}\frac{L(s)}{G_{\mathrm{r}}(T_j^{(r)})}-{\displaystyle \sum _{i=1}^k}{\displaystyle \sum _{T_{\mathit{\text{ij}}}\ge t}}\frac{L(s)}{G_i(T_{\mathit{\text{ij}}})}.$$ (31)

Theorem 13. Under the null hypothesis of UCIP performance, E (Z_OR) = 0.

Theorem 14. An unbiased estimate of the variance of Z_OR is given by,

$$\text{Var }({\mathrm{Z}}_{\text{OR}})(t)={\displaystyle \sum _{T_{\mathit{\text{ij}}}\le t}}\frac{L^2(T_{\mathit{\text{ij}}})}{Y_i^2(T_{\mathit{\text{ij}}})}+{\displaystyle \sum _{i=1}^k}{\displaystyle \sum _{T_{\mathit{\text{ij}}}\le t}}\frac{L^2(T_{\mathit{\text{ij}}})}{Y_i^2(T_{\mathit{\text{ij}}})}.$$

Theorem 15. Assume that there exists sequences of constants {a_n} and {c_n} such that,

$$\underset{n\to \mathrm{\infty }}{\text{lim}}{a}_n=\underset{n\to \mathrm{\infty }}{\text{lim}}{c}_n=\mathrm{\infty }\mathit{\text{ and}}$$

$$\frac{L^{(n)}(s)}{c_n}\stackrel{P}{\to }l(s)<\mathrm{\infty },\frac{Y_r^{(n)}(s)}{a_n^2}\stackrel{P}{\to }{y}_r(s)<\mathrm{\infty },$$

$$\frac{Y_i^{(n)}(s)}{a_n^2}\stackrel{P}{\to }{y}_i(s)<\mathrm{\infty }.$$

Further, assume that there exists some function d(s) such that for all δ,

$$\underset{n\to \mathrm{\infty }}{\text{lim inf}}\text{ Pr}\left\{{(a_n/c_n)}^2{\left(L^{(n)}(s)\right)}^2\left(\frac{1}{Y_r}+{\displaystyle \sum _{i=1}^k}\frac{1}{Y_i}\right)\le d(s)\mathit{\text{ for all }}s\in 𝒯\right\}\ge 1-\delta .$$

Then (a_n/c_n)Z_OR⁽ⁿ⁾ converges in distribution to a zero mean Gaussian process as the number of response times used in the estimate increases.

The Harrington–Fleming weight process (Harrington & Fleming, 1982) is one possible weight function,

$$L(t)=S{(t-)}^{\rho }\frac{Y_r(t){\displaystyle \sum }{Y}_i(t)}{Y_r(t)+{\displaystyle \sum }{Y}_i(t)}.$$ (32)

Here, S(t−) is an empirical survivor function estimated from the pooled response times from all conditions,

$$S(t)={\displaystyle \prod _{s\le t}}\left(1-\frac{\mathrm{\Delta }{N}_r(s)+{\displaystyle \sum }\mathrm{\Delta }{N}_i(s)}{Y_r(s)+{\displaystyle \sum }{Y}_i(s)+1}\right).$$ (33)

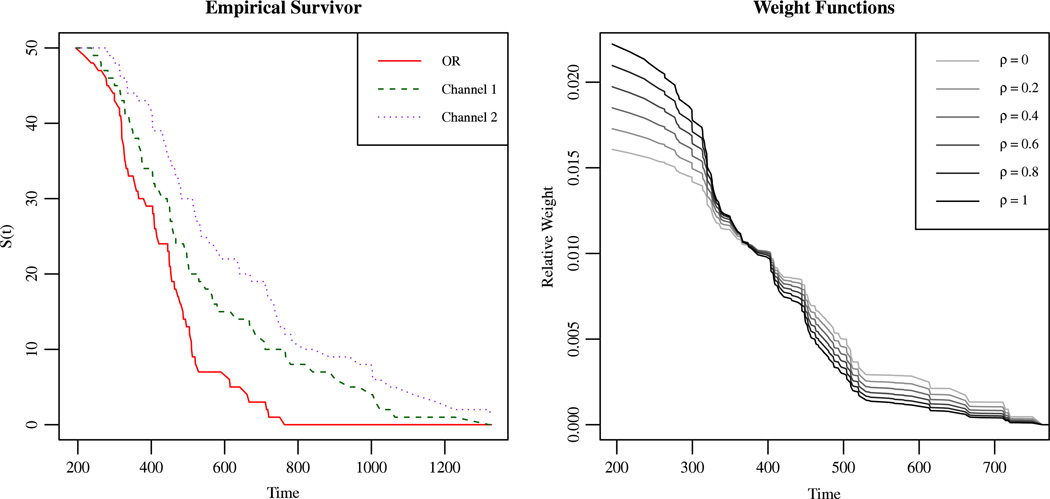
Fig. 2 depicts the relative values of the Harrington–Fleming weighting function across a range of response times and different values of ρ. Response times were sampled from a shifted Wald distribution and the estimators were based on 50 samples from each of the single channel and double target models. When ρ = 0, the test corresponds to a log-rank test (Mantel, 1966) between the estimated UCIP performance and the actual performance with redundant targets (see Andersen et al., 1993, Example V.2.1, for a discussion of this correspondence). As ρ increases, relatively more weight is given to earlier response times and less to later response times.

Fig. 2.

On the left, the empirical survivor function based on response times sampled from Wald distributions is shown. The right shows the relative values of the Harrington–Fleming (Harrington & Fleming, 1982) weighting function for the capacity test at various values of ρ.

Various other weight processes that satisfy the requirements for L(t) have also been proposed (see Aalen et al., 2008, Table 3.2, for a list). Because the null hypothesis distribution is unaffected by the choice of the weight process, it is up to the researcher to choose the most appropriate for a given application. In the simulation section, we use ρ = 0, essentially a log-rank (or Mann–Whitney if there are no censored response times) test of the difference between the estimated UCIP performance and the performance when all targets are present (Aalen et al., 2008; Mantel, 1966). We have chosen to present the Harrington–Fleming estimator here because of its flexibility and specifically with ρ = 0 for the simulation section because it reduces to tests that are more likely to be familiar to the reader. Any weight function that satisfies the conditions on L(t) could be used. A more thorough investigation of the appropriate functions for response time data will be an important next step, but is beyond the scope of this paper.

For a statistical test of C_AND(t), we simply switch Y(t) with G(t) and the bounds of integration.

Theorem 16. Under the null hypothesis of UCIP performance, E (Z_AND) = 0.

Theorem 17. An unbiased estimate of the variance of Z_AND is given by,

$$\text{Var }({\mathrm{Z}}_{\text{AND}})(t)={\displaystyle \sum _{T_{\mathit{\text{ij}}}\ge t}}\frac{L^2(T_{\mathit{\text{ij}}})}{G_i^2(T_{\mathit{\text{ij}}})}+{\displaystyle \sum _{i=1}^k}{\displaystyle \sum _{T_{\mathit{\text{ij}}}\ge t}}\frac{L^2(T_{\mathit{\text{ij}}})}{G_i^2(T_{\mathit{\text{ij}}})}.$$

Theorem 18. Assume that there exists sequences of constants {a_n} and {c_n} such that,

$$\underset{n\to \mathrm{\infty }}{\text{lim}}{a}_n=\underset{n\to \mathrm{\infty }}{\text{lim}}{c}_n=\mathrm{\infty }\mathit{\text{ and}}$$

$$\frac{L^{(n)}(s)}{c_n}\stackrel{P}{\to }l(s)<\mathrm{\infty },\frac{G_r^{(n)}(s)}{a_n^2}\stackrel{P}{\to }{g}_r(s)<\mathrm{\infty },$$

$$\frac{G_i^{(n)}(s)}{a_n^2}\stackrel{P}{\to }{g}_i(s)<\mathrm{\infty }.$$

Further, assume that there exists some function d(s) such that for all δ,

$$\underset{n\to \mathrm{\infty }}{\text{lim inf}}\text{ Pr}\left\{{(a_n/c_n)}^2{\left(L^{(n)}(s)\right)}^2\left(\frac{1}{G_r}+{\displaystyle \sum _{i=1}^k}\frac{1}{G_i}\right)\le d(s)\mathit{\text{ for all }}s\in 𝒯\right\}\ge 1-\delta .$$

Then (a_n/c_n)Z_AND⁽ⁿ⁾ converges in distribution to a zero mean Gaussian process as the number of response times used in the estimate increases.

This leads to a reverse hazard version of the Harrington–Fleming estimator,

$$L(t)=F{(t)}^{\rho }\frac{G_r(t){\displaystyle \sum }{G}_i(t)}{G_r(t)+{\displaystyle \sum }{G}_i(t)}$$ (34)

$$F(t)={\displaystyle \prod _{s\ge t}}\left(1-\frac{\mathrm{\Delta }{N}_r(s)+{\displaystyle \sum }\mathrm{\Delta }{N}_i(s)}{G_r(s)+{\displaystyle \sum }{G}_i(s)+1}\right).$$ (35)

Therefore, one can use the standard normal distribution for null-hypothesis-significance tests for UCIP-OR and UCIP-AND performance. Under the null hypothesis,

$${\mathrm{U}}_{\text{OR}}(t)=\frac{{\mathrm{Z}}_{\text{OR}}(t)}{\text{Var }({\mathrm{Z}}_{\text{OR}}(t))}\stackrel{d}{\to }𝒩(0,1)$$ (36)

$${\mathrm{U}}_{\text{AND}}(t)=\frac{{\mathrm{Z}}_{\text{AND}}(t)}{\text{Var }({\mathrm{Z}}_{\text{AND}}(t))}\stackrel{d}{\to }𝒩(0,1).$$ (37)

2. Simulation

In this section, we examine the properties of the NA estimator of UCIP performance as well as the new test statistic using simulated data. To estimate type I error rates for different sample sizes, we use three different distributions for the single target completion times, exponential, shifted Wald and exGaussian.

First, we simulated results for the test statistics with 10 through 200 samples per distribution. For each sample size, the type I error rate was estimated from 1000 simulations. In each simulation, the parameters for the distribution were randomly sampled. For the exponential rate parameter, we sampled from a gamma distribution with shape 1 and rate 500. For the shifted Wald model, we sampled the shift from a gamma distribution with shape 10 and rate 0.2. Parametrizing the Wald distribution as the first passage time of a diffusion process, we sampled the drift rate from a gamma distribution with shape 1 and rate 10 and the threshold from a gamma distribution with shape 30 and rate 0.6. The rate of the exponential in the exGaussian distribution was sampled from a gamma random variable with shape 1 and rate 250. The mean of the Gaussian component was sampled from a Gaussian distribution with mean 250 and standard deviation 100 and the standard deviation was sampled from a gamma distribution with shape 10 and rate 0.2. In each simulation, response times were sampled from the corresponding distribution with the sampled parameters. Double target response times were simulated by taking two independent samples from the single channel distribution, then taking either the minimum (for OR processing) or the maximum (for AND processing) of those samples.

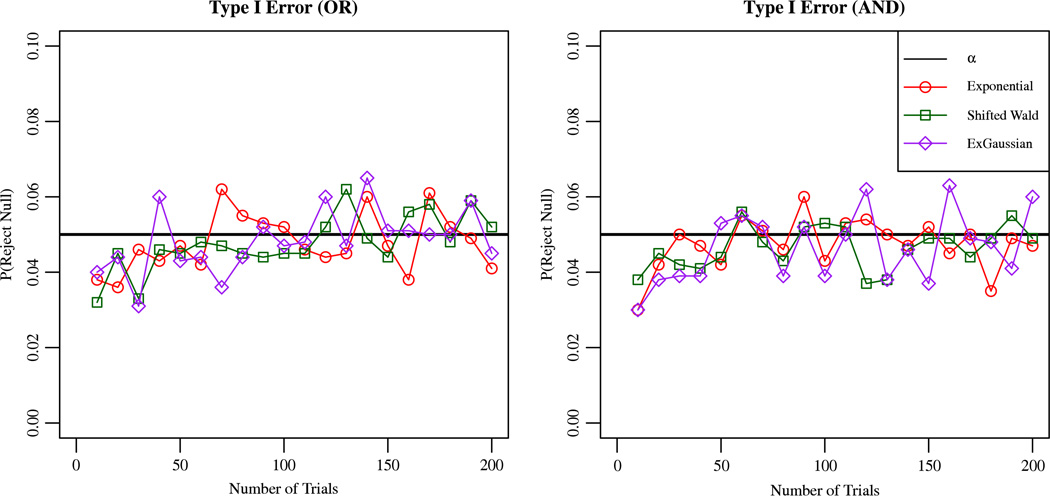
As shown in Fig. 3, the type I error rate is quite close to the chosen α, 0.05 across all three model types and for the simulated sample sizes. This indicates that, even with small sample sizes, using the standard normal distribution for the test statistic works quite well.

Fig. 3.

Type I error rates with α = 0.05 for three different channel completion times. For each model, double target response times were simulated by taking the min or max of independently sampled channel completion times for OR or AND models respectively. The error rates are based on 1000 simulations for each model with 10 through 200 trials per distribution.

Next, we examine the power as a function of the number of samples per distribution and the amount of increase/decrease in performance in the redundant target condition. To do so, we focus on models that have a simple relationship between their parameters and capacity. For OR processes, we use an exponential distribution for each individual channel, F_A(t) = F_B = 1 − e^−λt and H_A(t) = H_A(t) = λt. The prediction for a UCIP or model in this case would be H_AB(t) = 2λt. Thus, changes in will directly correspond to changes in the rate parameter. To explore a range of capacity, we used a range of multipliers for the rate parameters of each channel for simulating the double target response times, F_A,ρ(t) = F_B,ρ(t) = 1 − e^−ρλt so that H_AB,ρ(t) = 2ρλt. This leads to the formula H_AB,ρ/H_AB = ρ for the true capacity. For AND processes, we use F_A(t) = F_B(t) = (1 − e^−λt)^2/ρ as the distribution for simulating response times when both targets are present. Although ρλ no longer corresponds directly with the rate parameter, this approach maintains the correspondence α = C_AND.

In general, the power of these tests may depend on the distribution of the underlying channel processes. We limit our exploration to these models because of the analytic correspondence between the rate parameter and the value of the capacity coefficient. With other distributions, the relationship between the capacity coefficient and the differences in the parameters across workload can be quite complicated. These particular results are also dependent on the weighting function used. Here, we focus on the log-rank type weight function, but many other options are possible (e.g., Aalen et al., 2008, p. 107). These estimates apply to cases when the magnitude of the weighted difference in hazard functions between single and double target conditions match those predicted by the exponential models.

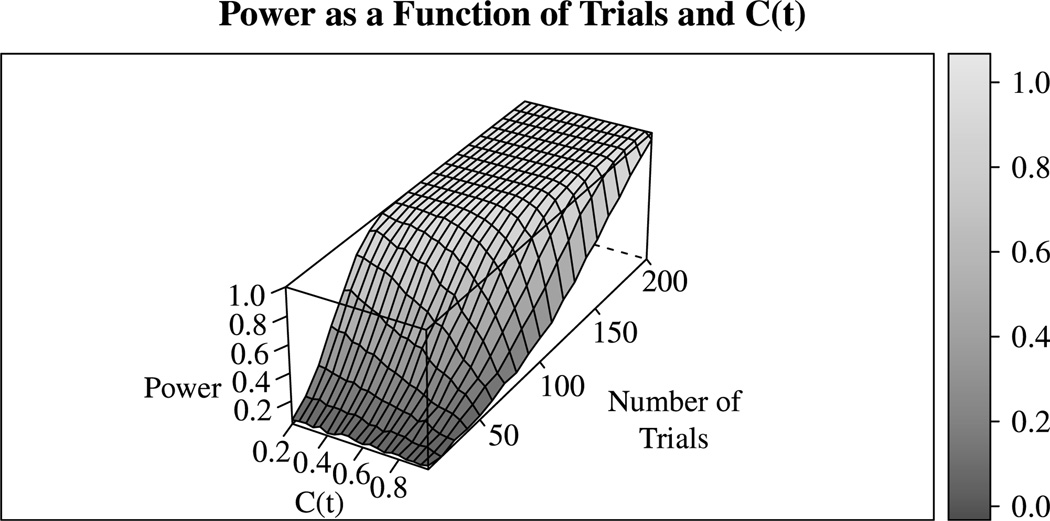
Both the U_OR and U_AND test statistics, applied to the corresponding OR or AND model, had the same power. Figs. 4 and 5 show the power of these tests as the capacity increases and as the number of trials used to estimate each cumulative hazard function increases. For much of the space tested, the power is quite high, with ceiling performance for nearly half of the points tested.

Fig. 4.

Power of the U_OR and U_AND statistics with α = 0.05 as a function of capacity and number of trials per distribution for capacity above 1. These results are based on two exponential channels, with either an OR or AND stopping rule, depending on the statistic. Using these models, the power of U_OR and U_AND is the same.

Fig. 5.

Power of the U_OR and U_AND statistics with α = 0.05 as a function of capacity and number of trials per distribution for capacity less than 1. These results are based on two exponential channels, with either an OR or AND stopping rule, depending on the statistic. Using these models, the power of U_OR and U_AND is the same.

With a true capacity of 1.1, the power remains quite low, even with up to 200 trials per distribution. However, with a higher number of trials, the increase in power is quite steep as a function of the true capacity. With 200 trials per distribution, the power jumps from roughly 0.5 to 0.9 as the true capacity changes from 1.1 to 1.2. On the low end of trials per distribution, i.e., 10 to 20, reasonable power is not achieved even up to a capacity of 3.0. With 30 trials per distribution, the power increases roughly linearly with the capacity, achieving reasonable power around C(t) = 2.5. The test was not as powerful with limited capacity. The power still increases with more trials and larger changes in capacity, however the increase is much more gradual than that in the super capacity plot.

Differences in the power as a function of capacity for super and limited are to be expected given that the capacity coefficient is a ratio, while the test statistics are based on differences. However, this does not explain the differences in power seen here. Part of the difference is due to a difference in scale. The super capacity plot has step sizes of 0.1 while the limited capacity plot has step sizes of 0.04. We chose different step sizes so that we could demonstrate a wider range of capacity values. Furthermore, the weighting function here may be more sensitive to super capacity. The effect of the weighting function on these tests, and determining the appropriate weights if one is interested in only one of super or limited capacity, is an important future direction of this work.

3. Application

In this section we turn to data from a recent experiment using a simple dot detection task. In this study, participants were shown one of four types of stimuli. In the single dot condition, a white 0.2° dot was presented directly above or below a central fixation on an otherwise black background. In the double dot condition, the dots were presented both above and below fixation. Each trial began with a fixation cross, presented for 500 ms, followed by either a single dot stimulus, a double dot stimulus or an entirely black screen presented for 100 ms or until a response was made. Participants were given up to 4 s to respond. Each trial was followed by a 1 s inter-trial interval. On each day, participants were shown each of the four stimuli 400 times in random order.

Participants completed two days worth of trials with each of two different instruction sets. In one version, the OR task, participants were asked to respond “Yes” to the single dot and double dot stimuli and only respond no when the entirely black screen was presented. In the other version, the AND task, participants were to respond “Yes” only to the double dot stimulus and “No” otherwise. See Fig. 1 for example stimuli. For further details of the study, see Eidels, Townsend, Hughes, and Perry (submitted for publication).

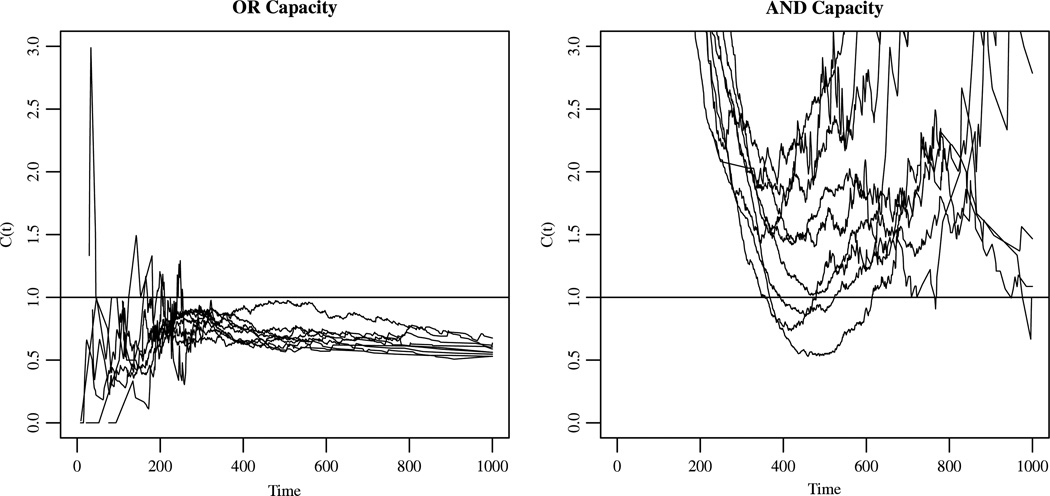
The capacity functions for each individual are shown in Fig. 6. Upon visual inspection, all participants seem to be limited capacity in the OR task. On the AND task, all of the participants had super capacity for some portion of time, with only three participants showing C(t) less than one, and those only for later times.

Fig. 6.

Capacity coefficient functions of the nine participants from Eidels et al. (submitted for publication). The left graph depicts performance on the OR task, evaluated with the OR capacity coefficient. The right graph depicts performance on the AND task, evaluated with the AND capacity coefficient.

Table 1 shows the values of the statistic for each individual. The test shows significant violations of the UCIP model for every participant on both tasks. These data are based on 800 trials per distribution, so based on the power analysis in the last section, it is no surprise that the test was significant for every participant. These data indicate that participants are doing worse than the predicted baseline UCIP processing on the OR task, and better than the UCIP baseline on the AND task. On the OR task, C_OR < 1 indicates either inhibition between the dot detection channels, limited processing resources, or processing worse than parallel (e.g., serial). On the AND task, C_AND > 1 indicates either facilitation between the dot detection channels, increased processing resources with increased load, or processing better than parallel (e.g. coactive). Given the nature of the stimuli and previous analyses (Houpt & Townsend, 2010), it is unlikely that the failure of the assumption of parallel processing is the explanation for these results. Likewise, there is no reason to believe that a change in the available processing resources would be different between the tasks, although resources may be limited for both versions (cf. Townsend & Nozawa, 1995). We believe the most likely explanation of these data is an increase in facilitation between the dot detection processes in the AND task.

Table 1.

Results of the test statistic applied to the results of the two dot experiment of Eidels et al. (submitted for publication).

	OR task	AND task
1	−10.12**	14.50**
2	−4.41**	13.81**
3	−8.22**	3.88**
4	−6.85**	18.62**
5	−9.21**	6.05**
6	−2.72*	22.27**
7	−5.14**	10.49**
8	−5.91**	11.59**
9	−5.53**	15.75**

^*p < 0.01.

^**p < 0.001.

4. Discussion

In this paper, we developed a statistical test for use with the capacity coefficient for both minimum-time (OR) decision rules and maximum-time (AND) decision rules. We did so by extending the properties of the Nelson–Aalen estimator of the cumulative hazard function (e.g., Aalen et al., 2008) to estimates of unlimited capacity, independent parallel performance. This approach yields a test statistic that, under the null hypothesis and in the limit as the number of trials increases, has a standard normal distribution. This allows investigators to use the statistic in a variety of tests beyond just a comparison against the UCIP performance, such as comparing two estimated capacity coefficients.

As part of developing the statistic, we demonstrated two other important results. First, we established the properties of the estimate of UCIP performance on an OR (AND) task given by the sum of cumulative (reverse) hazard functions estimated from single target trials. This included demonstrating that the estimator is unbiased, consistent and converges in distribution to a Gaussian process.

Furthermore, in developing the estimator for UCIP AND processing, we extended the Nelson–Aalen estimator of cumulative hazard functions to cumulative reverse hazard functions. Despite being less common than the cumulative hazard function, the cumulative reverse hazard function is used in a variety of contexts, recently including cognitive psychology (see Chechile, 2011; Eidels, Townsend et al., 2010; Townsend & Wenger, 2004). Nonetheless, we were unable to find existing work developing an NA estimator of the cumulative reverse hazard function. This estimator can also be used to estimate the reverse hazard function in the same way the hazard function is estimated by the muhaz package (Hess & Gentleman, 2010) for the statistical software R (R Development Core Team, 2011). In this method, the cumulative hazard function is estimated with the Nelson–Aalen estimator, then smoothed using (by default) an Epanechnikov kernel. The hazard function is then given by the first order difference of that smoothed function.

Although the statistical test is based on the difference between predicted UCIP performance and true performance when all targets are present, the test is valid for the capacity ratio. If one rejects the null-hypothesis that the difference is zero, this is equivalent to rejecting the hypothesis that the ratio is one. Nonetheless, we have not developed the statistical properties of the capacity coefficients. Instead, we have demonstrated the small-sample and asymptotic properties of the components of the capacity coefficients.

In future work, we hope to develop Bayesian counterparts to the present statistical tests. One advantage of this approach would be the ability to consider posterior distributions over the capacity coefficient in its ratio form, rather than being restricted to the difference. There are additional reasons to explore Bayesian alternatives as well. We will not repeat the various arguments in depth, but there are both practical and philosophical reasons why one might prefer such an alternative (cf. Kruschke, 2010).

We are also interested in a more thorough investigation of the weighting functions used in these tests. It could be that some weighting functions are more likely to detect super-capacity, while others are more likely to detect limited capacity. Furthermore, the effects of the weighting function are likely to vary depending on whether they are used with the cumulative hazard function or the cumulative reverse hazard function.

While the capacity coefficient has been applied in a variety of areas within cognitive psychology, the lack of a statistical test has been a barrier to its use. This work removes that barrier by establishing a general test for UCIP performance.

Appendix

Proofs and supporting theory

A.1. The multiplicative intensity model

The theory of the NA estimator for cumulative hazard functions is based on the multiplicative intensity model for counting processes. Here, we give a brief overview of the model and the corresponding model for counting processes with reverse time. For a more thorough treatment, see the Andersen et al. (1993) and Aalen et al. (2008). Also, Aalen et al. (2009) gives a good introduction to the topic.

Suppose we have a stochastic process N(t) that tracks the number of events that have occurred up to and including time t, e.g., the number of response times less than or equal to t. The intensity of the counting process λ(t) describes the probability that an event occurs in an infinitesimal interval, conditioned on the information about events that have already occurred, divided by the length of that interval. The process given by the difference of the counting process and the cumulative intensity, $M(t)=N(t)-{\displaystyle {\int }_0^t}\lambda (s)\mathit{\text{ ds}}$ turns out to be a martingale Aalen et al. (2008, p. 27). Under the multiplicative intensity process model, we rewrite the intensity process of N(t) by λ(t) = h(t)Y(t), where Y(t) is a process for which the value at time t is determined given the information available up to immediately before t. Of particular interest in this work is estimating the cumulative hazard function $H(t)={\displaystyle {\int }_0^t}h(t)\mathit{\text{ dt}}$.

We will also use the concept of the counting process in reverse time N̄. Hence, we will start at some t_max, possibly infinity, and work backward through time counting all of the events that happen at or after time t. The multiplicative model takes a similar form, with a process G(t) that is determined by all the information available after t, in place of Y(t), λ̄(t) = k(t)G(t). We will use this model when we are interested in estimating the cumulative reverse hazard function $K(t)=-{\displaystyle {\int }_t^{t_{\text{max}}}}k(t)\mathit{\text{ dt}}$.

One important consequence of the multiplicative intensity model is that the associated martingales are locally square integrable (cf. Andersen et al., 1993, p. 78), a requirement for much of the theory below.

A.2. Martingale theory

Before giving the full proofs of the theorems in this paper, we will first summarize the theoretical content that will be necessary, particularly some of the basic properties of martingales. Intuitively, martingales can be thought of as describing the fortune of a gambler through a series of fair gambles. Because each game is fair, the expected amount of money the gambler has after each game is the amount he had before the game. At any point in the sequence, the entire sequence of wins and losses before that game is known, but the outcome of the next game, or any future games is unknown. More formally, a discrete time martingale is defined as follows:

Definition 1. Suppose X₁, X₂, … are a sequence of random variables on a probability space (Ω, ℱ, P) and ℱ₁, ℱ₂, … is a sequence of σ-fields in ℱ. Then {(X_n, ℱ_n) : n = 1, 2, …} is a martingale if:

1. ℱ_n ⊂ ℱ_n+1,

2. X_n is measurable ℱ_n,

3. E(|X_n|) is finite and

4. E(X_n+1|ℱ_n) = X_n almost surely.

Assuming X_n corresponds to the gambler’s fortune after the nth game and ℱ_n corresponds to the information available after the nth game, the first two conditions correspond to the notion that after a particular game, the result of that game and all previous games is known. The third condition corresponds a condition that the expected amount of money a gambler has after any game is finite. The final condition corresponds to the fairness of the gambles; the expected amount of money the gambler has after one more game is the money he has already.

Martingales can also be defined for continuous time. In this case, the index set can be, for example, the set of all times t > 0, t ∈ ℝ. Then we require that for all s < t, ℱ_s ⊂ ℱ_t instead of (i). The second two conditions are the same after replacing the discretely valued index n with the continuously valued t. The final requirement for continuous time becomes E(X_t|ℱ_s) = X_s for all s ≤ t.

The expectation function of a martingale is fixed by definition, but the change in the variability of the process could differ among martingales and is often quite important. In addition to the variance function, there are two useful ways to track the variation, the predictable and optional variation processes. For discrete martingales the predictable variation process is based on the second moment of the process at each step conditioned on the σ-field from the previous step. Formally,

$${\langle X\rangle }_n\equiv {\displaystyle \sum _{i=1}^n}E\left({(X_i-X_{i-1})}^2|{ℱ}_{i-1}\right).$$ (A.1)

The optional (quadratic) variation process is similar, but the second moment at each step is taken without conditioning,

$${[X]}_n\equiv {\displaystyle \sum _{i=1}^n}{(X_i-X_{i-1})}^2.$$ (A.2)

To generalize these processes to continuous time martingales, evenly split up evenly split up the interval [0, t] into n subintervals, and use the discrete definitions, then take the limit as the number of sub-intervals goes to infinity,

$${\langle X\rangle }_t\equiv \underset{n\to \mathrm{\infty }}{\text{lim}}{\displaystyle \sum _{i=1}^n}E\left({(X_{\mathit{\text{it}}/n}-X_{(i-1)t/n})}^2|{ℱ}_{(i-1)t/n}\right)$$ (A.3)

$${[X]}_n\equiv \underset{n\to \mathrm{\infty }}{\text{lim}}{\displaystyle \sum _{i=1}^n}{(X_{\mathit{\text{it}}/n}-X_{(i-1)t/n})}^2.$$ (A.4)

For reverse hazard functions, the concept of a reverse martingale will also be useful. These processes are martingales, but with time reversed so that the martingale property is based on conditioning on the future, not the past. A sequence of random variables …, X_n, X_n+1, X_n+2, … is a reverse martingale if …, X_n+2, X_n+1, X_n, … is a martingale. The definition of a reverse martingale can be generalized to continuous time by the same procedure as a martingale.

Zero mean martingales will particularly useful in the proofs that follow. Similar to the equality of the variance and the second moment for zero mean univariate random variables, the variance of a zero mean martingale is equal to the optional variation process and the predictable variation process. Also, the stochastic integral of a predictable process with respect to a zero mean martingale is again a zero mean martingale. Informally, we can see this property by examining a discrete approximation to the martingale with [0, t] divided into n sub-intervals,

$$I(t)={\displaystyle \sum _{k=1}^n}{H}_k\left(M\left(\frac{\mathit{\text{kt}}}{n}\right)-M\left(\frac{(k-1)t}{n}\right)\right).$$ (A.5)

Then,

$$\mathrm{E}(I(t)-(n-1)t/n|{ℱ}_{n-1})={\displaystyle \sum _{k=1}^n}\mathrm{E}\left(H_k\left(M\left(\frac{\mathit{\text{kt}}}{n}\right)-M\left(\frac{(k-1)t}{n}\right)\right)|{ℱ}_{n-1}\right)-{\displaystyle \sum _{k=1}^{n-1}}\mathrm{E}\left(H_k\left(M\left(\frac{\mathit{\text{kt}}}{n}\right)-M\left(\frac{(k-1)t}{n}\right)\right)|{ℱ}_{n-1}\right)=\mathrm{E}\left(H_k\left(M(t)-M\left(\frac{(n-1)t}{n}\right)\right)|{ℱ}_{n-1}\right)=H_k\left(\mathrm{E}((M(t))|{ℱ}_{n-1})-M\left(\frac{(n-1)t}{n}\right)\right)=0.$$ (A.6)

Aalen et al. (2008) also give the predictable and optional variation processes of the integral of a predictable process, here H(t), with respect to a counting process martingale, M,

$$\langle {\displaystyle \int }H\mathit{\text{ dM}}\rangle (t)={\displaystyle {\int }_0^t}{H}^2(s)\lambda (s)\mathit{\text{ds}}$$ (A.7)

$$\left({\displaystyle \int }H\mathit{\text{ dM}}\right)(t)={\displaystyle {\int }_0^t}{H}^2(s)\mathit{\text{ dN }}(s).$$ (A.8)

Furthermore, if M₁, …, M_k are orthogonal martingales (i.e., for all i ≠ j, 〈M_i, M_j〉 = 0) then,

$$\langle {\displaystyle \sum _{j=1^k}}{\displaystyle \int }{H}_j{\mathit{\text{ dM}}}_j\rangle (t)={\displaystyle \sum _{j=1^k}}{\displaystyle {\int }_0^t}{H}_j^2(s){\lambda }_j(s)\mathit{\text{ ds}}$$ (A.9)

$$\left({\displaystyle \sum _{j=1^k}}{\displaystyle \int }{H}_j{\mathit{\text{ dM}}}_j\right)(t)={\displaystyle {\int }_0^t}{H}_j^2(s){\mathit{\text{ dN}}}_j(s).$$ (A.10)

From the reverse-time relationship, the same properties hold for reverse martingales, with the lower bound of integration set to t > 0 and the upper bound set to ∞ or t_max.

We will make use of the martingale central limit theorem for the proofs involving limit distributions of the estimators. This theorem states that, under certain assumptions, a sequence of martingales converges in distribution to a Gaussian martingale. There are various versions of the theorem that require various conditions. For our purposes, we will use the condition that there exist some non-negative function y(s) such that sup_s∈[0,t] |Y⁽ⁿ⁾(s)/n − y(s)| converges in probability to 0, where Y⁽ⁿ⁾(s) is as defined above (the number of responses that have not occurred by time s). With the additional assumption that the cumulative hazard function is finite on [0, t], this is sufficient for the martingale central limit theorem to hold. If the martingales are zero-mean and, assuming s₁ is the smaller of s₁ and s₂, $\text{cov}(s_1,s_2)={\displaystyle {\int }_0^{s_1}}h(u)/y(u)\mathit{\text{ du}}$ Andersen et al. (1993, pp. 83–84). In our applications, y(s) is the survivor function of the response time random variable.

We will also need an analogous theorem for reverse martingales for the theory of cumulative reverse hazard functions. With cumulative reverse hazard functions, we can no longer assume K(0) < ∞, but we can assume lim_t→∞ K(t) = 0. Thus, we will need a function g(t) such that ${\text{sup}}_{s\in [t,\mathrm{\infty }]}|G^{(n)}(s)/n-g(s)|\stackrel{P}{\to }0$ in place of the conditions on y(t). Furthermore, the covariance function of the limit distribution, cov(s₁, s₂), will depend on the larger of s₁ and s₂. In this case, g(s) is the cumulative distribution function of the response time random variable. Thus, if we additionally assume that when t > 0, K(t) < ∞, the distribution of the processes in the limit as the number of samples increases is again a Gaussian martingale (Loynes, 1969).

A.3. Proofs of theorems in the text

A.3.1. The cumulative reverse hazard function

As a reminder,

$$Q(t)\equiv I\{G(t)>0\}$$ (A.11)

$$\mathrm{K̂}(t)\equiv {\displaystyle \sum _{T_j\ge t}}\frac{1}{G(T_j)}$$

$$K^{*}(t)\equiv {\displaystyle {\int }_t^{t_{\text{max}}}}Q(s)k(s)\mathit{\text{ds}}.$$

Theorem 1. K̂(t) is an unbiased estimator of K*(t).

Proof. This can be derived in the same manner that the Ĥ is shown to be unbiased in Aalen et al. (2008, pp. 87–88), but with time reversed. Instead of using the definition of the counting process N(t) in Eq. (12), we use reversed counting processes N̄(t) which is 0 at some t_max, and increases as t decreases. We represent the intensity of this process as λ̄(t) = k(t)G(t), where k(t) is the reverse hazard function at time t and let M̄(t) be the reverse martingale $\mathrm{M̄}(t)=\mathrm{N̄}(t)-{\displaystyle {\int }_t^{t_{\text{max}}}}\mathrm{\lambda ̄}(s)\mathit{\text{ ds}}$. Then, the transitions of this process can be written informally as,

$$d\mathrm{N̄}(t)=k(t)G(t)\mathit{\text{dt}}+d\mathrm{M̄}(t).$$

Let Q(t)/G(t) = 0, then,

$$\frac{Q(t)}{G(t)}d\mathrm{N̄}(t)=Q(t)k(t)\mathit{\text{dt}}+\frac{Q(t)}{G(t)}d\mathrm{M̄}(t).$$

Integrating from t to t_max and multiplying through by −1, we have,

$$-{\displaystyle {\int }_t^{t_{\text{max}}}}\frac{Q(s)}{G(s)}d\mathrm{N̄}(s)=-{\displaystyle {\int }_t^{t_{\text{max}}}}Q(s)k(s)\mathit{\text{ds}}-{\displaystyle {\int }_t^{t_{\text{max}}}}\frac{Q(s)}{G(s)}d\mathrm{M̄}(s).$$

The left-hand side is K̂, the first term on the right is K*(t), and the final term is a zero mean reverse martingale. Hence, K̂(t) is an unbiased estimator of K*(t).

Theorem 2. An unbiased estimate of the variance of K̂(t) is given by,

$${\mathrm{\sigma ̂}}_K^2(t)\equiv {\displaystyle \sum _{T_j\ge t}}\frac{1}{G^2(T_j)}.$$ (A.12)

Proof. From Theorem 1, K̂(t) − K*(t) is a zero mean reverse martingale. Thus,

$$\text{Var }(\mathrm{K̂}(t)-K^{*}(t))=\mathrm{E}\left(\right[\mathrm{K̂}(t)-K^{*}(t)\left]\right)=\mathrm{E}\left(\right[{\displaystyle {\int }_t^{t_{\text{max}}}}\frac{Q(s)}{G(s)}d\mathrm{M̄}(s)\left]\right).$$

The integral ${\displaystyle {\int }_t^{t_{\text{max}}}}\frac{Q(s)}{G(s)}d\mathrm{M̄}(s)$ is with respect to a zero mean martingale with time reversed, so the optional variation process is,

$$[{\displaystyle {\int }_t^{t_{\text{max}}}}\frac{Q(s)}{G(s)}d\mathrm{M̄}(s)]={\displaystyle {\int }_t^{t_{\text{max}}}}\frac{Q(s)}{G^2(s)}d\mathrm{N̄}(s).$$

Hence,

$${\mathrm{\sigma ̂}}^2(t)={\displaystyle {\int }_t^{t_{\text{max}}}}\frac{Q(s)}{G^2(s)}d\mathrm{N̄}(s)={\displaystyle \sum _{T_j\ge t}}\frac{1}{G^2(T_j)}.$$

Lemma 1. $\langle \mathrm{K̂}(t)-K^{*}(t)\rangle ={\displaystyle {\int }_t^{t_{\text{max}}}}\frac{Q(s)}{G(s)}k(s)\mathit{\text{ds}}$.

Proof. From the proof of Theorem 1,

$$\mathrm{K̂}(t)-K^{*}(t)={\displaystyle {\int }_t^{t_{\text{max}}}}\frac{Q(s)}{G(s)}d\mathrm{M̄}(s).$$ (A.13)

Thus, the predictable variation process is (cf. Andersen et al., 1993, p. 71),

$${\displaystyle {\int }_t^{t_{\text{max}}}}{\left(\frac{Q(s)}{G(s)}\right)}^{2}d\langle M\rangle (s)={\displaystyle {\int }_t^{t_{\text{max}}}}{\left(\frac{Q(s)}{G(s)}\right)}^{2}G(s)k(s)\mathit{\text{ ds}}={\displaystyle {\int }_t^{t_{\text{max}}}}\frac{Q(s)}{G(s)}k(s)\mathit{\text{ ds}}.$$ (A.14)

Theorem 3. K̂(t) is a uniformly consistent estimator of K(t).

Proof. By Lenglart’s Inequality (e.g., Andersen et al., 1993, p. 86) and Lemma 1,

$$\text{Pr }\{\underset{s\in [t,t_{\text{max}}]}{\text{sup}}|{\mathrm{K̂}}^{(n)}-K^{*(n)}|>\eta \}\le \frac{\delta }{{\eta }^2}+\text{Pr }\{{\displaystyle {\int }_t^{t_{\text{max}}}}\frac{Q^{(n)}(s)}{G^{(n)}(s)}k(s)\mathit{\text{ds}}>\delta \}.$$

For each s ∈ [t, t_max], there is some positive probability of observing a response at or before s. Hence, as n → ∞, there will be infinitely many responses observed at or before s, so,

$$\underset{s\in [t,t_{\text{max}}]}{\text{inf}}{G}^{(n)}(s)\stackrel{P}{\to }\mathrm{\infty }.$$

Because Q⁽ⁿ⁾(s) ≤ 1 and k(s) < ∞,

$${\displaystyle {\int }_t^{t_{\text{max}}}}\frac{Q^{(n)}(s)}{G^{(n)}(s)}k(s)\mathit{\text{ ds}}\stackrel{P}{\to }0.$$

This implies that for any positive δ,

$$\underset{n\to \mathrm{\infty }}{\text{lim}}\text{Pr }\{{\displaystyle {\int }_t^{t_{\text{max}}}}\frac{Q^{(n)}(s)}{G^{(n)}(s)}k(s)\mathit{\text{ ds}}>\delta \}=0.$$

And thus for any positive ε,

$$\underset{n\to \mathrm{\infty }}{\text{lim}}\text{Pr }\left\{\underset{s\in [t,t_{\text{max}}]}{\text{sup}}\right|{\mathrm{K̂}}^{(n)}(s)-K^{*(n)}(s)|\ge \epsilon \}=0.$$

Additionally,

$$\underset{n\to \mathrm{\infty }}{\text{lim}}|K^{*}(s)-K(s)|={\displaystyle {\int }_s^{t_{\text{max}}}}(1-Q^{(n)}(s))\mathit{\text{ ds}}\stackrel{P}{\to }0.$$

Therefore, ${\text{sup}}_{s\in [t,t_{\text{max}}]}|{\mathrm{K̂}}^{(n)}(s)-K(s)|\stackrel{P}{\to }0$.

Theorem 4. $\sqrt{n}(\mathrm{K̂}(t)-K(t))$ converges in distribution to a zero mean Gaussian process as the number of response times used in the estimate increases.

Proof. In the limit as the number of samples n increases, for any t > 0, Q(t) = 0 only when k(t) = 0 so it is sufficient to demonstrate the convergence of K̂(t) − K(t). First, we must satisfy the condition that there must exist some g(t) such that $G(t)/n\stackrel{P}{\to }g(t)$ for all t ∈ [τ, t_max]. This follows directly from the Glivenko–Cantelli Theorem (e.g., Billingsley, 1995, p. 269) by noting that G(t)/n is the empirical cumulative distribution function. Then we may apply the reverse martingale central limit theorem and the conclusion follows.

A.3.2. Estimating UCIP performance

As a reminder,

$$J(t)\equiv I\{Y(t)>0\}$$ (A.15)

$$Ĥ(t)\equiv {\displaystyle \sum _{T_j\ge t}}\frac{1}{Y(T_j)}$$ (A.16)

$$H^{*}(t)\equiv {\displaystyle {\int }_0^t}J(s)h(s)\mathit{\text{ ds}}.$$ (A.17)

Theorem 5. Ĥ_UCIP(t) is an unbiased estimator of $H_{\text{UCIP}}^{*}(t)$.

Proof.

$$\mathrm{E}\left({Ĥ}_{\text{UCIP}}(t)\right)=\mathrm{E}\left({\displaystyle \sum _{i=1}^k}{Ĥ}_i(t)\right)={\displaystyle \sum _{i=1}^k}\mathrm{E}({Ĥ}_i(t))={\displaystyle \sum _{i=1}^k}{H}_i^{*}(t)=H_{\text{UCIP}}^{*}(t).$$

Theorem 6. An unbiased estimate of the variance of Ĥ_UCIP(t) is given by,

$${\mathrm{\sigma ̂}}^2(t)={\displaystyle \sum _{i=1}^k}{\displaystyle \sum _{T_{\mathit{\text{ij}}}\le t}}\frac{1}{Y_i^2(T_{\mathit{\text{ij}}})}.$$ (A.18)

Proof. To determine the variance, we use the optional variation of the martingale. Assuming that the counting processes for each process are independent, we have the following relation (e.g., Aalen et al., 2008, p. 56),

$$\left[{\displaystyle \sum _{i=1}^k}{\displaystyle {\int }_0^{t_0}}\frac{1}{Y_i(t)}{\mathit{\text{dM}}}_i(t)\right]={\displaystyle \sum _{i=1}^k}{\displaystyle {\int }_0^{t_0}}\frac{1}{Y_i^2(t)}{\mathit{\text{dN}}}_i(t).$$

Because, under the null hypothesis, ${Ĥ}_{\text{UCIP}}(t)-{\displaystyle {\sum }_{i=1}^k}{H}_i(t)$ is a zero mean martingale,

$$\text{Var }\left({Ĥ}_{\text{UCIP}}(t)-{\displaystyle \sum _{i=1}^k}{H}_i(t)\right)=\mathrm{E}\left[{Ĥ}_{\text{UCIP}}(t)-{\displaystyle \sum _{i=1}^k}{H}_i(t)\right]={\displaystyle \sum _{i=1}^k}{\displaystyle {\int }_0^t}\frac{1}{Y_i^2(s)}{\mathit{\text{dN}}}_i(s)={\displaystyle \sum _{i=1}^k}{\displaystyle \sum _{T_{\mathit{\text{ij}}}\le t}}\frac{1}{Y_i^2(T_{\mathit{\text{ij}}})}.$$

Theorem 7. Ĥ_UCIP(t) is a uniformly consistent estimator of H_UCIP(t).

Proof. Suppose n_i is the number of response times used to estimate Ĥ_i(t). For each i, Ĥ_i(t) is a consistent estimator of H_i(t), so

$$\underset{s\in [0,t]}{\text{sup}}\left|{Ĥ}_i^{(n_i)}(s)-H_i(s)\right|\stackrel{P}{\to }0.$$

Then,

$$\underset{s\in [0,t]}{\text{sup}}\left|{Ĥ}_{\text{UCIP}}^{(n)}(t)-H_{\text{UCIP}}(t)\right|=\underset{s\in [0,t]}{\text{sup}}\left|{\displaystyle \sum _{i=1}^k}{Ĥ}_i^{(n_i)}(s)-{\displaystyle \sum _{i=1}^k}{H}_i(s)\right|=\underset{s\in [0,t]}{\text{sup}}\left|{\displaystyle \sum _{i=1}^k}({Ĥ}_i^{(n_i)}(s)-H_i(s))\right|\le \underset{s\in [0,t]}{\text{sup}}\left({\displaystyle \sum _{i=1}^k}\left|{Ĥ}_i^{(n_i)}(s)-H_i(s)\right|\right)\stackrel{P}{\to }0.$$

Theorem 8. $n={\displaystyle {\sum }_{i=1}^k}{n}_i$ where n_i is the number of response times used to estimate the cumulative hazard function of the completion time of the ith channel. Then, $\sqrt{n}({Ĥ}_{\text{UCIP}}-H_{\text{UCIP}})$ converges in distribution to a zero mean Gaussian process as the number of response times used in the estimate increases.

Proof. For the distribution to converge, Y_i/n must converge in probability to some positive function y(t) for all i. This happens as long as the proportions of n_i/n converge to some fixed proportion p_i, and y_i(t) = p_i(1 − F_i(t)). Then, we have as the limit distribution a Gaussian process with mean 0 and covariance,

$$\text{Cov}(s,t)={\displaystyle \sum _{i=1}^k}{\sigma }_i^2(\text{min}(s,t))\text{ for }s,t>0.$$

Theorem 9. K̂_UCIP(t) is an unbiased estimator of $K_{\text{UCIP}}^{*}(t)$.

Proof.

$$\mathrm{E}\left({\mathrm{K̂}}_{\text{UCIP}}(t)\right)=\mathrm{E}\left({\displaystyle \sum _{i=1}^k}{\mathrm{K̂}}_i(t)\right)={\displaystyle \sum _{i=1}^k}\mathrm{E}({\mathrm{K̂}}_i(t))={\displaystyle \sum _{i=1}^k}{K}_i^{*}(t)={\text{UCIP}}^{*}(t).$$

Theorem 10. An unbiased estimate of the variance of K̂_UCIP(t) is given by,

$${\mathrm{\sigma ̂}}^2(t)\equiv {\displaystyle \sum _{i=1}^k}{\displaystyle \sum _{T_{\mathit{\text{ij}}}\ge t}}\frac{1}{G_i^2(T_{\mathit{\text{ij}}})}.$$ (A.19)

Proof. By Theorem 9, ${\mathrm{K̂}}_{\text{UCIP}}(t)-{\displaystyle {\sum }_{i=1}^k}{K}_i(t)$ is a zero mean martingale so,

$$\text{Var }\left({\mathrm{K̂}}_{\text{UCIP}}(t)-{\displaystyle \sum _{i=1}^k}{K}_i(t)\right)=\mathrm{E}\left[{\mathrm{K̂}}_{\text{UCIP}}(t)-{\displaystyle \sum _{i=1}^k}{K}_i(t)\right]={\displaystyle \sum _{i=1}^k}{\displaystyle {\int }_t^{t_{\text{max}}}}\frac{1}{G_i^2(t)}d{\mathrm{N̄}}_i(t)={\displaystyle \sum _{i=1}^k}{\displaystyle \sum _{T_{\mathit{\text{ij}}}\ge t}}\frac{1}{G_i^2(T_{\mathit{\text{ij}}})}.$$

Theorem 11. K̂_UCIP is a uniformly consistent estimator of K_UCIP.

Proof. Suppose n_i is the number of response times used to estimate K̂_i. For each i, K̂_i is a consistent estimator of K_i, so

$$\underset{s\in [t,t_{\text{max}}]}{\text{sup}}\left|{\mathrm{K̂}}_i^{(n_i)}(s)-K_i(s)\right|\stackrel{P}{\to }0.$$

Then,

$$\underset{s\in [t,t_{\text{max}}]}{\text{sup}}\left|{\mathrm{K̂}}_{\text{UCIP}}^{(n)}(s)-K_{\text{UCIP}}(s)\right|=\underset{s\in [t,t_{\text{max}}]}{\text{sup}}\left|{\displaystyle \sum _{i=1}^k}{\mathrm{K̂}}_i^{(n_i)}(s)-{\displaystyle \sum _{i=1}^k}{K}_i(s)\right|=\underset{s\in [t,t_{\text{max}}]}{\text{sup}}\left|{\displaystyle \sum _{i=1}^k}({\mathrm{K̂}}_i^{(n_i)}(s)-K_i(s))\right|\le \underset{s\in [t,t_{\text{max}}]}{\text{sup}}\left({\displaystyle \sum _{i=1}^k}\left|{\mathrm{K̂}}_i^{(n_i)}(s)-K_i(s)\right|\right)\stackrel{P}{\to }0.$$

Theorem 12. $\sqrt{n}({\mathrm{K̂}}_{\text{UCIP}}-K_{\text{UCIP}})$ converges in distribution to a zero mean Gaussian process as the number of response times used in the estimate increases.

Proof. Let $n={\displaystyle {\sum }_{i=1}^k}{n}_i$ where n_i is the number of response times used to estimate the cumulative hazard function of the completion time of the ith channel. For the distribution to converge, Y_i/n must converge in probability to some positive function y(t) for all i. This happens as long as the proportions of n_i/n converge to some fixed proportion p_i, and y_i(t) = p_i(1 − F_i(t)). Then, we have as the limit distribution a Gaussian process with mean 0 and covariance,

$$\text{Cov}(s,t)={\displaystyle \sum _{i=1}^k}{\sigma }_i^2(\text{min}(s,t))\text{ for }s,t>0.$$ (A.20)

A.3.3. Hypothesis testing

Lemma 2. Under the null hypothesis of UCIP performance,

$${\mathrm{Z}}_{\text{OR}}(t)={\displaystyle {\int }_0^t}\frac{L(s)}{Y_r(s)}{\mathit{\text{dM}}}_r(s)-{\displaystyle \sum _{i=1}^k}{\displaystyle {\int }_0^t}\frac{L(s)}{Y_i(s)}{\mathit{\text{dM}}}_i(s).$$

Proof.

$${\mathrm{Z}}_{\text{OR}}(t)={\displaystyle {\int }_0^t}\frac{L(s)}{Y_r(s)}{\mathit{\text{dN}}}_r(s)-{\displaystyle \sum _{i=1}^k}{\displaystyle {\int }_0^t}\frac{L(s)}{Y_i(s)}{\mathit{\text{dN}}}_i(s)={\displaystyle {\int }_0^t}\frac{L(s)}{Y_r(s)}{\mathit{\text{dM}}}_r(s)+{\displaystyle {\int }_0^t}\frac{L(s)}{Y_r(s)}{Y}_r(s)h_r(s)\mathit{\text{ ds}}-{\displaystyle \sum _{i=1}^k}{\displaystyle {\int }_0^t}\frac{L(s)}{Y_i(s)}{\mathit{\text{dM}}}_i(s)-{\displaystyle \sum _{i=1}^k}{\displaystyle {\int }_0^t}\frac{L(s)}{Y_i(s)}{Y}_i(s)h_i(s)\mathit{\text{ ds}}={\displaystyle {\int }_0^t}\frac{L(s)}{Y_r(s)}{\mathit{\text{dM}}}_r(s)-{\displaystyle \sum _{i=1}^k}{\displaystyle {\int }_0^t}\frac{L(s)}{Y_i(s)}{\mathit{\text{dM}}}_i(s)+{\displaystyle {\int }_0^t}L(s)h_r(s)-{\displaystyle \sum _{i=1}^k}L(s)h_i(s)\mathit{\text{ ds}}={\displaystyle {\int }_0^t}\frac{L(s)}{Y_r(s)}{\mathit{\text{dM}}}_r(s)-{\displaystyle \sum _{i=1}^k}{\displaystyle {\int }_0^t}\frac{L(s)}{Y_i(s)}{\mathit{\text{dM}}}_i(s)+{\displaystyle {\int }_0^t}L(s)\left(h_r(s)-{\displaystyle \sum _{i=1}^k}{h}_i(s)\right)\mathit{\text{ ds}}={\displaystyle {\int }_0^t}\frac{L(s)}{Y_r(s)}{\mathit{\text{dM}}}_r(s)-{\displaystyle \sum _{i=1}^k}{\displaystyle {\int }_0^t}\frac{L(s)}{Y_i(s)}{\mathit{\text{dM}}}_i(s).$$

Theorem 13. Under the null hypothesis of UCIP performance, E (Z_OR) = 0.

Proof. According to Lemma 2, Z_OR is the difference of two integrals with respect to zero mean martingales. The expectation of an integral with respect to a zero mean martingale is zero. Hence, the conclusion follows from the linearity of the expectation operator.

Theorem 14. An unbiased estimate of the variance of Z_OR is given by,

$$\text{Var }({\mathrm{Z}}_{\text{OR}})(t)={\displaystyle \sum _{T_{\mathit{\text{ij}}}\le t}}\frac{L^2(T_{\mathit{\text{ij}}})}{Y_i^2(T_{\mathit{\text{ij}}})}+{\displaystyle \sum _{i=1}^k}{\displaystyle \sum _{T_{\text{ij}}\le t}}\frac{L^2(T_{\mathit{\text{ij}}})}{Y_i^2(T_{\mathit{\text{ij}}})}.$$

Proof.

$$\text{Var }({\mathrm{Z}}_{\text{OR}}(t))=\mathrm{E}[{\mathrm{Z}}_{\text{OR}}(t)]=\mathrm{E}[{\displaystyle {\int }_0^t}\frac{L(s)}{Y_i(s)}{\mathit{\text{dM}}}_r(s)+{\displaystyle \sum _{i=1}^k}{\displaystyle {\int }_0^t}\frac{L(s)}{Y_i(s)}{\mathit{\text{dM}}}_i(s)]={\displaystyle {\int }_0^t}\frac{L^2(s)}{Y_i^2(s)}{\mathit{\text{dN}}}_r(s)+{\displaystyle \sum _{i=1}^k}{\displaystyle {\int }_0^t}\frac{L^2(s)}{Y_i^2(s)}{\mathit{\text{dN}}}_i(s)={\displaystyle \sum _{T_{\mathit{\text{ij}}}\le t}}\frac{L^2(T_{\mathit{\text{ij}}})}{Y_i^2(T_{\mathit{\text{ij}}})}+{\displaystyle \sum _{i=1}^k}{\displaystyle \sum _{T_{\mathit{\text{ij}}}\le t}}\frac{L^2(T_{\mathit{\text{ij}}})}{Y_i^2(T_{\mathit{\text{ij}}})}.$$

Theorem 15. Assume that there exists sequences of constants {a_n} and {c_n} such that,

$$\underset{n\to \mathrm{\infty }}{\text{lim}}{a}_n=\underset{n\to \mathrm{\infty }}{\text{lim}}{c}_n=\mathrm{\infty }\mathit{\text{ and}}$$

$$\frac{L^{(n)}(s)}{c_n}\stackrel{P}{\to }l(s)<\mathrm{\infty },\frac{Y_r^{(n)}(s)}{a_n^2}\stackrel{P}{\to }{y}_r(s)<\mathrm{\infty },$$

$$\frac{Y_i^{(n)}(s)}{a_n^2}\stackrel{P}{\to }{y}_i(s)<\mathrm{\infty }.$$

Further, assume that there exists some function d(s) such that for all δ,

$$\underset{n\to \mathrm{\infty }}{\text{lim inf }}\text{Pr}\left\{{(a_n/c_n)}^2{(L^{(n)}(s))}^2\left(\frac{1}{Y_r}+{\displaystyle \sum _{i=1}^k}\frac{1}{Y_i}\right)\le d(s)\mathit{\text{ for all }}s\in 𝒯\right\}\ge 1-\delta .$$

Then (a_n/c_n)Z_OR⁽ⁿ⁾ converges in distribution to a zero mean Gaussian process as the number of response times used in the estimate increases.

Proof. Here we use the version of the martingale central limit theorem as stated in Andersen et al. (1993, Section 2.23). First, we must show that the variance process converges to a deterministic process.

$$\langle \frac{a_n}{c_n}{{\mathrm{Z}}_{\text{OR}}}^{(n)}\rangle =\langle {\displaystyle {\int }_0^t}\frac{a_n}{c_n}\frac{L^{(n)}(s)}{Y_r^{(n)}(s)}{\mathit{\text{dM}}}_r^{(n)}(s)+{\displaystyle \sum _{i=1}^k}{\displaystyle {\int }_0^t}\frac{a_n}{c_n}\frac{-L^{(n)}(s)}{Y_i^{(n)}(s)}{\mathit{\text{dM}}}_i^{(n)}(s)\rangle ={\displaystyle {\int }_0^t}\frac{a_n^2}{c_n^2}\frac{{(L^{(n)}(s))}^2}{{\left(Y_r^{(n)}(s)\right)}^2}{Y}_r^{(n)}(s){\alpha }_r(s)\mathit{\text{ ds}}+{\displaystyle \sum _{i=1}^k}{\displaystyle {\int }_0^t}\frac{a_n^2}{c_n^2}\frac{{(L^{(n)}(s))}^2}{{\left(Y_i^{(n)}(s)\right)}^2}{Y}_i^{(n)}(s){\alpha }_i(s)\mathit{\text{ ds }}\mathrm{=}{\displaystyle {\int }_0^t}{\left(\frac{L^{(n)}(s)}{c_n}\right)}^2\left(\frac{a_n{\alpha }_r(s)}{Y_r^{(n)}(s)}+{\displaystyle \sum _{i=1}^k}\frac{a_n{\alpha }_i(s)}{Y_i^{(n)}(s)}\right)\mathit{\text{ ds}}.$$

Hence, from the assumptions and by the dominated convergence theorem,

$$\langle \frac{a_n}{c_n}{{\mathrm{Z}}_{\text{OR}}}^{(n)}\rangle \stackrel{P}{\to }{\displaystyle {\int }_0^t}{l}^2(s)\left(y_r(s){\alpha }_r(s)+{\displaystyle \sum _{i=1}^k}{y}_i(s){\alpha }_i(s)\right)\mathit{\text{ ds}}<\mathrm{\infty }.$$

The second condition holds because for all s ∈ [0, t],

$$\frac{a_{n}L(s)}{c_n{Y}_r(s)}\stackrel{P}{\to }0\text{ and }\frac{a_{n}L(s)}{c_n{Y}_i(s)}\stackrel{P}{\to }0\text{ for all }i.$$

Therefore, the conclusion follows from the martingale central limit theorem.

Lemma 3. Under the null hypothesis of UCIP performance,

$${\mathrm{Z}}_{\text{AND}}(t)={\displaystyle {\int }_t^{t_{\text{max}}}}\frac{L(s)}{G_r(s)}d{\mathrm{M̄}}_r(s)-{\displaystyle \sum _{i=1}^k}{\displaystyle {\int }_t^{t_{\text{max}}}}\frac{L(s)}{Y_i(s)}d{\mathrm{M̄}}_i(s).$$

Proof.

$${\mathrm{Z}}_{\text{AND}}(t)={\displaystyle {\int }_t^{t_{\text{max}}}}\frac{L(s)}{G_r(s)}d{\mathrm{N̄}}_r(s)-{\displaystyle \sum _{i=1}^k}{\displaystyle {\int }_t^{t_{\text{max}}}}\frac{L(s)}{G_i(s)}d{\mathrm{N̄}}_i(s)={\displaystyle {\int }_t^{t_{\text{max}}}}\frac{L(s)}{G_r(s)}d{\mathrm{M̄}}_r(s)+{\displaystyle {\int }_t^{t_{\text{max}}}}\frac{L(s)}{G_r(s)}{G}_r(s)h_r(s)\mathit{\text{ ds}}-{\displaystyle \sum _{i=1}^k}{\displaystyle {\int }_t^{t_{\text{max}}}}\frac{L(s)}{G_i(s)}d{\mathrm{M̄}}_i(s)-{\displaystyle \sum _{i=1}^k}{\displaystyle {\int }_t^{t_{\text{max}}}}\frac{L(s)}{G_i(s)}{G}_i(s)h_i(s)\mathit{\text{ ds}}={\displaystyle {\int }_t^{t_{\text{max}}}}\frac{L(s)}{G_r(s)}d{\mathrm{M̄}}_r(s)-{\displaystyle \sum _{i=1}^k}{\displaystyle {\int }_t^{t_{\text{max}}}}\frac{L(s)}{G_i(s)}d{\mathrm{M̄}}_i(s)+{\displaystyle {\int }_t^{t_{\text{max}}}}L(s)h_r(s)-{\displaystyle \sum _{i=1}^k}L(s)h_i(s)\mathit{\text{ ds}}={\displaystyle {\int }_t^{t_{\text{max}}}}\frac{L(s)}{G_r(s)}d{\mathrm{M̄}}_r(s)-{\displaystyle \sum _{i=1}^k}{\displaystyle {\int }_t^{t_{\text{max}}}}\frac{L(s)}{G_i(s)}d{\mathrm{M̄}}_i(s)+{\displaystyle {\int }_t^{t_{\text{max}}}}L(s)\left(h_r(s)-{\displaystyle \sum _{i=1}^k}{h}_i(s)\right)\mathit{\text{ ds}}={\displaystyle {\int }_t^{t_{\text{max}}}}\frac{L(s)}{G_r(s)}d{\mathrm{M̄}}_r(s)-{\displaystyle \sum _{i=1}^k}{\displaystyle {\int }_t^{t_{\text{max}}}}\frac{L(s)}{G_i(s)}d{\mathrm{M̄}}_i(s).$$

Theorem 16. Under the null hypothesis of UCIP performance, E (Z_AND) = 0.

Proof. According to Lemma 3, Z_AND is the difference of two integrals with respect to zero mean martingales. The expectation of an integral with respect to a zero mean reverse martingale is zero. Hence, the conclusion follows from the linearity of the expectation operator.

Theorem 17. An unbiased estimate of the variance of Z_AND is given by,

$$\text{Var }({\mathrm{Z}}_{\text{AND}})(t)={\displaystyle \sum _{T_{\mathit{\text{ij}}}\ge t}}\frac{L^2(T_{\mathit{\text{ij}}})}{G_i^2(T_{\mathit{\text{ij}}})}+{\displaystyle \sum _{i=1}^k}{\displaystyle \sum _{T_{\mathit{\text{ij}}}\ge t}}\frac{L^2(T_{\mathit{\text{ij}}})}{G_i^2(T_{\mathit{\text{ij}}})}.$$

Proof.

$$\text{Var }({\mathrm{Z}}_{\text{AND}}(t))=\mathrm{E}[{\mathrm{Z}}_{\text{AND}}(t)]=\mathrm{E}\left[{\displaystyle {\int }_t^{t_{\text{max}}}}\frac{L(s)}{G_i(s)}d{\mathrm{M̄}}_r(s)+{\displaystyle \sum _{i=1}^k}{\displaystyle {\int }_t^{t_{\text{max}}}}\frac{L(s)}{G_i(s)}d{\mathrm{M̄}}_i(s)\right]={\displaystyle {\int }_t^{t_{\text{max}}}}\frac{L^2(s)}{G_i^2(s)}d{\mathrm{N̄}}_r(s)+{\displaystyle \sum _{i=1}^k}{\displaystyle {\int }_t^{t_{\text{max}}}}\frac{L^2(s)}{G_i^2(s)}d{\mathrm{N̄}}_i(s)={\displaystyle \sum _{T_{\mathit{\text{ij}}}\ge t}}\frac{L^2(T_{\mathit{\text{ij}}})}{G_i^2(T_{\mathit{\text{ij}}})}+{\displaystyle \sum _{i=1}^k}{\displaystyle \sum _{T_{\mathit{\text{ij}}}\ge t}}\frac{L^2(T_{\mathit{\text{ij}}})}{G_i^2(T_{\mathit{\text{ij}}})}.$$

Theorem 18. Assume that there exists sequences of constants {a_n} and {c_n} such that,

$$\underset{n\to \mathrm{\infty }}{\text{lim}}{a}_n=\underset{n\to \mathrm{\infty }}{\text{lim}}{c}_n=\mathrm{\infty }\mathit{\text{ and}}$$

$$\frac{L^{(n)}(s)}{c_n}\stackrel{P}{\to }l(s)<\mathrm{\infty },\frac{G_r^{(n)}(s)}{a_n^2}\stackrel{P}{\to }{g}_r(s)<\mathrm{\infty },$$

$$\frac{G_i^{(n)}(s)}{a_n^2}\stackrel{P}{\to }{g}_i(s)<\mathrm{\infty }.$$

Further, assume that there exists some function d(s) such that for all δ,

$$\underset{n\to \mathrm{\infty }}{\text{lim inf }}\text{Pr}\left\{{(a_n/c_n)}^2{(L^{(n)}(s))}^2\left(\frac{1}{G_r}+{\displaystyle \sum _{i=1}^k}\frac{1}{G_i}\right)\le d(s)\mathit{\text{ for all }}s\in 𝒯\right\}\ge 1-\delta .$$

Then (a_n/c_n)Z_AND⁽ⁿ⁾ converges in distribution to a zero mean Gaussian process as the number of response times used in the estimate increases.

Proof.

$$\langle \frac{a_n}{c_n}{{\mathrm{Z}}_{\text{AND}}}^{(n)}\rangle =\langle {\displaystyle {\int }_t^{t_{\text{max}}}}\frac{a_n}{c_n}\frac{L^{(n)}(s)}{G_r^{(n)}(s)}d{\mathrm{M̄}}_r^{(n)}(s)+{\displaystyle \sum _{i=1}^k}{\displaystyle {\int }_t^{t_{\text{max}}}}\frac{a_n}{c_n}\frac{-L^{(n)}(s)}{G_i^{(n)}(s)}d{\mathrm{M̄}}_i^{(n)}(s)\rangle ={\displaystyle {\int }_t^{t_{\text{max}}}}\frac{a_n^2}{c_n^2}\frac{{\left(L^{(n)}(s)\right)}^2}{{\left(G_r^{(n)}(s)\right)}^2}{G}_r^{(n)}(s){\alpha }_r(s)\mathit{\text{ ds}}+{\displaystyle \sum _{i=1}^k}{\displaystyle {\int }_t^{t_{\text{max}}}}\frac{a_n^2}{c_n^2}\frac{{\left(L^{(n)}(s)\right)}^2}{{\left(G_i^{(n)}(s)\right)}^2}{G}_i^{(n)}(s){\alpha }_i(s)\mathit{\text{ ds}}={\displaystyle {\int }_t^{t_{\text{max}}}}{\left(\frac{L^{(n)}(s)}{c_n}\right)}^2\left(\frac{a_n{\alpha }_r(s)}{G_r^{(n)}(s)}+{\displaystyle \sum _{i=1}^k}\frac{a_n{\alpha }_i(s)}{G_i^{(n)}(s)}\right)\mathit{\text{ ds}}.$$

Hence, from the assumptions and by the dominated convergence theorem,

$$\langle \frac{a_n}{c_n}{{\mathrm{Z}}_{\text{AND}}}^{(n)}\rangle \stackrel{P}{\to }{\displaystyle {\int }_t^{t_{\text{max}}}}{l}^2(s)\left(g_r(s){\alpha }_r(s)+{\displaystyle \sum _{i=1}^k}{g}_i(s){\alpha }_i(s)\right)\mathit{\text{ ds}}<\mathrm{\infty }.$$

The second condition holds because for all s ∈ [t, t_max],

$$\frac{a_{n}L(s)}{c_n{G}_r(s)}\stackrel{P}{\to }0\text{ and }\frac{a_{n}L(s)}{c_n{G}_i(s)}\stackrel{P}{\to }0\text{ for all }i.$$

Therefore, the conclusion follows from the reverse martingale central limit theorem.