Efficient Moment Matrix Generation for Arbitrary Chemical Networks

Abstract

As stochastic simulations become increasingly common in biological research, tools for analysis of such systems are in demand. The deterministic analogue to stochastic models, a set of probability moment equations equivalent to the Chemical Master Equation (CME), offers the possibility of a priori analysis of systems without the need for computationally costly Monte Carlo simulations. Despite the drawbacks of the method, in particular non-linearity in even the simplest of cases, the use of moment equations combined with moment-closure techniques has been used effectively in many fields. The techniques currently available to generate moment equations rely upon analytical expressions that are not efficient upon scaling. Additionally, the resulting moment-dependent matrix is lower diagonal and demands massive memory allocation in extreme cases. Here it is demonstrated that by utilizing factorial moments and the probability generating function (the Z-transform of the probability distribution) a recursive algorithm is produced. The resulting method is scalable and particularly efficient when high-order moments are required. The matrix produced is banded and often demands substantially less memory resources.

1. Introduction

Stochastic simulations are becoming an increasingly popular tool in biological modeling and simulation due to the tendency of such systems to lie far from the thermodynamic limit (Kaznessis, 2006; Tuttle et al., 2005). This condition, common when only a handful of reactants exist in a system, renders deterministic models inaccurate (Gillespie, 1992a). The primary problem with stochastic simulations is the mathematical intractability of the govering equation, the Chemical Master Equations (CME), that makes analysis particularly difficult (Jahnke and Huisinga, 2007). The motivation for the following work is to propose and provide an efficient tool to be used in analysis of stochastic systems potentially without the need of the costly kinetic Monte Carlo sampling employed by the Gillespie Stochastic Simulation Algorithm (SSA) or its derivatives (Gillespie, 1992b; Li et al., 2008; Salis and Kaznessis, 2005; Gibson and Bruck, 2000).

An analogue to the CME proposed initially by Mc-Quarrie, among others, is the use of time differentials of the moments of the probablility distribution (McQuarrie et al., 1964). In principle, this deterministic analogue allows for system analysis without the need for Monte Carlo sampling. Such methods are in use, but predominantly in smaller systems like simple transient gene activation (Zechner et al.). While the moment viewpoint has not been applied to larger systems, the hope is that this work will facilitate this research by making matrix construction a quick and simple step. In particular, because biological systems often contain unknown or inaccurate kinetic constants, our hope is that this work can aid in more easily fitting such constants to experimental output. Traditionally, these constants are fit by running many Monte Carlo simulations and can take enormous computational time.

Complications arise when 2nd-order reactions are included in a chemical network. In such cases lower-order moments explicitly depend on higher-order moments, necessitating an infinitely large matrix (Gómez-Uribe and Verghese, 2007). The production and analysis of closure schemes for these open systems is an active area of research across several fields (Singh and Hespanha, 2006, 2011; Grima, 2012; Lee et al., 2009; Engblom, 2006). What is not often considered is the generation of the moment equations necessary once a particular closure scheme is chosen. Such sets of equations can become enormous considering that reproducing probability distributions accurately for complex systems have been shown to require as many as eight moments (Sotiropoulos and Kaznessis, 2011). Recent publications provide analytical solutions for the moment equations (Sotiropoulos and Kaznessis, 2011; Gillespie, 2009), but do not touch on the scaling problems or memory allocation of such systems.

The current work focuses on the efficient generation of a concise set of moment equations for arbitrary chemical networks. It should be noted that the method, as described, only works with elementary rate laws with integer stoichiometry. The method utilizes factorial moments (indicated by curly brackets {·}) instead of traditional polynomial moments (indicated by angled brackets 〈 · 〉) to conserve memory allocation. Factorial and polynomial moment formulation are entirely equivalent basis sets. The use of the probability generation function, the Z-transform of a probability distribution, also allows for a recursive algorithm as the moment equations are produced by the systematic differentiation of the Z-transformed CME (Z-CME). The results demonstrate the reduced memory load, reduced bandwidth, and computational efficiency in several example systems.

2. Theory

The traditional approach to chemical kinetic modeling is deterministic in nature. Stochastic models reframe chemical kinetics to take into account the randomness inherent to systems far from the thermodynamic limit. This viewpoint requires probability-based mathematics developed by McQuarrie, Van Kampen, Gardiner, and Gillespie, among others (McQuarrie et al., 1964; Gardiner, 1985; Gillespie, 1977; Van Kampen, 1992). The theory presented here focuses on Markov processes, the CME along with its Z-transform analogue, and the moment viewpoint of chemical reaction dynamics. The primary novel work is an alternative formulation of the moment equations for arbitrary chemical networks, including the unclosed matrices for systems with bimolecular reactions. The algorithm produces both the traditional and factorial moment equation matrix for either numerical or symbolic kinetic reaction rates for any desired order of moments.

2.1. Markov Processes and the Chemical Master Equation

For a stochastic process to be a Markov process the current state, x_n at time t_n, must be fully determined by the previous state, x_n−1 at time t_n−1. This condition is often called a “memoryless” condition, where the memory of states prior to the current state have no effect on the future dynamics. In the particular case of chemical kinetic systems the time scale is considered continuous, but the state space can be either continuous or discrete. Herein, the state space is considered to be strictly discrete by viewing the state X = [x₀, x₁, …, x_n]′ as a set of the number of molecules for each of the n chemical species. The state exists within a volume, O, that is well mixed to eliminate diffusive effects.

For stochastic processes the state can be described by a probability distribution P (X; t) at a given time t. This distribution is a continuous, bounded, n-dimensional, real-valued function. Given the Markov condition, the change in the probability distribution in time can thus be described generally by:

$$P(\underset{\_}{X};t+\delta t)=\left(1-\sum _{\underset{\_}{X^{\prime }}}T(\underset{\_}{X^{\prime }}\mid \underset{\_}{X})\delta t\right)P(\underset{\_}{X};t)+\sum _{\underset{\_}{X^{\prime }}}T(\underset{\_}{X}\mid \underset{\_}{X^{\prime }})\delta tP(\underset{\_}{X^{\prime }};t)$$ (1)

where X is the current state, X′ is any state that is not X, and T (Y|X) is the transition probability from state X to Y as a Poisson distributed event. By rearrangement one can reach what is known as the Chemical Master Equation (CME) for a discrete state space:

$$\frac{\partial P(\underset{\_}{X};t)}{\partial t}=\sum _{\underset{\_}{X^{\prime }}}[T(\underset{\_}{X}\mid \underset{\_}{X^{\prime }})P(\underset{\_}{X^{\prime }};t)-T(\underset{\_}{X^{\prime }}\mid \underset{\_}{X})P(\underset{\_}{X};t)]$$ (2)

The transition probability is a catch-all for any event that may bring the system into or out of a given state. In chemical kinetics these events will be reactions and thus the transition probabilities are equivalent to reaction propensities. For the general reaction $aA+bB\stackrel{k_{\mu }}{\to }cC+dD$ the propensity for a reaction event to occur is:

$$a_{\mu }(\underset{\_}{X})=k_{\mu }\left(\begin{array}{c}{x}_A\\ a\end{array}\right)\left(\begin{array}{c}{x}_B\\ b\end{array}\right)$$ (3)

Here x_A is the number of molecules of A in the system, and x_B is the number of molecules of B. Thus Equation 2 can be reformulated as a sum over the set of reactions in a chemical network:

$$\frac{\partial P(\underset{\_}{X};t)}{\partial t}=\sum _{\mu }\left[a_{\mu }\left(\underset{\_}{X}-\underset{\_}{{\nu }_{\mu }}\right)P\left(\underset{\_}{X}-\underset{\_}{{\nu }_{\mu }};t\right)-a_{\mu }(\underset{\_}{X})P(\underset{\_}{X};t)\right]$$ (4)

Here ν_μ is the stoichiometic vector for reaction μ. The CME is an equation which perfectly describes the time dynamics of any stochastic chemical network given an initial condition. The problem is that, except for a select few simple equations, analytically solving such a system is mathematically intractable.

To fully describe a system by probability states Equation 4 would form an infinite set of ODEs. Analysis is predominately performed using the Z-CME, the CME in terms of the probability generating function (Z-transform). The Z-transform is formed by a simple change of variables:

$$G(\underset{\_}{S};t)=\sum _{x_0=0}^{\infty }\sum _{x_1=0}^{\infty }\cdots \sum _{x_n=0}^{\infty }{s}_0^{x_0}{s}_1^{x_1}\cdots s_n^{x_n}P(\underset{\_}{X};t)$$ (5)

The vector S = [s₀, s₁, …, s_n]′ represents the continuous transform variables for an n-component system. The Z-transform simplifies the system by transforming from discrete space (X) to a continuous space (S).

The Z-CME is thus formed by mathematical manipulation of Equation 4:

$$\frac{\partial G(\underset{\_}{S};t)}{\partial t}=\sum _{\mu }\frac{k_{\mu }}{{\prod }_{i=1}^n{\nu }_{i,\mu }^{+}!}\left[\prod _{i=1}^n{s}_{i,\mu }^{{\nu }_{i,\mu }^{-}}-\prod _{i=1}^n{s}_{i,\mu }^{{\nu }_{i,\mu }^{+}}\right]\frac{{\partial }^{{\sum }_{i=1}^n{\nu }_{i,\mu }^{+}}G(\underset{\_}{S};t)}{\partial {\prod }_{i=1}^n{s}_{i,\mu }^{{\nu }_{i,\mu }^{+}}}$$ (6)

Here k_μ is modified since the differential creates permutations instead of combinations. Thus k_μ must be divided by the appropriate factorials. Also ${\nu }_{i,\mu }^{+}$ refers to product stoichiometries whereas ${\nu }_{i,\mu }^{-}$ refers to reactant stoichiometries. Both are strictly positive constants. This formulation may appear daunting, but is extremely simple to implement for any arbitrary chemical system with polynomial reaction rates (not non-linear rates). To make things clearer the Z-CME for a system with one general reaction $aA+bB\stackrel{k_1}{\to }cC+dD$ is:

$$\frac{\partial G(\underset{\_}{S};t)}{\partial t}=\frac{k_1}{a!·b!}[s_C^c{s}_D^d-s_A^a{s}_B^b]\frac{{\partial }^{a+b}G(\underset{\_}{S};t)}{\partial s_A^a\partial s_B^b}$$ (7)

The advantages of using the Z-CME will become clear after a brief discussion of different types of moments available to form the full moment equation matrix.

2.2. Moments and Factorial Moments

Moments are expected values that describe properties of a probability distribution. The common examples are the mean (first moment) and the variance (related to the second moment). For a molecular system the distribution is defined on the positive integer line. The polynomial moments are:

$$\langle x_1^{m_1}·x_2^{m_2}\cdots x_n^{m_n}\rangle =\sum _{x_1=0}^{\infty }\sum _{x_1=0}^{\infty }\cdots \sum _{x_1=0}^{\infty }{x}_1^{m_1}·x_2^{m_2}\cdots x_n^{m_n}·P(\underset{\_}{X};t)$$ (8)

When more than one chemical species has an order greater than zero these are known as joint moments. The order of the moment is defined by m = m₁ + m₂ + … m_n. While many distributions can be described primarily by low-order moments (m equals one or two), more complex systems can require as many as eight or ten moments to adequately reproduce the probability distribution (Sotiropoulos and Kaznessis, 2011).

The literature concerning moment equations and closure schemes has focused on the traditional set of polynomial moments (Gillespie, 2009; Sotiropoulos and Kaznessis, 2011; Singh and Hespanha, 2011), but any moment basis set is valid when describing a probability distribution. The following work utilizes factorial moments, an equivalent basis set. As will be shown shortly this has to do with the relationship between the Z-CME and the moments of a distribution. The factorial moments are defined as:

$$\{x_1^{m_1}·x_2^{m_2}\cdots x_n^{m_n}\}=\sum _{x_1=0}^{\infty }\sum _{x_1=0}^{\infty }\cdots \sum _{x_1=0}^{\infty }{(x_1)}_{m_1}·{(x_2)}_{m_2}\cdots {(x_n)}_{m_n}·P(\underset{\_}{X};t)$$ (9)

The form (x_i)_mi refers to the m_i-permutation of the variable x_i: (x₁)₂ = x₁ (x₁ − 1), (x₁)₃ = x₁ (x₁ − 1) (x₁ − 2), etc. The Z-transform of a distribution relates to the factorial moments as follows:

$$\begin{array}{l}G(\underset{\_}{S};t){\mid }_{\underset{\_}{S}=\underset{\_}{1}}=1\\ {\frac{\partial G(\underset{\_}{S};t)}{\partial s_i}|}_{\underset{\_}{S}=\underset{\_}{1}}=\{x_i\}\\ {\frac{{\partial }^{2}G(\underset{\_}{S};t)}{\partial s_i^2}|}_{\underset{\_}{S}=\underset{\_}{1}}=\{x_i^2\}\end{array}$$ (10)

Using the factorial moment basis there is a simple way to obtain the full set of factorial moment equations that has not been previously considered. By starting at the Z-CME (Equation 6) and then systematically differentiating by the elements of the S vector then setting S = 1 one can obtain the time derivatives for any factorial moment desired.

2.3. Matrix Equation Production

The analytical derivation of polynomial moment equations has been previously developed by several authors (Gillespie, 2009; Sotiropoulos and Kaznessis, 2011). The novelty of the following approach is that the described method lends itself to efficient regression. Higher-order moments are formed by applying an additional differentiation to a lower-order moment. In this way there is no need to re-derive information previously determined to form lower-order moments, thus saving substantial computational time. What is often not taken into consideration when producing a full analytical expression of moment equations is that it is almost never the case where only a select few moments are required. Typically, a system will require all moments up to a specific order (denoted as M throughout this paper). Providing an analyical expression does not provide an efficient way to fill a matrix of moment equations when all moments up to order M are necessary.

To expand on this last point a bit further, the available moment equation generation techniques exclusively rely on and provide an analytical equation for general moment equations (Gillespie, 2009; Sotiropoulos and Kaznessis, 2011). Sotriopoulos provided the following equation:

$$\frac{\partial \langle X_1^{m_1}{X}_2^{m_2}\cdots X_N^{m_N}\rangle }{\partial t}=\sum _{j_1,j_2,\dots ,j_N=0}^{m_1,m_2,\dots ,m_N}\left(\begin{array}{c}{m}_1{j}_1\end{array}\right)\left(\begin{array}{c}{m}_2\\ j_2\end{array}\right)\cdots \left(\begin{array}{c}{m}_N\\ j_N\end{array}\right)\times \langle X_1^{m_1-j_1}{X}_2^{m_2-j_2}\cdots X_N^{m_N-j_N}{a}_{j_1+j_2+\cdots +j_N}(\underset{\_}{X})\rangle$$ (11)

where

$$a_{j_1+j_2+\cdots +j_N}(\underset{\_}{X})=\sum _{k=1}^M\left[\prod _{i=1}^N{\nu }_{ik}^{j_i}\right]a_k(\underset{\_}{X})$$ (12)

Here a_k (X) is the propensity of reaction k given the current state X, and ν_ik is the stoichiometry of component i for reaction k.

There are three issues with this formulation. First, the summation is of indeterminate size. When there are N components there are N summations. When building a matrix generation program for any number of components not knowing how many for-loops are needed may be a problem in implementation. Second, the propensity term, $a_{j_1+j_2+\cdots +j_N}^{\mathit{index}}(\underset{\_}{X})$, does not have a computationally friendly form. Rather, it is a complex equation with multiple binomial terms and stoichiometric considerations (Equations 22 and 29 in Sotiropoulos and Kaznessis (2011)). Finally, as mentioned above, there is information waste in construction of the moment matrix that becomes costly as the number of components and moments increase. Note that the analytical form is not recursive: there is no intutive way to construct the higher-order moments from the moment equations previously determined. The proposed method may not provide an analytical equation for the moment equations, but by utilizing the Z-CME and factorial moments it does avoid this last problem in particular to produce an efficient recursive algorithm.

Using the Z-CME differentials can produce the moment equations. A quick application to Equation 7 illustrates this point. The left side of the equation is simple:

$${\frac{\partial }{\partial s_A}\frac{\partial G(\underset{\_}{S};t)}{\partial t}|}_{\underset{\_}{S}=\underset{\_}{1}}={\frac{\partial }{\partial t}\frac{\partial G(\underset{\_}{S};t)}{\partial s_A}|}_{\underset{\_}{S}=\underset{\_}{1}}=\frac{\partial \{A\}}{\partial t}$$

The full transformed equation before simplification is:

$$\frac{\partial \{A\}}{\partial t}={\left[-\frac{k_1}{a!·b!}[a·s_A^{a-1}{s}_B^b]\frac{{\partial }^{a+b}G(\underset{\_}{S};t)}{\partial s_A^a\partial s_B^b}+\frac{k_1}{a!·b!}[s_C^c{s}_D^d-s_A^a{s}_B^b]\frac{{\partial }^{a+b+1}G(\underset{\_}{S};t)}{\partial s_A^{a+1}\partial s_B^b}\right]|}_{\underset{\_}{S}=\underset{\_}{1}}$$

The reduced form then contains a single term:

$$\frac{\partial \{A\}}{\partial t}=-\frac{k_1}{(a-1)!·b!}\{A^a{B}^b\}$$ (13)

Taking the middle expression above it is easy to then produce ∂_t {A²} by applying a second differential. The final expression would be:

$$\frac{\partial \{A^2\}}{\partial t}=-\frac{k_1}{(a-2)!·b!}\{A^a{B}^b\}-2·\frac{k_1}{(a-1)!·b!}\{A^{a+1}{B}^b\}$$ (14)

This method is applicable to any arbirary set of chemical reactions.

A concern when producing moment matrices and moment closure schemes is a standardized and efficient indexing scheme for moments. Here it is proposed that the ideal indexing will achieve one main goal: keep the system as banded as possible. In the case of factorial moments the easiest way to band the matrix is to keep the moments of order-m together. In elementary chemical systems the stoichiometry of a chemical component in a reaction will rarely exceed an absolute value of two. In these cases then the factorial moment equations of order-m will only depend on the moments of order-(m−1), order-m, or order-(m+1). This tends to create systems with lower bandwidths. The only other consideration would be to put chemical species which are not involved in any common reactions apart. Within each order the moments are simply indexed in descending order for each of the components. For example, with three components the third-order moments are ordered: [ $\langle x_1^3\rangle ,\langle x_1^2{x}_2\rangle ,\langle x_1^2{x}_3\rangle ,\langle x_1{x}_2^2\rangle ,\langle x_1{x}_2{x}_3\rangle ,\langle x_1{x}_3^2\rangle ,\langle x_2^3\rangle ,\langle x_2^2{x}_3\rangle ,\langle x_2{x}_3^2\rangle ,\langle x_3^3\rangle$].

The final point to make is how the factorial moment matrix produced here relates to the polynomial moment matrix typically considered in the literature. The factorial moment matrix essentially takes the form:

$$\frac{\partial \{·\}}{\partial t}=M_f·\{·\}$$ (15)

The form {·} represents a vector containing all factorial moments up to order M. The number of moments up to order-M for N components is the same as the number of terms in a general polynomial with N variables and up to order-M:

$$\text{Number}\text{of}\text{Terms}=\frac{(N+M)!}{N!·M!}$$ (16)

Therefore, a system with four components, as decribed above, with eight moments would require 495 rows. The number of columns depends on the highest order reaction, but will be at least as much. This matrix can be quite large, especially when there is a large number of components involved in a system.

The polynomial matrix takes the same form and is the same size:

$$\frac{\partial \langle ·\rangle }{\partial t}=M·\langle ·〉$$ (17)

The polynomial moments and factorial moments are related through a similarity tranform. This means they have the same eigenvalues, just in a different basis set:

$$M_f=T^{-1}·M·T$$ (18)

The creation of this transform matrix T is rather simple and thus the programs provided are able to produce M_f and M, whichever is preferred.

3. Results and Examples

In the following section three examples of varying complexity and size are presented to show the primary advantages of the Z-CME approach. The algorithm used to produce the matrices of interest is written in Matlab. The matrices can be output for both numerical and symbolic kinetic constants. The main advantages claimed for the algorithm is speed, especially when producing high-order moments, and a reduced bandwidth and memory load in most cases. The three examples will be a simple reversible dimerization (2A ↔ B), a Michaelis-Menten system (S+E ↔ S : E → E + P), and a gene regulatory network model (9 components, 10 reactions). In all cases the matrices provided will utilize symbolic kinetic constants. In order to provide a better estimate of computational efficiencies, generation times are provided for these three matrices for the recursive algorithm, an equivalent non-recursive algorithm, and for the python code described by Gillespie (Gillespie, 2009). These represent a non-analytic recursive algorithm, a non-analytic non-recursive algorithm, and an analytic algorithm, respectively. We should stress that a direct comparison could not be rigorously developed and is of limited use, but we present these CPU times only to provide a sense of the computational efficiencies gained.

3.1. Reversible Dimerization

In reversible dimerization two monomers (A) combine in a second-order monomolecular reaction to form a dimer (B). This dimer can then split apart to reform the monomer bases. This reaction network is one of the simplest nonlinear systems available with only two reactions and two components. The network and Z-CME are as follows:

$$\begin{array}{c}2·A\stackrel{k_1}{\to }B\\ B\stackrel{k_2}{\to }2·A\\ \frac{\partial G(s_A,s_B;t)}{\partial t}=k_1(s_B-s_A^2)\frac{{\partial }^{2}G(s_A,s_B;t)}{\partial s_A^2}+k_2(s_A^2-s_B)\frac{\partial G(s_A,s_B;t)}{\partial s_B}\end{array}$$ (19)

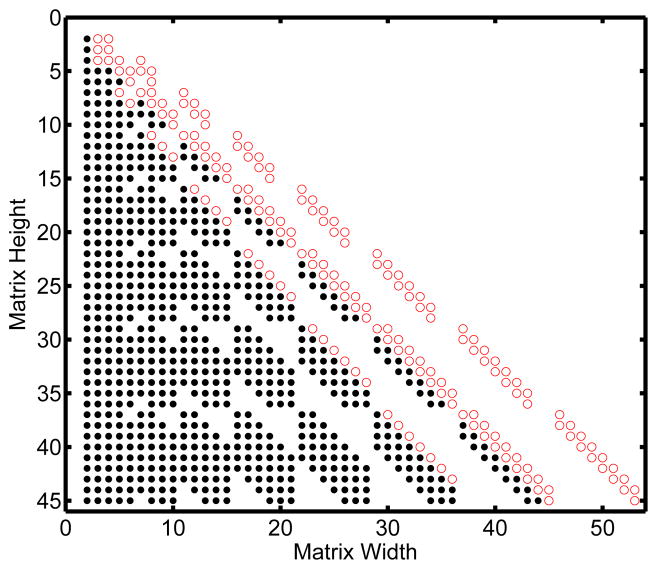
Table 1 and Table 2 show M_f and M respectively for the moment equations up to order-2. For the recursive algorithm the generation time for eight moments is on average 0.0502 seconds. This is compared to 0.962 seconds for the non-recursive version and 18.3 seconds for the code provided by Gillespie (Gillespie, 2009). Figure 1 highlights the non-zero entries in the factorial moment matrix compared to the polynomial moment matrix for 8 moments. In all cases the factorial moment matrix will have at most as many non-zero entries as the polynomial moment matrix. Here there are 179 non-zero entres for the factorial moment case and 846 non-zero entries for the polynomial moment case. The factorial moment matrix will also have a smaller bandwidth in all cases. The bandwidth for the factorial moment matrix is 16 (7 left bandwidth, 9 right bandwidth), and for the polynomial matrix is 52 (43 left bandwidth, 9 right bandwidth).

Table 1.

Moment Matrix for Dimerization - Factorial

	{A}	{B}	{A2}	{AB}	{B2}	{A3}	{A2B}
$\frac{\partial \{1\}}{\partial t}$	0	0	0	0	0	0	0
$\frac{\partial \{A\}}{\partial t}$	0	2k2	−2k1	0	0	0	0
$\frac{\partial \{B\}}{\partial t}$	0	−k2	k1	0	0	0	0
$\frac{\partial \{A^2\}}{\partial t}$	0	2k2	−2k1	4k2	0	−4k1	0
$\frac{\partial \{AB\}}{\partial t}$	0	0	0	−k2	2k2	k1	−2k1
$\frac{\partial \{B^2\}}{\partial t}$	0	0	0	0	− 2k2	0	2k1

Table 2.

Moment Matrix for Dimerization - Polynomial

	〈A〉	〈B〉	〈A2〉	〈AB〉	〈B2〉	〈A3〉	〈A2B〉
$\frac{\partial \langle 1\rangle }{\partial t}$	0	0	0	0	0	0	0
$\frac{\partial \langle A\rangle }{\partial t}$	2k1	2k2	−2k1	0	0	0	0
$\frac{\partial \langle B\rangle }{\partial t}$	−k1	−k2	k1	0	0	0	0
$\frac{\partial \langle A^2\rangle }{\partial t}$	−4k1	4k2	8k1	4k2	0	−4k1	0
$\frac{\partial \langle AB\rangle }{\partial t}$	2k1	−2k2	−3k1	2k1 − k2	2k2	k1	−2k1
$\frac{\partial \langle B^2\rangle }{\partial t}$	−k1	k2	k1	−2k1	−2k2	0	2k1

Figure 1.

Matrix Form For Reversible Dimerization

Comparison of the matrix form for the factorial moment equations and polynomial moment equations for reversible dimerization up to eight moments. The non-zero entries present in both matrices are represented by red empty circles, while the non-zero entries present only in the polynomial matrix are represented by black dots.

It should be noted that the system as described has a single degree of freedom since 2 · B = 2 · B₀ + A₀ − A, and thus the matrix could be reduced to include only the moments of A as a simplification.

3.2. Michaelis-Menten Network

The Michaelis-Menten reaction system is comprised of three reactions. First a substrate (S) complexes with an enzyme (E) to form a complex (S:E). Then the complex either degrades back to its original components or a product is formed (P). The network has four components and three reactions:

$$\begin{array}{l}S+E\stackrel{k_1}{\to }E:S\\ E:S\stackrel{k_2}{\to }S+E\\ E:S\stackrel{k_3}{\to }E+P\end{array}$$

This system has only two degrees of freedom. Using the following relations the system is reduced to two components (S and E): S + E : S + P = S_T and E + E : S = E_T. Using these relations the reduced Z-CME can be determined to be:

$$\frac{\partial G(\underset{\_}{S};t)}{\partial t}=k_1(1-s_S{s}_E)\frac{{\partial }^{2}G(\underset{\_}{S};t)}{\partial s_S\partial s_E}+k_2{E}_T(s_S{s}_E-1)G(\underset{\_}{S};t)-k_2(s_S{s^2}_E-s_E)\frac{\partial G(\underset{\_}{S};t)}{\partial s_E}+k_3{E}_T(s_E-1)G(\underset{\_}{S};t)-k_3({s^2}_E-s_E)\frac{\partial G(\underset{\_}{S};t)}{\partial s_E}$$ (20)

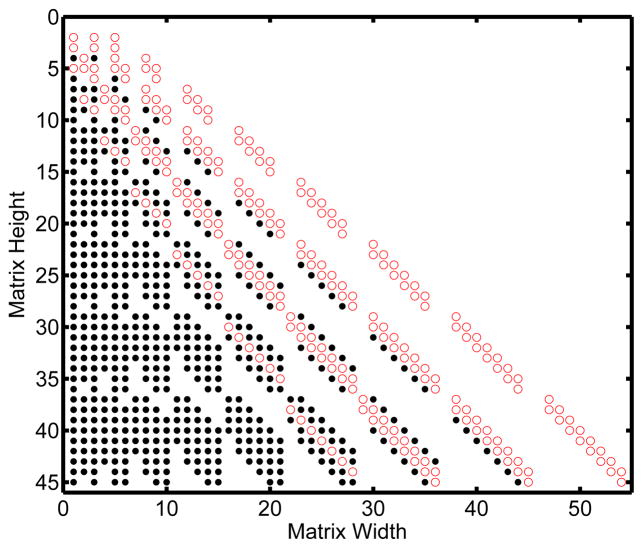
Table 3 and Table 4 show M_f and M respectively for the reduced Michaelis-Menten system up to order-2. For the non-reduced set of reactions the recursive algorithm generation time for eight moments is on average 0.126 seconds. This is compared to 21.9 seconds for the non-recursive version and 37.2 seconds for the code provided by Gillespie (Gillespie, 2009). Figure 2 highlights the non-zero entries in the factorial moment matrix compared to the polynomial moment matrix for 8 moments. There are 244 non-zero entires for the factorial moment case and 762 non-zero entries for the polynomial moment case. The bandwidth for the factorial moment matrix is 26 (16 left bandwidth, 10 right bandwidth), and for the polynomial matrix is 54 (44 left bandwidth, 10 right bandwidth).

Table 3.

Two Moment Matrix for Michaelis Menten System - Factorial

	{1}	{S}	{E}	{S2}	{S · E}	{E2}	{S3}	{S2 · E}	{S · E2}
$\frac{\partial \{1\}}{\partial t}$	0	0	0	0	0	0	0	0	0
$\frac{\partial \{S\}}{\partial t}$	ETk2	0	−k2	0	−k1	0	0	0	0
$\frac{\partial \{E\}}{\partial t}$	ET (k2 + k3)	0	−k2 − k3	0	−k1	0	0	0	0
$\frac{\partial \{S^2\}}{\partial t}$	0	2ETk2	0	0	−2k2	0	0	−2k1	0
$\frac{\partial \{S·E\}}{\partial t}$	ETk2	ET (k2 + k3)	(ET − 2) k2	0	−k1 − k2 − k3	−k2	0	−k1	−k1
$\frac{\partial \{E^2\}}{\partial t}$	0	0	2(ET − 1)(k2 + k3)	0	0	−2k2 − 2k3	0	0	−2k1

Table 4.

Two Moment Matrix for Michaelis Menten System - Polynomial

	〈1〉	〈S〉	〈E〉	〈S2〉	〈S · E〉	〈E2〉	〈S3〉	〈S2 · E〉	〈S · E2〉
$\frac{\partial \langle 1\rangle }{\partial t}$	0	0	0	0	0	0	0	0	0
$\frac{\partial \langle S\rangle }{\partial t}$	ETk2	0	−k2	0	−k1	0	0	0	0
$\frac{\partial \langle E\rangle }{\partial t}$	ET (k2+ k3)	0	−k2 − k3	0	−k1	0	0	0	0
$\frac{\partial \langle S^2\rangle }{\partial t}$	ETk2	2ET k2	−k2	0	k1 − 2k2	0	0	−2k1	0
$\frac{\partial \langle S·E\rangle }{\partial t}$	ETk2	ET (k2 + k3)	(ET − 1)k2	0	k1 − k2 − k3	−k2	0	−k1	−k1
$\frac{\partial \langle E^2\rangle }{\partial t}$	ET (k2 + k3	0	2(ET − 1)(k2 + k3)	0	k1	−2k2 − 2k3	0	0	−2k1

Figure 2.

Matrix Form For a Michaelis-Menten Network

Comparison of the matrix form for the factorial moment equations and polynomial moment equations for a Michaelis-Menten network up to eight moments. The non-zero entries present in both matrices are represented by red empty circles, while the non-zero entries present only in the polynomial matrix are represented by black dots.

3.3. Gene Network Model

While the previous two examples effectively show the memory conserving and bandwidth reducing advantages of the method, both were simple enough to require little time to complete. To demonstrate the final advantage, an ability to produce large matrices quickly, a larger network was chosen, that of a single gene model. The network consists of ten reactions involving nine components presented in Table 5.

Table 5.

Gene Network Model

DNA + RNAp	→	DNA:RNAp
DNA:RNAp	→	DNA + RNAp
DNA:RNAp	→	DNA + RNAp*
RNAp*	→	RNAp + mRNA
mRNA + rib	→	mRNA:rib
mRNA:rib	→	mRNA + rib
mRNA:rib	→	mRNA + rib*
rib*	→	rib + Product
mRNA	→	∅
Product	→	∅

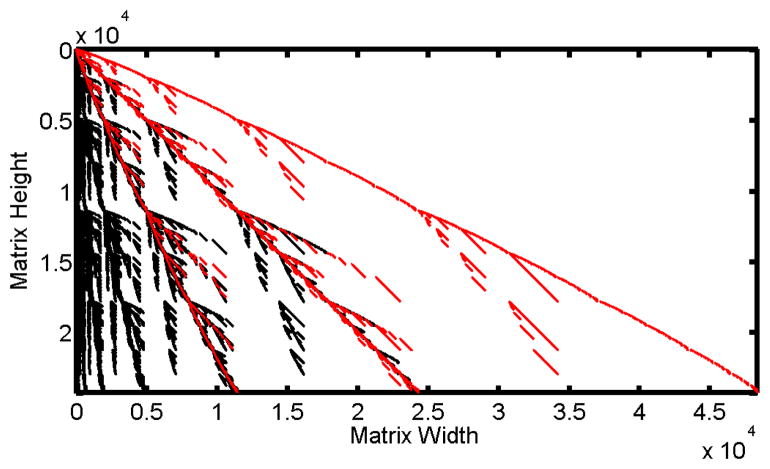
A two-moment matrix for nine components requires 55 rows and 194 columns. For the non-reduced set of reactions the recursive algorithm generation time for four moments is on average 0.251 seconds. This is compared to 12.8 seconds for the non-recursive version and 152.6 seconds for the code provided by Gillespie (Gillespie, 2009). For eight moments, the non-recursive and Gillespie’s code both run out of memory, but the recursive algorithm takes 105 seconds to complete. The Z-CME and two-moment matrix are not shown for size considerations. Figure 3 shows the non-zero entries for 8 moments. The factorial moment matrix is a 24310 by 48355 matrix, a staggeringly large matrix that pushes the memory limits of Matlab when produced. The program takes about two minutes to produce the symbolic matrix on a desktop computer The transform matrix is larger (48355 by 48355) and takes three minutes to produce. The number of non-zero en tires in the factorial moment matrix is 237299, whereas for the polynomial matrix there are 1439085 non-zero entries This matrix is far larger than what would be feasable for any type of computational method utilizing the moments of a stochastic simulation.

Figure 3.

Matrix Form For a Nine-Component Gene Network

Comparison of the matrix form for the factorial moment equations and polynomial moment equations for a nine component gene network up to eight moments. The non-zero entries present in both matrices are represented by red empty circles, while the non-zero entries present only in the polynomial matrix are represented by black dots.

4. Discussion

The first two reaction networks presented (Dimerization in Figure 1 and the Michaelis-Menten system in Figure 2) demonstrate advantages in bandwidth and memory allocation for the factorial moment matrix, M_f, compared to the polynomial moment matrix, M, present in the literature. In the dimerization system the factorial matrix is banded with three main bands corresponding to the (m−1)-order, m-order, and (m+1)-order moments. The polynomial moment matrix is nearly lower-triangular in nature and contains over five times as many non-zero entries. Similarly the Michaelis-Menten system has four main bands in the factorial moment matrix. The fourth band is an (m−2)-order moment resulting from the reduction using the conservation equation E + E : S = E_T. The polynomial moment matrix has about three times as many non-zero entries and is nearly lower triangular. Both systems take a negligible amount of time to produce up to order-eight moments. The important point is that the resulting matrix will have at most the same number of non-zero entries and bandwidth as the polynomial matrix, never more. As far as memory allocation and bandwidth reduction are concerned the factorial moment equations are unequivocally better than traditional polynomial moment equations in all elementary chemical networks. Although it would be obviously useful, we do not have a rigorous mathematical means for providing scaling arguments that show precisely how much sparser the factorial moment matrix is compared to the polynomial moment matrix or to what degree these matrices can take advantage of sparse algorithms.

The final system (Gene network, Figure 3) demonstrates the most impressive aspect of the method presented, its efficiency. The matrix produced is massive with over 10⁹ entries in the system, pushing the limit of memory allocation in many programs. The production of such a set of moment equations takes less than five minutes in total and shows that even in this extreme case the system does not require a prohibitively long period of time to run.

This final network also illustrates one of the drawbacks of utilizing the moments matrix in stochastic simulation for complex systems. Some systems will require four, six, or even eight moments to produce accurate results. For systems with, say, nine components this obviously becomes prohibitive in the analytical sense. The number of equations in deterministic systems scale O (N) where N is the number of components. On the other hand, the number of equations in stochastic systems will scale O (N^M) where M is the maximum order of moments. The work as presented shows that analysis using moment equations will have to take into careful consideration the number of components and valid moments necessary to produce accurate results.

5. Conclusion

The results provided in the previous section illustrate two main points: 1) The factorial moment basis produces a lower bandwidth and less memory intensive set of equations than the polynomial moment basis and in many cases should be preferentially chosen for analysis; 2) The use of the transforms of the CME (here the Z-CME, but other transforms could also be used) allow for efficient equation production through application within a recursive algorithm. These results show that for simple systems, and ignoring the closure problems still present in moment-based formulations, production of the set of equations necessary for analysis is not a time-consuming step.

Moment closure is the primary problem in the way of using such systems for stochastic analysis, and there is ongoing research in the area. The results as presented facilitate exploration of higher-order closure schemes. Such schemes are likely necessary in the case of complex probability systems, like bimodal systems, that are impossible to duplicate with anything less than six moments. Currently, it is not possible to compare the performance of polynomial moment matrices to the equivalent factorial moment matrices. Even with the proper algorithm, since current closure schemes are predominantly lower-order, there would likely not be significant improvement. We are working on a general purpose closure scheme that can be applied at any order and on arbitrary chemical networks that should facilitate the comparison of factorial moment matrices to their polynomial counterparts in the future.

Highlights.

• We show a method to efficiently generate Chemical Master Equation moment equations.

• The method uses a Z-transform of the Chemical Master Equation.

• The moment equations in the form of matrices of three example cases are generated.

• Very large matrices are produced quickly and the resulting matrix is banded.

• The method opens up avenues for research into high-order closure methods.