Optimal Nonbipartite Matching and Its Statistical Applications

Abstract

Matching is a powerful statistical tool in design and analysis. Conventional two-group, or bipartite, matching has been widely used in practice. However, its utility is limited to simpler designs. In contrast, nonbipartite matching is not limited to the two-group case, handling multiparty matching situations. It can be used to find the set of matches that minimize the sum of distances based on a given distance matrix. It brings greater flexibility to the matching design, such as multigroup comparisons. Thanks to improvements in computing power and freely available algorithms to solve nonbipartite problems, the cost in terms of computation time and complexity is low. This article reviews the optimal nonbipartite matching algorithm and its statistical applications, including observational studies with complex designs and an exact distribution-free test comparing two multivariate distributions. We also introduce an R package that performs optimal nonbipartite matching. We present an easily accessible web application to make nonbipartite matching freely available to general researchers.

1. INTRODUCTION

A major goal of many empirical studies in the health and social sciences is to evaluate the causal effect of an intervention, such as a medical treatment or a policy change. The ideal setup for conducting causal inference is a well-executed randomized experiment (Shadish, Clark, and Steiner 2008). However, random allocation of participants to treatments is often not feasible due to practical or ethical reasons, and observational studies have to be performed instead. For example, in most smoking cessation studies, participants are given the option to choose the treatment they would like to receive. In this case, participants who choose the treatment may differ from those who choose the control condition. Lack of adequate controls for treated participants often leads to biased treatment effect estimation, where the observed effect may be due, in part, to selection effects.

Matching is a popular approach to guard against such selection bias (Cochran and Chambers 1965). It classifies participants into homogeneous groups or strata according to certain criteria, such that the individuals within the same matched groups were comparable before they received a treatment. Provided the probability of treatment is influenced only by variables balanced through matching, the difference in their outcomes provides an unbiased estimate of the treatment effect. Matching is appealing for adjusting for measured confounding in observational studies for several reasons. First, well-matched sets provide easily interpretable analyses. Second, it draws the attention of the users to the covariate balance between matched groups to understand the limits of the analysis. Third, some matched analyses do not need the parametric assumptions required by most regression methods. Fourth, matching that produces nonoverlapped pairs (matching without replacement) maintains an independent structure and thus enables the proper use of the existing statistical inference methods (Hansen and Klopfer 2006). Fifth, the matching process itself does not use the outcome variable information, preventing inappropriate manipulation of the data. Matching-based analysis has been widely applied in various fields, including health care research, sociology, economics, business, and political science (see, e.g., Smith 1997; Dehejia and Wahba 1999; Harding 2003; Ho et al. 2007; Armstrong, Jagolinzer, and Larcker 2009).

Most of the existing matching methods in the literature are bipartite matching methods, which are adequate for simple designs with only two treatment options such as one treatment group and one control group. In many practical studies, however, participants may have the option to receive multiple different treatments. For example, in a study to investigate the influence of in-pregnancy smoking cessation, participants voluntarily go through one of the three treatments—standard care, a combination of enhanced counseling and self-help manual, and a combination of enhanced counseling and an interactive computer program (Aveyard et al. 2005). To conduct causal inference in studies with multiple treatment groups, nonbipartite matching methods have been proposed. However, in contrast to the extensive discussions on bipartite matching methods in the statistical literature (see Gu and Rosenbaum 1993; Ming and Rosenbaum 2001; Hansen 2004), the discussions on nonbipartite matching have been scarce. Moreover, as far as we know, there is no publicly available statistical software package to conduct nonbipartite matching.

The major thrust of this article is to provide a comprehensive description of the nonbipartite matching method, including clarifying its association to bipartite matching and introducing an optimal nonbipartite matching algorithm; and to demonstrate its applications in statistical analysis, including performing causal inference in observational studies with complex designs and conducting an exact distribution-free test between two multivariate distributions. Moreover, we implement this optimal nonbipartite matching algorithm in R, create a freely available R package, and provide an easily accessible web application for researchers in various scientific fields.

The article is organized as follows. In Section 2, we introduce general matching methodology and optimal nonbipartite matching. In Section 3, we discuss the applications of optimal nonbipartite matching in statistical analysis with various designs. Then in Section 4, we propose a new R package for conducting optimal matching and illustrate its implementation through an observational study on a media campaign. Finally, we summarize the major contributions of the article and discuss possible extensions.

2. OPTIMAL NONBIPARTITE MATCHING

2.1 The Basic Idea of Matching and Optimal Matching

In this subsection, we demonstrate the basic idea of matching methodology. To make the demonstration easier, we consider a simple design with only one treatment group and one control group. Matching in more complex designs will be discussed in the next subsection.

In graph-theoretic terminology, a graph consists of nodes and edges between nodes, usually denoted by G = (V, E), where V = {v_i, i = 1,…, n} denotes the set of nodes and E = {[v_i, v_j], v_i, v_j ∈ V } denotes the set of edges. In statistical applications, we may call each individual unit of interest a node; for example, in medical research, a node could be a hospital, a patient, or a cell line. A matching of a graph is a set of distinctive edges with no shared nodes. Denoted by M, a matching is a collection of paired nodes {[v_i, v_j]} between which an edge exists and each node can appear at most once. A matching is called complete or perfect if the cardinality of M is ⌋|V |/2⌊, which is the largest integer not greater than |V |/2 (|V | denotes the number of nodes in the graph). If |V | is an even number, a complete matching would cover all nodes in the graph.

In a two-group setup, we would match one node from the treatment group with one node from the control group, and represent this match by an edge in the graph. We could also evaluate the “closeness” of the matched nodes by assigning nonnegative weights to the matches. The weights can be calculated as the distance between units based on the available covariates information in a study, such as age difference, |age_i – age_j |. If each node has k ≥ 2 covariates, an appropriate distance measure in k-dimensional space may be chosen. Of course, for any two groups there could be numerous ways of matching. To evaluate the causal effect of a treatment, we would like to create homogenous pairs in which the two individual units have similar pretreatment covariates, and thus the outcome difference between the treatment group and the control group must be due to the treatment, provided that there is no unmeasured confounding. Therefore, matched pairs with smaller distance are preferable.

A traditional algorithm to create such pairs is the greedy matching algorithm (Rubin 1973). Using this algorithm, we first randomly order the units in one group. Then we pair the first unit in this group with its nearest neighbor in the other group based on the weights or distances. Next we match the second unit with its nearest neighbor in the other group’s remaining units and continue this procedure until no more pairs can be formed. This algorithm is very intuitive and easy to implement. However, it fails to produce the smallest total distance among all the pairs, because the units in later pairs can be very “far away” from each other.

The matching that minimizes the total distance among all the pairs is called an optimal matching. It can be formulated as the solution to a restricted minimization problem. Without loss of generality, we focus on complete matching with an even number of nodes in the following discussion. Assume that every edge [v_i, v_j] ∈ E is associated with a nonnegative weight w_ij. Then finding the optimal matching that minimizes the total distance is equivalent to finding a set of

$$x_{ij}=\{\begin{array}{cc}1,& \text{if}[v_i,v_j]\in M\\ 0,& \text{if}[v_i,v_j]\notin M\end{array}$$

which solves the restricted minimization problem

$$\begin{array}{l}min\sum _{[v_i,v_j]\in E}{w}_{ij}·x_{ij}\\ \text{s}.\text{t}.\sum _{j:[v_i,v_j]\in E}{x}_{ij}=1\text{for}{v}_i\in V.\end{array}$$ (1)

Rosenbaum (1989) discussed the optimal matching for two disjoint groups in detail. Simulation studies have shown that optimal matching is noticeably better than nearest neighbor matching in the sense of producing closely matched pairs in all cases (Gu and Rosenbaum 1993).

2.2 Optimal Bipartite Matching and Optimal Nonbipartite Matching

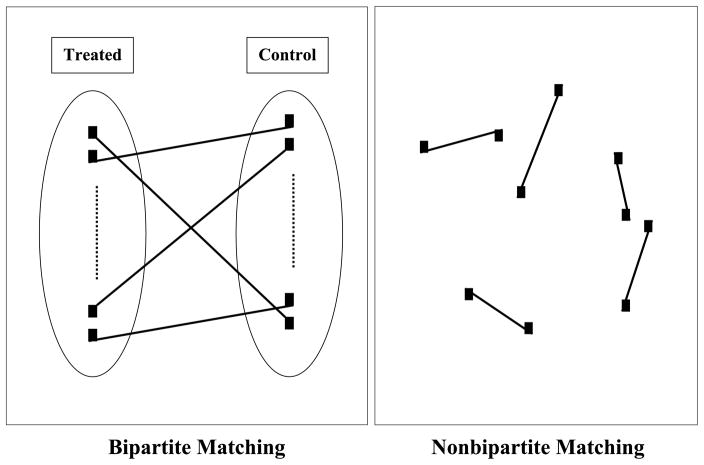
In general, a matching can be classified as bipartite or nonbipartite depending on the number of disjoint groups in the graph. Matching producing pairs in a bipartite graph that involves only two disjoint groups is known as bipartite matching. The group is defined in the sense that two nodes in the same group cannot be matched together, as illustrated in the left panel in Figure 1 (the ovals define two groups). Literally, the term “bipartite” refers to “two parts.” In contrast, when a graph has multiple groups, it is called a nonbipartite graph and the associated matching is referred to as nonbipartite matching. The right panel in Figure 1 shows an extreme case of nonbipartite matching in which every single node is considered to be a group and, as a result, any two nodes can be paired up in the matching.

Figure 1.

Bipartite matching and nonbipartite matching.

The bipartite matching corresponds perfectly to the classical two-arm design in observational studies, and so it has been extensively discussed in the literature. Optimal bipartite matching algorithms are available and usually implemented as a max-flow problem in the network flow framework (Rosenbaum 1989). Numerous statistical analyses of observational studies under various two-arm designs have used optimal bipartite matching to provide appropriate adjustments for unbiased estimation of treatment effects (see, e.g., Ming and Rosenbaum 2001; Hansen 2004).

In contrast, the optimal nonbipartite matching has received much less attention. The main reason is that the optimal nonbipartite matching problem requires a more complex algorithm to solve it. The simple optimal bipartite matching algorithm cannot be used for nonbipartite matching. Nonbipartite matching can only be reduced to an extension of the max-flow problem with bidirected graph, which has no easy solution. A widely accepted algorithm to solve nonbipartite matching is by searching augmenting paths (Papadimitriou and Steiglitz 1998). Our implementation of the optimal nonbipartite matching is based on Derig’s shortest augmentation path algorithm, discussed in Section 3.

Practically, the demand for nonbipartite matching is by no means meager. In many observational studies where the investigators have no control over the treatment given to each participant, the classic two-arm design is not satisfactory and a nonbipartite matching is required. For example, in a study investigating the effect of a media campaign on reducing illegal drug use by young Americans, the exposure to the media campaign is measured as the number of hours of antidrug advertisements the teenagers watched from various media sources. The treatment is perceived in a continuous scale rather than dichotomous. Lu et al. (2001) classified the kids into five ordinal dose groups and conducted an optimal nonbipartite matching to generate matched pairs that will be close on their covariates but far apart on the exposure levels. Then the within-pair response difference was aggregated to estimate the treatment effect for various levels of exposure differences.

Theoretically, optimal nonbipartite matching encompasses optimal bipartite matching as a special case, as shown in the following proposition.

Proposition 1

For a bipartite graph, the optimal nonbipartite matching produces the same result as the optimal bipartite matching, provided that the optimal matching for such graph is unique.

Proof

The bipartite graph differs from the nonbiparite graph structurally in terms of the number of disjoint groups. The bipartite graph has only two groups and the edges connect one node from each group. When the optimal matching algorithm is applied, it searches the entire set of possible edges to find the best result. Therefore, the optimal bipartite and the optimal nonbipartite matching algorithms have the same set of edges to search. Moreover, both algorithms minimize the same objective function (1). Hence, the two minimization problems are identical and would yield the same result provided that the optimal matching is unique.

In summary, optimal nonbipartite matching can be applied in observational studies with more complex designs and provides a unified framework for matched analyses in observational studies that encompasses optimal bipartite matching. Thus, it can be widely applied in statistical analysis with a variety of designs.

2.3 A Small Example of Optimal Nonbipartite Matching

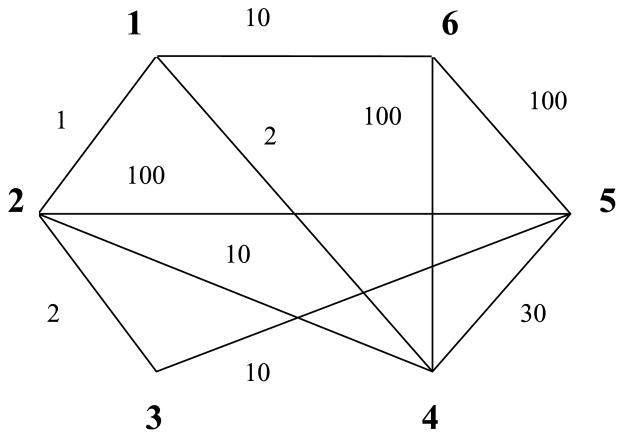
To illustrate the basic idea of optimal nonbipartite matching, consider a small matching example with six nodes (Figure 2). Assume that each node forms a different group, and so it could be matched with any other nodes in the figure. The lines between two nodes denote existing edges, and the numbers besides the lines denote the associated distances. If a line is missing between two nodes, such as between nodes 3 and 4, it means that the two nodes can not be matched (the distance between them is usually referred to as an infinite distance). We could also summarize the distances between the nodes in a distance matrix as in Table 1. This matrix is symmetric because the distance between the pair [i, j] is the same as the distance between the pair [j, i].

Figure 2.

Nonbipartite matching with six nodes.

Table 1.

Distance matrix for the small example.

Node	1	2	3	4	5	6
1	∞	1	∞	2	∞	10
2	1	∞	2	10	100	∞
3	∞	2	∞	∞	10	∞
4	2	10	∞	∞	30	100
5	∞	100	10	30	∞	100
6	10	∞	∞	100	100	∞

The goal of optimal matching is to create a matching that has three disjoint pairs and achieves the smallest total distance. Under formulation (1), the optimal matching for this figure is {[1, 6], [2, 4], [3, 5]}. The distances between these three pairs are highlighted in the distance matrix, and the total distance is 10 + 10 + 10 = 30. It is worth noting that node 1 is actually closer to node 2 than node 6, but if we matched node 1 with node 2, we would have to match node 6 with nodes 4 or 5 which incurs a very large distance. This illustrates a scenario when the optimal matching beats the greedy matching. Since the data cannot be clustered into two groups, the bipartite matching algorithm does not apply and the optimal nonbipartite matching algorithm must be used.

3. APPLICATIONS OF OPTIMAL NONBIPARTITE MATCHING IN STATISTICAL ANALYSIS

This section outlines the use of optimal nonbipartite matching in statistical analysis with different designs through four concrete scenarios. We focus on how nonbipartite matching can be used to generate comparable pairs, hence providing unbiased treatment effect estimates assuming strongly ignorable treatment assignment. Put simply, this assumption posits that the variables matched on are the only ones that influence treatment assignment. Naturally, if there exists an important variable that has not been balanced after matching, the estimates may still be biased. The detailed implementations in standard software are deferred to Section 4.

3.1 Observational Studies With Complex Design

A major advantage of nonbipartite matching is that it can lead to unbiased treatment effect estimation in complicated observational studies where the classic bipartite matching is not applicable.

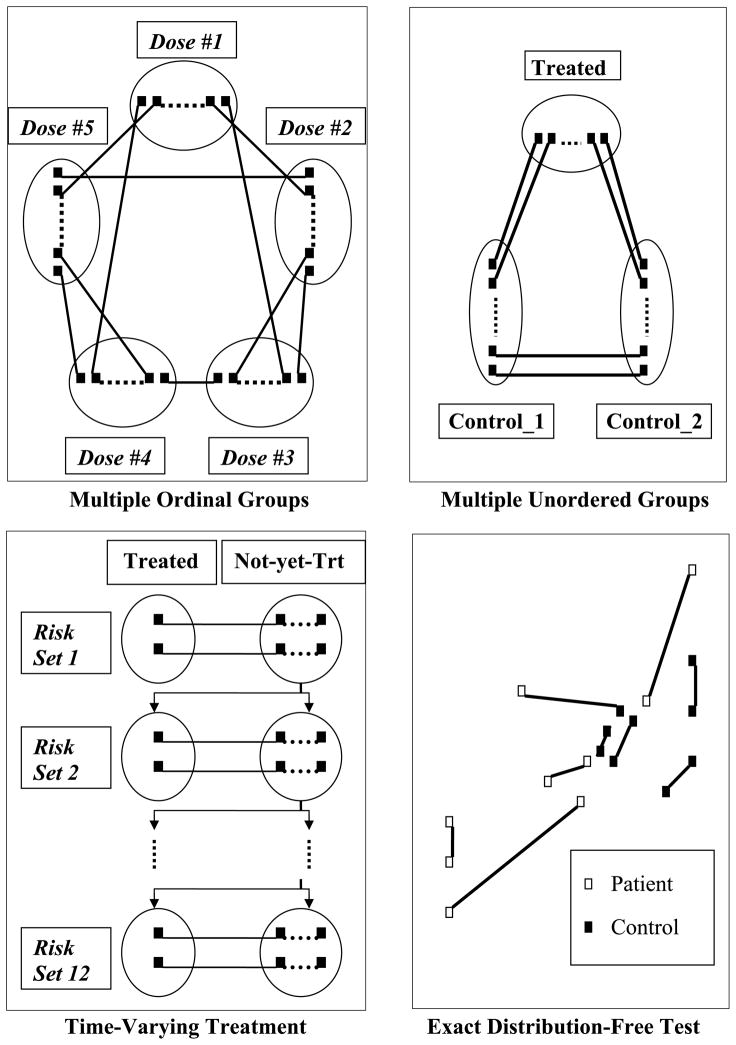
• Matching with multiple ordinal dose groups. In some nonexperimental studies, control groups might not be available and the level of exposure to treatment could vary significantly among the participants. For example, Flores-Kagybes, Gonzalez, and Neumann (2007) studied a job training program, in which the enrollment was voluntary and the time that the participants stayed in the program varied substantially. The level of exposure (the length of the program) would be an important factor in estimating the treatment effect. A nonbipartite matching can be used to compare the treatment effects among different “dose” groups. A reasonable approach is to first create propensity scores through an ordinal logit model and use them to measure distances between participants. Then conduct an optimal nonbipartite matching to match participants with similar pretreatment characteristics. This matching design is illustrated in the upper left panel of Figure 3. The detailed implementation with an antidrug media campaign dataset is shown in Section 4.

• Matching with multiple unordered groups. In order to detect hidden biases due to failure to control for an unobserved covariate, some observational studies use two control groups selected to systematically vary the unobserved covariate. There is usually no ordering among those three groups. Matched pairs are created not only between the treated group and the control groups, but also between the two control groups. Eventually, three two-group comparisons would be conducted, treated versus control 1, treated versus control 2, and control 1 versus control 2. If there is a treatment effect and no hidden bias with regards to the speculated unobserved variable, we would expect to see significant differences in the first two comparisons, but not in the third. Bipartite matching can only generate matched pairs between two groups. With three groups, bipartite matching needs to be applied three times and results in overlapped matched pairs. In contrast, nonbipartite matching can produce nonoverlapping matched pairs between three groups simultaneously. They can be easily analyzed as either a balanced incomplete block design or unbalanced incomplete block design as shown in Lu and Rosenbaum (2004). The upper right panel of Figure 3 illustrates this matching design.

• Matching with time varying covariates. Many observational studies on chronic diseases are longitudinal. A patient’s covariates may change over time, and at each time point, whether a patient receives the treatment depends on their symptoms at that time and on the physician’s judgment. Thus, there is a group of treated patients and a group of people not yet treated, at each time point. Matching can be conducted at each time point, and the treatment effect is estimated by taking the outcome difference between matched pairs. The overall treatment effect is the average of the treatment effects at all time points. This design is known as the risk set matching design (Li, Propert, and Rosenbaum 2001). If the bipartite matching algorithm is used, we need to conduct the matching separately at each time point, which can be very computationally intensive when the number of time points is large. The nonbipartite matching can reduce the computational burden significantly by treating risk sets at different time points as different groups, then running the matching once for all. For example, Lu (2005) investigated the effect of a certain surgical procedure on interstitial cystitis (IC) with a cohort of women who were followed up with every three months for up to four years. Therefore, there were 16 time points. An optimal nonbipartite matching was applied once to generate matched pairs between treated and not-yet-treated women at all time points. The lower left panel of Figure 3 illustrates this matching design.

Figure 3.

Complex nonbipartite matching designs.

3.2 Comparing Distributions Based on Adjacency

In addition to conducting matched pair analyses in observational studies with complex designs, optimal nonbiparite matching can be used to construct a distribution-free test for comparing two multivariate distributions. Rosenbaum (2005) used the optimal nonbipartite matching to develop an exact test for checking whether the outcomes from two populations, say the treated and the control populations, follow the same distribution. He first pooled the observations from these two populations together and ignored the grouping information. Then he used optimal nonbipartite matching to create matched pairs among all the observations. After the matching is done, he classified these matched pairs into three categories based on their compositions, namely, pairs consisting of treated subjects only, pairs consisting of control subjects only, and pairs consisting of one treated and one control subject. A substantially lower number in the third category would provide evidence against the null hypothesis that the two groups have exactly the same distribution. This test is known as the cross-match test. Rosenbaum also derived the normal approximation version of the exact test and compared the test with the well-known Kolmogorov–Smirnov test. He concluded that the cross-match test is consistent for comparing any two discrete distributions with finitely many mass points. It could also be extended to comparing continuous distributions given that the distributions can be approximated well by discrete distributions with finitely many mass points. The lower right panel of Figure 3 illustrates the nonbipartite matching design for the cross-match test.

4. SOFTWARE

The optimal matching problem is a combinatorial optimization problem that can be solved with a polynomial time algorithm. In general, it takes O(|V |³) arithmetic operations to finish a complete optimal bipartite matching and takes O(|V |⁴) arithmetic operations to finish a complete optimal nonbipartite matching, where |V | is the number of nodes in the graph. The complexity of nonbipartite matching can be brought down to O(|V |³) with some careful refinement to the original algorithm (Papadimitriou and Steiglitz 1998).

Matching routines are available for bipartite matching in many standard statistical software packages, such as R, Stata, and SAS. For example, King and his colleagues introduced a comprehensive R package MatchIt to conduct matching, check balance and perform post-matching analysis (Ho et al. 2007 and website http://gking.harvard.edu/matchit/). Hansen provided a R package for conducting optimal bipartite matching (http://cran.r-project.org/web/packages/optmatch). Sianesi and Leuven (2003) made a Stata package for conducting bipartite matching with either Mahalanobis distances or propensity score distances (see http://ideas.repec.org/c/boc/bocode/s432001.html). Moreover, Bergstralh, Kosanke, and Jacobsen (1996) implemented the optimal bipartite matching algorithm in SAS.

As far as we know, however, codes for the optimal nonbipartite matching exist in C and FORTRAN languages, but are not available in any standard statistical software. The C code may be downloaded from http://elib.zib.de/pub/Packages/mathprog/matching/weighted/index.html, which was based on Gabow’s (1973) algorithm. The objective of this algorithm is maximizing the total weights, that is, the weight between subject i and j is β_ij, rather than minimizing the total distance, that is, the distance between subject i and j is δ_ij. To use it in our setup, we must redefine the weights based on the distance measure, β_ij = max_{i, j} {δ_ij } −δ_ij. The FORTRAN codes for the optimal nonbipartite matching can be found in Derigs (1988). His algorithm—based on searching the shortest augmentation path with respect to an initial extreme matching—was intended to minimize the total cost in an undirected graph. His implementation is also efficient in terms of achieving a computational complexity of O(|V |³). Therefore, we used Derigs’ algorithm to create our R matching package.

4.1 A New R Package

The R language has become widely used for statistical research and data analysis, and its use is standard among statisticians for software development. We have created a new R package for the optimal nonbipartite matching based on Derig’s algorithm and made it freely available to public. It can be downloaded from the CRAN website http://cran.r-project.org/web/packages/nbpMatching or the Vanderbilt Biostatistics website http://biostat.mc.vanderbilt.edu/NonbipartiteMatching.

To use this package for the optimal nonbipartite matching, users need to first pass their distance matrices to function distancematrix(), which performs validity checks on the matrix and converts it into a readable object for the nonbimatch()function. In version 1.0, distancematrix() takes the integer part of the distance matrix values. Users may wish to rescale their distance matrix prior to passing it to distancematrix() by, for example, multiplying by 1000, to achieve the desired accuracy. Because Derig’s algorithm only solves the complete nonbipartite matching problem with an even number of subjects, the distancematrix() function automatically adds one artificial subject (known as sink, see Section 4.2 for details) to make the total number even. Users should make sure the generated distance matrices reflect their planned matching designs prior to performing matching. The function nonbimatch() in the package calls Derig’s FORTRAN codes and returns the optimal matching result in a complete list, which has all k subjects in column one and their respective matches in column two. It also returns a nonredundant list, which has k/2 subjects in column one with their respective matches in column two. Furthermore, for those not familiar with R, we implemented the package in an interactive webpage http://biostat.mc.vanderbilt.edu/NonbipartiteMatching, which calls the nbpMatching package’s functions using rapache by Horner (2008).

4.2 Matching Design and Distance Specification

Our R package is a general-purpose matching routine that can generate the optimal pairing under various matching designs. The only information that users need to input is the distance matrix. The grouping information is contained in the distance matrix because the distances between two subjects in the same group are set to be infinity, which prevents matching these subjects. To correctly specify the distance matrix, users should be familiar with the following common matching designs and understand how our matching algorithm works under these different designs.

• Bipartite 1–1 matching. Under a simplified bipartite matching design, each matched pair consists of one subject from the treatment group and one subject from the control group. Suppose that there are m₁ and m₂ subjects in these two groups, respectively. If m₁ = m₂ = m, our package produces m matched pairs using all the subjects. If m₁ < m₂, some subjects in the control group cannot be matched. Since Derigs’ algorithm only works with complete matching, we introduce artificial nodes (or sinks) to match with the extra control subjects. The sinks are set to have zero distances with all control subjects and have infinite distances with all treated subjects and among themselves. Thus, they can only be matched to the control group. Therefore, by including s = m₂ − m₁ sinks in the treated group, both groups have m₂ subjects and we can proceed with the complete matching.

• Bipartite 1–k matching. The 1–k matching design is an extension of the simple pair design. It was motivated by the matched sampling scenario described by Rubin (1973), where there is a huge pool of control subjects and only a limited number of treated subjects. To improve the efficiency of the treatment effect estimation, each treated subject is matched with k controls, where k is a prespecified integer. When k = 1, this is reduced to simple pair matching. To conduct a bipartite 1–k matching using our R package, we need to create k – 1 replicates for each of the treated subjects. These replicates will take exactly the same outcomes and covariates values as their original ones. Then the treated group has k × m₁ subjects and k should not exceed m₂/m₁. We may consider this as a regular bipartite 1–1 matching. Additional sinks may be needed to meet the complete matching required by the algorithm.

• Bipartite variable matching. The bipartite variable matching design further extends the 1–k design by allowing each treated subject to be matched with different number of controls. It can reduce more bias than simple pair matching (Ming and Rosenbaum 2000). To conduct a bipartite variable matching, we need to first specify the lower bound and the upper bound of the number of control subjects matched to each treated subject. By default, the lower bound is set to 1 and the upper bound is set based on the sample sizes of the two groups. Suppose that the upper limit is u, then up to u control subjects can be matched to each treated subject, so u – 1 replicates are created for each treated subject. Unlike the fixed 1–k design, these replicates can be matched to not only the control subjects, but also designated sinks (if less than u controls should be used). Again, additional sinks may be needed to meet the complete matching requirement.

• Nonbipartite multiple group 1–1 matching. As we have seen in Section 2.2, a nonbipartite matching could simultaneously match subjects from more than two groups. For example, suppose there are five dose groups, then a subject in dose one group can be matched to any subject in dose two, dose three, dose four or dose five groups. The optimal matching result minimizes the total distance among all possible parings between these five groups. A key to using the matching algorithm is to identify the correct distance matrix among groups. Usually we calculate the distance between two subjects from different groups based on their covariates. As in bipartite matching, artificial sinks will be introduced to satisfy the complete matching requirement if there is an odd number of subjects.

• Nonbipartite matching with no group classification. This no-group matching design is an extreme case of nonbipartite matching. Under this design, each subject is considered to form a separate group, so it can be matched to any other subject in the dataset. Rosenbaum (2005, sec. 3.2) used this matching design in his cross-match test for multivariate distributions. First, all subjects are pooled together and the grouping information is ignored. Then a nonbipartite matching is conducted with no group classification. Finally, the number of cross matches is identified and used as the pivotal quantity in the test.

Under any of the above matching designs, the distance matrix should be appropriately specified to reflect the matching design. The choice of the distance measure is up to users. Interested users are referred to Gu and Rosenbaum (1993), where an extensive simulation study was conducted to compare three popular distance metrics in observational studies, namely, the Mahalanobis distance, the propensity score distance, and the Mahalanobis distance with propensity score caliper. Since our focus in this article is to discuss nonbipartite matching, we do not discuss the choice of distance further here.

4.3 An Example: Optimal Nonbipartite Propensity Score Matching in an Observational Study With Multiple Ordinal Treatment Groups

This section reviews a concrete example where we used our R package to conduct optimal nonbipartite matching.

In 1998, the United States Office of National Drug Control Policy (ONDCP) launched a media campaign intended to reduce illegal drug use by young Americans. This made for a challenging observational study. Not only was each teenager’s exposure to media self-selected, but no natural control group existed for evaluating the campaign’s effects because the campaign was launched nationwide. In total 521 teenagers participated in the pilot study.

To evaluate the effect of the antidrug media campaign, Lu et al. (2001) classified the teenagers into five ordinal dose groups based on how often they reported seeing antidrug commercials in three major media sources. They used “1” to denote least exposure and “5” for most exposure. They used the following ordinal logit model to estimate the distribution of the doses:

$$log\frac{Pr(Z_k\ge d)}{Pr(Z_k<d)}={\theta }_k+{\beta }^T{x}_k,\text{for}d=2,3,4,5,$$

where Z_k is the dose level. Twenty-two covariates regarding the teenagers’ background information were included to fit this model. Note that the distribution of doses depends on the observed covariates only through e(x_k) = β^T x_k. Therefore, the maximum likelihood estimate β̂^T x_k was used as the propensity score component in the matching to balance the distributions of the covariates. If a dose-dependent treatment effect exists, subjects with similar covariates but very different dose exposures are more likely to show significant results. Therefore, in matching with doses, the goal is not only to balance the observed covariates, but also to produce pairs with very different doses. To this end, the following distance was considered:

$$\mathrm{\Delta }(x_i,x_j)=\frac{{({\widehat{\beta }}^T{x}_i-{\widehat{\beta }}^T{x}_j)}^2+\epsilon }{{(Z_i-Z_j)}^2},$$

where ε > 0 was a vanishingly small but strictly positive number, which serves two functions. First, it makes the distance between two subjects with the same dose equal ∞, regardless of their observed covariates. Second, when two subjects have identical covariates, the distance will be smaller as the dose difference increases. The addition of a sufficiently small ε > 0 would not affect the optimal matching result.

The teenagers from the same dose group cannot be matched to each other, so their distances are set to be ∞. In practice, a huge positive integer is often used to facilitate the computation, say 1,000,000. Derig’s algorithm works only for integer distances. When propensity score related distance is calculated, it often involves small decimal values which may lead to nonoptimal results with Derig’s algorithm. One practical remedy is to multiply all distances by 10 to an appropriate power. For example, if the desired accuracy is three decimal places, we can multiply all distances by 1000 and round them. Thus, a 521 × 521 distance matrix between all of the teenagers can be generated. Because the number of teenagers is odd, one sink is added to meet the complete matching requirement. The sink has zero distance to all 521 original subjects and infinity distance to itself. As a result, the final distance matrix is 522 × 522.

Using the optimal nonbipartite matching, we created 261 pairs and discarded one original subject by using the sink. Within each pair, the teenager with the higher dose was classified into the high dose group and the other was classified into the low dose group. As a result, two groups with 260 teenagers each were generated. Lu et al. (2001) showed that 7 of the 22 covariates were significantly associated with the dose levels before matching, and after matching, no significant differences were observed between high and low dose groups.

Specifically, to accomplish the optimal nonbipartite matching with ordinal dose groups, we take the following steps:

1. Estimate the ordinal propensity score with the ordinal logit model and save the propensity score component β̂^T x_k for each subject, k = 1,…, 521.

2. Generate a 521 × 521 distance matrix between all subjects with the above formula, denote it by distmx1. It is symmetric with infinity distance on the diagonal and between subjects with same dose. (A very large integer value is used to represent ∞ in practice.)

3. Expand the distance matrix to 522 × 522 by introducing a sink, which has zero distance to all 521 original subjects and infinity distance to itself. We add the sink at the very end and denote the matrix by distmx2 which looks like the following using the command distmx2<-distancematrix(distmx1)

   $$\text{distmx}2={\left(\begin{array}{cc}\text{distmx}{1}_{521\times 521}& {\mathbf{0}}_{1\times 521}\\ {\mathbf{0}}_{521\times 1}& \infty \end{array}\right)}_{522\times 522}$$
4. Conduct the optimal nonbipartite matching to create 261 matched pairs using the command:

   $$\text{nonbimatch}(\text{distmx}2)$$

5. The matched pair consisting of the sink (the 522nd node) should be discarded. The remaining 260 pairs are clustered into a high-dose and a low-dose group for checking balance after matching and for subsequent analyses.

5. SUMMARY

Matching plays a critical role in statistical study design and analysis. Many observational studies have a relatively small number of treated subjects and a much larger number of control subjects. Matched sampling is often used to select a group of control subjects who are comparable to the treated with regard to the background variables to allow valid treatment effect estimation (Rosenbaum and Rubin 1985). This is particularly important when the cost of obtaining the outcome is nontrivial for each subject.

Most of the matching algorithms discussed in the statistical literature are confined to two group matching. However, bipartite matching cannot accommodate more complex study designs. In this article, we provide a comprehensive description of the optimal nonbipartite matching methodology and demonstrate its applications in statistical analysis with various complex designs. Optimal nonbipartite matching has gained its popularity recently as being adopted in more and more publications to address various issues in observational studies (Rosenbaum and Silber 2009; Silber et al. 2009; Small and Rosenbaum 2009; Baiocchi et al. 2010; Heller et al. 2010). Nonbipartite matching can also be extended to randomized studies, especially when the sample size is small and the conventional randomization mechanism cannot guarantee the balance of the baseline covariates in both groups (Greevy et al. 2004). To aid in implementation, we develop a new R package that conducts optimal nonbipartite matching and encompasses optimal bipartite matching as a special case. The function is easy to use and runs quickly for moderately large cohorts. For users who are not familiar with R, we provide an interactive website to conduct the matching. Users may optionally have their matching results e-mailed to them and import those results into their preferred statistical software for analysis.

Our experience suggests that, for sample sizes up to a couple of thousand, the running times to solve a bipartite matching problem are similar for the optimal bipartite matching algorithm and the optimal nonbipartite matching algorithm. However, when the sample size is much larger than that, the nonbipartite algorithm is noticeably slower. Therefore, in a large study with well-defined dichotomous treatment options, the bipartite matching algorithm may be preferred. In a study with a polychotomous treatment, which will usually be intractable for the bipartite algorithm, nonbipartite matching provides a solution.

One limitation of our current R package is that it cannot perform full matching, which allows both multiple controls to be matched with one treated subject and multiple treated subjects to be matched with one control. Full matching can be viewed as an extension of bipartite matching, and may maximally eliminate observed bias (Hansen 2004). We are working on modifying our package to accommodate full matching. The idea is to add super sinks to increase the matching flexibility by allowing variable matching in both directions.

Many other interesting topics regarding matching are in the literature and are being developed. A practical issue is how to check the degree of balance after matching. One way is to perform hypothesis tests, such as two-sample tests after matching two groups and ANOVA or χ²-tests after matching multiple groups. Rosenbaum and Rubin (1985) pointed out that two-sample t -tests are relevant for comparing the distribution of the covariates between the treated and control group; whereas, paired t -tests are relevant for assessing residual biases. They suggested reporting standardized differences to examine the imbalance in covariates. In contrast, Imai, King, and Stuart (2008) argued against using tests to check balance because balance is a sample characteristic while most statistical tests infer about population quantities. Therefore, they recommended using graphical means to illustrate the balance and echoed the standardized difference approach. Love (2002) proposed forest plots as an effective way to show covariate balance before and after matching. Hansen extended the discussion in a series of papers that proposed a randomization-based test to appraise the balance for stratified and clustered designs (Hansen 2008; Hansen and Bowers 2008). Bowers and Hansen’s R package RItools implements both the balance test and the forest plot as a graphical diagnostic tool. Many good matching methodologies are available and more work is needed in this area, especially with regard to synthesizing the interpretation of the methods and making them more accessible.