Forces and moments generated by the human arm: Variability and control

Abstract

This is an exploratory study of the accurate endpoint force vector production by the human arm in isometric conditions. We formulated three common-sense hypotheses and falsified them in the experiment. The subjects (n=10) exerted static forces on the handle in eight directions in a horizontal plane for 25 seconds. The forces were of 4 magnitude levels (10 %, 20%, 30% and 40% of individual MVC). The torsion moment on the handle (grasp moment) was not specified in the instruction. The two force components and the grasp moment were recorded, and the shoulder, elbow, and wrist joint torques were computed. The following main facts were observed: (a) While the grasp moment was not prescribed by the instruction, it was always produced. The moment magnitude and direction depended on the instructed force magnitude and direction. (b) The within-trial angular variability of the exerted force vector (angular precision) did not depend on the target force magnitude (a small negative correlation was observed). (c) Across the target force directions, the variability of the exerted force magnitude and directional variability exhibited opposite trends: In the directions where the variability of force magnitude was maximal, the directional variability was minimal and vice versa. (d) The time profiles of joint torques in the trials were always positively correlated, even for the force directions where flexion torque was produced at one joint and extension torque was produced at the other joint. (e) The correlations between the grasp moment and the wrist torque were negative across the tasks and positive within the individual trials. (f) In static serial kinematic chains, the pattern of the joint torques distribution could not be explained by an optimization cost function additive with respect to the torques. Plans for several future experiments have been suggested.

Introduction

To move and manipulate objects people exert forces and moments of force (further addressed as simply “moments”) on the environment. Friedman et al.(2011) studied the production of two-dimensional force vectors by a two-joint arm (the wrist was braced). This design allowed mapping endpoint force vectors onto joint torques unambiguously. In the current study, we used more natural three-joint tasks (the wrist was free). When only the desired force is specified by an instruction, such a system is redundant because it can also produce a moment of force by the hand on the handle, the grasp moment (Zatsiorsky 2002). While many studies explored redundant kinematic tasks performed by multi-joint serial chains (Domkin et al. 2005; Yang et al. 2007) and redundant static tasks performed by several effectors acting in parallel (Li et al. 1998; Latash et al. 2002; Shim et al. 2004) to our knowledge performance in redundant static tasks performed by a serial chain has not been studied experimentally.

The presence of redundancy affords the system a possibility to use multiple solutions for any given task. In particular, when only the force magnitude and direction are specified, the performers can choose any moment magnitude and direction they prefer. Such preferences remain presently unknown. Common sense suggests that the performers — if not required — should exert no grasp moment at all to minimize effort.

In contrast to the moment production by a serial chain, the force production—especially the force magnitude variability — was an object of rigorous research. The dependence of the force magnitude variability on the target force level has been studied in detail (Carlton and Newell 1993). At low forces, standard deviation of force magnitude increases with the target force level (Schmidt et al. 1979; Newell and Carlton 1988; Sherwood et al. 1988b; Sherwood et al. 1988a; Slifkin and Newell 1999). At higher force magnitudes, the standard deviation peaks at about 65% of maximal force and then decreases at higher force levels (Sherwood and Schmidt 1980). Valero-Cuevas et al. (2009) examined muscle coordination using electromyograms during fingertip isometric force production and found that the variance was consistently lower for task-relevant variables than for muscle activation variables. According to our knowledge, there are no systematic data on the dependence of the force magnitude variability on the target force direction.

Studies on the variability of force vector direction are limited. These studies fall into one of the two groups dealing with the force production either in a single 2- or 3-D joint (Kutch et al. 2008) or in planar kinematic chains. Studies on the effects of the force direction on the force variability in multilink tasks (which is a topic of the present study) have been mainly limited to fingertip force production in the flexion–extension plane. It was observed that during the fingertip force production the target direction significantly affected the variable error of the force direction, but not the constant error (Gao et al. 2005). Fingertip force direction variability was shown to be larger for the force exerted downward and towards the body as compared to other directions (Kapur et al. 2010).

In studies on the control of the arm (van Bolhuis et al. (1998) and leg force production (Jacobs and van Ingen Schenau (1992) the researchers concluded that bi-articular muscles have a unique role in controlling the direction of the external force exerted on the environment. The validity of these conclusions was later questioned by Prilutsky (2000).

In the mentioned study by Friedman et al. (2011) the hand force direction variability decreased with an increase in the target force magnitude. This finding was in sharp contrast to the well-established increase in the force magnitude variability with the target force increase. In that study, the subjects grasped a handle and exerted forces of different magnitudes in various horizontal directions. The wrist joint was however braced, so the arm was mechanically reduced to the two-link kinematic chain. It remained unknown whether the negative relation between the force magnitude and its angular variability is valid for natural tasks when the wrist joint is not braced.

The variability of force production is generally assumed to reflect noise at some level of the neuromotor hierarchy (Newell et al. 2006). An increase in the amount of noise with the intensity of the neural signal is commonly referred to as the signal-dependent noise (Harris and Wolpert 1998). Peripheral sources may also contribute to the variability of the motor output, and attempts have been made to distinguish between these two sources (Wing and Kristofferson 1973). If the endpoint force variability is only due to the signal-dependent noise the variable intensity of the efferent signal, e.g. the signal to alpha-motoneuronal pools, should result in multi-joint kinematic chains in the synchronous variations of the produced joint torques, i.e. when the joint torques are in the same direction they should correlate positively and when they are in opposite directions they should correlate negatively.

Endpoint force variability is a function of the variability of the joint torques in the involved joints. There is a glaring gap in the literature on this topic.

In this work, we are specifically interested in the following:

1. The moment produced by the hand (the grasp moment);

2. The variability of the end-point force magnitude and direction as a function of the target force magnitude and direction; and

3. The torque variability at the contributing joints, the shoulder, elbow and wrist.

The following main hypotheses were explored:

Hypothesis 1: When subjects do not receive an explicit instruction that requires moment production they exert a zero moment on the environment.

Hypothesis 2: The variability indices of force magnitude and direction show similar dependencies on the target force magnitude and direction, e.g., in tasks where the force magnitude variability is maximal (minimal) the force direction variability is also maximal (minimal).

Hypothesis 3: The intra-trial correlations between the joint torques are positive in the tasks where the torques of similar sign are exerted (i.e. flexion-flexion or extension-extension) and the correlations are negative in the tasks that require the flexion (extension) torque at one joint and the extension (flexion) at another joint.

All these ‘commons sense’ hypotheses were falsified in the experiments.

We were also interested in whether the central controller selected the joint torques in redundant static tasks by following an optimization cost function that is additive with respect to the joint torques. This issue is addressed in Appendix 1. Similar to the above three hypotheses, the answer to this question was also negative.

Methods

Overall description of the experiment

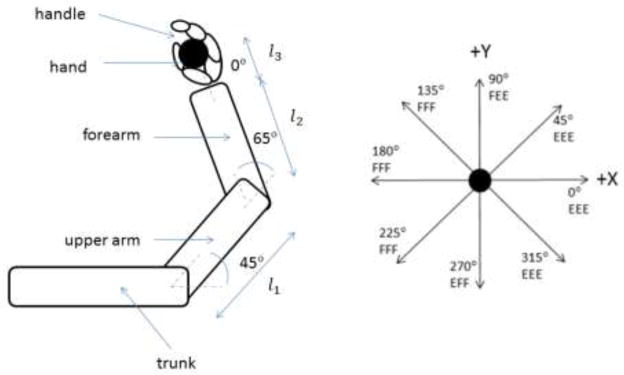
Subjects sat in a chair, grasped a handle and generated forces of different magnitudes in different directions (Figure 1). We restricted the right arm to a horizontal plane at the shoulder height, with the upper arm flexed at 45° from the frontal plane, and the elbow flexed at 65º (see Figure 1a). This configuration was selected to provide an insight into possible effects of combinations of the flexion or extension torques at the shoulder and elbow joints (the torque at the wrist joint always coincided in the direction with the elbow joint torque). The trunk was secured to the chair with seat belts. This reduced the task to a system with three degrees of freedom that produced a two-dimensional force and a moment. This allowed reconstructing the joint torques from the recorded endpoint force and moment (explained below).

Figure 1.

Schematic diagram of the experimental setup.

Left panel. The posture of the arm. The shoulder angle α₁ = 45°, the elbow angle α2 = 65°, and the wrist angle α3 = 0° l₁, l₂, and l₃ are the lengths of the upper arm, forearm and hand (from the wrist joint to the handle center), respectively.

Right panel. The directions in which forces were produced. The force production in the indicated directions requires the following combinations of the joint torques (under the assumption that the grasp moment is zero): (1) 45º - shoulder extension, elbow extension and wrist extension (EEE); (2) 90º-shoulder flexion, elbow extension, and wrist extension(FEE); (3) 135º - shoulder flexion, elbow flexion, and wrist flexion (FFF); (4) 180º - shoulder flexion, elbow flexion and wrist flexion (FFF); (5) 225º - shoulder flexion, elbow flexion, and wrist flexion (FFF); (6) 270º - shoulder extension, elbow flexion, and wrist flexion (EFF); (7) 315º - shoulder extension, elbow extension, and wrist extension (EEE). (8) 0º - shoulder extension, elbow extension, and wrist extension (EEE).

Subjects

Five male and five female right-hand dominant subjects took part in this study (mean age 24.7±3.2 yr, mass 65.8 ± 15.7 kg, height 1.70 ± 0.09 m, shoulder to elbow length (upper arm) 27.4 ± 2.3 cm, elbow to wrist length (forearm) 25.4 ± 2.0 cm, wrist to the center of the handle distance 7.3 ± 0.5 cm. All subjects were healthy, with no known neurological or peripheral disorders. All of the subjects gave informed consent according to the policies of the Office for Research Protections at the Pennsylvania State University.

Apparatus

The apparatus is shown in Figure 2. An aluminium cylindrical handle (height 16 cm, diameter 5 cm) was attached to a 6-DOF force/torque sensor (Mini85, ATI, Apex, NC USA, resolution of Fx and Fy is 7/144 N and resolution of Mz is 1/600 Nm). Such an arrangement allows recording both the force vector and the moment (‘grasp moment’) exerted on the handle. Surface of the handle was frosted, which provided greater static friction than polished surface.The friction was not measured but the subjects never reported slippage during tests. The force sensor was mounted on an aluminium block, which could slide left and right along two poles. These two poles were attached to blocks on the left and right side of the apparatus, which could slide forward and back on another two poles. Screws on the central block and on the two side blocks permitted fixing the handle at a desired location. The total workspace was 65 cm × 65 cm.

Figure 2.

Experimental setup

The subject sat on a large, heavy chair, and was strapped to the chair with two seatbelts to prevent movement of the trunk. The chair sat on a hydraulic lift, and its height was adjusted for each subject such that the bottom of the handle was at the shoulder height. The forearm was supported by a padded semicircular piece of plastic pipe, hanging down vertically from the ceiling. The location of the handle was adjusted for each subject such that the upper arm was at 45 degrees to the frontal plane and the elbow was flexed such that there was a 65° angle between the upper arm and forearm. The selected chair height ensured that the upper arm and forearm lay in a horizontal plane, at the height of the shoulder.

Experimental Procedure

Initially, the subjects were asked to produce maximal force (MVC) for 5 s along each of the 8 directions, in a clock-wise order. The subjects were provided with feedback on the horizontal force vector exerted on the handle by the right arm using a monitor placed directly in front of the subject. A blue arrow showed the amount and direction of force they were generating. Three concentric circles, marked in newtons, were subdivided by 8 directions. No feedback on the moment exerted on the handle (‘grasp moment’) was provided.

A total of 32 trials were performed to cover the combinations of four force magnitude levels (10 %, 20%, 30% and 40% MVC) and eight force directions. No instruction on the moment (grasp moment) production was given. Each trial took 53 s. The duration and composition of each trial was as follows: (1) Force production for 25 s → (2) Break 5s → (3) Force production without visual feedback for 25 s → (4) Rest 120 s. (The data on the force and moment production without visual feedback are not presented in this paper).

The visual feedback was adjusted for each trial such that an identical circle corresponded to varied force magnitude requirements. The target force level and direction were indicated by a red cross in visual feedback blocks. The subjects were instructed to keep the tip of the arrow as close as possible to the red cross for 25 s.

The target levels of force were presented in a random order. The force direction conditions were pseudo-randomized to prevent similar or same direction presenting in succession. Particularly, directions of the subsequent force exertion were randomly selected at either 180 º, 225 or 135 º from the previous direction. In total, 320 trials were analysed (8 instructed directions × 4 target force magnitudes × 10 subjects).

Data Collection and Analysis

The force signals were conditioned (9105 IFPS-1, ATI, Apex, NC USA) and digitized using a 16-bit A/D converter (PCI-6225, National Instruments, Ausin, TX) at 1000 Hz. The data were collected using a custom program written in LabVIEW (National Instruments). The data analysis was performed using a custom program written in Matlab (The MathWorks, Natick, MA). The first and the last 3 s of each trial were discarded; hence only 19-s long segments were analysed.

Mechanical model and the joint torque computations

The joint torques were computed from the recorded values of the endpoint force and moment by employing the equation (see Zatsiorsky, 2002, Chapter 2):

$$\mathbf{T}=J^T\mathbf{F}=J^T\left[\begin{array}{c}{F}_x\\ F_y\\ M_z\end{array}\right]$$ (1)

where T is a 3×1 vector of joint torques, F is a 3×1 vector of the endpoint force and moment (grasp moment), and J^T is the transpose Jacobian of the kinematic chain

$$J^T=\left[\begin{array}{ccc}-l_1{S}_1-l_2{S}_{12}-l_3{S}_{123}& l_{1}C+l_2{C}_{12}+l_3{C}_{123}& 1\\ -l_2{S}_{12}-l_3{S}_{123}& l_2{C}_{12}+l_3{C}_{123}& 1\\ -l_3{S}_{123}& l_3{C}_{123}& 1\end{array}\right]$$ (2)

where l₁, l₂, and l₃ are the lengths of the upper arm, forearm, and the hand (from the wrist to the centre of the handle), respectively; S and C refer to the sine and cosine, respectively; and the subscripts refer to the angles: 1 to the shoulder angle α₁ = 45°, 12 to (α 1 + α2), i.e. the upper arm angle with respect to axis X of the external system of coordinates, and 123 to the angle (α₁ + α₂ + α₃).

Data analysis

For all analyses the 3-s time periods at the beginning and at the end each trial were discarded and the computations were performed for the remaining 19-s time periods.

Force variance was calculated over each trial. The variance of the force magnitude in the target direction was computed and then standard deviation (SD) and coefficients of variation (CV= SD/average) computed within a trial. The same was done for the computed joint torque time series. For easier comparison with the previously published research on force variability that was mainly performed with single-direction force sensors, we analysed the force magnitude in the prescribed direction—essentially the projection of the force vector—rather than the force vector magnitude. Hence, the term ‘force magnitude’ in the present paper refers to its magnitude in the prescribed direction (the directional force magnitude). The force orthogonal to the prescribed direction was also measured but it will not be discussed in detail in the paper.

The instantaneous angle α_ACT of force vector was calculated as

$${\alpha }_{\text{ACT}}={tan}^{-1}\left(\frac{F_y}{F_x}\right)$$ (3)

where F_y and F_x are the force components along the coordinate axes, respectfully. The actual force direction was compared with the target force direction and the difference was treated as the angular deviation.

Calculation of the group mean values (n = 10) for the intra-trial standard deviations was performed by calculating the variances of the corresponding quantities for each subject, taking their group mean and then computing the square roots of the obtained values.

Statistical Analysis

Linear regression was used to model the relations between the target force magnitude (F_TASK), on the one hand, and the variability of the magnitude (F_ACT) and the direction (α_ACT) of the exerted forces, on the another hand.

To detect the effects of prescribed force direction (α_TASK) on the variability of the actual force magnitude (F_ACT) and direction (α_ACT) the Levene’s test for equality of variances was performed; p-value was set as 0.05.

Statistical analysis of the joint torques T₁, T₂ and T₃ included computation of the regression of the torque variability (the standard deviations, SD) on the average torque magnitude (i.e., on |T₁|, |T₂|, and |T₃|).

Intra-trial correlation analysis of the time histories of the recorded signals was performed at the zero-time lag between the two processes. Averaging of the correlation coefficients was done after Fisher’s z-transform.

RESULTS

The data are presented in the following sequence: (1) Maximal voluntary contractions. (2) Submaximal voluntary contractions: grasp moments. (3) Intra-trial performance variability: dependence on the prescribed force magnitude and direction: 3a. Force magnitude variability; 3b. Force direction variability; 3c. Grasp moment variability. (4) Joint torques: 4a. Correlation with the grasp moments; 4b. Joint torque variability; 4c. Intra-trial correlations.

1. Maximal voluntary contractions (MVC)

At the beginning of the test, we collected MVC data from all 10 subjects in all eight directions. MVCs of every subject were normalized by the maximum value across the directions. Then the mean values and standard deviation (SD) of the normalized forces across 10 subjects at each direction were computed. Results are shown in Figure 3.

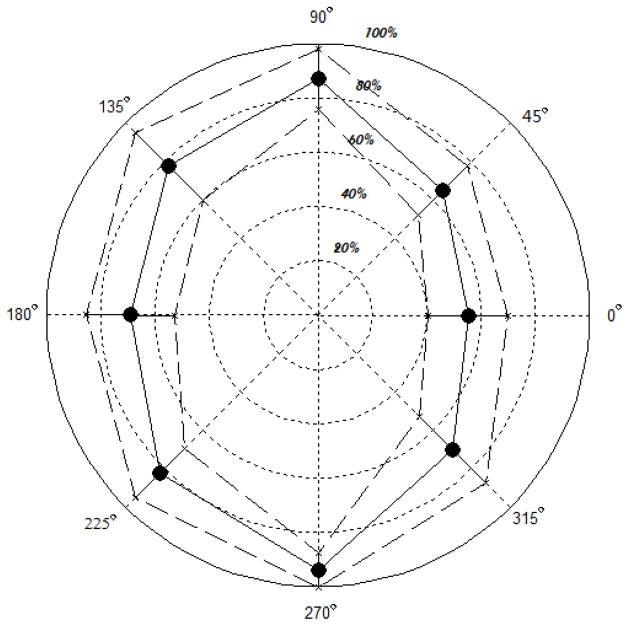
Figure 3.

MVC force vs. targeted force direction. The numbers around the outer circle are the target force directions. The average force magnitudes (in percent of the maximal MVC across all eight directions for each subject) are printed in italics. Dashed lines are the group SDs.

The group average MVCs were largest at the direction of 90º (87.10±11.05% of the maximal individual MVCs) and 270º (94.08±6.34%). In other words, the subjects tended to generate largest maximal forces in the ‘push’ and ‘pull’ directions. At these two directions, the group SDs of the normalized MVC values were the smallest (11.05% and 6.34%, respectively). These two directions are also the only two force directions which required torques in opposite directions at the shoulder and elbow (as well as the wrist), see Figure 1: At the direction of 90º, a joint torque combination of shoulder flexion, elbow extension and wrist extension (FEE) is required, while at the direction of 270, a joint torque combination of shoulder extension, elbow flexion and wrist flexion (EFF) is required. For other force directions, the joint torques were in the same direction, either EEE or FFF.

The MVC force distribution across the target directions (the force envelope) was approximately ellipse-like. This finding agrees well both with the previously published data (Fujikawa 1997) and with the mechanical analyses performed under the assumption that that the joint torque vector’s (T) Euclidian norm stays constant at all targeted endpoint force directions (Valero Cuevas 1997; Zatsiorsky et al. 2002).

2. Submaximal voluntary contractions: grasp moments

All subjects were able to complete the tasks successfully: they exerted force according to the prescribed values. The deviations of the trial-average data from the target values were relatively small, overall less than 4.3% of the target force magnitude.

While grasp moment production was not required by the instruction and no feedback on the grasp moment was provided, moments on the handle about its long axis (‘grasp moments’) were regularly exerted (Figure 4 and Table 1). Such a moment production represents a preference of the central controllers (the system is mechanically redundant and has certain freedom: three joint torques should satisfy two constraints associated with two endpoint force components).

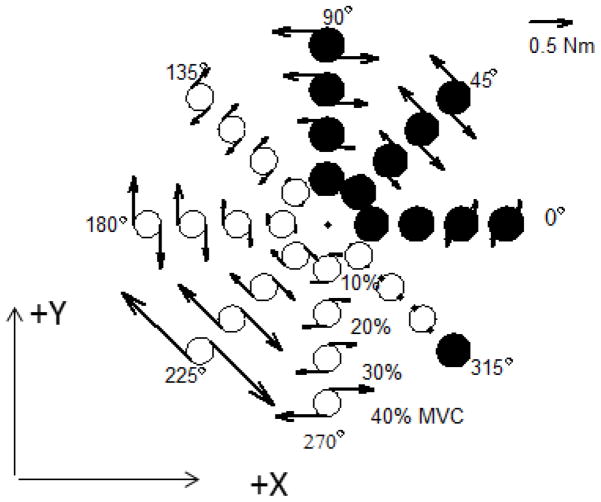
Figure 4.

The moments of force exerted on the handle (grasp moments), group averages. The arrows represent the moment magnitude and direction. Black circles – moments in counterclockwise direction; empty circles – clockwise moments. The locations of the circles correspond to the target force direction and magnitude. Counterclockwise grasp moments are in the direction of the flexion joint torques.

Table 1.

The number of subjects (out of 10) who generated torque on the handle in the positive (counterclockwise) direction

Target force direction (angleº)	Torques at the shoulder, elbow and wrist joints (F-flexion, E – extension)	Force level, % of MVC
		10	20	30	40
0	EEE	8	9	10	9
45	EEE	9	10	10	10
90	FEE	9	10	10	10
135	FFF	3	1	3	1
180	FFF	1	1	2	2
225	FFF	0	0	0	0
270	EFF	0	0	0	0
315	EEE	5	4	4	5

When the forces were exerted in 0º, 45º and 90º directions, majority of subjects generated counterclockwise torques. For force tasks in directions ranging from 135º to 270º clockwise torques were produced. At the angle of 315º, where the torque was close to zero, different subjects generated torques in different directions (Table 1). For 10 subjects, the probability of observing 9 or more cases of torque production in one direction by chance is 0.01 (p value for the one-tail sign test). Hence, for some force directions the observed directional preferences of the grasp moment production were statistically significant.

For all directions of force production, with the exception of the 315º (where grasp moments were around zero), the magnitude of grasp moments increased with the magnitude of the target force. Overall for the group r = 0.604 (p<0.01, n=32, correlation of group averages computed for each direction and force magnitude combination). At some force directions, e.g. 225º, the grasp moments at large target forces exceeded 1 Nm (approximately 20% of maximal grasp moments for this handle diameter and torque direction exerted by male subjects – Seo et al. 2007).

As a rule, the direction of the grasp moments was opposite to that of the joint torques at the elbow and wrist (cf. the grasp moment directions in Figure 4 and the joint torque directions presented in Table 1). For instance, for force directions of 225º and 270º, where the flexion torques were required at the elbow and wrist joints, none of the subjects exerted the grasp moment in the counterclockwise direction.

3. Intra-trial performance variability: dependence on the prescribed force magnitude and direction

3a. Force magnitude variability

Dependence of F_ACT on F_TASK

Force magnitude variability (SDs) increased monotonically with the target force level in all 8 directions (r = 0.91, p < 0.01, n = 32). However, after normalization by the average force there was no dependence of CV on F_TASK (r = −0.29, p > 0.05). Paired t-test indicated that for some force ranges (from 10% to 20% MVC, and from 10% to 30%), CV decreased with F_TASK (p value < 0.01) while there was no significant trend across other force levels (p value > 0.05).

Dependence F_ACT on α_TASK

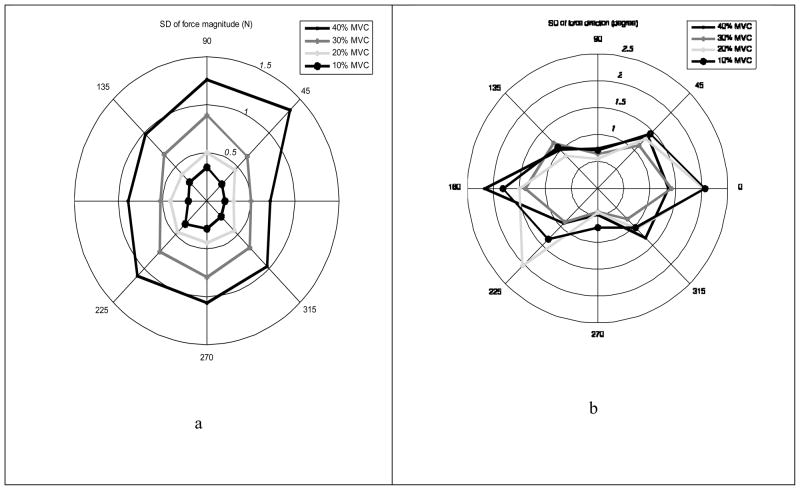
Levene’s test results showed that all subjects exhibited significantly different force magnitude variability (SD) across different directions (Levene’s statistic 6578, p<0.01), Figure 5a. The pattern of SD distribution across the force directions—especially at the levels 10 – 30%— was similar to the MVC pattern (see Figure 3), with maximal variance for the force directions of 90º and 270º. There were no systematic changes in CV with the target force level and direction.

Figure 5.

Dependence of the force magnitude variability (SDs) and force direction variability on the target force level and direction (panels a and b, respectively). In panel (a) note the systematic changes with the target force magnitude: outer contours always correspond to the larger target forces than the inner contours. This dependence is not seen in (b).

3b. Force direction variability

Dependence of α_ACT on F_TASK

Force direction variability (SD) did not show significant correlation with force level (r = −0.127, p > 0.05, n = 32). Figure 5b shows no systematic changes in the SD contours with F_TASK magnitude.

Dependence of α_ACT on α_TASK

Force direction variability depended on the targeted force direction. Levene’s test yielded p < 0.01 across the four force levels. The variability was largest for the force vector directions of 180º (1.72±0.35º, average across the force levels) and 0º (1.73±0.38º). It was smallest for the directions of 90º (0.66±0.09º) and 270º (0.53±0.14º) and relatively small for the directions of 45º (1.31±0.13º), 135º (1.04 ±0.14º), 225º (1.30±0.54º), 315º (1.05±0.20º), Figure 5b.

3c. Grasp moment variability

For all target force directions and levels combined, there was statistically significant correlation between the group averages of the grasp moment magnitude and its SDs (r = 0.80, p<0.01, n = 32). As the grasp moment averages depended on the target force magnitude and direction (see Figure 4), their variability (SDs) also depended on them. Systematic changes of the CVs with the force magnitude and direction were not observed.

4. Joint torques

The joint torques were computed using equation 1 from the recorded endpoint forces and grasp moment and measured arm link dimensions. These results follow trivial mechanics and, as such, they will not be presented in detail here. The ‘joint torque-endpoint force direction’ dependencies agreed well with the ones predicted theoretically from mechanical analysis (see Zatsiorsky 2002, Page 149, Figure 2.18).

4a. Correlation with grasp moments

For the group averages, across force directions and levels (n=32), the grasp moment values showed a strong negative correlation with the torques at the elbow (r = −0.92, p<0.001) and wrist (r = −0.86, p< 0.001) joints and a weaker correlation with the shoulder torque (r = −0.55, p<0.001). This pattern was seen in the individual data of 9 out of 10 subjects.

4b. Joint torque variability

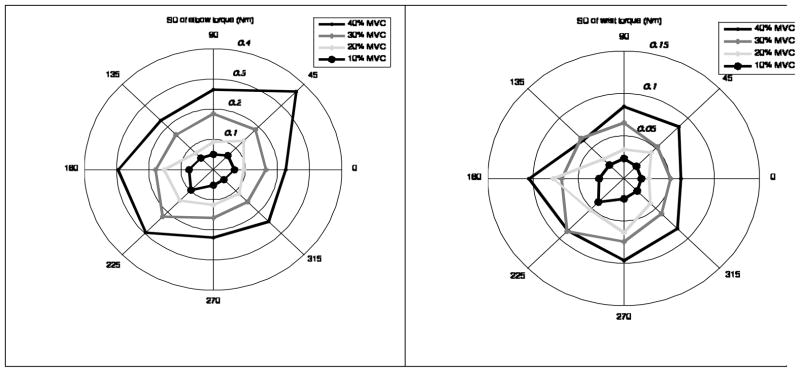
The intra-trial torque SDs for the elbow and wrist joints are presented in Figure 6. The SDs increase with the torque magnitude. The CVs do not change systematically. The shoulder joint torque is not affecting the grasp moment (this fact will be explained below in the Discussion section) and is not presented here.

Figure 6.

Torque variability (SD) at the elbow and wrist joints in the trials at different target force levels and directions, group average data. Note the different scales in the two panels. The ratios ‘SD (elbow joint)/SD (wrist joint)’ for different target force levels varied between 3.1 and 3.4.

4c. Intra-trial correlations

For each subject, the within-trials correlations of the force- and torque-time history processes —totally six: three endpoint force and moment components and three joint torques — at zero time lag were computed for all target force directions and levels. The obtained 4800 correlation coefficients (15 signal pairs × 32 tasks ×10 subjects) were then group averaged for individual force directions. The coefficients were computed for the signals that were digitized at 1000 Hz for 19 s. Hence, each coefficient was based on 19000 data pairs. Because consecutive observations in the continuous force recordings were not independent from each other and also due to the arbitrary selection of the digitization frequency, the classical methods of estimating statistical significance cannot be applied here.

The force component in the target direction showed close to zero correlation with both the force component in the orthogonal direction and grasp moment across all tasks. The first finding agrees well with the results reported by Friedman et al (2011) who analyzed the forces along the prescribed directions and perpendicular to them. In the tasks that required torque production both at the shoulder and elbow joints (the wrist joint was braced) force variance was approximately equal in both directions as it must be expected for a close-to-zero correlation. The within-trial correlations involving joint torques are described below.

Intra-trials correlations with the endpoint force

Across force directions, the correlations differed in magnitude but their sign, positive or negative, always corresponded to the joint function in force production at a given direction (Table 2). In some directions the correlations were very large, for instance for the zero degree direction the correlation with the shoulder torque was 0.97.

Table 2.

Intra-trials correlations between the force in the target direction and the joint torques in the individual trials. Group average data for different force directions (n=40; 4 force levels ×10 subjects).

Force direction, º	0.0	45.0	90.0	135.0	180.0	225.0	270.0	315.0
Torque direction	EEE	EEE	FEE	FFF	FFF	FFF	EFF	EEE
Shoulder	−0.97	−0.46	0.41	0.92	0.96	0.51	−0.33	−0.91
Elbow	−0.91	−0.88	−0.61	0.54	0.89	0.89	0.64	−0.51
Wrist	−0.68	−0.47	−0.16	0.38	0.59	0.43	0.22	−0.38

Intra-trial correlations with the grasp moment

The correlations between the grasp moment and the joint torques at the shoulder and elbow were low (around 0.1); hence, they are not presented here. The correlations with the wrist torque were strong and positive for all F_TASK directions (Table 3). Note that in contrast to the positive intra-trials correlations between the wrist torque and the grasp moment the correlation between these two variables across the tasks was negative (see section 4a above).

Table 3.

Intra-trials correlations between the grasp moment and the wrist torque. Group average data for different force directions (n=40; 4 force levels ×10 subjects).

Force direction, º	0.0	45.0	90.0	135.0	180.0	225.0	270.0	315.0
Joint torque direction	EEE	EEE	FEE	FFF	FFF	FFF	EFF	EEE
Correlation	0.65	0.65	0.76	0.70	0.68	0.71	0.80	0.77

Intra-trial correlations between the joint torques

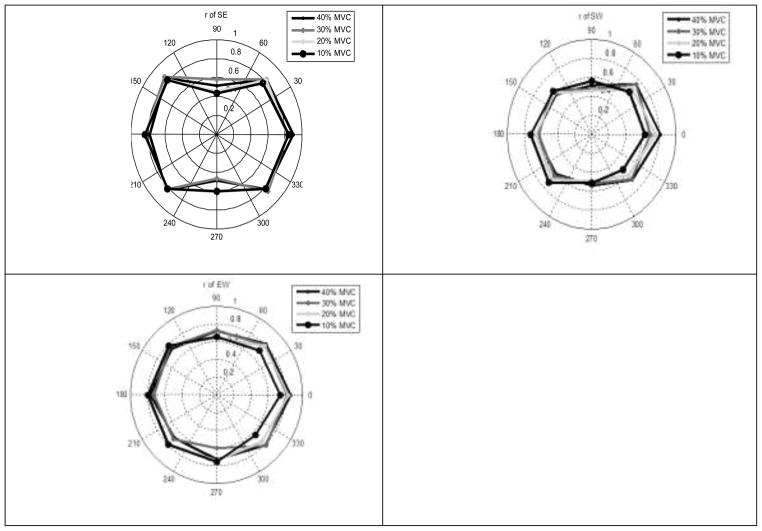
The coefficients are presented in Figure 7. The coefficients were positive for all force levels and directions. However, for α_TASK of 90º and 270º the correlations between the shoulder torque and the torques at the elbow and wrist joints were smaller than for other force directions. For instance, for α_TASK = 90º at 10%-force level; the shoulder-elbow correlation was only 0.43 while for α_TASK = 270º it was 0.60 – smaller than for all other force directions. When comparing group average data (1-way repeated measure ANOVA) the differences between the z-transformed coefficients of correlation were found to be significant (F_7,24= 49.07; p<0.01) and post hoc multiple comparisons also indicate significantly smaller coefficients at the direction 90º and 270º than at other directions. Note that at the directions of 90º and 270º the joint torques of the opposite signs are exerted: at 90º-FEE; at 270º - EFF, while at other force directions the joint torques were all either in flexion or in extension (see Figure 1).

Figure 7.

Intra-trial correlations between the joint torques at different force directions and force levels in individual trials. Group average data (n=10). Note that at the directions of 90º and 270º the intra-trial correlations are positive while the torques themselves are of opposite sense, FEE and EFF, respectively.

DISCUSSION

All three main hypotheses formulated in the Introduction have been falsified. Indeed:

Hypothesis 1: When subjects do not receive an explicit instruction that requires moment production they exert a zero moment on the environment. The data show that the subjects produced non-zero grasp moments of substantial magnitude.

Hypothesis 2: The variability indices of force magnitude and direction show similar dependencies on the target force magnitude and direction, e.g., in tasks where the force magnitude variability is maximal (minimal) the force direction variability is also maximal (minimal). The data show that the dependences of force magnitude and direction variability indices on task variables were opposite: In the directions where the variability of F_ACT was maximal directional of α_ACT was minimal and vice versa.

Hypothesis 3: The intra-trial correlations between the joint torques are positive in the tasks where the torques of similar sign are exerted (i.e. flexion-flexion or extension-extension) and the correlations are negative in the tasks that require the flexion (extension) torque at one joint and the extension (flexion) at another joint. The data show that in the tasks requiring the joint torque production in opposite directions the within-trial correlations between the joint torques were positive.

The following discussion covers the following topics: (1) grasp moments, (2) the end-effector force variability, and (3) joint torque variability and intra-trial correlations.

1. Grasp moments

The subjects generated the grasp moment in a very systematic manner (Figure 4 and Table1): the moment direction (clockwise or counterclockwise, as seen from the top) depended on the end-effector force direction and the moment magnitude depended on the force magnitude.

Across the tasks, i.e. across the directions and force levels, the grasp moments correlated negatively with the joint torques (see subsection 4a in the Results section). With increasing magnitude of the grasp moments the joint torques magnitudes decreased. It could be thought that the grasp moment production assisted in decreasing the joint torques. At first glance, the observed negative correlations can be explained by tendency to minimize the muscle efforts. However the actual situation is more complex. As well known, ‘correlation does not imply causation’ and at least some of the mentioned correlations can be false (spurious). It seems that they are.

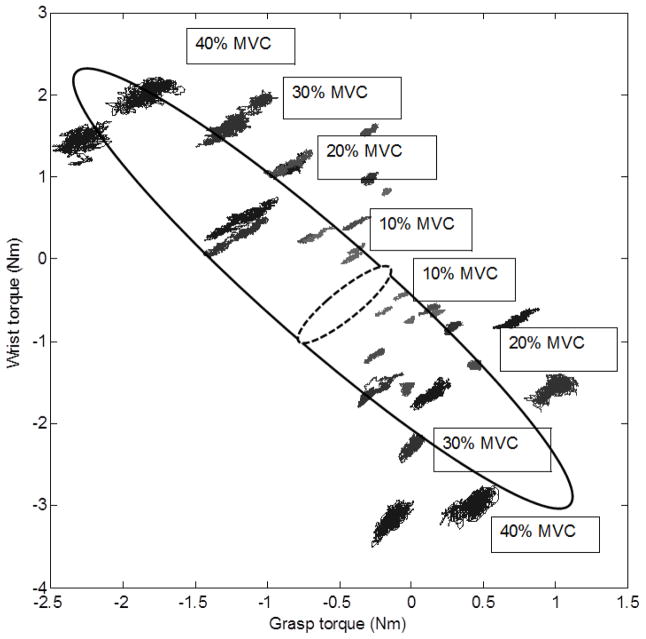
Consider the correlation between the grasp moment and the wrist torque. As mentioned above, the negative correlation between these two variables across the tasks was observed (subsection 4a in the Results section) while positive correlations within the trials were found (Figure 8, see also Table 3).

Figure 8.

Correlations between the grasp moment and the wrist torque. The figure is for a representative subject. Correlation across the target force levels and directions is negative (the large ellipse, r = −0.86, n= 32, p< 0.001) while the intra-trial correlations (small clouds of points) are all positive. For instance, for 315º direction the coefficients are: at 10% force r = 0.94, at 20% r = 0.92, at 30% r = 0.90 and at 40% r = 0.83.

We consider first biomechanical aspects of the grasp moment production and then the motor control issues.

Biomechanical aspects

For a three-link arm chain the relation between the joint torques and the endpoint force and moment is:

$$\mathbf{F}={[J^T]}^{-1}\mathbf{T}=\left[\begin{array}{ccc}\frac{C_{12}}{l_1{S}_2}& \frac{-l_2{C}_{12}-l_1{C}_1}{l_1{l}_2{S}_2}& \frac{C_1}{l_2{S}_2}\\ \frac{S_{12}}{l_1{S}_2}& \frac{-l_2{S}_{12}-l_1{S}_1}{l_1{l}_2{S}_2}& \frac{S_1}{l_2{S}_2}\\ \frac{l_3{S}_3}{l_1{S}_2}& \frac{-l_2{l}_3{S}_3-l_1{l}_3{S}_{23}}{l_1{l}_2{S}_2}& \frac{l_3{S}_{23}+l_2{S}_2}{l_2{S}_2}\end{array}\right]\left[\begin{array}{c}{T}_1\\ T_2\\ T_3\end{array}\right]=\left[\begin{array}{c}{F}_X\\ F_Y\\ M\end{array}\right]$$ (4)

where F is a 3×1 endpoint force vector, [J^T]¹ is the inverse of the transpose Jacobian, T is a 3×1 joint torque vector, T₁, T₂ and T₃ are the torques at the shoulder, elbow and wrist joints, respectively, and other symbols have been defined previously. The grasp (endpoint) moment M equals the dot product of the third row of the matrix and the joint torque vector. It is

$$M=\frac{l_3{S}_3}{l_1{S}_2}{T}_1+\left[\frac{-l_2{l}_3{S}_3-l_1{l}_3{S}_{23}}{l_1{l}_2{S}_2}\right]T_2+\frac{l_3{S}_{23}+l_2{S}_2}{l_2{S}_2}{T}_3$$ (5)

i.e. the grasp moment is an additive function of all three joint torques.

In the chain under consideration the wrist angle is 0º and hence S₃=0 and S₂₃=S₂. Therefore equation 5 can be simplified:

$$M=(1+\frac{l_3}{l_2})T_3-\frac{l_3}{l_2}{T}_2$$ (6a)

which for the average link length values in this research (l₂= 25.4 cm, l₃= 7.3 cm) yields

$$\text{M}=1.29T_3-0.29T_2$$ (6b)

Hence joint torque changes at the elbow and at the wrist of the same signs, i.e. both positive or both negative, induce the grasp moment changes in the opposite directions.

Because equation 6b predicts opposite effects of the wrist torque T₃ and elbow torque T₂ on the grasp moment M (the effects are positive for the wrist torque and negative for the elbow torque), it does not agree easily with the data presented in Table 1. For instance for the force vector directions of 225º and 270º, where the flexion—i.e. positive—torques were required at the elbow and wrist joints all subjects exerted grasp moments in the clockwise, i.e. negative, direction. Hence the expected positive effects of the wrist torque T₃ on the grasp moment M were not seen. Similar facts were observed for the 45º and 90º force directions where the negative (in extension) torques were produced at both joints while at least 9 subjects generated positive (counterclockwise) grasp moments. At the same time, there was excellent correspondence between the grasp moments predicted from equation 6b and the actual moments recorded in the experiment (r >0.99).

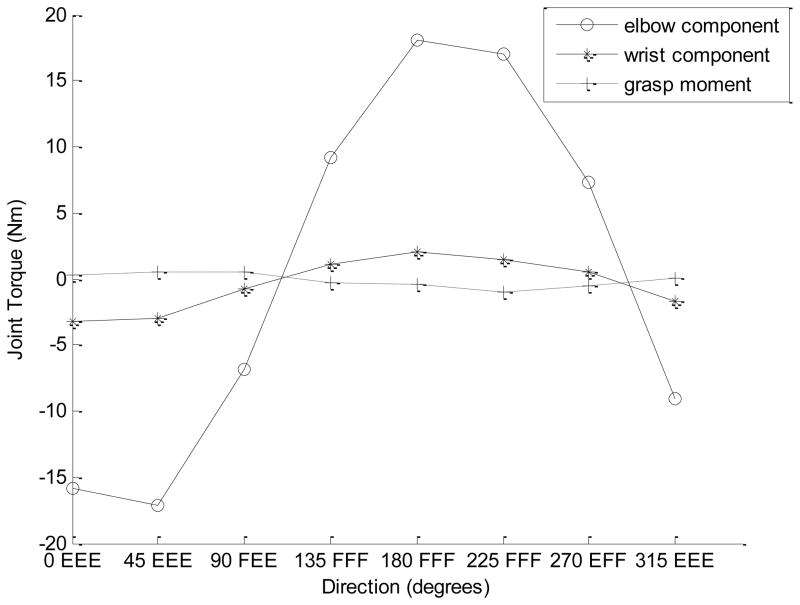
The disagreement between the negative ‘wrist torque-grasp moment’ correlation across the tasks and positive correlations within the trials is explained by the different magnitudes of the variations of T₂ and T₃, such that in different conditions effects of either T₂ (negative) or T₃ (positive) dominate (Figure 9).

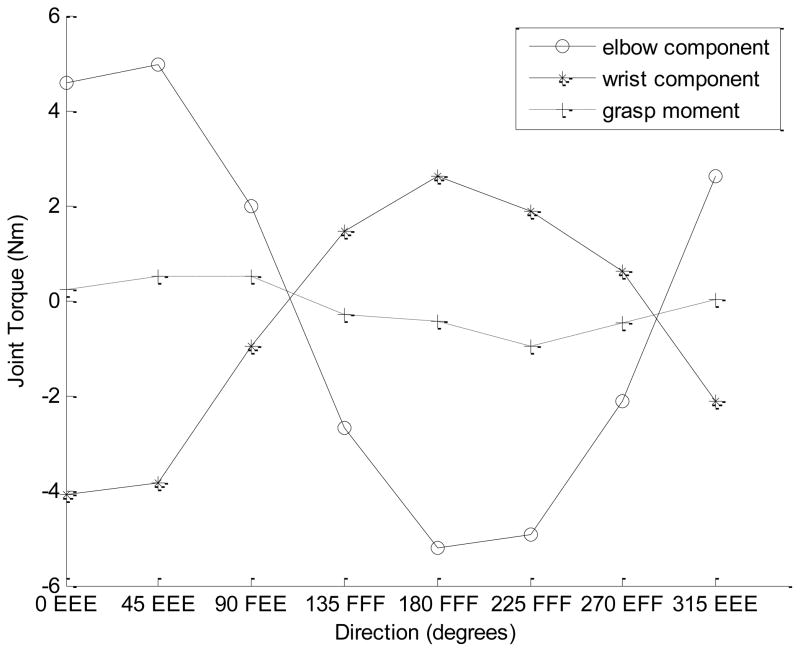
Figure 9.

Upper panel. Joint torques and the grasp moment across the target force directions (for 40% of MVC). The data are for a representative subject. Note that the grasp moment changes in the opposite directions to both joint torques (negative correlation).

Bottom panel. The joint torques multiplied by the coefficients from equation 6b: −0.29T₂ and 1.29T₃, respectively. The grasp moment changes in the same direction as the elbow joint component (−0.29T₂) and opposite to the wrist joint component (1.29T₃). This should result in the negative across tasks correlation between the T₃ and M despite their positive relation seen in equation 6.

From Figure 9 and the analysis presented in the figure caption it follows that the negative across trials correlations between T₃ and M are due to two factors: the inter-trial correlations between the joint torques and the much larger range of the elbow torque changes than the wrist torque changes (the upper panel in Figure 9). The same factors explain the negative correlation between the shoulder torque and grasp moment (r = −0.55) mentioned above in section 4a although, according to equation 6, shoulder torque does not immediately affect the grasp moment at all. The positive within-trials correlations between the grasp moment and wrist torque can be explained by two mechanisms. First, the positive relation is due to straightforward mechanics (see equation 6). Second, the negative effect of the intra-trial T₂ variations is smaller in this case: the T₃ coefficient (1.29) is 4.45 times larger than the T₂ coefficient (1.29/0.29=4.45) while the variations of T₂ are larger than those of T₃ only 3.1–3.4-fold (see the caption to Figure 6). Hence the positive effect of T₃ dominates over the negative effect of T₂.

Motor control aspects

Generating the non-required grasp moment is in accord with the reported in the literature tendency of the subjects to produce the static endpoint forces in the direction different from the instructed direction — when the visual feedback is not provided and the external object is mechanically constrained. For instance, during pedaling the athletes exert forces not only in a tangential direction but also in the normal directions along the crank thus either compressing or extending it (Cavanagh and Sanderson 1986). Such a pattern of pedaling is evidently suboptimal —the athletes spend efforts and energy on generating forces that are not necessary for the task. However, even the best athletes do this. Similar patterns of force production are reported for the manual wheelchair propulsion (van der Woude et al. 2000). Examples of producing force in a ‘wrong’ direction are abundant in the literature. Grieve and Pheasant (1981) called these directions ‘naturally preferred’ and introduced a measure for estimating the effectiveness of static force efforts – the maximum advantage of static force efforts (MACE). Pan et al. (2005) in an elegant study have shown that these results can be interpreted in terms of an unknown optimization used by the central controller. While the authors were not able to reconstruct the cost functions used by the central controller they derived from the experimental data the so-called “isocost” contours of objective functions. On the whole, these results suggest that the observed force patterns are due to some kind of optimization used by the central controller.

None of the above studies analyzed the grasp moment or any torque exerted on the environment. Application of the optimization methods in this case is however unusual: as follows from equation 6 the grasp moment is a function of the opposite —positive and negative—influences from the involved joint torques. Consider a task where both torques are of the same sign, for instance force should be exerted at 135º where both the elbow and wrist joint act in flexion. Suppose that the subject is also exerting a non-specified grasp moment while minimizing an unknown cost function of the joint torques. For simplicity assume that the shoulder joint is immobilized and its torque does not affect the grasp moment. If the performer decreases the wrist torque, the grasp moment will decrease but if the elbow torque is decreased the grasp moment will increase. The effect of the simultaneous increase or decrease of both joint torques on the grasp moment is unclear in this case.

In motor control studies addressing the issue of optimization additive cost functions have been commonly used (Nubar and Contini 1961; Yeo 1976; Crowninshield 1981; An et al. 1984; Herzog and Leonard 1991; Pandy and Zajac 1991; Tsirakos et al. 1997; Anderson and Pandy 2001; Raikova and Prilutsky 2001; Prilutsky and Zatsiorsky 2002; Zatsiorsky et al. 2002; Ackermann and van den Bogert 2010; Park et al. 2010). A newly developed analytic inverse optimization (ANIO) method that allows reconstructing the unknown cost function from experimental data—rather than assuming the function a priori—is also based on the presumption that the sought cost function is additive with respect to some ‘elemental’ variables, for instance individual finger forces in multi-finger tasks (Terekhov et al. 2010; Terekhov and Zatsiorsky 2011). The ANIO method was successfully applied to many multi-finger prehension and pressing tasks (Park et al. 2010; Niu et al. 2011; Park et al. 2011a; Park et al. 2011b; Niu et al. 2012; Park et al. 2012).

In search of the optimization cost function that could explain the findings of the present study we applied the ANIO method to the obtained experimental data (see Appendix). The outcome was unambiguous: the central controller does not use for the control of the endpoint force and moment a cost function additive with respect to the joint torques. This finding is in stark contrast with the arm movement control where such an additive cost function as the minimum torque change (the sum of the squared values of the time derivatives of the joint torques) has been suggested (Nakano et al. 1999) and validated (Wada et al. 2006). Developing optimization methods for static serial chains will be a challenge for researchers.

Future research

We are going to further test the mechanisms of the grasp moment generation in three sets of experiments: (a) the handle will be placed in a freely rotating housing (such that the grasp moment cannot be exerted), (b) the handle diameter will differ, and (c) the subjects will have to produce the grasp moments of different magnitude in clockwise and counterclockwise directions while simultaneously exerting the end-effector force of various magnitude in different directions such that the task becomes non-redundant.

2. The end-effector force variability

The increase of the force magnitude variability (SD) with the force level is a well known phenomenon discussed in detail in many publications (for a recent review see e.g. Friedman et al. 2011). This discussion will not be repeated here.

In contrast, the data on the force direction variability are relatively new. So far the dependence of SD(α_ACT) on F_TASK was addressed only in a recent study by Friedman et al. (2011) who found a counter-intuitive relation: SD(α_ACT) decreased with an increase in F_TASK. We were not able to confirm this finding quantitatively (in the present study the coefficient of correlation was only −0.127, p > 0.05), but taken together the results from the two studies provide sufficient evidence to conclude that force direction variability does not increase with the force level (see Figure 5b). The differences between the results of the two studies may be due to experimental details: In the Friedman et al. experiments the wrist was braced and hence the arm acted as a two-link system while in the present study more natural conditions of the arm functioning were preserved.

We would like to bring up one observation that can lead to a hypothesis that may explain the opposite trends of SD(F_ACT) and SD(α_ACT) as functions of F_TASK. Equation 3 is written in the external, X and Y, coordinates (explained in Figure 1) but it can be also written in the local coordinates, along the target force direction and normal to it. The force in the direction perpendicular to the target one is the main contributor to the angular deviation of the actual force from the target direction. For instance, if the target force is at 90° (in the ‘vertical’ direction in Figure 5), the angular deviation is a function of the force component in the ‘horizontal’ directions, i.e. in 0º and 180º directions. For 0º target force direction, the angular deviations of the force vector are determined by the ‘vertically’ oriented force components, i.e. the force components at 90º and 270º.

Comparing the data presented in Figures 5a and b suggests that across the targeted directions the variability of F_ACT and α_ACT exhibit opposite trends. In the directions where the variability of F_ACT is maximal (90 º and 270 º) directional of α_ACT is minimal and in the directions where α_ACT variability is maximal (0 º and 180 º) the F_ACT variability is minimal. Across the targeted force directions and levels, the coefficient of correlation between the F_ACT and α_ACT variability was r = −0.67 (n = 32; α <0.001). This observation, if confirmed, leads to a hypothesis that the force direction control is determined (or at least affected) by neural processes functioning in the body centered system of coordinates, i.e. in the system of coordinates with ‘forward-backward and left-right’ axes (and not, for instance, in the task relevant systems of coordinates with the axes along the target force direction and normal to it). This hypothesis agrees with the earlier postulate that the control is organized within the shoulder-centered referent frame (Soechting 1992). The accuracy of the control along the two shoulder-centered axes of coordinates is naturally different and this difference is manifested in the results shown in Figure 5. If this hypothesis is accepted as a starting point, a large body of experimental evidence would be necessary to either validate or compromise it.

Future research

We expect that systematic variations in the arm position can provide additional information on the mechanisms behind the data presented in Figure 5a and b.

3. Joint torque variability and intra--trial correlations

Intra-trial correlations were computed for the zero time lag between the two processes and hence these correlations characterize the level of synchronization between the processes.

We are specifically interested in the two tasks—with the force directions of 90º and 270º—in which the joint torques of the opposite signs were exerted: at 90º-FEE; and at 270º - EFF. As expected, for these force directions the within-trial correlations of the joint torques with the endpoint force of the opposite signs were found (Table 2). Hence when the end-effector force increased or decreased, the torques at the shoulder and other two joints changed in opposite directions, and the negative torque-torque correlations could be expected (Hypothesis 3).

In contrast, the torque-torque within-trial correlations were positive for the 90º and 270º force vector directions, similarly to all other directions (Figure 7). [Positive torque-torque correlations were also reported by Friedman et al. (2011) however in their study there were no tasks requiring the joint torque production in opposite directions.] The correlation coefficients at the 90º and 270º force directions were, however, smaller than at other directions. The discussion below attempts to address this controversy.

Let us assume that the endpoint force magnitude variations are due to the variability of a central, neural drive. If the drive ‘intensity’ (whatever it physiologically is) increases, the endpoint force also increases accompanied by an increase of the joint torque magnitudes. Because the torques are of opposite signs, a negative correlation between them should be expected following changes in the neural drive. Instead a positive correlation was observed..

It seems that more than one mechanism (the ‘neural drive’ variability) affect the result. Decreased intra-trial correlations for the 90º and 270º force directions, as compared with other directions, where either flexion-flexion or extension-extension torque combinations were required, speak in favor of this possibility. Such a second mechanism could be the activation of two-joint muscles—the long heads of the biceps brachii and triceps brachii—that serve both the shoulder and elbow joints. Activation of either one of these muscles results in producing flexion-flexion or extension-extension torque sets. In the tasks requiring the joint torques of the same sign the effects of the two abovementioned central drives are summed up (and very large intra-trial correlations are observed), while for the force directions requiring joint torques of opposite signs, the two drive effects are subtracted (and we observe smaller correlation).

Study limitations

The main limitation of this study was that only one arm position was used, and it is not known to what extent the observations depended on the arm posture.

Future research

We are planning to perform similar experiments with arm configurations that allow using a larger number of force directions for which the joint torques of opposite signs are required. We plan to concentrate on coordination of only two joints (the wrist will be braced). For the two-link arm, the end-point force can be represented by two force components (explained in Zatsiorsky 2002, Chapter 2, see Figure 2.19) that are due to: (a) shoulder torque – this force component is along the pointing axis – the axis along the forearm, and (b) elbow torque—this force component is along the radial axis – the axis along the line from the shoulder center to the endpoints. The forces that require the torques of opposite signs are located in the sectors limited by the two above axes. Due to the selected arm configuration (see Figure 1) these sectors were narrow in the present research. By changing the arm posture we will able to offer many force directions requiring the torques of opposite sign. We expect that this will allow shedding more light on the mechanism of the end-point force control.

Appendix

In this Appendix we demonstrate that the sharing of the joint torques cannot be explained by any additive cost function with respect to joint torques. An exact definition of such function will be given in the next paragraph. The general idea of the proof is as follows. We first show that if the experimental data are explained by an additive cost function then this cost function must be quadratic. Then we show that the data cannot be explained by any additive quadratic cost function. From these statements it follows that the data cannot be accounted by any additive cost function. Below we present elements used in the proof, which follows after.

Optimization problem

As emphasized in the main text, the problem of joint torques distribution is redundant if the instruction is given only with respect to the endpoint force. It is reasonable to assume that the distribution of the joint torques adopted by the subjects minimized a certain cost function. Mathematically this can be formalized as:

$$G(T_1,T_2,T_3)\to min$$

subject to the constraints on the end point force

$$[\mathbf{C}]\mathbf{T}=\mathbf{f},$$

where the matrix [C] comprises the first two rows of the inverse transpose Jacobian matrix [J^T]⁻¹ defined in equation (4) and f = [F_X, F_Y]^T is the endpoint force vector.

Uniqueness Theorem

Recently we formulated and proved the Uniqueness Theorem for inverse optimization problems (Terekhov et al 2010). The theorem suggests the conditions under which the cost function can be identified uniquely from experimental data. The main assumption of the Uniqueness Theorem is that the cost function is additive with respect to a known set of variables. If joint torques are chosen as such variables, this assumption means that the cost function is

$$G(T_1,T_2,T_3)=g_1(T_1)+g_2(T_2)+g_3(T_3),$$

where g₁, g₂, g₃ are unknown functions of individual torques.

For the current problem, the Uniqueness Theorem requires that, for different task values F_X and F_Y, the experimental data be distributed over a 2-d surface S. In addition it requires that the matrix [Č] = [I] − [C]^T([C][C]^T)⁻¹[C] cannot be made block-diagonal by simultaneous swapping of the columns and rows with the same indices (i.e. the problem is not-splittable). The reader can verify that the latter requirement is satisfied. Then, according to the Uniqueness Theorem, for every two functions G and G̃, such that

$$[\check{\mathbf{C}}]\text{grad}G=0\text{and}[\check{\mathbf{C}}]\text{grad}\stackrel{\sim }{G}=0$$ (A1)

on the experimental surface S, follows

$$G(T_1,T_2,T_3)=r\stackrel{\sim }{G}(T_1,T_2,T_3)+{[\mathbf{q}]}^T[\mathbf{T}],$$ (A2)

where grad stands for gradient, r is a non-vanishing scalar value, [q] is a 3-d vector, for which [Č][q] = 0.

Planarity of the data

A particular implication of this theorem is that if the experimental data are distributed along a plane, then the cost function — if it exists — must be a quadratic polynomial (for details see Terekhov et al. 2010; Terekhov, Zatsiorsky 2011). In line with this fact we begin with checking whether the data have planar distribution. We performed the principal component analysis (PCA) and found that the first two PCs accounted for 99.98±0.01% of the total variance. Since the wrist torque was significantly smaller in magnitude than the shoulder and elbow torques, such a high degree of planarity could result from the uneven spread of the magnitudes. To verify that it was not the case we normalized the torques by its standard deviation over all trials (SD) and repeated the PCA. For normalized data the planarity was still very high: the two first PCs accounted for 99.49±0.45% of the total variance. This finding suggests that the experimental data have planar distribution, i.e. they can be fitted by equation

$${[\mathbf{A}]}^T([\mathbf{T}]-[\overline{\mathbf{T}}])=0,$$ (A3)

where vector [A] is the normal to the plane formed by the data. The vector [A] coincides with the last PC (the one accounting for the smallest percentage of total variance); [T̄] is the average of the joint torques across the trials.

The planarity of the data suggests that the cost function — if it exists —must be searched on the class of quadratic polynomials.

Cost function coefficients

According to the Uniqueness theorem and the previous paragraph, if the central controller uses a cost function G, additive with respect to the joint torques, then this cost function must be quadratic:

$$G=k_1{(T_1-T_1^0)}^2+k_2{(T_2-T_0^2)}^2+k_3{(T_3-T_0^3)}^2$$ (A4)

According to the Lagrange principle for the inverse optimization problems proved in (Terekhov et al. 2010), if the experimental data minimize G, then G satisfies (A1) on the experimental plane (A3).

Now let us define a function

$$G={\stackrel{\sim }{k}}_1{({\stackrel{\sim }{T}}_1-{\stackrel{\sim }{T}}_1^0)}^2+{\stackrel{\sim }{k}}_2{({\stackrel{\sim }{T}}_2-{\stackrel{\sim }{T}}_2^0)}^2+{\stackrel{\sim }{k}}_3{({\stackrel{\sim }{T}}_3-{\stackrel{\sim }{T}}_3^0)}^2$$ (A5)

such that the coefficients k̃₁, k̃₂, k̃₃ satisfy

$$[\check{\mathbf{C}}][\stackrel{\sim }{\mathbf{K}}]=[\mathbf{A}],$$ (A6)

where [K̃] is a diagonal matrix with k̃₁, k̃₂, k̃₃ on the diagonal and $\left[\stackrel{\sim }{\mathbf{T}}\right]={[{\stackrel{\sim }{T}}_1^0,{\stackrel{\sim }{T}}_2^0,{\stackrel{\sim }{T}}_3^0]}^T=\left[\overline{\mathbf{T}}\right].$

One can verify that such a function G̃ also satisfies (A1) on the experimental plane (A3). Hence, according to Uniqueness Theorem, (A2) holds, and in particular the second-order coefficients of G (A4) and G̃ (A5) coincide up to normalization:

$$k_1=r{\stackrel{\sim }{k}}_1,k_2=r{\stackrel{\sim }{k}}_3,k_3=r{\stackrel{\sim }{k}}_3.$$ (A7)

We determined the second order coefficients k₁, k₂, k₃ of the presumed “true” cost function G using (A6) and (A7). Since a cost function can be determined only up to multiplication by a scalar value, we arbitrary choose r such that k₁² + k₂² + k₃² = 1. The computed coefficients were k₁: −0.02±0.01, k₂: −0.14±0.02, k₃: 0.99±0.01 (the units of the second-order coefficients are arbitrary). The signs of the coefficients were the same in all subjects. Clearly, the function G with negative second-order coefficients cannot be a cost function, because it does not have any local minima for the available constraints.

Proof

Assume that the experimental data can be explained by a function G additive with respect to the torques. Then, it must satisfy equation (A1) on the experimental data (A3). At the same time, there exists an additive quadratic function G̃ which satisfies (A1) on (A3) and its second-order coefficients have different signs. According to Uniqueness theorem, for the functions G and G̃ holds (A2) and hence G is also quadratic and its second-order coefficients also have different signs. But then G cannot be the cost function explaining the experimental data. Hence, G is not additive with respect to the joint torques. It proves that no function additive with respect to the torques can explain the joint torque sharing observed in the experiments.

Quality of estimation of the experimental plane

One can suggest that since the experimental plane is not ideal (the first 2 PCs account for less than 100%), its orientation is known imprecisely and hence even if the plane (A3) cannot be explained by an additive cost function, it may happen that some other plane, very close to (A3), can. This suggestion would be valid if the percentage of variance explained by the first 2 PCs was not so high. To illustrate this, we determined a plane, which could be explained by an additive cost function and which was the closest to the experimental plane in terms of the dihedral angle between the two planes (Niu et al. 2011; Niu et al. 2012). For such a plane we determined the cost function and then for each combination of F_X and F_Y we computed the torques this function predicted. The results for a representative subject are shown in the Figure A1.

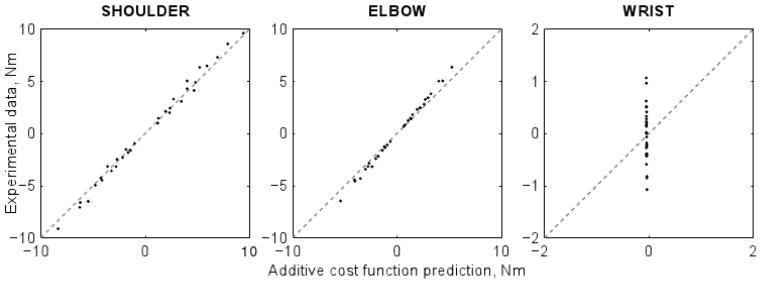
Figure A1.

The predictions of the joint torques by an additive cost function. The predictions were good for the shoulder and elbow torques and they fell short for the wrist torque.

One can see that, though such a cost function could rather well predict the shoulder and elbow torques, it failed completely for the wrist torque. Hence, it is not just a question of prediction quality: any cost function additive with respect to the joint torques will fail to reproduce the general tendency of the torque sharing. This, however, does not exclude that the data could be explained by another cost function, which would be, for example, additive with respect to the muscle forces, but not to the joint torques.