Variational multiscale models for charge transport

Abstract

This work presents a few variational multiscale models for charge transport in complex physical, chemical and biological systems and engineering devices, such as fuel cells, solar cells, battery cells, nanofluidics, transistors and ion channels. An essential ingredient of the present models, introduced in an earlier paper (Bulletin of Mathematical Biology, 72, 1562-1622, 2010), is the use of differential geometry theory of surfaces as a natural means to geometrically separate the macroscopic domain from the microscopic domain, meanwhile, dynamically couple discrete and continuum descriptions. Our main strategy is to construct the total energy functional of a charge transport system to encompass the polar and nonpolar free energies of solvation, and chemical potential related energy. By using the Euler-Lagrange variation, coupled Laplace-Beltrami and Poisson-Nernst-Planck (LB-PNP) equations are derived. The solution of the LB-PNP equations leads to the minimization of the total free energy, and explicit profiles of electrostatic potential and densities of charge species. To further reduce the computational complexity, the Boltzmann distribution obtained from the Poisson-Boltzmann (PB) equation is utilized to represent the densities of certain charge species so as to avoid the computationally expensive solution of some Nernst-Planck (NP) equations. Consequently, the coupled Laplace-Beltrami and Poisson-Boltzmann-Nernst-Planck (LB-PBNP) equations are proposed for charge transport in heterogeneous systems. A major emphasis of the present formulation is the consistency between equilibrium LB-PB theory and non-equilibrium LB-PNP theory at equilibrium. Another major emphasis is the capability of the reduced LB-PBNP model to fully recover the prediction of the LB-PNP model at non-equilibrium settings. To account for the fluid impact on the charge transport, we derive coupled Laplace-Beltrami, Poisson-Nernst-Planck and Navier-Stokes equations from the variational principle for chemo-electro-fluid systems. A number of computational algorithms is developed to implement the proposed new variational multiscale models in an efficient manner. A set of ten protein molecules and a realistic ion channel, Gramicidin A, are employed to confirm the consistency and verify the capability. Extensive numerical experiment is designed to validate the proposed variational multiscale models. A good quantitative agreement between our model prediction and the experimental measurement of current-voltage curves is observed for the Gramicidin A channel transport. This paper also provides a brief review of the field.

I Introduction

Charge transport is one of the most important processes in nature and man-made devices. Due to the continuous miniaturization of mechanical, optical, and electronic devices, molecular mechanism holds the key to the understanding of charge transport in a vast variety of complex nano-bio devices, such as deoxyribonucleic acid (DNA) nanowires, molecular junctions, solar cells, fuel cells, battery cells, molecular switches, nanotubes, field effect transistors, nanofibers, thin films, ion channels, ATPases, neuron synapses, etc. Apart from some oxidation and/or reduction in simple chemicals, which are described by ab initio quantum theories, most charge transport processes are associated with complex molecular structures or sophisticated devices in heterogeneous settings. As such, the molecular mechanism of the charge transport often involves an excessively large number of degrees of freedom and gives rise to enormous challenges to theoretical modeling and computations.¹⁸²

One typical system is the metal oxide semiconductor field effect transistor (MOSFET), or complementary metal oxide semiconductor (CMOS), which is the fundamental building block of large scale integrated circuits used in almost all electronic equipments. Nano-scale transistors, which are commonly used nowadays, still operate with the classical principle, while severe quantum effects, i.e., the channel tunneling and gate leakage, have to be suppressed by appropriate electrostatic potentials and designs.^54,134 Quantum structures, including nano-mechanical resonators, quantum dots, quantum wires, single electron transistors, and similar low dimensional structures, have been contemplated and/or prototyped.^70,102 They utilize the fundamental properties of nature, such as quantum coherence, i.e., the possibility for a quantum system to occupy several states simultaneously, and quantum correlation or entanglement which do not have direct analogs in classical physics. The charge transport and performance of quantum devices are subjects of intensive research.²⁷

Another example is the transport behavior of charge and water in the proton exchange membranes (PEMs) of fuel cells, which remains a subject of much interest in both theoretical and experimental studies.¹⁷⁹ The role of PEMs in the selective permeation of protons and effective blocking of anions is essential to the fuel cell performance. The molecular morphology of PEM polymers, including Nafion, most likely consists of negatively charged pores of nanometer diameter. Meticulous water management is crucial to avoid both dehydration and flooding of the fuel cell so as to sustain its continuous function.^74,86 The understanding of the PEM fuel cell's working principle and the improvement of fuel cell's performance are strategically important to alternative and environmentally friendly energy sources.¹³⁷ However, the underlying complex material structures, large spatial dimensions, chemical reactions, and charge and mass transport in the fuel cells pose severe challenges to their theoretical understanding.

Similar to fuel cells, battery cells have been intensively studied and will continue to be an important topic in chemistry, physics, engineering and material sciences for years to come.¹⁶¹ Battery cell unit typically consists of positive and negative electrode phases, separated by a functional polymer electrolyte, which selectively permeates certain ions. Battery charge/discharge cycling often induces volumetric change or deformation, which may lead to delamination at particle-binder and particle-current collector interfaces, and the loss of electrical connectivity.¹⁵² These problems contribute to the battery capacity fading and mechanical failure. A main task in battery cell design and modeling is to improve battery performance by reducing charge/discharge cyclic deformation. The Nernst-Planck equation is often used in the field to model the battery electrokinetics.^132,175 However, chemical, thermodynamic, mechanical and electrostatic properties of realistic microstructures are important aspects as well.

The other interesting subject concerns nanofluidics which is a new interdisciplinary field that makes use of precise control and manipulation of fluids at submicrometer and nanometer scales to study the behavior of molecular and biological systems. Fluids confined at the nanometer scale exhibit physical behaviors which are not observed in larger scales, because the characteristic length scale of the fluid coincides with the length scale of the biomolecule and the scale of the Debye length. Mirco/nano fluidic devices can be used to obtain a variety of interesting basic measurements including molecular diffusion coefficients,¹⁰⁵ pH values,^122,184 chemical binding affinities,¹⁰⁵ and enzyme reaction kinetics.^60,88 Nanobio fluidic techniques have been instrumented for polymerase chain reaction (PCR) amplifications,¹⁹ macromolecule accumulator,^40,186 electrokinetics,¹⁴ biomaterial separation¹¹⁰ membrane protein crystallization,¹²⁰ and DNA computing processor for gene expression analysis.¹⁹² Recently, the state of the art in nanofluidic dynamic arrays has been devised for high-throughput single nucleotide polymorphism genotyping.¹⁷⁶ Nanofluidic devices have also been widely used as electronic circuits,¹⁸⁸ local charge inversion,⁹¹ and photonic crystal circuits.⁶⁷ At the sub-millimeter scale, microfluidic and digital microfluidic devices have been widely used for electrowetting, electrode array, dielectrophoresis, DNA pyrosequencing, DNA miniaturized sequencing, immunoassay, cell manipulation, cell separation, and cell patterning. Currently, the development in microfluidics and nanofluidics is essentially empirical.¹⁶⁰ Since nanofluidic device prototyping and fabrication are technically challenging and financially costly, the lack of theoretical prediction and quantitative understanding hinders the further development of the field.

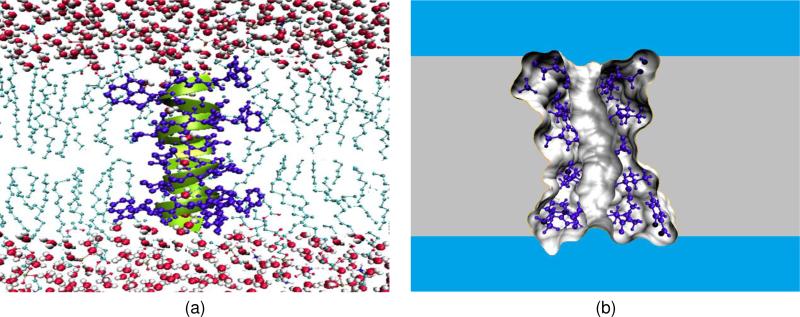
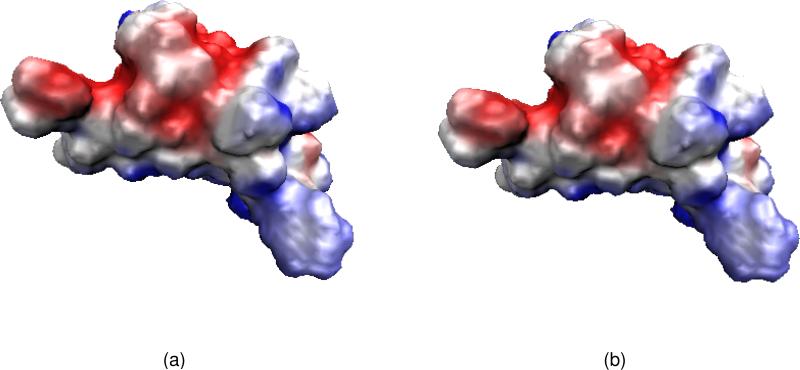
Finally, ion channels are transmembrane proteins that facilitate selected ion permeation and maintain proper cellular ion compositions.⁵⁵ The phospholipid bilayer provides a low dielectric hydrophobic barrier to the passage of charged ions, while strongly polar or even charged amino acids of ion channel proteins offer an ion conducting pathway across the hydrophobic interior of the membrane bilayer.^97,107 Figure 1(a) presents a graphic representation of an ion channel. Ion channels play critical roles in many physiological functions such as the conversion of chemical, physical, mechanical, photonic and thermal stimuli into electric signals so that they can pass through nerves and be analyzed by a brain.⁶⁹ Additionally, they maintain an intercellular material and charge balance, regulate signal transduction and control cardiac excitability. Therefore, ion channels are crucial to cell survival and function, and are key components in many biological processes. Physically, ion channels are mostly gated by ligands or voltages — the opening or closing of ligand-gated ion channels is controlled by the binding of ligands to the channel protein, while the state of voltage-gated ion channels depends on the electric field gradient across a plasma membrane. Ion channels can be regarded as nature-made nano-bio transistors. The health impact of ion channels has been well recognized — ion channels are common targets in the rational drug design.⁶⁹

Figure 1.

Illustration of ion channel and its multiscale simplification. (a) Atomic view of the Gramicidin A channel in the membrane and aqueous environment; (b) A cross section of the multiscale representation of the system.

A common feature of the aforementioned nano-transistor, fuel cell, battery cell, nanofluidic and ion channel systems is their involvement of charge transport. The main purpose of our theoretical modeling of charge transport is to predict device characteristics and performance. This amounts to the understanding of transport features, including the rate of charge movement, current-voltage (I-V) characteristics, output power, and efficiency, etc. One of most popular transport models is the Boltzmann equation, or the Boltzmann-Vlasov equation, which describes the kinetic of a typical particle, such as electron, phonon, or photon, in terms of distribution function, Wigner distribution¹⁰¹ or density operator,² due to the free motion, binary collision and/or external field effects.^21,38,90 The quantum Boltzmann equation, known as the Waldmann-Snider equation,^157,174 can provide quantum corrections to the classical transport expression. The Waldmann-Snider equation can be formally derived from the BBGKY hierarchy with an elegant binary collision closure.¹⁵⁷ Pair particle correlations in the framework of the quantum Boltzmann kinetic theory have been considered.^158,159 Stochastic approaches, such as the Monte Carlo algorithm, have also been widely used for charge transport in semiconductor device simulations.⁹⁹ Other methods, such as the FokkerPlanck equation and the Master equation,^71,98 describe the time evolution of the probability function. A commonly used transport model for nano-electronic devices is the non-equilibrium Green's function (NEGF) formalism^{50,51,114,164} originally developed by Schwinger,¹⁴⁹ and Kadanoff and Baym.¹⁰⁴ This approach is often used to solve the Poisson-Schrödinger equations for charge transport in nano-electronic devices.^4,9,121,166 Recently, coupled Poisson and Kohn-Sham equations have been derived from the variational principle to describe electron transport in MOSFETs via the density functional theory (DFT) formalism.²⁷ The reader is referred to Ref²⁷ for a review-style introduction to current issues in the charge transport of nano electronic devices.

Typically, fuel cell, solar cell, battery cell, nanofluidic and ion channel systems have a large number of degrees of freedom, and thus exclude the possibility of single-scale ab initio quantum mechanical descriptions, such as those used in the modeling of electron transfer in small molecules. Theoretical models in the field are mostly phenomenological and continuum in nature. They describe the hydrodynamic motion and change of velocity and mass in fuel cell and nanofluidic systems, which might be coupled to electric and/or electrostatic forces. In 1965, Rice and Whitehead proposed coupled Navier-Stokes and Poisson-Boltzmann (PB) equations for the continuum modeling of the transport of electrolyte solutions in long nanometer-diameter capillaries.¹³⁸ Navier-Stokes equations can be derived from the Boltzmann equation,^158,159 providing a description of density, velocity, and energy. Together with the PB equation, the Navier-Stokes equations are capable of coupling fluid motion with electric/electrostatic forces.

In early 1990s, Eisenberg and his coworkers^{7,30,63–65,155} pioneered the theory of the Poisson-Nernst-Planck (PNP) equations for ion transport in membrane channels and coined the name “Poisson-Nernst-Planck”, which is currently very popular in many fields, although a similar approach called drift-diffusion equations had been used in the electronic devices community for years. As a mean field theory, the PNP model treats the ion flow as the averaged ion concentration driven by the electrostatic potential force and ion concentration gradient. In general, the PNP theory goes beyond the DebyeHückel limiting law and the Guoy-Chapman theory. Unlike its use in electronic devices, fuel cells, battery cells, and nanofluidic systems, the PNP model in ion channel modeling incorporates the atomistic (permanent) charge description of channel proteins into the Poisson equation, and thus, it hybrids the macroscopic continuum description of ionic channel flows with the microscopic discrete representation of protein electrostatic charge sources, see Fig 1. Over the years, Coalson and his coworkers have intensively calibrated and validated the PNP and modified PNP models for realistic ion channel systems, which have significantly advanced the PNP theory.^{44,82,112,123} The PNP model is able to offer very good predictions of I-V curves for many channel proteins.^23,112,195 Because of the continuum representation of ions, the finite size effect and non-electrostatic interactions of ion species are not considered in the original PNP theory. To address these drawbacks, many modified PNP models, including the approaches of the potential of mean forces, have been proposed in the literature.^{48,96,103,109,119,123,154} It turns out that the potential force of the PNP model can be easily modified, while the essential structure of the equations remains unchanged. The advantages and limitations of all the abovementioned ion channel models have been a subject of intensive discussion in the literature.3,8,36,37,41,43,44,44,61,64,65,113,117,118,124,142,148,169 In addition to its success in biophysics, the PNP model is also widely used in semiconductor¹⁰⁰ and electrochemistry nowadays.^16,144

Recently, researchers have employed coupled PNP and the Navier-Stokes (NS) equations for nanofluidic simulations.^{30,32,42,47,100,171,172,178,182,197,199} These models are able to provide a more detailed description of the ionic distribution in nanopore channels. Chang et al compared the performance of the PB model and the PNP model for the streaming current in silica nanofluidic channels.²⁴ Adalsteinsson et al combined the Brownian dynamics of ions in the nanopore channel with the continuum PNP model for regions away from the nanopore channel.¹ Note that in ion channel models, Brownian dynamics typically describes individual ions of finite size in fluid regions, while treat the channel protein as a dielectric continuum.⁴³ Another important modeling aspect is the liquid-solid interface contact angle and interface morphology under an external electric field. The Lippmann-Young equation is utilized for the estimation of liquid-solid interface contact angle and droplet morphology in electrowetting-on-dielectric actuators.¹⁶⁰ Abovementioned models might work quite well in a particular circumstance, but none of them provides comprehensive predictions for general nanofluidic and fuel cell settings, because one or more important components are missing. For example, it is not uncommon for nanofluidic processes to induce structural modifications and even chemical reactions,^108,168 which are not described in the abovementioned models. Mechanical or structural stability of PEM polymers is crucial to the fuel cell performance and is often maintained via the water management in the literature.^74,86 Therefore, it is imperative to develop innovative models that are able to account for configurational changes induced by charge and mass transport processes.

It is very likely that maintaining a fluid flow balance between intracellular and extracellular spaces is one of the most important roles of ion channels in physiology. A comprehensive model, which constitutes coupled Poisson-Boltzmann, Navier-Stokes, Nernst-Plank and Laplace-Beltrami equations, was proposed for the dynamics and transport of ion channels as well as fuel cell and nanofluidic systems.¹⁸² However, currently, the main interest or the experimental measurement of ion channels is still focused on the current-voltage (I-V) curves to understand their electrophysiological properties. Consequently, the fluid modeling via the Navier-Stokes equation is often neglected by the ion channel community. Compared to the fuel cell and nanofluidic modeling, ion channel modeling places more emphasis on the microscopic structure and structural modification of channel proteins, and their impact to ion permeation. One of the most detailed ion channel models is constructed in light of the molecular dynamics (MD)^126,142 or explicit solvent molecular dynamics. MD approaches typically make use of classical force fields to describe molecular motions and are able to deal with an entire ion channel, including ions, counterions, solvent, lipids and proteins. To efficiently describe transport properties, Brownian dynamics (BD), based on the stochastic equation of motions of ion particles driven by some generalized potential functions, can effectively reduce the number of degrees of freedom, run up to the real time scale of ion permeation across channel membranes, and determine ion conductance.⁴³ A quite similar model is the Monte Carlo approach,⁹⁵ which computes the probability of the movement of a selected set of ion species using random samplings.

In the PNP theory as well as implicit solvent representations, a solvent-solute interface is needed for differentiating different regions with appropriate physical features, i.e., dielectric functions and diffusion constants, and for separating appropriate computational domains. Currently, the van der Waals surface, the solvent excluded surface,¹³⁹ and the solvent accessible surface are often utilized as solvent-protein interfaces. In combination with implicit solvent theories, these surface models have been applied to the biological modeling, computation and analysis, such as protein-protein interactions,⁴⁹ protein folding,¹⁶² DNA binding and bending,⁵⁹ to name only a few. However, from the physical perspective, these surface representations are simply ad hoc divisions of solute and solvent regions, and do not satisfy physical requirement of free energy minimization. Another problem associated with these surface representations is the admission of non-smooth interfaces, i.e., cusps, and self-intersecting surfaces, which could lead to computational instabilities in molecular simulations.^46,66,81,145 To remove geometric defects, we introduced one of the first partial differential equation (PDE) based approaches to construct biomolecular surfaces via curvature driven geometric flows in 2005.¹⁸³ In 2006, we proposed one of the first variational formulations of molecular surfaces, and the resulting molecular surface, called the minimal molecular surface (MMS), is constructed by the mean curvature flow.^12,13 Recently, we proposed a general framework for the construction of biomolecular surfaces by generalized geometric flows in which the surface evolution is determined by balancing curvature effects and potential effects.¹¹ The mathematical structure of the potential driven geometric flow was prototyped by Wei in 1999¹⁸¹ and is akin to the level set method devised by Osher and Sethian.¹³⁰ This approach enables incorporating microscopic interactions, such as van der Waals potentials, into the curvature motion. Similar smooth interfaces are used to impose boundary conditions on complex boundaries.¹⁸⁵

Recently, Wei has introduced a differential geometry based multiscale paradigm¹⁸² for large chemical and biological systems, such as fuel cells, nanofluidics, ion channels, molecular motors, and viruses, which, in conjunction with their aqueous environment, pose a challenge to both theoretical description and prediction. Therefore, it is crucial to perform dimensionality reduction and manifold contraction by multiscale approaches. The essential ingredient of this multiscale paradigm is to utilize the differential geometry theory of surfaces and the geometric measure theory as a natural means to separate macroscopic domain from the microscopic domain, and meanwhile, couple the continuum mechanical description of the aqueous environment with the discrete atomistic description of the macromolecule. The main tactic of the multiscale formalism is to construct multiscale free energy functionals, or multiscale action functionals as a unified framework to derive the governing equations for the dynamics of different scales and different descriptions. Differential geometry based multiscale models are constructed for three types of aqueous macromolecular complexes: ones that are near equilibrium, ones that are far from equilibrium, and ones that are excessively large. Coupled Poisson-Boltzmann and Laplace-Beltrami equations are derived for systems near equilibrium. For the micro-macro description of electrokinetics, electrohydrodynamics, electrophoresis, fuel cells, and ion channels, generalized Poisson-Nernst-Planck equations are coupled to generalized Navier-Stokes equations for fluid dynamics, Newton's equation for molecular dynamics, and the Laplace-Beltrami equation for the micro-macro interface. Finally, for excessively large aqueous macromolecular complexes, differential geometry based multiscale fluid-electro-elastic models are introduced to replace the expensive molecular dynamics description with an alternative elasticity formulation, which further reduces the dimensionality of the problem.

In the past two years, we have carried out intensive investigation to practically implement and further analyze differential geometry based multiscale models.^{26,28,33–35} In a series of efforts, both the Eulerian formulation³³ and the Lagrangian formulation³⁴ of differential geometry based solvation models have been studied. In our Lagrangian formalism, interface elements are directly evolved according to governing equations which prescribe a set of rules. In our Eulerian formalism, the interface is represented in a hypersurface function which is evolved according to the derived governing equations.³³ A Lagrangian representation can be obtained from the projection of the hypersurface function by using an isosurface extraction procedure. The Eulerian formulation is mathematically simple and computationally robust, while the Lagrangian formalism is straightforward for force prescription¹¹ and is computationally efficient, but usually encounters difficulties in handling the geometric break-up and/or surface merging. We have demonstrated the equivalence of these two formulations for the solvation analysis.³⁴ A good agreement between our theoretical prediction and experimental measurement has been observed for solvation energies of tens of compounds.^33,34 Independent confirmation of our differential geometry based solvation model has been reported in the literature.¹⁹³ For comprehensive background on the solvation analysis, the reader is referred to two review-style introductions.^33,34 Most recently, a quantum mechanical formulation has been introduced to extend our earlier two-scale solvation models to genuine multiscale formulations.³⁵ The use of density functional theory enables us to compute the charge distribution from the Kohn-Sham equation, and thus has significantly improved the predictive power of our earlier solvation models.

In another effort, we have developed differential geometry based multiscale models for proton transport which plays an important role in biological energy transduction, reproduction of influenza A viruses and sensory systems.^26,28 However, unlike other ion channel processes, proton permeation across membrane proteins involves significant quantum effect and needs to be treated by quantum mechanical formulations.^128,135 We have proposed a multiscale/multiphysics model for the understanding of the molecular mechanism of proton transport in transmembrane proteins via continuum, atomic and quantum descriptions, assisted with the differential geometry representation of membrane channel surfaces. To reduce the number of degrees of freedom, we have constructed a new density functional theory based on the Boltzmann statistics to describe proton dynamics quantum mechanically, while implicitly treat numerous solvent molecules as a dielectric continuum. A new density functional formalism is introduced to represent protein density according to the Boltzmann statistics, in contrast to the Fermi-Dirac statistics used in the traditional density functional theory (DFT) for electronic states. Such a change in statistics is necessary because the Hamiltonian operator of the proton transport admits the absolute continuous spectrum, while the Hamiltonian operator of the tradition DFT has a discrete spectrum. The densities of all the other ions in the solvent are treated by using Boltzmann distributions in a dynamic manner, an approach that has been validated in our earlier work.¹⁹⁶ An atomistic representation is given to protein molecular structures and their charge locations. The non-electrostatic interactions among all the ions, and between ions and proteins are denoted as generalized correlations and explored in detail.²⁸ The differential geometry based multiscale framework is utilized to put proton kinetic energy, proton potential energy, the free energy of all other ions, and the polar and nonpolar energies of the whole system on an equal footing. A comparison between experimental data and theoretical predictions validates our model.

The objective of the present work is to explore new differential geometry based multiscale formulations for heterogeneous chemical and biological systems that are far from equilibrium. In our earlier differential geometry based multiscale models, the chemical potential and the associated free energy are not accounted in the total energy functional.¹⁸² Consequently, the Nernst-Planck equation is introduced from the mass conservation of each individual chemical species with an appropriate argument for the “diffusion flow” of a species defined with respect to the barycentric motion of the homogeneous flow. As a result, the evolution and formation of the solvent-solute interface are independent of the entropy of mixing. In the present work, we construct alternative differential geometry based multiscale models for chemical and biological systems that are far from equilibrium by incorporating chemical potential related energy in the total free energy functional. We also investigate the effective reduction of the number of degrees of freedom by introducing the quasi-equilibrium Boltzmann distribution to selected charge species, which avoids the time-consuming solution of many three-dimensional (3D) Nernst-Planck equations.

The rest of this paper is organized as follows. Section II is devoted to the theory and formulation of our theoretical models. We first review our differential geometry based solvation models, which establishes the required notations and introduces some necessary modifications to our earlier formulations.^33,34,182 The modified solvation model also serves as a benchmark for non-equilibrium models when the system returns to the equilibrium. Based on this preparation, the chemical potential formulation of our variational multiscale models is presented in detail. In particular, the relations among different models are investigated. To highlight the perspective of fluid-dynamics driven charge transport, we present a differential geometry based chemo-electro-fluid model. This model is relevant to the nanofluidic and fuel cell systems. In Section III, a number of associated computational algorithms are presented and discussed. Some of these algorithms have been developed in our earlier work over many years for solving the Poisson-Boltzmann equation^{25,190,191,194,200,201} and the classical PNP equations.¹⁹⁵ Validation and application of the proposed new models are carried out in Section IV by using a set of ten proteins. We place a main emphasis on the demonstration of the consistency between the equilibrium solvation model and new non-equilibrium charge transport models. In fact, such a consistency provides a validation to new non-equilibrium models. We further apply our new models to the ion transport of the Gramicidin A channel protein. By a quantitative comparison, our model prediction of the I-V curves is found to be in a good accordance with experimental data in the literature. This paper ends with concluding remarks.

II Variational multiscale models

In this section, we discuss a family of variational multiscale models for the analysis of charge transport. Our formulation makes use of the differential geometry based multiscale models.¹⁸² The essence of our models is that the macroscopic description of the solvent is coupled to the microscopic description of the solute via the solvent-solute interface, which together with other physical properties, is determined by the variational principle. As charge transport is associated with mass transport, chemical potential comes to play a major role in our energy based formulation. Three different descriptions of charged species in the solvent, i.e., local equilibrium, local quasi-equilibrium and non-equilibrium descriptions, give rise to three distinct models. It is crucial to analyze the consistency among these models. In particular, the non-equilibrium models must reproduce the equilibrium model at equilibrium. Therefore, the consistency provides a theoretical validation to non-equilibrium models.

In this section, we start from a minor modification of the differential geometry based solvation model. Based on this foundation, we develop corresponding differential geometry based models for charge transport. The consistency between different models at equilibrium is established, which is a unique feature of the present work.

II.A Differential geometry based solvation model

Solvation is an elementary process in nature, and particularly in biological systems as 65% to 90% of cell mass is water. All other more sophisticated processes, such as charge and mass transport, signal transduction, transcription and translation, occur in aqueous environment under the physiological conditions. Consequently, the understanding of solvation is an elementary prerequisite for the quantitative description and analysis of the above-mentioned processes as well as many other physical systems, such as nanofluidics, fuel cells, batteries, etc. To establish the notation, provide the background, and illustrate our multiscale modeling procedure, we briefly review our differential geometry based solvation model.^33,182 In fact, we present a slightly modified solvation model in the present work. Changes are made to the solvent-solute interaction potentials and the Boltzmann distribution, which are necessary for the development of our present new models.

II.A.1 Total energy functional for solvation

Phenomenologically, solvation process can be described as the creation of a solute cavity in the solvent, the hydrogen bond breaking and formation at the solvent-solute interface, the surface reconstruction of the solute molecule, and the entropy effect due to the solvent-solute mixing. Microscopically, the solvation process involves a variety of solvent-solute interactions, such as the electrostatic, dipolar, induced dipolar and van der Waals interactions between the solvent and the solute. Solvation process is typically described by solvation free energies, which can be measured by experimental means. The experimental data provide a validation to solvation models. Typically, a solvation model provides a description of the solvation free energy, from which many other physical properties can be evaluated as well. It is a standard procedure to split the solvation free energy into two components: polar and nonpolar contributions. The polar part is accounted either by the Poisson-Boltzmann (PB) theory,^{52,73,115,151} the polarizable continuum theory,^127,165 or the generalized Born approximation.^10,58 Among them, the PB theory is the most popular and can be formally derived from basic theories.^17,92,129 One of commonly used nonpolar solvation models is the scaled particle theory (SPT), which includes the surface free energy and the mechanical work of creating a cavity of the solute size in the solvent.^133,163 However, it is well known that classical solvation models neglect the additional solvent-solute interaction and polar-nonpolar coupling.^33,62,173 An improved nonpolar solvation free energy is given as

$$G_{\text{nonpolar}}=\gamma \text{Area}+p\text{Vol}+{\int }_{{\Omega }_s}Ud\mathbf{r},\mathbf{r}\in {\mathbb{R}}^3,$$ (1)

where the first two terms come from the SPT model and the third term describes the solvent-solute interactions. Here “Area” and “Vol” are respectively the solute surface area and volume of the solute, γ is the surface tension, p is the hydrodynamic pressure, and U denotes the solvent-solute non-electrostatic interactions, such as the van der Waals interaction. The integration is over the solvent domain Ω_s.

We assume that the aqueous environment has multiple species. Under the assumption of pairwise solvent-solute interactions, U can be obtained by summing up all the interactions of each solute atom near the interface with the solvent species

$$U=\sum _{\alpha }{\rho }_{\alpha }{U}_{\alpha }$$ (2)

$$=\sum _{\alpha }{\rho }_{\alpha }\left(\mathbf{r}\right)\sum _j{U}_{\alpha j}\left(\mathbf{r}\right)$$ (3)

where ρ_α (r) is the density of αth solvent component, which may either charged or uncharged, and U_αj is an interaction potential between the jth atom of the solute and the αth component of the solvent. For a single component solvent that is free of salt, ρ_α (r) is the density of an uncharged solvent.^33,34 The solvent-solute non-electrostatic interactions can be approximated by the Lennard-Jones potential. In our recent work,^33,34 the Weeks-Chandler-Andersen (WCA) decomposition of the Lennard-Jones potential based on the original WCA theory¹⁸⁰ is utilized to split the Lennard-Jones potential into attractive and repulsive parts

$$U_{\alpha j}^{\text{att},\mathrm{WCA}}\left(\mathbf{r}\right)=\{\begin{array}{cc}-{\overline{∊}}_{\alpha j},\hfill & 0<\mid \mathbf{r}-{\mathbf{r}}_j\mid <{\sigma }_j+{\sigma }_{\alpha },\hfill \\ V_{\alpha j}^{\mathrm{LJ}},\hfill & \mid \mathbf{r}-{\mathbf{r}}_j\mid \ge {\sigma }_j+{\sigma }_{\alpha },\hfill \end{array}\phantom{\}}$$ (4)

$$U_{\alpha j}^{\text{rep},\mathrm{WCA}}\left(\mathbf{r}\right)=\{\begin{array}{cc}{V}_{\alpha j}^{\mathrm{LJ}}+{\overline{∊}}_{\alpha j},\hfill & 0<\mid \mathbf{r}-{\mathbf{r}}_j\mid <{\sigma }_j+{\sigma }_{\alpha },\hfill \\ 0,\hfill & \mid \mathbf{r}-{\mathbf{r}}_j\mid \ge {\sigma }_j+{\sigma }_{\alpha },\hfill \end{array}\phantom{\}}$$ (5)

where ${\overline{∊}}_{\alpha j}$ is the well-depth parameter, σ_j and σ_α are the radii of the jth solute atom and the αth solvent component, r denotes a point on the physical space and r_j represents the location of the jth atom in the protein. The WCA potential was found to provide a good account of the attractive dispersion interaction in our earlier work.^33,34 In fact, there are many other unaccounted interactions between the solvent and solute at their interface, including the dielectric effect of the polarizable solvent (water and complex ions). In the present work, we denote U for all possible solvent-solute interactions as shown in Eq. (2). Therefore, U contains part of the so called size effects as well.^28,96

The Lennard-Jones potential is singular and can cause computational difficulties.³³ Recently, Zhao has proposed a way to improve the integration stability in a realistic setting for proteins.¹⁹³ However, further mathematical algorithms are needed for this class of problems.

Furthermore, the surface area in Eq. (1) can be evaluated via a two-dimensional (2D) integral.^11,13 However, it is convenient for us to set up the total free functional as a 3D integral in ${\mathbb{R}}^3$ . To this end, we make use of the concept of mean surface area¹⁸² and the coarea formula⁶⁸

$$\text{Area}={\int }_0^1{\int }_{S^{-1}\left(c\right)\bigcap \Omega }d\sigma dc={\int }_{\Omega }\mid \nabla S\left(\mathbf{r}\right)\mid d\mathbf{r},\mathbf{r}\in {\mathbb{R}}^3,$$ (6)

where 0 ≤ S ≤ 1 is a characteristic function of the solute domain and is usually called a surface function. It embeds the 2D surface manifold in the 3D Euclidean space. Similarly, 1 – S is a characteristic function of the solvent domain. Here, Ω represents the whole computational domain. The validity of the mean surface area has been examined in our recent work.³³ By means of the hypersurface function S, the volume in Eq. (1) can be easily defined as

$$\text{Vol}={\int }_{{\Omega }_m}d\mathbf{r}={\int }_{\Omega }S\left(\mathbf{r}\right)d\mathbf{r},$$ (7)

where Ω_m is the macromolecular (i.e., solute) domain. Note that ${\Omega }_s\cap {\Omega }_m$ is not empty because the surface function S is a smooth function, which leads to the overlapping between Ω_s and Ω_m. The last term in Eq. (1) can be rewritten as

$${\int }_{{\Omega }_s}Ud\mathbf{r}={\int }_{\Omega }(1-S\left(\mathbf{r}\right))Ud\mathbf{r}.$$ (8)

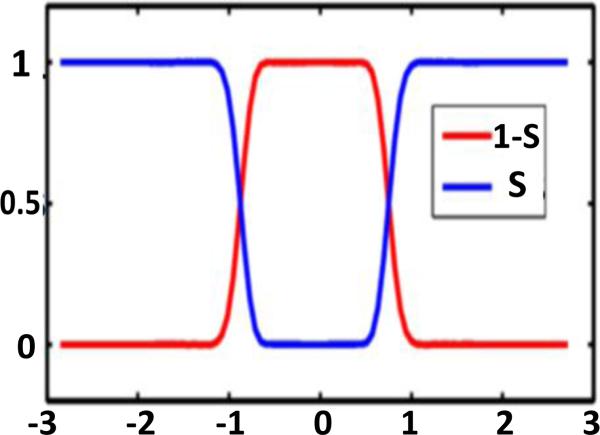
Figure 2 provides a one-dimensional (1D) illustration of the profiles of solute characteristic function S and solvent characteristic function 1 – S. The solute molecule is located from -0.8 to 0.8Å in the x-axis. Obviously, there is an overlapping between the solvent domain and the solute domain. As shown below, the surface function S is determined by the Laplace-Beltrami equation.

Figure 2.

Illustration of surface function S and solvent characteristic function 1 – S in a 1D setting.

In this work, we make use of the Poisson-Boltzmann theory for the polar solvation free energy. Variation formulation of the Poisson-Boltzmann theory was originally proposed by Sharp and Honig¹⁵⁰ in 1990 and was extended to the force derivation by Gilson et al.⁸⁰

By means of the surface function S, the polar solvation free energy can be expressed as¹⁸²

$$G_{\text{polar}}=\int \left\{S\left[-\frac{{∊}_m}{2}{\mid \nabla \Phi \mid }^2+\Phi {\rho }_m\right]+(1-S)\left[-\frac{{∊}_s}{2}{\mid \nabla \Phi \mid }^2-k_{B}T\sum _{\alpha }{\rho }_{\alpha 0}\left(e^{-\frac{q_{\alpha }\Phi +U_{\alpha }-{\mu }_{\alpha 0}}{k_{B}T}}-1\right)\right]\right\}d\mathbf{r},$$ (9)

where Φ is the electrostatic potential, ε_s and ε_m are the dielectric constants of the solvent and solute, respectively, and ρ_m represents the fixed charge density of the solute. Specifically, one has ρ_m = Σ_jδ(r – r_j), with Q_j denoting the partial charge of the jth atom in the solute. Here k_B is the Boltzmann constant, T is the temperature, ρ_α0 denotes the reference bulk concentration of the αth solvent species, and q_α denotes the charge valence of the αth solvent species, which is zero for an uncharged solvent component.

In Eq. (9), we assume the Boltzmann distribution of the form

$${\rho }_{\alpha }={\rho }_{\alpha 0}{e}^{-\frac{q_{\alpha }\Phi +U_{\alpha }-{\mu }_{\alpha 0}}{k_{B}T}}$$ (10)

with μ_α0 being a relative reference chemical potential which reflects the difference in the equilibrium concentrations of different solvent species, i.e., ρ_α ≠ ρ_β, given that ρ_α0 = ρ_β0. In Section II.B, it is seen that Boltzmann distribution (10) occurs naturally.

Note that the thermodynamic equilibrium is a state of full balance over the whole domain, which might not be achieved all the time at nanoscale, due to the recognition of microscopic interactions. The concept of local equilibrium, which is commonly used in the Boltzmann kinetic theory,^158,159 is appropriate. Therefore, we refer to equilibrium as a local one in this work.

Combining all the energy contributions mentioned above, the total free energy functional for the solvation system can be described as

$$G_{\text{total}}^{\mathrm{PB}}[S,\Phi ]=\int \left\{\gamma \mid \nabla S\mid +pS+S\left[-\frac{{∊}_m}{2}{\mid \nabla \Phi \mid }^2+\Phi {\rho }_m\right]+(1-S)\left[-\frac{{∊}_s}{2}{\mid \nabla \Phi \mid }^2-k_{B}T\sum _{\alpha }{\rho }_{\alpha 0}\left(e^{-\frac{q_{\alpha }\Phi +U_{\alpha }-{\mu }_{\alpha 0}}{k_{B}T}}-1\right)\right]\right\}d\mathbf{r}.$$ (11)

The total free energy functional (11) appears to differ much from that in our earlier work.^33,182 First, the Boltzmann distribution in Eq. (10) is used. Additionally, solvent-solute interactions (1 – S)U are omitted. To understand these modifications, let us assume k_BT >> q_αΦ + U_α – μ_α0 to obtain an expansion

$$-(1-S)k_{B}T\sum _{\alpha }{\rho }_{\alpha 0}\left(e^{-\frac{q_{\alpha }\Phi +U_{\alpha }-{\mu }_{\alpha 0}}{k_{B}T}}-1\right)\sim (1-S)\sum _{\alpha }{\rho }_{\alpha 0}(q_{\alpha }\Phi +U_{\alpha }-{\mu }_{\alpha 0}).$$ (12)

Therefore, it is seen that the solvent-solute interactions have already been accounted in the new Boltzmann distribution. In this sense, the present formulation (11) is consistent with that in our earlier work.^33,182 In fact, two more comments are in order. First, the division between polar and nonpolar parts is quite ad hoc. Particularly, the solvent-solute interactions can be included either in the nonpolar part or in the polar part. Additionally, by modifying the energy term in the Boltzmann distribution, one can easily take into consideration of more interactions, such as dipole,⁷⁶ multipole,^106,147 steric effects,²⁰ multiple dielectric constants¹⁴⁰ and van der Waals interactions in a generalized Poisson-Boltzmann equation. Such a generalized Poisson-Boltzmann equation may be able to show appropriate correlation corrections to the equilibrium density as those computed by more expensive integral equation theories.^79,141

II.A.2 Governing equations for solvation

The total solvation free energy in Eq. (11) is expressed as a functional of the surface function S and the electrostatic potential Φ. Our goal is to minimize the total solvation free energy functional with respect to S and Φ. By applying the variational principle, we have

$$\frac{\delta G_{\text{total}}^{\mathrm{PB}}}{\delta S}\Rightarrow -\nabla \cdot \left(\gamma \frac{\nabla S}{\mid \nabla S\mid }\right)+p-\frac{{∊}_m}{2}{\mid \nabla \Phi \mid }^2+\Phi {\rho }_m+\frac{{∊}_s}{2}{\mid \nabla \Phi \mid }^2+k_{B}T\sum _{\alpha }{\rho }_{\alpha 0}\left(e^{-\frac{q_{\alpha }\Phi +U_{\alpha }-{\mu }_{\alpha 0}}{k_{B}T}}-1\right)=0.$$ (13)

Based on the discussion in the earlier work,^13,33,34,182 the solution of Eq. (13) can be obtained by solving the following generalized Laplace-Beltrami equation after the introduction of an artificial time

$$\frac{\partial S}{\partial t}=\mid \nabla S\mid \left[\nabla \cdot \left(\gamma \frac{\nabla S}{\mid \nabla S\mid }\right)+V_1\right],$$ (14)

where the potential driven term is given by

$$V_1=-p+\frac{{∊}_m}{2}{\mid \nabla \Phi \mid }^2-\Phi {\rho }_m-\frac{{∊}_s}{2}{\mid \nabla \Phi \mid }^2-k_{B}T\sum _{\alpha }{\rho }_{\alpha 0}\left(e^{-\frac{q_{\alpha }\Phi +U_{\alpha }-{\mu }_{\alpha 0}}{k_{B}T}}-1\right).$$ (15)

The generalized Laplace-Beltrami equation (14) gives rise to the surface definition of the solvent-solute interface.

Taking the variation with respect to Φ, we have

$$\frac{\delta G_{\text{total}}^{\mathrm{PB}}}{\delta \Phi }\Rightarrow \nabla \cdot ([(1-S){∊}_s+S{∊}_m]\nabla \Phi )+S{\rho }_m+(1-S)\sum _{\alpha }{q}_{\alpha }{\rho }_{\alpha 0}{e}^{-\frac{q_{\alpha }\Phi +U_{\alpha }-{\mu }_{\alpha 0}}{k_{B}T}}=0.$$ (16)

From Eq. (16), one obtains the generalized Poisson-Boltzmann equation

$$-\nabla \cdot (∊\left(S\right)\nabla \Phi )=S{\rho }_m+(1-S)\sum _{\alpha }{q}_{\alpha }{\rho }_{\alpha 0}{e}^{-\frac{q_{\alpha }\Phi +U_{\alpha }-{\mu }_{\alpha 0}}{k_{B}T}},$$ (17)

where ε(S) = (1 – S)ε_s + Sε_m is the generalized permittivity function. As shown in our earlier work,^33,182 ε(S) is a smooth dielectric function gradually varying from ε_m to ε_s. The extra term $e^{-\frac{U_{\alpha }}{k_{B}T}}$ in Eq. (17) is due to the solvent (including ions) and solute interactions near the interface. Note that U_α is a relatively weak short range potential and has its largest impact near the solvent-solute interface. Therefore, $e^{-\frac{U_{\alpha }}{k_{B}T}}$ provides a non-electrostatic correction to the charge density near the interface.

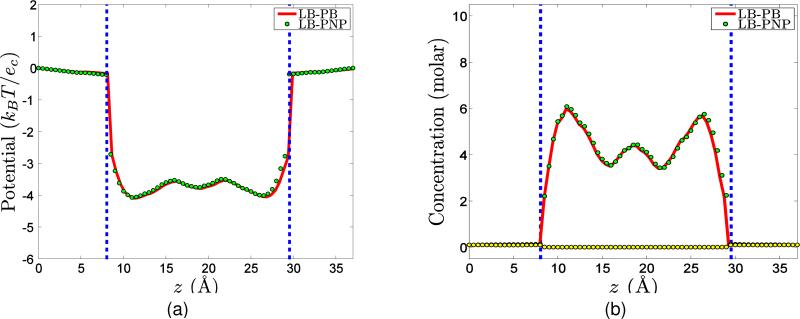
Equations (14) and (17) describe the surface evolution and the electrostatic potential, respectively. These coupled equations are called the Laplace-Beltrami and Poisson-Boltzmann (LB-PB) equations. They form a coupled system for the differential geometry based solvation model in the Eulerian representation. An essentially equivalent Lagrangian representation of the differential geometry based solvation model was derived.³⁴ It has been shown^33,34 that these solvation models provide very good predictions of solvation energies compared to experimental data.

The solvation model describes the system at equilibrium as the charge concentration is approximated by the Boltzmann distribution. However, for charge transport phenomena, charges typically undergo a dynamical process driven by the generalized electrochemical potential. As such, a non-equilibrium description for the charge concentration is required. In the rest of this section, we present variational multiscale models to describe charge transport in chemical and biological systems.

II.B Differential geometry based Poisson-Nernst-Planck model

In the above system, the generalized Poisson-Boltzmann and Laplace-Beltrami equations are obtained from the variational principle. For chemical and biological systems far from equilibrium, it is necessary to incorporate a kinetic equation to describe the dynamics of charged particles. Typically, the Nernst-Planck equation plays such a role. In our earlier work,¹⁸² the generalized Nernst-Planck equation was derived from the mass conservation. As such, the total free energy functional does not include the chemical energy density and the solvent-solute interface is not affected by the chemical potential. In the present work, we seek for an alternative formulation of charge transport, in which the total free energy functional encompasses the chemical potential contribution as well.

A variational approach to the Poisson-Boltzmann free energies that includes the concentration effect and chemical potential was considered by Fogolari and Briggs.⁷²

II.B.1 Total energy functional for a system with charged species

For simplicity, we assume that the flow stream velocity vanishes (|v| = 0). Additionally, we omit the chemical reactions in our present discussion. Chemical potential consists of a homogeneous reference term and the entropy of mixing. It can be derived from the free energy functional.⁷²

Chemical potential related free energy can be expressed as

$$G_{\text{chem}}=\int \sum _{\alpha }\left\{({\mu }_{\alpha }^0-{\mu }_{\alpha 0}){\rho }_{\alpha }+k_{B}T{\rho }_{\alpha }\ln \frac{{\rho }_{\alpha }}{{\rho }_{\alpha 0}}-k_{B}T({\rho }_{\alpha }-{\rho }_{\alpha 0})\right\}d\mathbf{r},$$ (18)

where ${\mu }_{\alpha }^0$ is a reference chemical potential of the αth species at which the associated ion concentration is ρ_0α given = Φ = U_α = μ_α0 = 0. Here $k_{B}T{\rho }_{\alpha }\ln \frac{{\rho }_{\alpha }}{{\rho }_{\alpha 0}}$ is the entropy of mixing, and –k_BT (ρ_α – ρ_α0) can be regarded as a relative osmotic term.¹²⁵

The chemical potential of species α can be obtained by the variation with respect to ρ_α

$$\frac{\delta G_{\text{chem}}}{\delta {\rho }_{\alpha }}\Rightarrow {\mu }_{\alpha }^{\text{chem}}={\mu }_{\alpha }^0-{\mu }_{\alpha 0}+k_{B}T\ln \frac{{\rho }_{\alpha }}{{\rho }_{\alpha 0}}.$$ (19)

Note that at equilibrium, ${\mu }_{\alpha }^{\text{chem}}\ne 0$ and ρ_α ≠ ρ_α0 because of possible external electrical potentials, solvent-solute interactions, and charged species. Even if the external electrical potential is absent and system is at equilibrium, the charged solute may induce the concentration response of ionic species in the solvent so that ρ_α ≠ ρ_α0.

Considering the aforementioned chemical potential related energy term, together with the polar and and nonpolar contributions discussed in the previous section, the total free energy for the system can be described as below

$$G_{\text{total}}^{\mathrm{PNP}}[S,\Phi ,\left\{{\rho }_{\alpha }\right\}]=\int \{\gamma \mid \nabla S\mid +pS+(1-S)U+S\phantom{\{}\left[-\frac{{∊}_m}{2}{\mid \nabla \Phi \mid }^2+\Phi {\rho }_m\right]+(1-S)\left[-\frac{{∊}_s}{2}{\mid \nabla \Phi \mid }^2+\Phi \sum _{\alpha }{\rho }_{\alpha }{q}_{\alpha }\right]+(1-S)\sum _{\alpha }\left[({\mu }_{\alpha }^0-{\mu }_{\alpha 0}){\rho }_{\alpha }+k_{B}T{\rho }_{\alpha }\ln \frac{{\rho }_{\alpha }}{{\rho }_{\alpha 0}}-k_{B}T({\rho }_{\alpha }-{\rho }_{\alpha 0})+{\lambda }_{\alpha }{\rho }_{\alpha }\right]\}d\mathbf{r},$$ (20)

where the first row is the nonpolar solvation free energy functional, the second row is the polar solvation free energy functional, and the third row is chemical potential related energy functional. Here λ_α is a Lagrange multiplier, which is required to ensure appropriate physical properties at equilibrium.⁷²

Note that we have employed the original nonpolar solvation free energy functional (1) in the present total free energy function formulation (20).

II.B.2 Generalized correlations — Size effect and channel confinement

Water is naturally abundant in nature. In an aqueous solution, charged particles do not exist by themselves, but constantly interact with solute, water molecules, and with other ions. Part of these interactions are electrostatic in nature and have been accounted in the above formulation. However, there are other interactions, including van der Waals interactions, dispersion interactions, ion-water dipolar interactions, ion-water cluster formation or dissociation, ion spin effects, ion-protein interaction, etc. These additional interactions are termed as generalized correlations in our recent work.²⁸ They give rise to many important effects in the behavior of charged particles. One obvious and intensively studied effect is the size effect.^28,96 Size effect typically offers a small correction to the ion distribution when the ion concentration is relatively small, but gets more important as the concentration increases. The effects of finite ion sizes in terms of volume exclusion were discussed by Bazant et al¹⁴ and many others.^84,116,170 Size effect in the variational multiscale solvation models has been accounted with the WCA potential for realistic proteins.^33,34 A treatment of pair particle interactions, including the so called size effects, in the Boltzmann kinetic theory was formulated by Snider et al in 1996.^158,159 They have demonstrated the impact of these interactions to the transport equations of density, velocity and energy, and transport coefficients. Another important effect of generalized correlation is an energy barrier to the ion transport due to the change in the solvation environment from the bulk solution to a relatively narrow channel pore.²⁸ It is commonly believed that the difference in this type of energy barriers for sodium and potassium leads to the selectivity of sodium and potassium channels. In the present work, we adopt the formulation of generalized corrections introduced in our earlier work.²⁸ This amounts to modify Eqs. (2) and (3) as

$$\begin{array}{cc}\hfill U& =\sum _{\alpha }{\rho }_{\alpha }{U}_{\alpha }\hfill \\ \hfill U_{\alpha }& =\sum _j{U}_{\alpha j}\left(\mathbf{r}\right)+\sum _{\beta }{U}_{\alpha \beta }\left(\mathbf{r}\right),\hfill \end{array}$$ (21)

where the solvent-solute interaction potential U_αj(r) was described in Section II.A.1 and the subscript β runs over all solvent components, including ions and water. In general, we denote U_α as any possible non-electrostatic interactions in the system.

If the solvent-solvent interaction is represented by the van der Waals potential, one has an explicit expression for U_αβ (r)

$$U_{\alpha \beta }\left(\mathbf{r}\right)={\overline{∊}}_{\alpha \beta }\int {\rho }_{\beta }\left({\mathbf{r}}^{\prime }\right)\left[{\left(\frac{{\sigma }_{\alpha }+{\sigma }_{\beta }}{\mid \mathbf{r}-{\mathbf{r}}^{\prime }\mid }\right)}^{12}-2{\left(\frac{{\sigma }_{\alpha }+{\sigma }_{\beta }}{\mid \mathbf{r}-{\mathbf{r}}^{\prime }\mid }\right)}^6\right]d{\mathbf{r}}^{\prime }$$ (22)

Note that there should be a factor of 1/2 in Eq. (22) when β = α. However, such a factor is eliminated after the variation. As pointed out in our earlier work,²⁸ the Lennard-Jones formula in our formulation is significantly different from the conventional Lennard-Jones potential, which traditionally represents short-range interactions between two explicit particles. Whereas in the present model, it characterizes solvent-solvent interactions in the continuum-continuum representation as both water and all ion species admit the continuum description. The repulsive 12-power term in the Lennard-Jones potential prevents any two particles from occupying the same space. It was shown in our earlier work that because the integration in Eq. (22) is restricted to a smaller volume in a narrow channel pore, the generalized correlation gives rise to an additional energy barrier. Physically, the channel confinement decreases the configurational entropy and increases the solvent-solvent interaction potential energy.

It is interesting to note that the inclusion of generalized correlation, i.e., adding an additional solvent-solvent interaction term U_αβ (r) to the total interaction potential U_α (r), does not change the derivation and the form of other expressions presented in the preceding section. It is expected that further modifications can be easily introduced to the present formulation.

II.B.3 Governing equations

The total free energy functional (20) is a function of the surface function S, electrostatic potential Φ and the ion concentration ρ_α. By applying the variational principle, we obtain governing equations for the system.

Generalized Nernst-Planck equation

First, we consider the variation with respect to the ion concentration ρ_α

$$\frac{\delta G_{\text{total}}^{\mathrm{PNP}}}{\delta {\rho }_{\alpha }}\Rightarrow {\mu }_{\alpha }^{\text{gen}}={\mu }_{\alpha }^0-{\mu }_{\alpha 0}+k_{B}T\ln \frac{{\rho }_{\alpha }}{{\rho }_{\alpha 0}}+q_{\alpha }\Phi +U_{\alpha }+{\lambda }_{\alpha }={\mu }_{\alpha }^{\text{chem}}+q_{\alpha }\Phi +U_{\alpha }+{\lambda }_{\alpha },$$ (23)

where ${\mu }_{\alpha }^{\text{gen}}$ is the relative generalized potential of species α. Note that it is ${\mu }_{\alpha }^{\text{gen}}$ , rather than ${\mu }_{\alpha }^{\text{chem}}$ , that vanishes at equilibrium. As such, one has

$${\lambda }_{\alpha }=-{\mu }_{\alpha }^0\text{and}{\rho }_{\alpha }={\rho }_{\alpha 0}{e}^{-\frac{q_{\alpha }\Phi +U_{\alpha }-{\mu }_{\alpha 0}}{k_{B}T}}.$$ (24)

From Eq. (24), the relative generalized potential ${\mu }_{\alpha }^{\text{gen}}$ can be expressed as

$${\mu }_{\alpha }^{\text{gen}}=k_{B}T\ln \frac{{\rho }_{\alpha }}{{\rho }_{\alpha 0}}+q_{\alpha }\Phi +U_{\alpha }-{\mu }_{\alpha 0}.$$ ( 25 )

A similar quantity was derived from a slightly different perspective in our earlier work.¹⁹⁶ Note that the relative generalized potential consists of contributions from the entropy of mixing, electrostatic potential, solvent-solute interaction and the relative reference chemical potential. The latter is position independent. By Fick's first law, the ion flux can be expressed as the gradient of the relative generalized potential ${\mathbf{J}}_{\alpha }=-D_{\alpha }{\rho }_{\alpha }\nabla \frac{{\mu }_{\alpha }^{\text{gen}}}{k_{B}T}$ with D_α being the diffusion coefficient of species α. Then the mass conservation of species α at the absence of steam velocity gives $\frac{\partial {\rho }_{\alpha }}{\partial t}=-\nabla \cdot {\mathbf{J}}_{\alpha }$ , which is the generalized Nernst-Planck equation:

$$\frac{\partial {\rho }_{\alpha }}{\partial t}=\nabla \cdot \left[D_{\alpha }\left(\nabla {\rho }_{\alpha }+\frac{{\rho }_{\alpha }}{k_{B}T}\nabla (q_{\alpha }\Phi +U_{\alpha })\right)\right],$$ (26)

where q_αΦ + U_α can be identified as a form of the potential of the mean field. Equation (26) reduces to the standard Nernst-Planck equation when the solvent-solute interactions vanish.

The steady state of Eq. (26) reads as

$$\nabla \cdot \left[D_{\alpha }\left(\nabla {\rho }_{\alpha }+\frac{{\rho }_{\alpha }}{k_{B}T}\nabla (q_{\alpha }\Phi +U_{\alpha })\right)\right]=0.$$ (27)

Generalized Poisson equation

The derivation of the generalized Poisson equation can be pursued in the same manner. We consider the variation of the total free energy functional with respect to the electrostatic potential Φ

$$\frac{\delta G_{\text{total}}^{\mathrm{PNP}}}{\delta \Phi }\Rightarrow \nabla \cdot ([(1-S){∊}_s+S{∊}_m]\nabla \Phi )+S{\rho }_m+(1-S)\sum _{\alpha }{\rho }_{\alpha }{q}_{\alpha }=0.$$ (28)

This gives rise to the desirable generalized Poisson equation

$$-\nabla \cdot (∊\left(S\right)\nabla \Phi )=S{\rho }_m+(1-S)\sum _{\alpha }{\rho }_{\alpha }{q}_{\alpha },$$ (29)

where ε(S) = (1 – S)ε_s + Sε_m is an interface dependent dielectric profile. Obviously, Eq. (29) involves the densities of ions ρ_α and the surface function S.

Generalized Laplace-Beltrami equation

As discussed earlier, the surface function S can be solved from the generalized Laplace-Beltrami equation. It is noted that although all Laplace-Beltrami equations in our formalisms share the same mean curvature operator obtained from the surface energy term, each system has its own potential driven term which can be derived from the Euler-Lagrange equation

$$\frac{\delta G_{\text{total}}^{\mathrm{PNP}}}{\delta S}\Rightarrow -\nabla \cdot \left(\gamma \frac{\nabla S}{\mid \nabla S\mid }\right)+p-U-\frac{{∊}_m}{2}{\mid \nabla \Phi \mid }^2+\Phi {\rho }_m+\frac{{∊}_s}{2}{\mid \nabla \Phi \mid }^2-\Phi \sum _{\alpha }{\rho }_{\alpha }{q}_{\alpha }-\sum _{\alpha }\left[-{\mu }_{\alpha 0}{\rho }_{\alpha }+k_{B}T{\rho }_{\alpha }\ln \frac{{\rho }_{\alpha }}{{\rho }_{\alpha 0}}-k_{B}T({\rho }_{\alpha }-{\rho }_{\alpha 0})\right]=0,$$ (30)

where we have made use of Eq. (24). As shown in our earlier work,^11,182 the solution of Eq. (30) can be obtained by solving the following parabolic equation via the introduction of an artificial time

$$\frac{\partial S}{\partial t}=\mid \nabla S\mid \left[\nabla \cdot \left(\gamma \frac{\nabla S}{\mid \nabla S\mid }\right)+V_2\right],$$ (31)

where

$$V_2=-p+U+\frac{{∊}_m}{2}{\mid \nabla \Phi \mid }^2-\Phi {\rho }_m-\frac{{∊}_s}{2}{\mid \nabla \Phi \mid }^2+\Phi \sum _{\alpha }{\rho }_{\alpha }{q}_{\alpha }+\sum _{\alpha }\left[k_{B}T\left({\rho }_{\alpha }\ln \frac{{\rho }_{\alpha }}{{\rho }_{\alpha 0}}-{\rho }_{\alpha }+{\rho }_{\alpha 0}\right)-{\mu }_{\alpha 0}{\rho }_{\alpha }\right].$$ (32)

Equations (26), (29), and (31) are coupled together to form a coupled system of equations for describing the surface function S, charge concentrations ρ_α and the electrostatic potential Φ, where the steady state of S and ρ_α are given in (30) and (27). This coupled system differs from the original PNP system in the sense that the surface characteristics is coupled to charge concentrations and the electrostatics. We call this system a Laplace-Beltrami Poisson-Nernst-Planck (LB-PNP) model.

II.B.4 Relation to the solvation model at the equilibrium

In this part, the relation between the non-equilibrium LB-PNP model and the equilibrium solvation model is investigated. If the charge flux is zero for the electrodiffusion system, the PNP model is known to be equivalent to the PB model.¹⁴² Note that at equilibrium, the relative generalized potential vanishes every-where and one has the equilibrium constraints given in Eq. (24). Therefore, by utilizing the constraints in Eq. (24), the total free energy functional in Eq. (20) becomes

$$\begin{array}{cc}\hfill G_{\text{total}}^{\mathrm{PNP}}& =\int \left\{\gamma \mid \nabla S\mid +pS+(1-S)U+S\left[-\frac{{∊}_m}{2}{\mid \nabla \Phi \mid }^2+\Phi {\rho }_m\right]+(1-S)\left[-\frac{{∊}_s}{2}{\mid \nabla \Phi \mid }^2+\Phi \sum _{\alpha }{\rho }_{\alpha }{q}_{\alpha }\right]+(1-S)\sum _{\alpha }\left[k_{B}T\left({\rho }_{\alpha }\ln \frac{{\rho }_{\alpha }}{{\rho }_{\alpha 0}}-{\rho }_{\alpha }+{\rho }_{\alpha 0}\right)-{\mu }_{\alpha 0}{\rho }_{\alpha }\right]\right\}d\mathbf{r}\hfill \\ \hfill & =\int \left\{\gamma \mid \nabla S\mid +pS+S\left[-\frac{{∊}_m}{2}{\mid \nabla \Phi \mid }^2+\Phi {\rho }_m\right]+(1-S)\left[-\frac{{∊}_s}{2}{\mid \nabla \Phi \mid }^2-k_{B}T\sum _{\alpha }{\rho }_{\alpha 0}\left(e^{-\frac{q_{\alpha }\Phi +U_{\alpha }-{\mu }_{\alpha 0}}{k_{B}T}}-1\right)\right]\right\}d\mathbf{r}\hfill \\ \hfill & =G_{\text{total}}^{\mathrm{PB}}.\hfill \end{array}$$ (33)

It shows that under the equilibrium assumption, the total free energy functional for the present charge transport model reduces to that of the solvation model given in Eq. (11). We emphasize that this consistency between LB-PNP and LB-PB models is a crucial aspect of the present non-equilibrium theory of charge transport.

Furthermore, for the surface driven functions of the generalized LB equation, it is easy to show that under the constraints of Eq. (24), one has

$$\begin{array}{cc}\hfill V_2& =-p+U+\frac{{∊}_m}{2}{\mid \nabla \Phi \mid }^2-\Phi {\rho }_m-\frac{{∊}_s}{2}{\mid \nabla \Phi \mid }^2+\Phi \sum _{\alpha }{\rho }_{\alpha }{q}_{\alpha }+\sum _{\alpha }\left[k_{B}T\left({\rho }_{\alpha }\ln \frac{{\rho }_{\alpha }}{{\rho }_{\alpha 0}}-{\rho }_{\alpha }+{\rho }_{\alpha 0}\right)-{\mu }_{\alpha 0}{\rho }_{\alpha }\right]\hfill \\ \hfill & =-p+\frac{{∊}_m}{2}{\mid \nabla \Phi \mid }^2-\Phi {\rho }_m-\frac{{∊}_s}{2}{\mid \nabla \Phi \mid }^2-k_{B}T\sum _{\alpha }({\rho }_{\alpha }-{\rho }_{\alpha 0})\hfill \\ \hfill & =-p+\frac{{∊}_m}{2}{\mid \nabla \Phi \mid }^2-\Phi {\rho }_m-\frac{{∊}_s}{2}{\mid \nabla \Phi \mid }^2-k_{B}T\sum _{\alpha }{\rho }_{\alpha 0}\left(e^{-\frac{q_{\alpha }\Phi +U_{\alpha }-{\mu }_{\alpha 0}}{k_{B}T}}-1\right)\hfill \\ \hfill & =V_1\hfill \end{array}$$ (34)

However, in general, the total free energy functional of the LB-PNP model in Eq. (20) differs from that of the LB-PB model in Eq. (11). Similarly, the surface driven term V₂ in the charge transport model differs from V₁ in the solvation model. Moreover, ρ_α in the charge transport model needs to be solved by the Nernst-Planck equation (26).

II.C Differential geometry based Poisson-Boltzmann-Nernst-Planck model

The LB-PNP model discussed above provides a good prediction of charge transport phenomena for non-equilibrium systems. However, the computational cost increases dramatically as the number of charge species in the system increases because the concentration of each charge species is governed by one Nernst-Planck equation. In a complex system with multiple charge species, the LB-PNP model can be very expensive. In our earlier work,¹⁹⁶ we introduced a Poisson-Boltzmann Nernst-Planck (PBNP) model in which the densities of target ions (ions of interest) are modeled by the Nernst-Planck equation while those of other ions are described by using the Boltzmann distribution. We have shown that the PBNP model is able to faithfully reproduce prediction of the PNP model for ion channel transport at non-equilibrium settings.¹⁹⁶ The validity and usefulness of the PBNP formulation have been quickly confirmed by independent researchers.¹¹¹ In the present work, we derive a set of coupled LB-PBNP equations for multiple charge species at non-equilibrium.

II.C.1 Total energy functional for Poisson-Boltzmann-Nernst-Planck model

Assuming that the total number of ion species in the system is N_c, and we are interested in certain charge species (or target charge species), while the rest of the species are not the ones of interest. Nevertheless, all species have similar impact on the system. Let us denote ρ_α (α = 1, ..., N_NP) as the densities of the target charge species, ρ_α (β = N_NP + 1, ..., N_c) as the densities of the remaining charge species in the system, where N_NP is the total number of charge species treated by using the non-equilibrium Nernst-Planck (NP) equation, and N_BD = N_c – N_NP is the total number of the remaining charge species which are represented by the equilibrium Boltzmann distribution. It was demonstrated in our earlier work that since all species are fully coupled, the non-equilibrium transport of the charge species can be effectively recovered although their densities are represented by the equilibrium Boltzmann distribution. Based on this consideration, the total free energy functional can be expressed by

$$\begin{gathered} G_{\text{total}}^{\mathrm{PBNP}}[S,\Phi ,\left\{{\rho }_{\alpha }\right\}]=\int \left\{\gamma \mid \nabla S\mid +pS+(1-S)\sum _{\alpha =1}^{N\mathrm{NP}}{\rho }_{\alpha }{U}_{\alpha } \\ +S\left[-\frac{{∊}_m}{2}{\mid \nabla \Phi \mid }^2+\Phi {\rho }_m\right]+(1-S)\left[-\frac{{∊}_s}{2}{\mid \nabla \Phi \mid }^2+\Phi \sum _{\alpha =1}^{N_{\mathrm{NP}}}{\rho }_{\alpha }{q}_{\alpha }-\sum _{\beta =N_{\mathrm{NP}} \\ +1}^{N_c}{k}_{B}T{\rho }_{\beta 0}\left(e^{-\frac{q_{\beta }\Phi +U_{\beta }-{\mu }_{\beta 0}}{k_{B}T}}-1\right)\right]+(1-S)\sum _{\alpha =1}^{N_{\mathrm{NP}}}\left[({\mu }_{\alpha }^0-{\mu }_{\alpha 0}){\rho }_{\alpha }+k_{B}T{\rho }_{\alpha }\ln \frac{{\rho }_{\alpha }}{{\rho }_{\alpha 0}}-k_{B}T({\rho }_{\alpha }-{\rho }_{\alpha 0})+{\lambda }_{\alpha }{\rho }_{\alpha }\right]\right\}d\mathbf{r}, \end{gathered}$$ (35)

where the first row is the nonpolar solvation free energy functional, followed by the polar and chemical potential related energy functionals in the second and third rows. Note that the charge source terms in the polar solvation free energy functional are modified to reflect the abovementioned different treatments of the charge species. The Lagrange multiplier λ_α is designed to enforce appropriate physical properties at equilibrium.

As shown in Eq. (2), the solvent-solute interaction potential U in Eq. (35) involves densities for all solvent species as well. As discussed above, these densities are described by the non-equilibrium Nernst-Planck (NP) equation and by the equilibrium Boltzmann distribution.

II.C.2 Governing equations

In our differential geometry based multiscale formalism, it has become a standard procedure to derive governing equations from the total energy functional. Here we present related governing equations for the system of charge transport.

Generalized Nernst-Planck equation

To calculate relative generalized potentials we take the variation of Eq. (35) with respect to the ion concentration ρ_α

$$\frac{\delta G_{\text{total}}^{\mathrm{PBNP}}}{\delta {\rho }_{\alpha }}\Rightarrow {\mu }_{\alpha }^{\text{gen}}={\mu }_{\alpha }^0-{\mu }_{\alpha 0}+k_{B}T\ln \frac{{\rho }_{\alpha }}{{\rho }_{\alpha 0}}+q_{\alpha }\Phi +U_{\alpha }+{\lambda }_{\alpha },\alpha =1,\cdots ,N_{\mathrm{NP}}$$ (36)

where ${\mu }_{\alpha }^{\text{gen}}$ is the relative generalized potential of species α. It must vanish at equilibrium, which leads to the constraint for the Lagrange multiplier and the equilibrium concentration

$$\begin{array}{cc}\hfill {\lambda }_{\alpha }& =-{\mu }_{\alpha }^0\hfill \\ \hfill {\rho }_{\alpha }& ={\rho }_{\alpha 0}{e}^{-\frac{q_{\alpha }\Phi +U_{\alpha }-{\mu }_{\alpha 0}}{k_{B}T}}.\hfill \end{array}$$ (37)

From Eqs. (36) and (37), the relative generalized potential can be expressed as

$${\mu }_{\alpha }^{\text{gen}}=-{\mu }_{\alpha 0}+k_{B}T\ln \frac{{\rho }_{\alpha }}{{\rho }_{\alpha 0}}+q_{\alpha }\Phi +U_{\alpha },\alpha =1,\cdots ,N_{\mathrm{NP}}$$ (38)

Note that μ_α0 does not have a position dependence. Therefore, by using the same procedure as that for deriving Eq. (26), we arrive at the generalized Nernst-Planck equation

$$\frac{\partial {\rho }_{\alpha }}{\partial t}=\nabla \cdot \left[D_{\alpha }\left(\nabla {\rho }_{\alpha }+\frac{{\rho }_{\alpha }}{k_{B}T}\nabla (q_{\alpha }\Phi +U_{\alpha })\right)\right],\alpha =1,2,\cdots ,N_{\mathrm{NP}}.$$ (39)

The combination of Eqs. (37) and (39) provides a full description of charge particles in the system. In practical applications, one wishes to solve as few NP equations as possible, while maintaining the given level of modeling accuracy.

Generalized Poisson-Boltzmann equation

By taking the variation of the total energy functional with respect to the electrostatic potential Φ, one has the generalized Poisson-Boltzmann equation

$$-\nabla \cdot (∊\left(S\right)\nabla \Phi )=S{\rho }_m+(1-S)\left(\sum _{\alpha =1}^{N_{\mathrm{NP}}}{q}_{\alpha }{\rho }_{\alpha }+\sum _{\beta =N_{\mathrm{NP}}+1}^{N_c}{q}_{\beta }{\rho }_{\beta 0}{e}^{-\frac{q_{\beta }\Phi +U_{\beta }-{\mu }_{\beta 0}}{k_{B}T}},\right),$$ (40)

where ε(S) = (1 – S)ε_s + Sε_m. The treatment of certain mobile charge species by the Boltzmann distribution has significantly reduced the number of NP equations to be solved. The combination of Eqs. (39) and (40) is called generalized PBNP equations.

Generalized Laplace-Beltrami equation

Furthermore, we can obtain the equation for the solvent-solute interface by the variation of Eq. (35) with respect to surface characteristic function S

$$\frac{\delta G_{\text{total}}^{\mathrm{PBNP}}}{\delta S}\Rightarrow -\nabla \cdot \left(\gamma \frac{\nabla S}{\mid \nabla S\mid }\right)+p-\sum _{\alpha =1}^{N_{\mathrm{NP}}}{\rho }_{\alpha }{U}_{\alpha }-\frac{{∊}_m}{2}{\mid \nabla \Phi \mid }^2+\Phi {\rho }_m+\frac{{∊}_s}{2}{\mid \nabla \Phi \mid }^2-\Phi \sum _{\alpha =1}^{N_{\mathrm{NP}}}{\rho }_{\alpha }{q}_{\alpha }-\sum _{\alpha =1}^{N_{\mathrm{NP}}}\left[k_{B}T\left({\rho }_{\alpha }\ln \frac{{\rho }_{\alpha }}{{\rho }_{\alpha 0}}-{\rho }_{\alpha }+{\rho }_{\alpha 0}\right)-{\mu }_{\alpha 0}{\rho }_{\alpha }\right]+\sum _{\beta =N_{\mathrm{NP}}+1}^{N_c}{k}_{B}T{\rho }_{\beta 0}\left(e^{-\frac{q_{\beta }\Phi +U_{\beta }-{\mu }_{\beta 0}}{k_{B}T}}-1\right)=0.$$ (41)

Similarly, the solution of Eq. (41) can be obtained by solving the following generalized Laplace-Beltrami equation

$$\frac{\partial S}{\partial t}=\mid \nabla S\mid \left[\nabla \cdot \left(\gamma \frac{\nabla S}{\mid \nabla S\mid }\right)+V_3\right],$$ (42)

where the potential driven term is given by

$$V_3=-p+\sum _{\alpha =1}^{N_{\mathrm{NP}}}{\rho }_{\alpha }{U}_{\alpha }+\frac{{∊}_m}{2}{\mid \nabla \Phi \mid }^2-\Phi {\rho }_m-\frac{{∊}_s}{2}{\mid \nabla \Phi \mid }^2+\Phi \sum _{\alpha =1}^{N_{\mathrm{NP}}}{\rho }_{\alpha }{q}_{\alpha }+\sum _{\alpha =1}^{N_{\mathrm{NP}}}\left[k_{B}T\left({\rho }_{\alpha }\ln \frac{{\rho }_{\alpha }}{{\rho }_{\alpha 0}}-{\rho }_{\alpha }+{\rho }_{\alpha 0}\right)-{\mu }_{\alpha 0}{\rho }_{\alpha }\right]-k_{B}T\sum _{\beta =N_{\mathrm{NP}}+1}^{N_c}{\rho }_{\beta 0}\left(e^{-\frac{q_{\beta }\Phi +U_{\beta }-{\mu }_{\beta 0}}{k_{B}T}}-1\right)$$ (43)

The generalized LB equation (42), PB equation (40) and NP equation (39) are coupled together to form the system for the present LB-PBNP model. The solution to these equations gives rise to an optimized surface function S, electrostatic potential Φ and a set of charge densities {ρ_α}. The convergent solutions of S, Φ and {ρ_α} provide the minimal total energy $G_{\text{total}}^{\mathrm{PBNP}}$ given in Eq. (35).

II.C.3 Relation to the LB-PB and LB-PNP models

It is easy to show that at equilibrium, the constraints given in Eq. (37) reduce the LB-PBNP total energy $G_{\text{total}}^{\mathrm{PBNP}}$ given in Eq. (35) to the LB-PB total energy $G_{\text{total}}^{\mathrm{PB}}$ given in Eq. (11)

$$\begin{array}{cc}\hfill G_{\text{total}}^{\mathrm{PBNP}}& =\int \left\{\gamma \mid \nabla S\mid +pS+(1-S)\sum _{\alpha =1}^{N_{\mathrm{NP}}}{\rho }_{\alpha }{U}_{\alpha }+S\left[-\frac{{∊}_m}{2}{\mid \nabla \Phi \mid }^2+\Phi {\rho }_m\right]+(1-S)\left[-\frac{{∊}_s}{2}{\mid \nabla \Phi \mid }^2+\Phi \sum _{\alpha =1}^{N_{\mathrm{NP}}}{\rho }_{\alpha }{q}_{\alpha }-\sum _{\beta =N_{\mathrm{NP}}+1}^{N_c}{k}_{B}T{\rho }_{\beta 0}\left(e^{-\frac{q_{\beta }\Phi +U_{\beta }-{\mu }_{\beta 0}}{k_{B}T}}-1\right)\right]+(1-S)\sum _{\alpha =1}^{N_{\mathrm{NP}}}\left[-{\mu }_{\alpha 0}{\rho }_{\alpha }+k_{B}T{\rho }_{\alpha }\ln \frac{{\rho }_{\alpha }}{{\rho }_{\alpha 0}}-k_{B}T({\rho }_{\alpha }-{\rho }_{\alpha 0})\right]\right\}d\mathbf{r}\hfill \\ \hfill & =\int \left\{\gamma \mid \nabla S\mid +pS+S\left[-\frac{{∊}_m}{2}{\mid \nabla \Phi \mid }^2+\Phi {\rho }_m\right]+(1-S)\left[-\frac{{∊}_s}{2}{\mid \nabla \Phi \mid }^2-k_{B}T\sum _{\alpha =1}^{N_{\mathrm{NP}}}({\rho }_{\alpha }-{\rho }_{\alpha 0})-k_{B}T\sum _{\beta =N_{\mathrm{NP}}+1}^{N_c}{\rho }_{\alpha 0}\left(e^{-\frac{q_{\alpha }\Phi +U_{\alpha }-{\mu }_{\alpha 0}}{k_{B}T}}-1\right)\right]\right\}d\mathbf{r}\hfill \\ \hfill & =G_{\text{total}}^{\mathrm{PB}}.\hfill \end{array}$$ (44)

Similarly, one can demonstrate that under the constraints of Eq. (37), the surface driven function V₃ given in Eq. (43) reduces to the surface driven function V₁ of the LB-PB model

$$\begin{array}{cc}\hfill V_3& =-p+\sum _{\alpha =1}^{N_{\mathrm{NP}}}{\rho }_{\alpha }{U}_{\alpha }+\frac{{∊}_m}{2}{\mid \nabla \Phi \mid }^2-\Phi {\rho }_m-\frac{{∊}_s}{2}{\mid \nabla \Phi \mid }^2+\Phi \sum _{\alpha =1}^{N_{\mathrm{NP}}}{\rho }_{\alpha }{q}_{\alpha }+\sum _{\alpha =1}^{N_{\mathrm{NP}}}\left[k_{B}T\left({\rho }_{\alpha }\ln \frac{{\rho }_{\alpha }}{{\rho }_{\alpha 0}}-{\rho }_{\alpha }+{\rho }_{\alpha 0}\right)-{\mu }_{\alpha 0}{\rho }_{\alpha }\right]-k_{B}T\sum _{\beta =N_{\mathrm{NP}}+1}^{N_c}{\rho }_{\beta 0}\left(e^{-\frac{q_{\beta }\Phi +U_{\beta }-{\mu }_{\beta 0}}{k_{B}T}}-1\right)\hfill \\ \hfill & =-p+\frac{{∊}_m}{2}{\mid \nabla \Phi \mid }^2-\Phi {\rho }_m-\frac{{∊}_s}{2}{\mid \nabla \Phi \mid }^2-k_{B}T\sum _{\alpha =1}^{N_{\mathrm{NP}}}({\rho }_{\alpha }-{\rho }_{\alpha 0})-k_{B}T\sum _{\beta =N_{\mathrm{NP}}+1}^{N_c}{\rho }_{\beta 0}\left(e^{-\frac{q_{\beta }\Phi +U_{\beta }-{\mu }_{\beta 0}}{k_{B}T}}-1\right)\hfill \\ \hfill & =-p+\frac{{∊}_m}{2}{\mid \nabla \Phi \mid }^2-\Phi {\rho }_m-\frac{{∊}_s}{2}{\mid \nabla \Phi \mid }^2-k_{B}T\sum _{\alpha =1}^{N_c}{\rho }_{\alpha 0}\left(e^{-\frac{q_{\alpha }\Phi +U_{\alpha }-{\mu }_{\alpha 0}}{k_{B}T}}-1\right)\hfill \\ \hfill & =V_1.\hfill \end{array}$$ (45)

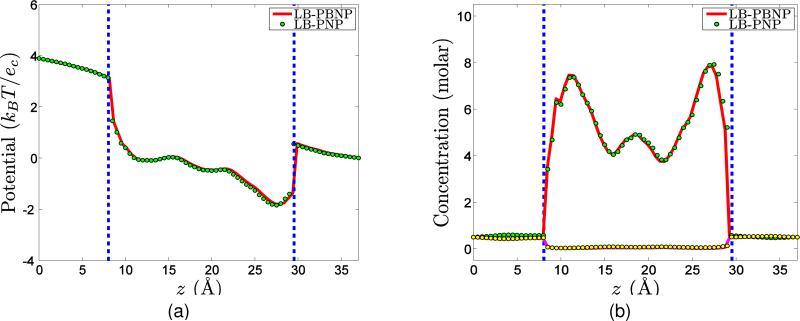
However, it is not easy to show that the LB-PBNP total energy $G_{\text{total}}^{\mathrm{PBNP}}$ is a faithful representation of the LB-PNP total energy $G_{\text{total}}^{\mathrm{PNP}}$ . In other words, it is not clear whether the reduced LB-PBNP model is able to recover the full predictions of the LB-PNP model. The representability of the LB-PNP model by the present simplified LB-PBNP model is one of the major issues to be addressed by the numerical analysis and experiments in following sections. The success of the present LB-PBNP model depends on its ability to reproduce the full predictions of the computationally more expensive LB-PNP model.

The LB-PNP and LB-PBNP models neglect possible fluid flows and chemical reactions. In fact, in practical applications, such as fuel cells and nanofluidic systems, fluid motion and chemical reaction commonly occur. In the next section, we present a differential geometry based chemo-electro-fluid model.

II.D Differential geometry based chemo-electro-fluid model

At nanoscale, fluid flows play a crucial role in the density distribution of charge species and electrostatic properties of immersed macromolecules. In nano-fluidic devices and fuel cell systems, the description of fluid motion is mostly required. The interface description is important in PEM fuel cells, where a hydrophobic polymer membrane is functionalized by acidic side chains. The polymer membrane behaves as an electrode separator and allows certain types of ion species (e.g., protons) to pass through so as to convert the chemical energy into electric power. However, fluid particles involve an excessively large number of degrees of freedom and are better described by using continuum models. On the other hand, we wish to describe the immersed molecules, such as proteins, DNAs and ion channels, by using discrete atomistic models because their charge locations are important to the ion selectivity, gating effect, and transport. It is well-known that the relevant distance is determined by the Debye length ${\lambda }_D={({∊}_s{k}_{B}T∕{\sum }_{\alpha }{\rho }_{\alpha 0}{q}_{\alpha }^2)}^{1∕2}$ . In biological systems, the electrostatic potential impacts over a few orders of magnitude, from atomic to cellular scales, depending on the temperature and ion density. Similar effects can be found in mechanical and chemical systems as well. As such, a multiscale model is desirable for nanofluidic and fuel cell systems as introduced in our earlier work.¹⁸² In classical kinetic theory, the distribution of charge species is often described by equations of the conservation law. Therefore, we have provided a conservation law based derivation of the Nernst-Planck equation in our earlier work.¹⁸² It was shown that the “diffusion flow” of each individual species defined with respect to the barycentric motion is crucial to the derivation of the Nernst-Planck equation. All other governing equations, including Navier-Stokes, Laplace-Beltrami and Poisson equations, were derived from the variational principle.

In the present work, we offer an alternative derivation of coupled Navier-Stokes, Laplace-Beltrami, Poisson and Nernst-Planck equations. Specifically, we do not resort to the conservation law argument for the Nernst-Planck equation. Instead, all governing equations are derived from the variational framework, which is able to put microscopic and macroscopic description on an equal footing. An important advantage of this framework is that it is easy to put different theories in contact and eliminate inconsistency in governing equations. An essential tactic in our multiscale variational framework is to make use of fundamental laws of physics, while avoiding phenomenological descriptions.

II.D.1 The action functional for the chemo-electro-fluid model

In this work, we develop differential geometry based approaches so that the surface formation is coupled to the Navier-Stokes equation and Poisson-Nernst-Planck equations. We slightly modify the formulation developed in Section II.B with an appropriate fluid term. Let us consider the following total action functional

$$G_{\text{total}}^{\mathrm{NS}-\mathrm{PNP}}[S,\Phi ,\left\{{\rho }_{\alpha }\right\}]=\int \int \{\gamma \mid \nabla S\mid +pS+(1-S)U+S\phantom{\{}\left[-\frac{{∊}_m}{2}{\mid \nabla \Phi \mid }^2+\Phi {\rho }_m\right]+(1-S)\left[-\frac{{∊}_s}{2}{\mid \nabla \Phi \mid }^2+\Phi \sum _{\alpha }{\rho }_{\alpha }{q}_{\alpha }\right]+(1-S)\sum _{\alpha }\left[({\mu }_{\alpha }^0-{\mu }_{\alpha 0}){\rho }_{\alpha }+k_{B}T{\rho }_{\alpha }\ln \frac{{\rho }_{\alpha }}{{\rho }_{\alpha 0}}-k_{B}T({\rho }_{\alpha }-{\rho }_{\alpha 0})+{\lambda }_{\alpha }{\rho }_{\alpha }\right]-(1-S)\left[\rho \frac{{\mathbf{v}}^2}{2}-p+\frac{{\mu }_f}{8}{\int }^t{\left(\frac{\partial {\mathbf{v}}_i}{\partial {\mathbf{r}}_j}+\frac{\partial {\mathbf{v}}_j}{\partial {\mathbf{r}}_i}\right)}^{2}d{t}^{\prime }\right]\}d\mathbf{r}dt,$$ (46)

where ρ = Σ_α ρ_α is the total solvent mass density, v is the flow stream velocity, and μ_f is the viscosity of the fluid. The Einstein summation convention is used in the viscosity term. The first few rows in Eq. (46) have been discussed in the earlier sections. The last row in Eq. (46) describes the Lagrangian of an incompressible viscous flow with the kinetic energy, potential energy and viscous energy lost due to friction.¹⁸²

II.D.2 Governing equations

Generalized Nernst-Planck equation

With a non-vanishing flow velocity, the derivation of the generalized Nernst-Planck is slightly different from that in Section II.B.3. One first computes the generalized potential via the variation of the total action functional (46) with respect to the ion concentration ρ_α.

$${\mu }_{\alpha }^{\text{gen}}={\mu }_{\alpha }^0-{\mu }_{\alpha 0}+k_{B}T\ln \frac{{\rho }_{\alpha }}{{\rho }_{\alpha 0}}+q_{\alpha }\Phi +U_{\alpha }+{\lambda }_{\alpha }-\frac{{\mathbf{v}}^2}{2},$$ (47)

where ${\mu }_{\alpha }^{\text{gen}}$ is the relative generalized potential of species α. We assume that ${\mu }_{\alpha }^{\text{gen}}$ vanishes at “dynamical equilibrium”. As such, one has

$${\lambda }_{\alpha }=-{\mu }_{\alpha }^0\text{and}{\rho }_{\alpha }={\rho }_{\alpha 0}{e}^{-\frac{q_{\alpha }\Phi +U_{\alpha }-{\mu }_{\alpha 0}-\frac{{\mathbf{v}}^2}{2}}{k_{B}T}}.$$ (48)

Of course, more classical equilibrium state is described by Eq. (24). From Eq. (48), the relative generalized potential ${\mu }_{\alpha }^{\text{gen}}$ can be expressed as

$${\mu }_{\alpha }^{\text{gen}}=k_{B}T\ln \frac{{\rho }_{\alpha }}{{\rho }_{\alpha 0}}+q_{\alpha }\Phi +U_{\alpha }-{\mu }_{\alpha 0}-\frac{{\mathbf{v}}^2}{2}.$$ (49)

With the above relative generalized potential, we obtain the generalized flux as

$${\mathbf{J}}_{\alpha }=-D_{\alpha }{\rho }_{\alpha }\nabla \frac{{\mu }_{\alpha }^{\text{gen}}}{k_{B}T}.$$

With the consideration of chemical reactions and fluid flows, the generalized Fick's law reads¹⁸²

$$\frac{\partial {\rho }_{\alpha }}{\partial t}+\mathbf{v}\cdot \nabla {\rho }_{\alpha }=-\nabla \cdot {\mathbf{J}}_{\alpha }+\sum _j{\stackrel{‒}{\nu }}_{\alpha j}{J}^j$$ (50)

where ${\stackrel{‒}{\nu }}_{\alpha j}{J}^j$ is the density production of α species per unit volume in the jth chemical reaction. Therefore, we have the generalized Nernst-Planck equation

$$\frac{\partial {\rho }_{\alpha }}{\partial t}+\mathbf{v}\cdot \nabla {\rho }_{\alpha }=\nabla \cdot D_{\alpha }\left[\nabla {\rho }_{\alpha }+\frac{{\rho }_{\alpha }}{k_{B}T}\nabla \left(q_{\alpha }\Phi +U_{\alpha }-\frac{{\mathbf{v}}^2}{2}\right)\right]+\sum _j{\stackrel{‒}{\nu }}_{\alpha j}{J}^j.$$ (51)

Here, $q_{\alpha }\Phi +U_{\alpha }-\frac{{\mathbf{v}}^2}{2}$ is a generalized potential, which is similar to the “potential of mean forces” for the system. Consequently, $-\nabla \left(q_{\alpha }\Phi +U_{\alpha }-\frac{{\mathbf{v}}^2}{2}\right)$ is a generalized force. It is interesting to note that the local gradient of fluid flow kinetic energy also contributes to the density flux. When |v| = 0 and there is no chemical reactions, Eq. (51) reduces to Eq. (26), which further reduces to the standard Nernst-Planck equation if the solvent-solute interactions vanishes.

Generalized Navier-Stokes equation

The variation of the total action functional (46) also leads to the generalized Navier-Stokes equation which governs the flow stream velocity of incompressible flows¹⁸²

$$\rho \left(\frac{\partial \mathbf{v}}{\partial t}+\mathbf{v}\cdot \nabla \mathbf{v}\right)=-\nabla p+\frac{1}{1-S}\nabla \cdot (1-S)\mathbb{T}+{\mathbf{F}}_{\mathrm{E}},$$ (52)

where $\mathbb{T}$ is the flow stress tensor¹⁸²

$$\mathbb{T}=\frac{{\mu }_f}{2}\left(\frac{\partial {\mathbf{v}}_i}{\partial {\mathbf{r}}_j}+\frac{\partial {\mathbf{v}}_j}{\partial {\mathbf{r}}_i}\right)=\frac{{\mu }_f}{2}[\nabla \mathbf{v}+{(\nabla \mathbf{v})}^T],$$ (53)

where symbol T denotes the transpose. In Eq. (52), F_E is the total force given by

$${\mathbf{F}}_{\mathrm{E}}=\frac{S}{1-S}{\mathbf{f}}_{\mathrm{np}},$$ (54)

where the nonpolar force is

$${\mathbf{f}}_{\mathrm{np}}=-\nabla p-\frac{1-S}{S}\nabla U+\frac{{\rho }_m}{S}\nabla \left(S\Phi \right).$$ (55)

It is interesting to note that compared with the classical Navier-Stokes equation under electric field,¹⁸² the generalized reaction field force ${\mathbf{f}}_{\mathrm{E}}=\frac{1}{1-S}{\sum }_{\alpha }{q}_{\alpha }{\rho }_{\alpha }\nabla (1-S)\Phi$ (i.e., the classical electric field (E) term $-{\sum }_{\alpha }{q}_{\alpha }{\rho }_{\alpha }\mathbf{E}$ for electro-osmotic flows) is absent from the present force expression because the density of each species is regarded as a variable in the variation. For the same reason, generalized Nernst-Planck equation (51) has gained an extra term associated with the fluid energy. Therefore, by using the total energy functional formulation, one can eliminate the inconsistency in governing equations.

Generalized Laplace-Beltrami equation

By using the same procedure as that used in Section II.B.3, we end up with the generalized Laplace-Beltrami equation

$$\frac{\partial S}{\partial t}=\mid \nabla S\mid \left[\nabla \cdot \left(\gamma \frac{\nabla S}{\mid \nabla S\mid }\right)+V_4\right],$$ (56)

where

$$V_4=-p+U+\frac{{∊}_m}{2}{\mid \nabla \Phi \mid }^2-\Phi {\rho }_m-\frac{{∊}_s}{2}{\mid \nabla \Phi \mid }^2+\Phi \sum _{\alpha }{\rho }_{\alpha }{q}_{\alpha }+\sum _{\alpha }\left[k_{B}T\left({\rho }_{\alpha }\ln \frac{{\rho }_{\alpha }}{{\rho }_{\alpha 0}}-{\rho }_{\alpha }+{\rho }_{\alpha 0}\right)-{\mu }_{\alpha 0}{\rho }_{\alpha }\right]-\left[\rho \frac{{\mathbf{v}}^2}{2}-p+\frac{{\mu }_f}{8}{\int }^t{\left(\frac{\partial {\mathbf{v}}_i}{\partial {\mathbf{r}}_j}+\frac{\partial {\mathbf{v}}_j}{\partial {\mathbf{r}}_i}\right)}^{2}d{t}^{\prime }\right].$$ (57)

Compared with Eq. (32), the additional fluid energy term contributes to the solvent-solute interface evolution.

Finally, the variation of the total action functional (46) with respect to does not lead to a new equation — the generalized Poisson equation (29) is obtained again.

The generalized Nernst-Planck equation (51), Navier-Stokes equation (52) and Laplace-Beltrami equation¹⁸² are coupled to the generalized Poisson equation (29). These coupled equations provide a description to a chemo-electro-fluid system of multiple charge species far from equilibrium. They offer a reference to the charge transport models formulated in earlier sections so as to enhance our understanding.

As discussed in our earlier work,¹⁸² the total charge current density I_c is given by

$${\mathbf{I}}_{\mathbf{c}}=\rho q\mathbf{v}+{\mathbf{i}}_c=\mathbf{v}\sum _{\alpha }{\rho }_{\alpha }{q}_{\alpha }+\sum _{\alpha }{q}_{\alpha }{\mathbf{J}}_{\alpha }$$ (58)

where ρqv is the charge convection current due to flow motion and i_c is the charge conduction current. The charge convection current vanishes for a charge neutral system.

III Computational algorithms

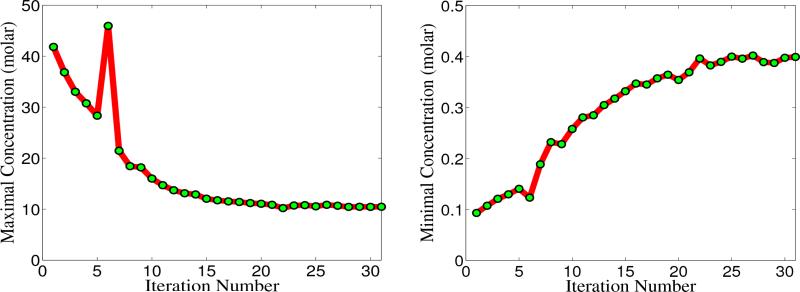
The development of rigorous numerical techniques and computational algorithms is enormously important for the study and understanding of realistic chemical, physical, biological and engineering problems. This section concerns the implementation of the proposed charge transport models for ion channel transport in membrane proteins. Since ion channel measurements are usually conducted without fluid motion, we focus our effort on two charge transport models given in Sections II.B and II.C. In these models, essentially three types of coupled equations with appropriate initial/boundary conditions need to be solved in a self-consistent manner. In this section, the algorithms of solving the coupled system are discussed by referring to the generalized LB-PNP equations, the algorithms for LB-PBNP follow similar procedures.

As discussed in the previous work,^33,34 either the Eulerian representation or the Lagrangian representation can be utilized for the multiscale analysis. Here we discuss the computational algorithms for both formulations.

III.A Eulerian representation

The main feature of the Eulerian representation is that a smooth solvent-solute interface is produced, which avoids many numerical problems in dealing with the Poisson equation or the Poisson-Boltzmann equation.

III.A.1 Generalized Laplace-Beltrami equation

To solve Eq. (31) with V₂ being represented by Eq. (34), the initial condition is defined below

$$S(\mathbf{r},0)=\{\begin{array}{cc}1,\hfill & \mathbf{r}\in {\Omega }_1,\hfill \\ 0,\hfill & \text{otherwise},\hfill \end{array}\phantom{\}}$$ (59)

where ${\Omega }_1={\bigcup }_{\beta =1,\dots ,N_a}O({\mathbf{r}}_{\beta },r_{\beta }+r_m)$ , that is, if r lies in any of the sphere $(O({\mathbf{r}}_{\beta },r_{\beta }+r_m):\{\mathbf{r}\in {\mathbb{R}}^3,\mid \mathbf{r}-{\mathbf{r}}_{\beta }\mid \le r_{\beta }+r_m\})$ defined by atomic coordinates, then the value for S is 1, otherwise, S = 0. Here, r_β and r_β (β = 1; ..., N_a) are respectively the coordinate and specific radius of βth atom in the molecule with N_a being the total number of atoms, and r_m is the probe radius. The atomic specific radius can be chosen as the atomic van der Waals (vdW) radius.

To evaluate the LB equation, we set t′ = tγ and $V_{\gamma }=\frac{V}{\gamma }$ . To avoid the blowup when the magnitude of ∇ S is very close to zero, we modify the LB equation as

$$\frac{\partial S}{\partial t^{\prime }}=\sqrt{\widehat{\delta }+{\mid \nabla S\mid }^2}\left[\nabla \cdot \left(\frac{\nabla S}{\sqrt{\widehat{\delta }+{\mid \nabla S\mid }^2}}\right)+V_{\gamma }\right],$$ (60)

where $\widehat{\delta }$ is a small positive number. Denote ${\Omega }_2={\bigcup }_{\beta =1,\dots ,N_a}O({\mathbf{r}}_{\beta },r_{\beta })$ as the protection zone, then the surface function S is only updated in domain ${\Omega }_1\bigcap {\overline{\Omega }}_2$ as

$$\frac{\partial S}{\partial t^{\prime }}=\frac{(S_x^2+S_y^2)S_{zz}+(S_x^2+S_z^2)S_{yy}+(S_y^2+S_z^2)S_{xx}-(2S_x{S}_y{S}_{xy}+2S_x{S}_z{S}_{xz}+2S_y{S}_z{S}_{yz})}{\widehat{\delta }+S_x^2+S_y^2+S_z^2}+\sqrt{\widehat{\delta }+S_x^2+S_y^2+S_z^2}{V}_{\gamma }.$$ (61)

Here Eq. (61) can be solved explicitly³⁵ where the time discretization is implemented by the forward Euler scheme and the spatial discretization is done by the standard central finite difference scheme. Alternatively, it can also be solved implicitly by the semi-implicit scheme and alternating-direction implicit (ADI) methods.¹¹ Implicit schemes allow the use of a relatively large time step.

III.A.2 Generalized Poisson and Nernst-Planck equations

The discretization of Eq. (27) and Eq. (29) can follow the standard finite difference scheme. To discretize Eq. (29) along x direction at point (i, j, k), we use

$${\left(∊{\Phi }_x\right)}_x=\frac{{∊}_{i+\frac{1}{2}}{\Phi }_{i+1,j,k}-({∊}_{i+\frac{1}{2}}+{∊}_{i-\frac{1}{2}}){\Phi }_{i,j,k}+{∊}_{i-\frac{1}{2}}{\Phi }_{i-1,j,k}}{{\left(\Delta x\right)}^2},$$ (62)

where Δx is the mesh size in the x direction, ε_i = ε(S_i,j,k). As for the delta functions on the right hand side, they can be distributed to the neighboring points round (i, j, k).

As D_α is the position dependent diffusion coefficient of the α species, we define D_α (S) = (1 – S)D_α . By using this definition, we can observe that when S = 1, D_α(S) is 0, which means that there is no diffusion in the protection zone, then the steady state Eq. (27) can be written as

$$\nabla \cdot \left[D_{\alpha }\left(S\right)\left(\nabla {\rho }_{\alpha }+\frac{{\rho }_{\alpha }}{k_{B}T}\nabla (q_{\alpha }\Phi +U_{\alpha })\right)\right]=0.$$ (63)

To discretize Eq. (63) along the x direction at point (i, j, k), the following scheme can be utilized,

$${\left[D_{\alpha }\left(S\right)({\rho }_{\alpha x}+{\eta }_{\alpha }{\rho }_{\alpha }({\Phi }_x-U_{\alpha }∕q_{\alpha }))\right]}_x=D_{\alpha i+\frac{1}{2},j,k}\left[{\rho }_{\alpha i+1,j,k}-{\rho }_{\alpha i,j,k}+\frac{{\eta }_{\alpha }}{2}({\rho }_{\alpha i+1,j,k}+{\rho }_{\alpha i,j,k})\left({\Phi }_{i+1,j,k}-{\Phi }_{i,j,k}+\frac{U_{\alpha i+1,j,k}-U_{\alpha i,j,k}}{q_{\alpha }}\right)\right]\frac{1}{{\left(\Delta x\right)}^2}-D_{\alpha i-\frac{1}{2},j,k}\left[{\rho }_{\alpha i,j,k}-{\rho }_{\alpha i-1,j,k}+\frac{{\eta }_{\alpha }}{2}({\rho }_{\alpha i,j,k}+{\rho }_{\alpha i-1,j,k})\left({\Phi }_{i,j,k}-{\Phi }_{i-1,j,k}+\frac{U_{\alpha i,j,k}-U_{\alpha i-1,j,k}}{q_{\alpha }}\right)\right]\frac{1}{{\left(\Delta x\right)}^2}$$ (64)

where ${\eta }_{\alpha }=\frac{q_{\alpha }}{k_{B}T}$ and D_i,j,k = (1 – S_i,j,k)D. Here one problem is how to implement the boundary condition for Eq. (63). To enforce the non-flux boundary condition, we set J_α = 0 on ∂Ω₂. Therefore, every time Eq. (31) is updated to the steady state, then ε(S) and D_α (S) can be determined from the surface function S. Therefore, Eqs. (29) and (27) can be solved iteratively until the steady state is reached, which provides new Φ and ρ_α for updating S.

In the Ith inner loop for computing Φ and ρ_α, the successive over relaxation scheme is utilized³³

$$\begin{array}{cc}\hfill {\Phi }^{I+1}& ={\zeta }_1{\Phi }^I+(1-{\zeta }_1){\Phi }^{I+1}\hfill \\ \hfill {\rho }_{\alpha }^{I+1}& ={\zeta }_2{\rho }_{\alpha }^I+(1-{\zeta }_2){\rho }_{\alpha }^{I+1},\hfill \end{array}$$ (65)

where ζ₁ and ζ₂ are in the range of zero and one. This algorithm delivers a stable scheme with appropriate choice of relaxation factors, ζ₁ and ζ₂. A larger value will lead to slower convergence, while a smaller values may cause instability.³³ Alternatively, the Gummel iteration⁵³ can also be used to handle this type of problems as shown in our earlier work.¹⁹⁵

III.B Lagrangian representation

Although the free energy functional is presented in the Eulerian formulation, an alternative free energy functional can be provided by using the Lagrangian representation. Based on such a free energy functional, one can derive the governing equations in a way similar to that in Ref.³⁴ We skipped the description in the present work. The final governing equations are presented below, while the reader is referred to Ref.³⁴ for more details about the derivation procedure.

III.B.1 Poisson equation

In the Lagrangian representation, the total domain $\widehat{\Omega }$ is divided into two domains ${\widehat{\Omega }}_m$ and ${\widehat{\Omega }}_s$ by a sharp interface $\widehat{\Gamma }$ such that $\widehat{\Omega }={\widehat{\Omega }}_m\cup {\widehat{\Omega }}_s$ and $\widehat{\Gamma }={\widehat{\Omega }}_m\cap {\widehat{\Omega }}_s$ . Here the interface $\widehat{\Gamma }$ is determined by the hyperfunction S via an isosurface extraction procedure

$$\widehat{\Gamma }=\{\mathbf{r}\mid S\left(\mathbf{r}\right)=c,0<c<1,\mathbf{r}\in {\mathbb{R}}^3\}.$$ (66)

The matched cubes algorithm is used for the isovalue extraction. Typically, we set c = 0.5 although other values may be used for a particular purpose of illustration. In Eq. (66), the surface function S is still determined by the steady state of evolution equation (31).

The governing equation for electrostatic potential Φ is given by

$$-\nabla \cdot (∊\nabla \Phi )={\rho }_m+\sum _{\alpha }{\rho }_{\alpha }{q}_{\alpha },$$ (67)

where the sharp dielectric function is given by

$$∊=\{\begin{array}{cc}{∊}_m,\hfill & \mathbf{r}\in {\widehat{\Omega }}_m,\hfill \\ {∊}_s,\hfill & \mathbf{r}\in {\widehat{\Omega }}_s.\hfill \end{array}\phantom{\}}$$ (68)

For charge densities ρ_α, Eq. (27) is used. However, it is defined in the present domain of ${\widehat{\Omega }}_s$ .

The solution of Eqs. (67) and (27) involves elliptic equations with discontinuous coefficients and singular sources in biomolecular context. This numerical problem is extremely challenging. The algorithms developed in our recent work¹⁹⁵ can be utilized. Many of essential ideas for treating the irregular points in the discretization of the governing elliptic equations close to the interface are developed in our earlier work.^{187,189–191} Notice that in this representation the zero-flux boundary condition is enforced on $\widehat{\Gamma }$ . A brief discussion of computational techniques is presented below so that the reader can have an essential idea about what are involved.

III.B.2 Dirichlet to Neumann mapping

In order to remove the Dirac delta functions describing partial charge sources in ρ_m from the Poisson equation, the Green's function can be utilized^78,202 and Φ can be decomposed into the regular part $\tilde{\Phi }\left(\mathbf{r}\right)$ and the singular part $\overline{\Phi }\left(\mathbf{r}\right)$ . Specifically, $\Phi =\tilde{\Phi }+\overline{\Phi }$ , where $\overline{\Phi }\left(\mathbf{r}\right)$ is defined only in ${\widehat{\Omega }}_m$ .^39,78 We define $\overline{\Phi }\left(\mathbf{r}\right)={\Phi }^{\ast }\left(\mathbf{r}\right)+{\Phi }^0\left(\mathbf{r}\right)$ , where Φ*(r) is the analytical Green's function given as

$${\Phi }^{\ast }\left(\mathbf{r}\right)=\frac{1}{4\pi }\sum _{j=1}^{N_a}\frac{Q_j}{{∊}_m\mid \mathbf{r}-{\mathbf{r}}_j\mid }.$$ (69)

To compensate the values induced by the Green's function Φ* on the interface $\widehat{\Gamma },{\Phi }^0\left(\mathbf{r}\right)$ is introduced and satisfies the following Laplace equation with a Dirichlet boundary condition

$$\{\begin{array}{cc}{\nabla }^2{\Phi }^0\left(\mathbf{r}\right)=0,\hfill & \mathbf{r}\in {\widehat{\Omega }}_m\hfill \\ {\Phi }^0\left(\mathbf{r}\right)=-{\Phi }^{\ast }\left(\mathbf{r}\right),\hfill & \mathbf{r}\in \widehat{\Gamma }.\hfill \end{array}\phantom{\}}$$ (70)

This decomposition of Φ gives rise to a Poisson equation for $\tilde{\Phi }\left(\mathbf{r}\right)$ without the singular source term, i.e., delta functions,

$$\{\begin{array}{cc}-\nabla \cdot (∊\nabla \tilde{\Phi }\left(\mathbf{r}\right))=\sum _{\alpha }{q}_{\alpha }{\rho }_{\alpha }\hfill & \mathbf{r}\in \widehat{\Omega }\hfill \\ \left[\tilde{\Phi }\left(\mathbf{r}\right)\right]=0\hfill & \mathbf{r}\in \widehat{\Gamma }\hfill \\ \left[∊{\tilde{\Phi }}_{\mathbf{n}}\left(\mathbf{r}\right)\right]={∊}_m\nabla ({\Phi }^{\ast }\left(\mathbf{r}\right)+{\Phi }^0\left(\mathbf{r}\right))\cdot \mathbf{n}\hfill & \mathbf{r}\in \widehat{\Gamma },\hfill \end{array}\phantom{\}}$$ (71)

where n is the interface norm. Due to the introduction of the new Neumann interface condition in Eq. (71), this method is also called Dirichlet to Neumann mapping (DNM). Note that after the decomposition, $\overline{\Phi }$ depends on the geometry of the computational domain and fixed protein charge information, and is independent of the concentration. Therefore, $\overline{\Phi }$ needs to be solved only once. In contrast, since $\tilde{\Phi }$ is coupled to the ion concentrations, $\tilde{\Phi }$ is to be solved in each iteration step. The DNM enhances the stability, improves the accuracy and enables the use of larger mesh sizes.

III.B.3 Matched interface and boundary (MIB) method

To solve Eq. (71) rigorously, the discretization of Eq. (71) requires the enforcement of interface jump conditions while taking care of discontinuous coefficients (68) to ensure certain order accuracy for complex biomolecular surfaces. In this work, we utilize the matched interface and boundary (MIB) method^{25,187,189–191,194,200,201} for the discretization of Eq. (71). Three generations of MIB based Poisson-Boltzmann solvers, MIBPB-I,¹⁹⁸ MIBPB-II¹⁸⁹ and MIBPB-III,⁷⁸ have developed. The MIBPB-I is the first PB solver that explicitly enforces the interface conditions in the biomolecular context. However, it encounters an accuracy reduction in the presence of molecular surface singularities.¹⁴⁶ The MIBPB-II has addressed this problem by utilizing an advanced MIB technique developed by Yu et al.¹⁹⁰ to achieve the second order accuracy for the molecular surfaces of proteins. However, the MIBPB-II is limited to small mesh sizes, namely, sizes smaller than half of the smallest van der Waals radius in a protein structure, because of the interference of the interface and singular charges in the MIBPB-II scheme. This problem has been addressed in our MIBPB-III⁷⁸ by using the Dirichlet to Neumann mapping approach as discussed above. To our knowledge, the MIBPB-III is the only numerical method that delivers second order accuracy in solving the Poisson-Boltzmann equation with discontinuous coefficients, singular sources and primitive geometric singularities in the biomolecular context at present.^25,78

In the MIB method, we define a regular point as the point where its nearest neighboring points involved in the discretization are in the same domain, that is, the point itself is away from the interface. An irregular point is defined as the point where at least one of its nearest neighboring points lies on the other side of the interface, that is, the point itself is close to the interface. The main idea of the MIB method is that to maintain the designed order of accuracy, the finite difference schemes for regular points and irregular points are different. For the discretization along x direction at a regular point (i – 1, j, k), we use the standard finite difference scheme,

$${\left(∊{\tilde{\Phi }}_x\right)}_x=\frac{{∊}_{i-\frac{1}{2}}{\tilde{\Phi }}_{i,j,k}-({∊}_{i-\frac{1}{2}}+{∊}_{i-\frac{3}{2}}){\tilde{\Phi }}_{i-1,j,k}+{∊}_{i-\frac{3}{2}}{\tilde{\Phi }}_{i-2,j,k}}{{\left(\Delta x\right)}^2}\text{at}(i-1,j,k),$$ (72)

where Δx is the mesh size in the x direction. However, for the irregular point (i, j, k), assuming point (i + 1, j, k) lies on a different subdomain, and the solution might not be smooth across the interface, a fictitious value is utilized for the discretization

$${\left(∊{\tilde{\Phi }}_x\right)}_x=\frac{{∊}_{i+\frac{1}{2}}{f}_{i+1,j,k}-({∊}_{i+\frac{1}{2}}+{∊}_{i-\frac{1}{2}}){\tilde{\Phi }}_{i,j,k}+{∊}_{i-\frac{1}{2}}{\tilde{\Phi }}_{i-1,j,k}}{{\left(\Delta x\right)}^2}\text{at}(i,j,k),$$ (73)

where f_i+1,j,k is the fictitious value defined at point (i + 1, j, k) and the value is interpolated by using the interface jump conditions shown in Eq. (71). This is nontrivial for complex biomolecules since the discretization of the jump conditions is defined on the interface, and in most cases the interface points are off grid. The discretizations from both sides of the interface are required for the enforcement of the jump conditions, which needs many auxiliary points. The details of the technique are referred to the related work on the MIB method.^{190,191,194,200,201} Essentially, the MIB method makes use of simple Cartesian grids, standard finite difference schemes, lower order physical jump conditions and the idea of fictitious values defined on irregular points close to the interface. While the physical jump conditions are enforced at each intersecting point of the interface and the mesh lines, the MIB method takes care of the interface condition in a systematic way. As a result, whenever it is possible, the MIB method reduces a multidimensional interface problem into one-dimensional ones. So far, it is the only known method that has been shown to achieve the second order accuracy in solving the PB equation with realistic molecular surfaces of proteins and associated singular charges, to our best knowledge.²⁵

III.C Iterative procedure and algebraic equation solver

The iteration loop for the linear implementation starts from an initial guess of Φ⁰ and ${\rho }_{\alpha }^0$ , then ${\rho }_{\alpha }^0$ is obtained by solving

$$\nabla \cdot \left[D_{\alpha }\left(\nabla {\rho }_{\alpha }^1+\frac{q_{\alpha }{\rho }_{\alpha }^1}{k_{B}T}\nabla ({\Phi }^0+U_{\alpha }∕q_{\alpha })\right)\right]=0.$$ (74)

Then, Φ¹ can be obtained by

$$-\nabla \cdot (∊\nabla {\Phi }^1)=\sum _{\alpha }{q}_{\alpha }{\rho }_{\alpha }^1.$$ (75)

Here the superscripts of Φ and ρ_α indicate the iteration step. The solution of the formed linear algebraic system is credited to a preconditioner algorithm²⁵ from the SLATEC library (http://people.sc.fsu.edu/~jburkardt/f_src/slatec/slatec.html). The following implementation procedure is used in the present work for proteins or ion channels.

• Step 1: Initial atomic position and partial charge generation. The initial atomic positions of a protein are taken from the Protein Data Bank (PDB) (www.pdb.org), and the partial charge prescription is obtained by the software PDB2PQR,^56,57 which provides r_j and Q_j values in the formulation.

• Step 2: Give an initial guess of Φ and ρ_α, the surface function S is obtained by the initial value problem Eq. (31). After the surface function S is determined, an isosurface is extracted for the interface Γ.

• Step 3: Based on the interface Γ, normal direction n is computed by $\frac{\nabla S}{\mid \nabla S\mid }$ on the isosurface; the coupled Eqs. (29) and (27) are solved iteratively by above mentioned schemes.

• Step 4: Go to Steps 2 and 3 for updating S, Φ and ρ_α until a convergence is reached based on a given tolerance. Noticed that in the lth outer loop for updating S, we use S^l+1 = λ₃S^l+(1 – λ₃)S^l+1. In each outer loop, the total free energy functional is evaluated for checking the convergence criteria.

IV Validation and Application

Rigorous validation of mathematical models via advanced computational techniques in realistic settings is perhaps one the of most challenging and time-consuming aspects of theoretical studies. In fact, without quantitative validations with experimental data in realistic settings, it is extremely easy for mathematical models to admit unphysical components. Therefore, rigorous validation should become a standard procedure to calibrate mathematical and theoretical models in the field.

This section studies the validity of the proposed variational multiscale models, investigates their feasibility for realistic proteins and ion channels, and test the accuracy, stability and robustness of our computational algorithms. First, we describe the computational setup for proteins and ion channels. Additionally, we carry out numerical experiments on proteins to examine the consistency of proposed multiscale models. Finally, we perform numerical simulations on a realistic ion channel.

It is noted that the solvent-solvent interaction U_αβ(r), i.e., the generalized correlation, is omitted in our present numerical experiments. However, such effects were numerically explored in our earlier work²⁸

IV.A Computational setups of proteins and ion channels

We discuss the computational setup for proteins and ion channels. The essential procedure is similar to that used in our earlier work.^{33,78,189,195}

IV.A.1 Preparation for the protein study

A set of ten protein molecules is employed in the present work. The initial atomic positions of proteins are taken from the Protein Data Bank (PDB) (www.pdb.org), and the partial charge prescription is obtained by the software PDB2PQR.^56,57 Here, the PDB2PQR is a Python software package that automates many of the common tasks of preparing structures for continuum electrostatic calculations, providing a platform-independent utility for converting protein files in the PDB format to the so called PQR format. The following procedures are involved in the conversion: adding a limited number of missing heavy atoms to biomolecular structures, placing missing hydrogens, optimizing the protein for favorable hydrogen bonding, and assigning charge and radius parameters from a variety of force fields. The details are described in the software webpage (www.poissonboltzmann.org/pdb2pqr/). In our models, the function S is obtained by solving the parabolic evolution equation, and the surface is obtained by extracting the isovalue of 0.5. A uniform mesh with the mesh size of 0.5Å is utilized for the computation. After the surface is obtained, all the mesh points are identified either in the solvent domain or in the solute domain. For the whole computation, the stopping criteria is that the energy difference between two iterations in the outer loop is less than 0.01 kcal/mol. The parameters developed in our previous work for the nonpolar solvation model³³ are considered as the reference in the present work. In the protein test cases, the following parameters are utilized: ρ_s/ρ = 2, σ_s = 0.65 Å and p/γ = 0.5 where ρ_s is the solvent density. Since we only consider very low ion densities in the present work, we neglect interactions between the protein and solvent ions in the nonpolar model. For the value of γ, it may be chosen due to different sizes of the molecule. In this computation, γ is scaled to be 1/3 for the surface generation to incorporate the time evolution scale, while in the final total energy computation, γ = 0.0065 kcal/(mol Ų).

IV.A.2 Preparation for the ion channel study

The ions are charged particles solvated to the solvent environment, including both bulk solvent and channel pore solvent. In ion channels, many microscopic interactions take place during ion transport processes, as ion channel proteins interact with ions and the solvent at atomic scale. Essentially, the ion channel protein and lipid bilayer are immersed in a solvent environment.^195,196 In the present study, we consider Gramicidin A (GA) channel (PDB ID: 1mag, see Fig. 1), which is a benchmark ion channel for testing various theoretical models. As shown in Fig. 1, the computational domain of the GA channel incorporates four different regions, i.e., the channel region, bulk region, protein region and a membrane lipid bilayer. The channel and bulk regions are set to Ω_s and the protein and membrane regions are set to Ω_m. The structural preparation of GA is done according to the following procedure. First, the initial atomic positions of the GA channel protein are obtained from the PDB. The partial charge for each atom in the protein is obtained by using the PDB2PQR software, and is accounted in Φ*. The channel protein is combined with an implicit slab representation of the membrane lipid bilayers to form the molecular domain Ω_m. We set the GA channel pore as along the z direction, which is the same as that in the literature.²³ The corresponding diffusion coefficient profile and unit conversion detail are described in our previous work.¹⁹⁵

The value S is obtained by solving the Laplace-Beltrami equation, and the surface can be extracted by choosing an isovalue between 0 and 1. In the following computation, the surface is obtained by extracting an isovalue of 0.7 so that the protein channel pore diameter is similar to that used in our earlier computation.¹⁹⁵ A uniform mesh with the mesh size of 0.5Å is utilized for the present study. After the surface is obtained, mesh points are identified as either in the solvent domain or in the solute domain, then mesh points in the pore region can be located accordingly. For the whole computation, the stopping criteria is that the energy difference between two iterations in the outer loop is less than 0.01 kcal/mol. In our calculations, we set γ = 1/15 kcal/(molŲ), ρ_s/γ = 2, σ_s = 0.65Å and p/γ = 0.5.

IV.B Protein study

Using a set of ten proteins, we test the proposed LB-PNP and LB-PBNP models. Comparison is given to the traditional PB model and our earlier LB-PB model. The latter has been intensively validated by using both accurate theoretical predictions and experimental data of solvation energies.³⁵

IV.B.1 Free energies at equilibrium

In this subsection, the electrostatic solvation energies of proteins with salt effect are studied by using three models. The first model is the PB equation with the solvent excluded surface generated by using the MSMS package.¹⁴⁵ Another model is the LB-PB equations proposed in our earlier work.³³ The other model is the LB-PNP system introduced in the present paper.

For the LB-PNP model, the numerical procedure discussed in the previous section is utilized. The surface function, electrostatic potential and ion densities are obtained by solving the coupled equations. As discussed in our earlier work,³⁴ the electrostatic potential can be computed in different units. By applying the Gaussian units and defining the dimensionless potential as $u\left(\mathbf{r}\right)=\frac{e_c\Phi }{k_{B}T}$ , Eq. (29) can be written as

$$-\nabla \cdot (∊\left(S\right)\nabla u)=\frac{4\pi e_c}{k_{B}T}S{\rho }_m+\frac{4\pi e_c}{k_{B}T}(1-S)\sum _{\alpha }^{N_c}{\rho }_{\alpha }{q}_{\alpha },$$ (76)

and the boundary condition is given by⁹³

$$u\left(\mathbf{r}\right)=\frac{4\pi e_c^2}{k_{B}T}\sum _j^{N_a}{Q}_j\frac{e^{-\kappa \mid \mathbf{r}-{\mathbf{r}}_j\mid }}{{∊}_s\mid \mathbf{r}-{\mathbf{r}}_j\mid }$$ (77)

on ∂Ω, here $\kappa =\frac{\overline{\kappa }}{\sqrt{{∊}_s}}$ and ${\overline{\kappa }}^2=8.486902807{\mathrm{Å}}^{-2}{I}_s$ , where I_s is the ionic strength measured in molar (molars per liter).⁹³ For the concentration ρ_α (α = 1, 2), the uniform Dirichlet boundary condition of ρ₀ = 0.1molar is imposed on ∂Ω_s. For the surface function S, zero boundary condition is imposed.

The reduced electrostatic free energy is computed after solving the Poisson equation or the PB equation

$$\Delta G_{\text{ele}}=\frac{1}{2}\sum _j{Q}_j{\Phi }_{rf}\left({\mathbf{r}}_j\right)$$ (78)

where Φ_rf is the reaction field potential which is defined as ${\Phi }_{\mathrm{rf}}=\Phi -{\Phi }_{\text{vac}}={\Phi }^0+\tilde{\Phi }$ , with Φ_vac being the electrostatic potential in vacuum. Note that ΔG_ele is not the total free energy of the system.

The PDB IDs of 10 proteins are listed in Table 1. We set the bulk salt (KCl) concentration as n₀ = 0.1molar (i.e. the bulk ion concentrations of cations and anions are 0.1 molar, respectively). Electrostatic solvation free energies are computed using PB, LB-PNP and LB-PB models. Results are listed in Table 1, where the first column shows the PDB IDs obtained from the PDB. The second column lists the electrostatic energies computed by using MIBPB package²⁵ which is based on the MSMS surface. The third column provides the electrostatic energies computed based on the LB-PNP model and the last column lists the electrostatic energies computed from the LB-PB model. Figure 3 gives a graphic representation of our comparison. The diagonal line is the reference, or PB vs PB. Obviously, there is an extraordinary consistency between the LB-PB and LB-PNP predictions. Therefore, the equilibrium solution of the Nernst-Planck equation indeed reproduces the Boltzmann distribution of the ion concentration. This consistency provides a confirmation of our non-equilibrium formulation. This result is in a good accordance with our earlier findings.¹⁹⁶

Table 1.

Comparison of electrostatic energies (in kcal/mol) computed with three models for 10 protein molecules

PDB ID	PB	LB-PNP	LB-PB
1ajj	-1142.69	-1121.24	-1121.45
1bbl	-989.35	-984.12	-984.20
1bor	-854.93	-839.80	-839.87
1cbn	-303.90	-295.15	-295.16
1frd	-2867.84	-2832.13	-2832.73
1r69	-1089.81	-1068.40	-1068.55
1sh1	-756.61	-732.49	-732.54
1hpt	-812.56	-787.23	-787.24
1mbg	-1354.62	-1343.01	-1343.29
1neq	-1733.12	-1710.26	-1710.45

Figure 3.

Consistency of electrostatic free energies of 10 proteins among the PB, LB-PB and LB-PNP predictions (protein IDs are listed in Table 1).

Figure 3 also reveals that the results of the present variational interface based LB-PB and LB-PNP models are in a good agreement with those obtained from the traditional PB model equipped with solvent excluded surfaces generated by the MSMS software. As shown in Table 1, the energy differences from these two types of models are within 3% for all proteins examined in this study.

IV.B.2 Variational surface and surface electrostatic potentials

Another important product of the present differential geometry based multiscale models is the variational solvent-solute interface. As discussed in the Introduction, the interface definition underpins a wide range of biomolecular applications. After solving the coupled equations, the surface is extracted at the isovalue of S = 0.5. As an illustrating example, the variational surface of protein 1ajj is shown in Fig. 4 (b), while the molecular surface generated by MSMS package¹⁴⁵ is shown in Fig. 4 (a). Our visualization is aided with the VMD software.

Figure 4.

Surface representations for protein 1ajj. (a) Molecular surface generated by the MSMS package with probe radius 1.4 and density 10; (b) Variational surface extracted from the isovalue of S = 0.5 based on the LB-PNP model.

Obviously, there is a similarity between these two types of surfaces. Technically, the molecular surface is subject to geometric singularities, i.e., non-smooth interfaces, which may devastate numerical simulations. Whereas, our variational interface is free of geometric singularities.^11,13

The other utility of the present multiscale model is the surface electrostatic potential, which is crucial to the protein-protein and protein-ligand interactions, as well as rational drug design. In the present work, we are interested in the consistency between surface electrostatic potentials obtained from the LB-PNP and LB-PB models in the absence of the external force or voltage. Figure 5 provides a comparison of surface electrostatic potentials computed from both models at the iosvalue of S = 0.5. The surface electrostatic potentials are projected on surfaces and illustrated with appropriate colors. Figure 5(a) shows the result obtained from the LB-PNP model and Fig. 5(b) depicts the profile from the LB-PB model. Clearly, a good consistency between two models can be observed. On the one hand, this consistency validates the theoretical formulations of our models; on the other hand, it confirms the computational codes as the results are obtained by solving different sets of coupled equations.

Figure 5.

Comparison of surface electrostatic potentials computed at ρ₀ = 0.1molar for protein 1ajj. (a) Surface electrostatic potential profile obtained from the LB-PNP model; (b) Surface electrostatic potential profile obtained from the LB-PB model.

IV.B.3 Convergence of the total free energy

Another important issue regarding the present variational paradigm is the minimization of the total free energy functional. If the formulation is correct, the total free energy should be gradually reduced in the course of the numerical solution of the coupled equations until a steady state is reached. The computational detail for the evaluation of the nonpolar free energy has been described and validated in our earlier work.³³ Figure 6 plots the total free energy, the electrostatic free energy and the volume of protein 1ajj obtained from the LB-PNP model at the absence of the external voltage. Obviously, all three quantities decrease as the number of outer iterations increases. In particular, at each given time, the difference between the total free energy and the electrostatic free energy is relatively small. Therefore, the nonpolar energy contribution to the total free energy is much smaller than the electrostatic free energy contribution. Moreover, the volume converges slightly faster than the energies do. We have tested that the LB-PB model shows essentially the same convergence characteristic.

Figure 6.

Convergence history of total free energy (kcal/mol), electrostatic energy (kcal/mol) and scaled volume (ų) at ρ₀ = 0.1 molar for protein 1ajj.

Here, we would like to point out that an unreasonable formulation of the total energy functional may lead to abnormal behaviors in the total energy integration history. Monotonic decay to a steady value is the normal behavior. Whereas, increase and/or discontinuous drop in the total energy integration history are unacceptable behaviors and may be caused by unphysical terms in the total energy functional.

IV.C Ion channel study

In this subsection, we study the proposed differential geometry based models for the ion transport problem using a realistic ion channel, the GA channel. Figure 1 provides an illustration of the GA channel and its computational setup. It is important to verify that the consistency between the proposed equilibrium LB-PB model and non-equilibrium LB-PNP model at equilibrium, and the ability of the quasi-equilibrium LP-PBNP model to recover the predictions of the non-equilibrium LB-PNP model at non-equilibrium. After this verification, we explore the GA channel electrostatic potential characteristic and ion density profiles under a variety of typical experimental conditions. Finally, we compare our model predictions with experimental data.

First, the GA channel parameters of the present differential geometry based models are calibrated by the solvation free energies. After the calibration, we study the channel morphology by using two approaches, the conventional MSMS and the present LB equation. Figure 7 depicts two surface representations of the GA channel. Clearly, the surface generated by the LB equation is much smoother, while that generated by the MSMS software usually has geometric singularities.¹⁹⁵ Apart from the surface regularity, the channel pore radius is another important feature. It appears that LB surface pore radius is slightly smaller. This is reasonable because in the Eulerian representation generated by the LB equation, the channel pore domain overlaps with the protein domain. A smaller pore radius also reflects the fact that there is a boundary effect, which means many physical properties at the solvent-solute interface are different from those away from the pore boundary.

Figure 7.

Surface representations of the Gramicidin A channel protein structure. (a) MSMS Surface with probe radius 1.4 and density 10; (b) Surface extracted from the LB equation with S = 0.7.

IV.C.1 Convergence of the ion concentration

Although the convergence of the iteration is judged by the energy, it is also important to examine the behavior of the ion concentration during the iteration process. Figure 8 depicts the concentration profiles along the cross section of the Gramicidin A channel at different numbers of outer iterations. Initially, the cation concentration is relatively high and the anion concentration is relatively low because the fixed charges in the channel protein dominate the electrostatic potential. Figure 9 shows the convergence history and trend of the peak concentration value along the cross section of the Gramicidin A channel. Clearly, cation concentration decreases and anion concentration increases during the iterations, due to the fact that ions themselves also contribute to the electrostatic potential, in addition to many other effects. Note that the scale for the anion profile is different from that for the cation profile.

Figure 8.

Concentration profiles along the cross section of the Gramicidin A channel at different numbers of iterations with ρ₀ = 2.0 molar, Φ₀ = 0 mV. Two vertical dashed lines indicate the channel region. (a) Cation; (b) Anion.

Figure 9.

Convergence history of the peak concentration value along the cross section of the Gramicidin A channel with ρ₀ = 2.0 molar, Φ₀ = 0 mV. (a) Maximal concentration values for cations; (b) Minimal concentration values for anions.

IV.C.2 Consistency between the equilibrium LB-PB model and the non-equilibrium LB-PNP model

As discussed in Section II, the non-equilibrium LB-PNP model reproduces the equilibrium LB-PB model when the flux is zero. Here, computations are carried out with a bulk concentration of ρ_α0=0.1 molar, where α = K⁺ and Cl^–, and without external voltage, i.e., Φ₀ = 0mV. The computational results for two different sets of governing equations are solved, and the cross sections of concentration and potential profiles are plotted in Fig. 10. As shown in Fig. 10(a), the electrostatic potential is negative in the channel region, which indicates that the GA selects positive ions. The concentrations of both cations and anions are plotted in Fig. 10(b) and labeled with green and yellow dots, respectively. In this figure and many other figures, two vertical dashed lines indicate the channel region. Apparently, the cation density peaks at the electrostatic valleys, as expected. Whereas, the density of anions is suppressed in the channel region by the electrostatic potential and is about zero. Obviously, there is an excellent consistency between these two models at equilibrium. This consistency validates our multiscale formulations and computational algorithms.

Figure 10.

Comparison of cross sections of electrostatic potential and concentration profiles with Φ₀ = 0mV and ρ₀ = 0.1molar for Gramicidin A channel. The concentrations of cations and anions are labeled with green and yellow dots, respectively. Two vertical dashed lines indicate the channel region.. (a) Electrostatic potential profiles; (b) Concentration profiles.

Figure 11 presents a comparison of surface electrostatic potentials of two models. The red color indicates the negative potential while blue color stands for a positive potential. As expected, the GA channel possesses predominantly negative electrostatic potentials in the channel mouth region and the pore region. The GA channel repulses anions not only inside the channel pore, but also outside the channel pore region. As shown in Figs. 11 and 12, two differential geometry based models provide essentially the same surface electrostatic potential profiles.

Figure 11.

Comparison of surface electrostatic potential profiles with Φ₀ = 0mV and ρ₀ = 0.1molar for Gramicidin A channel. (a) Surface electrostatic potential profile of the LB-PB model; (b) Surface electrostatic potential profile of the LB-PNP model.

Figure 12.

Comparison of surface electrostatic potential cross sections with Φ₀ = 0 mV and ρ₀ = 0.1molar for Gramicidin A channel. (a) Surface electrostatic potential profile of the LB-PB model; (b) Surface electrostatic potential profile of the LB-PNP model.

IV.C.3 Consistency between the quasi-equilibrium LB-PBNP model and the non-equilibrium LB-PNP model

So far, we have shown the consistency between proposed differential geometry based models and classic PB model in terms of the solvation free energy at equilibrium. We have also demonstrated the consistency between our LB-PB and LB-PNP models in terms of electrostatic potential and density at equilibrium. However, what remains unknown is the ability of the proposed quasi-equilibrium LB-PBNP model to recover the full predictions of the non-equilibrium LB-PNP model at non-equilibrium settings. This ability is important for the reduction of model complexity, because densities of certain ion species are represented by the Boltzmann distribution, instead of being computed by computationally expensive Nernst-Planck equations.

Figure 13 provides the comparison of the cross sections of electrostatic potential and concentration profiles obtained from LB-PNP and LB-PBNP models. The external voltage is set to Φ₀ = 100mV and the salt (KCl) concentration is ρ₀ = 0.5molar. Here we represent Cl^– density ρ_Cl^– (r) by using the Boltzmann distribution, while solve the Nernst-Planck equation for K⁺ density ρ_K⁺ (r). Clearly, electrostatic potential computed by the reduced LB-PBNP model is able to near perfectly recover that of the full LB-PNP model. For the density profile, reduced LB-PBNP model does an excellent job in the channel region, which is the region of main interest. Note that in the bulk regions, it may appear that there is a discrepancy between two models. In fact, two models have an excellent agreement in the bulk regions too.

Figure 13.

Comparison of cross sections of electrostatic potential and concentration profiles with Φ₀ = 100mV, ρ₀ = 0.5molar. The concentrations of cations and anions are labeled with green and yellow dots, respectively. (a) Electrostatic potential profiles; (b) Concentration profiles.

In Figs. 14 and 15, we also plot the comparison of surface electrostatic potentials obtained from the LB-PNP and LB-PBNP models. The top views of surface electrostatic potential profiles are demonstrated in Fig. 14. It is interesting to compare these profiles with those given in Fig. 11, which are attained without any external voltage. Clearly, the applied external voltage has significantly changed the landscape of electrostatic potentials at the top channel mouth region shown in Fig. 14. However, one can still notice the negative surface potential profile inside the channel pore, which ensures original GA channel selectivity. To further confirm this property, we illustrate the cross section profiles of the surface electrostatic potentials in Fig. 15. Indeed, the inner part of the channel pore remains negatively charged, giving rise to the GA selectivity of cations.

Figure 14.

Comparison of the top views of surface electrostatic potentials with Φ₀ = 100mV and ρ₀ = 0.1molar. (a) Surface electrostatic potential profile of the LB-PBNP model; (b) Surface electrostatic potential profile of the LB-PNP model.

Figure 15.

Comparison of the cross sections of surface electrostatic potentials with Φ₀ = 100mV and ρ₀ = 0.1molar for Gramicidin A channel. (a) Surface electrostatic potential profile of the LB-PBNP model; (b) Surface electrostatic potential profile of the LB-PNP model.

It is also interesting to compare Figs. 12(b) and 15(b). The cross sections of electrostatic potentials are clearly affected by the change in external voltages. However, under the applied voltage, the channel pore region remains negative in terms of electrostatic potentials.

Finally, we emphasize that surface electrostatic potentials obtained from the LB-PNP and LB-PBNP models are visually identical, which implies that the proposed LB-PBNP model can be as useful as, but is computationally less expensive than the LB-PNP model for realistic ion channel simulations.

IV.C.4 Electrostatic potentials and densities under different experimental settings

Having validated the consistency of proposed variational multiscale models for ion channel transport, we are interested in the behavior of the GA channel at different external voltages and bulk salt concentrations. To this end, we investigate ion concentration profiles and electrostatic potential distributions at different boundary conditions. In the first set of numerical experiments, we fix the external voltage as V₀ = 150mV and study the system at five different bulk concentrations, namely ρ₀ = 0.1molar, ρ₀ = 0.2molar, ρ₀ = 0.5molar, ρ₀ = 1.0molar and ρ₀ = 2.0molar. Our results are plotted in Fig. 16. It is observed that a higher bulk salt concentration elevates the electrostatic potential profile, and increases the concentrations of both ions in the channel pore region. It is interesting to note that the local concentrations in the channel pore can be as high as 10molar, due to the local protein charge environment. In general, there are more cation accumulations at the right hand side of the channel because of the relatively low electrostatic potentials there.

Figure 16.

Electrostatic potential and concentration profiles with Φ₀ = 150mV for Gramicidin A channel. (a) Electrostatic potential profiles; (b) Concentration profiles.

In the second set of numerical experiments, we let external voltage vary from 0mV to 200mV with the increment of 50mV, while fixing the bulk concentration as ρ₀ = 0.1molar. Figure 17 displays the electrostatic potential and concentration profiles for five different applied voltage values. It can be seen that on the left hand side (close to higher potential), the changes in the potential values are larger than those on the right hand side (close to lower potential), which corresponds to more dramatical changes in the concentration profiles on the left. Additionally, note that concentrations of cations K⁺ and anions Cl^–, are essentially the same in the bulk regions. However, in the channel region, the concentrations of K⁺ are high, but those of Cl^– are nearly 0, which is consistent with the general property that the GA is a positive monovalent ion channel.

Figure 17.

Electrostatic potential and concentration profiles with ρ₀ = 0.1molar for Gramicidin A channel. (a) Electrostatic potential profiles; (b) Concentration profiles.

It is particularly interesting to note that the ion concentrations in the channel region can be about 70 times as high as their bulk concentrations. Similar findings have been reported in the literature.¹⁹⁵ Electrostatic certainly plays a major role in this phenomenon at nanoscale. Microscopic structure, charge and polarization contribute to the variability and complexity of biomolecular electrokinetics.

IV.C.5 Consistency between theoretical prediction and experimental measurement

In electrophysiology, I-V curves of ion channels are frequently measured. In this situation, the voltage refers to the voltage across a membrane, and the current is the flow of charged ions across protein pore. The current is determined by the conductances of the channel protein. The experimental I-V curves of the GA channel for KCl were reported by Cole et al.⁴⁵ The right panel of their Fig. 8 is used as the reference data for the present study.

To compute the electric current across the membrane protein pore, we employ an expression¹⁹⁵

$$I=\sum _{\alpha =1}^{N_c}{q}_{\alpha }{\int }_{L_x,L_y}{D}_{\alpha }\left[\frac{\partial {\rho }_{\alpha }}{\partial z}+\frac{{\rho }_{\alpha }}{k_{B}T}\left(q_{\alpha }\frac{\partial \Phi }{\partial z}+\frac{\partial U_{\alpha }}{\partial z}\right)\right]dxdy.$$ (79)

For the bulk diffusion coefficients of K⁺ and Cl^–, the experimental data are used. As in our earlier work,¹⁹⁵ the diffusion coefficients in the bulk region are set to their experimental values: D_K⁺ = 1.96 × 10^–5cm²/s and D_Cl^– = 2.03 × 10^–5cm²/s for K⁺ and Cl^–, respectively. However, the diffusion coefficients in the channel pore are not known in general, to our knowledge. Usually, smaller diffusion coefficients are to be used in the channel region due to the restricted diffusion in most ion channels. Here we assume that the diffusion coefficients inside the channel is a constant and we use the same current value as that used in the experiment, i.e., at Φ₀ = 200mV to obtain the range of diffusion coefficients. We find that a diffusion coefficient which is 25 times smaller than the bulk coefficient shows a reasonable match. The comparison between the present predictions using the LB-PBNP model and experimental data⁴⁵ is shown in Fig. 18. Although there are some minor deviations between our model predictions and experimental values, overall, there is a very good agreement between two sets of data, considering the fact that experimental measurements are also subject to certain errors.

Figure 18.

A comparison of simulated I-V curves and experimental data from Ref.⁴⁵ for Gramicidin A channel.

We notice that the prediction of the present LB-PBNP model or LB-PNP model is much closer to the experimental measurement than the result of the PNP model studied in our earlier work.¹⁹⁵ A possible reason is that the present models take care of nonpolar solvation effects, including solvent-solute interactions. The close agreement with experimental measurement further validates the proposed variational multiscale models for ion channel transport.

V Concluding remarks

Charge transport phenomena are omnipresent in nature and man-made devices, and become fascinating when charge transport is regulated by multiple components or occurs in a heterogeneous environment. Electrokinetics is a fast growing field which is devoted to the study of complex charge transport phenomena. The complexity of electrokinetic systems increases dramatically at nanoscale, where macroscopic meets microscopic. Typical examples include fuel/solar cells, battery cells, nanofluidic systems and ion channels. Theoretical modeling and computation of these complex systems pose a formidable challenge due to the excessively large number of degrees of freedom. It is commonly believed that dimensionality reduction via multiscale modeling should provide viable approaches. The question is how to pursue the multiscale modeling, given the intriguing nature of the aforementioned nano-bio systems.

Recently, Wei has introduced a new multiscale paradigm for the modeling and computation of aqueous chemical and biological systems.¹⁸² The novelty of this multiscale paradigm is the use of differential geometry theory of surfaces as a natural means to geometrically divide the total domain into macroscopic and microscopic ones, while dynamically coupling discrete and continuum descriptions. Typically, the biomolecular domain is equipped with discrete atomistic descriptions while the solvent domain is represented by macroscopic continuum mechanics. A main strategy to couple macro-micro descriptions in our differential geometry based multiscale models is the total free energy (or action) functional. By the variation of the total free energy functional with respect to the variables of interest, we systematically derive the generalized Poisson- Boltzmann (PB) equations for electrostatic interactions, Navier-Stokes equations for the fluid dynamics, Newton's equation for the molecular dynamics (MD), and the Laplace- Beltrami (LB) equation for the hypersurface dynamics. These equations are coupled with the Nernst- Planck (NP) equation to describe the charge transport in chemical and biological systems. For excessively large macromolecular complexes, such as viruses, protein complexes and molecular motors, differential geometry based multiscale fluid- electro- elastic models are proposed to replace the expensive MD description with an alternative elasticity formulation.¹⁸² More recently, the differential geometry based solvation models have been carefully analyzed and validated by an intensive comparison with experimental data.³³ The Lagrangian representation of our new solvation models has also been developed.³⁴ However, in our original formulation,¹⁸² the NP equation was not derived from the variation of the total free energy functional. Instead, it was obtained from the mass conservation analysis. As a consequence, the chemical potential energy plays no role in the surface formation and evolution.

In the present work, we provide an alternative formulation of differential geometry based multiscale models for charge transport. One main new feature of the present variational multiscale formulation is the inclusion of the chemical potential related energy in the total energy functional. Consequently, the entropy of mixing is able to drive the solvent-solute interface and influence the surface morphology. By the variation of the new total free energy functional, we derive coupled Laplace- Beltrami and Poisson- Nernst- Planck (LB- PNP) equations for the modeling of charge transport.

Another main new feature of the proposed variational multiscale formulation is the consistency between the equilibrium Laplace- Beltrami and Poisson Boltzmann (LB- PB) model and the non-equilibrium LB- PNP model. The present LB- PNP model is designed to reproduce LB- PB model at equilibrium. It is believed that this consistency is a crucial criterion for validating new non-equilibrium theories. In the present formulation, we show that when the charge distribution reaches its equilibrium profile, the LB-PNP system can be well described by the LB- PB model.

The other main new feature of the proposed variational multiscale models is the reduced representation of charge species at non-equilibrium. In our recent work,¹⁹⁶ we have shown that for multi-species ion channel transport, the computationally expensive PNP model can be replaced by an inexpensive Poisson- Boltzmann- Nernst- Planck (PBNP) model. In the PBNP model, we describe the density of charge species of interest by the NP equation, while, represent the density of other ion species by the quasi-equilibrium Boltzmann distribution obtained from the Poisson- Boltzmann (PB) equation, which avoids the expensive solution of NP equations. The validity of our PBNP model has been confirmed with Monte Carlo simulations by independently researchers.¹¹¹ In the present work, we have incorporated this approach into our variational multiscale models. It is easy to demonstrate that the resulting LB- PBNP model recovers the LB- PB model at equilibrium. However, our goal is to have the LB- PBNP model to fully reproduce the prediction of the LB- PNP model at non-equilibrium settings so as to dramatically reduce computational cost for multi-species chemical and biological systems.

Finally, we present a differential geometry based chemo- electro- fluid model for charge transport in nanofluidic, fuel cell and other systems where the fluid motion contributes to the charge transport. It is found that both the generalized Nernst- Planck equation and the generalized Navier- Stokes equation have new features that are not accounted for in the classical governing equations for electro- osmotic flows.

To implement the above mentioned variational multiscale models, we have designed a number of computational algorithms. Both the Eulerian formulation³³ and Lagrangian formulation³⁴ of our new models are considered in the present work. In the Lagrangian formulation, the second-order PNP solver developed in our earlier work¹⁹⁵ plays a significant role. The Dirichlet to Neumann mapping and matched interface and boundary (MIB) methods are also employed in the present work to deal with sharp interfaces. A successive over-relaxation like algorithm is used to ensure the convergence in solving the coupled equations.

To validate the abovementioned new variational multiscale models, we have considered two types of realistic numerical tests. In the first type of numerical tests, we explore the free energies of ten protein molecules computed with equilibrium PB, equilibrium LB- PB, and non-equilibrium LB- PNP models. The consistency among the predictions of these models has been observed. We further examine the surface morphology and surface electrostatic potential profiles generated by a number of models: solvent excluded surface based PB, LB- PB and LB- PNP approaches. The results obtained from PB and LB- PB models agree within 3% deriations. Excellent consistency between LB- PB and LB- PNP model predictions is found. The present differential geometry based surface models are able to overcome the well known defects of many other traditional surface models, namely, geometric singularities and unphysical features (i.e., no energy minimization). Finally, we demonstrate the decay of the total free energy with respect to the time integration or the iteration of coupled equations, which indicates the reasonable design of the total free energy functional.

To further validate the proposed variational multiscale models for ion channel transport, we have employed a standard test case, the Gramicidin A (GA) channel, in our numerical experiments. We first illustrate the consistency between the equilibrium LB- PB model and the non-equilibrium LB- PNP model in terms of electrostatic potentials and ion concentration profiles along the channel pore direction, and surface electrostatic potentials of the GA channel. Additionally, we demonstrate the ability of the quasi-equilibrium LB- PBNP model to faithfully reproduce the predictions of the non-equilibrium LB-PNP model. Such an ability enables us to reduce computational cost for multi-species systems. Moreover, we explore electrostatic potentials and density profiles under different experimental settings for the GA channel. A number of external voltages and bulk concentrations are considered in our investigation. Finally, we show that the proposed variational multiscale models provide excellent predictions of current-voltage (I-V) curves. In electrophysiology, I-V curves are major experimental measurements. They are frequently used to validate theoretical models in biophysics. The agreement between the present theoretical predictions and experimental measurement further validates the proposed variational multiscale models.

Although the present multiscale models originate from geometric flow theory, differential geometry theory of surfaces, and geometric measure theory, they are akin in spirit to earlier variational models in implicit solvent theories^80,150 and phase field models proposed by Cahn and Hilliard in 1958. In fact, our hypersurface function is quite similar to the phase field function, of which a similar treatment of smooth boundaries dates back to 1893 by van der Waals (see Ref.¹⁴³ for a translation and critical discussion). However, it is well-known that phase field models in materials science or Landau-Ginzburg models in physics are phenomenological approaches. Whereas the present variational multiscale models are based on the fundamental laws of physics with realistic physical descriptions, which is essential because the model prediction is to be quantitatively, rather than qualitatively, compared with experimental measurement. For example, in standard phase field models, interfacial tension density is represented as K|∇S|² with K being a parameter, while in our approach, we deal with the physically measurable surface energy as defined in Eq. (1). The mathematical realization using the geometric measure theory given in Eq. (6) leads to surface energy density γ|∇S|, which gives rise to the mean curvature term after the variation. Nevertheless, diffuse interface methods and energy variational approaches offer a powerful qualitative description for complex physical and chemical systems, including electrochemical systems,⁸⁷ electrodeposition^136,153 and electro-osmotic fluid flows.⁸³ For example, phase-field models have found their success in describing ion intercalation phenomena in batteries.^22,89,156 It is interesting to note that in phase field models, volume-exclusion correlations can be treated with nonlocal kernels, e.g., as the “weighted density approximation”.⁵ However, it is not clear if a similar nonlocal approach is appropriate for the biomolecular systems due to the constraint of physical interactions.

This paper presents only an introduction to variational multiscale models for charge transport in complex systems. Many important aspects are not considered or not numerically implemented in the present work. First, the flow transport and its coupling to the charge transport are of crucial importance to the mass and charge balance of living cells and to the water management of fuel cells. In fact, fluid dynamics is an essential ingredient in nanofluidic systems. Therefore, an obvious task is to numerically implement fluid dynamics and validate new governing equations against experiment data in future work.

Additionally, in the present work, ion channels are treated as rigid and channel structural response to the ion permeation is not accounted. The theoretical framework for such a development has been given in our earlier work.¹⁸² Numerical implementation of multiscale molecular dynamics or implicit molecular dynamics has been developed in our recent work.⁷⁷ It is interesting to incorporate such a molecular dynamics to allow local modifications of channel protein structures.

Moreover, although non-electrostatic interactions among various species, including part of the so called size effects in the continuum description of ion densities, are considered in the present models, our numerical simulation does not include the numerical test of finite size effects. This type of interactions has been numerically studied in terms of “generalized correlations” in our other variational multiscale formulation, namely, the quantum dynamics in continuum model.²⁶ It is desirable to explore the impact of finite size effects in the present models as well. Typically, correlations produced by the size of particles lead to atomic scale corrections to the density distributions of liquids.⁷⁵ More expensive integral equation theories, such as hyper-netted chain equation, Carnahan-Starling equation, Percus-Yevick equation and density functional theory of liquids, are employed to deliver corrections at equilibrium.^{18,75,79,141,167} However, it takes much additional effort to construct effective integral equation approaches for the description of charge transport in large scale complex chemical and biological systems.

Further, the correction of ion correlation to electrostatic potential due to nonlinear polarizations is needed for a dense multivalent ion fluid.^6,85 An interesting variational “Landau- Ginzburg” model for electrostatic correlations leads to a higher order Poisson equation.¹⁵ Recently, we have proposed a nonlinear Poisson equation to account for hyperpolarization effects in heterogeneous media.⁹⁴ These effects can be considered in our variational multiscale models too.

Furthermore, it is useful to consider quantum effects in the solvation process, which will lead to an extra scale in the present formulation of change transport. Similar multiscale variational model for solvation analysis has been studied by using the electronic DFT¹³¹ in our recent work.³⁵ Indeed, the consideration of quantum effects significantly improves the prediction of solvation free energies.³⁵ Anotrher related approaches include polarizable continuum models (PCM)^127,165 and Poisson-Boltzmann based quantum solvation models.^31,177

Yet, another interesting issue is the quantum effect in charge transport processes, concerning light charge carriers such as electrons and protons. When the thermal De Broglie wavelength is of the same scale as the channel length and/or Debye length, the quantum effect becomes important. Variation multiscale models have been proposed in our recent work to account for quantum effects in nano-electronic devices²⁷ and proton channels.^25,29 The incorporation of quantum effects in the present charge transport models can be easily formulated.

Finally, the other important issue associated with charge transport is the protonation, ligand binding, Stern layer and/or chemical reactions. This issue becomes increasingly important for fuel cells and many ion channels, such as potassium and proton channels.⁵⁵ The present work gives a simplified account to this issue in Section II.D. More sophisticated considerations of chemical reactions are needed to address localized reaction, reaction induced charge transport, charge transport induced reaction, and strongly coupled reaction and transport.

Giving the importance of charge transport to physical, chemical, and biological systems, as well as nano-technology and device engineering, we expect increased interest and rapid progress in terms of theoretical modeling, numerical algorithms, mathematical analysis and realistic applications in the near future.