Phase response theory extended to nonoscillatory network components

Abstract

New tools for analysis of oscillatory networks using phase response theory (PRT) under the assumption of pulsatile coupling have been developed steadily since the 1980s, but none have yet allowed for analysis of mixed systems containing nonoscillatory elements. This caveat has excluded the application of PRT to most real systems, which are often mixed. We show that a recently developed tool, the functional phase resetting curve (fPRC), provides a serendipitous benefit: it allows incorporation of nonoscillatory elements into systems of oscillators where PRT can be applied. We validate this method in a model system of neural oscillators and a biological system, the pyloric network of crustacean decapods.

I. INTRODUCTION

The topic of synchronization and patterned organization of oscillators is of general interest in physics [1–6]. More specifically, the study of pulse-coupled oscillators has commanded substantial interest [7–14]. Networks of pulse-coupled oscillators are used to study many natural phenomena [15], e.g., plate tectonics [16], heart rhythms [17], and neural networks [18]. Synchrony is a dynamical feature of such networks [19–21]. These systems consist of oscillators coupled by discrete pulses. Phase response theory (PRT) is often used to study network synchrony. PRT breaks the network into its component oscillators and analyzes the response of each to input. In the past and as referenced above, only systems consisting of oscillatory components have previously been amenable to analysis using PRT. Most physical systems, however, consist of a mixture of components, some nonoscillatory. To overcome this limitation, we propose that a recently established metric, the functional phase response curve (fPRC), provides a means to extend PRT to analyze networks with nonoscillatory components. We validate this method in both a computational model and a biological network comprised of an oscillator coupled to a nonoscillatory element. In each system, we show that knowledge of the fPRC is sufficient to determine the existence, stability, and precise timing of a 1:1 mode of phase-locking, even in the presence of noise seen in the biological preparation.

II. METHODS

A. How the fPRC predicts phase-locking

As recently defined, the functional phase response curve (fPRC) is tabulated as the steady-state phase shift of an oscillator in response to a dynamically generated train of stereotyped input pulses precisely timed relative to a dynamical reference point such as a spike or a burst from this oscillator [22]. The fPRC is a variant of the single-pulse PRC (spPRC) [23] wherein transient effects such as adaptation are allowed to stabilize during the experimental protocol so that the fPRC is a direct measure of steady-state behavior.

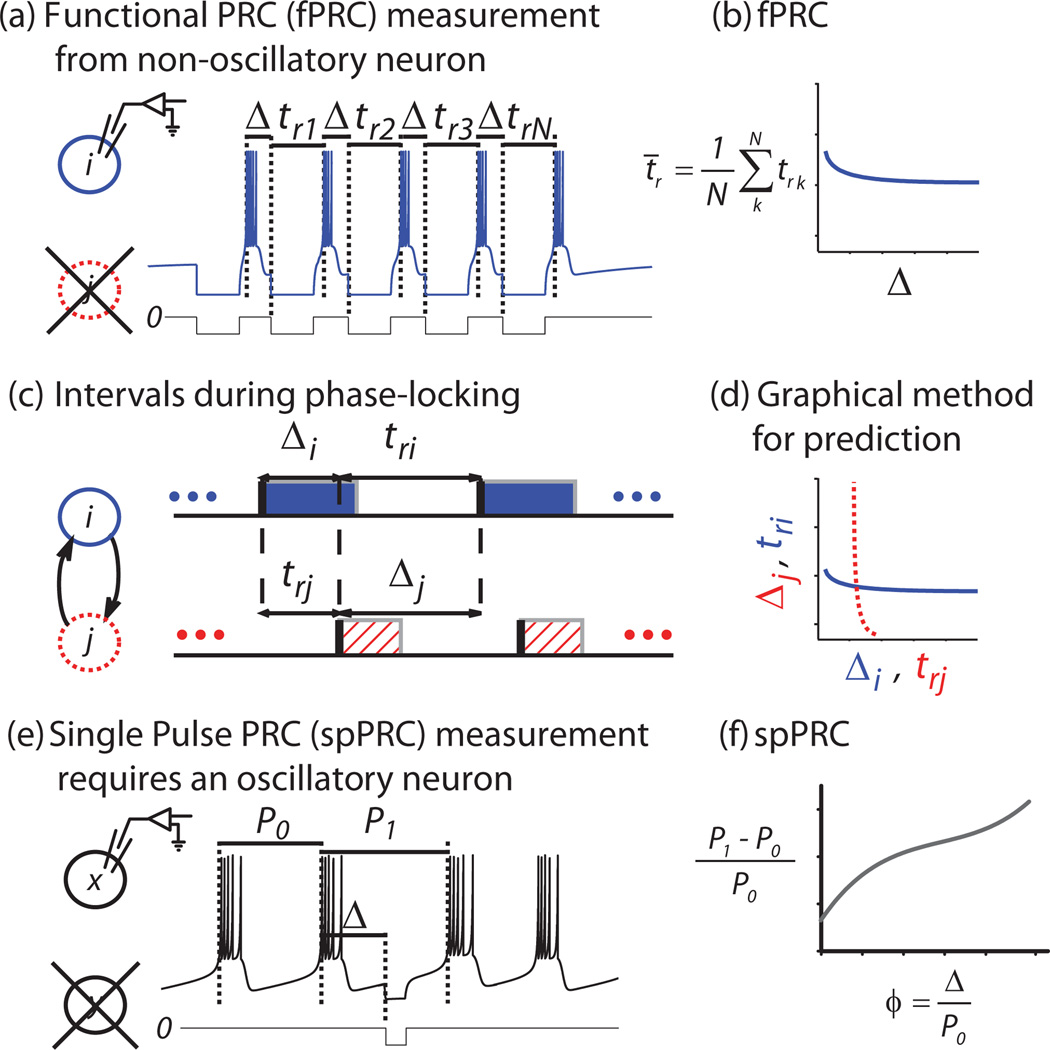
In Fig. 1, we schematize the prediction of phase-locking using the fPRC method. First, we measure the fPRC from each neuron in an isolated state. In the case of a bursting neural oscillator, an online protocol is created to detect burst initiation and deliver an artificial synaptic input to the target neuron i at a fixed delay Δ after each burst initiation for several cycles [22] [Fig. 1(a)]. For the given burst shape, we detected bursts using a threshold on the upward edge of the slow oscillation (vertical dotted lines). Response time t_rk is measured in each of N = 10 cycles and then averaged; resulting in Fig. 1(b), where each point of the fPRC represents the average response time t̄_r for the neuron to burst after stimulus initiation at the given value of Δ. For the remainder of the paper, we use t_r to refer to this average. In our example, the neuron is silent until after the first pulse forces a response, then subsequent inputs are delivered as described above for an oscillatory neuron. In a 1:1 mode of phase-locking, Δ represents the delay from burst initiation to receipt of input [Fig. 1(c)].

FIG. 1.

(Color online) Schematized protocols for PRC measurement in neurons. (a) Protocol for fPRC measurement: isolated nonoscillatory neuron i is silent at rest, but emits a burst in response to an initial input. An online protocol detects this burst and thereafter delivers a stimulus at fixed delay Δ after the initiation of each subsequent burst for N cycles. Response times t_rk are measured after each input. (b) The fPRC consists of averages t̄_r tabulated across Δ. (c) Definition of terms: stimulus delay Δ and response time t_r during 1:1 phase-locking are shown for bursting neurons i and j . The shaded and hatched regions correspond to the burst duration. (d) Graphical method for prediction: fPRCs for each component neuron are plotted on the appropriate axes such that any point of intersection gives a solution mode of 1:1 phase-locking. Stability is calculated as described in the text. (e) Protocol for spPRC measurement provided for comparison: phase shift to an ongoing oscillatory rhythm with period P₀ is measured in isolated neuron x by delivering a single-pulse stimulus at delay Δ and measuring the resulting interval P₁. (f) The spPRC consists of the relative change in period P₁−P₀ tabulated across delay Δ. Both terms are scaled to phase ϕ on [0,1) by normalizing by P₀.

We solve for the existence of the fixed points graphically [Fig. 1(d)] by plotting F_i(Δ_i) = t_ri together with $F_j^{-1}(t_{rj})={\mathrm{\Delta }}_j$, where F is a function of Δ and F⁻1 is the inverse of F, and looking for the intersections (t_ri = Δ_j, Δ_i = t_rj). These intersections represent fixed points in the system’s behavior, which may be stable or unstable.

To determine stability, we construct the following map (for cycle n) Δ_i[n] = F_j{F_i(Δ_i[n − 1])} by substitution, following Ref. [22] (p. 393). Taking the first term of its Taylor expansion to linearize the system around a fixed point of interest (${\mathrm{\Delta }}_i^{*},{\mathrm{\Delta }}_j^{*}$), we analyze the eigenvalues resulting from an infinitesimal perturbation δΔ, which describe whether the system will relax back to the fixed point or move away from it, resulting in the stability criterion −1 < $F_i^{\prime }({\mathrm{\Delta }}_i^{*})·F_j^{\prime }({\mathrm{\Delta }}_j^{*})$ < 1, where an asterisk indicates a fixed point and a prime indicates the slope at that point [22].

To compare the newer fPRC method against the classic spPRC, we provide an analogous example trace of spPRC measurement protocol (E) and the tabulated spPRC (F). Modes of 1:1 phase-locking can be predicted graphically [26] in an analogous manner to fPRCs (not illustrated).

B. Model systems

In a basic demonstration of this theory, we constructed Izhikevich-type bursting neurons

$$\upsilon \prime =0.04{\upsilon }^2+5\upsilon +140-u+J+1,$$

$$u\prime =a(b\upsilon -u),$$

with after-spike resetting

$$\text{if }\upsilon ⩾30\text{ mV},\text{ then }\{\begin{array}{c}\upsilon \leftarrow c\hfill \\ u\leftarrow u+d\hfill \end{array}$$

where υ and u are dimensionless variables, and a = 0.02, b = 0.2, c = −50, and d = 2, and ′ = d/dt, where t is time [24]. We set one neuron in the oscillatory regime (J = 10) and set one in a nonoscillatory regime (J = 3). A post-inhibitory rebound (PIR) neuron is silent or irregularly firing at rest, and when released from inhibition it becomes active, firing a stereotyped spike or burst, in this case, a burst ([25], p. 64). When isolated, the PIR neuron is silent, but after receiving an inhibitory input, it rebounds with a burst. Two neurons i and j were coupled by reciprocal inhibition I_i = g_ji(υ_i − E), which activated a square conductance pulse at a threshold θ as follows: if υ_i > θ then g_ij = ḡ, else g_ij = 0, where E = −85, θ = −55, and ḡ = 50 is the interaction strength equivalent to g_s , below. Conductance pulse length was chosen to match a typical burst duration in the oscillatory neuron.

C. Biological system

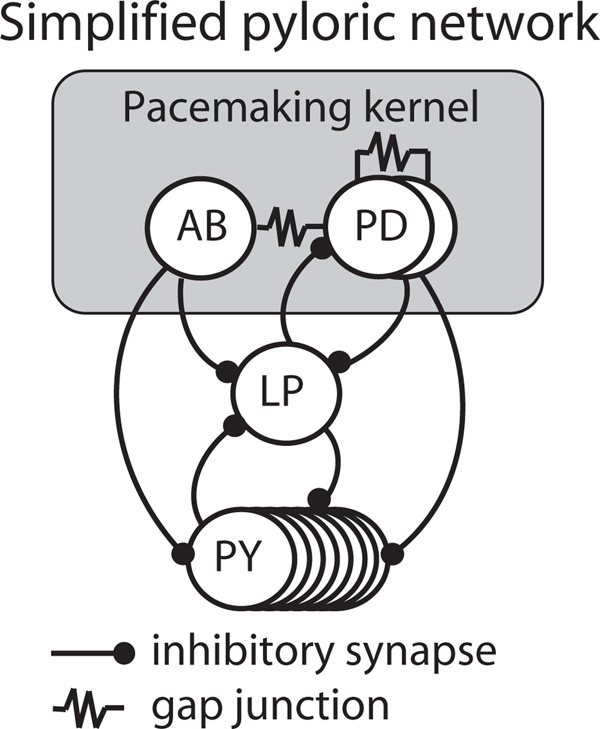
To show that our method is robust to experimental conditions, we applied it in a biological system. We chose a well-studied system that can be decomposed into an oscillating component and a PIR component. The pyloric network of the stomatogastric ganglion (STG) is a central pattern generator in decapod crustaceans, mediating aspects of digestion that consists of an oscillatory component—the AB/PD complex, a tightly electrically coupled group composed of one anterior burster (AB) and two pyloric dilator (PD) neurons—and two nonoscillatory components—the lateral pyloric (LP) neuron and a group of eight electrically coupled pyloric (PY) neurons (Fig. 2; [25]). In the intact network, the AB/PD complex rhythmically inhibits the LP and PY components, which then become active via the PIR mechanism and inhibit each other. LP alone provides feedback to the AB/PD complex. In the Results section, we refer to the AB/PD complex as the oscillator “Osc” and LP as “PIR” for consistency.

FIG. 2.

Schematic of the pyloric network.

This network is well suited to analysis here because the rhythm of active phases in each component is robust and stereotyped [26–28], yet the nonoscillatory nature of the PIR components previously prevented analysis using PRT. Due to the fact that PY plays a lesser role in the timing of network activity, we were able to simplify our analysis by examining only AB/PD and LP while ignoring PY, resulting in a two-node network analogous to the model system described above. We performed the following experiments in either Homarus americanus (American lobster) or Cancer borealis (Jonah crab).

Dissection of the nervous tissue and electrophysiology was done using standard procedures as in [29]. In all experiments, AB/PD was accessed by impaling one PD neuron with an intracellular electrode, and LP was also impaled. In lobster, nonreversible synaptic isolation of AB/PD was achieved by bath application of 10⁻⁵ M picrotoxin (PTX), and further isolation of LP was done by photoinactivation of both PD neurons using Alexa 568 dye (Invitrogen; [30]). In crab, reversible isolation of both network components was achieved by hyperpolarizing the complementary neuron.

III. RESULTS

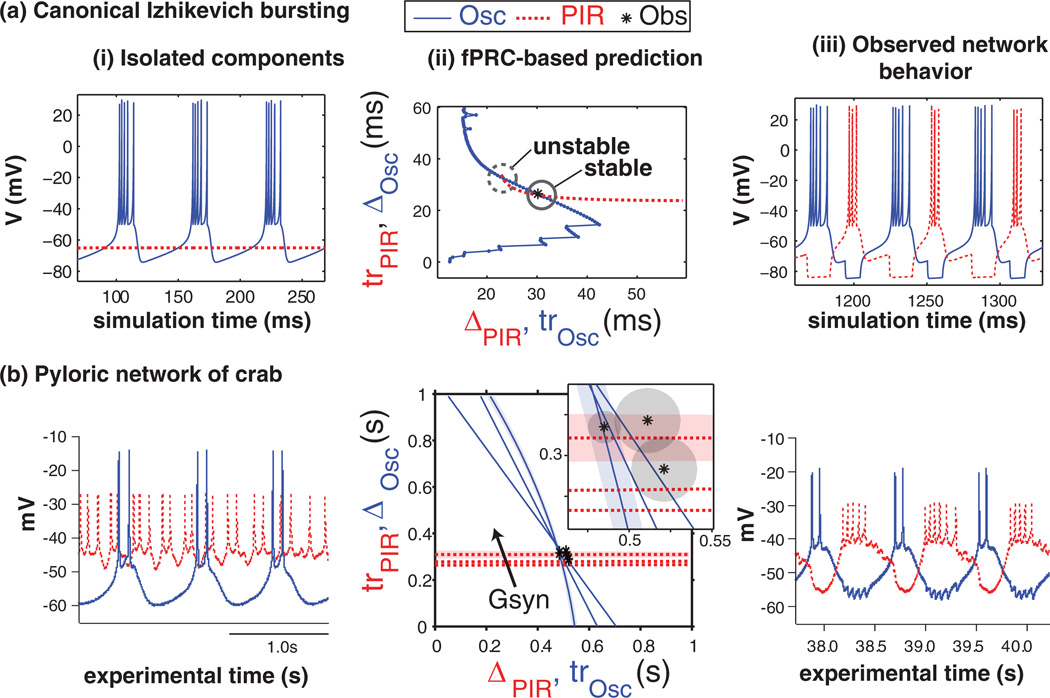
We present our results as proof of concept in Fig. 3 and summary statistics in Fig. 4. For model and biological neurons, Fig. 3 shows (i) time-series data from the isolated component neurons, (ii) the graphical method for prediction of phase-locked behavior, and (iii) time-series data from the coupled network (iii).

FIG. 3.

(Color online) Comparison of (a) model and (b) biological results showing that fPRCs measured in (i) isolated component neurons make (ii) predictions that match (iii) simulated or experimental observations of network activity. Summarized observations from column (iii) are indicated by asterisks (*) plotted in column (ii). Parameter g_s was varied to produce families of three fPRCs for each neuron in (b)(ii). All intersections in (b)(ii) were calculated to be stable. To avoid clutter in (b)(ii), confidence bounds of +/−1 standard error are shown as the shaded area for only one fPRC from each component neuron and for the observed activity. Observations at multiple points in experimental time were necessary in (b) to determine the degree of stationarity of the biological system.

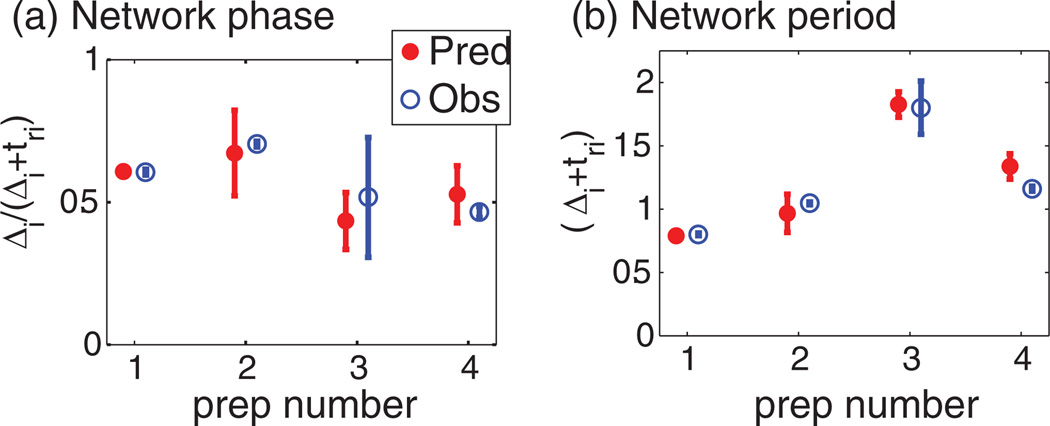
FIG. 4.

(Color online) Summary of results. Predicted (Pred) network (a) phase and (b) period are compared to observed (Obs) behavior for four experimental preparations.

In Fig. 3(a)(i), it can be seen that one model neuron is bursting (see legend, Osc), while the other is silent. As described in the Methods section, this neuron is a post-inhibitory rebound (PIR) neuron, which responds to inhibition with a rebound burst. Transient activity due to initial conditions not on the limit cycle was allowed to dissipate prior to showing the model data. Figure 3(a)(ii) shows the result of the graphical method for prediction of phase-locked modes. Essentially, the fPRC for each component neuron is plotted on the appropriate axes such that an intersection of the curves gives a fixed point (see Methods for further detail). We calculated the stability of these fixed points as described in the Methods and annotated the plot appropriately. In this case, note that there are two predicted modes of 1:1 phase-locking; however, only one is stable. The asterisk (*) on the plot marks our result from numerical simulation, which is close to the stable fixed point calculated from the fPRCs (intersection). Figure 3(a)(iii) shows simulated time series of the connected network. Intervals of phase-locking are indicated by the asterisk in Fig. 3(a)(ii). In the coupled network, the neurons fire alternately phase-locked in a 1:1 pattern.

Our biological results are conceptually similar to the modeling results but illustrate the broader applicability of the method. Whereas the model PIR neuron is silent when isolated, the biological PIR neuron exhibits an irregular spiking mode [Fig. 3(b)(i)]. This is nonoscillatory for our purposes, because the bursting oscillation is the relevant oscillation for the purposes of the central pattern generating circuit. Several fPRCs are shown in Fig. 3(b)(ii). Due to the uncertainty regarding the precise value of this parameter in the intact circuit, we measured families of fPRCs for each neuron by varying g_s [Fig. 3(b)(ii)]. The fPRC for the PIR neuron was increased at higher values of g_s (arrow, plotted are g_s = {50,100,150}nS), while there was a complex relationship in the Osc neuron (plotted g_s ={50,60,100}nS).All intersections occurred in a small area of the state space (inset), where we show noise envelopes (+/− standard error) for one fPRC from each neuron as a shaded area. All intersections were determined to be stable. Three asterisks (*) appear. Due to experimental variability, we measured the connected network activity over the course of 1.5 h and we show that data as three points, each representing the average intervals of a window 10 min in duration. Each shaded area represents a noise envelope. For clarity, noise envelopes are plotted for only two fPRCs. While there is some variability, network activity stayed within the noise in the measured fPRCs over 1.5 h. Figure 3(b)(iii) shows a time series of the connected network behavior.

In Fig. 4, we summarize our biological results over four preparations. Noise measured in the fPRC is compared to the noise measured in the intact network. Prep 1 is the exemplar from Fig. 3(b). As explained previously [26,27], we expect that variability will destroy a fixed point only if the edge of the noise envelope in Fig. 3, column (ii) falls off of the intersecting curve. It is interesting to note that the observed noise (shaded region around the asterisk) has an area of similar size to the region bounded by both noise envelopes. We use the terms noise and variability interchangeably because it is unknown why the signal varies in this system, yet it is understood that noise sources are important in characterizing dynamics of the behavior of the system. The Δ-tr curve (fPRC) of the PIR component tends to be flat because of its stereotyped response to input.

IV. DISCUSSION

In model networks, we verified that the fPRC predicts the observed phase-locked mode of activity (and no other modes; Fig. 3(a)(ii). The predictions are accurate, but they are not precise due to small changes in burst shape between isolated (open loop) and coupled (closed loop) configurations [Fig. 3(a)(ii), asterisk]. Burst PRCs can be more complicated than PRCs of spiking neurons due to the possibility of an added or deleted spike in the burst [31].

In biological experiments, as opposed to the model systems above, we must deal with variability. We have included measures of experimental variability at two time scales: first as +/− standard error around fPRC and experimental interval measurements, which represents variability in the short-term recording on the order of 10 min [Fig. 3(b)(ii), shaded areas; Fig. 4, error bars]; and second as a set of three experimental interval measurements taken over the course of 1.5 h [Fig. 3(b)(ii), asterisks].

Under the assumptions of pulsatile coupling, it is necessary to measure the PRC in an open loop using the same input perturbation as would be received by the component in a closed loop; however, it is currently impossible to know the exact coupling in these neurons because they interact at a location that is electrotonically distant from our electrode. For this reason, we chose our input perturbation carefully for each component, using a square pulse of conductance with duration equal to the burst length of the complimentary neuron and repeating the entire fPRC protocol while varying the synaptic strength g_s. Our goal was to survey the Δ-tr space within reasonable boundaries, and see if the functional coupling of the intact network fell within our survey. For this reason, we plot six fPRCs in Fig. 3(b)(ii), a family of three for each component.

Our methods implicitly assume that the system is stationary over the duration of the experiment. Consider that our experiment takes almost 2 h to complete, including isolation of network components, measurement of fPRCs for each component, network recomposition, and observation of network activity. Although the pyloric network ranks among the most stationary neurobiological systems to our knowledge, it is not perfectly stationary; however, the drift is acceptable during the experiment. In the time interval between fPRC measurement and observation of network activity, changes occur in the biological system that we are unable to measure. To gain an understanding of how this affects our predictions, we recorded 10-min segments of unperturbed activity of the intact network at three times during the experiment—before, during, and after our fPRC measurements—and found that while the system drift was negligible during each segment, it was important over the 1.5-h experiment [Fig. 3(b)(ii), asterisks]. Thus, considering the measured nonstationarity of the system, the predictions are accurate.

The effect of noise in networks of coupled oscillators has been an area of recent interest [32–37]. We do not go into detail to determine how noise magnitude or phase dependence in the fPRCs, measured from isolated neurons, interact in the coupled network. It is interesting to note that the scale of noise (standard error) measured in a 10-min segment from the intact network is on the order of the area on the Δ-tr plot enclosed by the fPRC’s noise envelopes (Fig. 3(b)(ii), shaded areas), which each required 6 min to record. This may indicate that the noise measured is an effect of a drifting set point for the system.

The pyloric circuit has been widely studied. The biological implications of our work for understanding the pyloric circuit are that the PY group contributes little to network patterning but that pharmacological or electrical manipulation of LP or the AB/PD group should impact patterning in a predictable way. The reason PY has no effect on the timing of LP is clear from the fPRC, which corresponds to a fixed recovery interval; at the end of a long-lasting hyperpolarization, all memory for previous input is lost. In the pyloric circuit, the firing order is PY-AB/PD-LP, therefore we are justified in ignoring the effect of PY on LP in this context.

V. CONCLUSIONS

Previously [22], fPRC methods were derived as a way to incorporate spiking neural oscillators exhibiting adaptation on the scale of one period into a framework allowing examination using tools from PRT. We assert that this recent advance gives a serendipitous benefit. The key insight we provide is that when the same protocol used to measure the fPRC in a network component with an adaptation mechanism is applied to a nonoscillatory component such as an irregularly spiking or silent neuron or a PIR neuron, the resulting fPRC gives a valid measure of phasic response to input in an oscillatory regime even though the subject is not itself oscillatory and thus does not have a defined phase. This relatively simple observation and the validation presented in this paper greatly extend the potential for application of PRT. To validate our assertion, we show results from one model and one biological system. Both are from neurobiology, the area that motivated Cui et al.’s work [22]; however, the methods are generally applicable to any system containing mixed oscillatory and nonoscillatory components. This work thus addresses mixed systems in the context of PRT. Applications extend to any pulse coupled system and not just to synaptic coupling between neurons. Recent work by others [38] applied the fPRC to light pulses used in optogenetic techniques.

As stated in [22], the strength of the fPRC is to reduce the set of assumptions necessary when using the spPRC from three to one. Previously, the assumptions were as follows: (1) each neuron in the network can be represented as a limit cycle oscillator, (2) the trajectory of each neuron returns to its limit cycle between inputs (this is the assumption of pulsatile coupling), and (3) the input received by each neuron has the same effect in the closed-loop circuit as in the open-loop circuit used to generate the phase response curves. Under the fPRC, only the third assumption is necessary; however, this is not always a good assumption. Even in simple models [Fig. 3(a) and unpublished data], there is some error due to changes in spike or burst shape between open- and closed-loop configurations.

Phase resetting theory is broadly defined here, as we use it to include the characterization using our framework of defined time intervals in neurons that are not endogenous bursters, such as PIR neurons. Nevertheless, to our knowledge, these methods have been used so far only to gain general insights, and not to work out in detail the operation of a specific biological circuit. In this paper, we apply our methods to an intact and biologically relevant network, the pyloric network from the STG. We did not include the entire circuit in our analysis, only the pacemaker neuron complex and the main input to that complex, but nonetheless obtained a reasonable explanation of the observed electrical activity of the intact circuit.