Using Trait-State Models to Evaluate the Longitudinal Consistency of Global Self-Esteem From Adolescence to Adulthood

Abstract

The present research used a latent variable trait-state model to evaluate the longitudinal consistency of self-esteem during the transition from adolescence to adulthood. Analyses were based on ten administrations of the Rosenberg Self-Esteem scale (Rosenberg, 1965) spanning the ages of approximately 13 to 32 for a sample of 451 participants. Results indicated that a completely stable trait factor and an autoregressive trait factor accounted for the majority of the variance in latent self-esteem assessments, whereas state factors accounted for about 16% of the variance in repeated assessments of latent self-esteem. The stability of individual differences in self-esteem increased with age consistent with the cumulative continuity principle of personality development.

Global self-esteem reflects a person’s overall evaluation of personal value and adequacy and high self-esteem is often regarded as an important component of psychological health (Donnellan, Trzesniewski, & Robins, 2011; Greenberg 2008; Harter, 2006; Jahoda, 1958; McClure, Tanski, Kingsbury, Gerrard, & Sargent, 2010; Orth, Robins, & Roberts, 2008; Rogers, 1961; Rosenberg, 1965; Swann, Chang-Schnieder, & McClarty, 2007; Tangney & Leary, 2003;Trzesniewski, Donnellan, Moffitt, Robins, Poulton, & Caspi, 2006; but see Baumeister, Campbell, Krueger, & Vohs, 2003 for an alternative perspective). Although self-esteem is one of the most widely studied constructs in psychology, debates surround a number of issues related to this individual difference (reviewed in Donnellan et al., 2011). One such debate concerns whether self-esteem is more trait-like or state-like (see Marsh & Grayson, 1994). That is, is self-esteem primarily a fluctuating state that gauges an individual’s social standing with others (e.g., a sociometer; Leary, Tambor, Terdal, & Downs, 1995) or is self-esteem a more enduring personality trait that becomes increasingly more consistent with age (e.g., Trzesniewski, Donnellan, & Robins, 2003)? The goal of the present research is to apply trait-state statistical models to address this particular issue. Specifically, we evaluate the extent to which self-esteem consists of trait-like and state-like components and test whether self-esteem shows increasing consistency during the transition to adulthood.

The Trait-State Debate

There is a longstanding debate as to whether global self-esteem is best conceptualized as a psychological trait or state (e.g., Conley, 1984; Harter, 2006; Harter & Whitesell, 2003; Trzesniewski et al., 2003). A critical issue in resolving this debate concerns the defining features of a psychological trait as opposed to a state. Following contemporary conceptualizations (e.g., Caspi & Roberts, 2001) and drawing on Allport’s (1937) seminal treatment of the trait construct, we consider differential or rank-order consistency over time (i.e., the extent to which people maintain their relative ordering over time) as the major criterion for making trait attributions (see also Asendorpf, 1992; Conley, 1984; Roberts & DelVecchio, 2000).

Constructs that exhibit a relatively high degree of rank-order consistency are considered more trait-like, whereas constructs that do not are more state-like (see alsoKenny & Zautra, 2001, p. 243). A focus on rank-order or differential stability (as opposed to other types of consistency such as absolute consistency) allows constructs that show normative developmental trends (i.e., mean-level changes associated with age) such as cognitive abilities and core personality attributes to be considered psychological traits. A given attribute might increase or decrease in terms of absolute levels with age and development but the central issue for making trait designations is whether the relative ordering of individuals on that dimension remains consistent over time. Differential stability is often assessed by correlating scores at one point with scores at a second point over an appreciable span of time (e.g., years). These coefficients provide an estimate of the degree to which individuals that are high or low relative to their peers in self-esteem at one time point are similarly positioned at a future time point.

It is important to emphasize, however, that most psychological constructs are neither completely trait-like nor completely state-like. As noted by Hertzog and Nesselroade (1987), “psychological variables may contain both state-like and trait-like components” (p. 105). Thus, researchers have attempted to determine where constructs fall on a trait-state continuum (see e.g., Conley, 1984) using statistical models applied to longitudinal data (see Steyer & Schmitt, 1990 for an early example of a trait-state model in the literature). Following in this psychometric tradition, Kenny and Zautra (2001) provide a general framework for decomposing longitudinal assessments of attributes into state and trait components. They articulate three latent factors that are useful for capturing variability in repeated measures: a completely stable trait factor, slow-changing trait factors, and state factors. The stable trait factor captures individual differences that are completely stable across all time points. Slow-changing trait factors called autoregressive traits capture variability that demonstrates relatively gradual and orderly changes with time. There is also a stability coefficient associated with these factors. Last, state factors capture variance that is unique to any single measurement occasion. State factors reflect fleeting individual differences and measurement errors in many models (e.g., Kenny & Zautra, 1995). All three sources of variability are inevitability confounded at any single measurement occasion and therefore trait-state models applied to longitudinal data are required to isolate these sources of variance (e.g., Cole, 2006; Cole, Martin, & Steiger, 2005; Kenny & Zautra, 2001; Steyer, Schmitt, & Eid, 1999).

In sum, trait-state models have potential to provide a relatively precise understanding of the nature of self-esteem. If self-esteem is best characterized as a relatively enduring individual difference construct, then trait factors should account for a substantial amount of variance. In terms of the Kenny and Zautra (2001) model, the variance attributed to the stable trait and autoregressive traits should be large and the autoregressive traits should show an appreciable amount of consistency over time (i.e., the stability coefficients for the autoregressive traits should be relatively large). On the other hand, if self-esteem is best conceptualized as a transitory state, then state factors should account for a substantial amount of variance in repeated measures of self-esteem.

Previous studies investigating the consistency of self-esteem have not used trait-state models to address this issue. This has perhaps led to an impoverished understanding of the construct. Advocates for more trait-like conceptualizations have relied on the analysis of simple test-retest correlations across long intervals without specific attention to quantifying the trait-like and state-like components of global self-esteem (e.g., Trzesniewski et al., 2003). In contrast, those interested in the state-like aspects of self-esteem have developed separate, single timepoint, measures to capture such components (e.g., Heatherton & Polivy, 1991) and have not focused on the consistency of these “state” measures over appreciable periods of time. Accordingly, the present research seeks to extend existing work on the nature of self-esteem by applying trait-state models to a dataset in which global self-esteem was repeatedly assessed across intervals of a considerable length of time (i.e. years) for a considerable number of intervals (i.e., 10 assessments made from 1989 to 2007).

Developmental Considerations

Even if self-esteem is best conceptualized as a relatively enduring individual difference for much of the life span (e.g., Trzesniewski et al., 2003), it is nonetheless possible that there is a developmental aspect to the consistency of self-esteem. Most notably,Trzesniewski et al. (2003) found that there was a pattern of increasing consistency from adolescence to adulthood in their meta-analysis of self-esteem retest correlations. The self-esteem results converged with earlier findings by Roberts and DelVecchio (2000; see also Ferguson, 2010) with respect to the increasing consistency of broad personality traits from childhood to adulthood. Both of these findings are in accord with Bloom (1964) who argued that many human attributes are more malleable earlier in development rather than later in development (e.g., p. 207). This observation that psychological traits become even more consistent with age has been formalized into the cumulative continuity generalization about personality development (see Caspi, Roberts, & Shiner, 2005).

Trzesniewski et al. (2003) argued that lower levels of consistency are expected during periods of environmental and maturational change. The periods of development in between childhood and adulthood are marked by dramatic changes in the biological, cognitive, and social domains (see Donnellan, Trzesniewski, & Robins, 2006). For example, individuals experience physiological changes associated with puberty as well as cognitive changes involving increased speed of cognitive processing (e.g., Kail, 1991), improved reasoning skills, and increased abilities to think in abstract terms (e.g., Keating, 2004). Social relationships are also transformed as individuals negotiate new connections outside of their families of origin and begin to form intimate interpersonal bonds with peers and romantic partners (Donnellan et al., 2006). Individuals also explore issues of identity during adolescence and emerging adulthood in a more thorough and psychologically nuanced way than in childhood (Arnett, 2000). In short, individuals experience a considerable number of changes during the transition from childhood to adulthood in many domains of development. This observation might explain why the consistency of individual differences increases during this phase of the life span.

Fortunately, it is possible to modify trait-state models to allow for increasing degrees of consistency for the autoregressive or “changing trait” component of the model. Such a modification permits a test of whether relatively enduring individual differences in self-esteem become more consistent with development because it is possible to evaluate whether models that specify increasing consistency with age for the autoregressive trait factors account for observed data better than simpler models that specify a constant rate of consistency for autoregressive components. In this way trait-state models can be used to test specific hypotheses about personality development and help to quantify the increasing consistency of self-esteem during the transition to adulthood.

The Present Study

The present research evaluates the consistency of self-esteem issue using a novel application of trait-state models applied to 10 repeated assessments of the Rosenberg Self-Esteem Scale (Rosenberg, 1965), the most widely used measure of global self-esteem in the literature (Blascovich & Tomaka, 1991; Schmitt & Allik, 2005). The assessments were collected between 1989 and 2007 for a longitudinal sample that was an average age of 13 years in 1989 and an average age of 32 years in 2007. Thus, this study covers a period of development in which self-esteem is thought to increase in consistency. We use latent variable extensions of Kenny and Zautra’s (1995, 2001) STARTS model for our primary analyses. In particular, we test whether a model that permits increasing auto-regressive consistency fits the observed data better than models that specify a constant stability coefficient across all waves. If such a developmental trait model demonstrates adequate fit, then it is possible to extrapolate backward from the observed data to estimate the age at which the autoregressive trait component of self-esteem would have first emerged.

Method

Sample

Participants were initially focal adolescents in the 7^th grade (52.3% female) from the Iowa Youth and Families Project (IYFP; see Appendix A of Elder & Conger, 2000). The project began in 1989 with a sample of 451 two-parent European-American, lower-middle and middle class families living in north central Iowa. Families were recruited from all 34 public and private schools with a seventh-grade class in communities of 6,500 or less in eight Iowa counties. After receiving a letter explaining the project, families were contacted by telephone and invited to participate. A personal visit was made to families without telephones. About 78% of the eligible families agreed to take part in the study. The IYFP cohort was merged with the Iowa Single Parent Project in 1994 and that combined sample is the subject of an ongoing longitudinal study known as the Family Transitions Project (see Conger & Conger, 2002). However, data analyzed here are restricted to the IYFP participants to maximize the number of waves of self-esteem assessment. In each year of the study, participants were visited in their homes where they completed a series of questionnaires that included the Rosenberg Self-Esteem scale. We often refer to these waves by the year of primary data collection (1989, 1990, 1991, 1992, 1994, 1995, 1997, 1999, 2005, and 2007). The RSE was not administered in 2001 and 2003 but was again administered in 2005 and 2007 so these waves represent the available RSE data collected to date on the IYFP sample. The average age in years at each wave was 13.18, 14.09, 15.09, 16.07, 18.14, 19.18, 21.15, 23.79, 29.61, and 31.70 for the 10 waves, respectively. Participants were paid approximately $10 per hour of participation. More complete demographic details about the IYFP are available in Conger and Conger (2002) and Elder and Conger (2000).

Measures

Self-Esteem

The Rosenberg Self-Esteem scale (RSE; Rosenberg, 1965) was used to measure global self-esteem. Participants answered 10 items using a 5-point scale ranging from 1 “Strongly agree” to 5 “Strongly Disagree.” Sample items include, “I feel that I have a number of good qualities” and “All in all, I am inclined to feel that I’m a failure.” Items were then scored so that higher scores reflected higher self-esteem. These self-esteem assessments had high levels of internal consistency at each time point (range of alphas = .844 to .908 across the 10 assessments). A table of descriptive statistics for the composite scale scores at each assessment including estimates of internal consistency is available upon request from the first author. Item parcels were created for use in latent variable models as described below.

Basic Specification of the Latent Variable STARTS Model

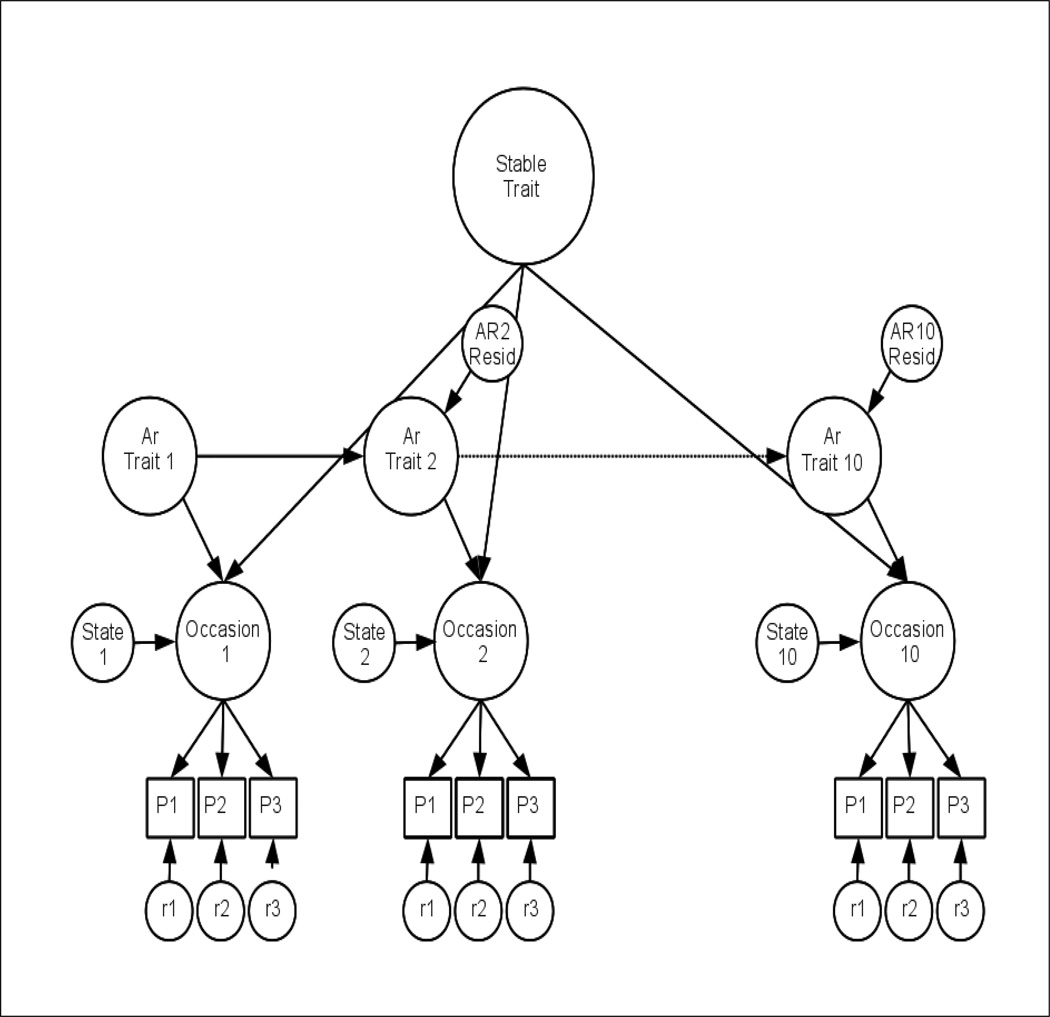
Kenny and Zautra (1995, p. 54) provide complete details for the basic STARTS model using manifest variables and the model displayed in Figure 1 is a latent variable extension of their basic model. This latent variable approach has the advantage of distinguishing measurement error due to unreliability from reliable (but transitory) state variance.¹ As seen in Figure 1, there are latent self-esteem variables at each measurement occasion which are created from three manifest indicators. Different researchers may choose a different number of indicators for each latent factor in any given application but the choice of three indicators has a compelling conceptual basis (Little, Lindenberger, & Nesselroade, 1999). We created 3 sets of “item parcels” drawn from the 10 Rosenberg items administered at each wave to serve as indicators of self-esteem in the present study.

Figure 1. Multiple Indicator STARTS Model.

Note: AR = Autoregressive Trait; P1, P2, and P3 = Self-Esteem Item Parcels 1, 2, and 3. r1, r2, r3 = Parcel-specific residuals, 1, 2, and 3. Overtime correlations between parcel-specific residuals (r1, r2, and r3) are not shown to enhance clarity.

One important issue in longitudinal studies of consistency is the assumption of metric invariance or the idea that the measure ranks people in the same way at each assessment occasion. Metric invariance is achieved when the factor loadings for the indicators of self-esteem are the same at all waves (see Schmitt & Kuljanin, 2008 for a review of measurement invariance issues). If factor loadings vary across measurement occasions, then individuals would not be ranked in the same way at each measurement occasion and this fact will complicate the interpretation of any longitudinal result. Metric invariance can be tested by imposing equality constraints on the factor loadings for indicators at each wave and comparing the fit of this model to the fit of the model in which factor loadings are freely estimated.

The latent self-esteem variables at each measurement occasion are the primary focus of the STARTS model variance decomposition. Figure 1 illustrates that variability in these latent self-esteem variables at each measurement occasion are themselves described by three latent factors: the completely stable trait (ST), autoregressive traits (ART), and true state factors (S). Given that latent variables capture reliable variance, the state factors in this model reflect systematic variance in the construct of self-esteem that is unexplained by a stable trait or an autoregressive trait. State variance is therefore reliable variance that is unique to each measurement occasion (i.e., this reliable variance is unrelated to components at any other occasion). This isolation of reliable state variance from measurement error is the major advantage of the latent variable version of the STARTS model over the manifest variable version. Although not shown in Figure 1 to enhance clarity, across time correlations between the respective parcel-specific residuals are included to account for the possibility that parcel specific variance demonstrates consistency over time that is not accounted for by factors operating on the general self-esteem factor – the factor of primary interest in the current application.

Four parameters are of primary interest in a typical STARTS analysis: the variance for the stable trait (V_ST), which indicates how much variance in repeated assessments of self-esteem is captured by a completely stable trait factor; the variance for the changing or autoregressive trait factors (V_ART), which indicates how much variance in self-esteem is captured by relatively enduring factors whose changes are statistically predictable; variance for the state factors (V_S), which indicates how much variance in self-esteem is unique to each individual measurement occasion; and last, the autoregressive path coefficient (b), which indicates the over-time consistency or stability of the autoregressive factors. This path coefficient provides an indication of the enduringness of the autoregressive traits. The interval associated with this path coefficient is usually defined by the design of the study such that when data are collected yearly then the path coefficient represents a 1-year stability coefficient. Typically the relative, not raw, variances are reported such that V_ST/(V_ST + V_ART + V_S) equals the proportion of completely stable trait variance captured by the assessment.

A number of constraints are typically imposed on the STARTS model to identify the latent factors and to facilitate estimation (see Kenny & Zautra, 2001). The first specification is that the three STARTS components are independent of each other (this reflects the independence assumption of the model; Kenny & Zautra, 1995). The one exception is that adjacent autoregressive trait factors are connected to each other (known as the autoregressive structure assumption; Kenny & Zautra, 1995). The original STARTS model did not allow the total amount of variance to change over time and thus, the variance for all of the autoregressive trait factors (one for each occasion of measurement) and the variance for all of the state factors (one for each occasion of measurement) were fixed to the same value. Likewise, it was originally stipulated that the stability coefficients linking the autoregressive factors have the same value. In terms of identification, factor loadings for the stable trait are fixed to 1.0 to instantiate the idea that this latent factor captures variability that is present at all occasions. Factor loadings for each of the autoregressive traits are also fixed to 1.0 as are loadings for each of the state factors. Equality constraints are placed on the model such that there is a single variance estimate for the state factors and for the autoregressive traits.

The stationarity assumption of the STARTS model holds that the stable trait, autoregressive traits, and state factors explain the exact same amount of variance in the latent factors at each occasion. Under this assumption, the variance of the disturbance of the autoregressive trait factor is constrained by the autoregressive path coefficient and the variance of the autoregressive trait factor (V_ART) such that variance of the disturbance of the autoregressive trait factor equals V_ART(1 – b²). Because of the stationarity assumption, b (the stability path for the autoregressive factors) can be interpreted as a correlation coefficient which makes it easier to interpret than an unstandardized regression coefficient which does not have a constrained metric. This nonlinear constraint is easy to implement in the Mplus software package (complete syntax is posted on David Kenny’s website).

The latent variable STARTS model can be viewed as a more restrictive version of the general longitudinal model with multiple indicators described by Marsh and Grayson (1994, see their Figure 2, p. 326). This model identified by Marsh and Grayson is a longitudinal factor model that includes all possible correlations between latent self-esteem variables at each wave. The Marsh and Grayson general longitudinal model (hereafter referred to as the general longitudinal model) therefore provides zero-order estimates of the stability of individual differences in self-esteem without attenuation concerns due to unreliability. The latent STARTS model imposes a more restrictive structure on those correlations just as the manifest STARTS model imposes a more restrictive structure on the correlations between observed variables (see Kenny & Zautra, 1995).

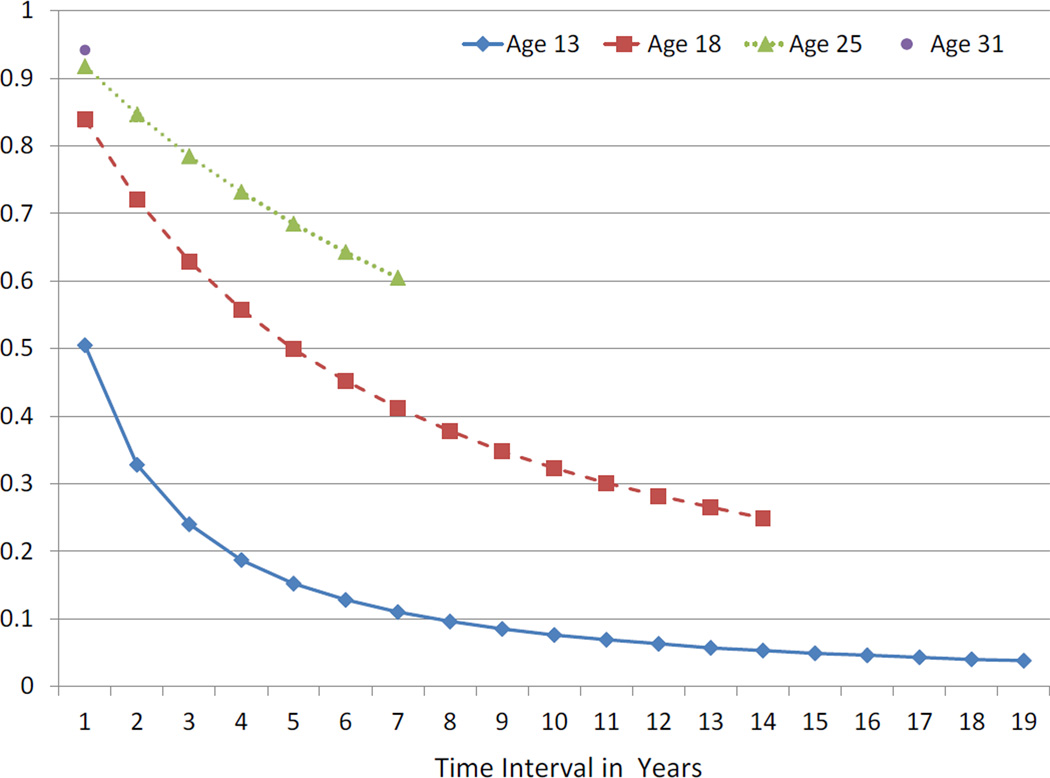
Figure 2.

Increasing Autoregressive Stability Coefficients for Selected Ages Across Selected Intervals from Model 5

Varieties of STARTS Models

In this section we describe extensions of the latent variable STARTS model used in the current analyses. First and foremost, we needed to allow for a more precise accounting for the passage of time in our analyses. In the basic STARTS specification, the model assumes that measurement occasions are equally spaced across time and the autoregressive coefficient is therefore defined across a fixed interval determined by the data collection strategy. However, there were varying intervals of time between waves in the IYFP (i.e., data were initially collected more or less every year in the early waves but this data collection strategy changed as the participants moved into adulthood). In the current application, we used information about the average age of the participants at the time of each measurement occasion to help address this issue. Each participant’s age was calculated by taking the difference between the actual dates of observation and each participant’s birthdates. (Results were similar when we used self-reports of the participants’ age in years at their last birthday). This information about the average age at each occasion was incorporated in the specification of the model by imposing a nonlinear constraint on the autoregressive path coefficients. Specifically, to allow for unequal spacing between waves of data collection, we can define b (which in the standard STARTS model represents the stability of the autoregressive factors from one occasion to the next) as the rate of change expected in one year and we can then constrain b between any wave t and wave t-1 to equal b^ΔA where ΔA is the change in average age between the two waves. In other words, stability from one wave to the next is expected to be a function of the yearly change in age that occurred between those two waves. Note that when the average ages differ by exactly one year then b^ΔA equals b. This approach is more precise than specifying that assessments occur at equal intervals as is the case in the canonical STARTS model specification. Finkel (1995) provides a detailed discussion about how information about time can be made more meaningful when using panel data.

Second, we also tested models that relaxed the stationarity assumption to what has been called the quasi-stationarity assumption (Kenny & Campbell, 1989; Kenny & Zautra, 1995). Specifically, we allowed for the possibility that the total variance in self-esteem may change over time, but we stipulated that the relative amounts of stable trait, autoregressive trait, and state variances were constant across time. Put differently, we allowed the total amount of variance to fluctuate over time but we specified that the three components of the STARTS model must account for the same proportion of variance at all occasions. Kenny (1979) noted that “stationarity implies that a variable has the same proportions of ‘ingredients’ at [multiple] points in time” (p. 239). Changes in observed variance could occur because of methodological factors, such as differential attrition (i.e., more extreme members of a panel study are perhaps more likely to be missing data at a given wave) or for substantive reasons, such as the accentuation of individual differences (e.g. Caspi & Moffitt, 1993). The imposition of quasi-stationarity ensures that the estimated unstandardized path coefficients linking one autoregressive trait to the next are in a standardized metric. It also makes it possible to report an overall decomposition of variance in the form of the proportion of variance in self-esteem attributable to three STARTS factors.²

To specify quasi-stationarity we modified the model in Figure 1 as follows. First, we fixed the paths from the stable trait, autoregressive trait, and state latent factors to self-esteem at the first occasion to 1.0. We then imposed equality constraints on these three paths within each subsequent wave. In other words, the paths from the stable trait, the autoregressive trait, and the state factors to self-esteem at the second occasions were all constrained to have the same value. This value could, however, differ across the remaining occasions. These constraints allow for there to be different amounts of variance at each occasion while maintaining the assumption that the three STARTS factors account for the same proportion of variance at each wave. Mplus script showing how this is specified is available on David Kenny’s website.

The last and most important modification is to allow for the anticipated increase in the consistency or stability of the autoregressive trait factor. As noted earlier, theoretical models of personality development (e.g., Fraley & Roberts, 2005) and previous research on self-esteem (Trzesniewski et al., 2003) have suggested that differential or rank-order consistency increases with age. One way to model this increasing stability across the lifespan is to replace the observed time interval between assessment occasions with coefficients that incorporate the natural logarithm of age. This approach is motivated by theoretical writings proposed by Bloom (1964) as it is expected that a 1-year period has a different meaning to the average 10-year-old as compared to the average 20-year-old (i.e., such an interval represent 10% versus 5% of their total life spans, respectively). By logging time, we can impose a restriction that makes the influence of time in the model depend on the ratio of time that has passed between assessments and not simply the difference in the number of years that have passed between assessments. For example, under this scheme, the amount of change that occurs over a 10 year period from ages 10 to 20 would be equal to the amount of change that would occur over a 20 year period from ages 20 to 40, a 2 to 1 ratio. Thus, with logarithmic time, the autoregressive coefficient is not the difference in years but the ratio of years, and allows us to account for more consistency in later waves as opposed to earlier waves.

Taking the log of time presumes that time is a ratio scale with a meaningful score at zero. In the present context if we were to use age in years, we would be presuming that time zero is at birth. But for self-esteem, the starting point might occur at a later point in development than birth. It is instructive therefore to determine the age when the variance in the observed autoregressive trait first emerges. We can empirically estimate the zero point for the latent autoregressive self-esteem traits by using the natural logarithm of Age minus k where k is a value estimated from the data, a term we label, A₀. The value of A₀ is interesting because it indicates when variance in the autoregressive trait would have emerged based on the observed data. Note for instance that if k were equal to 10, then the rate of change in the autoregressive trait from 12 to 14 [(14 – 10)/(12 – 10) = 2] would be the same as from 15 to 30 [(30 – 10)/(15 – 10) = 2].

In total, we evaluate the results of five statistical models – the general longitudinal model and four STARTS models:

Model 1 – General Longitudinal Model. In this model, all of the latent self-esteem variables were allowed to correlate with each other and metric invariance is imposed on the factor loadings.

Model 2 - Basic STARTS model using the average age at each assessment to identify the autoregressive stability coefficient. In this model, the autoregressive path coefficient captured stability over a 1-year interval based on the average age difference between measurement occasions.

Model 3 – STARTS model using the average age at each assessment to identify the autoregressive stability coefficient and specifying a constant ratio for the STARTS variance components. This model relaxed the specification that the absolute amount of variance ascribed to each STARTS factor was constant across all waves. Instead we stipulated that the ratio of stable trait, autoregressive trait, and state variances was constant across all waves.

Model 4 –STARTS model using the average age at each assessment to identify the autoregressive stability coefficient and allowing for increasing stability in the autoregressive trait paths. This model re-imposed stationarity on the three STARTS variances but allowed for increasing stability for the autoregressive traits from age 13 to 32 using the logarithmic specification described earlier. This specification allowed us to estimate when variance in the autoregressive trait factor observed in this study would have first emerged in development.

Model 5 – Model 4 but with a constant ratio for the STARTS variance components. This model was identical to Model 4 with the exception that we made a less restrictive assumption about variance by fixing the ratio of stable trait, autoregressive trait, and state variances constant across all waves (as in Model 3). We expect this model to provide the closest representation of the underlying data.

Results

As in most longitudinal studies, some data were missing at waves subsequent to the initial assessment. In the present study, 280 participants had complete data across all observations (i.e., self-esteem data at all 10 waves) whereas 414 participants had three or fewer missing waves of data (92% of the 451). To address concerns over missing data, all models were estimated using a structural equation modeling program with full information maximum likelihood estimation (FIML) procedures. We evaluated omnibus tests of model fit using the χ² exact-fit test and the Root Mean Square Error of Approximation (RMSEA). As the sample sizes exceeded 200, we considered models generally acceptable if the RMSEA value was around .05. We also examined the TLI and the SRMR and used conventions of .95 and above for the TLI and values of .08 or below for the SRMR.

Preliminary Analyses to Identify Item Parcels

We conducted a series of preliminary analyses to evaluate the dimensionality of the Rosenberg scale and to select items for creating parcels for the latent variable STARTS models. For our purposes, the use of item parcels over individual scale items has at least two advantages (see Little, Cunningham, Shahar, & Widaman, 2002 for a review of the pros and cons of parceling). First, item parcels tend to be more reliable than single-item responses and they tend to have distributions that more closely approximate normality than single-item responses. This makes the data more appropriate for maximum likelihood estimation techniques. Second, the use of three item parcels has the practical advantage of reducing the number of observed variables for use in our analysis. Nonetheless, we acknowledge that parceling has critics and refer readers toLittle et al. (2002) for a review of the issues.

One of the important issues in debates over parceling is whether the underlying measure is unidimensional. Parceling is not a terribly controversial approach with undimensional measures (see Little et al., 2002). On the one hand, pure unidimensionality is difficult to achieve for many personality measures and thus researchers are becoming accustomed to thinking in terms of essential unidimensionality (Slocum-Gori, Zumbo, Michalos, & Diener, 2009). A single substantive factor perspective on the Rosenberg items, however, is consistent with previous work using item response theory approaches (Gray-Little, Williams, & Hancock, 1997) and factor analytic procedures (Pullmann & Allik, 2000). To be sure, even researchers who have proposed multi-dimensional solutions for the Rosenberg have acknowledged that “a common factor account[s] for the lion’s share of reliable variance” in the items (e.g., Tafarodi & Milne, 2002, p. 456). Moreover, Marsh, Scalas, and Nagengast (2010) recently argued that the Rosenberg item pool was best represented by a single substantive factor and two method factors. In short, we believe that our decision to create parcels from the Rosenberg is reasonable given our focus on the overarching construct of global self-esteem and our desire to reduce the number of manifest variables from 100 to a more manageable set of a 30. At the same time, we acknowledge that other groups may hold different perspectives on the factor structure of this measure.

To construct parcels, we first conducted separate maximum likelihood exploratory factor analyses on the RSE items at each wave using Mplus 5.2 (Muthén, & Muthén, 1998–2007). Across the ten waves, there was evidence of a strong first dimension based on an inspection of the initial eigenvalues provided by Mplus (average first eigenvalue: 5.225, SD = .478; Min. = 4.357, Max. = 5.695). The second eigenvalue was considerably smaller than the first eigenvalue at each wave (average second eigenvalue: 1.224, SD = .096; Min. = 1.101, Max. = 1.404) and the third eigenvalue was never above 1.0 (average third eigenvalue: 0.805, SD = .048; Min. = 0.732, Max. = 0.864). Thus, the scree plots all suggested extracting a single factor and likewise a supplementary parallel analysis using the 1989 and 2007 data suggested extracting a single factor (the largest and smallest samples, respectively). Such results are consistent with our view that this measure is essentially unidimensional.

We computed an overall index of how well each item was related to the latent self-esteem construct by averaging the 10 pattern/structure loadings for each item across each wave (i.e., we averaged the ten loadings for item 1 from 1989 to 2007). These loadings are reported in Table 1 and they were very consistent over time (Range of SDs for loadings: .03 to .09). Finally, scores for Parcel 1 were created by averaging responses to the items with 1^st, 6^th, and 7^th highest average loadings, scores for Parcel 2 were created by averaging responses to the items with the 2^nd, 5^th, and 8^th highest average loadings, and scores for Parcel 3 were created by averaging response to the items with the 3^rd, 4^th, 9^th, and 10^th highest average loadings. Table 1 lists the items included in each of the three parcels. As seen in Table 1, each parcel involves a mixture of positively and negatively worded items.

Table 1.

Average Factor Loadings for a Single Factor Model for the Rosenberg Items across 10 Waves of Data

	Item	Average Loading	Standard Deviation	Parcel
1.	I feel that I'm a person of worth, at least on an equal level with others.	.69	.08	3
2.	I feel that I have a number of good qualities.	.73	.07	3
3.	All in all, I am inclined to feel that I'm a failure.	.66	.06	1
4.	I am able to do things as well as most other people.	.68	.07	1
5.	I feel that I do not have much to be proud of.	.52	.05	3
6.	I take a positive attitude toward myself.	.83	.03	1
7.	On the whole, I am satisfied with myself.	.77	.03	2
8.	I certainly feel useless at times.	.63	.06	2
9.	I wish I could have more respect for myself.	.60	.09	3
10.	At times I think I am no good at all.	.68	.06	2

General Longitudinal Model

Model 1. We first estimated a general longitudinal model following Marsh and Grayson (1994) without metric invariance. Latent self-esteem factors at each wave were indicated by the three respective parcels (i.e., the 3 parcels in 1989 were used to identify a latent self-esteem factor in 1989). The variance of each factor was freely estimated and the loadings of the first parcel were fixed to 1.0 for identification purposes. We allowed for correlated uniquenesses between the respective parcels at different waves (i.e., we allowed for all possible correlations between the various residuals for parcel 1 at different time points; e.g., 1989 with 1990, 1990 with 1991, 1989 with 2007, and so on). This model had good fit to the data (chi-square = 296.725, df = 225; RMSEA = 0.027; TLI = 0.987; SRMR = 0.028).

We then imposed invariance constraints on the factor loadings to make sure that the parcels exhibited metric invariance across time. For example, we constrained the loadings for parcel 2 to the same values at each measurement occasion. (Recall that Parcel 1 was set to 1.0 to identify the latent variables). This general longitudinal model with metric invariance model had good fit to the data by our conventions (chi-square = 319.117, df = 243: RMSEA = 0.026; TLI = 0.987; SRMR = 0.035) and the difference in fit between this model and the longitudinal factor model without metric invariance was not statistically significant (Δ chi-square = 23.392, Δ df = 18). In short, there was no reason to question the assumption that individuals were being ranked in the same way at each measurement occasion (i.e., we satisfied the condition of metric invariance for the parcels). This is the level of measurement invariance required to draw meaningful inferences from STARTS models because STARTS models do not include construct means (see Kenny & Zautra, 2001, p. 256–257). The fit of this general model with metric invariance served as a point of comparison for evaluating the fit of more restricted models like the latent-variable STARTS model.

The matrix of latent variable correlations from the model with constraints on the factor loadings is reported in Table 2. These coefficients are test-retest correlations that are not attenuated by unreliability. As seen in Table 2, there is evidence that self-esteem scores in 1989 were correlated with scores in 2007 (r = .369, p < .05). Likewise, there was evidence that self-esteem scores became more consistent with age. For example, the correlation between scores in 1990 and 1991 (an approximately 1-year interval when sample members were adolescents) was .725 whereas the correlation between scores in 2005 and 2007 was .802 (an approximately 2-year interval when sample members were adults). These coefficients in Table 2 therefore provide an important context for understanding the STARTS model results. It is also useful to note that the latent variable variances fluctuated over time (Min = .256 in 1990; Max = .384 in 1995) but the pattern did not indicate a clear linear trend toward increasing variance with age.

Table 2.

Latent Variable Correlations for 10 Waves of Self-Esteem from 1989 to 2007 from Model 1

	1989	1990	1991	1992	1994	1995	1997	1999	2005	2007
1989	1.000
1990	.609	1.000
1991	.544	.725	1.000
1992	.501	.606	.762	1.000
1994	.405	.536	.552	.635	1.000
1995	.390	.480	.532	.598	.739	1.000
1997	.345	.471	.507	.499	.590	.691	1.000
1999	.339	.456	.430	.488	.557	.609	.655	1.000
2005	.418	.445	.422	.442	.537	.568	.606	.694	1.000
2007	.369	.404	.400	.431	.487	.522	.589	.605	.802	1.000
Average Age	13.18	14.09	15.09	16.07	18.14	19.18	21.15	23.79	29.61	31.70
SD Age	0.42	0.42	0.42	0.42	0.41	0.41	0.41	0.42	0.40	0.50

Note: Unstandardized factor loading for Parcel 2 was 1.156 and 0.991 for Parcel 3 (Parcel 1 was fixed to 1.0 for identification purposes). Factor variances were 0.293, 0.256, 0.329, 0.364, 0.354, 0.384, 0.320, 0.319, 0.294, and 0.281 for the 10 years, respectively.

STARTS Models

Fit statistics for all models are reported in Table 3. Key estimates from these models are reported in Table 4.

Table 3.

Selected Fit Statistics for Latent Variable Models 1 to 5

Model	χ2	df	RMSEA	90% CI	TLI	SRMR
1. General Longitudinal Model w/ Metric Invariance	319.117	243	0.026	0.018 to 0.034	0.987	0.035
2. Basic STARTS	471.773	294	0.037	0.030 to 0.043	0.975	0.092
3. Constant Ratio for the Variances	424.997	285	0.033	0.026 to 0.039	0.980	0.089
4. Increasing Stability	398.411	293	0.028	0.021 to 0.035	0.985	0.080
5. Increasing Stability   and Constant Ratio     for the Variances	360.882	284	0.024	0.016 to 0.032	0.989	0.045

Table 4.

Stable Trait (ST), Autoregressive Trait (ART), and State (S) Variances and the Size of the Autoregressive (AR) Path Coefficient for the STARTS Models Evaluated

	Variance Components (and 95% Confidence Intervals)						AR Path Coefficient
	Stable Trait		AR Trait		State
Model	Estimate	95% CI	Estimate	95% CI	State	95% CI	Estimate	95% CI
2. Basic STARTS	43.1%	33.7% to 50.5%	39.4%	31.7% to 45.6%	17.6%	9.8% to 24.8%	.765	.646 to .864
3. Constant Ratio for the Variances	41.1%	28.0% to 49.9%	41.7%	33.5% to 48.5%	17.2%	10.5% to 24.0%	.810	.684 to .898
4. Increasing Stability	35.8%	22.6% to 44.3%	48.1%	39.8% to 56.5%	16.1%	9.0% to 22.5%	.868a	.773 to .926
5. Increasing Stability and Constant Ratio for the Variances	35.1%	22.1% to 44.1%	49.0%	40.2% to 57.6%	15.9%	10.1% to 21.7%	.886a	.794 to .934

Note: AR Trait = Autoregressive Traits. All variances and AR coefficients are greater than zero (p < .05). 95% Confidence Intervals are based on bias-corrected bootstrapped estimates using 500 draws.

^aFor models in which the AR stability coefficient were allowed to increase with age (Models 4 and 5), the reported coefficient is the estimate between ages 21 and 22.

Model 2. As shown in Table 4, all three primary sources of variance were statistically detectable; however, the largest source of variance was the stable trait followed closely by the autoregressive trait factor. One interesting question concerns the implied stability of the autoregressive traits over long periods of time. This can be evaluated by taking the autoregressive stability path and raising it to a power that reflects the length of the study, 19 years. The correlation between the autoregressive trait scores at age 13 and age 32 is estimated to be .006. (This figure was derived by taking the .765 path coefficient and raising it to the 19^th power to reflect 19 yearly intervals between the ages of 13 and 32.) The implication is that the connection between autoregressive variance in adolescence and adulthood was minimal, despite the relatively high degree of 1-year stability in the autoregressive factor. This further suggests that the correlation between scores at 1989 and 2007 (i.e., r = .369, Table 2) almost exclusively reflects the influence of the stable trait factor. The reasoning is that the observed correlation cannot reflect shared state influences by definition and the autoregressive effect from 1989 to 2007 is virtually nil.

Model 3. This model relaxed the canonical STARTS stationarity assumption and required that the ratio of stable trait, autoregressive trait, and state variances were constant across all waves. The fit indices and chi square difference test (see Table 3) suggest that allowing for unequal variances resulted in a better fitting model than Model 2. As seen in Table 4, the variance decomposition from this model indicated that the stable trait and autoregressive traits accounted for roughly similar amounts of variance. The correlation between autoregressive trait scores at age 13 and at age 32 was estimated to be .018 (taking .810 to the 19^th power). Thus, as in Model 2, scores on the autoregressive trait at the first (early adolescence) and last wave (adulthood) were virtually uncorrelated.

Model 4. This model retained the stationarity assumption regarding total variance but specified a logarithmic function for age to capture an increasing degree of stability for the autoregressive trait factors with increasing age. The decomposition of variance shifted more to the autoregressive trait factors than the stable trait factor. The estimate of A₀, the model implied age when variance in the autoregressive factor that is detectable from ages 13 to 32 first emerged was 11.189.

Model 5. This model extended Model 4 by relaxing the stationarity assumption to stipulate that the ratio of variance components was constant over time. This model therefore captures increasing stability and a fixed ratio of variances for three focal components. It had a relatively good fit to the data as seen in Table 3 especially when compared to the fit of the general longitudinal model with metric invariance imposed (i.e., Model 1: Δ chi-square = 41.765, Δ df = 41, p = ns). Factor loadings from the latent self-esteem variable to the three STARTS components were (1.00, 0.926, 1.040, 1.108, 1.119, 1.167, 1.071, 1.054, 0.985, and 0.964 for the ten occasions). The squares of these paths estimated the change in variance relative to the first occasion which was fixed to 1.00. For example, given that we used the 1989 assessment as the reference point, the .926 path for the 1990 occasion indicates that there was less variance in 1990 than in 1989). The stable trait factor accounted for 35% of the variance whereas the autoregressive trait accounted for 49% in self-esteem scores. Pure state variance accounted for about 16% of the variance in self-esteem scores. The estimate of A₀ was 11.716. This means that the autoregressive variance that carries over from ages 13 to 32 was predicted to start before age 12.

As a more direct check on the ability of this model to reproduce the underlying data, we examined the model implied correlation matrix for the latent self-esteem factors from 1989 to 2007. These values are reported in Table 5 and we noted that they were generally quite close to the values reported in Table 2. Indeed, there were only 4 discrepancies ≥ |.10| and none exceeded |.12|. These discrepancies are reported in Appendix A. Accordingly, we focused our interpretations on this model given issues of model fit and the conceptual advantages of Model 5 over the other models.

Table 5.

Latent Variable Correlations for 10 Waves of Self-Esteem from 1989 to 2007 from Model 5

	1989	1990	1991	1992	1994	1995	1997	1999	2005	2007
1989	1.000
1990	.628	1.000
1991	.533	.674	1.000
1992	.486	.590	.713	1.000
1994	.436	.502	.580	.660	1.000
1995	.422	.477	.543	.610	.761	1.000
1997	.405	.447	.496	.547	.662	.723	1.000
1999	.392	.423	.459	.498	.583	.628	.717	1.000
2005	.377	.396	.419	.443	.497	.525	.581	.659	1.000
2007	.374	.391	.411	.432	.479	.504	.553	.621	.781	1.000

In particular, Model 5 allows for a developmental trend for increasing stability with age for the autoregressive traits. This progression is evident in Figure 2 which plots selected model implied one-year autoregressive stability coefficients at different starting ages (13, 18, and 25). We selected these intervals because they roughly correspond to different developmental periods (adolescence, emerging adulthood, and adulthood). We also include the single yearly interval between ages 31 and 32 to provide the most extreme point of contrast for the 13 to 14 stability coefficient. The estimate of autoregressive stability was .505 between the ages of 13 and 14 versus .942 between the ages of 31 and 32. The predicted correlation between autoregressive trait scores at age 13 and autoregressive trait scores at age 32 was less than .040. This once again points to the conclusion that the observed correlation between scores in 1989 and 2007 reflects the influence of the completely stable trait. In short, Figure 2 illustrates the pattern of increasing autoregressive stability with age and conveys the point that the consistency between autoregressive traits approaches zero as the time between measurement occasions increases. The caveat is that consistency approaches zero more quickly at younger starting ages as opposed to older starting ages. Note that the pattern for overall stability has the same shape as is depicted in Figure 2.

Follow-Up Analyses of Model 5

We also compared Model 5 to reduced models that omitted one of the STARTS components. A model that dropped the ST factor had significantly worse fit to these data than Model 5 (i.e., an ARTS model: Chi-Square = 376.588, df = 285; TLI: .987; RMSEA = .027; SRMR = .043; Δ chi square = 15.706, Δ df = 1, p < .05). A model that dropped the ART factors also had a significantly worse fit to these data than Model 5 (i.e., a STS model: Chi-Square = 743.460, df = 287; TLI: .934; RMSEA = .059; SRMR = .083; Δ chi square = 382.578, Δ df = 3, p < .05). Likewise, a model that dropped the S factors fit significantly worse than Model 5 (i.e., a START model: Chi-Square = 390.303, df = 285; TLI: .985; RMSEA = .029; SRMR = .051; Δ chi square = 29.421, Δ df = 1, p < .05). This model without state factors also yielded generally lower b coefficients than the STARTS model. For example, the model implied coefficient between ages 13 and 14 was .343 (versus .505 in the STARTS), .624 between ages 18 and 19 (versus .839 in the STARTS), .768 between ages 25 and 26 (versus .918 in the STARTS), and .825 between ages 30 and 31(versus .939 in the STARTS). The explanation is that the autoregressive factors in this type of START model must now capture systematic variance that is unique to that occasion. The inclusion of this variance into the autoregressive factors likely depresses the overtime stability coefficients. Stability coefficients increase in the latent variable STARTS model because this approach permits a distinction between reliable variance that is occasion specific from the autoregressive trait variance. All in all, these follow-up tests suggest that all three sources of variance in the STARTS framework are necessary elements when attempting to explain the longitudinal structure of self-esteem.

Summary of Results

The results across models converged on a set of conclusions about the longitudinal consistency of latent self-esteem from adolescence to adulthood. Moreover, the use of latent variable modeling approaches allowed us to isolate systematic variance from measurement error. First, the smallest component of variance in repeated assessments of latent self-esteem was state variance. This factor accounted for about 16% of the total variance in latent self-esteem. The more stable components of self-esteem accounted for the majority of the variance in repeated assessments of latent self-esteem. Second, models that specified an increasing degree of consistency in the autoregressive trait factor and relaxed assumptions about the total amount of variance fit better than models without such assumptions. Third, scores on the autoregressive trait at age 13 were virtually uncorrelated with scores on the autoregressive trait at age 32 across all models. This means that the observed correlation between self-esteem scores obtained at 1989 and 2007 (i.e., ages 13 versus 32 years) largely reflects the influence of the stable trait factor. This pattern occurred despite fairly substantial 1-year stability coefficients for autoregressive traits in all models, especially at older ages.

Discussion

We evaluated the longitudinal consistency of latent global self-esteem during a particularly salient transition in the life span – the transition from early adolescence to adulthood. Results from a latent variable extension of Kenny and Zautra’s (1995, 2001) STARTS model indicated that approximately 35% of the variance in latent global self-esteem was due to a stable trait factor, whereas 49% was due to an autoregressive trait factor. The remaining 16% of systematic variance was due to transient state factors. These findings add additional and methodologically rigorous support to the notion that self-esteem is an enduring individual difference construct rather than a transitory or ephemeral state-like construct. We now turn to more detailed discussion of our key findings.

Global Self-Esteem Is a Relatively Enduring Individual Difference Construct

We concluded that global self-esteem is a relatively enduring individual difference construct because the completely stable trait factor and autoregressive trait factors combined to account for 84% of the reliable variance in latent self-esteem assessments. This interpretation raises an important issue with respect to whether autoregressive trait variance should be considered as evidence for judging a construct as more trait-like than state-like. In the present study, we have made such an assumption and we note that this is a judgment call based on design considerations and the statistical results. As it stands, we believe that researchers should jointly consider three pieces of information when evaluating this issue -- the amount of variance attributed to the autoregressive factor, the size of the autoregressive path coefficient, and the length of the interval in question. These issues of judgment and perspective are placed in better relief when considering a study conducted by Campbell and Kenny (1999) who used the STARTS model to evaluate the longitudinal stability of physical attractiveness from childhood to adulthood (e.g., ages 10 to 56; see Zebrowitz, Olson, & Hoffman, 1993).

Campbell and Kenny found no statistical evidence for a stable trait factor and instead reported evidence of a substantial autoregressive trait factor with considerable stability for attractiveness (i.e., they estimated b to be .97 for yearly intervals). From the point of view of a few years, a coefficient of this size indicates that physical attractiveness is extremely stable. On the other hand, such an interpretation is not as straightforward from the vantage point of 50 years. Consider what happens to the size of the autoregressive coefficient of .97 when it is raised to the 50^th power – the model implied correlation is .22. Different scholars will hold different opinions as to the impressiveness of this figure. Nonetheless, it is hard to dismiss the fact that .22 is much smaller than .97. Viewed from such a long term-longitudinal perspective, it is clear that a substantially sized autoregressive trait with even an extremely high yearly stability coefficient simply points to some non-zero degree of consistency over many waves of data. This is a useful perspective to keep in mind when conceptualizing the nature of autoregressive traits. That is, multiplied over enough waves, even relatively high stability coefficients produce trivial net correlations for autoregressive traits across long intervals.

Global Self-Esteem Becomes More Consistent with Development

Despite our interpretation that self-esteem is a relatively enduring psychological construct, the current results also point to an important developmental aspect to self-esteem. Indeed, the observed pattern of increasing consistency in self-esteem with age is perhaps even more interesting than the variance decompositions we reported. This general finding converges with research on global personality traits such as the Big Five domains (Roberts & DelVecchio, 2000) and with the classic suggestion by Bloom (1964; see also Fraley & Roberts, 2005) that inconsistency is more common earlier in the life span rather than later. A broad generalization is that individual difference constructs become more consistent with age and development (i.e., the cumulative continuity principle of personality development; Caspi et al. 2005).

The changing aspects of self-esteem were captured by the autoregressive traits and the results suggest that changes in these attributes are fairly modest from one year to the next but can be substantial when viewed from a longer term perspective. For example, Figure 2 shows that scores on the autoregressive self-esteem factor at age 13 have virtually no connection with scores on that factor at age 32 although there is a connection between the autoregressive traits at ages 13 and 14. The “slings and arrows of outrageous fortune” can contribute to the development of relatively high self-esteem in adulthood for adolescents who had relatively low self-esteem and vice versa. Nonetheless, there is still an observable connection between overall self-esteem scores at ages 13 and 32 (i.e. see Table 2). This connection, however, is explained almost exclusively by the contribution of the stable trait element of self-esteem.

The observation of the increasing consistency of self-esteem with age has methodological and perhaps even applied implications. One methodological implication is that it will be difficult to discern much inconsistency in self-esteem with only a few waves of data covering a small amount of the life span (say two to three years). Changes in self-esteem are more likely to be evident when evaluated over a longer interval. Such a consideration points to the need for long-term studies on personality development (i.e., studies that cover intervals of say 10 to 20 years). Short-term longitudinal designs also make it difficult to distinguish autoregressive trait variance and stable trait variance. The issue is that the observed stability coefficients need to show an asymptote in the decay of their magnitude for the STARTS model to be able to isolate the completely stable component from the autoregressive trait. This pattern of diminishing decay is evident in Table 2. As seen in Table 2, the various longer-term correlations (i.e., between 1989 and 2007 or between 1991 and 2007) do not appear to as different from each either as would be predicted by a strict first-order simplex pattern (see Fraley & Roberts, 2005 for a more technical discussion of this issue).

The current results may also have applied implications given that they hint that early self-esteem interventions might be more successful than interventions aimed at older adolescents or adults. The major caveat is that these results are based on a community sample that was not specifically targeted for psychological intervention. Although self-esteem becomes increasingly more consistent with age, this observation does not necessarily mean that changing self-esteem would be more difficult in adulthood as opposed to early adolescence in a targeted investigation. Naturalistic studies based on “normal samples” do not provide insights into what could happen if interventions were attempted. Nonetheless, it is plausible that interventions might have a greater chance of impacting self-esteem change if they are targeted to periods in the life span marked by greater inconsistency (see Trzesniewski et al., 2003).

One of the potentially intriguing aspects of modeling increasingly stable autoregressive components of self-esteem with development is the possibility of estimating backwards from the observed data to the point when that observed consistency in the autoregressive traits would have emerged. The value in the present study was somewhere between the ages of 11 and 12. Put differently, we found that the increasingly consistent autoregressive component of self-esteem assessed from ages 13 to 32 seems to first emerge before an individual’s 12^th birthday. We emphasize that this figure is simply an extrapolation from the observed data and it is not a fixed number. This model implied starting age applies to the autoregressive traits under investigation and therefore depends on the design of the study. The figure in the current study simply highlights that some of the observed variance in self-esteem at age 13 has its origins earlier in development.

Limitations and Conclusions

Despite considerable intuitive appeal, there are relatively few published examples of trait-state models in the substantive literature (Kenny & Zautra, 2001; but see Cole & Martin, 2005). In this respect, the present investigation is a novel contribution to the self-esteem literature. Even so, there are limitations and caveats that are worth noting. Certain limitations concern the limited diversity of the present sample which was based on European Americans who were originally based in Iowa. Future work should examine more diverse samples. Moreover, we examined consistency using self-reports of self-esteem and it might be profitable to obtain informant report measures in future studies. In addition, the trait-state decomposition of self-esteem might differ had we assessed self-esteem in a more intensive fashion such as taking measures daily, weekly, or monthly. The current results may not generalize to those kinds of assessment strategies. Likewise, different measures of self-esteem may yield different results. However, the measure we used in this study (the Rosenberg) is the mostly widely used measure of global self-esteem in the literature. Aside from these specific concerns, there are other more general considerations that have to do with trait-state models.

Foremost,Cole et al. (2005) and Kenny and Zautra (2001) emphasized that the STARTS model can be difficult to estimate and these authors have noted that inadmissible solutions are obtained with some regularity. This was not a concern in the present study as we had 10 waves of data, a reasonably large sample size, and we were dealing with a construct that was neither too stable nor unstable. These conditions apply in certain research contexts only. We therefore encourage users of trait-state models to inspect statistical output carefully to detect inadmissible solutions (e.g., negative variances). A second concern has to do with the estimate of the starting point for the autoregressive trait factor. It is very likely that we would have obtained a different starting value had we elected to study a different phase of the life span. Thus, it is important to remember that such a figure has meaning only in relation to the design of the study. Future research is needed to replicate these particular results and to obtain estimated starting points for autoregressive traits using data that cover different phases of the life span.

In closing, there has been ongoing debate over whether global self-esteem is best conceptualized as a trait-like or state-like construct. Results using a latent variable trait-state model indicate that self-esteem has both trait-like and state-like components but that the state component is comparatively smaller than the more stable components. Global self-esteem is therefore best conceptualized as a relatively enduring psychological attribute that becomes increasingly consistent with age, at least when considering the years between adolescence to adulthood. Moreover, the current findings for global self-esteem illustrate the cumulative continuity principle of personality development because the consistency of self-esteem increased with age.

1. The longitudinal consistency of global self-esteem was evaluated from age 13 to age 32

2. Latent trait-state models were used to quantify how much state variance was in self-esteem.

3. Stable factors accounted for the majority of the variance in longitudinal assessments of self-esteem.

Appendix A

Difference Between the Model Implied Latent Variable Correlations for the 10 Waves of Self-Esteem from Model #5 and the Correlations from Model #1.

	1989	1990	1991	1992	1994	1995	1997	1999	2005	2007
1989	-	.031	−.015	−.020	.038	.038	.070	.061	−.049	.006
1990		-	−.100	−.025	−.047	−.004	−.030	−.041	−.059	−.015
1991			-	−.107	.041	.015	−.015	.036	−.004	.013
1992				-	.043	.019	.066	.013	.001	.001
1994					-	.050	.118	.039	−.055	−.010
1995						-	.064	.031	−.061	−.024
1997							-	.117	−.039	−.053
1999								-	−.064	.026
2005									-	−.056
2007										-

Note: Coefficients are the differences between the latent variable correlations from Model 1 (Table 2) and the model implied values from Model 5 (Table 5). Positive numbers indicate the model implied value from Model 5 was larger than latent variable correlation. Differences were calculated by first r-to-z transforming the correlations, taking the difference, and then back transforming to the difference to the r metric. Discrepancies ≥ |.10| are bolded.