Abstract
Cells are complex, dynamic systems that actively adapt to various stimuli including mechanical alterations. Central to understanding cellular response to mechanical stimulation is the organization of the cytoskeleton and its actin filament network. In this manuscript, we present a minimalistic network Monte Carlo based approach to model actin filament organization under cyclic stretching. Utilizing a coarse-grained model, a filament network is prescribed within a two-dimensional circular space through nodal connections. When cyclically stretched, the model demonstrates that a perpendicular alignment of the filaments to the direction of stretch emerges in response to nodal repositioning to minimize net nodal forces from filament stress states. In addition, the filaments in the network rearrange and redistribute themselves to reduce the overall stress by decreasing their individual stresses. In parallel, we cyclically stretch NIH 3T3 fibroblasts and find a similar cytoskeletal response. With this work, we test the hypothesis that a first-principles mechanical model of filament assembly in a confined space is by itself capable of yielding the remodeling behavior observed experimentally. Identifying minimal mechanisms sufficient to reproduce mechanical influences on cellular structure has important implications in a diversity of fields, including biology, physics, medicine, computer science, and engineering.
Keywords: stochastic, computational, actin, mechanobiology, modeling, biomechanics
1. INTRODUCTION
The cytoskeleton is directly linked to the mechanical environment of cells through multiple sites of interaction, including focal adhesions, integrins, cellular junctions and the extracellular matrix. The cytoskeleton is a dynamic structure capable of rearranging to adapt to changing environments, even though the specifics of these active adaptations are not well understood. Among the major components of the cytoskeleton is its network of actin filaments, which assemble into specialized bundles, arrays and complex branching structures to influence cell functions such as cell motility, spreading, and adhesion. For example, stress fibers, which are cross-linked bundles of actin filaments, maintain tensile forces in the cell to assist in cell adhesion and cytokinesis. From a physiological perspective, the mechanical stimulation experienced by individual cells is often comprised of multiple mechanical modes (e.g., stretching and shear), thus presenting a challenge to characterize their influence on cell structure. Endothelial mechanotransduction has been a topic of significant interest (Hahn & Schwartz, 2009). Endothelial cells are classically considered to undergo three mechanical stresses: shear from blood flow, hydrostatic pressure from blood pressure, and cyclic hoop stress due vessel deformation (Sato & Ohashi, 2005). In addition, fibroblasts form a major component (tunica externa) of the vasculature in a layer surrounding the endothelial cells (tunica intima) and thus experience similar forces to the endothelium. The responses of cells to mechanical stimuli are often directly linked to their actin cytoskeleton. For example, in vivo experiments performed in flow-regulating chambers using cultured endothelial cells revealed that cells and their stress fibers dynamically reorient themselves parallel to the direction of flow, which is perpendicular to the direction of hoop stress (Franke et al., 1984). Physiologically, endothelial cells are similarly found to align themselves parallel to direction of flow and perpendicular to the direction of hoop stress (Wong et al., 1983). Fibroblasts have also been shown to align perpendicular to the direction of cyclic stretch in vivo (Danciu et al., 2004; Joshi & Webb, 2008; Pender & McCulloch, 1991), suggesting that a biomechanical similarity could cause comparable behavior in both cell types under cyclic stretching. This pattern of cyclic stretch alignment has been shown to occur in the absence of microtubules in cultured cells (Wang et al., 2001) and in the absence of shear flow in intact rat arteries (Sipkema et al., 2003).
Computational models can provide a valuable complement to experimental work in understanding the complex responses of cellular systems to heterogeneous mechanical environments. For example, they provide a basis for rationalizing complex experimental observations and a platform to test the sufficiency of theories and minimal models of the experimental system. They are therefore in principal well suited to understanding how mechanical stimulation influences actin cytoskeleton structure and dynamics. Actin in particular has attracted considerable interest in the modeling and simulation area due to its relative simplicity and the wealth of experimental data available for it. Specifically, mechanical modeling of the actin cytoskeleton has contributed much to understanding the interplay between these polymer networks and mechanics. Properties at many scales have been examined, from atomic-scale models of small numbers of actin monomers (Chu & Voth, 2006), through models of properties of single filaments (Ming et al., 2003), through coarse-grained models of the overall mechanical properties of full actin networks (Satcher & Dewey, 1996; Stamenovic & Coughlin, 2000; Stamenovic & Ingber, 2002; Stamenovic & Wang, 2000; Wilhelm & Frey, 2003). A key observation of the field is that multiscale modeling approaches make it possible to infer detailed mechanical properties of filaments at the atomic scale and translate these into coarse-grained models of large filaments or filament networks (Bausch & Kroy, 2006; Chu & Voth, 2006). One can thus use insights from the more computationally expensive models, as well as experimental studies of the mechanical properties of filaments and filament bundles, to set parameters for simplified but far more tractable models of the macroscopic behaviors of full actin networks.
In this work, our objective was to design a coarse-grained Monte Carlo model of the actin filament network in a cell undergoing uniaxial cyclic stretch. We demonstrate a gradual alignment of the actin filaments that reflects the observed physiological and in vivo response of both endothelial cells and fibroblasts under cyclic stretch. We corroborate our model with experimental data showing gradual alignment of fibroblasts perpendicular to cyclic stretch over a period of 24 hours. Previous work on cyclic stretch simulations on actin networks have focused on areas such as continuum mechanics models (Hsu et al., 2009; Na et al., 2007; Palmer & Boyce, 2008) or cytoskeletal dynamics (Civelekoglu et al., 1998). While there has been work on discrete models involving force-generating actin-myosin networks (Silveira et al., 2005; Silveira & Fredberg, 2005) and passive actin networks under static stretch (DiDonna & Levine, 2006), to our knowledge this is the first discrete filament model that accurately captures the observed passive response of actin filament alignment under cyclic stretch. While we believe that incorporating active elements such as myosin as well as different cross-linking proteins will be a next great step, in this manuscript, we have focused on developing a new model and showing its responses compared to defined experimental results
2. MATERIALS AND METHODS
2.1 Simulation methods
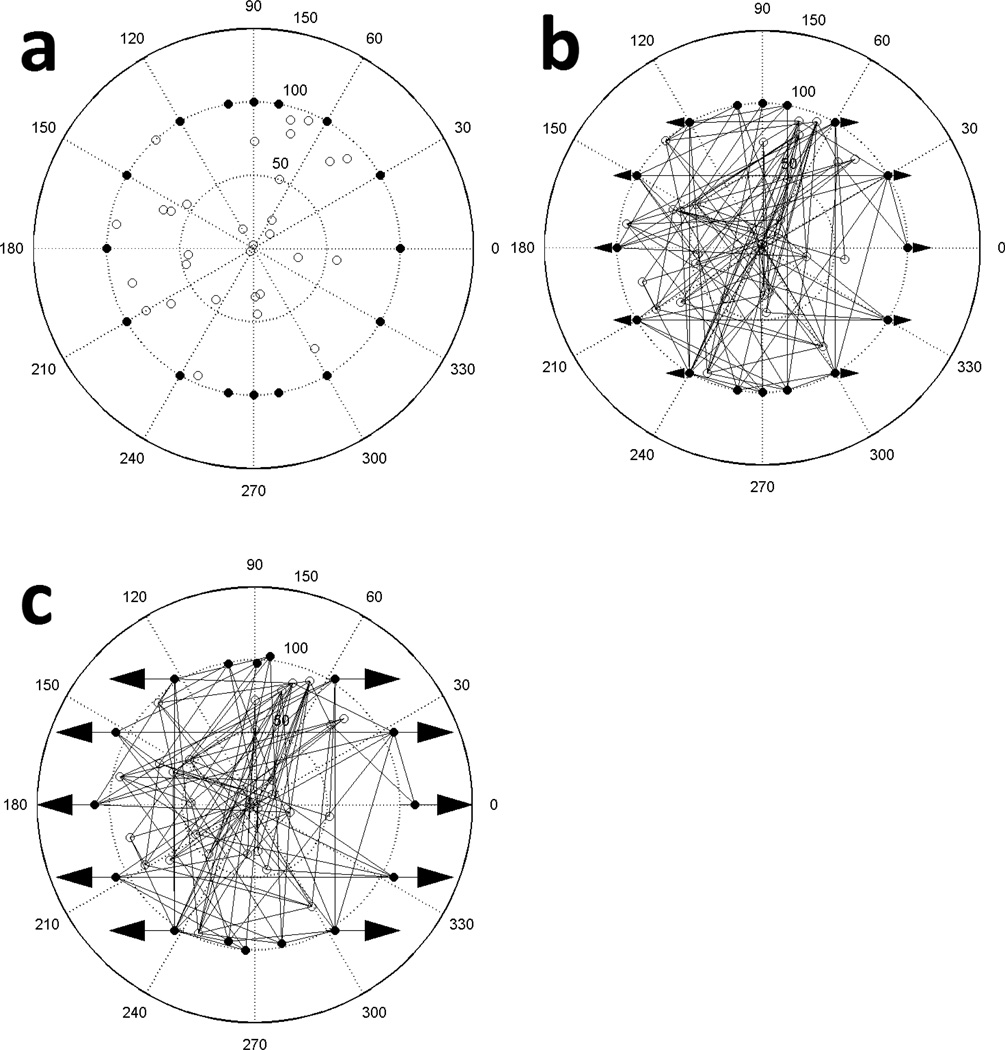
A stochastic model was developed to examine the distribution of forces and the reorganization of actin filament structures in response to cyclic stretching. We used a two-dimensional circular solution space of prescribed radius. This radius was chosen to be 100 arbitrary units, representing an adhered and spread cell whose bulk lies in an approximately circular region of diameter 30 µm, such as a fibroblast. So as not to restrict the angular orientation of the filaments, an off-lattice model was chosen. The space is considered fixed to an underlying substrate by perimeter nodes at prescribed locations on the circumference of the circle (Fig. 1a). Within its interior, additional nodes are randomly placed that are not fixed to the substrate and can move when a net imbalanced force is applied to them. The nodes on the perimeter act as anchoring proteins, which are representative of focal adhesions, and the interior nodes model cross-linking proteins between filaments, such as filamin; multiple filaments per node are possible. A prescribed quantity of filaments is created by randomly assigning two nodes per filament, which locates the filament ends and establishes its length and orientation within the space (Fig. 1b). These filaments are assumed to represent either cross-linked single actin filaments or bundled filaments found in stress fibers. The filaments are considered linear members able to support both tensile and compressive loads. This assumption is reasonable if the applied stretch is at short time intervals, or the stress is weak, or for short filaments in the range of 0.1–1 µm long, which account for 80–90% of filaments found in vivo (Cano et al., 1991; Xu et al., 1999). The filaments and nodes are initially assembled in an unstressed state. All perimeter nodes except for those between 80–100° and 260–280° are then stretched horizontally on both sides (i.e., uniaxially) by an amount proportional to their initial X-axis positions so that those on the X-axis experience full stretching. The excluded nodes are near the vertical positions and are not considered fixed; this approach is used to simulate uniaxial stretching (Fig. 1c; see Movie S1 in the Supporting Material). The substrate is assumed to be sufficiently wide to exclude edge effects. A key assumption of the model is that mechanical stress on actin filaments is primarily responsible for the network’s response and all other influences, including the properties of the binding proteins, are accounted for in the probabilities assigned for filament fracture.
Figure 1.
Our computational model for representing a simplified actin filament network of an approximately circular cell under mechanical stimulation. (a) The node distribution of the network of 100 arbitrary unit radius with filaments removed. 16 nodes are assigned to specific locations on the perimeter (filled circles) and can act as fixed connections (mimicking focal adhesions). 30 interior nodes (open circles) are placed randomly and function as links between filaments (mimicking linking proteins such as filamin). (b) 138 filament network with both nodes and filaments represented. Linear fibers are formed by randomly selecting two nodes for each fiber; the nodes locate the ends of a fiber and define its length and orientation. Arrows denote which perimeter nodes will be stretched and the direction of stretch. (c) Configuration after stretching the arrowed perimeter nodes by 10% of their X-axis position in the direction of the arrows and after node network equilibrium has been achieved. The model was considered in equilibrium when the summation of the absolute magnitude of all the nodal forces was less than a prescribed tolerance.
The displacement of the nodes on the perimeter may cause some filaments to elongate and some to shorten. The resulting mechanical strain in a filament is defined as the ratio of the change in length to the original length. Using the assumption that filaments behave as Hooke’s Law springs, strain is directly proportional to stress by the elastic modulus, which for actin filaments is approximately 2 GPa (Isambert et al., 1995; Xu et al., 1998). It has been shown that individual actin filaments in living cells have a linear stress/strain relationship up to at least 12% strain (Lu et al., 2008) and that at frequencies <100 Hz, overall cytoskeletal elasticity is relatively independent of frequency (Deng et al., 2006). The strain in our model is then directly proportional to the applied force and the forces exerted by the filaments on their connected nodes are equal and opposite; multiple filament connections per node are possible. A force balance--which translates to a strain balance--was applied to all internal nodes and the perimeter nodes at 80–100° and 260–280° (i.e. all nodes except for the fixed perimeter nodes). Based on the resultant forces, the position of the nodes were adjusted by an amount proportional to and in the direction of the resultant force. A Gauss-Seidel relaxation iteration was applied to adjust the node positions until all the nodal forces were balanced, minimizing the nodal stress in the network. However, repositioning of the nodes can either increase or decrease stresses in the connected filaments. We consider the system to be at equilibrium when the sum of the absolute magnitudes of all the nodal forces is less than a prescribed tolerance (0.1 Pa in our model). We imposed a 10% total displacement by displacing perimeter nodes in 1% increments and relaxing forces in the system after each 1% adjustment until a total specified displacement of 10% was reached. Note that at equilibrium, individual filaments may contain large positive (tensile) or negative (compressive) stress values but the net balance of these stresses on each node must be small. Once the total prescribed displacement was reached and the model was in equilibrium (Fig. 1c), the final strains in the individual filaments were checked to determine, which would break. This was accomplished by first normalizing the strains using the largest strain value. The probability for any individual filament to break was then defined to be the absolute value of the normalized strain. Random numbers were generated between 0 and 1 to determine which filaments were removed, with a new filaments generated in the relaxed state between a random pair of nodes to replace each removed filament. This process of stretching, energy minimizing, and breaking and replacing filaments was considered a complete cycle. A new cycle was initiated by returning the nodes back to their original positions with the filaments in an unscretched state. The network was again stretched and the cycle repeated. This continued for a prescribed number of cycles while the distribution of filaments, their orientations, and their stresses were determined. See Movie S2 for a simulated actin filament network undergoing 25 cycles of horizontal uniaxial 10% stretching with filament breakage and replacement. To calculate the variability in our model, we calculated the standard error of the mean of our measurements of filament angle and stress. The means are taken at each cycle over n=10 uniquely generated filament networks. These variabilities are shown in the relevant figures as error bars representing 95% confidence intervals. One assumption that makes this approach more computationally tractable is that the peripheral nodes acting as focal adhesions do not move freely. While it has been shown that focal adhesions can move in response to tensional stress (Chen et al., 2003), in the scope of this work we have not incorporated this yet.
2.2 Experimental methods
2.2.1 Mechanical Stimulation System
A device was fabricated to impose cyclic uniaxial tension on living cells (Kubicek et al., 2004). A stretch frequency of 1 Hz was chosen since a normal adult resting heart rate is 60–100 beats per minute and experiments show that maximal alignment does not occur at less than 1 Hz (Hsu et al., 2009). The substrate used in our cell-substrate interactions was a ½ cm thick polydimethylsiloxane (PDMS) membrane. PDMS is created using a prescribed base-tocuring agent ratio, which was 10:1 for this study, resulting in an Elastic Modulus of 1882 kPa. We used the PDMS membrane to generate forces on adhered cells by clamping and stretching it in an air pressurization system. For the cyclic stretching, the cyclic pressure supply to the PDMS membrane was created through a bypass mechanism. This mechanism was constructed by modifying the feedback pressure control system of a microfluidic interface approach (Kim et al., 2009). This control device enabled cyclic regulation of pressurized air onto the bottom surface of the membrane, which deformed the cells attached to the upper surface of the membrane. Nearly complete uniaxial (ratio of 20:1 of stretch in desired vs normal direction) stretching was imposed on PDMS membranes through elliptically constraining the periphery of the membrane, and the cells which were attached to the membrane, were stretched simultaneously. Cyclic uniaxial strain at 20% was applied by adjusting the pressure to 10 psi using a frequency of 1 Hz for 3, 6, and 12 hour time periods.
2.2.2 Cell Culture
NIH 3T3 fibroblasts were washed once with phosphate-buffered saline (PBS), and then exposed to 0.05% trypsin-ethylenediamine-tetraacetate (Trypsin-EDTA) for 5 minutes. Following dissociation, the cells were counted and seeded, at a concentration of 1000 cells/cm2, on PDMS substrates that were pre-coated with fibronectin (10 µg in 1 mL PBS; BD Biosciences, San Jose, CA, USA; No.: 39410). Cell cultures were maintained at 37°C under 5% carbon dioxide in Dulbecco's modified Eagle's medium supplemented with 10% calf serum, glutamine, 0.3 mg/mL, streptomycin, 100 µg/mL, penicillin, 100 U/mL, and 20 mM N-2-hydroxyethylpiperazine-N'-2-ethanesulfonic acid at pH of 7.4. Cells were incubated for a minimum of 6 hours to allow for attachment and spreading; the media was replenished 24 hours before testing. A thermostatically regulated heat source maintained a temperature of 37°C during the experiments.
2.2.3 Optical Microscopy
Following the application of mechanical stimulation, pressure was removed and the cells were immediately fixed for imaging with an optical microscope. Filamentous actin (F-actin) was visualized to investigate the effects of mechanical stimulation on actin filaments. F-actin were visualized by fixing the cells with 4% paraformaldahyde and then permeablizing them with 0.2% Triton-X 100, followed by staining with 6 µM Alexa Flour® 488 phalloidin (Molecular Probes, Carlsbad, CA, USA; No.: A12379). The cells were then mounted with fluoromount-G, sealed under a coverslip and examined using an inverted optical microscope (Zeiss Axiovert 200; Zander IVF, Vero Beach, FL, USA) with a 63X high numerical aperture oil immersion objective. A fluorescein isothiocyanate (FITC; correspondingly pseudo-colored green) filter set allowed us to visualize these filaments.
2.2.4 Analysis of Actin Filament Orientation
Following mechanical stimulation, the cells were stained for F-actin and fluorescent images were imported into ImageJ software (download from the National Institutes of Health; http://rsb.info.nih.gov/ij/download.html), which were used for analysis of actin filament orientation. Microfilament orientation was examined by fitting an ellipse to the cellular outline based upon an initial tracing of the cell periphery. A major and minor x' and y' axes was then defined on this ellipse. Because cellular orientation is a predictor of actin filament orientation (Suciu et al., 1997; Swailes et al., 2004), we then quantified actin filament orientation by comparing the ellipse major axis orientation to the direction of uniaxial stretch. Only cells whose actin filaments exhibited a single orientation were used for analysis.
3. RESULTS
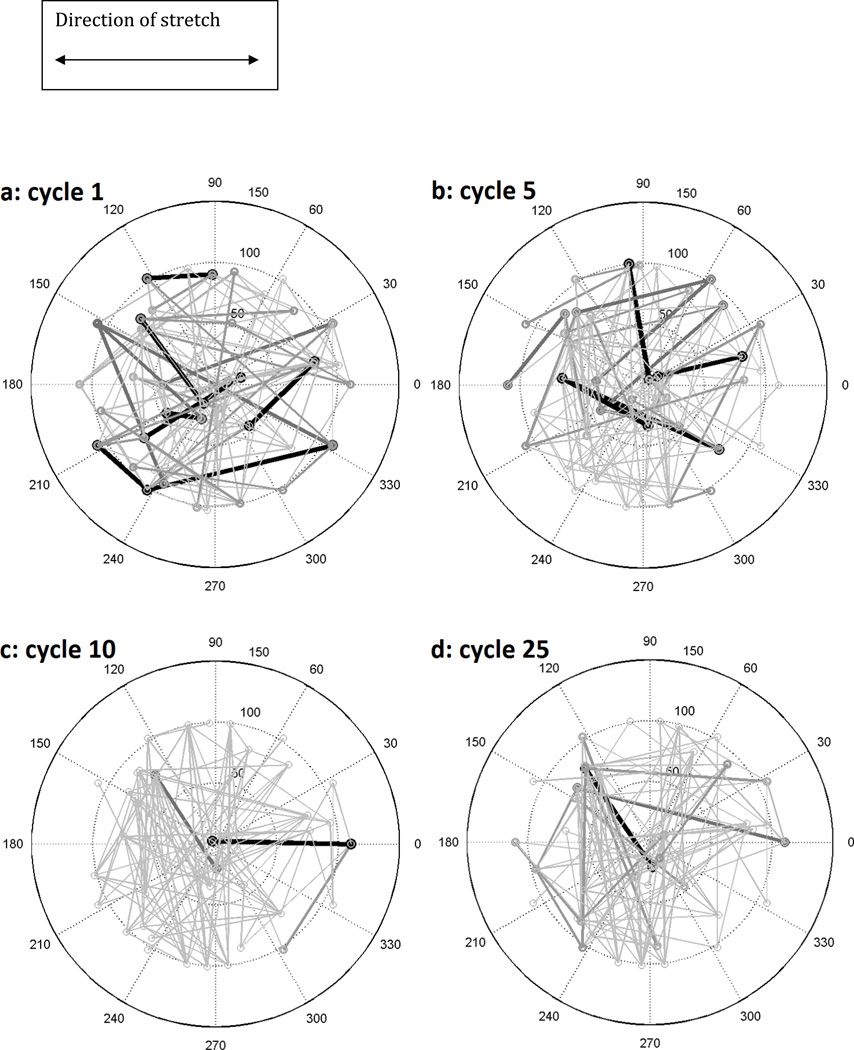
We studied the response of the actin filament model network by examining the network over time as mechanical stimulation was imposed on the system. Figures 2a–d show initial, intermediate, and final configurations of an actin filament network subjected to cyclic stretching corresponding to 1, 5, 10, and 25 cycles of stretching. There are 16 nodes on the perimeter of a circle of radius 100 units and 30 interior nodes with 138 filaments. In dividing non-muscle vertebrate cells, the number of actin filaments has been estimated to be in the tens of thousands (Alberts, 2002; Lee et al., 2010; Mitsui & Schneider, 1976) but due to the computational challenges with these number of filaments, we are assuming a model with fewer filaments. We have though examined the changes associated with our model response with respect to the number of filaments. Nodes located on the perimeter from 80° to 100° and 260° to 280° are not stretched. Nodes from −60° to 60° and 120° to 240° are stretched 10% for 25 cycles. After each cycle, the normalized filament stress determines the probability for breaking. “Breaking” is a term used to encompass all of the different mechanisms by which a filament might cease linking two nodes, whether this is through depolymerization, disassembly, or physical breaking (Janmey et al., 1991; Krendel et al., 1998; Mitchison & Cramer, 1996; Ono, 2003; Tsuda et al., 1996). These are replaced by filaments which are randomly assigned new locations such that the total number of filaments is conserved.
Figure 2.
A filament network of 138 filaments, 16 prescribed perimeter nodes, and 30 randomly placed internal nodes under 10% uniaxial horizontal stretch after (a) 1, (b) 5, (c) 10, and (d) 25 iterative cycles. Stretch was imposed in 1% increments on all peripheral nodes from −60° to 60° and 120° to 240°followed by Gauss-Seidel relaxation to achieve network nodal force equilibrium. The depicted thickness/darkness of the filaments correspond to their relative stresses with the thickest/darkest being >75% of the maximum stress of the network and the thinnest/lightest being <25%. The length scale in this model is 100 arbitrary units, representing a cell whose bulk lies in an approximately circular region of diameter 30 µm, such as a fibroblast.
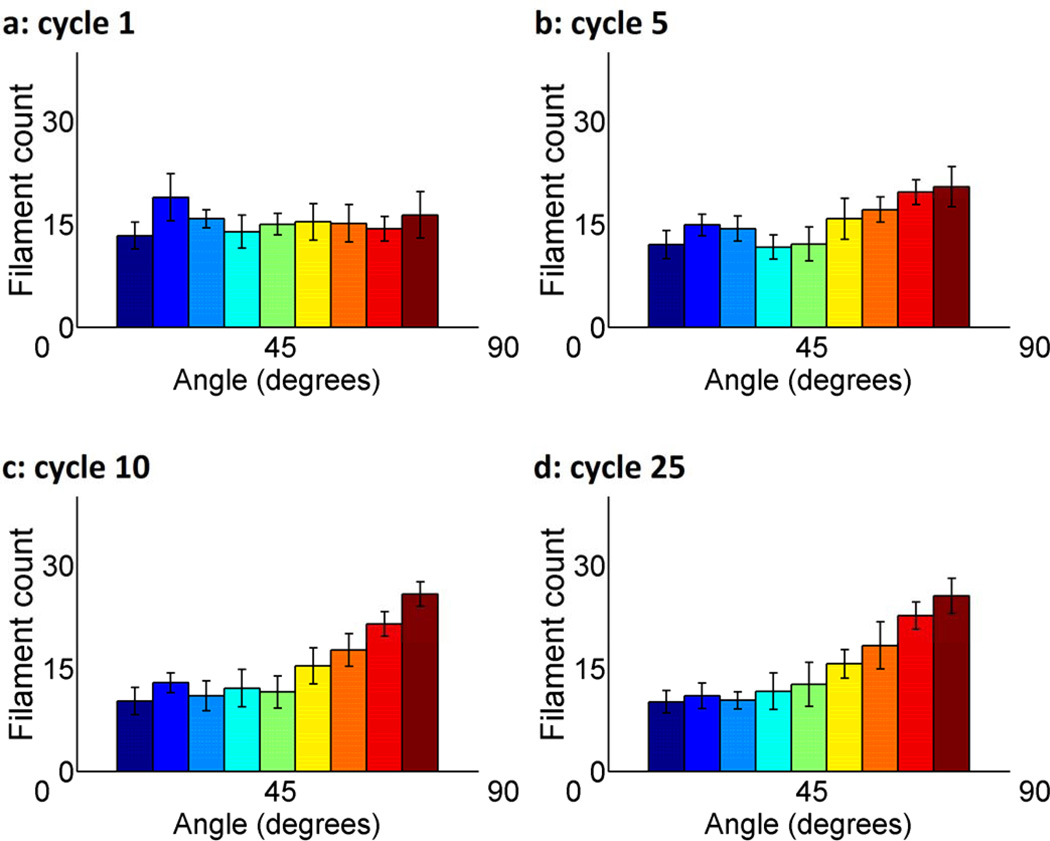
In order to quantify filament orientation, we create histograms of all filament angles in the network, averaged over 10 uniquely generated networks (Figure 3a–d). A clear affinity for 90° vertical alignment appears as cycle number increases. This shift though can be detected in as few as 5 cycles. The error bars reveal that there is a small amount of variation in the distribution of the filament alignment, which is not unexpected in a stochastic model. Note that all filament angles have been transposed to the first quadrant of the Cartersian coordinate system to create these histograms so that we are able to similarly portray filaments from 90° to 360°.
Figure 3.
Histograms of angular orientation of filaments in nodal equilibrium after (a) 1, (b) 5, (c) 10, and (d) 25 iterative cycles of 10% uniaxial horizontal stretch. Averaged over ten uniquely generated filament networks, each of which consisted of 138 filaments distributed among 16 prescribed perimeter nodes and 30 randomly placed interior nodes. Each filament connects two nodes. Error bars denote 95% confidence interval.
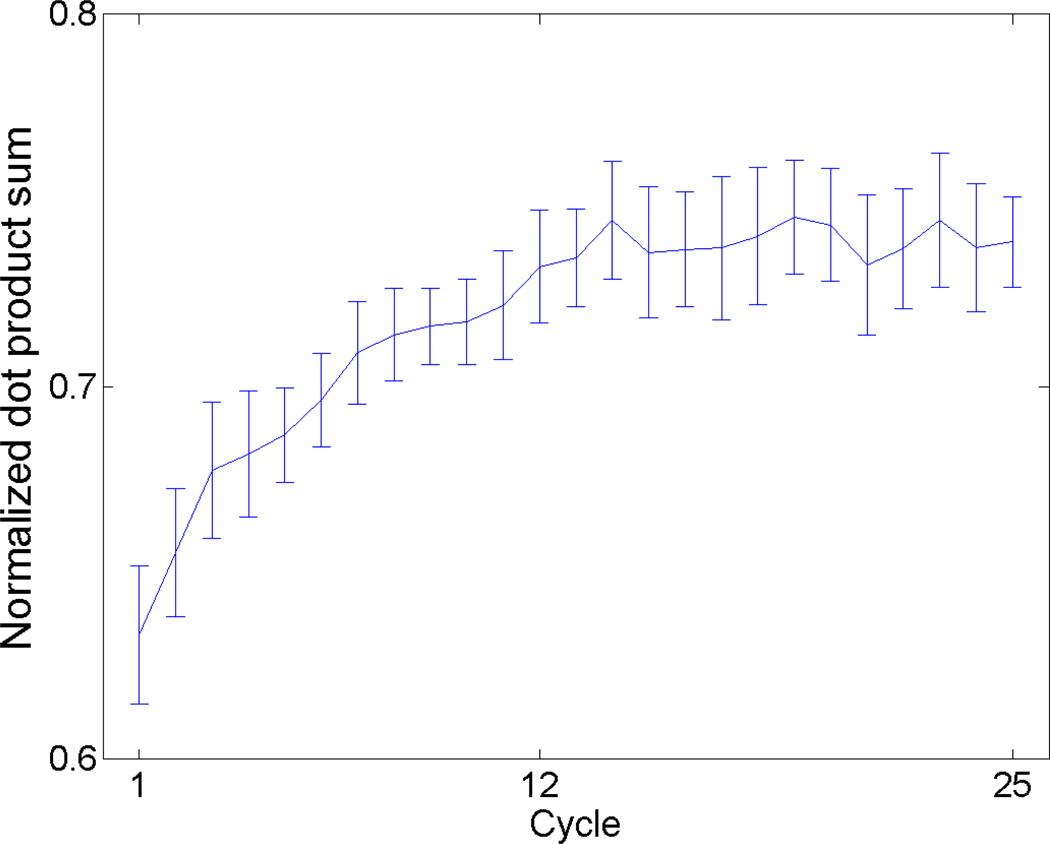
To quantify filament angle alignment over all cycles, we normalized all filament lengths to 1 and determined the dot products between each filament angle and the mean filament angle of the network. We calculated this normalized dot product for each cycle from 1 through 25 and averaged the results over ten uniquely generated 138-filament networks (Fig. 4). The normalized dot product increases immediately in the early cycles until a steady state is reached at approximately 14 cycles. The decision to normalize all filament lengths to 1 was made to allow equal representation among all filaments. If all of the 138 filaments aligned exactly with the filament network mean angle, the normalized dot product sum would be 1.0 for that cycle.
Figure 4.
Normalized dot product between filament angles and the filament network mean angle at nodal equilibrium over cycles 1–25. For each cycle, filament lengths were all assumed to equal 1 and the average dot product between each filament angle and the mean filament network angle were averaged over 10 uniquely generated networks. All filament lengths were normalized to 1 to maintain equal representation among all filaments. If all of the 138 filaments aligned exactly with the filament network mean angle, the normalized dot product sum would be 1.0 for that cycle. Error bars denote 95% confidence interval.
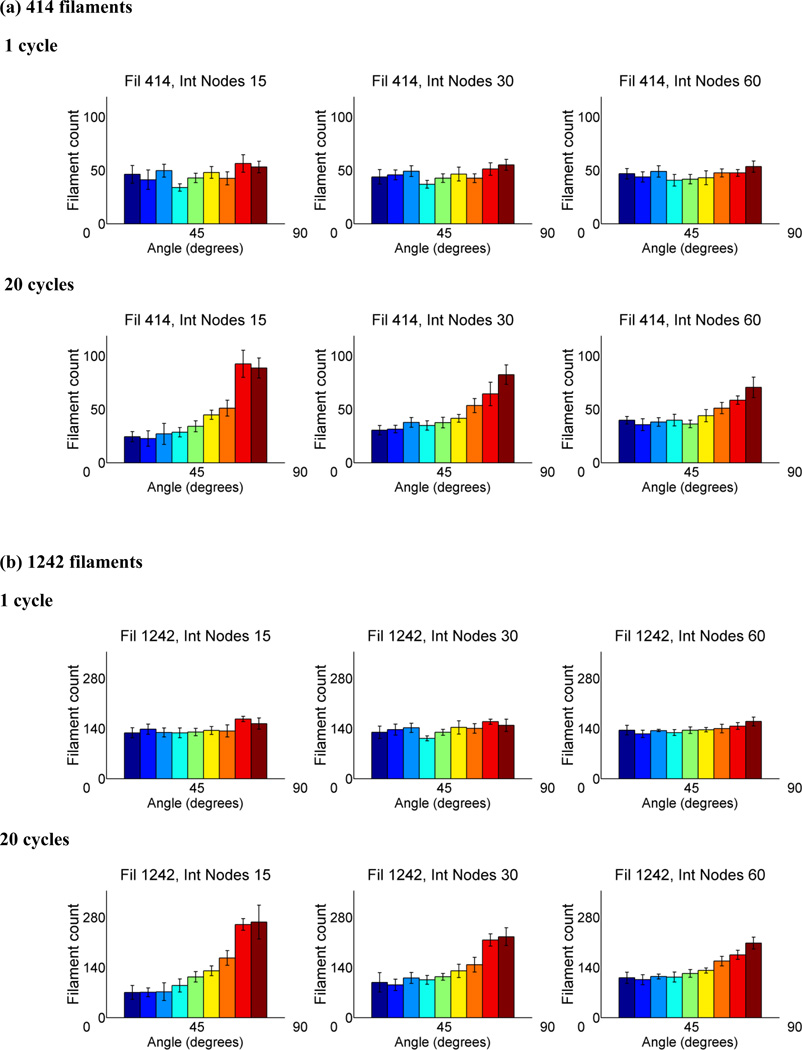
To determine the changes to our model under important parameters including filament number and internal node number, we increased the number of filaments to 414 and 1242 while varying the number of internal nodes between 15, 30, and 60. We tracked filament angle orientation and present the results at cycle 1 and 20 (Fig. 5). While there is no obvious alteration in filament orientation when increasing filament number, there is a slight shift towards vertical alignment when the number of internal nodes is decreased. We observed that with decreased number of internal nodes, more breakages occur while holding the filament number steady (data not shown). It is possible that fewer degrees of freedom to alleviate stress are causing higher filament strains when node number decreases, which subsequently leads to faster convergence to the perpendicularly aligned state.
Figure 5.
Histograms of angular orientation of filaments in nodal equilibrium after 1 cycle and 20 cycles for networks with (A) 414 and (B) 1242 filaments, which are 3 fold and 9 fold multiples of the previous filament number, 138. The number of internal nodes was varied as well from 15, 30, to 60 while peripheral nodes were held constant at 16. The results were averaged over eight uniquely generated filament networks. Error bars denote 95% confidence interval.
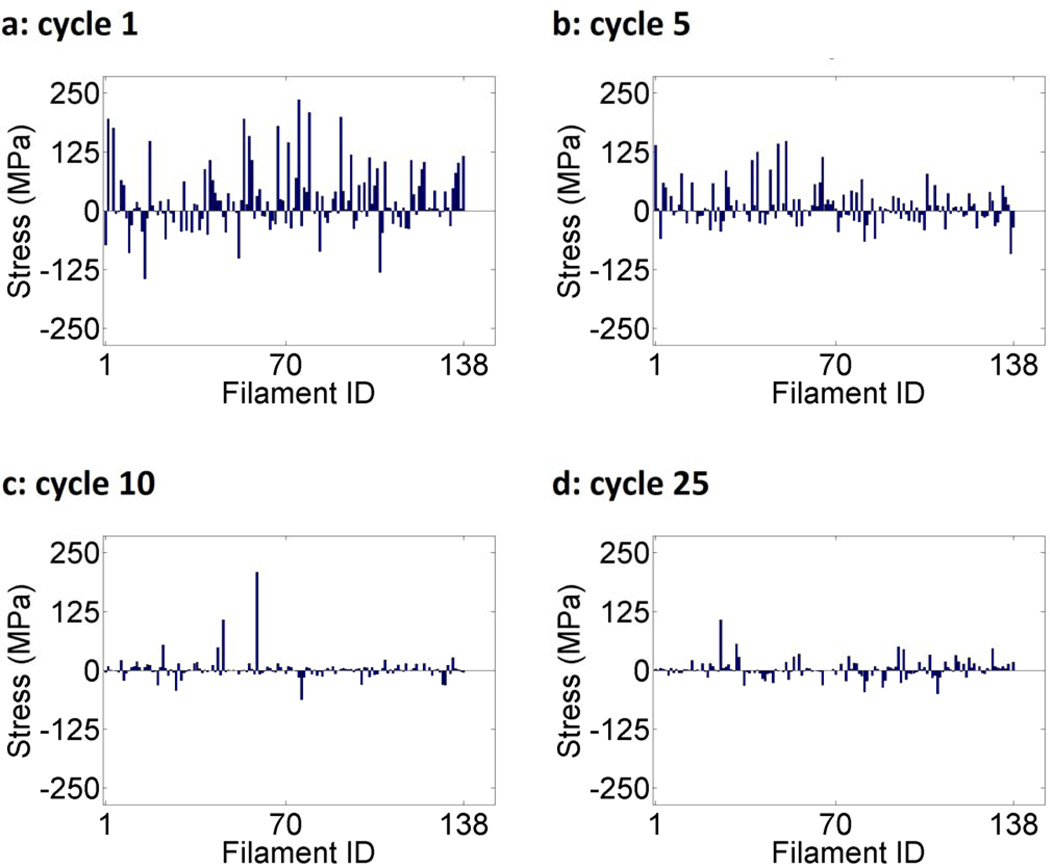
The filament stresses for each of the 138 filaments in the network for 1, 5, 10, and 25 cycles of stretching are analyzed (Fig. 6). Positive stress (i.e., tension) denotes an increase in the length of the filament relative to the start of the stretch cycle and negative stress (i.e., compression) denotes a decrease in length. As the cycle number increases in Figures 6a–d, a clear trend towards decreasing stress is observed. At cycle 1, the range of filament stresses is [−150,250] MPa. By cycle 9, this has been reduced to [−100,100] MPa and by cycle 25, the range is [−50,50] MPa with one outlier at 100 MPa. These results are non-obvious as the model implies that stresses in not only tension but also compression are reducing in this uniaxial stretch based approach.
Figure 6.
Individual filament stress values in nodal equilibrium for 138 filaments, 16 perimeter nodes, and 30 internal nodes after a network was stretched uniaxially by 10% for (a) 1, (b) 5, (c) 10, and (d) 25 cycles. Positive stress (i.e., tension) denotes an increase in the length of the filament relative to the length before the stretching cycle and negative stress (i.e., compression) denotes a decrease in length. At the end of each cycle, filament breakage probability was defined to be the absolute value of the strain normalized to the largest strain value.
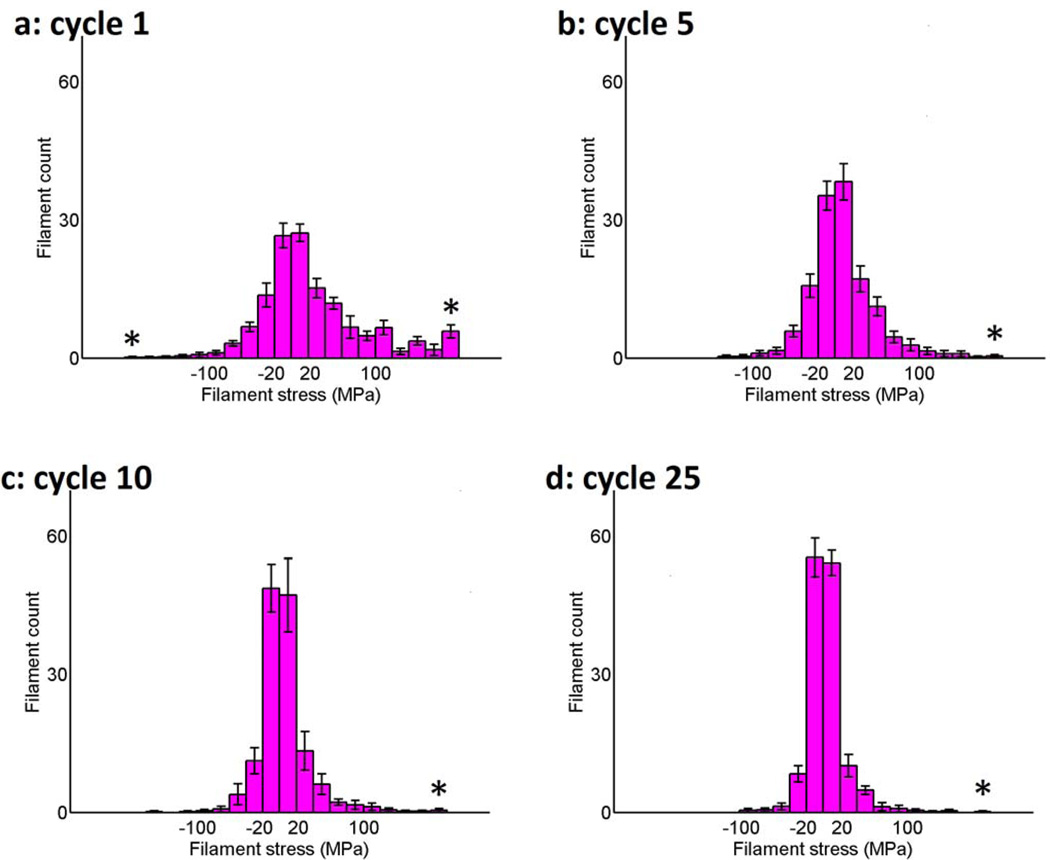
Figure 7 quantifies the filament stress through histograms comparing tensile (positive) and compressive (negative) stresses for 1, 5, 10, and 25 cycles of stretching. Each category bin covers a range of 10 MPa. The left-most and rightmost starred (*) bins contain filaments with stresses less than and greater than −190 and 190 MPa, respectively, as these contained much smaller numbers of filaments. Initially the filament stresses are relatively widely distributed but as the number of cycles increases, a shift to a much higher number of filaments in the bins of lower tension and compression occurs. This result is consistent with the results presented in Figure 6. The peak in the right-most bin for the 1st cycle in Figure 7(a) is the result of a large number of high-stress filaments initially in the network, which decreases with greater number of cycles (Fig. 7(b–d)).
Figure 7.
Histogram of filament stresses in nodal equilibrium after (a) 1, (b) 5, (c) 10, (d) 25 iterative cycles of 10% uniaxial stretch averaged over 10 uniquely generated filament networks of 138 filaments, 16 perimeter nodes, and 30 internal nodes. The starred (*) leftmost and rightmost bins contain filaments with stresses less or greater than −180 and 180 MPa, respectively. Positive stress (i.e., tension) denotes an increase in the length of the filament relative to that before each stretching cycle and negative stress (i.e., compression) denotes a decrease in length. Note the large rightmost bin in Figure 7(a) represents a large number of high-stress filaments initially present in the network, which decreases with additional cycles (Fig. 7(b–d)). Error bars denote 95% confidence interval.
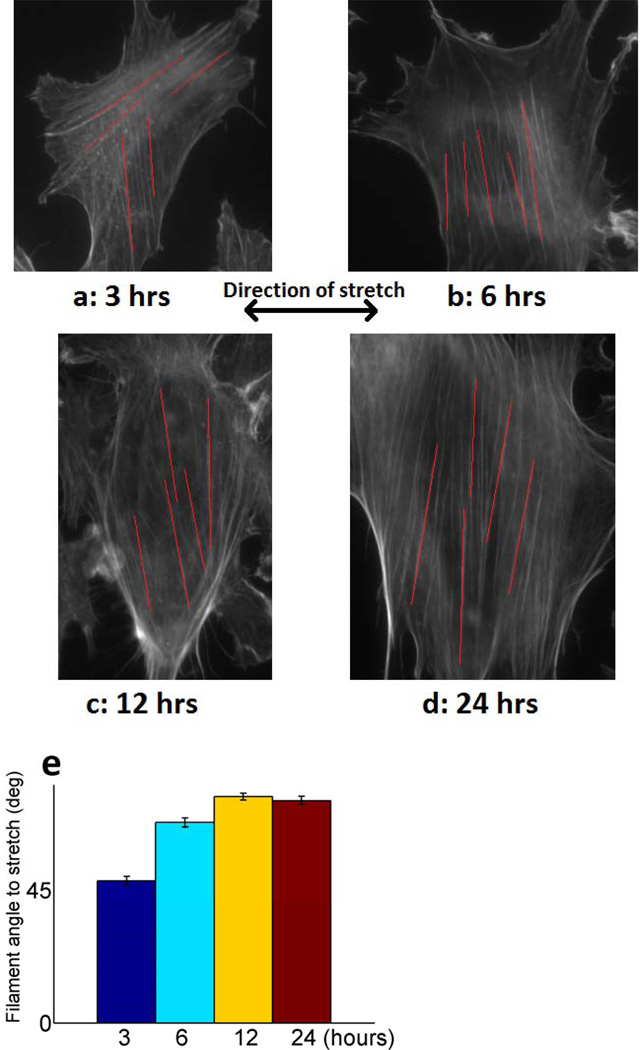
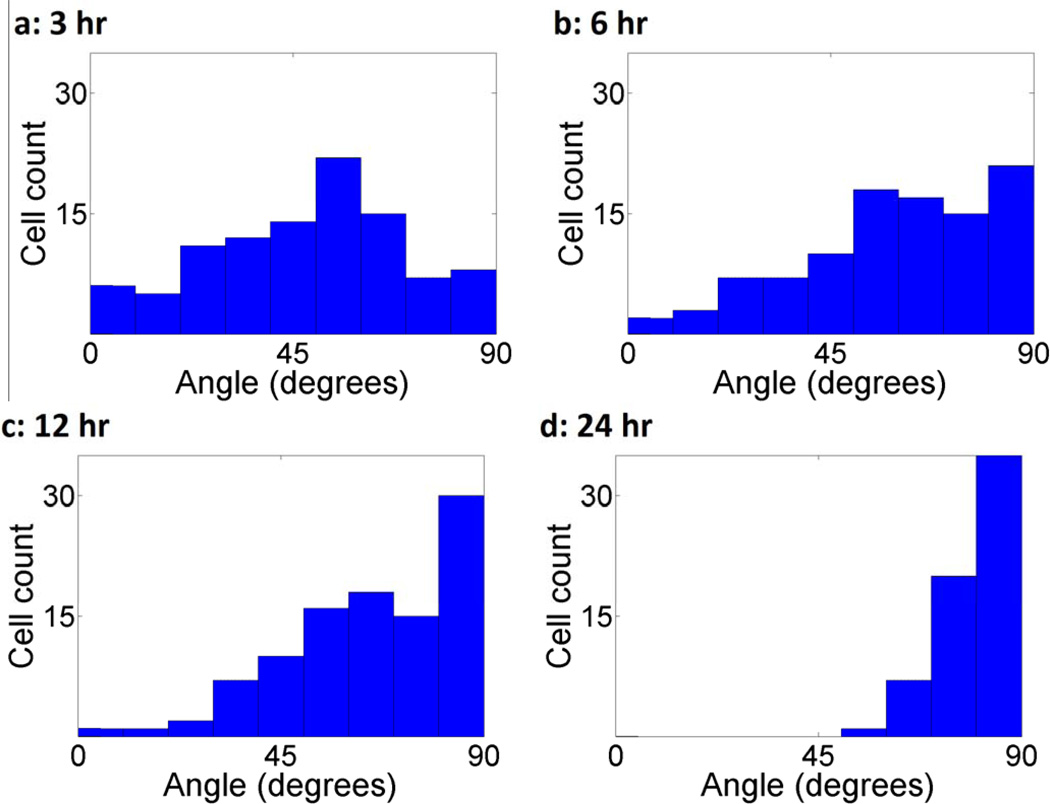
The orientation of cytoskeletal actin in NIH 3T3 fibroblasts exposed to 1 Hz cyclic uniaxial stretch after 3, 6, 12, and 24 hours was observed (Fig. 8a–d). The cells were strained using the elastomeric membrane, fixed with paraformaldahyde, and then labeled using 6 µM Alexa Flour® 488 phalloidin stain for F-actin (green pseudo-colored). The filament outlines were enhanced in software using the convolution feature in ImageJ. For each time point, the angles of ten representative filaments relative to that of the cyclic stretch were measured and their average computed (Fig 8e). At 3 hours, we see that prominent actin filaments are arranged both parallel to and perpendicular to the axis of stretch. Over time, with an increasing number of stretch cycles, steadily increasing F-actin alignment in the direction normal to stretch is observed. To further support our observations, we measured the orientation of whole cells at the same time points as whole cell orientation generally follows intracellular cytoskeletal alignment (see Fig. 8). This alignment is quantified showing a strong pattern moving toward vertical alignment (Fig. 9). These experimental results reflect the modeling results in Figure 3 and 4.
Figure 8.
Images of NIH 3T3 fibroblasts exposed to 1 Hz vertical cyclic stretch uniaxial stretching after (a) 3, (b) 6, (c) 12, (d) 24 hours. Red lines indicate representative actin filaments measured for angle relative to stretch direction. (e) Average filament angle relative to stretch direction at all time points. 5 filament angles were measured per clearly visible non-dividing cell. For the 3, 6, 12, 24 hour time points, we measured filaments in 47, 31, 22, and 10 cells, respectively. The cells were cultured on an elastomeric substrate, stretched, fixed with paraformaldahyde, and then stained with 6 µM Alexa Flour® 488 phalloidin stain for F-actin. These images were captured on an inverted Zeiss Axiovert optical microscope with a 63X high numerical aperture oil immersion objective. A fluorescein isothiocyanate (FITC) filter set allowed us to visualize the actin filaments. Error bars denote 95% confidence interval.
Figure 9.
Angular orientation histogram of NIH 3T3 fibroblasts after (a) 3, (b) 6, (c) 12, and (d) 24 hours of uniaxial horizontal cyclic stretch. Following mechanical stimulation, the cells were stained for F-actin and fluorescent images were imported into ImageJ software for analysis of actin filament orientation. Microfilament orientation was examined by fitting an ellipse to the cellular outline based upon an initial tracing of the cell periphery. A major and minor x' and y' axes was then defined on this ellipse. Actin filament orientation was then quantified by comparing the ellipse major axis orientation to the direction of uniaxial stretch. Only cells whose actin filaments exhibited a single orientation were used for analysis. 100 cells were sampled.
4. DISCUSSION
4.1 Filament alignment patterns
Through our computational simulations, we have shown that a minimal model of coupling of mechanics to a stress based approach results in a realignment of filament networks under cyclic stretching. Initially the filaments in the model are randomly oriented (Fig. 3a) but begin to exhibit a distinct alignment in the vertical direction as they experience additional cycles of stretching (Fig. 3b–d). Figure 4 clearly shows a trend towards filament co-alignment with further cycles. Taken together, Figures 3 and 4 show that under cyclic stretch, our model demonstrates not only gradual vertical alignment but also increased similarities in the distribution of filament angles. As shown in Figures 8 and 9, a comparable alignment in response to cyclic stress occurs in cultured cells. Initially, the cells show little alignment, but with increasing time, at 12 hours under uniaxial cyclic stimulation, the cytoskeletal actin and whole cell alignment of NIH 3T3 cells acquire a defined alignment in the vertical direction. This alignment begins to appear as early as 6 hours. Our model predicts this alignment by 25 cycles, which would correspond to approximately half a minute assuming a typical heart rate of 60 cycles per minute. We believe this discrepancy results from the fact that the probabilistic method of our network realignment algorithm forces at least one filament to break and reform on each iteration of energy relaxation, while the true system might pass through many cycles of stretching between filament breakages. In this regard, then, each cycle in our method can be considered to represent a sequence of potentially many cycles without any filament breakage culminating in a cycle in which some rearrangement occurs. This decision to effectively simulate only “eventful” rounds of cycling is needed because the computational cost of each individual cycle would make it prohibitive to directly simulate the tens of thousands of cycles needed to explicitly simulate every cycle of the true multi-hour time course of realignment. While the selective sampling procedure we use prevents us from attaching an explicit time scale to our simulations, we plan in future work to extend it using standard stochastic simulation methods to allow more realistic sampling of times between eventful cycles (Hsu et al., 2009; Rathinam et al., 2003; Slepoy et al., 2008).
4.2 Filament stress patterns and imposed strain
Along with the alignment perpendicular to the direction of cyclic stretch, the stress within the individual filaments was observed to decrease with increasing number of cycles. The alignment can be attributed in part to the model being stretched in the horizontal direction and the highest strains therefore occurring in the horizontally positioned filaments. There were, however, several further interesting and non-obvious findings. For the nodes from 80–100° and 260–280°, which were not fixed to the underlying substrate, the vertical filaments attached to these nodes could be expected to experience higher compressive strains similar to that experienced in a uniaxial stretch of a solid body obeying Poisson’s ratio, described as a simple elongation model (Wang et al., 2001). This, though, did not seem to be the case here. The stress plots suggest that both tensile (positive) and compressive (negative) stress levels proceeded toward a low baseline with more cycles of stretching (Fig. 6). Figure 7 quantifies this trend and, when taken with the alignment of the filaments, indicates that the filaments may have reorganized to minimize stress. However, if the filaments in compression were assigned a higher probability of breaking, as has been suggested in prior experimental work (Takemasa et al., 1998) , the final results may have been more biased towards an oblique alignment of the filaments. In addition, if all the perimeter nodes were fixed in a different initial configuration, the filament response may have differed. Furthermore, the results may be dependent on the total magnitude of stretching applied as experiments have shown that cell reorientation is primarily dependent on stretch magnitude as opposed to rate (Wang et al., 2001). A strain of 10% was used based on previous cellular and physiological experiments and conditions. For example, under normotensive conditions, stretch has been reported to be 9–12% in the aorta and 6–10% in the pulmonary arteries in humans (Luchsinger et al., 1962; Nakajima, 1968; Patel et al., 1962). In addition, arterial motion is predominantly in the circumferential direction with little longitudinal movement (Dobrin, 1978), which suggests that a uniaxial circumferential stretch model may accurately simulate physiological arterial stretch. Previous studies have demonstrated that cytoskeletal elasticity's relationship with frequency lies in two domains; at high frequencies >100 Hz, the elasticity is dependent on frequency with a universal exponent of 3/4 in a regime akin to semiflexible polymers whereas at lower frequencies the elasticity is relatively independent of frequency consistent with a soft-glass regime (Deng et al., 2006; Trepat et al., 2007). While our model is independent of frequency and these cytoskeletal elasticities relate to the whole cell rather than individual filaments, in the future, the alignment and stress patterns could be compared to empirical results after parameterizing the elastic modulus of our filaments for frequencies between 60–100Hz and beyond 100 Hz.
4.3 Filament breakage and reassembly
In our model, we normalize probabilities of filament breakage to the highest individual stress value of the given filament network. Our goal is to have a single measure that attempts to account of the variety of different filament responses that might occur at high stresses, including physical breaking and depolymerization. However, it has been shown in vitro that actin breakage might be more accurately modeled as occurring reliably at a threshold strain (Janmey et al., 1991) rather than probabilistically over a range of strains. This observation may hold in vivo as well. Our data shows the maximum stress averaged over 10 runs consistently is between 140 and 180 MPa with few exceptions after the 5th cycle (Cycle 16: 106 MPa; Cycle 20:127 MPa; Cycle 25:114 MPa). These data suggest that even though our model uses a relative probability for filament breakage, the model still is relatively effective at simulating pseudo-thresholds in these cycle ranges. In addition, new filaments are assumed to form instantaneously and independently of current fiber orientation or shape in our model. In reality, new filament formation may be more gradual and dependent on multiple factors including current cell orientation. It has been reported that endothelial elongation can drive filament orientation (Civelekoglu-Scholey et al., 2005). Conversely, stress fiber orientation has been suggested to drive endothelial cell elongation (Noria et al., 2004). An interesting result during reassembly that we observed in our simulations was when nodes moved outside the boundaries of the cell during the force equilibrium phases (see Movie S2). Our model was not formulated to constrain this from occurring and interestingly, this might have implications for cell motility as motility is directly related to polymerization of the actin cytoskeleton (Mitchison & Cramer, 1996). As our model is based on passive force balance, one factor that we have not modeled is the generation of active force by myosin motors. While it is known that myosin II is involved in unbundling individual actin filaments and their depolymerization, the functions of various myosins, actin turnover separate from actin-based motility is not well understood (Haviv et al., 2008) thus in this manuscript, we presented a minimalistic model without multiple layers of complexity. Additionally, while it is known that various focal adhesion and actin cross-linking proteins such as α-actinin and zyxin have different mechanical properties related to adhesion, motility and orientation (Ngu et al., 2010), in this current work, we are not modeling these specific differences in this minimalistic model.
5. CONCLUSION
We have developed a simulation model to investigate the response of actin filaments under mechanical stimulation. We present this minimalistic model to isolate observed behavior and test the sufficiency of a defined set of components critical to understanding complex biological systems, as modeling billions of molecules in single cells completely in terms of spatial and temporal organization will be far beyond computational resources for the foreseeable future. These minimal or coarse-grained models are in principal suited to understanding how mechanical stimulation influences actin cytoskeleton structure and dynamics. With this model, we are able test the hypothesis that a firstprinciples mechanical model of filament assembly in a confined space may be capable of yielding the remodeling behavior observed both experimentally and in vivo for cytoskeletal actin networks subjected to mechanical stimulation. We have found that the filaments in our model align preferentially in the vertical direction when experiencing cyclic horizontal stretching, which were similar to our experimental cyclic cell stretching responses. We also observed that the stress in the individual filaments decreased with the increasing numbers of stretch cycles, indicating that the aggregate behavior of this network can decrease the local stress in the individual filaments. While this is a simplified model of cell structure, it is intended to approach a minimal model to allow exploration of fundamental questions about the mechanisms underlying cytoskeleton rearrangement in response to mechanical stimulus that do not lend themselves to direct experimental investigation. It therefore contains only those mechanisms we propose to be necessary to the observed phenomena, in order to test whether those mechanisms specifically are sufficient to give the observed behaviors. Future directions of this work include correlating our simulation and experimental data to find an accurate physiological threshold stress, integrating multiple modes of mechanical stimulation, and linking these network responses to biochemical alterations. We believe this computational model in combination with experimental results will provide insight into a wide range of areas at the intersection of mechanics and biochemistry, including mechanobiology, material science, and polymer physics.
Supplementary Material
ACKNOWLEDGEMENTS
The authors thank Shlomo Ta'asan for his assistance in developing the iterative force balance algorithm in our computational actin network model. This work was supported in part by the National Science Foundation CAREER, NSF, and the Office of Naval Research.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
REFERENCES
- Alberts B. Molecular biology of the cell. 4th edit. New York: Garland Science; 2002. [Google Scholar]
- Bausch AR, Kroy K. A bottom-up approach to cell mechanics. Nat Phys. 2006;2(4):231–238. [Google Scholar]
- Cano ML, Lauffenburger DA, Zigmond SH. Kinetic analysis of F-actin depolymerization in polymorphonuclear leukocyte lysates indicates that chemoattractant stimulation increases actin filament number without altering the filament length distribution. J Cell Biol. 1991;115(3):677–687. doi: 10.1083/jcb.115.3.677. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen CS, Alonso JL, Ostuni E, Whitesides GM, Ingber DE. Cell shape provides global control of focal adhesion assembly. Biochem Biophys Res Commun. 2003;307(2):355–361. doi: 10.1016/s0006-291x(03)01165-3. [DOI] [PubMed] [Google Scholar]
- Chu JW, Voth GA. Coarse-grained modeling of the actin filament derived from atomistic-scale simulations. Biophys J. 2006;90(5):1572–1582. doi: 10.1529/biophysj.105.073924. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Civelekoglu-Scholey G, Orr AW, Novak I, Meister JJ, Schwartz MA, Mogilner A. Model of coupled transient changes of Rac, Rho, adhesions and stress fibers alignment in endothelial cells responding to shear stress. J Theor Biol. 2005;232(4):569–585. doi: 10.1016/j.jtbi.2004.09.004. [DOI] [PubMed] [Google Scholar]
- Civelekoglu G, Tardy Y, Meister JJ. Modeling actin filament reorganization in endothelial cells subjected to cyclic stretch. Bull Math Biol. 1998;60(6):1017–1037. doi: 10.1006/S0092-8240(98)90001-5. [DOI] [PubMed] [Google Scholar]
- Danciu TE, Gagari E, Adam RM, Damoulis PD, Freeman MR. Mechanical strain delivers anti-apoptotic and proliferative signals to gingival fibroblasts. J Dent Res. 2004;83(8):596–601. doi: 10.1177/154405910408300803. [DOI] [PubMed] [Google Scholar]
- Deng L, Trepat X, Butler JP, Millet E, Morgan KG, Weitz DA, Fredberg JJ. Fast and slow dynamics of the cytoskeleton. Nat Mater. 2006;5(8):636–640. doi: 10.1038/nmat1685. [DOI] [PubMed] [Google Scholar]
- DiDonna BA, Levine AJ. Filamin cross-linked semiflexible networks: fragility under strain. Phys Rev Lett. 2006;97(6):068104. doi: 10.1103/PhysRevLett.97.068104. [DOI] [PubMed] [Google Scholar]
- Dobrin PB. Mechanical properties of arterises. Physiol Rev. 1978;58(2):397–460. doi: 10.1152/physrev.1978.58.2.397. [DOI] [PubMed] [Google Scholar]
- Franke RP, Grafe M, Schnittler H, Seiffge D, Mittermayer C, Drenckhahn D. Induction of human vascular endothelial stress fibres by fluid shear stress. Nature. 1984;307(5952):648–649. doi: 10.1038/307648a0. [DOI] [PubMed] [Google Scholar]
- Hahn C, Schwartz MA. Mechanotransduction in vascular physiology and atherogenesis. Nat Rev Mol Cell Biol. 2009;10(1):53–62. doi: 10.1038/nrm2596. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haviv L, Gillo D, Backouche F, Bernheim-Groswasser A. A cytoskeletal demolition worker: myosin II acts as an actin depolymerization agent. J Mol Biol. 2008;375(2):325–330. doi: 10.1016/j.jmb.2007.09.066. [DOI] [PubMed] [Google Scholar]
- Hsu HJ, Lee CF, Kaunas R. A dynamic stochastic model of frequency-dependent stress fiber alignment induced by cyclic stretch. PLoS One. 2009;4(3):e4853. doi: 10.1371/journal.pone.0004853. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Isambert H, Venier P, Maggs AC, Fattoum A, Kassab R, Pantaloni D, Carlier MF. Flexibility of actin filaments derived from thermal fluctuations. Effect of bound nucleotide, phalloidin, and muscle regulatory proteins. J Biol Chem. 1995;270(19):11437–11444. doi: 10.1074/jbc.270.19.11437. [DOI] [PubMed] [Google Scholar]
- Janmey PA, Euteneuer U, Traub P, Schliwa M. Viscoelastic properties of vimentin compared with other filamentous biopolymer networks. J Cell Biol. 1991;113(1):155–160. doi: 10.1083/jcb.113.1.155. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Joshi SD, Webb K. Variation of cyclic strain parameters regulates development of elastic modulus in fibroblast/substrate constructs. J Orthop Res. 2008;26(8):1105–1113. doi: 10.1002/jor.20626. [DOI] [PubMed] [Google Scholar]
- Kim Y, Kuczenski B, LeDuc PR, Messner WC. Modulation of fluidic resistance and capacitance for long-term, high-speed feedback control of a microfluidic interface. Lab Chip. 2009;9(17):2603–2609. doi: 10.1039/b822423d. [DOI] [PubMed] [Google Scholar]
- Krendel M, Sgourdas G, Bonder EM. Disassembly of actin filaments leads to increased rate and frequency of mitochondrial movement along microtubules. Cell Motil Cytoskeleton. 1998;40(4):368–378. doi: 10.1002/(SICI)1097-0169(1998)40:4<368::AID-CM5>3.0.CO;2-7. [DOI] [PubMed] [Google Scholar]
- Kubicek JD, Brelsford S, Ahluwalia P, LeDuc PR. Integrated Lithographic Membranes and Surface Adhesion Chemistry for Three-Dimensional Cellular Stimulation. Langmuir. 2004;20(26):11552–11556. doi: 10.1021/la0487646. [DOI] [PubMed] [Google Scholar]
- Lee H, Ferrer JM, Nakamura F, Lang MJ, Kamm RD. Passive and active microrheology for cross-linked F-actin networks in vitro. Acta Biomater. 2010;6(4):1207–1218. doi: 10.1016/j.actbio.2009.10.044. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lu L, Oswald SJ, Ngu H, Yin FC. Mechanical properties of actin stress fibers in living cells. Biophys J. 2008;95(12):6060–6071. doi: 10.1529/biophysj.108.133462. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Luchsinger PC, Sachs M, Patel DJ. Pressure-radius relationship in large blood vessels of man. Circ Res. 1962;11:885–888. doi: 10.1161/01.res.11.5.885. [DOI] [PubMed] [Google Scholar]
- Ming D, Kong Y, Wu Y, Ma J. Simulation of F-actin filaments of several microns. Biophys J. 2003;85(1):27–35. doi: 10.1016/S0006-3495(03)74451-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mitchison TJ, Cramer LP. Actin-based cell motility and cell locomotion. Cell. 1996;84(3):371–379. doi: 10.1016/s0092-8674(00)81281-7. [DOI] [PubMed] [Google Scholar]
- Mitsui Y, Schneider EL. Relationship between cell replication and volume in senescent human diploid fibroblasts. Mech Ageing Dev. 1976;5(1):45–56. doi: 10.1016/0047-6374(76)90007-5. [DOI] [PubMed] [Google Scholar]
- Na S, Meininger GA, Humphrey JD. A theoretical model for F-actin remodeling in vascular smooth muscle cells subjected to cyclic stretch. J Theor Biol. 2007;246(1):87–99. doi: 10.1016/j.jtbi.2006.11.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nakajima H. Measurement of the normal and hypertensive heart and great vessels based on cardiosynchronous angiocardiography. Jpn Circ J. 1968;32(1):79–98. doi: 10.1253/jcj.32.79. [DOI] [PubMed] [Google Scholar]
- Ngu H, Feng Y, Lu L, Oswald SJ, Longmore GD, Yin FC. Effect of focal adhesion proteins on endothelial cell adhesion, motility and orientation response to cyclic strain. Ann Biomed Eng. 2010;38(1):208–222. doi: 10.1007/s10439-009-9826-7. [DOI] [PubMed] [Google Scholar]
- Noria S, Xu F, McCue S, Jones M, Gotlieb AI, Langille BL. Assembly and reorientation of stress fibers drives morphological changes to endothelial cells exposed to shear stress. Am J Pathol. 2004;164(4):1211–1223. doi: 10.1016/S0002-9440(10)63209-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ono S. Regulation of actin filament dynamics by actin depolymerizing factor/cofilin and actin-interacting protein 1: new blades for twisted filaments. Biochemistry. 2003;42(46):13363–13370. doi: 10.1021/bi034600x. [DOI] [PubMed] [Google Scholar]
- Palmer JS, Boyce MC. Constitutive modeling of the stress-strain behavior of F-actin filament networks. Acta Biomater. 2008;4(3):597–612. doi: 10.1016/j.actbio.2007.12.007. [DOI] [PubMed] [Google Scholar]
- Patel DJ, De Freitas FM, Mallos AJ. Mechanical function of the main pulmonary artery. J Appl Physiol. 1962;17:205–208. doi: 10.1152/jappl.1962.17.2.205. [DOI] [PubMed] [Google Scholar]
- Pender N, McCulloch CA. Quantification of actin polymerization in two human fibroblast sub-types responding to mechanical stretching. J Cell Sci. 1991;100(Pt 1):187–193. doi: 10.1242/jcs.100.1.187. [DOI] [PubMed] [Google Scholar]
- Rathinam M, Petzold LR, Cao Y, Gillespie DT. Stiffness in stochastic chemically reacting systems: The implicit tau-leaping method. The Journal of Chemical Physics. 2003;119(24):12784–12794. [Google Scholar]
- Satcher RL, Jr, Dewey CF., Jr Theoretical estimates of mechanical properties of the endothelial cell cytoskeleton. Biophys J. 1996;71(1):109–118. doi: 10.1016/S0006-3495(96)79206-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sato M, Ohashi T. Biorheological views of endothelial cell responses to mechanical stimuli. Biorheology. 2005;42(6):421–441. [PubMed] [Google Scholar]
- Silveira PS, Butler JP, Fredberg JJ. Length adaptation of airway smooth muscle: a stochastic model of cytoskeletal dynamics. J Appl Physiol. 2005;99(6):2087–2098. doi: 10.1152/japplphysiol.00159.2005. [DOI] [PubMed] [Google Scholar]
- Silveira PS, Fredberg JJ. Smooth muscle length adaptation and actin filament length: a network model of the cytoskeletal dysregulation. Can J Physiol Pharmacol. 2005;83(10):923–931. doi: 10.1139/y05-092. [DOI] [PubMed] [Google Scholar]
- Sipkema P, van der Linden PJ, Westerhof N, Yin FC. Effect of cyclic axial stretch of rat arteries on endothelial cytoskeletal morphology and vascular reactivity. J Biomech. 2003;36(5):653–659. doi: 10.1016/s0021-9290(02)00443-8. [DOI] [PubMed] [Google Scholar]
- Slepoy A, Thompson AP, Plimpton SJ. A constant-time kinetic Monte Carlo algorithm for simulation of large biochemical reaction networks. J Chem Phys. 2008;128(20):205101. doi: 10.1063/1.2919546. [DOI] [PubMed] [Google Scholar]
- Stamenovic D, Coughlin MF. A quantitative model of cellular elasticity based on tensegrity. J Biomech Eng. 2000;122(1):39–43. doi: 10.1115/1.429631. [DOI] [PubMed] [Google Scholar]
- Stamenovic D, Ingber DE. Models of cytoskeletal mechanics of adherent cells. Biomech Model Mechanobiol. 2002;1(1):95–108. doi: 10.1007/s10237-002-0009-9. [DOI] [PubMed] [Google Scholar]
- Stamenovic D, Wang N. Invited review: engineering approaches to cytoskeletal mechanics. J Appl Physiol. 2000;89(5):2085–2090. doi: 10.1152/jappl.2000.89.5.2085. [DOI] [PubMed] [Google Scholar]
- Suciu A, Civelekoglu G, Tardy Y, Meister JJ. Model for the alignment of actin filaments in endothelial cells subjected to fluid shear stress. Bull Math Biol. 1997;59(6):1029–1046. doi: 10.1007/BF02460100. [DOI] [PubMed] [Google Scholar]
- Swailes NT, Knight PJ, Peckham M. Actin filament organization in aligned prefusion myoblasts. Journal of Anatomy. 2004;205(5):381–391. doi: 10.1111/j.0021-8782.2004.00341.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Takemasa T, Yamaguchi T, Yamamoto Y, Sugimoto K, Yamashita K. Oblique alignment of stress fibers in cells reduces the mechanical stress in cyclically deforming fields. Eur J Cell Biol. 1998;77(2):91–99. doi: 10.1016/S0171-9335(98)80076-9. [DOI] [PubMed] [Google Scholar]
- Trepat X, Deng LH, An SS, Navajas D, Tschumperlin DJ, Gerthoffer WT, Butler JP, Fredberg JJ. Universal physical responses to stretch in the living cell. Nature. 2007;447(7144) doi: 10.1038/nature05824. 592-+. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tsuda Y, Yasutake H, Ishijima A, Yanagida T. Torsional rigidity of single actin filaments and actin-actin bond breaking force under torsion measured directly by in vitro micromanipulation. Proc Natl Acad Sci U S A. 1996;93(23):12937–12942. doi: 10.1073/pnas.93.23.12937. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang JH, Goldschmidt-Clermont P, Wille J, Yin FC. Specificity of endothelial cell reorientation in response to cyclic mechanical stretching. J Biomech. 2001;34(12):1563–1572. doi: 10.1016/s0021-9290(01)00150-6. [DOI] [PubMed] [Google Scholar]
- Wilhelm J, Frey E. Elasticity of stiff polymer networks. Phys Rev Lett. 2003;91(10):108103. doi: 10.1103/PhysRevLett.91.108103. [DOI] [PubMed] [Google Scholar]
- Wong AJ, Pollard TD, Herman IM. Actin filament stress fibers in vascular endothelial cells in vivo. Science. 1983;219(4586):867–869. doi: 10.1126/science.6681677. [DOI] [PubMed] [Google Scholar]
- Xu J, Casella JF, Pollard TD. Effect of capping protein, CapZ, on the length of actin filaments and mechanical properties of actin filament networks. Cell Motil Cytoskeleton. 1999;42(1):73–81. doi: 10.1002/(SICI)1097-0169(1999)42:1<73::AID-CM7>3.0.CO;2-Z. [DOI] [PubMed] [Google Scholar]
- Xu J, Wirtz D, Pollard TD. Dynamic cross-linking by alpha-actinin determines the mechanical properties of actin filament networks. J Biol Chem. 1998;273(16):9570–9576. doi: 10.1074/jbc.273.16.9570. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.