On the Performance of Local Density Approximation in Describing the Adsorption of Electron Donating/Accepting Molecules on Graphene

Abstract

In order to asses performance of the LDA in describing physisorption on graphene, adsorptions of TCNE, TCNQ, TNF, TTF, and DMPD as well as four benzene derivatives on C₅₄H₁₈ and C₁₁₀H₃₀ were explored with a variety of DFTs such as MPWB1K, M06-2X, PBE-D and LSDA. Although it is well known that the LDA considerably overestimate non-covalent interaction, the LSDA predicted adsorption energies except for TCNE on C₁₁₀H₃₀ are systematically lower than those from the M06-2X by 0.4–3.2 kcal/mol, and they are more significantly lower than those from the PBE-D for all the molecules by 3–6 kcal/mol. However, the LSDA adsorption energy sequence is consistent with that from the PBE-D, TNF~TCNQ>TCNE~DMPD>TTF. Moreover, the domain interaction between the electron donor and acceptor molecules with graphene through cooperative π···π, C-H···π and N-H···π were visualized with sign(λ₂)×ρ, and the relationships between the binding energy with London force, molecular electronegativity, and frontier orbital level were extensively discussed.

Introduction

Adsorptions of electron donor and acceptor molecules on graphene have attracted wide attention since the electronic property of graphene can be considerably changed by the physical functionalization. Analogous to silicon semiconductors with electrons doped by germanium or gallium, it is realized that graphene can exhibit similar properties of the n- and p-type semiconductors through adsorption of electron donating and accepting organic molecules, respectively.¹ Thus, it was proposed that graphene may become a new generation of semiconductor material in future.² Some authors recently reported their experimental results for the functionalized graphene with several organic molecules. Chen et al. performed angle-resolved photoemission spectroscopy experiment and showed the p-type doping effect of tetrafluoro-tetracyanoquinodimethane (F4-TCNQ) molecule for the functionalized graphene.^1a Varghese et al. investigated the interaction of electron donor and acceptor molecules with single-walled carbon nanotube (SWCNT) and graphene through isothermal titration calorimetry (ITC)³ and the trend in the relative binding energies was predicted for the molecules such as tetracyanoethylene (TCNE), tetracyanoquinodimethane (TCNQ), 2,4,7-trinitrofluorenone (TNF), tetrathiafulvalene (TTF), and N,N-dimethyl paraphenylenediamine (DMPD). Wang et al.^1b employed Kelvin probe force microscopy (KPFM) to investigate both n-type and p-type surface doping of exfoliated graphene by organic molecules vanadyl phthalocyanine (VPOC) and tetrafluoro-tetracyanoquinodimethane (F4-TCNQ), respectively. Barja et al. studied the intermolecular interaction between two electron acceptor molecules on graphene surface with scanning tunneling microscope (STM) image of the moiré pattern.⁴ They showed that the molecular ordering of TCNQ molecules on graphene is dominated by intermolecular attraction while repulsion determines the ordering for the F4-TCNQ.

In addition to the above experimental investigations, in the most recent years this subject was also explored by density functional theories; however, the most applied local spin density approximation (LSDA) or LDA, is well known to considerably overestimate physisorption or non-covalent interaction systems. Lu et al. studied the adsorption of TCNE on graphene with the LSDA.⁵ They demonstrated that p-type graphene can be obtained through TCNE adsorption with the binding energy of approximately 0.9 eV for a variety of adsorption configurations. Saha et al. applied both the LDA and GGA type of DFT (PBE) to the adsorptions of aniline (PhNH₂) and nitrobenzene (PhNO₂) on graphene.⁶ They predicted strong adsorptions by the LDA, e.g. the respective adsorption energies of 0.341 and 0.412eV for PhNH₂ and PhNO₂ on 5×5 graphene supercell; however, similar to its performance on other non-covalent systems the PBE brings about rather small binding. The LDA predicted an adsorption energy for F4-TCNQ on graphene was around 1.26 eV by Pinto et al.,⁷ 1.28eV by Sun et al.,⁸ yet 1.95eV by Tian et al.⁹ The binding energies obtained by the LDA for benzene (PhH) and TTF on graphene are 0.24 and 0.51 eV, respectively.¹⁰ For the adsorption of the TTF on graphene, its binding energy with the LDA obtained by Sun et al.⁸ is 0.72 eV, and those of TCNQ and F4-TCNQ on graphene are 1.15, and 1.28 eV, respectively. With the LDA the adsorption energies for PhH and naphthalene on graphene predicted by AlZahrani are 0.30 and 0.47 eV, respectively.¹¹ Most recently, Chi et al still applied the PBE to the adsorption of TCNE and TCNQ on graphene, and it is not surprising that the adsorption energies are only one fifth of the LDA predicted ones, 0.233 and 0.255 eV.¹² Besides the adsorption energies, the electron transfer between graphene and the organic molecules were also theoretically discussed. For example, the amounts of electron transferred from graphene are estimated to be 0.27–0.44e to TCNE,^5,12 and 0.263-0.34e to TCNQ,^8,12 and 0.07e to TTF.⁸ However, for the PhH and TTF on graphene Zhang et al.¹⁰ predicted that electrons are transferred from Ph-H and TTF to graphene with 0.02e and 0.26e, respectively, which is opposite to the previous result.⁸

Accordingly, there exists a controversy for both the binding energy and the electron transfer for the adsorptions of the electron donor and acceptor molecules on graphene. It is generally believed that the adsorptions are dominated by the non-covalent weak interactions, such as π···π and other weak C/N-H···π interactions, which are usually not well described by the LDA and GGA density functional theories. The novel hybrid meta-GGA functionals, M05-2X and M06-2x, developed by Truhlar et al ¹³ are proven to reasonably represent the non-covalent interactions. The Grimme’s empirical dispersion-corrected density functional theory (DFT-D), ¹⁴ has better performance on the noncovalent systems through directly accounting for long-range dispersion effects with a damped interatomic potential. Thus, one of the objectives of the present investigation is to assess the LDA method widely applied in aforementioned plane-wave calculations through comparing its results with those from the M06-2X and the DFT-D methods.

In addition, although theoretical and experimental studies on the adsorptions of the electron donors and acceptors on graphene were carried out, a relationship between electron transfer characteristics of adsorbates with their electronic structure properties such as IP, EA, and frontier orbital level has not yet been well established. It should be an important issue how to estimate electron withdrawing or donating capacity for molecules adsorbed on graphene. A good semiconductor material should have significant electronic transfer between the organic molecule and graphene, while on the other hand the interaction between the organic molecule and graphene should not essentially change π orbital framework of graphene. In order to better understand the relationship and to find some regulations to identify electronic donor and acceptor molecules, we systematically investigated the adsorption of a series of some organic molecules, including PhH, PhNH₂, PhOH, PhNO₂, TCNE, TTF, DMPD, TCNQ, and TNF, on graphene in the current study.

Graphene Model and Computational Method

Full optimizations and property calculations for the adsorptions of the organic molecules on graphene were performed with the MPWB1K,¹⁵, LSDA and M06-2X¹⁶ methods implemented in Gaussian09.¹⁷ The basis set superposition error¹⁸ (BSSE) of the intermolecular interaction was applied to the energy correction of the binding complexes. In addition, an empirical dispersion-corrected density functional theory (DFT-D) of Grimme’s scheme^14,19 was adopted for long-range dispersion effects in the noncovalent systems with the ORCA suite of programs.²⁰ Because of employing the Perdew-Burke-Ernzerhof (PBE) exchange-correlation functional²¹ in the DFT part of the Grimme’s scheme, the DFT-D method was therefore referred to as PBE-D. The above four calculation methods were carried out with Dunning’s correlation-consistent polarized valence basis sets (cc-pVDZ and cc-pVTZ).²² The adsorption energy is calculated by the equation: E_ads = E^A + E^B − E^AB, where AB, A and B respectively represent the optimized adsorption complex and the separate monomers. Charges carried by the electron donor and acceptor molecules, such as PhH, PhNH₂, PhOH, PhNO₂, TCNE, TTF, DMPD, TCNQ, and TNF, were calculated with electrostatic potential fitting scheme(CHelpG).²³ For the sake of comparison, London’s empirical formula²⁴ $E_{ab}^{\mathit{disp}}=-\frac{3{\alpha }_A{\alpha }_B{I}_A{I}_B}{4(I_A+I_B)R^6}$ may help understand the non-covalent interaction of the organic molecule with graphene. Here, α and I are the polarizability and ionization potential, respectively, for monomers A and B; R is the interplanar distance between A and B.

Two clusters C₅₄H₁₈ (G₅₄) and C₁₁₀H₃₀ (G110) were used to model graphene layer. The cluster models together with the hybrid meta-GGA method (M06-2X) implemented in Gaussian 09 and the PBE-D in ORCA, which may not be available in the plane-wave based DFT packages, will allow assessing the accuracy of the LDA method for the non-covalent adsorptions on graphene.

Results and Discussions

Geometry and Binding Energy

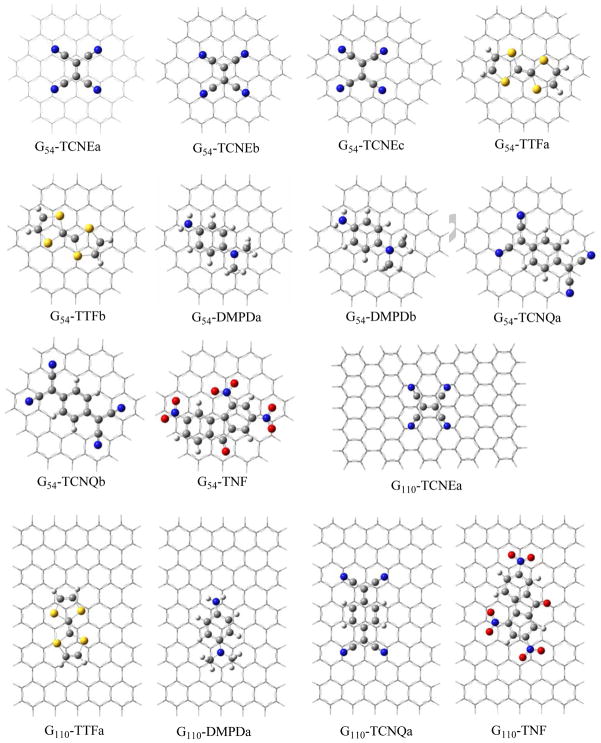
The fully optimized geometries for the adsorptions of TCNE, TTF, DMPD, TCNQ, and TNF on G₅₄ and G₁₁₀ with the MPWB1K, PBE-D, M06-2X, and LSDA methods are shown in Figure 1, and the adsorption energies are listed in Table 1. From the results of G₅₄ at the MPWB1K/cc-pVDZ level, it can be seen that the bridge type complexes (a) are more stable than other structures. For example, the adsorption energy of G₅₄-TCNE-a is greater than those of G₅₄-TCNE-b and G₅₄-TCNE-c by 0.8 and 2.2 kcal/mol, respectively; the adsorption energies of G₅₄-TTF-a, G₅₄-DMPD-a, and G₅₄-TCNQ-a are also 4.1, 0.9 and 3.2 kcal/mol higher than those of G₅₄-TTF-b, G₅₄-DMPD-b, G₅₄-TCNQ-b, respectively. Comparing with the result at the PBE-D/cc-pVDZ level, the MPWB1K only provides less than one half of the adsorption energy predicted by the PBE-D. Even after the BSSE correction is included at the PBE-D level, the adsorption energies of G₅₄-TCNE, G₅₄-TTF, and G₅₄-DMPD are still one time higher than the corresponding ones from the MPWB1K method. The BSSE corrections at the PBE-D/cc-pVDZ level are 3.5, 3.8, 4.6, 5.0, and 10.5kcal/mol for G₅₄-TCNE, G₅₄-TTF, G₅₄-DMPD, G₅₄-TCNQ, and G₅₄-TNF, respectively, which exhibits an increase with the size of the adsorbed organic molecule. Although the adsorption energies with the cc-pVTZ basis set without BSSE correction are improved about 1–5 kcal/mol over those with the cc-pVDZ basis set, there is only a slight variation of approximately 1 kcal/mol after the BSSE is included. Thus, with the BSSE correction the cc-pVDZ basis set is able to provide similar binding energies to those from the cc-pVTZ for the current systems. The most stable G₁₁₀-molecule adsorption complexes, i.e., bridge adsorptions were therefore calculated at the PBE-D, M06-2X and LSDA levels with the cc-pVDZ basis set. Due to more van der Waals contact, Table 1 shows that the BSSE corrected adsorption energies of G₁₁₀-TCNE-a, G₁₁₀-TTF-a, G₁₁₀-DMPD-a, G₁₁₀-TCNQ-a, and G₁₁₀-TNF are 3.1, 2.9, 1.1, 3.6, and 3.0 kcal/mol higher than those of G₅₄-TCNE-a, G₅₄-TTF-a, G₅₄-DMPD-a, G₅₄-TCNQa, and G₅₄-TNF, respectively, at the PBE-D/cc-pVDZ level. Although the cluster model is rather extended from G₅₄ to G₁₁₀ the adsorption energy only changes less than 10%. This trend is similar to that of the adsorption of DNA bases on the clusters C₂₄H₁₂ and C₅₄H₁₈.²⁵ The PBE-D predicted sequence of the adsorption energies on the both clusters is TNF (28.5 kcal/mol for G110) ~TCNQ (28.1) >DMPD (19.1)~TCNE (19.2)>TTF (17.4). However, the M06-2X method considerably underestimates the adsorption energy of G₁₁₀-TCNE-a so that the order reverses to be TNF (25.3 kcal/mol for G110) > TCNQ (23.0) > DMPD (18.1) > TTF (16.6) >TCNE (13.2). This implies that the M06-2X may be insufficient to describe the dispersion for the non-ring conjugated systems like the TCNE.

Figure 1.

Structures of adsorption complexes of TCNE, TTF, DMPD, TCNQ and TNF with C₅₄H₁₈ and C₁₁₀H₃₀. G₅₄ and G₁₁₀ represent C₅₄H₁₈ and C₁₁₀H₃₀, respectively.

Table 1.

Adsorption energies (E_ads, kcal/mol) with BSSE correction (E_ads+BSSE) for adsorptions of TCNE, TTF, DMPD, TCNQ, and TNF on C₅₄H₁₈ (G₅₄) and C₁₁₀H₃₀ (G₁₁₀) from theoretical methods

Complex	G54					G110							Literature LDA
	MPWB1K/cc-pVDZ	PBE-D/cc-pVDZ		PBE-D/cc-pVTZ		PBE-D/cc-pVDZ		M062x/cc-pVDZ		CPCM-M062x	LSDA/cc-pVDZ
	Eads	Eads	Eads+BSSE	Eads	Eads+BSSE	Eads	Eads+BSSE	Eads	Eads+BSSE	Eads	Eads	Eads+BSSE	Eads
Gx-TCNEa	9.3	19.6	16.1	18.7	17.7	22.3	19.2	16.1	13.2	14.0	19.4	15.8	21.3,a 5.4d
Gx-TCNEb	8.5
Gx-TCNEc	7.1
Gx-TTFa	10.6	18.3	14.5	15.9	14.8	21.3	17.4	20.2	16.6	17.7	17.9	13.5	16.6,b 11.8c
Gx-TTFb	6.5
Gx-DMPDa	9.4	22.6	18.0	19.5	17.7	24.7	19.1	22.8	18.1	24.1	20.8	15.3
Gx-DMPDb	8.5
Gx-TCNQa	14.2	29.5	24.5	25.9	24.5	33.6	28.1	27.6	23.0	25.6	28.5	22.6	26.5,b 5.9d
Gx-TCNQb	11.0
Gx-TNF	21.1	35.7	25.2	29.9	26.3	39.7	28.5	35.5	25.3	37.2	32.9	22.1

^aRef.5;

^bRef. 8;

^cRef.10;

^dRef. 12

Comparing the result of the PBE-D method with those of the M06-2X method for G₁₁₀ in Table 1, the BSSE corrected adsorption energies of G₁₁₀-TCNE-a, G₁₁₀-TTF-a, G₁₁₀-DMPD-a, G₁₁₀-TCNQ-a, and G₁₁₀-TNF at the M06-2X level are 6.0, 0.8, 1.0, 5.1, and 3.2 kcal/mol less than the corresponding ones at the PBE-D level. Obviously, the M06-2X estimation slightly deviates from the PBE-D result for G₁₁₀-TTF-a, G₁₁₀-DMPD-a; however, it provides considerably weaker binding for G₁₁₀-TCNE-a, G₁₁₀-TCNQ-a and G₁₁₀-TNF so that the binding sequence is different from what is predicted by the PBE-D as aforementioned. The solvent effect in the aqueous solution on these five adsorption systems was estimated with the conductor-like polarizable continuum model (CPCM) at the M06-2X/cc-pVDZ level. Because of low polarity of the molecules, as expected the solvent effects only change the binding energies by 1–2 kcal/mol. For example, the dipole moments of the molecules TNF and DMPD at M06-2X/cc-pVDZ level are only 1.083 and 0.158 Debye, respectively; while the dipole moments of the high symmetric molecules, TCNE, TCNQ and TTF, are almost negligible.

Performance of LSDA/LDA

The five adsorption complexes were fully optimized at the LSDA level of theory implemented in Gaussian program with the cc-pVDZ basis set. Although it is well known that the LDA considerably overestimate non-covalent interaction, Table 1 shows that the BSSE corrected adsorption energies of G₁₁₀-TCNE-a, G₁₁₀-TTF-a, G₁₁₀-DMPD-a, G₁₁₀-TCNQ-a, and G₁₁₀-TNF at the LSDA level are systematically less than the corresponding ones at the PBE-D level by 3.4, 3.9, 3.8, 5.5, and 6.4 kcal/mol, respectively. The deviation is in the range of 13–22%. It can be seen that the LSDA result has slightly bigger deviation than that of M06-2x except for the G₁₁₀-TCNE-a adsorption complex, which is up to 31% at the M06-2X level. However, the sequence of the adsorption energies at the LSDA level is same as that at the PBE-D level, TNF (22.1 kcal/mol for G110)~TCNQ (22.6) >DMPD (15.3)~TCNE (15.8)>TTF (13.5).

Most of the previous adsorption energies for TCNE, TTF and TCNQ on graphene were achieved by the LSDA together with ultrasoft pseudopotential plane-wave basis and periodic boundary condition. In general, the binding energies from the periodic LSDA agree well in 1–2 kcal/mol with those from the present PBE-D with the cluster model, G₁₁₀. For the TCNE-graphene the Lu’s binding energy 21.3 kcal/mol ⁵ is 2.1 kcal/mol bigger than the current PBE-D result (21.3 vs 19.2 kcal/mol), and 8.1 and 5.5 kcal/mol bigger than the M06-2X and LSDA values, respectively. For TTF-graphene, Zhang et al.¹⁰ and Sun et al.⁸ reported their theoretical values, 11.8 and 16.6 kcal/mol. The latter one is the same as the M06-2X result and only 0.8 kcal/mol less than the PBE-D result (17.4 kcal/mol). In the same publication, Sun et al.⁸ also reported the adsorption energy of TCNQ-graphene, 26.5 kcal/mol, which is 3.5 kcal/mol higher than the M062x value and 1.6 kcal/mol less than the PBE-D one. However, Chi et al. considerably underestimated the adsorption energies for TCNE and TCNQ on graphene (5.4 and 5.9kcal/mol) with the PBE method although a 8×8 graphene supercell (128 carbon atoms per graphene layer) was used.¹²

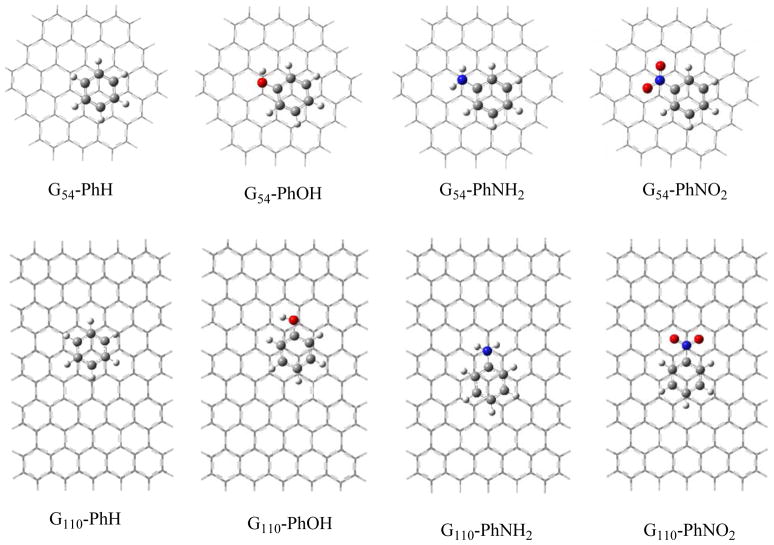
In addition to the above five organic molecules, the binding of benzene and three derivatives (PhNH₂, PhOH, and PhNO₂) with graphene clusters (G₅₄ and G₁₁₀) are also calculated at MPWB1K and M06-2X levels, respectively. The geometries of these adsorption complexes are shown in Figure 2 and their adsorption energies are listed in Table 2. It can be seen that the adsorption energies at the MPWB1K level are only a half of those at the M06-2X level, similar to the case of the above five adsorption complexes. At the M062X level the BSSE corrected adsorption energies of G₁₁₀-PhH, G₁₁₀-PhOH, G₁₁₀-PhNH₂, and G₁₁₀-PhNO₂ are 8.0, 8.9, 8.6, and11.0 kcal/mol, respectively. According to Table 2 the binding energies are slightly higher than the previous values predicted by the periodic LDA density functional theory with pseudopotential. For example, for PhH-graphene Zhang’s ¹⁰ and AlZahrani’s¹¹ binding energies are lower than the current one from the M06-2X by 2.5 and 1.1 kcal/mol, respectively (5.5 and 6.9 vs 8.0 kcal/mol); Saha’s ⁶ respective values for the PhNH₂-graphene and PhNO₂-graphene are 7.9 and 9.5 kcal/mol, which deviate from the current M06-2X results in the range of 0.7–2.5 kcal/mol.

Figure 2.

Top views of structures for adsorption complexes of PhH, PhOH, PhNH₂ and PhNO₂ with C₅₄H₁₈ and C₁₁₀H₃₀. G₅₄ and G₁₁₀ represent C₅₄H₁₈ and C₁₁₀H₃₀, respectively.

Table 2.

Adsorption energies (E_ads, kcal/mol) with BBSE correction (E_ads+BSSE) for adsorptions of PhH, PhOH, PhNH₂, and PhNO₂ on C₅₄H₁₈ (G₅₄) with MPWB1K nd C₁₁₀H₃₀ (G₁₁₀) with M06-2X.

Comlex	G54	G110		LDA
	MPWB1K/6-31G(d)	M06-2x/cc-pVDZ
	Eads	Eads	Eads+BSSE
Gx-PhH	4.0	9.9	8.0	5.5,a 6.9b
Gx-PhOH	4.0	11.9	8.9
Gx-PhNH2	5.3	11.5	8.6	7.9c
Gx-PhNO2	6.6	15.1	11.0	9.5c

^aRef.¹⁰;

^bRef.¹¹;

^cRef.⁶

Correlation of binding energy with London dispersion, and polarizability

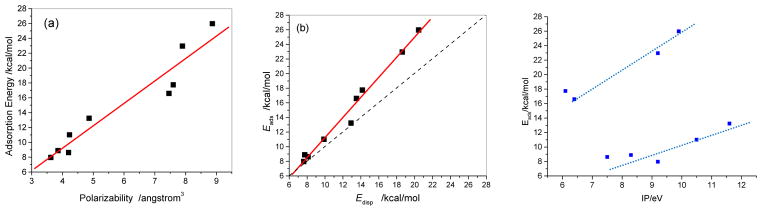
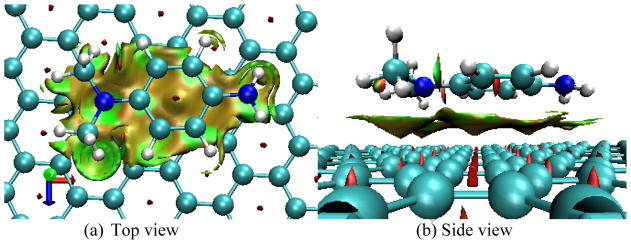
Table 3 lists the interplanar distances between adsorbed molecules and graphene, adsorption energies, London dispersion energies, and the charges carried by the adsorbed molecules in the adsorption complexes at the M062x/cc-pVDZ level. According to Table 3, all of the interplanar distances are approximately 3.2 Å. For G₁₁₀-PhNO₂, G₁₁₀-TCNE, G₁₁₀-TCNQ, and G₁₁₀-TNF the distances are slightly less than 3.2 Å while the others are slightly larger than 3.2 Å. This small variation may be caused by the electron accepting and donating groups in the adsorbed organic molecules. Comparing the charges carried by the adsorbed molecules, PhNO₂, TCNE, TCNQ, and TNF carry considerable negative charge with −0.0680e, −0.1337e, −0.2144e, and −0.1477e, respectively, implying that partial electrons are transferred from graphene to these molecules and the basic planar structure of graphene keeps almost invariance. The similar E_ads and E_disp in Table 3 imply that the adsorption interaction dominantly arises from the dispersion. One can further see that the plot of E_ads versus E_disp in Figure 4b exhibits a good linear relationship with a slope of 1.2 and a correlation coefficient of 0.9918. The deviation from the diagonal line (dashed line in Figure 4b) becomes gradually significant with E_disp increasing. Especially for G₁₁₀-TTF-a, G₁₁₀-DMPD-a, G₁₁₀-TCNQ-a, and G₁₁₀-TNF E_ads are 3.1, 3.6, 4.3, and 5.5 kcal/mol higher than E_disp, respectively, which indicates that the strong adsorbed molecule enhances its electrostatic interaction with graphene. Figure 3, the isosurface of sign(λ₂)×ρ defined by Yang et al.,²⁶ of the G₁₁₀-DMPD adsorption complex provides a clear visualization of the van der Waals interaction between graphene and DMPD. According to the color code that green shows vdW interaction and red strong nonbonded overlap, vdW interaction between DMPD and graphene is very obvious via cooperative π···π, N-H···π as well as C-H···π. The sign(λ₂)×ρ isosurfaces for G₁₁₀-TCNE and G₁₁₀-TTF were provided as the supporting information.

Table 3.

Vertical separation (R), adsorption energies (E_ads), and dispersion energies ( $E_{\mathit{disp}}=-E_{ab}^{\mathit{disp}}$) of adsorption complexes and CHelpG net charges (q) of adsorbed monomer parts on graphene (C₁₁₀H₃₀) at M062x/cc-pVDZ level.

Complex	R/Ǻ	Eads/kcal/mol	Edisp/kcal/mol	q/e
G110-PhH	3.230	7.96	7.63	−0.0547
G110-PhOH	3.237	8.89	7.74	−0.0516
G110-PhNH2	3.238	8.62	8.11	−0.0092
G110-PhNO2	3.196	11.01	9.88	−0.0680
G110-TCNE	3.144	13.23	12.90	−0.1337
G110-TTF	3.237	16.59	13.51	−0.0450
G110-DMPD	3.210	17.74	14.17	0.0712
G110-TCNQ	3.170	22.95	18.62	−0.2144
G110-TNF	3.193	25.97	20.45	−0.1477

Figure 4.

Correlation of adsorption energy with polarizability (a), dispersion energy (b), and adiabatic IP (c). Solid squares are the calculated points and the red lines are linear fitting.

Figure 3.

Reduced density gradient isosurface (0.5 au) for G₁₁₀-DMPD. Green and yellow indicates vdW interaction and red strong nonbonded overlap.

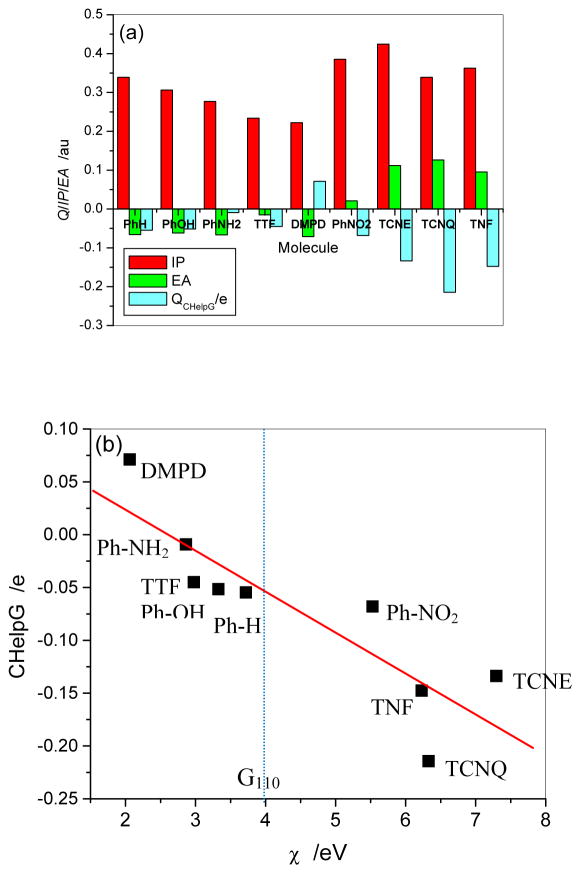
In addition, the correlation between E_ads and adiabatic ionization potential IP and polarizability (α) of the electron donors and acceptors were searched for. As shown in Figure 4c, it seems that the E_ads respectively correlates with the IP of four benzene derivates and another five organic molecules. However, it is found that the E_ads directly relates to α of the organic molecules perpendicular to the molecular plane. Figure 4(a) well demonstrates that E_ads linearly correlates (correlation coefficient 0.9584) with the polarizability of the organic molecule, positively depending on the polarizability of the organic molecule.

Electron transfer with molecular electronegativity and frontier orbital level

Table 4 summarizes the IP, electron affinity (EA), and HOMO and LUMO calculated at the M06-2X/cc-pVDZ level. For the IP of a molecule, the larger the ionization potential, the more difficult the molecule loses its electron to form a cation. However, the positive electron affinity makes a molecule obtain an electron easily to form an anion. The four molecules PhNO₂, TCNE, TCNQ, and TNF clearly exhibit electron acceptor property because of their larger IP values and positive EA values. From the IP and EA of C₁₁₀H₃₀, one can see that the graphene would have dual properties as electron donor as well as acceptor because of its low IP value (4.5270 eV) and positive EA (3.4630 eV). Figure 5(a) intuitively shows the CHelpG charges carried by the adsorbed molecules in adsorption complexes, the IP and EA of the organic molecules. It is obvious to see that partial electrons are transferred from graphene to the four molecules with positive EA, PhNO₂, TCNE, TCNQ, and TNF. DMPD exhibits electron donor property because of high negative EA and relative low IP, only transferring a small amount of electron to graphene. Because of high positive IP and negative EA, other molecules (PhH, PhOH, PhNH₂, and TTF) on graphene appear a negligible electron withdrawing property, which shows they hardly modify graphene to become n-type or p-type semiconductor. This prediction is consistent with the previous theoretical results,^5,8 but it is different from Zhang’s theoretical result for TTF,¹⁰ which showed that TTF is a good electron donator.

Table 4.

Ionization potential (IP), electron affinity (EA), polarizability (α), electronegativity (χ=(IP+EA)/2), and HOMO and LUMO of interacting monomers calculated at M062x/cc-pVDZ level.

species	IP/eV	EA/eV	χ/eV	α/Å3	εHOMO/au	εLUMO/au
PhH	9.2288	−1.7910	3.7189	3.6236	−0.30382	0.03115
PhOH	8.3321	−1.6782	3.3269	3.8562	−0.27477	0.02901
PhNH2	7.5354	−1.8091	2.8631	4.1986	−0.25340	0.03623
PhNO2	10.4878	0.5676	5.5277	4.2298	−0.33466	−0.04646
TCNE	11.5503	3.0390	7.2946	4.8651	−0.39017	−0.14781
TTF	6.3633	−0.4133	2.9750	7.4591	−0.21126	0.00752
DMPD	6.0516	−1.9320	2.0598	7.6000	−0.19928	0.04506
TCNQ	9.2256	3.4317	6.3286	7.8983	−0.31521	−0.15073
TNF	9.8615	2.5976	6.2295	8.8690	−0.34291	−0.11547
C110H30	4.5270	3.4630	3.9950	45.5361	−0.15497	−0.13978

Figure 5.

(a) CHelpG charges of adsorbed molecule in adsorption complex and adiabatic inonization potential (IP) and electron affinity (EA) for monomers of organic molecules (b) CHelpG charges of adsorbed molecule in adsorption complex with electronegativities (χ) of organic molecules.

Moreover, to unify the effects of IP and EA on electron transfer the molecular electronegativity was defined as χ IP+EA 2. It is interesting to see that the four electron acceptors (TCNE, TCNQ, TNF and Ph-NO₂) have higher χ than the graphene, and oppositely other electron donators (Ph-H, Ph-OH, TTF, Ph-NH₂, and DMPD) have lower χ than the graphene. As shown in Figure 5b, the charge carried by the molecules also shows a good linear relationship with the electronegativity (correlation coefficient of 0.8709). Thus, molecular electronegativity χ can be used as an index to predict electron transfer property, and further n- and p-type semiconductors for the functionalized graphenes.

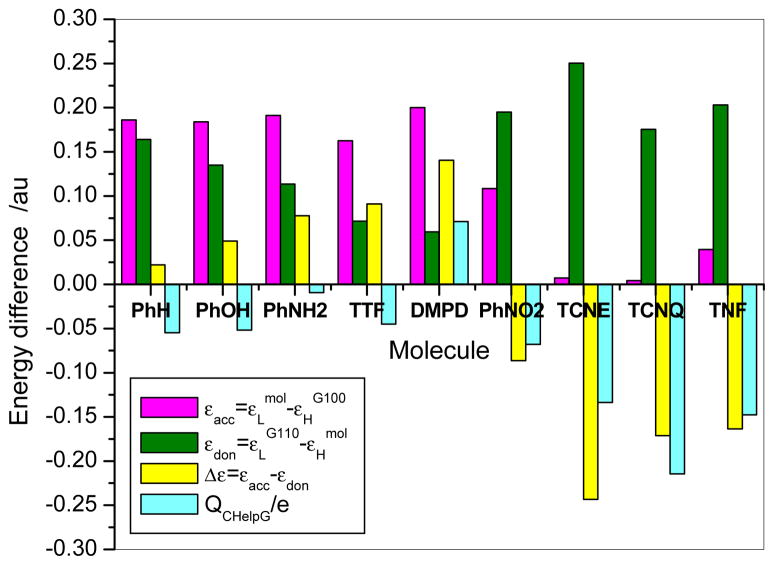
Figure 6 presents the molecular accepting and donating capacities (q/e), and the defined factors: ${\epsilon }_{\mathit{acc}}={\epsilon }_L^{\mathit{mol}}-{\epsilon }_H^{G110}$ and ${\epsilon }_{\mathit{don}}={\epsilon }_L^{G110}-{\epsilon }_H^{\mathit{mol}}$. Here, ε_L^mol and ε_H^mol respectively are the HOMO and LUMO orbital energies of an organic molecule, while ε_L^G110 and ε_H^G110 are those of graphene C₁₁₀. Apparently, the electron transfer is determined by the competence of ε_acc with ε_don. If ε_acc < ε_don, the organic molecule will be an electron acceptor, otherwise it will be a donator. Thus, to simply correlate electron transfer and frontier orbital energy we define Δε = ε_acc − ε_don. The more negative Δε, the easier a molecule accepts electrons; while the more positive Δε, the easier a molecule donates electrons. Figure 6 clearly shows that the considerable negative Δε of Ph-NO₂, TCNE, TCNQ, and TNF agrees excellently with the charge (q) accepting from the graphene. In contrary, the high positive Δε value of DMPD is also good consistent with the charge (q) donating to the graphene. It is apparently to see that the former four molecules might make graphene become a p-type semiconductor and the latter one could make graphene an n-type one.

Figure 6.

CHelpG charges of adsorbed molecule in adsorption complex and difference of frontier orbital energy levels for monomers of organic molecules and graphene at M06-2x/cc-pVDZ level. ε_L^mol and ε_H^mol, LUMO and HOMO orbital energy of organic molecule; ε_L^G110 and ε_H^G110, LUMO and HOMO orbital energy of graphene.

Conclusion

Using a variety of DFT methods such as MPWB1K, M06-2X, PBE-D and LSDA, the adsorptions of TCNE, TCNQ, TNF, TTF, DMPD as well as four benzene derivatives on C₅₄H₁₈ and C₁₁₀H₃₀ were extensively investigated. Although it is well known that the LSDA considerably overestimate non-covalent interaction, the LSDA predicted adsorption energies for the above organic molecules except for TCNE on C₁₁₀H₃₀ are systematically lower than those from the M06-2X by 0.4–3.2 kcal/mol, and they are more significantly lower than those from the PBE-D for TCNE, TTF, DMPD, TCNQ, and TNF by 3.4, 3.9, 3.8, 5.5, and 6.4 kcal/mol, respectively. However, the LSDA adsorption energy sequence is consistent with that from the PBE-D, TNF~TCNQ>TCNE~DMPD>TTF. Thus, regarding the DFT methods for describing physisorption or noncovalent interaction on pristine graphene layer it can be concluded that the GGA methods are indeed improper; the LDA or LSDA method underestimates the weak interactions to some extent; M06-2X performs slightly better than the LDA; however, the dispersion correction is essential to further quantitatively improve the theoretical results. Remarkably, it was found that the adsorption energies well linearly correlate with London dispersion and polarizability rather than ionization potential, indicating that the dominant interaction between the electron donor and acceptor molecules with graphene is van der Waals interaction through cooperative π···π, C-H···π and N-H···π, which are well visualized with sign(λ₂)×ρ. In addition, molecular electronegativity χ can be used as an index to predict electron transfer property, and further n- and p-type semiconductors for the functionalized graphenes. The bigger the electronegativity χ, the more electron the organic molecules will accept from graphene. As for Δε, the higher the negative Δε, the easier the organic molecules will gain electron from graphene. The PhNO₂, TCNE, TCNQ, and TNF molecules therefore exhibit strong electron acceptors, while the DMPD molecule acts as an electron donator. However, the PhH, PhOH, PhNH₂, and TTF molecules only show rather low electron withdrawing property.