Abstract
Deep brain stimulation (DBS) has expanded as an effective treatment for motor disorders, providing a valuable opportunity for intraoperative recording of the spiking activity of subcortical neurons. The properties of these neurons and their potential utility in neuroprosthetic applications are not completely understood. During DBS surgeries in 25 human patients with either essential tremor or Parkinson's disease, we acutely recorded the single-unit activity of 274 ventral intermediate/ventral oralis posterior motor thalamus (Vim/Vop) neurons and 123 subthalamic nucleus (STN) neurons. These subcortical neuronal ensembles (up to 23 neurons sampled simultaneously) were recorded while the patients performed a target-tracking motor task using a cursor controlled by a haptic glove. We observed that modulations in firing rate of a substantial number of neurons in both Vim/Vop and STN represented target onset, movement onset/direction, and hand tremor. Neurons in both areas exhibited rhythmic oscillations and pairwise synchrony. Notably, all tremor-associated neurons exhibited synchrony within the ensemble. The data further indicate that oscillatory (likely pathological) neurons and behaviorally tuned neurons are not distinct but rather form overlapping sets. Whereas previous studies have reported a linear relationship between power spectra of neuronal oscillations and hand tremor, we report a nonlinear relationship suggestive of complex encoding schemes. Even in the presence of this pathological activity, linear models were able to extract motor parameters from ensemble discharges. Based on these findings, we propose that chronic multielectrode recordings from Vim/Vop and STN could prove useful for further studying, monitoring, and even treating motor disorders.
Introduction
Neurosurgical implantation of deep brain stimulation (DBS) electrodes is an efficacious treatment for both Parkinson's disease (PD) and essential tremor (ET) (Ondo et al., 1998; Koller et al., 2001; Kumar et al., 2003; Rodriguez-Oroz et al., 2005; Deuschl et al., 2006). Common DBS targets include the subthalamic nucleus (STN; for PD patients) and the ventral intermediate nucleus of thalamus (Vim; for ET patients). Both structures are involved in motor control (Parent and Hazrati, 1995; Guillery and Sherman, 2002). The dorsolateral STN receives afferents from motor cortex, premotor cortex, and supplementary motor areas (Parent and Hazrati, 1995; Hamani et al., 2004). Vim projects to these areas as well as receiving afferents from the ipsilateral cerebellum.
Individual human Vim/STN neurons are active during voluntary and passive movement, somatosensation, and motor imagery (Lenz et al., 1990, 1994, 2002; Raeva et al., 1999; Magariños-Ascone et al., 2000; Magnin et al., 2000; Rodriguez-Oroz et al., 2001; Abosch et al., 2002; Benazzouz et al., 2002; Theodosopoulos et al., 2003; Williams et al., 2005). Many reports have examined single-unit activity in these regions with respect to tremor (Lenz et al., 1988, 1994, 2002; Zirh et al., 1998; Magariños-Ascone et al., 2000; Magnin et al., 2000; Rodriguez-Oroz et al., 2001; Brodkey et al., 2004; Hua and Lenz, 2005; Amtage et al., 2008) and pathological synchronous oscillations (Levy et al., 2000, 2002; Amirnovin et al., 2004). However, the number of simultaneously recorded cells in these studies was low (≤2), providing limited information about the pathological activity of larger neuronal ensembles.
Ensembles of simultaneously recorded neurons have been used to enable brain-machine interfaces (BMIs) for neuroprosthetic control in animal models (Chapin et al., 1999; Wessberg et al., 2000; Nicolelis, 2001; Serruya et al., 2002; Taylor et al., 2002; Hochberg et al., 2006; Fetz, 2007; Patil and Turner, 2008; Nicolelis and Lebedev, 2009; Lebedev et al., 2011; O'Doherty et al., 2011). However, recordings in humans have rarely been extracted from neuronal ensembles (Kennedy and Bakay, 1998; Kennedy et al., 2000, 2004; Patil et al., 2004; Quiroga et al., 2005). Human subcortical ensembles have only been used in a sole study (Patil et al., 2004), in which our laboratory demonstrated the feasibility of a subcortical motor BMI using motor control signals from neuronal ensembles recorded in motor thalamus [Vim/ventral oralis posterior motor thalamus (Vop)] or STN during DBS surgery to decode modulations of hand force during a one-dimensional target-tracking task.
We now examine neuronal population firing patterns during a voluntary motor task in a new sample of 25 human patients. While patients performed contralateral hand movements to acquire visual targets, up to 23 subcortical neurons were recorded simultaneously and acutely in Vim/Vop and STN to elucidate the relationship between neuronal modulations, rhythmic oscillations, and neuronal synchrony. A linear decoder model was applied to reconstruct cursor position from spiking activity. Neurons were classified by oscillatory firing patterns, tremor association, synchrony, and tuning to target and movement parameters.
Materials and Methods
Intraoperative recordings were conducted in 25 human patients undergoing placement of therapeutic DBS implants in either Vim or STN. All studies were approved by the Duke University Institutional Review Board and human ethics committees, and all participating patients understood and signed all required consent forms.
Patient characteristics and operative plan.
All patients selected for this study underwent either Vim (N = 14, 10 male, 4 female) or STN (N = 11, 10 male, 1 female) DBS electrode implantation surgery. Patients whose symptom presentation was dominated primarily by medication-resistant tremor (either essential tremor or severe parkinsonian tremor) were candidates for implantation in Vim, while patients with severe PD (typically akinetic/rigid variant with on/off fluctuations and dyskinesia) were candidates for implantation in STN. Both groups of patients were off their medications before and during surgery.
Patients first underwent Leksell frame placement, followed by a MRI scan to localize the implantation target. For Vim patients, the target was typically estimated according to anterior–posterior commissure (AC-PC) criteria, located ∼5–6 mm in front of the PC, on the AC-PC line with a lateral measure depending on the width of the third ventricle (typically 12–15 mm). Figure 1A shows a typical electrode trajectory. The first penetration for approaching Vim was the localization pass from a frontal burr hole, with the upper 5 mm of the recording track near the border of Vop and Vim, and the lower 5 mm in Vim and close to ventralis caudalis at the most posterior extent. Typically, the upper 5 mm was the best for multineuron recordings, reflecting more of the anterior motor thalamus (Vop rather than Vim), as shown in Figure 1A. For STN patients, the target was calculated by indirect methods, based on the AC-PC and 1 mm axial cuts of spoiled gradient recalled acquisition in the steady-state imaging. The initial target was located at 11–12 mm from the midline, 2–3 mm posterior to the midpoint of the AC-PC line, and 4 mm below the AC-PC line (Deuschl et al., 2006). Single-unit recordings were first performed to define the borders of the STN, according to standard electrophysiological criteria, with the goal of attaining at least 5.5–6 mm of STN. Typically, 2–3 passes were performed. Localization was performed using single-channel tungsten microelectrodes.
Figure 1.
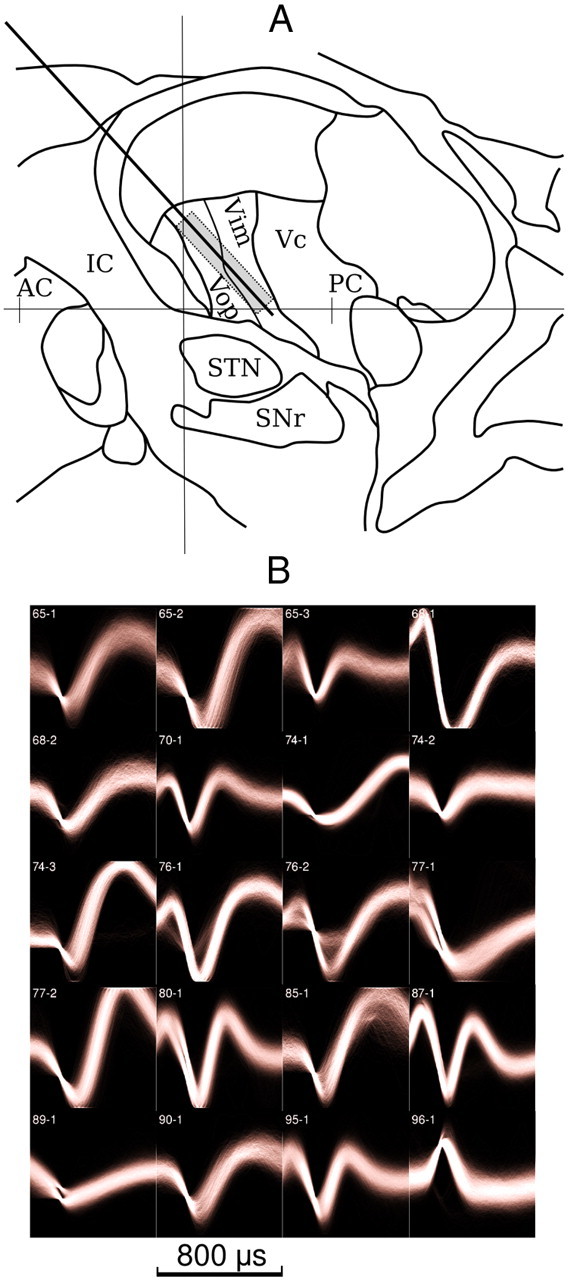
A, Sagittal diagram of the human brain at 15 mm off the midline. The vertical line represents the midpoint of the AC-PC line, which is arbitrarily set here as 24 mm in total length. The distance from the midpoint to the PC is 12 mm. The angled line represents a typical electrode trajectory, with the box emphasizing the best location (in terms of cell density) for the placement of the electrode array. This area overlaps Vim/Vop in the motor thalamus. Note that the DBS electrode would typically be placed deeper, at the border of Vim and ventralis caudatus (Vc, the sensory nucleus). The exact angle of the trajectory varied slightly from patient to patient, depending on the frame orientation and location of the frontal burr hole in front of the coronal suture. IC, Internal capsule; SNr, substantia nigra pars reticulata. B, Visualization of all waveforms from 20 sorted units from Patient M (Vim/Vop). Waveforms are 32 samples long and triggered by threshold crossing at sample 8. Individual traces were smoothed and summed into an accumulation buffer. Lighter colors represent a higher density of voltage traces. Traces are labeled by channel followed by unit number. Voltage amplitudes are normalized for display and are therefore represented in arbitrary units.
For both targets, once single-unit recordings had been performed for localization, a 32-channel Pt/Ir microwire (35 μm diameter) array (Ad-Tech Medical Instrument) was passed to the appropriate depth via an outer cannula (Patil et al., 2004), where significant activity was noted with the single-unit electrode. After allowing a few minutes for initial recordings to stabilize, the microwire array was slowly advanced through the cannula. Once the number of clearly distinguishable single units was maximized, the microwire array was left in place. At each electrode depth, the patient was instructed to proceed with the voluntary motor task.
Following completion of the multichannel recording sessions, the microwire array was removed and the DBS treatment electrodes were implanted. As a clinical routine, a brain computed tomography scan was performed within 12 h of the surgery procedure, and in no instance was a hemorrhage or other complication noted. Hence, the clinical risks of temporary placement of the 32 channel microwire array were demonstrated to be very low, as previously reported (Patil et al., 2004). Furthermore, in our research, we have used this electrode in many (N = 72) patients over several years with no post-op evidence of hemorrhage.
Electrophysiological recording.
The 32-channel microwire recordings were performed with a Plexon MAP system. Since this study was performed intraoperatively during electrophysiological mapping of the implantation sites, the recordings for each patient consisted of one or more epochs (up to 8, mean = 3.8), between which the electrode depths were altered. For each recording epoch, single units were sorted offline using custom software developed in-house. Extracted spikes consisted of 32 samples each, sampled at 40 kHz, aligned on the crossing of a linear voltage threshold. Sorting was done by projecting these waveforms into a two-dimensional principal component space. Clusters in principal component space were determined visually and selected by use of a lasso tool to define spatial boundaries. If the electrodes were moved (clearly visible as the microdrive corrupted the recording traces) or threshold was otherwise changed during a recording epoch, the record was broken into separate epochs. Recorded neuronal discharges on a given channel that could not be sorted and isolated as single units were classified as belonging to a multiunit, indicating a collection of individual discharges whose identity could not be firmly established. Figure 1B shows the sorted unit waveforms from a single recording session. We estimated the signal-to-noise ratio (SNR) by dividing the variance of the extracted spike samples by an estimate of the noise variance (Bankman et al., 1993), yielding a mean SNR of 4.69 for all sorted units.
Voluntary motor task.
Patients were placed in a supine, semisitting position in front of a computer monitor. A 5DT Systems Data Glove 5 Ultra haptic glove was placed over the hand contralateral to the microelectrode array. This glove was used to measure flexion/extension of the fingers, sampled at 1 kHz. The average flexion/extension signal, which effectively measured opening/closing of the hand, was used to control the one-dimensional position of the cursor on a video screen, placed directly in front of the patient for high visibility. Patients were trained to modulate the opening and closing of their hand to acquire targets by moving the cursor into a box placed randomly along a horizontal line (Fig. 2A). The required target hold time was 200 ms. Once the target was acquired, the box disappeared for 300 ms before reappearing in a new random position, chosen from a uniform distribution representing the horizontal extent of the screen. Therefore, movements did not strictly alternate between left and right; successive jumps would frequently occur in the same direction.
Figure 2.
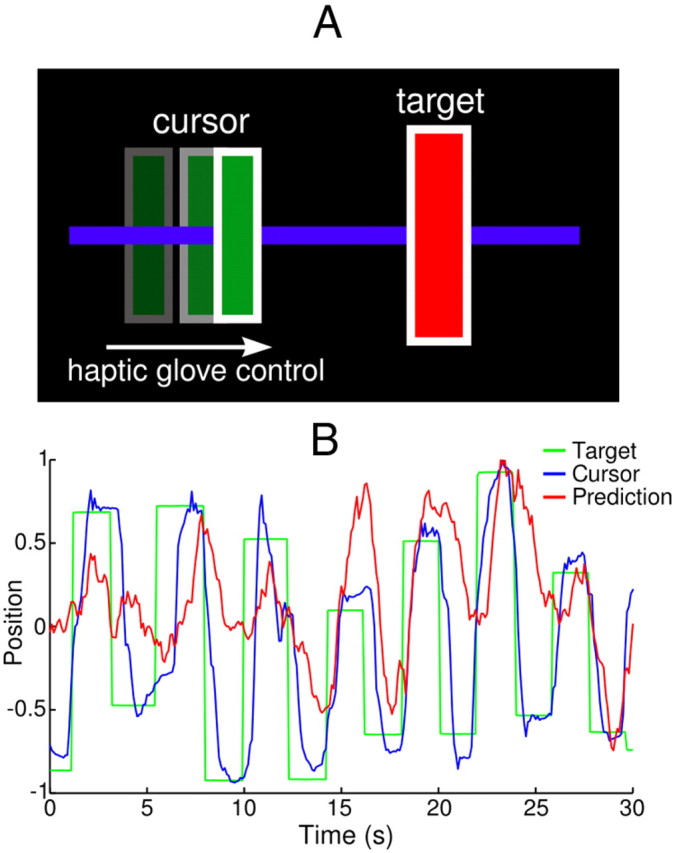
A, Diagram of the bidirectional hand task. The patient uses graded opening/closing of the hand to actuate a one-dimensional cursor toward randomly appearing targets. B, Example off-line prediction of hand/cursor position. Prediction was obtained using a linear Kalman filter with a 500 s training period, from Patient M (Vim/Vop). Forty-eight units (16 single units, 32 multiunits) were included in the ensemble. Position is given in normalized units.
During the preliminary training/calibration phase, the cursor gain, offset, and target box size were systematically calibrated by the experimenters to compensate for variations in physical ability. Specifically, in patients exhibiting limited hand mobility, the gain from hand movement to cursor motion was increased. In patients with pronounced hand tremor, the size of the target was increased. Finally, the offset was set so that the resting position of the patient's hand corresponded to the middle of the screen. During the recordings that followed, the length of individual motor task sessions varied depending on electrophysiological recording quality and the level of patient fatigue. Figure 2B shows a representative snapshot of the motor task performed by an ET patient. Note the slight 5 Hz tremor that occurred during target hold periods.
Neuronal tuning to target and movement.
All subsequent data analyses were performed using Matlab (MathWorks). We use the term “tuning” to refer to modulation of neuronal firing rates that is correlated to an external parameter and “tuning strength” to refer to the extent of those modulations.
For all sorted single units and multiunits, perievent time histograms (PETHs) of neuronal activity (Awiszus, 1997) were generated using one of two event triggers: (1) the appearance of a new target or (2) movement time. PETHs triggered on target appearance were constructed using a window beginning 0.5 s before each event trigger and ending 1.5 s after, whereas a symmetric 2 s window was used for PETHs triggered on movement time. Movement time was defined as the moment at which the cursor crossed the midpoint between initial cursor position (at target appearance) and the endpoint target position. We chose this standard as a robust definition of movement execution in light of patient tremor and occasional incorrect movements. Regardless of reaction time, this event trigger was locked to movement, being in close proximity to the point of maximum hand velocity before target acquisition. Trials with anomalous movement times <200 ms (premature movement) or >1000 ms (inattention) were discarded. Only neurons with at least 50 valid target acquisition trials were chosen for further analysis.
Neuronal tuning to either target or movement was determined by quantifying the deviation of each PETH from a bootstrap distribution of PETHs generated by uncorrelated triggers. We calculated significance using the one-sample Kuiper's test (Kuiper, 1962; Batschelet, 1981; Zar, 1999), a nonparametric test related to the Kolmogorov–Smirnov (K-S) test (Zar, 1999) but better suited for nonbiased PETH analysis. Unlike the K-S test, Kuiper's test is equally sensitive throughout the distribution, a useful property in scenarios in which the locations of the peak modulations are not known a priori. Variations of the K-S test have been used previously in the significance evaluation of neuronal PETHs (Ghazanfar et al., 2001; Wiest et al., 2005; Gutierrez et al., 2006). In this study, we used Kuiper's test to distinguish an observed distribution of event-triggered spike times from the null hypothesis (uniform probability distribution). Kuiper's test requires the calculation of the maximum positive and negative deviations of the observed PETH cumulative distribution function (CDF) from a uniform distribution CDF (ramp function); the sum of these two deviations is the statistic V: V = max[CDFsample − CDFuniform] + max[CDFuniform − CDFsample].
The Kuiper statistic, K, is a normalized version of V, taking into account the size of the observed sample size N, in this case, the number of binned spikes: (K = VN1/2 + 0.155 + 0.24N−1/2). To distinguish the test statistic Kobs from the null hypothesis, we generated a bootstrapped distribution of 1000 simulated Kuiper statistics (Ksim). Preliminary analysis determined shuffling of spike timestamps to be a suboptimal control; the process eliminates spike autocorrelations from the bootstrap distribution, thereby potentially biasing the evaluation of the observed distribution in favor of significance. Instead, each value of Ksim was calculated using a PETH constructed from the original spike timestamps but processed using a distribution of randomized event triggers; the triggers were drawn uniformly from the time span of the recording session. In other words, in each bootstrapped trial, the timestamps of the events (target appearance, movement) are randomly and independently assigned to decorrelate them from the spiking data. For each sorted unit, the resulting bootstrapped distribution of Ksim was used to produce a p value: p = (number of trials for which Ksimn > Kobs)/(N + 1).
Units were deemed to be tuned to task events (target or movement onset) using the threshold p < 0.05. These units exhibited temporal modulations in firing rate relative to newly appearing targets and/or target-directed movements. Tuning strength was defined as the z-score of the observed PETH relative to the bootstrap distribution.
Directional tuning.
The directional tuning of each sorted unit or multiunit was defined as the difference in neuronal response for leftward versus rightward movements. Significance of directional tuning was determined using the two-sample Kuiper's test. This test applied the calculation of the maximum positive and negative deviations between the spike CDFs for leftward and rightward movements: V = max[CDFsample 1 − CDFsample 2] + max[CDFsample 2 − CDFsample 1].
The Kuiper statistic K was calculated from V using the same equation as the one-sample Kuiper's test, but in the case of the two-sample Kuiper's test, the effective sample size (Neff) replaced N to account for the combined contributions of the individual sample sizes N1 and N2: Neff = (N1N2)/(N1 + N2).
Two PETHs triggered on movement time were generated, one for leftward movements and one for rightward movements. As with the one-sample Kuiper's test, each unit's Kobs statistic was compared with a bootstrapped distribution of Ksim generated from randomized trigger times. Units were deemed to be directionally tuned using the threshold p < 0.05. Tuning strength was defined as the z-score of the observed PETHs relative to the bootstrap distribution.
Tremor sensitivity.
Although concurrent surface EMG recordings were not permitted under our approved experimental protocol, haptic/position tracking have been used repeatedly to analyze tremor (Bardorfer et al., 2001; Su et al., 2003; Vinjamuri et al., 2009), as has accelerometry (Ghika et al., 1993; Grimaldi et al., 2007; Birdno et al., 2008).
For all sorted single units, perievent phase histograms (PEPHs) of neuronal activity were generated using phase of the patient's tremor as an event trigger, similar to the approach of Lebedev et al. (1994). Tremor was determined from hand velocity, and tremor periods within the range of 100–2000 ms (0.5–10 Hz) were analyzed. To exclude the impact of voluntary movements, hand velocity peaks occurring within 250 ms of a movement trigger were excluded. Each tremor period was defined in units of phase, with neuronal spike activity captured into 100 bins of equivalent phase aperture (3.6° each). The zero phase for each cycle was defined by a local maximum in hand velocity. Only sorted units with at least 500 valid tremor periods were chosen for further analysis.
Each resulting PEPH was a measurement of neuronal firing rate with respect to tremor phase. The one-sample Kuiper's test, in addition to possessing uniform sensitivity, is also rotationally invariant, meaning that the arbitrary choice of zero phase has no effect on the assessment of statistical significance. For analysis of tremor tuning, we generated a bootstrapped distribution of 1000 simulated Kuiper statistics (Ksim); each was calculated using a PEPH constructed from trials whose binned spike counts were circularly rotated by uniformly random phase offsets. For each analyzed unit, the bootstrapped distribution was used to produce a p value. Units were deemed to be tremor associated (tuned) using the threshold p < 0.05. Tuning strength was defined as the z-score of the observed PEPH relative to the bootstrap distribution.
Oscillatory neurons.
For all sorted units with at least 1000 extracted spikes, we used Welch's method (Oppenheim and Schafer, 1975) with eight nonoverlapping segments to determine the spike train autopower spectral density. The power spectra were smoothed using a 0.5 Hz rectangular sliding window. For each unit, the peak autopower frequency was determined in the 1–25 Hz range, with frequency content <1 Hz discarded for the remainder of the analysis. For the peak frequency, we determined the SNR by dividing peak power by the mean power (assessed from 1 Hz up to the Nyquist frequency of 500 Hz). For the purpose of comparison, the same spectral analysis was performed on hand acceleration traces for all recorded sessions.
Preliminary analysis indicated a functional separation of peak frequencies at ∼2.5 Hz. Units with a peak power frequency <2.5 Hz tended to be dominated by low-frequency power and were therefore judged not to be sufficiently oscillatory in a physiologically relevant frequency range. As in previous studies (Lenz et al., 1988; Amtage et al., 2008), only units with a peak SNR >2 were classified as oscillatory. Sharpness of the peaks in either the spike train or hand acceleration autopower spectra was determined by calculating the maximum power concentrated in a 1 Hz band within the physiologically relevant 2.5–7.5 Hz window. “Peakedness” was defined as the ratio of the power in this band relative to the total power in the 1–25 Hz band.
In addition to established linear methods, we developed a heterodyne method for detecting nonstationary or wide-bandwidth synchronized activity between each neuron's firing rate and associated hand velocity. This method, inspired by the frequency shifting scheme used in radio frequency transceivers, was applied to all sorted units that fulfilled the selection criteria for both target tuning analysis and oscillatory analysis. The spike train and hand velocity recordings were first bandpass filtered (fourth-order Butterworth, zero phase method) between 2 and 12 Hz, leaving both signals with negligible 0 Hz (DC) energy. The two signals were then multiplied, yielding a third time series from which to extract spectral energy. Because multiplication in the time domain is equivalent to convolution in the frequency domain (and vice versa), any synchronous frequency-modulated components in both neuronal firing rate and hand velocity are transferred to DC. The ratio of spectral energy (Eobs) from 0 to 0.125 Hz (signal) over that from 0.25–2 Hz (baseline) was considered as a metric of heterodyne correlation between neuronal activity and hand movement. To provide a control for this estimate, a bootstrap distribution (Esim) was generated by shuffling spike timestamps 1000 times and repeating the above analysis. Since all low-frequency information is filtered out before multiplication, shuffling timestamps was determined to be a suitable control. For all single units, the resulting bootstrapped distribution was used to produce a p value. Units were deemed to be heterodyne-tuned to tremor if the heterodyne correlation between neuronal activity and movement was significant using the threshold p < 0.05. Heterodyne tremor tuning strength was defined as the z-score of the observed spectra relative to the bootstrap distribution.
Efficacy of neuronal recordings for kinematic predictions.
Prediction algorithms from the BMI literature were applied to subcortical neuronal populations to extract behavioral parameters. Several algorithms were tested, including the linear Kalman filter, unscented Kalman filter, and the Wiener filter. Figure 2B shows an example off-line prediction for a 30 s window of task performance.
Since all three algorithms achieved the same approximate fidelity in preliminary testing, we chose the Wiener filter for further analysis due to its computational simplicity and extensive presence in the BMI literature (Wessberg et al., 2000; Carmena et al., 2003; Patil et al., 2004). Individual Wiener filters were fit by binning neuronal data into 100 ms time slices with 10 causal lags and regressing against recorded hand position. Model training was performed by the random selection of 50% of these time slices; predictions were then made on a distinct random 25%. This process was repeated with 100 draws of fit and predict time slices. Correlation coefficient (R) between predicted hand position and actual hand position was measured for each of the draws; the mean correlation coefficient was reported for each recording session. Offline prediction results are reported for all sessions with at least 50 presented targets.
We generated neuron dropping curves for selected sessions (Wessberg et al., 2000) by drawing random subsets from the neuronal ensemble. For each subset ensemble size N, we performed 1000 draws of random ensemble subset and Wiener filter fit and prediction; the R values for these draws were averaged to form a smooth neuron dropping curve. Following Wessberg et al. (2000), the resulting curve was then fit to the following hyperbolic function to extrapolate the performance results to larger ensemble sizes: R2 = cN/(1 + cN).
Neuronal synchrony.
The use of simultaneous ensemble recordings allows for the analysis of pairwise synchrony between neurons. To determine the statistical significance of the synchrony between two neurons, we analyzed the cross-correlation peak between pairs of spike trains. Pairs were analyzed if they each contained at least 100 spikes and corresponded to a session with at least 50 targets. The cross-correlation coefficient was first calculated for the observed spike trains of the two neurons, then smoothed using a 5 ms rectangular sliding window. The observed test statistic Cobs was defined as the peak coefficient in the ±10 ms time lag range. Bootstrap simulations (n = 1000) of the two spike trains were generated by convolving the spike trains with a Gaussian kernel (σ = 250 ms) and then generating new spike trains via an inhomogeneous Poisson process. The smoothing filter was used to extinguish correlated high-frequency content in the bootstrap distribution while maintaining low-frequency correlation in mean firing rate. Each of these bootstrap simulations was used to produce a cross-correlation coefficient Csim. The bootstrapped distribution was used to produce a p value, and neuron pairs were deemed to be significantly synchronous using the threshold p < 0.05.
To visualize the time dependence of pairwise synchrony, we generated joint peristimulus time histograms (JPSTHs) for neuron pairs, as originally proposed by Aertsen et al. (1989). Our JPSTHs were adjusted by subtracting the shift predictor histogram and normalizing (bin-by-bin) by the standard deviation, a procedure referred to by Aertsen et al. (1989) as the “true normalization” of the JPSTH.
Results
A total of 25 DBS implantation patients were examined. In these patients, we simultaneously recorded from ensembles of up to 23 well isolated neurons from either Vim/Vop or STN, depending on the site of electrode location. Recording sessions varied substantially in terms of duration and target acquisition rate, as limited by individual patient pathology and motivation. Neurons from these subcortical areas were classified by oscillatory firing patterns and tuning to target, movement, direction, and tremor. Moreover, neuronal ensemble data served as input for an offline linear prediction model to reconstruct cursor position. Finally, neuronal pairs were analyzed for evidence of functional synchrony.
STN cells (N = 168) exhibited a higher (p < 0.01, Mann–Whitney U test) mean firing rate than Vim/Vop cells (N = 83): 15.8 ± 1.95 Hz and 11.7 ± 1.02 Hz, respectively (mean ± 1 SE in both cases). In both subcortical areas, we found substantial populations of oscillatory neurons, as well as neurons strongly tuned to target, movement, direction, and tremor. Furthermore, neurons in both subcortical areas tended to show tuning to multiple parameters (Table 1) rather than belonging to disjoint sets. For example, the number of Vim/Vop cells tuned to both target and tremor was higher than would be expected under statistical independence (two-tailed Fisher's exact test, p < 0.05). At the ensemble level, a substantial number of analyzed cell pairs were found to exhibit synchrony. Curiously, all tremor-associated neurons exhibited synchrony within the recorded neuronal ensemble.
Table 1.
Pairwise classifications for single units
| Target | Movement | Direction | Tremor | Oscillatory | Heterodyne | |
|---|---|---|---|---|---|---|
| Vim/Vop cells | ||||||
| Target | 29.2% (N = 168) | 32.0%(+)** (N = 75) | 16.0% (N = 75) | 9.5%(+)† (N = 126) | 5.1% (N = 158) | 3.8% (N = 158) |
| Movement | — | 34.7% (N = 75) | 14.7%(+)† (N = 75) | 13.8% (N = 65) | 1.4%(−)* (N = 74) | 4.1% (N = 74) |
| Direction | — | — | 25.3% (N = 75) | 12.3%(+)† (N = 65) | 4.1% (N = 74) | 8.1%(+)† (N = 74) |
| Tremor | — | — | — | 12.4% (N = 169) | 2.4% (N = 169) | 6.3%(+)* (N = 126) |
| Oscillatory | — | — | — | — | 21.5% (N = 274) | 3.8% (N = 158) |
| Heterodyne | — | — | — | — | — | 13.3% (N = 158) |
| STN cells | ||||||
| Target | 22.9% (N = 83) | 38.5%(+)** (N = 26) | 11.5% (N = 26) | 4.1% (N = 74) | 4.9% (N = 81) | 2.5% (N = 81) |
| Movement | — | 42.3% (N = 26) | 11.5% (N = 26) | 12.5% (N = 24) | 8.3% (N = 24) | 8.3% (N = 24) |
| Direction | — | — | 19.2% (N = 26) | 0.0% (N = 24) | 4.2% (N = 24) | 0.0% (N = 24) |
| Tremor | — | — | — | 15.9% (N = 82) | 1.2% (N = 82) | 4.1% (N = 74) |
| Oscillatory | — | — | — | — | 17.9% (N = 123) | 6.2% (N = 81) |
| Heterodyne | — | — | — | — | — | 17.3% (N = 81) |
N, Number of analyzed cells per entry. Off-diagonal table entries have a smaller number of analyzed cells because they must fulfill the criteria of two independent classification tests. (+, −), Significantly (high, low) level of pairwise classification (Two-tailed Fisher's exact test: †p < 0.05, *p < 0.01, **p < 0.001).
Neuronal tuning to target and movement
Both Vim/Vop and STN neurons represented target appearance and movement onset (Table 2). Of all single units tested, 29.2% of 168 Vim/Vop cells and 22.9% of 83 STN cells were found to be tuned to target appearance. Both of these percentages represent significant populations (binomial test, p ≪ 0.001 in both cases). Figure 3A shows example PETHs for three highly responsive neurons.
Table 2.
Behavioral tuning of subcortical neurons
| Parameter | Unit type | Area | No. of units | # Tuned |
|---|---|---|---|---|
| Target | Single | Vim/Vop | 168 | 49** (29.2%) |
| Target | Single | STN | 83 | 19** (22.9%) |
| Target | Multi | Both | 753 | 87** (11.6%) |
| Movement | Single | Vim/Vop | 75 | 26** (34.7%) |
| Movement | Single | STN | 26 | 11** (42.3%) |
| Movement | Multi | Both | 414 | 48** (11.6%) |
| Direction | Single | Vim/Vop | 75 | 19** (25.3%) |
| Direction | Single | STN | 26 | 5* (19.2%) |
| Direction | Multi | Both | 414 | 36* (8.7%) |
Tuned population tested for significance (Binomial test: †p < 0.05, *p < 0.01, **p < 0.001).
Figure 3.
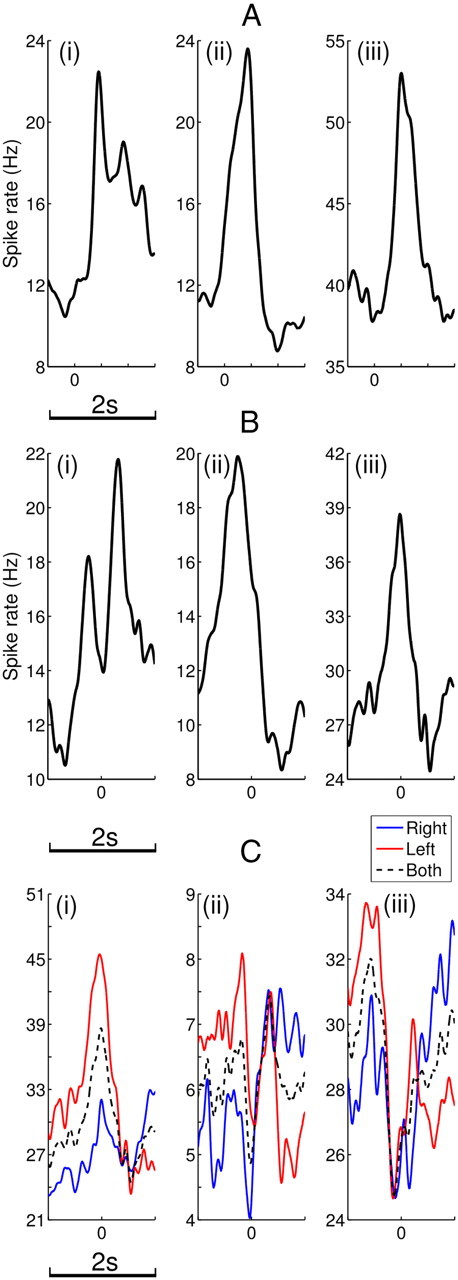
Example PETHs. A, Strongly tuned units to target appearance. i, Vim/Vop cell, Patient M, 465 trials. ii, Vim/Vop cell, Patient M, 375 trials. iii, STN cell, Patient H, 310 trials. B, Strongly tuned units to movement time. i, Vim/Vop cell, Patient M, 390 trials. ii, Vim/Vop cell, Patient M, 310 trials. iii, STN cell, Patient H, 201 trials. C, Strongly direction tuned units. i, STN cell, Patient H, 201 trials. ii, Vim/Vop cell, Patient M, 416 trials. iii, Vim/Vop cell, Patient M, 394 trials. For A, reported time is relative to target appearance. For B and C, reported time is relative to movement time. All plots were smoothed using a Gaussian kernel, σ = 40 ms.
As explained above, trials with reaction times outside the 200–1000 ms range were discarded for movement tuning, and only sessions with at least 50 valid trials were subjected to further statistical analysis. Because of the additional reaction-time criterion, fewer single units were analyzed for movement tuning than for target tuning. Of these, 34.7% of 75 Vim/Vop cells and 42.3% of 26 STN cells were found to be tuned to movement. Both of these percentages represent statistically significant populations (binomial test, p ≪ 0.001 in both cases). Figure 3B shows example PETHs for three highly responsive neurons.
We also found a strong positive correlation between the strength of target appearance tuning and that of movement tuning, for both Vim/Vop and STN cells. When controlling for the number of session trials, target tuning strength significantly predicted movement tuning strength (β = 0.70, p ≪ 0.001 for Vim/Vop; β = 0.71, p ≪ 0.001 for STN). This result is consistent with Table 1, which indicates that a larger-than-expected number of neurons in both subcortical areas were tuned to both target and movement.
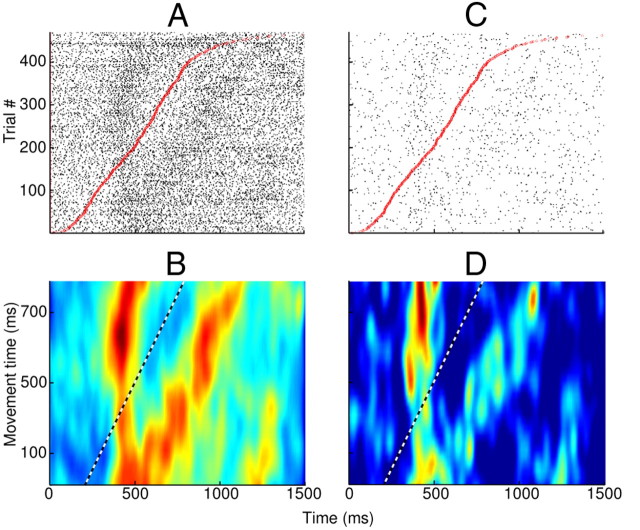
A portion of the correlation between target tuning and movement tuning may be explained by a tight temporal offset between target appearance and movement time. However, visual inspection of some tuned units indicated a clear decoupling of the neural encoding of target appearance and movement. Sorted raster plots from example neurons are shown in Figure 4, A and C. From these, we derived the color maps in Figure 4, B and D, each showing two clear bands of increased spike density. In both panels, the vertical bands are independent of movement time and are clearly related to target appearance (∼450 ms postappearance). The diagonal bands have a near-unity slope, indicating a clear time-locked relationship between neuronal activity and movement time. For both units, the second peak in firing rate occurred ∼300 ms after the defined movement time. From these data, it can be concluded that these neurons were tuned to both target appearance and movement; they modulated their firing rates in relation to both events.
Figure 4.
Separation between single-unit response to target appearance and movement time. Time along the x-axis is relative to target appearance. A and C show spike raster plots relative to target appearance, with individual trials sorted by movement time (red circles). B and D show smoothed color plots for the same two units as A and C, using the relative timing of all spikes and the movement time of their corresponding trials. The dashed line (unity slope) depicts movement time. For generation of the color plots, the data were smoothed using a two-dimensional Gaussian kernel, with σ = 20 ms along the x-axis and σ = 40 ms along the y-axis. Both units are Vim/Vop cells from Patient M.
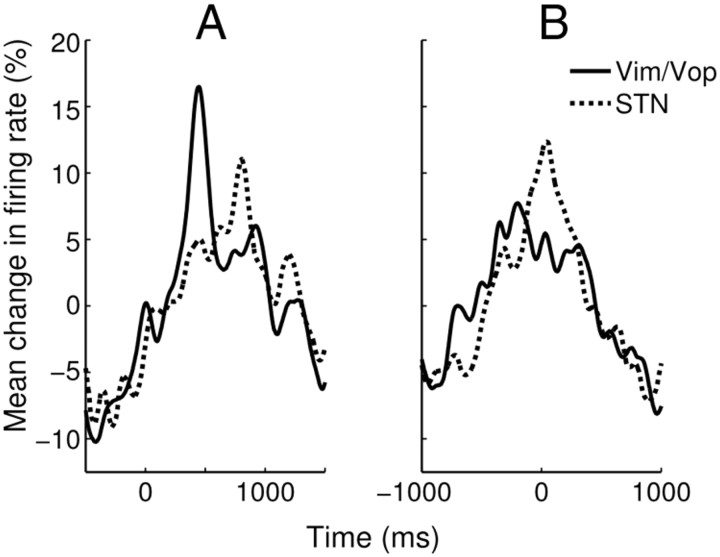
Modest differences were seen in the aggregate response patterns of Vim/Vop and STN cells classified as responsive to either target or movement (Fig. 5). Both cell types exhibited a mean response that peaked following target appearance (Fig. 5A); STN cells peaked later on average. The mean response of the Vim/Vop cells peaked immediately before movement while that of the STN cells peaked concurrently with movement (Fig. 5B). Differences in the relative lags for Vim/Vop and STN neuronal activation likely reflect the position of thalamic and STN neurons in the network hierarchy of motor control (Marsden et al., 2001; Guillery and Sherman, 2002; Gradinaru et al., 2009). The motor regions of the thalamus are more involved with intention, with signals arriving before motor cortex activation, whereas the collaterals from motor cortex to STN deliver signals at the time of motor activation.
Figure 5.
A, B, Mean normalized PETHs for all responsive units (p < 0.05) from both subcortical areas using two event triggers: target appearance (A), and movement time (B). Reported time is relative to the event trigger. Before aggregation, individual PETHs were convolved with a Gaussian kernel (σ = 40 ms) and normalized relative to mean firing rate. For both panels, the differences between the mean Vim/Vop and STN responses were statistically significant (χ2 test, p ≪ 0.001).
For both aggregates, the differences between the mean Vim/Vop and STN responses were statistically significant (χ2 test, p ≪ 0.001). However, similar proportions of Vim/Vop and STN cells were tuned to target appearance; the same was also true for movement tuning (two-tailed Fisher's exact test, p > 0.05 in both cases).
Directional tuning
Another metric of interest for the behavioral responsiveness of subcortical neurons was directional tuning; Table 2 gives the directional tuning results for both single units and multiunits. Of all tested single units, 25.3% of 75 Vim/Vop cells and 19.2% of 26 STN cells were found to exhibit directional tuning. Both of these percentages represent statistically significant populations (binomial test, p < 0.001 for Vim/Vop, p < 0.01 for STN). Figure 3C shows example PETHs for three strongly tuned neurons. Similar proportions of Vim/Vop and STN cells were tuned to direction (two-tailed Fisher's exact test, p > 0.05).
Despite the clear separation in the neuronal response to leftward and rightward movements, note the transient regions of convergence that occurred in Figure 3C. In Figure 3Ciii, for example, the neuronal responses to each direction converged just before movement. For many tuned neurons in both Vim/Vop and STN, the degree of directional modulation varied throughout the temporal window.
For both Vim/Vop and STN cells, we found strong positive correlations between directional tuning strength and the strength of both target tuning and movement tuning. When controlling for the number of session trials, target tuning strength significantly predicted directional tuning strength (β = 0.16, p < 0.05 for Vim/Vop; β = 0.38, p < 0.01 for STN). Similarly, movement tuning strength significantly predicted directional tuning strength (β = 0.24, p < 0.01 for Vim/Vop; β = 0.43, p < 0.05 for STN). The latter finding is consistent with the Vim/Vop pairwise classification result in Table 1.
Properties of multiunits
Whereas single units are identifiable as distinct neurons, a multiunit is likely comprised of distant neurons with lower SNR spike profiles. From Table 2, it can be seen that a significant population of analyzed multiunits were tuned to target, movement, and direction (binomial test, p < 0.01 in all cases). A substantial number of these tuned multiunits were found on the same recorded channel as tuned sorted units. Furthermore, when controlling for the number of session trials, the target tuning strength of single units significantly predicted the target tuning strength of same-channel multiunits (β = 0.18, p < 0.01). This confirms the presence of correlated tuning in nearby neurons. Thus, a substantial amount of encoded information was present in subcortical multiunits, arguing for the potential inclusion of these signals in future analyses of ensemble activity.
Tremor sensitivity
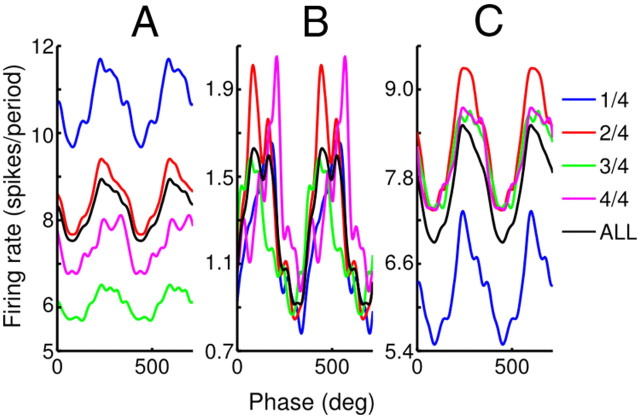
To identify potentially pathological neurons within the recorded subcortical populations, we analyzed the tremor sensitivity of single units using the discussed PEPH approach; the results are given in Table 3. Of all single units tested, 12.4% of 169 Vim/Vop cells and 15.9% of 82 STN cells were found to be correlated to observable hand tremor. Both of these percentages represent statistically significant populations (binomial test, p < 0.001 in both cases). Figure 6 shows example PEPHs for three strongly tremor-sensitive neurons. These results demonstrate that for highly tuned units, the dependence of spike rate on tremor phase remained stable throughout the recording session (Fig. 6), even if the mean firing rate varied substantially Figure 6, A and C. Similar proportions of Vim/Vop and STN cells were tuned to tremor (two-tailed Fisher's exact test, p > 0.05).
Table 3.
Tremor tuning of subcortical neurons
Tuned population tested for significance (Binomial test: †p < 0.05, *p < 0.01, **p < 0.001).
Figure 6.
Example PEPHs triggered on hand tremor phase for strongly tremor tuned units. A, Vim/Vop cell, Patient M, 4478 tremor periods. B, Vim/Vop cell, Patient M, 1259 tremor periods. C, Vim/Vop cell, Patient M, 4642 tremor periods. Zero phase is aligned to local peaks in hand velocity. All panels show individual PEPHs for each temporal quarter of their respective sessions, overlaid with the aggregate PEPH for the session as a whole (ALL). All plots in this figure are smoothed using a Gaussian kernel, σ = 15°.
For Vim/Vop cells (but not STN cells), we found a positive correlation between the strength of tremor tuning and that of directional tuning. When controlling for the number of session trials, directional tuning strength significantly predicted tremor tuning (β = 0.34, p < 0.05). However, we found no relationship between tremor tuning and either undirected target or movement tuning (p > 0.05 for all cases).
However, these results do not distinguish whether these tremor-tuned neurons are involved in a pathological mechanism that causes tremor or merely reflect somatosensory signals indicative of tremor.
Oscillatory behavior
To explore neuronal oscillations in Vim/Vop and STN and their relationship to patient pathology, we inspected the autopower spectra of single-unit spike trains for strong frequency peaks, yielding peak frequency and SNR (Fig. 7A). Of all tested single units with SNR > 2, the distribution of peak frequencies showed a clear bimodal distribution with a border between low- and high-frequency oscillations at ∼2.5 Hz (Fig. 7B).
Figure 7.
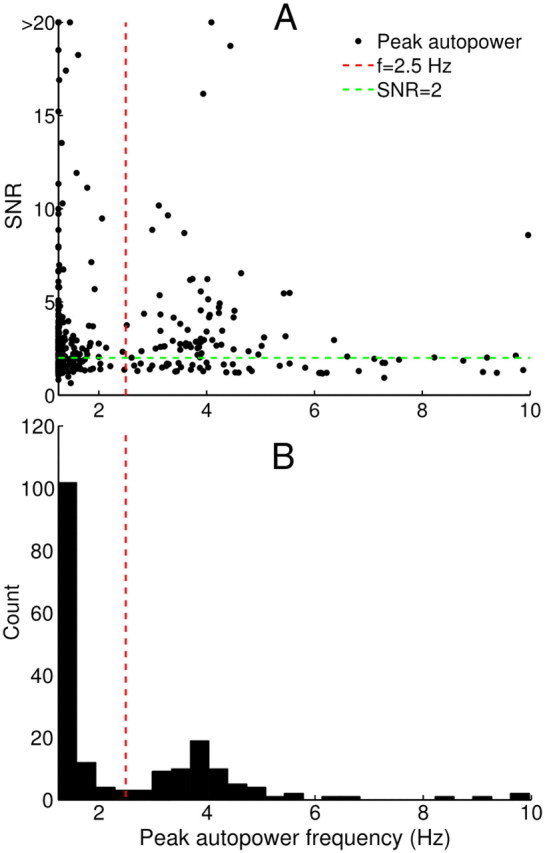
A, Distribution of peak frequencies for the spike train autopower spectra of 397 analyzed single units. Units with peak frequency >10 Hz (17.4% of all units) are not shown in this figure; they are distributed with near uniformity in the 10–25 Hz range with SNR mostly below the classification threshold of 2. B, Histogram showing the number of oscillatory (SNR > 2) units at each peak frequency. A clear separation between two subpopulations is clear at ∼2.5 Hz.
Spike train spectra from Vim/Vop and STN neurons also tended to possess large amounts of energy at low frequencies, suggestive of 1/f (pink) noise. This power-law distribution has been described for cortical neurons as a stochastic process (Davidsen and Schuster, 2002), but may also be related to slow modulations of patient attention and arousal. The observed distribution may explain the 2.5 Hz trough (Fig. 7) that separates neurons dominated by 1/f noise from those exhibiting strong oscillations in the tremor-relevant frequency range (2.5–7.5 Hz). Only neurons with sufficient power within this frequency range were eligible to be classified as oscillatory.
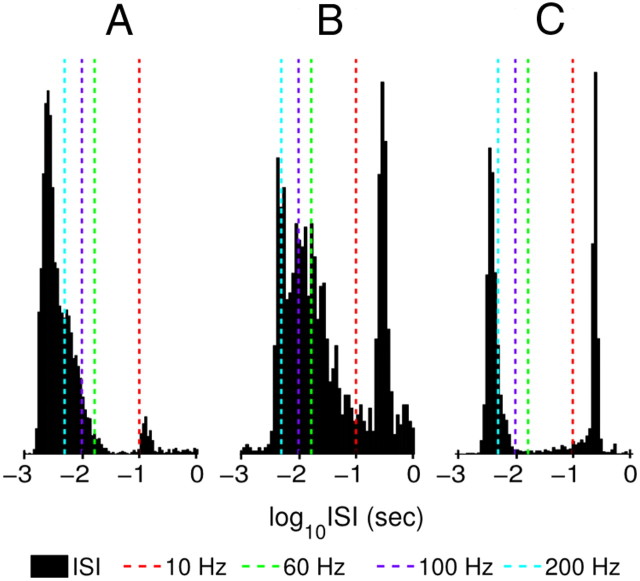
The oscillatory classification results are shown in Table 4; 21.5% of 274 Vim/Vop cells and 17.9% of 123 STN cells were classified as oscillatory. No difference was seen in the proportions of oscillatory Vim/Vop and STN cells (two-tailed Fisher's exact test, p > 0.05). Figure 8 shows example interspike interval (ISI) plots for three highly oscillatory cells. Note that all three ISI histograms exhibit some degree of bimodality, indicative of periodic bursting behavior.
Table 4.
Oscillatory Units
| Area | Unit type | No. of units | No.of oscillatory |
|---|---|---|---|
| Vim/Vop | Single | 274 | 59 (21.5%) |
| STN | Single | 123 | 22 (17.9%) |
Figure 8.
Example ISI histograms for highly oscillatory neurons. A, Vim/Vop cell, Patient W. B, STN cell, Patient V. C, Vim/Vop cell, Patient J.
Figure 9A shows the smoothed autopower spectra of spike trains for all analyzed single units, with each individually normalized horizontal trace corresponding to a distinct unit. From this figure, one can visually identify some of the highly oscillatory units as well as observe the congruity between multiple units from the same patient. The difference between the mean normalized spectra for Vim/Vop and STN cells (Fig. 9B) is statistically significant (χ2 test, p ≪ 0.001). From Figure 9B, it is clear that STN cells tended to concentrate power at a lower frequency (3 rather than 4 Hz).
Figure 9.
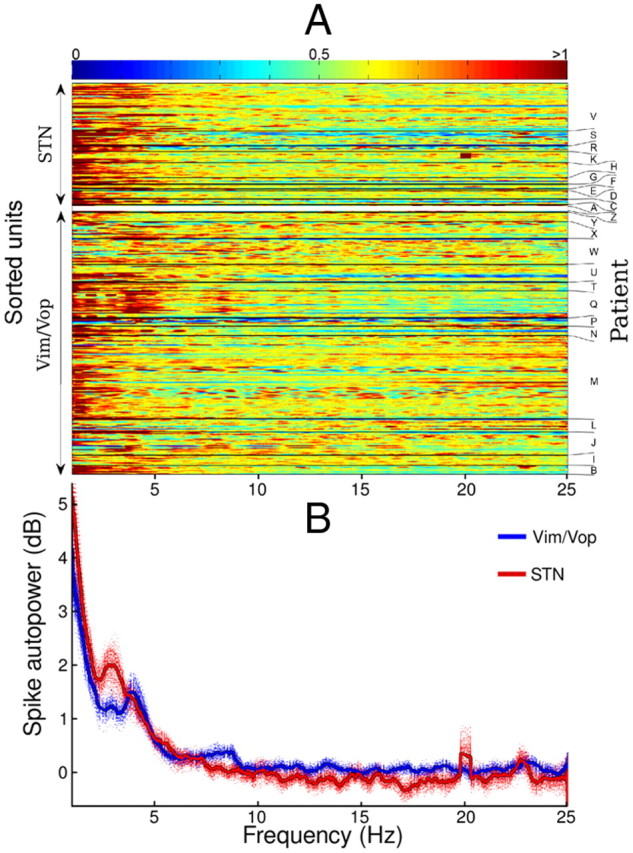
A, Smoothed autopower of spike trains for all sorted units with sufficient spike count. The autopower spectra (determined by Welch's method) of each horizontal trace, corresponding to a distinct unit, has been individually smoothed (using a 0.5 Hz sliding window) and normalized. The horizontal traces are grouped by patient and recording area. The color bar represents arbitrary units of normalized energy density. B, Mean autopower spectra from all analyzed Vim/Vop and STN cells. Spectra are individually smoothed using a 0.5 Hz sliding window and normalized before aggregation. Each of the dashed traces represents a bootstrap simulation in which only half of all analyzed units are aggregated. The difference between the mean Vim/Vop and STN spectra is statistically significant (χ2 test, p ≪ 0.001).
The pairwise classification results in Table 1 reject the notion that oscillatory neurons and behaviorally tuned neurons form disjoint sets. Furthermore, we found no relationship between spike autopower peakedness and the strength of any of the three (target, movement, direction) behavioral tuning metrics (p > 0.05 for all cases, for both Vim/Vop and STN). The lack of a clear anticorrelation suggests that the sets of behavioral neurons and oscillatory neurons are far from disjointed. Instead, they appear to exist as overlapping populations.
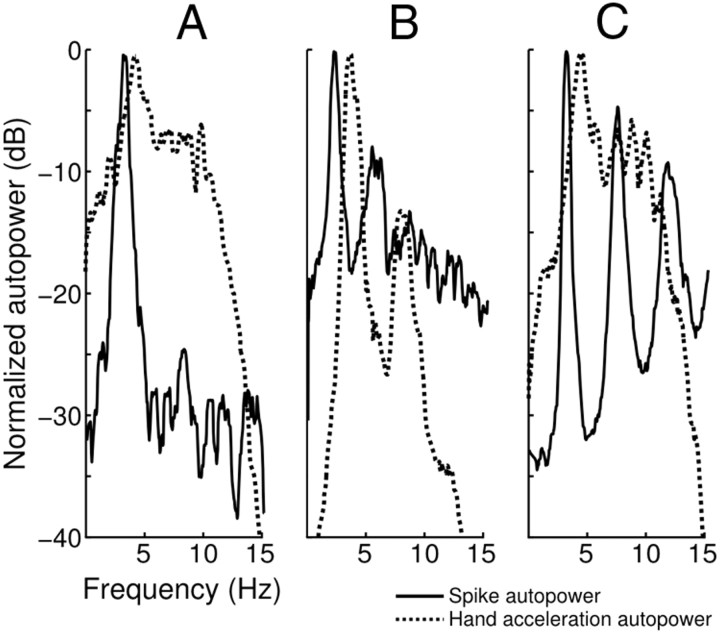
Our next analysis intended to uncover a relationship between strong oscillatory neuronal patterns and observable hand tremor. However, we did not find any clear relationship. Linear regression analysis revealed no relationship between peak frequency (2.5–7.5 Hz range) of spike train autopower spectra and corresponding hand acceleration autopower spectra (p > 0.05 for both Vim/Vop and STN). No relationship was found between the sharpness of the two spectra for Vim/Vop neurons (p > 0.05), but we did observe a marginally significant positive relationship for STN neurons (β = 0.72, p = 0.038). Figure 10 shows overlaid spectra for the spike train autopower and hand acceleration autopower of three highly oscillatory units. For all three cells (representative of the population as a whole), the peak frequencies do not coincide. However, we did find a marginally significant (β = 0.24, p = 0.055) correlation between spike autopower peakedness and tremor tuning strength for Vim/Vop cells (p > 0.1 for STN cells). These findings call into question the presumed causal linear relationship between the two, suggesting the possibility of an elusive nonlinear relationship.
Figure 10.
Comparison of spike train autopower and hand acceleration autopower for three highly oscillatory units. A, Vim/Vop cell, Patient W. B, STN cell, Patient V. C, Vim/Vop cell, Patient J. Note that for all three cells, peak frequency does not coincide.
Our heterodyne decoding analysis further explored this relationship by applying a nonlinear frequency shifting approach to the autopower spectra. Of 239 analyzed single units, 13.3% of Vim/Vop cells and 17.3% of STN cells were found to be tremor associated via heterodyne decoding (Table 5). Both of these percentages represent statistically significant populations (binomial test, p ≪ 0.001), but the difference between them is not significant (two-tailed Fisher's exact test, p > 0.05).
Table 5.
Heterodyne tremor tuning
Tuned population tested for significance (Binomial test: †p < 0.05, *p < 0.01, **p < 0.001).
Heterodyne decoding is a more sensitive method for detecting tremor correlations than spectral peak analysis if the tremor signal is wide-bandwidth or prone to phase changes. Indeed, this schema may better serve to explain the relationship between the oscillatory activity of neurons and observed tremor. In fact, this can explain the similarity in the proportions of tuned neurons in Tables 3 and 5. Furthermore, Vim/Vop firing indicated a strong positive correlation between tremor tuning strength, identified using PEPHs, and heterodyne tremor tuning strength (β = 0.31, p < 0.001). This relationship was marginally significant in STN cells (β = 0.28, p = 0.086). These findings are consistent with the pairwise classification results in Table 1, which indicated a higher than expected joint classification for the two tremor tuning analyses for Vim/Vop cells.
Efficacy of neuronal recordings for kinematic predictions
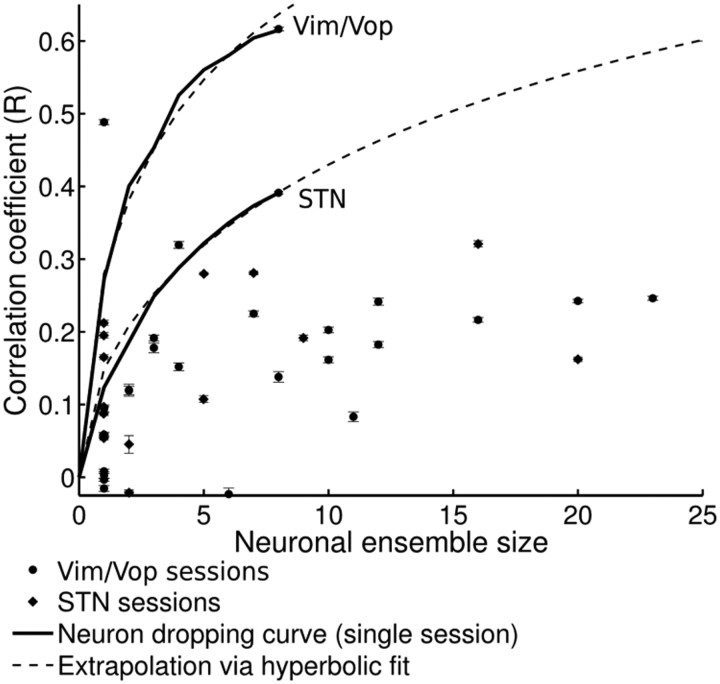
We also performed off-line predictions of cursor motion using the recorded ensembles. The correlation coefficient (mean ± 1.98 SE) for each of the sessions is shown in Figure 11. Although the predictions varied greatly across sessions and patients, the results compared favorably with our previous study (Patil et al., 2004). The best session for each subcortical area (Vim/Vop, STN) was chosen for further analysis, and neuron dropping curves were generated for these two sessions and fitted to a hyperbolic function (Wessberg et al., 2000). Extrapolation of the hyperbolic fit produced estimates of the approximate ensemble sizes required to achieve R2 = 0.9: 106 Vim/Vop neurons or 397 STN neurons.
Figure 11.
Dependence of off-line BMI predictions on neuron ensemble size. Each data point corresponds to a recording session. Correlation coefficient (R) is indicated as mean ± 1.98 SE. The best session for each subcortical area (Vim/Vop, STN) was chosen for further analysis. Neuron dropping curves are shown for each of these sessions and fitted to a hyperbolic function (Wessberg et al., 2000). Extrapolation calculations are presented in Results.
Neuronal synchrony
We analyzed neuronal synchrony in pairs of sorted units and investigated how its prevalence varied across subcortical areas; the results are given in Table 6. Using the cross-correlation approach, 43.0% of Vim/Vop pairs and 25.8% of STN pairs were found to be significantly synchronous. Both of these percentages represent significant populations (binomial test, p ≪ 0.001 for both cases). Figure 12A shows example cross-correlation plots for three highly synchronous pairs, while Figure 12B shows the normalized JPSTH for the same three pairs. Whereas Figure 12B, i and ii, clearly shows temporal synchronization along the diagonal (and off-diagonals), the same result is not visually discernible in Figure 12Biii.
Table 6.
Pairwise neuronal synchrony
Tuned population tested for significance (Binomial test: †p < 0.05, *p < 0.01, **p < 0.001).
Figure 12.
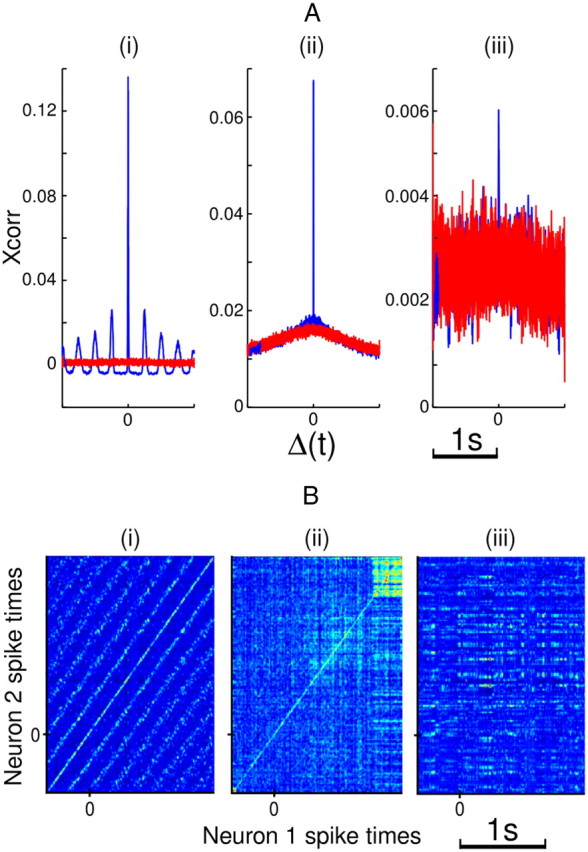
A, Example plots of cross-correlation coefficient for three highly synchronous neuron pairs. Bootstrapped simulations of coefficient shown in red. B, Example normalized JPSTHs for the same three neuron pairs. i, Pair of Vim/Vop cells, Patient I. ii, Pair of STN cells, Patient H. iii, Pair of Vim/Vop cells, Patient Q. For B, reported time is relative to target appearance.
We found highly significant differences between the Vim/Vop and STN in terms of the proportions of synchronous pairs. A significantly higher proportion of Vim/Vop pairs were synchronous than STN pairs (two-tailed Fisher's exact test, p ≪ 0.001).
It has been reported that the level of tremor in parkinsonian patients is positively correlated to the degree of pairwise synchrony among STN cells (Levy et al., 2000). To test the relationship between tremor tuning and local synchrony, we compared the subpopulation of both Vim/Vop and STN neurons that were synchronous with at least one other neuron in their respective ensembles to the subpopulation of neurons tuned to hand tremor (PEPH method). Only neurons fulfilling the criteria of both individual analyses were considered. The results are shown in Table 7. The observed proportions are significantly different (two-tailed Fisher's exact test, p < 0.01), indicating a clear interaction between tremor tuning and local synchrony. Only units synchronized to at least one other unit were tuned to tremor, whereas no unsynchronized units were tuned to tremor.
Table 7.
Comparison of synchrony (cross-correlation method) and tremor tuning (PEPH method)
| Tremor tuning (PEPH method) | Synchronized to ≥1 unit | Not synchronized |
|---|---|---|
| Tremor tuned | 28 | 0 |
| Not tremor tuned | 137 | 30 |
Discussion
In this study, we analyzed ensemble activity of human subcortical neurons (either Vim/Vop or STN) in 25 patients, recorded in patients who performed visually guided hand movements. To our knowledge, this constitutes the largest sample of human subcortical ensemble recordings to date. We quantitatively evaluated the representation of motor parameters in these neurons, as well as activity thought to be related to pathological states—tremor sensitivity, oscillations, and pairwise synchrony. The present work also supports our previous proposition that a sufficiently large ensemble of subcortical neurons could enable a motor BMI (Patil et al., 2004). We further propose that chronic subcortical microelectrode technology could serve as the basis of a new generation of neuroprosthetic devices aimed at both monitoring and actively reducing oscillatory firing and elevated levels of network synchrony.
Subcortical encoding of behavior
Neurons in both subcortical areas (Vim/Vop and STN) were found to encode features of patient motor behavior, both voluntary (target tracking) and involuntary (tremor). During voluntary behavior, a substantial number of neurons were found to be tuned to target appearance, movement onset, and movement direction (Table 2). This finding likely indicates that neurons in both structures are broadly tuned across multiple modalities and muscle groups. This observation is consistent with previous studies in which STN neurons have been reported to have large receptive fields that respond to multiple joints (Abosch et al., 2002), with 40% of STN cells tuned to movement in a simple two-dimensional joystick task (Williams et al., 2005). It has been reported that 42% of STN neurons respond to passive movement of either arm or leg, and of these, 25% responded to multiple joint movements (Theodosopoulos et al., 2003), whereas 51% of Vim/Vop neurons are tuned to sensory stimuli, with an overlapping 10% of these cells tuned to volitional movements (Lenz et al., 1990).
Some thalamic and STN neurons exhibited bimodal encoding of target and movement (Fig. 4), demonstrating what appears to be superposition of two independent neural representations. Furthermore, we observed a significant overlap between tuning to target appearance and to movement onset in both structures. Additionally, directional tuning strength was positively correlated to movement tuning strength, indicating that individual neurons encoded both parameters by exhibiting both common-mode and differential activity relative to movement onset (Fig. 3). Thus, neurons from both subcortical areas exhibited rate modulations based on a broad superposition of task parameters (Table 1).
Our analysis of involuntary motor activity (tremor) yielded phase histograms demonstrating clear phase-locking between neuronal activity and tremor periods (Fig. 6). Overall, we report significant populations of tremor tuned cells (12.4% for Vim/Vop, 15.9% for STN). The literature reports a large range in the prevalence of tremor-related cells. For STN, researchers have reported 11% (Magariños-Ascone et al., 2000), 19% (Rodriguez-Oroz et al., 2001), and 52% (Amtage et al., 2008). For Vim/Vop, researchers have reported 34% (Lenz et al., 1988), 35.6% (Zirh et al., 1998), and 51% (Hua and Lenz, 2005). These disparities are probably due to differences in recording parameters and classification methodology. For example, whereas many researchers have classified tremor tuning using linear coherence between spike train and recorded EMGs, we used kinematic hand position recorded by a haptic glove.
We found substantial overlap between tremor-tuned neurons and those tuned to parameters of voluntary motor behavior (Table 1). Moreover, we also observed a positive correlation between tremor tuning strength and directional tuning strength (Vim/Vop cells only). These results are consistent with earlier studies (Magariños-Ascone et al., 2000; Rodriguez-Oroz et al., 2001) that reported a large proportion of tremor-related STN cells to be simultaneously related to voluntary movements either through motor or sensory loops.
Elusive relationship between oscillatory activity and tremor
Within a tremor-relevant frequency range (2.5–7.5 Hz), we observed a substantial population of Vim/Vop and STN cells exhibiting strong oscillations (Table 4). Furthermore, we found that the mean autopower spectra for recorded Vim/Vop cells had a higher peak frequency than that of recorded STN cells (Fig. 9B). This finding is consistent with reports of higher mean tremor frequency in ET patients (4–12 Hz) than in PD patients (3–6 Hz) (Deuschl et al., 1998).
Whereas Rodriguez-Oroz et al. (2001) reported that oscillatory cells in STN did not represent movements, we found moderate overlap (Table 1) between Vim/Vop and STN neurons exhibiting oscillations and those tuned to voluntary behavioral parameters (target, movement, direction). This important finding indicates that there is not a strict dichotomy between pathological neurons and those encoding motor signals.
Similarly, we found overlap but no significant correlation between the presence of oscillatory patterns and tremor tuning in both subcortical areas. This finding corroborates the claims of earlier studies of ventral thalamus and STN (Magnin et al., 2000; Rodriguez-Oroz et al., 2001), in which the sets of tremor-related neurons and oscillatory neurons show modest intersection. In other words, not all tremor-related neurons exhibited oscillations, and some oscillatory neurons exhibited no clear association with tremor.
Furthermore, spectral peak detection methods revealed no relationship between spike train and hand acceleration (Fig. 10), though there may be an elusive nonlinear or nonstationary relationship between neuronal oscillations and hand tremor. We hypothesized that for some cells, spike train and tremor comodulated with relatively large bandwidth. Our heterodyne decoding results suggest that a substantial number of cells in both subcortical areas may be tremor-tuned in this manner (Table 5). Overall, no consensus in the field has been reached regarding the definitive relationship between oscillatory behavior and tremor tuning, and our results support the idea that pathological oscillations are idiopathic across both neurons and patients.
Network synchrony
Dopamine depletion in PD has been reported to promote neuronal synchrony within the basal ganglia (Heimer et al., 2006). In this study, a high percentage of neuronal pairs from both subcortical areas exhibited synchronous behavior (Table 6). This is generally consistent with reports of pairwise synchrony in the majority of analyzed STN pairs (Levy et al., 2000, 2002). However, we observed high levels of functional synchrony in neuronal pairs much further apart than the submillimeter separation in Levy et al. (2000, 2002). Furthermore, Vim/Vop neuron pairs (from ET patients) exhibited significantly higher synchrony than STN pairs.
Remarkably, only cells exhibiting synchrony with another cell in the ensemble were found to be tremor-tuned; no unsynchronized cells were tremor-tuned (Table 7). This finding corroborates reports that the prevalence of STN pairs synchronized at high frequencies is correlated to the degree of parkinsonian tremor (Levy et al., 2000) and that patients without observable tremor do not exhibit high-frequency STN synchrony (Levy et al., 2002). Others have reported correlations between STN synchrony and bradykinesia/rigidity (Weinberger et al., 2009). Our findings have extended Levy et al.'s (2000, 2002) results to combinatorial pairs in neuronal ensembles from both STN and Vim/Vop. It remains unclear to what degree network synchrony is indicative of tremor pathology, although the effective disruption of unstable network activity by DBS stimulation suggests a connection.
Chronic subcortical ensemble recordings
Acute intraoperative recordings exhibit instability and other limitations, whereas long-term recordings from subcortical structures will offer greater signal quality following the recovery of the electrode-tissue interface. Thousands of subcortical DBS implantations are performed every year with minimal risk (Bronstein et al., 2011). Furthermore, long electrode tracts have been shown to yield more stable extracellular recordings (Porada et al., 2000; Krüger et al., 2010) by mitigating the problem of electrode micromotion seen in cortical implants.
We suggest that chronic subcortical ensemble recordings may bring about the viability of subcortical BMI systems, first discussed in our previous study (Patil et al., 2004). Our reported offline prediction results from our best Vim/Vop and STN sessions are comparable to those reported from selected rhesus macaque cortical regions with similar neuron count (Wessberg et al., 2000; Carmena et al., 2003). However, hyperbolic extrapolation (Wessberg et al., 2000) suggests an ensemble size greater than 100 to achieve prediction fidelity above R2 = 0.9. This would of course necessitate the design of microelectrode arrays for cannula-based implantation with more recording sensors and demonstrable long-term safety and recording efficacy.
We propose that clinical studies using chronic ensemble recordings in humans will permit both the continued study of the neurophysiological mechanisms involved in motor control as well as long-term monitoring of pathological activity. Chronic recordings will facilitate continuous examination of changes in tuning, oscillations, and synchrony as a function of the patient's symptomatic state both on and off treatment. Specifically, this wealth of electrophysiological data may well be used to instruct the improvement of closed-loop DBS systems that are currently in initial stages of development (Rosin et al., 2011; Rouse et al., 2011).
We have shown that within the STN and Vim/Vop thalamus, there is an idiopathic mixture of pathology and behavior tuning; these sites are worthy of more targeted treatment than the current dominant approach of delivering high-frequency DBS through macroelectrodes. Subcortical ensembles remain an untapped resource, with the potential to advance both neuroscience and neurorehabilitation alike.
Footnotes
This work was supported by funding from the National Science Foundation Graduate Research Fellowship award DGE-1106401-004 to A.M.F.; the VA Merit Review Award, and NIH Grants R21NS066115 and RO1AG037599 to D.A.T.; and by Defense Advanced Research Projects Agency Grant N66001-06-C-2019, NIH Grant R01NS073125, and the NIH Director's Pioneer Award DP1OD006798 to M.A.L.N. The content is solely the responsibility of the authors and does not necessarily represent the official views of the Office of the NIH Director or the NIH. We thank Daniel Clayton for surgical assistance and expertise, Susan Halkiotis for manuscript editing and preparation, and Joseph E. O'Doherty for technical, scientific, and programming help.
The authors declare no financial conflicts of interest.
References
- Abosch A, Hutchison WD, Saint-Cyr JA, Dostrovsky JO, Lozano AM. Movement-related neurons of the subthalamic nucleus in patients with Parkinson disease. J Neurosurg. 2002;97:1167–1172. doi: 10.3171/jns.2002.97.5.1167. [DOI] [PubMed] [Google Scholar]
- Aertsen AM, Gerstein GL, Habib MK, Palm G. Dynamics of neuronal firing correlation: modulation of “effective connectivity.”. J Neurophysiol. 1989;61:900–917. doi: 10.1152/jn.1989.61.5.900. [DOI] [PubMed] [Google Scholar]
- Amirnovin R, Williams ZM, Cosgrove GR, Eskandar EN. Visually guided movements suppress subthalamic oscillations in Parkinson's disease patients. J Neurosci. 2004;24:11302–11306. doi: 10.1523/JNEUROSCI.3242-04.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Amtage F, Henschel K, Schelter B, Vesper J, Timmer J, Lücking CH, Hellwig B. Tremor-correlated neuronal activity in the subthalamic nucleus of Parkinsonian patients. Neurosci Lett. 2008;442:195–199. doi: 10.1016/j.neulet.2008.06.087. [DOI] [PubMed] [Google Scholar]
- Awiszus F. Spike train analysis. J Neurosci Methods. 1997;74:155–166. doi: 10.1016/s0165-0270(96)02246-7. [DOI] [PubMed] [Google Scholar]
- Bankman IN, Johnson KO, Schneider W. Optimal detection, classification, and superposition resolution in neural waveform recordings. IEEE Trans Biomed Eng. 1993;40:836–841. doi: 10.1109/10.238472. [DOI] [PubMed] [Google Scholar]
- Bardorfer A, Munih M, Zupan A, Primozic A. Upper limb motion analysis using haptic interface. IEEE/ASME Trans Mechatronics. 2001;6:253–260. [Google Scholar]
- Batschelet E. Circular statistics in biology. New York: Academic; 1981. [Google Scholar]
- Benazzouz A, Breit S, Koudsie A, Pollak P, Krack P, Benabid AL. Intraoperative microrecordings of the subthalamic nucleus in Parkinson's disease. Mov Disord. 2002;17(Suppl 3):S145–S149. doi: 10.1002/mds.10156. [DOI] [PubMed] [Google Scholar]
- Birdno MJ, Kuncel AM, Dorval AD, Turner DA, Grill WM. Tremor varies as a function of the temporal regularity of deep brain stimulation. Neuroreport. 2008;19:599–602. doi: 10.1097/WNR.0b013e3282f9e45e. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brodkey JA, Tasker RR, Hamani C, McAndrews MP, Dostrovsky JO, Lozano AM. Tremor cells in the human thalamus: differences among neurological disorders. J Neurosurg. 2004;101:43–47. doi: 10.3171/jns.2004.101.1.0043. [DOI] [PubMed] [Google Scholar]
- Bronstein JM, Tagliati M, Alterman RL, Lozano AM, Volkmann J, Stefani A, Horak FB, Okun MS, Foote KD, Krack P, Pahwa R, Henderson JM, Hariz MI, Bakay RA, Rezai A, Marks WJ, Jr, Moro E, Vitek JL, Weaver FM, Gross RE, DeLong MR. Deep brain stimulation for Parkinson disease: an expert consensus and review of key issues. Arch Neurol. 2011;68:165. doi: 10.1001/archneurol.2010.260. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carmena JM, Lebedev MA, Crist RE, O'Doherty JE, Santucci DM, Dimitrov DF, Patil PG, Henriquez CS, Nicolelis MA. Learning to control a brain-machine interface for reaching and grasping by primates. PLoS Biology. 2003;1:E42. doi: 10.1371/journal.pbio.0000042. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chapin JK, Moxon KA, Markowitz RS, Nicolelis MA. Real-time control of a robot arm using simultaneously recorded neurons in the motor cortex. Nat Neurosci. 1999;2:664–670. doi: 10.1038/10223. [DOI] [PubMed] [Google Scholar]
- Davidsen J, Schuster HG. Simple model for 1/f(alpha) noise. Phys Rev E Stat Nonlin Soft Matter Phys. 2002;65 doi: 10.1103/PhysRevE.65.026120. 026120. [DOI] [PubMed] [Google Scholar]
- Deuschl G, Bain P, Brin M. Consensus statement of the movement disorder society on tremor. Ad Hoc Scientific Committee. Mov Disord. 1998;13(Suppl 3):2–23. doi: 10.1002/mds.870131303. [DOI] [PubMed] [Google Scholar]
- Deuschl G, Schade-Brittinger C, Krack P, Volkmann J, Schäfer H, Bötzel K, Daniels C, Deutschländer A, Dillmann U, Eisner W, Gruber D, Hamel W, Herzog J, Hilker R, Klebe S, Kloss M, Koy J, Krause M, Kupsch A, Lorenz D, et al. A randomized trial of deep-brain stimulation for Parkinson's disease. N Engl J Med. 2006;355:896–908. doi: 10.1056/NEJMoa060281. [DOI] [PubMed] [Google Scholar]
- Fetz EE. Volitional control of neural activity: implications for brain-computer interfaces. J Physiol. 2007;579:571–579. doi: 10.1113/jphysiol.2006.127142. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ghazanfar AA, Krupa DJ, Nicolelis MA. Role of cortical feedback in the receptive field structure and nonlinear response properties of somatosensory thalamic neurons. Exp Brain Res. 2001;141:88–100. doi: 10.1007/s002210100849. [DOI] [PubMed] [Google Scholar]
- Ghika J, Wiegner AW, Fang JJ, Davies L, Young RR, Growdon JH. Portable system for quantifying motor abnormalities in Parkinsons-disease. IEEE Trans Biomed Eng. 1993;40:276–283. doi: 10.1109/10.216411. [DOI] [PubMed] [Google Scholar]
- Gradinaru V, Mogri M, Thompson KR, Henderson JM, Deisseroth K. Optical deconstruction of parkinsonian neural circuitry. Science. 2009;324:354–359. doi: 10.1126/science.1167093. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grimaldi G, Piet L, Manto M. Effects of wrist oscillations on contralateral neurological postural tremor using a new myohaptic device (‘wristalyzer’). Proceedings of the 4th IEEE-EMBS; Cambridge: IEEE; 2007. pp. 44–48. [DOI] [PubMed] [Google Scholar]
- Guillery RW, Sherman SM. The thalamus as a monitor of motor outputs. Philos Trans R Soc Lond B Biol Sci. 2002;357:1809–1821. doi: 10.1098/rstb.2002.1171. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gutierrez R, Carmena JM, Nicolelis MA, Simon SA. Orbitofrontal ensemble activity monitors licking and distinguishes among natural rewards. J Neurophysiol. 2006;95:119–133. doi: 10.1152/jn.00467.2005. [DOI] [PubMed] [Google Scholar]
- Hamani C, Saint-Cyr JA, Fraser J, Kaplitt M, Lozano AM. The subthalamic nucleus in the context of movement disorders. Brain. 2004;127:4–20. doi: 10.1093/brain/awh029. [DOI] [PubMed] [Google Scholar]
- Heimer G, Rivlin M, Israel Z, Bergman H. Synchronizing activity of basal ganglia and pathophysiology of Parkinson's disease. J Neural Transm Suppl. 2006;70:17–20. doi: 10.1007/978-3-211-45295-0_4. [DOI] [PubMed] [Google Scholar]
- Hochberg LR, Serruya MD, Friehs GM, Mukand JA, Saleh M, Caplan AH, Branner A, Chen D, Penn RD, Donoghue JP. Neuronal ensemble control of prosthetic devices by a human with tetraplegia. Nature. 2006;442:164–171. doi: 10.1038/nature04970. [DOI] [PubMed] [Google Scholar]
- Hua SE, Lenz FA. Posture-related oscillations in human cerebellar thalamus in essential tremor are enabled by voluntary motor circuits. J Neurophysiol. 2005;93:117–127. doi: 10.1152/jn.00527.2004. [DOI] [PubMed] [Google Scholar]
- Kennedy PR, Bakay RA. Restoration of neural output from a paralyzed patient by a direct brain connection. Neuroreport. 1998;9:1707–1711. doi: 10.1097/00001756-199806010-00007. [DOI] [PubMed] [Google Scholar]
- Kennedy PR, Bakay RA, Moore MM, Adams K, Goldwaithe J. Direct control of a computer from the human central nervous system. IEEE Trans Rehabil Eng. 2000;8:198–202. doi: 10.1109/86.847815. [DOI] [PubMed] [Google Scholar]
- Kennedy PR, Kirby MT, Moore MM, King B, Mallory A. Computer control using human intracortical local field potentials. IEEE Trans Neural Syst Rehabil Eng. 2004;12:339–344. doi: 10.1109/TNSRE.2004.834629. [DOI] [PubMed] [Google Scholar]
- Koller WC, Lyons KE, Wilkinson SB, Troster AI, Pahwa R. Long-term safety and efficacy of unilateral deep brain stimulation of the thalamus in essential tremor. Mov Disord. 2001;16:464–468. doi: 10.1002/mds.1089. [DOI] [PubMed] [Google Scholar]
- Krüger J, Caruana F, Volta RD, Rizzolatti G. Seven years of recording from monkey cortex with a chronically implanted multiple microelectrode. Front Neuroeng. 2010;3:6. doi: 10.3389/fneng.2010.00006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kuiper NH. Tests concerning random points on a circle. Proc Koninkl Neder Akad Wetensch. 1962;63:38–47. [Google Scholar]
- Kumar R, Lozano AM, Sime E, Lang AE. Long-term follow-up of thalamic deep brain stimulation for essential and parkinsonian tremor. Neurology. 2003;61:1601–1604. doi: 10.1212/01.wnl.0000096012.07360.1c. [DOI] [PubMed] [Google Scholar]
- Lebedev MA, Denton JM, Nelson RJ. Vibration-entrained and premovement activity in monkey primary somatosensory cortex. J Neurophysiol. 1994;72:1654–1673. doi: 10.1152/jn.1994.72.4.1654. [DOI] [PubMed] [Google Scholar]
- Lebedev MA, Tate AJ, Hanson TL, Li Z, O'Doherty JE, Winans JA, Ifft PJ, Zhuang KZ, Fitzsimmons NA, Schwarz DA, Fuller AM, An JH, Nicolelis MA. Future developments in brain-machine interface research. Clinics (Sao Paulo) 2011;66(Suppl 1):25–32. doi: 10.1590/S1807-59322011001300004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lenz FA, Tasker RR, Kwan HC, Schnider S, Kwong R, Murayama Y, Dostrovsky JO, Murphy JT. Single unit analysis of the human ventral thalamic nuclear group: correlation of thalamic “tremor cells” with the 3–6 Hz component of parkinsonian tremor. J Neurosci. 1988;8:754–764. doi: 10.1523/JNEUROSCI.08-03-00754.1988. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lenz FA, Kwan HC, Dostrovsky JO, Tasker RR, Murphy JT, Lenz YE. Single unit analysis of the human ventral thalamic nuclear group: activity correlated with movement. Brain. 1990;113:1795–1821. doi: 10.1093/brain/113.6.1795. [DOI] [PubMed] [Google Scholar]
- Lenz FA, Kwan HC, Martin RL, Tasker RR, Dostrovsky JO, Lenz YE. Single unit analysis of the human ventral thalamic nuclear group: tremor-related activity in functionally identified cells. Brain. 1994;117:531–543. doi: 10.1093/brain/117.3.531. [DOI] [PubMed] [Google Scholar]
- Lenz FA, Jaeger CJ, Seike MS, Lin YC, Reich SG. Single-neuron analysis of human thalamus in patients with intention tremor and other clinical signs of cerebellar disease. J Neurophysiol. 2002;87:2084–2094. doi: 10.1152/jn.00049.2001. [DOI] [PubMed] [Google Scholar]
- Levy R, Hutchison WD, Lozano AM, Dostrovsky JO. High-frequency synchronization of neuronal activity in the subthalamic nucleus of parkinsonian patients with limb tremor. J Neurosci. 2000;20:7766–7775. doi: 10.1523/JNEUROSCI.20-20-07766.2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Levy R, Ashby P, Hutchison WD, Lang AE, Lozano AM, Dostrovsky JO. Dependence of subthalamic nucleus oscillations on movement and dopamine in Parkinson's disease. Brain. 2002;125:1196–1209. doi: 10.1093/brain/awf128. [DOI] [PubMed] [Google Scholar]
- Magariños-Ascone CM, Figueiras-Mendez R, Riva-Meana C, Córdoba-Fernández A. Subthalamic neuron activity related to tremor and movement in Parkinson's disease. Eur J Neurosci. 2000;12:2597–2607. doi: 10.1046/j.1460-9568.2000.00127.x. [DOI] [PubMed] [Google Scholar]
- Magnin M, Morel A, Jeanmonod D. Single-unit analysis of the pallidum, thalamus and subthalamic nucleus in parkinsonian patients. Neuroscience. 2000;96:549–564. doi: 10.1016/s0306-4522(99)00583-7. [DOI] [PubMed] [Google Scholar]
- Marsden JF, Limousin-Dowsey P, Ashby P, Pollak P, Brown P. Subthalamic nucleus, sensorimotor cortex and muscle interrelationships in Parkinson's disease. Brain. 2001;124:378–388. doi: 10.1093/brain/124.2.378. [DOI] [PubMed] [Google Scholar]
- Nicolelis MA. Actions from thoughts. Nature. 2001;409:403–407. doi: 10.1038/35053191. [DOI] [PubMed] [Google Scholar]
- Nicolelis MA, Lebedev MA. Principles of neural ensemble physiology underlying the operation of brain-machine interfaces. Nat Rev Neurosci. 2009;10:530–540. doi: 10.1038/nrn2653. [DOI] [PubMed] [Google Scholar]
- O'Doherty JE, Lebedev MA, Ifft PJ, Zhuang KZ, Shokur S, Bleuler H, Nicolelis MA. Active tactile exploration using a brain-machine-brain interface. Nature. 2011;479:228–231. doi: 10.1038/nature10489. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ondo W, Jankovic J, Schwartz K, Almaguer M, Simpson RK. Unilateral thalamic deep brain stimulation for refractory essential tremor and Parkinson's disease tremor. Neurology. 1998;51:1063–1069. doi: 10.1212/wnl.51.4.1063. [DOI] [PubMed] [Google Scholar]
- Oppenheim AV, Schafer RW. Digital signal processing. Englewood Cliffs, NJ: Prentice-Hall; 1975. [Google Scholar]
- Parent A, Hazrati LN. Functional anatomy of the basal ganglia. II. The place of subthalamic nucleus and external pallidum in basal ganglia circuitry. Brain Res Brain Res Rev. 1995;20:128–154. doi: 10.1016/0165-0173(94)00008-d. [DOI] [PubMed] [Google Scholar]
- Patil PG, Turner DA. The development of brain-machine interface neuroprosthetic devices. Neurotherapeutics. 2008;5:137–146. doi: 10.1016/j.nurt.2007.11.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Patil PG, Carmena JM, Nicolelis MA, Turner DA. Ensemble recordings of human subcortical neurons as a source of motor control signals for a brain-machine interface. Neurosurgery. 2004;55:27–35. discussion 35–38. [PubMed] [Google Scholar]
- Porada I, Bondar I, Spatz WB, Krüger J. Rabbit and monkey visual cortex: more than a year of recording with up to 64 microelectrodes. J Neurosci Methods. 2000;95:13–28. doi: 10.1016/s0165-0270(99)00139-9. [DOI] [PubMed] [Google Scholar]
- Quiroga RQ, Reddy L, Kreiman G, Koch C, Fried I. Invariant visual representation by single neurons in the human brain. Nature. 2005;435:1102–1107. doi: 10.1038/nature03687. [DOI] [PubMed] [Google Scholar]
- Raeva S, Vainberg N, Tikhonov Y, Tsetlin I. Analysis of evoked activity patterns of human thalamic ventrolateral neurons during verbally ordered voluntary movements. Neuroscience. 1999;88:377–392. doi: 10.1016/s0306-4522(98)00230-9. [DOI] [PubMed] [Google Scholar]
- Rodriguez-Oroz MC, Rodriguez M, Guridi J, Mewes K, Chockkman V, Vitek J, DeLong MR, Obeso JA. The subthalamic nucleus in Parkinson's disease: somatotopic organization and physiological characteristics. Brain. 2001;124:1777–1790. doi: 10.1093/brain/124.9.1777. [DOI] [PubMed] [Google Scholar]
- Rodriguez-Oroz MC, Obeso JA, Lang AE, Houeto JL, Pollak P, Rehncrona S, Kulisevsky J, Albanese A, Volkmann J, Hariz MI, Quinn NP, Speelman JD, Guridi J, Zamarbide I, Gironell A, Molet J, Pascual-Sedano B, Pidoux B, Bonnet AM, Agid Y, et al. Bilateral deep brain stimulation in Parkinson's disease: a multicentre study with 4 years follow-up. Brain. 2005;128:2240–2249. doi: 10.1093/brain/awh571. [DOI] [PubMed] [Google Scholar]
- Rosin B, Slovik M, Mitelman R, Rivlin-Etzion M, Haber SN, Israel Z, Vaadia E, Bergman H. Closed-loop deep brain stimulation is superior in ameliorating parkinsonism. Neuron. 2011;72:370–384. doi: 10.1016/j.neuron.2011.08.023. [DOI] [PubMed] [Google Scholar]
- Rouse AG, Stanslaski SR, Cong P, Jensen RM, Afshar P, Ullestad D, Gupta R, Molnar GF, Moran DW, Denison TJ. A chronic generalized bi-directional brain-machine interface. J Neural Eng. 2011;8 doi: 10.1088/1741-2560/8/3/036018. 036018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Serruya MD, Hatsopoulos NG, Paninski L, Fellows MR, Donoghue JP. Instant neural control of a movement signal. Nature. 2002;416:141–142. doi: 10.1038/416141a. [DOI] [PubMed] [Google Scholar]
- Su Y, Allen CR, Geng D, Burn D, Brechany U, Bell GD, Rowland R. 3-D motion system (“data-gloves”): application for Parkinson's disease. IEEE Trans Instr Meas. 2003;52:662–674. [Google Scholar]
- Taylor DM, Tillery SI, Schwartz AB. Direct cortical control of 3D neuroprosthetic devices. Science. 2002;296:1829–1832. doi: 10.1126/science.1070291. [DOI] [PubMed] [Google Scholar]
- Theodosopoulos PV, Marks WJ, Jr, Christine C, Starr PA. Locations of movement-related cells in the human subthalamic nucleus in Parkinson's disease. Mov Disord. 2003;18:791–798. doi: 10.1002/mds.10446. [DOI] [PubMed] [Google Scholar]
- Vinjamuri R, Crammond DJ, Kondziolka D, Lee HN, Mao ZH. Extraction of sources of tremor in hand movements of patients with movement disorders. IEEE Trans Inf Technol Biomed. 2009;13:49–56. doi: 10.1109/TITB.2008.2006403. [DOI] [PubMed] [Google Scholar]
- Weinberger M, Hutchison WD, Dostrovsky JO. Pathological subthalamic nucleus oscillations in PD: can they be the cause of bradykinesia and akinesia? Exp Neurol. 2009;219:58–61. doi: 10.1016/j.expneurol.2009.05.014. [DOI] [PubMed] [Google Scholar]
- Wessberg J, Stambaugh CR, Kralik JD, Beck PD, Laubach M, Chapin JK, Kim J, Biggs SJ, Srinivasan MA, Nicolelis MA. Real-time prediction of hand trajectory by ensembles of cortical neurons in primates. Nature. 2000;408:361–365. doi: 10.1038/35042582. [DOI] [PubMed] [Google Scholar]
- Wiest MC, Bentley N, Nicolelis MA. Heterogeneous integration of bilateral whisker signals by neurons in primary somatosensory cortex of awake rats. J Neurophysiol. 2005;93:2966–2973. doi: 10.1152/jn.00556.2004. [DOI] [PubMed] [Google Scholar]
- Williams ZM, Neimat JS, Cosgrove GR, Eskandar EN. Timing and direction selectivity of subthalamic and pallidal neurons in patients with Parkinson disease. Exp Brain Res. 2005;162:407–416. doi: 10.1007/s00221-004-2035-6. [DOI] [PubMed] [Google Scholar]
- Zar JH. Biostatistical analysis. 4th edition. Upper Saddle River, NJ: Prentice Hall; 1999. [Google Scholar]
- Zirh TA, Lenz FA, Reich SG, Dougherty PM. Patterns of bursting occurring in thalamic cells during parkinsonian tremor. Neuroscience. 1998;83:107–121. doi: 10.1016/s0306-4522(97)00295-9. [DOI] [PubMed] [Google Scholar]