Case/Control Studies With Follow-up: Constructing the Source Population to Estimate Effects of Risk Factors on Development, Disease, and Survival

Abstract

If individuals in a case/control study are subsequently observed as a cohort of cases and a cohort of controls, weighted regression analyses can be used to estimate the association between the exposures initially recorded and events occurring during the follow-up of the 2 cohorts. Such analyses can be conceptualized as being undertaken on a reconstructed source population from which cases and controls stem. To simulate this population, the cohort of cases is added to the cohort of controls expanded with the reciprocal of the case disease incidence odds (the sampling weight) to include all individuals in the source population who did not develop the case disease. We use a simulated dataset to illustrate how weighted generalized linear model regression can be used to estimate the association between an exposure captured during the case/control study component and an outcome that occurs during follow-up.

By including a larger fraction of individuals in a source population who develop a disease than of those who do not, case/control (CC) studies are more efficient than the corresponding cohort studies in obtaining measures of association between exposures and disease risk [1–3]. With decreasing disease incidence, this sampling fraction decreases, and the relative efficiency of CC studies increases. In CC studies nested inside a defined cohort, the sampling fraction can be calculated directly as the number of controls, that is, the disease-free individuals in whom exposures are recorded, divided by the total number of individuals who did not develop the disease during the course of the cohort study [2–5].

Even CC studies that are not undertaken within a defined cohort can be conceptualized as being nested in a source population [2]. This population, or the underlying, “hypothetical” cohort, is elusive because it is neither captured in a roster nor followed to record outcomes. In CC studies that reuse data for measuring associations between exposures and an outcome other than that defined by being a case, the occurrence of the case disease can be used to calculate weights for appropriate regression analyses [6]. Once the disease risk is estimated, subsequent follow-up of CC study participants in a cohort of cases (CoCa) and a cohort of controls (CoCo) enables us to measure the association between exposures recorded at recruitment into the study and an outcome during follow-up, such as growth, disease, or death. Provided there is an association between an exposure and becoming a case, and cases have a higher risk of outcomes measured during follow-up than controls, CC studies with follow-up (CCF) are more efficient in identifying an association between the exposure and such outcomes than the corresponding cohort study, because the exposure is condensed in the CoCa.

We created an imagined population with a known exposure, case disease occurrence, and outcome distribution in order to present a conceptual framework of CCF data analysis using what we call the reconstructed population method (RPM). We then show how this framework can be translated into weighted regression analysis.

DECOMPOSING THE POPULATION AND THEN RECONSTRUCTING THE UNDERLYING COHORT FROM THE CASES AND THE CONTROLS

Let us imagine a population with N individuals where we recruit 1 control per case into a CC study and follow up the CoCa and the CoCo. The exposure (E) and outcome (O) are distributed as shown in Figure 1.

Figure 1.

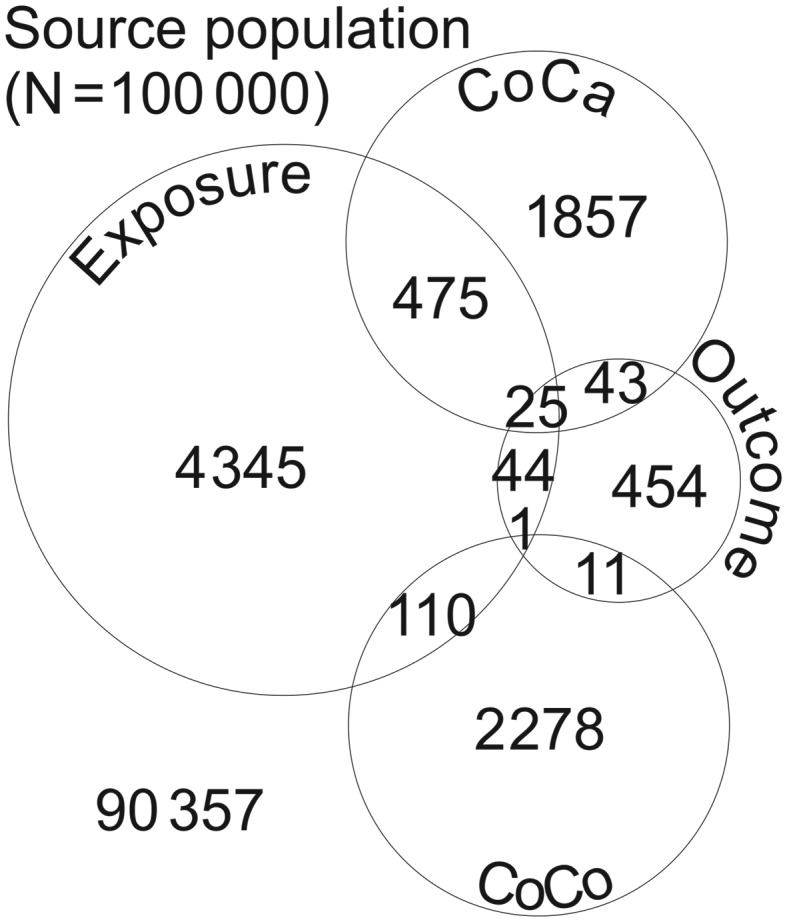
Venn diagram showing the distribution of 2400 cases and 2400 controls in relation to an exposure and an outcome in a population of 100 000 individuals. The numbers were generated using functions found in the Supplementary Appendix. Abbreviations: CoCa, cohort of cases; CoCo, cohort of controls.

Our incident cases are recruited into this CCF study within a short time window after the onset of a case-defining event (D); those who do not develop D within that time window are noncases (NC). The population was generated using functions (given in the Supplementary Appendix) that describe how E influences D, and how E and D separately and in combination, influence O (Figure 2).

Figure 2.

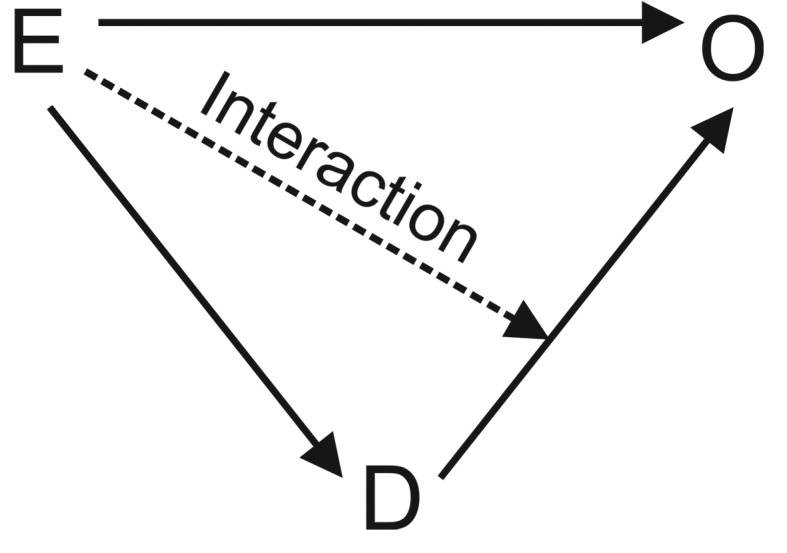
Schematic presentation of associations between an exposure (E), a case disease (D), and an outcome (O) in a population, where arrows indicate the direction of causality.

Because our study recruits an equal number of cases and controls, n, the number of NC in the population is N-n. Because n of all NC are recruited into the CoCo, the sampling fraction is calculated as n/(N-n), and the sampling weight as (N-n)/n [7]. In our example, where n = 2400 and N = 100 000, the sampling fraction is 2400/(100 000–2400) = 0.02459, the corresponding sampling weight (100 000–2400)/2400 = 40.67.

The relative risk (RR) of experiencing O given E for the whole population, in the CoCa, among the NC, and in the CoCo is shown in Table 1, rows A–D. The slight difference in RR between NC (Table 1, row C) and the CoCo (Table 1, row D) is an artifact of rounding.

Table 1.

Two-by-Two Tables Showing Distributions of Exposure (E) and Outcome (O) or Disease Defining Case Status (D) as a Basis for the Conceptual Framework of the Reconstructed Population Method

			O
			+	−	Total	Risk	RR	95% CI
A	Source Population
	E	+	70	4930	5000	0.014	2.6
		−	508	94 492	95 000	0.005
B	CoCa
	E	+	25	475	500	0.050	2.2
		−	43	1857	1900	0.023
C	NC
	E	+	45	4455	4500	0.010	2.0
		−	465	92 635	93 100	0.005
D	CoCo
	E	+	1	110	111	0.009	1.9
		−	11	2278	2289	0.005
			D
			+	−	(Odds)	(OR)
E	CC study
	E	+	500	111	4.505	5.4
		−	1900	2289	0.83
			O
			+	−
F	CoCa
	E	+	25	475	500	0.050	2.2	1.4–3.6
		−	43	1857	1900	0.023
G	CoCo
	E	+	1	110	111	0.009	1.9	.24–14.4
		−	11	2278	2289	0.005
H	CoCa + CoCo
	E	+	26	585	611	0.043	3.3	2.1–5.2
		−	54	4135	4189	0.013

Abbreviations: CC, case/control; CI, confidence interval; CoCa, cohort of cases; CoCo, cohort of controls; D, case-defining illness; NC, noncases; OR, odds ratio; RR, relative risk.

The odds ratio (OR) describing the association between E and getting D (ie, becoming a case) can be calculated from Table 1, row E (derived from Table 1, rows B and D), which distributes E among the cases (D⁺) and the controls (D⁻).

We now make a shift to the real world of epidemiology where only the CCF study represented by the CoCa (Table 1, row B) and the CoCo (Table 1, row D) is known. It is only conceptually nested in the source population (Figure 1). When analyzing the CCF study with the RPM, the exposure-outcome distributions in the CoCa and the CoCo should be identical but because they represent samples of our population, estimated associations should be provided with confidence intervals (CIs) (Table 1, rows F and G).

As an estimate for the association between E and O in the source population, it may seem tempting to ignore the CC sampling scheme and simply calculate RR on the combined data of the 4800 individuals in CoCa and CoCo (Table 1, row H). This corresponds to what Jiang et al lists as the first ad hoc approach to secondary analysis of CC data [8]. However, this approach assumes that D is conditionally independent of O given E, ie, when none of the effect of E on O is mediated by D. When getting D, on the other hand, does change the risk of O, this approach yields an unbiased estimate of the association between E and O only when the ratio of cases to NC in the source population is 1:1, ie, when D risk is 50%. In many situations, including in the Global Enteric Multicenter Study (GEMS) [9, 10], not only may E increase the incidence risk of D, this risk is usually much lower than 50%, and such an approach would accordingly overestimate the strength of the association between E and O (Table 1, row H).

Another approach, which is suggested by Nagelkerke et al, is to base the estimates only on the 2400 CoCo individuals (Table 1, row G) [4]. Jiang et al argues that this, in what they call the second ad hoc approach, may be approximately valid when D is rare [8], but emphasizes, just as do Reilly et al [6], that it is inefficient because it discards the case data. If there is an interaction between E and D on O, ie, when the association between E and O differs between CoCa and CoCo individuals, the bias may be substantial and even more unpredictable.

A third approach is to calculate RRs for the CoCa and for the CoCo, and, if there is no interaction between E and D on O, report the average of the 2 RRs using Mantel-Haenszel stratified analysis. This corresponds to Jiang et al's third ad hoc approach where the combined analysis of CoCa and CoCo individuals is adjusted for D [8]. This approach, which gives an RR estimate of 2.2 (95% CI, 1.4–3.5) in our example, not only disregards the fact that cases are oversampled (see Table 1, row H and the first ad hoc approach) but also de facto removes the effect of E on O that operates through, ie, is mediated by, D.

To use CCF data to estimate the association between E and O in a given population, we need to perform the analysis on the population reconstructed from the CoCa plus the NC. The sampling fraction needed to estimate NC cannot be calculated directly, but must be derived from an independent source of D incidence risk. Thus, if R is the incidence risk of D in the time window during which cases are recruited, and because we assume equal numbers of cases and controls, the sampling fraction of controls is proportional to the corresponding incidence odds, ie, R/(1 – R). If we assign a weight of 1 to the cases, the sampling weight of the controls is its reciprocal, (1 – R)/R.

In our example, let us assume that the D incidence risk, derived from a perfectly representative survey in the population, is 0.024. To reconstruct the population's NC, we multiply the number of individuals in the CoCo with the reciprocal of its corresponding incidence odds, the sampling weight, ie, 40.67, to obtain the reconstructed number of exposed and unexposed noncases (rNC) (Table 2, row A). We can then estimate the association between E and O in our reconstructed population consisting of the CoCa plus the rNC (Table 2, row B).

Table 2.

Reconstructing the Population

			O
			+	−	Total	Risk	RR
A	rNC
	E	+	1 × 40.67 = 40.67	110 × 40.67 = 4473.33	4514	0.013	1.9
		−	11 × 40.67 = 447.33	2278 × 40.67 = 92 639.67	93 086	0.005
B	Reconstructed populationa
	E	+	40.67 + 25 = 65.67	4473.33 + 475 = 4948.33	5014	0.013	2.5
		−	447.33 + 43 = 490.33	92639.67 + 1857 = 94 496.67	94 986	0.005

Two-by-two tables showing distributions of exposure, outcome, and disease that defines case status in the reconstructed noncases and in the reconstructed source population.

Abbreviations: D, case-defining illness; E, exposure; O, outcome; rNC, reconstructed noncases; RR, relative risk.

^a rNC + cohort of cases.

The difference in cell numbers between the imagined (Table 1, row A) and this reconstructed population is an artifact of the rounding we undertook to generate the CoCo (Table 1, row D). We do not include a 95% CI for this RR estimate because the sampling error should be derived from the CoCa and CoCo, not from the reconstructed population.

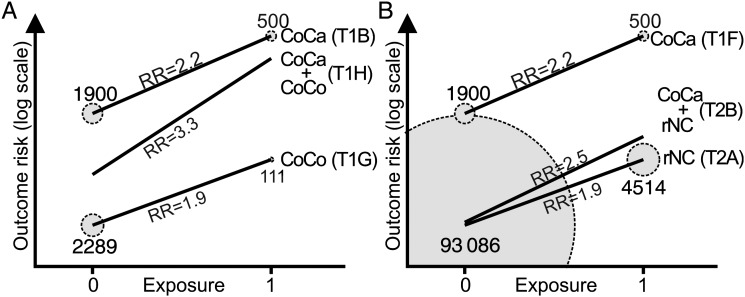
To explain the difference between the RR in the combined CoCa and the CoCo (Table 1, row H) and that in the reconstructed population (Table 2, row B), and to provide a transition into regression analysis of such data, Figure 3 illustrates how the weighting of the data influences the estimated effect of E on O.

Figure 3.

Regression lines reflecting the relative risk for an outcome during follow-up for (A) the cohort of cases (CoCa) + the cohort of controls (CoCo) and (B) the reconstructed population (CoCa + noncases that have been reconstructed from the CoCo × sampling weight [rNC]). The data underlying each line corresponds to the 2 × 2 tables in Table 1 and Table 2, so that (T1B) is the 2 × 2 in row B of Table 1, and (T2A) is the 2 × 2 table in row A of Table 2. Notice that the change in weights, or individuals, between (A) and (B) alters the end-point positions, and thus the slope of the middle line. (A) depicts the ill-advised approach to analyze the combined CoCo and CoCa data (Table 1, row H). The area of each circle is proportional to the number of exposed (Exposure = 1) and unexposed (Exposure = 0) individuals in the CoCa and the CoCo. (B) depicts the reconstructed population method (Table 2, row B). The area of each circle is proportional to the number of exposed and unexposed individuals in the CoCa and the rNC. Abbreviations: CoCa, cohort of cases; CoCo, cohort of controls; rNC, noncases that have been reconstructed from the CoCo × sampling weight; RR, relative risk.

ANALYSIS OF CCF DATA USING WEIGHTED REGRESSION ANALYSIS

As a more versatile analytic approach than that depicted in the previous section, we will now describe a weighted generalized linear model (GLM), illustrated graphically in Figure 3B). It is based on a dataset containing individual records for the 4800 individuals in the CCF, with variables indicating E and O status, as well as the above-mentioned sampling weight. Our Supplementary Appendix contains instructions for the use of R-functions and a spreadsheet to generate the data we have used in this paper and data with other underlying associations between E, D, and O.

We further address how weighted GLM can be used to depict interactions between E and D on O, and show how to estimate the extent to which getting D mediates an effect that E has on O. We have chosen to use Stata version 12.1 (Stata Corp) to illustrate the analyses, but other statistical software, such as R (The R Foundation for Statistical Computing; www.r-project.org) can also be used for the weighted regression analysis, notably using survey weights [11, 12].

The 3 above-mentioned ad hoc approaches disregard the fact that in CC studies where D incidence risk is <50%, the cases are oversampled [4]. Several of the cited papers advise weighting the cases and the controls according to their relative probability of being sampled into the study [4, 6, 8]. For the analysis of CCF studies where 1 control is included per case, and the sampling weight for each individual in the CoCa, ie, for each case, is set to 1, the weight for the controls is then (1 – R)/R, as described above. If there are n cases and m controls, the weights are 1 for cases and (n/m)(1 – R)/R for controls. Specifying sampling weights (called pweight in Stata, and hereafter given the variable name Pw) in the regression model de facto reconstructs the source population while basing the estimation of the corresponding standard error of the association between E and O on the actual observations in (Table 1, rows B and D), rather than on the reconstructed population in (Table 2, row B), the latter being an approach that would underestimate the standard error and thereby overestimate the precision of the RR.

To estimate the RR of outcome O given exposure E using a GLM of the binomial family with a log link and with sampling weight = Pw requires the following command in Stata:

eform directs Stata to yield RR instead of ln(RR), which is the default. In our example, the RR is 2.5 with a 95% CI spanning .67 to 9.6. This RR corresponds to the RR point estimate derived from the reconstructed population (Table 2, row B).

Failing to account for the fact that the cases are oversampled, by omitting the sampling weights, as in

depicted graphically in Figure 3A, yields an RR identical to that derived from the exposure-outcome distribution in the combination of the CoCa and the CoCo (Table 1, row H), ie, a substantial overestimation.

Regression analyses carry several other benefits, including the ease of adjusting estimates of associations between E and O for both categorical and continuous confounders. By including an interaction term, they enable us to effectively identify and estimate the size and statistical precision of any effect measure modification between E and D on O. An interaction means that RR_CoCa and RR_CoCo are different; ie, that getting D changes the risk of getting O given E. Simply adjusting for D would under such circumstances not only violate regression model assumptions, but also iron out any differential effect of E on O between those getting D and the NC.

When estimating the effect of E on O in the underlying cohort, one should refrain from adjusting for D, so that the resulting RR incorporates any effect of E on O mediated through D as well as any interaction between E and D on O. There are, however, situations where adjustment for D is warranted. For instance, to advise public health action, it may be important to break down the effect of E on O by the extent to which it is mediated through D. The size of such mediation can be measured as the relative change in the RR associated with E when estimated from models including and excluding, respectively, D as a covariate. The change in RR of O given E observed by including D as a covariate, ie,

corresponding to Jiang et al's third ad hoc approach [8] but now with an appropriate balance between cases and NC, would describe the relative change in O risk given E above and beyond that mediated by D. In our example, this adjusted RR is 1.97 (95% CI, .49–8.0). The mediation is accordingly 1.97/2.5 = 0.78.

If the 2 models were run on independent data sets, the estimated log RR values for E could be compared using their asymptotic standard errors and their independence. In the present case, however, the 2 models are run on the same data and the 2 estimates of log RR are thus dependent. The dependence may be accounted for with either of 2 different approaches. In Stata, the postestimation command suest stores individual score values from the weighted maximum (pseudo)likelihood estimation. The score values are then utilized to compute a robust standard error for the difference of the log RR values in the 2 models. The syntax for a log-binomial regression is

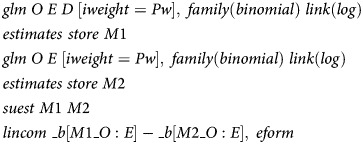The suest command requires the sampling weights to be used as “importance weights” (iweight) rather than “probability weights” (pweight).

This yields the (same) point estimate of 0.78 for the mediation and provides us with its 95% CI, which spans .64 to .93. Summarizing, one could say that of the RR = 2.5 that describes the effect of E on O, D contributes with 22% (95% CI, 7%–36%).

Alternatively, a bootstrap approach can be followed. For each bootstrap sample from the observed data, both models are fitted and the difference between log RR values is computed. The usual bootstrap standard errors and CIs can then be computed for the difference, and the CI can be converted to a CI for the ratio of the 2 RRs [13, 14].

If a GLM with a log link for the binomial family does not converge, as may be the case when O is common, or we for other reasons wish to describe the association between E and O with an OR using logistic regression, we can replace the log link with a logit link. GLM of the binomial family with an identity link estimates the absolute risk difference rather than the RR. Using this link enables us to model interactions on an additive scale, which may well be more relevant than doing so on a multiplicative scale in studies such as GEMS, which addresses exposures against which public health interventions, such as vaccination, may be warranted [2, 3, 15].

We have so far considered binary E and O variables, but the RPM is also valid for continuous outcomes. Thus, we can model symmetrically distributed continuous variables, such as infant development scores [16] and growth [17] using an identity link combined with a Gaussian distribution:

which is equivalent to the simpler linear regression command:

The effect estimate describes the change in O associated with E.

The RPM approach can also be used to model the effects of E on a count, such as that captured in an incidence rate or incidence density, using Poisson regression analysis:

or, when there is overdispersion, using a negative binomial distribution:

The effect estimate describes the incidence rate ratio for O where the exposure is E.

Finally, switching from GLM to time-to-event analysis, the Cox proportional hazards model is well adapted to weighted analysis. Time-to-event analysis requires 2 outcome variables, T is the time from recruitment into the CCF to censoring or to the occurrence of O, which here has the value 1 when the event (eg, death) occurs, or 0 if the individual is censored. In Stata, the sampling weights are included when the data is declared to be time-to-event data:

The hazard ratios for the event where E is the exposure is returned by

As in CC studies, having served as a control in a CCF study does not preclude an individual from later serving as a case or again being recruited as a control for another case [2, 3]. Similarly, having been enrolled as a case should not bar an individual from again being included as a case, nor from later being included as a control.

The presentation hitherto assumes that we have access to an exact sampling weight. The weight is calculated from the incidence risk, which we cannot obtain from the CCF study. In GEMS, the risk of D is estimated using healthcare utilization and attitude surveys (HUAS), which are undertaken every 4–6 months throughout the study [9, 18]. These estimates carry sampling errors, which need to be taken into account when ultimately estimating the effect of E on O in the underlying cohort.

In the Supplementary Appendix, we provide an Excel sheet, “Data,” in the workbook “RPMParametersAndTablesAug2012.xlsx,” which generates joint probabilities and 2 × 2 tables describing an imagined source population based on chosen parameters explained in the sheet “Codes.” We used it to generate the 2 × 2 tables presented in the current manuscript. This population (ie, the underlying cohort) has an exposure (E), a case disease (D), and a dichotomous outcome (O), the latter recorded during follow-up. “Data” enables the user to change the underlying probabilities and associations. In cell C30, it produces an R command highlighted in yellow which, using our R function “rpmBootstrap.R,” also provided in the Supplementary Appendix, estimates the composite measures of association, ie, the RR describing the effect of E on O in the reconstructed population (“Unadjusted RR”), the effect of E on O above and beyond that mediated by D (“Adjusted RR”), and the proportion of the Unadjusted RR which is mediated by D (“Mediation RR”). These estimates incorporate not only the sampling error of the CCF study but also that of the D incidence risk estimate obtained from an independent survey. This sampling weight is calculated based on the number of individuals who developed D (Huas.D) and the number of individuals who did not (Huas.NoD). The analysis might be modified in a variety of ways. For example, the effect of E on O might be modeled in terms of an OR in logistic regression; as a dichotomous outcome on an additive scale, using an identity link to measure risk difference (RD); as the numerator of incidence density or rate in Poisson or negative binomial regression; as a continuous variable in linear regression; or as a hazard ratio in Cox regression.

“rpmBootstrap.R” also generates a Stata (test.dta) and a comma-separated values (test.csv) data set, which contain data from the imagined CCF study and which can be used in a weighted GLM regression of the binomial family to estimate the RR, OR, and RD describing the effect of E on a dichotomous O. This approach, described in some detail in this paper, does not, however, incorporate the sampling error of the sampling weight estimate, and should accordingly be used only when this value is known, as when analyzing data from a CCF study nested in a defined cohort, or when surveys used to estimate D incidence risk are of a size that the derived sampling weights can be considered known values.

EFFECTS OF CHANGING THE POPULATION PARAMETERS

To illustrate how a change in parameters that define critical associations in the underlying population influences the observed effect and to guide the reader on how to use the material in the Supplementary Appendix, let us consider the alterations that occur if we change the association between E and D so that RR changes from 5 to 3. This is achieved by changing RR.D.E in cell D7 of the spreadsheet “Data” in the Workbook “RPMParametersAndTablesAug2012.xlsx” accordingly. The reader will in cell Q84 find that the association described by the RR in the reconstructed population between E and O is reduced from 2.5 to 2.3. Moreover, because we in this example keep the exposure prevalence in the population unchanged at 0.05, the incidence of D is reduced accordingly, in this example from 0.0240 to 0.0220. Such an incidence can be obtained in a survey of 273 individuals that identifies 6 new cases of D.

By running the command returned in cell C30 using the function “rpmBootstrap.R” in R and then the command “glm O E [pweight = Pw], family(binomial 1) link(log) eform” on the generated dataset “test.dta,” Stata will return not only the RR of 2.3 but also its 95% CI of .48–11.1. This assumes that the incidence risk of 0.0220 is a fixed number, an assumption which is questionable unless the survey has a very large sample size. Encompassing the sampling error of the sampling weight, our R bootstrap run yielded an RR of 2.4 (95% CI, .26–6.9). Adjusting for D reduced the RR to 2.0 (95% CI, .24–6.3) and quantified the mediation to be 0.86 (95% CI, .69–.96), ie, D contributing with 14% (95% CI, 4%–31%) of the effect of E on O.

If, on the other hand we change the association between E and D so that the RR changes from 5 to 10, the incidence increases to 0.0299, which can be obtained by a survey of 276 individuals of which 8 develop D. Under this scenario, cell Q84 in the sheet “Data” returns an RR of 3.1; Stata also yields its 95% CI of 1.2–7.9. Taking the sampling error of the survey-derived incidence estimate into account using rpmBootstrap, R yielded an RR of 3.4 (95% CI, .95–8.1), which was reduced to 1.9 (95% CI, .58–5.3) after adjustment for D; the mediation was 0.57 (95% CI, .42–.82), so according to this analysis, D contributed with 43% (95% CI, 18%–58%) of the effect of E on O.

The Supplementary Data can also be used to illustrate Jiang et al's argument that, if D changes the risk of O, the first ad hoc approach is valid only if incidence risk is 50% or 0.5. An incidence risk of 50% can be achieved by for example changing the population incidence of D for individuals not exposed to E, ie, p.0.D, to 0.41667. It can be seen that in this unrealistic scenario, Jiang's first ad hoc approach (cell Q54) yields an estimate identical to that obtained with the RPM (cell Q84).

DISCUSSION

We have presented a conceptual framework and illustrate analyses of data from CCF studies. If cases and controls are sampled independently of the exposures and a reliable measure of case disease occurrence can be obtained, such studies can with high efficiency estimate the association between the exposure recorded when the individuals are recruited into the CCF study and outcomes captured during follow-up thereafter. CCF studies exploit the condensation of individuals who develop the case disease into the CoCa, and are thereby more efficient than the corresponding cohort studies.

Previous reports have explored the reuse of CC data to estimate the association between exposures and alternative outcomes [6, 8, 19, 20]. While the suggested approaches range from inverse probability weighting to semiparametric marginal and full likelihood models, the key issue of obtaining appropriate sampling weights is hidden from view. Moreover, there is no suggestion of how to incorporate the standard error of the sampling weight into the composite effect measure generated by the proposed analyses. In general, the rarer the case disease and the smaller the surveys, the more extensive is the contribution from the sampling weight estimates to this joint sampling error.

A well-designed CCF study should be planned with the intent of estimating the association between antecedent exposures and outcomes during follow-up of the 2 cohorts. To enable the necessary weighting, such studies will ensure that appropriate estimates of case disease incidence, and thereby sampling weight, is captured. This poses particular challenges for CCF studies of infectious diseases, of which the GEMS [10]—to our knowledge—is a conspicuous first. Because the incidence of infectious diseases, such as diarrhea, varies over time and often between relatively closely situated locales, this risk in GEMS is estimated using HUAS rounds undertaken periodically during the study [9, 18], and not as a one-time snapshot [21]. The HUAS-based sampling weights are thereby likely to approach a “real-time” representation of the exposures, case disease, and outcomes, thus increasing the validity of the weighted regression analyses. An estimate of incidence risk derived from such survey data pooled over the duration of the study might be used, if estimates for individual survey rounds seem sufficiently similar. When incidence risk estimates from sequential surveys differ substantially and pooling over time accordingly is questionable, our advice is to first estimate the composite estimates, which describe the effect of E on O for each survey round. This may be of particular relevance for studies that describe microbial agents' contribution to infectious disease, where microepidemics can cause substantial monthly, seasonal, and year-to-year variations [22, 23]. When relevant and appropriate, one can thereafter pool the composite effect sizes, thereby ensuring transparency and epidemiological clarity.

This paper deals with single-population CCF studies that do not recruit controls matched to their corresponding cases, when sampling weights may need to be estimated differently (manuscript in preparation). Further, in a pooled analysis across populations (strata), the weights should be based on the relative stratum sizes and the incidence of D within each stratum.

In most CCF studies relatively few children will be enrolled more than once. Even in a cohort study in Guinea-Bissau, where children were followed with weekly stool specimen examination to identify infections with enteropathogens from birth up to 2 years of age, generalized estimating equations or frailty correction to account for between-child differences did not substantially alter point estimates or precision [24–26]. We suggest that if such correction yields no or little effect on point estimates and their precision, it need not be incorporated in the bootstrapping approaches that capture the sampling error of the sampling weight estimates. It is beyond the scope of this paper to describe in further detail how to take into account between-individual differences in the occurrence of exposures and/or outcomes [27, 28].

In this paper, we describe how a CCF study can be analyzed using weighted regression analysis and, using a bootstrap approach, incorporate the sampling error not only of the CCF component but also of the sampling weight derived from concurrently undertaken survey. Using the spreadsheet and an R function supplied in the Supplementary Appendix, we also show how changes in population parameters, exemplified by a change in the association between E and D, will change the association between E and O in the reconstructed population.

It is our contention that if reliable data on disease incidence are captured, thereby allowing sampling weights to be estimated, weighted regression analysis of CCF data can provide a useful, flexible, and effective analytic tool. We hope that by presenting the conceptual framework for CCF study design and guidance for RPM analysis using weighted regression, we will foster collaboration among infectious disease specialists, epidemiologists, and biostatisticians. Such collaboration in conceptualizing, designing, undertaking, analyzing, and interpreting CCF studies will improve the studies and make it more likely that the analyses and results will address issues of relevance to clinical infectious diseases and communicable disease epidemiology. With constraints on financial and human resources to address critical questions of relationships between specific infections and outcomes (such as clinical sequelae, nutritional impact of infection as well as illness- and infection-associated mortality), CCF studies, because of their efficiency, become particularly attractive. The RPM described in this paper provides a basis for estimating relationships in the population between infection with a pathogen (eg, a diarrheal pathogen as detected in GEMS) and consequences of infection over the period of follow-up. With respect to death possibly related to infection with a diarrheal pathogen, for example, CCF and RPM provide a way to go beyond describing case fatality among enrolled cases who are infected with the pathogen of interest to assessment of the association between the pathogen and mortality in the source population. One would anticipate that this addition to the toolbox of analytic epidemiology might also be useful in estimating the impact of interventions that decrease the frequency of a particular infection on specific outcomes (eg, stunting or death). This can help set priorities for choosing among potential interventions aimed at control of infectious diseases encountered by clinicians on the frontline of clinical care.

Supplementary Data

Supplementary materials are available at Clinical Infectious Diseases online (http://www.oxfordjournals.org/our_journals/cid/). Supplementary materials consist of data provided by the author that are published to benefit the reader. The posted materials are not copyedited. The contents of all supplementary data are the sole responsibility of the authors. Questions or messages regarding errors should be addressed to the author.