Fe²⁺ Block and Permeation of Ca_V3.1 (α1G) T-Type Calcium Channels: Candidate Mechanism for Non–Transferrin-Mediated Fe²⁺ Influx

Abstract

Iron is a biologically essential metal, but excess iron can cause damage to the cardiovascular and nervous systems. We examined the effects of extracellular Fe²⁺ on permeation and gating of Ca_V3.1 channels stably transfected in HEK293 cells, by using whole-cell recording. Precautions were taken to maintain iron in the Fe²⁺ state (e.g., use of extracellular ascorbate). With the use of instantaneous I-V currents (measured after strong depolarization) to isolate the effects on permeation, extracellular Fe²⁺ rapidly blocked currents with 2 mM extracellular Ca²⁺ in a voltage-dependent manner, as described by a Woodhull model with K_D = 2.5 mM at 0 mV and apparent electrical distance δ = 0.17. Extracellular Fe²⁺ also shifted activation to more-depolarized voltages (by ∼10 mV with 1.8 mM extracellular Fe²⁺) somewhat more strongly than did extracellular Ca²⁺ or Mg²⁺, which is consistent with a Gouy-Chapman-Stern model with surface charge density σ = 1 e⁻/98 Ų and K_Fe = 4.5 M⁻¹ for extracellular Fe²⁺. In the absence of extracellular Ca²⁺ (and with extracellular Na⁺ replaced by TEA), Fe²⁺ carried detectable, whole-cell, inward currents at millimolar concentrations (73 ± 7 pA at −60 mV with 10 mM extracellular Fe²⁺). With a two-site/three-barrier Eyring model for permeation of Ca_V3.1 channels, we estimated a transport rate for Fe²⁺ of ∼20 ions/s for each open channel at −60 mV and pH 7.2, with 1 μM extracellular Fe²⁺ (with 2 mM extracellular Ca²⁺). Because Ca_V3.1 channels exhibit a significant “window current” at that voltage (open probability, ∼1%), Ca_V3.1 channels represent a likely pathway for Fe²⁺ entry into cells with clinically relevant concentrations of extracellular Fe²⁺.

Introduction

Iron enters cells not only through the well characterized transferrin receptor-endocytosis pathway for ferric iron but also through the poorly defined non–transferrin-bound iron (NTBI) mechanism for both ferric and ferrous iron entry (Anderson and Vulpe, 2009). Candidate mechanisms for NTBI involve divalent metal ion transporter 1 (Gunshin et al., 1997), Zrt- and Irt-like protein 14 (Liuzzi et al., 2006), the nonselective transient receptor potential canonical 6 channel (Mwanjewe and Grover, 2004), and voltage-gated calcium channels. Both L-type (Tsushima et al., 1999; Oudit et al., 2003) and T-type (Kumfu et al., 2011) calcium channels have been implicated in Fe²⁺ uptake through the use of selective blockers. Currents carried by Fe²⁺ were recorded electrophysiologically for L-type channels (Tsushima et al., 1999) but not T-type channels.

Iron overload typically is caused by excess dietary absorption of iron in genetic hemochromatosis (Clark et al., 2010) or repeated blood transfusions, when red blood cells are broken down and the heme-bound iron is released (Kwiatkowski, 2011). Plasma NTBI levels can reach ∼5 μM (Loréal et al., 2000). NTBI is highly reactive and can cause the formation of damaging free radicals. Excess iron accumulates mainly in the liver and the heart (Andrews, 1999). In myocardial cells, iron overload affects cellular structure (Iancu et al., 1987), gene expression (Parkes et al., 2000), Ca²⁺ handling (Kim et al., 1995), and ion channel properties (Kuryshev et al., 1999). Because Ca_v3.1 channels are widely expressed in excitable and nonexcitable cells, including brain, ovary, placenta, heart, liver, and vascular smooth muscle (Perez-Reyes, 2003; Yunker and McEnery, 2003; Rodman et al., 2005), understanding the mechanism of Fe²⁺ transport by these channels is necessary for understanding their role in organ damage in conditions associated with iron overload.

In addition to acting as a pore blocker and permeant ion (Winegar et al., 1991; Tsushima et al., 1999), Fe²⁺ might have significant effects on channel gating, as is the case for other divalent cations (Elinder and Arhem, 2003). Gating changes induced by divalent cations may arise from pore occupancy, allosteric effects of binding to sites outside the pore (Beedle et al., 2002; Kang et al., 2006; Traboulsie et al., 2007), or screening or binding to surface charges (Zhou and Jones, 1995).

We found that Fe²⁺ blocks currents carried by Ca²⁺ or Ba²⁺ through voltage-dependent block within the pore. Fe²⁺ also permeates, less well than Ca²⁺ or Ba²⁺. Effects of Fe²⁺ on gating are consistent with a surface charge mechanism, in which Fe²⁺ both screens and binds to surface charges. The effects of Fe²⁺ to block and to shift gating would be minimal at clinically observed concentrations of Fe²⁺. However, the estimated rates of Fe²⁺ permeation suggest that Ca_V3.1 may be a significant source of Fe²⁺ entry into cells even at the resting potential.

Materials and Methods

Electrophysiological Studies.

Patch-clamp experiments were performed in the whole-cell configuration by using HEK293 cells stably transfected with Ca_V3.1 (α1G) calcium channels, as described (Khan et al., 2008). Electrodes were made from borosilicate glass, with open-pipet resistances of 1.8 to 2.3 MΩ and access resistances of 5 ± 1 MΩ before compensation (80%). Currents were digitally sampled at 50 kHz, with 10-kHz analog filtering, by using an Axopatch 200 amplifier and pClamp 8.2 software (Molecular Devices, Sunnyvale, CA). Leak and capacitative currents were subtracted online by using a −P/4 protocol. Experiments were performed at room temperature (∼22°C).

We evaluated the effects of Fe²⁺ by using two basic voltage protocols, i.e., direct depolarization to different voltages (I-V protocol) and preactivation of channels through strong brief depolarization, followed by steps to different voltages (II-V protocol) (Figs. 1 and 2). With the assumption that the effects of Fe²⁺ are effectively instantaneous (as we conclude below), this approach allows separation of effects on permeation versus gating (Hodgkin and Huxley, 1952; Serrano et al., 1999; Khan et al., 2008; Obejero-Paz et al., 2008; Lopin et al., 2012). Currents measured immediately after repolarization with the II-V protocol should be directly proportional to the current through a single open channel (Fig. 1A). Therefore, effects of Fe²⁺ on the II-V relationship would reflect the inhibition of currents through open channels. Effects on the I-V relationship, in contrast, would reflect the net effects of the ion on both permeation and gating.

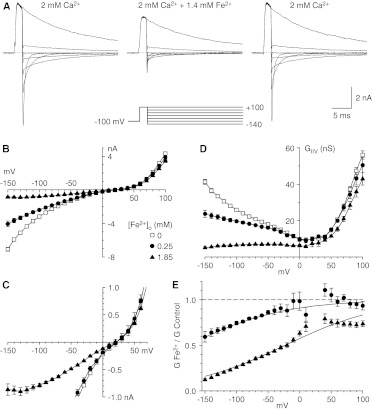
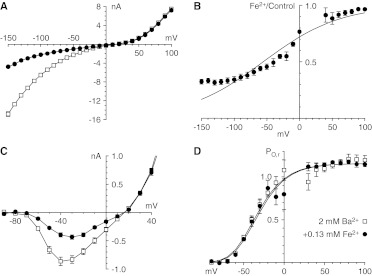
Fig. 1.

Block by Fe²⁺ of currents carried by Ca²⁺ with the II-V protocol. A, sample currents recorded by using the protocols illustrated below the middle records, under control conditions (left), after the addition of Fe²⁺ (middle), and after washout of Fe²⁺ (right) (3-kHz Gaussian filter). Currents are shown in 40-mV increments. B, II-V relationships from the protocol used in A, under control conditions (0 mM Fe²⁺) and with two concentrations of Fe²⁺ (n = 4 for each concentration). C, expanded view of II-V relationships. D, chord conductances calculated for the data in B. E, inhibition by Fe²⁺, expressed as the ratio of the chord conductance with Fe²⁺ to the chord conductance under control conditions. Data are not shown near the reversal potential, where errors in conductance calculations can be large. Solid curves, fits to the model described by Woodhull (1973). Symbols shown in B apply to B to E.

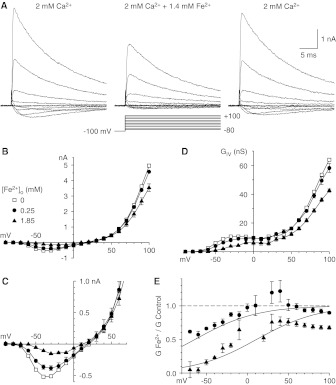
Fig. 2.

Block by Fe²⁺ of currents carried by Ca²⁺ with the I-V protocol. A, sample records, shown in 20-mV increments (3-kHz Gaussian filter). B, I-V relationships with the protocol used in A, with the same cells as in Fig. 1. C, I-V relationships on an expanded scale. D, chord conductances calculated from the data in B. E, inhibition by Fe²⁺, determined as chord conductance ratios and fitted to the model described by Woodhull (1973). Data near the reversal potential are not shown. Symbols shown in B apply to B to E.

Standard Recording Solutions.

The intracellular solution contained 2 mM CaCl₂, 1 mM MgCl₂, 120 mM NaCl, 10 mM HEPES, 4 mM MgATP, and 11 mM EGTA, adjusted to pH 7.2 with NaOH (total Na⁺ concentration, 145 mM; calculated free Ca²⁺ concentration, 70 nM). The normal extracellular solution contained 2 mM CaCl₂, 128 mM NaCl, 5 mM ascorbic acid, 10 mM glucose, and 20 mM HEPES, adjusted to pH 7.2 with NaOH (total Na⁺ concentration, 145 mM). Where noted, CaCl₂ was replaced by BaCl₂.

Extracellular Solutions Containing Fe²⁺.

Extreme care must be taken to maintain iron in the soluble Fe²⁺ state. To do this, FeCl₂ was added to the solution only after cell patches were prepared and control currents were being recorded, to reduce the amount of time Fe²⁺ could oxidize. Solutions were prepared 1 to 2 min before they were applied to the cells and were used within 6 min after preparation. Fe²⁺ was added to the final desired concentration from a 200 mM stock solution of FeCl₂·4H₂O in 1% (v/v) HCl. The free Fe²⁺ concentration in each solution was measured, by using the ferrozine method (Dorey et al., 1993; Viollier et al., 2000), while the electrophysiological experiments were being performed. To this end, a sample of the extracellular solution was diluted to a final concentration of 100 μM Fe²⁺ with a solution containing the same components (except FeCl₂) or a solution containing 5 mM ascorbate (pH 3.3), to reduce all iron forms; 0.75 ml of those samples was mixed with the same volume of 2 mM ferrozine [3-(2-pyridyl)-5,6-diphenyl-1,2,4-triazine-4′,4″-disulfonic acid], and absorbance was measured (at 562 nm) with a Beckman DU640B spectrophotometer (Beckman Coulter, Fullerton, CA). Standard solutions in the range of 10 to 100 μM Fe²⁺ were prepared through dilution of a stock solution of 20 mM FeCl₂·4H₂O, with a final concentration of 5 mM ascorbic acid. Measured free Fe²⁺ concentrations ranged from 28 to 95% of the nominal value. Throughout this article, Fe²⁺ concentration values are the actual values measured with this procedure.

For experiments examining block by Fe²⁺, Fe²⁺ was added to the normal extracellular solutions (2 mM Ca²⁺ or 2 mM Ba²⁺). To investigate whether Ca_V3.1 currents allowed Fe²⁺ influx, we designed extracellular solutions in which Fe²⁺ was the only charge carrier. To this end, extracellular NaCl was replaced by TEA-Cl, Ca²⁺ was replaced by Fe²⁺, and solutions were maintained at pH 7.0 to reduce the rate of iron oxidation; pH values of 6.8 to 7.05 measured at the end of the experiment were considered acceptable. A control solution containing 2 mM Ca²⁺ was applied to the cell before and after the test solution. Because inward currents with Fe²⁺ were small, we performed experiments to evaluate the contributions of gating currents, by using an extracellular solution containing 140 mM NaCl, 2 mM CdCl₂, and 1 mM LaCl₃.

Data Analyses.

Most methods were as described (Lopin et al., 2012). Throughout the article, data are presented as mean ± S.E.M. We used the paired t test implemented in Origin 7.0 (OriginLab Corp., Northampton, MA) to assess differences between means when control values were from the same cell. We used one-way analysis of variance to investigate differences between means from different groups. Two-tailed p values of <0.05 were considered statistically significant.

Fe²⁺ Block.

The voltage dependence of block by Fe²⁺ was described with a model that assumed that Fe²⁺ binds within the electrical field of the membrane, with Fe²⁺ entry and exit exclusively from the extracellular solution (Woodhull, 1973),

where f is the fraction of peak tail current remaining in the presence of Fe²⁺ and K_D,0 is the K_D at 0 mV.

Permeation Model.

The classic two-site/three-barrier model of channel permeation (Almers and McCleskey, 1984; Hess and Tsien, 1984) was extended to Fe²⁺, as for Cd²⁺ (Lopin et al., 2010, 2012). Parameters for the energy profile of Fe²⁺ were chosen to minimize the sum of absolute errors attributable to Fe²⁺ block and permeation for recorded currents. The parameters for Ca²⁺, Ba²⁺, Mg²⁺, and Na⁺ were fixed to the values reported by Lopin et al. (2010), which were fit to a wide range of ionic conditions. The minimization procedure produced multiple parameter sets with similar errors (within 15%), all with qualitatively similar currents and energy profiles (all energy parameters varied in a 1-kT range across parameter sets). Because we use the model to predict Fe²⁺ transport rates, we chose the parameter set that best fit the currents carried by Fe²⁺. All other parameter sets predicted Fe²⁺ currents larger than those observed, as well as predicting Fe²⁺ transport rates up to twice as high as the rate observed with the chosen parameter set.

Because control currents in Fe²⁺ permeation experiments were significantly larger than control currents in the experiments reported by Khan et al. (2008), we assumed 18,000 channels/cell, rather than 8000 channels/cell. We expected that Fe²⁺ currents would be minimally affected by the 0.2-pH unit difference between solutions. Because it was not always possible to record control currents after application of the test solution, we used the first control current for normalization, a procedure that would underestimate iron currents in the presence of current rundown.

Gating.

To investigate the effects of Fe²⁺ on channel activation, we fitted simultaneously the relative open probability (P_o,r) values measured under control conditions and with Fe²⁺ to a fourth-power Boltzmann function,

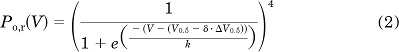where V_0.5 is the half-point of activation for an individual voltage sensor, k is the voltage sensitivity, ΔV_0.5 is the shift in V_0.5 induced by Fe²⁺, and δ is the Kronecker δ function, which takes the value of 1 with Fe²⁺ and 0 for control conditions.

The effect of Fe²⁺ on the rate of channel opening was addressed indirectly by studying changes in the time to peak (TP). To this end, we simultaneously fitted data from control and Fe²⁺ experiments to eq. 3,

where V_1−TP∞ is the voltage at which the time to peak is equal to 1 minus the asymptotic value of TP (TP_∞), k is the voltage sensitivity, and ΔV_1−TP∞ is the shift along the voltage axis.

The effect of Fe²⁺ on the closing rate was investigated by fitting simultaneously the deactivating time constants between −70 and −120 mV to eq. 4,

where V_τ2ms is the voltage at which the time constant (τ) equals 2 ms, ΔV_τ2ms is the displacement induced by Fe²⁺ along the voltage axis, and k is the slope factor. Gating shifts were calculated by using the Minerr procedure (Mathcad; Adept Scientific, Letchworth Garden City, Herts, UK) to calculate the values of σ_t and K_Fe that minimized χ² for ΔV_0.5, ΔV_1−TP∞, and ΔV_τ2ms.

⁵⁹Fe²⁺ Kinetic Transport Studies.

For cellular ⁵⁹Fe²⁺ uptake experiments, ⁵⁹Fe²⁺ was generated from ⁵⁹FeCl₃ [specific activity, >5 Ci (185 GBq)/g of FeCl₃ in 0.5 M HCl; Perkin-Elmer, Rodgau, Germany] as described elsewhere (Garrick et al., 2006). ⁵⁹Fe²⁺ uptake (18.5 kBq/ml ⁵⁹FeCl₂ in 200–400 μM FeSO₄) was assessed with confluent monolayers of HEK293 cells or HEK293-Ca_V3.1 cells, with or without 25 μM (1S,2S)-2-(2-(N-[(3-benzimidazol-2-yl)propyl]-N-methylamino)ethyl)-6-fluoro-1,2,3,4-tetrahydro-1-isopropyl-2-naphtyl cyclopropanecarboxylate dihydrochloride (NNC 55-0396), a selective inhibitor of T-type calcium channels (Huang et al., 2004). Monolayers were washed with 2 mM desferrioxamine mesylate and solubilized with 1 N NaOH, and cellular radioactivity was measured with a gamma counter.

Results

Effects of Fe²⁺ on Permeation.

Extracellular application of Fe²⁺ reversibly inhibited currents through Ca_V3.1 channels that were evaluated by using the II-V protocol (Fig. 1A). Under these ionic conditions (2 mM extracellular Ca²⁺ and 145 mM intracellular and extracellular Na⁺ levels), Ca_V3.1 channels exhibited inward currents carried mostly by Ca²⁺ and outward currents carried by Na⁺. It should be noted that the inward tail currents were smaller and faster with Fe²⁺. Peak tail currents were reduced immediately after repolarization, which suggests that Fe²⁺ reached steady-state block rapidly. Block was concentration- and voltage-dependent, with strong inhibition at negative voltages but little effect on outward currents (Fig. 1B). Fe²⁺ had no clear effect on the reversal potential (Fig. 1C). The voltage dependence of block was best illustrated by chord conductances, especially near the reversal potential (Fig. 1D). The fractional inhibition determined from chord conductances was well described by the model reported by Woodhull (1973) (Fig. 1E), which suggests negligible relief of block with hyperpolarization. The data were fit best with K_D = 2.5 mM at 0 mV and electrical distance δ = 0.17.

Effects of Fe²⁺ on Gating.

Fe²⁺ also inhibited currents that were examined by using the I-V protocol and evoking currents through direct depolarization from the holding potential (Fig. 2A). The peak current at each voltage is shown in Fig. 2B, on an expanded scale in Fig. 2C, and as chord conductances in Fig. 2D. With this protocol, inhibition by Fe²⁺ was voltage-dependent and stronger at more-negative voltages, and the voltage that produced the peak inward current was shifted to more-positive voltages (Fig. 2C). Inhibition of peak current also could be described with the model reported by Woodhull (1973), with K_D = 1.4 mM at 0 mV and δ = 0.33.

Why does the effect of Fe²⁺ appear to be more potent and more voltage-dependent with the I-V protocol? The currents recorded in that manner are affected not only by permeation (e.g., channel block) but also by gating (e.g., surface charge effects of Fe²⁺).

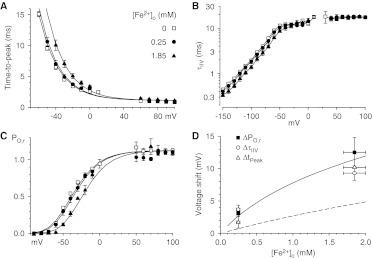
We examined the effects of Fe²⁺ on activation with three measures, i.e., effects on the time courses of channel activation (Fig. 3A) and deactivation (Fig. 3B) and on the voltage dependence of peak activation (Fig. 3C). Activation curves were measured as the relative open probability, calculated as the ratio of the peak current from the I-V protocol divided by the current at the same voltage from the II-V protocol (Fig. 3C) (Serrano et al., 1999; Khan et al., 2008). This parameter is a more-accurate reflection of channel open probability than is the more commonly used chord conductance, because the open-channel conductance is not constant with voltage (Fig. 1D) and thus the chord conductances measured with the I-V protocol (Fig. 2D) are not pure measures of channel activation (Khan et al., 2008). The three measures of the voltage dependence of channel gating were affected by Fe²⁺ in similar manners (Fig. 3D), demonstrating positive shifts along the voltage axis with Fe²⁺. It is noteworthy that Fe²⁺ did not affect the limiting rates for channel activation (Fig. 3A) or inactivation (Fig. 3B) at strongly depolarized voltages.

Fig. 3.

Effects of Fe²⁺ on gating. A, effects of Fe²⁺ on the time to peak currents with the I-V protocol. B, effects of Fe²⁺ on the time constants for deactivation with the II-V protocol. C, effects of Fe²⁺ on channel activation, determined as the ratio of the peak I-V current to the II-V current at the same voltage. D, voltage shifts for the data shown in A to C, for the activation curve (ΔP_O,r), for deactivation (Δτ_IIV), and for time to peak (Δt_Peak). Solid curve, fit to the Gouy-Chapman-Stern theory. Dashed curve, fit to voltage shifts induced by Ca²⁺, Ba²⁺, and Mg²⁺ (Khan et al., 2008). Symbols shown in A apply to A to C. Data near the reversal potential are not shown in A to C (same cells as Figs. 1 and 2).

Qualitatively, the observed voltage shifts were as expected on the basis of a surface charge mechanism, with cations screening a negative surface charge on the extracellular side. Quantitatively, the effect was approximately twice as large as those observed previously for Ca²⁺, Ba²⁺, and Mg²⁺ (Khan et al., 2008) (Fig. 3D). Because simple charge-screening (Gouy-Chapman theory) assumes that all divalent cations are equivalent, we considered the possibility that Fe²⁺ could bind to the surface charge as well as screening it (Gouy-Chapman-Stern theory), as observed for Cd²⁺ (Lopin et al., 2012). Figure 3D demonstrates that the data could be described well by using the surface charge density determined previously for the effects of Ca²⁺, Ba²⁺, and Mg²⁺ (σ = 1 e⁻/98 Ų⁾ (Khan et al., 2008) but allowing binding of extracellular Fe²⁺ to the surface charge with K_Fe = 4.5 M⁻¹.

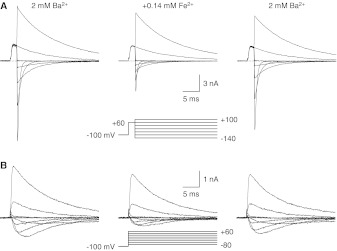
Effects of Fe²⁺ with 2 mM Ba²⁺.

Ca_V3.1 calcium channels are selective for Ca²⁺ over Ba²⁺ on the basis of the classic criterion of permeability ratios, which reflects a more-positive reversal potential with Ca²⁺ and indicates greater selectivity versus monovalent cations (Serrano et al., 2000). Divalent and trivalent cations, e.g., Mg²⁺ (Serrano et al., 2000), Ni²⁺ (Obejero-Paz et al., 2008), Y³⁺ (Obejero-Paz et al., 2004), and Cd²⁺ (Lopin et al., 2012), block more rapidly and/or strongly when Ba²⁺ is the charge carrier, which reflects stronger competition versus the less-permeant Ba²⁺ ion; this was also observed for Fe²⁺ (Figs. 4 and 5). Fe²⁺ at 0.13 mM blocked strongly at hyperpolarized voltages, with either the II-V (Figs. 4A and 5A) or I-V (Figs. 4B and 5C) protocol. Inhibition measured from chord conductances determined by using the II-V protocol was described with a Woodhull model with K_D = 0.33 mM at 0 mV and δ = 0.21 (Fig. 5B). Block was slightly overestimated with the model at the most negative voltages, which suggests relief of block through the exit of Fe²⁺ into the cell. That low concentration of Fe²⁺ had minimal effects on channel activation (Fig. 5D). The activation curve was shifted by 2.8 ± 1.0 mV and the time constants for activation and deactivation were shifted by 2.9 ± 0.5 mV and −1.0 ± 1.6 mV, respectively.

Fig. 4.

Effects of Fe²⁺ with 2 mM Ba²⁺ as the charge carrier. A, sample records with the II-V protocol, shown in 40-mV increments. B, sample records with the I-V protocol, shown in 20-mV increments (3-kHz Gaussian filter).

Fig. 5.

Analysis of effects of Fe²⁺ with 2 mM Ba²⁺. A, II-V relationships under control conditions and with 0.13 mM Fe²⁺. B, inhibition by Fe²⁺, determined as chord conductance ratios (Fe²⁺/control) and fitted to a Woodhull model. C, I-V relationships (currents from 50 to 100 mV not shown). D, activation curves determined from I-V/II-V current ratios. Data near the reversal potential are not shown in B and D (n = 4 for all panels).

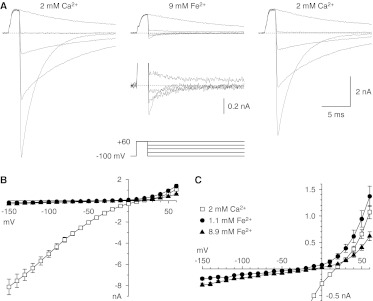
Permeation by Fe²⁺.

When extracellular Ca²⁺ and Na⁺ were replaced by Fe²⁺ and TEA (respectively), inward currents were small but clearly detectable (Fig. 6). Currents were larger with 9 mM Fe²⁺ than 1 mM Fe²⁺ (Fig. 6C), as expected for permeation by Fe²⁺. The chord conductance with 9 mM Fe²⁺ was 1.5 ± 0.2-fold larger than that with 1 mM Fe²⁺, averaged from −150 to −50 mV (p < 0.01).

Fig. 6.

Permeation by Fe²⁺. A, sample records with the II-V protocol, in 40-mV increments (3-kHz Gaussian filter). Inset below the middle record, currents from −100 to +20 mV, on a 5× expanded scale. B, II-V relationships. C, II-V relationships on an expanded scale. Symbols shown in C also apply to B. Data in B and C are from seven cells, four with 1.1 mM Fe²⁺, and five with 8.9 mM Fe²⁺.

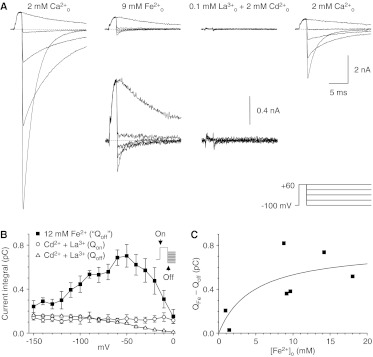
An alternative interpretation is that the inward currents observed with Fe²⁺ might be “off” gating currents. To evaluate that possibility, we compared the integrated tail current amplitudes with gating currents isolated by using a combination of 0.1 mM extracellular La³⁺ and 2 mM extracellular Cd²⁺ to block ionic currents (Fig. 7). Figure 7A, insets, shows that the inward currents were larger with extracellular Fe²⁺. Quantitatively, the integrated Fe²⁺ tail current greatly exceeded the gating currents at voltages at which tail currents were relatively large and slowly decaying (Fig. 7B). The amplitude of the integrated tail current increased with the extracellular Fe²⁺ concentration (Fig. 7C). There was considerable scatter in the data, which presumably reflects cell-to-cell variations in channel expression levels; therefore, the apparent K_D of 4.7 mM for current saturation with extracellular Fe²⁺ should be considered an estimate.

Fig. 7.

Comparison of tail currents with Fe²⁺ with gating currents. A, sample records with the II-V protocol, in 40-mV increments. Partial recovery (right) after superfusion with the solution used to isolate gating currents (La³⁺ plus Cd²⁺) should be noted. Insets below the middle records, recordings on a 5× expanded scale, to show tail currents with Fe²⁺ and on- and off-gating currents with La³⁺ plus Cd²⁺ (3-kHz Gaussian filter). B, integrated tail currents with Fe²⁺, compared with the on-gating current (measured during depolarization to 60 mV) and off-gating current (measured after repolarization) (Fe²⁺ tails, n = 5; on- and off-gating currents, n = 4). C, portion of the integrated tail current amplitude attributable to Fe²⁺ entry, as a function of Fe²⁺, for the five cells in B and two cells tested with ∼1 mM Fe²⁺. Solid curve, fit to a single saturable binding site with a K_D of 4.7 mM and a maximal current of 0.78 pC.

Reversal potentials were less positive with Fe²⁺ than with Ca²⁺ (Fig. 6C), i.e., −26.1 ± 4.7 mV (n = 4) with 1.1 mM Fe²⁺ and −9.0 ± 3.7 mV (n = 5) with 8.9 mM Fe²⁺. Those values correspond to Fe²⁺/Na⁺ permeability ratios of 16 and 5, respectively, which compare with a Ca²⁺/Na⁺ permeability ratio of 87 and a Ba²⁺/Na⁺ permeability ratio of 44 (Khan et al., 2008) and indicate a Fe²⁺/Ca²⁺ permeability ratio of 0.06 to 0.18. Incubation studies with ⁵⁹Fe²⁺ showed a trend toward increased Fe²⁺ uptake by Ca_v3.1 channels, but results were inconclusive because of high background levels of Fe²⁺ uptake and increased cell death rates (data not shown).

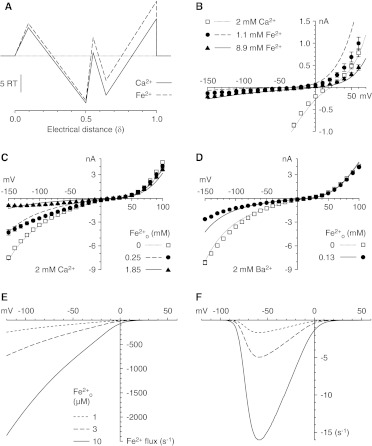
Model for Fe²⁺ Permeation and Block.

We fitted the data on Fe²⁺ permeation and block to a two-site/three-barrier Eyring rate theory model (Almers and McCleskey, 1984). The fit of the model to the data is shown for Fe²⁺ permeation (Fig. 8B) and for block of current carried by extracellular Ca²⁺ (Fig. 8C) or Ba²⁺ (Fig. 8D).

Fig. 8.

Two-site/three-barrier Eyring model for permeation and block by Fe²⁺. A, energy levels and electrical distances for barriers and wells for Ca²⁺ and Fe²⁺. Energy levels (outside to inside) were 9.32, −12.73, 5.26, −6.97, and 15.65 RT. The electrical distances and energy profiles for Na⁺, Mg²⁺, and Ba²⁺ are from the report by Lopin et al. (2010). B to D, fits of the model to experimental II-V data are shown for permeation (B), block of the current carried by 2 mM Ca²⁺ (C), and block with 2 mM Ba²⁺ (D). E, calculation of the rate of Fe²⁺ entry with the indicated extracellular Fe²⁺ concentrations, in the presence of 2 mM extracellular Ca²⁺, for a single open channel. F, calculation of the steady-state rate of Fe²⁺ entry by considering channel gating (activation and inactivation). The steady-state open probability-voltage relationship calculated with the model described by Serrano et al. (1999) was convolved with the curves in E.

We used the model to estimate the extent of Fe²⁺ permeation at concentrations more relevant to physiological or pathophysiological conditions (Fig. 8, E and F). Simulated addition of 1 to 10 μM Fe²⁺ (to extracellular solutions also containing 2 mM Ca²⁺) yielded predicted Fe²⁺ influx rates of up to several hundred ions per second through a single open channel (Fig. 8E). The mechanism of Fe²⁺ permeation predicted by the model is similar to the permeation of Ca²⁺, with quantitative differences. The two ions seem to enter the pore and to bind to the first site similarly; however, Fe²⁺ is slower to move to the second site and binds less tightly to the second site, and the energy barrier to Fe²⁺ exit from the pore is higher.

Ca_V3.1 channels inactivate rapidly and strongly but inactivation is incomplete, with 1 to 2% of channels remaining open even after 0.3 s, i.e., 20 times the time constant for inactivation (Serrano et al., 1999). This produces a “window current” that can potentially allow maintained entry of divalent cations into the cell even near the resting potential. When the two-site/three-barrier model for permeation was combined with the model described by Serrano et al. (1999) for gating of Ca_V3.1 channels, the predicted steady-state Fe²⁺ influx peaked at 6 ions/s near −60 mV, with 10 μM extracellular Fe²⁺ (Fig. 8F). Correction for slow inactivation would decrease these values by ∼35% (Hering et al., 2004).

Discussion

Overall Findings.

We conclude that Fe²⁺ affects currents through Ca_V3.1 channels through three mechanisms, i.e., block of the open pore by Fe²⁺, shifts in channel activation, and permeation by Fe²⁺. Fe²⁺ permeates Ca_V3.1 pores poorly, compared with Ca²⁺ or Ba²⁺ or even Cd²⁺ (Lopin et al., 2012), but the estimated rate of Fe²⁺ entry suggests that Ca_V3.1 is a strong candidate for Fe²⁺ influx under conditions in which free extracellular Fe²⁺ is present at micromolar concentrations. We discuss first the biophysical mechanisms of Fe²⁺ interactions with calcium channels and then the potential implications for iron overload.

Block by Fe²⁺.

The effect of Fe²⁺ on the II-V relationship was consistent with block through occupancy of the pore, presumably at the selectivity filter responsible for selectivity for Ca²⁺ and other divalent and trivalent cations. First, block was voltage-dependent and was well approximated with the model described by Woodhull (1973), with the assumption of binding to a site within the electrical field of the membrane. Second, block was ∼4-fold stronger when 2 mM Ba²⁺ was the charge carrier (compared with 2 mM Ca²⁺), which suggests ion-ion competition within the pore. Reduction of the current measured instantaneously indicates that Fe²⁺ equilibrates rapidly with the open pore, on the time scale of the voltage clamp (∼0.1 ms). For the lowest concentration used (0.13 mM Fe²⁺, for experiments with Ba²⁺), that indicates binding with a bimolecular rate constant of 10⁸ M⁻¹ s⁻¹ or faster, near the diffusion limit.

Effects of Fe²⁺ on Gating.

The effect of Fe²⁺ on the peak current measured with the I-V protocol was stronger and more voltage-dependent than that observed with the II-V protocol. Because currents measured with the I-V protocol are affected by both permeation and gating (i.e., changes in the probability that a channel would be open at a particular voltage and time), this finding suggests that Fe²⁺ affects the response of the channel to voltage. Figure 3 shows that the effect of Fe²⁺ could be attributed to screening and binding to surface charge. We assumed a Guoy-Chapman-Stern model for simplicity, but the possibility of a specific binding site on the channel cannot be excluded.

Fe²⁺ Permeation.

In the absence of extracellular Ca²⁺ and Na⁺, Ca_v3.1 channels carry a significant Fe²⁺ current that is saturated in the millimolar range. The currents measured with Fe²⁺ were small (which indicates that Fe²⁺ is a poorly permeant ion) but were noticeably larger than could be attributed to gating charge movement (Fig. 7B). This current increased as the external Fe²⁺ concentration was increased, which suggests that the current was carried by Fe²⁺ and not contaminating cations.

Ca_V3.1 as Pathway for Fe²⁺ Entry.

To explain the effects of Fe²⁺ on permeation, we expanded a model of permeation for Ca_v3.1 channels to account for Fe²⁺. The model fit the data well, although block of outward currents with 1.1 mM Fe²⁺ was underestimated (Fig. 8B). The model could assess Fe²⁺ permeation when Ca²⁺ and Mg²⁺ were present at physiological concentrations. Figure 8, E and F, shows the calculated transport rates for Fe²⁺ at external concentrations in the range of 1 to 10 μM and the membrane potentials encountered at rest and during action potentials. Ca_v3.1 channels have a window current attributable to incomplete inactivation (Serrano et al., 1999) that leaves ∼1 to 2% of channels open at resting membrane potentials. Because channels are open even at resting membrane potentials, we used our model of Ca_v3.1 channel gating to calculate the fraction of channels expected to be open at steady state (Serrano et al., 1999). This value multiplied by the transport rate calculated for Fig. 8F is the number of Fe²⁺ ions transported per second per channel (Fig. 8D).

Comparison of Fe²⁺ with Other Divalent Cations.

We have examined the effects of several divalent cations, including Ca²⁺, Ba²⁺, Mg²⁺, Ni²⁺, and Cd²⁺, on the permeation and gating of Ca_V3.1 (Khan et al., 2008; Obejero-Paz et al., 2008; Lopin et al., 2012). To a surprising extent, the channel can easily distinguish between the ions. As previously established for L-type calcium channels, there is a spectrum from highly permeant ions to strong blockers. Ca²⁺ and Ba²⁺ are the most permeant at millimolar concentrations, although they potently block currents carried by Na⁺ at micromolar concentrations. Mg²⁺ is nearly impermeant but blocks currents carried by Ca²⁺ from either side of the membrane (Khan et al., 2008). Fe²⁺ appears to be a Mg²⁺-like blocker, but it can carry small inward currents. The classic calcium channel blocker Cd²⁺ produces surprisingly large inward currents and exhibits reversed voltage dependence of channel block (Lopin et al., 2012). Ni²⁺ seems to be unique in blocking rapidly at an extracellular site (that cannot distinguish Ca²⁺ from Ba²⁺), in addition to blocking slowly at the selectivity filter (Obejero-Paz et al., 2008). Except for the fast-block site for Ni²⁺, these effects can be explained with the two-site/three-barrier model as subtle quantitative changes in the energetic parameters of ion binding, as opposed to distinct biophysical mechanisms.

Iron Overload.

Iron levels normally are tightly regulated in the body (Zhang and Enns, 2009). Increased intracellular iron levels have been associated with disorders involving the heart (Horwitz and Rosenthal, 1999; Kremastinos and Farmakis, 2011) and the brain (Stankiewicz and Brass, 2009), including neurological disorders such as amyotrophic lateral sclerosis, Parkinson's disease, and Alzheimer's disease (Oshiro et al., 2011). Intracellular iron leads to the production of reactive oxygen species that cause oxidative damage to proteins, lipids, and DNA (Giorgio et al., 2007).

Pathways for NTBI Influx.

In neurons, voltage-gated calcium channels (Gaasch et al., 2007) and N-methyl-d-aspartate receptors (Pelizzoni et al., 2011) have been implicated in NTBI influx. Studies with calcium channel blockers implicated both L-type channels and non–L-type, high-voltage–activated channels in Fe²⁺ entry into hippocampal neurons (Pelizzoni et al., 2011). The cerebrospinal fluid has levels of iron that saturate transferrin, leaving ∼1 μM free iron (Bradbury, 1997). This iron should be maintained in its ferrous form (Fe²⁺) with high levels of ascorbate (Bradbury, 1997) and ferrireductases (Lane et al., 2010; Mills et al., 2010). In the case of cerebral hemorrhage, free iron levels were observed to peak at >10 μM and to remain above 5 μM for 28 days (Wan et al., 2006). Such levels could provide sufficient free Fe²⁺ for entry into neurons through calcium channels.

The mechanism of Fe²⁺ uptake into cardiomyocytes is still being debated (Chattipakorn et al., 2011). Block of L-type and T-type calcium channels in cardiomyocytes in vivo (Oudit et al., 2003; Kumfu et al., 2012) can decrease iron uptake into the heart, which is an indication that sufficient free Fe²⁺ for calcium channels is available in the plasma and it can permeate in the presence of physiological levels of Ca²⁺.

Although the main mechanism for preventing excess iron in cells is preventing iron uptake, cells have mechanisms to efflux excess iron out of the cell, with the main protein being ferroportin 1 (Donovan et al., 2000). To maintain iron homeostasis, the liver releases hepcidin when iron levels are increased (Park et al., 2001); hepcidin binds to ferroportin 1 and causes its endocytosis and degradation (Nemeth et al., 2004). Normally this reduces plasma iron levels by decreasing ferroportin 1 levels in intestinal cells, which decreases iron absorption from the diet (Ganz, 2011). Under conditions of iron overload, in which iron absorption is not regulated in this way because of repeated transfusions to treat a blood disorder, the mechanism involving hepcidin down-regulation of ferroportin 1 might cause iron-handling problems. In cells with unregulated Fe²⁺ entry, such as cardiomyocytes and neurons, which have large numbers of calcium channels, hepcidin release causes ferroportin 1 levels to decrease (Wang et al., 2010), which decreases the capacity of cells to export Fe²⁺, but calcium channels continue to allow unregulated Fe²⁺ entry. Our results indicate that Ca_v3.1 channels can constitute a pathway for iron entry at resting membrane potentials and possibly during the course of action potentials, when extracellular Fe²⁺ levels reach concentrations in the micromolar range.

Authorship Contributions

Participated in research design: Lopin, Obejero-Paz, Thévenod, and Jones.

Conducted experiments: Lopin, Gray, Obejero-Paz, and Thévenod.

Performed data analysis: Lopin, Obejero-Paz, Thévenod, and Jones.

Wrote or contributed to the writing of the manuscript: Lopin, Obejero-Paz, Thévenod, and Jones.