Solitons Beyond Binary: Possibility of Fibre-Optic Transmission of Two Bits per Clock Period

Abstract

Optical telecommunication employs light pulses travelling down optical fibres; in a binary format logical Ones and Zeroes are represented by the presence or absence of a light pulse in a given time slot, respectively. The fibre's data-carrying capacity must keep up with increasing demand, but for binary coding it now approaches its limit. Alternative coding schemes beyond binary are currently hotly debated; the challenge is to mitigate detrimental effects from the fibre's nonlinearity. Here we provide proof-of-principle that coding with solitons and soliton molecules allows to encode two bits of data per clock period. Solitons do not suffer from nonlinearity, rather, they rely on it; this endows them with greater robustness. However, they are universally considered to be restricted to binary coding. With that notion now refuted, it is warranted to rethink future systems.

Today massive streams of short light pulses are sent down optical fibres to carry the world's telephone, telefax, and internet traffic. The fibre's data-carrying rate is by and large limited by Shannon's celebrated theorem¹, with some modifications to take the particular nature of optical signals into account²,³. The channel capacity is limited by the available bandwidth (≈ 30 THz) and by a factor depending on the coding scheme. In binary coding a logical One is represented by a pulse, and a logical Zero by its absence within a certain clock period. Clock periods of commercial systems are now often 25 ps (corresponding to 40 GBits/s transmission rate). Many such ‘channels', at staggered wavelengths, may be transmitted simultaneously through the same fibre, a concept known as wavelength division multiplexing. This way a fibre provides a capacity of several tens of Terabits per second. Current technology already comes quite close to that mark, and there is now much discussion about the upcoming “capacity crunch”⁴. Several coding schemes have been suggested that all abandon the binary format.

To code more than one bit of information per clock period, one might use pulses with different peak powers as different symbols. However, the fibre's optical nonlinearity affects pulses of different peak powers in different ways, and considerable signal distortions would arise. Therefore, constant-power schemes exploiting the phase or the state of polarization of the light pulse, or a combination thereof, are now favored, and quite a few variants have been proposed and tested. The challenge is to find formats robust enough to be insensitive to the multitude of detrimental effects and perturbations that a signal may encounter during transmission. To avoid problems from nonlinearity, either the power is kept quite low, or some complex correction is employed – and often a combination of both. Highly respectable results have been obtained along these lines by using sophisticated coding schemes combined with complex error compensation techniques (for a recent review see5), and some of these methods are in commercial use already.

We pursue a quite different approach. As discovered in 1973⁶ and first demonstrated in 1980⁷, there is a kind of light pulses that does not suffer from nonlinearity precisely because it relies on it. These pulses, known as solitons, have been considered by many to be the natural bits for optical telecommunication on grounds that they constitute the stable solutions of the underlying nonlinear propagation equation, the nonlinear Schrödinger equation⁸,⁹.

In solitons a stable balance exists between the nonlinearity-induced phase modulation on one hand, and dispersive effects on the other. Solitons are remarkably robust in the presence of perturbations, to the point that after suffering distortion they can self-heal to some degree. They are used in a few commercial systems, but in most recent research they were discounted as supposedly useful for binary coding only.

To understand why this may have been premature one needs to consider the fibres employed today. For several years now, the preferred type is so-called dispersion-managed fibre. It consists of periodically alternating segments of two fibre types with opposite-sign group velocity dispersion coefficients. With the path-average dispersion then close to zero, dispersive effects are reduced. It has been shown that soliton-like pulses still exist in the sense that they are stabilized by nonlinearity; however, their shape is different from the conventional solitons in constant-dispersion fibre, and it expands and contracts again in each dispersion period. These pulses are therefore somewhat different from conventional solitons and are known as dispersion managed (DM, for short) solitons.

A few years ago we have demonstrated experimentally that two DM solitons can form a stable bound state¹⁰. The phenomenon was also noted in theoretical work¹¹,¹²,¹³,¹⁴ and is recently also pursued in¹⁵,¹⁶. The binding mechanism ultimately results from the optical Kerr effect which creates interaction forces between light pulses, and solitons in particular¹⁷,¹⁸. In constant-dispersion fibres two equal-energy copropagating pulses, depending on their relative phase, can only either collide or fly apart, but a stable equilibrium separation exists in the DM case. If pulses get perturbed away from that position, they move right back – much like the nuclei in diatomic molecules. We therefore called this structure a “soliton molecule”; its binding mechanism has been studied in detail in¹⁹. One may wonder whether use of a set of different molecules would allow enhanced coding of data.

For the sake of completeness we mention that the basic idea has been raised before in Ref.20 where a solution of the NLSE (non-DM fibre) was found that is basically a three-soliton compound. However, given the large separation of the pulses the binding forces must be quite weak (if they exist at all²¹,). Also, two-pulse molecules would need to have two very unequal pulse powers which is awkward from the technical standpoint of detection at the receiver. A similar, quite rigorous recent study²² is silent about molecules larger than two pulses. DM fibre, now the commonly deployed fibre type, is not treated in Refs.²⁰,²². In Ref.23 an information-theoretical treatment shows that bound 2-soliton compounds can enhance transmission capacity to just below twice the single-soliton value; the paper is silent about physical and technical considerations. It must further be mentioned that inside the resonator of fibre lasers a wealth of soliton phenomena has been observed, including soliton molecules²⁴,²⁵. However, in these systems the underlying equation is not the nonlinear Schrödinger equation but the complex Ginzburg-Landau equation²⁶; these compounds (with properties different from the ones studied here) therefore do not exist in passive fibres and thus are unlikely to be of much use for data transmission.

Results

We have investigated whether there are also molecules of more than two pulses. Here we report experimental demonstration that three-pulse molecules exist. As expected on theoretical grounds¹⁹, neighboring pulses of the molecule are in antiphase. In the experiment we prepare a three-pulse compound of suitable shape, and compare its fibre input and output shape. The setup is sketched in Fig. 1; for further details see below in Methods.

Figure 1. Sketch of the experimental setup.

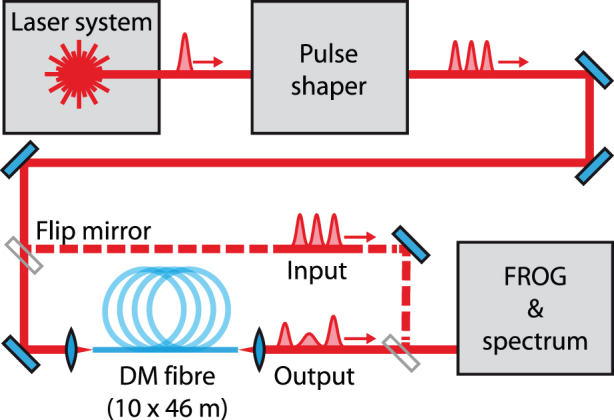
Top half, symbol generator: The pulse shaper carves the desired structures from the laser pulses. Bottom half, propagation and data acquisition: Flip mirrors allow easy comparison of shapes before and after fibre propagation.

A perfect preservation of shape is not achieved, and was not expected. We intentionally use an entirely passive system, to rule out any doubt about a possible influence of amplifier gain dynamics on the pulse shapes, but must then accept some impact from loss. Further limitations are set chiefly by the Raman effect which in our experiment is more severe than it would in a real-world installation (see below). The Raman effect causes the pulses to receive power-dependent frequency shifts; as soon as differences in the peak heights arise, these cause differential phase shifts which distort the structure. Moreover, by dispersive effects there is then a transfer of power between the pulses; once the relative phases have evolved on, this transfer would reverse itself. In effect, the structure found at the fibre end is asymmetric, pulses have unequal power, and the phase jumps of originally π are smeared out. Nonetheless, it still hangs together as a unit, and maintains the pulse-to-pulse separation.

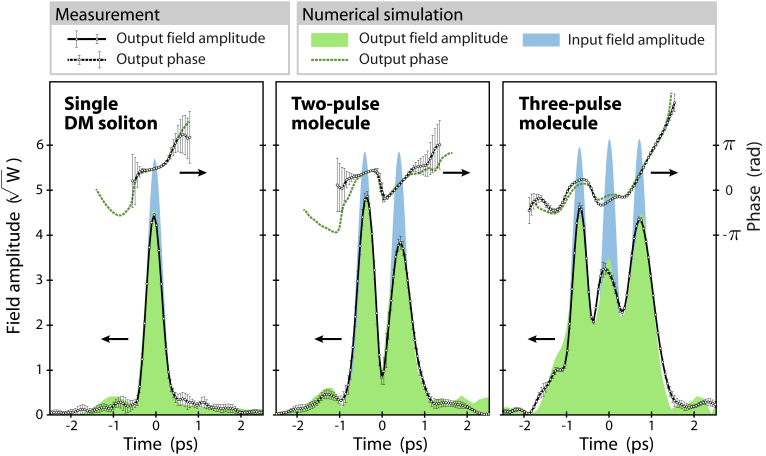
In Fig. 2 we show the pulse shapes at launch and at the fibre end, the latter both from simulation and from measured data. The overall shape deviations are visible, but it is equally clear that simulation and measurement agree very closely. This shows that all perturbing effects are well understood. They will set an ultimate limit to the span over which soliton molecules can be transmitted error-free, but for reasonable distances such transmission is feasible.

Figure 2. Temporal shape of complex waveform of single DM soliton (left), two-pulse molecule (center) and three-pulse molecule (right).

Shown are field amplitude envelopes (lower part, left axis) and phases (upper part, right axis). Points with error bars are experimental data.

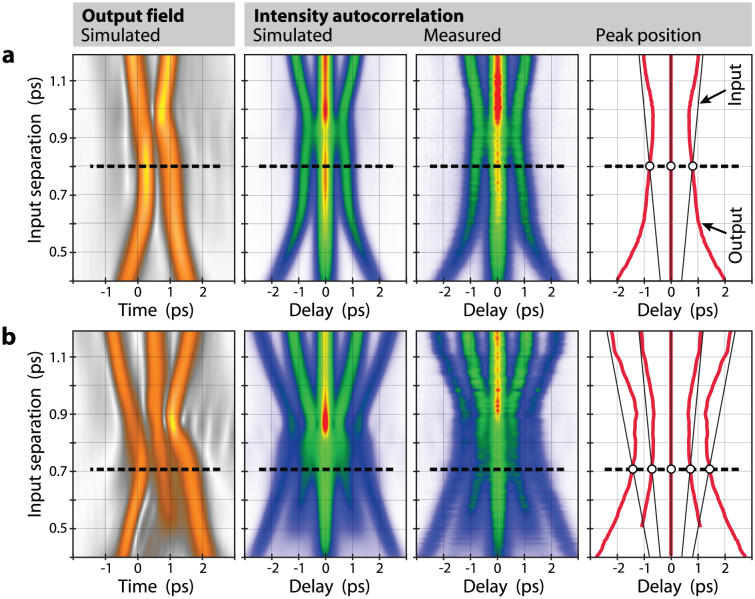
We turn to a discussion of parameter dependencies. We convinced ourselves that antiphase pulses are indeed required; for initial phase differences sufficiently different from π no stable transmission was observed. We then tested whether the separation between neighbors exhibits a particular equilibrium value. In Fig. 3 we show experimental data in comparison to simulations for the output temporal profile when the pulse separation at launch is varied. Data shown represent a two-pulse molecule (upper row) and a three-pulse molecule (lower row). The first column shows the simulated temporal profiles of the pulse groups. The shapes are not perfectly preserved in the presence of all the perturbations, in particular the Raman effect, and some asymmetry arises. Nevertheless, the basic structure holds up well. To acquire substantial amounts of data as in these scans we forgo a full amplitude-and-phase characterization and resort to autocorrelation measurements. Simulated data are therefore self-convoluted to autocorrelation traces in the second column for the convenience of direct comparison with measured data in the third column. In the fourth column, positions of maxima are extracted from the measurements for the sake of clarity. Straight lines indicate the loci where input separation equals output separation, in other words, the expected positions in the absence of any interaction. The measured traces cross these lines at positions of equilibria (marked by circles). The direction of the crossing distinguishes stable and unstable equilibria; here the equilibria are stable. The data of Fig. 2 were taken at these positions.

Figure 3. Study of temporal structure of (a) double and (b) triple pulses.

The temporal separation of pulses at launch is varied (vertical axes), and the resulting output profiles are recorded. Color scale indicates power levels. From left to right: Simulated temporal profile; same but self-convoluted for autocorrelation; measured autocorrelation profile; same but maxima extracted for better visibility, with auxiliary lines indicating positions in the absence of interaction. The equilibrium distances are highlighted by dashed horizontal lines; equilibrium positions are marked as circles in the right panels.

Discussion

The existence of a three-pulse molecule is a significant result because it makes an alphabet of four different symbols complete: no pulse, single soliton, two-pulse molecule, and three-pulse molecule. There with two bits of information can be coded into a single time slot (clock period). We experimentally confirmed that the same fibre can support all four symbols. This completes our proof-of-principle demonstration that a data stream using all four symbols is possible: Coding of two bits per clock period has thus been demonstrated for a soliton-based format for the first time.

Note that solitons and soliton molecules, like any other light signal, can exist in two orthogonal states of polarization, and they have a well-defined phase structure. Therefore, all presently investigated schemes of phase modulation and/or polarization multiplexing can potentially be combined with the soliton approach. Soliton molecules would provide an extra bit, or in other words a doubling of the data-carrying capacity of the fibre, to augment any of those schemes. Due to considerable added complexity over the case shown here, an experiment to test this suggestion must be consigned to the future. However, we anticipate that as an added benefit detection noise problems would be reduced because the transmitted power would be higher than in conventional schemes. This is possible because for solitons nonlinearity is natural, rather than an external nuisance to be avoided.

Methods

An overview of our setup is sketched in Fig. 1. As a light source we employ an optical parametric oscillator (Coherent Inc. /APE GmbH) tunable near 1540 nm wavelength. It is pumped by a modelocked Ti:sapphire laser (Coherent Inc. model Mira, modified for 250 fs pulse duration), which in turn is pumped by 10 W of 532 nm light from a solid state laser (Coherent, Inc. model Verdi V10). From these pulses we generate a Gaussian with defined width and peak power as an approximation for a single DM soliton, and two or three Gaussians with defined separations and relative phases for the pulse pairs and triplets, respectively. This is done by carving the target shapes from laser pulses in a pulse shaper arrangement²⁷ involving two gratings and a liquid crystal light modulator (CRI, Inc. model SLM-128-D-NM) controlled by a desktop computer. The same computer also controls massive sequences of data acquisitions as in Fig. 3.

We use ten dispersion periods, each consisting of a 22 m segment of OFS TrueWave RS with β₂ = +4.259 ps²/km at 1540 nm, and a 24 m segment of OFS TrueWave SRS with β₂ = −5.158 ps²/km at 1540 nm, respectively; this puts the path average dispersion at −0.655 ps²/km. (The fibre begins and ends with a half-segment of SRS fibre). Dispersion values were verified and measured up to fifth order by white light interferometry. The fibre's nonlinearity coefficient and Raman time have previously been obtained for this particular fibre line in the context of other work. Splice losses were carefully measured individually when the fibre was assembled; they total 1.55 dB. The energy of a single DM soliton depends on pulse width and wavelength, but is typically about 10 pJ.

This fibre line is a scale model of a typical commercial fibre line with 40 GBit/s bit rate using 7.5 ps wide pulses. When the pulse duration τ is scaled down, fibre length must be reduced accordingly in proportion to τ². With the ≈ 250 fs pulses provided by the source, the dispersion map period is therefore scaled down 900-fold. With a total length of ten dispersion map periods, or 460 m of fibre, our scale model thus corresponds to a real-life version with a span of just above 400 km. Note that some perturbations grow faster as τ⁻², e.g. the Raman effect as τ⁻⁴; this implies that in assessing complications from these effects our experiment is very conservative.

To assess pulse shapes and compare fibre input and output we use flip mirrors. In order to obtain a full amplitude-and-phase characterization we use the frequency-resolved optical gating (FROG)²⁸ technique in a homemade setup; data with excessive FROG error are discarded. Likewise, possible false reconstructions as described in Ref.29 are detected by simultaneous check of the optical spectra with an optical spectrum analyzer (Anritsu model MS 9740A), and are also discarded. For Fig. 3 FROG traces were reduced to those of an optical autocorrelator.

Numerical simulations are employed to back up the experiments. A standard split-step Fourier method is applied to the nonlinear Schrödinger equation with additional terms taking into account higher-order dispersion up to fifth order, losses (mostly at splices), and the Raman effect⁸, with all parameters as pertaining to the fibre used. The only parameters tuned to match experimental data are the chirp of the laser pulses and the pulse peak power in the fibre. The chirp is known only approximately because it changes with adjustment; we account for that by slight variations of the assumed value. The peak power is derived from average power measurements; for best correspondence of experiment and simulation we corrected by a few percent which remains within the uncertainty of the nonlinearity coefficient and the power meter calibration.

Author Contributions

All authors contributed extensively to the work presented in this paper.