Abstract
Although observations from biochemistry and cell biology seemingly illustrate hundreds of examples of exquisite molecular adaptations, the fact that experimental manipulation can often result in improvements in cellular infrastructure raises the question as to what ultimately limits the level of molecular perfection achievable by natural selection. Here, it is argued that random genetic drift can impose a strong barrier to the advancement of molecular refinements by adaptive processes. Moreover, although substantial improvements in fitness may sometimes be accomplished via the emergence of novel cellular features that improve on previously established mechanisms, such advances are expected to often be transient, with overall fitness eventually returning to the level before incorporation of the genetic novelty. As a consequence of such changes, increased molecular/cellular complexity can arise by Darwinian processes, while yielding no long-term increase in adaptation and imposing increased energetic and mutational costs.
Keywords: genetic load, cellular evolution, robustness, nonadaptive evolution
Although natural selection is one of the most powerful forces in the biological world, it is not all powerful. However, so ingrained is the belief in the extraordinary power of selection that when confronted by biological imperfections at the molecular and morphological levels, most investigators simply invoke pleiotropic constraints, i.e., negative functional relationships between two traits influenced by the same genes, resulting from molecular limitations, metabolic tradeoffs, etc. When made in the absence of any direct evidence, as is often the case, such adherence to the adaptationist paradigm discourages the likelihood of recognizing nonadaptive paths to the origin of organismal features (1–3).
Random genetic drift imposes a fundamental constraint on the level of perfection achievable by natural selection. As a consequence of the finite sampling of gametes and the linked nature of genomes, all populations experience stochastic fluctuations in allele frequencies that compromise the efficiency of selection. Once a high enough level of molecular perfection has been achieved so that further refinements in fitness are smaller than the prevailing force of drift, natural selection will be incapable of promoting any additional improvement (4, 5). Depending on the nature of the potential genetic variation underlying an adaptation, this drift barrier may be reached before selection is confronted with any physical, chemical, or bioenergetic constraints.
If, however, drift prevents natural selection from inexorably moving cellular features toward a state of molecular perfection, how do we account for the abundant examples of organisms using layered mechanisms for dealing with intracellular problems? For example, genome replication involves highly selective DNA polymerases, but the small fraction of initial base misincorporations are subject to correction by subsequent proofreading, and the still smaller fraction of errors that escape proofreading are generally subject to mismatch repair. The accuracy of translation also depends on a series of quality-control steps: proper loading of tRNA synthetases by their cognate amino acids, proper recognition of tRNAs by their cognate synthetases, proper codon recognition by tRNAs, and a variety of mRNA surveillance mechanisms. In many cases, proper protein folding depends on a series of chaperone systems, and numerous mechanisms exist for the disposal of terminally misfolded proteins.
Although these layered lines of defense are clearly advantageous and in many cases essential to cell health, because the simultaneous emergence of all components of a system is implausible, several questions immediately arise. How can selection promote the establishment of additional layers of fitness-enhancing mechanisms if the established primary lines of defense are already highly refined? When such changes are assimilated into a population, does an increase in overall fitness necessarily follow? Do the preexisting mechanisms retain their full efficiency, with a permanent increase in adaptation being achieved, or does an added layer of protection inevitably result in the relaxation and eventual degeneration of earlier established mechanisms (6, 7)?
Results
Limits to Perfection.
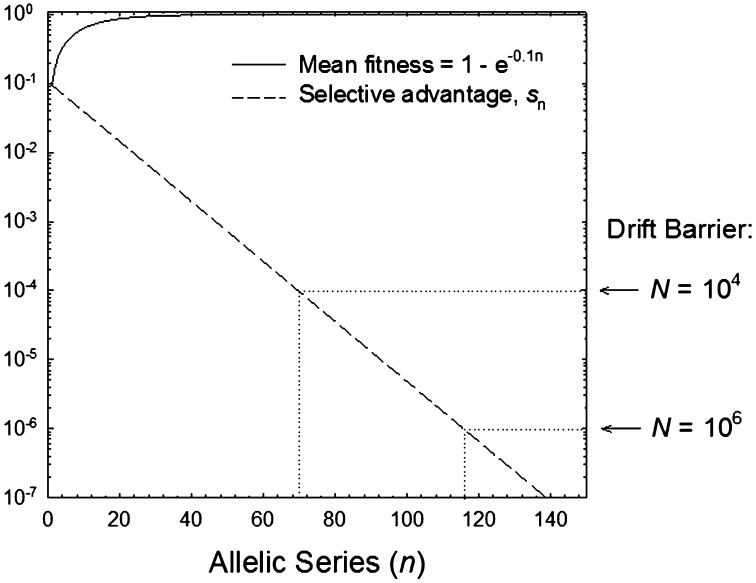
As a point of departure, we first consider the evolutionary features of an arbitrary character under a simple mutational model. A discrete array of alleles is assumed, with the upper limit to fitness being scaled to 1.0, and the selective disadvantage of allele i, si = e−ki, asymptotically approaching zero with increasing i (Fig. 1). A homogeneous stepwise mutation process is assumed, such that each allele i mutates to the next highest fitness class i + 1 at rate u and to the next lowest class i − 1 at rate v. Under this model, a population is expected to evolve upwardly in the allelic series until the point is reached where the advantage of the next highest allele is so weak that selection is rendered ineffective either by the power of random genetic drift or by mutation pressure in the downward direction. This point will depend on the effective size of the population (N, assumed here to be haploid, which defines the magnitude of genetic drift 1/N), by the granularity of the fitness effects of adjacent allelic classes (k), and by the ratio of downward to upward mutation rates (v/u).
Fig. 1.
Fitness function and selection coefficients for an allelic series defined by the exponential model described in the text. The drift barrier to allelic improvement is illustrated for two population sizes.
Although the behavior of loci harboring multiple alleles can be quite complicated, two limiting cases for this stepwise-mutation model yield simple generalizations. At the small-population size extreme, (u + v)N < 1, there will generally be only a few alleles segregating in the population at any point in time. Such a population will then typically move between adjacent classes in a nearly stepwise fashion, and can thus be categorized reasonably well by the feature of its most recent common ancestor (8). Letting ϕx,y denote the probability of fixation of a single mutant allele of class y arising on a background of allele x, the approximate rate of transition of class i to i + 1 is Nuϕi,i+1 and to i − 1 is Nvϕi,i−1.
Using Kimura’s (9) diffusion approximation for the fixation probabilities, noting that si − si+1 is the net selective advantage of allele i + 1 in an i background, and taking advantage of the fact that the ratio of fixation probabilities of advantageous and deleterious mutations with the same s is e2Ns in a haploid population (10), a simple solution can be obtained for the equilibrium mean frequencies of each allele,
 |
where T is the sum of the numerators for all 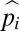 . Under this model,
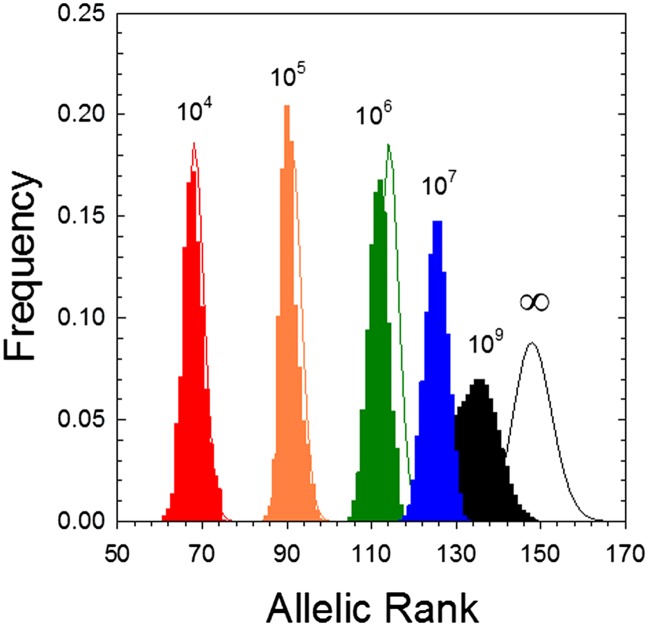
. Under this model, 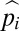 can be interpreted as the probability that allele i is the most recent common ancestor of the full collection of alleles in the population, with adjacent allelic classes (i − 1 and i + 1) potentially segregating in between fixation periods. As shown in Fig. 2, this expression closely approximates the average long-term representation of alleles in a steady-state population with (u + v)N < 1, derived from the results of stochastic computer simulations.
can be interpreted as the probability that allele i is the most recent common ancestor of the full collection of alleles in the population, with adjacent allelic classes (i − 1 and i + 1) potentially segregating in between fixation periods. As shown in Fig. 2, this expression closely approximates the average long-term representation of alleles in a steady-state population with (u + v)N < 1, derived from the results of stochastic computer simulations.
Fig. 2.
Allele-frequency distributions at various effective population sizes (from 104 to 109). The histograms were derived from simulations of a Wright–Fisher population, whereas the three leftmost line graphs depict the expectations given by Eq. 1, and the results for an infinite population size were obtained from the recursion equations Eqs. 3a–3c. In all cases, the total mutation rate is u + v = 10−6, u/(u + v) = 0.1, and k = 0.1.
The drift barrier to further adaptive progress is defined by the threshold allele (i = n*) at the point in the array where the rate of establishment of the next best allele (the product of the upward mutation rate and the fixation probability) is approximately equal to that in the opposite direction (i.e., the rate of reversion). Because the ratio of fixation probabilities for beneficial and deleterious alleles with equal absolute effects is e2Ns, the critical selection coefficient at stochastic equilibrium is s* ≃ [ln(v + u)]/(2N) assuming v > u. Using the above definition for s, at stochastic selection–mutation–drift equilibrium, the population is then expected to stall near allelic position
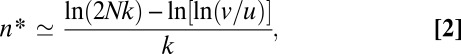 |
assuming k ≪ 1. Allelic position n* closely approximates the peaks of the three leftmost plots in Fig. 2.
For an effectively infinite population size, the dynamics of allele-frequency change (p to p′) can be expressed as
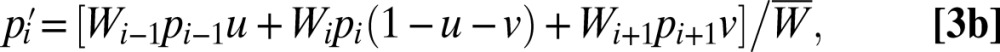 |
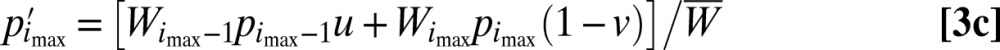 |
where the middle equation applies to all but the first and final alleles in the series, and 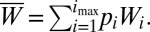 Iteration of these equations from any starting point, with imax set at an arbitrarily large value, leads to the limiting equilibrium distribution of allele frequencies.
Iteration of these equations from any starting point, with imax set at an arbitrarily large value, leads to the limiting equilibrium distribution of allele frequencies.
Although a population can wander slightly above the n* allelic state by stochastic mutation and drift, such alleles cannot be maintained by selection. Thus, for relatively small population sizes, provided there is a mutational bias in the downward direction, which seems certain in virtually all cases of molecular adaptation, a fairly tight distribution of allelic probabilities is maintained over evolutionary time, despite the fact that all allelic classes are accessible by mutation. For the extreme case in which u = v (no mutational bias), alleles in states beyond the drift barrier are free to randomly evolve in both directions, and a flat distribution of 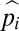 is expected beyond n* (8). However, because a random walk from n* to some substantially higher state (n′) requires on the order of
is expected beyond n* (8). However, because a random walk from n* to some substantially higher state (n′) requires on the order of 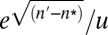 generations (11), such a distribution may rarely ever be realized in nature.
generations (11), such a distribution may rarely ever be realized in nature.
The limits to adaptation can be quantified as the magnitude of fitness load resulting from the inability of selection to promote the most advantageous alleles, i.e., as the reduction of the equilibrium mean population fitness relative to the scaled maximum of 1.0,
 |
where the sum is over all alleles with nonzero equilibrium frequencies. Provided the rate of deleterious mutation exceeds the rate of adaptive mutation (v > u) and (u + v)N < 1, an equilibrium population will generally be close to the state defined by Eq. 2, and
 |
This expression for the fitness load (in effect, a measure of allelic imperfection) differs from previous results that assumed the presence of just two possible alleles (e.g., ref. 12), often with mutations only producing the disadvantageous allele (e.g., ref. 13), and also from prior results with multiallelic models that have assumed either symmetrical mutation patterns (i.e., u = v), or Fisher’s (14) geometric model in which v/u effectively increases with the degree of adaptation (8, 15, 16). Nevertheless, although the exact expression for the drift load appears to be model dependent, a unifying feature of Eq. 5 and all prior work is an inverse relationship between the equilibrium level of molecular imperfection and the effective population size. A strong fitness gradient among alleles (large k) reduces the load because adjacent alleles are more easily discriminated by selection, and a relatively high incidence of adaptive (forward) mutations (low v/u) further reduces the load because selection is less opposed by mutation pressure.
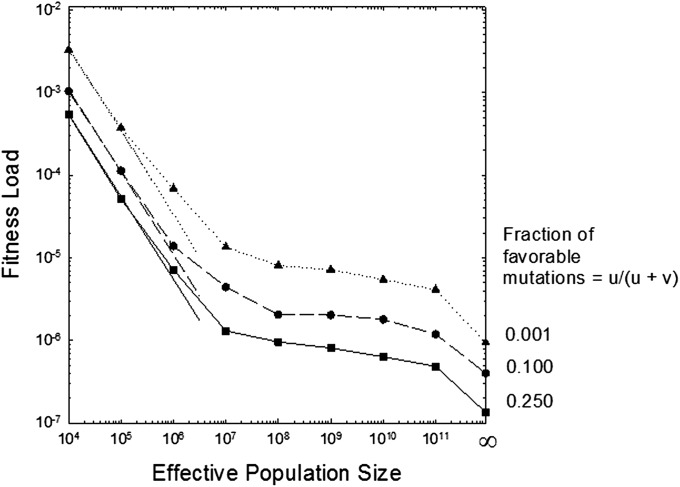
At the other extreme, as N → ∞, the population approaches the expected distribution of segregating allele frequencies under selection–mutation balance, obtainable from Eqs. 3a–3c. In this case, provided v/u > 5, i.e., the equilibrium load is
independent of k, although N must be enormous for this limit to be reached (Fig. 3). Eq. 6 shows that Haldane’s (13) classical result of the genetic load being equal to the deleterious mutation rate in an effectively infinite population even holds with multiple alleles, provided there are no advantageous mutations, but gives an overestimate when u ≠ 0.
Fig. 3.
Equilibrium fitness loads as a function of the effective population size. Solid, dashed, and dotted lines are for u/v = 1/3, 1/9, and 1/999, respectively. Straight lines to the left are given by Eq. 5, and data points were obtained by computer simulation of a Wright–Fisher model. The final (rightmost) data points for each curve are the infinite-population size limits obtained by use of Eqs. 3a–3c. In all cases, the total mutation rate is u + v = 10−6, and k = 0.1.
Establishment of a Secondary Line of Defense.
Supposing the genotypic distribution of a primary line of defense has settled into the steady-state selection–mutation–drift equilibrium, the possibility still exists that a second line of defense with a sufficiently large initial effect on fitness can be promoted by at least transient positive selection. In a large population, such establishment will be least likely if the new mutation arises in a low background-fitness class, as such individuals are destined to be lost by selection, but colonization of a high background-fitness genotype may give a sufficiently high boost in total fitness to promote fixation of the two-layered system. To have a reasonable chance of success, the boost in fitness would need to be greater than the incremental effects of beneficial mutations for the primary line of defense. A small population transiently fixed for a relatively low quality allele may also provide a viable path to invasion of a second layer.
Consider the situation in which the mutation to a secondary layer of defense causes an improvement in fitness in a carrier equivalent to moving up the allelic ladder by j steps, so that the absolute selective disadvantage of an individual in class i at the first layer would be reduced to si+j = e−k(i+j), and the probability of fixation of the new layer is given by ϕi,i+j. The overall probability of establishment depends on the frequency distribution of the background trait in which the mutation for the new layer of defense arises,
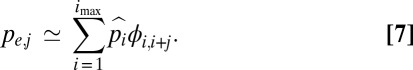 |
The maximum probability of establishment arises when the second layer completely eliminates all deficiencies of the first layer, which implies a relative selective advantage equal to si.
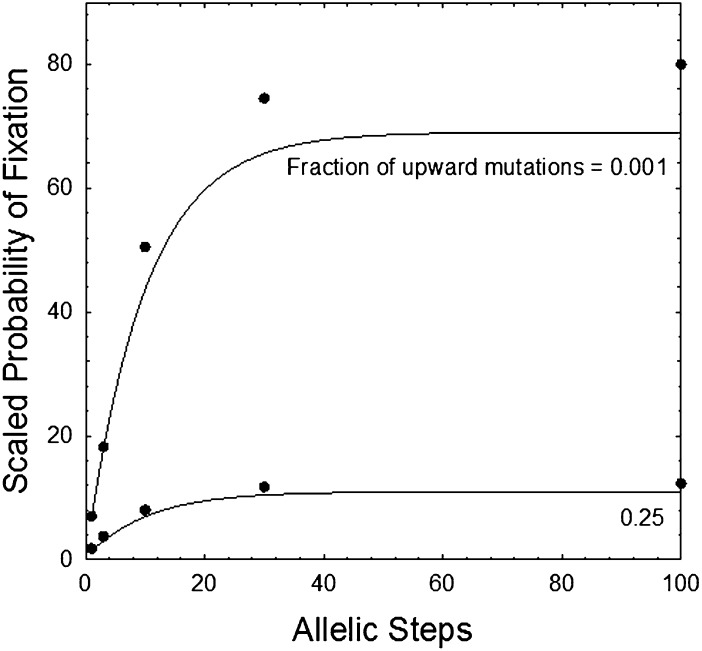
An example of the sensitivity to fixation of a second layer of defense in the small population-size domain is shown in Fig. 4, where 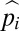 is defined by Eq. 1. With the fitness model used, virtually identical results are obtained for all population sizes in the domain satisfying N(u + v) < 1. The fact that the probability of fixation exceeds the neutral expectation of 1/N in all cases clearly demonstrates that the establishment of a second layer of defense can be promoted by selection even if the first layer is at the drift barrier. Simulations with small population sizes give slightly higher probabilities of establishment than the theoretical approximations, and those with larger population sizes yield even higher probabilities.
is defined by Eq. 1. With the fitness model used, virtually identical results are obtained for all population sizes in the domain satisfying N(u + v) < 1. The fact that the probability of fixation exceeds the neutral expectation of 1/N in all cases clearly demonstrates that the establishment of a second layer of defense can be promoted by selection even if the first layer is at the drift barrier. Simulations with small population sizes give slightly higher probabilities of establishment than the theoretical approximations, and those with larger population sizes yield even higher probabilities.
Fig. 4.
Probability of establishment of a second layer of defense as a function of the initial improvement, given for the small population-size domain using Eqs. 1 and 5. In both cases, the total mutation rate is u + v = 10−6, and k = 0.1. Virtually identical results are obtained for N = 104 and 105. The probability of fixation is scaled to the neutral rate, being given as Np(j), so a value equal to 1.0 implies simple drift to fixation without any assistance by selection. Data points were obtained from simulations of a Wright–Fisher model with complete linkage.
Consequences of Evolutionary Layering.
Having been promoted by natural selection, establishment of a second layer of defense will initially lead to an increase in mean population fitness. However, this boost in fitness may also be transitory unless the presence of a second layer somehow magnifies the fitness-enhancing effects separating adjacent allelic classes (k in the above model). Consequently, depending on the nature of the molecular adaptation, the initial excursion below the drift barrier resulting from the invasion of a second layer of defense may gradually dissipate as deleterious alleles with effects too small to be opposed by selection accumulate at one or both loci, with the joint effects of the two-layered system eventually returning to the same layer of perfection as the initial one-layered system. In principle, this means that the efficiency of the first layer is unlikely to ever improve from its initial state, assuming that the equilibrium state had been reached. Likewise, assuming a similar magnitude of mutational effects for both layers (e.g., constant k), the efficiency of the secondary layer is unlikely to improve any further unless it comes at the expense of the first layer.
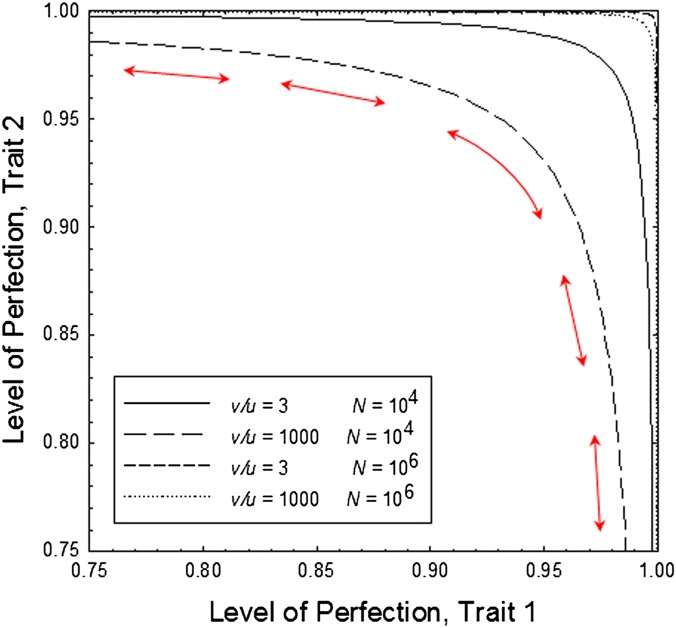
For the model presented above, an explicit statement can be made by considering the joint combination of alleles across both loci satisfying 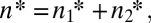 as defined in Eq. 2, with the level of perfection at each layer then being defined as
as defined in Eq. 2, with the level of perfection at each layer then being defined as 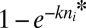 . In effect, this leads to a ridge of combinations of states at the two loci defining the bivariate drift barrier s* = [ln(v + u)]/(2N) (Fig. 5). This implies that a negative relationship is expected to evolve between the levels of perfection of the two traits in independent populations, or at various points of time within a lineage containing the two traits. With all points on the equilibrium ridge having equivalent fitness, such populations are free to drift in one direction or the other, even to the point of losing one of the traits, although directional bias may be induced by the pattern of mutation pressure.
. In effect, this leads to a ridge of combinations of states at the two loci defining the bivariate drift barrier s* = [ln(v + u)]/(2N) (Fig. 5). This implies that a negative relationship is expected to evolve between the levels of perfection of the two traits in independent populations, or at various points of time within a lineage containing the two traits. With all points on the equilibrium ridge having equivalent fitness, such populations are free to drift in one direction or the other, even to the point of losing one of the traits, although directional bias may be induced by the pattern of mutation pressure.
Fig. 5.
Bivariate drift barrier for two ratios of rates of beneficial and deleterious mutation (u/v), and two effective population sizes (N), as defined by the model in the text, and Eq. 2. All points along each line have equal fitness, providing ridges for the drift of the bivariate system.
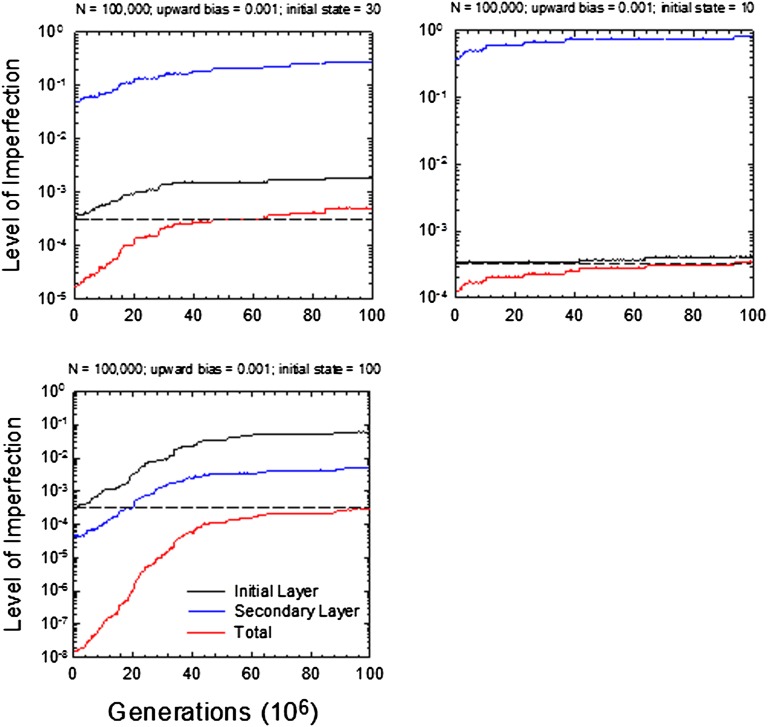
A few examples of this behavior, generated by stochastic simulations of populations following the fixation of a newly arisen allele for the second trait, are given in Fig. 6. In all cases, the initial improvement in overall fitness resulting from the establishment of the second layer is followed by a gradual loss of perfection in each trait, until a point on the bivariate drift barrier is reached where mean fitness is essentially the same as that before invasion of the second layer.
Fig. 6.
Stochastic dynamics of the average levels of imperfection of two traits, individually and jointly. Horizontal dashed lines demarcate the initial level of imperfection of the one-layered system.
Discussion
Although the preceding results rely on just one of many possible mutation–selection models, they clarify the general roles that random genetic drift plays in defining the ability of natural selection to refine the performance of molecular/cellular features. In general, the level of sustainable molecular perfection is inversely proportional to the effective size of a population, with small populations experiencing the fixation of suboptimal alleles and large populations experiencing an additional segregational load from recurrent mutational introduction. In both cases, the vast majority of alleles that are likely rise to moderate frequencies are effectively neutral with respect to each other.
The concept of a drift barrier to adaptive performance is implicit in several previous theoretical studies. For example, Hartl et al. (4) suggested that enzyme activities evolve to levels at which further mutational improvements in fitness have effects smaller than 1/(4N), leading to the conclusion that effective neutrality is an expected outcome of natural selection. Wylie and Shakhnovich (17) provide a very similar explanation for the marginal stability of proteins, i.e., the tendency to be just one or two mutations away from misfolding (18). In effect, they argue that smaller populations will typically move down the fitness-stability function to a point that ensures larger (but still effectively neutral) effects of mutations. The idea of evolved effective neutrality is also implicit in theory on the evolution of quantitative traits under stabilizing selection in finite populations (19, 20).
Any selection coefficient between adjacent classes of s* ≃ [ln(v + u)]/(2N) defines an approximate point at which selective progress will be stalled, regardless of the relationship of s across an entire allelic series. Although the model used here assumed an exponential decline in fitness costs between consecutive allelic states, more complex allelic topographies might exhibit irregularities. For example, some adjacent classes of intermediate-state alleles might have small enough selection differentials that adaptive progress cannot be promoted by selection, even though sufficient advancement might lead to a domain where the selection gradient becomes sufficiently steep to allow further progress. Such conditions do not violate the principle of a drift barrier, but simply broaden considerations to allow for multiple possible stalling points depending on initial circumstances. For sufficiently large populations, however, such hurdles may only be transient in nature, as rare instances may arise in which multiple mutations in segregating alleles enable populations to move efficiently into a new domain (21, 22). An additional complication worth further consideration is the change in the ratio of beneficial to deleterious mutations (presumably a decline) that may arise as traits move closer and closer to the point of perfection (14), which will further inhibit progress toward molecular perfection in accordance with the preceding expression.
Despite the generality of the concepts outlined above, it appears that a drift barrier can occasionally be surmounted by the introduction of a novel feature endowing a sufficiently large improvement in a molecular pathway. However, such enhancements in fitness may often be transient, as subsequent mutations with mildly deleterious effects in one or both components cause the joint system to revert back to a point where the magnitude of mutational effects again exceeds the power of drift. There will then inevitably be a series of alternative multivariate states that are equivalent in terms of overall fitness, resulting in the evolution of negative correlations between the efficiencies of redundant pathways, as populations wander over a ridge of equivalent multitrait fitness combinations. It may be useful to consider this passive mechanism for the emergence of negative associations between functionally related traits as an alternative to the widespread notion that tradeoffs between fitness components always evolve as a direct consequence of pleiotropic constraints and/or correlated selection (23–25).
If the components of a multitiered system are completely substitutable, each component is expected to be lost with equal probability. However, mechanisms likely exist that encourage a greater probability of loss of one component of a layered system relative to another, e.g., differential metabolic costs, differential vulnerabilities to mutational breakdown, and/or the acquisition of secondary beneficial functions that ensure preservation by natural selection. One might also imagine that an overall increase in molecular refinement could be achieved if the addition of a second layer somehow altered the mutational landscape in a way that magnified the fitness differences between alleles in adjacent classes, as this would provide the system with greater resistance to invasion of deleterious mutations. Such a condition might arise, for example, if the first layer becomes stalled at a level above the drift barrier by physical/chemical constraints, and indeed a key unresolved issue concerns the conditions under which such constraints are reached before the point at which drift takes on significance.
A number of empirical observations appear to be consistent with the drift-barrier hypothesis, just a few of which are given here. First, replication fidelities of DNA polymerases are lower in taxa with smaller effective population sizes, and also lower for enzymes involved in fewer nucleotide transactions per cell cycle, which presumably reduces the intensity of selection associated with error propagation (5). Second, although the restriction of licensing of DNA replication origins to one event per cell cycle is critical to maintaining genome integrity, there is substantial variation among eukaryotic lineages in the mechanisms regulating such behavior (26, 27). As redundant mechanisms of replication licensing control appear to be common within species, these observations are consistent with the concept of evolutionary layering and random wandering of independent lineages over a multivariate drift barrier. Third, despite the centrality of amino acid production to all organisms, substantial differences in biosynthetic pathways exist among lineages (e.g., refs. 28–30), again suggestive of divergent resolution of redundant pathways in ancestral species. Fourth, in Escherichia coli, genes whose protein products are clients of the molecular chaperone GroEL harbor significantly lower frequencies of optimal codons (and hence experience higher rates of misfolding associated with translational errors, ref. 31) than do sporadic clients (32). This suggests a bivariate drift barrier with respect to solutions to the problem of protein folding. Finally, the fact that the magnitude of selection associated with alternative codons in organisms ranging from prokaryotes to vertebrates is typically on the order of 1/(2N) (33) is consistent with the hypothesis that translation mechanisms within cells evolve to levels of refinement inversely proportional to the power of drift.
In summary, the results of this study demonstrate that increasingly complex mechanisms for dealing with cellular challenges can often be promoted in a population by natural selection without any long-term advantage in terms of mean population fitness. In fact, such increments in complexity can impose at least two costs: (i) the energetic demands associated with maintaining an additional cellular component; and (ii) the increased vulnerability of the overall system to inactivating mutations, owing to the increased number of mutational targets. Indeed, if the features of individual members of jointly reinforcing suites of genes evolve to reduced levels of refinement, as suggested by Fig. 5, mutants that return to a single-gene state (e.g., null mutations) are expected to have reduced performance relative to the ancestral single-gene condition. As pointed out by Frank (6), an appreciation for the internal evolutionary dynamics of redundant systems provides an alternative perspective on the origin and maintenance of the myriad of molecular attributes often interpreted as acquired enhancements of cellular robustness (34).
Acknowledgments
I am grateful to S. Frank for stimulating my interest in this problem. This work was supported by National Institutes of Health Grant R01 GM036827 to M.L. and W. K. Thomas, National Science Foundation Grant EF-0827411 to M.L., and US Department of Defense Grant W911NF-09-1-0444 to M.L., P. Foster, H. Tang, and S. Finkel.
Footnotes
The author declares no conflict of interest.
References
- 1.Gould SJ, Lewontin RC. The spandrels of San Marco and the Panglossian paradigm: A critique of the adaptationist programme. Proc R Soc Lond B Biol Sci. 1979;205(1161):581–598. doi: 10.1098/rspb.1979.0086. [DOI] [PubMed] [Google Scholar]
- 2.Stoltzfus A. On the possibility of constructive neutral evolution. J Mol Evol. 1999;49(2):169–181. doi: 10.1007/pl00006540. [DOI] [PubMed] [Google Scholar]
- 3.Lynch M. The frailty of adaptive hypotheses for the origins of organismal complexity. Proc Natl Acad Sci USA. 2007;104(Suppl 1):8597–8604. doi: 10.1073/pnas.0702207104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Hartl DL, Dykhuizen DE, Dean AM. Limits of adaptation: The evolution of selective neutrality. Genetics. 1985;111(3):655–674. doi: 10.1093/genetics/111.3.655. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Lynch M. The lower bound to the evolution of mutation rates. Genome Biol Evol. 2011;3:1107–1118. doi: 10.1093/gbe/evr066. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Frank SA. Maladaptation and the paradox of robustness in evolution. PLoS ONE. 2007;2(10):e1021. doi: 10.1371/journal.pone.0001021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Gros PA, Tenaillon O. Selection for chaperone-like mediated genetic robustness at low mutation rate: Impact of drift, epistasis and complexity. Genetics. 2009;182(2):555–564. doi: 10.1534/genetics.108.099366. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Sella G, Hirsh AE. The application of statistical physics to evolutionary biology. Proc Natl Acad Sci USA. 2005;102(27):9541–9546. doi: 10.1073/pnas.0501865102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Kimura M. On the probability of fixation of mutant genes in a population. Genetics. 1962;47:713–719. doi: 10.1093/genetics/47.6.713. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Bulmer M. The selection-mutation-drift theory of synonymous codon usage. Genetics. 1991;129(3):897–907. doi: 10.1093/genetics/129.3.897. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Noskowicz SH, Goldhirsch I. Average versus typical mean first-passage time in a random random walk. Phys Rev Lett. 1988;61(5):500–502. doi: 10.1103/PhysRevLett.61.500. [DOI] [PubMed] [Google Scholar]
- 12.Kimura M, Maruyama T, Crow JF. The mutation load in small populations. Genetics. 1963;48:1303–1312. doi: 10.1093/genetics/48.10.1303. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Haldane JBS. The effect of variation on fitness. Am Nat. 1937;71:337–349. [Google Scholar]
- 14.Fisher RA. Genetical Theory of Natural Selection. Oxford: Clarendon; 1930. [Google Scholar]
- 15.Hartl DL, Taubes CH. Compensatory nearly neutral mutations: Selection without adaptation. J Theor Biol. 1996;182(3):303–309. doi: 10.1006/jtbi.1996.0168. [DOI] [PubMed] [Google Scholar]
- 16.Poon A, Otto SP. Compensating for our load of mutations: Freezing the meltdown of small populations. Evolution. 2000;54(5):1467–1479. doi: 10.1111/j.0014-3820.2000.tb00693.x. [DOI] [PubMed] [Google Scholar]
- 17.Wylie CS, Shakhnovich EI. A biophysical protein folding model accounts for most mutational fitness effects in viruses. Proc Natl Acad Sci USA. 2011;108(24):9916–9921. doi: 10.1073/pnas.1017572108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Taverna DM, Goldstein RA. Why are proteins marginally stable? Proteins. 2002;46(1):105–109. doi: 10.1002/prot.10016. [DOI] [PubMed] [Google Scholar]
- 19.Lynch M. The selective value of alleles underlying polygenic traits. Genetics. 1984;108(4):1021–1033. doi: 10.1093/genetics/108.4.1021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Bürger R, Wagner GP, Stettinger F. How much heritable variation can be maintained in finite populations by mutation-selection balance? Evolution. 1989;43(8):1748–1766. doi: 10.1111/j.1558-5646.1989.tb02624.x. [DOI] [PubMed] [Google Scholar]
- 21.Weissman DB, Desai MM, Fisher DS, Feldman MW. The rate at which asexual populations cross fitness valleys. Theor Popul Biol. 2009;75(4):286–300. doi: 10.1016/j.tpb.2009.02.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Lynch M. Scaling expectations for the time to establishment of complex adaptations. Proc Natl Acad Sci USA. 2010;107(38):16577–16582. doi: 10.1073/pnas.1010836107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Lande R. The genetic covariance between characters maintained by pleiotropic mutations. Genetics. 1980;94(1):203–215. doi: 10.1093/genetics/94.1.203. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Arnold SJ, Bürger R, Hohenlohe PA, Ajie BC, Jones AG. Understanding the evolution and stability of the G-matrix. Evolution. 2008;62(10):2451–2461. doi: 10.1111/j.1558-5646.2008.00472.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Futuyma DJ. Evolution. Sunderland, MA: Sinauer; 2009. [Google Scholar]
- 26.Drury LS, Diffley JF. Factors affecting the diversity of DNA replication licensing control in eukaryotes. Curr Biol. 2009;19(6):530–535. doi: 10.1016/j.cub.2009.02.034. [DOI] [PubMed] [Google Scholar]
- 27.Cross FR, Buchler NE, Skotheim JM. Evolution of networks and sequences in eukaryotic cell cycle control. Philos Trans R Soc Lond B Biol Sci. 2011;366(1584):3532–3544. doi: 10.1098/rstb.2011.0078. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Hébert A, Casaregola S, Beckerich JM. Biodiversity in sulfur metabolism in hemiascomycetous yeasts. FEMS Yeast Res. 2011;11(4):366–378. doi: 10.1111/j.1567-1364.2011.00725.x. [DOI] [PubMed] [Google Scholar]
- 29.Gophna U, Bapteste E, Doolittle WF, Biran D, Ron EZ. Evolutionary plasticity of methionine biosynthesis. Gene. 2005;355:48–57. doi: 10.1016/j.gene.2005.05.028. [DOI] [PubMed] [Google Scholar]
- 30.Song J, Bonner CA, Wolinsky M, Jensen RA. The TyrA family of aromatic-pathway dehydrogenases in phylogenetic context. BMC Biol. 2005;3:13. doi: 10.1186/1741-7007-3-13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Drummond DA, Wilke CO. Mistranslation-induced protein misfolding as a dominant constraint on coding-sequence evolution. Cell. 2008;134(2):341–352. doi: 10.1016/j.cell.2008.05.042. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Warnecke T, Hurst LD. GroEL dependency affects codon usage—support for a critical role of misfolding in gene evolution. Mol Syst Biol. 2010;6:340. doi: 10.1038/msb.2009.94. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Lynch M. The Origins of Genome Architecture. Sunderland, MA: Sinauer; 2007. [Google Scholar]
- 34.Wagner A. Robustness and Evolvability of Living Systems. Princeton: Princeton Univ Press; 2005. [Google Scholar]