Acid–base chemical reaction model for nucleation rates in the polluted atmospheric boundary layer

Abstract

Climate models show that particles formed by nucleation can affect cloud cover and, therefore, the earth's radiation budget. Measurements worldwide show that nucleation rates in the atmospheric boundary layer are positively correlated with concentrations of sulfuric acid vapor. However, current nucleation theories do not correctly predict either the observed nucleation rates or their functional dependence on sulfuric acid concentrations. This paper develops an alternative approach for modeling nucleation rates, based on a sequence of acid–base reactions. The model uses empirical estimates of sulfuric acid evaporation rates obtained from new measurements of neutral molecular clusters. The model predicts that nucleation rates equal the sulfuric acid vapor collision rate times a prefactor that is less than unity and that depends on the concentrations of basic gaseous compounds and preexisting particles. Predicted nucleation rates and their dependence on sulfuric acid vapor concentrations are in reasonable agreement with measurements from Mexico City and Atlanta.

Nucleation of atmospheric trace gases occurs regularly throughout the continental boundary layer (1). Nucleated particles grow at typical rates of 1–10 nm/h, and can be a significant source of condensation nuclei (2) and cloud condensation nuclei (CCN) (3). The cloud albedo effect is a major source of uncertainty in estimates of climate radiative forcing (4). Because nucleation may affect CCN concentrations, there is a need for microphysical models that reliably predict atmospheric nucleation rates.

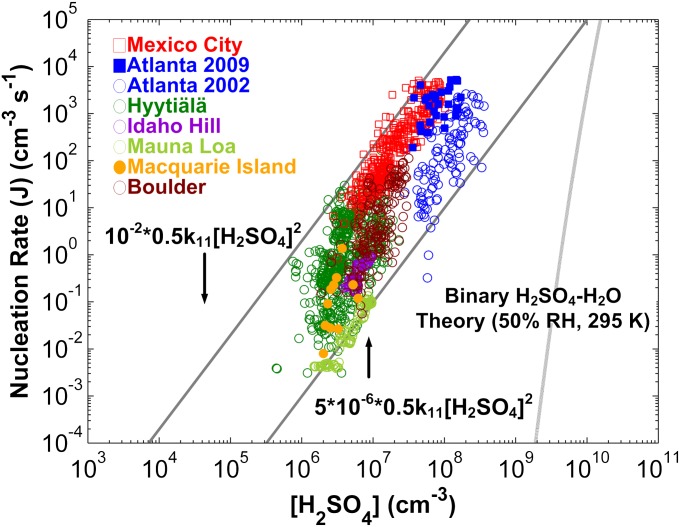
Fig. 1 summarizes results for the dependence of boundary layer nucleation rates on the number concentration of sulfuric acid vapor, “[H₂SO₄],” measured by the University of Minnesota-National Center for Atmospheric Research (NCAR) research team over the past two decades (5). Also included are data from the University of Helsinki group (6, 7). The considerable scatter in the measurements of the nucleation rate 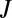at a given value of [H₂SO₄] may be due to factors including dependencies on other nucleation precursor gases, temperature, and relative humidity (RH), as well as uncertainties introduced when J is deduced from measurements. Significantly, Fig. 1 shows that for all of these studies nucleation rates range from 1 × 10⁻² to 5 × 10⁻⁶ times the sulfuric acid vapor collision rate, 0.5k₁₁[H₂SO₄]², where k₁₁ is the hard-sphere collision rate constant for sulfuric acid vapor (8).

Fig. 1.

Dependence of nucleation rates (J = J_{1 nm}) in the atmospheric boundary layer on [H₂SO₄]. The solid diagonal lines, which provide bounds for atmospheric observations, show that nucleation rates range from 10⁻² to 5 × 10⁻⁶ times the sulfuric acid vapor collision rate (428 data points for Mexico City, 31 data points for Atlanta 2009, 115 data points for Atlanta 2002, 602 data points for Hyytiälä, 86 data points for Idaho Hill, 107 data points for Mauna Loa, 11 data points for Macquarie Island, 180 data points for Boulder).

The literature includes a lively debate about the relative importance of ion-induced and neutral nucleation (9, 10). Our work aims to explain nucleation rates observed in the polluted boundary layer atmospheres of Atlanta and Mexico City, where estimated nucleation rates (∼1–10³ cm⁻³⋅s⁻¹) were often much greater than typical ion production rates (∼2–30 cm⁻³⋅s⁻¹). Therefore, although ion-induced nucleation could contribute to particle production in these locations it is not the dominant mechanism. Accordingly, this paper focuses on nucleation involving condensation/evaporation of neutral molecules.

The classical theory for multicomponent homogeneous nucleation is often used to model nucleation in the atmosphere. This theory predicts that nucleation rates, J, can be expressed as (11)

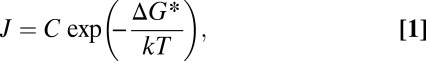where 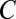is a kinetic prefactor and 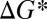is the change in Gibbs free energy associated with forming the critical nucleus from its gas-phase constituents. In this theory, critical nuclei gain vapor molecules by condensation and lose them by evaporation at equal rates. Particles smaller than the critical size evaporate faster than they grow, whereas larger particles grow faster than they evaporate. As shown in Fig. 1, classical binary homogeneous nucleation theory for sulfuric acid and water (12) underpredicts observations by over 10 orders of magnitude for typical ambient daytime concentrations of sulfuric acid vapor (10⁶ to 3 × 10⁸ cm⁻³). A recent ternary nucleation theory (13), which assumes that nucleation arises from clustering of ammonia, water vapor, and sulfuric acid vapor, does not predict any nucleation over the range of ambient [H₂SO₄] temperatures and RHs for the measurements shown in Fig. 1. In brief, no nucleation model based on classical theory predicts either the observed rates or the observed functional dependence on [H₂SO₄] shown in Fig. 1. Clearly, there is a need for better models for atmospheric nucleation.

A promising alternative approach, which treats cluster formation as a sequence of reactions between acidic and basic gases, has recently been described by several groups. Vehkamäki and coworkers (14, 15) have used computational chemistry to model the formation and growth of clusters from basic gases and sulfuric acid. Consistent with laboratory experiments (16–19), this work provides evidence that both ammonia and amines enhance ternary nucleation, and that for equal concentrations the amines have the greater effect. Dawson et al. (20) described a simplified mechanism for nucleation of methanesulfonic acid, amines, and water that explicitly accounted for the sequence of reactions that leads to stable particle formation. This study, which included both experimental and computational results, showed that all three reactants play a significant role in nucleation.

Results and Discussion

The acid–base nucleation model developed in this paper is based on observations from an intensive field campaign in Atlanta, and on observations obtained in chamber studies at the University of Minnesota. The model is based on new measurements of neutral molecular clusters, particle number distributions down to about 1 nm geometric diameter (21), and precursor gas concentrations. Information about these studies is provided in Materials and Methods and in SI Text.

We define “monomer (A₁),” “dimer (A₂),” “trimer (A₃),” and “tetramer (A₄)” as clusters that contain, respectively, one, two, three, and four sulfuric acid molecules. Although those clusters may also contain some water and alkaline species before chemical ionization and sampling, we assume that after ionization and background subtraction they correspond to the species detected at masses 160, 195, 293, and 391 by the Cluster CIMS (chemical ionization mass spectrometer). These masses correspond to HSO₄⁻HNO₃, HSO₄⁻H₂SO₄, HSO₄⁻ (H₂SO₄)₂, and HSO₄⁻ (H₂SO₄)₃. In the chamber studies, trimer sometimes contained amines, and in those cases reported concentrations of A₃ include aminated and nonaminated clusters. However, aminated trimer concentrations were not measured in Atlanta. We assume that the monomer drives the nucleation process. The approach used to determine cluster concentrations from Cluster CIMS measurements is discussed in SI Text.

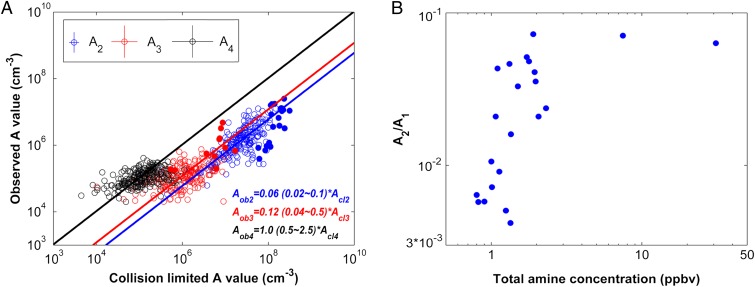
Fig. 2A plots concentrations of dimer, trimer, and tetramer measured with the Cluster CIMS versus calculated values, assuming that clusters are formed at the collision-limited rates. For example, the collision-limited tetramer concentration equals the steady-state tetramer concentration that would occur if measured monomer and trimer were to react at the collision rate and evaporation did not occur. Fig. 2A shows that measured tetramer concentrations are approximately equal to the collision-limited values, but that measured trimer and dimer concentrations are, respectively, factors of 8 and 16 below collision-limited values. These measurements suggest that monomer evaporation from dimer and trimer is the bottleneck to nucleation. This role of the dimer is consistent with laboratory measurements reported by Hanson and Eisele (22) at 30–100 parts per trillion by volume (pptv) [H₂SO₄], 10% RH, and 270 K. They concluded that “critical clusters contained 2 or less H₂SO₄ molecules and may contain as little as one ammonia molecule.” Because the data show that evaporation from tetramer is not significant under these conditions, and because evaporation rates typically decrease with increasing cluster size, we assume that evaporation from clusters larger than tetramer is also negligible. This is supported by recent work of Kuang et al. (23), who show that growth rates of 1–3 nm particles are typically equal to or greater than sulfuric acid vapor condensation rates; tetramers are about 1 nm in size. Further information on sub-3-nm growth rates for Atlanta (2009) is provided in SI Text.

Fig. 2.

(A) Observed dimer, trimer, and tetramer concentrations versus collision-limited values. ○, from 2009 measurements in Atlanta; ●, from chamber experiments. Tetramer was below the detection limit in the chamber. The diagonal lines are best log–log fits with fit parameter ranges in parentheses (235 data points for A₂, 214 data points for A₃, 235 data points for A₄. The numbers indicate estimated ranges that include 90% of the data). The crosses on the legend show estimated systematic uncertainties for all data points. Estimated random uncertainties, which must be equal to or less than the observed scatter in the data, are assumed approximately equal to the systematic uncertainties. (B) Ratio of steady-state dimer to monomer concentrations (m/z 195/160) as a function of total amine concentration in chamber experiments (22 data points).

Fig. 2B shows that the concentration ratio of steady-state “dimer” to “monomer” ([A₂]/[A₁]) in the chamber experiments increases as total amine concentrations (protonated m/z 32+46+60+74+88) increase. The observed increase in dimer concentrations is due to stabilization of dimer by the base. The model assumes there are two types of dimers: more volatile (MV) and less volatile (LV). As the concentration of basic gases increases, more MV dimers are converted to LV dimers, and this leads to the observed increase of mass 195. For amine concentrations that exceed several parts per billion by volume (ppbv), the concentration of the more volatile clusters is insignificant and saturation is observed. The observed asymptotic value of [A₂]/[A₁] is about a factor of 2 below the theoretical upper limit of [A₂]/[A₁] = 0.18 that occurs for collision-controlled nucleation when monomer is formed chemically at a constant rate and evaporation from clusters is neglected (24). The model also accounts for evaporation from trimer, as suggested by the results shown in Fig. 2A, but assumes that evaporation is insignificant for clusters of size four and larger.

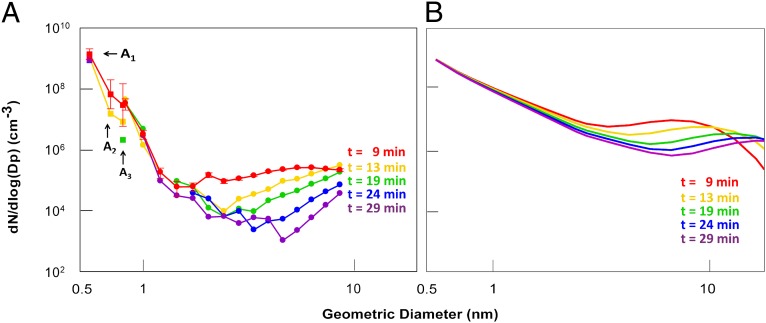
Fig. 3 compares size distributions measured in a chamber experiment with those predicted theoretically for collision-controlled nucleation in the absence of preexisting aerosol (24). The measured distributions show some qualitative similarities to theoretical results. Beginning with the monomer, number distributions decrease monotonically with size until reaching a minimum. The concentration of particles at this minimum decreases as time increases, and the size increases with time. However, there are also important qualitative differences. The measured minima occur at significantly smaller values of particle concentration, and the distribution functions fall more rapidly than theoretically predicted. These differences reflect the effects of evaporation from the smallest clusters, as demonstrated by the results shown in Fig. 2.

Fig. 3.

Time-dependent particle size distributions formed by gas-phase nucleation in a chamber. (A) Obtained from the UMN chamber measurements, where SO₂ undergoes oxidation in the presence of amines (total amine = 0.9 ppbv). Size distributions shown in B were obtained by assuming that monomer is formed at the same rate as in the experiment shown in A, and that coagulation is collision controlled (i.e., monomer and clusters always stick when they collide and evaporation from clusters does not occur).

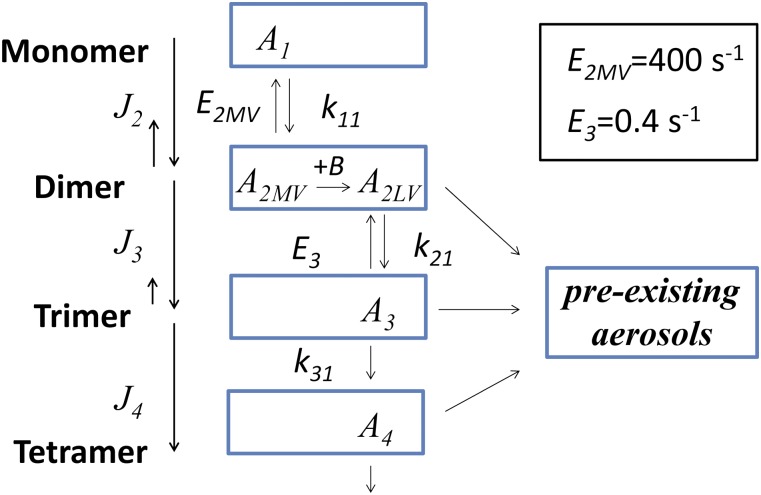
Fig. 4 illustrates the conceptual model for neutral atmospheric nucleation that was developed based on the observations shown in Fig. 2. Rows correspond to the number of sulfuric acid (A) molecules per cluster. MV dimers are formed by monomer–monomer coagulation, and therefore contain two sulfuric acid molecules and possibly some water and basic compounds. An LV dimer is formed when additional reactions of an MV dimer with the basic gas B further stabilize the cluster. The evaporation rate constants E_2MV and E₃ were used as empirical fitting parameters to reconcile measured and modeled dimer and trimer concentrations, as explained in SI Text.

Fig. 4.

Conceptual acid–base reaction model for nucleation. Measured monomer concentrations are an input to the model and are determined by chemical-formation and condensation-loss rates. Rows represent the number of sulfuric acid molecules per cluster. Dimer (row 2) includes MV and LV clusters. Trimer includes a single type of cluster that is volatile to some extent. Clusters larger than trimer are not volatile.

Cluster CIMS measurements indicate that ammonia and amines enhance the dimer concentrations to a similar extent (see SI Text). Therefore, at this point we do not distinguish between different bases (i.e., ammonia and the various amines are assumed to behave identically); a more complex theory might include accounting for the base-dependent chemistry. Aside from explicitly accounting for the transformation of MV dimer to LV dimer, the model does not explicitly account for reactions between larger clusters and the basic gases, but rather assumes that the larger clusters are in equilibrium with the base. The lengths of the vertical arrows in Fig. 4 (Left) qualitatively illustrate rates of monomer uptake or evaporation. Forward reactions are assumed to occur at the collision rate. As shown in SI Text, modeled dimer concentrations for Atlanta are consistent with measurements only when the total concentration of basic gaseous compounds (ammonia plus amines) is used. Predicted dimer concentrations are much lower than measured values if only amines (and not ammonia) are included in the model.

The data shown in Fig. 2 lead to sulfuric acid evaporation rate constants of E_2MV = 400 s⁻¹ (range 100–1,000 s⁻¹) and E₃ = 0.4 ± 0.3 s⁻¹. These values were obtained by fitting Eqs. S23 and S24 (E_2MV) and S27 (E₃) to monomer, dimer, and trimer concentrations measured with the Cluster CIMS. Uncertainties in E_2MV and E₃ are affected by uncertainties in measured number concentrations of clusters containing a specified number of sulfuric acid molecules. As detailed in SI Text, a root-sum-square analysis was used to determine the cumulative contributions of known systematic and random uncertainties in parameters used to calculate cluster concentrations. That analysis led to the conclusion that overall uncertainties in reported concentrations of monomer, dimer, trimer, and tetramer are, respectively, factors of 1.5, 3, 5, and 5. A parametric error analysis was carried out to estimate the propagated uncertainties on E_2MV and E₃ associated with uncertainties in cluster concentrations. The uncertainty limits given above encompass the range of evaporation rate constants revealed by this analysis.

Sulfuric acid evaporation rates from clusters likely are highly sensitive to cluster composition. For example, using quantum chemical calculations Ortega et al. (15) predict sulfuric acid evaporation rates equal to 1.5 × 10⁴ s⁻¹, 2.45 × 10⁻⁵ s⁻¹, 5.88 × 10⁻¹⁷ s⁻¹, 3.41 × 10⁻¹⁸ s⁻¹, 4.27 × 10⁻²⁰ s⁻¹, respectively, from dimer that contains 0, 1, 2, 3, or 4 molecules of dimethyl amine. Hanson and Lovejoy (25) measured the equilibrium constants for sulfuric acid dimer at low temperatures. An evaporation rate constant of E₂ = 1 × 10⁵ s⁻¹ is obtained by extrapolating their data to 300 K. The empirically determined value of E_2MV (400 s⁻¹) from this study is a factor of 40–250 below the values for pure sulfuric acid clusters, but orders of magnitude greater than the computed values for aminated clusters. Similarly, Ortega et al. (15) predict sulfuric evaporation rates equal to 2.0 × 10⁵ s⁻¹, 3.7 s⁻¹, 90.8 s⁻¹, 1.44 × 10⁻¹⁰ s⁻¹, 7.17 × 10⁻¹⁵ s⁻¹, respectively, for trimers that contain 0, 1, 2, 3, or 4 molecules of dimethyl amine. Our empirical value of E₃ (0.4 ± 0.3 s⁻¹) falls between calculated values for trimers that contain two and three molecules of dimethyl amine.

In principle, dissociation of 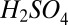could also lead to errors in measured cluster concentrations. We believe this is an insignificant source of uncertainty relative to other factors. As discussed in SI Text, the Cluster CIMS was tuned to minimize breakup of the chemically ionized monomer (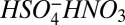). Therefore, the monomer is detected primarily at m/z 160 and not at 97 (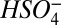). The computed bond enthalpy for 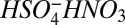is 27.4 kcal mol⁻¹, whereas the corresponding bond enthalpies for the dimer (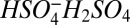) and trimer (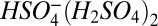) are, respectively, 41.8 and 27.4 kcal mole⁻¹ (26, 27), indicating that the dimer is more stable than 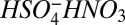and the trimer is equally stable. If the monomer does not undergo dissociation, then neither should the dimer or trimer. Loss of sulfuric acid from larger clusters cannot be ruled out using similar arguments but, as shown above, measurements indicate that tetramer is present at collision-limited levels. If tetramer dissociation had occurred to a significant extent, measured concentrations would have been significantly lower than that. In contrast, in measurements with the chemical ionization with the atmospheric pressure interface time-of-flight mass spectrometer (CI-APi-TOF), Jokinen et al. (28) detected the monomer primarily at mass 97, indicating that the 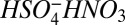largely underwent dissociation. This may be one reason that neutral clusters have not been detected with the CI-APi-TOF.

However, following chemical ionization, neutral clusters may undergo chemical alterations that result in the loss of alkaline species (29), as has been observed for ammonia (22). At any moment, atmospheric monomer, dimer, trimer, tetramer, etc., may contain a distribution of types and numbers of basic compounds (29, 30). Because the Cluster CIMS cannot accurately measure the abundance of those basic compounds, our reported values of E_2MV and E₃ correspond to ensemble average sulfuric acid evaporation rates from dimer and trimer of unknown alkaline composition. These empirical values for evaporation rates will constrain future theoretical models. A fundamental understanding of nucleation will require knowledge of the exact cluster composition.

Based on the evidence shown in Fig. 2A, nucleation rates are assumed to be equal to the tetramer formation rate for the polluted conditions pertinent to this work. As shown in SI Text, the chemical nucleation model illustrated in Fig. 4 leads to the following expression for tetramer formation rates:

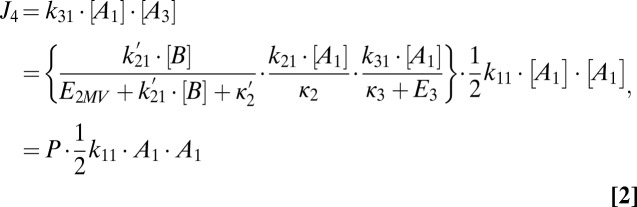where the prefactor P is less than unity and κ₂ and κ₃ are the first-order rate constants for coagulation loss of dimer and trimer with clusters/particles of all sizes. Fig. 5 compares measured 1-nm nucleation rates with values predicted by Eq. 2. The predicted values (J_model) were calculated with the second line of Eq. 2, using empirically determined values for the evaporation rate constants E_2MV and E₃ given above and assuming that [B] is the total measured concentration of basic gases. Because ammonia was the dominant basic gaseous compound in these studies, [B] is approximately equal to the ammonia concentration.

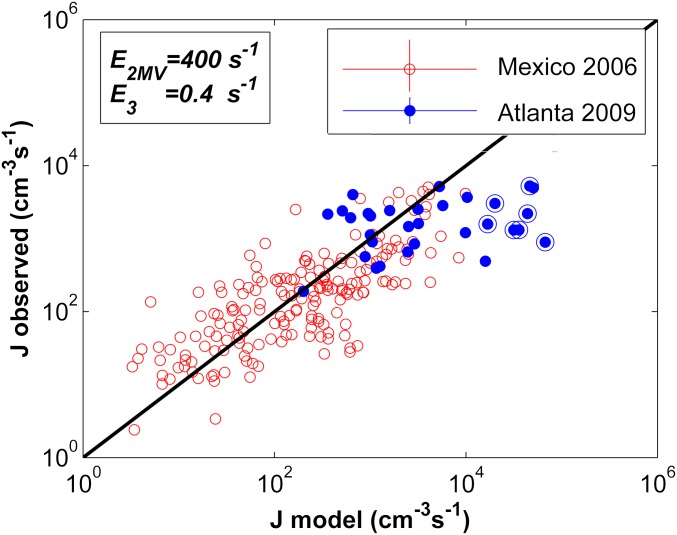
Fig. 5.

Comparison of observed and calculated (Eq. 2) atmospheric nucleation rates. The red symbols are from Mexico City (2006). The blue symbols are from Atlanta (2009). The 1:1 correlation is indicated by the diagonal black line (31 data points for Atlanta 2009, 186 data points for Mexico City 2006). The error bars shown in the legend apply to all data points. The seven circled blue symbols are from measurements on August 22, 2009.

Results in Fig. 5 show that modeled nucleation rates for Mexico City mostly agree with independently observed nucleation rates to within a factor of 10. Modeled and measured nucleation rates for Atlanta are also within a factor of 10 for all but 5 of the 31 measurements. However, the model predicts a greater variability in nucleation rates than was observed in Atlanta, with modeled rates exceeding measurements by up to a factor of 100. Measurements that were carried out on August 22, 2009, are circled. Those measurements account for most of the days where modeled nucleation rates were high. The available data do not explain the reasons for the discrepancy. However, the measured and modeled nucleation rates for August 22 can be reconciled if evaporation of sulfuric acid from the tetramer is included in the model, using evaporation rate constants of E_2MV = 400 s⁻¹, E₃ = 1 s⁻¹, and E₄ = 0.3 s⁻¹. This result suggests that on August 22, concentrations of an important stabilizing compound were lower than for other days. This result also implies that in cleaner environments, where concentrations of stabilizing compounds are lower than in Atlanta or Mexico City, it might be necessary to alter the model to include evaporation from clusters larger than trimer. This would lead to the inclusion of additional terms in the prefactor P, similar to those for dimer and trimer evaporation shown above.

In summary, a conceptually unique approach for modeling nucleation rates in the polluted boundary layer is described. The model is based on new measurements of neutral molecular clusters and aerosol number distributions carried out in the laboratory and in urban Atlanta. This model treats nucleation as a sequence of chemical reactions between clusters and acidic and basic gaseous compounds. It uses evaporation rate constants determined from direct measurements of cluster concentrations to infer nucleation rates. Determining evaporation rates from clusters is the greatest source of uncertainty in any nucleation theory. Although uncertainties remain about the effects of RH or specific basic gaseous compounds (and mixtures thereof) on cluster evaporation rates, this model predicts nucleation rates observed in Mexico City and Atlanta to within a factor of 10. This is a significant improvement over the classical theory, which differs from measurements by factors of 10¹⁰ or more. This model shows that basic gaseous compounds play an important role in stabilizing clusters in the atmosphere. The discovery that the bottleneck to nucleation occurs for clusters that contain just two and three sulfuric acid molecules shows that, at least for polluted conditions similar to those studied here, it is sufficient to understand the formation and evaporation rates for those small clusters. This simplifies significantly the theoretical hurdles to understanding nucleation.

It is possible that for cleaner environments, the model would need to be extended to include evaporation from clusters larger than trimer. Also, just as this model accounts for the existence of MV and LV dimer, it might also be necessary to account for larger clusters having varying composition and therefore volatility. Accounting for these effects would lead to the inclusion of additional terms in the prefactor P in Eq. 2 similar in form to those for the dimer and trimer.

Materials and Methods

The model is based on new measurements of neutral molecular clusters and aerosol number distributions down to 1 nm. These measurements include both laboratory chamber studies at the University of Minnesota (31) and atmospheric measurements in Atlanta (2009). Model predictions, which require measurements of concentrations of sulfuric acid vapor and basic gaseous compounds, are compared with independent measurements of nucleation rates from intensive atmospheric campaign studies in Mexico City (2006) and Atlanta (2009). Details of these measurements and campaigns are described in previous publications (21, 23, 32–39). Additional information on Cluster CIMS measurements during the 2009 intensive study in Atlanta are provided in SI Text. The analysis of the ambient data focuses on periods with high concentrations of sulfuric acid vapor and basic gaseous compounds. Typically, sulfuric acid monomer (m/z 160) concentration varied from 10⁷ to 5 × 10⁸ cm⁻³, and concentrations of basic gaseous compounds (ammonia and amines) exceeded 1 ppbv during these studies. Ammonia concentrations were about 10 times higher than amines in Atlanta. Ammonia concentrations in Mexico City were even higher than in Atlanta, but amines were not measured. The chamber studies were aimed at investigating the dependence of cluster concentrations on dimethyl amine concentrations. Sulfuric acid monomers were produced by photochemical reactions in a roughly 1000-L, climate-controlled, Teflon film batch reactor within an insulated stainless steel enclosure. The sulfuric acid concentration was maintained at 2.3 ± 0.8 × 10⁸ cm⁻³ for all experiments. Dimethyl amine was the only basic gaseous compound that was intentionally added to the chamber, and the ammonia and amines were below detection limits (<1 pptv) in the zero air used to fill the chamber. However, various amines (protonated m/z 32+46+60+74+88) were detected in the chamber at levels of at least several tens of pptv whether or not they were intentionally added. Therefore, some experiments were carried out without adding amines. Experiments were carried out with total concentrations of amines ranging from 0.8 to 31 ppbv. At the higher concentration, dimethyl amine was the dominant amine, whereas at lower concentrations an amine mixture was measured. Further information about these chamber studies is given in SI Text.

Clusters and sulfuric acid vapor were measured with the Cluster CIMS (40). Further information about how the Cluster CIMS was optimized to detect neutral molecular clusters is provided in SI Text. Evidence suggests (22) that the most highly neutralized clusters do not undergo chemical ionization by the nitrate ion and are therefore not detected by the Cluster CIMS, although the extent to which this affects our measurements is unknown. In our analysis we assume that all clusters undergo chemical ionization. These uncertainties and limitations place constraints on the information that can be obtained with the Cluster CIMS. Nevertheless, the data provide clues about nucleation processes that were exploited in this paper. In analyzing the Cluster CIMS data we focus on the clusters’ sulfuric acid content, which is measured with greater confidence, and avoid the need to know explicitly the clusters’ water or alkaline content, which cannot be measured with the Cluster CIMS.