Mobility of a semiflexible chain confined in a nanochannel

Abstract

The classic results of de Gennes and Odijk describe the mobility of a semiflexible chain confined in a nanochannel only in the limits of very weak and very strong confinement, respectively. Using Monte Carlo sampling of the Kirkwood diffusivity with full hydrodynamic interactions, we show that the mobility of a semiflexible chain exhibits a broad plateau as a function of extension before transitioning to an Odijk regime, and that the width of the plateau depends on the anisotropy of the monomers. For the particular case of DNA in a high ionic strength buffer, which has highly anisotropic monomers, we predict that this Rouse-like behavior will be observed over most of the measurable chain extensions seen in experiments.

The configurations and dynamics of a flexible chain confined in a tube were described quite some time ago by de Gennes [1–3] and Odijk [4]. Emerging genomics technologies such as DNA barcoding [5, 6] have brought to the forefront the comparable problem of describing semiflexible chains when they are confined in a nanochannel [7, 8]. In this Letter, we show that the classical results for the mobility in the de Gennes [3] and Odijk regimes [4], which we will confirm describe the dynamics of flexible chains over the full range of confinement, are only the limiting cases for semiflexible chains such as DNA. Moreover, when DNA in a high ionic strength buffer is used as a model polymer, we predict that the mobility is independent of the fractional extension of the chain over the experimentally relevant range of chain extensions [8] (~ 20% to ~ 80%). Thus, the commonly invoked ansatz [3] that the friction coefficient of a confined, semiflexible chain is proportional to its extension fails for DNA.

Let us first define what we mean by a semiflexible chain, since this term changes in different contexts [9]. The polymer is described by its contour length L, persistence length l_p, and effective width w, such that the chain consists of N = L/l_p persistence lengths. Often, the term “semiflexible” is used in a global context to describe a chain where L ≈ l_p, corresponding to a semiflexible filament such as actin. In our study of chains confined in nanochannels, we are concerned with the local flexibility of the chain on the length scale of the channel size, D ≈ l_p. In this context the anisotropy of the “monomers” matters, with a flexible chain corresponding to l_p/w ≈ 1 and a semiflexible chain corresponding to $l_p∕w\gg 1$ [10].

In particular, we will focus on double-stranded DNA in a high ionic strength buffer that screens electrostatic interactions, which has frequently been used as a model system for a confined polymer [11]. In these conditions, DNA is clearly a semiflexible chain, with l_p = 53 nm [12] and w = 4.6 nm [13]. As we will see, this high degree of anisotropy limits de Gennes’ model [1–3] to very small values of the fractional extension. The DNA used in experiments can be quite long, normally tens of microns in length. As a result, the chain is flexible in the global sense since $L\gg l_p$.

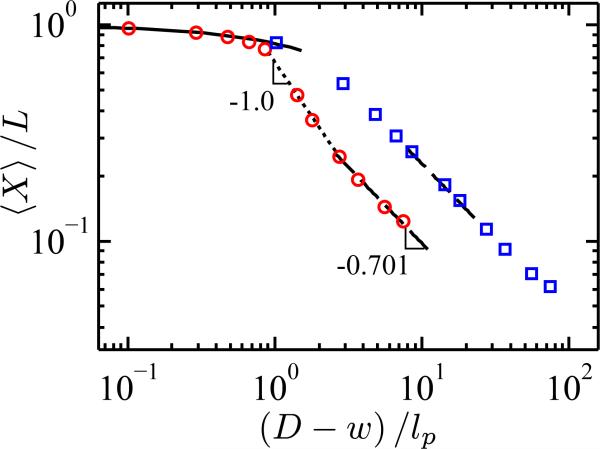
We already know that the semiflexible nature of DNA strongly affects its equilibrium extension [13–16]. Figure 1 shows how the average chain extension, 〈X〉, depends on the degree of confinement for a flexible chain and semiflexible chain. These data were generated by modeling the chain as a series of N_b = 2048 touching beads [17] of size w that interact by a hardcore excluded volume interactions. To give the chain a persistence length of l_p, a bending potential is enforced between trios of beads according to the discrete wormlike chain model [15, 18]. Analogous to our prior work [15], we generated an equilibrium ensemble of chain configurations using Monte Carlo simulations with reptation, crankshaft and pivot moves [19]. The simulation was run in each case until the statistical errors, corrected for the time series autocorrelation [20], were smaller than the size of the plot symbols.

FIG. 1.

(color online) Averaged extension of a flexible (l_p = 5.3 nm, blue squares) and a semiflexible (l_p = 53 nm, red circles) chain containing 2048 touching beads of width w = 4.6 nm as a function of the effective channel width, D – w, available to the chain. To aid the eye, lines corresponding to the Odijk regime (solid), transition regime (dotted), and extended de Gennes/de Gennes regimes (long dashed) are shown.

The classical theories [1, 2, 4] provide a complete description for the extension of the flexible chain. Over almost the full range of extension, the flexible chain is in the de Gennes regime [1, 2]. Here, the chain consists of isometric compression blobs of characteristic volume D³ containing a subchain of length L_sub ≅ D^5/3 (wl_p)^–1/3 [14]. The corresponding extension is 〈X〉 ≅ L(wl_p)^1/3 D^–2/3. A more precise calculation yields 〈X〉 ~ D^{(ν – 1)/ν} with ν = 0.5877 being the Flory parameter [15]. In the tightest channels, the chain crosses over into the Odijk regime [4], where the chain consists of a series of deflection segments. The extension here is 〈X〉 = L[1 – 2α (D/l_p)^2/3] with α = 0.09137 a universal prefactor [21].

In contrast, we already know [13–16] that the classical theories [1, 2, 4] only correspond to the limiting cases for the extension of a semiflexible chain. Indeed, in order for a semiflexble chain to be able to reach a de Gennes regime, the polymer must have a length of at least L ≅ l_p³/w² in a channel that is larger than D ≅ l_p²/w [14, 15]. As a semiflexible chain is compressed by decreasing the channel size, the blobs become anisometric [13–15] with size D²H, where H ≅ (Dl_p)^2/3w^–1/3. Each one of these cylindrical blobs contains a subchain of length L_* ≅ l_p^1/3D^4/3w^–2/3. This regime was named the “extended” de Gennes regime [15] because the scaling for the extension in the de Gennes regime, 〈X〉 ≅ L(wl_p)^1/3D^–2/3, extends to the case of anisometric compression blobs. When the channel size approaches the order of the persistence length, D ≈ l_p, the chain can no longer form blobs. Here the behavior crosses into a transition regime where several simulations [15, 16], as well as our results in Fig. 1, indicate that the extension scales like 〈X〉 ~ D^–1 [15, 16]. The free energy of these configurations is unknown, and it is not clear yet if the behavior is universal. Finally, when $D\ll l_p$, the other classical limit of Odijk [4] is recovered.

For DNA confined in a nanochannel, semiflexibility is a crucial aspect. As the anisotropy of the monomers increases, the width of the transition regime grows; the maximum extension in the extended de Gennes regime is compressed to 〈X〉/L ≅ (w/l_p)^1/3. When DNA in a high ionic strength buffer is used as a model for a confined polymer [7, 8], the extended de Gennes regime and, in particular, the transition regime encompass almost the entire experimental range of extensions [15]. Indeed, the existence of these additional regimes explains [15] the disagreement between early experiments on DNA extension in nanochannels [8] and the de Gennes model.

Let us now consider the mobility of a confined semiflexible chain. By applying an infinitesimal force f_x that is uniformly distributed along the chain, the corresponding velocity along the channel axis is

$$v_x=\mu f_x=\langle {\Omega }_{xx}\rangle f_x$$ (1)

where μ is the mobility of the chain. As seen in eq. (1), we can obtain the Kirkwood approximation to the mobility [22, 23] from the appropriate component of the hydrodynamic tensor, Ω_xx, where the brackets refer to an average over the equilibrium distribution of chain configurations.

For a flexible chain, the number of monomers inside the volume D³ where the walls screen long-range hydrodynamic interactions is sufficiently high to permit a simple scaling law. Simplifying eq. (1) in terms of the pair-correlation function, g(r), following de Gennes [2], yields

$$\mu =N^{-1}\int g\left(r\right)\Omega \left(r\right)d^3\mathbf{r}$$ (2)

In the blob theory [3] the pair-correlation function is replaced with c, the number concentration of segments inside a blob, and the hydrodynamic screening by the walls is approximated by Ω(r) = 1/ηr for r < D and an exponential decay for r > D [2, 3], where η is the solvent viscosity. Since we only need an approximate result, the remainder of the calculation is simplified by using spherical coordinates and integrating over the solid angle [2],

$$\mu =\frac{4\pi c}{N}{\int }_0^D\frac{1}{\eta r}{r}^{2}dr\approx \frac{c{D}^2}{\eta N}$$ (3)

In the de Gennes regime, the monomer concentration in the blobs is c ≅ (L_sub/l_p)/D³, which yields $c\cong w^{-1∕3}{l}_p^{-4∕3}{D}^{-4∕3}$. Recalling that N = L/l_p, we recover the classic result [3]

$$\mu \sim (1∕\eta L){\langle X∕L\rangle }^{-1}$$ (4)

In the extended de Gennes regime, the density of segments is (L_*/l_p)/(D²H), which again yields $c\cong w^{-1∕3}{l}_p^{-4∕3}{D}^{-4∕3}$. As a result, the blob theory predicts the diffusion in the extended de Gennes regime is also given by eq. (4).

The key assumption leading to eq. (4) is that the number of segments in the screening volume, cD³, is large enough so that each blob is non-draining (Zimm). In other words, the subchain comprising a blob entrains the fluid inside it, whereupon the segment-segment hydrodynamics dominate and the subchain behaves hydrodynamically like a solid object. Free draining (Rouse) behavior at the subchain level should arise when D ≈ 2l_p. There is now approximately one Kuhn length inside D³, which causes each segment to be an independent friction center. In other words the segment-fluid hydrodynamic interactions are dominant. In this limit, we would expect

$$\mu \sim (1∕\eta L){\langle X∕L\rangle }^0$$ (5)

The question is whether the chain reaches the scaling of eq. (5) before it reaches the Odijk regime $(D\ll l_p)$. In the latter case, the chain is like a slender, confined rod. Its mobility [24]

$$\mu \approx \frac{1}{2\pi }\ln \left(\frac{l_p}{2a}{\left[\frac{1-\langle X∕L\rangle }{2\alpha }\right]}^{3∕2}\right)$$ (6)

reflects the dominance of segment-wall interactions. The latter expression involves the bead hydrodynamic radius, a. We chose a = 1.38 nm so that the chain mobilities in free solution for l_p = 53 nm matched experimental values for DNA [25]. While we raise this issue for nanochannels, similar concerns about the draining behavior have been expressed for DNA in slits [26].

To determine if and when the chain crosses over to eq. (5), we computed the Kirkwood mobility through a Monte Carlo integration of eq. (1) [27]. For a given chain configuration, we computed the 3×3 chain hydrodynamic tensor

$$\Omega =\frac{1}{{N_b}^2}\sum _{i,j}^{N_b}\left[\frac{{\delta }_{ij}}{6\pi \eta a}\mathbf{I}+(1-{\delta }_{ij}){\Omega }^{\mathrm{OB}}\left({\mathbf{r}}_{ij}\right)+{\Omega }^{\mathrm{W}}({\mathbf{r}}_i,{\mathbf{r}}_j)\right]$$ (7)

In the latter, δ_ij is the Kronecker delta, r_i and r_j are the positions of bead i and j respectively and r_ij = r_j – r_i. The hydrodynamic tensor includes a self-diffusion term, a free-solution Oseen-Burgers tensor [28], Ω^OB, and a wall term, Ω^W, due to the effects of the no-slip condition at the channel boundaries. The Oseen-Burgers tensor is acceptable in this calculation because the beads are hard spheres, and do not suffer from unphysical behavior caused by bead-bead overlap. The wall term was calculated using a numerical solution of Stokes equation, similar to Jendrejack et al. [28]. We employed a second-order finite difference approach with a staggered, three-dimensional, uniform, Cartesian mesh [29] and mass-conserving boundary conditions. Due to the prohibitive computational time needed to solve the hydrodynamic problem for each chain configuration, the wall term was calculated and stored on a grid, and subsequently linearly interpolated during Monte Carlo averaging. Finally, we note that in each case the statistical errors of the computed diffusivity, corrected for the time series autocorrelation [20], are smaller than the size of all plot symbols.

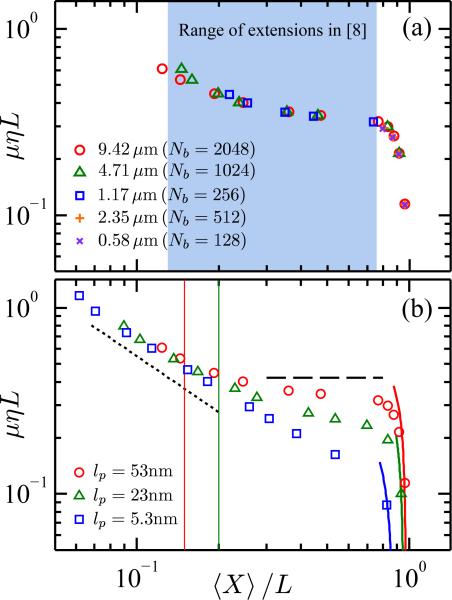
Figure 2a shows the results for the mobility of DNA as a function of its extension. In the largest channels, corresponding to the smallest fractional extensions, the channel provides minimal confinement and the chains are approaching the Zimm free solution mobility, μ ~ L^–3/5. Outside of this limit, the friction due to the walls is substantial. If we neglect the wall term in eq. (7) for a channel size of 80 nm, the resultant mobility is more than 5 times larger.

FIG. 2.

(color online) Mobility versus extension. All simulations correspond to w = 4.6 nm and a = 1.38 nm. (a) Results for five different chain lengths for l_p = 53 nm. The shaded region corresponds to the extensions seen in DNA experiments [8]. (b) Results for three different persistence lengths for L = 9:42 μm (N_b = 2048 beads). The dotted line is the scaling of eq. (4) and the dashed line shows the scaling of eq. (5). The solid lines are the approximation in eq. (6). The vertical lines are the values for the onset of the scaling 〈X〉/L ~ D^–1 for the 53 nm chain (red, 〈X〉/L = 0.15) and the 23 nm chain (green, 〈X〉/L = 0.2).

The key result is that the Rouse scaling in eq. (5) encompasses all of the extensions seen in experiments for DNA [8]. In contrast, Fig. 2b shows that eq. (4) is a reasonable description for the flexible chain all the way to the transition to the Odijk regime of eq. (6). To be more quantitative, linear regression gives μ ~ 〈X〉^–0.874 (R² = 0.998) which agrees very well with the value of μ ~ 〈X〉^{–0.61/0.7015} obtained from other flexible chain calculations [30]. We also simulated an intermediate persistence length l_p = 23 nm and found an intermediate result; for short extension this chain obeys de Gennes scaling but it still exhibits a broad transition towards the Odijk result.

In the case of the flexible chain, the crossover between de Gennes and Odijk mobilities is narrow, mirroring the extension behavior. If the confinement does not force a rod-like conformation, this chain is so flexible that it can only form non-draining blobs. In the semiflexible case, the large monomer anisotropy leads to a wide gap between the de Gennes regime and the Odijk regime for the extension. This gap closely aligns with the beginning and ending of the mobility plateau in Fig. (2)b. Thus the existence of additional regimes for the extension of semiflexible chains explains both the existence of the mobility plateau and the fact that it grows with increasing persistence length.

While we have focused exclusively on the dynamics of DNA in a high ionic strength buffer, where electrostatic interactions are screened, there are DNA barcoding devices [5] that use high ionic strengths to stiffen the DNA backbone. As the ionic strength decreases, the predicted values for the effective width and persistence length begin to converge [31]. Our analysis thus predicts that DNA will obey the de Gennes prediction in eq. (4) in a sufficiently low ionic strength such that l_p/w ≈ 1 and a large enough channel such that this very high persistence length chain can form compression blobs. These experiments are technically challenging, since the length of DNA required to reach the de Gennes regime in a low ionic strength buffer is enormous.

In this Letter, we have clearly shown that the hydrodynamics of confined semiflexible chains deviate significantly from the classic prediction for a flexible chain in eq. (4) [2, 3]. As there are a large number of publications using DNA in a high ionic strength buffer as a model polymer, it is important to keep in mind the stark differences between the dynamics of semiflexible chain such as DNA and the more flexible chains often encountered in polymer physics [11].