Abstract
Knowledge of how crash severity influences injury risk in car crashes is essential in order to create a safe road transport system. Analyses of real-world crashes increase the ability to obtain such knowledge.
The aim of this study was to present injury risk functions based on real-world frontal crashes where crash severity was measured with on-board crash pulse recorders.
Results from 489 frontal car crashes (26 models of four car makes) with recorded acceleration-time history were analysed. Injury risk functions for restrained front seat occupants were generated for maximum AIS value of two or greater (MAIS2+) using multiple logistic regression. Analytical as well as empirical injury risk was plotted for several crash severity parameters; change of velocity, mean acceleration and peak acceleration. In addition to crash severity, the influence of occupant age and gender was investigated.
A strong dependence between injury risk and crash severity was found. The risk curves reflect that small changes in crash severity may have a considerable influence on the risk of injury. Mean acceleration, followed by change of velocity, was found to be the single variable that best explained the risk of being injured (MAIS2+) in a crash. Furthermore, all three crash severity parameters were found to predict injury better than age and gender. However, age was an important factor. The very best model describing MAIS2+ injury risk included delta V supplemented by an interaction term of peak acceleration and age.
INTRODUCTION
In order to design a safe road transport system, including all safety technologies, it is important to understand the whole chain of events in a crash, especially how the forces related to the impact speed can influence the injury outcome. Knowledge of the human injury tolerance and biomechanics is fundamental. Analyses of real-world car crashes are useful to gain such knowledge and to identify the effectiveness of safety technologies.
The human tolerance for injury has traditionally been achieved from crash tests with volunteers, PMHS (Post Mortem Human Subjects) or animals. Several previous studies have also used real-world data to correlate crash severity, often defined as change of velocity (delta V), with risk of occupant injury (Augenstein et al., 2003; Bahouth et al., 2004; Sunnevång et al., 2009; Kononen et al., 2011). The delta V has traditionally been estimated from the vehicle post-crash deformation. The quality of real-world data has often been a limiting factor in establishing injury tolerance (Kullgren and Lie, 1998). However, during the last 15 years, studies aimed at evaluating injury tolerance based on real-world crashes with recorded crash severity have been presented (Gabauer and Gabler, 2006; Gabauer and Gabler, 2008; Kullgren and Krafft, 2008; Ydenius, 2010). In these studies, injury risks for different injury types versus recorded impact severity have been established. Nowadays, vehicles are often equipped with event data recorders (EDR) that makes it possible to measure change of velocity time history or acceleration time history during the crash phase. However, these data are often restricted to being used by the manufacturer, and studies from only four databases have been published to the author’s knowledge: Volvo, NHTSA, Winterthur and Folksam, see for example (Andersson et al., 1997; Kullgren et al., 1999; Ydenius and Kullgren, 2001; Krafft et al., 2002; Krafft et al., 2005; Gabauer and Gabler, 2006; Gabler and Gabauer, 2006; Sinzig, 2010) .
The crash severity level to which a human is exposed during a crash depends on several factors, such as relative velocity between the vehicles, the mass and structure of the vehicles, as well as the crash situation, including impact angle, overlap etc. As mentioned earlier, several approaches such as crash tests with volunteers, PMHS, animals, dummies and numerical models, have been used to estimate the human response to impact. However, the knowledge of human injury tolerance is still limited. The risk of human injury is influenced by, and differs depending on, several parameters, such as road user groups, age, gender, crash type, type of restraint systems etc. Analysis of real-world crashes have increased the understanding of how crash severity correlates with e.g. impact speed, type of striking object and injury outcome (Krafft et al., 2002; Gabauer and Gabler, 2006; Stigson, 2009; Stigson et al., 2009; Sunnevång et al., 2009; Ydenius, 2010). To understand the biomechanical limits and mechanisms of injuries, it is important to study how crash severity influences the risk of injury.
The aim of this study is therefore to present injury risk functions based on real-world frontal crashes with crash severity measured with on-board crash pulse recorders.
METHODS
In order to analyze the correlation between crash severity and injury outcome, real-world crashes in Sweden collected by Folksam involving cars fitted with two kinds of on-board crash pulse recorders named CPR (Crash Pulse Recorder) and ECR (Electronic Crash Recorder) were used. Since 1992, approximately 240,000 CPRs and 35,000 ECRs have been installed in passenger cars in Sweden, comprising twenty-six different car models of four car makes (Honda, Opel, Saab, and Toyota) aimed at measuring frontal and rear-end impacts. The ECR also measures lateral impacts. The CPRs and ECRs were fitted in all new cars of the models included, which are connected to a car damage warranty insurance in Folksam. The installation is made irrespective of the age, sex or insurance claims history of the insurance policy holder.
The CPR/ECR measures acceleration time history in the impact phase. Crash pulses were filtered according to CFC60. The ECR records the complete crash pulse (30 ms before triggering and a total of 500 ms). The CPR records the complete acceleration after triggering. The trigger level is between 3 and 5 g (Kullgren, 1998). The acceleration before the triggering is approximated based on the first 15 ms of the recorded acceleration.
Change of velocity and mean and peak acceleration were calculated from the measured crash pulses. To calculate mean acceleration the pulse duration (start and end of the pulse) were decided according to a procedure where the acceleration-time history is filtered at 30 Hz and the start and end is decided based on the intersection with the y-axis.
The recordings from the CPR are calculated to show the acceleration in the principal direction of force. The ECR measures the acceleration in the x–y plane, and resultant acceleration was calculated. The accuracy of the CPR has been shown to be within 5% in impacts between 23 and 81 km/h (Kullgren, 1998). The accuracy was lower (7%) in low-speed tests (23–31 km/h), while in high-speed tests (43–81 km/h) it was 4%. And the accuracy of the ECR is higher than the CPR(Ydenius et al., 2012).
The inclusion criteria in this study were as follows:
frontal crashes (within +/− 30 degrees from straight frontal) with a repair cost exceeding 5,000 EUR (1995–2007) and 7,000 EUR (from 2007) respectively
vehicle model year 1992 or later (the mean model year was 2000)
airbag fitted cars
two-vehicle crashes and single-vehicle crashes
restrained drivers and front seat passengers
Multiple event crashes were excluded (unless one of the events had a minor crash severity in comparison to the one included). Crashes with unknown injury data were also excluded.
With these criteria applied, 391 crashes occurring between 1993 and 2011 involving 391 drivers and 110 front seat passengers remained for analysis. In 12 cases the age was unknown and in five cases gender was unknown. The use of seat belt was verified from inspections of the seat belt systems. Intrusion into the occupant compartment was not considered.
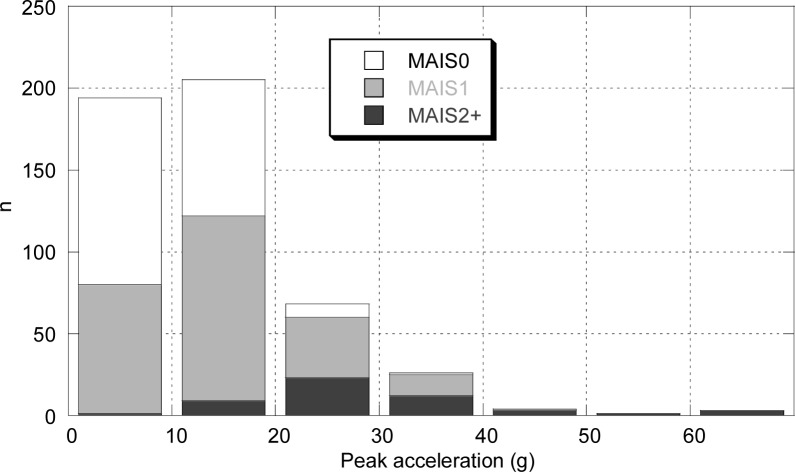
Injury data were collected from hospital records, questionnaires sent to the occupants, or insurance claims. All initial diagnoses, even self-reported minor injuries, were classified according to AIS 2005 (AAAM, 2005). Cases collected prior to the release of AIS 2005 were all converted manually. Only the maximum AIS (MAIS) for each injured occupant was used. Figure 1–3 shows the distribution of injuries in crashes with different change of velocity, mean acceleration and peak acceleration intervals. Empirical injury risks were calculated as the proportion of injured in each interval of each crash severity parameter.
Figure 1.
Number of crashes and injuries in intervals of change of velocity
Figure 3.
Number of crashes and injuries in intervals of peak acceleration.
Statistical methods
The predictor variables were grouped in two categories, occupant characteristics and crash violence, Table 1. Average pulse duration for the sample was 102 ms with a standard deviation of 32 ms. The minimum and maximum duration was 47 and 427 ms respectively. In the logistic regression analysis, all variables were linear continuous variable except from age that was defined as a nominal variable. The distribution of each variable was investigated for the total sample (N=489) and the MAIS2+ injured (N=52). Simple and multiple logistic regression analyses were applied to the sample in order to derive an analytical expression for the MAIS2+ risk. The probability of MAIS2+ injury, P(X), was then assumed to have the following form:
| (1) |
where X is a vector with the predictor variables, and a, B parameters to be estimated by the method of maximum likelihood (McCullagh and Nelder, 1989; Dobson, 2002). Note that B is a vector of the same length as X. A confidence band for the risk curve was derived following Kutner et al (2004). The main objective of this analysis was to find a multivariate function describing occupant risk of sustaining MAIS2+ injuries. The model selection was based on a subset of 379 cases, including 489 occupants, for which all predictor variables were known.
Table 1.
Predictor variables.
| Occupant characteristics | Type | N | Mean | Median | Minimum | Maximum | S.D. |
|---|---|---|---|---|---|---|---|
| Gender | Nominal | 496 | |||||
| Age | Continuous | 489 | 45.9 years | 47.0 years | 6.0 years | 93.0 years | 18.6 years |
| Crash severity | |||||||
| Change of velocity | Continuous | 501 | 21.3 km/h | 16.7 km/h | 3.9 km/h | 126.2 km/h | 14.6 km/h |
| Mean acceleration | Continuous | 501 | 5.8 g | 4.9 g | 1.2 g | 22.8 g | 3.1g |
| Peak acceleration | Continuous | 501 | 14.4 g | 11.5 g | 2.8 g | 66.2 g | 9.0 g |
Multiple logistic regression models should not be applied to collinear predictor variables. In this data, some variables were likely collinear, e.g., peak acceleration, mean acceleration and delta V. This was checked by studying scatter plots of these variables, two at the time.
Model selection was based on Akaike’s information criterion, AIC (Akaike, 1974). A great number of models (i.e. combinations of predictor variables) were tested, and the one with lowest AIC was chosen as the best model. AIC is a function of the maximum of the log-likelihood function, L, (see e.g. Dobson 2002) and the number of predictor variables, k–1: AIC=−2(log L – k). In this way, models with high likelihood and small number of parameters are preferred. Adding new variables always increase L but does not necessarily improve AIC. Furthermore, significance of the individual predictor variables was checked considering Wald Chi-square statistics. Proceeding from the best model according to AIC, various interaction effects between the predictor variables were introduced. AIC was still considered to evaluate if the models improved by the interaction effects. The software package SAS 9 was used for all statistical analyses.
Descriptive statistics for the explanatory variables for the sample are presented in Table 1. In the present study, 30 percent of the occupants were over 60 years of age and these accounts for 40 percent of the MAIS2+ injuries. The percentage of females was 40 for the total sample and a slightly higher proportion of the MAIS2+ injuries, 46%. In eight cases the passenger occupant age was less than 15 years. These cases were excluded and all analysis was repeated for the remaining cases. The simple as well as multiple regressions were not affected.
RESULTS
MAIS2+ injury prediction based on simple analysis
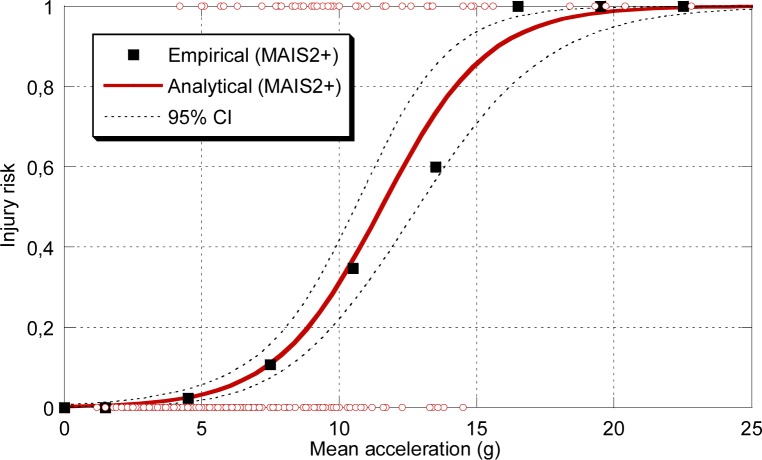
Logistic regression analysis was applied to fit an analytical function to predict injury outcome in real-world crashes, in total 489 occupants. Figure 4–6 show the MAIS 2+ injury risk curves with crash severity for the restrained front seat occupants in cars fitted with airbags in frontal crashes. For example, at a delta V of 28 km/h the injury risk was 10% of having a MAIS2+ injury. The mean acceleration (AIC=211.9), followed by delta V(AIC=215.9), was the single variable that best could predict injury outcome, Table 2 and Figure 7. Peak acceleration (AIS=223.5) was not quite as accurate as the other crash severity parameters. Age as a single variable could not predict MAIS2+injury as good as the crash severity variables (AIC= 327.7). The effect of gender was not significant.
Figure 4.
Risk of a MAIS2+ injury for front seat occupants versus delta V in frontal impacts
Figure 6.
Risk of a MAIS2+ injury for front seat occupants versus peak acceleration in frontal impacts
Table 2.
The value of the logistic regression parameters
| Estimate | Lower limit | Upper limit | Standard error | Wald X2 | p-value | |
|---|---|---|---|---|---|---|
| Simple variable analysis | ||||||
| Intercept | −5.35 | −6.31 | 4.40 | 0.49 | 121.57 | <0.0001 |
| Delta V (km/h) | 0.11 | 0.086 | 0.14 | 0.014 | 66.97 | <0.0001 |
| Intercept | −5.99 | −7.07 | −4.92 | 0.55 | 119.30 | <0.0001 |
| Mean acc. (g) | 0.52 | 0.40 | 0.64 | 0.062 | 70.88 | <0.0001 |
| Intercept | −5.37 | −6.31 | −4.43 | 0.48 | 125.0 | <0.0001 |
| Peak acc. (g) | 0.17 | 0.13 | 0.21 | 0.020 | 71.2 | <0.0001 |
| Multiple variable analysis | ||||||
| Intercept | −5.9 | −6.96 | −4.81 | 0.55 | 114.7 | <0.0001 |
| Delta V (km/h) | 0.08 | 0.05 | 0.11 | 0.015 | 26.2 | <0.0001 |
| Peak acc. (g) x age (year) | 0.0016 | 0.0016 | 0. 0024 | 0.00040 | 15.7 | <0.0001 |
Figure 7.
AIC was calculated for all models and the one with lowest AIC (marked with a triangle) was chosen as the best model.
MAIS2+ injury prediction based on multiple variable analysis
Multiple logistic regression analysis was applied to the sample. In total 31 models that relate crash conditions to the risk of MAIS2+ injury were presented. Model selection was based on Akaike’s information criterion, Figure 7. Some models are not included in the scatter plot, since AIC was too high (AISmaximum=334.3). The best of the models without interaction effects (AIC provided in Figure 7) included delta V, peak acceleration and age as independent predictors (AIC=203.8). However, by investigating various interaction models of these variables (and also including mean acceleration) an even better model was found, according to AIC. Hence, the very best model included delta V supplemented by an interaction term of peak acceleration and age (AIC=201.6), Eq. (2) and Table 2.
The resulting risk function is presented in Eq. (2):
| (2) |
Model accuracy
The area under the Receiver Operator Characteristics Curve (AUROC) for the final model, based on the variable delta V together with age multiplied by peak acceleration, was 0.92, which indicates that the model had excellent predictive power. The higher the AUROC, the better, with a 0.50 value indicating random performance and 1.00 denoting perfect performance.
A collinearity between peak acceleration, mean acceleration and delta V was found. It is obvious that these crash severity parameters are highly correlated since delta V is based on mean acceleration and the crash duration. This could be seen when studying the estimate for change of velocity. The estimate changes when adding peak or mean acceleration, but not when adding age to the model. This shows that there is collinearity between the crash severity parameters. The relation between delta V and age multiplied by peak acceleration can be studied in the scatter plots of these variables, Figure 8.
Figure 8.
Scatter plot of delta V and the age multiplied by peak acceleration
DISCUSSION
Analysis of real-world crashes is essential in order to obtain knowledge of influence of crash severity on injury outcome in the variety of crashes occurring under real-world conditions. The crash severity data used in this study are of high quality due to the fact that all crashes involved cars fitted with crash pulse recorders. The criterion for being included in the database used for this study is a certain repair cost. The advantage with this is that uninjured occupants are also included. Often the inclusion criterion in databases is that at least one occupant is injured or that the vehicle is towed away. This would result in the injury risk being overestimated at lower speeds. It is important that the inclusion criterion is not linked to injury outcome in order to get an unbiased injury risk.
Figures 4–6 shows the risk of MAIS2+ injury with crash severity for three different descriptors of crash severity; delta V, peak acceleration and mean acceleration. The risk curves show that small changes in crash severity have a considerable influence on the risk of injury. The risk of sustaining an injury with a MAIS2+ was found to be 10 percent at either a delta V of 28 km/h or a mean acceleration of 2.7 g. At a delta V of 48 km/h or a mean acceleration of 11.5 g the risk of sustaining an MAIS2+ injury was 50 percent. In a comparable study from Gabauer and Gabler (2008) based on 145 crashes with EDR data from the USA, the 50 percent risk of an MAIS2+ injury for a belted and airbag restrained occupants was found to be identical to the one presented in Figure 4. It is interesting to see that although the two studies are based on different car fleets, the risk of an MAIS2+ injury appears to be very similar. The car fleets in the study by Gabauer and Gabler was based on GM cars in the USA and this study was based on mainly Toyota cars in Sweden.
Delta V has traditionally been used to correlate crash severity with risk of occupant injury (Augenstein et al., 2003; Bahouth et al., 2004; Sunnevång et al., 2009; Kononen et al., 2011). Results from the present study show that delta V as a single predictor of MAIS2+ injury is still useful although mean acceleration had a lower AIC. From many EDRs it is possible to calculate mean acceleration even if they do not record the complete acceleration-time history.
Although mean acceleration as a single parameter was found to best predict MAIS2+ injury risk, single parameters other than those studied could be even better. Examples worth further evaluations could be the mean acceleration of the first 50 ms of the pulse or the maximum mean acceleration in a moving window of a fixed time frame. In this study the complete acceleration-time history was used to calculate mean and peak acceleration. Having the complete acceleration-time history makes it possible to also study how other crash severity parameters influence the injury risk. This should be further investigated.
The results also show that a mix of factors better predict injury than mean acceleration itself. The accuracy of the final model, based on the variable delta V together with age multiplied by peak acceleration, was denoting excellent performance (AUROC=0.92). Of course, parameters other than those included in this study may have importance. This needs to be further investigated.
An important issue is how good the regression technique is in mirroring the true injury risk. Comparing the analytical risk function with the empirical there seems to be a good correlation for both change of velocity and mean acceleration, and not as good for peak acceleration, which is also reflected by the higher AIC value.
Several previous studies have correlated crash severity with risk of injury risk using logistic regression. The method is suitable for this type of analysis. However, other statistical models could probably be more suitable to predict other injury risks, e.g. whiplash injuries in frontal impacts. These do not show a continuously increasing risk, Figure 9 (Kullgren et al., 2000), which has some implications for the statistical model to be used.
Figure 9.
Risk of whiplash injury in frontal impacts (Kullgren and Stigson, 2010)
It is known from previous studies conducted on wider datasets that both age and gender influence the risk of being fatally injured in a car crash (Bedard et al., 2002; Funk et al., 2008). In particular, age and fatality risk are strongly correlated with each other (Braver and Trempel, 2004). Age as a single variable could not predict MAIS2+injury as well as the crash severity variables but it was an important factor in the multiple regression analysis. Based on another subset of Folksam CPR data it has been shown that occupants above 60 years of age have over 60 percent higher risk for MAIS2+injuries compared with other occupants (Ydenius, 2010). In the present study 30 percent of the occupants were above 60 years of age and these accounted for 40 percent of the MAIS2+ injuries. In order to offer a safe road transport system to all road users, the road traffic system should also be designed for the most vulnerable road users. Therefore, it is important to study injury risk for all ages. Furthermore, gender was not a significant predictor of injury risk in the present study. Adding gender to other predictor variables never improved the models according to AIC. However, in all models tested the odds ratio between males and females was approximately 0.7, indicating that males have a lower risk than females. A previous study has shown that the risk is 50 percent higher of having serious injuries (ISS>14) in crashes with at least one female occupant (Kononen et al., 2011). However, Mackay and Hassan (2000) have shown that gender did not have a great effect on MAIS2+ injuries based on UK data. They found that the influence of age was more important for the injury risk, which is in line with the results of the current study. As mentioned earlier the best model was the one with interaction between peak acceleration and age together with change of velocity. The interpretation is that age has a significant importance when it comes to the tolerance to high peak acceleration.
Limitations of the Study
The data were limited to twenty-six car models from four car makers, with on-board crash pulse recorders. Therefore, it is not possible to generalise the results to the whole car fleet. One of the inclusion criteria for frontal crashes was a repair cost of at least 5,000 EUR. This limit excludes most of the crashes in which the delta V was below 10 km/h. The number of crashes at high crash severity (delta V above 60 km/h)was low, and the number of occupants with MAIS-3+ injuries was only 13, so no risk functions for MAIS3+ was presented. Delta V, mean and peak acceleration were used as crash severity measurements. Intrusion into the occupant compartment was not considered in this study. In two-car crashes delta V is dependent of vehicle mass, while mean acceleration is linked to vehicle stiffness. And lower intrusion gives higher mean acceleration. It would be of interest to study influence on injury outcome of a combination of intrusion and acceleration.
The included cars were all fitted with airbags and seat belt pretensioners. However, there was a mix of cars with and without seat belt load limiters. Load limiters have the ability to filter high peak accelerations and thereby reduce the injury risk. Further studies should be made addressing this issue.
CONCLUSIONS
Mean acceleration, followed by change of velocity, was found to be the crash severity parameters that best explained the risk of being injured (MAIS2+) in a frontal crash. Furthermore, the three crash severity parameters studied were found to predict injury better than age and gender. However, age was an important factor in the multiple regression analysis. The very best model describing MAIS2+ injury risk included delta V supplemented by an interaction term of peak acceleration and age.
Figure 2.
Number of crashes and injuries in intervals of mean acceleration.
Figure 5.
Risk of a MAIS2+ injury for front seat occupants versus mean acceleration in frontal impacts
APPENDIX
A confidence band for the risk curve was derived following Kutner et al.(2004). In short, an approximate 95% confidence interval for the probability of MAIS2+ injury at an delta V, dv, is given by 1/(1 + exp(–ˆa –ˆbdv ± 1.96(XT S2 X)1/2)). Here X is a column vector with entries (1, dv); ˆa, ˆb are the maximum likelihood estimates of a, b; and S2 is the estimated approximate variance-covariance matrix for the regression parameters when the sample size is large. The final result of the confidence interval as a function of delta V, mean and peak acceleration are presented in Eq. (3)–(5).
| (3) |
| (4) |
| (5) |
REFERENCES
- AAAM Abbreviated Injury Scale Barrington, IL, USA, Association for the Advancement of Automotive Medicine 2005.
- Akaike H. “A new look at the statistical model identification”. IEEE Trans. Automat Control. 1974;19:716–723. [Google Scholar]
- Andersson U, Koch M, Norin H. IRCOBI International Conference on the Biomechanics of Impact. Hannover; Germany: 1997. The Volvo Digital Accident Research Recorder (DARR) Converting Accident DARR-pulses into Different Impact Severity Measures. [Google Scholar]
- Augenstein J, Perdeck E, Stratton J, Digges K, Bahouth G. “Characteristics of crashes that increase the risk of serious injuries.”. Annu Proc Assoc Adv Automot Med. 2003;47:561–576. [PMC free article] [PubMed] [Google Scholar]
- Bahouth GT, Digges KH, Bedewi NE, Kuznetsov A, Augenstein JS, Perdeck E. “Development of URGENCY 2.1 for the Prediction of Crash Injury Severity.”. Topics in Emergency Medicine. 2004;26(2):157–165. [Google Scholar]
- Bedard M, Guyatt GH, Stones MJ, Hirdes JP. “The independent contribution of driver, crash, and vehicle characteristics to driver fatalities.”. Accid Anal Prev. 2002;34(6):717–727. doi: 10.1016/s0001-4575(01)00072-0. [DOI] [PubMed] [Google Scholar]
- Braver ER, Trempel RE. “Are older drivers actually at higher risk of involvement in collisions resulting in deaths or non-fatal injuries among their passengers and other road users?”. Inj Prev. 2004;10(1):27–32. doi: 10.1136/ip.2003.002923. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dobson AJ. An Introduction to Generalized Linear Models, Chapman & Hall/CRC. 2002. [Google Scholar]
- Funk JR, Cormier JM, Gabler HC. “Effect of delta-V errors in NASS on frontal crash risk calculations.”. Ann Adv Automot Med. 2008;52:155–164. [PMC free article] [PubMed] [Google Scholar]
- Gabauer DJ, Gabler HC. “Comparison of delta-v and occupant impact velocity crash severity metrics using event data recorders.”. Annu Proc Assoc Adv Automot Med. 2006;50:57–71. [PMC free article] [PubMed] [Google Scholar]
- Gabauer DJ, Gabler HC. “Comparison of roadside crash injury metrics using event data recorders.”. Accid Anal Prev. 2008;40(2):548–558. doi: 10.1016/j.aap.2007.08.011. [DOI] [PubMed] [Google Scholar]
- Gabler HC, Gabauer DJ. Safety Audit of Fatalities and Injuries Involving Guide Rail, Report to the New Jersey Department of Transportation. FHWA-NJ-2007-001. 2006.
- Kononen DW, Flannagan CA, Wang SC. “Identification and validation of a logistic regression model for predicting serious injuries associated with motor vehicle crashes.”. Accident Analysis and Prevention. 2011;43(1):112–122. doi: 10.1016/j.aap.2010.07.018. [DOI] [PubMed] [Google Scholar]
- Krafft M, Kullgren A, Malm S, Ydenius A. Influence of Crash Severity on Various Whiplash Injury Symptoms: A Study Based on Real-life Rear-end Crashes with Recorded Crash Pulses. 19th International Conference on the Enhanced Safety Vehicles (ESV); Washington DC, USA. 2005. [Google Scholar]
- Krafft M, Kullgren A, Ydenius A, Tingvall C. “Influence of Crash Pulse Characteristics on Whiplash Associated Disorders in Rear Impacts--Crash Recording in Real Life Crashes.”. Traffic Inj Prev. 2002;3(2):141–149. [Google Scholar]
- Kullgren A. Validity and Reliability of Vehicle Collision Data: Crash Pulse Recorders for Impact Severity and Injury Risk Assessments in Real-Life Frontal Impacts. . . Stockholm, Folksam Research. Phd. 1998.
- Kullgren A, Krafft M. Influence of change of velocity and mean accelration on whiplash injury risk: Results from real-world crashes. 2nd International Conference on Whiplash: Neck pain in car crashes; Erding, Munich. 2008. [Google Scholar]
- Kullgren A, Krafft M, Malm S, Ydenius A. The Influence of Crash Pulse Characteristics on Injury Risks in Real-Life Frontal Impacts. JSAE Conf; Yokohama. 1999. [Google Scholar]
- Kullgren A, Krafft M, Malm S, Ydenius A, Tingvall C. “Influence of Airbags and Seatbelt Pretensioners on AIS1 Neck Injuries for Belted Occupants in Frontal Impacts.”. Stapp Car Crash J. 2000;44(SAE P-362):117–125. doi: 10.4271/2000-01-SC09. [DOI] [PubMed] [Google Scholar]
- Kullgren A, Lie A. “Vehicle Collision Accident Data - Validity and Reliability.”. Journal of Traffic Medicine. 1998;26(3–4):77–98. [Google Scholar]
- Kullgren A, Stigson H. WP1 - Task 1.2 report from Folksam, ADSEAT, Project no. 233904, CP Sustainable Surface Transport. 2010. Stockholm, Folksam Research.
- Kutner MH, Nachtsheim CJ, Neter J, Li W. Applied Linear Statistical Models. New York: McGraw-Hill/Irwin; 2004. [Google Scholar]
- Mackay M, Hassan AM. “Age and gender effects on injury outcome for restrained occupants in frontal crashes: a comparison of UK and US data bases.”. Annu Proc Assoc Adv Automot Med. 2000;44:75–91. [PMC free article] [PubMed] [Google Scholar]
- McCullagh P, Nelder JA. Generalized Linear Models. London: Chapman & Hall; 1989. [Google Scholar]
- Sinzig B. Crash Recorder: acceleration data of real world accidents. 3rd International Conference Whiplash 2010 - Neck Pain in Car Crashes; Munich, Germany. 2010. [Google Scholar]
- Stigson H. “Evaluation of safety ratings of roads based on frontal crashes with known crash pulse and injury outcome.”. Traffic Inj Prev. 2009;10(3):273–278. doi: 10.1080/15389580902864107. [DOI] [PubMed] [Google Scholar]
- Stigson H, Ydenius A, Kullgren A. “Variation in crash severity depending on different vehicle types and objects as collision partner.”. International Journal of Crashworthiness. 2009;14(6):613–622. [Google Scholar]
- Sunnevång C, Rosén E, Bostrom O. “Real-life fatal outcome in car-to-car near-side impacts--implications for improved protection considering age and crash severity.”. Traffic Inj Prev. 2009;10(2):194–203. doi: 10.1080/15389580802594127. [DOI] [PubMed] [Google Scholar]
- Ydenius A. “Influence of crash pulse characteristics on injury risk in frontal impacts based on real-life crashes.”. Traffic Inj Prev. 2010;11(5):526–534. doi: 10.1080/15389588.2010.492053. [DOI] [PubMed] [Google Scholar]
- Ydenius A, Kullgren A. Injury Risk Functions in Frontal Impacts Using Recorded Crash Pulses. Int. IRCOBI Conf. on the Biomechanics of Injury; Isle of Man UK. 2001. [Google Scholar]
- Ydenius A, kullgren A, Stigson H. Comparison between Electronic Crash Recorder (ECR) and laboratory accelerometer data in frontal and side impact crash tests. 2012. Internal report. Stockholm, Folksam.