Abstract
A central question in intertemporal decision making is why people reverse their own past choices. Someone who initially prefers a long-run outcome might fail to maintain that preference for long enough to see the outcome realized. Such behavior is usually understood as reflecting preference instability or self-control failure. However, if a decision maker is unsure exactly how long an awaited outcome will be delayed, a reversal can constitute the rational, utility-maximizing course of action. In the present behavioral experiments, we placed participants in timing environments where persistence toward delayed rewards was either productive or counterproductive. Our results show that human decision makers are responsive to statistical timing cues, modulating their level of persistence according to the distribution of delay durations they encounter. We conclude that temporal expectations act as a powerful and adaptive influence on people’s tendency to sustain patient decisions.
Keywords: decision making, intertemporal choice, dynamic inconsistency, statistical learning, interval timing
1. Introduction
1.1. Failures of persistence
Intertemporal decision behavior can appear to be dynamically inconsistent. As Ainslie (1975) framed the problem, “people often change their preferences as time passes, even though they have found out nothing new about their situation” (p. 464). Reversals of choices in domains as diverse and consequential as diet, addiction, and financial planning create the impression that preferences are fundamentally unstable. Understanding the cause of these reversals is important, since a tendency to sustain the pursuit of delayed rewards correlates with numerous positive life outcomes (Duckworth & Seligman, 2005; Mischel, Shoda, & Peake, 1988; Shoda, Mischel, & Peake, 1990).
The predominant theoretical explanations for such reversals hold that multiple internal subsystems trade off control over behavior. The relevant subsystems have been variously characterized as cool vs. hot (Loewenstein, 1996; Metcalfe & Mischel, 1999), controlled vs. automatic (Baumeister, Bratslavsky, Muraven, & Tice, 1998; Stanovich & West, 2000), farsighted vs. myopic (Laibson, 1997; McClure, Laibson, Loewenstein, & Cohen, 2004) or instrumental vs. Pavlovian (Dayan, Niv, Seymour, & Daw, 2006). A related idea is that preference instability can arise from non-exponential temporal discounting functions (Ainslie, 1975; Laibson, 1997; McClure et al., 2004; Strotz, 1955).
Previous theoretical enterprises have focused largely on situations where decision makers hold full information about the times at which future outcomes will occur. However, the timing of real-world events is not always so predictable. Decision makers routinely wait for buses, job offers, weight loss, and other outcomes characterized by significant temporal uncertainty. Timing uncertainty is also a central feature of the well-known delay-of-gratification paradigm (Mischel & Ebbesen, 1970), where young children must decide how long to continue waiting for a preferred food reward, while lacking any information about how long the delay will last. Even though persistence is usually associated with successful self-control, temporal uncertainty can create situations where limits on persistence are appropriate (Dasgupta & Maskin, 2005; Rachlin, 2000). Our aim in the present paper is to demonstrate that behavior resembling persistence failure can arise as the rational response to uncertainty about an awaited outcome’s timing.
1.2. Persistence under temporal uncertainty
A temporally uncertain outcome can be described in terms of a probability distribution over its potential times of arrival. Different timing distributions will apply to different categories of events, and the shape of the distribution determines how the expected remaining delay will change as time passes. This general phenomenon has been described previously in the contexts of survival and reliability analysis (e.g., Elandt-Johnson & Johnson, 1980) and Bayesian cognitive judgment (Griffiths & Tenenbaum, 2006). Here we present an overview focusing on the implications for intertemporal decision making (for quantitative details see Section 2.3, below).
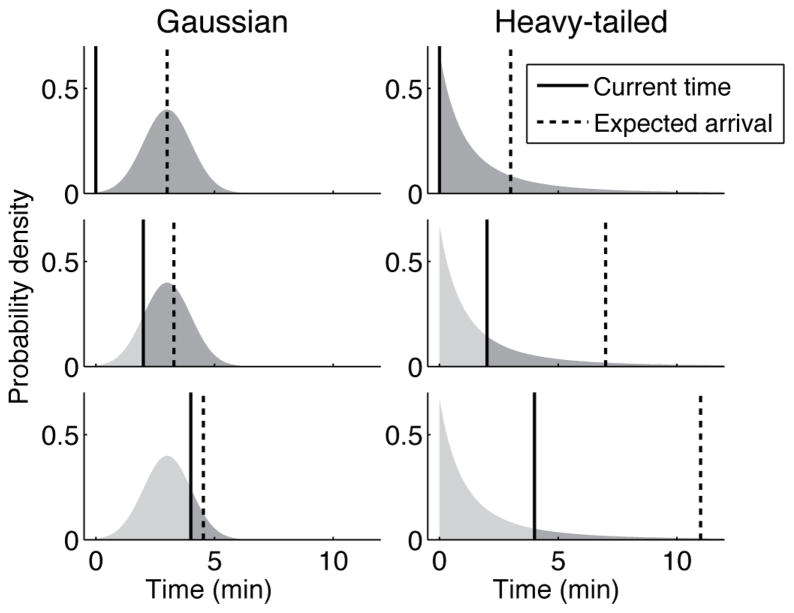
If delay durations in a given environment follow a uniform or Gaussian distribution, the expected remaining delay will become steadily shorter as time elapses. Gaussian distributions characterize delimited events, such as movies or human lifetimes (Griffiths & Tenenbaum, 2006). Consider, for example, the case of waiting for a talk to end. If it has gone on longer than expected, one might be inclined to assume that only a small amount of time still remains. Figure 1 illustrates this phenomenon for a Gaussian distribution (specifically, a truncated Gaussian with a lower bound corresponding to the current time).
Figure 1.
Schematic illustration of how time passage may change a reward’s expected time of arrival. The left and right columns represent different kinds of beliefs one might hold about an awaited outcome’s timing. The solid line represents the current time (shown at 0, 2, and 4 minutes). The dashed line represents the outcome’s expected arrival time, defined as the mean of the area to the right of the current time. For Gaussian beliefs (mean=3, SD=1), the expected delay starts at 3 minutes and grows shorter with time. For heavy-tailed beliefs (generalized Pareto distribution [see Equation 2], k=0.5, σ=1.5), the delay starts at 3 minutes and rises with time.
Under the standard assumption that rewards are subjectively discounted as a function of their delay (Samuelson, 1937), rewards with Gaussian timing will tend to increase in present subjective value over time while they are being awaited. If a delayed reward is initially preferred relative to other alternatives that are available immediately, this preference should strengthen as time passes. All else equal, the initial patient choice should be sustained.
A very different situation can occur if the reward’s timing follows a heavy-tailed distribution (e.g., a power function; see Figure 1). In this case, the expected remaining delay can increase with the passage of time. Heavy-tailed distributions describe open-ended events, where some delays are short but others are indefinitely long. Consider the example of waiting for a reply to an email (Barabási, 2005). One might initially expect a reply to come quickly, but if it does not, one might conclude that the remaining delay will be longer than initially expected.
If a reward is characterized by a heavy-tailed timing distribution, its expected delivery time grows more distant with time elapsed, implying that its present subjective value progressively deteriorates. Even if the delayed reward were initially preferred, it might eventually become so remote that it no longer outcompeted immediately available alternatives. Under these circumstances, decision makers could produce reversing sequences of choices, equivalent to the patterns often attributed to self-control failure: they might choose a delayed reward, wait for a period of time, and then shift to an immediate outcome instead. Such a decision maker would not be dynamically inconsistent, but would instead be responding rationally to new information gained from observing the passage of time. There is precedent for the idea that mere time passage may be informative in this way, warranting reassessments of both the delay and the degree of risk associated with future events (Dasgupta & Maskin, 2005; Fawcett, McNamara, & Houston, 2012; Rachlin, 2000; Sozou, 1998).
Heavy-tailed distributions characterize timing in a variety of real-life situations where intervals are open-ended. Distributions with this form have been empirically documented in examinations of the time between emails (Barabási, 2005), the length of hospital stays (Harrison & Millard, 1991), and time between retrievals of the same memory (Anderson & Schooler, 1991). Heavy-tailed distributions also provide a reasonable prior when the true distribution is unknown (Gott, 1993, 1994; Jeffreys, 1983). It seems plausible that decision makers routinely encounter environments characterized by heavy-tailed timing statistics, in which they must continually reassess whether a formerly preferred delayed outcome remains worth pursuing.
Decision makers are also likely to encounter situations where timing is uncertain but delimited. For example, endogenous variability in time-interval perception and memory can produce a Gaussian pattern of subjective uncertainty (i.e., scalar variability; Gallistel & Gibbon, 2000; Gibbon, 1977). This kind of situation would call for persistence: if a delayed reward was worth pursuing in the first place, it should be pursued until it is obtained.
The above observations lead to a hypothesis: a person’s willingness to continue waiting ought to depend on a dynamically updated estimate of the time at which an awaited outcome will arrive. This estimate, in turn, should depend on the applicable timing statistics. Environments with Gaussian or uniform timing statistics should elicit strong persistence. In contrast, environments characterized by heavy-tailed timing statistics should cause people to limit how long they are willing to wait.
Existing evidence suggests it is plausible that people form context-sensitive time estimates and update these estimates dynamically. Properties of statistical distributions can be encoded rapidly from direct experience (Körding & Wolpert, 2004), and processes resembling valid Bayesian inference support both explicit temporal judgments (Griffiths & Tenenbaum, 2006, 2011; Jazayeri & Shadlen, 2010) and time-dependent reward-seeking behavior (Balci, Freestone, & Gallistel, 2009; Bateson & Kacelnik, 1995; Catania & Reynolds, 1968). However, little evidence as yet bears on the role of temporal inference during choices that involve waiting for delayed outcomes. Even though preference reversals may sometimes be theoretically rational (Dasgupta & Maskin, 2005; Fawcett et al., 2012), empirical data to date have been interpreted largely in terms of limitations on people’s capacity to exert self control (Baumeister et al., 1998).
1.3. The present work
Here we seek direct empirical evidence that human decision makers calibrate their willingness to tolerate delay on the basis of experience with time-interval distributions. Participants in our first experiment were given repeated opportunities to wait for randomly timed delayed rewards, and could decide at any time to stop waiting and accept a small immediate reward instead. We placed participants in environments with either uniform or heavy-tailed distributions of time intervals, hypothesizing that the two conditions would elicit different degrees of willingness to persist.
2. Experiment 1
2.1. Overview
Participants were given a fixed time period to harvest monetary rewards. They therefore faced a rate-maximization objective, akin to a foraging problem. Each reward took a random length of time to arrive, and participants could wait for only one reward at a time. At any time they could quit waiting, receive a small immediate reward, and continue to a new trial after a short inter-trial interval. Delay durations were governed by different probability distributions in two groups of participants.
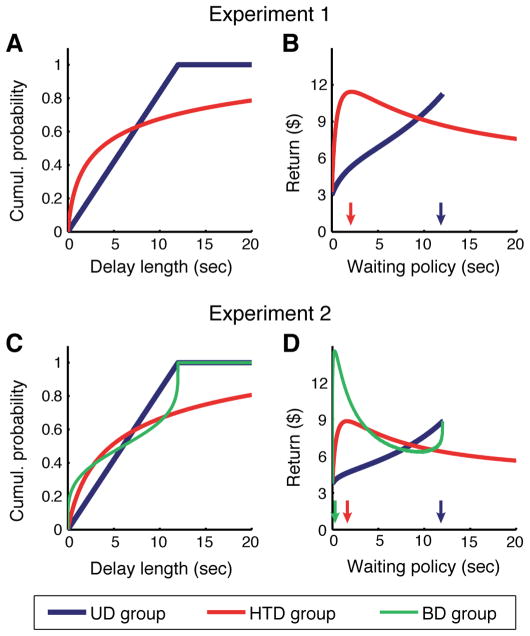
One group experienced a uniform distribution (UD; see Fig 2A), spanning 0–12 sec. The expected remaining delay declined over time, and the reward-maximizing strategy was always to continue waiting (see Section 2.3). To understand this intuitively, consider a decision maker who has already waited 6 sec. The delayed reward is guaranteed to arrive within the next 6 sec, and is therefore an even better prospect than initially, when it was guaranteed to arrive within 12 sec. If the delayed reward was preferred at the outset, it should be preferred by a still greater margin after some time has passed.
Figure 2.
Delay distributions and the resulting payoff functions in each experiment. A: Cumulative probability of the large reward arriving after a given delay length, for each condition of Experiment 1. Delays in the UD group followed a uniform distribution (lower bound a=0, upper bound b=12). Delays in the HTD group followed a generalized Pareto distribution (shape k=8, scale σ=3.4, location θ=0) truncated at 90 sec. B: Expected total monetary return under a range of waiting policies for Experiment 1. A waiting policy is defined by the time at which a subject would give up waiting if the reward had not yet been delivered. Arrows mark the optimal waiting policy in each condition. C: Cumulative probability distributions for delay lengths in Experiment 2. The UD group received a uniform distribution (a=0, b=12), the HTD group received a truncated generalized Pareto distribution (k=4, σ=5.75, θ=0, truncated at 60 sec), and the BD group received a scaled beta distribution (shape parameters α=0.25, β=0.25, scaling factor of 12). D: Expected total monetary return under a range of waiting policies for Experiment 2. Arrows mark each condition’s reward-maximizing policy.
The second group experienced a truncated heavy-tailed distribution of delays (HTD group; see Fig. 2A). Here the expected remaining delay initially increased with time waited. The maximizing strategy called for quitting whenever the reward failed to arrive within the first few seconds (for details, see Section 2.3). If participants calibrate persistence adaptively, they should exhibit greater persistence in the UD condition than the HTD condition.
2.2. Methods
2.2.1. Participants
Participants were recruited in a New Jersey shopping mall (n=40; 23 female), age 18–64 (mean=32), with 11–20 years of education (mean=15). Each participant was randomly assigned to either the UD or HTD condition (n=20 each). The proportion female was 10/20 in the UD group and 13/20 in the HTD group. The two groups did not significantly differ with respect to age (UD group median=25, interquartile range [IQR]=20.5–48.5; HTD group median=24.5, IQR=22.5–44.5; Mann-Whitney U=194, nUD=20, nHTD=20, p=0.88) or years of education (based on the 35 participants who reported their level of education; UD group median=15, IQR=12–16; HTD group median=15, IQR=14–16; Mann-Whitney U=137, nUD=17, nHTD=18, p=0.61).
Assignment to conditions was automated and concealed from the experimenter, and all participants received identical instructions. Participants were informed that they could expect to make $5–10 depending on performance, but were not told anything about the distribution of possible delay times. In both experiments, procedures for testing human subjects were approved by the applicable institutional review board.
2.2.2. Materials and procedure
The task was programmed using the Psychophysics Toolbox (Brainard, 1997; Pelli, 1997) extensions for Matlab (The MathWorks, Natick, MA). Figure 3 shows the interface. A yellow light would stay lit for a random duration before delivering a 15¢ reward. Participants could choose to wait by leaving the mouse cursor in a box marked, “Wait for 15¢.” Alternatively, by shifting to a box marked “Take 1¢,” participants could receive 1¢ and proceed to a new trial. Each outcome (15¢ or 1¢) was followed by a 2-sec inter-trial interval (ITI). The cursor could remain in either box across multiple trials. The task duration was 10 min, and the screen continuously displayed the time remaining and total earned. Final compensation was rounded up to the next 25¢.
Figure 3.
Interface for the behavioral choice task used in both experiments.
Delays varied randomly from trial to trial, and were scheduled according to a different distribution in each condition (see Figure 2A). The large reward was delivered at the end of the scheduled delay on each trial unless the participant chose to take the small reward earlier. For the UD group, delays were drawn from a continuous uniform distribution described by the following cumulative distribution function:
| (1) |
Parameters were a=0 and b=12 sec, so quartile upper boundaries fell at 3, 6, 9, and 12 sec.
For the heavy-tailed distribution we used a truncated generalized Pareto distribution. An unbounded generalized Pareto distribution has the following cumulative distribution function:
| (2) |
Note that Equation 2 omits the location parameter θ, which we set to zero, implying that zero is the shortest possible delay. Applying an upper bound T gives the following cumulative distribution function for a truncated generalized Pareto:
| (3) |
We used parameters k=8, σ=3.4, and T=90 sec, which set quartile upper boundaries at 0.78, 3.56, 15.88, and 90 sec.
We wished to ensure that even short spans of experience would be representative of the underlying distribution. To accomplish this, delays were not drawn fully randomly on each trial, but were sampled from each quartile in random order before a quartile was repeated. This approach has the disadvantage of introducing subtle sequential structure, but the important advantage of reducing within-condition variability in the timing statistics participants experienced.
Two demonstration trials preceded the main task. On the first, participants were instructed to wait for the large reward, which arrived after 5 sec. On the second, participants were instructed to take the small reward.
2.3. Normative analysis
We define a waiting policy as the time at which a decision maker will give up waiting on each trial if the large reward has not yet arrived. The expected return for a policy of quitting at time t may be calculated as follows. Let pt be the proportion of rewards delivered earlier than t. Let τt be the mean duration of these rewarded trials. One trial’s expected return, in dollars, is Rt = 0.15(pt) + 0.01(1−pt). Its expected cost, in seconds, is Ct = τt(pt) + t(1−pt) + 2 (including the 2-sec ITI). The expected return for policy t over the 600-sec experiment is 600 × Rt/Ct. This is the quantity participants should seek to maximize.
For each condition, we calculated the expected return for a grid of waiting policies spaced every 0.01 sec from 0 to 20 sec. For policy t, the large-reward probability pt is simply the value of the cumulative probability distribution function at t (see Equations 1–3). The value of τt is easy to calculate in the UD condition: τt = t/2. For the HTD condition the calculation of τt is more complex, though still tractable; in practice, we estimated τt by taking the mean of 100,000 random samples from the distribution between 0 and t.
Figure 2B shows the expected monetary return for a range of waiting policies. At one extreme, a policy of quitting every trial immediately yields 1¢ every 2 sec, for $3.00 total (in either condition). At the other extreme, complete persistence in the UD condition would yield 15¢ every 8 sec on average, for $11.25. Complete persistence in the HTD condition would yield poorer results, with a large reward occurring approximately every 15 sec on average, leading to an expected return of $6.00. The best-performing policy in the HTD condition is to quit if the reward has not arrived after 2.13 sec; this yields an expected return of $11.43. A participant who perfectly implemented this policy would obtain the large reward on 41% of trials, with an average delay on these trials of 725ms. On the remaining trials the small reward would be selected after a wait of 2.13 sec.
2.4. Data analyses
Individual trials differ in the amount of information they provide regarding a participant’s waiting policy. Quit trials are the most informative, as they offer a direct estimate of the limit on an individual’s willingness to persist. When a reward is delivered, however, we observe only that the person was willing to wait at least the duration of the trial. We accommodate this situation using statistical methods from survival analysis. Analyses assessed how long a trial would “survive” without the participant quitting. Rewarded trials were considered right-censored, analogous to patients who drop out of a clinical study and yield only a lower bound on their survival.
We constructed a Kaplan-Meier survival curve on the basis of each participant’s responses. The Kaplan-Meier is a nonparametric estimator of the survival function (Kaplan & Meier, 1958). For each time t, it plots the participant’s probability of waiting at least until t if the reward is not delivered earlier. Analyses were restricted to the 0–11 sec interval for which we have observations in both conditions. (Note that we can only observe an individual’s willingness to wait t seconds if we have trials where the scheduled delay equals or exceeds t.) The area under the survival curve (AUC) is a useful summary statistic, representing the average number of seconds an individual was willing to wait within the analyzed interval. Someone who never quit earlier than 11 sec would have an AUC of 11. One who was willing to wait up to 3 sec on half the trials and up to 9 sec on the other half would have an AUC of 6.
Differences in AUC between groups were evaluated using two-tailed nonparametric Mann-Whitney U tests (also known as Wilcoxon rank sum tests). Single-sample comparisons were performed using two-tailed nonparametric Wilcoxon signed rank tests.
To assess the change in persistence over time, we separately calculated a local, nonparametric estimate of each subject’s willingness to wait (WTW) every 1 sec throughout the experiment. During quit trials, this estimate simply consisted of the observed waiting time. During rewarded trials, the estimate was the longest time waited since the last quit trial. The WTW estimate was capped at 12 sec to make the two conditions comparable.
2.5. Results
2.5.1. Earnings
Total earnings provide a rough gauge of task success. Each group’s best possible return was about $11.25. Median earnings were $10.69 (IQR=9.47–11.11) in the UD group and $7.29 (IQR=6.09–8.70) in the HTD group, which differed significantly (Mann-Whitney U=32.5, nUD=20, nHTD=20, p<0.001). In the UD group, 12 of 20 participants obtained within $1 of the theoretical optimum. No one performed this well in the HTD group, where the most any participant earned was $9.83.
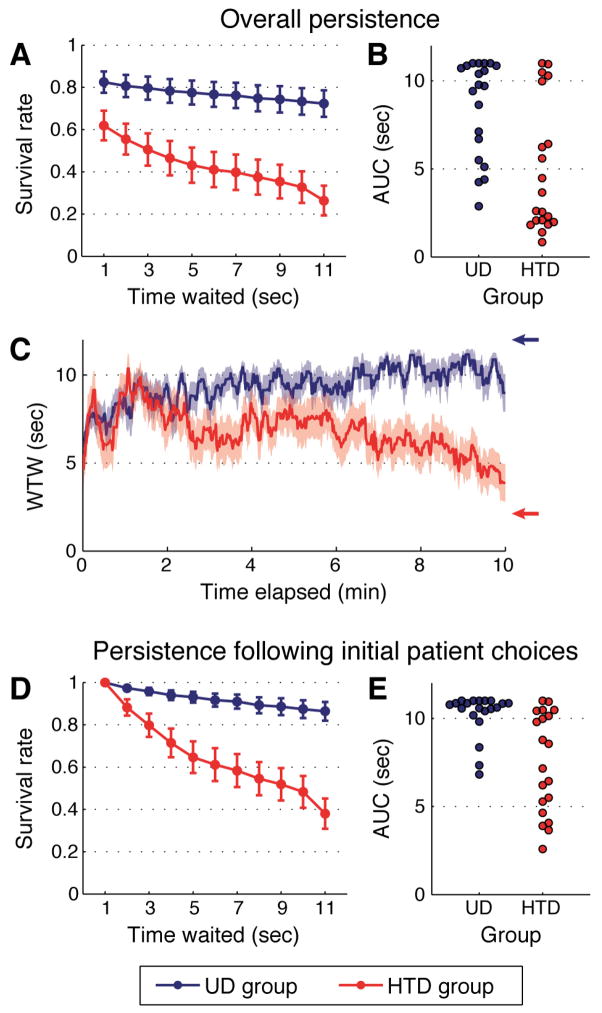
2.5.2. Survival analysis
Figure 4A shows survival curves summarizing participants’ persistence, sampled at 1-sec intervals and averaged across subjects in each condition. Figure 4B shows the corresponding AUC values for each individual. Comparing AUC values in the two groups confirms the study’s central prediction: the UD group (median AUC=9.74 sec, IQR=6.10–10.86) showed greater persistence than the HTD group (median AUC=3.14 sec, IQR=2.02–8.20; Mann-Whitney U=87, nUD=20, nHTD=20, p=0.002). HTD-group participants waited significantly longer than the reward-maximizing point of 2.13 sec (signed-rank T=36, n=20, p=0.01). (The equivalent test for the UD group would not be meaningful, because it was only possible to err on the side of waiting too little.)
Figure 4.
Results of Experiment 1. A: Mean survival curves, with standard error of the mean (SEM), sampled at 1-sec intervals, reflecting participants’ willingness to wait in each condition. B: Area under the survival curve (AUC) for each individual, calculated over the range from 0–11 sec. Values reflect how long each individual was willing to wait within the first 11 sec of the delay period. C: Mean estimated willingness to wait (WTW), as a function of time elapsed in the experimental session (with SEM). Arrows mark the reward-maximizing policies. D: Mean survival curves (with SEM) restricted to trials in which participants waited at least 1 sec. E: Each individual’s AUC value for the analysis in Panel D.
2.5.3. Learning over time
Results in Fig 4A–B aggregate over the 10-min task, but participants started out knowing nothing about the relevant timing distributions. Figure 4C shows local WTW as a function of time. Median linear trend coefficients differed between the two groups (Mann-Whitney U=46, nUD=20, nHTD=20, p<0.001), and differed from zero in each group individually (+0.19sec per min in the UD condition, signed-rank T=10, n=20, p<0.001; −0.17sec per min in the HTD condition, signed-rank T=43, n=20, p=0.02).
2.5.4. Dynamic reversals
Differences in overall willingness to wait could stem from two qualitatively different types of behavior. The first involves initially choosing the delayed outcome but subsequently failing to persist. Such reversals are necessary for success in the HTD condition (see Figure 2B), even though they could superficially appear to reflect unstable preferences.
To assess reversals of this type, we ran a version of the survival analysis restricted to trials with waiting times of 1 sec or greater (Fig. 4D). This fixes each survival curve’s first point at 1, while leaving the remaining points free to vary. Results show that even when participants made an initial choice to wait, they sustained that choice for less time in the HTD condition (median AUC=7.86 sec, IQR=4.95–10.28) than in the UD condition (median AUC=10.70 sec, IQR=10.29–10.93; Mann-Whitney U=68.5, nUD=20, nHTD=20, p<0.001; see Fig 4E), consistent with our normative predictions.
Besides reversals, participants can also exhibit outright impatience: they might spend periods of time ignoring the delayed reward entirely and simply collecting small rewards as rapidly as possible. We considered a trial “skipped” if the small reward was obtained within 100ms (suggesting the subject chose “Take 1¢” before the trial began). Skipping trials was an unproductive strategy (see Section 2.3, above). The number of skipped trials varied substantially across individuals, and was greater in the HTD condition (median=37.5 trials, IQR=2–88) than the UD condition (median=2 trials, IQR=0–19.5; Mann-Whitney U=112.5, nUD=20, nHTD=20, p=0.02). Thus, in addition to persisting less, the HTD group was also more likely to forego the large reward altogether. Given the 2-sec ITI, the HTD-group median corresponds to about 75 sec spent skipping trials (1/8 of the session).
There was no evidence that subjects capitalized on nonrandom aspects of the trial sequence to skip trials with long scheduled delays. The scheduled duration of skipped trials was 0.70 sec shorter on average (SD=2.60) than non-skipped trials.
2.6. Discussion of Experiment 1
Consistent with our hypothesis, decision makers calibrated persistence according to the time-interval distributions they experienced. Participants showed high persistence when delays were drawn from a uniform distribution, implying that waiting posed little difficulty when its value was supported by direct statistical experience. In contrast, a heavy-tailed distribution of delays elicited limited persistence, with participants selecting delayed rewards and then giving them up after short periods of waiting. It also elicited increased impatience, with participants more often skipping the delayed reward altogether. The latter behavior was counterproductive, but reversals were necessary under the reward-maximizing strategy.
The two timing conditions were matched for their highest potential earnings, but differed in a number of specific respects. Delay lengths in the HTD condition were greater on average, higher-variance, spanned a greater range, and led to lower earnings in practice. Behavioral differences could, in principle, have stemmed from any of these individual factors. For example, HTD-group participants might have adopted a lower level of persistence in response to low earnings, or perhaps in reaction to occasional very long delays.
To narrow the space of possibilities, we replicated the design while introducing a third timing condition in Experiment 2.
3. Experiment 2
3.1. Overview
Experiment 2 added a condition in which delay lengths followed a bimodal distribution (BD group; see Fig. 2C). As in the HTD condition, the reward-maximizing strategy was to wait only a short time for each reward (see Fig. 2D). Many rewards arrived in the first 1 sec, but those delays that exceeded 1 sec often continued for an additional 10 sec, making it more productive to quit and move on to a new trial.
The bimodal distribution had the same range, mean, and median as the uniform distribution, with greater variance. Because mean delays were matched, UD and BD participants could earn equal amounts of money under a strategy of always waiting. However, those in the BD group could earn still more under a low-persistence strategy. Participants were not initially told anything about the range of potential incentive payments, removing any explicit benchmark. The duration of the task was increased to 20 min.
We hypothesized that decision makers would calibrate persistence advantageously in each timing environment, waiting longer in the UD condition than in either the HTD or BD conditions.
3.2. Methods
3.2.1. Participants
Participants were 48 members of the University of Pennsylvania community (27 female), age 18–38 (mean=21), with 12–20 years of education (mean=14). Each individual was randomly assigned to the UD, HTD, or BD group (n=16 per group). Condition assignment was automated and concealed from the experimenter. The proportion female was 8/16 in the UD group, 8/16 in the HTD group, and 11/16 in the BD group. There were no significant pairwise group differences in age (UD median=20.5, IQR=19–23.5; HTD median=19, IQR=18–21.5; BD median=19.5, IQR=18.5–23; UUD-HTD=91.5, nUD=16, nHTD=16, p=0.17; UUD-BD=108.5, nUD=16, nBD=16, p=0.47; UHTD-BD=113, nHTD=16, nBD=16, p=0.58). There also were no pairwise group differences in education (based on the 44 participants who reported their education level; UD median=14, IQR=13–16; HTD median=12.5, IQR=12–14; BD median=13, IQR=12.25–15.75; UUD-HTD=73, nUD=16, nHTD=14, p=0.11; UUD-BD=101.5, nUD=16, nBD=15, p=0.48; UHTD-BD=82, nHTD=14, nBD=15, p=0.33).
Participants received a $10 show-up payment plus incentives earned during the task. Instructions provided no information about the distribution of delay times or the range of possible incentive payments.
3.2.2. Materials and procedure
Several parameters were adjusted from Experiment 1 to achieve the desired payoff functions while keeping overall incentive levels moderate. Participants continuously chose between two boxes labeled “Wait for 20 points” and “Take 1 point.” Points were converted to money at 400pts to $1, paid to the nearest 1¢. Delays were drawn from one of three distributions, depending on an individual’s condition assignment (see Fig. 2C). The BD condition used a beta distribution as implemented in Matlab, with parameters α=0.25, β=0.25, rescaled to span 0–12 sec. Note that this distribution does not have a simple closed-form expression akin to Equations 1–3 above. Its density is symmetrical and U-shaped, with quartile upper boundaries at 0.54, 6.00, 11.46, and 12.00 sec. The HTD condition used a truncated generalized Pareto distribution (see Equations 2–3), with parameters modified from Experiment 1 (k=4, σ=5.75, T=60 sec) so that quartile upper boundaries fell at 1.35, 4.70, 15.06, and 60 sec. Each outcome was followed by an 800ms ITI. The task and analysis methods otherwise matched those in Experiment 1.
The expected return for various waiting policies was calculated as in Experiment 1. In the BD condition, the average wait time for large rewards received under each policy was estimated by taking the mean of 100,000 random draws from the distribution between 0 and t. The reward-maximizing policy for the UD group was to wait the full 12 sec, implying an expected incentive payment of $8.82 (5¢ every 6.8 sec for 20 min; see Fig 2D). HTD-group participants could do similarly well by giving up waiting between 1.3 and 1.9 sec on each trial; further persistence would reduce earnings. In the BD group, waiting the full 12 sec implied the same $8.82 return as in the UD group; that is, the expected return under full persistence for the BD and UD groups was equated. However, BD participants could earn up to $14.59 if they quit waiting after only 0.26 sec on each trial. Quitting at any point up to 3.1 sec would yield better outcomes than waiting the full time.
To summarize, timing statistics implied that persistence was the best strategy for the UD group, but the other two groups could perform best by waiting less than 2 sec per trial.
3.3. Results
3.3.1. Total earnings
Median earnings were as follows: in the UD group $8.37 (IQR=8.10–8.68), in the HTD group $5.71 (IQR=5.25–6.28), and in the BD group $8.58 (IQR=7.25–9.23). Earnings were significantly lower in the HTD group than either the UD group (Mann-Whitney U=6, nUD=16, nHTD=16, p<0.001) or the BD group (Mann-Whitney U=12, nHTD=16, nBD=16, p<0.001). Earnings did not differ between the UD and BD groups (Mann-Whitney U=114, nUD=16, nBD=16, p=0.61). Thirteen of 16 participants in the UD group (and no participants in the other two groups) earned within $1 of the maximum possible amount.
3.3.2. Survival analysis
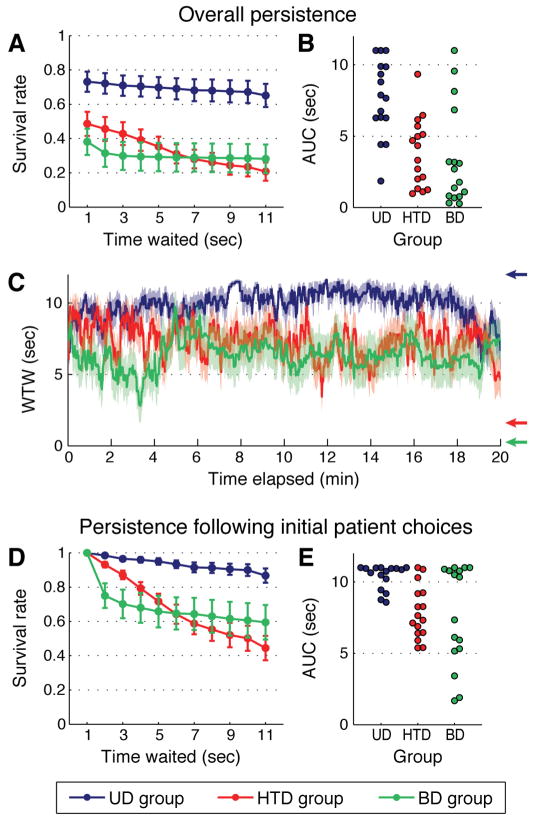
Figures 5A–B show mean survival curves reflecting willingness to wait in each condition, together with individual participants’ AUC values. Consistent with our predictions, AUCs were greater in the UD group (median=7.77 sec, IQR=6.28–9.87) than in either the HTD group (median=3.83 sec, IQR=1.66–5.40; Mann-Whitney U=36, nUD=16, nHTD=16, p<0.001) or the BD group (median=2.24 sec, IQR=0.80–5.02; Mann-Whitney U=45.5, nUD=16, nBD=16, p=0.002). The HTD and BD groups did not significantly differ (Mann-Whitney U=99, nHTD=16, nBD=16, p=0.28).
Figure 5.
Results of Experiment 2. Panels correspond to those in Figure 4. A: Mean survival curves (with SEM) reflecting persistence in each condition. B: AUC values for individual participants. C: Mean local WTW estimate (with SEM) as a function of time on task, with arrows marking reward-maximizing policies. D: Mean survival curves (with SEM) restricted to trials lasting at least 1 sec. E: Individual AUC values corresponding to Panel D.
3.3.3. Learning over time
Figure 5C shows estimated WTW over time in each condition. Unlike Experiment 1, the trajectory was not characterized by a significant linear trend in any of the three conditions. Average waiting policies appear roughly steady from minutes 10–18, with an unpredicted shift in the final 1–2 min (see Section 3.4 for discussion).
Linear trends do largely replicate those in Experiment 1 if analyses are confined to the same 0–10-min window tested in that experiment. Within that period, the UD group shows a rising linear trend (median coefficient +0.17sec per min, signed-rank T=22, n=16, p=0.02), while the HTD and BD groups show no trend. The UD group differs significantly from the HTD group (Mann-Whitney U=60, nUD=16, nHTD=16, p=0.01) but not the BD group (Mann-Whitney U=108, nUD=16, nBD=16, p=0.46).
3.3.4. Dynamic reversals
To assess participants’ willingness to continue waiting after having initially chosen patiently, we restricted a followup survival analysis to trials where participants waited 1 sec or longer (see Fig 5D–E). Median AUC values were 10.80 sec (IQR=9.82–10.96) in the UD group, 7.48 sec (IQR=6.42–9.21) in the HTD group, and 8.84 sec (IQR=5.24–10.83) in the BD group. Differences were significant between the UD and HTD groups (Mann-Whitney U=33.5, nUD=16, nHTD=16, p<0.001) and marginal between the UD and BD groups (Mann-Whitney U=79.5, nUD=16, nBD=16, p=0.07), while the HTD and BD groups did not differ (Mann-Whitney U=124.5, nHTD=16, nBD=16, p=0.91).
We also assessed the frequency of sub-100ms selections of the small reward, which indicate a strategy of skipping the large reward entirely. As before, the occurrence of this strategy was highly variable. The median number of skipped trials was 52 (IQR=7.5–94.5) in the UD group, 88.5 (IQR=54.5–332) in the HTD group, and 308.5 (IQR=74.5–610.5) in the BD group. Given the 800ms ITI, these medians correspond to time periods of about 42 sec, 71 sec, and 247 sec, respectively. Differences were significant for the HTD vs. UD group (Mann-Whitney U=72.5, nUD=16, nHTD=16, p=0.04), and BD vs. UD group (Mann-Whitney U=53.5, nUD=16, nBD=16, p=0.005), but not the HTD vs. BD groups (Mann-Whitney U=96, nHTD=16, nBD=16, p=0.24). Thus, individuals in the HTD and BD conditions exhibited both reduced waiting times and more frequent skipped trials.
Again, there was no evidence that participants could selectively anticipate and skip trials with long scheduled delays. Scheduled durations of skipped trials were 0.11 sec longer on average than non-skipped trials (SD=1.37).
3.4. Discussion of Experiment 2
Experiment 2 replicated the main findings of Experiment 1 despite several minor changes involving the participant pool, compensation, and task duration. In an extension of the previous findings, the newly introduced BD condition elicited low persistence despite matching the UD condition for its average delay, maximum delay, and rates of earnings actually obtained. This result bolsters the conclusion that decision makers calibrate persistence using temporal inference. It counters the possibility that the differences observed in Experiment 1 depended on secondary aspects of the timing environments, such as the range of possible delays or the monetary rate of return.
The longer duration of Experiment 2 provides an extended picture of performance over time. Group-level performance appeared to level off near the 8-min mark, with the overall trajectory no longer well characterized by linear trends. Not all individuals converged on reward-maximizing levels of persistence even with additional experience, especially in the HTD and BD groups (see Figure 5B). Timecourses also appeared to shift near minute 19, when several UD-group participants adopted a trial-skipping strategy. Though we have no a priori explanation for this observation, we suspect it may reflect an effect of time pressure on participants’ preference for low-variance outcomes (given that time remaining was continuously displayed).
4. General discussion
Using a timing manipulation, we created laboratory environments that demanded either consistent adherence to one’s own previous intertemporal choices, or else the frequent reversal of such choices. Decision makers adjusted their persistence in the appropriate direction after short periods of direct experience. These results imply that temporal beliefs and inferences act as an adaptive influence on people’s willingness to persist toward delayed outcomes. Our findings are qualitatively consistent with the idea that decision-making mechanisms function to promote reward rate over time, in agreement with principles of optimal foraging theory (Brunner, Kacelnik, & Gibbon, 1996; Kacelnik, 2003; Krebs, Kacelnik, & Taylor, 1978; Mark & Gallistel, 1994). Similar principles have been applied productively in several other complex decision-making settings (e.g., Cain, Vul, Clark, & Mitroff, 2011; Simen et al., 2009).
In theoretical examinations of intertemporal choice and delay of gratification, it has occasionally been noted that reversals can be economically rational if decision makers believe event timing is governed by a high-variance distribution (Dasgupta & Maskin, 2005; Rachlin, 2000) or if time passage supports updated assessments of risk (Fawcett et al., 2012; Sozou, 1998). Our experiments offer empirical support for the importance of these theoretical observations. Despite the ubiquity of temporal uncertainty in real-life decisions, most research on delay of gratification focuses on identifying cognitive mechanisms that could undermine persistence irrespective of temporal expectations (Ainslie, 1975; Baumeister et al., 1998; Dayan et al., 2006; Loewenstein, 1996; McClure et al., 2004; Metcalfe & Mischel, 1999).
In light of our findings, it may be possible to reduce the number of situations in which intrinsically unstable preferences need to be posited. Several of the best-known empirical demonstrations of persistence failure involve tasks where some kind of limit on persistence clearly seems appropriate, such as puzzles that are actually impossible (Baumeister et al., 1998) or delays with no identified endpoint (Mischel & Ebbesen, 1970). Behavior in these tasks has been theoretically interpreted as reflecting an intrinsic limitation on people’s ability to wait for delayed rewards. In our view, the most compelling evidence for such a limitation would involve showing that some manipulation (e.g., self-regulatory depletion) diminished persistence even in an environment such as our UD condition, where statistical cues unambiguously establish that persistence is advantageous.
We suggest that in order to understand reversals of intertemporal choices, it is essential to recognize that decision makers can often err by waiting too long as well as too little. Decision makers face a computational-level problem of calibrating persistence appropriately to their environment, not merely of maximizing persistence in all cases. Revisiting our opening quotation from Ainslie (1975), we agree that it is important to understand why decision makers change their preferences over time in the absence of new information. In uncertain environments, however, time passage serves as an important source of information in its own right (Dasgupta & Maskin, 2005; Fawcett et al., 2012; Rachlin, 2000; Sozou, 1998). If an outcome could have occurred at a short delay, its non-occurrence supports a revised estimate of the time at which it will arrive in the future. Our empirical results demonstrate that valid temporal inferences can suffice to produce overt reversals of intertemporal decisions. Further work should seek to extend this principle to longer time spans and more naturalistic contexts.
At the same time, it is important to emphasize that performance was not quantitatively optimal (see Figures 4–5). Participants fell short of the highest available rates of return, particularly in conditions where limited persistence was the best strategy. One reason may be the relatively short period of experience. Although performance did not appear to improve across the final 10 minutes of Experiment 2, we cannot rule out the possibility that substantial additional experience might yield further gains. If, for example, participants entered the task with strong prior beliefs about the timing they were likely to encounter, a large amount of experience might be required for these beliefs to be revised. It is also possible that providing individuals with additional explicit information about the task’s structure (e.g., potential ranges of parameters) would help them discover better-performing strategies.
An important goal for future work, therefore, will be to examine the temporal prior beliefs that decision makers apply in particular situations, and test how these beliefs are updated and generalized across contexts. Temporal beliefs presumably depend on past experience (and perhaps evolutionary history; Stevens, Hallinan, & Hauser, 2005). The qualitative pattern in our results is consistent with a view that cognitive judgment approximates Bayesian inference (Griffiths & Tenenbaum, 2006, 2011; Jazayeri & Shadlen, 2010; Körding & Wolpert, 2004), but a full mechanistic account must accommodate the fact that individuals differ in the degree of successful calibration they achieve.
Such a mechanistic account might take several forms. One possibility is that participants develop an internal model of the environment, using previously observed delays to forecast the consequences of a given persistence policy (akin to our own optimality analysis of the task). Alternatively, decision makers might rely on simpler approximations of this strategy such as giving up waiting if the instantaneous probability of reward is perceived as low. It would also be possible to approach the task in a model-free manner, exploring a range of different quitting policies and comparing their rates of return.
One aspect of the findings that may prove particularly useful in guiding future theorizing is that participants were generally more successful (i.e., came closer to the maximum available earnings) in environments requiring high rather than low persistence. One likely reason is that low-persistence conditions allow participants to make errors in both directions, waiting either too long or not long enough. Indeed, errors in both directions were observed: participants waited too long on average, but also sometimes chose impatiently by ignoring the delayed reward altogether. A second important difference between high- and low-persistence environments involves the information that decision makers can gain from individual events. Quitting provides the participant with only a censored observation of a delay’s duration (just as, during our data analyses, rewarded trials provide us with only a censored observation of how long a participant was willing to wait.) Adopting the reward-maximizing strategy for a low-persistence environment therefore involves sacrificing information, setting up a potential exploration/exploitation tradeoff. In a changing environment, this asymmetry of information might make it easier for individuals to shift from persistence to nonpersistence than vice versa.
As a final point, our findings suggest new potential avenues toward modifying socially consequential behaviors (involving diet, finances, substance abuse, etc.) that are traditionally understood in terms of self-control. Building upon the well-established principle that intermittent reinforcement yields extinction-resistant learning (Jenkins & Stanley, 1950), our findings imply that one way to encourage (or curb) persistence would be to intervene on an individual’s beliefs about the timing environment in which decisions take place.
5. Conclusion
By manipulating the probabilistic timing of rewards, we created environments in which it was productive either to wait persistently or to abandon rewards after a short time. These environments elicited very different patterns of behavior, with human participants adopting either high or low levels of persistence after short periods of direct experience. Our results suggest that reversals of patient intertemporal choices need not signify a cognitive limitation, but may instead reflect an adaptive response to temporal uncertainty.
Highlights.
Participants decided how long to wait for temporally uncertain rewards.
The distribution of possible delays determines whether persistence is productive.
Different conditions, matched for reward rate, required high or low persistence.
With experience, decision makers appropriately adjusted their willingness to wait.
Apparent failures of persistence can reflect adaptive temporal judgments.
Acknowledgments
This research was supported by NIH grants DA029149 to JWK and DA030870 to JTM. Portions of these results were presented at the 2011 meetings of the Cognitive Science Society and the Society for Neuroeconomics.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
Contributor Information
Joseph T. McGuire, Email: mcguirej@psych.upenn.edu.
Joseph W. Kable, Email: kable@psych.upenn.edu.
References
- Ainslie G. Specious reward: A behavioral theory of impulsiveness and impulse control. Psychological Bulletin. 1975;82:463–496. doi: 10.1037/h0076860. [DOI] [PubMed] [Google Scholar]
- Anderson JR, Schooler LJ. Reflections of the environment in memory. Psychological Science. 1991;2:396–408. [Google Scholar]
- Balci F, Freestone D, Gallistel CR. Risk assessment in man and mouse. Proceedings of the National Academy of Sciences of the United States of America. 2009;106:2459–2463. doi: 10.1073/pnas.0812709106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barabási AL. The origin of bursts and heavy tails in human dynamics. Nature. 2005;435:207–211. doi: 10.1038/nature03459. [DOI] [PubMed] [Google Scholar]
- Bateson M, Kacelnik A. Preferences for fixed and variable food sources: Variability in amount and delay. Journal of the Experimental Analysis of Behavior. 1995;63:313–329. doi: 10.1901/jeab.1995.63-313. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baumeister RF, Bratslavsky E, Muraven M, Tice DM. Ego depletion: Is the active self a limited resource? Journal of Personality and Social Psychology. 1998;74:1252–1265. doi: 10.1037//0022-3514.74.5.1252. [DOI] [PubMed] [Google Scholar]
- Brainard DH. The psychophysics toolbox. Spatial Vision. 1997;10:433–436. [PubMed] [Google Scholar]
- Brunner D, Kacelnik A, Gibbon J. Memory for inter-reinforcement interval variability and patch departure decisions in the starling, Sturnus vulgaris. Animal Behaviour. 1996;51:1025–1045. [Google Scholar]
- Cain MS, Vul E, Clark K, Mitroff SR. An optimal foraging model of human visual search. In: Carlson L, Hölscher C, Shipley T, editors. Proceedings of the 33rd Annual Conference of the Cognitive Science Society. Boston, MA: Cognitive Science Society; 2011. pp. 184–189. [Google Scholar]
- Catania AC, Reynolds GS. A quantitative analysis of the responding maintained by interval schedules of reinforcement. Journal of the Experimental Analysis of Behavior. 1968;3:327–383. doi: 10.1901/jeab.1968.11-s327. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dasgupta P, Maskin E. Uncertainty and hyperbolic discounting. American Economic Review. 2005;95:1290–1299. [Google Scholar]
- Dayan P, Niv Y, Seymour B, Daw ND. The misbehavior of value and the discipline of the will. Neural Networks. 2006;19:1153–1160. doi: 10.1016/j.neunet.2006.03.002. [DOI] [PubMed] [Google Scholar]
- Duckworth AL, Seligman MEP. Self-discipline outdoes IQ in predicting academic performance of adolescents. Psychological Science. 2005;16:939–944. doi: 10.1111/j.1467-9280.2005.01641.x. [DOI] [PubMed] [Google Scholar]
- Elandt-Johnson RC, Johnson NL. Survival models and data analysis. New York: John Wiley & Sons; 1980. [Google Scholar]
- Fawcett TW, McNamara JM, Houston AI. When is it adaptive to be patient? A general framework for evaluating delayed rewards. Behavioural Processes. 2012;89:128–136. doi: 10.1016/j.beproc.2011.08.015. [DOI] [PubMed] [Google Scholar]
- Gallistel CR, Gibbon J. Time, rate, and conditioning. Psychological Review. 2000;107:289–344. doi: 10.1037/0033-295x.107.2.289. [DOI] [PubMed] [Google Scholar]
- Gibbon J. Scalar expectancy theory and Weber’s law in animal timing. Psychological Review. 1977;84:279–325. [Google Scholar]
- Gott JRI. Implications of the Copernican principle for our future prospects. Nature. 1993;363:315–319. [Google Scholar]
- Gott JRI. Future prospects discussed. Nature. 1994;368:108. [Google Scholar]
- Griffiths TL, Tenenbaum JB. Optimal predictions in everyday cognition. Psychological Science. 2006;17:767–773. doi: 10.1111/j.1467-9280.2006.01780.x. [DOI] [PubMed] [Google Scholar]
- Griffiths TL, Tenenbaum JB. Predicting the future as Bayesian inference: People combine prior knowledge with observations when estimating duration and extent. Journal of Experimental Psychology: General. 2011 doi: 10.1037/a0024899. [DOI] [PubMed] [Google Scholar]
- Harrison GW, Millard PH. Balancing acute and long-term care: The mathematics of throughput in departments of geriatric medicine. Methods of Information in Medicine. 1991;30:221–228. [PubMed] [Google Scholar]
- Jazayeri M, Shadlen MN. Temporal context calibrates interval timing. Nature Neuroscience. 2010;13:1020–1026. doi: 10.1038/nn.2590. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jeffreys H. Theory of Probability. 3. Oxford: Clarendon Press; 1983. [Google Scholar]
- Jenkins WO, Stanley JC., Jr Partial reinforcement: A review and critique. Psychological Bulletin. 1950;47:193–234. doi: 10.1037/h0060772. [DOI] [PubMed] [Google Scholar]
- Kacelnik A. The evolution of patience. In: Loewenstein G, Read D, Baumeister RF, editors. Time and Decision: Economic and Psychological Perspectives on Intertemporal Choice. New York: Russell Sage Foundation; 2003. pp. 115–138. [Google Scholar]
- Kaplan EL, Meier P. Nonparametric estimation from incomplete observations. Journal of the American Statistical Association. 1958;53:457–481. [Google Scholar]
- Körding KP, Wolpert DM. Bayesian integration in sensorimotor learning. Nature. 2004;427:244–247. doi: 10.1038/nature02169. [DOI] [PubMed] [Google Scholar]
- Krebs JR, Kacelnik A, Taylor P. Test of optimal sampling by foraging great tits. Nature. 1978;275:27–31. [Google Scholar]
- Laibson D. Golden eggs and hyperbolic discounting. Quarterly Journal of Economics. 1997;112:443–477. [Google Scholar]
- Loewenstein G. Out of control: Visceral influences on behavior. Organizational Behavior and Human Decision Processes. 1996;65:272–292. [Google Scholar]
- Mark TA, Gallistel CR. Kinetics of matching. Journal of Experimental Psychology Animal Behavior Processes. 1994;20:79–95. [PubMed] [Google Scholar]
- McClure SM, Laibson DI, Loewenstein G, Cohen JD. Separate neural systems value immediate and delayed monetary rewards. Science. 2004;306:503–507. doi: 10.1126/science.1100907. [DOI] [PubMed] [Google Scholar]
- Metcalfe J, Mischel W. A hot/cool-system analysis of delay of gratification: Dynamics of willpower. Psychological Review. 1999;106:3–19. doi: 10.1037/0033-295x.106.1.3. [DOI] [PubMed] [Google Scholar]
- Mischel W, Ebbesen EB. Attention in delay of gratification. Journal of Personality and Social Psychology. 1970;16:329–337. doi: 10.1037/h0032198. [DOI] [PubMed] [Google Scholar]
- Mischel W, Shoda Y, Peake PK. The nature of adolescent competencies predicted by preschool delay of gratification. Journal of Personality and Social Psychology. 1988;54:687–696. doi: 10.1037//0022-3514.54.4.687. [DOI] [PubMed] [Google Scholar]
- Pelli DG. The VideoToolbox software for visual psychophysics: Transforming numbers into movies. Spatial Vision. 1997;10:437–442. [PubMed] [Google Scholar]
- Rachlin H. The science of self-control. Cambridge, MA: Harvard University Press; 2000. [Google Scholar]
- Samuelson PA. A note on measurement of utility. Review of Economic Studies. 1937;4:155–161. [Google Scholar]
- Shoda Y, Mischel W, Peake PK. Predicting adolescent cognitive and self-regulatory competencies from preschool delay of gratification: Identifying diagnostic conditions. Developmental Psychology. 1990;26:978–986. [Google Scholar]
- Simen P, Contreras D, Buck C, Hu P, Holmes P, Cohen JD. Reward rate optimization in two-alternative decision making: Empirical tests of theoretical predictions. Journal of Experimental Psychology: Human Perception and Performance. 2009;35:1865–1897. doi: 10.1037/a0016926. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sozou PD. On hyperbolic discounting and uncertain hazard rates. Proceedings of the Royal Society B: Biological Sciences. 1998;265:2015–2020. [Google Scholar]
- Stanovich KE, West RF. Individual differences in reasoning: Implications for the rationality debate? Behavioral and Brain Sciences. 2000;23:645–665. doi: 10.1017/s0140525x00003435. [DOI] [PubMed] [Google Scholar]
- Stevens JR, Hallinan EV, Hauser MD. The ecology and evolution of patience in two New World monkeys. Biology Letters. 2005;1:223–226. doi: 10.1098/rsbl.2004.0285. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Strotz RH. Myopia and inconsistency in dynamic utility maximization. Review of Economic Studies. 1955;23:165–180. [Google Scholar]