The glmS Ribozyme Cofactor is a General Acid-Base Catalyst

Abstract

The glmS ribozyme is the first natural self-cleaving ribozyme known to require a cofactor. The D-glucosamine-6-phosphate (GlcN6P) cofactor has been proposed to serve as a general acid, but its role in the catalytic mechanism has not been established conclusively. We surveyed GlcN6P-like molecules for their ability to support self-cleavage of the glmS ribozyme and found a strong correlation between the pH dependence of the cleavage reaction and the intrinsic acidity of the cofactors. For cofactors with low binding affinities the contribution to rate enhancement was proportional to their intrinsic acidity. This linear free-energy relationship between cofactor efficiency and acid dissociation constants is consistent with a mechanism in which the cofactors participate directly in the reaction as general acid-base catalysts. A high value for the Brønsted coefficient (β ~ 0.7) indicates that a significant amount of proton transfer has already occurred in the transition state. The glmS ribozyme is the first self-cleaving RNA to use an exogenous acid-base catalyst.

INTRODUCTION

The glmS ribozyme provides feedback regulation of the glucosamine- 6-phosphate synthase gene in bacteria and is the first natural self-cleaving ribozyme known to require a cofactor for activity.¹ Binding of the cognate cofactor, D-glucosamine-6- phosphate (GlcN6P), initiates ribozyme cleavage, which triggers the degradation of the mRNA.² Since glmS ribozyme cleavage regulates gene expression, it is a riboswitch as well as a ribozyme. The glmS ribozyme may be the first of a class of cofactor-activated catalytic RNAs that take advantage of exogenous molecules to expand the number of accessible reactions. ³

The glmS ribozyme exhibits high selectivity for GlcN6P, relative to similar molecules that also stimulate activity.^4–6 Moreover, only the α-anomer of GlcN6P binds in the active site and promotes catalysis.⁷ Initial studies showed that cofactor activity requires an amino group with a vicinal hydroxyl group.⁴ Subsequent efforts to identify new types of cofactors⁶ or to design new sugar-based cofactors^{5, 6} have had limited success, and only molecules very closely related to GlcN6P have been shown to promote efficient catalysis.^{1, 4–6}

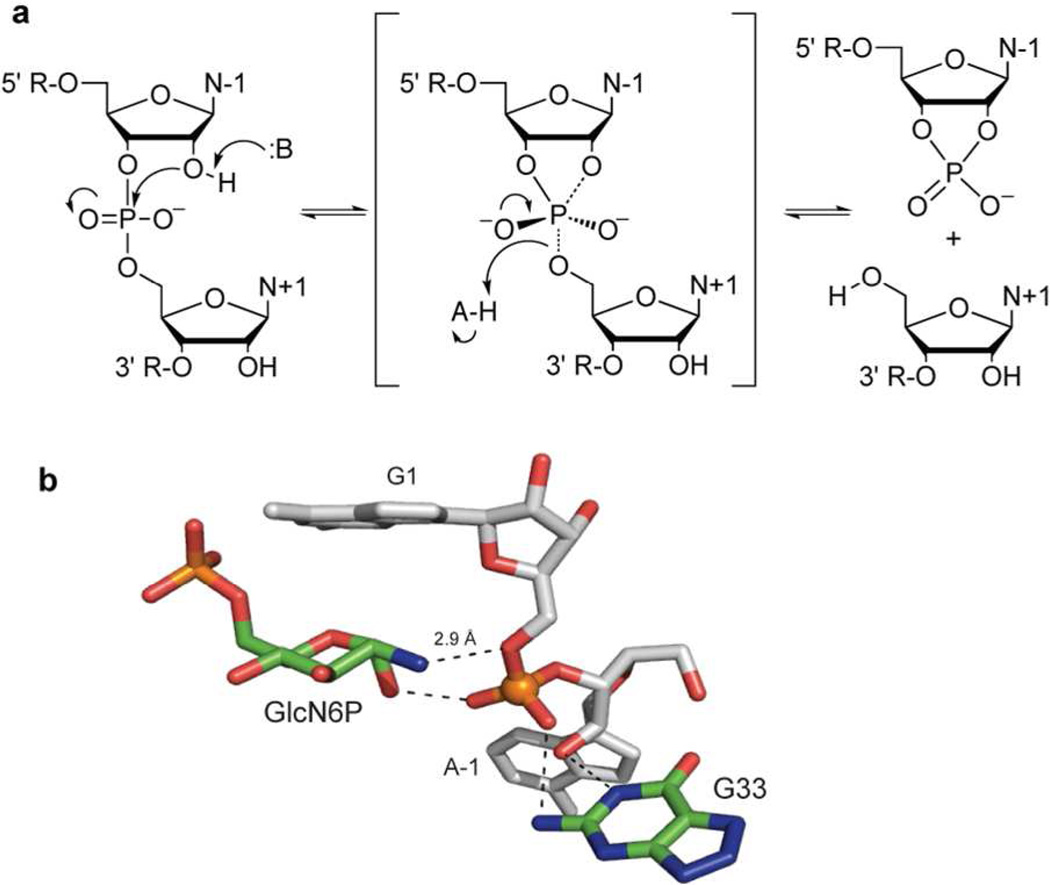
The glmS ribozyme catalyzes site-specific phosphodiester cleavage that involves nucleophilic attack of the 2'-oxygen on the adjacent phosphorus and cleavage of the 5'-P-O bond to generate a 5'-product with a 2',3'-cyclic phosphate and a 3'- product with a 5'-OH terminus (Figure 1a). The glmS ribozyme promotes cleavage rates 10⁷-fold faster than the uncatalyzed reaction.^{8, 9} To achieve these high rates, small ribozymes likely combine several catalytic strategies, including positioning and orientation of reactive groups, ground state destabilization, transition state stabilization, and general acid-base catalysis.^{10, 11}

Figure 1.

Chemical mechanism and active site of the glmS ribozyme. a) General mechanism for the phosphodiester transfer reaction catalyzed by small self-cleaving ribozymes. b) Active site of the glmS ribozyme showing the scissile phosphate and the two important elements for catalysis: GlcN6P and G33 (based on the X-Ray structure of the pre-cleavage ribozyme from Bacillus anthracis, PDB entry 2NZ4).¹²

The role of the GlcN6P cofactor in the catalytic mechanism is a key question. Crystal structures place the amino group of GlcN6P within hydrogen bonding distance of the scissile phosphate (Figure 1b).^{12, 13} The pK_a value of the amino group is close to neutrality in the active site,¹⁴ making it a suitable general acid-base catalyst. Thus, GlcN6P could act as a general acid catalyst to protonate the departing 5'-O.^{12, 15} Alternatively, GlcN6P could serve as a general base catalyst through a proton relay mechanism and act as a general acid catalyst once protonated.¹⁵ The cofactor could also participate in catalysis by orienting and positioning the reactive groups and by providing electrostatic stabilization through hydrogen bonding.^{12, 15} The precise role of GlcN6P in the catalytic mechanism remains to be established conclusively.

We examined the participation of the glmS ribozyme cofactor as a general acid-base catalyst by analyzing reactions with several cofactors that differ in Brønsted acid-base strength. If the cofactor donates or removes a proton in the transition state, the rate constant for the reaction should be proportional to the intrinsic acid or base strength of the cofactor.¹⁶ This proportionality generates a linear free-energy relationship between the pK_a values of different cofactors and the logarithm of the rate constants obtained from their corresponding reaction kinetics. This type of Brønsted analysis has been applied to the hepatitis delta virus (HDV) ribozymes to confirm that an active site cytosine participates directly in proton transfer.^{17, 18} For cofactors with low binding affinities, we found a linear free-energy relationship between the second-order rate constant, k_B, and the acid dissociation constant of the primary amine. This relationship provides compelling evidence that the cofactor participates directly in proton transfer in glmS ribozyme catalysis.

RESULTS

Cofactors that promote glmS ribozyme self-cleavage

We worked with the well-characterized glmS ribozyme named G18, which comprises 161 nt, A-16 to A145, of the Bacillus anthracis sequence, with 18 nt upstream of the cleavage site.^{9, 19} This variant cleaves virtually completely with reproducible, monophasic kinetics and the cleavage step can be monitored independently of metal or cofactor binding, or product dissociation.^{9, 20, 21} Thus, the pseudo-first-order rate constant, k_obs, corresponds to k_cleav.

In order to probe the cofactor contribution to catalysis, we tested 18 molecules containing the minimal ethanolamine moiety required for catalysis,⁴ including 10 that had not been described previously. Most of these accelerated cleavage above the background cleavage rate in the absence of cofactor at pH 7.5. However, many did not exhibit the expected increase in rates with increasing cofactor concentration, suggesting that reactions were complicated by nonproductive interactions. Therefore, we focused on the eight cofactors listed in Table 1 for further study. For some cofactors, binding affinities could be calculated from the dependence of cleavage rate constants on cofactor concentrations (K_m = K_d,app, Eq 5, Table 1). For cofactors lacking a sugar skeleton, however, k_cleav values increased linearly with increasing cofactor concentrations as high as 200 mM at pH 7.5 and 25 °C, and apparent equilibrium dissociation constants were estimated to be greater than 1 M. In subsequent experiments, we measured second-order rate constants at subsaturating cofactor concentrations, below 20% of Km values, under so-called k_cat/K_m conditions (Eq 2). The cofactor concentration dependence of reaction rates was monitored to ensure that k_cat/K_m conditions were maintained under all experimental conditions.

Table 1.

Rate and equilibrium constants for glmS ribozyme reactions with different cofactors.

Cofactor	Structure	kobs (min−1) 10 mM, pH 7.5, 25 °C	Kd,app (mM) pH 7.5, 25 °C	kcat/Km (mM−1min−1) pH 7.5, 25 °C
D-glucosamine-6-phosphate (GlcN6P)		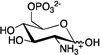92.9 ± 5.3	0.96 ± 0.11	98 ± 5
D-glucosamine-6-sulfate (GlcN6S)		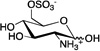3.1 ± 0.6	270 ± 64	0.22 ± 0.01
D-glucosamine (GlcN)		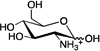0.65 ± 0.01	~ 500	0.062 ± 0.001
serinol (2-amino-propane-1,3-diol)		0.013 ± 0.002	≥ 1000	0.00047 ± 0.00007
TRIS (2-amino-2-hydroxymethyl- propane-1,3-diol)		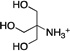0.0096 ± 0.0006	≥ 1000	0.00035 ± 0.00014
L-serine		0.0095 ± 0.0001	≥ 1000	0.00029 ± 0.00005
ethanolamine		0.003 ± 0.001	≥ 1000	0.000058 ± 0.000003
*L-prolinol		0.0007 ± 0.0003	≥ 1000	0.000023 ± 0.000009
no cofactor	-	0.0001	--	--

^*not previously described

Apparent pK_a values determined from self-cleavage kinetics correlate with microscopic pK_a values for protonation of the cofactors in solution

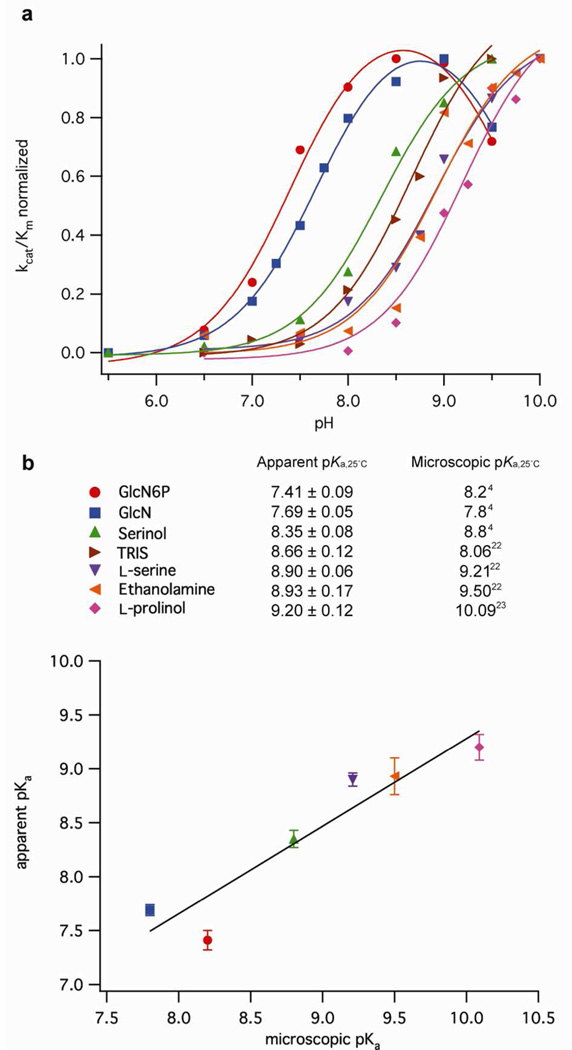
To study the pH dependence of cleavage kinetics, we measured apparent second-order rate constants (k_cat/K_m) at various pH values. pH-rate profiles for reactions with GlcN6P and GlcN fit an equation with two ionizable groups to give two apparent pK_a values (Eq 4, Figure 2a). The first pK_a value near neutrality corresponded to the pH where rates were half maximal. The second pK_a value near 9.7 likely reflected the decrease in cofactor binding affinity that occurs above pH 8.5,⁹ as well as the destabilization of ribozyme structure upon deprotonation of G and U hydrogen bond donors. The pH-rate profiles for reactions with cofactors other than GlcN6P and GlcN fit an equation with a single ionizable group (Eq 3, Figure 2a). These plots could not be fit to Eq 4 by fixing a second pK_a value because the two inflection points were too similar. If cleavage rates decreased in all reactions at high pH due to loss of cofactor binding or structural destabilization, as is likely, a second deprotonation event would cause underestimation of the first pK_a value by approximately 0.2 units. This underestimation causes a small discrepancy between apparent pK_a values determined from self-cleavage kinetics and microscopic pK_a values for the amino groups of the cofactors in solution.

Figure 2.

Correlation of apparent pK_a values determined from pH-rate profiles with microscopic pK_a values for protonation of the cofactors in solution. a) Normalized pH-rate profiles for different cofactors were fit to Eq 3 or 4. Each point is the mean of two or more experiments. Normalized standard deviations ranged from 0.0002 to 0.28 (not shown for the sake of clarity). b) Linear correlation of apparent pK_a values obtained from pH-rate profiles versus microscopic pK_a values of the cofactors in solution. Errors correspond to the error of the fit in panel a.

Nonetheless, apparent pK_a values calculated from the pH dependence of k_cat/K_m values correlated well with the microscopic pK_a values of the amino group of the cofactors in solution (Figure 2 b),^{4, 14, 22, 23} with TRIS as the single exception. TRIS was the only cofactor that showed an apparent pK_a from cleavage kinetics higher than the microscopic pK_a value of its amino group in solution. The plot of log(k_cat/K_m) versus pH for self-cleavage promoted by TRIS had a slope much less than one (Figure S1), suggesting that more than one ionization event was taking place. Because the apparent pK_a value determined from self-cleavage kinetics reflected more than one ionization event, it did not correlate well with the microscopic pK_a value of the TRIS amino group in solution.

The apparent pK_a value of G18 ribozyme self-cleavage promoted by GlcN6P under k_cat/K_m conditions (7.41 ± 0.09) was not significantly different (Welch t-test, P > 0.05) from the one that we previously determined at a saturating concentration of GlcN6P (7.62 ± 0.05).⁹ GlcN6P was the cofactor that exhibited the largest difference between its microscopic pK_a value in solution and the apparent pK_a value obtained from self-cleavage kinetics. We attributed this discrepancy to an effect of phosphate ionization on GlcN6P binding because K_m values for reactions with GlcN6P have been shown to depend on pH with an apparent pK_a of 6.7 ± 0.2.⁷ This pK_a corresponds roughly to the pK_a of the phosphate in the active site,¹⁴ and it is protonation of this phosphate that is believed to be responsible for the decrease in affinity at low pH. The rest of the ligands assayed do not have a phosphate group and did not show this behavior. The correlation between apparent pKa values determined from pH-rate profiles and microscopic pKa values for ionization of cofactor amines in solution shows that the protonation state of the cofactor affects activity.

Self-cleavage of the glmS ribozyme is subject to general acid-base catalysis

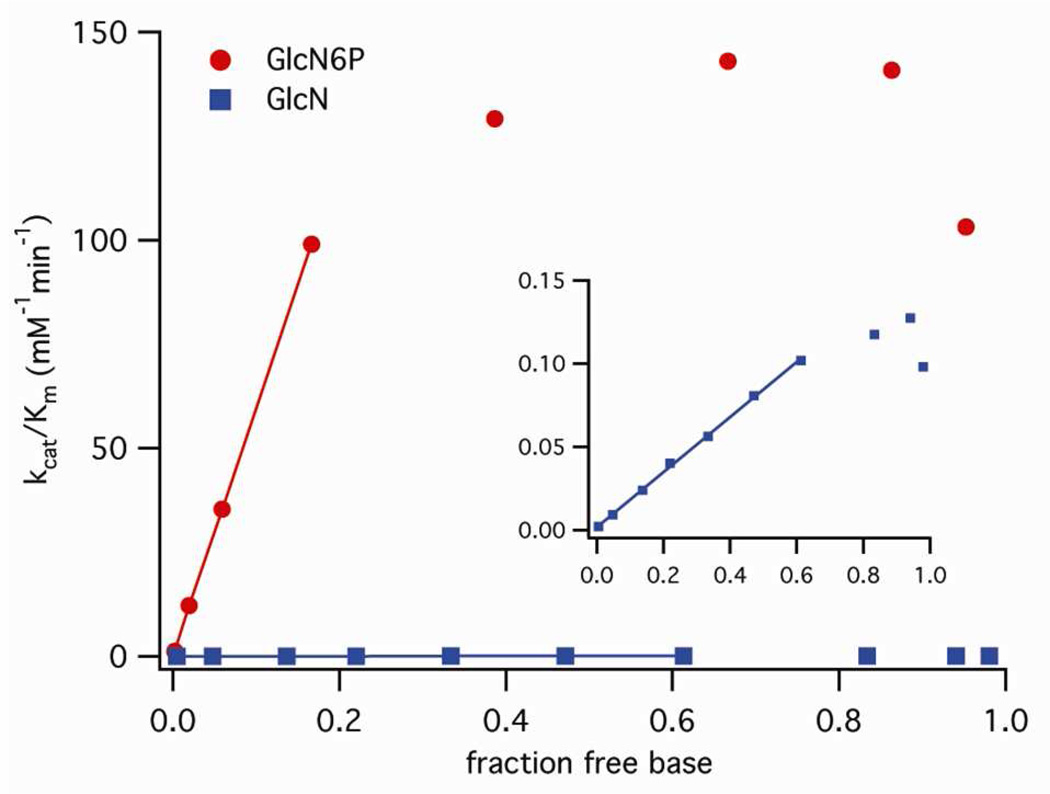
The way in which second-order rate constants change as the relative amounts of the basic and acidic forms of the cofactor shift with pH reveals the relative contributions of each form of the cofactor to catalysis (Eq 7).¹⁶ Apparent second-order rate constants (k_cat/K_m) showed linear dependence on the fraction of the free base form of the cofactors (α = [B]/([B]+[BH⁺])), calculated using microscopic pK_a values in solution (Eq 6).^{4, 14, 22, 23} This dependence deviated from linearity when the fraction of free base (α) corresponded to the apparent pK_a value obtained from self-cleavage reactions (Figure 3), due to the small difference between microscopic pK_a values in solution and apparent pK_a values determined from self-cleavage kinetics. Plots constructed using the apparent pK_a values obtained from self-cleavage kinetics were linear across a broader range of pH values (Figure S2). The y-axes of plots of k_cat/K_m versus α (Figures 3 and S2) approached zero (Eq 7, k_BH ~ 0), indicating that the reaction obeys a rate law consistent with general base catalysis with no contribution from the acidic form of the cofactor.¹⁶ That is, the first-order rate constant follows the rate-law for general base catalysis: k_cleav = k_B [B] + k₀, where k_B is the second-order rate constant with respect to the free base form of the cofactor.

Figure 3.

Dependence of cleavage rates on the concentration of the free base form of the cofactors. Linear fits of second-order rate constants, k_cat/K_m, versus the fraction of the free base forms of GlcN6P and GlcN (for free base concentrations below apparent pK_a values) intercept the origin. Each point represents the average of two or more experiments at a single pH.

Due to the principle of kinetic ambiguity,¹⁶ this kinetic behavior is equally consistent with a mechanism in which the cofactor participates as a true general base catalyst or with a mechanism in which the cofactor participates as a general acid catalyst together with a hydroxyl anion that acts as a specific base catalyst to deprotonate the 2'-OH nucleophile (k_cleav = (k_BK_a/K_w) [OH⁻] [BH⁺ ] + k₀). These two cases are kinetically indistinguishable because both exhibit the same pH dependence, with rates that increase as pH increases, and apparent pK_a values that track the intrinsic pK_a of the cofactor.

The second-order rate constant k_B was obtained from the slope of the plot of k_cleav versus the cofactor free base concentration [B], calculated using microscopic pK_a values in solution.^{4, 14, 22, 23} The value of kB varied somewhat with pH, exhibiting a small decrease with increasing pH (Figure S3). This behavior could point to a minor contribution from the acidic form of the cofactor. However, the data did not fit well to a rate equation that included a contribution from the acidic form, (k_cleav = kB [B] + kBH [BH⁺] + k₀), because the slope of the plot of k_cleav versus [B], which should correspond to (kBH/Ka) [H+] + k_B, did not vary linearly with [H⁺] across the full pH range. The variation of k_B with pH arises in part from experimental uncertainty associated with the small difference between microscopic pK_a values of the cofactors in solution and apparent pK_a values obtained from self-cleavage kinetics; use of apparent pK_a values to calculate k_B gave less variability (Figure S3). It is also possible that the acidic form BH⁺ contributes to catalysis through a different mechanism, such as electrostatic stabilization, or that multiple catalytic strategies operate simultaneously and their contributions vary with pH.

To evaluate the relationship between catalytic efficiency and intrinsic Brønsted acid-base strength, we used values of k_B obtained from data at pH 9.0 in order to isolate the contribution of the basic form of the cofactor. For comparison, we also calculated k_B from the slope of the plot of k_cleav versus the cofactor free base concentration [B] using all data obtained at pH values between 7.5 and 9.5 (Table 2).

Table 2.

Second-order rate constants, k_B (mM⁻¹ min⁻¹), calculated from data obtained under different pH conditions.

Cofactor	kB (pH 9.0)	kB (pH 7.5–9.5)
GlcN6P	163 ± 13	134 ± 22
GlcN	0.135 ± 0.009	0.122 ± 0.008
TRIS	0.0013 ± 0.0001	0.0014 ± 0.0003
Serinol	0.0047 ± 0.0003	0.0056 ± 0.0003
L-Serine	0.0050 ± 0.0004	0.0058 ± 0.0005
Ethanolamine	0.0205 ± 0.0022	0.0123 ± 0.0008
L-Prolinol	0.0019 ± 0.0001	0.0008 ± 0.0001

Brønsted analysis of proton transfer

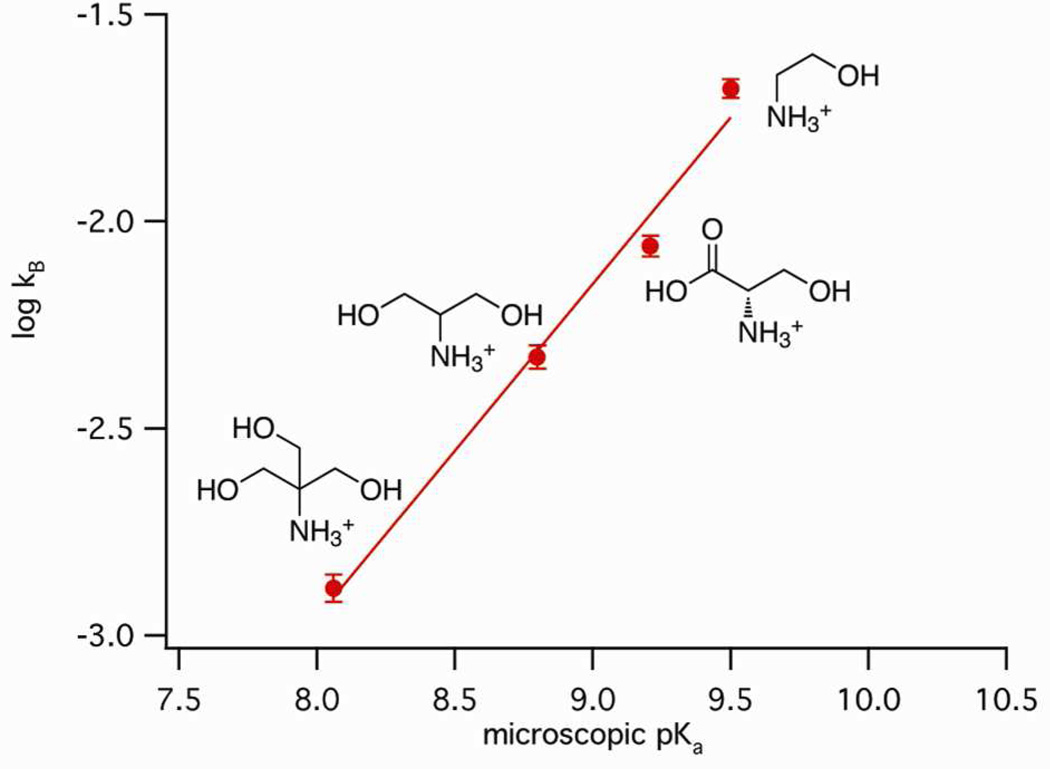
In general acid-base catalysis, second-order rate constants k_BH or k_B show a log-linear relationship with the pK_a value of the Brønsted acid or base for a series of catalysts, following the Brønsted equations: log k_BH = C_BH - α pK_a or log k_B = CB + β pK_a, respectively.¹⁶ The slope of this so-called Brønsted plot (α or β) is a measure of the sensitivity of the reaction to the acid-base strength of the catalyst and reflects the amount of proton transfer in the transition state.

To gain insight into the transition state of glmS ribozyme catalysis, we applied a Brønsted analysis to a selected number of cofactors. The Brønsted plot is very sensitive to small variations in the structure of the catalysts.^{16, 17, 24} Thus, to minimize complications arising from variation in cofactor structures, we compared primary amines that bind the glmS ribozyme with low affinity, excluding L-prolinol, which is a cyclic secondary amine, and GlcN6P and GlcN, which bind the ribozyme with much higher affinity and produce much greater rate enhancements than the other the cofactors. Plots of the logarithm of k_B versus cofactor pK_a values for reactions with TRIS, serinol, L-serine and ethanolamine produced a straight line with a positive slope (Figure 4). The Brønsted coefficient β varied from 0.80 ± 0.07, when the plot was constructed with k_B values determined at pH 9.0 (Figure 4), to 0.65 ± 0.13, when the plot was constructed with k_B values calculated using data at pH values from 7.5 to 9.5 (Figure S4). These two β values fall within the range of experimental uncertainty. The linearity of the Brønsted plot links cofactor efficiency to acid-base strength, evidence that the cofactor participates in proton transfer in the transition state.

Figure 4.

Correlation of base strength with rate acceleration. Brønsted plot represents the linear free-energy relationship between the second-order rate constant, k_B, calculated at pH 9.0 and the microscopic acidity constant K_a of low affinity cofactors with primary amines in solution (R² = 0.98).

DISCUSSION

We show the direct participation of the cofactor in proton transfer in glmS ribozyme catalysis, consistent with previous biochemical and structural data. High-resolution structures had implicated the GlcN6P cofactor and an active-site guanine as the general acid and general base catalysts, respectively, in the catalytic mechanism of the glmS ribozyme (Figure 1b).^{12, 15} These roles were inferred from the similarity of their positions in the active site to the positions of two histidine residues that fulfill the same roles in the mechanism of RNAse A.²⁵ Previously, we demonstrated that the microscopic pK_a value of the active site guanine G33 does not correlate well with the apparent pK_a value obtained from the pH dependence of cleavage kinetics.⁹ This result contradicts the idea that the pH-dependent step in catalysis reflects activation of the nucleophilic oxygen by the deprotonated form of G33. We now present evidence supporting the model that the cofactor acts as a general acid-base catalyst in the rate-limiting step. We show that apparent pK_a values obtained from cleavage kinetics correlate well with microscopic pK_a values for ionization of the primary amines of several cofactors in solution. Most importantly, we report that catalytic efficiency correlates well with the intrinsic acidity of the cofactors, as expected if cofactors participate directly in general acid-base catalysis.

It was shown previously that apparent pK_a values obtained from glmS self-cleavage reactions with GlcN and serinol shifted about one unit, corresponding to the difference between the microscopic pK_a values of the two compounds in solution.⁴ We have extended this correspondence to several more cofactors, including both sugar-based and non-sugar based cofactors, as well as primary and secondary amines with vicinal hydroxyl groups. Agreement between apparent pK_a values obtained from reaction kinetics and intrinsic pK_a values of the free cofactors in solution was expected because the pH dependence of k_cat/K_m values reflects ionization of the free enzyme and free cofactor.²⁶ The microscopic pK_a value for ionization of bound GlcN6P has been shown to shift towards neutrality. ^{7, 14} The active site of the glmS ribozyme might tune the acid dissociation constants of the other cofactors in the same way. Consistent with the notion that the apparent pK_a value obtained from cofactor-ribozyme self-cleavage kinetics tracks the microscopic pK_a value of the cofactor, the apo ribozyme exhibited a log-linear pH-rate profile with a slope of approximately one between pH 6.5 and pH 10.⁹ The relationship between cofactor ionization state and ribozyme cleavage activity suggests that the cofactor participates in proton transfer during catalysis. However, this relationship alone is not sufficient to prove that the cofactor is a general acid base catalyst; the same relationship could be seen if the protonation state of the cofactor affects binding affinity or the active site structure of the cofactor-ribozyme complex.

The Brønsted equation describes a linear free-energy relationship that correlates the Gibbs free energy of proton dissociation with the activation energy of the catalytic step.¹⁶ This relationship between the free energies translates to a linear correlation between pK_a values for ionization of the cofactors’ amine groups to the logarithm of the rate constants determined from reactions supported by each cofactor. The first application of a Brønsted analysis to a protein enzyme catalyzed reaction was made possible by creating an inactive mutant missing a catalytic lysine and rescuing activity with exogenous amines.²⁴ More recently, a Brønsted analysis of proton transfer was applied to both the genomic¹⁸ and antigenomic¹⁷ HDV ribozymes by rescuing inactive mutants with exogenous imidazole analogues.

For the construction of a Brønsted plot to analyze proton transfer in the transition state, we selected cofactors with low affinity and similar structures to ethanolamine, the smallest molecule that promotes catalysis. Deviations from the Brønsted plot are usually found for bases that differ structurally.^{16, 17, 24} We observed this effect with L-prolinol, which clearly deviated from the fit. GlcN6P and GlcN promoted cleavage rates much more efficiently than the other cofactors, presumably due to differences in binding interactions.²⁷ No correction for molecular volume of the cofactors was required for the remaining cofactors.²⁴ The linear free energy relationship reflected in the Brønsted plot is consistent with a model in which the amino group of the cofactor participates in proton transfer in the transition state. This result is strong evidence that the cofactor acts as a general acid-base catalyst in the transition state of the rate-determining step.

The value of the Brønsted coefficient can be interpreted as a measure of the degree of proton transfer between the cofactor and the ribozyme in the transition state.^{16, 28} A value of zero would mean that the reaction is not sensitive to the acid-base strength of the cofactor, indicating that the cofactor does not participate in proton transfer in a rate-determining step. Conversely, a value of one would signify that the free energy of acid dissociation accounts for all of the free energy of activation for proton transfer, meaning that proton transfer is complete in the transition state. The estimated Brønsted coefficient near 0.7 indicates that ~70% of proton transfer has already occurred in the transition state. This value is close to Brønsted coefficients of ~ 0.5 that were reported previously for proton transfer in phosphodiester bond cleavage by RNase A²⁹ and HDV ribozymes.^{17, 18} In glmS ribozyme catalysis, a substantial amount of proton transfer between the cofactor and the ribozyme has already occurred in the transition state. Thus, the reaction proceeds through a late transition state that resembles the 2',3'-cyclic phosphate and 5'-hydoxyl products more than the phosphodiester starting material.

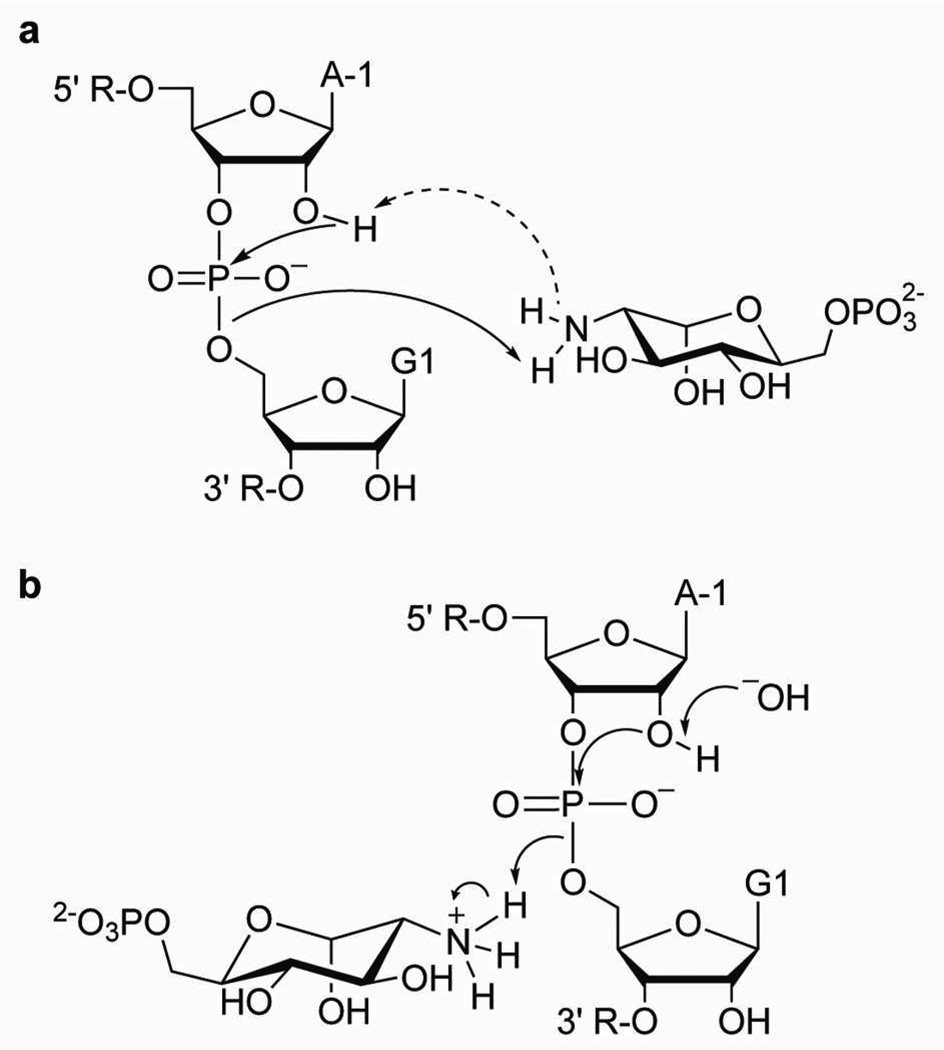
Our results provide conclusive evidence for a direct role of the cofactor in proton transfer, but Brønsted analyses do not eliminate the ambiguity inherent to rate laws for proton transfer reactions. Therefore, our kinetic data alone do not allow us to distinguish whether the cofactor activates the 2'-OH nucleophile as a general base catalyst (Figure 5a), or whether it stabilizes the 5'-O leaving group as a general acid catalyst while a specific base catalyst activates the nucleophile (Figure 5b). However, the position of the cofactor in the active site, with its amino group within Van der Waals distance (~ 3 A) of the 5'-O leaving group^{12, 13} supports a role for the cofactor in protonating and activating the leaving group as a general acid catalyst, as originally proposed.^{12, 15} Moreover, previous studies of spontaneous and ribozyme-catalyzed reactions, studies of model systems, and computational studies concluded that cleavage of the exocyclic 5'-P-O bond presents the highest activation energy barrier and is rate-limiting for this type of phosphodiester transfer.^30–34 Also, physical organic studies of phosphodiester cleavage support a substantially anionic character of the 5'-bridging oxygen (β_{leaving group} ~ −1).^{33, 35, 36} Taken together, these data support the model that the cofactor acts as a general acid catalyst to protonate the 5'-O leaving group in combination with a hydroxide ion which deprotonates the 2'-OH nucleophile (Figure 5b).

Figure 5.

Kinetically equivalent mechanisms that include participation of the cofactor in proton transfer. a) Mechanism where GlcN6P acts as the general base catalyst through a proton shuttle and, once protonated, acts as the general acid catalyst. b) Mechanism where GlcN6P acts as a general acid catalyst together with specific base catalysis by a hydroxide ion.

This model agrees with the observed decrease of nearly one unit in the pK_a of GlcN6P upon binding to the active site.¹⁴ The shift in the pK_a value in the acidic direction upon cofactor binding facilitates the release of its proton.³⁷ General acid catalysis is common in RNA self-cleavage and general acid catalysts often ionize with pK_a values shifted towards neutrality.^38–42 Our model suggests that this is also the case for the glmS ribozyme; the pK_a value for ionization of the amino group of the exogenous cofactor shifts towards neutrality when bound in the active site so it can better perform its role as a general acid catalyst.

CONCLUSION

We have applied a linear free-energy Brønsted analysis of proton transfer to the first known cofactor-dependent RNA self-cleavage reaction. A correlation between the efficiency of the cofactor and its basic strength indicates that the cofactor participates directly in proton transfer in the transition state of the rate-determining chemical step. It is reasonable to think that other ribozymes might harness the catalytic properties of an exogenous molecule. The ability of RNA to bind and exploit the chemical versatility of an exogenous cofactor greatly enhances its ability to catalyze more diverse and efficient reactions.

pH-rate profiles for glmS self-cleavage followed the rate-law that defines general base catalysis. While kinetic data alone cannot distinguish general base from general acid catalysis, structural information as well as comparison with other phosphodiester cleavage reactions support the original hypothesis that the cofactor is a general acid catalyst that protonates the 5'-O leaving group during 5'-O-P bond cleavage. From the value of 0.7 for the Brønsted coefficient, we can infer a late transition state in the phosphodiester cleavage of the RNA-cofactor complex, in which the 2'-O-P bond is nearly completely formed and the 5'-O-P bond is nearly completely broken. This late transition state confirms the idea that breaking the 5'-O-P bond poses the highest activation energy making general acid catalysis essential for RNA self-cleavage.

EXPERIMENTAL SECTION

All chemicals were purchased from Sigma-Aldrich (St. Louis, MO) or Alfa Aesar (Ward Hill, MA) and used as received.

Preparation of RNAs

The plasmid template used to transcribe the glmS ribozyme from B. anthracis (pTG18) has been previously described.⁹ Homogeneously labeled RNAs were prepared using T7 RNA polymerase transcription with 10 nM linearized pTG18 at 37 °C for 2 h in 20 mM HEPES pH 8, 1 mM spermidine, 5 mM dithiothreitol, 0.01% Triton X-100, 4 mM NTPs, 25 mM MgCl₂ and 0.3 µM [α-³²P]ATP. RNAs were fractionated by denaturing gel electrophoresis and converted into sodium salts by DEAE-650M chromatography (Toyopearl).

Self-cleavage kinetics

Kinetic assays were performed with pre-annealed RNAs and with saturating concentrations of MgCl₂ in order to avoid a slow folding step that precedes formation of the native structure.^{8, 20} Standard conditions were 50 mM buffer (piperazine pH 5-6, PIPES pH 6-7, HEPES pH 7- 8.25, HEPPS pH 8.25-9, CHES pH 9-10), 0.1 mM EDTA, 50 mM MgCl₂, 25 °C. [α-³²P]ATP-labeled G18 (5–20 nM) in 50 mM buffer and 0.1 mM EDTA was pre-folded following an annealing cycle: 85 °C for 1 min, cooled to 25 °C, MgCl₂ added and incubated at 25 °C for 15 min. Reactions were started by addition of the cofactor at the appropriate concentration (2×) in the same buffer solution. For self-cleavage rates below 5 min⁻¹, cleavage was initiated by manually mixing 30 µL of pre-folded RNA with 30 µL of cofactor solution in the same buffering system. 6 µL samples were taken at various time points and quenched with 5 volumes of 90% formamide, 50 mM EDTA, 0.1 % bromophenol blue, 0.1 % xylene cyanol. For intervals of 5 seconds or less, each time point was taken independently: 3 µL of the pre-folded RNA solution and 3 µL of the cofactor solution were mixed by hand and quenched with 30 µL of the quenching solution described above. Rates above 5 min⁻¹ were measured using a Rapid Quench System RQF-3 (KinTek Corp.), where the driving solutions had the same composition as the reaction buffer. Solutions of 200 µL were prepared for both pre-folded RNA and cofactor. Samples were mixed in the reaction loop (~ 14 µL of each) for each time point and collected onto 40 µL of quenching buffer, for a total dilution of 1:5. Aliquots were fractioned on denaturing 10% (19:1) polyacrylamide gels. The fraction of cleaved product was quantified by radioanalytic imaging (PhosphorImager Storm 820 and ImageQuant software, Molecular Dynamics).

Data Analysis

First-order cleavage rate constants (k_cleav) were calculated by fitting the fraction of cleaved product versus time to a single-exponential equation (1):

$$f=f_0+f_{\mathrm{\infty }}\left(1-e^{-k_{clev}t}\right)$$ (1)

First-order cleavage rates were obtained at different concentrations of the cofactor in the linear range of a Michaelis-Menten plot (cofactor concentration < 0.2 × apparent K_m value) and were fit by linear regression to obtain apparent second-order rate constants k_cat/K_m (Eq 2):

$$k_{\text{cleav}}=\frac{k_{\text{cat}}}{K_{\mathrm{m}}}[\text{cofactor}]+k_{\text{min}}$$ (2)

where k_min represents the background cleavage rate in the absence of cofactor.

pH-rate profiles were constructed by plotting second-order rate constants versus pH. Apparent pK_a values for ribozyme self-cleavage were determined by fitting second-order averaged rate constants (from at least two replicates) to equations (3) or (4):

$$k_{\text{cat}}/K_{\mathrm{m}}=\frac{{\left(k_{\text{cat}}/K_{\mathrm{m}}\right)}_{\text{max}}}{1+{10}^{(p{K}_a-pH)}}+{\left(k_{\text{cat}}/K_{\mathrm{m}}\right)}_{\text{min}}$$ (3)

$$k_{\text{cat}}/K_{\mathrm{m}}=\frac{{\left(k_{\text{cat}}/K_{\mathrm{m}}\right)}_{\text{max}}}{1+{10}^{(p{K}_{a1}-pH)}+{10}^{(pH-p{K}_{a2})}+{10}^{(p{K}_{a1}-p{K}_{a2})}}+{\left(k_{\text{cat}}/K_{\mathrm{m}}\right)}_{\text{min}}$$ (4)

The reported errors for the apparent pK_a values are the errors from the fits. To prepare Figure 2a, data were normalized using the maximum and minimum values of k_cat/K_m. For the sake of clarity, standard deviations for each point are not shown; normalized standard deviations ranged from 0.0002 to 0.28.

Binding curves were constructed by plotting pseudo-first-order rate constants versus total cofactor concentration. Apparent equilibrium dissociation constants (K_m = K_d,app) for cofactor binding were determined from first-order cleavage rates using equation (5):

$$k_{\text{cleav}}=\frac{k_{\text{max}}\left[\text{cofactor}\right]}{\left[\text{cofactor}\right]+K_m}$$ (5)

Second-order rate constants with respect to free base (k_B) were determined from the slopes of plots of k_cleav versus the free base form of the cofactor [B] obtained at several cofactor concentrations (in the linear range of the Michaelis-Menten plot) and at a single pH (9.0) or pH values ranging from 7.5 to 9.5. The Brønsted plot was constructed from log k_B versus microscopic pK_a values for ionization of the amino group of each cofactor in solution. The microscopic pK_a for ionization of the cofactors in solution was used for these calculations because the bulk of the cofactor is in solution, not bound, and because the measurements were made under k_cat/K_m conditions, where the process concerned is the interaction of the free enzyme with free cofactor.

The fraction of free base form of the cofactor (α) was calculated using equation (6), where pK_a is the microscopic pK_a value of the amino group in solution:

$$\alpha =\frac{[\mathrm{B}]}{[\mathrm{B}]+[\mathrm{B}{\mathrm{H}}^{+}]}=\frac{1}{1+{10}^{\left(p{K}_a-pH\right)}}$$ (6)

The dependence of k_cat/K_M on the fraction of free base form of the cofactor α is given by equation (7):

$$k_{\text{cat}}/K_{\mathrm{m}}=\left(k_{\mathrm{B}}-k_{\mathrm{BH}}\right)\cdot \alpha +k_{\mathrm{BH}}$$ (7)

ABBREVIATIONS

GlcN6P

D-glucosamine-6-phosphate

GlcN

D-glucosamine

GlcN6S

D-glucosamine-6-sulfate

TRIS

2-amino-2-hydroxymethyl-propane-1,3-diol

PIPES

1,4-piperazinediethanesulfonic acid

HEPES

2-[4-(2-hydroxyethyl)piperazin-1-yl]ethanesulfonic acid

HEPPS

3-[4-(2-hydroxyethyl)piperazin-1-yl]propane-1-sulfonic acid

CHES

2-(cyclohexylamino)ethanesulfonic acid

EDTA

ethylenediaminetetraacetic acid

NTP

nucleotide 5'-triphosphate

HDV

hepatitis delta virus.