Smaller sample sizes for phase II trials based on exact tests with actual error rates by trading-off their nominal levels of significance and power

Abstract

Background:

Sample sizes for single-stage phase II clinical trials in the literature are often based on exact (binomial) tests with levels of significance (alpha (α) <5% and power >80%). This is because there is not always a sample size where α and power are exactly equal to 5% and 80%, respectively. Consequently, the opportunity to trade-off small amounts of α and power for savings in sample sizes may be lost.

Methods:

Sample-size tables are presented for single-stage phase II trials based on exact tests with actual levels of significance and power. Trade-off in small amounts of α and power allows the researcher to select from several possible designs with potentially smaller sample sizes compared with existing approaches. We provide SAS macro coding and an R function, which for a given treatment difference, allow researchers to examine all possible sample sizes for specified differences are provided.

Results:

In a single-arm study with P₀ (standard treatment)=10% and P₁ (new treatment)=20%, and specified α=5% and power=80%, the A’Hern approach yields n=78 (exact α=4.53%, power=80.81%). However, by relaxing α to 5.67% and power to 77.7%, a sample size of 65 can be used (a saving of 13 patients).

Interpretation:

The approach we describe is especially useful for trials in rare disorders, or for proof-of-concept studies, where it is important to minimise the trial duration and financial costs, particularly in single-arm cancer trials commonly associated with expensive treatment options.

Phase II clinical trials are common in medical research, particularly in oncology. They are often based on a relatively small or moderate number of patients (typically 40–70), and allow a preliminary assessment of a new intervention before embarking on a larger and expensive randomised controlled trial (i.e., phase III). Many new drugs are not investigated beyond phase II, because of evidence that they are ineffective. The Fleming single-stage procedure (Fleming, 1982 (for the situation where K=1); Machin et al, 1997; A’Hern, 2001) has been a widely used approach in early-phase drug development. It involves having a single treatment group, and all patients are given the test intervention (often called a single-arm, single-stage design). The observed data are considered in relation to historical data expected to be associated with the control/standard treatment in order to design a subsequent phase III study.

Multistage designs involve conducting one or more interim analyses to decide whether all patients planned for a trial should be recruited. A decision to proceed to phase III is determined by using patient data from all stages of accrual. One important advantage of a multistage design relates to fewer patients on ineffective experimental treatments, with the opportunity to stop a trial earlier for futility (Schlesselman et al, 2006).

Recently, randomised controlled phase II trials are becoming more popular, particularly for common cancers, in which patients are randomly allocated to receive either the test intervention or the control (e.g., the standard treatment or placebo), or they are randomised to several experimental treatments. An important advantage of this approach is that the control group data are collected prospectively, that is, at the same time as those given the new intervention, and this usually yields more reliable data from which to design a subsequent phase III trial. A review and discussion of phase II designs is given in Rubinstein et al (2005), Ratain and Sargent (2009), Daniel et al (2009) and Sargent and Taylor (2009).

The basic idea of a phase II design is that a new therapy is worth considering further if it demonstrates a level of treatment response, P₁ (e.g., tumour response or lower disease progression), which is greater than the response rate for the current or standard treatment, P₀. Values of P₁ and P₀ are estimates of π₁ and π₀, respectively, the true probability of response, and used for sample-size calculations, along with desired statistical power and level of statistical significance.

The sample-size method in a single-stage Fleming design uses a normal approximation to the binomial distribution, and this helped facilitate the calculations for multiple stage testing. However, the sample sizes using this approximation result in differences in sample sizes compared with exact methods, particularly for relatively small studies. This is discussed in A’Hern (2001), who also provided sample-size tables using exact methods, which are larger than those obtained using the Fleming (1982) design. The difference is noticeable for studies of say <50 patients. The Fleming design can also produce anomalous results in that the confidence interval for the observed proportion could include P₀, even though the P-value is <0.05 (A’Hern, 2001). It is therefore better to use exact tests. Although the idea of using alpha (α) levels greater than threshold values, such as 5 or 10%, was mentioned briefly, the impact on sample size was not discussed (A’Hern, 2001). A’Hern (2001) provides sample sizes based on approximate α levels and power.

Sample-size software (Hintze, 2001; Machin et al, 2009) and tables (A’Hern, 2001; Machin et al, 2009) are available for the Fleming design and A’Hern exact sample sizes. However, they are based on conventional significance levels, such as 5 or 10%, and power, such as 80 or 90%. This means that the sample sizes produced are based on ensuring an α ⩽5% and power ⩾80% but researchers might think that α=5% and power=80%. In some situations, smaller sample sizes for α=5.1% and power=79.9% might be possible and therefore ignored. It can be difficult to choose from a wider set of possible sample sizes if software or tables only offer a solution where α is ⩽5% and power is ⩾80%. Even with some specialist software, such as PASS (Hintze, 2001), it would require inputting a large number of non-standard α and power values either one at a time or in some other way. If we accept an α level that is ‘around’ 10% and power ‘around’ 80%, then more than one possible sample size can arise (shown later). The consequence of this is that software programs and the tables presented by A’Hern (2001) give sample sizes based on approximate α levels and power.

This paper considers the implications of such approximations in clinical trials in practice and presents sample size for exact α levels based on the exact test. We can then use this approach to examine several sample sizes for the same treatment effect and choose one that is the smallest. This would be especially useful for studies of novel agents (where little is known about the treatment) or for rare disorders, where it is appropriate to minimise the sample size.

Materials and methods

With a single-stage design, the standard response rate is assumed to be P₀ (under the null hypothesis); and the new therapy is considered worthy of further research if we can reject the null hypothesis in favour of the alternative hypothesis, where the response rate is P₁. For example, a current therapy may be associated with a 50% tumour response rate for a given cancer, and a new agent or intervention is considered potentially useful if it can increase the rate to at least 65%. The consequent decision rule provides the sample size (n) and minimum number of responders (i.e., ⩾r) that are required to warrant further investigation of the new therapy, such that statistical significance is achieved. If the number of responders is <r, then this number is the maximum number of responders for which statistical significance is not achieved.

The above can be formally stated as:

H₀ : P₀ ⩽50% vs H₁ : P₁ ⩾65%

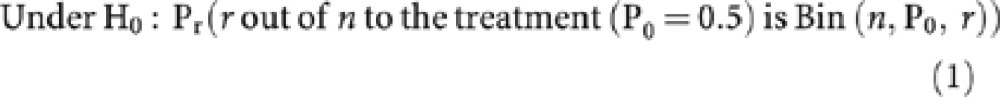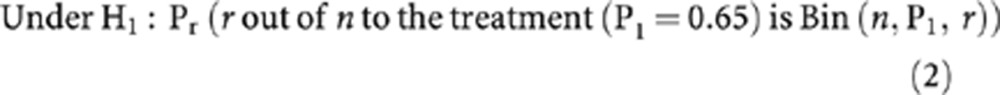The term Bin(n, P₁, r) states that responses are from a Binomial distribution with parameters P₁, the probability of a response, r, the number of responders to the new treatment and n, the sample size.

The approach to computing (1) and (2) is shown below in (3) and (4) respectively, as described by Chow et al (2003).

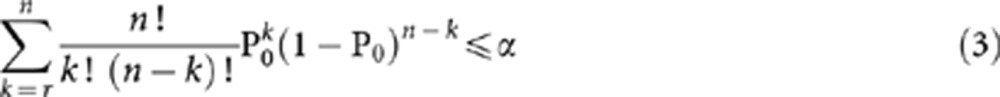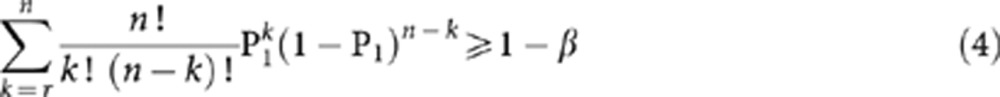From Equation 3, we generate the observed significance level (α) and this value is compared against the pre-specified significance level (i.e., 5 or 10%). We also require values from Equation 4 to be ⩾80%. Sample sizes are then chosen when the observed α levels are <5% (or 10%) and when the power is ⩾80%.

Results

Table 1 uses a range of differences between P₀ and P₁ to show how sample size can vary if we accept a significance level or power that are not exactly equal to conventionally accepted levels. Interest is in whether there is a value of α that is not much larger than the usual specified level of 5 or 10%, or a value of power which is not much <80%, but where there is a reduction in sample size. Table 1 shows the exact α and power values compared with the tables from A’Hern (2001). In Table 1, we show only the first five solutions ordered by sample size where available, for sample sizes >20, for absolute differences between P₀ and P₁ ranging 10–30%. Smaller differences (i.e., <10%) are not considered clinically important in most trials. The value of α has been increased to a limit of 8% where the planned (target) α was 5% (target +3%). For a target α of 10%, the limit is 13%. The sample sizes are presented with power always ⩾77%. The exact α and power values are computed only when the sample size requirement is >20, because sample sizes <20 pose less of a problem in recruitment terms. A SAS macro is also provided (Appendix I), which can be used to derive sample sizes, power and α values for all possibilities of P₀ and P₁, but other software such as R can also be used. The SAS program requires the user to input ranges of P₀ and P₁ and also uses cut-offs of 0.08 for α (i.e., target α +3%) and 0.77 for power, which we consider as constituting a ‘small trade-off’. We illustrate the use of Table 1 using some examples. A Corresponding R function is also available in the Clinfun package written by Seshan (2012), see Appendix II.

Table 1. Sample sizes based on exact binomial test.

		Target α=5% (+3%)			Target α=10% (+3%)
P 0	P 1	Exact α (%)	Exact Power	r \ n	Exact α (%)	Exact Power	r \ n
0.10	0.20	4.53	80.81	13\78	7.99	80.41	10\61
		7.31	78.68	10\60	10.21	77.08	8\48
		7.99	80.41	10\61	11.19	79.09	8\49
		5.67	77.71	11\65	12.21	80.96	8\50
		6.21	79.42	11\66	10.30	81.49	9\56
		6.79	81.04	11\67	11.20	83.11	9\57
0.10	0.25	4.19	81.80	8\40	8.34	82.35	6\31
		7.32	79.74	6\30	11.18	81.56	5\26
		5.52	80.80	7\35	12.66	84.17	5\27
		6.28	83.16	7\36
		7.11	85.28	7\37
		8.00	87.18	7\38
0.10	0.30	3.33	80.65	6\25	9.81	83.54	4\18
		5.22	80.16	5\21			n<20
		6.21	83.55	5\22
		7.31	86.44	5\23
0.10	0.35	2.81	81.11	5\18	5.55	82.73	4\15
				n<20			n<20
0.15	0.25	4.33	80.42	22\101	8.88	80.54	16\75
		6.90	78.11	17\78	12.50	77.65	12\56
		7.61	79.90	17\79	11.74	78.94	13\61
		5.91	77.52	18\82	12.92	80.90	13\62
		6.53	79.30	18\83	10.00	78.18	14\65
		7.19	80.98	18\84	11.03	80.13	14\66
0.15	0.30	4.77	81.85	12\48	9.23	82.37	9\37
		5.79	77.59	10\39	11.52	77.98	7\28
		6.72	80.41	10\40	11.07	81.78	8\33
		7.74	82.95	10\41	12.67	84.42	8\34
		5.66	81.15	11\44
		6.51	83.53	11\45
0.15	0.35	4.85	81.79	8\28	9.99	83.71	6\22
		5.72	78.94	7\24	12.06	81.14	5\18
		6.95	82.66	7\25	11.89	86.91	6\23
0.15	0.40	3.68	84.15	7\21	7.90	83.34	5\16
		6.17	78.27	5\15			n<20
		7.91	83.34	5\16
		5.37	83.71	6\19
		6.73	87.44	6\20
0.15	0.45	4.67	83.28	5\14	6.94	80.88	4\11
				n<20			n<20
0.20	0.30	4.86	80.72	31\116	9.84	81.71	23\88
		7.99	77.93	23\86	12.03	77.63	18\68
		7.70	78.80	24\90	11.56	78.54	19\72
		6.67	77.72	25\93	12.83	80.62	19\73
		7.42	79.62	25\94	11.10	79.40	20\76
		6.44	78.58	26\97	12.30	81.38	20\77
0.20	0.35	4.32	80.64	17\56	8.57	81.96	13\44
		7.33	79.08	13\43	12.87	77.53	9\30
		6.15	78.75	14\46	10.68	77.01	10\33
		7.21	81.57	14\47	12.54	80.45	10\34
		5.17	78.45	15\49	10.46	79.92	11\37
		6.07	81.22	15\50	12.19	82.91	11\38
0.20	0.40	3.43	80.48	12\35	8.91	80.80	8\24
		5.92	77.45	9\26	10.85	79.98	7\21
		7.37	81.61	9\27
		6.11	82.37	10\30
		7.46	85.66	10\31
		5.08	83.10	11\33
0.20	0.45	4.30	80.29	8\21	8.16	80.24	6\16
		5.13	77.42	7\18			n<20
		6.76	82.73	7\19
0.20	0.50	3.76	83.80	7\17	7.25	80.61	5\12
				n<20			n<20
0.25	0.35	4.93	80.39	41\129	9.93	80.91	30\96
		7.80	78.79	32\101	12.65	77.11	23\73
		7.31	78.75	33\104	11.81	77.03	24\76
		6.85	78.72	34\107	12.39	79.28	25\80
		7.68	80.64	34\108	11.58	79.18	26\83
		6.43	78.69	35\110	12.94	81.32	26\84
0.25	0.40	4.28	80.31	22\62	8.96	80.78	16\46
		7.53	77.51	16\45	11.09	77.83	13\37
		7.04	78.56	17\48	10.32	78.88	14\40
		6.59	79.54	18\51	12.22	82.19	14\41
		7.81	82.45	18\52	11.35	82.97	15\44
		5.17	77.41	19\53
0.25	0.45	4.61	81.67	14\36	9.08	80.64	10\26
		6.79	78.65	11\28	12.99	80.29	8\21
		6.44	81.13	12\31	12.13	82.70	9\24
		6.10	83.26	13\34
		7.56	86.56	13\35
		5.77
0.25	0.50	4.00	83.65	11\26	7.74	82.03	8\19
		7.96	77.28	7\16			n<20
		7.75	82.04	8\19
		5.61	80.83	9\21
		7.46	85.69	9\22
		5.47	84.63	10\24
0.25	0.55	4.02	81.65	8\17	8.02	82.12	6\13
				n<20			n<20
0.30	0.40	4.73	80.67	53\144	9.00	80.13	39\107
		7.98	77.06	38\103	11.99	77.04	30\82
		7.96	77.94	39\106	11.93	77.98	31\85
		7.94	78.79	40\109	11.88	78.88	32\88
		6.99	77.41	41\111	10.43	77.33	33\90
		7.92	79.59	41\112	11.82	79.73	33\91
0.30	0.45	4.66	81.46	27\67	8.48	80.26	20\50
		7.17	78.99	21\52	11.51	78.58	16\40
		6.05	77.74	22\54	11.69	80.84	17\43
		7.31	81.04	22\55	11.83	82.83	18\46
		6.20	79.87	23\57	10.02	81.54	19\48
		7.44	82.88	23\58	11.94	84.60	19\49
0.30	0.50	4.99	83.16	17\39	8.44	81.92	13\30
		7.98	77.90	12\27	12.01	79.76	10\23
		6.52	77.09	13\29	12.53	83.65	11\26
		6.94	81.15	14\32	10.28	82.75	12\28
		5.71	80.42	15\34	12.94	86.75	12\29
		7.31	84.47	15\35
0.30	0.55	4.42	81.73	12\25	8.39	81.58	9\19
		6.76	81.59	10\21			n<20
		5.46	81.64	11\23
		7.42	86.59	11\24
0.30	0.60	4.02	80.10	9\17	9.32	84.98	7\14
				n<20			n<20
0.35	0.45	4.86	80.00	62\148	9.39	80.17	46\111
		7.54	77.01	47\112	12.87	78.37	36\87
		7.94	78.68	48\115	11.80	77.47	37\89
		7.30	77.93	49\117	12.40	79.27	38\92
		6.70	77.18	50\119	11.38	78.41	39\94
		7.68	79.52	50\120	12.99	80.93	39\95
0.35	0.50	4.60	80.19	31\68	9.77	80.41	22\49
		7.87	79.49	24\53	12.39	78.52	18\40
		7.07	79.06	25\55	11.07	77.96	19\42
		6.35	78.65	26\57	12.15	81.44	20\45
		7.78	82.09	26\58	10.89	80.92	21\47
		5.70	78.25	27\59
0.35	0.55	4.80	83.09	20\41	9.77	81.99	14\29
		5.78	77.28	16\32	12.54	81.73	12\25
		7.68	82.32	16\33	11.06	81.85	13\27
		5.14	77.64	17\34
		6.82	82.51	17\35
		6.06	82.69	18\37
0.35	0.60	3.77	80.06	14\26	9.99	80.10	9\17
		7.72	82.56	11\21			n<20
		6.82	83.64	12\23
		6.04	84.62	13\25
		5.36	85.53	14\27
		7.36	89.75	14\28
0.35	0.65	3.46	81.45	11\19	7.53	81.64	8\14
		7.53	81.64	8\14
		6.71	84.06	9\16			n<20
		5.97	86.09	10\18
		5.32	87.82	11\20
		7.72	92.28	11\21
0.40	0.50	4.79	80.92	74\158	9.87	80.24	52\112
		7.75	77.21	54\115	12.48	77.21	41\88
		7.39	77.02	55\117	12.51	79.40	44\95
		7.81	79.24	57\122	11.92	79.16	45\97
		7.46	78.05	58\124	11.36	78.92	46\99
		7.12	78.86	59\126	10.82	78.69	47\101
0.40	0.55	4.37	80.17	36\71	9.78	80.33	25\50
		6.61	77.24	28\55	12.98	78.70	20\40
		6.27	77.64	29\57	12.25	79.04	21\42
		7.87	81.54	29\58	11.57	79.37	22\44
		5.96	78.03	30\59	10.93	79.70	23\46
		7.46	81.83	30\60	10.34	80.02	24\48
0.40	0.60	3.75	80.31	23\42	9.70	82.46	16\30
		6.77	78.06	17\31	12.07	77.20	12\22
		6.45	79.41	18\33	11.43	78.70	13\24
		6.15	80.65	19\35	10.82	80.07	14\26
		5.86	81.80	20\37	10.25	81.32	15\28
		7.84	86.24	20\38	12.84	87.16	16\31
0.40	0.65	4.99	85.72	16\28	8.84	81.45	11\19
		5.51	79.16	13\22			n<20
		5.35	81.67	14\24
		7.78	87.46	14\25
		5.18	83.84	15\26
		7.43	88.94	15\27
0.40	0.70	3.50	81.80	12\19	9.76	83.46	8\13
				n<20			n<20
0.45	0.55	4.95	80.03	80\154	9.90	82.20	62\121
		7.10	77.07	63\121	12.13	77.32	47\91
		7.01	77.44	64\123	11.96	77.70	48\93
		6.93	77.79	65\125	11.80	78.07	49\95
		6.85	78.14	66\127	11.64	78.43	50\97
		6.77	78.48	67\129	11.49	78.78	51\99
0.45	0.60	4.66	80.39	39\70	9.98	82.29	29\53
		7.79	77.87	29\52	10.17	77.77	25\45
		7.78	79.06	30\54	10.14	79.02	26\47
		7.76	80.18	31\56	12.91	83.47	26\48
		7.74	81.23	32\58	10.09	80.18	27\49
		6.01	78.05	33\59	12.79	84.38	27\50
0.45	0.65	4.15	81.82	25\42	9.92	82.07	17\29
		7.14	78.02	18\30	9.59	77.11	15\25
		7.29	80.43	19\32	9.78	79.76	16\27
		7.42	82.57	20\34
		5.36	78.91	21\35
		7.52	84.46	21\36
0.45	0.70	4.39	81.05	16\25	8.71	81.80	12\19
		5.80	77.23	13\20			n<20
		6.17	81.35	14\22
		6.48	84.72	15\24
		6.74	87.47	16\26
0.45	0.75	4.86	81.03	11\16	7.69	85.16	10\15
				n<20			n<20
0.50	0.60	4.72	80.56	90\158	9.57	80.45	65\115
		7.98	77.28	65\114	12.31	77.52	51\90
		7.27	77.73	69\121	12.57	78.52	52\92
		7.44	78.63	70\123	12.82	79.48	53\94
		7.61	79.49	71\125	11.14	77.92	55\97
		6.48	77.28	72\126	11.38	78.88	56\99
0.50	0.65	4.55	80.20	42\69	8.44	80.32	32\53
		6.68	77.27	33\54	12.79	77.49	23\38
		7.04	79.30	34\56	11.10	78.50	26\43
		7.40	81.16	35\58	11.63	80.60	27\45
		5.87	78.32	36\59	12.15	82.51	28\47
		7.75	82.86	36\60	12.64	84.22	29\49
0.50	0.70	4.94	80.70	24\37	9.24	80.86	18\28
		6.80	77.08	19\29	10.50	77.09	15\23
		7.48	80.76	20\31	11.48	81.06	16\25
		5.51	77.17	21\32	12.39	84.34	17\27
		6.07	80.71	22\34
		6.62	83.73	23\36
0.50	0.75	4.65	80.36	16\23	8.35	82.51	13\19
		5.77	78.58	14\20			n<20
		6.69	83.85	15\22
0.50	0.80	4.81	86.70	13\18	8.97	87.01	10\14
				n<20			n<20
0.55	0.65	4.97	80.45	93\150	9.44	80.35	69\112
		7.47	77.77	72\116	12.95	78.02	53\86
		7.92	79.21	73\118	11.81	77.31	55\89
		6.83	77.15	74\119	12.50	78.98	56\91
		7.25	78.65	75\121	11.40	78.30	58\94
		7.68	80.06	76\123	12.07	79.88	59\96
0.55	0.70	4.52	82.01	46\70	9.48	81.00	32\49
		7.65	78.22	33\50	11.96	77.45	25\38
		6.87	78.44	35\53	10.67	77.62	27\41
		7.64	81.25	36\55	11.84	80.81	28\43
		6.17	78.66	37\56	10.59	80.90	30\46
		6.86	81.39	38\58	11.65	83.59	31\48
0.55	0.75	4.26	80.59	26\37	9.12	83.36	20\29
		7.74	78.59	19\27	12.99	78.58	14\20
		6.94	80.34	21\30	11.52	80.37	16\23
		5.22	77.10	22\31	10.24	81.95	18\26
		6.23	81.90	23\33	11.87	86.15	19\28
		7.29	85.79	24\35
0.55	0.80	3.64	81.10	18\24	7.77	83.69	14\19
		7.77	83.69	14\19			n<20
		5.53	80.42	15\20
		7.05	86.70	16\22
		5.10	84.02	17\23
0.55	0.85	4.24	82.26	12\15	9.95	82.01	8\10
							n<20

The value of r denotes the number of responders required. Comparison with the numbers in bold shows the potential saving in sample sizes

The first entry of each P₀ and P₁ row (i.e., in bold) refers to the sample size from A’Hern (2001), which is also produced from software.

Example 1: single-arm phase II study

Aogi et al (2011) report a single-arm trial designed to detect a small difference of 10% in Japanese breast cancer patients. We use the same parameters in the context of a single-arm trial with P₀=10% and P₁=20%, α=5% (one sided) and power=80% to demonstrate the impact of trading-off type I and II error rates. There is no exact solution for this design. Fleming approximation using the formulae as presented in Machin et al (2009) gives the solution as sample size n=69 and number of response r=12, which (based on exact method) is actually coming from exact α=4% and exact power=75.04%. The A’Hern method in the sample-size software (Machin et al, 2009) gives the solution to the same problem as 13 out of 78, which actually come from α=4.53% and power=80.81% (Table 1, first row entries in bold).

Further examination of Table 1 shows alternative sample sizes obtained by relaxing α and power (savings in sample sizes are shown by comparing the bold figures in the first row with the sample sizes immediately below), and also for differences >10%. By accepting α=5.67% and power=77.7%, both of which are reasonably close to the specified levels of 5 and 80%, and the solution is 11 out of 65, which is smaller than Fleming (12 out of 69) but the power is also higher. Compared with A’Hern, the sample size 78, there is a saving of 13. This means that the chance of declaring the new agent as being beneficial when in reality it is not has only increased by 1.14 (from 4.53% to 5.67%) percentage points, and power has decreased by 3.10 percentage points. On the other hand, the increase of α is only 0.67% when compared with the conventional 5%. This could be considered worthwhile in relation to the potential saving in financial costs and accrual time, as well as exposing fewer patients to a novel agent that may have serious side effects.

Example 2: randomised controlled phase II study (1 : 1 allocation)

We take P₀=30% and P₁=40% and specify α=10% and power=80%. Again, there is no exact solution for this when α=10% and power=80%. Sample-size software and tables from A’Hern (2001) give the solution as n=107 and r=39, which has an exact α=9.00% and power=80.13%. However, by accepting α=10.43% and power=77.33% (Table 1), both of which are reasonably close to the specified levels of 10 and 80%, the sample size could be 90 patients in one treatment group (instead of 107). Because there are an equal number of patients in the other treatment group (which could be another new treatment or a control group), there would be a total saving of 34 patients. The increase in α has therefore been 1.43 percentage points (and only 0.43 percentage points from the usual α of 10%); and power has decreased by only 2.8 percentage points. If the same trial had a 2 : 1 allocation instead of a 1 : 1 (in favour of the new intervention group), the saving would be 25 patients (17 in the experimental plus roughly half the number in the control). It should be noted that although this approach to randomised studies was common, a more efficient approach is to have a design that involves a direct comparison of the two treatment groups (Rubinstein et al, 2005; Jung, 2008).

A practical example

We extend the trade-off approach to an example of a phase II randomised trial in lung cancer patients using a two-stage design, which was stopped for lack of efficacy after stage I. A Simon’s two-stage minimax design with P₀=50% and P₁=65%, α=10% and power=90% using the software by Machin et al (2009) gives the required sample size at stage 1 of 20 out of 40, and total sample size was 42 out of 72 in each intervention arm. Therefore, total sample size was 144 due to randomisation. Our exact calculation reveals that the actual α was 9.7% and power was 90.4% in the sample-size calculation. The trial had major recruitment problems and it could have been designed with α=10.4% and power=88.8% to give a stage 1 sample size of 13 out of 27 and stage II sample size of 38 out of 65, saving 26 patients at stage I and 14 patients in total. It is worth noting that both the original design (n=144) and the alternative design (n=130) have probabilities of early termination under the null hypothesis of <50%.

Discussion

There are an increasing number of early phase II trials being conducted, given the availability of many new therapies, which are used on their own or in combination with the standard treatments. Furthermore, there is an emerging preference for randomised controlled phase II studies, which increases the total trial size (Lee and Feng, 2005; Cannistra, 2009). Phase II trials need to be conducted as quickly as possible with the minimum of resources, in order to reject apparently ineffective interventions early on in drug development and move on to other treatments, or to further investigate those that look promising. Traditionally, phase II trials are designed on the basis of the active (new) treatment arm only, in that the sample size is based on the expected treatment effect in that arm. If there is a control arm, the number of patients may be taken to be the same as or half of that in the active arm, depending on 1 : 1 or 2 : 1 allocation, respectively.

The financial costs of conducting a clinical trial have increased, particularly in light of the current regulations and governance, so that it can take many months (>6) to set up a study (Hackshaw et al, 2008). Having a small study, where acceptable, can therefore have clear benefits in terms of shorter trial duration, which is associated with lower costs. Another benefit is that fewer patients are exposed to a novel agent that has serious side effects but is eventually shown to be ineffective. Minimising sample size is particularly important for rare disorders where recruiting even 10–15 patients could take several months.

When designing studies, most researchers use established values for α of 5 or 10% and power of 80% (occasionally 90%). In our paper, we show that by allowing slightly higher α and lower power for these exact tests, there could be a material reduction in sample size, particularly for studies with say <50 patients. We believe that such an approach is useful for two reasons. First, phase II trials are usually only meant to provide preliminary evidence of efficacy, therefore relaxing the design parameters should not be of great concern. Second, the conventional values of α=5% and power 80% were somewhat arbitrary when originally stipulated; they were not selected on the basis of scientific principles (α=5% was judged sufficiently low and power=80% as sufficiently high). However, these values were primarily meant for large confirmatory studies, but researchers and reviewers involved in grant applications have not often relaxed them for exploratory studies, such as phase II trials. Recently, it has become more common to have values of α of ⩾10% in cancer trials (Rubinstein et al, 2005). Therefore, accepting α of 7% instead of 5%, or power of 77% instead of 80%, could be considered a worthwhile trade-off for having a smaller study, particularly when the largest savings are made with randomised controlled phase II trials.

Our approach to sizing studies is not just limited to single-stage designs, but can also be extended to two-stage (Simon, 1989) and other n-stage designs where exact methods are used. In some two-stage design, trade-offs in the expected sample size are considered for smaller overall sample sizes (Jung et al, 2001). By compromising α and power in addition to the expected sample size, it is possible that savings in sample size are even greater. However, additional complexities such as the probability of early termination might also be important when considering any trade-off.

The implications of trading-off type I and II errors is that the risk of a false-positive or -negative may be slightly above or below the conventional 5% and 80%, respectively. The specific type of trade-off is likely to be based on feasibility and may vary from trial to trial. However, in phase II trials, which are often about finding preliminary evidence of effect, a trade-off in either direction may be possible. It is important to point out that such a trade-off does not influence the size of the treatment benefit.

A limitation of our suggested approach is that the final result ideally needs to be considered in relation to the α level used in the sample-size calculation, which is not a round number such as 5% or 10%. However, even when sample sizes come from A’Hern (2001) or software, the interpretation of the primary result is based on α=5%, even though the actual value might be 4.5%. Moreover, reported P-values such as ‘0.052’ or ‘0.057’ (in the context of phase III trials) are not readily dismissed for lack of effect (Hackshaw and Kirkwood, 2011), and therefore powering a trial with non-standard α and power may also be considered a reasonable approach for phase II study designs. Nevertheless, the decision on whether or not to investigate a new treatment further should not be based on a single numerical cut-off for α, but perhaps on consideration of several pieces of information, including other clinically important efficacy end points, safety and accrual rates. It is often the case that a smaller treatment effect is observed, and precision would be lost by having a study that is too small, making it difficult to determine whether to investigate the new therapy further or not. We therefore do not recommend that sample sizes be reduced to <20 patients per treatment group.

In conclusion, it is worthwhile examining a fuller range of sample sizes when using exact methods for single-stage phase II trials, so that the smallest acceptable sample size could be chosen after allowing a slightly higher α level (error rate) than the conventional 5 or 10%, and lower power than the nominal 80%. This can lead to benefits such as shorter study duration and lower financial costs, which are key considerations when investigating treatments for uncommon disorders or new agents in proof-of-concept studies, and this could make a project proposal being considered for funding more attractive when peer-reviewed. When the decision rule is based on the experimental arm alone, but the study is a randomised parallel group design, the differences in sample size between the approaches described here and those presented by A’Hern can be up to 25% lower after allowing for small trade-offs in α and power.

Appendix I

SAS macro for sample sizes for single-stage phase II designs based on exact binomial test

Appendix II

R Function in package Clinfun

Example function call: ph2single(P₀, P₁, alpha, beta and n)

Where,

P0, unacceptable response rate

P1, response rate that is desirable

Alpha, threshold for the probability of declaring drug desirable under P0

Beta, threshold for the probability of rejecting the drug under P1

n: number of designs with given alpha and beta

The ph2single wall gives values of: n, r, alpha and the type I and type II errors.