Abstract
We studied how similar postsynaptic responses are maintained in the face of interindividual variability in the number of presynaptic neurons. In the stomatogastric ganglion of the lobster, Homarus americanus, the pyloric (PY) neurons exist in variable numbers across animals. We show that each individual fiber of the stomach muscles innervated by PY neurons received synaptic input from all neurons present. We performed intracellular recordings of excitatory junction potentials (EJPs) in the muscle fibers to determine the consequences of differences in the number of motor neurons. Despite the variability in neuron number, the compound electrical response of muscle fibers to natural bursting input was similar across individuals. The similarity of total synaptic activation was not due to differences in the spiking activity of individual motor neurons across animals with different numbers of PY neurons. The amplitude of a unitary EJP in response to a single spike in a single motor neuron also did not depend on the number of PY neurons present. Consequently, the compound EJP in response to a single stimulus that activated all motor axons present was larger in individuals with more PY neurons. However, when axons were stimulated with trains of pulses mimicking bursting activity, EJPs facilitated more in individuals with fewer PY neurons. After a few stimuli, this resulted in depolarizations similar to the ones in individuals with more PY neurons. We interpret our findings as evidence that compensatory or homeostatic regulatory mechanisms can act on short-term synaptic dynamics instead of absolute synaptic strength.
Introduction
Homeostatic regulation of neuronal activity encompasses various cellular mechanisms that lend stability to neural and neuromuscular function in the face of changing internal states and experience, for example, during development and learning (Davis and Bezprozvanny, 2001; Marder and Prinz, 2002; Turrigiano and Nelson, 2004; Pérez-Otaño and Ehlers, 2005; Davis, 2006; Marder and Goaillard, 2006; Turrigiano, 2007, 2011; Pozo and Goda, 2010). The central tenet is that set-point levels of activity are maintained through modulation of synaptic efficacy and membrane excitability, often involving activity-dependent feedback mechanisms. The cellular and molecular loci of regulation are diverse across different systems and contexts (Turrigiano, 2011), as are the regulatory set-points, which include postsynaptic depolarization (Paradis et al., 2001), firing rate (Turrigiano and Nelson, 2004), or activity type (Turrigiano et al., 1994; Soto-Treviño et al., 2001; Bucher et al., 2005).
Homeostatic regulation of synapses has been described in two contexts. First, in a connection between two cells, synaptic strength itself can be kept constant in the face of perturbations; for example, to ensure stable depolarizations at the Drosophila neuromuscular junction (NMJ) (Davis and Bezprozvanny, 2001; Paradis et al., 2001; Davis, 2006). Second, synaptic strength can be adjusted to compensate for other changes in excitability. Thus, scaling of synaptic strength across a population of presynaptic inputs, as well as changes in the balance of excitatory and inhibitory inputs, can ensure stable overall activation of the postsynaptic neuron (Turrigiano et al., 1998; Marder and Prinz, 2002; Turrigiano, 2007). However, one aspect of homeostatic regulation of synaptic strength is often neglected. During repetitive activity, postsynaptic depolarization is a compound response shaped by summation and short-term synaptic dynamics (Regehr and Stevens, 2001; Zucker and Regehr, 2002; Abbott and Regehr, 2004). Due to facilitation and depression, the effective strength of a synaptic connection during highly repetitive activity like bursting stabilizes at a level dependent on the rate of presynaptic activity (Nadim et al., 1999; Nadim and Manor, 2000). Therefore, responses to single presynaptic activation may not be an appropriate measure of synaptic strength as a target value for regulatory mechanisms. On the flipside, experimental findings of synaptic homeostasis at the level of single responses do not necessarily translate into constant responses to repetitive input, as short-term synaptic dynamics and summation may differ (Pulver et al., 2005; Davis, 2006).
While homeostatic regulation of synaptic strength is usually assessed with experimental perturbations that disrupt normal activity, here we make use of naturally occurring variability across individuals to identify compensatory synaptic mechanisms. We recently described that pyloric (PY) neurons, a group of simultaneously active and continuously bursting motor neurons in the stomatogastric nervous system (STNS) of the lobster, Homarus americanus, are present in variable numbers (Bucher et al., 2007). Thus, target muscles are innervated by different numbers of motor axons across individuals. We show that compound electrical muscle responses to bursting input are not dependent on the number of PY neurons present. This constancy is not achieved through differences in individual synaptic strength, but through differences in the magnitude of synaptic enhancement.
Materials and Methods
Experimental preparation.
Experiments were conducted on the STNS and stomach muscles of adult lobsters (∼500 g), H. americanus, of either sex. Animals were shipped from Commercial Lobster and kept in flow-through aerated filtered sea water tanks at 10−13°C. Animals were anesthetized in ice for 40 min before dissection. Parts of the STNS and musculature were dissected from the stomach and transferred into a transparent Sylgard-lined (Dow Corning) dish in physiological saline. The saline composition was as follows (in mm): 479 NaCl, 12.8 KCl, 13.7 CaCl2, 10 MgSO4, 3.9 Na2SO4, and 10 HEPES, pH 7.4–7.5.
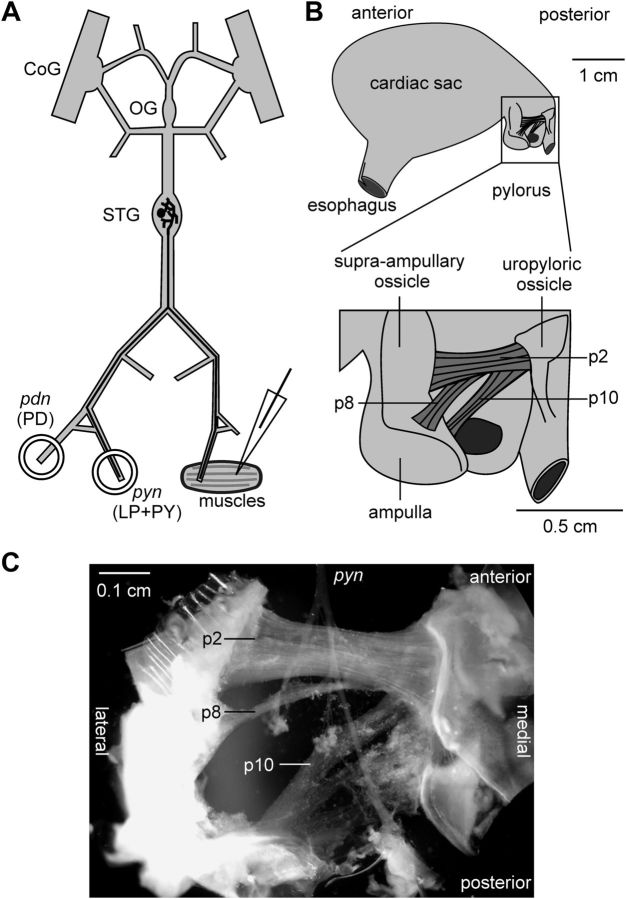
In a subset of experiments, all muscles were discarded and only the STNS, including the paired commissural ganglia, the esophageal ganglion, and the stomatogastric ganglion (STG), was used. In these experiments, we recorded PY neurons intracellularly from the soma during spontaneous rhythmic activity. For these recordings, the perineural sheath around the STG was carefully removed. In all other experiments, the STNS was kept connected to the posterior part of the stomach (Fig. 1A). The pylorus was cut along both the dorsal and ventral midlines, and the halves were pinned with the stomach lining facing upward. The stomach lining and connective tissues were carefully removed to expose the pyloric muscles p2, p8, and p10 (Fig. 1B), all of which are innervated by the PY neurons (Maynard and Dando, 1974). Because the motor nerves run on top of these muscles (Fig. 1C), this technique allowed us to record intracellularly from the underside of these muscles without damaging innervations.
Figure 1.
The nerve-muscle preparation of the stomatogastric system used in this study. A, Schematic of the STNS and muscle indicating intracellular and extracellular recording sites. B, Schematic of the lobster stomach showing the location of the PY-innervated muscles p2, p8, and p10 in the pylorus. C, Photomicrograph of the surgically isolated muscles with intact innervation. CoG, Commissural ganglion; OG, oesophageal ganglion; PD, pyloric dilator.
Electrophysiological recording and stimulation.
During recordings, preparations were continuously superfused with cooled saline (12°C). Extracellular recordings of PY axon activity were obtained by building petroleum jelly wells (diameter ≈ 1 mm) around motor nerves and placing one lead of a pair of stainless steel wire electrodes into a well, and the other lead into the bath. Signals were differentially amplified and filtered using an A-M Systems AC amplifier (model 1700). The same electrodes were used for axon stimulations. Pulses of 0.5 ms duration and varying amplitudes were delivered to the nerves using an isolated pulse stimulator (A-M Systems, model 2100). In some experiments, custom-made suction electrodes attached to the cut ends of nerves were used for axon stimulations instead. Intracellular recordings of PY neuron somata, as well as intracellular recordings of excitatory junction potentials in muscle fibers, were achieved using sharp glass microelectrodes filled with 0.6 m K2SO4 and 20 mm KCl. Electrode holders and headstages were mounted on Leica mechanical micromanipulators. Electrode resistances were between 10 and 20 MΩ. Signals were amplified and recorded using Axoclamp 2B amplifiers (Molecular Devices), micro 1401 digitizer boards (Cambridge Electronic Design), and Spike 2 acquisition software (versions 6 and 7, Cambridge Electronic Design).
Photoablations.
In soma mapping experiments to count PY cells, neurons were sequentially photoablated to remove their rhythmic spiking activity from peripheral motor nerve recordings. PY somata were dye injected using glass microelectrodes with their tips backfilled with Alexa Fluor 568 hydrazide (sodium salt, 10 mm in 200 mm KCl; Invitrogen). Dye was passed by applying −10 to −20 nA direct current for 5–20 min. Subsequently, the STG was illuminated with a 20 mW green laser (wavelength: 532 nm; Beta Electronics, model MGM20), and Kodak gel filters attached to the eyepieces of the rig microscope allowed visual inspection of the cell morphology and completeness of the fill. Sufficiently filled neurons continued to be recorded intracellularly and illuminated for 5–30 min, until the membrane potential broke down and the cell morphology clearly deteriorated.
Data analysis.
Electrophysiological recordings were analyzed using custom programs written in the Spike2 script language (version 6 and 7). Secondary analyses and statistical tests were performed using StatView (version 5, SAS Institute). Graphs were generated using StatView or Origin (version 6, Microcal Software), and final figure layout and labeling was done in CorelDraw (version 15, Corel). Statistical comparisons were one-way ANOVA with subsequent Fisher's PLSD post hoc tests, or paired t tests where appropriate. Data, unless otherwise indicated, are presented as combined box and scatter plots, showing single data points, median, first and third quartile, and 10th and 90th percentile. Statistical significance is indicated by asterisks.
Results
Individual muscle fibers received input from all PY neurons present in a preparation
The PY neurons are a set of motor neurons in the STG that form glutamatergic synapses on several constrictor muscles of the pylorus (Lingle, 1980). In H. americanus, their number can vary between 3 and 7 across animals (Bucher et al., 2007). Therefore, differences in numbers of neurons potentially have to be compensated to ensure similar postsynaptic activation. PY neurons, like most of the neurons in the STG, serve a dual function as parts of a central pattern generating network and as motor neurons (Marder and Bucher, 2007). They innervate constrictor muscles of the pylorus, named p2, p8, and p10 (Maynard and Dando, 1974). Figure 1B shows a schematic of the anatomical location of these muscles and Figure 1C shows a photomicrograph of the muscle preparation along with the pyloric nerve (pyn) containing the PY neuron axons. Due to their separate anterolateral insertion sites, it was straightforward to distinguish the different muscles. Pyloric muscles are slowly contracting and do not generate action potentials (Govind et al., 1975; Jahromi and Govind, 1976; Hoyle, 1983; Thuma et al., 2007). Figure 2 shows intracellular muscle fiber recordings of compound excitatory junction potentials (EJPs) during rhythmic pyloric activity in the semi-intact STNS-muscle preparation. As a reference, we simultaneously recorded the triphasic pyloric rhythm extracellularly from the motor nerves. Bursts of the pyloric dilator neurons recorded from the pyloric dilator nerve (pdn) were followed by bursts of the pyloric (LP) neuron, and the PY neurons, recorded from the pyn. All three examples show dual intracellular recordings from two different muscle fibers. Compound EJPs were similar between p2 and p8, with a sharp rising phase and relatively constant depolarization level over most of the burst input. In contrast, p10 showed different dynamics, with a very small initial response and slow rising phase, only peaking toward the end of the burst input.
Figure 2.
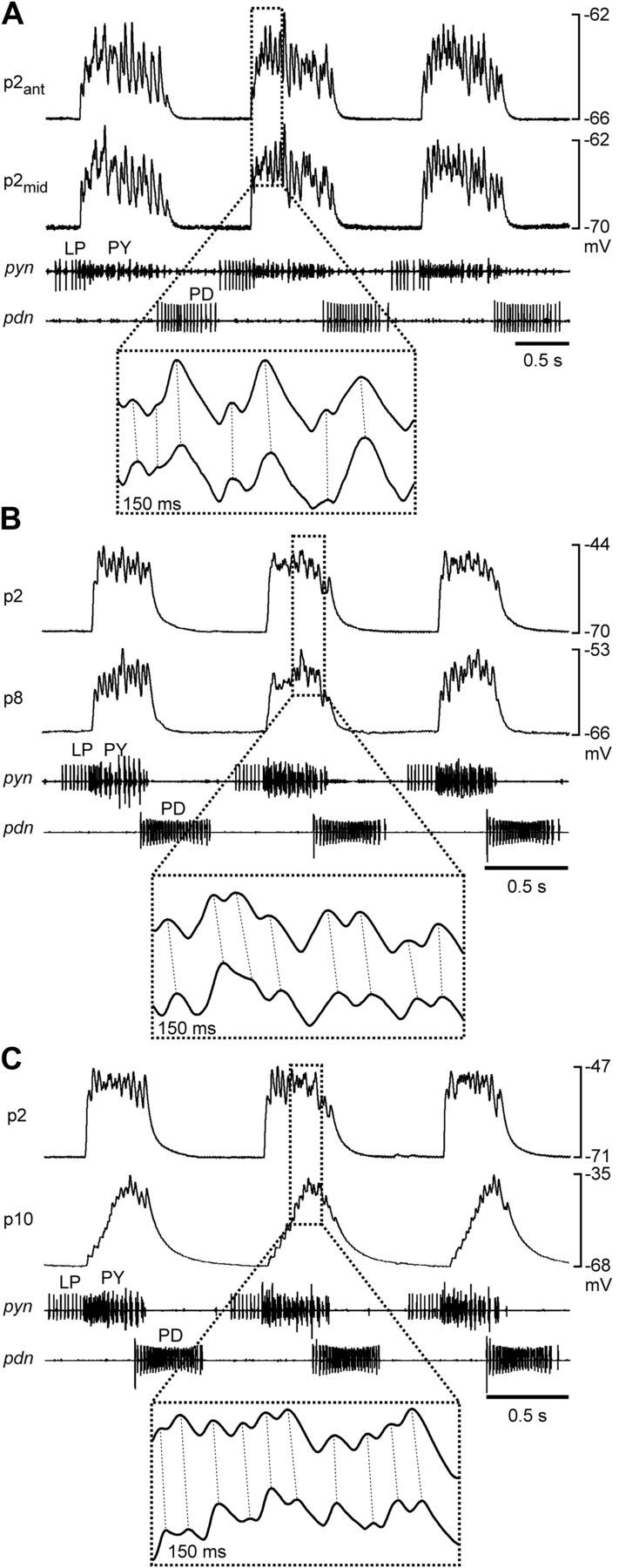
Electrical muscle responses during spontaneous rhythmic pyloric activity. A, Simultaneous recordings of two different fibers in the p2 muscle, one from the anterior end, and one from the middle. B, Simultaneous recordings of a p2 and a p8 fiber. C, Simultaneous recordings of a p2 and a p10 fiber. Extracellular nerve recordings in all panels show the phasing of the pyloric rhythm. The magnified insets indicate the 1:1 relationship of EJPs in the paired recordings (dashed lines).
One possible way how interindividual differences could be compensated is that individual muscle fibers are innervated by the same number of presynaptic axons across animals, independent of the total numbers of PY neurons present. Different PY neurons within one preparation do not produce synchronous spikes, and in the spiny lobster Panulirus interruptus, whole muscles are innervated by different subsets of PY neurons (Hartline et al., 1987). However, the inserts in Figure 2 show that there was a 1:1 correspondence between individual peaks in the intracellular recordings in all pairs (dashed lines), both within p2, and across different muscles. This correspondence was observed in all dual recordings in 39 preparations, with up to 14 different fiber pairs within each preparation. In p1, a pyloric muscle innervated by the LP neuron, adjacent fibers are strongly electrically coupled (Pulver et al., 2005). We therefore recorded from 1–3 adjacent pairs of fibers in the p2 muscles in 8 experiments. Depolarizing current (10 nA) injections into one fiber in no case elicited electrical responses in the adjacent fiber. We conclude that the correspondence between individual peaks in different fibers of the same muscle was not due to extensive electrical coupling between fibers. Because the different PY neurons within one preparation do not produce synchronous spikes, we conclude that each fiber in each muscle we recorded from was innervated by all PY axons present.
Electrical responses of muscle fibers to natural bursting input were independent of the number of motor axons present
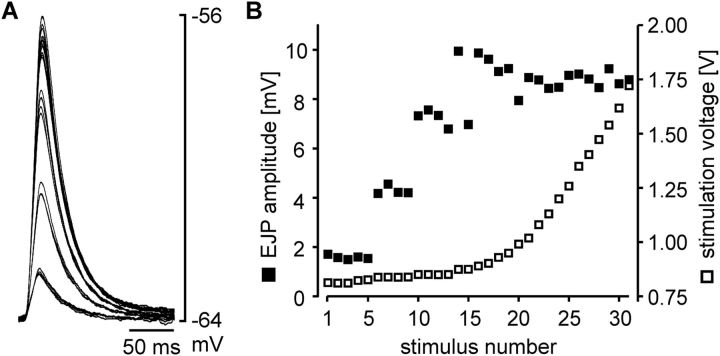
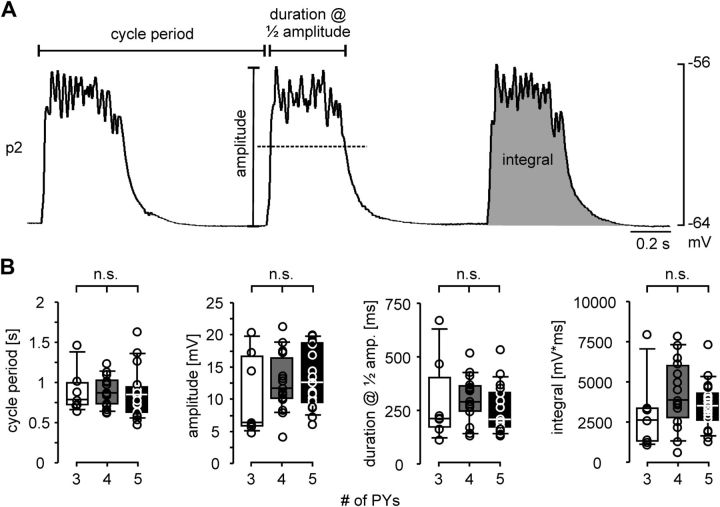
Recordings of p2 fibers showed larger unitary responses than p10 fibers, and p2 was easier to record from than p8, due to its larger size. Therefore, we conducted all experiments described in the following on p2. To compare the compound electrical muscle responses to natural rhythmic pyloric input across preparations with different numbers of PY neurons, we needed to establish the number of PY neurons in each preparation. After recording responses to rhythmic drive, we eliminated natural rhythmic inputs by cutting the pyn, which carries all PY axons. We then stimulated the distal part of the cut nerve with single pulses. Gradually increasing stimulus voltages successively recruited more PY axons, reflected in a stepwise increase in EJP amplitudes. Figure 3A shows overlaid EJPs from one preparation with 4 PY neurons, and Figure 3B shows a plot of stimulation voltage and EJP amplitudes at different successive stimuli from the same experiment. Despite some variability in EJP amplitude, distinct amplitude ranges were discernible in most experiments, and therefore allowed us to determine the number of PY neurons present. We discarded all experiments that showed ambiguous amplitude changes. In 39 experiments, we were able to determine the number of PY neurons as 3, 4, or 5. In only 4 experiments, >5 PY neurons were present. Because it was difficult to determine whether those preparations contained 6 or 7 PY neurons, and because the low incidence made statistical comparisons problematic, we discarded those data. Figure 4A shows an example recording of a p2 fiber during ongoing rhythmic pyloric activity, indicating the measurements we took to quantify the responses. We measured the cycle period between the beginning of one response to the beginning of the next, the amplitude as the difference between the voltage maximum within the response to a PY burst and the resting membrane potential, the duration of the response at half of the amplitude, and the voltage integral of each response. In each experiment, measurements were obtained as means of at least 13 consecutive cycles. Figure 4B shows the values across experiments for preparations with 3 (n = 7), 4 (n = 15), and 5 (n = 17) PY neurons. ANOVA revealed that none of the parameters were significantly different across preparations with different numbers of PY neurons (cycle period: p = 0.967; amplitude: p = 0.518; duration: p = 0.617; integral: p = 0.350). Because the responses of muscle fibers to bursting input were independent of the number of motor neurons innervating them, we concluded that some aspect of synapse function had to compensate for differences in number of motor neurons.
Figure 3.
Recruitment of presynaptic PY neuron axons in response to nerve stimulation with gradually increasing amplitude. A, Overlaid traces of EJP responses in p2. Gradually increasing stimulation amplitude led to stepwise increases in EJP amplitude, indicating successive recruitment of additional PY axons. B, Plot of EJP amplitude and stimulation voltage from the same experiment.
Figure 4.
Similarity of electrical responses of p2 fibers to spontaneous rhythmic pyloric input across preparations with different numbers of PY neurons. A, Intracellular p2 fiber recording, indicating the measurements taken. B, Box and scatter plots of the electrical response parameters indicated in A (3 PY neurons: n = 7; 4 PY neurons: n = 15; 5 PY neurons: n = 17). None of the parameters showed significant differences across preparations with different numbers of PY neurons.
Individual PY activity did not differ between preparations with different numbers of neurons
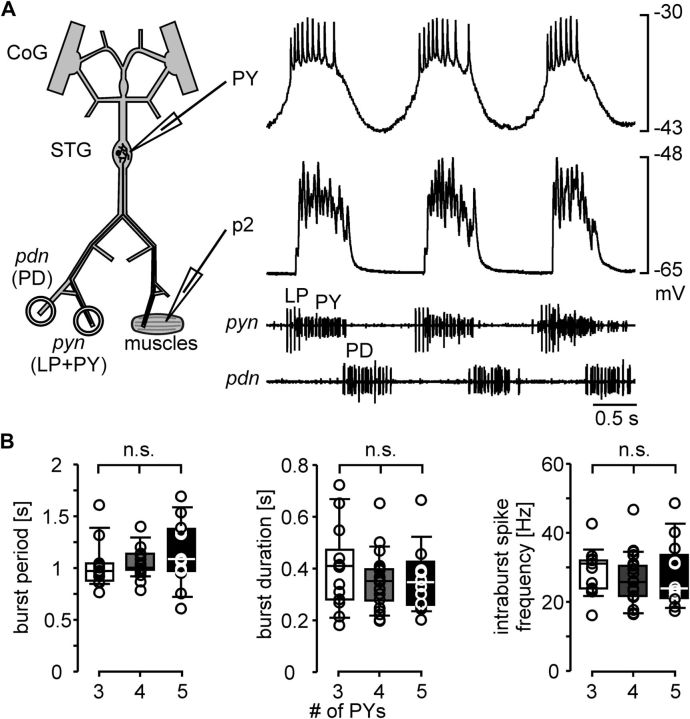
Different numbers of PY neurons could be compensated at the level of the efficacy of synaptic connections, or at the level of the neuronal activity patterns. Postsynaptic muscle responses could have been similar across preparations because individual PY neurons produced more action potentials in animals with fewer PY neurons. We performed intracellular recordings from PY neuron somata in the STG to determine their individual spike patterns. In 9 experiments, we recorded simultaneously from a PY neuron soma and a p2 fiber (Fig. 5A). We subsequently cut the pyn and determined the number of PY neurons with threshold stimulation, as shown in Figure 3. In other experiments, we counted PY neurons in a different way, in the absence of muscles. We recorded somata in the STG and identified as many neurons as possible and mapped their location, in the same manner originally used to determine the number of PY neurons in H. americanus (Bucher et al., 2007). However, because we frequently did not succeed in recording from all STG neurons within one preparation, we used dye killing to increase our success rate. To this end, we successively stained and photoablated PY neurons to remove their spiking activity from the extracellular pyn recording. We did this in as many PY neurons as necessary to determine the total number of PY neurons, either until all nerve activity ceased, or until we could distinguish the number of remaining PY neuron spikes with distinct amplitudes in the pyn recordings. In 5 experiments, we used both soma counting and muscle recordings with nerve stimulations in the same preparations, and verified that they yielded the same results. In 37 preparations, we could determine whether there were 3, 4, or 5 PY neurons present. We discarded data from all experiments in which it was ambiguous if there were 5 or more PY neurons. In the 46 preparations from combined soma/muscle recordings and photoablation experiments, we selected only those PY recordings that showed no obvious change in spike pattern and phasing in response to electrode penetration. We determined the mean burst period, mean burst duration, and mean intraburst spike frequency from a minimum of 5 cycles. When more than one PY neuron was recorded, we determined the means of these values across PY neurons within one preparation. Figure 5B shows the values across experiments for preparations with 3 (n = 13), 4 (n = 21), and 5 (n = 12) PY neurons. ANOVA revealed that none of the parameters were significantly different across preparations with different numbers of PY neurons (burst period: p = 0.327; burst duration: p = 0.511; intraburst spike frequency: p = 0.681). We conclude that different numbers of motor neurons were not compensated at the level of the neural pattern. A compensatory mechanism therefore had to reside at the level of the efficacy of the synaptic connections between PY neurons and muscle.
Figure 5.
Similarity of PY neuron activity across preparations during spontaneous pyloric rhythms. A, Simultaneous recordings of a PY neuron soma in the STG, a p2 muscle fiber, and two motor nerves during spontaneous rhythmic pyloric activity. B, Box and scatter plots of PY burst parameters (3 PY neurons: n = 13; 4 PY neurons: n = 21; 5 PY neurons: n = 12).
Unitary EJP amplitude and time course were independent of the number of PY neurons
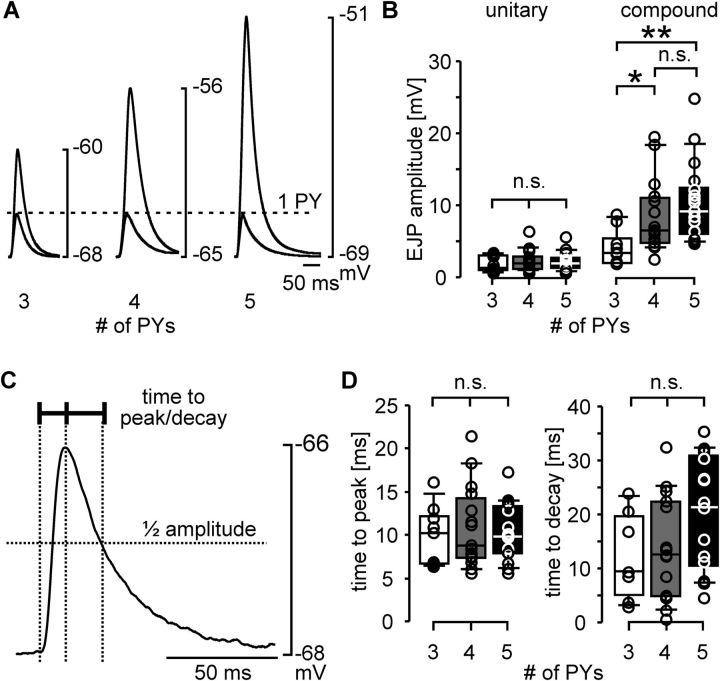
Postsynaptic muscle responses could have been similar across preparations because individual PY neuron action potentials produced larger unitary EJPs in animals with fewer PY neurons. In this case, the amplitude of a unitary response would differ across preparations with different numbers of PY neurons, but the amplitude of the compound EJP in response to simultaneous activation of all PY neurons present would be similar. We compared the EJP amplitudes in response to single nerve stimulation pulses across preparations. We did so both for the minimal stimulation voltages that elicited a unitary response, and for stimulation voltages that elicited the maximal compound response (as in Fig. 3). Figure 6A shows example recordings of both unitary and compound responses from preparations with 3, 4, and 5 PY neurons. Unitary response amplitudes were similar across these preparations (dashed line), whereas the compound EJP amplitudes were larger the more PY neurons were present. Figure 6B shows comparisons of EJP amplitudes across preparations with 3 (n = 9), 4 (n = 15), or 5 (n = 17) PY neurons. ANOVA revealed that unitary EJP amplitudes were not significantly different across preparations with different numbers of PY neurons (p = 0.785). In contrast, compound EJP amplitudes were different (p = 0.012). Fisher's PLSD post hoc tests showed that compound EJP amplitudes in preparations with 3 PY neurons were significantly smaller than those from preparations with 4 PY neurons (p = 0.040) and 5 PY neurons (p = 0.003). The difference in mean compound EJP amplitudes between preparations with 4 and 5 PY neurons was not statistically significant (p = 0.270). The similarity of unitary responses strongly suggests that different numbers of PY neurons were not compensated at the level of synaptic strength.
Figure 6.
EJP parameters across preparations with different numbers of PY neurons. A, Examples of unitary EJPs (one PY axon activated) and compound EJPs (all PY axons activated) in response to single stimulation pulses (3 PY neurons: n = 9; 4 PY neurons: n = 15; 5 PY neurons: n = 17). B, Box and scatter plots of EJP amplitudes in unitary and compound responses across preparations with different numbers of PY neurons. C, Unitary EJP indicating the measurements taken to describe the time course. D, Box and scatter plots of unitary EJP time course measurements from the same data shown in B. *p < 0.05, **p < 0.01.
Preparations with fewer PY neurons could also achieve similar depolarizations if EJPs during bursting input showed more summation, for example due to larger decay time constants of unitary EJPs. We therefore also compared the time course of unitary EJPs across preparations with different numbers of PY neurons. Because it was inconsistent if single or dual exponentials yielded better fits to determine time constants, we simply measured the time from the half amplitude voltage to the peak, and the time from the peak to decay to half the amplitude (Fig. 6C). Figure 6D shows the values for time to peak and time to decay across experiments. ANOVA revealed that neither parameter was significantly different across preparations with different numbers of PY neurons (time to peak: p = 0.802; time to decay: p = 0.087). We conclude that different numbers of PY neurons were unlikely to be compensated by differences in how EJPs summate during bursting input.
Change in compound EJP amplitude during train stimulations was dependent on the number of PY neurons
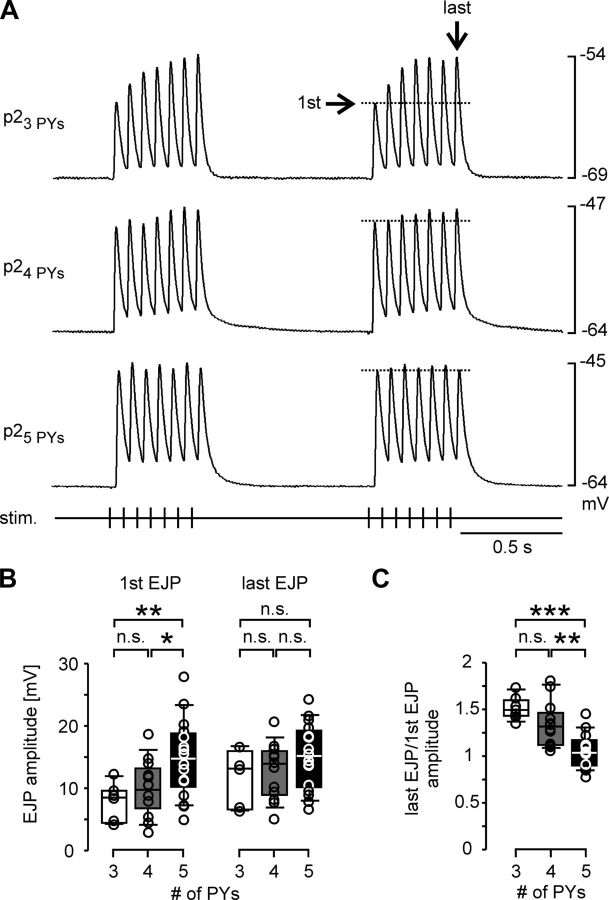
Because unitary EJP amplitude and time course were independent of the number of PY neurons present, similar responses during rhythmic activity could only be due to differences in the dynamics of how bursting input was integrated. We therefore activated the PY axons with repeating trains of stimuli to mimic bursting input. We used 400 ms trains at 15 Hz stimulation frequency (7 stimuli per train), and repeated the train 25 times with a period of 850 ms. We did not succeed in stimulating just one PY axon in these experiments because changing thresholds during trains led to stimulation failures, or activation of additional axons when the stimulation voltage was increased. We therefore only used stimulus voltages substantially larger than needed to activate all PY neurons in response to a single stimulus. The trajectory of compound EJP amplitudes over each train showed changes in the first few cycles, with a large degree of variability across preparations. However, toward the end of the stimulation, EJP changes were consistent in consecutive trains. We therefore only analyzed responses to the last train in each experiment. Figure 7A shows example recordings of the responses to the last two trains in preparations with different numbers of PY neurons. Note that the EJP trajectory looks different from that during natural bursting input. This is due to the fact that PY axons do not fire synchronously during natural bursts, while nerve stimulations activate different axons at the same time. In the preparation with 3 PY neurons, the compound EJP at the beginning of a train was relatively small, but EJP amplitude increased substantially within one train (dashed line). In the preparations with 4 and 5 PY neurons, initial compound EJP amplitudes were larger but did not increase as much toward the end of the train. Figure 7B shows the amplitudes for the first and last compound EJPs across preparations with 3 (n = 7), 4 (n = 12), and 5 (n = 16) PY neurons. As expected from the results shown in Figure 6, ANOVA revealed that the compound EJPs in response to the first stimulus in a train were different across preparations with different numbers of PY neurons (p = 0.009). Fisher's PLSD post hoc tests showed that the amplitudes in preparations with 5 PY neurons were larger than the ones in preparations with 3 (p = 0.005) or 4 (p = 0.027) PY neurons. Differences between preparations with 3 or 4 neurons were not significant (p = 0.311). In contrast to the differences between initial compound EJP amplitudes, the mean values for the amplitudes of the last (seventh) EJPs were more similar across preparations with different numbers of PY neurons, and differences were not statistically significant (ANOVA, p = 0.22). Therefore, despite the initially smaller depolarization in preparations with fewer PY neurons, compound responses to train stimulation reached similar levels of depolarizations. Figure 7C shows the mean ratios between the last and first compound EJP amplitudes. The increase in amplitude over the course of a train was significantly different across preparations with different numbers of PY neurons (ANOVA, p < 0.0001). Fisher's PLSD post hoc tests showed that amplitudes increased less in preparations with 5 PY neurons compared with those with 4 (p = 0.001) or 3 (p < 0.0001) PY neurons. The difference in ratios between preparations with 3 and 4 PY neurons was not significant (p = 0.076). Nevertheless, we conclude that differences in the number of PY neurons across preparations were at least partially compensated by differences in the short-term dynamics of signal integration in the muscle fibers.
Figure 7.
Short-term synaptic dynamics in compound EJP responses. A, Examples of responses to repeated train stimulations of all PY axons. Shown are the 24th and 25th trains in preparations with different numbers of PY neurons. The dashed line indicates the peak voltage of the first response in the train. B, Box and scatter plots of compound EJP amplitudes for the first and last pulses in the last (25th) train across preparations with different numbers of PY neurons (3 PY neurons: n = 7; 4 PY neurons: n = 12; 5 PY neurons: n = 16).C, Box and scatter plots of the ratios between the compound EJP amplitudes in response to the last and first pulse of the last (25th) train. *p < 0.05, **p < 0.01, ***p < 0.001.
The dynamics of electrical muscle responses to repeated activation were due to short-term synaptic plasticity
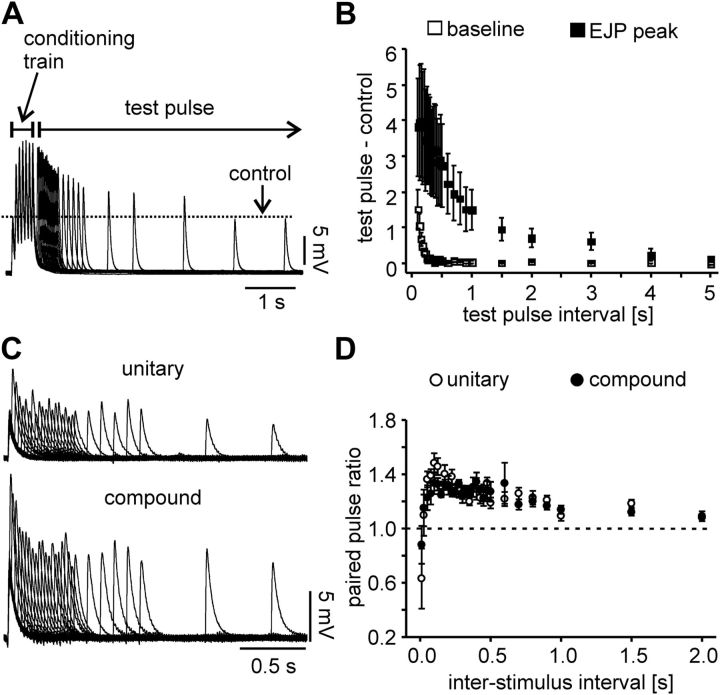
The results shown in Figure 7 compared compound responses to train stimulations with intratrain frequencies that lead to summation of EJPs. As shown in Figure 6, C and D, the time course of EJPs was not significantly different across preparations with different numbers of PY neurons, suggesting that differences in integration of repetitive input were not due to differences in summation. However, the time constants of repolarization could have changed in a differential manner over the course of the train responses, which would be hard to quantify in summating signals. Alternatively, changes in EJP amplitudes could have been solely due to short-term synaptic plasticity. However, in this scenario the nature of short-term synaptic plasticity is ambiguous. Neuromuscular synapses in the stomatogastric system can express mixtures of facilitation and depression, revealed at different time scales of repetitive activation (Sen et al., 1996; Stein et al., 2006). The data shown in Figure 7 suggest that this may have also been the case in the p2 muscle. In the analysis shown, we defined the amplitude as the difference of peak and resting membrane potential, and not the potential from which each EJP started. In the recording from a preparation with 3 PY neurons shown in Figure 7A, the peak depolarization increases more than the preceding trough voltages, i.e., total amplitude changed more than was accounted for by summation. In contrast, the peak voltage did not change substantially in the preparation with 5 PY neurons (see also Fig. 7B), even though later EJPs rose from a more depolarized membrane potential than the first one. We therefore also wanted to investigate the predominant change of amplitude during repetitive activation in the absence of summation. To this end, we elicited compound responses to a conditioning train followed by test pulses at different intervals. A 15 Hz train of 7 pulses was followed by test pulses at varying intervals from the last pulse in the train, between 0.1 and 5 s. Figure 8A shows overlaid recording traces from one experiment, indicating that compound EJPs in response to test pulses had increased peak voltages compared with the initial response, even at intervals that by far outlasted the depolarization of the baseline potential due to summation. We measured the amplitudes of the responses to the test pulses and compared them to the amplitude of the first compound EJP in the conditioning train response. We also measured the preceding trough potentials from which each compound EJP rose and compared them to the resting membrane potential before the start of the conditioning train. Figure 8B shows the difference of peaks and baseline voltages as means from 5 preparations, 3 of them with 3, 1 with 4, and 1 with 5 PY neurons. In each experiment, we determined the intervals at which peak voltage and baseline voltage had returned to a value within 5% of the control value. The baseline voltage returned within 0.32 s (± 0.03 SEM), whereas the increase in peak voltage lasted 4.20 s (± 0.37 SEM). These values were statistically different (paired t test, p = 0.0004). We conclude that the dynamics of EJP amplitudes observed during train stimulation were predominantly due to short-term synaptic plasticity.
Figure 8.
A, Overlaid compound EJP recordings from a stimulation protocol with a conditioning train and single test pulses at varying intervals, showing the synaptic enhancement and the time course of recovery. The dashed line indicates the EJP amplitude in response to the first pulse in the conditioning train. B, Plot of the mean response difference (n = 5) between test pulse and first pulse in the conditioning train for EJP peak voltages and preceding baseline voltages, as a function of test pulse interval. Note that summation ceases after a few hundred microseconds as the baseline voltage in between pulses returns to normal, while the increase of EJP amplitude persists for several seconds. C, Overlaid EJP recordings from paired-pulse stimulations with varying intervals (10 ms–2 s). Unitary and compound EJP recordings are from the same experiment. D, Mean paired-pulse response amplitude ratios as a function of interstimulus intervals (n = 5). Both unitary and compound responses show similar paired-pulse ratios at all interstimulus intervals.
The results shown in Figures 3 and 6A suggest that compound EJP amplitudes are the linear sum of unitary EJP amplitudes. We wanted to test whether the changes in amplitude during repeated activation were also proportional between stimulating either one or all PY axons present. As stated before, because of changing thresholds we did not succeed in performing single PY axon train stimulations. However, we used paired-pulse stimulations to compare synaptic dynamics between unitary and compound responses. We delivered paired pulses at intervals between 10 ms and 2 s. Figure 8C shows overlaid recording traces from one experiment, for both unitary and compound responses. Figure 8D shows the mean paired-pulse amplitude ratios as a function of interval from five preparations, 1 of them with 3, 3 with 4, and 1 with 5 PY neurons. Paired-pulse ratios have similar values between unitary and compound EJPs at all intervals. In both cases, there is depression at 10 ms, followed by enhancement which is increasing up to an interval of 100 ms, and decreasing subsequently over the whole interval range up to 2 s. These experiments differ from the train stimulations shown in Figure 7. During repeated train stimulations, the magnitude of synaptic dynamics over a single train changed and then stabilized over consecutive trains, whereas paired pulses were delivered from an initial state not influenced by preceding activity. However, we interpret our results as evidence that the synapses from each PY neuron onto the muscle act independently and the compound EJP amplitudes as well as their dynamics are the linear sum of unitary responses.
Discussion
Interindividual variability of neuron numbers
In the STG, network output is remarkably similar across different individual animals (Bucher et al., 2005, 2006), and both experimental and theoretical studies suggest that very different combinations of properties can give rise to this invariant output (Golowasch et al., 1999a,b; Prinz et al., 2003, 2004; Schulz et al., 2006). The number of neurons appears to be among the parameters that are compensated, as neither centrally generated activity patterns nor the muscle responses to rhythmic motor drive differ across individuals with different numbers of PY neurons. At the NMJ, we show that interindividual differences in the number of presynaptic neurons are compensated at the level of short-term synaptic dynamics. Because it appears unlikely that the relationship between number of neurons and magnitude of synaptic enhancement is genetically hard-wired, we interpret this as a novel form of homeostatic plasticity.
Homeostatic plasticity is usually understood as a mostly activity-dependent negative feedback loop that ensures stable overall activity levels (Davis and Bezprozvanny, 2001; Marder and Prinz, 2002; Turrigiano and Nelson, 2004; Pérez-Otaño and Ehlers, 2005; Davis, 2006; Marder and Goaillard, 2006; Turrigiano, 2007, 2011; Pozo and Goda, 2010). It is most often studied as a mechanism that allows recovery of function after experimental disruption of normal activity. However, presumably it is a continuous process ensuring stability not only in response to drastic perturbations, but also in the face of constant molecular turnover and interindividual component variability (Marder and Goaillard, 2006; Bucher, 2009). Instead of perturbing activity experimentally, we used the interindividual variability in neuron number to study compensatory regulation of synapses. While this did not provide us with direct evidence of activity-dependent regulation, correlation of physiological parameters with natural variability provides a window into long-term compensatory regulation without the risk of artifacts or ambiguities arising from harsh perturbations.
Furthermore, variable numbers of neurons occur in many networks, suggesting that compensatory regulation for differences in circuit architecture is a common phenomenon. How much variability exists appears to depend on the size of the neuron population (Williams and Herrup, 1988). In arthropods and other invertebrates, large individually identifiable neurons are usually invariant in number (Govind and Atwood, 1982; Sandeman, 1982; Burrows, 1996), although some variability has been observed in several systems (Goodman, 1974; Kuffler and Muller, 1974; Newcomb et al., 2006). While cell numbers in vertebrates are relatively tightly controlled in systems with relatively few neurons (Ma and Lopez, 2003), larger networks can show substantial variability (Williams et al., 1996, 1998; Whitney et al., 2011). Interesting insights into how such variability might be compensated come from mutant animals with supernumerary numbers of neurons. For example, zebrafish with supernumerary Mauthner cells show relatively normal escape responses, due to a compensatory division of synaptic output regions in the spinal cord (Liu et al., 2003). We did not study the structural consequences of PY neuron variability. However, our finding that single muscle fiber responses elicited by stimulating individual axons did not differ across individuals with different numbers of PY neurons suggests that compensation is not simply achieved by dividing the same numbers of synaptic contact sites among varying numbers of motor axons.
Short-term synaptic dynamics as a novel target for long-term homeostatic regulation
The challenge in the study of compensatory plasticity phenomena is to identify both the locus of regulation, i.e., the effectors that are regulated to maintain physiological function, and the actual target that is maintained, i.e., the physiological parameter that serves as a set-point for regulation. In cases where the gain of a specific synaptic connection is maintained, like at the Drosophila NMJ (Davis and Bezprozvanny, 2001; Paradis et al., 2001; Davis, 2006), the focus has been on the amplitude of single postsynaptic responses. However, differences in synaptic dynamics and summation during repetitive activation may lead to different compound responses even if responses to single presynaptic spikes are similar. In a crustacean stomatogastric muscle, the EJP amplitude in response to single motor neuron spikes stays constant from juvenile to adult, but the compound responses to bursting input are significantly larger in juveniles (Pulver et al., 2005).
Interpreting the relationship between responses to single and repetitive activation is even less straightforward in the context of changes in synaptic strength, as changes in short-term dynamics may occur concomitantly. Long-term regulatory mechanisms at a developmental time scale clearly specify not only the strength but also the dynamics of synapses, as the same neuron can express different forms of short-term plasticity at synapses to different postsynaptic neurons (Davis and Murphey, 1994; Dittman et al., 2000). In addition, Hebbian forms of long-term plasticity like LTP can change short-term synaptic dynamics in a computationally significant manner (Gundlfinger et al., 2007; Leibold and Bendels, 2009). To our knowledge, long-term regulation of short-term synaptic dynamics in the context of homeostatic plasticity has not been explicitly addressed. Visual deprivation in rat pups leads to compensatory shifts in the excitation/inhibition balance in the visual cortex, and most of the changes in synaptic strength are accompanied by altered short-term synaptic plasticity (Maffei et al., 2004; Maffei and Turrigiano, 2008). However, the degree to which these changes are functionally significant or an epiphenomenon of changes in the synaptic machinery is not clear. Similarly, homeostatic plasticity at an identified synapse in the locust involves changes in individual postsynaptic responses and synaptic dynamics during repetitive activity (Rogers et al., 2007). The data presented here clearly differ from such findings because differences in short-term synaptic dynamics of the PY neuron motor synapse are not solely accompanying changes in absolute synaptic strength. Rather, single synaptic responses are relatively constant, while the magnitude of dynamics during repetitive activation appears to be the physiological parameter that actually acts as the compensatory mechanism.
The possible loci of compensatory changes
Our finding that differences in short-term synaptic dynamics compensate for different numbers of presynaptic neurons suggests that the loci for such regulation are among the cellular mechanisms giving rise to transient changes in transmitter release and/or postsynaptic receptor activation. Short-term synaptic plasticity encompasses various cellular mechanisms that can lead to enhancement or depression of postsynaptic potentials (Regehr and Stevens, 2001; Zucker and Regehr, 2002). In many cases, several forms of these dynamics are present (Sen et al., 1996; Dittman et al., 2000; Zucker and Regehr, 2002; Abbott and Regehr, 2004; Blitz et al., 2004). Enhancement occurs at several time scales, classified as facilitation in the range of up to hundreds of milliseconds, augmentation in the range of several seconds, and post-tetanic potentiation in the range of tens of seconds to minutes (Regehr and Stevens, 2001; Zucker and Regehr, 2002). The results shown here suggest that more than one process acts at the p2 NMJ, as enhancement and possibly depression occur over the course of single bursts (Fig. 7A), while enhancement also persists for several seconds after the end of a burst (Fig. 8). In most cases, short-term synaptic dynamics are predominantly due to presynaptic changes in calcium concentration, transmitter release probability, and vesicle recruitment (Regehr and Stevens, 2001; Zucker and Regehr, 2002). However, these changes can be accompanied by, and functionally interact with, postsynaptic changes like receptor desensitization or saturation (Jones and Westbrook, 1996; Chen et al., 2002; Foster et al., 2002, 2005; Sun and Beierlein, 2011).
Crustacean stomach muscle fibers are multiterminally innervated along their length, do not show miniature potentials, and have inhomogeneous synaptic contact sites (Atwood, 1976; Atwood et al., 1977, 1978; Pulver et al., 2005). Our initial attempts at quantal analysis did not show clear peaks in amplitude histograms (data not shown), similar to what has been found in a different stomach muscle (Atwood et al., 1977). We therefore could not determine whether the differences in short-term dynamics were expressed presynaptically or postsynaptically, or both. If the set-point for regulation is the depolarization level of the muscle fiber, postsynaptic regulation of receptor densities and function could be achieved cell-autonomously, while regulation of presynaptic transmitter release would require a retrograde signal. In the context of homeostatic regulation of synaptic strength, both possibilities are realized. It is well documented for mammalian excitatory synapses that synaptic scaling involves regulation of receptor trafficking to adjust the number of glutamate receptors at postsynaptic sites (Turrigiano, 2008). At the Drosophila NMJ, synaptic homeostasis involves both regulation of postsynaptic receptors and retrograde signaling affecting presynaptic transmitter release (Davis et al., 1998; Davis and Bezprozvanny, 2001; Davis, 2006; Frank et al., 2009). Homeostatic regulation of mammalian synapses can also be accompanied by presynaptic changes in transmitter release (Murthy et al., 2001; Moulder et al., 2006; Branco et al., 2008; Pozo and Goda, 2010).
It is undetermined to which degree changes in short-term synaptic dynamics might play a role in homeostatic regulation of synapses in other systems. However, repetitive activity is common in many neural circuits and almost always accompanied by short-term plasticity (Regehr and Stevens, 2001; Zucker and Regehr, 2002; Abbott and Regehr, 2004). Therefore, long-term regulation of short-term synaptic dynamics would be an effective way to control activity levels in many systems.
Footnotes
This work was supported by National Institute of Neurological Disorders and Stroke Grant NS058825 (D.B.), and Stipend DA 1188 of the Deutsche Forschungsgemeinschaft (N.D.).
References
- Abbott LF, Regehr WG. Synaptic computation. Nature. 2004;431:796–803. doi: 10.1038/nature03010. [DOI] [PubMed] [Google Scholar]
- Atwood HL. Organization and synaptic physiology of crustacean neuromuscular systems. Prog Neurobiol. 1976;7:291–391. doi: 10.1016/0301-0082(76)90009-5. [DOI] [PubMed] [Google Scholar]
- Atwood HL, Govind CK, Jahromi SS. Excitatory synapses of blue crab gastric mill muscles. Cell Tissue Res. 1977;177:145–158. doi: 10.1007/BF00221078. [DOI] [PubMed] [Google Scholar]
- Atwood HL, Govind CK, Kwan I. Nonhomogeneous excitatory synapses of a crab stomach muscle. J Neurobiol. 1978;9:17–28. doi: 10.1002/neu.480090103. [DOI] [PubMed] [Google Scholar]
- Blitz DM, Foster KA, Regehr WG. Short-term synaptic plasticity: a comparison of two synapses. Nat Rev Neurosci. 2004;5:630–640. doi: 10.1038/nrn1475. [DOI] [PubMed] [Google Scholar]
- Branco T, Staras K, Darcy KJ, Goda Y. Local dendritic activity sets release probability at hippocampal synapses. Neuron. 2008;59:475–485. doi: 10.1016/j.neuron.2008.07.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bucher D. Neuronal homeostasis: does form follow function or vice versa? Curr Biol. 2009;19:R64–R67. doi: 10.1016/j.cub.2008.11.042. [DOI] [PubMed] [Google Scholar]
- Bucher D, Prinz AA, Marder E. Animal-to-animal variability in motor pattern production in adults and during growth. J Neurosci. 2005;25:1611–1619. doi: 10.1523/JNEUROSCI.3679-04.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bucher D, Taylor AL, Marder E. Central pattern generating neurons simultaneously express fast and slow rhythmic activities in the stomatogastric ganglion. J Neurophysiol. 2006;95:3617–3632. doi: 10.1152/jn.00004.2006. [DOI] [PubMed] [Google Scholar]
- Bucher D, Johnson CD, Marder E. Neuronal morphology and neuropil structure in the stomatogastric ganglion of the lobster, Homarus americanus. J Comp Neurol. 2007;501:185–205. doi: 10.1002/cne.21169. [DOI] [PubMed] [Google Scholar]
- Burrows M. The neurobiology of an insect brain. Oxford: Oxford UP; 1996. [Google Scholar]
- Chen C, Blitz DM, Regehr WG. Contributions of receptor desensitization and saturation to plasticity at the retinogeniculate synapse. Neuron. 2002;33:779–788. doi: 10.1016/s0896-6273(02)00611-6. [DOI] [PubMed] [Google Scholar]
- Davis GW. Homeostatic control of neural activity: from phenomenology to molecular design. Annu Rev Neurosci. 2006;29:307–323. doi: 10.1146/annurev.neuro.28.061604.135751. [DOI] [PubMed] [Google Scholar]
- Davis GW, Bezprozvanny I. Maintaining the stability of neural function: a homeostatic hypothesis. Annu Rev Physiol. 2001;63:847–869. doi: 10.1146/annurev.physiol.63.1.847. [DOI] [PubMed] [Google Scholar]
- Davis GW, Murphey RK. Long-term regulation of short-term transmitter release properties: retrograde signaling and synaptic development. Trends Neurosci. 1994;17:9–13. doi: 10.1016/0166-2236(94)90028-0. [DOI] [PubMed] [Google Scholar]
- Davis GW, DiAntonio A, Petersen SA, Goodman CS. Postsynaptic PKA controls quantal size and reveals a retrograde signal that regulates presynaptic transmitter release in Drosophila. Neuron. 1998;20:305–315. doi: 10.1016/s0896-6273(00)80458-4. [DOI] [PubMed] [Google Scholar]
- Dittman JS, Kreitzer AC, Regehr WG. Interplay between facilitation, depression, and residual calcium at three presynaptic terminals. J Neurosci. 2000;20:1374–1385. doi: 10.1523/JNEUROSCI.20-04-01374.2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Foster KA, Kreitzer AC, Regehr WG. Interaction of postsynaptic receptor saturation with presynaptic mechanisms produces a reliable synapse. Neuron. 2002;36:1115–1126. doi: 10.1016/s0896-6273(02)01106-6. [DOI] [PubMed] [Google Scholar]
- Foster KA, Crowley JJ, Regehr WG. The influence of multivesicular release and postsynaptic receptor saturation on transmission at granule cell to Purkinje cell synapses. J Neurosci. 2005;25:11655–11665. doi: 10.1523/JNEUROSCI.4029-05.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Frank CA, Pielage J, Davis GW. A presynaptic homeostatic signaling system composed of the Eph receptor, ephexin, Cdc42, and CaV2.1 calcium channels. Neuron. 2009;61:556–569. doi: 10.1016/j.neuron.2008.12.028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Golowasch J, Casey M, Abbott LF, Marder E. Network stability from activity-dependent regulation of neuronal conductances. Neural Comput. 1999a;11:1079–1096. doi: 10.1162/089976699300016359. [DOI] [PubMed] [Google Scholar]
- Golowasch J, Abbott LF, Marder E. Activity-dependent regulation of potassium currents in an identified neuron of the stomatogastric ganglion of the crab Cancer borealis. J Neurosci. 1999b;19:RC33. doi: 10.1523/JNEUROSCI.19-20-j0004.1999. (1-5) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goodman C. Anatomy of locust ocellar interneurons: constancy and variability. J Comp Physiol A Neuroethol Sens Neural Behav Physiol. 1974;95:185–201. [Google Scholar]
- Govind CK, Atwood HL. Organization of neuromuscular systems. In: Atwood HL, Sandeman DC, editors. The biology of crustacea: Neurobiology: structure and function. New York: Academic; 1982. pp. 63–98. [Google Scholar]
- Govind CK, Atwood HL, Maynard DM. Innervation and neuromuscular physiology of intrinsic foregut muscles in the blue crab and spiny lobster. J Comp Physiol A Neuroethol Sens Neural Behav Physiol. 1975;96:185–204. [Google Scholar]
- Gundlfinger A, Leibold C, Gebert K, Moisel M, Schmitz D, Kempter R. Differential modulation of short-term synaptic dynamics by long-term potentiation at mouse hippocampal mossy fibre synapses. J Physiol. 2007;585:853–865. doi: 10.1113/jphysiol.2007.143925. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hartline DK, Gassie DV, Sirchia CD. PY cell types in the stomatogastric ganglion of Panulirus. In: Selverston AI, Moulins M, editors. The crustacean stomatogastric system. Berlin: Springer; 1987. pp. 75–77. [Google Scholar]
- Hoyle G. Muscles and their neural control. New York: Wiley; 1983. [Google Scholar]
- Jahromi SS, Govind CK. Ultrastructural diversity in motor units of crustacean stomach muscles. Cell Tissue Res. 1976;166:159–166. doi: 10.1007/BF00227037. [DOI] [PubMed] [Google Scholar]
- Jones MV, Westbrook GL. The impact of receptor desensitization on fast synaptic transmission. Trends Neurosci. 1996;19:96–101. doi: 10.1016/s0166-2236(96)80037-3. [DOI] [PubMed] [Google Scholar]
- Kuffler DP, Muller KJ. The properties and connections of supernumerary sensory and motor nerve cells in the central nervous system of an abnormal leech. J Neurobiol. 1974;5:331–348. doi: 10.1002/neu.480050405. [DOI] [PubMed] [Google Scholar]
- Leibold C, Bendels MH. Learning to discriminate through long-term changes of dynamical synaptic transmission. Neural Comput. 2009;21:3408–3428. doi: 10.1162/neco.2009.12-08-929. [DOI] [PubMed] [Google Scholar]
- Lingle C. The sensitivity of decapod foregut muscles to acetylcholine and glutamate. J Comp Physiol. 1980;138:187–199. [Google Scholar]
- Liu KS, Gray M, Otto SJ, Fetcho JR, Beattie CE. Mutations in deadly seven/notch1a reveal developmental plasticity in the escape response circuit. J Neurosci. 2003;23:8159–8166. doi: 10.1523/JNEUROSCI.23-22-08159.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ma PM, Lopez M. Consistency in the number of dopaminergic paraventricular organ-accompanying neurons in the posterior tuberculum of the zebrafish brain. Brain Res. 2003;967:267–272. doi: 10.1016/s0006-8993(02)04238-5. [DOI] [PubMed] [Google Scholar]
- Maffei A, Turrigiano GG. Multiple modes of network homeostasis in visual cortical layer 2/3. J Neurosci. 2008;28:4377–4384. doi: 10.1523/JNEUROSCI.5298-07.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maffei A, Nelson SB, Turrigiano GG. Selective reconfiguration of layer 4 visual cortical circuitry by visual deprivation. Nat Neurosci. 2004;7:1353–1359. doi: 10.1038/nn1351. [DOI] [PubMed] [Google Scholar]
- Marder E, Bucher D. Understanding circuit dynamics using the stomatogastric nervous system of lobsters and crabs. Annu Rev Physiol. 2007;69:291–316. doi: 10.1146/annurev.physiol.69.031905.161516. [DOI] [PubMed] [Google Scholar]
- Marder E, Goaillard JM. Variability, compensation and homeostasis in neuron and network function. Nat Rev Neurosci. 2006;7:563–574. doi: 10.1038/nrn1949. [DOI] [PubMed] [Google Scholar]
- Marder E, Prinz AA. Modeling stability in neuron and network function: the role of activity in homeostasis. Bioessays. 2002;24:1145–1154. doi: 10.1002/bies.10185. [DOI] [PubMed] [Google Scholar]
- Maynard DM, Dando MR. The structure of the stomatogastric neuromuscular system in Callinectes sapidus, Homarus americanus and Panulirus argus (Decapoda Crustacea) Philos Trans R Soc Lond B. 1974;268:161–220. doi: 10.1098/rstb.1974.0024. [DOI] [PubMed] [Google Scholar]
- Moulder KL, Jiang X, Taylor AA, Olney JW, Mennerick S. Physiological activity depresses synaptic function through an effect on vesicle priming. J Neurosci. 2006;26:6618–6626. doi: 10.1523/JNEUROSCI.5498-05.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Murthy VN, Schikorski T, Stevens CF, Zhu Y. Inactivity produces increases in neurotransmitter release and synapse size. Neuron. 2001;32:673–682. doi: 10.1016/s0896-6273(01)00500-1. [DOI] [PubMed] [Google Scholar]
- Nadim F, Manor Y. The role of short-term synaptic dynamics in motor control. Curr Opin Neurobiol. 2000;10:683–690. doi: 10.1016/s0959-4388(00)00159-8. [DOI] [PubMed] [Google Scholar]
- Nadim F, Manor Y, Kopell N, Marder E. Synaptic depression creates a switch that controls the frequency of an oscillatory circuit. Proc Natl Acad Sci U S A. 1999;96:8206–8211. doi: 10.1073/pnas.96.14.8206. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Newcomb JM, Fickbohm DJ, Katz PS. Comparative mapping of serotonin-immunoreactive neurons in the central nervous systems of nudibranch molluscs. J Comp Neurol. 2006;499:485–505. doi: 10.1002/cne.21111. [DOI] [PubMed] [Google Scholar]
- Paradis S, Sweeney ST, Davis GW. Homeostatic control of presynaptic release is triggered by postsynaptic membrane depolarization. Neuron. 2001;30:737–749. doi: 10.1016/s0896-6273(01)00326-9. [DOI] [PubMed] [Google Scholar]
- Pérez-Otaño I, Ehlers MD. Homeostatic plasticity and NMDA receptor trafficking. Trends Neurosci. 2005;28:229–238. doi: 10.1016/j.tins.2005.03.004. [DOI] [PubMed] [Google Scholar]
- Pozo K, Goda Y. Unraveling mechanisms of homeostatic synaptic plasticity. Neuron. 2010;66:337–351. doi: 10.1016/j.neuron.2010.04.028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Prinz AA, Billimoria CP, Marder E. Alternative to hand-tuning conductance-based models: construction and analysis of databases of model neurons. J Neurophysiol. 2003;90:3998–4015. doi: 10.1152/jn.00641.2003. [DOI] [PubMed] [Google Scholar]
- Prinz AA, Bucher D, Marder E. Similar network activity from disparate circuit parameters. Nat Neurosci. 2004;7:1345–1352. doi: 10.1038/nn1352. [DOI] [PubMed] [Google Scholar]
- Pulver SR, Bucher D, Simon DJ, Marder E. Constant amplitude of postsynaptic responses for single presynaptic action potentials but not bursting input during growth of an identified neuromuscular junction in the lobster, Homarus americanus. J Neurobiol. 2005;62:47–61. doi: 10.1002/neu.20066. [DOI] [PubMed] [Google Scholar]
- Regehr WG, Stevens CF. Physiology of synaptic transmission and short-term plasticity. In: Cowan WM, Sudhof TC, Stevens CF, editors. Synapses. Baltimore: The Johns Hopkins UP; 2001. pp. 135–176. [Google Scholar]
- Rogers SM, Krapp HG, Burrows M, Matheson T. Compensatory plasticity at an identified synapse tunes a visuomotor pathway. J Neurosci. 2007;27:4621–4633. doi: 10.1523/JNEUROSCI.4615-06.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sandeman DC. Organization of the central nervous system. In: Atwood HL, Sandeman DC, editors. The biology of crustacea: Neurobiology: structure and function. New York: Academic; 1982. pp. 1–54. [Google Scholar]
- Schulz DJ, Goaillard JM, Marder E. Variable channel expression in identified single and electrically coupled neurons in different animals. Nat Neurosci. 2006;9:356–362. doi: 10.1038/nn1639. [DOI] [PubMed] [Google Scholar]
- Sen K, Jorge-Rivera JC, Marder E, Abbott LF. Decoding synapses. J Neurosci. 1996;16:6307–6318. doi: 10.1523/JNEUROSCI.16-19-06307.1996. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Soto-Treviño C, Thoroughman KA, Marder E, Abbott LF. Activity-dependent modification of inhibitory synapses in models of rhythmic neural networks. Nat Neurosci. 2001;4:297–303. doi: 10.1038/85147. [DOI] [PubMed] [Google Scholar]
- Stein W, Smarandache CR, Nickmann M, Hedrich UB. Functional consequences of activity-dependent synaptic enhancement at a crustacean neuromuscular junction. J Exp Biol. 2006;209:1285–1300. doi: 10.1242/jeb.02133. [DOI] [PubMed] [Google Scholar]
- Sun YG, Beierlein M. Receptor saturation controls short-term synaptic plasticity at corticothalamic synapses. J Neurophysiol. 2011;105:2319–2329. doi: 10.1152/jn.00942.2010. [DOI] [PubMed] [Google Scholar]
- Thuma JB, Harness PI, Koehnle TJ, Morris LG, Hooper SL. Muscle anatomy is a primary determinant of muscle relaxation dynamics in the lobster (Panulirus interruptus) stomatogastric system. J Comp Physiol A Neuroethol Sens Neural Behav Physiol. 2007;193:1101–1113. doi: 10.1007/s00359-007-0261-7. [DOI] [PubMed] [Google Scholar]
- Turrigiano G. Homeostatic signaling: the positive side of negative feedback. Curr Opin Neurobiol. 2007;17:318–324. doi: 10.1016/j.conb.2007.04.004. [DOI] [PubMed] [Google Scholar]
- Turrigiano G. Too many cooks? Intrinsic and synaptic homeostatic mechanisms in cortical circuit refinement. Annu Rev Neurosci. 2011;34:89–103. doi: 10.1146/annurev-neuro-060909-153238. [DOI] [PubMed] [Google Scholar]
- Turrigiano G, Abbott LF, Marder E. Activity-dependent changes in the intrinsic properties of cultured neurons. Science. 1994;264:974–977. doi: 10.1126/science.8178157. [DOI] [PubMed] [Google Scholar]
- Turrigiano GG. The self-tuning neuron: synaptic scaling of excitatory synapses. Cell. 2008;135:422–435. doi: 10.1016/j.cell.2008.10.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Turrigiano GG, Nelson SB. Homeostatic plasticity in the developing nervous system. Nat Rev Neurosci. 2004;5:97–107. doi: 10.1038/nrn1327. [DOI] [PubMed] [Google Scholar]
- Turrigiano GG, Leslie KR, Desai NS, Rutherford LC, Nelson SB. Activity-dependent scaling of quantal amplitude in neocortical neurons. Nature. 1998;391:892–896. doi: 10.1038/36103. [DOI] [PubMed] [Google Scholar]
- Whitney IE, Raven MA, Ciobanu DC, Poché RA, Ding Q, Elshatory Y, Gan L, Williams RW, Reese BE. Genetic modulation of horizontal cell number in the mouse retina. Proc Natl Acad Sci U S A. 2011;108:9697–9702. doi: 10.1073/pnas.1103253108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Williams RW, Herrup K. The control of neuron number. Annu Rev Neurosci. 1988;11:423–453. doi: 10.1146/annurev.ne.11.030188.002231. [DOI] [PubMed] [Google Scholar]
- Williams RW, Strom RC, Rice DS, Goldowitz D. Genetic and environmental control of variation in retinal ganglion cell number in mice. J Neurosci. 1996;16:7193–7205. doi: 10.1523/JNEUROSCI.16-22-07193.1996. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Williams RW, Strom RC, Goldowitz D. Natural variation in neuron number in mice is linked to a major quantitative trait locus on Chr 11. J Neurosci. 1998;18:138–146. doi: 10.1523/JNEUROSCI.18-01-00138.1998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zucker RS, Regehr WG. Short-term synaptic plasticity. Annu Rev Physiol. 2002;64:355–405. doi: 10.1146/annurev.physiol.64.092501.114547. [DOI] [PubMed] [Google Scholar]