Exact Relation between Potential of Mean Force and Free-Energy Profile

Abstract

We apply concepts of covariant and contravariant vector space in differential geometry and general relativity to derive new, general, exact relations between potential of mean force and free-energy profile. These relations are immensely practical in free-energy simulations because a full Jacobian transformation (which is usually unknown) is not required; rather, only knowledge of the (constraint) coordinate of interest is needed. We reveal that in addition to the Jacobian determinant, the Jacobian scale factor and Leibnizian contributions must also be considered, as well a Fixman term with correct mass dependence. Our newly derived relations are verified with new non-trivial benchmark numerical examples for which exact results can be computed, and compared with relations available in the literature that turn out to exhibit significant deviations from the exact values.

Free-energy profiles derived from molecular simulations are widely used in computational physics, biophysics, and chemistry^1–3 to provide valuable insight into biochemical or physical events ranging from folding and conformational changes in proteins ^{4, 5}, lipid-driven aggregation of nanoparticles ⁶ to chemical reactions ^{7, 8} that occur on material surfaces ⁹, in aqueous solution ¹⁰, and in the catalytic active sites of RNA ¹¹ or protein ^{12, 13} enzymes. Two of the most commonly applied approaches for simulating free-energy profiles involve methods based on reweighting biased probability distributions (e.g., umbrella sampling) ¹⁴, and constrained mean-force (CMF) samplings (e.g., blue-moon sampling) ^{15, 16}. The former delivers the free-energy profile directly from the probability distribution along the coordinate of interest, whereas the latter relies on relation between free-energy profile and potential of mean force (PMF), first introduced by Kirkwood over three quarters of century ago ¹⁷, which subsequently has become a central underpinning in free-energy simulations (e.g., the two terms, “PMF” and “free-energy profile”, are sometimes written as synonyms in the literature).

Advantages of constrained mean-force (CMF) sampling approaches are that they neither have inherent assumptions imposed by reweighting algorithms, nor binning/overlapping histograms, and also do not require biasing forces/potentials ^14–16. Furthermore, it is trivial for the CMF simulations to have identical number of samples (sample uniformly) at any value of the coordinate of interest (e.g., the number of ‘rare’ samples at the transition state can easily be as many as the number of ‘abundant’ samples at the ground state). However, in order to exactly equate PMF with free-energy profile, we must consider the Jacobian contribution. Explicitly expressing the Jacobian contribution for any curvilinear coordinate in analytical form is not straightforward, and in practice, applications are (thus) often limited to use of fairly simple coordinates to describe the events of interest ^{5, 15, 18}.

Substantial theoretical efforts have been made to generalize the original Kirkwood relation, and have led to different, sometimes inconsistent relations between PMF and free-energy profile involving discrepant relation with the integrated mean Lagrange multiplier of the constraint, and incorrect mass-dependence of the Fixman term ^15–29. Further, there is a lack of non-trivial numerical examples, in which exact values can be computed, and thus serve as benchmarks to rigorously test different formulations.

In this paper, we first (I) reveal a new free-energy-profile term contributed from Leibniz’s rule ³⁰, and then apply the equivalence between the orthogonal covariant and contravariant vector space from differential geometry and general relativity to (II) formulate general equations for the Jacobian contribution to the free-energy profile that requires knowledge only of the (constraint) coordinate of interest (full Jacobian transformation is not needed), (III) present the Fixman term with correct mass dependence, and (IV) disclose a Jacobian scale factor term that is required to exactly relate the integrated mean Lagrange multiplier to the free-energy profile. All new results are compared with those calculated from other relations reported in the literature^15–29 using new rigorous numerical examples that serve as validation benchmarks.

I: Leibnizian contribution (full Jacobian case)

Suppose q_ξ is the generalized coordinate of interest for describing a biochemical or physical process, and is a member of at least one complete set of curvilinear coordinates, say {q}^N. Then the (canonical) free-energy profile as a function of q_ξ = ξ₀ is:^1–3

$$G_{\xi }({\xi }_0)=\frac{-1}{\beta }ln\int \left|\overleftrightarrow{J}\left({\xi }_0,{\left\{q\right\}}^{N-1}\right)\right|{dq}^{N-1}{e}^{-\beta V({\xi }_0,{\left\{q\right\}}^{N-1})}+C$$ (1)

where N is number of degrees of freedom, β = 1/k_BT, k_B is Boltzmann’s constant, T is absolute temperature, |J↔| is the determinant of the Jacobian transformation J↔ for {q}^N, dq^N−1 is a set of integration variables without dq_ξ, and C is a normalization constant from integrating the entire momentum space. Note that in this paper, integrals without explicit limits imply the entire space is integrated. Generalization of Eq. (1) to the isothermal-isobaric ensemble is straightforward ^{2, 3, 31} [and for the cases in the alchemical free-energy simulations,⁵ if the extended degree of freedom, say q_λ, is completely independent of the original configuration space, such that its Jacobian scale factor is always unity in the extended version of Eq. (1), then there is no Jacobian and Leibnizian contribution in the following Eq. (2)]. Practically, it is rare to determine the constant C because what we often care about is the free-energy differences with various values of ξ₀. To exactly equate PMF with the free-energy profile in Eq. (1), we first differentiate it with respect to ξ₀:

$$\begin{array}{l}\frac{{dG}_{\xi }({\xi }_0)}{d{\xi }_0}={\langle {\left(\frac{\partial V}{\partial q_{\xi }}\right)}_{{\left\{q_{m\ne \xi }\right\}}^{N-1}}\rangle }_{{\xi }_0}-\frac{1}{\beta }{\langle \frac{1}{\left|\overleftrightarrow{J}\right|}{\left(\frac{\partial \left|\overleftrightarrow{J}\right|}{\partial q_{\xi }}\right)}_{{\left\{q_{m\ne \xi }\right\}}^{N-1}}\rangle }_{{\xi }_0}\\ -\frac{1}{\beta }{\langle \sum _{m\ne \xi }^{N-1}\left[\delta \left(q_m-l_{U_m}\right)\frac{{dl}_{U_m}\left(q_{\xi }\right)}{{dq}_{\xi }}-\delta \left(q_m-l_{L_m}\right)\frac{{dl}_{L_m}\left(q_{\xi }\right)}{{dq}_{\xi }}\right]\rangle }_{{\xi }_0}\end{array}$$ (2)

where 〈···〉_ξ0 is the ensemble average over all configurations with q_ξ= ξ₀ (Supp. Info.), l_Um and l_Lm are the upper and lower integration limits for q_m, respectively. Eq. (2) establishes an important exact relation between free-energy profile and ensemble averages (or mean values) of some physical quantities.

The first term in Eq. (2) is the negative value of the mean force. Integrating the first term over the coordinate of interest provides us with the potential of mean force (PMF). The second term is the contribution due to the Jacobian determinant. These two ensemble-average terms are sometimes collectively referred to in the literature as the mean value of “generalized force”, although we avoid this designation in the present work.

The third term in Eq. (2), which is not found in the literature, derives from the change of domains of {q_m≠ξ}^N−1 with respect to q_ξ, i.e., from Leibniz’s rule ³⁰. This term arises in the Jacobian transformation between two complete sets of coordinates that have coupling of their integration domains, and is herein referred to as the Leibnizian contribution. In Eq. (2), we restrict ourselves to the cases that if there are domains of q_m≠ξ depending on q_ξ, then all are functions of q_ξ only, independent of q_j≠m,ξ. For all other domains of q_j≠m,ξ, even depending on q_m≠ξ, as long as they are independent of q_ξ, then we treat these domains as constants. A general expression without such restrictions can be found in Ref. ³⁰.

To demonstrate the importance of the Leibnizian contribution in Eq. (2), we consider a three-atom system, initially involving nine degrees of freedom: {x_A, y_A, z_A, x_B, y_B, z_B, x_C, y_C, z_C}. The motions of the two atoms: A and C are restricted such that they are always located at the z-axis with the values of R/2 and −R/2, respectively, although their separation, R, is a variable. So the degrees of freedom is down to four: {R, x_B, y_B, z_B}. We would like to express these four degrees of freedom in terms of a set of four elliptic coordinates {R, ξ_s, ξ_a, φ}, in which the coordinate of interest ξ_a ∈ [−R,R] is ${\xi }_a\equiv \sqrt{x_B^2+y_B^2+{(z_B-R/2)}^2}-\sqrt{x_B^2+y_B^2+{(z_B+R/2)}^2}$. Note that ξ_a is an effective coordinate to describe atom-transfer reaction ^{3, 10–13, 32} (from atom A to C), and the domains for {R, ξ_s, ξ_a} are related. With the definition of the coordinate of interest ξ_a, and with a three-body double-well potential and full Jacobian transformation (details for the coordinate transformation and the potential are in Supp. Info.), the exact free-energy profile can be directly calculated from Eq. (1).

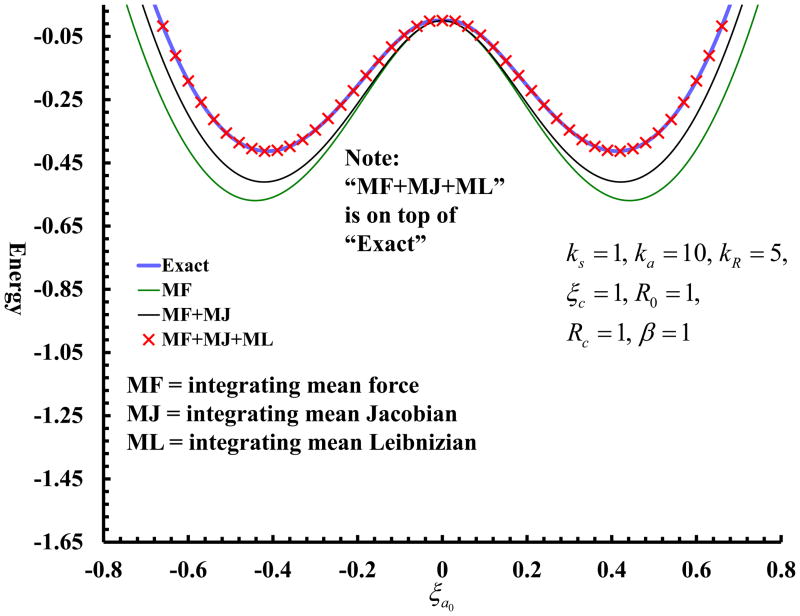
Fig. 1 shows that integration of Eq. (2) does give back the exact free-energy profile in Eq. (1), but requires consideration of all three (mean force, Jacobian and Leibnizian) contributions.¹ In this example, neglect of the Leibnizian contribution disclosed in this work leads to an overestimate the free-energy barrier (between minimum and maximum points) by about 25%.

Fig. 1.

Exact free-energy profile [Eq. (1)] compared with integrated mean force with and without Jacobian and Leibnizian contributions [Eq. (2)]. All plots are symmetric and anchored at zero value when ξ_a0 = 0.

II: Orthogonal contravariant space formulation (no full Jacobian requirement)

To use Eq. (2), we have to express Cartesian coordinates {x}^N and then V in terms of {q}^N for the instantaneous Jacobian and force contributions, respectively. In the language of differential geometry or general relativity, Eq. (2) is in the covariant vector space representation ³³. However, working in the covariant space is often not practical since we usually only know the definition of q_ξ in terms of {x}^N, rather than having the ability to express all {x}^N in terms of {q}^N.

It would thus be desirable to determine dG_ξ(ξ₀)/dξ₀ in the contravariant space, which is the vector space expressing {q}^N in terms of {x}^N. Note that if and only if q_ξ is orthogonal to the subspace spanned by the rest of coordinates, then the covariant vector space for q_ξ is identical (or trivially related) to the contravariant vector space for q_ξ ³³. We designate these vector spaces as orthogonal covariant and orthogonal contravariant spaces, respectively. Nevertheless, as long as q_ξ can be a member of at least one complete set of coordinates, then the orthogonal space always exists, because the rest of the subspace can be simply adjusted to be perpendicular to q_ξ by orthogonalization.

In the orthogonal contravariant space, the unit vector for q_ξ is:¹

$${\widehat{q}}_{\xi }=\overrightarrow{\nabla }{q}_{\xi }/\left|\overrightarrow{\nabla }{q}_{\xi }\right|$$ (3)

which is identical to the unit vector in the orthogonal covariant space (Supp. Info.). Similarly, in the orthogonal contravariant space, the Jacobian scale factor for q_ξ is:¹

$$h_{q_{\xi }}=|\overrightarrow{\nabla }{q}_{\xi }{|}^{-1}$$ (4)

which is identical to the scale factor in the orthogonal covariant space (Supp. Info.). Notably, the Jacobian scale factor in Eq. (4) is misinterpreted as the full Jacobian determinant in Ref. [²⁰]. Eq. (3) and (4) are key results for this paper, and in particular the gradient operator in Eq. (3) and (4) that can be calculated in Cartesian coordinates (and in any complete curvilinear coordinates), i.e., Eq. (3) and (4) depend only on the definition of q_ξ.

Additionally, if we define $q_{\xi }^{\prime }\equiv q_{\xi }$, it is always possible that we keep orthogonalizing the subspace {q_m≠ξ}^N−1 such that we find a complete set of coordinates {q′}^N which are all orthogonal to one another. Using Eq. (3), Eq. (4), and the orthogonality of {q′}^N, we find:¹

$$\stackrel{\rightharpoonup }{\nabla }V·\left(h_{q_{\xi }}{\widehat{q}}_{\xi }\right)={\left(\frac{\partial V}{\partial q_{\xi }}\right)}_{{\left\{q_{m\ne \xi }^{\prime }\right\}}^{N-1}}=\stackrel{\rightharpoonup }{\nabla }V·\left(\frac{\overrightarrow{\nabla }{q}_{\xi }}{|\overrightarrow{\nabla }{q}_{\xi }{|}^2}\right)$$ (5)

Eq. (5) is the instantaneous force in the orthogonal contravariant space that depends only on q_ξ.

Similarly, using Eq. (3), (4), the Jacobian determinant for {q′}^N as $\left|{\overleftrightarrow{J}}^{\prime }\right|={\displaystyle \prod _{m=1}^N}{h}_{q_m^{\prime }}$ (due to the orthogonality in {q′}^N), and $q_{\xi }^{\prime }\equiv q_{\xi }$, now we have the divergence of h_qξq̂_ξ, i.e., ∇⃑ · (h_qξq̂_ξ), as:¹

$$\overrightarrow{\nabla }·\left(\frac{\overrightarrow{\nabla }{q}_{\xi }}{|\overrightarrow{\nabla }{q}_{\xi }{|}^2}\right)=\frac{1}{{\displaystyle \prod _{m=1}^N}{h}_{q_m^{\prime }}}{\left(\frac{\partial }{\partial q_{\xi }}\left[h_{q_{\xi }^{\prime }}\prod _{m\ne \xi }^{N-1}{h}_{q_m^{\prime }}\right]\right)}_{{\left\{q_{m\ne \xi }^{\prime }\right\}}^{N-1}}=\frac{1}{\left|{\overleftrightarrow{J}}^{\prime }\right|}{\left(\frac{\partial \left|{\overleftrightarrow{J}}^{\prime }\right|}{\partial q_{\xi }}\right)}_{{\left\{q_{m\ne \xi }^{\prime }\right\}}^{N-1}}$$ (6)

Eq. (6) is the instantaneous Jacobian contribution in the orthogonal contravariant space that depends only on the (constraint) coordinate, q_ξ.

Towards this end, since the coordinates in {q′}^N are orthogonal to one another, the domains of all coordinates should not be related, and should be constants. Thus, there should be no Leibnizian contribution in Eq. (2) with {q′}^N. Finally, we can express dG_ξ(ξ₀)/dξ₀ in the orthogonal contravariant space ^{16, 21} by substituting Eq. (5) and (6) into Eq. (2):¹

$$\frac{{dG}_{\xi }({\xi }_0)}{d{\xi }_0}={\langle \stackrel{\rightharpoonup }{\nabla }V·\left(\frac{\overrightarrow{\nabla }{q}_{\xi }}{|\overrightarrow{\nabla }{q}_{\xi }{|}^2}\right)\rangle }_{{\xi }_0}-\frac{1}{\beta }{\langle \overrightarrow{\nabla }·\left(\frac{\overrightarrow{\nabla }{q}_{\xi }}{|\overrightarrow{\nabla }{q}_{\xi }{|}^2}\right)\rangle }_{{\xi }_0}$$ (7)

Unlike Eq. (2) which is in the covariant space, Eq. (7) is in the orthogonal contravariant space for q_ξ, which depends only on the definition of q_ξ (without full Jacobian transformation). The desired result, Eq. (7), is correct and general, as long as q_ξ can be a member of a complete set of coordinates.¹

We note that Ref. [²¹] presents a similar (but different) formulation as the above Eq. (7), and it also indicates the orthogonality requirement that is ignored in Ref. [¹⁶]; however, using the formula given in Ref. [²¹] cannot return us the correct unit or dimension of the mean force when the coordinate of interest is not in the dimension of length. This is because, as opposed to our Eq. (7), in which we have a squared power in our denominator, i.e., |∇⃗q_ξ|², the corresponding denominator in Ref. [²¹] does not have any power index, i.e., |∇⃗q_ξ| (instead of |∇⃗q_ξ|²).

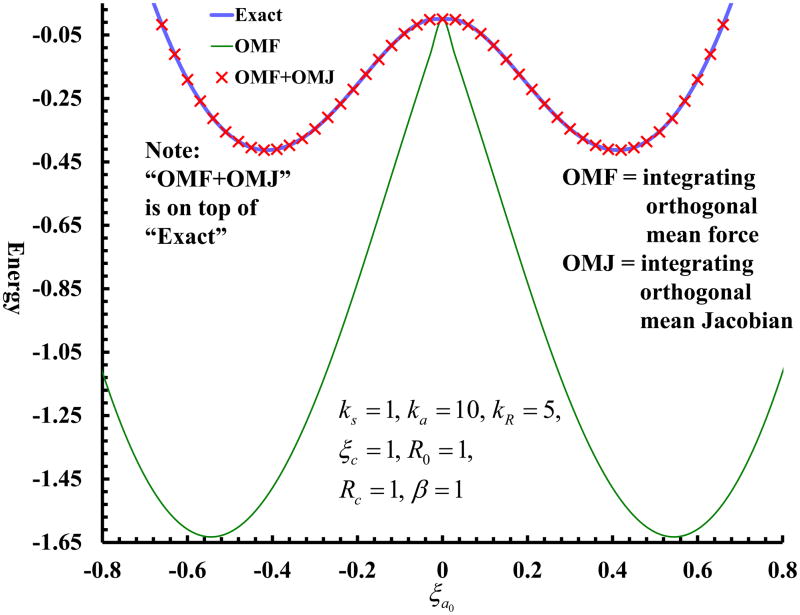
Figure 2 illustrates that integration of Eq. (7) indeed returns the exact free-energy profile in Eq. (1) without requiring the full Jacobian transformation. Note that no Leibnizian contribution to the free energy profile is in the orthogonal contravariant space, and that the mean force and the mean Jacobian contributions in the orthogonal contravariant space respectively differ from their own counterparts in the non-orthogonal covariant space. In the present example, integrating the non-orthogonal mean force would overestimate the exact free-energy barrier by about 40% (Fig. 1), whereas integrating the orthogonal mean force would cause the overestimate by about 300% (Fig. 2).

Fig. 2.

Exact free-energy profile [Eq. (1)] compared with integrated orthogonal mean force with and without Jacobian contributions [Eq. (7)], in which the Leibnizian term vanishes. All curves are symmetric and anchored at zero value when ξ_a0 = 0.

III: Fixman term (constrained MD)

In MD simulations, once we put a constraint to eliminate a degree of freedom in configuration space, e.g., q_ξ = ξ₀, then the degree of freedom of its velocity must vanish, i.e., q̇_ξ = 0. Thus, the constant nature of C in Eq. (1) does not exist because we no longer integrate the entire momentum space with q̇_ξ = 0. To figure out the consequence of this, we re-express Eq. (1) in the phase space explicitly consisting of q_ξ and q̇_ξ. First, we transform the Cartesian coordinates and momenta to the mass-scaled coordinates {s}^N, $s_i=\sqrt{M_i}{x}_i$, and the mass-scaled velocities {ṡ}^N, ${\stackrel{.}{s}}_i=p_i/\sqrt{M_i}=\sqrt{M_i}{\stackrel{.}{x}}_i$, respectively. We denote J↔_s as the Jacobian transformation for mass-scaled ds_j in terms of a complete set of orthogonal coordinates {w}^N, in which w_ξ ≡ q_ξ. J↔_s is a function of masses and {w}^N only. The same J↔_s is also the transformation for the kinetic energy and for mass-scaled dṡ_j in terms of {ẇ}^N, in which ẇ_ξ ≡ q̇_ξ. So Eq. (1) in the phase space of {w}^N and {ẇ}^N is (Supp. Info.):

$$G_{\xi }({\xi }_0)=\frac{-1}{\beta }ln\iint \frac{\left|{\overleftrightarrow{J}}_s\right|{dw}^{N-1}\left|{\overleftrightarrow{J}}_s\right|d{\stackrel{.}{w}}^N}{h^N}{e}^{\frac{-\beta }{2}\left[\sum _{j=1}^N{h}_{w_j}^2{\stackrel{.}{w}}_j^2+V({\xi }_0,{\left\{W\right\}}^{N-1})\right]}$$ (8)

where h is Planck’s constant, h_wj is a Jacobian scale factor with $\left|{\overleftrightarrow{J}}_s\right|={\displaystyle \prod _{m=1}^N}{h}_{w_m}$. By putting one more constraint: ẇ_ξ ≡ q̇_ξ = 0 in Eq. (8), then integrating out all velocities, the modified free-energy profile G_ξξ̇ is:

$$G_{\xi \xi }({\xi }_0)=\frac{-1}{\beta }ln\int h_{w_{\xi }}\left|{\overleftrightarrow{J}}_s\right|{dw}^{N-1}{e}^{-\beta V\left({\xi }_0,{\left\{W\right\}}^{N-1}\right)}\frac{1}{h}{\left(\frac{k_{B}T}{2\pi {\hslash }^2}\right)}^{\frac{N-1}{2}}$$ (9)

By Zwanzig’s free-energy perturbation theory ³⁴, Eq. (8) and (9) are related (Supp. Info.):

$$G_{\xi }({\xi }_0)=G_{\xi \xi }({\xi }_0)-k_{B}Tln{\langle h_{w_{\xi }}^{-1}\rangle }_{{\xi }_0{\stackrel{.}{q}}_{\xi }}-k_{B}Tln\sqrt{2\pi k_{B}T}$$ (10)

The second term on the RHS of Eq. (10) is called the Fixman term ²⁸.

Now if we do the perturbation on ensemble average, then Eq. (7) can be obtained from the constrained MD (Supp. Info.):

$$\frac{{dG}_{\xi }({\xi }_0)}{d{\xi }_0}=\frac{1}{{\langle h_{w_{\xi }}^{-1}\rangle }_{{\xi }_0{\stackrel{.}{q}}_{\xi }}}\left({\langle \frac{1}{h_{w_{\xi }}}\stackrel{\rightharpoonup }{\nabla }V·\left(\frac{\overrightarrow{\nabla }{q}_{\xi }}{|\overrightarrow{\nabla }{q}_{\xi }{|}^2}\right)\rangle }_{{\xi }_0{\stackrel{.}{q}}_{\xi }}-\frac{1}{\beta }{\langle \frac{1}{h_{w_{\xi }}}\overrightarrow{\nabla }·\left(\frac{\overrightarrow{\nabla }{q}_{\xi }}{|\overrightarrow{\nabla }{q}_{\xi }{|}^2}\right)\rangle }_{{\xi }_0{\stackrel{.}{q}}_{\xi }}\right)$$ (11)

The V in Eq. (11) is the original potential energy. Following from Eq. (4), it is now straightforward to yield the Jacobian scale factor h_wξ for w_ξ ≡ q_ξ in the mass-scaled orthogonal contravariant space:

$$\frac{1}{h_{w_{\xi }}}=\left|{\stackrel{\rightharpoonup }{\nabla }}_{\left\{s\right\}}{w}_{\xi }\right|=\left|\sum _{j=1}^N{\left(\frac{\partial w_{\xi }}{\partial s_j}\right)}_{{\left\{s_{m\ne j}\right\}}^{N-1}}{\widehat{s}}_j\right|=\left|\sum _{j=1}^N{\left(\frac{\partial q_{\xi }}{\partial x_j}\right)}_{{\left\{x_{m\ne j}\right\}}^{N-1}}\frac{{\widehat{x}}_j}{\sqrt{M_j}}\right|$$ (12)

Eq. (12) correctly indicates the velocity contribution to the partition function in Eq. (10) and. (11) decreases with mass, as opposed to momentum (see Supp. Info. for a simple one-dimensional one-body example).¹ Notably, the entire correction term in Eq. (10), i.e., $h_{w_{\xi }}^{-1}$, is the inverse of the entire term reported in other literature ^{15, 16, 18, 22–27, 29}.

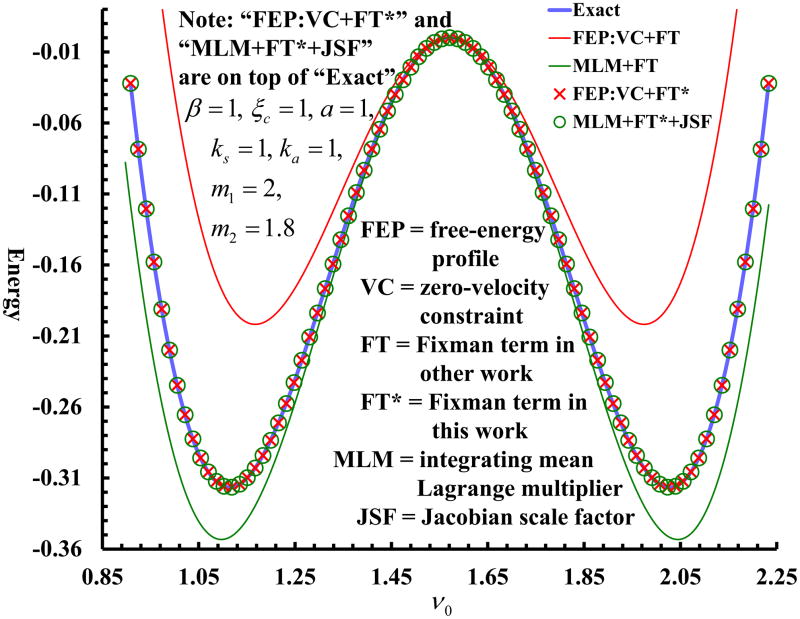
To verify the mass-dependence of the Fixman term shown in Eq. (10) and (12) is correct, we consider a two-degree-of-freedom system: x₁ and x₂ with mass m₁ and m₂, respectively. We would like to express these two degrees of freedom in terms of a set of two standard elliptic coordinates {μ,ν}, in which the coordinate of interest ν ∈ [0,2π]is: $2acos\nu \equiv \sqrt{{(x_1+a)}^2+x_2^2}-\sqrt{{(x_1-a)}^2+x_2^2}$. Fig. 3, which is plotted from Eq. (1), (9), and (10) (details for the two-body double-well potential and full Jacobian transformation are in the Supp. Info.) assures the mass-dependence of the Fixman term derived in Eq. (10), (11), and (12) is correct and exact (i.e., FEP:VC+FT*), while using the Fixman term found in the literature^{15, 16, 18, 22–27, 29} (i.e., FEP:VC+FT) does not return the exact results and underestimates the exact free-energy barrier by about 35%.

Fig. 3.

Comparison of exact free-energy profile [Eq. (1)], profile with zero-velocity constraint [Eq. (9)], Fixman term in this work: “FT*” [Eq. (12)], Fixman term in the literature: “FT” [i.e., inverse of Eq. (12) ^{15, 16, 18, 22–27, 29}], and integrated mean Lagrange multiplier with and without Jacobian scale factor derived in this work [i.e., Eq. (14) and (13), respectively]. All curves are symmetric and anchored at zero value when ν₀ = π/2.

IV: Integrated mean Lagrange multiplier (constrained MD)

Certain literature ^{15, 16, 22–27} suggests that integration of the mean of the Lagrange multiplier λ_ν associated with the constraint force would return G_νν̇(ν₀) [Eq. (9)]. If generally true, then this would be a convenient approach because the explicit knowledge of the Laplacian of the coordinate of interest in Eq. (11) is not required. In their derivations ^{23, 26, 27} that equate λ_ν with the exact free-energy profile, the Jacobian contribution is not discussed (or else is assumed to vanish) and the Fixman term is the inverse of the Fixman term shown in Eq. (10) and (12). As a result, the following quantity has been claimed to be equal to the original free-energy profile G_ν(ν₀) [Eq. (1)] ^{15, 16, 22–27}:

$$\underset{}{\overset{{\nu }_0}{\int }}{\langle {\lambda }_{\nu }\rangle }_{{\nu }^{\prime }\stackrel{.}{v}}d{\nu }^{\prime }-k_{B}Tln{\langle h_{\nu }\rangle }_{{\nu }_0\stackrel{.}{v}}$$ (13)

From Fig. 3, in contrast to our exact relation (i.e., FEP:VC+FT*), it is clear that Eq. (13) (i.e., MLM+FT) does not return us the exact G_ν(ν₀), and in fact (not shown in Fig. 3) integrating 〈λ_ν〉_νν̇(ν₀) (i.e., MLM) also does not return G_νν̇(ν₀) (i.e., FEP:VC). The use of Eq. (13), for this example, would lead to an overestimate of the exact free-energy barrier by about 10%. In order to correct Eq. (13) to obtain the exact free-energy profile, not only do we first need to use the Fixman term derived in this work [i.e., Eq. (10) and (12)], but also we need to add a new contribution from mass-scaled Jacobian scale factor as follows:

$$G_{\nu }({\nu }_0)=\underset{}{\overset{{\nu }_0}{\int }}{\langle {\lambda }_{{\nu }^{\prime }}\rangle }_{{\nu }^{\prime }\stackrel{.}{v}}d{\nu }^{\prime }-k_{B}Tln{\langle h_{\nu }^{-1}\rangle }_{{\nu }_0\stackrel{.}{v}}-2k_{B}T\underset{}{\overset{{\nu }_0}{\int }}{\langle {\stackrel{\rightharpoonup }{\nabla }}_{\left\{s\right\}}{h}_{\nu }·\left(\frac{{\stackrel{\rightharpoonup }{\nabla }}_{\left\{s\right\}}\nu }{\left|{\stackrel{\rightharpoonup }{\nabla }}_{\left\{s\right\}}\nu \right|}\right)\rangle }_{{\nu }^{\prime }\stackrel{.}{v}}d{\nu }^{\prime }+\text{constant}$$ (14)

This exact relation is illustrated in Fig. 3 (MLM+FT*+JSF). The new third term on the RHS of Eq. (14) is associated with the differentiation of the mass-scaled Jacobian scale factor of the coordinate of interest, and arises from the inherent ν̇ = 0 condition in constrained MD simulation where the corresponding coordinate is held fixed. With the zero-velocity constraint, this differentiation information is unavailable in the Lagrange multiplier and requires explicit knowledge of the Laplacian of the coordinate of interest to recover it fully ^{18, 29} (Supp. Info.).

V: Conclusion

In this work, new exact relations between PMF and free-energy profile (with or without full Jacobian transformation) are presented. Specifically, we apply mathematical and physical concepts of covariant and contravariant vector space [e.g., Eq. (3), (4), (12)] from differential geometry and general relativity to derive explicit, practical expressions that equate the PMF obtained from (constrained) MD simulations with the free-energy profile in terms of the Cartesian coordinates [i.e., Eq. (7) and (11)]. These general expressions require knowledge only of the (constraint) coordinate of interest, and thus are immensely practical in molecular simulations that may require complex coordinate constraints used as basic variables in the free-energy profile. Further, we demonstrate that, in general, in addition to the Jacobian contribution, the Leibnizian contribution derived here still needs to be considered when there is an interdependence of the integration domains [Eq. (2)] (even if a full Jacobian transformation is available). Moreover, we illustrate that the individual contribution from the mean force, and from the Jacobian can vary significantly (e.g., from ~140% to ~400% in terms of the free-energy barriers considered in Figs. 1 and 2) with different complete sets of coordinates for which the (constraint) coordinate of interest is a simultaneous member. A sufficient condition to make the contributions be invariant is to be in the orthogonal contravariant space [Eq. (5) and (6)], in which the Leibnizian contribution vanishes. Next, we present a definition of the Fixman term with correct dependence on mass in constrained MD simulations [Eq. (10), (11), (12)]. Finally, we divulge that an additional term arising from the Jacobian scale factor contribution that requires explicit knowledge of the Laplacian of the coordinate of interest [Eq. (14)] must be included in order to exactly equate the integrated mean Lagrange multiplier with the free-energy profile. All formulations presented here are verified and illustrated by new non-trivial benchmark numerical results, and are compared with those reported in other literature, which, for the examples studied here, result in discrepancies from the exact values by about 10% to 35% in terms of free-energy barriers (Figs. 1–3). Future work will involve application of the present formulations to simulations of more complex, real-world molecular processes, and comparison with other methods to determine the free-energy profiles.