Coupling quantum interpretative techniques: another look at chemical mechanisms in organic reactions

Abstract

A cross ELF-NCI analysis is tested over prototypical organic reactions. The synergetic use of ELF and NCI enables the understanding of reaction mechanisms since each method can respectively identify regions of strong and weak electron pairing. Chemically intuitive results are recovered and enriched by the identification of new features. Non covalent interactions are found to foresee the evolution of the reaction from the initial steps. Within NCI, no topological catastrophe is observed as changes are continuous to such an extent that future reaction steps can be predicted from the evolution of the initial NCI critical points. Indeed, strong convergences through the reaction paths between ELF and NCI critical points enable to identify key interactions at the origin of the bond formation. VMD scripts enabling the automatic generation of movies depicting the cross NCI/ELF analysis along a reaction path (or following a Born-Oppenheimer molecular dynamics trajectory) are provided as S.I.

Revealing the formation, reorganization or breaking of the chemical bonds of any molecular systems forms the foundation of chemistry. However theoretical chemists are limited by the fact that bonds do not appear in the Hamiltonian. Thus interpretative tools are necessary to recover chemical structure and reactivity and more specifically to understand the process of bond formation and bond breaking during reactions.

Over the years, different approaches have been developed. Molecular Orbital (MO) theory has been very useful and successful for the theoretical analysis of chemical reactions and chemical reactivity. The frontier orbital theory¹ and the orbital symmetry rules of Woodward and Hoffman² are paradigmatic examples of the possibilities of quantum chemistry within the MO theory. To reduce the dimensionality of the problem, three dimensional interpretative approaches have been introduced. The conceptual density functional theory pioneered by R.G. Parr³ has been at the origin of very useful reactivity descriptors. Another low dimensional approach has originally been developed by Bader^4,5: the topological approach. Within these approaches, 3D space is divided into mutually disjoint regions following the gradient of a scalar function. Bader’s QTAIM (Quantum Theory of Atoms In Molecules) theory is based on the topological analysis of the density and provides a picture of the system formed by atoms. Following the same philosophy, ELF^6–8 (Electron Localization Function) topological analysis divides the space into chemically intuitive regions associated to electron pairs so that electron shells, bonds and lone pairs are revealed. This approach appears therefore attractive to interpret reaction mechanisms, and it has indeed given rise to the bonding evolution theory by Krokidis et al.⁹

The crucial role of weak interactions in chemical reactions can also be analyzed in an indirect manner through property computations (from population to electrostatic moments)¹⁰. However, these fluctuations are not easily visualized. Very recently, some of us have introduced the reduced density gradient s(ρ) as a new scalar function based on the electron density ρ(r) to map and analyze non-covalent interactions^11,12, providing a rich representation of van der Waals interactions, hydrogen bonds, and steric repulsions (NB: This includes both attractive and repulsive interactions)^13,14.

The s(ρ) function is defined using the electron density and its first derivatives:

$$s(\rho )=\frac{1}{2{(3{\pi }^2)}^{1/3}}\frac{|\mathrm{\nabla }\rho |}{{\rho }^{4/3}}$$

It is a dimensionless quantity used in DFT to describe the deviation from a homogenous electron distribution. In density tails (i.e. regions far from the molecule, in which the density is decaying to zero exponentially), the reduced gradient has very large positive values. On the contrary, the s(ρ) function assumes very small values, when approaching zero, for regions of both covalent bonding and non-covalent interactions.

These low s(ρ) regions are traced back to molecular space and give rise to isosurfaces, enabling the visualization of the weak interactions in the system. In order to differentiate between the different types of interactions, we will use the following color code:

• Blue for the highly attractive weak interactions (such as hydrogen bonds).

• Green for the extremely weak interactions (such as dispersive-like van der Waals).

• Red for repulsive interactions (such as steric clashes).

In this contribution we attempt for the first time to explain chemical reactivity using cross interpretative analysis that includes covalent and non-covalent interactions, all of them needed for understanding atomic reorganization. Representative examples from textbook organic chemistry have been chosen in order to show the applicability and the interest of the method: SN2, cycloadditions and 2-steps reactions. Given the fact that previous ELF studies on many different reactions^15–17 are already available, the work will focus on the interest of using the cross ELF/NCI approach. Indeed both approaches are complementary because ELF will encompass high density regions whereas NCI will reveal low density areas. Given the visual nature of these cross interpretative analyses, we suggest the reader to look at the different videos and pictures provided in the Supporting Information.

Geometry optimizations of reactants, products and intermediate states were performed at the B3LYP^18,19/6-31++G** ²⁰ level using the Gaussian 09 software²¹. Transition states were obtained by the STQN (Synchronous Transit and Quasi- Newton) method²², and characterized by their imaginary frequency after vibrational analysis on the optimized geometries. Connectivity between transition states and stationary points were established with IRC calculations²³. The ELF and AIM interpretative analyses were performed using the Top_Mod software²⁴. The NCI approach was carried out as implemented in NCIPLOT¹⁴. Additional methodological details can be found in the Supporting Information (S.I.-1).

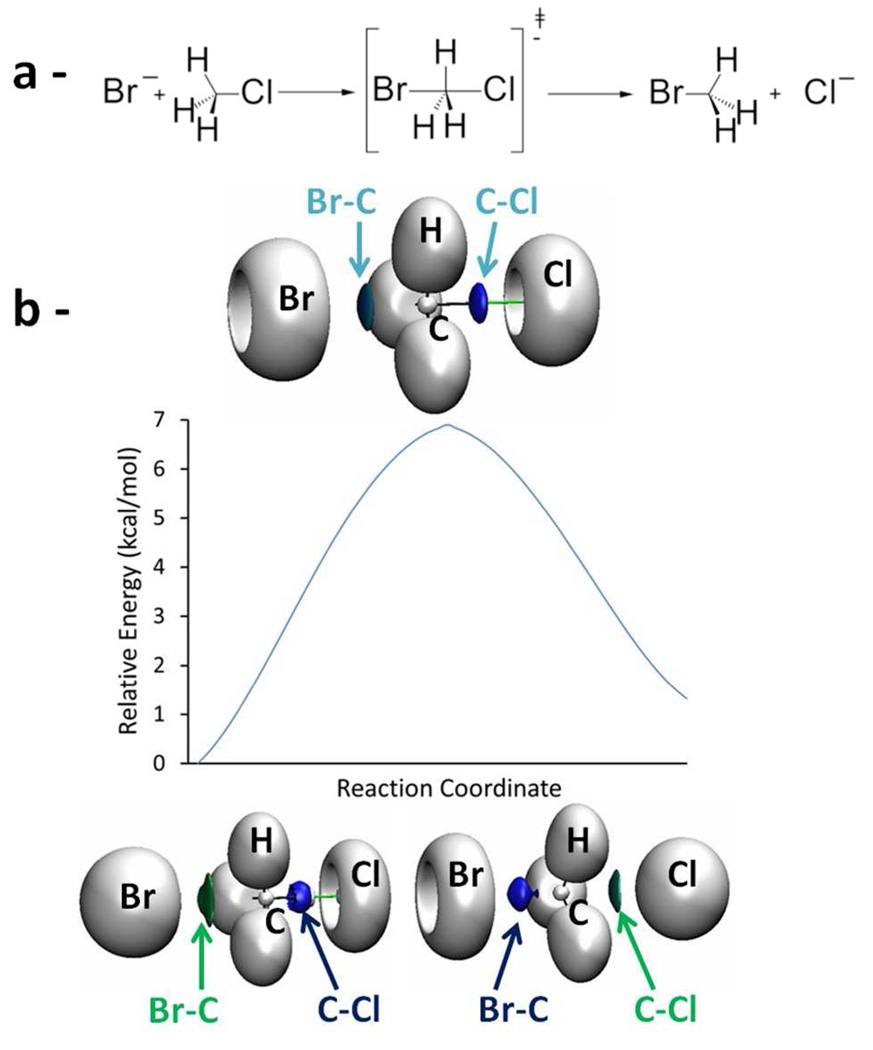
The cross ELF/NCI analysis has first been tested on prototypical SN2 reactions: chloromethanebromide ion substitution reaction (movie S.I.-M1) and chloromethane-fluorine substitution reaction. The results discussed here about the chloromethane-bromide ion substitution reaction can be generalized to the other SN2 reactions we studied. The initial and final stages (regions of strong bonding ) of the reaction are being well captured by the ELF analysis whereas NCI is more suited in order to define the nature of the weak bonds involved in the TS structure. Around the TS, the NCI piece associated to the forming C-Br bond becomes bluer (stronger) along the path, whereas the disappearing C-Cl bond becomes greener (weaker). As the reaction profile is roughly symmetric, at the transition state, the formed and broken bonds appear similarly in NCI (same light blue color). When the bond is getting stronger, the NCI approximation becomes less accurate and cannot account for the changes in covalent binding. On the contrary, in this regime, the ELF approach is perfectly adapted to such strong interactions. ELF pieces (in gray in the movies) appear in the regions where new bonds are formed.

It is here interesting to compare the position of the NCI Interaction Critical Point (ICP) with the ELF attractors (see movie in SI-M3). Critical points of the ELF, or points of zero density gradient, are related to each of the bonds (in pink in the movie). Indeed in the range of NCI-ELF overlap, the NCI ICPs (in blue in the movie) are localized exactly at the same position as the ELF attractors for (strong) covalent bonds. The two methods appear therefore in very good agreement for interactions that are in both ranges of validity. Thus, the similarity of their topologies in the overlap region validates the cross analysis. Furthermore, this analysis highlights the capabilities of NCI to unravel the key interactions at the origin of a bond formation. It is important to note that there is no formal “topological catastrophe” event appearing within the NCI analyzed path as changes are continuous: all the NCI critical points are already found at the beginning of the reaction. Thus, it appears that the location of the final ELF transition-state ICP within the strong electron pairing regime can be foreseen by following the evolutions of the NCI initial ICPs within the weak electron pairing regime through the path separating the initial and transition states.

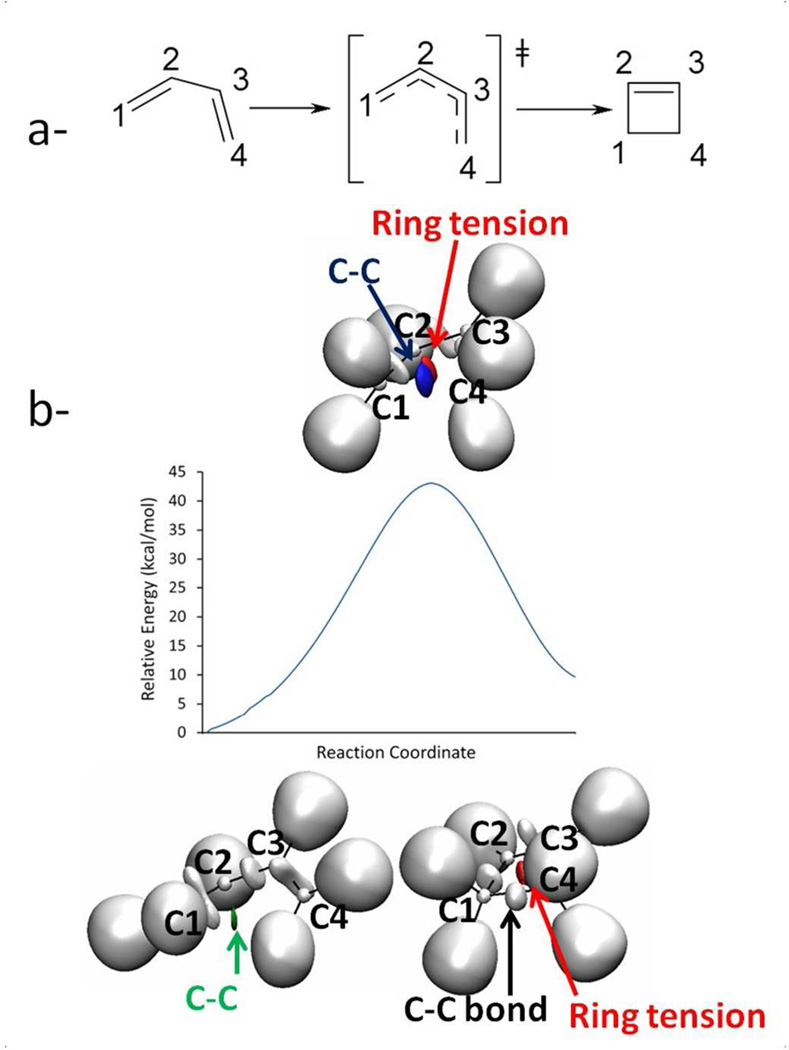
As with SN2 reactions, electrocyclization and Diels-Alder reactions have been widely studied through the computational community ^{11,15,25–27}. The use of NCI analysis coupled with the ELF approach yields however to new (steric) information. Indeed as we can see during the electrocyclization reaction of butadiene in Figure 2, the following of the modification of the ELF basins of the single and double bonds allows us to monitor the electronic reorganization along the reaction. Within the ELF analysis, double bonds are characterized by showing two basins, which in 3D give rise to an oblong isosurface, whereas single bonds are centered on the internuclear line. Following the changes in the cycloaddition, it can be seen that the C₁-C₂ and C₃-C₄ basins are changing from a double to a simple bond basin along the reaction whereas the C₂-C₃ basins undergo the opposite change.

Figure 2.

(a) Lewis scheme of electrocyclization of butadiene. (b) IRC path for electrocyclization of butadiene with ELF-NCI snapshots of reactants, transition state and products. Relative Energy = E-E_react were E_react is the energy of the initial state and E the energy of an IRC point.

The NCI analysis shows an interaction in the cyclobutene molecule that is not localized on a bond (or an incoming bond) but at the center of the ring and which corresponds to the future bond and ring tension. Such an interaction was not present in the reactant state which exhibits a single stabilizing interaction (light blue). Indeed this initial interaction appears to bifurcate along the reaction coordinate into the C₂-C₃ bond interaction (blue) and ring tension (red) (see movie in SI-M2). The NCI ring tension seems to already preexist as it has been prepared in the initial interaction even if such ring did not exist. This opens up possibilities in the analysis of reaction mechanism and the search for transition states.

To complement these results we resort to the ELF analysis. Therefore to follow the density reorganization, we can monitor distributed properties within the ELF basins, such as populations and electrostatic moments (see SI-1.I for details about the ELF moments use and evaluation). These data (Figures in SI-1.II) show the reorganization of the different bond and lone pairs. Important modifications of such quantities can be observed around the transition state when the bond multiplicity varies. Along the cyclization, the C₂-C₃ bond becomes double, therefore its population increases so do the M1 and M2 moments. On the contrary, the bonds which become single, C₁-C₂ and C₃-C₄, show a decrease in population and moments.

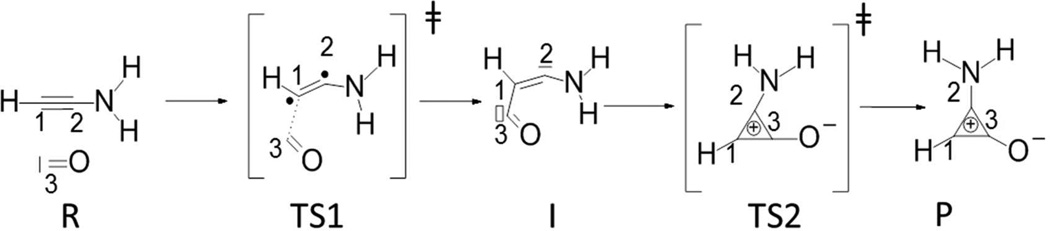
As a last example, the ELF/NCI cross analysis was applied to a two-step [2+1] cycloaddition of carbon monoxide to ethynamine15 in order to test more complicated reaction mechanisms. During the first step, the interaction between C1 and C3 can be followed by NCI analysis (the interaction goes from green to deep blue). However, for the second step, the electronic density is too high to consider interactions in the NCI approximation. This can be seen in the movie SI-M5, where the NCI isosurfaces are so strong that it is difficult to follow the changes. ELF analysis is thus preferred to explain high density reorganization. Results are thus presented in Table 1. The evolution of ELF basins (see movies SI-M4) shows that, in a first time, the C3 lone pair seems to transfer electrons into the C1-C3 bond corresponding to a mechanism of nucleophilic attack from the C3 lone pair to the C1 atom. In the second step, the C2 lone pair attacks C3 carbon to form the C2-C3 bond (as shown by the diminution of the population of V(C2) in Table 1). As within this step, the NCI approximation is less useful; we can resort to the ELF analysis and monitor ELF distributed properties within ELF basins. These data bring additional information allowing us to determine mesomeric species (Table 1). For instance, at the intermediate state, the C1-C3 bond has characteristics of double bonds (double basin) but its population is only of 3 e⁻. The remaining electron appears localized on the C1 lone pair. The C1-C2 bond appears as a single bond (M1 and M2) whereas C2-N bond has an important double bond character and the N atom lone pair basin has disappeared. All these observations prove that an important delocalization is present at the intermediate state, thus stabilizing it. Likewise, population analysis of the product state leads us to assume that the structure has with a delocalized positive charge in the cycle and a negative charge on the oxygen atom.

Table 1.

Population (MO), norm of dipolar (Ml) and quadrupolar moments (M2) of different ELF basins at different points of the cycloaddition of carbon monoxide on ethynamine). If several basins have the same name for one point (double basins), their populations are added and their moments are not indicated (the acronym DB is used).

	Basin	R	TS1	I	TS2	P
M 0 (a.u.)	V(C1,C2)	5.57	3.43	2.03	1.91	2.85
	V(C1,C3)	×	×	3.38	2.87	2.61
	V(C2,C3)	×	×	×	1.41	2.45
	V(C2,N)	2.25	2.36	3.65	2.1	2
	V(C1)	×	0.87	0.71	0.54	×
	V(C2)	×	1.29	2.08	1.29	×
	V(C3)	2.56	2.64	×	×	×
	V(O)	4.17	4.53	4.8	5.36	5.43
	V(N)	1.71	1.49	×	1.59	1.81
M 1 (a.u.)	V(C1,C2)	5.377	DB	0.116	0.608	0.415
	V(C1,C3)	×	2.741	DB	0.69	0.378
	V(C2,C3)	×	×	×	0.348	0.376
	V(C2,N)	0.123	0.535	1.924	0.1	0.054
M2 (a.u.)	V(C1,C2)	6.569	DB	0.579	1.003	2.059
	V(C1,C3)	×	3.008	DB	1.032	1.249
	V(C2,C3)	×	×	×	0.377	0.87
	V(C2,N)	0.453	1.152	2.576	0.624	0.443

This approach is general to the study of any structure modification in a system. Therefore it can be generalized to the study of ab initio dynamic simulations (see SI-M6). The test presented here is a 225 fs simulation (at B3LYP level) of the water dimer (6-31G basis set). This very first dynamical application of ELF/NCI opens the doors of interpretative analysis for dynamic systems by cross interpretative techniques. The approach completely recovers the intuitive chemical evolution of the lone pair (ELF) and hydrogen bond (NCI) modifications along the trajectories. The evolution of the hydrogen bond goes along with a modification of the volume and moments of the lone pair. Such capabilities of observations should be of interest for the development of next generation polarizable force fields.²⁸

The present work highlights the complementarity of ELF and NCI analysis for the study and the understanding of reaction mechanisms. ELF and topological analysis have proved to be a powerful tool to study density modification along a reaction path. However weak interactions remain difficult to visualize. Using a recently introduced complementary technique, NCI, we have developed a new ELF-NCI cross interpretative approach that enables to follow the full range of interactions. This approach has been automated and gives intuitive and visual results as demonstrated in the prototypical organic reactions. Along the reaction paths some interesting features have been identified:

• Within NCI, no topological catastrophe is observed as changes are continuous, NCI analysis contains therefore the information of the future reaction steps and should then be able to predict them.

• A correspondence was found between the interaction seen by ELF and that revealed by NCI in the region where information is available for both (ELF attractors and NCI ICPs overlap). This observation reinforces the consistency of the cross analysis at different ranges of interactions and enables to identify key interactions at the origin of the formation of chemical bond.

Finally, it is worth noting that this method can easily be generalized to any kind of reaction or dynamic system: enzymatic reaction, molecular dynamic, inorganic reactions, and catalytic system. Indeed, the first application to first principle molecular dynamics has been hereby presented. It should be also pointed out that a synergetic use of QTAIM and NCI could be also automatically handled using the NCI and TopMod programs.

VMD scripts enabling the automatic generation of movies depicting the cross NCI/ELF analysis along a reaction path (or following a Born-Oppenheimer molecular dynamics trajectory) are provided as S.I..

Extension of the ELF/NCI approach is presently underway in the framework the 4-component fully relativistic framework as coupling of the Electron Pair Function (EPLF)²⁹ with NCI is also underway.

Figure 1.

(a) Lewis scheme of SN2 reaction between chloromethane and bromide ion. (b) IRC path for SN2 reaction between chloromethane and bromide ion with ELF-NCI snapshots of reactants, transition state and products. Relative Energy = E-E_react were E_react is the energy of the initial state and E the energy of an IRC point.

Figure 3.

Lewis scheme of [2+1] cycloaddition of carbon monoxide to ethynamine.