Emission guided radiation therapy for lung and prostate cancers: A feasibility study on a digital patient

Abstract

Purpose: Accurate tumor tracking remains a challenge in current radiation therapy. Many strategies including image guided radiation therapy alleviate the problem to certain extents. The authors propose a new modality called emission guided radiation therapy (EGRT) to accurately and directly track the tumor based on its biological signature. This work is to demonstrate the feasibility of EGRT under two clinical scenarios using a 4D digital patient model.

Methods: EGRT uses lines of response (LOR’s) from positron emission events to direct beamlets of therapeutic radiation through the emission sites inside a tumor. This is accomplished by a radiation delivery system consisting of a Linac and positron emission tomography (PET) detectors on a fast rotating closed-ring gantry. During the treatment of radiotracer-administrated cancer patients, PET detectors collect LOR's from tumor uptake sites and the Linac responds in nearly real-time with beamlets of radiation along the same LOR paths. Moving tumors are therefore treated with a high targeting accuracy. Based on the EGRT concept, the authors design a treatment method with additional modulation algorithms including attenuation correction and an integrated boost scheme. Performance is evaluated using simulations of a lung tumor case with 3D motion and a prostate tumor case with setup errors. The emission process is simulated by Geant4 Application for Tomographic Emission package (GATE) and Linac dose delivery is simulated using a voxel-based Monte Carlo algorithm (VMC++).

Results: In the lung case with attenuation correction, compared to a conventional helical treatment, EGRT achieves a 41% relative increase in dose to 95% of the gross tumor volume (GTV) and a 55% increase to 50% of the GTV. All dose distributions are normalized for the same dose to the lung. In the prostate case with the integrated boost and no setup error, EGRT yields a 19% and 55% relative dose increase to 95% and 50% of the GTV, respectively, when all methods are normalized for the same dose to the rectum. In the prostate case with integrated boost where setup error is present, EGRT contributes a 21% and 52% relative dose increase to 95% and 50% of the GTV, respectively.

Conclusions: As a new radiation therapy modality with inherent tumor tracking, EGRT has the potential to substantially improve targeting in radiation therapy in the presence of intrafractional and interfractional motion.

INTRODUCTION

Despite the significant advances in external beam radiation therapy over the last several decades, accurate tumor tracking remains a major challenge due to the uncertainties originating from a variety of factors including tumor volume delineation, patient setup, and physiologic motion.¹ Treatment efficacy is limited by this difficulty. For example, intensity modulated radiation therapy (IMRT) is capable of generating highly conformal dose distributions to spare healthy tissues.^{2, 3} However, IMRT treatment performance is heavily determined by the accuracy of tumor tracking, which cannot be guaranteed in the presence of intrafractional organ motion^{4, 5, 6} and interfractional patient setup errors.^{5, 7, 8} To compensate for tumor location uncertainties, treatment margins up to 1.5 cm are routinely added to the clinical target volume (CTV) to obtain the planning target volume (PTV) as the target for the prescription dose.^{9, 10, 11} Although the added treatment margin ensures dose coverage of the tumor, the benefits may be counteracted by the extra dose to the normal tissue surrounding the target.

In order to reduce treatment margins, it is critical to minimize tumor location uncertainty with tumor localization. Many techniques and devices have been proposed and implemented clinically. They have shown certain success but with different drawbacks. For example, respiratory gating techniques attempt to track large and periodic tumor motion by monitoring an external surrogate.^{12, 13} The performance of these indirect tracking methods relies on the unfaithful correlation between the tumor and the surrogate motion.^{14, 15} For enhanced correlation and improved treatment guidance accuracy, more effective tumor targeting is clinically achieved by implanting electromagnetic fiducial transponders or internal fiducial markers^{16, 17} into the disease sites.¹⁸ These invasive procedures are not only costly but also sacrifice patient comfort and may cause severe side effects, such as pneumothorax.¹⁹ Moreover, implanted internal markers cannot accurately depict the whole tumor volume and shape by showing only several points on the tumor, and possible marker migration is also an issue. Some researchers have proposed direct tumor targeting methods using fluoroscopic images without implanting markers.^{20, 21} In these studies, tumor motion phase or position is determined by matching the real-time acquired fluoroscopic images with the prebuilt templates, which may fail when the tumor boundary is unclear in fluoroscopic images.²² Even if perfect localization is achieved, the uncertainties arising from tumor volume delineation are difficult to address.

Besides tumor localization, a further challenge of high-performance radiation therapy is to accurately deliver the dose to a fast moving target. A popular approach is delivery gating.²³ A gated delivery scheme turns the treatment beam on only when the monitored tumor position falls into the preplanned area. This method ensures that the beam always hits the tumor, at the price of a low duty cycle. Dynamic motion compensation strategies achieve much higher duty cycles through real-time patient-beam alignment technologies. Typical methods of dynamic motion compensation include couch shifting,^{24, 25} dynamic multileaf collimator (DMLC) tracking,^{26, 27, 28} and robotic tracking.²⁹ Couch shifting may introduce continuous back-and-forth patient motion, which leads to problems of patient discomfort and low treatment tolerance.¹ DMLC tracking may require leaf speeds that may at times exceed the MLC speed limit.¹ It also involves nontrivial adjustments to the base treatment plan for satisfactory performance.³⁰ Robotic tracking offers more degrees of freedom in space for dose delivery through the use of a miniature Linac mounted on a flexible robotic arm. However, it usually requires the implantation of fiducial markers for image guidance.

In search of a new method that inherently and automatically integrates accurate tumor tracking and dose delivery, we have proposed the concept of emission guided radiation therapy (EGRT).^{31, 32, 33, 34, 35} In EGRT, positron emission tracers are first administrated to patients. As in conventional positron emission tomography (PET) imaging, lines of response (LOR’s) are continuously detected from photon pairs produced by positron annihilation events within the tracer. Each detected LOR gives an approximate line-of-sight to the emission source almost instantaneously due to the intrinsic collimation effect of coincidence detection.³⁶ Instead of waiting minutes for enough LOR's to form PET images, an EGRT system delivers beamlets of therapeutic radiation along LOR paths individually as they are detected. The nearly real-time LOR response is made possible with a fast rotating Linac and collimation system to align the beam along the LOR path with a minimal lag time. The feasibility of rotating a Linac and a binary multileaf collimator (bMLC) has been previously demonstrated, as well as a rotating PET system.^{37, 38, 39, 40, 41} With the integration of real-time emission detection and radiotherapy, tumor localization and dose delivery are more naturally unified. The emission guidance of EGRT stems from the physical principle of positron annihilation in PET imaging. Therefore, EGRT can be classified as a new type of broadly defined image-guided radiation therapy (IGRT) method. It should be noted that the treatment guidance in EGRT is not provided by PET images, but rather by individual emission rays.

The goal of this work is to demonstrate the feasibility of EGRT in two clinical scenarios using computer simulations of a digital patient model and to evaluate its performance compared to a conventional therapy approach. Both positron emission and beamlet-based radiation delivery are simulated using Monte Carlo (MC) simulations on the digital anthropomorphic XCAT phantom.⁴² In this paper, we first describe the design of the EGRT treatment system as well as a corresponding treatment scheme. We then present the simulation framework and the simulation studies with results and finally we discuss other considerations, benefits, and limitations of this new therapy approach.

METHODS

Proposed geometry

Figure 1 shows the proposed EGRT treatment system design. The system is composed of two major components: two arcs of symmetrically opposed PET detectors and a compact Linac equipped with both a primary collimator and a rapidly switching bMLC. The Linac design is based on current technology,⁴³ with a photon beam energy of 6 MV and a maximum dose rate delivery capability of 800 MU/min. The bMLC system is also based on a current pneumatic-driven system with 64 binary leaves made of 10-cm-thick tungsten. The Linac, collimation system, and PET detectors are mounted together on a fast rotating slip-ring gantry in the same transverse plane. The primary collimator defines the slice width of the fan beam of radiation and the bMLC selects among individual beamlets within this fan beam in order to direct radiation along the detected LOR paths. In EGRT, only LOR's that meet predefined criteria (noted as qualified LOR's) are used for emission guidance. These predefined criteria are specified by the EGRT algorithm, as presented in detail in a later section. Based on the qualified LOR’s, the Linac delivers therapeutic dose from designated points (referred to as firing positions), which are equally spaced around the circular gantry. During treatment, the system rotates around the system isocenter with a constant rotation period while the patient is being translated slowly through the system bore with a fixed translation speed, resulting in a helical dose delivery scheme. In order to accurately track tumor motion, the gantry rotation period should be small relative to the respiratory cycle or the motion period of the tumor in consideration. In this work, we model a constant rotation period of 1 s. On the proposed system, if the PET activity distribution is relatively uniform, the average angular separation between a detected LOR and the Linac position at any given time is about 90°. With a 1 s rotation period, the expected average lag time of Linac response to a qualified LOR is 250 ms. This inherent latency in the system is modeled in all simulations to assess the EGRT system's ability to track tumor motion.

Figure 1.

Cross-sectional diagram of the proposed treatment system geometry for EGRT. The PET detector arcs are symmetrically opposed, with a span of 2 cm in the longitudinal direction. During treatment, PET detectors, Linac system, and MV x-ray detectors rotate together around the system isocenter on a slip-ring gantry. The patient table moves in the longitudinal direction so that the treatment is delivered helically.

We model 256 firing positions around the gantry circle, which is similar to the number of angular bins assigned to LOR data in conventional clinical PET imaging. At a 1 s revolution period, there is about 4 ms between firing positions and we assume the bMLC can switch to a new configuration within this travel time to prepare for dose delivery at the next firing position. Current high speed pneumatically driven tungsten leaves can switch as fast as within 10–20 ms.⁴⁴ If 4 ms cannot be physically achieved for our proposed system, either a slower rotation speed or fewer firing positions or a combination of both can be employed to ensure the feasibility of the designed bMLC configurations. In this work, bMLC configurations refer to the set of information that defines beamlet responses including the spatial coordinates of the firing points, the leaf numbers that are opened, and the phase number of the phantom when a leaf is opened (for evaluation purposes). Current medical Linacs operate in a pulsed mode, with a very low duty cycle. Each pulse is on for a few microseconds, with a few milliseconds between pulses, yielding duty cycles on the order of 0.1%. Thus, the bMLC motion speed will most likely be the main limiting factor with respect to timing in the EGRT system design.

Basic EGRT treatment algorithm

The EGRT algorithm is based on the concept of backprojecting beamlets of radiation along detected LOR paths. Figure 2 is an illustration of the proposed treatment scheme. Figure 2a shows two distinct events during EGRT treatment: the moment when one LOR is detected (Linac and PET detector arcs are displayed with solid lines) and the moment when the Linac responds to this LOR by backprojecting a beamlet along the LOR path (Linac and PET detector arcs are displayed with dotted lines). Figure 2a also illustrates the procedures of an EGRT treatment: (1) PTV is defined, at the tumor contouring stage, to contain the gross tumor volume (GTV) motion, i.e., internal target volume (ITV), with additional margins as in the case of conventional radiation therapy. The patient is administered with a PET radiotracer and undergoes setup and registration using megavoltage CT (MVCT) images after the patient is positioned on the table to align the PTV. MVCT can provide sufficient image quality for tumor identification and patient setup.⁴⁵ (MVCT x-ray detectors and patient table are shown in Fig. 1 but not in Fig. 2 for simplicity.) (2) The EGRT system performs in-plane rotation continuously with a constant period on the slip-ring gantry while the patient bench undergoes through-plane translation for a helical treatment. (3) LOR's are detected. (4) A LOR that meets certain criteria (explained below) is stored as a qualified LOR. When the Linac arrives at the firing position for this LOR, the corresponding collimator leaf is opened, resulting in a radiation beamlet delivered along this particular LOR path. LOR detection and selective LOR response [steps (3) and (4)] are repeated to achieve the full helical treatment covering the PTV.

Figure 2.

Illustration of EGRT treatment scheme. (a) shows the process of LOR detection and the beamlets of radiation response. (b) and (c) are enlarged views of the corresponding blocks as labeled in (a). (b) shows the EGRT spatial window, one of the LOR response criteria of the basic EGRT treatment scheme. The LOR (solid/dashed line in (b)) that intersects the source trajectory at a point that falls within the EGRT spatial window (arrow arc in (b)) is qualified for radiation response. (b) and (c) together show the collimator leaf (shaded) closest to the line that connects the source and the midpoint of the LOR-PTV intersection [indicated in (c)].

The margins added to the CTV to define the PTV account for tumor location uncertainties including intrafractional/interfractional motion and setup errors such that the tumor is always inside the PTV during treatment. The PTV is assumed to be static throughout the treatment and provides an approximate region in which the GTV is contained. Only the LOR's intersecting the PTV are used for treatment guidance, so that the EGRT system can track and locate the GTV for dose delivery with minimal interference from background emissions.

Besides the PTV criterion, other criteria are also used in EGRT to optimally use the LOR's in guiding radiation beamlets. In the basic EGRT algorithm, these predefined criteria include: the EGRT time window, PTV intersection, and the EGRT spatial window. To ensure nearly real-time tracking, the Linac only responds to LOR's that are detected within a short period of time relative to the current firing time, referred to as the EGRT time window. In this work, the EGRT time window is fixed to be 500 ms. The PTV intersection criterion excludes LOR's that do not intersect the PTV, so that the LOR's originating from activity outside the target are largely avoided. Finally, the LOR's whose intersection with the source trajectory is more than a predetermined distance away from the closest firing position are also excluded to minimize azimuthal error. This small tolerance is referred to as the EGRT spatial window, specified using angular separation along the source/firing trajectory [see Fig. 2b]. It should be noted that due to this spatial tolerance, beamlets may not be backprojected exactly along the corresponding LOR paths. Figure 2b shows, in an enlarged view, the deviation of the actual delivery path (dotted line) from the detected LOR path (solid/dashed line). The actual path of delivery is selected along the line that passes through the source point and the midpoint of the LOR-PTV intersection, as illustrated together by Figs. 2b, 2c. Figure 2b also illustrates the LOR passing the EGRT spatial window criterion (arrow arc), as well as the shaded leaf that will be opened. Note that at each firing position, a set of leaves may be opened for a set of qualified LOR’s. In all simulations presented in this paper, the EGRT spatial window is fixed at ±0.5°. We find that the average leaf openings for each of the 256 firing positions, accumulated over all rotations within a 2 mm slice, are within a range of 2-6 for the PTV sizes used.

EGRT modulation

The resultant dose distribution of EGRT treatment is the summation of doses from beamlets backprojected along paths of qualified LOR’s. In the proposed helical geometry, with fast rotation, slow translation, and small PET detector extent in the longitudinal direction, the LOR's are approximately detected and responded to in a series of 2D slices. This particular “3D parallel” geometry samples the delivery space into a stack of 2D fan-beam sinograms, referred to as sinogram space. Each bin in sinogram space corresponds to a spatial orientation of a beamlet response path for a specific slice. Every detected LOR path can then be mapped into one of the sinogram bins according to a nearest neighbor approximation. Under such an approximation, the delivered dose of EGRT can be written as

$$d=D·\Sigma ·b,$$ (1)

where vector b has a length of number of elements in the sinogram space and specifies the total number of qualified LOR's for each sinogram bin in the EGRT treatment. Matrix D is a group of beamlet kernels. The jth column of D is the vectorized 3D dose distribution resulting from a beamlet with unit intensity along the LOR path specified by the jth element of the sinogram. Σ is a diagonal matrix (referred to as the modulation matrix), whose jth diagonal element corresponds to the modulation we apply on the jth sinogram bin (i.e., slice number and bMLC leaf) to improve the dose performance of EGRT. Note that, for simplicity, Eq. 1 implicitly assumes that the modulation is the same for all qualified LOR's at the same sinogram bin.

An inverse treatment planning of EGRT optimizes the modulation variables [i.e., diagonal elements of Σ in Eq. 1] such that the calculated dose best matches the prescribed dose. This task can be implemented by minimizing, for example, the L2 norm of the difference between the calculated dose and the prescribed dose for given constraints.^{46, 47, 48} Such a full characterization of EGRT treatment planning is beyond the scope of this work. In this feasibility study, we propose basic EGRT modulation methods without optimization to demonstrate the potential of dose planning. The modulation on the effective beamlet intensity is achieved by applying leaf opening probabilities on the bMLC for different sinogram bins. In the future, the beam intensity and/or duration for each leaf opening could also be modulated to provide more flexibility for dose control.

Attenuation correction

The sinogram vector b in Eq. 1 is determined by the activity distribution of positron annihilation on the patient. For the delivered dose to concentrate in the tumor, it is desired that the qualified LOR's from the tumor substantially overwhelm those from normal tissues. Although such a situation is expected when the tumor uptake ratio is significantly higher than the background, the dose concentration could be degraded in the presence of photon attenuation. In PET imaging, attenuation of the annihilation photons within the subject leads to lower signal along highly attenuating paths. If not accounted for, the reconstructed image will reflect this attenuation bias with lower activity estimates within the attenuating regions.³⁶ Attenuation correction is now routine in PET/CT imaging by using the CT scan to estimate the attenuation map of the subject at photon energies in the PET range (i.e., 511 keV), followed by using this estimate to weight LOR's according to the attenuation along their individual paths. In EGRT, the same issue arises as the LOR detection rate is inversely proportional to the attenuation of the two annihilation photons. Attenuation can be highly nonuniform across all directions, resulting in nonuniform LOR detection rates and therefore a nonuniform radiation response distribution.

To correct for the attenuation effect, we apply a modulation probability on each beamlet in sinogram space [i.e., diagonal elements of modulation matrix Σ in Eq. 1] that is inversely proportional to the LOR detection rate of that sinogram bin. Specifically, the line integrals of attenuation coefficients are first efficiently precalculated using Siddon's algorithm⁴⁹ from the planning patient CT images for all sinogram bins. The leaf opening probability is a value between 0 and 1, calculated from the attenuation of the associated bin. Let us denote the maximum line integral value across all bins as a_max. For the sinogram bin with an index j and a line integral value a_j, its leaf opening probability is given as

$$p_j=\exp (-a_{\max }+a_j).$$ (2)

Depending on the strength of the attenuation, the leaf open probability for each bin ranges from 0 to 1 to compensate for the change of LOR detection rate. Figure 3 illustrates how the response to an individual LOR is adjusted when attenuation correction modulation is enabled.

Figure 3.

Illustration of EGRT modulation in the case of attenuation correction. The workflow starts with the shaded module. When one LOR is qualified for response, i.e., it passes the three criteria of the basic EGRT algorithm, the leaf will be opened if the attenuation correction algorithm is not enabled. However, if the modulation algorithm is enabled, the open probability will not be 1. Rather, this LOR will first find its corresponding bin in terms of its spatial orientation in the precalculated attenuation map and the response probability of this LOR, p_j, is determined as shown. Note that since only LOR's that intersect the PTV may be responded to, the attenuation map is only calculated for the PTV region.

Integrated boost

Target dose boosting is often utilized in current radiation therapy to ensure that the target receives adequate dose.⁵⁰ In an integrated boost scheme, a subvolume within the PTV is prescribed a higher dose than the remaining PTV. Note that the subvolume is defined at the tumor contouring stage and is assumed static during the treatment as it is defined relative to the PTV. To achieve a target dose boost in EGRT, the same boost region is constructed within the PTV. Using Eq. 1, we can construct a modulation matrix Σ whose diagonal elements corresponding to the boost region (i.e., in the beamlet directions that intersect the boost subvolume) are larger than those that correspond to the nonboost PTV region. In this work, the ratio of the boost and nonboost modulation values (diagonal elements of Σ) is the ratio of the prescription dose to these two regions and the modulation matrix is scaled to a range of [0 1]. In the case where both modulation methods are applied, the final modulation matrix is obtained by componentwise multiplication of the individual modulation matrices from each method.

EGRT simulation workflow

An anthropomorphic digital phantom, the 4D XCAT phantom, is used in our studies.⁴² Both cardiac and respiratory motions are simulated. The phantom consists of an attenuation distribution and an activity distribution with the same anatomical geometry, and it is constructed based on real patient anatomy and typical radiotracer uptake distributions measured in nuclear medicine imaging. The activity distribution specifies how the radioactive tracers are distributed inside the phantom, and the attenuation distribution is used in the calculation of radiation dose distributions. The XCAT phantom has a voxel resolution of 2 mm for all simulation studies included in this work. Other simulation parameters can be found in Table 1.

Table 1.

A summary of major simulation parameters.

	Parameter	Value	Parameter	Value
EGRT	PET detector extent	2 cm	Leaf aperture at iso(x-y)	0.5 cm
	PET detector coverage	180° arc	Leaf aperture at iso (z)	1 cm
	PET ring radius	50 cm	EGRT spatial window	±0.5° arc
	Linac rotating frequency	1 Hz	EGRT time window	500 ms
	Linac radius	60 cm	Helical pitch (conventional)	0.2
	Background activity	3 kBq/cc
	Collimator radius	50 cm	Radiotracer	FDG
	Collimator leaves	64	Firing positions	256
GATE	Version	V5.0.0.p01	Light decay time (LSO)	40 ns
	Coincidence window	10 ns	Energy resolution	0.26
	Scatter threshold (keV)	350, 650	Multiple coincidence policy	takeWinnerofGoods
XCAT-lung	Respiration period	4.2 s	Phantom size	256 × 256 × 35
	Respiration phases	12	Voxel resolution	2 mm
	GTV size	9.40 cm3	Sinogram bin size	256 × 64 × 35
	ITV size	17.01 cm3	Tracer uptake ratio	8:0.5:1
	PTV size	153.90 cm3
XCAT-prostate	PTV margin	6 mm	Phantom size	256 × 256 × 39
	Setup error	6 mm	Voxel resolution	2 mm
	GTV/ITV size	33. 27 cm3	Sinogram bin size	256 × 64 × 39
	PTV size	71.73 cm3	Tracer uptake ratio	8.5:1

Two MC software tools are used to simulate the positron emission and the high-energy treatment beams of the EGRT system. Geant4 Application for Tomographic Emission (GATE) is a software package (http://www.opengatecollaboration.org/) that simulates the process of positron emission after the radioactive tracer injection, based on the PET geometry, the activity, and attenuation distributions of the phantom.^{51, 52} Major physical processes including Rayleigh scatter, photoelectric, and Compton scatter are simulated. The simulation also includes the effects of photon noncollinearity, positron range, and realistic detector response. The software package has been well validated for commercial PET systems.⁵³ Modeling the proposed EGRT system geometry is simplified by using the benchmark full ring PET scanner geometry provided in the GATE package. Some important GATE simulation parameters are listed in Table 1. A voxel-based Monte Carlo algorithm (VMC++) is used for dose delivery. VMC++ is a highly efficient Monte Carlo dose calculation software for radiation therapy treatment planning and has been validated against well established codes.^{54, 55, 56} VMC++ takes the phantom attenuation map and the sequence of leaf openings as inputs and computes the dose distributions for both EGRT and conventional methods.

To simulate a dynamic EGRT treatment and examine the feasibility of EGRT, the following simulation workflow is designed as shown in Fig. 4.

Figure 4.

The simulation flow chart (starting from the shaded module). In an EGRT treatment, there are two major processes to simulate: positron emission and dose delivery. For simulation of the positron emission and detection process, the 4D XCAT phantom is input into the GATE package to obtain the LOR data for dose delivery. The LOR data are used as input for the basic EGRT algorithm and optional EGRT modulation algorithms, such as attenuation correction and integrated dose boost. The resultant set of bMLC configurations is used as inputs to the VMC++ dose calculation engine. The components that enable dynamic EGRT delivery are collectively referred to as “EGRT Engine,” as labeled in the figure.

The LOR detection and dose delivery processes are separately simulated for convenience. Both the activity and attenuation XCAT phantoms are input into the GATE package. The output coincidence data are stored in list-mode form. In this format, each recorded coincidence event includes its timestamp and 3D coordinates of the two LOR endpoints. Note that these data contain both the scattered and random coincidence events. Since the GATE simulation adopts the full ring geometry, the events that do not intersect the actual PET detector arcs in the proposed system are discarded. The resultant coincidence list forms the LOR queue for dose delivery. Dose delivery estimation involves two processes: the determination of bMLC configurations and subsequent Monte Carlo dose calculation. When dose delivery starts, the Linac rotates around the circle continuously and goes through different firing points along the whole treatment helix. At each firing point, it scans through the current LOR queue and checks whether each individual LOR meets the three criteria. If at least one LOR is determined to be eligible for response, the EGRT modulation algorithms can be enabled to determine its response probability. The final bMLC configuration is recorded for each firing point. Once all firing points have been processed, the final set of bMLC configurations is obtained and subsequently the VMC++ dose calculation engine calculates the final dose map for evaluation.

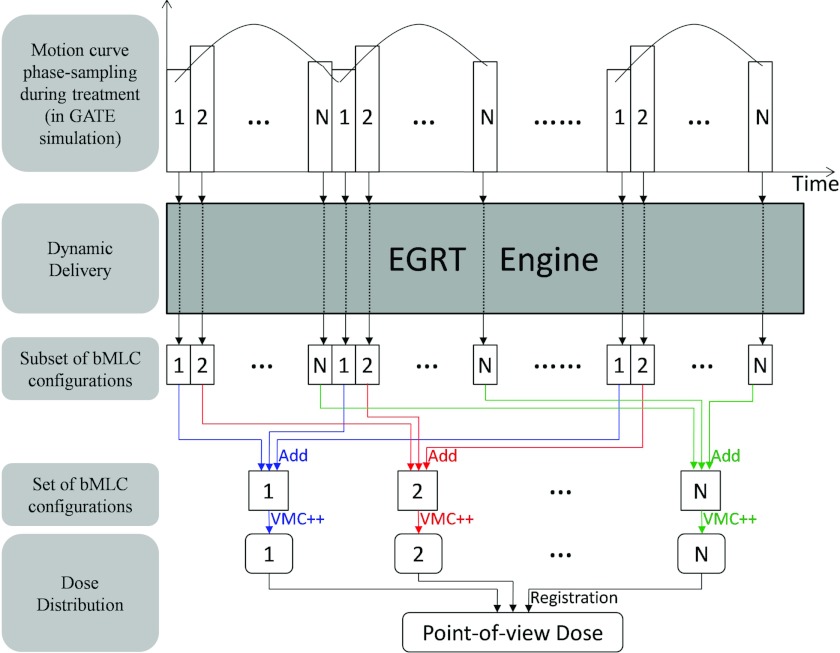
In the case of a moving phantom, the dose is first estimated separately for each phase of motion. To calculate the total dose of a moving structure, dose maps of different phases are registered to the same reference phase through rigid image registration. The multiple dose maps are then summed to produce a point-of-view map relative to the moving structure. A detailed description of the dose evaluation scheme for a moving phantom is shown in Fig. 5.

Figure 5.

The dose evaluation scheme for a moving phantom. The periodic motion curve is sampled into N phases. The number (i.e., 1, 2, …, N) in this figure indicates the corresponding phase index. EGRT engine refers to our dynamic EGRT delivery algorithm used to determine the qualified LOR responses. The included components of EGRT engine are labeled in the simulation workflow (Fig. 4). While the gantry and couch are constantly moving in one direction, subsets of bMLC configurations are generated continuously until the treatment ends. Note that these subsets of bMLC configurations are phase-labeled, i.e., each subset belongs to a particular phase. To evaluate the dose that has been accumulated in each phase during the whole treatment, the set of bMLC configurations for each phase is obtained as a summation of subsets of bMLC configurations that correspond to that particular phase. To evaluate the dose accumulated for a specific moving structure (e.g., GTV) during the whole treatment, rigid image registration is used.

A summary of the main EGRT simulation parameters is shown in Table 1. Choices of parameters take into account typical engineering design considerations and actual clinical uptake of the FDG radiotracer.^{57, 58} For performance evaluation, we compare the proposed EGRT method and a conventional helical IMRT method without optimized intensity modulation. Both simulations use nearly the same system settings (i.e., the same MLC system, the same number of 256 firing positions, and the same firing geometry with a more suitable helical pitch). The main difference is that EGRT opens the leaves that correspond to qualified LOR's from the tumor, while the conventional treatment opens the leaves that intersect the PTV without tracking the tumor position.

Evaluation studies

Six simulation studies have been conducted to validate the feasibility of EGRT for two clinical cases. Two typical disease sites are studied: a lung tumor scenario and a prostate tumor scenario.

Lung tumor scenario

The lung tumor simulation includes both respiratory motion and heart motion, with periods of 4.2 and 1 s, respectively, sampled in 12 phases. The GTV is modeled using an ellipsoid with a set of semiaxis lengths of 1.5, 1, 1.5 cm and placed in the right lung. The GTV motion path is based on an XCAT built-in 3D periodic tumor motion trajectory with typical lung motion behavior and amplitude. The trajectory of the lung tumor motion is shown in Fig. 6. The PTV is modeled using a cylinder that contains the full range of GTV motion with a total height of 7 cm and an ellipsoidal cross section whose semiaxis lengths are 2 and 2.5 cm. Two cases are evaluated with and without attenuation correction. 100 Gy is prescribed to 95% of the GTV volume. For the case without attenuation correction, the EGRT treatment time is 300 s with a table speed of 0.023 cm/s; for the case with attenuation correction, the EGRT treatment time is 1000 s with a table speed of 0.007 cm/s. The mean of 12 phases of the XCAT attenuation phantom is used for the PTV attenuation map calculation. The tumor, lung, and background activity uptake ratio is assumed to be 8:0.5:1. The phantom geometry can be seen in Fig. 8.

Figure 6.

The 3D lung tumor trajectory (first phase at the origin). The star and circle markers depict each direction of the tumor round trip, respectively. The peak-to-peak tumor motion amplitude is 16.6, 3.5, and 0.02 mm for superior-inferior (SI), anterior-posterior (AP), lateral-medial (LM) directions, respectively.

Figure 8.

Point-of-view dose maps and associated DVHs for the lung case with (a) EGRT (dashed-dotted lines), (b) conventional method (dashed lines), and (c) EGRT with attenuation correction (solid lines). The GTV is contoured using a black solid line. Note that the curves on OAR's are mostly overlapping with each other.

Prostate tumor scenario

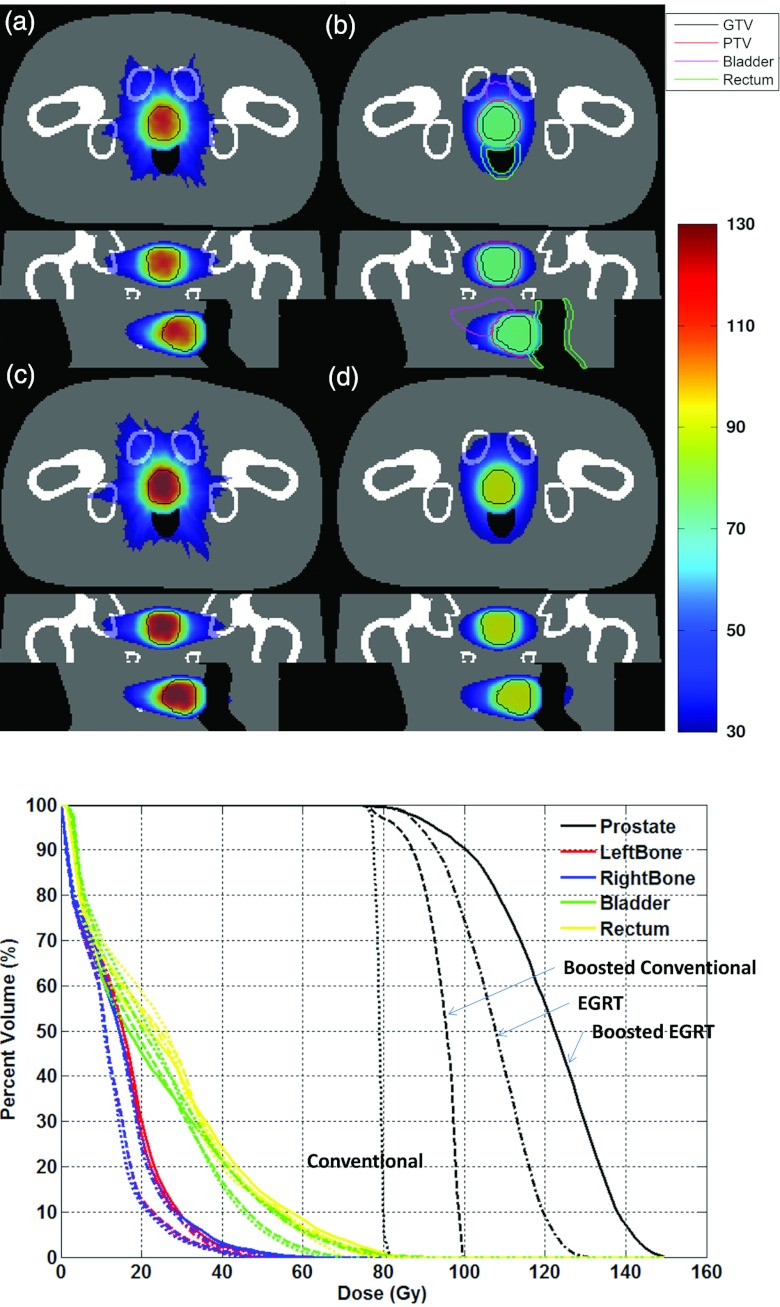
To evaluate the feasibility of EGRT treatment in a different disease site, more studies have been conducted for a prostate tumor case. In this work, four prostate cases are modeled: with and without setup errors and with and without an integrated boost. The GTV is modeled using the XCAT built-in prostate profile with a volume size of 33.27 cm³. No motion during treatment is modeled in the prostate case. The PTV is constructed with a 6 mm margin around the GTV in all directions, resulting in a volume size of 71.73 cm³. Due to strong inhomogeneous attenuation, all cases of prostate cancer have been simulated with the attenuation correction EGRT modulation. The 6 mm setup error is simulated in the lateral-medial direction. In order to make use of the same set of GATE data, the setup error is simulated by shifting the PTV in the corresponding direction. The boost region is set to be the GTV if there is no setup error and is shifted with the PTV in the presence of setup error since the boost region is defined relative to the PTV. 78 Gy is prescribed to 95% of the GTV volume. When the integrated boost algorithm is enabled, the same amount of dose is prescribed to the boost region. The treatment time is 1000 s for all cases, with a table translation speed of 0.007 cm/s. The XCAT attenuation phantom is used for the PTV attenuation map calculation. The tumor to background activity ratio is selected to be 8.5:1. The phantom setup including the contouring of the GTV, PTV, and important organs at risk (OAR’s) can be found in Figs. 9b, 10b.

Figure 9.

The dose distributions for (a) original EGRT (dashed-dotted lines), (b) conventional method (dotted lines), (c) boosted EGRT (solid lines), and (d) boosted conventional method (dashed lines) with the associated DVH. The GTV is contoured with a solid line in all scenarios. Contoured PTV, bladder, and rectum are shown only in (b) for simplicity. The boost region is equivalent to the GTV in this case (without a setup error). Note that the curves on OAR's are mostly overlapping with each other.

Figure 10.

The dose distribution for (a) original EGRT (dashed-dotted lines), (b) conventional method (dotted lines), (c) boosted EGRT (solid lines), and (d) boosted conventional method (dashed lines) with the associated DVH in the presence of simulated setup error. The GTV is contoured with a solid line in all scenarios. Contoured PTV, bladder, rectum, and boost region are shown only in (b) for simplicity.

RESULTS

Lung

The GATE simulation resulted in 39 084 and 47 925 beamlet responses in the treatment of 300 and 1000 s for the cases without and with attenuation correction, respectively. Figure 7 depicts the dose maps of all 12 simulated phases for the EGRT algorithm in both coronal and sagittal views in the absence of attenuation correction. The results with attenuation correction are similar. Dose concentration in the moving target can be observed, which indicates that the EGRT method is able to track the tumor's motion.

Figure 7.

Dose maps of all 12 simulated phases in both (a) coronal and (b) sagittal views. Dashed lines are overlaid for positional reference. Each image has a display window of [min max] of itself.

Figure 8 shows the GTV point-of-view dose maps assembled from all 12 motion phases for each case, as well as the associated dose volume histogram (DVH) curves comparing the conventional helical IMRT method with EGRT in the cases with and without attenuation correction. In both EGRT cases, there is a peaking of dose in the center of the GTV. However, even with this inhomogeneity, there is a 31%, 41% relative increase in dose to 95% of the GTV and a 44%, 55% relative increase in dose to 50% of the GTV for the cases without and with attenuation correction, respectively, when comparing the EGRT methods with the conventional method. All dose distributions are normalized for the same integral dose to the lung.

The GTV dose relative increase is higher when attenuation correction is enabled in the EGRT method. This is due to the fact that after attenuation correction, dose is redistributed more toward the heart rather than the lung to which the dose distribution is normalized. In other words, the GTV dose increase is achieved at the price of heart dose increase. This may be favored in the case where the heart dose increase is still within the planning limit. This study also demonstrates that EGRT modulation through customization of the response probabilities can be used to reshape the dose distribution.

Prostate

Without setup errors

The GATE simulation results in 22 231 and 19 128 beamlet responses in the treatment of 1000 s for the cases without and with the integrated boost, respectively. The number of beamlet responses is reduced for the boost case since a portion of beamlets is discarded in the EGRT modulation. Figure 9 depicts the DVH and the dose distributions for all four scenarios comparing the original EGRT case, the boosted EGRT case, the conventional case, and the boosted conventional case in the absence of a setup error.

Using the conventional method without boost as a basis for comparison, when evaluating the dose to 95% and 50% of the GTV, the boosted conventional method results in a 8% and 20% relative increase, the EGRT method yields a 14% and 36% relative increase, while the boosted EGRT method results in a 19% and 55% relative dose increase, respectively. All methods are normalized for the same integral dose to the rectum.

With setup errors

When a setup error is simulated by shifting the PTV, the GATE simulation results in 22 172 and 18 929 beamlet responses in the treatment of 1000 s for the cases without and with integrated boost, respectively. Figure 10 depicts the DVH and the dose distributions for all four scenarios comparing the EGRT case, the boosted EGRT case, the conventional case, and the boosted conventional case in the presence of a setup error.

Compared with the conventional method, when evaluating the dose to 95% and 50% of the GTV, the boosted conventional method results in a dose increase of 2% and 21%, the EGRT method yields a 19% and 35% dose increase and the boosted EGRT method yields a 21% and 52% relative dose increase, respectively. All methods are normalized for the same integral dose to the rectum.

DISCUSSION

In this work, we integrate positron emission into the process of radiation therapy dose delivery for treatment guidance by directing radiation beamlets along detected LOR paths in near real-time. Since PET imaging serves as the gold standard for noninvasive cancer detection and staging,⁵⁹ and is increasingly being used for treatment planning,^{60, 61} this proposed biological targeting method may provide a way to close the loop between detection and radiation treatment.

In the current implementation of EGRT, a few items require further consideration. First, we want to discuss several issues on the EGRT results. It should be noted that the EGRT dose increase in the prostate case is smaller than that observed in the lung case, which could be explained by the PTV-ITV ratio used. As EGRT is able to concentrate the dose to the PET-avid region while the conventional method irradiates the whole PTV, the larger the PTV-ITV ratio used, the larger the anticipated advantage. The advantage of EGRT still exists when the boost scheme is implemented, which indicates that the dose increase in EGRT is due to the inherent tumor targeting. Also, as indicated by the results, both the positron range uncertainty and angle divergence in PET do not compromise the accuracy of emission guidance. There are two possible reasons for this. One is that the uncertainty due to the positron range and angle divergence is small compared to the treatment beam resolution. The other is that the uncertainty has a zero-mean stochastic nature and while it may add a small blurring component, there should be no bias in the tumor tracking accuracy. The results take into account the decay of PET signals during treatment. Given current simulation settings, treatment time can be generally controlled to be less than 20 min. Most clinical PET tracers are ¹⁸F based, which has an approximate half life of 110 min. Therefore, at the end of a 20 min treatment, the activity remains 88% of the maximum, which have casted little effect on the treatment delivery efficiency. Furthermore, unlike in the conventional method, dose peaking is observed in the center of a uniformly PET-avid target. This phenomenon is due to the backprojection effect. There are more LOR's that intersect the center of the GTV than the edge, as the detected LOR rate spatial profile is the projection of the target onto the PET detector array. Therefore, more beamlet responses will be directed toward the center of the target. Due to the dose peaking effect, the results are presented in the form of dose escalation. Note that the EGRT dose benefits due to inherent tumor tracking are generic and thus will not vanish if assessment criteria are changed. For example, if the results are normalized to the target (GTV) dose, the benefit may be in the form of reduced dose to critical structures. However, given the current EGRT algorithm design, the benefits may not be in the form of some particular criteria, such as target dose uniformity without modification of the current algorithm.

Second, special care is needed in the practical implementation of EGRT for cancer treatment. For example, EGRT performance is dependent on the target-to-background activity uptake ratio. In the extreme case where there is no significant difference between target and background activity, there would be no advantage of EGRT over other methods. Also, although the attenuation correction EGRT modulation algorithm can help to reduce the attenuation effect, a negative consequence is an increase in treatment time if approximately the same number of beamlet responses is to be maintained since many beamlet responses are suppressed. In addition, patient and therapist are expected to receive similar levels of dose as in a standard clinical PET exam. Studies have shown that a conventional whole-body ¹⁸F-FDG PET/CT examination gives an average effective patient dose equivalent to 2.5cGy.⁶² This dose should be taken into account when evaluating patient or therapist dose. It is also worth noting that the selection of radioactive tracers for different tumor sites is possible in EGRT. EGRT can benefit from new radiotracers that are developed to target various aspects of cancer biology and function. ¹⁸F-fluorodeoxyglucose (FDG), which measures the metabolic activity of glucose, is currently the gold standard in noninvasive cancer detection, with higher sensitivity and specificity than CT or MRI across a broad range of cancers.⁵⁹ FDG is effective for many lung tumors. However, for prostate cancer, ¹⁸F-fluorocholine (FCH) and ¹⁸F-fluorocyclobutane-1-carboxylic acid (FACBC) may be more effective.^{59, 63, 64}

Finally, EGRT performance could be further improved by better engineering and algorithm designs in several aspects. For example, no attempt has been made to compensate for both the scattered and random events from the raw PET coincidence dataset. Although the PTV intersection requirement reduces the error that these false events introduce, correction for scatter and random events should be implemented to further improve EGRT performance. Moreover, simulation settings are not optimized. Each beamlet response is assumed to have the same beam intensity and duration. The patient couch also has a constant translation speed. To achieve more degrees of freedom for a more optimized delivery or shorter treatment time, it is viable to modulate the intensity or duration of each beamlet or apply a variable couch speed to allocate more treatment time for desired regions. In addition, the EGRT implementation can be extended to treat multiple targets without major modifications. This is another potential advantage of EGRT since conventional methods typically have to treat the targets sequentially with multiple isocenters and plans, which can impact the overall time, cost, and complexity of treatment. Also, it is shown by many studies that microscopic disease can extend beyond the region of FDG uptake that is easily visualized in PET. To treat such disease, the addition of CTV margins can be incorporated into the EGRT framework through a margin extension algorithm. If we assume the CTV margin motion is very similar to the GTV motion, one possible method could allow for adjacent bMLC leaves toward the margin extension direction to be opened when the current beamlet-response is substantially perpendicular to the direction of desired margin extension. Most of all, current EGRT algorithm design does not incorporate a conventional treatment planning component. The EGRT modulation simulations have demonstrated the feasibility of dose modulation by making use of leaf opening probabilities. The overall leaf opening probability distribution resembles the beamlet weighting distribution in conventional inverse planning. In the future development of EGRT treatment planning where a detailed plan is specified, the conventional weighting distribution may first be calculated using inverse optimization and then converted into a corresponding leaf opening probability distribution. This future work will enable a fair comparison of planned EGRT with current state-of-the-art conventional external beam therapy.

CONCLUSION

In this work, we introduce EGRT as a new radiation therapy technique to improve treatment performance. The feasibility of EGRT has been demonstrated using the XCAT digital phantom as well as Monte Carlo simulations of PET acquisition and radiation delivery. An EGRT treatment scheme with attenuation correction and boost algorithms are proposed as an implementation of the EGRT concept in two clinical scenarios. The treatment scheme and associated algorithms are designed based on realistic hardware and software technology. Compared with a conventional method, dose concentration is observed for both moving and static targets. EGRT has the potential to enable true biological targeting and guidance in radiation delivery.