Moments of click-evoked otoacoustic emissions in human ears: Group delay and spread, instantaneous frequency and bandwidth

Abstract

A click-evoked otoacoustic emission (CEOAE) has group delay and spread as first- and second-order temporal moments varying over frequency, and instantaneous frequency and bandwidth as first- and second-order spectral moments varying over time. Energy-smoothed moments were calculated from a CEOAE database over 0.5–15 kHz bandwidth and 0.25–20 ms duration. Group delay and instantaneous frequency were calculated without phase unwrapping using a coherence synchrony measure that accurately classified ears with hearing loss. CEOAE moment measurements were repeatable in individual ears. Group delays were similar for CEOAEs and stimulus-frequency OAEs. Group spread is a frequency-specific measure of temporal spread in an emission, related to spatial spread across tonotopic generation sites along the cochlea. In normal ears, group delay and spread increased with frequency and decreased with level. A direct measure of cochlear tuning above 4 kHz was analyzed using instantaneous frequency and bandwidth. Synchronized spontaneous OAEs were present in most ears below 4 kHz, and confounded interpretation of moments. In ears with sensorineural hearing loss, group delay and spread varied with audiometric classification and amount of hearing loss; group delay differed between older males and females. CEOAE moments reveal clinically relevant information on cochlear tuning in ears with normal and impaired hearing.

INTRODUCTION

Upon presentation of a brief transient sound (i.e., a “click”) within the ear canal, the resulting evoked sound response in the ear canal is a click-evoked (CE) otoacoustic emission (OAE) (Kemp, 1978). Its largest amplitude occurs in the initial 20 ms. The emission persists for longer durations in many ears, and its spectral content is measured as a synchronous spontaneous (SS) OAE over a time window including this late energy (i.e., at times $\ge 20$ ms). Kemp confirmed the cochlear place of origin of the CEOAE through measurements of an instantaneous frequency, which was defined over time in terms of a local zero-crossing rate, and by the latency of the maximum amplitude of an emission generated by a narrow-band stimulus. A CEOAE measurement also provides phase information that may help interpret how the emission is generated. Analyses of the CEOAE phase gradient, defined as the group delay of the emission at each frequency, gave further evidence that CEOAEs were generated within the cochlea (Wilson, 1980). The stimulus reemission mechanism underlying generation of both CEOAEs and stimulus-frequency (SF) OAEs is a place-fixed mechanism along the tonotopically organized basilar membrane, and further explained as a coherent reflection from a random distribution of scatterers along the basilar membrane (Shera and Guinan, 1999). These emissions are non-invasive measures of the compressive nonlinearity of cochlear mechanics related to outer hair cell function. SFOAE group delay in normal ears is proportional to the sharpness of cochlear tuning in human and other mammalian ears (Shera et al., 2010), which suggests its potential clinical use to non-invasively estimate tuning in human ears. However, large measurement variabilities in SFOAE group delay have limited clinical applications. To the extent that the cochlear source mechanisms are similar for SFOAEs and CEOAEs in human ears, then CEOAE group delay might also serve to estimate cochlear tuning.

As an initial research goal, the group delay (GD) is calculated as a smoothed, first-order temporal moment of a CEOAE to make possible highly reproducible measurements of GD in an individual ear. One reason why GD measurements are not used in clinical assessments is that the signal phase gradient comprising GD (as normally calculated) is more sensitive to noise than is signal magnitude. Its value also fluctuates as a result of the underlying random scatterers generating the cochlear reflections. Phase-unwrapping is typically performed on evoked OAE signals prior to calculating a phase gradient, but ambiguities in phase unwrapping may arise for signals in noise. A coherence synchrony measure (CSM) is introduced to detect CEOAEs with sufficient synchrony to reliably interpret as a measurement of GD, and GD is calculated without using phase unwrapping.

As broader research goals, additional CEOAE moments are formulated and their properties are studied in normal and impaired ears. A group spread (GS) is defined as a smoothed, second-order temporal moment of the CEOAE as a frequency-specific measure of the effective dispersion in timing that is associated with a CEOAE component having a particular GD. An instantaneous frequency (IF) is defined as a smoothed, first-order spectral moment to provide a time-domain measure of the local frequency of a CEOAE. An instantaneous bandwidth (IB) is defined as a smoothed, second-order spectral moment to provide a time-domain measure of the local bandwidth of a CEOAE.

After quantifying the repeatability of CEOAE moment measurements, CEOAE data are used to calculate the level dependence of each moment. A hypothesized relationship between IF and inverse GD is examined, which links the first-order moments of the CEOAE waveform and its spectrum based on a theory of cochlear scaling and symmetry. Synchronized spontaneous (SS) OAE responses are analyzed in the same set of ears to examine their relationships to CEOAE responses. Cochlear tuning is directly estimated in terms of IF and IB at frequencies above 4 kHz.

CEOAE signal level and signal-to-noise ratio (SNR) across frequency are commonly used clinically to identify sensorineural hearing loss (SNHL) in human ears. The test accuracy of detecting SNHL using evoked OAEs is objectively quantified using a receiver operator characteristic curve analysis (Prieve et al., 1993). The ability of CEOAEs and SSOAEs to detect SNHL is assessed using such an analysis to compare predictors based on CEOAE CSM and SNR in the frequency and time domains.

Studies in normal ears provide a baseline to interpret measurements of CEOAE moments in ears with SNHL. CEOAE moments are analyzed in groups of ears with similar audiometric configuration to evaluate how the moments change with characteristics of SNHL. Variations in each moment are evaluated as a function of the magnitude of the hearing loss to evaluate the extent to which CEOAE moments provide information on impairments in outer hair cell function. CEOAE GDs are compared in ears of older female and male subjects ($\ge 60$ years) to examine effects of age and sex.

Background on CEOAE timing in adult ears

CEOAE latency is defined at each frequency as the time interval between the peak envelopes of the click stimulus and the frequency-specific CEOAE. The response may be a bandpass-filtered CEOAE at frequency $f,$ or a toneburst- (TB-) evoked OAE generated by a narrowband stimulus centered at frequency $f,$ as these result in similar latencies (Prieve et al., 1996). A CEOAE GD is the negative of the spectral phase gradient at frequency $f.$ Thus, latency is obtained from the time-domain amplitude function using a frequency-specific stimulus or filtered response, while GD is obtained from the frequency-domain phase function. The similar values of latency and GD measured in early experimental studies of CEOAEs confirmed its cochlear generation site (Kemp, 1978; Wilson, 1980), i.e., the characteristic times associated with ear-canal and middle-ear function were much shorter than the characteristic times of CEOAEs.

CEOAE GD and latency are predicted to be approximately equal by a one-dimensional model of cochlear mechanics with the long-wavelength approximation in a cochlea with scale symmetry and linearized mechanics (Sisto et al., 2007). GD and latency may differ in measured CEOAEs due to effects of cochlear scale asymmetry, nonlinearity, and the three-dimensional nature of the cochlear traveling wave in the tonotopic region. They may also differ due to cochlear suppression effects, multiple internal reflections within the cochlea, and procedural factors.

For example, a SSOAE is a measure of particularly strong internal reflections within the cochlea. In a CEOAE measurement, the time interval between adjacent click presentations typically lies within the duration of a SSOAE, so that the SSOAE associated with previous click presentations may be present at short time delays after the onset of the next click. One possible empirical result may be an apparently short characteristic time in a low-frequency CEOAE response due to SSOAEs, which would be unrelated to any basal emission generators of low-frequency emissions that may also be present. Studies to detect such putative generators should control for SSOAEs. The operational difference between a CEOAE and SSOAE response is that CEOAEs are typically measured in the initial 20–25 ms, whereas SSOAEs are measured at later times.

Concerning experimental studies of CEOAE GD, GDs measured using clicks in young adults with normal hearing increased with increasing frequency between 1.7–2.4 kHz in a manner similar to SFOAE GDs, but differently from the GDs of distortion product (DP) OAEs (Knight and Kemp, 1999). CEOAE GD was measured using phase unwrapping with correction strategies applied depending on SNR. Kalluri and Shera (2007) compared signal level and unwrapped phase of CEOAEs and SFOAEs in four subjects from 1 kHz up to as high as 3 kHz in one subject. They concluded that CEOAEs and SFOAEs were both generated, in general, by a mechanism of coherent reflection of the cochlear traveling wave from a distribution of random discontinuities along the basilar membrane. In two of these subjects without SSOAEs, level and phase spectra of SFOAEs and CEOAEs were nearly equivalent after correcting for stimulus-level conditions. In two other subjects with SSOAEs, the level and phase spectra of SFOAEs and CEOAEs were similar from 1 kHz up to 2.3 kHz in one subject and up to 1.6 kHz in the other, but their phase spectra differed above those frequencies. Sisto et al. (2007) compared CEOAE latency obtained via a wavelet transform and CEOAE GD calculated via the phase gradient with smoothing across frequency in ten young adult subjects from 0.5 to 5 kHz. Ambiguities in phase gradient calculations were resolved by arbitrarily translating the measured GD to fit in a 20-ms range (in steps of $\pm 20$ ms) in which CEOAE data were acquired. The absolute limits of the 20-ms acceptance window for wavelet latency depended on frequency. CEOAE timing estimates generally agreed, except that GDs were sometimes close to zero or negative. This was explained as consistent with causality constraints on correlated fluctuations in amplitude and phase, although a possible contribution from wave-fixed generation was also described.

Concerning experimental studies of CEOAE latency, CEOAE latencies in normal human ears have been measured using time-frequency analyses based on wavelets (Tognola et al., 1997; Sisto and Moleti, 2002), cone kernel (Konrad-Martin and Keefe, 2003), and matching pursuit algorithms (Jedrzejczak et al., 2004). These latter techniques have been refined to identify apparently anomalous latency values on the time-frequency plane using SNR and model-based criteria (Notaro et al., 2007). The authors concluded that the large variability in CEOAE latency makes it difficult to use wavelets and matching pursuit estimates of latency in diagnostic tests on individual subjects.

Goodman et al. (2009) reported group norms for CEOAE latency over a frequency range from 1 to 16 kHz and a 18-dB range of stimulus level. A trend of decreased CEOAE latency with increasing stimulus level was observed across frequency, in agreement with earlier studies performed up to 4 kHz (Prieve et al., 1996; Tognola et al., 1997). However, this level effect on CEOAE latency was smaller than that reported for SFOAE GD (Schairer et al., 2006). CEOAE latencies in Goodman et al. (2009) were similar to SFOAE GD (Shera et al., 2010) at 1–2 kHz, slightly shorter between 2–4 kHz, and shorter by a factor of the order of one half above 5 kHz. CEOAE latency was similar to SFOAE GD reported by Schairer et al. (2006) from 1–4 kHz, in which the SFOAE GD was calculated by smoothing the unwrapped phase prior to calculating the phase gradient. High-frequency timing differences may be due to differences in emission type (CEOAE or SFOAE), effective stimulus level, type of timing response (latency or GD), or methodology.

Mild to moderate SNHL typically involves a reduction or elimination of outer hair function in its role in the cochlear amplifier. In a non-human mammalian ear with normal function, increased stimulus level is associated with a relative reduction in the amplitude of the traveling wave on the basilar membrane and a reduced GD compared to linear growth. These are associated with cochlear tuning that is less sharp at higher compared to lower stimulus levels. For example, GD near the characteristic frequency at a basal location on the basilar membrane of the chinchilla was reduced by about 38% (from 990 to 610 $\mu \text{s}$) at stimulus levels elevated by 80 dB relative to low levels (Robles and Ruggero, 2001). This finding is similar to those measurements described above in human ears with normal function, which show decreased CEOAE latency and SFOAE GD at increased stimulus level. Cochlear tuning is also reduced in ears with SNHL due to impairments in the functioning of outer hair cells. The preponderance of evidence reported by Robles and Ruggero (2001) shows that the GD in non-human mammalian ears on the basilar membrane near its characteristic frequency is reduced by acoustic overstimulation and by furosemide administration. The latter reduces the endocochlear potential within outer (and inner) hair cells, which attenuates their role in producing sharp tuning. This suggests the hypotheses in human ears that CEOAEs are more likely to be absent as SNHL increases, and that CEOAE latency and GD decrease in ears with mild to moderate SNHL relative to normal ears.

Concerning CEOAE latency measurements in hearing-impaired ears, all studies confirm that the prevalence of detectable CEOAEs is lower in SNHL ears than in normal ears, and lower in SNHL ears with greater amounts of hearing loss. Avan et al. (1993) reported differences in the amplitude latency of CEOAEs at 1 and 2 kHz, with a tendency for longer latencies in impaired ears. Prieve et al. (1996) reported no difference in tone-burst (TB) evoked OAE latency between normal-hearing and hearing-impaired groups. While large variability of wavelet latency between subjects was reported, group analyses of CEOAEs in normal ears and ears with a hearing loss above 3 kHz showed longer latencies between 1–2 kHz in impaired ears (Sisto and Moleti, 2002). TBOAE latencies at 4 kHz were shorter in ears with SNHL compared to normal ears, but interpretation was complicated by a small number of test ears (Konrad-Martin and Keefe, 2005). The relatively few studies addressing the effects of SNHL on CEOAE and TBOAE latency have produced inconsistent results on whether SNHL results in an increased, unchanged, or decreased CEOAE latency compared to a normal ear.

CEOAE timing measurements have been limited to a maximum frequency of 5 kHz except for measurements to 16 kHz in Goodman et al. (2009), and most previous measurements have examined CEOAE latency. The present study extends the maximum measurement frequency of CEOAE GD up to 15.3 kHz through improvements in how GD is smoothed and detected, assesses its repeatability, and compares GD in normal and hearing-impaired groups. Since the report in (Kemp, 1978), a literature review has identified no other reports of CEOAE IF measurements based on zero-crossing rate. No measurements of GS and IB have been reported for OAEs.

METHODS

The database of CEOAE recordings analyzed in the present study consisted of 446 ears from the normal-group subjects tested in Goodman et al. (2009), and the normal-group and hearing-impaired subjects tested in Keefe et al. (2011). The overall measurement methods were presented in those articles. This section outlines the methods and describes any procedural differences in the present study compared to these previous studies.

Subjects

All subjects had normal middle-ear function based on 226-Hz admittance tympanometry (Tympstar, Grason-Stadler, Inc.). Air-conduction audiograms were measured with a clinical audiometer (Model 61, Grason-Stadler, Inc.) at octave frequencies from 0.5 to 8 kHz, and bone-conduction audiograms were measured at octaves from 0.5 to 4 kHz. Subjects were included in the normal group (age 14 to 38 years) if their air-conduction hearing thresholds did not exceed 15 dB HL at any test frequency. The remaining subjects in a SNHL group had air-conduction thresholds of 20 dB HL or more at one or more test frequencies.

An additional criterion imposed in this study was to include only those ears with an air-bone gap of 15 dB or less at octave frequencies between 0.5 and 4 kHz. This excluded ears with conductive hearing loss. A subset of 41 ears in the normal group were retested on a different test date to evaluate OAE test repeatability. The average time between the initial test 1 and follow-up test 2 was 8.5 days.

General OAE procedures

The computer-measurement system used custom software to record OAEs with a 24-bit sound card (CardDeluxe) operating at a sample rate of 44.1 kHz. Sound stimuli were generated using a pair of ER-2 receivers (Etymotic) and the acoustical pressure response was measured using an ER10B+ microphone (Etymotic). An electrical stimulus was designed for each receiver such that the voltage waveform from the microphone output in response to the sound generated by the receiver approximated the impulse response of a finite impulse response Kaiser filter (pass band 0.5 to 16 kHz). That is, the incident click pressure approximated a band-limited acoustic impulse. A source of error in this approximation was that the microphone sensitivity varied with frequency above 8 kHz. The sensitivity was within $\pm 2$ dB up to 12.7 kHz except for an increase of 6 dB in a narrow bandwidth around 11.7 kHz (Keefe et al., 2011).

The microphone sensitivity magnitude and phase were measured in the present study using the approach of Siegel (2007) as implemented by Rasetshwane and Neely (2011). The microphone sensitivity impulse response was calculated using an inverse discrete Fourier transform (DFT). All OAE responses were filtered using the Kaiser bandpass filter. Each impulse response was convolved with the microphone sensitivity impulse response, and the resulting response was truncated in length at early and late times by zeroing amplitudes less than 0.0005 of the peak amplitude. Thus, even though the sound source spectrum level of the click stimulus varied above 8 kHz, the pressure waveforms used to analyze OAEs were calibrated for the frequency dependence of the microphone.

CEOAE procedures

A CEOAE waveform was measured as a nonlinear residual of three successive pressure measurements, each of duration 25.5 ms: the response to the first receiver at the reference peak-to-peak equivalent sound pressure level (peSPL), the response to the second receiver at a peSPL 15 dB larger than the reference peSPL, and the response to the simultaneous presentation of sound from both receivers at the same peSPLs as in the first pair of responses. The reference peSPL was that measured for the incident click pressure in the absence of reflections in a long tube of circular cross-section (8-mm diameter) based on a time-gated response. This CEOAE stimulus set of duration 76.5 ms was repetitively output for 4050 presentations, and the entire response over the 5.16 min duration was recorded. This response was calibrated in terms of pressure and partitioned into individual responses.

A CEOAE waveform was calculated as the sum of the first pair of responses (at the reference peSPL and elevated by 15 dB) minus the third response (i.e., the simultaneous presentation condition). This CEOAE waveform would be zero for a linear, noise-free system. CEOAEs were recorded in Goodman et al. (2009) at reference peSPLs in 6-dB steps from 43 to 73 dB, and in Keefe et al. (2011) at 61, 67, and 73 dB peSPL. The majority of analyses in the current study used data measured at reference peSPLs of 61, 67, and 73 dB, although some normal-group analyses also used data recorded at lower peSPLs. Each CEOAE waveform was windowed to extend from 0.25 to 20 ms after the onset of the acoustic click. Outliers in the 4050 CEOAE waveforms were rejected using a median absolute deviation test Keefe et al. (2011). The remaining valid CEOAE waveforms were time-averaged into 32 buffers for subsequent processing, and their CEOAE spectra were calculated in each buffer using the DFT. CEOAE spectra were analyzed in half-octave bins ranging from 0.5–11.3 kHz. Because of intermittent noise from the microphone output close to 16 kHz, the highest-frequency CEOAE responses in the upper frequency bin was reduced to 15.3 kHz, so that the maximum center (geometric) frequency was reduced from 16 to 14.3 kHz. CEOAE waveforms were analyzed in half-doublings of time in centered intervals from 0.35 to 16 ms.

SSOAE procedures

The presence of SSOAEs is associated with increased CEOAE levels and lower hearing thresholds. SSOAE spectra typically share the same narrow-band components as appear in a spontaneous (S)OAE spectrum measured in the same ear, but a SSOAE spectra has additional narrow-band components absent from the SOAE spectrum (Burns et al., 1998). Using a matching pursuit algorithm, the presence of SSOAEs influenced the measurements of CEOAE latency because the SSOAE-related components of the CEOAE tended to have large CEOAE amplitudes (Jedrzejczak et al., 2008).

SSOAEs were recorded in the same test session using the same probe and ear-canal placement as for CEOAEs, although SSOAE data were not analyzed in the pair of previous studies. The stimulus set used to elicit a SSOAE was the same stimulus set used to record a CEOAE at 73 dB peSPL, except that the duration of each of the three individual measurements was extended to 46.4 ms (2048 samples). This stimulus set was repeated for 1 minute and data were recorded. The voltage waveform was convolved with the calibration impulse response to give a pressure waveform that was partitioned into individual click responses. The SSOAE-relevant section of each click response from 20 to 42 ms after stimulus onset was extracted (972 samples).

The click peSPL varied for each of the three clicks in the CEOAE stimulus set, which slightly influenced the SSOAE levels recorded 20 ms after each click. For purposes of characterizing the individual SSOAE frequencies in each ear, these windowed sections from 20–42 ms were averaged across all click presentations, and therefore over the varying peSPL values. This resulted in a total of 1198 responses (the intent had been to measure SSOAEs using a click at the reference peSPL, but the software was implemented in this other manner). Each response was multiplied by a 972-sample Hanning window, and then zero padded to 2048 samples so that the DFT bin sizes of SSOAE and CEOAE spectra were identical.

Analytic signal

Using a continuous-time, continuous-frequency representation, a CEOAE pressure waveform $p(t)$ is zero for negative times for an ideal impulse at $t=0,$ and is a real waveform for non-negative times. Its complex Fourier transform $P(f)$ is the spectrum of the real waveform. It has conjugate symmetry for negative frequencies, i.e., $P(-f)=P^{\ast }(f)$ in which the superscript asterisk denotes complex conjugation. The complex analytic signal $s(t)$ (Gabor, 1946) of the CEOAE waveform is defined using the unit imaginary number j and the Hilbert transform $p_h(t)$ of $p(t)$ by

$$s(t)=p(t)+j\hspace{0.17em}\hspace{0.17em}{p}_h(t).$$ (1)

The Hilbert transform $p_h(t)$ is real because $p(t)$ is real. A key reason to use the analytic signal formulation is that it provides straightforward definitions of waveform envelope and phase. The analytic signal $s(t)$ is zero for negative times, and represented for $t\ge 0$ in terms of real amplitude $A(t)$ and phase $\mathrm{\Phi }(t)$ functions by

$$s(t)=A(t)\hspace{0.17em}\hspace{0.17em}{e}^{j\mathrm{\Phi }(t)}.$$ (2)

The temporal envelope of the real waveform $p(t)$ is $A(t),$ and its temporal fine structure resides in $\mathrm{\Phi }(t).$ The time rate of change of $A(t)$ and $\mathrm{\Phi }(t)$ are used below to define spectral moments of the CEOAE.

The spectrum $S(f)$ of the analytic signal is zero for negative frequencies, and represented for non-negative frequencies in terms of the spectrum $P(f)$ of the real waveform $p(t)$:

$$S(f)=2\hspace{0.17em}\hspace{0.17em}P(f).$$ (3)

Thus, the analytic signal is a one-sided complex waveform that has a one-sided complex spectrum.1 The spectrum of the analytic signal is represented for $f\ge 0$ in terms of real amplitude $B(f)$ and phase $\Psi (f)$ functions by

$$S(f)=B(f)\hspace{0.17em}\hspace{0.17em}{e}^{j\Psi (f)}.$$ (4)

The spectral envelope of the spectrum $P(f)$ of the real waveform $p(t)$ is $B(f),$ and its spectral fine structure resides in $\Psi (f).$ The frequency rate of change of $B(f)$ and $\Psi (f)$ are used below to define temporal moments of the CEOAE.

Multi-window analyses to improve SNR

A measured CEOAE waveform has shorter-latency components weighted to higher frequencies and longer-latency components weighted to lower frequencies. This is due to the tonotopic organization of the basilar membrane, and the observation in human ears that CEOAEs are predominantly generated in the tonotopic region. This property may be used to improve the overall spectral SNR of a CEOAE measurement through a multi-window spectral analysis that uses shorter-duration windows at earlier times for improved SNR at higher frequencies, and longer-duration windows at later times for improved SNR at lower frequencies. Keefe et al. (2011) used early, middle, and late temporal windows with early and middle windows overlapping at 2 ms, and middle and late windows overlapping at 8 ms to improve the SNR of measurements of CEOAE magnitude.

The multi-window analyses in Keefe et al. (2011) retained spectral magnitude and discarded phase. In contrast, the present study performed a multi-window spectrum analysis of the CEOAE waveform that retained spectral phase and magnitude information, because both of these were needed to calculate the GD and GS of the CEOAE. Early, middle and late temporal windows were defined that overlapped at 4 and 8 ms after the onset time of the click. The early window extended from 0.25 to 4.33 ms with onset ramp of 0.34 ms and offset ramp of 0.66 ms. The middle window extended from 3.67 to 8.65 ms with onset ramp of 0.66 ms and offset ramp of 1.29 ms. The late window extended from 7.35 to 25 ms with onset ramp of 1.29 ms and offset ramp of 10 ms. Each overlapping pair of windows summed to one at each time step within their ramps. Ramp durations increased at later times because the local OAE period was longer at later times.

The three temporal windows are denoted as $h_i(t)$ for $i=1,2,$ and $3.$ In each buffer, the CEOAE waveform is $p(t),$ and the ith windowed CEOAE waveform is $p_i(t)=h_i(t)\times p(t).$ Each windowed waveform $p_i(t)$ was zero-padded out to 46.4 ms (2048 samples) prior to calculating its complex spectrum $P_i(f)$ (other analyses used other lengths of zero padding as described below). The spectrum $P_i(f)$ of the ith windowed waveform was calculated using the DFT of $p_i(t).$ A weighting coefficient $W_i(f)$ for the ith windowed signal was defined as the SNR of the spectrum $P_i(f)$ across all 32 buffers. The CEOAE signal and noise sound pressure spectra were calculated using coherent and incoherent averaging (Goodman et al., 2009), and combined to form the SNR at each frequency $f.$ The total complex CEOAE spectrum $P(f)$ was defined in terms of the windowed complex spectra by2

$$P(f)=\frac{W_1(f)P_1(f)+W_2(f)P_2(f)+W_3(f)P_3(f)}{W_1(f)+W_2(f)+W_3(f)}.$$ (5)

A measured CEOAE spectrum has shorter-latency components weighted to higher frequencies and longer-latency components weighted to higher frequencies. This property was used to improve the temporal SNR of a CEOAE measurement by means of a multi-window temporal analysis of the signal processed through three bandpass filters. Narrower bandpass filters were used at higher frequencies to improve the SNR at shorter times, and wider bandpass filters at lower frequencies to improve the SNR at longer times. For the overall bandwidth (0.35–15.3 kHz), three bandpass filters $G_k(f),$ with $k=1,2,3$ were calculated with conjugate symmetry above the Nyquist frequency so that their inverse DFTs were real. Each was defined with equal bandwidth on a logarithmic frequency axis. Each filter had unity gain except for onset and offset ramps (cosine-squared) at lower and upper band edges to control for spectral splatter. The bandwidth of each ramp was 20% of the overlap frequency between adjacent filters; i.e., the ramp bandwidth was 0.25 kHz between lower- and mid-frequency windows overlapping at 1.24 kHz, and was 0.87 kHz between mid- and high-frequency windows overlapping at 4.36 kHz. Each overlapping pair of bandpass filter magnitude functions summed to one at each frequency within the onset and offset ramps.

An analytic waveform $s_k(t)$ associated with the kth bandpass filter ($k=1,2,3$) was calculated as follows based on the spectrum $P(f)$ of the measured CEOAE for each of the 32 buffered CEOAE waveforms. The output waveform $p_k(t)$ of the kth bandpass filtered spectrum was calculated using the inverse DFT, i.e., $p_k(t)={\text{DFT}}^{-1}(G_k(f)\times P(f)).$ The analytic waveform $s_k(t)$ associated with the real $p_k(t)$ was calculated using Eq. 1 for each of 32 buffered waveforms. The mean and standard error of the mean (SE) of the analytic waveforms were calculated across the 32 buffers. The temporal SNR ${\sigma }_k(t)$ was defined as the ratio of the square of the waveform envelope of the mean analytic waveform at time t and the square of the SE of the waveform envelope at time $t.$ This definition of a (real) SNR waveform at each time step was adopted as leading to the best performance compared to several alternative definitions that were considered. A real CEOAE waveform $\tilde{p}(t)$ was defined in terms of an SNR-weighted sum of the filtered real waveforms by

$$\tilde{p}(t)=\frac{{\sigma }_1(t)p_1(t)+{\sigma }_2(t)p_2(t)+{\sigma }_3(t)p_3(t)}{{\sigma }_1(t)+{\sigma }_2(t)+{\sigma }_3(t)}.$$ (6)

The total CEOAE analytic signal $s(t)$ was re-calculated with $\tilde{p}(t)$ and its Hilbert transform replacing $p(t)$ and $p_h(t)$ in Eq. 1, and used in subsequent moment analyses. Properties of multi-window temporal analyses were formally similar to the properties of multi-window spectral analyses described in Keefe et al. (2011) and in Eq. 5 after reversing the roles of time and frequency.

An example of these temporal SNR responses are shown for a subject A with normal hearing in Fig. 1. The SNR level of the unfiltered CEOAE waveform (solid line) had a maximum of 19–21 dB at several times between 1 and 12 ms. The SNR levels ($10{\log }_{10}\left[{\sigma }_k(t)\right]$) of the CEOAE waveforms calculated from each bandpass filter had larger SNRs at some times, which exceeded the SNR of the unfiltered CEOAE waveform. Except for times $\le 0.5$ ms, one or more of the bandpass filtered CEOAE waveforms had larger SNR than the unfiltered CEOAE waveform at all times. The CEOAE SNR level from the high-frequency filtered response had a maximum of 25 dB near 1.5 ms, that from the mid-frequency filtered response had a maximum of 31 dB between about 5 to 9 ms (with peak levels exceeding 24 dB between 1.3 and 19 ms), and that from the low-frequency filtered response had a maximum of 30 dB near 12 ms.

Figure 1.

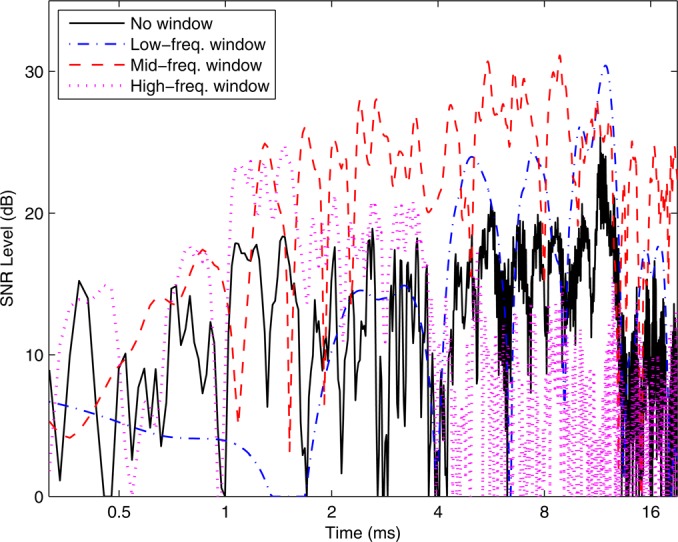
(Color online) Temporal SNR plotted (subject A) for originally measured CEOAE waveform (“no window” in legend), and waveforms from low-, mid-, and high-frequency bandpass-filtered spectra (line styles in legend). SNR plotted as level (in dB).

There was considerable overlap between the three SNRs at each time step, so that the averaging associated with Eq. 6 was influenced by multiple terms.3 An important property in Fig. 1 is that the SNR was increased at most times using the bandpass-filtered waveforms relative to the SNR of the unfiltered waveform. Because each SNR was localized to a low-, mid-, or high-frequency band, the overall OAE waveform $\tilde{p}(t)$ preferentially captured those band-limited OAE components with larger SNR, and attenuated those band-limited components that were dominated by noise. Subsequent smoothing of moments calculated from the analytic waveform associated with $\tilde{p}(t),$ which is described below, greatly reduced effects related to the temporal fluctuations of SNR in this figure.

THEORY UNDERLYING CEOAE MOMENTS

The CEOAE moments are formulated based on the analytic signal and time-frequency analysis. These subjects are described in detail in Cohen (1995). The spectral moments of the general analytic signal in Eq. 2 are

$$\begin{array}{c}\mathrm{I}\mathrm{F}(t)=\frac{1}{2\pi }\frac{d\mathrm{\Phi }(t)}{\mathit{d}\mathit{t}},\\ \mathrm{I}\mathrm{B}(t)=\frac{1}{2\pi }\left|\frac{d\hspace{0.17em}\ln \hspace{0.17em}A(t)}{\mathit{d}\mathit{t}}\right|.\end{array}$$ (7)

The instantaneous frequency (IF) is the temporal phase gradient, and the instantaneous bandwidth (IB) with unit of frequency is the magnitude of the temporal gradient of the log-amplitude. Aside from a numerical constant, IB (Cohen and Lee, 1990) is the temporal gradient of the sound pressure level of the CEOAE, i.e., its decay rate. A steep decay rate over a brief time interval is associated with a large bandwidth over that time interval.

A rationale for considering IB is illustrated using the analytic impulse response $g(t)$ of a two-pole filter resonator with constant resonance frequency $f_0$ and constant decay time $\tau ,$ namely, $g(t)=g_0{e}^{j2\pi f_{0}t}{e}^{-t/\tau }.$ Its IB from Eq. 7 is $1/(2\pi \tau ),$ so that its 3-dB quality factor is $Q=1/2\times \text{IF}/\text{IB}$ (Barnes, 1993). Using the equivalent rectangular bandwidth (ERB) of a two-pole filter (Hartmann, 1998), it follows that its spectral quality factor $Q_{\text{ERB}}=2Q=\text{IF}/\text{IB}.$ This motivates a definition of $Q_I(t)$ for a general signal by

$$Q_I(t)=\text{IF}(t)/\text{IB}(t).$$ (8)

The equality $Q_I=Q_{\text{ERB}}$ is satisfied only for a second-order resonant filter, and is not satisfied for a cochlear filter. Nevertheless, the quantities $\text{IB}$ and $Q_I$ provide estimates of the local bandwidth and “tuning” of a CEOAE to the extent that the CEOAE is predominantly a single-component signal at time $t.$ The presence of multiple internal reflections within the cochlea would result in a multiple-component signal.

The temporal moments of the spectrum of an analytic signal in Eq. 4 are (Cohen and Lee, 1990)

$$\begin{array}{c}\text{GD}(f)=-\frac{1}{2\pi }\frac{d\Psi (f)}{\mathit{d}\mathit{f}},\\ \text{GS}(f)=\frac{1}{2\pi }\left|\frac{d\hspace{0.17em}\ln \hspace{0.17em}B(f)}{\mathit{d}\mathit{f}}\right|.\end{array}$$ (9)

The group spread (GS) with a unit of time is the magnitude of the spectral gradient of the log-amplitude. GS is the effective duration or local temporal spread of the CEOAE with delay GD at frequency $f.$ Aside from a numerical constant, GS is the slope (i.e., level per unit frequency) of the CEOAE sound pressure level spectrum. A peakier spectrum around a particular frequency f is associated with increased $\text{GS}(f).$ GS is a measure of the temporal dispersion associated with the spatial spread of tonotopically organized CEOAE-reflection sites along the basilar membrane.

A dimensionless ratio $Q_G(f)$ is defined as a CEOAE temporal quality factor by

$$Q_G(f)=\text{GD}(f)/\text{GS}(f).$$ (10)

Whereas $Q_I(t)$ is a ratio of a center or mean frequency to its bandwidth, $Q_G(f)$ is a ratio of a center or mean delay to its temporal spread or duration about its mean delay.

A peak in the spectrum has a bandwidth and hence a spectral quality factor $Q_I(t).$ A peak in the maximum waveform envelope at a time equal to the group delay is associated with a duration or spread in the envelope at times around the group delay, and hence a temporal quality factor $Q_G(f).$

The definitions of these moments are placed in the context of time-frequency analysis in Appendix A, which explains the sense in which IF, IB, GD, and GS are understood as moments of conditional time-frequency distributions. The material in this appendix is not used elsewhere in the manuscript.

Phase and level gradient calculations

OAE phase gradients have been calculated in previous studies by first unwrapping the phase, which may be contaminated by noise effects. Phase gradients in this study were calculated without evaluating phase (Barnes, 1992). The $S(f)$ is expressed using its rectangular components $S(f)=U(f)+jV(f)$ with real functions $U(f)$ and $V(f).$ GD is

$$\text{GD}(f)=-\frac{1}{2\pi }\left(\frac{U(f)(dV(f)/df)-(dU(f)/df)V(f)}{U^2(f)+V^2(f)}\right).$$ (11)

A similar operation is performed for $s(t)$ in rectangular components to calculate $\text{IF}(t).$

In discrete-time, discrete-frequency calculations with CEOAE data for sampling period T, both two- and three-sample approximations were used to calculate the derivatives (Barnes, 1992). The two-sample approximations for GD and GS at the kth frequency are

$$\begin{array}{c}\text{GD}[k]=-\frac{1}{2\pi T}\arctan \left(\frac{U[k]V[k+1]-U[k+1]V[k]}{U[k]U[k+1]+V[k]V[k+1]}\right),\\ \text{GS}[k]=\frac{1}{4\pi T}\left|\ln \left(\frac{{(U[k+1])}^2+{(V[k+1])}^2}{{(U[k])}^2+{(V[k])}^2}\right)\right|.\end{array}$$ (12)

Analogous discrete-time, discrete-frequency approximations were used for IF and IB. In preliminary analyses of GD and GS, the three-sample approximations of GD and GS over a time interval $2T$ required approximately twice the zero padding of the CEOAE waveform prior to the DFT as compared to the two-sample approximation over an interval $T.$ Insufficient zero padding produced anomalously small values of GD at low frequencies (between 0.5 and 2 kHz). All reported CEOAE moment analyses used two-sample approximations and a CEOAE waveform length of $N_F=2048$ samples.4

Smoothing of moments

Shera and Guinan (2003) concluded that fluctuations in SFOAE GDs were not caused by noise inasmuch as results were reproducible within each subject (although no degree of reproducibility was specified). Frequency-dependent phase variations were described as correlated with amplitude variations, as predicted by the coherent reflection emission theory, and produced by variations in the cochlear impedance perturbations that generate the reflected wave forming the SFOAE. Based on the close relationship of CEOAEs and SFOAEs, a similar scattering mechanism would affect CEOAE GDs as well. The presence of any noise would further exacerbate the ability to measure GD and other moments.

An effective strategy to reduce the effect of fluctuations arising from any source is to smooth $\text{GD}(f)$ and $\text{GS}(f)$ over frequency, and $\text{IF}(t)$ and $\text{IB}(t)$ over time. Inasmuch as audiometric measurements are commonly interpreted at half-octave spacings, $\text{GD}(f)$ and $\text{GS}(f)$ were smoothed over each half octave at center frequencies from 0.5 to 11 kHz, and smoothed at the center frequency of 14.3 kHz for the highest frequencies between 13.3 and 15.3 kHz. Aside from slightly larger variability, similar results were obtained using third-octave spacings. An octave in frequency corresponds to a doubling in time. A set of doublings in time was defined based on a reference value of 1 ms. $\text{IF}(t)$ and $\text{IB}(t)$ were smoothed over time, and reported at half-doublings of time from 0.35–16 ms.

GD and GS were smoothed within the frequency range centered at $f_0$ using the squared magnitude $B^2(f)$ of the CEOAE spectrum as a weighting coefficient. In the continuous-frequency representation, the smoothed moments $\langle \text{GD}(f_0)\rangle$ and $\langle \text{GS}(f_0)\rangle$ at $f_0$ were defined by

$$\begin{array}{c}\langle \text{GD}(f_0)\rangle =-\frac{1}{2\pi }\frac{\int (d\Psi (f)/df)B^2(f)df}{\int B^2(f)df},\\ \langle \text{GS}(f_0)\rangle =\frac{1}{2\pi }\frac{\int \left|d\ln B(f)/df\right|B^2(f)df}{\int B^2(f)df},\end{array}$$ (13)

in which the expressions for $\text{GD}(f)$ and $\text{GS}(f)$ in Eq. 9 were used within the integrands. Each integral extended over frequencies within a band centered at $f_0.$ This smoothing used squared magnitude (or “spectral energy density” in a signal-processing sense) to attenuate the integrand at those frequencies where trouble would occur in calculating GD and GS. Fine structure within each half octave was discarded in order to more accurately extract the slower variation of GD and GS across frequency.

IF and IB were smoothed within the range of times centered at $t_0$ using the squared magnitude $A^2(t)$ (or “temporal energy density”) of the CEOAE waveform as a weighting coefficient. The smoothed moments $\langle \text{IF}(t_0)\rangle$ and $\langle \text{IB}(t_0)\rangle$ at $t_0$ were defined using Eq. 7 as

$$\begin{array}{c}\langle \text{IF}(t_0)\rangle =\frac{1}{2\pi }\frac{\int (d\mathrm{\Phi }(t)/dt)A^2(t)dt}{\int A^2(t)dt},\\ \langle \text{IB}(t_0)\rangle =\frac{1}{2\pi }\frac{\int \left|d\ln A(t)/dt\right|A^2(t)dt}{\int A^2(t)dt}.\end{array}$$ (14)

Each integral extended over times within the interval centered at $t_0.$

Smoothing was performed in the discrete-time, discrete-frequency representation by replacing integrals by sums. In the Sec. 4, each measured CEOAE moment is understood to be the result of the smoothing operations in Eq. 13 or 14, although simpler variable names are used therein for convenience.

OAE detection criteria based on SNR and CSM

CEOAE moments were calculated for each ear only at those frequencies and times for which the CEOAE was detectable. As described in Sec. 2A, CEOAE waveforms and spectra were calculated in each of $K=32$ buffers. In the frequency domain, the CEOAE signal and noise sound pressure spectra were calculated across the K buffers using coherent and incoherent averaging (Goodman et al., 2009). The frequency-averaged SNR was calculated as the ratio of the summed squared magnitude of the CEOAE signal to the summed squared magnitude of CEOAE noise over each half-octave band. A CEOAE magnitude was detected if this SNR exceeded a criterion SNR. This criterion SNR, which is derived from the underlying Rice distribution of signal magnitude in noise, is the minimum SNR to achieve correct detection of the signal in noise with an error rate p in a two-alternative forced-choice paradigm (Green and McGill, 1970); it has been used for SFOAE detection (Goodman and Keefe, 2006). The criterion SNR as a level (in dB) is

$$\mathrm{S}\mathrm{N}{\mathrm{R}}_{\text{crit}}=10{\log }_{10}(-2\ln (2p)),$$ (15)

which is 6.6 dB for $p=\mathrm{0.05.}$ The SNR and this criterion were also applied in the time domain using the CEOAE analytic waveform at each time step, after summing at times within each half-doubling of time.

An alternative detection criterion for a CEOAE response was based on the degree of synchrony of the CEOAE with respect to the click stimulus. Such a coherence synchrony measure (CSM) was introduced to detect 80 Hz auditory steady state responses in neural recordings based on synchrony (Valdes et al., 1997). Müller-Wehlau et al. (2005) used CSM to detect the presence of the acoustic stapedius-muscle reflex. CSM was used in the present study to detect CEOAE synchrony.

The spectrum in the ith buffer is parameterized at each frequency by its measured magnitude $B_i(f)$ and complex phasor $e^{j{\Psi }_i(f)}.$ CSM(f) is defined at each DFT frequency as the length of the sum of the spectral phasors in the K buffers divided by $K,$ i.e.,

$$\text{CSM}(\mathrm{f})=\frac{1}{K}{\displaystyle \sum }_{i=1}^K{e}^{j{\Psi }_i(f)}.$$ (16)

Each phasor, and therefore CSM as well, is unaffected by phase unwrapping. CSM ranges from near zero in the limit that the phasors are independent samples of noise on the complex plane up to one in the limit that all phasor angles (modulo $2\pi$) are equal. A criterion CSM is defined such that a smaller CSM satisfies the null hypothesis that the phasor distribution is uniform on the complex plane and any larger CSM is evidence that a CEOAE is present. Greenwood and Durand (1955) provided asymptotic function approximations with which to calculate a criterion CSM for K buffers and a specified p value. Their approximations to two terms imply

$${\text{CSM}}_{\text{crit}}=\frac{1}{2K}{\left[{(1+2K)}^2-{(\ln p+(1+2K))}^2\right]}^{1/2}.$$ (17)

This expression is accurate to within 0.001 for $K\ge 10,$ which sufficed for present analyses. The ${\text{CSM}}_{\text{crit}}=0.305$ for $K=32$ and $p=\mathrm{0.05.}$ These CSM(f) values measured at each DFT frequency were averaged within each half-octave bin to give CSM(f) for that bin.

CSM(t) at each sample time t was similarly defined and calculated in terms of the temporal phasor $e^{j{\mathrm{\Phi }}_i(t)}$ in each of K buffers by

$$\text{CSM}(\mathrm{t})=\frac{1}{K}{\displaystyle \sum }_{i=1}^K{e}^{j{\mathrm{\Phi }}_i(t)}.$$ (18)

These CSM(t) values measured at each sample were averaged within each half-doubling in time to give CSM(t) for that time step. The criterion CSM for CSM(t) was ${\text{CSM}}_{\text{crit}}$ defined in Eq. 17. CEOAE synchrony was judged as significant for each frequency bin when CSM(f) exceeded ${\text{CSM}}_{\text{crit}}$, and similarly for CSM(t) at each time step.

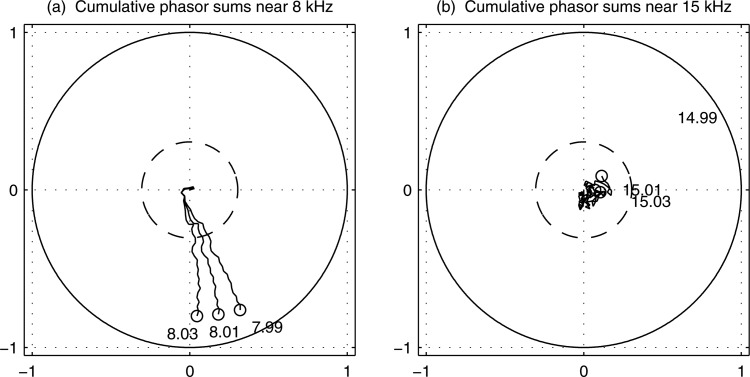
An example of a CSM(f) measurement in a single test ear is shown in Fig. 2 for three adjacent DFT bin frequencies close to 8 kHz, and three bin frequencies close to 15 kHz (i.e., prior to half-octave averaging). ${\text{CSM}}_{\text{crit}}$ is shown as the radius of the dashed-line circle. The CSMs exceeded ${\text{CSM}}_{\text{crit}}$ near 8 kHz, which was consistent with a present CEOAE response in these DFT bins; the CSMs were less than ${\text{CSM}}_{\text{crit}}$ near 15 kHz, which was consistent with an absent CEOAE response. This latter CSM near 15 kHz shows the phase response of a “random walk,” i.e., each phasor represents a step in a random direction on the complex plane so that their sum remains close to the starting point (95% of trials would end up within the circle of radius ${\text{CSM}}_{\text{crit}}$). The CSM value used to detect the CEOAE is the average CSM over all DFT bin frequencies within each half octave frequency, so the results in this figure show an intermediate stage of calculation. Nonetheless, they are consistent with CEOAE measurements described in Results in Fig. 4 (see the plot panel in row 2 and column 4) for the same test ear. These showed CEOAEs present at 8 kHz based on CSM, and absent at 14.3 kHz (i.e., in the bin including frequencies near 15 kHz).

Figure 2.

Cumulative sums of phasors of CEOAE spectrum plotted at three frequencies close to 8 kHz (left) and close to 15 kHz (right). Solid-line circle is circle of radius one; dashed-line circle is a circle ofradius ${\text{CSM}}_{\text{crit}}=\mathrm{0.305.}$ Circle marker at the end of each line segment denotes its CSM across all 32 buffers. Each cumulative sum of phasors labeled by its spectral frequency (in kHz).

Figure 4.

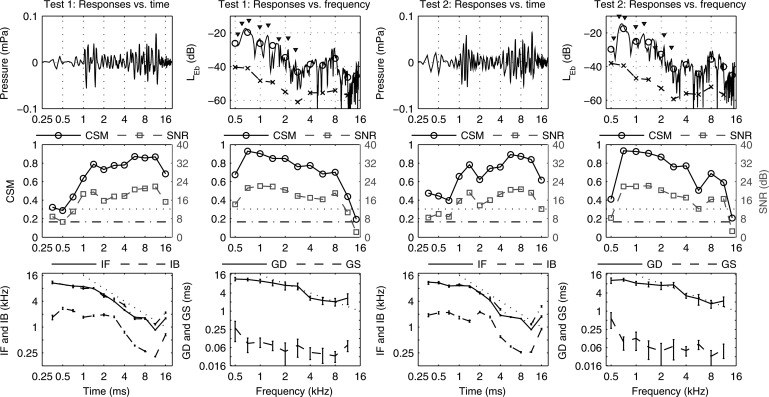
CEOAE data in subject A (left ear) shown in columns 1 and 2 for test 1, and columns 3 and 4 for test 2. Columns 1 and 3 with time abscissa—Row 1: Mean CEOAE waveform. Row 2: CSM (left ordinate, solid line) and ${\text{CSM}}_{\text{crit}}$ (dotted line). SNR (right ordinate, dashed line) and ${\text{CSM}}_{\text{crit}}$ (dash-dot line). Row 3: Mean $\pm 1$ SE of IF (solid line) and IB (dashed line). Mean $\pm 1$ SE of CEOAE waveform zero-crossing rate (${\text{IF}}_z$) (dash-dot line). Dotted line slope of −1. Columns 2 and 4 with frequency abscissa—Row 1: CEOAE spectrum level (solid line). Mean CEOAE signal spectrum level (black line, marker ○); mean CEOAE noise spectrum level (dashed line, marker ×). Triangles placed above SSOAE frequencies as in Fig. 3. Row 2: CSM (left ordinate, solid line) and ${\text{CSM}}_{\text{crit}}$ (dotted line). SNR (right ordinate, dashed line) and ${\text{SNR}}_{\text{crit}}$ (dash-dot line). Row 3: Mean $\pm 1$ SE of GD (solid line) and GS (dashed line). Dotted line slope of −1.

The phase-gradient moments IF and GD used CSM as the detection criterion. This eliminated any problem associated with using a SNR criterion based on signal envelope to interpret a CEOAE phase-gradient in the time or frequency domain. The log-amplitude-gradient moments IB and GS used SNR as the detection criterion.

The CSM for a SSOAE spectrum was measured in each of $N_B=687$ frequency bins between $0.35$ and $15.3$ kHz, in which $0.35$ kHz was the lower edge frequency in the half octave centered at $0.5$ kHz. A Bonferroni correction of $p=0.05/N_B=0.000072$ was applied to correct for multiple comparisons across frequency. This p was used to calculate ${\text{CSM}}_{\text{crit}}$ with the number of valid SSOAE buffers $K_S$ after artifact rejection calculated individually for each ear (i.e., $K_S\le 1198$). For example, the SSOAE results to be described in Fig. 3 had $K_S=1153$ valid buffers resulting in ${\text{CSM}}_{\text{crit}}=0.091$ using Eq. 17.

Figure 3.

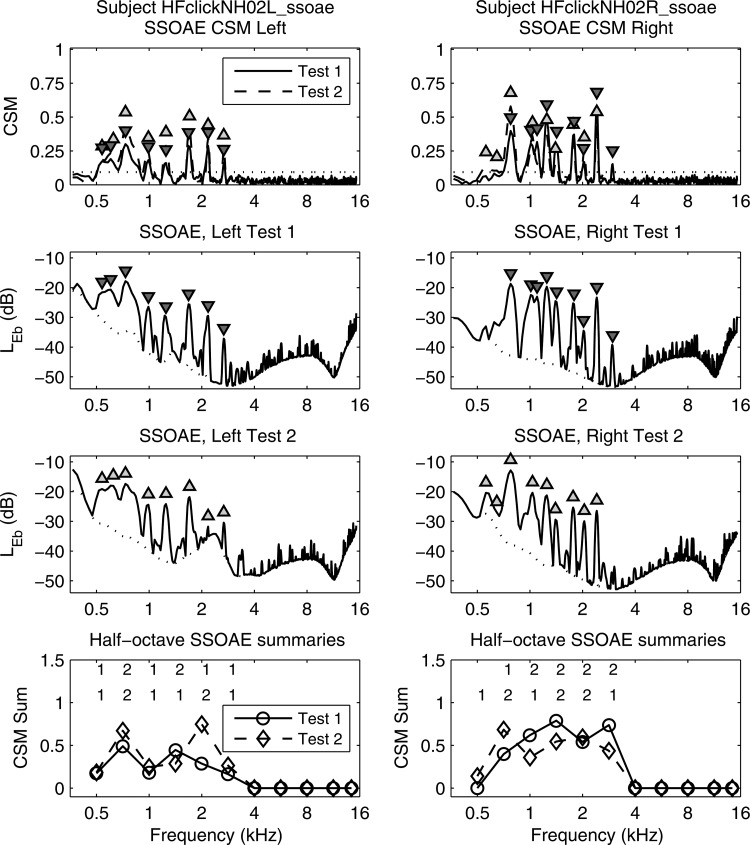
SSOAE response vs frequency (subject A) in left column (left ear) and right column (right ear) for tests 1 and 2. Row 1: CSM (lines), triangle markers at SSOAE peak frequencies: apex up for SSOAEs in test 1 and down for test 2. ${\text{CSM}}_{\text{crit}}=0.091$ (dotted line). Row 2: $L_{\mathit{E}\mathit{b}}$ in test 1 for SSOAEs (solid line) and noise (dotted line). Triangles specify peaks from CSM in row 1. Row 3: $L_{\mathit{E}\mathit{b}}$ in test 2 using similar format to row 2. Row 4: CSM Sum. Upper row of numbers are # of SSOAEs at each frequency for test 1, and lower row for test 2.

RESULTS

Individual ear results

SSOAEs

Properties of SSOAEs in both ears of a subject A with normal hearing are shown in Fig. 3 for test 1 and test 2. CSM in row 1 of the figure had 8-9 narrow peaks that were localized to spectral frequencies between 0.5 and 3 kHz, and identified as SSOAEs based on $\text{CSM}>{\text{CSM}}_{\text{crit}}.$ In the absence of any Bonferroni correction for ${\text{CSM}}_{\text{crit}},$ many more SSOAE frequencies would have been spuriously identified. The observed SSOAE frequencies were highly repeatable between tests 1 and 2. The frequencies at which the SSOAE was present according to ${\text{CSM}\hspace{0.17em}>\hspace{0.17em}\text{CSM}}_{\text{crit}}$ essentially coincided with the frequencies at which the SNR was large in the SSOAE spectrum (see test 1 levels in row 2 and test 2 levels in row 3). SSOAE levels $L_{\mathit{E}\mathit{b}}$ are plotted as band sound-exposure spectrum levels with reference time equal to the DFT buffer duration (Goodman et al., 2009).5

For subsequent interpretation of CEOAE results, the number of SSOAEs in each frequency bin (nominally at half-octave frequencies except for the 14.3 kHz bin) are presented in row 4 using a CSM Sum variable. CSM Sum is defined at each frequency bin as the sum of the CSMs occurring at all SSOAE frequencies within the bin.6 CSM Sum is a more refined measure of overall SSOAE strength in each frequency bin compared to the number of SSOAEs per bin, which varied between 1–2 for this subject up to 2.8 kHz. The fact that the right ear had nine SSOAEs and a slightly larger CSM Sum than the left ear (with its eight SSOAEs) exemplifies an ear effect described below in group results. Left- and right-ear SSOAEs tended to be similar within a given subject in the numbers of SSOAEs and their approximate levels, as was observed for subject A in Fig. 3.

CEOAEs

Properties of CEOAEs recorded in the left ear of subject A at 73 dB peSPL are shown in Fig. 4 for test 1 (columns 1 and 2) and test 2 (columns 3 and 4). For test 1, the CEOAE waveform was detected using CSM at all time steps from 0.35 to 16 ms except at 0.5 ms, and using SNR at all time steps. Means and SEs of CEOAE moments were calculated across 32 buffers, with data shown only at times (column 1) and frequencies (column 2) at which their detection criteria were satisfied.

IF exceeded 8 kHz at short times and decreased to 2 kHz at increasing times with a slope less than −1. The zero-crossing rate (${\text{IF}}_z$) of the CEOAE waveform was nearly identical to IF, a property found in all test ears. IB was about 3 kHz at short times, and decreased to a minimum of 0.14 kHz at 11 ms. The small IB at long times suggests that the CEOAE waveform was dominated by frequency components that would be also detected as SSOAEs (compare Figs. 34), inasmuch as a SSOAE might occur as a CEOAE component with an extremely narrow bandwidth.7

As functions of frequency (see column 2 of Fig. 4), CEOAEs were detected based on CSM and SNR at all frequencies except 14.3 kHz. GD exceeded 10 ms at low frequencies and decreased more slowly than $f^{-1}$ at higher frequencies (to about 3 ms). GS ranged from 0.06–0.2 ms at lower frequencies to about 0.03–0.09 ms at higher frequencies.

These results illustrate the salience of SSOAE properties (Fig. 3) in understanding CEOAE moments (Fig. 4). When one or more SSOAEs were present in an ear in which a CEOAE was measured, the SSOAE components were present at all times with frequency components up to 3 kHz. The presence of SSOAEs influenced IF and IB at short times. Even with the use of multi-window signal processing in time and frequency domains, the presence of any low-frequency SSOAEs remained as a complicating factor in interpreting CEOAE moments. The underlying property is that a click stimulus generates both CEOAEs and SSOAEs, and the difference in the responses arises from when each is measured, early or late.

The SEs plotted as error bars in Fig. 4 for the four CEOAE moments were based on the SE across the 32 buffers, i.e., each moment was calculated in each buffer, and then averaged across buffers. This shows that the variabilities in measuring IF, IB, GD and GS were small within test 1 and within test 2. The CEOAE moment measurements were generally repeatable in test 1 and test 2 (i.e., compare columns 1 and 3, and columns 2 and 4). This repeatability is quantified in group analyses.

Group results on SSOAEs

The prevalence of one or more SSOAEs was 85% in the group of 110 ears with normal hearing. This is larger than the 72% reported by Sisto et al. (2001), which may be due to the fact that their study used a time interval out to 80 ms after the synchronizing click, whereas the present study extended only out to 42 ms. This SSOAE prevalence was also larger than the 72% prevalence reported for SOAEs in normal ears (Talmadge et al., 1993). SSOAE prevalence in the present study was 3% larger in right than left ears, replicating a similar trend in Sisto et al. (2001). The median number of SSOAEs per ear was 4 for all ears, 5 for all right ears, and 4 for all left ears, although this ear difference was not significant based on $p=\mathrm{0.05.}$

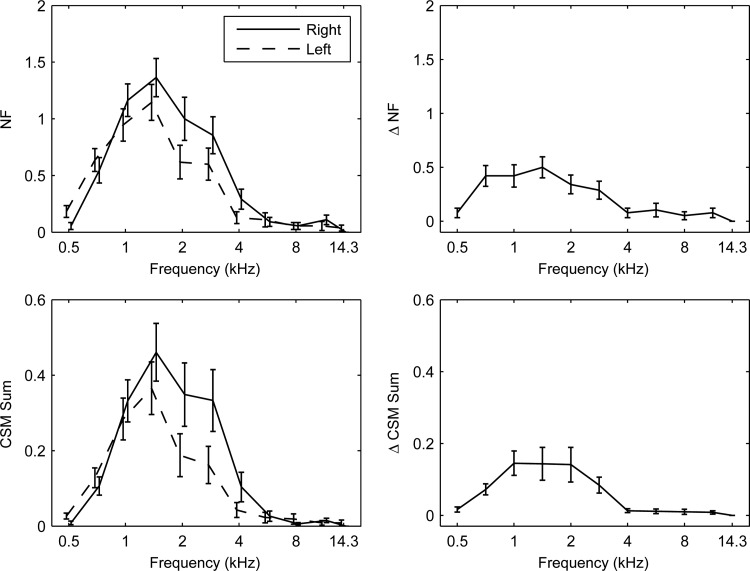
Ear differences were investigated in SSOAEs in the normal group (see left column of Fig. 5). The mean numbers of SSOAEs (NF) per half-octave frequency bin were largest between 1 and 3 kHz, and the mean NF at 2 kHz was significantly larger in right than left ears. The maximum frequency at which SSOAEs were detected was 4 kHz, and SSOAEs at 4 kHz occurred more often in the right ear. The mean CSM Sum across ears was largest in the same frequency range, and larger in the right than the left ear at 2, 3, and 4 kHz. These results are similar to the right-ear advantage found in SOAEs (Bilger et al., 1990; Burns et al., 1992).

Figure 5.

SSOAE normal group data using mean $\pm 1$ SE. Test 1 data in left column; magnitude difference data from tests 1 and 2 plotted in right column. Left column—Row 1: Number (NF) of SSOAEs per frequency bin. Row 2: CSM Sum. Separate plots for left/right ears slightly displaced along abscissa for clarity. Right column—Row 1: $\Delta \text{NF}$, magnitude difference in NF. Row 2: $\Delta \text{CSM}$ Sum, magnitude difference in CSM Sum.

The repeatability of SSOAE measurements was examined in 73 normal ears (see right column of Fig. 5). When averaged across both ears, the magnitude differences between test 1 and test 2 of NF (denoted $\Delta \text{NF}$) and of CSM (denoted $\Delta \text{CSM}$) were each small below 4 kHz compared to measured values in test 1 (i.e., compared to the midline of right- and left-ear results in the left column of Fig. 5). For example, the mean CSM of 0.41 at 1.4 kHz contrasts with the mean $\Delta \text{CSM}$ of 0.15. Some fluctuation in the repeatability of these SSOAE variables is due to fluctuations in the biological mechanisms underlying SSOAE generation, and test variability. A high level of repeatability of SSOAEs in test ears over a time span of approximately 8.5 days is consistent with the high level of repeatability of SOAEs in ears over many years (Burns, 2009).

Group results on CEOAE moments

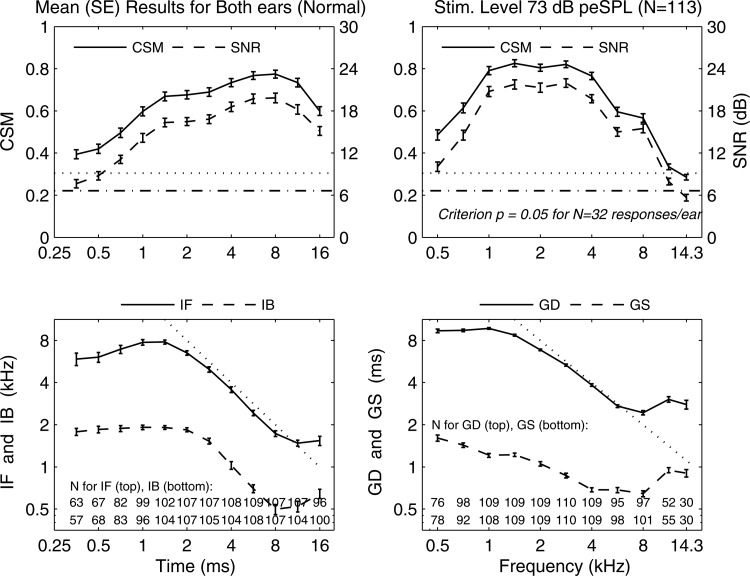
The mean and SE of each CEOAE moment are plotted in Fig. 6 (row 2) for the normal group of 113 ears at a stimulus level of 73 dB peSPL, along with the number of ears at each time or frequency step with a detectable moment. In the plots versus time in the left column, the mean $\text{CSM}(\mathrm{t})$ and $\text{SNR}(t)$ showed significance at all time steps, but were smaller at shorter times. The mean $\text{IF}(t)$ (in the subset of ears with detected IF) had a maximum of about 8 kHz at $1-1.4$ ms, and decreased more slowly than $t^{-1}$ at longer times. The mean $\text{IB}(t)$ had a similar trend versus time to the mean $\text{IF}(t)$ with reduced values.

Figure 6.

CEOAE-moment normal group data using mean $\pm 1$ SE. Left column, time abscissa—Row 1: CSM (solid line) and ${\text{CSM}}_{\text{crit}}$ (dotted line) [left ordinate], and SNR (dashed line) and ${\text{SNR}}_{\text{crit}}$ (dashed-dotted line) [right ordinate]. Row 2: IF and IB. # of ears at each time listed at bottom for detected IF and IB. Dotted line slope of −1. Right column, frequency abscissa—Row 1: CSM (solid line) and ${\text{CSM}}_{\text{crit}}$ (dotted line) [left ordinate], and SNR (dashed line) and ${\text{SNR}}_{\text{crit}}$ (dashed-dotted line) [right ordinate]. Row 2: GD and GS. # of ears at each frequency listed at bottom for detected GD and GS. Dotted line slope of −1.

In the plots vs frequency in the right column, the mean $\text{CSM}(\mathrm{f})$ and $\text{SNR}(f)$ exceeded their criterion values at all frequencies except $14.3$ kHz, and decreased more slowly than $f^{-1}$ with increasing frequency. The mean $\text{GD}(f)$ had a maximum of about 10 ms at $0.5-1$ kHz, and decreased more slowly than $f^{-1}$ at longer times to $2.2-3$ ms at frequencies above 6 kHz. The mean $\text{GS}(f)$ had a generally similar trend vs frequency to the mean $\text{GD}(f),$ but its values were reduced. The SEs were small relative to their means for IF and IB at all times, and for GD and GS at all frequencies.

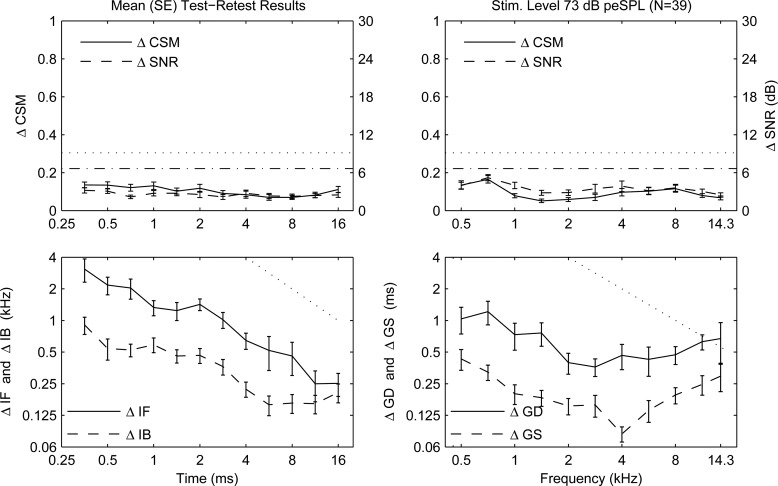
The within-ear repeatability in the normal-hearing group was assessed by the mean magnitude of the difference in test 1 and test 2 between the criteria ($\Delta \text{CSM}$ and $\Delta \text{SNR}$), and between their moment values (see Fig. 7). The mean and SE were calculated by averaging the magnitude difference across all ears. The mean magnitude differences $\Delta \text{CSM}$ and $\Delta \text{SNR}$ were small compared to their respective single-test criterion levels. The mean magnitude difference of each moment was less than one-quarter of the measured moment in most conditions. Exceptions were that the mean magnitude differences $\Delta \text{IF}$ and $\Delta \text{IB}$ were as much as one-half of the measured mean moment for times less than 1 ms. The SEs between ears were small compared to the mean magnitude difference values.

Figure 7.

Magnitude difference (mean $\pm 1$ SE) in subset of normal ears ($N=41$) between tests 1 and 2 for CSM and SNR, and CEOAE moments. Left column, time abscissa—Row 1: $\Delta \text{CSM}$ (solid line) and ${\text{CSM}}_{\text{crit}}$ (dotted line) [left ordinate], and $\Delta \text{SNR}$ (dashed line) and ${\text{SNR}}_{\text{crit}}$ (dashed-dotted line) [right ordinate]. Row 2: $\Delta \text{IF}$ and $\Delta \text{IB}$. Dotted line slope of −1. Right column, frequency abscissa—Row 1: CSM (solid line) and ${\text{CSM}}_{\text{crit}}$ (dotted line) [left ordinate], and SNR (dashed line) and ${\text{SNR}}_{\text{crit}}$ (dashed-dotted line) [right ordinate]. Row 2: $\Delta \text{GD}$ and $\Delta \text{GS}$. Dotted line slope of −1.

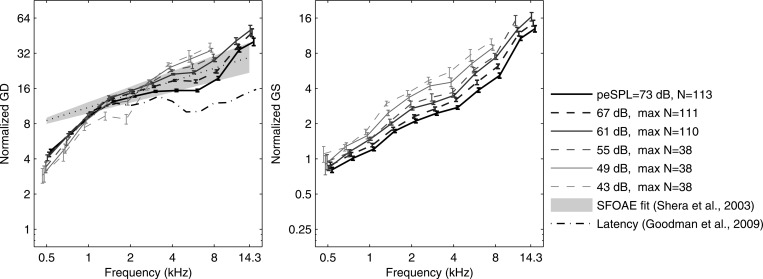
A normalized GD was defined as the ratio of GD to the sample period, and a normalized GS was defined as the ratio of GS to the sample period. Each was measured in units of the number of periods at each frequency. The mean $\pm 1$ SE of normalized GD and GS in normal ears are shown in Fig. 8 at peSPLs between 43 and 73 dB. These moment statistics were plotted only if five or more ears had detected moments. GD increased slowly with increasing peSPL at frequencies below 1 kHz, and decreased with increasing peSPL at frequencies above 3 kHz. The normalized GD shows a low-frequency breakpoint near 1.4 kHz, a high-frequency breakpoint near 11 kHz (at 73 dB peSPL), and an approximate power-law dependence at intermediate frequencies. The model fit for the corresponding SFOAE GD measurements of Shera et al. (2010) at intermediate frequencies and a stimulus level of 40 dB SPL is shown for comparison. A more detailed trend line of SFOAE GD in Shera et al. (not shown) was similar to CEOAE GD at frequencies from 1.4 to about 8 kHz, but lower than their model fit at frequencies below 1 kHz, and higher than the model fit above about 8 kHz. These details generally agree with the mean CEOAE GD results in the present study. The CEOAE latency at 73 dB peSPL measured by Goodman et al. (2009) using the same database as the present study was smaller than CEOAE GD and SFOAE GD (see left panel, Fig. 8). The mean normalized GS increased with increasing frequency with a slope slightly less than 1, and decreased uniformly with increasing stimulus level.

Figure 8.

Normalized GD and GS (mean $\pm 1$ SE) as ratios of GD and GS, respectively, to sample period (units, # periods) over stimulus peSPL range 43–73 dB. Left: Normalized GD from CEOAEs. Fit line of normalized GD for SFOAEs (dotted line) with 90th percentiles of fit (gray shading) (Shera et al., 2010). CEOAE latency at 73 dB peSPL (Goodman et al., 2009). Right: Normalized GS from CEOAEs. (Data displaced horizontally for clarity.)

The mean, median, or local trend average measurements for GDs in CEOAEs and SFOAEs are in general agreement across studies, while greater differences are present in the variabilities in GD, however these are defined. This study showed that the CEOAE GD was shown in this study to be repeatable in individual ears to within about 25%, and thus a potential candidate for clinical utilization.

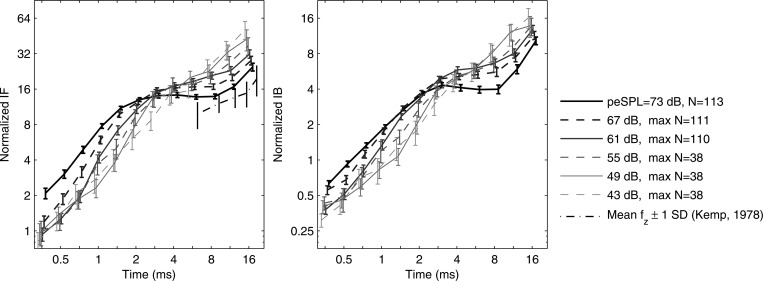
A normalized IF was defined as the product of IF and the sample period, and a normalized IB as the product of IB and the sample period. Each was measured in units of the number of cycles. The mean $\pm 1$ SE of normalized IF and IB in normal ears are shown in Fig. 9 at peSPLs between 43 and 73 dB (responses plotted only if data from five or more ears were included). IF increased with increasing peSPL at times shorter than 2.5 ms, and decreased with increasing peSPL at frequencies at times longer than 5 ms. The normalized IF at the highest peSPL (73 dB) showed a short-time breakpoint near 1.4 ms, a long-time breakpoint above about 10 ms, and an approximate power-law dependence at intermediate times. The group mean of the CEOAE zero-crossing rate (not shown) was essentially identical (i.e., to within 0.1%) to the group mean of CEOAE IF, which was consistent with the single-subject results in Fig. 4. In contrast, the group mean of the CEOAE zero-crossing rate measured at times 5–20 ms by Kemp (1978) was less than IF in the present study.

Figure 9.

Normalized IF and IB (mean $\pm 1$ SE) as products of IF and IB, respectively, and sample period (units, # cycles) over stimulus peSPL range 43–73 dB. Left: normalized IF from CEOAEs. Mean $\pm 1$ standard deviation of normalized zero-crossing rate (Kemp, 1978). Right: normalized IB from CEOAEs. (Data displaced horizontally for clarity.)

The mean normalized IB increased with increasing time with a slope slightly less than 1 (depending on stimulus level). IB tended to increase with increasing stimulus level for times shorter than 2.5 ms, and to decrease with level at times longer than 6 ms. The mean normalized IB showed a similar scaling region between about 2 and 8 ms to that observed for mean normalized IF.

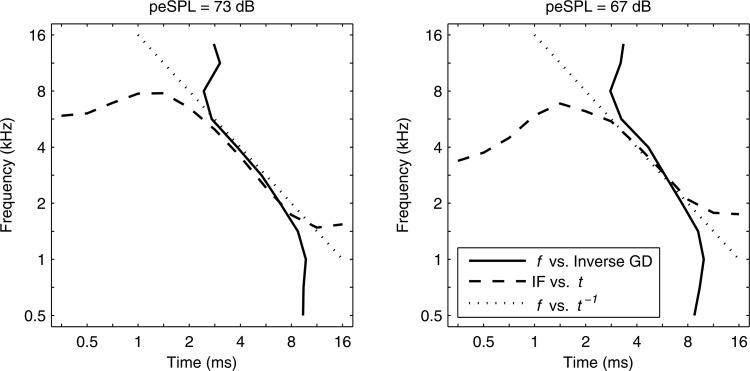
The shape similarities in normalized GD and IF at 73 dB peSPL in Figs. 89 hinted at an underlying symmetry. Relative to a fixed measurement location on the mammalian basilar membrane, auditory nerve recordings and mechanical measurements showed a symmetry between IF derived from impulse response recordings and GD derived from the spectral transfer function of basilar-membrane velocity relative to stapes velocity (Shera, 2001). When expressed in dimensionless forms, the measured IF and inverse GD functions were approximately equal over a range of characteristic times in guinea pig and chinchilla ears.

Assuming that frequency-specific CEOAEs are mainly generated from the tonotopic region associated with each frequency in the CEOAE, then it is hypothesized that the IF and inverse GD of CEOAEs recorded in normal-hearing human ears are approximately equal. In contrast to mechanical and neural responses measured at a fixed location on the basilar membrane, a CEOAE is generated over a range of generator sources, each localized to its tonotopic place along the basilar membrane. IF is a frequency measure obtained as a function of time, while GD is a temporal measure obtained as a function of frequency. By interchanging ordinate and abscissa, the inverse GD is a frequency measure obtained as a function of time. This hypothesis was partially confirmed in results shown for the two highest stimulus levels in Fig. 10. IF and inverse GD were approximately equal at the highest peSPL (73 dB) at times from 2.8 to 8 ms, and at frequencies from 1.6 to 5.7 kHz. However, the breadth of the region of equality was reduced at the next highest peSPL (67 dB), and was absent at lower peSPLs (not shown) except for a narrow time-frequency region close to 6 ms and 3 kHz.

Figure 10.

Mean IF (dashed line) and inverse GD (solid line) in normal group plotted at stimulus peSPLs of 73 dB (left) and 67 dB (right). Dotted line shows $f=t^{-1}$ (tonal frequency versus inverse of its period).

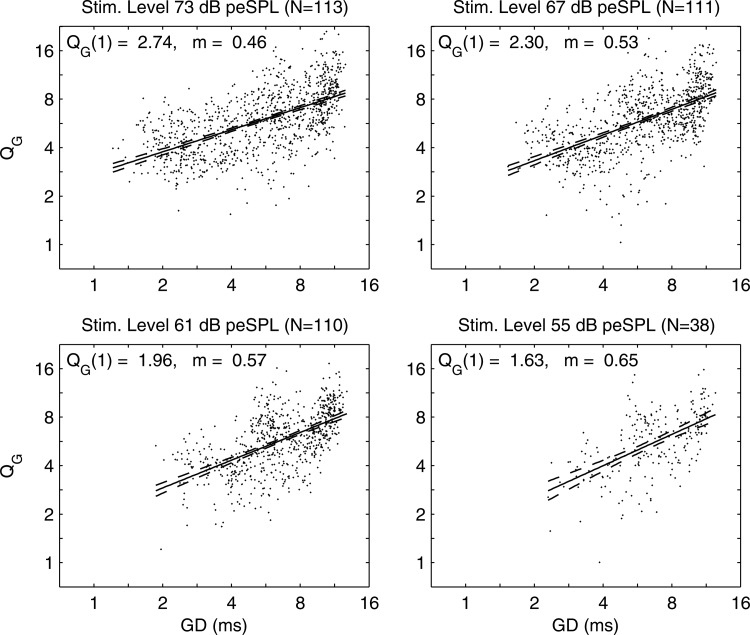
The implicit dependence on f of $Q_G(f)$ and $\text{GD}(f)$ values in each ear with detectable GD(f) and GS(f) were eliminated by a parametric scatter plot of $Q_G$ versus $\text{GD}$ in Fig. 11. Each dot in the scatter plot represents the value in a single normal ear. A linear regression showed a significant model fit with narrow 95% confidence interval (CI) at each peSPL: the temporal $Q_G$ increased with increasing GD. The relative dispersion of the delayed emission was larger at longer times, which corresponds to lower stimulus frequencies. The implicit dependences on t of $Q_I(t)$ and $\text{IF}(t)$ values in each ear with detectable IF(t) and IB(t) were eliminated by a parametric scatter plot of $Q_I$ versus IF in Fig. 12. There was large variability in $Q_I$ for $\text{IF}<4$ kHz, which coincides with the upper frequency of the SSOAE spectrum (see Fig. 5). This is evidence that CEOAE measurements of IF and IB were strongly influenced at frequencies up to 4 kHz by the presence of SSOAEs. A linear regression for the logarithm of $Q_I$ was calculated as a function of the logarithm of IF for the subset of data with $\text{IF}\ge 4$ kHz; this regression line and its 95% CI are shown in the figure. The exponent m of the regression line $Q_I(f)=Q_I(1)\times {(\text{IF}(f))}^m$ varied only slightly between 0.84 and 0.89 at peSPLs between 55 and 73 dB. This suggests the cochlear tuning is sharper in an ear with normal hearing at frequencies above 4 kHz. At frequencies above 11 kHz at the two highest peSPLs, the $Q_I$ data were almost always larger than that predicted using the regression model. There was no systematic dependence of $Q_I(f)$ on stimulus peSPL.

Figure 11.

Parametric scatter plots of $Q_G(f)$ vs $GD(f)$ in normal ears at stimulus peSPLs from 73 dB down to 55 dB. Regression model fit (solid line) and 95% CI (dashed lines). Model intercept $Q_G(1)$ at $GD=1$ ms and exponent $m,$ i.e., $Q_G=Q_G(1)\times G{D}^m.$

Figure 12.

Parametric scatter plots of $Q_I(t)$ vs $IF(t)$ in normal ears at stimulus peSPLs from 73 dB down to 55 dB. Regression model fit (solid line) and 95% CI (dashed lines) for subset of data with $IF\ge 4$ kHz. Model intercept $Q_I(1)$ at $IF=1$ kHz and exponent $m,$ i.e., $Q_I=Q_I(1)\times I{F}^m.$

This relationship between $Q_I$ and IF was not present when a $Q_I$ was calculated as the ratio of the mean IF to the mean IB (mean IF and mean IB are plotted in Fig. 6). The relationship was revealed only when $Q_I$ and IF were compared in each ear.

OAE predictions of SNHL

CEOAE studies reviewed in Keefe et al. (2011) used SNR to detect SNHL with test accuracies based on the area (AUC) under the receiver operating characteristic curve. The present results on CSM and SNR suggest the possibility of using either measure to classify ears as having normal hearing or a SNHL. No OAE study has reported the statistical significance of any difference in accuracy between multiple tests on the same group of subjects using AUC. Statistical significance was assessed in the present study using a bootstrap method to determine whether a particular test was more or less accurate than any other test performed on the same subject group according to a difference in their nonparametric AUC values.

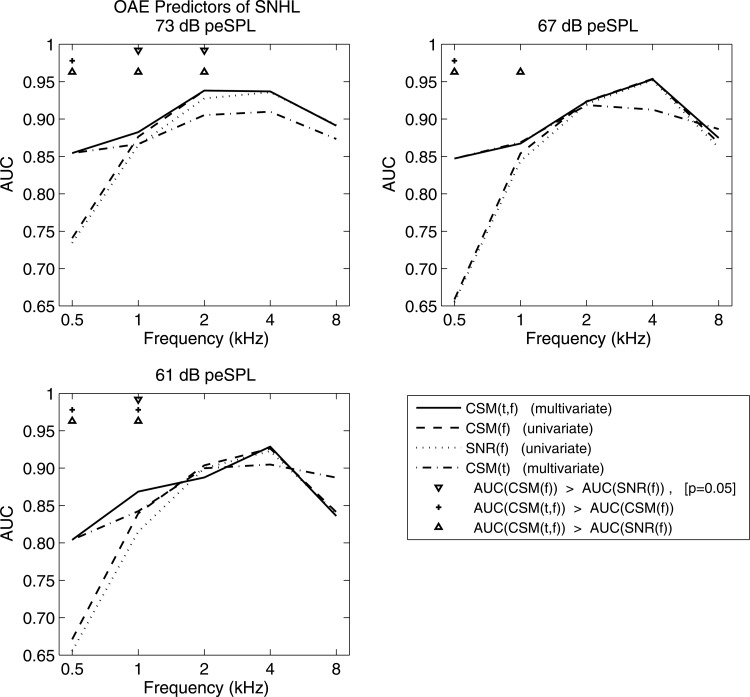
A distribution of AUC for a given test was calculated by 10 000 resamplings with replacement of the measured data in which AUC was evaluated in each resampling. AUC between two tests significantly differed from zero at the $p=0.05$ level when their AUC difference was outside to the 95% CI of the resampled distribution of AUC. The CI of the AUC difference was calculated using a bias-corrected and accelerated method (Efron, 1987). This method accounted for within-ear correlations between tests, which are important to consider in studies comparing the performance of multiple tests on the same group of ears. This is because AUCs and their pairwise differences were compared for tests in the same set of ears in each resampling. A distribution of the pairwise differences in AUC was constructed across all resamplings for each pair of tests. At 73 dB peSPL, the total number of test ears was 402 such that the numbers of ears with SNHL were 130 at 0.5 kHz, 163 at 1 kHz, 219 at 2 kHz, 253 at 4 kHz, and 251 at 8 kHz.

AUC was larger at 73 and 67 dB peSPL than at 61 dB and lower peSPLs (see Fig. 13). AUCs as large as 0.93–0.95 occurred at 2 and 4 kHz, with values as large as 0.87–0.89 at 1 and 8 kHz. The lowest AUCs occurred at 0.5 kHz. Comparing different CEOAE predictor variables at the same audiometric frequency $f,$ AUC for CSM(f) was larger than AUC for SNR(f) at 14 of 15 conditions (i.e., across three peSPLs and five frequencies). This suggested that CSM might be a more accurate predictor than SNR. Results showed that CEOAE CSM(f) was significantly more accurate than CEOAE SNR(f) for 3 of 15 conditions, i.e., at 1 and 2 kHz at 73 dB peSPL, and at 1 kHz at 61 dB peSPL. There was no significant difference in accuracy between these tests in the other 12 conditions.

Figure 13.

AUC at stimulus peSPLs of 73 dB (upper left), 67 dB (upper right) and 61 dB (lower left) using CEOAE predictors CSM(t), CSM(f), SNR(f), and CSM(t,f). As specified by markers at bottom of legend, tops rows in each panel list frequencies at which one of a pair of predictors is more accurate than another (at $p=0.05$).

A multivariate predictor of SNHL based on the time-domain CSM(t) [e.g., see CSM(t) for subject A in row 2 and columns 1 and 3 of Fig. 4] was constructed for each audiometric frequency using the log likelihood ratio, as explained in Appendix B. AUC for performance at each audiometric frequency was calculated using a log likelihood ratio of CSM(t) across a sub-range of time, with iterative pruning of the sub-range to maximize AUC. The resulting sub-ranges were 5.7–16 ms at 0.5 and 1 kHz, 2.8–11.3 ms at 2 kHz, and 1.4–11.3 ms at 4 and 8 kHz. When compared to the frequency-specific predictors CSM(f) and SNR(f) at 73 dB peSPL, the multivariate predictor for CSM(t) had a much larger AUC at 0.5 kHz, slightly smaller AUC at 1 kHz, and smaller AUC above 1 kHz (see Fig. 13).

An overall multivariate predictor of SNHL named CSM(t,f) was constructed by combining CSM in the time and frequency domains.8 The CSM(t,f) predictor was set equal to the log likelihood ratio of CSM(t) at 0.5 kHz, and to the CSM(f) predictor above 1 kHz. The best performance at 1 kHz was achieved by calculating CSM(t,f) as the sum of the log likelihood ratio of CSM(t) and five times the log likelihood ratio of CSM(f) at 1 kHz. CSM(t,f) outperformed both CSM(t) and CSM(f) at 1 kHz (see Fig. 13). Combinations of CSM(t) and CSM(f) had no benefit at other frequencies.

CSM(t,f) was significantly more accurate in predicting SNHL than SNR(f) for 7 of 15 conditions (i.e., at 0.5 and 1 kHz at all stimulus levels, and at 2 kHz at 73 dB peSPL). It was significantly more accurate than CSM(f) for 4 of 15 conditions (i.e., at 0.5 kHz at all stimulus levels, and at 1 kHz at 61 dB peSPL).

The finding that SSOAEs were prevalent in 85% of normal ears suggested that a multivariate combination of CEOAE and SSOAE variables might be more accurate in predicting a SNHL than CEOAEs alone. The test accuracy increased slightly in some conditions by combining CEOAE and SSOAE responses using CSM predictors (in which CSM Sum illustrated in Fig. 5 was used as the SSOAE predictor). Nevertheless, the benefit from combining the CEOAE CSM(f) and CSM(t) into CSM(t,f) was much greater at 0.5 kHz than any benefit gained from adding SSOAE information.

CEOAE moments in ears with sloping SNHL

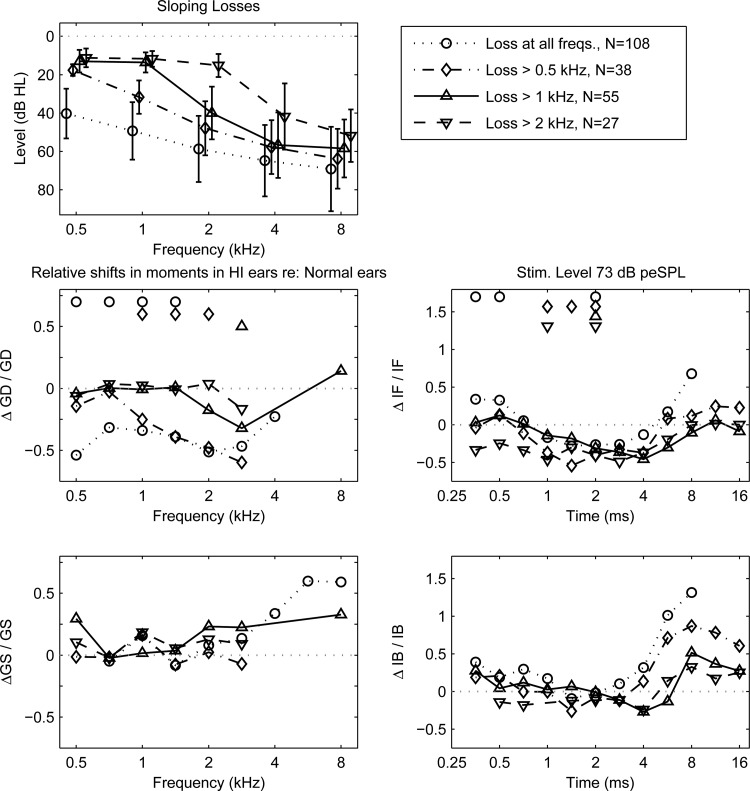
The CEOAE spectrum across frequency was examined for groups of ears with similar audiometric classifications (Pittman and Stelmachowicz, 2003). The goal was to relate changes in CEOAE moments to the audiometric pattern of hearing loss. Groups with sloping losses were examined in which hearing was within normal limits ($\text{HL}\le$ 20 dB) from 0.5 kHz up to a specified transition frequency, with $\text{HL}>20$ dB above the transition frequency. Sloping-loss groups were defined using transition frequencies of 0.5, 1, and 2 kHz with audiograms shown in Fig. 14 (top panel). A so-called flat-loss group of ears with $\text{HL}>20$ dB at all test frequencies was also defined.

Figure 14.

CEOAE moments at 73 dB peSPL in sloping SNHL re: normal group. Left column with frequency abscissa—Top: Audiometric HL for sloping-loss groups. Middle: $\Delta GD/GD$ in GD for SNHL re: normal groups. Significant changes ($p=0.05$) indicated by marker above frequency (top of panel). Similar plotting style used in remaining panels. Bottom: $\Delta GS/GS.$ Right column with time abscissa—Middle: $\Delta IF/IF.$ Bottom: $\Delta IB/IB.$

CEOAE moments measured at 73 dB peSPL were analyzed, inasmuch as this maximum peSPL resulted in the most accurate predictions of SNHL. The mean CEOAE moment in each SNHL group was compared with the mean CEOAE moment in the normal group. An unpaired Welch t test based on unequal sample size and unequal variance was used to evaluate whether these means differed at the $p=0.05$ significance level at each time step for IF and IB, and at each frequency bin for GD and GS.

Results in Fig. 14 (rows 2 and 3) are plotted in terms of the mean difference in each CEOAE moment relative to the mean in the normal group, e.g., $\Delta \text{GD}/\text{GD}$ had GD in the SNHL group minus GD in the normal group in the numerator, and GD in the normal group in the denominator. A plotting marker is present in a horizontal row at the top of each panel for each condition in which a CEOAE moment was significantly different in normal and SNHL groups.

The mean GD in SNHL ears relative to normal ears significantly decreased between 0.5–1.4 kHz for the flat-loss group, decreased between 1–2 kHz for the group with loss above 0.5 kHz, and decreased at 2.8 kHz (with a similar trend at 2 kHz) for the group with loss above 1 kHz. The mean GD trended to decreased values at 2.8 kHz in the group with loss above 2 kHz (the statistical power was reduced in this group because of its smaller number of ears). The mean GD was never reduced in any SNHL group at an audiometric frequency within the normal range of hearing. Any reductions in mean GD occurred at frequencies at which a SNHL was present. The mean GD was never larger in the SNHL group than the mean GD in the normal group.

The mean IF in SNHL ears relative to normal ears significantly increased for the flat-loss group at 0.35–0.5 ms, and decreased at 2 ms. The mean IF significantly decreased in SNHL ears in groups with a loss above 0.5 kHz at 1–2 ms, with a loss above 1 kHz at 2 ms, and with a loss above 2 kHz at 1 and 2 ms. The reductions in mean GD and mean IF were on the order of −0.5, which corresponds to a 50% reduction in mean GD and mean IF in ears with SNHL. Although non-zero trends in $\Delta \text{GS}/\text{GS}$ and $\Delta \text{IB}/\text{IB}$ were apparent, neither the mean GS nor the mean IB significantly differed in any SNHL group compared to the normal group.

A set of 15 ears had a U-shaped audiogram based on a mid-frequency mean loss of 50 dB HL at 4 kHz, with inclusion criteria that the thresholds were improved by at least 20 dB at a lower and higher frequency. Mean hearing levels were about 20 dB at 0.5, 1, and 8 kHz. The mean $\Delta \text{GD}/\text{GD}$ was reduced to −0.4 at 4 kHz, but the change was not significant for GD or any other moment. This was probably due to insufficient statistical power.

Frequency-specific GD and GS in ears with SNHL

CEOAE moments were analyzed as a function of hearing loss at each audiometric frequency. A histogram of the number of ears with HL is plotted in Fig. 15 (right ordinate, dotted line, diamond plot markers) for audiometric frequencies 0.5, 1 2, 4, and 8 kHz. The peak number of ears typically occurred in the range from 0 to 20 dB HL, inasmuch as ears were included that were normal at all audiometric frequencies. Otherwise, secondary peaks showed the contribution of SNHL ears with smaller HL at 0.5 and 1 kHz, and larger HL at frequencies above 1 kHz.

Figure 15.

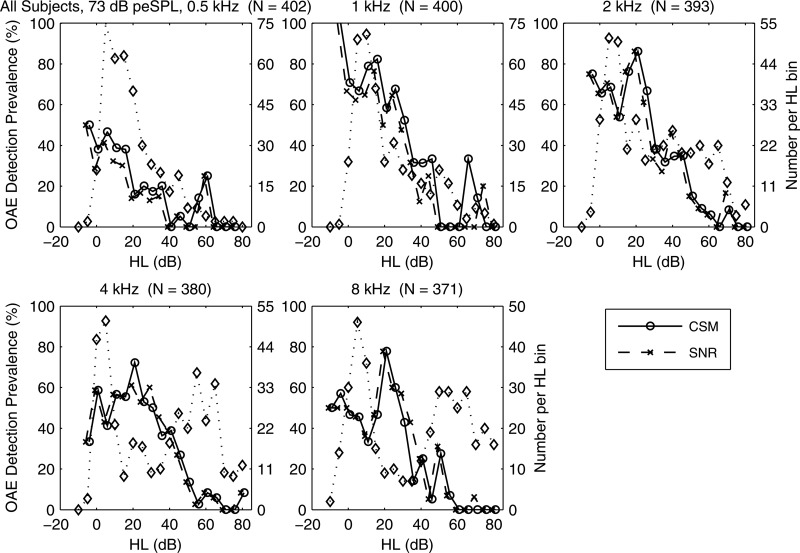
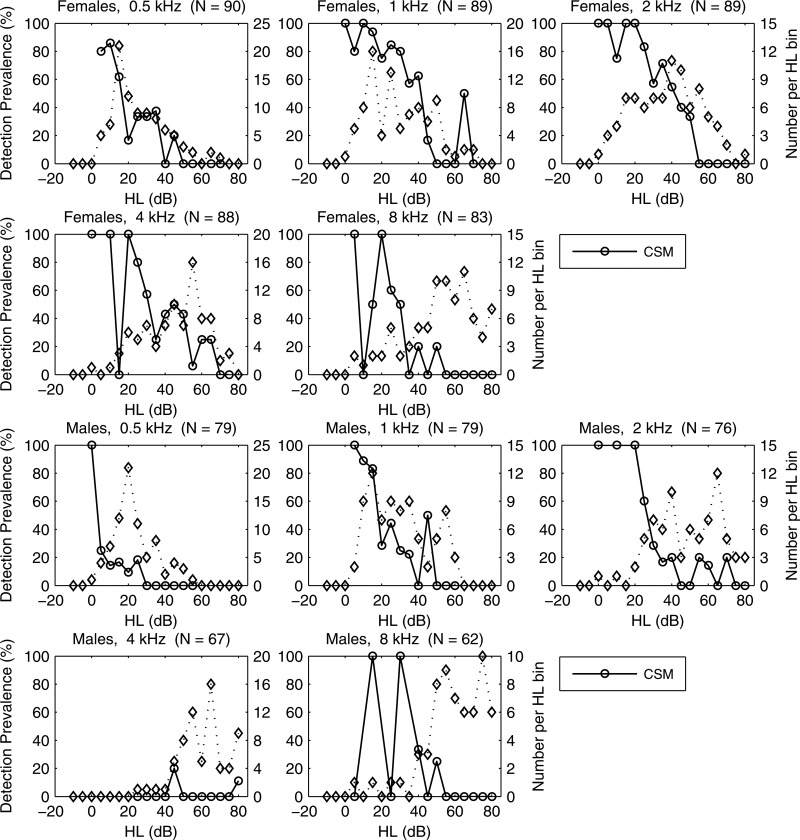
At 73 dB peSPL, the prevalence (in %) for CEOAE detection (left ordinate) for CSM (solid line) and SNR (dashed line) vs HL at octave frequencies 0.5, 1, 2, 4, and 8 kHz. Number of ears per HL bin (in 5 dB bins) also plotted (right ordinate, dotted line, diamond markers). Total # of test ears listed in title. (CSM/SNR data displaced horizontally for clarity.)

The CEOAE detection prevalence is plotted in Fig. 15 (left ordinate) at each audiometric frequency as a percentage of the number of ears with detected CEOAEs in each HL bin based on both CSM and SNR at the $p<0.05$ level of significance. Prevalences tended to be largest in the normal range of HL and to decrease as HL increased. The relatively small numbers of ears with HL in some conditions contributed to variability. Prevalences of CSM and SNR were similar overall, which confirmed the performance consistency of statistical detection criteria evaluated at the same p value. Any residual dissimilarity indicated ears in which only one of the phase-gradient and amplitude-gradient moments was detected.

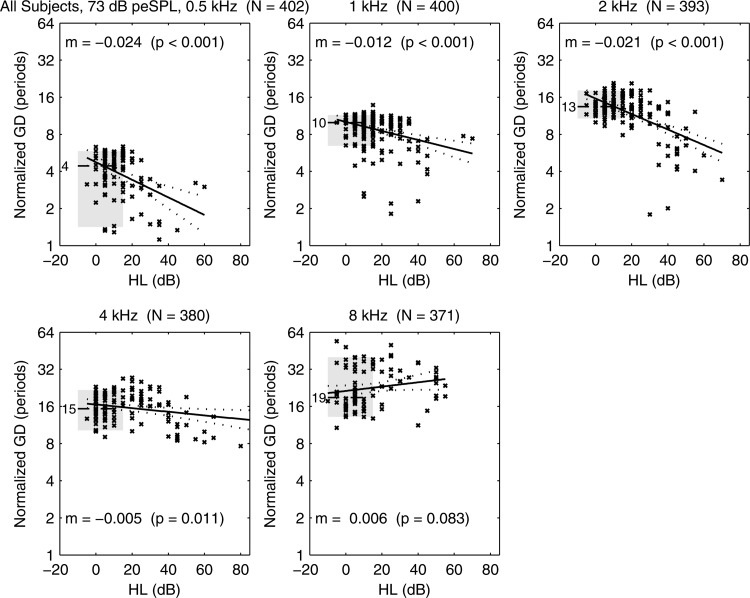
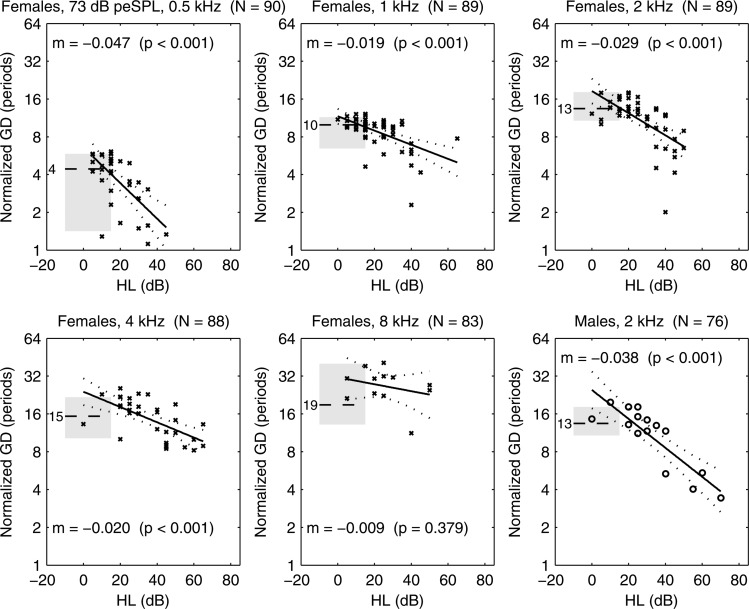
The fact that some ears with HL had detectable CEOAEs allowed for measurements of the dependence of each CEOAE moment on HL. Results are presented for GD and GS at CEOAE half-octave frequencies aligned with the audiometric frequency of the HL. A scatter plot is shown in Fig. 16 of the normalized GD (in number of periods) of each ear with SNHL at one or more frequencies. For purposes of comparison, a horizontal line and gray fill show the median and inter-quartile range (IQR), respectively, of normalized GD for the normal group. For example, the median normalized GD in normal ears was four periods at 0.5 kHz and ten periods at 1 kHz. A linear regression model was calculated for ears in the SNHL group at each audiometric frequency, and the model fits with 95% CIs are plotted in the figure. The text reports the slope m of the regression line with its calculated p value. For example, $m=-0.021$ at 2 kHz, which means that GD would decrease by a factor of one-half as HL increased by 48 dB (i.e., $48\approx 1/\left|m\right|$). Such a 50% reduction in GD was observed in ears with sloping- and flat-loss audiograms at some frequencies (see Fig. 14). A significant decrease in GD with increasing HL was observed at all octave frequencies between 0.5 and 4 kHz (see Fig. 16). The regression slope did not differ from zero at 8 kHz.

Figure 16.

At 73 dB peSPL, normal-group median GD plotted (horizontal dashed line) with median listed to left of line (e.g., 4 periods at 0.5 kHz), and IQR plotted (gray shading). Scatter plot of SNHL ears shows GD vs HL with × marker. Regression model for SNHL ears (solid line) with 95% CI (dotted lines). Text lists regression slope m (i.e., $\mathrm{G}\mathrm{D}\sim \mathrm{H}{\mathrm{L}}^m$) and $p.$

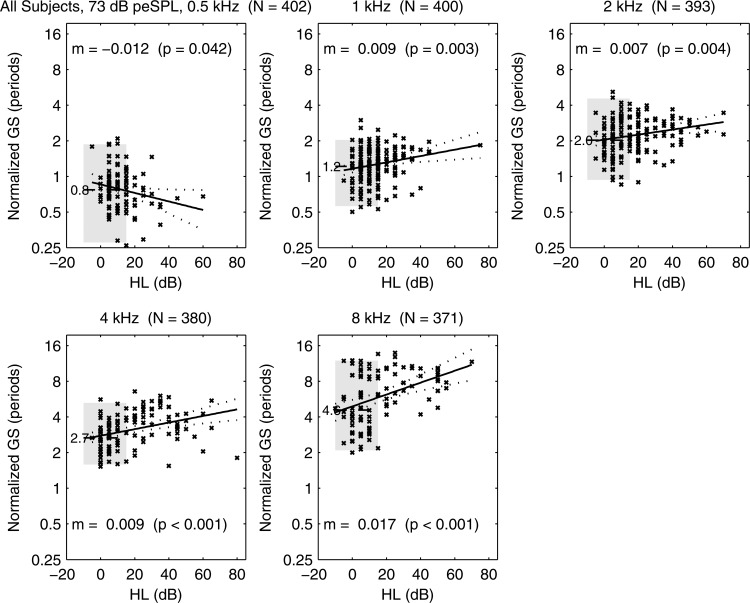
A plot of normalized GS is shown in Fig. 17 for the group of ears with SNHL at one or more frequencies. The plot also includes the median and IQR for the group of ears that were within the normal range at all audiometric frequencies. GS increased with increasing HL between 1 and 8 kHz, which would correspond in SNHL ears to a broadening in the range of cochlear sites contributing to CEOAE delay at the audiometric frequency. At 0.5 kHz, the opposite effect was observed with borderline significance ($p=0.042$), i.e., GS decreased with increasing HL. Except for two ears, the range of HL at 0.5 kHz extended only up to 35 dB HL.

Figure 17.

At 73 dB peSPL, normal-group median GS plotted (horizontal dashed line) with median listed to left of line (e.g., 0.8 periods at 0.5 kHz), and IQR plotted (gray shading). Scatter plot of SNHL ears shows GS vs HL with × marker. Regression model for SNHL ears (solid line) with 95% CI (dotted lines). Text lists regression slope m (i.e., $\mathrm{G}\mathrm{S}\sim \mathrm{H}{\mathrm{L}}^m$) and $p.$

The regression slopes at all audiometric frequencies for IF and IB as functions of HL in the group of ears with SNHL at one or more frequencies were not significantly different from zero.

CEOAEs in older adults with SNHL

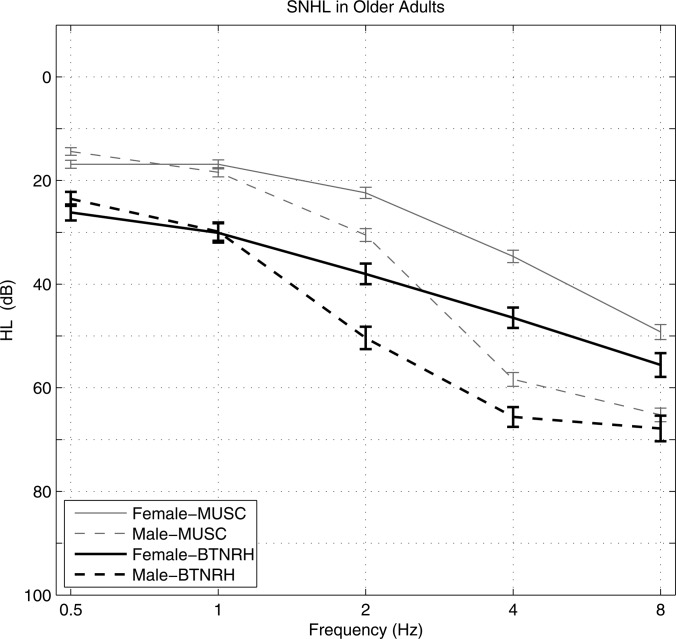
As part of a longitudinal study at the Medical University of South Carolina (MUSC) on age-related hearing loss and speech recognition (Dubno et al., 2008), audiograms of males and females (mean age 66.8 years) were measured on their initial research visit, as reproduced in Fig. 18. Inclusion criteria for these subjects were absence of conductive hearing loss or active otologic or neurologic disease.

Figure 18.

Audiograms in older males and females from MUSC study (Dubno et al., 2008) and current study (BTNRH).

Based on studies in other mammalian ears, Dubno et al. (2008) concluded that HL in older females, which is characterized by a flat 10–40 dB hearing loss at low frequencies increasing to 60 dB at higher frequencies, was consistent with a metabolic presbyacusis. A principal metabolic component is a decrease in the endocochlear potential of the outer hair cells (and inner hair cells), which is thought to reduce the gain of the cochlear amplification mechanism. Dubno et al. also concluded that the additional HL present in older males above 1 kHz, and especially above 2 kHz, included a mixture of metabolic presbyacusis and sensory presbyacusis effects, with the latter related to loss of outer hair cells due to noise exposure.

The mean and SE of auditory thresholds in the present BTNRH study for males and females of age 60 years and older are also plotted in Fig. 18 (mean age 69.8 years, standard deviation 5.5 years). Inclusion criteria for these subjects partially controlled for otologic disease by requiring normal 226-Hz tympanometry and absence of conductive hearing loss, but did not control for neurologic disease (although no subjects used cochlear implants). Older subjects were included if they had SNHL at one or more frequencies. The mean HL was larger for the BTNRH group than the MUSC group, especially at 2 and 4 kHz. This may be related to the facts that some subjects with hearing within normal limits were included in the MUSC group, and some ears with HL for etiologies unrelated to presbyacusis were included in the BTNRH group. Most HL subjects in the BTNRH group were recruited from the general population of otolaryngological patients receiving an audiometric test. Nevertheless, the HL in both male groups exceeded that for female groups at all frequencies above 1 kHz, with no sex-related differences at 0.5 and 1 kHz. This suggests for the BTNRH group that the older female ears may have had a larger representation of ears with metabolic presbyacusis than older male ears, and that older male ears may have had a larger representation of ears with a mix of metabolic and sensory presbyacusis.

An analysis was performed for CEOAEs measured in these older subjects to evaluate any sex-related functional differences. Separate histograms of the numbers of older female and male ears with a loss in each HL bin are plotted in Fig. 19 (right ordinate) at each audiometric frequency. Results for older female ears are shown in rows 1 and 2 and for older male ears in rows 3 and 4. As shown by the left ordinate of Fig. 19, the CEOAE detection prevalence based on CSM was different in older female ears than in older male ears (detection prevalences based on SNR were similar). Large fluctuations in prevalence were associated with small numbers of test ears in certain HL ranges, especially for older males. Few CEOAEs were detected in older ears for HLs exceeding 50 dB. What emerges is a larger CEOAE detection prevalence in older female than male ears at 1, 2, and 4 kHz, and at 0.5 kHz to a lesser extent, in the range of moderate HL between 20 and 50 dB. This provides physiological evidence that outer-hair cell function differs, on average, between older females and males, and is consistent with an increased outer-hair-cell loss in older male ears. Increased outer-hair-cell loss is predicted to lead to decreased prevalence of CEOAEs.

Figure 19.

Rows 1 and 2—For older females tested at 73 dB peSPL, % prevalence for CEOAE detection (left ordinate) vs HL for CSM (solid line). Number of ears per HL bin (in 5 dB bins) also plotted (right ordinate, dotted line, diamond marker). Title lists audiometric frequency and total # of test ears. Rows 3 and 4 show similar results for older male ears.

In those older ears with detectable CEOAEs, GS, IF, and IB did not vary significantly with HL. In contrast, the measured GD decreased with increasing HL in older female ears, with significant regression-model slopes found at 0.5, 1, 2, and 4 kHz (see Fig. 20), but not at 8 kHz. All significant GD slopes in older ears (see Fig. 20) were more steeply negative than the corresponding GD slopes in all SNHL ears (see Fig. 16). This would predict broader cochlear tuning in older subjects compared to all subjects with the same amount of HL. GD in older male ears decreased significantly with increasing HL only at 2 kHz (see Fig. 20). This is consistent with the fact that few CEOAEs were detected in older male ears for $\text{HL}>20$ dB at 0.5 and 4 kHz (see Fig. 19).

Figure 20.

For tests at 73 dB peSPL, normalized GD vs HL of older female ears (marker ×). Regression model (solid line) with 95% CI (dotted lines). Text lists model slope m and $p.$ For comparison, median GD (horizontal dashed line) and IQR (gray shading) of younger normal group are shown; median GD listed (left of line). Five panels show data for older females at octaves 0.5–8 kHz. Lower right panel shows GD vs HL at 2.0 kHz for older males (marker ○).

DISCUSSION

A set of four signal-processing moments (Cohen and Lee, 1990) were applied to measured CEOAEs that included and extended the use of GD in parameterizing a CEOAE response. The SNR of CEOAE spectra and waveforms were improved using artifact rejection and multi-window signal processing. GD and GS are first- and second-order temporal moments, respectively, that describe the group delay and group spread in delays as a function of frequency in the CEOAE spectrum. IF and IB are first- and second-order spectral moments, respectively, that describe the instantaneous frequency and instantaneous bandwidth as a function of time in the CEOAE analytic waveform. The phase-gradient moments (GD and IF) were calculated using a procedure that did not require phase unwrapping. Discrete-time and discrete-frequency procedures were applied with smoothing across time and frequency using the squared amplitude of the CEOAE. A CSM criterion was used to detect CEOAEs with interpretable phase gradients (for GD and IF), and a SNR criterion was used to detect CEOAEs with interpretable amplitude gradients (for GS and IB).

CEOAE moments in ears with normal hearing

CSM measurements were effective at identifying the narrow-band frequencies at which SSOAEs were detected (Fig. 3). These SSOAE frequencies were associated with CEOAE frequencies with large spectral levels (Fig. 4). The use of 32 multiple analysis buffers facilitated measurement of the means and SEs of the CEOAE moments. The SEs obtained were small compared to their means in individual ears.

There were 8–9 SSOAEs present in test 1 for subject A, which were aligned with corresponding peaks in the CEOAE spectrum below 3 kHz (see Fig. 3). SSOAEs were localized in frequency but were present across all times within the CEOAE waveform, and thus influenced temporal measurements of IF and IB. SSOAEs are generated by a highly tuned generation mechanism in the cochlea that includes multiple internal reflections within the cochlea, middle ear and ear canal.

The CEOAE waveform is a multiple-component signal, including components at an arbitrary time with a varying number of multiple internal reflections within the ear (i.e., SSOAE components), and, therefore, a varying set of frequencies. The use of multiple spectral and temporal windows to boost those CEOAE components with larger SNR was effective in measuring the CEOAE moments, but it did not completely address the multiple-component nature of the CEOAE. A promising approach in future research might be to use a time-frequency, wavelet- or model-based procedure to detect and identify each of the multiple components of a CEOAE response. Such studies were reviewed in the Introduction for CEOAE latency. Conceptually, the goal would be to calculate IF and IB for each component of the CEOAE waveform. Criteria to separate multiple components are that the distance on the time-frequency plane between any pair of IF of distinct components be large compared to either of their IBs (Cohen, 1995). Such an approach would also facilitate interpretation of GD and GS.

The repeatability across test dates was assessed in the normal group of ears in terms of the magnitude difference of the response. SSOAE measurements were highly repeatable as quantified by results in Fig. 5. The repeatability of the CEOAE detection variable CSM and all CEOAE moments were quantified by results in Fig. 7. This was similar to the repeatability measured for CEOAE level and SNR in substantially the same group of normal ears (Keefe et al., 2011). The least repeatable moment measurements occurred at high frequencies for which the magnitude difference of GD was as much as 0.25 times GD, and similarly for GS (Fig. 7). The demonstrated ability to make repeatable measurements of GD and other CEOAE moments has significance for clinical testing. The relative smallness of these magnitude differences was due to the overall procedures, which included the use of 5-min recordings, artifact rejection, multiple-window filtering, improved calculations of phase-gradient moments, moment smoothing, and statistical detection criteria. The remaining variability was due, in part, to inherent biological variability.

A goal of the study was to compare CEOAE GD across frequency and level with other studies of CEOAE latency and SFOAE GD. The comparison in Fig. 8 is in terms of the normalized or dimensionless GD measured in terms of the number of periods at each frequency. At the highest peSPLs of 73, 67, and 61 dB SPL that included the largest number of test ears with normal hearing, the normalized CEOAE GD was similar to previous measurements of SFOAE GDs analyzed by Shera et al. (2010). This is evidence of similarity in generation mechanisms underlying SFOAEs and CEOAEs as reported in Kalluri and Shera (2007), although a broader frequency range was analyzed in the present CEOAE study.

The moments of CEOAEs and SFOAEs may not be equivalent. For example, the SFOAE GD at 1 kHz was 11 periods according to a trend value in Shera et al. (2010) and mean in Schairer et al. (2006), whereas its mean and median CEOAE GD in the present study were 10 periods. Suppression, and possibly distortion, processes within the cochlea would influence CEOAEs and SFOAEs differently due to their differing stimulus content, even if the principal generation mechanism is coherent reflection for both emission types. A low-frequency breakpoint occurred in the slope of normalized CEOAE GD at about 1.4 kHz in Fig. 8. This is similar to the breakpoint of 1 kHz reported for normalized SFOAE GD, which was related to an apical change in the underlying basilar-membrane mechanics (Shera et al., 2010).

Figure 8 also shows a high-frequency breakpoint in the slope of normalized CEOAE GD above approximately 8 kHz (e.g., at 73 dB peSPL). A high-frequency breakpoint may be present just above 10 kHz in SFOAE GD data analyzed in Shera et al. (2010). Shera et al. concluded that a steeper slope in normalized SFOAE GD at higher frequencies predicted sharper cochlear tuning. This is also a possible interpretation of the present CEOAE GD data. However, it appears unlikely that cochlear tuning would continue to sharpen as the stimulus frequency approaches the maximum limit of human hearing (20 kHz). Cochlear tuning may begin to degrade at frequencies approaching 20 kHz from below. The frequency dependence of normalized OAE GD is unknown at frequencies above the maximum frequency of 15.3 kHz in this study. A larger OAE GD at high frequencies would reflect changes in basilar-membrane mechanics in the most basal region. More research is needed to address these issues, including measurements of OAE GD and behavioral tuning up to 20 kHz.

SFOAE GD reported by Schairer et al. (2006) was smaller than SFOAE GD of Shera et al. and smaller than CEOAE GD in the present study above about 1.5 kHz. SFOAE GD in Schairer et al. decreased with increasing stimulus level at all frequencies between 0.5 and 4 kHz, in contrast to the level dependence of CEOAE GD below 1 kHz, and in agreement above 3 kHz. The variability in CEOAE GD was much less than that reported for SFOAEs (Shera et al., 2010; Schairer et al., 2006), and was likely due to procedural differences.

Shera et al. (2010) calculated GD using the gradient of the unwrapped phase, and then used a local regression to extract a smooth trend line over frequency. The present procedures to calculate GD were shown to be highly repeatable in the same ear across test dates and would therefore be potentially useful in clinical OAE testing in an individual ear. In contrast, the local regression procedure to extract a trend line for GD over a group of ears has not been demonstrated to given repeatable results on the same ear tested on different dates.

Schairer et al. (2006) calculated GD using the gradient of a smoothed unwrapped phase in an attempt to address inaccuracies related to phase unwrapping at frequencies where the SNR is relatively small. The present results on CEOAE GD demonstrated that a calculation of the phase gradient without phase unwrapping was effective in combination with the use of a phase-sensitive detector of the CEOAE (based on CSM), and an energy-weighted smoothing of phase gradients over each half-octave frequency band. The procedures used by Schairer et al. to first unwrap the evoked OAE phase and then smooth it prior to calculating a phase gradient are not recommended.

CEOAE latencies based on envelope delays that were measured for substantially the same subject group at the same stimulus level (Goodman et al., 2009) were smaller than the CEOAE GDs in the present study (see Fig. 8). That is, CEOAE latency and GD are not equivalent measures of CEOAE timing, with a mean difference more than a factor of two larger at the highest bin frequency of 14.3 kHz. The presence of SSOAEs may influence latency and GD in different ways below 4 kHz.

Both GD and GS varied with stimulus level (see Fig. 8). Because the SSOAE bandwidth also straddled 0.5–4 kHz, it is likely that the level dependences of GD and GS up to 4 kHz would be related to the level dependence of SSOAEs. GD and GS decreased with increasing stimulus level above 4 kHz, which substantially agrees with the level dependence reported for SFOAEs over lower frequencies from 0.5 to 4 kHz (Schairer et al., 2006). SFOAE detection procedures were narrow band, and thus would be approximately independent of any SSOAEs unless their frequencies were similar (i.e., amplitude and frequency modulation effects would then occur).

At larger peSPLs, the mean normalized IF varied slowly with time between 2 and 8 ms, and increased more rapidly with increasing time at shorter and longer times (see Fig. 9). The temporal breakpoints at about 2 and 8 ms may be related to the spectral breakpoints at 8 and 1.4 kHz, respectively, in Fig. 8. Both mean IF and mean IB generally increased with increasing stimulus level for times earlier than about 2 ms, and decreased with increasing level for times later than 4 ms.

The mean IF varied with stimulus level (see Fig. 9). This contrasts with the near-invariance in the zero-crossing rate (and, thus, in the IF) of basilar-membrane click responses in non-human mammals that was summarized from the physiological literature in Shera (2001). An essential difference is that the basilar-membrane responses are measured at a single location whereas IF is calculated based on the CEOAE arising from multiple locations. The level dependence of mean IF and mean IB in CEOAEs may have been strongly influenced by SSOAEs. For example, the mean IF at 0.5 ms was about three cycles or 6 kHz at 73 dB peSPL (see also Fig. 6), but it was reduced by more than 50% to less than 1.5 cycles (or 3 kHz) at all $\text{peSPLs}\le 61$ dB. The latter was in the range of SSOAEs.

It is likely that high-frequency generation of CEOAEs, which would be associated with a high IF at short times, was of relatively small amplitude in many ears at lower stimulus peSPLs, so that the short-time CEOAE waveforms were dominated by lower-frequency SSOAEs elicited by some previous click stimulus. This would reduce IF at short times. Conversely, the high-frequency generation of CEOAEs might have been sufficiently strong at the maximum peSPL so that the mean IF at short times increased. It is also possible that the amplitude dependence of the mean IF was due to some as yet unknown source of low-frequency distortion in the basal region of the basilar membrane; however, there is no physiological evidence to support this conjecture. Inasmuch as a single SSOAE would have a smaller IB than a single CEOAE component unrelated to any SSOAE, a dominance of SSOAEs at short times may have also affected the normalized IB responses at lower stimulus levels. Notwithstanding that effect, the presence of multiple strong SSOAEs at the same time step would tend to increase IB. This is another example of the desirability of a multiple-component analysis of CEOAE moments.

The finding that IF and inverse GD were nearly equal in their functional time dependence at the maximum peSPL (73 dB) over a range of delays (see Fig. 10) revealed an underlying symmetry in the CEOAE generation mechanism over a spatially extended region of the basilar membrane. The characteristic times and frequencies of the CEOAE moments suggest that the CEOAE was generated at the tonotopic place within the scaling region. Otherwise, either the time dependence of IF or the GD dependence on frequency would have differed. A relative absence of this symmetry at reduced stimulus levels may be related to a more dominant role of SSOAEs and other multiple internal reflections of CEOAEs, or perhaps these stimulus levels were insufficient to generate CEOAEs at higher frequencies in many test ears.

CEAOE moments as measures of tuning

$Q_G$ was plotted versus $\text{GD}(f)$ for each ear at each frequency bin at which both $\text{GD}(f)$ and $\text{GS}(f)$ were measured. A parametric scatter plot (see Fig. 11) eliminated their mutual dependence on bin frequency to show all individual-ear data. $Q_G$ increased with increasing GD, i.e., the relative temporal dispersion of CEOAE responses increased with increasing GD. Because larger GDs were associated with lower bin frequencies in the range of SSOAE frequencies (0.5–4 kHz), this increased relative dispersion may have been strongly influenced by SSOAEs.

$Q_I$ was plotted versus $\text{IF}(t)$ for each ear at each time step at which both $\text{IF}(t)$ and $\text{IB}(t)$ were measured. A parametric scatter plot (see Fig. 12) eliminated the mutual dependence on time to show all individual-ear data. $Q_I$ was highly variable for IF below 4 kHz due to the presence of SSOAEs, but it increased with increasing IF at and above 4 kHz with greatly reduced variability.

Attention is restricted to $Q_I$ measurements at $\text{IF}\ge 4$ kHz that were unaffected by SSOAEs. $Q_I$ is a direct measure of the tuning of the cochlear source mechanism generating the CEOAE with local frequency IF. If this emission-source tuning is assumed to be invariant with respect to the underlying $Q_{\text{ERB}}$ associated with basilar-membrane tuning, then the frequency dependences of $Q_I$ and $Q_{\text{ERB}}$ would be the same, and $Q_I$ would serve as a measure of relative changes in the cochlear $Q_{\text{ERB}}$ with frequency.

GD provided an indirect or model-based measure of $Q_{\text{ERB}}$ based on estimating a tuning ratio as the ratio of $Q_{\text{ERB}}$ to normalized GD (Shera et al., 2010). This tuning ratio was assumed to be transformable across mammalian species based on a single species-specific breakpoint. The findings of the present study may complicate the estimation of this tuning ratio if a high-frequency breakpoint, which occurred at about 11 kHz for CEOAE GD at 73 and 67 dB peSPL in Fig. 8, might also require estimation across species (assuming that such a cross-species breakpoint exists at high frequencies). An estimation of cochlear tuning based on $Q_I$ may require fewer assumptions and no parameter transformations across species compared to one based on GD. Nevertheless, the indirect measure of $Q_{\text{ERB}}$ based on GD was estimated over a broader frequency region than that based on $Q_I$ in the present study, which was limited to frequencies between 4 and 14.8 kHz. The latter value was the maximum IF at 73 dB peSPL in Fig. 12.

SFOAE GD in Shera et al. (2010) and CEOAE GD (see Fig. 8) showed a high-frequency breakpoint near 11 kHz. A more precisely localized breakpoint in slope near 11 kHz was present in the scatter plots of $Q_I$ at each stimulus level (see Fig. 12), and especially so at the larger peSPLs with more data. This similarity in high-frequency breakpoints is evidence that the direct and indirect measures of cochlear tuning ($Q_I$ and GD, respectively) are mutually consistent. Comparable data at and above 11 kHz are unavailable for behavioral $Q_{\text{ERB}}.$

Auditory-system tuning $Q_{\text{ERB}}(f)$ was measured behaviorally in human ears using forward masking at frequencies from 1 to 8 kHz, with results fitted by (Oxenham and Shera, 2003),

$$Q_{\text{ERB}}(f)=11.1\times f^{0.27}.$$ (19)

Any CEOAE leading to a measured IF would be generated within the cochlea at a tonotopic place with frequency f identified with $\text{IF}(t),$ and with a corresponding behavioral tuning $Q_{\text{ERB}}(f).$ The measured $Q_I(f)$ data for CEOAEs at 73 dB peSPL (see Fig. 12) were fitted for frequencies above 4 kHz by

$$Q_I(f)=0.66\times f^{0.87}.$$ (20)

This transposition from f to $\text{IF}(t)$ in the time domain is also supported by the symmetry between CEOAE IF and inverse GD at the maximum peSPL (73 dB) (see Fig. 10), which is approximately satisfied over much of the frequency range of the behavioral measurements of $Q_{\text{ERB}}.$

A tuning ratio $R_I(f)$ was formally defined as the ratio of the behavioral $Q_{\text{ERB}}(f)$ to the CEOAE-derived $Q_I(f).$ For $f\ge 4$ kHz, the tuning ratio is

$$R_I(f)=\frac{Q_{\text{ERB}}(f)}{Q_I(f)}=17\times f^{-0.60}.$$ (21)

This tuning ratio signifies that $Q_I$ was smaller than $Q_{\text{ERB}}$ overall, and increased more rapidly with frequency than behavioral $Q_{\text{ERB}}.$ A contributor to this difference is that $Q_I$ was defined in general signal processing terms by analogy with $Q_{\text{ERB}}$ for a second-order resonator, whereas the underlying cochlear/behavioral filters are much more sharply tuned [see Eq. 8 and related discussion]. For example, the behavioral $Q_{\text{ERB}}$ was larger than $Q_I$ by a factor $R_I=7.4$ at 4 kHz, and $R_I=4.9$ at 8 kHz. A detailed theory that incorporates cochlear mechanics including CEOAE generation and the transformation between cochlear and behavioral tuning would be needed to predict $R_I$ and its frequency dependence.

Improved CEOAE procedures to detect SNHL

The use of CSM derived from the measurement of an evoked OAE to predict a SNHL is a novel aspect of this study. AUC results for CEOAE testing showed that CSM(f) at the audiometric frequency was a significantly more accurate predictor of SNHL in adult ears than SNR(f) in 3 of 15 conditions. Their accuracies did not differ in the remaining 12 conditions (see Fig. 13). The use of CSM in OAE testing has significance as a potential screening test for SNHL. CSM is no more difficult to measure than is SNR, with the key difference that CSM is a phase-sensitive detector of the CEOAE and SNR is an energy detector.

The accuracy of CEOAE SNR(f) to predict SNHL was previously examined for this database in Keefe et al. (2011) in relation to other evoked OAE studies predicting SNHL. The main difference is that ears with an air-bone gap of 20 dB or more were included in the previous study, but excluded in the present study. Despite this difference, AUCs for CEOAE SNR(f) at a stimulus level of 73 dB peSPL were generally similar in the two studies. The largest difference based on SNR occurred at 0.5 kHz with an AUC of 0.63 in Keefe et al. (2011) compared to an AUC of 0.74 in the present study. The average AUC between 1 and 8 kHz was 0.89 in Keefe et al. (2011) compared to 0.91 in the present study for SNR(f). The exclusion of ears with an air-bone gap may have contributed to slightly better performance in the present study, but was not a major factor. This relative invariance would be an attractive property in practical hearing screening programs in which some ears would have a conductive hearing loss.

Considering CSM predictors of SNHL based on CEOAE testing, a CSM(t,f) predictor defined in terms of CSM(t) and CSM(f) was significantly more accurate based on AUC than SNR(f) in 7 of 15 conditions, and more accurate than CSM(f) in 4 of 15 conditions. The largest improvement occurred at 0.5 kHz, e.g., AUC measured at 73 dB peSPL increased from 0.74 for CSM(f) to 0.86 for the CSM(t,f). This substantial improvement in test accuracy was a result of adding information from CSM(t) of the CEOAE waveform at time steps between 5.7 and 16 ms. Information on CSM(t) slightly improved test accuracy at 1 kHz but decreased accuracy at 2, 4, and 8 kHz compared to CSM(f) at the audiometric frequency of the loss. Thus, the CSM(t,f) is the recommended predictor in CEOAE testing for SNHL: it combines information from CSM(t) at 0.5 and 1 kHz with information from CSM(f) at frequencies between 1 and 8 kHz.

For predicting SNHL at at 0.5 kHz using CSM(t,f), the AUC of 0.86 in the present study was equal to the largest AUC previously reported for CEOAEs (Hurley and Musiek, 2004). As reviewed for previous studies in more detail elsewhere Keefe et al. (2011), this AUC was slightly larger than the AUC of 0.84 for SFOAE SNR (Ellison and Keefe, 2005) and the AUC of 0.77 for DPOAE SNR (Gorga et al., 1993). TBOAE responses using a 0.5 kHz gated stimulus are more reproducible than CEOAE responses measured using conventional procedures, and TBOAEs are detectable in some ears with sloping hearing loss (Jedrzejczak et al., 2009). Therefore, a CEOAE or SFOAE test is recommended for detecting SNHL at 0.5 kHz, while a TBOAE test shows promise. Other differences between OAE types in predicting SNHL at higher frequencies were smaller. No other conclusions are drawn concerning any smaller differences between test performance across studies that differed in OAE type, measurement procedures and subject groups.

While a combination of SSOAE and CEOAE responses may slightly improve test performance compared to CEOAE testing, a larger benefit was found by combining time- and frequency-domain CEOAE responses. Based on an overall maximum test duration that might be available in any clinical application, it is recommended to maximize the CEOAE test time rather than to split the available test time into separate CEOAE and SSOAE tests, or separate CEOAE and TBOAE tests. A cochlear source mechanism leading to a response at any SSOAE frequency would also contribute at earlier times to the CEOAE response.

CEOAE moments in ears with SNHL

Measurements in ears with similar audiometric patterns revealed significant changes in the patterns of CEOAE GD and IF (see Fig. 14). In ears with a sloping SNHL, the GD was significantly reduced at a subset of the frequencies of the HL, but remained in the normal range at frequencies with normal hearing. A reduction in GD is consistent with a reduced level of outer-hair cell function, which would be associated with a reduction in the gain of cochlear amplification in ears with SNHL. With a sloping loss, hearing is normal at lower frequencies corresponding to more apically tuned regions of the basilar membrane, but hearing loss is present at higher frequencies corresponding to more basally tuned regions. The cochlear traveling wave at lower frequencies must propagate through the basal region in which some dysfunction exists due to the high-frequency hearing loss. The fact that GD was within normal limits at lower frequencies in ears with a sloping hearing loss supports the theory that propagation at these lower frequencies through the basal region was not significantly affected by any impairment of outer hair cell function. This is consistent with theories of normal cochlear function inasmuch as the region of cochlear amplification is thought to lie just basal to the tonotopic place, while even more basal regions have passive mechanical properties that are more nearly linear. In this view, the passive mechanical properties in the basal region were undamaged in the sloping loss groups characterized by a high-frequency HL.

IF was significantly reduced at times between 1 and 2 ms in the sloping-loss groups with transition frequencies of 0.5, 1, and 2 kHz compared to the normal group, but IF was always within normal limits at longer times. This reduced IF at short times is consistent with impaired cochlear function in the basal region corresponding to the region of hearing loss.

The averaged audiograms are also shown in Fig. 14 for ears with the flat-loss group. This flat-loss group (only approximately so) had a mean HL of 40–50 dB at 0.5 and 1 kHz and larger mean losses at higher frequencies (e.g., 70 dB HL at 8 kHz). These means were accompanied by large SEs at all frequencies, emphasizing the diverse range of SNHL in this group, and, probably, their diverse etiologies. The mean HL at 0.5 and 1 kHz in the flat-loss group was much larger than in the mean audiograms of subjects of age 60 years and older (see Fig. 18), which are further described below in the context of presbyacusis. This suggests etiologies for SNHL in the flat-loss group that were at least partially distinct from those for presbyacusis.

The mean GD for the flat-loss group showed greater reductions compared to normal ears at all frequencies between 0.5 and 1.4 kHz (with fewer detected CEOAEs at higher frequencies), whereas IF was significantly larger by 33% in the flat-loss group at 0.35−0.5 ms, but smaller by 26% at 2 ms (see Fig. 14). The increased IF in the flat-loss group at short times was not observed in any sloping-loss group. This finding suggests that the basilar-membrane mechanics in the basal region may have differed for these audiometric classes of SNHL, even though both classes showed a high-frequency hearing loss.

These and other results on CEOAE moments in ears with SNHL relate only to those ear tests in which CEOAEs were detected. All that can be concluded from the remaining ear tests is that CEOAEs were absent, which is consistent with a high degree of outer hair cell dysfunction. Another general point is that the mean relative changes in GD and IF between normal and SNHL groups was as large or larger than 50%, whereas the repeatability of GD and IF in normal ears was approximately 25%. This suggests the possibility of using GD and IF in longitudinal programs to detect SNHL based on changes in CEOAEs, e.g., in monitoring programs for ototoxic effects and noise-induced hearing loss. This is a topic for future research.

An alternative approach to analyzing CEOAE moments in impaired ears was to investigate each moment as a function of the amount of hearing loss. The prevalence of detected CEOAEs decreased as a function of increasing hearing loss (see Fig. 15). A summary analysis of these data reveals that the hearing loss at the 95th percentile of cumulative CEOAE prevalence based on CSM (termed HL95) was 35 dB at 0.5 and 1 kHz, 45 dB at 2 kHz, and 50 dB at 4 and 8 kHz. CEOAEs were rarely observed in ears with hearing loss exceeding HL95 (i.e., based on $p<0.05$). These HL95 values are interpreted as representing a dynamic range of the compressive nonlinearity associated with outer hair cell function that would give rise to a detectable CEOAE. This dynamic range of outer hair cell function increased with increasing frequency between 0.5 and 8 kHz, which suggests a more robust cochlear amplification mechanism at higher frequencies in a normal ear (inasmuch as HL = 0 dB represents normal hearing). Audiometric losses exceeding HL95 at any frequency is consistent with additional hearing loss related to inner hair cell or neural pathology, although that does not preclude their involvement as well in some ears with milder losses.

The range of HL95 across frequency in impaired ears is in general agreement with cochlear gain estimates in normal ears across frequency that were derived from suppression tip-to-tail difference measurements for SFOAEs (Keefe and Schairer, 2011) and DPOAEs (Gorga et al., 2011). For example, the estimated cochlear gain from SFOAEs based on absorbed sound power was about 26 dB at 0.5 and 1 kHz increasing to 46 dB at 8 kHz (compared to HL95 values from CEOAEs in SNHL ears of 35 dB at 0.5 kHz and 50 dB at 8 kHz). These evoked OAE studies collectively support the theory that SNHL is commonly associated with a loss in outer hair cell function that attenuates the gain of the cochlear amplifier.

As described in the Introduction, previous studies examining the relationship between CEOAE timing measures and hearing loss have reached no consensus on the nature of this relationship. In contrast, the present study found significantly shorter CEOAE GDs with increasing hearing loss at all audiometric frequencies between 0.5 and 4 kHz (see Fig. 16), although CEOAE GD did not vary with hearing loss at 8 kHz. The fact that GD was similar in CEOAEs and SFOAEs recorded in ears with normal hearing and the theory that increasing SFOAE GD is related to increasing $Q_{\text{ERB}}$ (Shera et al., 2010) would jointly predict that these reductions in CEOAE GD in ears with hearing loss were associated with reduced cochlear tuning. It remains to sort out the relationships at 8 kHz inasmuch as GD is predicted to be associated with a maximum across frequency in $Q_{\text{ERB}}$ across normal ears, yet GD was not significantly reduced in ears with hearing loss.

A significantly larger CEOAE GS was observed with increasing hearing loss at all audiometric frequencies between 1 and 8 kHz (see Fig. 17), but GS decreased with increasing hearing loss at 0.5 kHz. Interpretation of GS in normal ears was confounded by the presence of SSOAEs at frequencies below 4 kHz. The finding of increased GS with increasing hearing loss at 4 and 8 kHz is consistent with broader temporal tuning in the CEOAE generator in impaired ears, which is associated with CEOAE source contributions from a broader spatial region along the basilar membrane. The robust GS effect with HL at 8 kHz is interesting in conjunction with the absence of any GD effect at 8 kHz. The fact that the positive regression slopes of GS were similar in magnitude at 1 and 2 kHz to the slope at 4 kHz suggests that a generally similar spatial broadening along the basilar membrane occurred at these lower frequencies despite any influence of SSOAE-related components. This might arise because a low-frequency hearing loss would attenuate the influence of any SSOAEs on the CEOAE at frequencies within the bandwidth of the hearing loss. The pattern of GS in ears with hearing loss at 0.5 kHz requires further study, as there were only two ears with $\text{HL}>35$ dB.

Aging effects

CEOAEs and audiograms (see Fig. 18) were measured in female and male ears in adults of age 60 years and older. In ears with a detectable CEOAE GD based on CSM, CEOAE prevalence was generally larger in older female than older male ears at frequencies between 0.5 and 4 kHz and over a range of mild to moderate HL from 25 to 45 dB HL (see Fig. 19). The median differences in prevalence across this HL range in female compared to male ears were 20%, 41%, 35%, and 43% at 0.5, 1, 2, and 4 kHz, respectively. The median differences in prevalence across this frequency range in female compared to male ears were 32%, 44%, 36.5%, 38%, and 25% at 25, 30, 35, 40, and 45 dB HL, respectively. The grand median difference in prevalence across these ranges of frequency and HL was 35%. The 8-kHz datasets were omitted from this analysis because the numbers of ears at each HL step in this range were too few.

The hearing loss at the 95th percentile of cumulative CEOAE prevalence based on CSM (i.e., HL95) was calculated for older subject groups only at those frequencies for which the number of ears with detectable CEOAEs was 20 or more. The HL95 for older females was 35 dB at 0.5 kHz, 40 dB at 1 kHz, 45 dB at 2 kHz, and 65 dB at 4 kHz (based on 33 ears at 4 kHz). The HL95 for older males was 35 dB at 1 kHz (based on 31 ears at 1 kHz). Except for older female ears at 4 kHz, HL95 in older subjects was within 5 dB of HL95 in all subjects, and usually these HL95s were equal.

When comparing the prevalence of CEOAEs in older female and male ears at the same HL in the range of mild to moderate loss, CEOAE prevalence was larger in female ears by 25%–44% across frequencies from 0.5 to 4 kHz. This finding supports the theory of Dubno et al. (2008) that metabolic presbyacusis is important in both females and males, whereas sensory presbyacusis is more important in males in combination with metabolic effects. A reduction in endocochlear potential would reduce the cochlear amplifier gain, and, thus, reduce the amplitude and synchrony of the CEOAE response. Nonetheless, it might not eliminate the possibility of detecting CEOAEs. Sensory presbyacusis, which is more prevalent in males, would tend to eliminate the outer-hair-cell nonlinearity, and thus eliminate a CEOAE response. These mechanisms would predict a higher prevalence of CEOAEs in female ears, as was observed.

Moreover, the predicted reduction in cochlear gain in older ears with increasing HL due to metabolic presbyacusis would linearize the cochlear mechanics and result in reduced GD in CEOAE measurements. A reduction in GD with increasing HL was observed in older females at all frequencies between 0.5 and 4 kHz, and in older males at 2 kHz (see Fig. 20). The lack of a significant effect on GD due to HL in older males at frequencies other than 1 kHz was related to insufficient power: CEOAEs were detected in only nine older male ears at 0.5 kHz, two ears at 4 kHz and five ears at 8 kHz. Although not plotted, the regression slope at 1 kHz for 31 male ears with CEOAEs was $m=-0.008,$ but did not differ significantly from zero. The large differences observed in CEOAE responses between older female and male ears suggest that sex-dependent baselines in CEOAE responses may be helpful in identifying older ears with SNHL.

CONCLUDING REMARKS

This report introduces a group of signal-processing moments to summarize CEOAE properties in the time domain via instantaneous frequency and instantaneous bandwidth (spectral moments), and in the frequency domain via group delay and group spread (temporal moments). Instantaneous bandwidth is a measure of the frequency dispersion of CEOAE waveform energy density about its instantaneous frequency. Group spread is a measure of the temporal dispersion of CEOAE spectral energy density about its group delay. Measurement procedures avoided phase unwrapping for phase-gradient moments, and used energy-weighted smoothing and statistical detection criteria for all moments. In normal ears, measurements of CEOAE moments were highly repeatable in ears tested on two different dates. Moments were strongly influenced in most ears by the presence of SSOAEs at frequencies up to 4 kHz. The mean CEOAE moments showed aspects of cochlear function with smaller measurement variabilities in group delay than in previous studies on SFOAE group delay. CEOAE group delay was longer than CEOAE latency analyzed at the same stimulus level. A time-frequency symmetry was observed between instantaneous frequency and group delay measurements, which confirmed the place of CEOAE generation within the tonotopic region of the basilar membrane. A direct measure of cochlear tuning based on CEOAE instantaneous frequency and bandwidth above 4 kHz showed sharper tuning at higher frequencies, which became even more pronounced above 11 kHz.

Coherence synchrony measures derived from CEOAEs in time and frequency domains accurately predicted hearing loss, such that a combined time-frequency predictor performed best overall in identifying ears with hearing loss at frequencies between 0.5 and 8 kHz. In ears with a sloping hearing loss compared to normal ears, group delay and instantaneous frequency were generally reduced at frequencies of hearing loss and unchanged at frequencies of normal hearing. Group delay decreased with increasing hearing loss at all frequencies up to 4 kHz, confirming a progressive loss of outer hair cell function. Group spread increased with increasing hearing loss at frequencies from 1 to 8 kHz, which was consistent with a loss in cochlear tuning. In subjects 60 years and older, the prevalence of CEOAEs in ears with mild-to-moderate hearing loss (25–45 dB HL) was reduced by 35% in males compared to females. CEOAE group delay decreased with increasing hearing loss in older female ears at frequencies from 0.5 to 4 kHz, and in older males at 2 kHz. These CEOAE moment measurements provide physiological evidence in human ears to support the theory (Dubno et al., 2008) that metabolic presbyascusis affects older subjects with an increased relative importance of sensory presbyacusis in older males.

CEOAE moments have potential for clinical utilization based on their demonstrated repeatability, their ability to non-invasively measure cochlear function including tuning, and the systematic changes observed in ears with sensorineural hearing loss compared to normal ears.

While all experimental results were obtained in human ears, CEOAE moments and their properties may also be applied in non-human mammalian ears over a bandwidth in which CEOAEs and SSOAEs can be reliably recorded. The extent to which SSOAEs influence interpretation of CEOAE moments is expected to be species dependent.

NOMENCLATURE

AUC

Area under the receiver operating characteristic curve

CEOAE

Click-evoked OAE

CI

Confidence interval

CSM

Coherence synchrony measure

DFT

Discrete Fourier transform

DPOAE

Distortion product OAE

ERB

Equivalent rectangular bandwidth

GD

Group delay

GS

Group spread

HL95

HL at 95% cumulative CEOAE prevalence

IB

Instantaneous bandwidth

IF

Instantaneous frequency

IQR

Inter-quartile range

NF

Mean # of SSOAEs per half-octave frequency band

OAE

Otoacoustic emission

peSPL

Peak-to-peak equivalent SPL

SE

Standard error of the mean

SFOAE

Stimulus frequency OAE

SNHL

Sensorineural hearing loss

SNR

Signal to noise ratio

SOAE

Spontaneous OAE

SSOAE

Synchronized spontaneous OAE

TBOAE

Tone-burst evoked OAE

APPENDIX A: MOMENTS OF CONDITIONAL TIME-FREQUENCY DISTRIBUTIONS

This appendix places the definitions for CEOAE moments in the context of time-frequency analysis. Except where otherwise referenced, proofs of all time-frequency relations are given in Cohen (1995). A standard terminology in time-frequency analysis uses radian frequency $\omega =2\pi f$ rather than frequency f to reduce the number of occurrences of $2\pi ;$ this convention is used here.

The spectrum $S(\omega )$ or Fourier transform of the (CEOAE) analytic signal $s(t)$ for $\omega >0$ is

$$S(\omega )=\frac{1}{\sqrt{2\pi }}\int s(t)e^{-j\omega t}dt,$$ (A1)

with inverse Fourier transform for $t>0,$

$$s(t)=\frac{1}{\sqrt{2\pi }}\int S(\omega )e^{j\omega t}d\omega .$$ (A2)

The analytic signal is normalized for unit energy, and it follows that its spectrum is also normalized:

$$\begin{array}{c}1=\int {\left|s(t)\right|}^{2}dt,\\ 1=\int {\left|S(\omega )\right|}^{2}d\omega .\end{array}$$ (A3)

A general Cohen class of time-frequency representations that is bilinear in the analytic signal $s(t)$ is defined by the time-frequency distribution $C(t,\omega )$,

$$C(t,\omega )=\frac{1}{4{\pi }^2}{\displaystyle \int \int \int }{s}^{\ast }(u-\frac{1}{2}\tau )s(u+\frac{1}{2}\tau )\hspace{0.17em}\varphi (\theta ,\tau )e^{-j\theta t-j\tau \omega +j\theta u}du\hspace{0.17em}d\tau \hspace{0.17em}d\theta ,$$ (A4)

in terms of a two-dimensional kernel function $\varphi (\theta ,\tau )$ that uniquely defines the distribution. The simplest kernel $\varphi (\theta ,\tau )=1$ is the Wigner distribution. The spectrogram is represented by a kernel specified using a filter function. A class of product kernels satisfies $\varphi (\theta ,\tau )=\varphi (\theta \tau ).$

The marginal distributions $P(t)$ in time and $P(\omega )$ in frequency are defined by

$$\begin{array}{c}P(t)=\int C(t,\omega )d\omega ,\\ P(\omega )=\int C(t,\omega )dt.\end{array}$$ (A5)

The time marginal is said to be satisfied if

$$P(t)=\int C(t,\omega )\hspace{0.17em}d\omega ={\left|s(t)\right|}^2=A^2(t),$$ (A6)

in which Eq. 2 is used. The frequency marginal is said to be satisfied if

$$P(\omega )=\int C(t,\omega )dt={\left|S(\omega )\right|}^2=B^2(\omega ),$$ (A7)

in which Eq. 4 is used. Satisfaction of the marginals ensures that $A^2(t)$ is the energy density in time and $B^2(\omega )$ is the energy density in frequency. The time marginal is satisfied for any kernel with $\varphi (\theta ,0)=1,$ and the frequency marginal is satisfied for a kernel with $\varphi (0,\tau )=1.$ Both marginals are satisfied if $\varphi (0,0)=1,$ which reduces to $\varphi (0)=1$ for a product kernel. In either case, the total energy satisfies

$$1={\displaystyle \int {\displaystyle \int C(t,\omega )\hspace{0.17em}dt\hspace{0.17em}d\omega }}.$$ (A8)

For an arbitrary kernel, the conditional density distribution $C(\omega |t)$ of frequency for a given time is

$$C(\omega |t)=\frac{C(t,\omega )}{P(t)},$$ (A9)

and the conditional density distribution $C(t|\omega )$ of time for a given frequency is

$$C(t|\omega )=\frac{C(t,\omega )}{P(\omega )}.$$ (A10)

The expectation value of any power of time $t^n$ for positive integer n at a given frequency over the conditional distribution is

$${\langle t^n\rangle }_{\omega }=\int t^n\hspace{0.17em}C(t|\omega )\hspace{0.17em}dt=\frac{1}{P(\omega )}\int t^n\hspace{0.17em}C(t,\omega )dt.$$ (A11)

The expectation value of any power of frequency ${\omega }^n$ for positive integer n at a given frequency over the conditional distribution is

$${\langle {\omega }^n\rangle }_t=\int {\omega }^n\hspace{0.17em}C(\omega |t)\hspace{0.17em}d\omega =\frac{1}{P(t)}\int {\omega }^2\hspace{0.17em}C(t,\omega )d\omega .$$ (A12)

${\langle t^n\rangle }_{\omega }$ is the nth order (conditional) moment of time as a function of frequency, and ${\langle {\omega }^n\rangle }_t$ is the nth order (conditional) moment of frequency as a function of time.

The average frequency $\langle \omega \rangle$ at a given time t is the first spectral moment

$${\langle \omega \rangle }_t=\frac{1}{P(t)}\int \omega C(t,\omega )\hspace{0.17em}d\omega .$$ (A13)

Suppose that a kernel is selected that satisfies the time marginal ($\varphi (\theta ,0)=1$) and that satisfies $\partial \varphi (\theta ,\tau )/\partial \tau {|}_{\tau =0}=0.$ These conditions for a product kernel are $\varphi (0)=1$ and ${\varphi }^{\prime }(0)=0,$ in which the prime denotes differentiation with respect to the argument of the kernel. It follows that

$${\langle \omega \rangle }_t=\frac{d\mathrm{\Phi }(t)}{\mathit{d}\mathit{t}},$$ (A14)

in which $\mathrm{\Phi }(t)$ is the phase of the analytic signal in Eq. 2. IF(t) in Eq. 7 is equal to $\left(1/2\pi \right){\langle \omega \rangle }_t,$ i.e., IF(t) is the first spectral moment. When the kernel function is selected as a spectrogram, IF(t) is equal to $\left(1/2\pi \right){\langle \omega \rangle }_t$ in the limit that the spectrogram filter function has short duration.

The second-order moment of frequency $\langle {\omega }^2\rangle$ at a given time t is

$${\langle {\omega }^2\rangle }_t=\frac{1}{P(t)}\int {\omega }^{2}C(t,\omega )d\omega .$$ (A15)

The special case of a product kernel is considered in which it and its derivatives satisfy $\varphi (0)=1,$${\varphi }^{\prime }(0)=0,$ and ${\varphi }^{″}(0)=1/4$ at $\tau =0.$ It follows that

$${\langle {\omega }^2\rangle }_t={\left(\frac{d\hspace{0.17em}\ln \hspace{0.17em}A(t)}{\mathit{d}\mathit{t}}\right)}^2+{\left(\frac{\mathrm{\Phi }(t)}{\mathit{d}\mathit{t}}\right)}^2.$$ (A16)

Particular examples of such product kernels are described (Cohen and Lee, 1988; Loughlin and Davidson, 2001). A standard deviation ${\sigma }_{\omega |t}^2$ is defined in terms of the moments of order 1 and 2 by

$${\sigma }_{\omega |t}^2={\langle {\omega }^2\rangle }_t-{\langle \omega \rangle }_t^2.$$ (A17)

It follows from Eq. A16 that

$${\sigma }_{\omega |t}^2={\left(\frac{d\hspace{0.17em}\ln \hspace{0.17em}A(t)}{\mathit{d}\mathit{t}}\right)}^2.$$ (A18)

${\sigma }_{\omega |t}$ is the second-order spectral moment normalized by its first-order moment. IB(t) in Eq. 7 is equal to ${\sigma }_{\omega |t}/2\pi$ after conversion from radian frequency to frequency. Thus, IB(t) is the second-order spectral moment in the form of a standard deviation.

However, when the kernel function is selected as the spectrogram, IB(t) is not equal to $\left|d\hspace{0.17em}\ln \hspace{0.17em}A(t)/dt\right|$ in the limit that the filter function has short duration. Nevertheless, the relation corresponding to Eq. A18 for ${\sigma }_{\omega |t}^2$ for the spectrogram is equal to ${\left(d\ln A(t)/dt\right)}^2$ plus other window-dependent terms.

A similar analysis in the time domain shows that GD(f) and GS(f), as defined in Eq. 9, are interpreted as first and second temporal moments of the conditional distribution $C(t|\omega )$ using Eq. A11. In summary, the moments of the conditional time-frequency distributions characterize the IF, IB, GD, and GS of the signal.

The Cohen class of kernels leads to time-frequency distributions that are negative at some times and frequencies, which is undesirable based on the intuitive notion of a time-frequency distribution as a positive energy density on the time-frequency plane. Manifestly positive time-frequency distributions have a more complicated form than that of the bilinear distributions considered herein, i.e., their kernels become signal dependent. Nevertheless, the interpretation of IF, IB, GD, and GS as moments of the conditional distributions would remain valid.

These moments do take on a more complicated form for the case of multiple-component signals, and weighted averaging techniques for such moments have been developed (Loughlin and Davidson, 2001). The present work assumes the validity of interpreting the moments based on the single-component expressions in Eqs. 7, 9. This assumption is valid above 4 kHz where SSOAEs were rarely observed, but the interpretation at lower frequencies is complicated by inaccuracies in these relations. These inaccuracies were partially addressed by smoothing the moments over time or frequency.

APPENDIX B: LOG LIKELIHOOD RATIO CLASSIFIER OF SNHL

A log likelihood ratio classifier combines test information across multiple variables, in this case the evoked CSM(t) at various times, into a univariate predictor to classify a particular response from the ith ear into one or the other of two groups (normal or impaired). The test variable for the ith test ear is $x(i,j,k),$ in which $j=1,2,\dots ,J$ ranges over the J test variables [i.e., CSM(t) at each of J time steps], and in which $k=1,2,\dots ,K$ ranges over the $K=32$ buffers. The predictor is constructed for the jth test variable based on the measured mean ${\mu }_I(j)$ and standard deviation ${\sigma }_I(j)$ of the impaired group over K buffers and $N_I$ impaired ears, and the mean ${\mu }_N(j)$ and standard deviation ${\sigma }_N(j)$ of the normal group over K buffers and $N_N$ impaired ears. The ear index i ranges over all ears, normal and impaired.

Assuming that the response in each buffer is an independent Gaussian random variable, the log likelihood $L(i,j)$ for ear i and test variable j that a test response $x(i,j,k)$ is from an impaired ear is

$$L_I(i,j)=-\frac{K}{2}\hspace{0.17em}\ln \hspace{0.17em}2\pi -K\hspace{0.17em}\ln \hspace{0.17em}{\sigma }_I(j)-\frac{1}{2}{\displaystyle \sum }_{k=1}^K{\left[\frac{(x(i,j,k)-{\mu }_I(j))}{{\sigma }_I(j)}\right]}^2.$$ (B1)

The above relation is a generalization of cases described in Van Trees (2001). Assuming that each test variable is an independent Gaussian random variable, the log likelihood $L(i)$ that the ith test ear is selected from the impaired group is

$$L_I(i)={\displaystyle \sum }_{j=1}^J{L}_I(i,j).$$ (B2)

The log likelihood $L_N(i)$ that the ith test ear is selected from the normal group is calculated in an analogous manner to $L_I(i),$ but using the mean ${\mu }_N(j)$ and standard deviation ${\sigma }_N(j)$ of ears from the normal group. The log likelihood ratio classifier is defined for each test ear by $l(i)=L_I(i)-L_N(i),$ with $l(i)>0$ indicating greater likelihood that the ith test ear is impaired, and $l(i)<0$ that it is normal. The classifier has larger relative weightings at times for which the distributions of the two test groups have the least overlap. In the actual measurements wherein the test responses were not independent across the J test variables (e.g., a CEOAE waveform at one time was correlated with the waveform at other times), the success of a log-likelihood ratio classifier was assessed by its AUC value relative to other predictors. Test predictors based on likelihood ratios are useful even when the assumption of statistical independence is not satisfied, but only if the resulting AUC is significantly larger than the AUCs of other available tests.