Analysis of the cochlear microphonic to a low-frequency tone embedded in filtered noise

Abstract

The cochlear microphonic was recorded in response to a 733 Hz tone embedded in noise that was high-pass filtered at 25 different frequencies. The amplitude of the cochlear microphonic increased as the high-pass cutoff frequency of the noise increased. The amplitude growth for a 60 dB SPL tone was steeper and saturated sooner than that of an 80 dB SPL tone. The growth for both signal levels, however, was not entirely cumulative with plateaus occurring at about 4 and 7 mm from the apex. A phenomenological model of the electrical potential in the cochlea that included a hair cell probability function and spiral geometry of the cochlea could account for both the slope of the growth functions and the plateau regions. This suggests that with high-pass-filtered noise, the cochlear microphonic recorded at the round window comes from the electric field generated at the source directed towards the electrode and not down the longitudinal axis of the cochlea.

INTRODUCTION

Hearing loss occurs as a result of damage to anatomic structures in the cochlea; this leads to degeneration of auditory nerve fibers and changes in central auditory structures (Suzuka and Schuknecht, 1988;Dodson, 1997; Leake et al., 2006). Presently, the majority of audiologic diagnostic tests are not designed to determine the site of damage either within the cochlea or across neural and brain stem structures. Future developments in biologic rehabilitative approaches (i.e., virus-mediated hair cell regeneration and stem cell transplantation) will require new diagnostic procedures to target the location of damaged structures and pathophysiology resulting in the loss of hearing.

The cochlear microphonic may be a useful physiologic measure to estimate the location of missing outer hair cells along the cochlear partition. The cochlear microphonic (CM) is a voltage that occurs as a result of an alternating current produced by ions passing mainly through outer hair cells (OHC) into scala tympani as a function of the displacement of the basilar membrane (Dallos and Durrant, 1972). Historically, the clinical and scientific use of the CM to estimate OHC function has been limited due to two problems. One problem is that in response to high frequency stimuli, the instantaneous basilar membrane wave form has both positive and negative deflections spaced over a short distance. These opposing displacements initiate deflections of OHC stereocilia in opposite directions and result in receptor currents that are not coherent in phase. An electrode at the round window records the summed currents as a vector sum. In cases of cochlear damage, a change in the amplitude of the CM could be due to missing hair cells or a change in vector summation, making a diagnosis regarding location and health of OHCs difficult. A second problem is the location of the recording electrode (either round window for animal studies or promontory or tympanic membrane for human recordings). The OHCs that are closest to the electrode dominate the CM. For example, at low frequencies and high signal levels, the CM recorded from an electrode on the round window will be dominated by the OHCs in the base even though the maximum basilar membrane displacement is apical to the round window (Patuzzi et al., 1989). Thus determining the location of missing OHCs in remote cochlear turns with normal OHCs in the base could be difficult.

A possible solution to the vector summation and electrode location problem is to use a low-frequency tone embedded in high-pass masking noise. A low-frequency tone results in basilar membrane deflection that is in phase along the majority of the cochlear partition, thereby reducing, if not eliminating, the confounding influence of vector summation. Furthermore, depending on the cutoff frequency, the high-pass masking noise should limit the contribution of basal OHCs to the CM and emphasize those that are remote from the electrode location. The use of masking to limit electrophysiologic responses to specific cochlear regions is not unique. Many researchers have used masking and derived band techniques to estimate the cochlear locations contributing to the compound action potential (Teas et al., 1962; Elberling, 1974; Eggermont, 1976; Spoor et al., 1976; Zerlin and Naunton, 1976; Evans and Elberling, 1982; Shore and Nuttall, 1985; Earl and Chertoff, 2012), auditory brain stem response (Klein, 1986; Conijn et al., 1992; Boettcher et al., 1995; Oates and Stapells, 1997a,b), and CM (Ponton et al., 1992).

Recording the CM to a low-frequency tone embedded in noise filtered with various high-pass cutoffs may be useful for identifying regions of missing OHCs. The idea is to choose cutoff frequencies of the noise to allow OHCs ranging from the apical end of the cochlea to the basal end of the cochlea to sequentially contribute receptor currents to the CM. As the high-pass masker cutoff frequency increases, more OHCs will contribute to the response, and the amplitude of the CM should increase. In a case with missing OHCs in the cochlea, the amplitude of the CM would increase until the high-pass cutoff frequency matched the region of missing OHCs. At this point, the CM amplitude would remain constant.

This increase in CM amplitude with increasing frequency of the high-pass filtered noise may be related to the space constant in the cochlea. In a normal cochlea, the space constant along the longitudinal axis is approximately 1 mm (Misrahy et al., 1958; Mistrik et al., 2009). That is, for a source at a given location, the voltage recorded by an electrode should decay by 1/e for every mm in distance between the voltage source and the electrode. Or, contrarily, as the source moves closer to the electrode, as is the case in this study, the amplitude of the CM should increase exponentially at a rate of ∼1/e for every mm released from the noise. The purpose of this study was to (1) quantify the growth of the amplitude of the CM to a low-frequency tone as a function of high-pass noise cutoff frequency (or cochlear distance), (2) determine the influence of signal level of the low-frequency tone on the CM amplitude growth in the filtered noise conditions, and (3) provide a geometric model of the cochlea that explains the amplitude growth functions.

MATERIALS AND METHODS

Subjects

Mongolian gerbils weighing between 45 and 70 g were used as subjects. Gerbils were chosen because (1) the ease of surgical approach to the cochlea, (2) they have hearing thresholds similar to humans in the low frequencies, and (3) we have a large normative database on the CM and other physiologic measures of hearing. For the CM, a 733 Hz tone burst was delivered at 80 dB SPL to 15 animals and at 60 dB SPL to another 15 animals (some animals were the same as those in the 80 dB SPL condition) at a rate of 41.66/s. The experiments with the 80 dB SPL tone were performed twice with each animal. For each animal, a total of 25 CM measures corresponding to 25 distances from the apex were obtained. Data analysis was completed on 13 of the 15 animals because 2 animals had hearing thresholds above our normal criteria.

Surgery

The surgical methods to record the CM is similar to those reported previously (Chertoff et al., 1996; Choi et al., 2002) and are only briefly described. Initially, gerbils were sedated with pentobarbital (64 mg/kg) and maintained with injections of 1/3 the initial dose given every hour. Rectal temperature was monitored and maintained at 37 °C with a heating pad (Harvard, Holliston, MA). The bulla was opened with a small pick, and a cotton wick placed in the niche to absorb condensation. A silver wire ball electrode was lowered into the niche and placed against the round window of the cochlea. A needle electrode placed in the muscle of the contralateral forelimb served as ground.

Stimuli

A 733 Hz tone was used to evoke the CM. This frequency was chosen so that the spectrum of the CM did not contain frequencies at 1 kHz or its harmonics. One thousand hertz is the frequency of the compound action potential and if present in the spectrum of the response would confound the measurement of the amplitude of the CM. Furthermore, the frequency matched a point equal to the frequency point in the spectrum of the response to eliminate bias error when transforming the CM into the frequency domain via the Fourier transform. The 733 Hz tone burst was 15 ms in duration with a 2 ms rise/fall time. Tone bursts (10 ms in duration and 1.5 ms rise/fall time) were also used to record compound action potentials (CAPs). CAP thresholds were used as a physiologic measure of hearing, and obtained at 1, 2, 4, 8, and 16 kHz. In some animals, the frequency range was extended to include 24 kHz. All tone burst stimuli were created in a 16 bit array processor [Tucker-Davis-Technologies (TDT), AP2] sampling at 250 000 Hz.

Broad-band noise was created in a real-time signal processor (TDT, RP2) and high-pass filtered (fifth-order BiQuad digital filter, RP2) at 25 specific cut-off frequencies. The cutoff frequencies were chosen to assess 1/2 to 1/4 mm intervals along the cochlear partition. Pilot data showed that fewer frequencies did not yield enough data points to get an accurate description at the steepest segment of the CM amplitude growth curve. The gerbil frequency place map developed by Müller (1996) was used to convert masker cutoff frequency to place.

Stimulus delivery and physiologic recordings

The tone and noise signals were presented free field from a speaker (TDT, FF1) with a frequency response of 1000–50 000 Hz to span almost the complete range of hearing in gerbil. The speaker was shielded with mu metal (MμShield; Manchester, NH) to decrease electromagnetic artifact. The sound pressure and spectrum were monitored by a Bruel and Kjaer microphone (1/8 in., 4138) placed in front of the ear canal of the animal, and the output of the microphone was attached to an oscilloscope (Tektronix, TDS 2014) for calibration purposes.

The CM and CAP were recorded from a ball-tip electrode placed next to the round window, and an electrode placed in the contralateral forelimb musculature served as ground. The physiologic signals were filtered (0.3–3000 Hz), amplified (5000 times), digitized (TDT, AD2) at 250 000 Hz, averaged (∼500 times) and stored on disk. For the CM, the 733 Hz tone burst was delivered at 60 dB SPL and 80 dB SPL at a rate of 41.66/s. The CAP was recorded in response to tone bursts ranging from 100 dB SPL to 5 dB SPL in 5 dB increments and presented at 33.33/s. The amplitude and phase of the CM was obtained by windowing the time-domain signal with a Hanning window, and converting to the frequency domain with a fast Fourier transform (matlab). The amplitude of the CM was considered the amplitude of the peak at 733 Hz, and the phase was the angle at 733 Hz in the spectrum.

Procedure

Animals were sedated with pentobarbital (64 mg/kg), the bulla opened, and the electrode positioned in the round window niche. CAPs were recorded, and if thresholds across all frequencies were within normative values for our laboratory, the animal was included in the study. The 733 Hz tone was delivered repetitively and the amplitude of the CM was monitored in the frequency domain on a spectrum analyzer (Hewlett Packard, 3561 A) averaging in the time domain. After 100–200 signal averages, the time-domain CM was recorded and saved to disk. The stimulus was presented again, and the response monitored via the spectrum analyzer while noise was introduced and increased in level until the amplitude of the CM was reduced to 20% of its original size. Although somewhat arbitrary, 20% was chosen because at this value the amplitude of the CM was stable and still visible on the spectrum analyzer. This “fully suppressed” response was saved to disk. Next, the CM was recorded to the tone embedded in 25 different high-pass noise conditions. For each high-pass noise condition, the noise level was adjusted to account for the decrease in energy as the noise spectrum narrowed. The high-pass noise conditions were randomized to reduce any order effect. Furthermore, two recordings of unsuppressed responses of the CM were obtained randomly during the experimental session to monitor the stability of the CM and the animal. Reliability of the responses was examined by repeating the CM recording procedure after allowing the animals to rest for 20 min. No signal was delivered during this time.

RESULTS

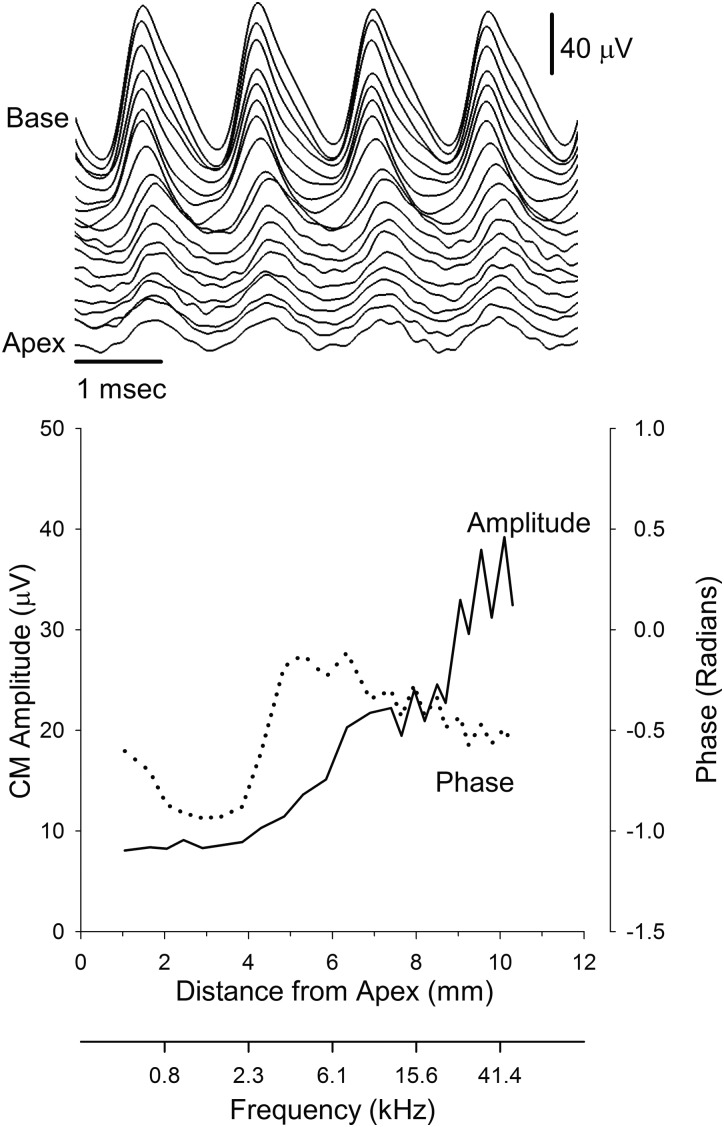
The amplitude and the morphology of the time-domain CM waveform changed as the high-pass cutoff frequency of the filtered noise increased. An example from one representative animal in response to the 733 Hz tone presented at 80 dB SPL is illustrated in the top and bottom panels of Fig. 1. As the cutoff of the high-pass noise increased, the amplitude of the waveform increased and the morphology changed from a “pure” sinusoidal response to a triangular-shaped waveform (top panel). Furthermore, the peaks of the response occurred slightly earlier as the cutoff frequency of the noise increased.

Figure 1.

The top panel illustrates an example of the CM recorded in response to a 733 Hz tone at 80 dB SPL in the presence of filtered noise. The waveform labeled Apex was obtained with the noise filtered with a high-pass cutoff frequency of 594 Hz. Each successive waveform represents the CM in response to increasing the high-pass cutoff frequency of the filtered noise. The bottom panel is the amplitude (left axis) and phase (right axis) of the CM obtained from the waveforms in the top panel. Filter cutoff frequency was converted to cochlear distance using the equation from Müller (1996).

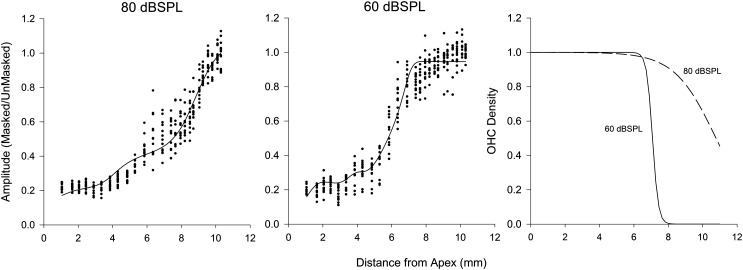
These observations were quantified by extracting the magnitude and phase of the CM at 733 Hz via a fast Fourier transform. Plotted as a function of cochlear distance (or cochlear frequency), the amplitude of the CM increased at ∼4 mm from the apex when the high-pass cutoff frequency of the noise neared 2.3 kHz (Fig. 1, bottom panel). The growth continued and reached a plateau at a distance of 6-8 mm from the apex. After the plateau, the amplitude of the CM increased and saturated at approximately 10 mm from the apex. The phase of the CM also varied as a function of distance. The phase showed a minimum between 2 and 4 mm, followed by a maximum at 4-6 mm, and then the phase decreased with a shallow slope until it recovered to baseline.

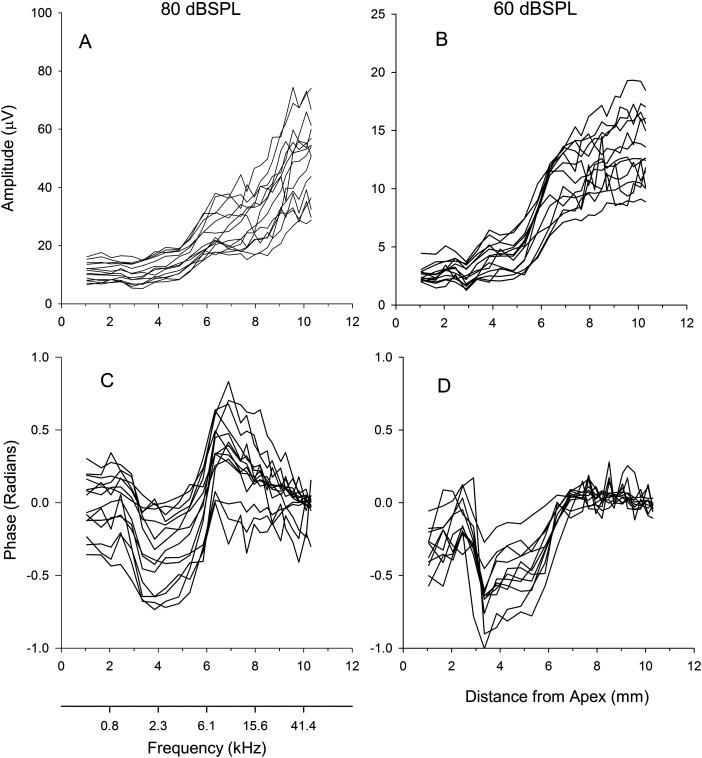
The general trend from the one animal was apparent in the group data along with differences between responses obtained for signals presented at 80 dB SPL and 60 dB SPL. The amplitude of the CM for the 60 dB SPL tone increased more steeply between 5 and 6 mm than it did in response to the 80 dB SPL tone, and the growth thereafter was shallower for the 60 dB SPL stimulus compared to the growth from the 80 dB SPL signal [Figs. 2A, 2B]. Initially, the phase from the response to the 60 dB SPL stimulus was similar to that of the 80 dB SPL stimulus. However, after 6 mm, the phase of the CM in response to the 60 dB SPL signal [Figs. 2C, 2D] lacked a maximum and corresponding return to baseline.

Figure 2.

Top panels show the amplitude of the CM as a function of distance from apex for the 80 and 60 dB SPL tones. The bottom panels show the corresponding CM phases relative to the unsuppressed condition.

Normalized data

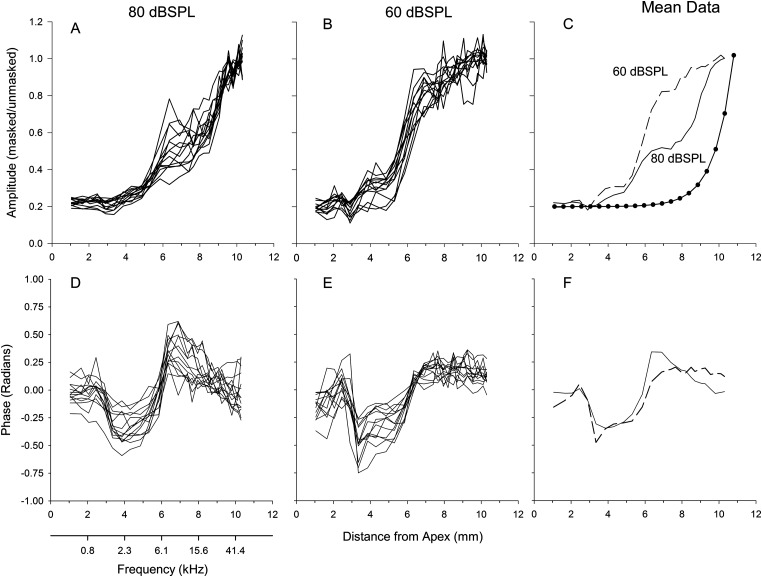
The amplitude of the CM was normalized by dividing each animal's response in the presence of noise to the response without noise. We refer to the normalized growth functions as the cumulative amplitude function or CAF. The CAFs showed similar trends to the raw amplitude functions, but the between-animal variability decreased when the functions were normalized [Figs. 3A, 3B]. After normalization many of the CAFs started at 0.2, verifying the 20% masking criteria considered as “fully suppressed.”

Figure 3.

Cumulative amplitude functions (CAFs), defined as the noise-suppressed response relative to the unsuppressed response, for the 80 and 60 dB SPL conditions from all animals, along with the mean CAFs. The curve with filled symbols is an exponential function with a space constant of 1 mm (panel C). Bottom panels are the phase of the CM normalized by subtracting the individual mean from each waveform for all animals. The corresponding mean phase for 80 and 60 dB SPL are shown in the bottom right panel.

The within-animal reliability of the CAFs between the two trials was determined by computing a correlation between the first and second CAF recording at 80 dB SPL for each animal. The average correlation was 0.97 with a between animal standard deviation of 0.05, indicating that the shapes of the CAFs were very similar within an animal.

Features present in the raw amplitude functions became more apparent after computing the mean CAF across animals at each examined distance from apex [Fig. 3C]. The CAF from the 80 dB SPL condition showed various inflections which occurred at approximately 3, 5, and 7.5 mm from the apex. Similar inflections in the CAF occurred for the 60 dB SPL stimulus but were more defined at 3 and 5 mm from the apex than those that occurred at the same distance for the 80 dB SPL stimulus.

The initial phase (i.e., the phase at 1 mm from the apex) of the CM as a function of distance from the apex differed among animals but showed maxima and minima that were common to a majority of the animals. To emphasize the similarity in morphology, the mean of the phase from each animal was subtracted from each individual's data [Figs. 3D, 3E], and then the phase was averaged across animals to illustrate the trends [Fig. 3F]. At 80 dB SPL and 60 dB SPL, the phase of the CM changed by approximately –0.25 radians between 2 and 4 mm from the apex. After, the phase increased and reached 0.25 radians at a distance of 6 mm from the apex for the 80 dB SPL signal, whereas for the 60 dB SPL stimulus, the phase recovered to baseline.

The 80 dB SPL and 60 dB SPL CAFs showed both similarities and differences to the growth predicted by a simple exponential function with a space constant of 1 mm [Fig. 3C, the dotted function was shifted along the ordinate to match the 20% criteria of the CAF data]. At 80 dB SPL, the CAF slope was similar to the exponential between 9 and 10 mm from the apex. Similarly, at 60 dB SPL, the CAF slope at 5–6 mm was similar to the exponential between 9 and 10 mm. However, for both signal levels, over a majority of distances the slope of the CAF curves did not match the exponential function. Moreover, the CAFs had regions where the curves plateaued which could not happen for a simple exponential growth.

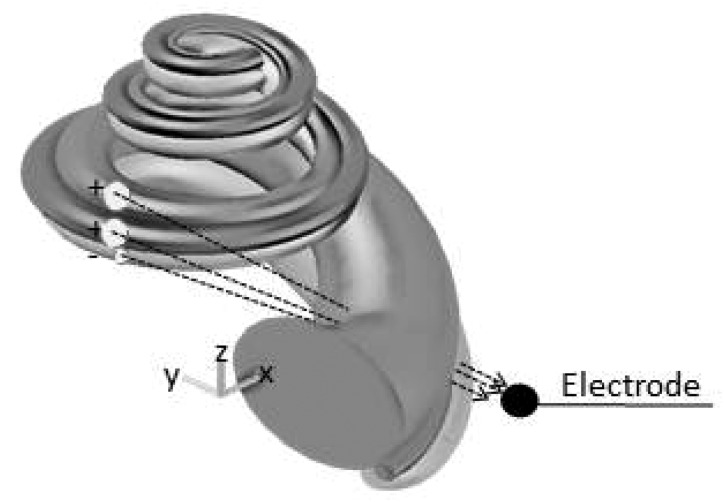
Model

Instead of the potential measured at the round window coming from along the longitudinal cochlear axis, which predicts an exponential growth, we proposed that the electric field in the scala vestibuli, media, and tympani, projected directly toward the electrode. The motivation for this theory was from the observation that the plateaus in the CAFs occurred when cochlear segments released from noise were on the side where the modiolus intervened between the electrode and the OHC sources. To test this hypothesis, equations that describe the geometry of the gerbil cochlea were developed (see the Appendix for details). Figure 4 shows the geometric model of the cochlea used to determine the potential at the electrode given the electric potential generated by hair cells along the cochlear partition. The initial source was considered a group of charges located in scala media [Mq, Eq. 1], produced by OHCs along the length of the cochlea. The charge in scala tympani (Tq) and the charge in scala vestibuli (Vq) were both proportional to that created in scala media with the charge in tympani being negative compared to the other chambers (Tasaki et al., 1952; Zidanic and Brownell, 1992). Thus the CAF, as a function of distance from the apex (x), was modeled as

$$\text{CAF}(x)={\displaystyle {\int }_o^x\left(\frac{1}{1+e^{a+by}}\right)\left(\frac{-Tq}{R_T(y)}+\frac{\mathit{M}\mathit{q}}{R_M(y)}+\frac{\mathit{V}\mathit{q}}{R_V(y)}-c\right)dy+\mathrm{d}.}$$ (1)

The first factor in the integrand of Eq. 1 (a logistic function) represents the contribution of OHCs along the cochlear partition to the CM, which depends on two parameters, a and b. The value of this function is approximately equal to 1 along the length of the cochlea but will decrease and reach 0.5 at −a/b. The parameter c represents the resting voltage when no stimulus is presented, and d shifts the function along the ordinate to fit the data. $R_T$, $R_M$, and $R_V$ are the respective Euclidean distances from the midpoint of scala tympani, scala media, and scala vestibuli to the recording electrode, as a function of an arclength distance from apex (y) that is measured along the respective scala.

Figure 4.

Spiral geometry of the gerbil cochlea obtained from the anatomical measurements and fitted equations described in the Appendix. The arrows indicate a possible path of the electric field from the source to the electrode.

Equation 1 was fit separately to both the data from the animals at 80 dB SPL and the data from animals at 60 dB SPL tone levels using least squares nonlinear regression (Fig. 5). Initial values for charges ($T_q$, $M_q$, and $V_q$), resting voltage (c) and shift parameter (d) were obtained by fitting a model without the logistic-function factor in the integrand to the data corresponding to measurements before a distance of about 7 mm (for which the logistic factor should have been essentially equal to 1 according to the observed curves in Fig. 3). Then, for the 60 dB SPL data, the complete model was fitted by starting with these initial values along with a set of a and b initial parameter values that were consistent with a ratio −a/b of about 8, a number that is close to the point where the logistic factor should drop sharply from 1 to 0, which was suggested by the fact that the observed curves tended to level off after 8 mm. For the 80 dB SPL data, ratios with higher values were used to obtain initial values for a and b.

Figure 5.

Left and middle panels illustrate the CAFs (dots) from the 80 and 60 dB SPL conditions. The lines represent the estimated model fits showing growth similar to the animal data. The right panel is the solution to the logistic function estimating the percentage of OHCs contributing to the CAF for the 80 dB SPL (dashed line) and 60 dB SPL (solid line) conditions.

The fitted model with the parameters and coefficients that produced the lowest sum of squares for the 80 dB SPL signal is reported in Tables 1, TABLE II. for the 60 dB SPL condition. For 80 dB SPL data, the model fit well with adjusted R² = 0.93 for trial 1, and R² = 0.94 for trial 2. Moreover, the values of the parameters for the two trials at 80 dB SPL were similar. The fit of the model at 60 dB SPL (Table TABLE II.) was also good with an R² = 0.92. Importantly, at both signal levels, the model curves showed growth rates and plateau regions similar to the data. From the model parameters, the logistic function representing the effective OHC density along length of the cochlea was solved (Fig. 5). For the 80 dB SPL signal, the majority of hair cells along the cochlear partition contribute to the CAF whereas at 60 dB SPL, mainly hair cells from the apex to 7.08 mm contribute to the CAF.

TABLE I.

Parameters, coefficient values, standard errors of the estimated coefficients, and confidence intervals for the coefficients obtained from fitting Eq. 1 to the CAF data from the first trial at 80 dB SPL. Values in parentheses were obtained from fitting the equation to the second trial recordings.

Parameter	Coefficient	Standard error	95% CI
Tq	0.1729	0.0302	0.1135, 0.2323
(Tq)	(0.1795)	(0.0300)	(0.1204, 0.2386)
Mq	0.3215	0.0245	0.2733, 0.3697
(Mq)	(0.3284)	(0.0338)	(0.2620, 0.3949)
Vq	0.3249	0.0345	0.2570, 0.3929
(Vq)	(0.3079)	(0.0381)	(0.2330, 0.3828)
d	0.1465	0.0106	0.1257, 0.1673
(d)	(0.1403)	(0.0110)	(0.1186, 0.1619)
a	−8.9480	0.9449	−10.8067, −7.0894
(a)	(−8.5100)	(0.9600)	(−10.3970, −6.6221)
b	0.8301	0.0827	0.6674, 0.9928
(b)	(0.7322)	(0.0807)	(0.5735, 0.8910)
c	0.1461	0.0090	0.1284, 0.1639
(c)	(0.1386)	(0.0090)	(0.1217, 0.1555)

TABLE II.

Parameters, coefficient estimates, standard errors, and 95% confidence intervals obtained from fitting Eq. 1 to CAF data obtained at 60 dB SPL.

Parameter	Coefficient	Standard error	95% CI
Tq	15.4668	0.8267	13.8411, 17.0925
Mq	0.5427	0.0589	0.4268, 0.6686
Vq	19.1288	0.9703	17.2208, 21.0369
d	0.1191	0.0286	0.0628, 0.1754
a	−41.6984	6.3786	−54.2415, −29.1553
b	5.8885	0.8780	4.1620, 7.6149
c	1.2328	0.8574	1.0642, 1.4014

DISCUSSION

Assumptions

The long term goals of this research are to determine if the CM can be used to locate regions of missing OHCs along the cochlear partition, or, if present, provide a physiologic description of their health. In this study, the CM in response to a low-frequency tone was suppressed by the addition of noise. This was likely due to the noise driving the hair-cell transducer function in to saturation, thereby reducing the hair cells ability to respond to the low frequency tone. As the high-pass cutoff frequency of the noise increased, the amplitude of the CM increased. One assumption in this study is that the recorded electrophysiologic signal was the CM representing voltage changes due to OHC and perhaps some IHC receptor currents. For low frequency tones, however, the phase locking from auditory nerve fibers (i.e., auditory neurophonic) may contribute to the response (Henry, 1995; Lichtenhan et al., 2012). In gerbil, Henry (1995) and others (He et al., 2012) showed that the auditory neurophonic contributes to the recording at the round window for low-frequency tones presented at low signal levels. At high signal levels such as 80 dB SPL, a difference between responses with and without TTX is not observable. Thus at least for the high-level condition, we conclude that the contribution of neural phase locking in this study, if present, was small.

Another assumption in this study is that the growth in amplitude of the CM was due to the sequential release of OHCs along the cochlear partition from the noise, allowing their receptor currents to sum and contribute to the amplitude of the CM. This assumption is supported for the following reasons. First, if the noise-suppressed CM was solely dominated by basal OHCs located near the electrode, the CAF would remain at its initial “fully suppressed” value (i.e., 20% of unsuppressed value) as the high-pass cutoff frequency of the noise increased until the cutoff frequency place was close to the electrode location (approximately 1 mm from the base). Then the amplitude would grow rapidly. This, however, did not happen. The CM amplitude began to increase from the 20% criteria at ∼4 mm from the apex and then grew steadily.

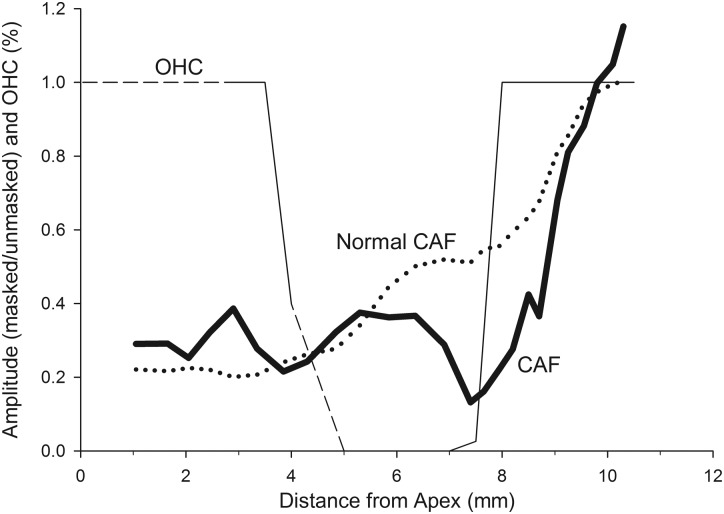
Another piece of supporting evidence is from an animal with OHC loss in the second turn of the cochlea. As part of a subsequent study, animals are being exposed to tones of different frequencies to damage hair cells in different cochlear turns. Histology is completed and missing OHC locations are correlated with the CAF. In one animal exposed to a 1000 Hz tone for 2 h, the CAF differed from the normal CAF obtained at 80 dB SPL (Fig. 6). The CAF remained relatively flat until ∼8 mm from the apex, followed by a rapid rise to a maximum. This was related to the presence of OHCs. The CAF was small in the region of missing OHCs but increased rapidly when the present OHCs in the base were released from the noise. If the amplitude of the CM in the noise conditions only reflected basal OHCs, the CAF in this animal would be normal. However, the CAF rose only when the segment of the cochlea with present OHCs was able to respond. Thus we conclude that the growth of the CM amplitude with increasing cutoff frequency of the noise reflects contributions from OHCs along the cochlear partition progressively being released from noise.

Figure 6.

The solid thin line is the percentage of OHC present along the length of the cochlea. The dashed line indicates regions wherein OHCs were uncountable due to error/artifacts of the histologic preparation. The CAF from this animal (solid thick line) is abnormal through the cochlear region with missing OHCs, then the curve increases over the region where OHCs are present in the base. The dotted line is the average CAF computed across all of the animals.

Signal level

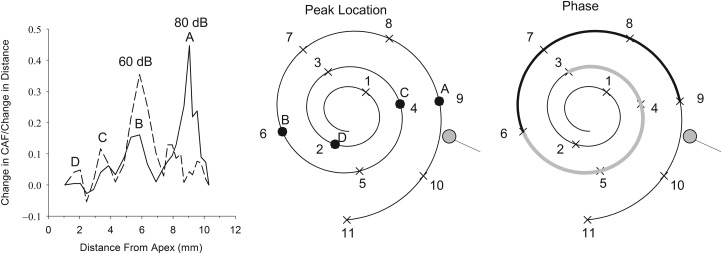
The shape of the CAF varied as a function of signal level. For the 60 dB SPL signal, the slope of the CAF was steeper than the slope of the CAF from the 80 dB SPL signal between 5 and 7 mm from the apex. Closer to the base, the slope of the CAF for the 60 dB SPL condition was more shallow than that for the 80 dB SPL signal. The different shapes of the CAFs indicate that the contribution of OHCs to the amplitude of the CM shifts along the cochlear partition when signal level was varied. The shift can be represented by differentiating the average CAFs for both signal levels with respect to distance (Fig. 7). The largest peak in the differentiated CAF curve differed between the 2 signal levels. For the 60 dB SPL stimulus, the peak occurred at 6 mm from the apex and for the 80 dB SPL signal, the peak occurred at 9 mm from the apex. This indicates that the OHCs that dominate the CM shifted basally as signal level increased. A change of 20 dB caused a 3 mm change in the predominant location of OHCs contributing to the CM. This result is consistent with Honrubia and Ward (1968), who reported a 4 mm basal shift in the distribution of the CM in guinea pig with increasing signal level.

Figure 7.

Left panel is the derivative of the mean CAF with respect to distance for the 80 dB SPL (solid line) and 60 dB SPL conditions (dashed lines). The middle panel illustrates a two-dimensional view of the cochlear spiral with locations of the peaks for the 80 dB SPL condition from the differentiated CAF indicated by letters A–D. The right panel is the same two-dimensional cochlear view with the location where the phase is negative (light grey line) or positive (dark line) relative to the no-noise condition.

Cochlear model

Space constant

The results from the geometric model of the gerbil cochlea showed that the growth and inflections in the CAF could be accounted for by a combination of the charge in the cochlear scalae, an OHC density function, and the Euclidean distance to the electrode. Moreover, the growth of the CAF differed from that predicted by an exponential growth with a space constant of 1 mm [Fig. 3C]. This is in contrast with previous investigations that recorded the potential in the cochlea as a function of longitudinal distance from the source to the electrode (Békésy, 1951; Misrahy et al., 1958; Johnstone and Johnstone, 1966) or models of cochlear potentials (Strelioff, 1973; Mistrik et al., 2009). In the physiological studies, an ac or dc source was fixed at a given cochlear location, and the voltage was recorded as an electrode was moved along the scalae. The results were consistent across investigations indicating a space constant of 1 mm. In our study, the experimental situation was similar in that we measured voltage as a function of distance between the source and the electrode. Only in this study the location of the source varied and the electrode remained fixed. Thus we expected the results to be similar. Some possible explanations for the discrepancy may be that the older studies used guinea pig as experimental subjects, which may have different bioelectric tissue properties than gerbil. Another possibility is that signal averaging allowed us to record smaller signals than previously done. Misrahy et al. (1958) reported no signal could be recorded in the second turn of the guinea pig cochlea with the source in the first turn. It is possible a small signal existed but was not visible with the recording techniques of those years.

Spiral geometry

The spiral nature of the cochlea as described by the cochlear model helps provide some insight into the influence of the cochlear geometry on the CAF. The peaks in the differentiated CAF (Fig. 7) occurred at somewhat regular spatial intervals, indicating a spatial periodicity in the change in voltage with distance along the cochlea. When peak locations were plotted on a cochlear map (Fig. 7, middle panel), the locations of the peaks were not randomly distributed along the cochlear spiral. The peaks occurred every 1/2 cycle of the cochlear spiral. That is, starting at the apex, when the frequency cutoff of the noise released a 2 mm cochlear segment, the amplitude of the CM increased. This occurred again after another 1/2 cycle (4 mm) and repeated at 6 mm and at 9 mm from the apex.

The periodic changes in the amplitude of the CM as cochlear segments were released from noise may be explained by the interaction of the sign and magnitude of the voltage in the three scalae and the distance from the source to the electrode. In particular, the Euclidean distance from the source to the electrode and the different sign of the charges in the scalae could create the plateau regions in the CAFs. Given that the electrode position and the charge are fixed, the distances from the three scalae to the electrode and the potential at the electrode trade off. That is, as the distance from one chamber decreases the others must increase for the voltage at the electrode to remain constant. Interestingly, this predicts that in different animal species, the location of the plateau would depend on the geometry of the species' cochlea and location of the recording electrode.

Another observation was that the phase of the CM was not randomly distributed along the cochlear spiral (Fig. 7, right panel). The phase was negative when 3-6 mm from the apex was freed from the noise and then it was positive from 6 to 9 mm from the apex. The phase changes when the source is on either side of the modiolus. This may reflect the dielectric properties of the tissue that the electric field passes through and eventually recorded as a potential at the round window. The cochlea consists of tissue and bone with various conductivities and capacitances, which are most likely not isotropic. It is possible that when the field is created in the cochlea where the modiolus intervenes between the source and the electrode, the dielectric properties of the bone alter the field (Foster and Schwan, 1989). At the frequency used in this study, the relative permittivity of bone is approximately 4000 (Kosterich et al., 1983), contributing to the bone's capacitance. In combination with the conductivity of the bone and other tissues, this could cause changes in the phase of the CM as it propagates from various locations along the cochlear spiral.

Phenomenological and physical interpretation of cochlear model

The CAF model was derived from general principles of electric potentials produced by electric fields (charge and distance). However, many of the parameters of the model serve as phenomenological descriptors. In the simplest and classic model of an electric field, the electrostatic potential in free space is given as

$$P=\frac{1}{4\pi \epsilon }{\displaystyle \sum _{i=1}^n\frac{q_i}{R_i}}$$ (2)

where P is the potential at the electrode, q is charge, R is the Euclidean distance from the source to the electrode, and ε is the permittivity of free space. The charge parameters in our model are not static charges because their values were obtained from the CM, which is a measure of the change in voltage in the cochlear chambers as a result of the flow of ionic current through fluids and tissue. A more appropriate physically interpretable model would be to replace the charge parameters with a current source element and the permittivity of free space by the conductivity and capacitance of the fluid and tissue spaces of the cochlea. Conductivity values have been reported in guinea pig (Békésy, 1951; Misrahy et al., 1958; Johnstone and Johnstone, 1966) and gerbil (Kumar et al., 2010). Moreover, values from these studies have been incorporated into electric circuit models of the cochlea to help understand cochlear potentials (Békésy, 1951; Strelioff, 1973; Mistrik et al., 2009). However, because of the influence of the spiral geometry found in the present study the directional dependence of the conductivity and capacitance would be important to consider before embarking on a physically realizable model.

The logistic function in the model may be physically interpretable. This function represents the percentage of present hair cells along the cochlear partition contributing to the CM. The parameters a and b indicate the location where the percentage of hair cells reduces to 50%. The results of this study showed that for the 60 dB SPL condition, hair cells basal to 7 mm (−a/b) contributed less to the CM than for the 80 dB SPL signal level. This has implications for the long term goal of this research to use this study's paradigm to estimate the location of missing hair cells along the length of the cochlea. That is, −a/b may indicate the location of missing hair cells in animals with hearing loss due to cochlear damage. An on-going study examining the relation between the physiologic prediction and anatomic location of hair cell loss will determine the success of the parameters of the logistic function.

Limitations

The results of this study point to at least one possible limitation of the current procedure for identifying regions of missing OHCs. At 6 mm from the apex, a plateau of ∼1.5 mm in extent existed in the CAF obtained from normal-hearing animals. This plateau appears to be related to the geometry of the cochlea and not missing OHCs. Thus at this location and extent, it may be difficult to distinguish missing OHCs from a geometrically induced field problem. One solution may be to present a tone in noise with a frequency gap centered over the plateau and examine the influence of signal level on the amplitude of the CM. If the amplitude of the CM increased, one may conclude the presence of OHCs, whereas if the CM amplitude does not change, it may indicate the absence of functioning OHCs. Other issues requiring further research include determining the range of severity that can be identified by the CAF as well as the ability to distinguish missing OHCs from IHCs.

Conclusions

High-pass noise can be used to limit the contribution of hair cells along the cochlear partition that produce the low-frequency-evoked CM. The contribution of OHCs shifts depending on signal level. As signal level increases, the population of hair cells contributing to the CM shifts from apical to basal hair cells. The increase in amplitude and shape of the CM growth function (CAF) at the round window as a function of high-pass cutoff frequency of the noise, differed from previous investigations examining voltage decay along the longitudinal cochlear axis. Aided by a geometric cochlear model, we suggest that the noise-suppressed response is due to an electric field that projects directly from a source to the round window electrode and not along the longitudinal axis of the cochlea.

APPENDIX

Tissue dissection and staining

x and y coordinates

Seven right-ear gerbil cochleae were harvested. For each cochlea, a small hole was made in the apex, and the stapes was removed from the oval window. A syringe filled with paraformaldehyde was used to perfuse the solution through the oval window. The cochleae were then placed in the paraformaldehyde overnight. After fixation, the cochleae were decalcified in ethylenediaminetetraacetic acid (EDTA) for 2 days and then stored in 1% phosphate-buffered saline (PBS). A razor was used to slice each cochlea into three sections. The cuts were made through the stria vascularis on a plane that paralleled the rise of the basilar membrane from base to apex.

Once each cochlea was in three pieces, the tissue was put in a combination of 1 part Triton to 100 parts 1% PBS for 10 min. The tissue then underwent three 5-min baths of 1% PBS before being placed in a combination of 1 part fetal bovine serum to 10 parts 1% PBS for 10 min. Again, the tissue then had three 5-min baths of 1% PBS. At this point, the tissue was placed in a container that did not allow light to access the tissue. For 30 min, the tissue was placed in a blend of 1 part phalloidin to 10 parts 1% PBS, then underwent three more 5-min baths of 1% PBS. The tissue was then stored in 1% PBS until it was ready to image.

z coordinate

Five right cochleae underwent the same fixing process as previously described. After the fixation process, the bone was picked away around the outside of each cochlea leaving only the modiolus and spiral lamina. The cochlea was then submerged in 1% Osmium for 2 min. This stained the nerve fibers and made the spiral lamina visually pronounced. The spiral lamina was used as the marker for the missing basilar membrane.

Imaging

x and y Cartesian coordinates

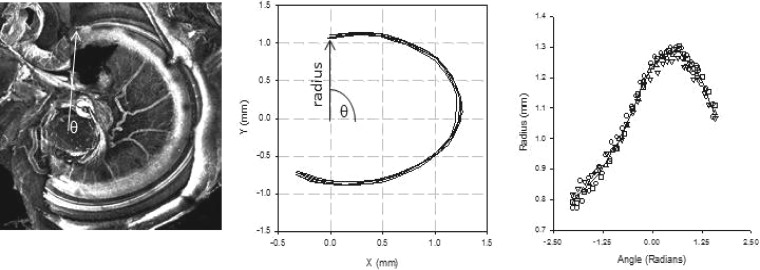
An inverted confocal microscope (Nikon T3 2000U with a 488 nanometer Melles Griot argon laser) using EZ-C1 software was used to image the basilar membrane on each of the three pieces. The investigator focused the microscope at the beginning of the tissue and then at the end of the tissue. This distance was divided into 20 optical segments and images were captured at 4× magnification. The confocal microscope software overlaid all the images and made a composite image for each turn of the cochlea. This allowed for one image where the whole basilar membrane was in focus. A 4× confocal image of the base of the cochlea is shown in Fig. 8 (left panel).

Figure 8.

A 4× image of the basal turn of the gerbil cochlea obtained with a confocal microscope. The arrow points to the beginning of the cochlear partition but also serves as the radius of the cochlear partition rotated around angle theta (θ), located in the center of the modioulus (left panel). Middle panel shows the result of five tracings of the cochlear partition. The coordinates of these tracings were converted to polar coordinates and fit with a cubic spline (right panel).

z Cartesian coordinate (elevation)

The bone was picked away, and the basal side of the cochlea was epoxied to a small square of plastic and adhered to the wheel of a DC motor. A Krohne-Hite 5200 A function generator was connected to the motor and delivered a square-wave pulse that would rotate the wheel 36° when manually triggered. The motor, with cochlea attached, was placed under a Nikon SMZ1500 stereomicroscope that had a Nikon DS-2Mv camera attachment and nis elements f 3.00 imaging software by Nikon. The cochlea was manipulated until it rotated around the central axis of the wheel and was not tilting. After the first picture of the cochlea was taken, the researcher triggered the motor to turn 36°, and another picture was taken. This sequence was repeated for three full rotations.

Image processing and quantification

x and y coordinates

imagej (version 1.37v), was used to alter the brightness and contrast of the images to improve visualization of the basilar membrane. Images were loaded into matlab (MathWorks, Inc.), and a software program was developed to obtain the x and y coordinates along the basilar membrane. First, a computer mouse was positioned over the modiolus and chosen as a center point (base of arrow, Fig. 8, left panel). Next the mouse was moved along the basilar membrane, and points were selected and recorded. This process was repeated four more times to examine and minimize measurement error in the selection of the coordinates. Figure 8, middle panel, shows the x and y coordinates for the five tracings from cochlea in the left panel. From the x and y coordinates, the radius and angle from the modioulus were computed from

$$r=\sqrt{x^2+y^2},$$ (A1)

$$\theta ={\tan }^{-1}\left(\frac{y}{x}\right).$$ (A2)

These are plotted in the right panel of Fig. 8, along with a cubic spline fit to the five angle and radii estimates.

z coordinate

The pictures of the mounted cochleae were uploaded into imagej. A midpoint was taken as the average distance from the right to left side of the cochlea and used to assess the elevation of the spiral lamina in each of the pictures. On each picture of a given cochlea, the elevation of the spiral lamina at the midpoint along the x axis was recorded. In the first 10 pictures of the cochlea, the base spiral lamina height was recorded; in the next 10 pictures, the middle spiral lamina elevation was recorded; and in the last 10 pictures, the apical spiral lamina elevation was recorded. One cochlea was used as a reliability measure and was imaged and analyzed twice. Between the first and second imaging and analyses, it was un-mounted from the motor and other cochleae were imaged. The Pearson correlation between the first and second trials was 0.99. Figure 9 (lower left panel) shows the elevation of the spiral lamina as a function of rotation.

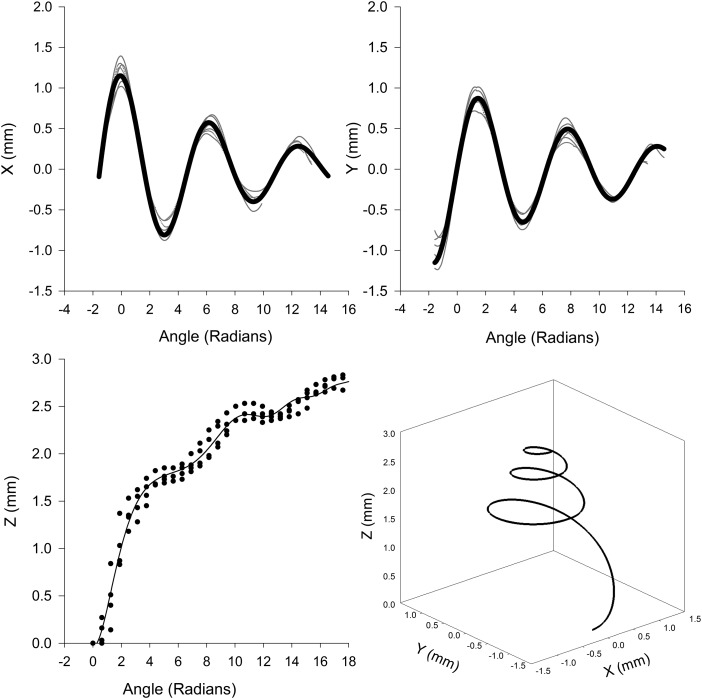
Figure 9.

The top two panels are the values of the x and y coordinates (thin grey lines) as a function of angle theta obtained from the cochlea. The solid dark lines are the fit of Eq. A3. The value of the z coordinate from the cochlea and the corresponding fit of Eq. A3 is illustrated in the bottom left panel. Plot of the parametric equation of thebasilar membrane is illustrated in the bottom right panel.

Parametric equations

For the x and y coordinates, cubic splines were fit to the five replications of each of the basal, middle, and apical turn polar coordinate data. The cubic splines from each turn were attached to each other to make one continuous line for the x coordinate and one line for the y coordinate. These lines represent the x and y coordinates of the basilar membrane as the cochlea spirals from base to apex. The z coordinate did not require stitching because the cochlea was not sectioned to obtain the data.

The x and y coordinate as a function of spiral angle appeared as a decaying sinusoidal function (Fig. 9, top panels). The z coordinate steeply increased with angle of rotation up to about 6 radians, followed by a shallow slope and varying oscillations. The following function was used to fit each of the Cartesian coordinates to the spiral angle,

$$\text{Coordinate}(\theta )=A{e}^{a\theta }\sin (2\pi (f-b\theta )\theta +Ø)+c\theta +d,$$ (A3)

where θ is the angle of rotation. As illustrated in Fig. 9 and as noted by the squared correlation coefficients in Table TABLE III., Eq. A3 fit the Cartesian coordinates well. The lower right panel of Fig. 9 shows a plot of the cochlear partition obtained from the x, y, and z coordinates from Eq. A3.

TABLE III.

Values of the parameters for obtaining the Cartesian coordinates for the cochlear partition.

Coordinate	A	a	f	b	Ø	c	d	R2a
x	1.148	−0.112	−0.162	−0.0002	1.610	0.000	0.000	0.984
y	1.000	−0.900	0.158	−0.00002	0.011	0.000	0.000	0.976
z	−1.951	−0.306	−0.124	−0.016	2.043	0.059	1.713	0.980

^aAdjusted for the number of parameters.

Scala tympani, media, and vestibuli area

The cross-sectional area of scala vestibuli, media, and tympani as a function of distance was obtained from Alec Salt's web site (http://oto2.wustl.edu/cochlea/mrgbvol.htm). An analytic expression was fit to each of the scalae as a function of distance. The area of the scala vestibule was fit by

$$SV=a{e}^{-bx}+c{e}^{-dx},$$ (A4)

where x was the percent distance from base, a = 0.992, b = 0.097, c = 0.017, and d = 0.008. The adjusted R² was 0.972. Scala media was fit with the following function,

$$SM=\frac{a+bx+c{x}^2}{1+dx+e{x}^2},$$ (A5)

where, a = 0.17, b = −0.001, c = 1.657 × 10⁻⁵, d = −0.069, and e = 0.001. The goodness of fit to the data, i.e., the adjusted R², was 0.881. Finally, scala tympani was fit with a similar ratio of polynomial functions to Eq. A5, but with more terms. That is,

$$ST=\frac{a+bx+c{x}^2+d{x}^3+e{x}^4}{1+fx+g{x}^2+h{x}^3+i{x}^4},$$ (A6)

where a = 0.044, b = −0.002, c = 0.001, d = −0.8983 × 10⁻⁵, e = 2.213 × 10⁻⁶, f = −0.285, g = 0.036, h = −0.002, and i = 3.863 × 10⁻⁵. The adjusted R² was 0.987.

Using autocad (http://usa.autodesk.com/autocad/), artificial, digital cross sections were created at 59 discrete points along the length of the basilar membrane (BM) and oriented perpendicular to the BM. The area of each scala was approximated using a circle the area of which was defined by Eqs. A4 through A6. A point on the perimeter of each circle was anchored to the basilar membrane and then rotated into position. The scala vestibuli, media, and tympani are located at 120°, 0°, and 270°, respectively. Using the BM as a guide, autocad interpolated a curved cylinder between each successive circle for each scala.