Molecular Dynamics Trajectory Compression with a Coarse-Grained Model

Abstract

Molecular dynamics trajectories are very data-intensive thereby limiting sharing and archival of such data. One possible solution is compression of trajectory data. Here, trajectory compression based on conversion to the coarse-grained model PRIMO is proposed. The compressed data is about one third of the original data and fast decompression is possible with an analytical reconstruction procedure from PRIMO to all-atom representations. This protocol largely preserves structural features and to a more limited extent also energetic features of the original trajectory.

1 Introduction

Molecular dynamics (MD) simulations are well established for studying the dynamics of macromolecules in the condensed phase, such as proteins, nucleic acids, and polymers. Enabled by ever-increasing computational power, modern simulations are capable of describing the dynamics of more than 10⁵ atoms for up to microsecond time scales [1], [2], [3]. The primary data resulting from such simulations are trajectories that consist of snapshots of the atomic coordinates at fixed time intervals. Because coordinates are typically saved as 4-byte real numbers, a system with 10⁵ atoms simulated for 1 ns with one snapshot per picosecond generates a trajectory file of about 1 gigabyte (GB) in size, and a microsecond-scale simulation of the same system will thus generate terabytes (TB) of data. The management of such large amounts of data, in particular, permanent storage and network transfer, is a major challenge. This is an especially serious issue hindering efforts to develop public simulation databases, such as SimDB [4], Dynameomics [5], the Ascona B-DNA Consortium [6], BioSimGrid [7], and Molecular Dynamics Extended Library [8].

Simulations of biomedical systems often consist of a solute of interest immersed in an explicit representation of the environment, typically aqueous solvent. While the explicit presence of solvent atoms provides physical accuracy during the simulation, the solvent atoms are often not needed for analysis. If only the coordinates of the solute atoms are stored or transferred, the amount of data can be decreased by a typical factor of 2 to 10 depending on the system. While this is a significant reduction, the resulting data for just the solute atoms still amounts to hundreds of GB up to TB for microsecond-scale simulations of large biomolecular systems. Further reduction of the data size requires compression. Loss-less compression can be achieved through the use of general-purpose compression methods [9], [10], [11], such as Lempel–Ziv–Markov chain (LZMA/LZMA2 in 7Zip) [12], gzip [13], bzip2 [14], or RAR [15]. Because atomic coordinate data are typically stored in compact binary form with few easily exploitable redundancies or repetitive patterns, general-purpose methods typically do not perform well when applied directly to trajectory data achieving compression by only 5–25% (see below). It is possible to achieve better compression of MD trajectories when the nature of the trajectory data is taken into account. One such approach is to reorder the coordinate data and transform the reordered data into differences between subsequent frames to enhance the occurrence of repetitive patterns before employing standard compression algorithms. With this method it was possible to compress the trajectory of a small system by about 39% [16]. Further compression was achieved by using a lossy protocol [10] based on the MPEG-4 algorithm [17] commonly used for media streams. In this case, the original trajectory could be compressed by 60% by converting the coordinates to MPEG-4 BIFS scenes [18], [19] and then compressing the scenes via the reduction of the number of bits used to store the numeric data [16]. However, MPEG-4 encoding is computationally expensive and limits a practical application to trajectories of relatively small systems.

Another set of lossy compression algorithms stores trajectory data at reduced precision. This approach is especially effective when the limited variation in typical atomic coordinates is considered. Given a fixed precision, such data can then be stored with much fewer bits than full 32- or 64-bit floating point numbers. For example, coordinate differences between frames could be multiplied by 1000 and then stored as 16-bit integers to achieve a precision of 0.001. These ideas were explored extensively in a recent paper[20] with a practical implementation in the xtc trajectory format that is used by Gromacs[21] and achieves a compression to about a third of the original, full-precision data (see below).

In an alternative approach that considers the nature of MD trajectories more directly, MD trajectories were compressed by reducing a given trajectory to its essential dynamics based on principal component analysis [22]. The essential dynamics technique decomposes a given trajectory into collective modes of fluctuations and then projects the dynamics from the given atomistic trajectory onto the so-called “essential subspace” that is spanned by relatively few collective modes thereby reducing the dimension of the data [23]. Atomistic trajectories are readily recovered through an inverse transformation based on the collective modes stored in the essential dynamics trajectories. For simulations, where the fluctuations of molecular motions involve only relatively limited degrees of freedom, it was possible to cover 99% of the variance of fluctuations in the original trajectory with a relatively small essential subspace resulting in an effective reduction in file size by 94.6% [22]. The average root mean square deviation (RMSD) between the original and back-projected trajectories was only 0.3±0.02 Å. However, for systems where structural fluctuations involved more degrees of freedom, a larger essential subspace was required to capture 99% of the dynamic variance and the compression ratio was lower at 80% [22]. The essential dynamics technique works well for large biomolecular solutes where slow collective modes dominate the dynamic behavior. However, this method is not effective for compressing solvent dynamics, which are dominated by diffusive motions.

In this study, we present an alternative strategy for compressing MD trajectories using coarse-graining (CG). The main idea is to reduce each coordinate frame to a coarse-grained representation during compression. Decompression then involves reconstruction of atomistic representations from the CG model. In principle, this approach can be applied to both solute and solvent parts of a given system, but it relies on the availability of appropriate CG models that allow accurate atomistic reconstructions. Here, we focus on the compression of trajectories of biomolecular solutes and in particular protein systems to take advantage of the recently introduced PRIMO model which provides an intermediate-resolution CG model of proteins [24]. Unlike most other CG models [25], [26], [27], PRIMO was specifically designed to allow accurate and rapid reconstruction of atomistic representations. Popular C_α- or side chain center-based representations require reconstruction of atomistic models with iterative techniques to 1.0 – 2.0 Å RMSD at a cost that may range from seconds to minutes for a single coordinate frame [28], [29], [30]. Such accuracy is generally not sufficient to preserve the essential structural information provided by a fully atomistic trajectory. Furthermore, the computational cost for decompression would be impractical for large trajectories with as many as 10⁶ frames. In contrast, PRIMO maintains quasi-atomistic accuracy at the CG level and allows very fast analytical reconstruction of atomistic models based on the assumption that standard molecular bonding geometries are maintained for the degrees of freedom lost during coarse-graining. PRIMO therefore provides both the accuracy and speed that is required for MD trajectory compression.

In the following, we will first briefly introduce the original PRIMO model, describe model updates, and then present results of using PRIMO for trajectory compression in terms of efficiency, speed, and accuracy.

2 PRIMO Model

The PRIMO coarse-grained model for proteins has been introduced by us earlier [24]. It involves three interaction sites for the backbone (C_α, N, and CO at the center of the carbonyl bond) and up to five sites for the side chains. The level of resolution and location of interaction sites was chosen to allow reconstruction of atomistic sites based on geometric considerations using standard bonding geometries with a minimum number of CG sites. As a result, the PRIMO model as originally published provides an overall reconstruction accuracy of about 0.1 Å RMSD for heavy atoms and very fast reconstruction speeds compared to other CG representations [24].

After publication of the original version of the PRIMO model, we have modified the location of interaction sites for some side chains and the C-terminus. We also adjusted the reconstruction procedure to improve the reconstruction accuracy further. We have also developed a reconstruction procedure for hydrogen atoms that was not available in the first version of PRIMO. Finally, we are also proposing an alternative reconstruction scheme that compromises accuracy to gain improved energetics of the reconstructed structures. The modifications and additions are described in more detail in the following:

2.1 General modifications to the reconstruction protocol

Many atomistic sites are calculated from CG sites and from already reconstructed sites according to internal coordinates (bond distances, angles, and dihedrals). This procedure is called “scheme 1” in the original PRIMO paper [24]. The values for bond distances, angles, and dihedrals are chosen according to average values to reflect standard bonding geometries. Here, we are using updated values (given in Table S1) that slightly improve the overall reconstruction accuracy.

2.2 Isoleucine model and reconstruction

The side-chain interaction site SC1 of isoleucine was moved to C_γ2 while SC2 now reflects the center of geometry between C_γ1 and C_δ1 (see Fig. 1).

Fig. 1.

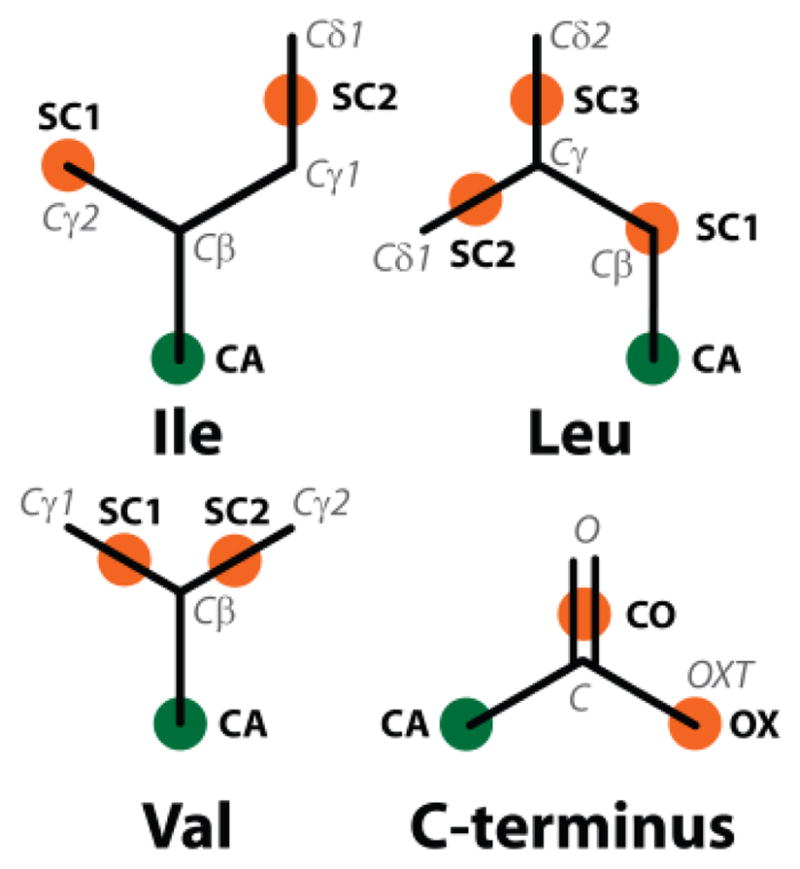
The updated PRIMO CG interaction sites for the side-chain and backbone of amino acids. Orange spheres represent the side-chain interaction sites and green spheres represent the C_α atom on the backbone

Because of the new interaction sites, a new reconstruction scheme was also devised. The resulting reconstruction scheme for isoleucine is more elaborate than for other amino acids because accurate isoleucine reconstruction proved to be more difficult than for other side chains.

The position of C_γ2 is directly given from SC1. Reconstruction of C_β and C_γ1 is achieved by simultaneously solving the geometric relations between C_α, C_β, C_γ1, SC1 (i.e. C_γ2), and SC2 ((C_γ1+C_δ1)/2). For simplification, the reconstruction of C_β and C_γ1 is carried out in a different frame of reference where the C_α-SC1 vector is aligned with the z-axis and C_α is at the origin. This requires an initial transformation of SC1 and SC2 positions and back transformation of the reconstructed C_β and C_γ1 into the original frame of reference once their positions are determined. We begin by assuming that the following distances between atomistic and CG sites are known:

$$\begin{array}{l}\left|{\stackrel{\rightharpoonup }{r}}_{C_{\beta }}-{\stackrel{\rightharpoonup }{r}}_{C_{\alpha }}\right|={\ell }_{BA};\left|{\stackrel{\rightharpoonup }{r}}_{C_{\beta }}-{\stackrel{\rightharpoonup }{r}}_{SC2}\right|={\ell }_{BS2};\left|{\stackrel{\rightharpoonup }{r}}_{C_{\alpha }}-{\stackrel{\rightharpoonup }{r}}_{C_{\gamma 1}}\right|={\ell }_{AG1};\\ \left|{\stackrel{\rightharpoonup }{r}}_{SC1}-{\stackrel{\rightharpoonup }{r}}_{C_{\gamma 1}}\right|={\ell }_{S1G1};\left|{\stackrel{\rightharpoonup }{r}}_{SC2}-{\stackrel{\rightharpoonup }{r}}_{C\gamma 1}\right|={\ell }_{SC2G1};\left|{\stackrel{\rightharpoonup }{r}}_{C_{\beta }}-{\stackrel{\rightharpoonup }{r}}_{C_{\gamma 1}}\right|={\ell }_{BG1}.\end{array}$$

Furthermore, C_α-C_β-SC1 and C_α-C_β-C_γ1 angles are assumed to be known and are calculated as:

$$cos(C_{\alpha }{C}_{\beta }SC1)=\frac{({\stackrel{\rightharpoonup }{r}}_{C_{\alpha }}-{\stackrel{\rightharpoonup }{r}}_{C_{\beta }})·({\stackrel{\rightharpoonup }{r}}_{SC1}-{\stackrel{\rightharpoonup }{r}}_{C_{\beta }})}{\left|{\stackrel{\rightharpoonup }{r}}_{C_{\alpha }}-{\stackrel{\rightharpoonup }{r}}_{C_{\beta }}\right|\times \left|{\stackrel{\rightharpoonup }{r}}_{SC1}-{\stackrel{\rightharpoonup }{r}}_{C_{\beta }}\right|};cos(C_{\alpha }{C}_{\beta }{C}_{CG1})=\frac{({\stackrel{\rightharpoonup }{r}}_{C_{\alpha }}-{\stackrel{\rightharpoonup }{r}}_{C_{\beta }})·({\stackrel{\rightharpoonup }{r}}_{C_{\gamma 1}}-{\stackrel{\rightharpoonup }{r}}_{C_{\beta }})}{\left|{\stackrel{\rightharpoonup }{r}}_{C_{\alpha }}-{\stackrel{\rightharpoonup }{r}}_{C_{\beta }}\right|\times \left|{\stackrel{\rightharpoonup }{r}}_{C_{\gamma 1}}-{\stackrel{\rightharpoonup }{r}}_{C_{\beta }}\right|}.$$

In the transformed coordinate system, the positions for C_α and SC1 are (0,0,0) and (0,0, z_sc1), respectively. With the bond and angle relationships given above one obtains the z-coordinate of C_β as

$$z_{C_{\beta }}=\frac{{\ell }_{BA}^2-{\ell }_{BA}{\ell }_{BS1}cos(C_{\alpha }{C}_{\beta }SC1)}{z_{SC1}}$$ (1)

while the y-coordinate of C_β is given as:

$$y_{C_{\beta }}=\frac{1}{2y_{sc2}}({\ell }_{BA}^2-{\ell }_{BS2}^2+x_{SC2}^2+y_{SC2}^2+z_{SC2}^2-2z_{C_{\beta }}{z}_{SC2})-\frac{z_{SC2}}{y_{SC2}}{x}_{C_{\beta }}$$ (2)

and if y_Cβ is rewritten as y_Cβ = a + bx_Cβ the x-coordinate of C_β becomes:

$$x_{C_{\beta }}=\frac{1}{1+b^2}\left[-ab\pm {(z_{C_{\beta }}^2+{\ell }_{BA}^2-a^2-b^2{z}_{C_{\beta }}+b^2{\ell }_{BA}^2)}^{1/2}\right]$$ (3)

Similarly, the coordinates for C_γ1 are described according to:

$$z_{C_{\gamma 1}}=\frac{{\ell }_{AG1}^2-{\ell }_{S1G1}^2+z_{SC1}^2}{2z_{SC1}}$$ (4)

$$y_{C_{\gamma 1}}=\frac{1}{2y_{SC2}}({\ell }_{AG1}^2-{\ell }_{SC2G1}^2+x_{SC2}^2+y_{SC2}^2+z_{SC2}^2-2z_{C\gamma 1}{z}_{SC2})-\frac{x_{SC2}}{y_{SC2}}{x}_{C_{\gamma 1}}$$ (5)

$$x_{C_{\gamma 1}}=\frac{1}{x_{C\beta }}\left[-y_{C_{\beta }}{y}_{C_{\gamma 1}}-z_{C_{\beta }}{z}_{C_{\gamma 1}}+{\ell }_{BA}^2-{\ell }_{BA}{\ell }_{BG1}cos(C_{\alpha }{C}_{\beta }{C}_{CG1})\right]$$ (6)

Because Eq. 3 has two solutions, there are two sets of coordinates for C_β and C_γ1 that are consistent with the given bond distances and angles. The two solutions correspond to different chiral isomers (2S,3S and 2S,3R), only one of which (2S,3S) is found in biologically relevant isoleucine. The correct isomer is selected based on a positive value of the improper dihedral between C_α, C_γ2, C_γ1, and C_β atoms. So far we have assumed standard bond lengths and angles to be used in Eqs. 1–6. The reconstruction of isoleucine can be improved further by taking advantage of correlations between different bonds and angles. For example, C_α-C_γ1 and C_α-SC2 bond distances are correlated as shown in Fig. S2. Other correlations are shown in Figs. S1 (C_α-C_β vs. C_α-SC2 distances), S3 (C_α-C_β-C_γ1 angles vs. C_α-SC2 distances), S4 (C_β-SC2 vs. C_α-SC2 distances), S5 (SC1-C_γ1 vs. SC1-SC2 distances), and S6 (C_α-C_β-SC1 vs. C_α-SC2-SC1 angles). We used here interpolated values for bond and angles according to the average correlations shown as blue lines in Fig. S1–S6.

Once positions for C_β and C_γ1 are determined, the position of C_δ1 can be obtained using the C_γ1-SC2 vector.

2.3 Leucine model and reconstruction

The SC1 position of leucine now coincides with C_β while SC2 and SC3 are determined from the centers of geometry between C_γ, C_δ1 and C_γ, C_δ2, respectively.

The C_γ atom is reconstructed based on the distance to C_β, the angle between C_γ, C_β, SC2, and the dihedral between C_γ, C_β, SC2, and SC3. C_δ1 and C_δ2 are then reconstructed using the C_γ-SC2 and C_γ-SC3 vectors, respectively.

2.4 Valine model and reconstruction

The SC1 interaction site of valine was changed to the center between C_β and C_γ1 and a new interaction site (SC2) was placed at the center between C_β and C_γ2.

Similar to C_γ in leucine, the C_β atom is reconstructed based on the coordinates of C_α, SC1, and SC2 with. C_γ1 and C_γ2 are reconstructed based on the C_β-SC1 and C_β-SC2 vectors, respectively.

2.5 Threonine reconstruction

The reconstruction protocol for threonine was modified to improve the accuracy of the C_β reconstruction. In the new protocol, C_β is now estimated based on the distances and angles relative to C_α, SC1, and SC2. O_γ1 is subsequently reconstructed using the C_β-SC1 vector.

2.6 C-terminus model and reconstruction

An additional PRIMO site, OX, was introduced for charged C-termini at one of the carboxylate oxygen atoms to improve reconstruction accuracy.

Previously, the C-terminal carbonyl atoms were reconstructed assuming that they were in the same plane as the C_α and N particles resulting in a less accurate reconstruction of the carbonyl atoms [24]. With the additional particle, the position of C can be reconstructed based on the distance to CO, the angle between C, CO, OX, and the dihedral between C, CO, OX, and C_α. Atom O was then reconstructed from the position of the C atom.

2.7 Hydrogen atom reconstruction

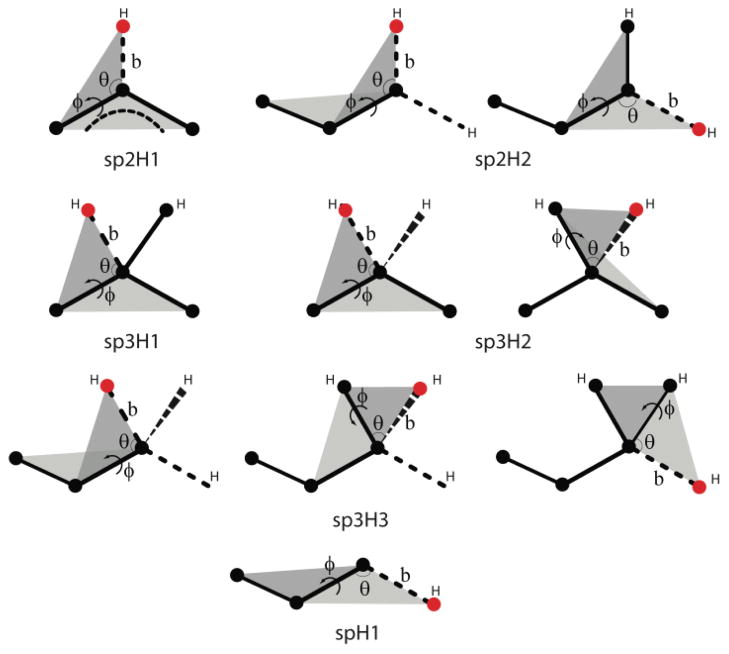
The original PRIMO paper did not describe a reconstruction method for hydrogen atoms. We have since devised such a procedure, which is used here during trajectory decompression. Hydrogen atoms were categorized into subgroups according the hybridization state of the connected heavy atom as suggested by Li et al. [31]. The reconstruction protocol for all types of hydrogens is based on internal coordinates relative to heavy atoms (see Fig. 2). For example, the coordinate of H_ζ in phenylalanine, which is of sp2H1 type, is reconstructed based on the bond distance to C_ζ, the angle between H_ζ, C_ζ, C_ε1, and the dihedral between H_ζ, C_ζ, C_ε1, and C_ε2. H_δ21 in asparagine, which is an sp2H2 hydrogen, is reconstructed based on the bond distance to N_δ2, the angle between H_δ21, N_δ2, C_γ, and the dihedral between H_δ21, N_δ2, C_γ, O_δ1. H_β in valine, an sp3H1 hydrogen, is reconstructed using the bond distance to C_β, the angle between H_β, C_β, C_γ1, and the dihedral between H_β, C_β, C_γ1, and C_γ2. H_β1 in arginine, which is of type sp3H2, is reconstructed based on the bond distance to C_β, the angle between H_β1, C_β, C_γ, and the dihedral between H_β1, C_β, C_β, and C_α. H_β1 in alanine, an sp3H3 hydrogen, is reconstructed based on the bond distance to C_β, the angle between H_β1, C_β, C_α, and dihedral between H_β1, C_β, C_α, and N. Finally, H_γ1 in cysteine, an spH1 hydrogen, is reconstructed based on the bond distance to S_γ, the angle between H_γ1, S_γ, C_β, and the dihedral between H_γ1, S_γ, C_β, and C_α. Other hydrogen atoms were reconstructed in an analogous fashion. Assumed standard bonds, angles, and dihedrals are given in Table S2.

Fig. 2.

Reconstruction sequence for hydrogen atoms of the following categories: sp3H1, sp3H2, sp3H3, sp2H1, sp2H2, and spH1. Note: black circles represent the atomistic site that has been reconstructed, while red ones are the ones being reconstructed. Parameters, such as bond distance (b), bond angle (θ), dihedral angle (ϕ), being used for the reconstruction are also illustrated.

2.8 Alternative reconstruction scheme

The reconstruction protocol described above maximizes reconstruction accuracy and largely maintains a one-to one correspondence between PRIMO and atomistic representations. We found that despite the high accuracy, reconstructed structures often have relatively high energies due to unfavorable bonding or van der Waals energies (see ‘Results’ section).

In the case of two bonded atoms, A and B, where one of the atoms is known, e.g. B, and a PRIMO site S is located at the center between A and B, the other atom, in this case A, is calculated in the original protocol according to what is called “scheme 2” [24]:

$${\overrightarrow{r}}_A={\overrightarrow{r}}_B+2{\overrightarrow{r}}_{BS}$$ (7)

This scheme preserves the one-to-one mapping between atomistic and CG sites but does not guarantee that the distance between A and B, r⃗_AB, is near the equilibrium value for the bond between A and B. Alternatively, r⃗_A can be calculated according to the normal vector along AB, n̂, and the equilibrium bond length between A and B, ℓ_AB:

$${\stackrel{\rightharpoonup }{r}}_A={\stackrel{\rightharpoonup }{r}}_B-{\ell }_{AB}\ast \widehat{n}$$ (8)

With Eq. 8, the one-to-one CG/atomistic mapping is violated but the reconstructed structures are energetically better behaved. In the alternative reconstruction protocol, Eq. 8 is applied to reconstruct the carbonyl oxygens on the backbone C.

This idea can be taken further to enforce not just equilibrium bond distances but also standard bond angles and torsion angles. Some side chain heavy atoms are reconstructed with such a scheme in the alternative reconstruction protocol even in cases where the atomistic sites are otherwise defined by PRIMO sites (see Table S4). In this alternate protocol the atoms given in Table S4 are reconstructed based on the given internal coordinates. Other atoms not given in the table are reconstructed as in the standard scheme.

3 Test Sets

Trajectory compression was tested with all-atom trajectories of ubiquitin (22 ns, 110,000 frames, 76 residues, 1231 atoms, file size: 1.52 GB) and the B1 domain of protein G (50 ns, 250,000 frames, 56 residues, 855 atoms, file size: 2.41 GB). The trajectories stem originally from explicit solvent simulations described previously [32], but the trajectories used here contained only the dynamics of the solute atoms.

An additional test set consisted of a temperature replica exchange simulation of (AAQAA)₃ that was used primarily to examine the reconstruction accuracy of hydrogen bonds and resulting helical propensities after decompression. The replica exchange simulation was carried out using the program CHARMM [33] along with the MMTSB toolset [34] with the CHARMM22 force field [35] including CMAP [36], [37], [38]. The solvent was represented by the GBSW implicit solvent model [39]. Eight temperature windows exponentially spaced from 300 to 500 K were used in the simulation (300, 322, 347, 373, 401, 432, 464, and 500K). Each replica was simulated for 37.5 ns with exchange attempts at 0.75 ps intervals (50,000 frames).

Reconstruction accuracy with the updated PRIMO model was tested with a previously introduced set of 601 non-homologous single-chain PDB structures ranging from small protein fragments to very large structures with more than 800 residues and covering a wide variety of native folds [24], [40]. Structures 1A2S, 1BA9, 1BUY, 1DBD, 1E6U, 1EHJ, 1HCD, 1PCN, and 2A3D were removed from the original set because of non-canonical chirality in N-terminal residues and isoleucine, threonine side chains. Accuracy of hydrogen reconstruction was tested with a set of selected structures from high-resolution X-ray crystallography and neutron diffraction established by Li et al. [31] to allow comparison with other methods (see Table S3).

4 Results and Discussion

4.1 Reconstruction accuracy with updated PRIMO model

The accuracy of the updated PRIMO model and modified reconstruction procedure was tested by converting a set of structures (see Methods section) to the PRIMO level and subsequently reconstructing atomistic structures. The root mean square deviation (RMSD) between the initial and reconstructed models then reflects reconstruction accuracy. Table 1 shows the accuracy for different parts of protein structures. The overall accuracy is improved significantly from about 0.1 Å in the original model to 0.06 Å as a result of improvements in both backbone and side chain reconstruction. While most amino acids show small improvements, improvements that are more significant were found for cysteine, isoleucine, leucine, threonine, and valine.

TABLE 1.

Heavy-Atom Reconstruction accuracy

	No. of Residues	RMSD (Å)	RMSD (Å) from Ref [22]
All/Average	57,685	0.057 (0.020)	0.099 (0.04)
Backbone	57,685	0.022 (0.021)	0.046 (0.02)
Side chains	57,685	0.076 (0.027)	0.131 (0.06)
ARG	3,326	0.043 (0.032)	0.056 (0.04)
ASN	3,127	0.012 (0.007)	0.011 (0.01)
ASP	3,922	0.017 (0.010)	0.018 (0.01)
CYS	1,612	0.088 (0.055)	0.105 (0.06)
GLN	2,828	0.055 (0.033)	0.067 (0.05)
GLU	4,542	0.079 (0.045)	0.098 (0.05)
HIS	1,520	0.063 (0.037)	0.075 (0.04)
ILE	3,555	0.144 (0.118)	0.244 (0.15)
LEU	5,778	0.023 (0.013)	0.205 (0.13)
LYS	4,702	0.057 (0.034)	0.067 (0.04)
MET	1,404	0.067 (0.038)	0.067 (0.04)
PHE	2,467	0.062 (0.030)	0.059 (0.03)
PRO	3,118	0.105 (0.078)	0.110 (0.07)
SER	4,254	0.114 (0.057)	0.114 (0.06)
THR	3,954	0.034 (0.014)	0.136 (0.05)
TRP	909	0.055 (0.022)	0.053 (0.03)
TYR	2,192	0.055 (0.029)	0.059 (0.03)
VAL	4,475	0.025 (0.020)	0.291 (0.16)

Reconstruction accuracy for side-chain and backbone heavy atoms with updated PRIMO model and reconstruction procedure. Standard deviations are given in parentheses. Significantly improved values over the original version are highlighted in bold.

Results for the new hydrogen reconstruction procedure are presented in Table 2 and compared with force-field based hydrogen reconstruction (HBUILD function in CHARMM[33]) and the Hydrogen Atom ADdition (HAAD) method recently introduced by Li et al.[31]. The overall reconstruction accuracy with PRIMO is 0.19 Å, which is only slightly worse than HAAD and force field based hydrogen reconstruction with CHARMM. As with HBUILD and HAAD, the accurate reconstruction of spH1-type hydrogens is problematic. The positions of these hydrogens, involving hydroxyl-hydrogens in tyrosine, serine, and threonine, depend strongly on interactions with the environment, which are neglected by the internal geometry-based reconstruction procedure used here. It should be emphasized again that the hydrogen reconstruction protocol described here does not involve any iterative steps as with HBUILD and HAAD so that full atomistic reconstruction from the PRIMO model can be accomplished with minimal computational cost.

TABLE 2.

Hydrogen Reconstruction accuracy

	HBUILD (Å)	HAAD (Å)	PRIMO (Å)
All/Average	0.158 (0.188)	0.134 (0.192)	0.192 (0.209)
sp3H3	0.227 (0.184)	0.182 (0.201)	0.240 (0.199)
sp3H2	0.116 (0.072)	0.081 (0.069)	0.194 (0.158)
sp3H1	0.112 (0.075)	0.109 (0.085)	0.118 (0.078)
sp2H2	0.108 (0.063)	0.107 (0.061)	0.131 (0.061)
sp2H1	0.099 (0.058)	0.079 (0.021)	0.126 (0.060)
spH1	0.989 (0.614)	1.036 (0.538)	1.028 (0.614)

Reconstruction accuracy of hydrogen atoms with PRIMO protocol compared with HBUILD (in CHARMM) and HAAD[31]. Standard deviations are given in parentheses.

4.2 Trajectory compression with PRIMO

We will now discuss the application of the PRIMO model for the compression of MD trajectories in terms of efficiency and accuracy of structural and energetic properties extracted from decompressed trajectories.

4.2.1 Compression efficiency

Compression efficiency measures the ratio of the compressed data to the original data and is one of the key performance features of any compression algorithm. We evaluated compression efficiencies for two MD trajectories of typical protein systems (see Methods section). Note that these trajectories only contained the coordinates for the solute since PRIMO does not provide a coarse-grained model for solvent. The results shown in Table 3 demonstrate that conversion of an atomistic trajectory to PRIMO results in a significant reduction to slightly more than a third of the original data size. The reduction directly reflects the reduced number of interaction sites in PRIMO vs. fully atomistic models. The compression with PRIMO is significantly better than with general-purpose compression algorithms, which only reduce the data by 6–25%. However, PRIMO compression by itself does not quite reach the level of compression that can be achieved with PCAZIP based on essential subspace projection (up to 78% reduction in data size). It is interesting to compare these results also with the compression achieved with the Gromacs xtc format. Conversion from DCD format to xtc results in similar compression ratios as with PRIMO (about 30%) with very fast compression and decompression speeds.

TABLE 3.

Compression/Decompression Performance

	Compression Ratio (%)	Compression Speed (MB/sec)	Decompression Speed (MB/sec)
PRIMO	34.6	483.8	21.5
	36.4	442.3	21.9
PRIMO +RAR	27.2	24.5	17.3
	27.8	23.4	17.5
PRIMO +PCAZIP	11.2c	79.4	11.0a
	11.7d	82.6	12.4a
PRIMO +xtci	11.6	184.9	20.0
	12.4	169.4	20.0
PCAZIP	22.2e	17.6	3.9a
	22.3f	23.5	5.7a
	35.5g	17.6	2.4a
	35.2h	22.0	3.5a
PCAsuite	22.2e	0.15	0.53
	22.3f	0.22	0.72
bzip2	93.6	4.8	10.0
	92.7	4.8	10.1
7Zip	83.0	3.5	11.2
	80.4	3.4	11.3
RAR	77.2	9.0	32.3
	74.8	9.1	33.1
Gzip	91.6	15.9	77.6
	90.7	15.3	77.3
xtci	31.9	128.2	106.3
	32.0	126.6	102.8

Compression performance of the PRIMO-based method in comparison with PCAZIP, PCAsuite, Bzip2/bunzip2, 7Zip (LZMA2), RAR, and gzip/gunzip for ubiquitin (first values) and protein G (second values) trajectories. Compression ratio is calculated as percentage of reduced file size relative to original size. Compression/decompression speeds are relative to original data size and determined on a tmpfs file system (RAM disk) on a Linux workstation with an Intel Core i7 2.8 GHz CPU.

^aoutput in binary format (see text);

^c410 eigenvectors/99% variance of fluctuations;

^d301 eigenvectors/99% variances;

^e795 eigenvectors/99% variance;

^f567 eigenvectors/99% variance;

^g1275 eigenvectors/99% variance;

^h900 eigenvectors/99% variance;

ⁱcompression and decompression speed between Gromacs trj and Gromacs xtc formats using trjconv script from Gromacs 4.5.4

PRIMO-based compression relies on a reduction of the spatial degrees of freedom that does not prevent a combination with general-purpose loss-less compression algorithms such as RAR, compression algorithms that exploit correlations between subsequent frames, such as PCAZIP, or other methods, such as conversion to xtc format. We therefore also tested the combination of PRIMO with RAR, PCAZIP, or xtc. As Table 3 shows, further compression is possible resulting in a 73% reduction with PRIMO/RAR, nearly 90% with PRIMO followed by PCAZIP or conversion to the xtc format. For comparison, we also tested PCAZIP in combination with RAR and found only marginal improvement (data not shown).

4.2.2 Compression/decompression speed

The second important feature of any compression algorithm is the speed for compression and decompression, which becomes critical when large amounts of trajectory data are to be processed. We report here compression and decompression speeds based on timing tests with a RAM disk where the files were read from main memory instead of a hard drive. The speeds given here therefore focus on the computational throughput of the compression/decompression algorithms. When trajectory data is stored on disks, the maximum throughput is limited by the type of disk hardware, which may reduce the RAM-disk based performance reported here in actual applications.

The speed for compressing data is highest with PRIMO-based compression (around 450 MB/s, see Table 3) because the conversion from an atomistic representation to the CG level requires very little computation. The other algorithms are significantly slower because they involve more expensive calculations, especially for the loss-less, general-purpose compression algorithms where compression speeds are between 3 and 15 MB/s. As would be expected, the combination of PRIMO compression with RAR or PCAZIP slows down compression speeds. But because of the smaller amount of data after PRIMO compression that needs to be processed by either RAR or PCAZIP the effective compression speeds still reach 24 and 80 MB/s, respectively.

In the context of MD trajectory databases or archives where compress trajectory data may need to be decompressed frequently to allow analysis calculations, the data decompression speed is of greater practical importance. As the data in Table 3 shows, decompression is slower than compression for PRIMO- and PCAZIP-based algorithms while the opposite is the case for loss-less compression algorithms. The PRIMO decompression speed is about 21 MB/s. This is remarkable because it means that complete all-atom reconstruction of a single frame can be accomplished in well under a millisecond. Furthermore, PRIMO decompression is much faster than decompression with PCAZIP, which achieves at best 6 MB/s. It should be noted that the decompression speeds for PCAZIP in Table 3 are a result of code optimizations of the distributed PCAZIP code and a switch to a more I/O-friendly binary output format. The original PCAZIP code was in fact much slower, by a factor of about 40. In principle, decompression with PCAZIP should be fast because it involves only a single matrix multiplication between the eigenvectors and subspace projections. However, the actual performance is limited by slow main memory access times that become dominant when large amounts of data are processed. For comparison we also show results for PCAZIP when the number of eigenvectors is increased to match the compression ratio of PRIMO. In that case, the compression speeds remain essentially the same but decompression becomes slower. Furthermore, we tested another implementation of PCA-based compression, PCAsuite[41]. To use this program we first had to convert our DCD trajectories to AMBER format but the times listed in Table 3 do not include the format conversion. PCAsuite achieves very similar compression ratios but its speed was found to be much slower than PCAZIP and in fact any other method that we tested here.

The combination of PRIMO with RAR or PCAZIP reduces the decompression speeds because of the additional calculations to about 17 MB/s with PRIMO/RAR and 11–12 MB/s with PRIMO/PCAZIP.

A decompression speed of 15 MB/s means that it takes about 3 minutes to decompress the 50 ns trajectory of protein G with 250,000 frames while microsecond trajectories would take on the order of hours for decompression. While such decompression speeds may or may not be acceptable, the performance could be improved through distributed storage and parallel decompression. PRIMO-based compression is ideally suited for parallel processing because compression/decompression of one frame does not depend on other frames. In contrast, other compression methods, in particular the PCAZIP method, take advantage of correlations between different frames of the trajectory data and become less efficient when applied to fragments of a given trajectory.

4.2.3 Loss of information after compression

PRIMO-based compression is a lossy compression algorithm, which means that after compression and decompression with PRIMO the original atomistic coordinates are not recovered exactly. As described above, the reconstruction accuracy from PRIMO to full atomistic detail is on average 0.06 Å RMSD for heavy atoms and about 0.2 Å RMSD for hydrogen atoms. In this section we will examine whether this accuracy is sufficient to preserve the essential structural and energetic features of the original trajectory.

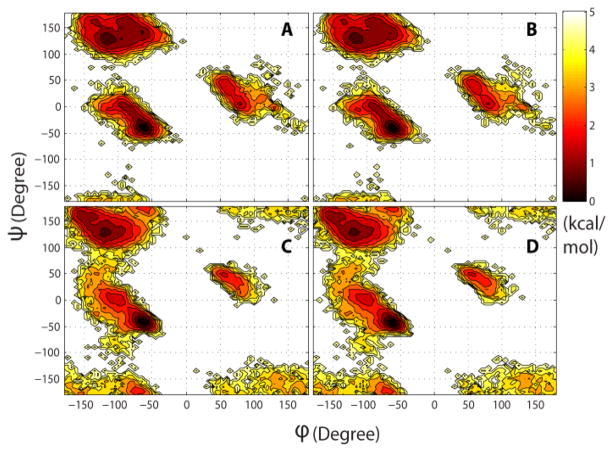
We begin by discussing the effect on structural features. Table 4 compares the calculation of common structural properties from the original and reconstructed trajectories. The deviations between average values are very small, well below 1% for all but two properties, and individual values along the trajectory exhibit very high correlation. Slightly larger but still small deviations are found for χ₁ torsion angles and for the average helical content. The deviation in χ₁ reflects uncertainties in reconstructing side chain atoms while the calculation of the helical content is very sensitive to the placement of hydrogens since it is based on a minimum distance hydrogen bonding criterion. However, comparison with the standard deviations given in Table 4 suggests that even the slightly larger deviations for χ₁ and helical content are on the order of statistical uncertainties. Further comparisons of structural properties extracted from the original and reconstructed trajectories are shown in Figs. 3, 4, and 5. Fig. 3 shows backbone torsion φ/ψ sampling that is virtually identical to the original data when analyzed from reconstructed trajectories. Fig. 4 compares the calculation of experimental observables: NMR residual dipolar couplings (RDCs) and root mean square fluctuations (RMSF) that are directly related to crystallographic B-factors. Again, there are no appreciable differences between the original and reconstructed trajectories. Finally, we calculated helical content of (AAQAA)₃ as a function of residue and temperature from implicit solvent replica exchange folding simulations (see Fig. 5). In this comparison, there are also only minor deviations after compression/decompression of the trajectory.

TABLE 4.

Preservation of Structural Properties

	Orig.	Recon.	Δ	r	m	n
RMSD (Å)	1.937 (0.183)	1.938 (0.182)	+0.05%	1.000	0.994	0.01
	1.545 (0.183)	1.545 (0.182)	+0.05%	1.000	0.997	0.01
Radius of gyration (Å)	11.92 (0.072)	11.92 (0.071)	−0.01%	1.000	0.999	0.01
	10.77 (0.075)	10.76 (0.075)	−0.04%	1.000	0.998	0.02
SASA (Å2)	5083.9 (76.49)	5085.2 (77.03)	+0.03%	0.997	1.004	−20.0
	3863.8 (78.99)	3865.2 (78.87)	+0.03%	0.998	0.997	13.8
φ RMSD (o)	19.36 (1.77)	19.33 (1.74)	−0.12%	0.995	0.977	0.42
	22.97 (4.52)	22.91 (4.50)	−0.28%	0.999	0.996	0.03
ψ RMSD (o)	23.46 (3.18)	23.43 (3.18)	−0.14%	0.997	0.997	0.04
	23.97 (5.01)	23.89 (4.99)	−0.35%	0.999	0.994	0.06
χ1 RMSD (o)	47.67 (7.12)	48.14 (7.0)	+1.00%	0.987	0.969	1.95
	54.57 (8.13)	54.98 (8.13)	+0.75%	0.989	0.988	1.06
Average helical content	0.150 (0.015)	0.152 (0.015)	+1.57%	0.860	0.844	0.03
	0.231 (0.024)	0.235 (0.024)	+1.75%	0.839	0.824	0.05
Fraction of native contacts	0.850 (0.028)	0.849 (0.028)	−0.16%	0.912	0.908	0.08
	0.885 (0.041)	0.886 (0.040)	+0.13%	0.962	0.944	0.05

Average structural properties calculated before (“original”) and after compression/decompression (“reconstructed”) using PRIMO from trajectories of ubiquitin (first values) and protein G (second values). RMSD values are calculated for heavy atoms after superposition with respect to the first frame of the trajectory. Radius of gyration was calculated based on all atoms, including hydrogen atoms. Solvent-accessible surface area (SASA) calculations involved all heavy atoms and were performed with CHARMM[33]. Helical content was calculated based on backbone N(i)-H – O-C(i-4) distances of less than 2.6 Å. Native contacts were defined as residue separations of less than 4.2 Å for residues separated by at least 5 residues along the polypeptide chain in model 1 of the experimental NMR structure ensemble. Standard deviations are given in parentheses. Original and reconstructed values were compared with a linear regression analysis to obtain correlation coefficients (r), slope (m), and intercept (n).

Fig. 3.

Potential of mean force from sampling of backbone torsion angles (φ: C-N-C_α-C, ψ: N-C_α-C-N) from original (A, C) and reconstructed (B, D) trajectories of ubiquitin (A, B) and the B1 domain of protein G (C, D).

Fig. 4.

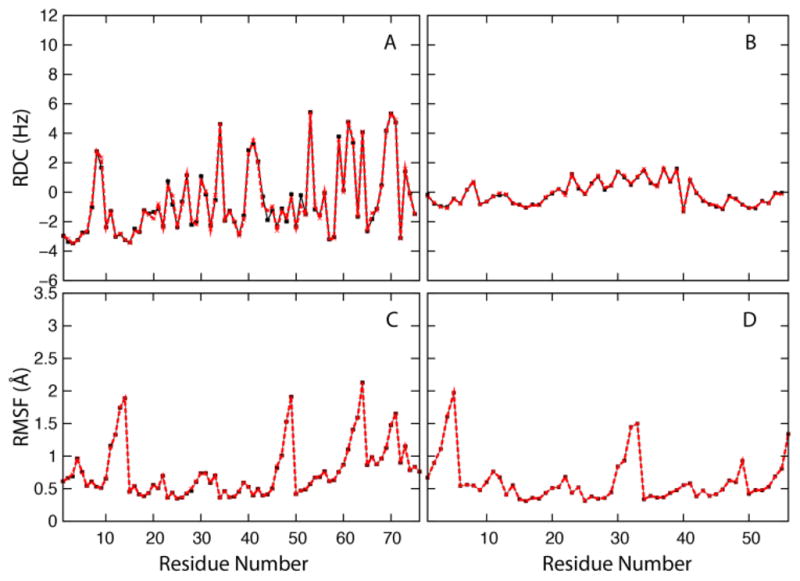
Top: Residual dipolar coupling (RDC) between backbone N and H nuclei from trajectories of ubiquitin (A) and the B1 domain of protein G (B) according to 〈D〉 = D_a {〈3 cos² θ − 1〉 + 3/2R 〈 sin² θ cos 2ϕ〉} where Da is the principal axis component, R is the rhombicity of the alignment tensor (Da = 5 Hz and R=0), θ and φ is the angle between the NH vector of each residue with respect to the alignment tensor, and the angular brackets denote conformational averaging. Bottom: Root mean square atomic fluctuation (RMSF) with respect to average structure from trajectories of ubiquitin (C) and protein G B1 domain (D). In all plots, black lines with square symbols show quantities calculated from the original trajectories while red lines with crosses show quantities calculated from the reconstructed trajectories.

Fig. 5.

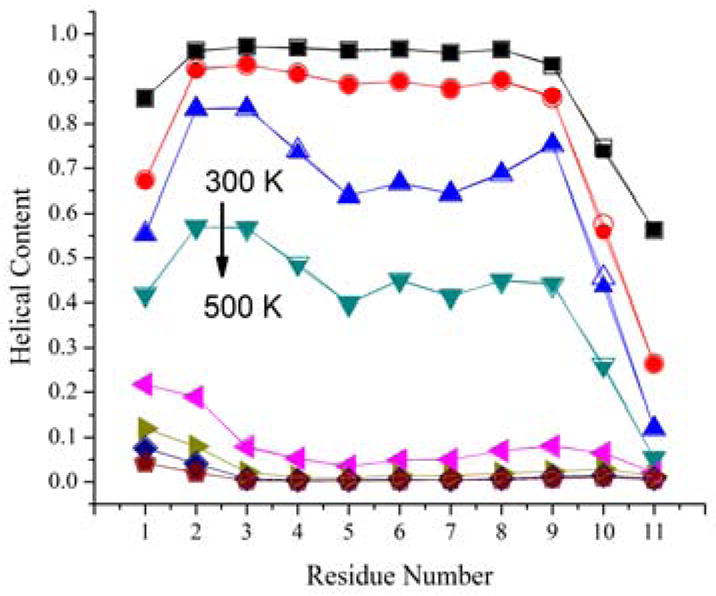
Residue helical content of (AAQAA)₃ peptide as a function of temperature calculated from a temperature replica exchange simulations. 8 temperature windows exponentially spaced from 300 to 500 K were used in the simulation (top to bottom: 300, 322, 347, 373, 401, 432, 464, and 500K). Closed symbols show quantities from the original structures, open symbols from reconstructed structures.

A more stringent test is the preservation of energetic features. In order to address this point, we compared all-atom energies from the CHARMM force field[35] before and after compression/decompression. The results are shown in Table 5. It can be seen that the total energies are not well preserved with the standard reconstruction protocol. There is poor preservation of bonded energies (bonds, angles, Urey-Bradley, dihedrals, improper torsions) and Lennard-Jones energies. Furthermore, there are significant outliers with very large energies due to van der Waals clashes. This, of course, reflects the sensitivity of packing and bonding interactions to sub-Å perturbations. In contrast, CMAP, electrostatic, and solvation energies are highly correlated before and after reconstruction since they are less sensitive to minor structural deviations. The overall unsatisfactory preservation of energetic properties with the standard reconstruction protocol prompted us to explore an alternative reconstruction protocol where certain side chain heavy atoms are reconstructed based on standard bonding geometries rather than from PRIMO sites (see Methods). The resulting protocol has somewhat lower reconstruction accuracy for heavy atoms (see Table S5) of around 0.1 Å RMSD but achieves similar hydrogen atom reconstruction accuracy as before (see Table S6). Using the alternate protocol for reconstruction, the energetic accuracy is significantly improved. In particular, the correlation of bonds and angles is improved and gross outliers are now avoided for the Lennard-Jones potential. Further improvement in energetic accuracy after reconstruction can be gained by following the reconstruction by force field–based minimization. We tried various protocols and found that 5 steps of steepest descent under restraints on C_α and C_β atoms to maintain backbone and sidechain orientations were sufficient to significantly improve the energetic accuracy (see Table 5) of the total energy (to correlation coefficients of 0.38–0.40 for the total energy), due primarily to better-correlated Lennard-Jones energies. Correlations of bonds and angles actually became slightly worse after minimization. The reason is likely that the snapshots taken from an MD simulation at 300 K are not at the energetic minimum (corresponding to 0 K). This affects bonds and angles most during short minimization runs where the gradients are largest. We should also point out that the minimization step adds significantly to the overall reconstruction cost because now the full atomistic potential has to be evaluated several times during the minimization iterations. Consequently, the decompression speed including such minimization is significantly lower, to less than 1 MB/sec.

TABLE 5.

ENERGETIC CONSERVATION

		Ubiquitin				Protein G
		r	m	n	Δ	r	m	n	Δ
Total	Std	0.02	**	**	**	0.12	0.79	119	139
	Alt.	0.15	0.53	−1197.8	84.4	0.19	0.49	−732	54.6
	Min	0.38	0.38	−1829.1	27.1	0.40	0.36	−1096	21.9
Bond	Std	0.09	1.25	555.1	155.9	0.15	1.21	293	77.6
	Alt.	0.50	0.64	84.6	13.3	0.40	0.59	81	13.5
	Min	0.35	0.15	30.4	10.8	0.38	0.15	25	8.8
Angle	Std	0.22	0.75	98.0	54.8	0.26	0.64	76	33.1
	Alt	0.35	0.47	58.7	22.7	0.49	0.42	43	13.0
	Min	0.34	0.25	82.2	16.9	0.45	0.23	46	12.3
Urey-Bradley	Std	0.11	1.63	113.4	56.5	0.08	0.61	72	22.2
	Alt	0.19	0.21	20.3	5.2	0.07	0.09	16	4.8
	Min	0.06	0.02	12.4	4.1	0.06	0.03	7.0	2.3
Dihedral	Std	0.55	0.67	95.0	9.0	0.50	0.57	100	7.7
	Alt.	0.56	0.65	99.4	8.6	0.57	0.52	105	6.3
	Min	0.55	0.60	109.0	8.4	0.58	0.49	109	6.1
Improper	Std	−0.02	0.00	0.7	4.0	0.08	0.00	0.3	3.3
	Alt	0.01	0.00	0.7	4.0	0.03	0.00	0.3	3.3
	Min	0.09	0.01	4.1	4.0	0.09	0.01	3.1	3.3
CMAP	Std	0.98	0.98	−1.3	0.9	0.99	0.99	0.1	0.8
	Alt	0.98	0.98	−1.3	0.9	0.99	0.99	0.1	0.8
	Min	0.96	0.92	−10.2	1.8	0.98	0.96	−5.5	0.9
L.-J.	Std	−0.01	**	**	**	0.22	0.90	19	42.2
	Alt	0.15	0.97	76.7	79.0	0.22	1.07	52	50.3
	Min	0.60	0.71	−89.0	12.4	0.66	0.67	−68	8.9
Electrostatic	Std	0.95	0.97	44.4	24.6	0.95	0.87	−54	26.6
	Alt	0.91	0.95	−1.2	32.3	0.93	0.85	−68	30.9
	Min	0.91	0.93	13.6	31.4	0.94	0.84	−54	29.5
ASP	Std	0.88	0.89	8.8	0.7	0.93	0.93	4.2	0.6
	Alt	0.86	0.86	10.8	0.8	0.91	0.92	4.7	0.6
	Min	0.86	0.86	11.2	0.8	0.91	0.92	4.7	0.6
GB	Std	0.96	1.00	−18.0	20.0	0.97	0.92	−87	18.7
	Alt	0.93	0.98	−38.6	26.0	0.96	0.91	−97	21.7
	Min	0.93	0.98	−31.6	25.6	0.96	0.90	−98	21.4

Comparison of all-atom CHARMM force field energies obtained from the frames of the original and reconstructed atomistic trajectories of ubiquitin and protein G. The correlation coefficient (r), slope (m), and intercept (n) (in kcal/mol) resulting from linear regression are given as well as the root mean square deviation (Δ, in kcal/mol) after subtracting the difference in average energies. ‘Std’ refers to the new high-accuracy reconstruction protocol introduced here. ‘Alt’ is the alternative protocol (see Methods section) and ‘Min’ refers to reconstruction with the alternative protocol followed by a brief energy minimization with CHARMM (5 steps steepest descent with positional restraints on C_α and C_β atoms.

^**: Unmeaningful large values. ASP: Atomic solvation potential; CMAP: cross-correlation map; GB: Generalized Born; L.-J.: Lennard Jones

One common energetic analysis based on simulation snapshots follows the MM-PB/SA (or MM-GB/SA) scheme[42] where free energies are estimated as a sum of solute vacuum energies and free energies of solvation from a continuum model (PB or GB). This approach has become popular for estimating relative conformational free energies [43] or binding free energies[44]. To test whether the energetics of the snapshots from the reconstructed trajectory match the original structures, we first clustered the snapshots of the original trajectory. For each cluster, we then calculated average MMGB/SA free energy estimates before and after reconstruction. Table 6 lists those energies relative to the cluster with the lowest free energy for each method. The results show that the standard reconstruction scheme does not provide useful total energy estimates due to outliers with large bond and Lennard-Jones energies. However, better results are obtained with the alternative reconstruction scheme. For ubiquitin, the lowest free energy cluster is correctly identified with and without minimization but only after minimization all five clusters are ranked correctly. Nevertheless, some of the total average energies still deviate significantly from the energies for the original trajectory, by as much as 11 kcal for cluster 2. For protein G, even after minimization the correct ranking is not fully recovered. While clusters 1 and 2 have very similar low energies based on the original trajectory, cluster 2 has a significantly higher energy after reconstruction. We also compared our results with PCAZIP-based compression and found that in this case the overall energetic accuracy is worse, apparently mostly due to problems with unfavorable bonded interactions (Table 6). This is still the case when more modes are included in PCAZIP to match the PRIMO compression ratio. However, non-bonded interactions are reproduced well when a larger number of eigenvectors is used to match the PRIMO compression ratio.

TABLE 6.

MM-GB/SA Analysis

Ubiquitin		#3 (446)	#4 (279)	#5 (151)	#1 (67)	#2 (57)
Total [kcal/mol]	Orig	0.0	0.9	3.3	6.2	22.8
	Std	382.7	9335.1	11.9	91.4	0.0
	Alt	0.0	10.2	8.1	10.5	27.7
	Min	0.0	2.9	5.9	9.1	11.2
	PCAZIPa	0.0	9.3	58.5	114.0	193.5
	PCAZIPb	0.0	5.3	12.9	55.7	78.3
Internal [kcal/mol]	Orig	8.1	10.2	0.0	10.5	27.7
	Std	0.0	19.7	35.1	95.5	14.8
	Alt	3.3	4.8	4.8	12.7	0.0
	Min	0.5	0.9	0.0	4.8	0.8
	PCAZIPa	2.7	0.0	43.5	107.4	163.9
	PCAZIPb	0.0	0.9	3.0	49.4	53.9
Nonbonded [kcal/mol]	Orig	0.0	3.0	8.4	5.2	20.1
	Std	405.9	9338.6	0.0	19.1	8.4
	Alt	0.0	8.7	6.6	1.2	31.0
	Min	0.0	2.5	6.5	4.9	10.9
	PCAZIPa	0.0	11.9	17.7	9.2	32.3
	PCAZIPb	0.0	4.4	9.9	6.3	24.4
Protein G		#2 (118)	#1 (255)	#3 (426)	#4 (45)	#5 (155)
Total [kcal/mol]	Orig	0.0	0.6	2.2	8.5	14.1
	Std	25.9	8.3	0.0	0.0	17.4
	Alt	12.3	0.0	0.2	4.4	8.7
	Min	14.4	0.0	6.3	7.5	16.9
	PCAZIPc	55.7	31.7	0.0	141.6	109.3
	PCAZIPd	3.0	0.0	2.5	42.8	24.3
Internal [kcal/mol]	Orig	6.4	5.5	0.0	4.8	3.9
	Std	23.2	18.9	0.0	7.9	2.5
	Alt	6.5	4.4	0.0	4.6	2.1
	Min	2.8	3.0	0.0	3.1	0.4
	PCAZIPc	62.2	38.5	0.0	133.4	97.6
	PCAZIPd	9.3	4.2	0.0	37.3	11.9
Nonbonded [kcal/mol]	Orig	0.0	1.5	8.6	10.1	16.6
	Std	13.3	0.0	10.7	2.7	25.5
	Alt	10.2	0.0	4.6	4.2	10.9
	Min	14.7	0.0	9.4	7.4	19.5
	PCAZIPc	0.3	0.0	6.8	15.1	18.5
	PCAZIPd	0.0	2.1	8.8	11.8	18.7

MM-GB/SA analysis of conformational sub-states identified through K-means clustering. Clusters were generated from 1000 snapshots for each of the ubiquitin and protein G trajectories using the MMTSB Tool Set[45] using a cluster radius of 1 Å. For ubiquitin all clusters are shown; for protein G a sixth cluster with only one element was omitted. Relative MM-GB/SA energy estimates (total, internal, and non-bonded energies) are shown for standard and alternative reconstruction protocols (with and without minimization). Results for reconstructed snapshots are compared with the snapshots extracted from original trajectories and with snapshots reconstructed with the PCAZIP method.

^a795 eigenvectors/99% variance;

^b1275 eigenvectors99% variance;

^c567 eigenvectors/99% variance;

^d900 eigenvectors/99% variance

It is clear from this analysis that the level of energetic accuracy that is maintained after decompression may not be sufficient for some applications. A possible solution would be to store certain energies along with the compressed trajectory. For example, in order to facilitate MMGB/SA analysis one could simply store total solute energy components for each snapshot.

5 Conclusions

In this study, we have presented the novel idea of using a coarse-grained model as a means for compressing atomistic molecular dynamics simulations. We find that using PRIMO as the coarse-grained model it is possible to achieve significant reduction in size to about 30% of the original trajectory at fast compression and decompression speeds. Because of a highly accurate reconstruction protocol from PRIMO to a full atomistic representation it is possible to largely preserve structural features and with some limitations even energetic properties. Because PRIMO-based compression does not exploit redundancies between subsequent frames, it is possible to achieve further reduction in data size through combination with general purpose programs such as RAR or with PCA-based compression. We suggest PRIMO-based trajectory compression as an attractive option for the archival of MD data and in particular the development of MD databases.

A program for compressing and decompressing molecular dynamics trajectories as described in this paper can be obtained by contacting the authors.

Biographies

Yi-Ming Cheng is currently a postdoctoral fellow at Michigan State University focusing on the development of coarse-grained simulation methods. He received B.S. and M.S. degrees from National Chung Cheng University, Taiwan and a Ph.D. degree from National Taiwan University. His graduate research was focused on the application of femtosecond laser spectroscopy to probe the early time-domain kinetics of several types of chemical reactions. He then worked as a postdoctoral associate at the National Tsing Hua University, Taiwan focusing on transition metal complexes suited for organic light emitting diode (OLED), both with experimental and theoretical approaches.

Srinivasa Murthy Gopal is currently a postdoctoral fellow at Michigan State University. He received a B.S. degree from Bangalore University, India, a M.S. degree in Physics from the Indian Institute of Technology Madras, India, and a PhD degree in Physics from Dortmund University, Germany. in 2007. His research interests broadly encompass computational biophysics and include coarse-grained models, protein-protein interactions and protein structure prediction and refinement.

Sean M. Law is a senior graduate student in the Department of Biochemistry & Molecular Biology of Michigan State University. He graduated from York University, Toronto, Canada with a B. S. in Biology and Applied Mathematics. His research interests include molecular dynamics simulations, enhanced sampling methods, and protein-DNA interactions.

Michael Feig is an Associate Professor of Biochemistry & Molecular Biology and Chemistry and an Adjunct Professor of Computer Science & Engineering at Michigan State University. He received a Diplom degree in Physics from the Technical University of Berlin, Germany, and a Ph.D. in Computational Chemistry from the University of Houston. He is a member of the American Chemical Society, the Protein Society, and the Biophysical Society. His current research interests revolve around the development and application of molecular dynamics simulation techniques for the study of biomolecular systems. His research is currently funded by both NIH and NSF and has resulted in a total of 70 mostly peer-reviewed publications.