Molecular Modeling to Provide Insight into the Substrate Binding and Catalytic Mechanism of Human Biliverdin-IXα Reductase

Abstract

Human biliverdin-IXα reductase (hBVR-A) catalyzes the conversion of biliverdin-IXα to bilirubin-IXα in the last step of heme degradation and is a key enzyme in regulating a wide range of cellular responses. Though the X-ray structure of hBVR-A is available including cofactor, a crystal structure with a bound substrate would be even more useful as a starting point for protein-structure based inhibitor design, but none has been reported. The present study employed induced fit docking (IFD) to study the substrate binding modes to hBVR-A of biliverdin-IXα and four analogues. The proposed substrate binding modes were examined further by performing molecular dynamics (MD) simulations followed by Molecular Mechanics Poisson-Boltzmann Surface Area (MM-PBSA) calculations. The predicted binding free energies for the five biliverdin-IXα analogues match well with the relative potency of their reported experimental binding affinities, supporting that the proposed binding modes are reasonable. Furthermore, the ternary complex structure of hBVR-A binding with biliverdin-IXα and the electron donor cofactor NADPH obtained from MD simulations was exploited to investigate the catalytic mechanism, by calculating the reaction energy profile using the quantum mechanics/molecular mechanics (QM/MM) method. Based on our calculations, the energetically preferred pathway consists of an initial protonation of the pyrrolic nitrogen on the biliverdin substrate followed by hydride transfer to yield the reduction product. This conclusion is consistent with a previous mechanistic study on human biliverdin IXβ reductase (hBVR-B).

1. Introduction

Heme is a prosthetic group utilized by hemoproteins including hemoglobin, myoglobin, and cytochromes. The conversion of heme to bilirubin occurs in a pathway sequentially catalyzed by two enzymes, heme oxygenase (HO) and biliverdin reductase (BVR). Regulation of that pathway controls homeostasis of heme, biosynthesis of pigments, and oxidative stress.^1-3 Human HO1 catalyzes the oxidative ring opening of heme at its α meso bridge carbon, generating CO, which may be an important neurotransmitter,⁴ and a biliverdin structural isomer designated biliverdin IXα (Figure 1).⁵ Other biliverdin structural isomers, IXβ, IXγ, and IXδ (Figure 1), have been produced by various human HO1 mutants.⁵ Biliverdin-IXα reductase (BVR-A), often simply called biliverdin reductase A, catalyzes the regiospecific addition of hydrogen to the reducible C10 in the γ-methylene bridge of biliverdin-IXα to produce bilirubin-IXα, which is subsequently converted to glucuronide conjugates by bilirubin glucuronosyl transferase for excretion by the hepatobiliary system.⁶ Biliverdin-IXβ reductase (BVR-B), a relatively nonspecific enzyme, catalyzes the reduction of the IXβ, IXγ, and IXδ isomers of biliverdin. However, it is not capable of catalyzing the reduction of biliverdin-IXα due to steric hindrance during substrate binding.⁷ BVR-B is less important than BVR-A in human metabolism, since the HO cleavage produces exclusively IXα isomers of biliverdin.⁸

Figure 1.

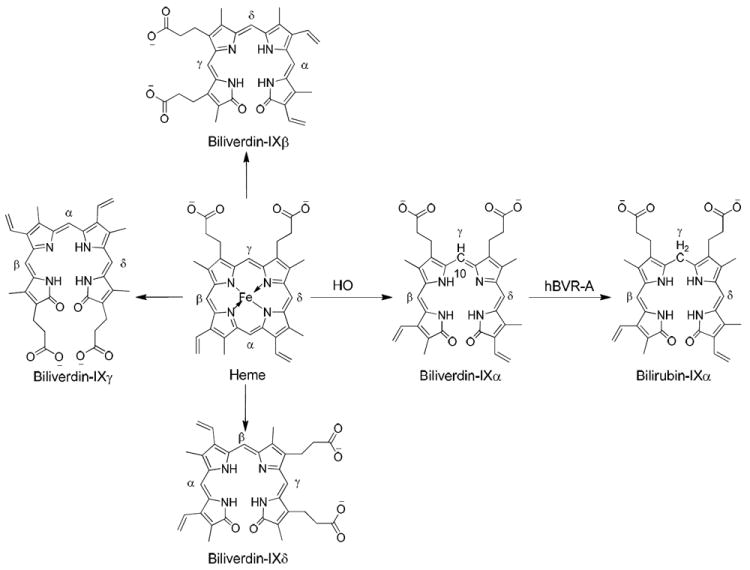
A schematic representation of the heme degradation pathway.

Bilirubin-IXα is a major physiologic antioxidant and cytoprotectant which can protect cells from a 10,000-fold excess of H₂O₂ through a redox-cycling mechanism.⁹ Thus, cellular depletion of bilirubin-IXα increases tissue levels of reactive oxygen species leading to apoptosis. Furthermore, low serum levels of bilirubin-IXα increase the chances of coronary artery disease. However, high levels of bilirubin-IXα are also cytotoxic. A high level of bilirubin-IXα can cause clinical jaundice in neonates and excessive production of bilirubin-IXα in the brain may result in kernicterus causing major brain damage. Since human BVR-A (hBVR-A) is the key enzyme which modulates bilirubin-IXα levels it is highly relevant to the above-mentioned cellular functions. Studies in recent years further have led to the identification of hBVR-A as a pivotal enzyme in cell-signaling cascades through distinct mechanisms.¹⁰ Its pleiotropic functions in cellular signaling and regulation of gene expression have been reviewed.¹¹ It has emerged as a dual-specificity kinase (Ser/Thr and Tyr) in the insulin-signaling pathway, which controls functions such as glucose metabolism, cell growth, and differentiation.¹² Its involvements have been recognized most recently in the regulation of an inflammatory response to endotoxins,¹³ in modulating aging through adjusting the cellular oxidative status,¹⁴ in protecting against cardiomyocyte apoptosis,¹⁵ and in the cell response to stress that is commonly found in neurodegenerative disorders such as Alzheimer’s disease.¹⁶ Since hBVR-A is important to a wide range of cellular functions, it is a potential therapeutic target for many diseases.¹⁷

hBVR-A is an oxidoreductase displaying a high degree of regiospecificity for reduction of C10 in the γ-methylene bridge of biliverdin-IXα. During the reaction, hBVR-A uses one proton and two electrons from a pyridine nucleotide cofactor; therefore it most likely forms a ternary complex with biliverdin-IXα and the cofactor. Though the X-ray structure of hBVR-A is available including cofactor, a crystal structure with a bound substrate would be even more useful as a starting point for protein-structure based inhibitor design, but none has been reported. Such structural information could provide useful guidance for understanding substrate binding and specificity. There is, however, some experimental information available on cofactor binding and specificity. hBVR-A is unique in its recognition of cofactors with a different pH optimal for catalysis: β-nicotinamide adenine dinucleotide (NADH) is used in the lower pH range of 6.7-6.9, whereas β-nicotinamide adenine dinucleotide phosphate (NADPH) is used at the higher pH value of ~8.7.¹⁸ This dual cofactor and dual pH-dependent behavior has been explained by the evidence of a distinct cofactor activation mechanism, in which inorganic phosphate can assist NADH to interact with BVR-A in the same way that the 2’-phosphate of NADPH acts.¹⁹ However, the lack of a clearly defined substrate binding mode has slowed investigations on the catalytic mechanism of this particular enzymatic reduction.

Herein, we report the binding modes of biliverdin-IXα and four analogues, obtained via induced fit docking (IFD) and simulations of the five systems in explicit solvent using molecular dynamics (MD). We carried out Molecular Mechanics Poisson-Boltzmann Surface Area (MM-PBSA) calculations for the snapshots collected from MD simulations to obtain binding free energies for the five biliverdin analogues. The method of using in sequence molecular docking, MD simulations, and MM-PBSA analysis has been extensively explored to predict the binding mode of ligand–protein complexes.^20,21

In previous research, the proposed catalytic mechanism of hBVR-A has been suggested to be either a two-step mechanism²² or a concerted reaction² (Figure 2). In principle the two-step mechanism can involve the hydride transfer first, from the nicotinamide C4 position to the biliverdin C10, and then subsequent protonation to yield bilirubin-IXα. Alternatively, protonation of the pyrrolic nitrogen could occur first followed by hydride transfer. In a previous mutagenesis study, Whitby et al. proposed Tyr97 in rat BVR-A to be the proton source and suggested that the catalysis is driven by hydride transfer from NADPH, since Tyr97Ala or Tyr97Phe substitution only reduced catalytic activity by ~50%.²³ Whitby et al. did not reach a conclusion on whether the reaction steps were concerted or sequential. By contrast, Smith et al. used quantum mechanics/molecular mechanics (QM/MM) methodology to study human BVR-B and concluded that for that isoform hydride transfer occurs after protonation of the pyrrolic N.²² To evaluate which pathway is energetically preferred for hBVR-A, we calculated the QM/MM reaction energy profile, using structures obtained from the MD simulations.

Figure 2.

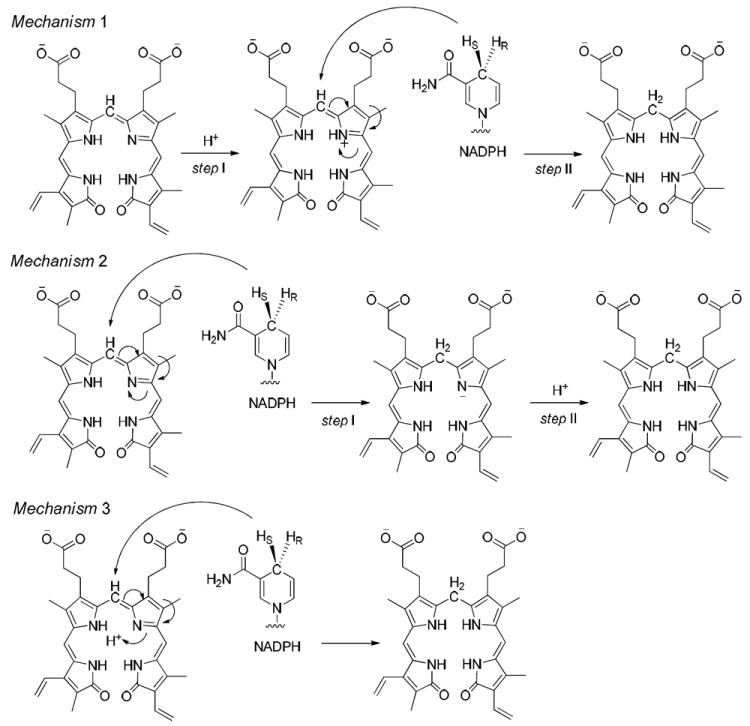
The three possible catalytic mechanisms for hBVR-A. Mechanism 1 represents protonation first followed by hydride transfer. Mechanism 2 represents hydride transfer first followed by protonation. Mechanism 3 represents the concerted reaction.

2. Computational methods

2.1 Initial structure preparation

To date, several BVR-A crystal structures including NAD(P)H have been determined,^7,18,23 but there is only one crystal structure available for human BVR-A in complex with NADPH (PDB code 2H63 at 2.7 Å resolution). The structure is a tetramer consisting of four equivalent chains (A, B, C and D). Chain A, which is comprised of a protein fragment of residues 6-291 and the NADPH cofactor, was selected as the starting structure for our calculations. Since two amino acids in the protein fragment are missing, Glu195 and Asp196, the starting structure was reconstructed by comparative modeling using the Prime program.²⁴ The final structure without any gaps in the protein fragment was used for flexible docking to construct the ternary complexes of protein, NADPH and substrate.

Biliverdin-IXα (I) and its four open-chain tetrapyrrole analogues (Figure 3), including mesobiliverdin-XIIIα (II), 12-ethyl-mesobiliverdin-XIIIα (III), mesobiliverdin-IVα (IV), and α,α,α’,α’-tetramethyl-mesobiliverdin-XIIIα (V), were used for investigation of ligand-protein interactions and structure-activity relationships.²⁵ The initial three-dimensional (3D) structure of substrate I was obtained from a crystal structure of nonproductive binding of I with hBVR-B (PDB code 1HE2 at 1.2 Å resolution)⁷. In the crystal structure, substrate I adopts a helical porphyrin-like conformation which is similar to the global minimum found in careful systematic conformational studies of biliverdin and other open-chain tetrapyrroles.^26,27 The 3D structures of the other four biliverdin analogues were built based on the conformation of substrate I.

Figure 3.

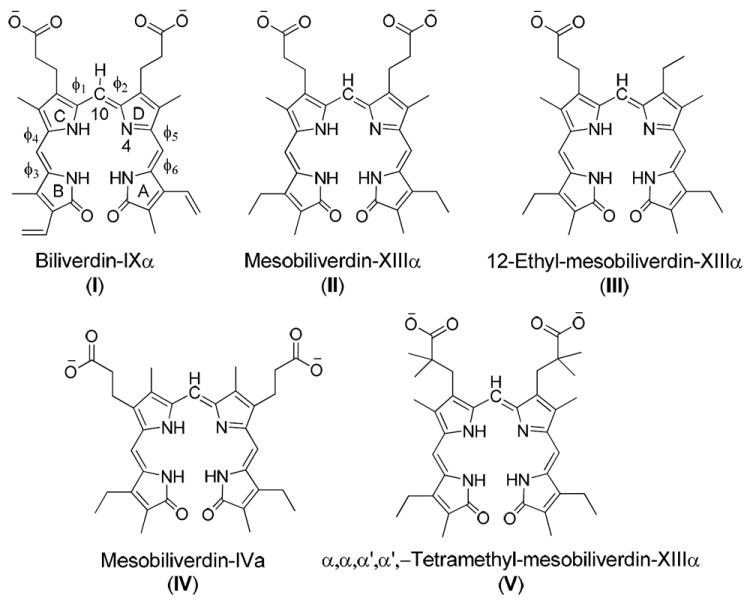
Structures of the five biliverdin reductase substrates considered in this work.

2.2 Induced fit docking (IFD)

The ternary complex consisting of the protein chain, NADPH, and the substrate was constructed by IFD implemented in the Schrödinger Suite.²⁸ The original crystal structure is only a binary complex without any substrate binding in the catalytic site, and we found that the narrow cavity is too limited to accommodate a large substrate such as substrate I. The protein must undergo substantial conformational changes during ligand binding. IFD is an algorithm that accounts for both ligand and protein flexibility by iteratively combining flexible ligand docking into a rigid protein and flexible protein structure prediction. IFD first utilizes softened-potential force fields (with scaling factor of 0.5) to dock a flexible ligand into a rigid protein binding pocket with the Glide program.²⁹ Since the side chain of Tyr98 protrudes into the binding pocket and blocks attempts at substrate docking due to steric hindrance, we trimmed the side chain through mutation of Tyr98 to Ala. After initial docking, the best predicted binding pose is used for protein structure prediction via the Refinement module of the Prime program, in which any residues having at least one atom within 5 Å of the ligand are treated as flexible, while all other residues are held fixed. Residue 98 was mutated back from Ala to Tyr during protein structure prediction. Each refined protein structure is ranked by total Prime energy, and the top-ranked protein structure is then used for redocking of the ligand with the Glide program, using a hard (conventional) potential function without scaling.

2.3 Partial charges and force fields assignments

To calculate the partial charges required for force field calculations on the ternary complex, the geometries of the open-chain tetrapyrrole substrates and of cofactor NADPH were separately optimized at the Hartree-Fock level with the 6-31G* basis set using the Gaussian03 program.³⁰ Partial atomic charges were assigned based on the optimized structures and fitted with the RESP procedure.³¹ The atom types were assigned using the ANTECHAMBER module in Amber9.³² The AMBER ff03 all atom force field³³ was used for the protein and the general AMBER force field³⁴ was used for parameters for the substrates and cofactor.

2.4 Molecular dynamics simulations

The final best-ranked ternary complex structures from IFD were minimized and used for molecular dynamics simulations. The models were solvated with TIP3P³⁵ water molecules in a truncated octahedron periodic box. The distance between the box walls and the protein was set to 10 Å. The systems were neutralized by adding the corresponding number of counterions (Na⁺) using the LEaP module.

Energy minimizations and MD simulations were performed using the Amber9 package.³⁶ Energy minimization was conducted in four steps. First, only water molecules and counterions were allowed to move. Next, the movement was extended to the hydrogen atoms. After that, constraints were only retained on the backbone C_α’s in the protein. Finally, all atoms were allowed to move freely. In each step, energy minimization was carried out by a combination of the steepest descent method for 1000 steps followed by the conjugate gradient method for 4000 steps. After minimization, each system was used for a MD simulation which consisted of thermalization, equilibration, and production stages. The systems were first gradually heated from 0 to 303 K over 100 ps while maintaining a constant number of particles, volume, and temperature (NVT conditions). Then, the systems were maintained at a temperature of 303 K using a Langevin thermostat³⁷ with a coupling time constant of 5.0 ps^-1 for the rest of the equilibration and for all subsequent production runs. All subsequent stages were carried out in the isothermal isobaric ensemble (NPT conditions) with a target pressure of 1.0 atm and a pressure coupling time constant of 1.0 ps. In the equilibration stage, the systems were first equilibrated for 400 ps while maintaining the force constants of 4.0 kcal mol^-1 Å^-2 on the restrained atoms, the backbone C_α atoms in the protein, to allow for thorough solvation of the complex and to prevent structural collapse. Then, the systems were fully equilibrated without any restraints for another 400 ps. Finally, 3.6 ns unrestrained production simulations were conducted for each system using an integration time step of 2.0 fs. During the production stage, coordinates were saved every 5000 time steps, to be used for energy calculations and structure evaluation. The convergence of energies, temperature, and pressure of the systems, and the root-mean-square deviation (RMSD) of the backbone C_α’s in the protein were used to monitor and verify the stability of the systems. All the MD simulations were performed employing periodic boundary conditions with a 10 Å cutoff for nonbonded interactions, and the particle-mesh Ewald (PME) method³⁸ was used for a suitable treatment of long range electrostatic interaction. The SHAKE algorithm³⁹ was used to constrain the covalent bonds containing hydrogens.

2.5 Binding free energy calculations

Multiple snapshots were generated from the production phase of the MD simulations. For every snapshot, after stripping off the water molecules and counterions, the free energy was calculated for the tetrapyrrole substrate, binary complex, and ternary complex. The substrate binding free energy was computed as:

$$\mathrm{\Delta }{G}_{\mathrm{bind}}=G_{\mathrm{ternary\; complex}}-(G_{\mathrm{binary\; complex}}+G_{\mathrm{substrate}})$$ (1)

where G_{ternary complex}, G_{binary complex}, and G_substrate represent the free energies of the ternary complex, binary complex, and substrate averaged over 360 snapshots from the 3.6 ns MD production runs.

The binding free energy, which was calculated using the MM-PBSA procedure, contains an enthalpic and an entropic contribution:

$$\mathrm{\Delta }{G}_{\mathrm{bind}}=\mathrm{\Delta }H-T\mathrm{\Delta }S$$ (2)

TΔS is the entropy contribution, and the enthalpy of binding ΔH is composed of ΔG_MM, the change in the molecular mechanics free energy upon ternary complex formation, and ΔG_solv, the solvated free energy contribution:

$$\mathrm{\Delta }H=\mathrm{\Delta }{G}_{\mathrm{MM}}+\mathrm{\Delta }{G}_{\mathrm{solv}}$$ (3)

The molecular mechanics energy ΔG_MM is further divided into internal, van der Waals, and electrostatic energy in the gas phase:

$$\mathrm{\Delta }{G}_{\mathrm{MM}}=\mathrm{\Delta }{G}_{\mathrm{int}}+\mathrm{\Delta }{G}_{\mathrm{vdW}}+\mathrm{\Delta }{G}_{\mathrm{elec}}$$ (4)

in which the internal term, including the bond, angle, and torsional angle energies, remains the same after binding, whereas the intermolecular van der Waals and electrostatic energies change noticeably.

The solvation free energy is divided into a polar and a nonpolar part,

$$\mathrm{\Delta }{G}_{\mathrm{solv}}=\mathrm{\Delta }{G}_{\mathrm{solv}­\mathrm{pol}+}\mathrm{\Delta }{G}_{\mathrm{solv}­\mathrm{nonpol}}$$ (5)

where ΔG_solv-pol is the electrostatic contribution to the solvation energy, and ΔG_solv-nonpol is the nonpolar solvation term. Here, the polar contribution was calculated by solving the Poisson-Boltzmann (PB) equation⁴⁰ as implemented in Amber9. Grid spacing of 0.5 Å was employed for the cubic lattice, and 360 linear iterations were performed. The values of the interior dielectric constant and exterior dielectric constant were set to 1 and 80, respectively.

The nonpolar solvation energy ΔG_solv-nonpol was calculated from the solvent-accessible surface area (SASA) using the hard-sphere atomic model. The probe radius of the solvent was set to 1.4 Å. The atomic radii for the solute were taken from the PARSE parameter set.⁴¹ ΔG_solv-nonpol is determined using,

$$\mathrm{\Delta }{G}_{\mathrm{solv}­\mathrm{nonpol}}=\gamma (\mathrm{SASA})+\beta$$ (6)

where the surface tension γ and the offset β were set to the standard values of 0.00542 kcal mol⁻¹ Å⁻² and 0.92 kcal/mol, respectively.

Normal-mode analysis (NMA) is useful for estimating the change in solute entropy during ligand association; however, the NMA calculation is considered to be problematic and time-consuming. The NMA approach also does not take into consideration the solvent entropy. In addition, the structural modifications on the five substrates in the present study are relatively small, and they all have the same open-chain tetrapyrrole structure. Based on previous studies,^42,43 the entropy differences should be very small and NMA would not greatly improve the correlation between the experimental K_m and the calculated binding free energy. Thus, the calculation of the solute entropy term has been omitted in the present study.

To obtain a detailed view of the substrate binding, the interaction energies were further decomposed into contributions from each hBVR-A residue and cofactor NADPH. Due to the high computational demand of PB calculations, the residue-based pair-wise interactions were computed using the Molecular Mechanics Generalized Born Surface Area (MM-GBSA) decomposition process implemented in Amber9. In contrast to the MM-PBSA approach, the polar contribution to the solvation free energy (ΔG_solv-pol) was computed using the generalized Born (GB) model.⁴⁴

2.6 QM/MM calculations

The QM/MM calculations were performed using the QSite program.⁴⁵ For the QM region, geometries were optimized using the hybrid density functional B3LYP^46-48 with the LACVP* basis set. Relative energies for the QM region were obtained by performing single point calculations at the B3LYP/LACV3P+** level. The OPLS 2005 force field was used for the MM region. The above computational method can be described as B3LYP/LACV3P+**/OPLS_2005//B3LYP/LACVP*/OPLS_2005. For certain reaction steps, potential energy surface scans were performed at the B3LYP/LACVP*/OPLS_2005 level. The scanned bond distances were varied by a stepsize of 0.1 Å and constrained geometry optimizations were performed at each step with the scanned bond distance fixed. The applicability of QM/MM methods for studying the mechanisms of enzymatic reactions has been previously reviewed in depth.^49-52 The QM/MM protocol as implemented in QSite has been shown to give small errors for relative energies,^53-61 in particular for enzymatic barriers, which are typically accurate within 2-3 kcal/mol compared to experiment.

The last snapshot from the MD simulation for the hBVR-A/NADPH/I complex was taken as the starting geometry for QM/MM calculations. The water molecules within 5 Å of the protein surface were retained while the waters beyond 5 Å as well as the counterions were removed to reduce computational cost. From this snapshot, after minimization with the OPLS2005 force field, a H₂O molecule forms a hydrogen bond with N4 of the substrate, which is the only basic pyrrolic nitrogen that can be protonated during the reaction. It is not likely for a neutral H₂O to itself act as an acid since the resulting OH⁻ would be quite unstable in a biological system. Hence, we manually protonated this water molecule to form an oxonium ion before proceeding with further studies. The QM region included the complete substrate molecule, the H₃O⁺ and the nicotinamide moiety of NADPH, while all the rest of the atoms were included in the MM region. The complete system for QM/MM calculations contained 10175 atoms, in which 96 atoms were treated using the QM method.

3. Results and discussion

3.1 Ternary complex models of BVR-A and cofactor with substrate

According to the X-ray crystal structure of the binary complex, the cofactor NADPH binds in an extended conformation, and the Si-face of the nicotinamide moiety is accessible for hydride transfer. It is challenging to predict the binding pose of biliverdin-IXα and its analogs, because the original putative binding pocket in the crystal structure was too small to fit the large substrates. To obtain the binding pose for Substrate I, we tried several docking protocols and procedures (including AUTODOCK). Only the induced fit docking (IFD) protocol implemented in the Schrödinger Suite provided a reasonable docking solution. In contrast, other docking methods failed to generate any binding pose.

Cunningham et al. investigated the substrate specificity of hBVR-A and suggested that three basic residues on the top of the binding site, including Arg172, Arg225 and Arg227, contribute significantly to the substrate binding.²⁵. So during the initial docking in the IFD process, the grid was generated by centering on those three basic residues. During the Prime prediction of protein structure, Arg225 underwent significant conformational change to accommodate the two large propionates straddling the C10 methylene carbon of the substrates. The final binding mode was obtained after redocking the ligand into the binding pocket (Figure 4).

Figure 4.

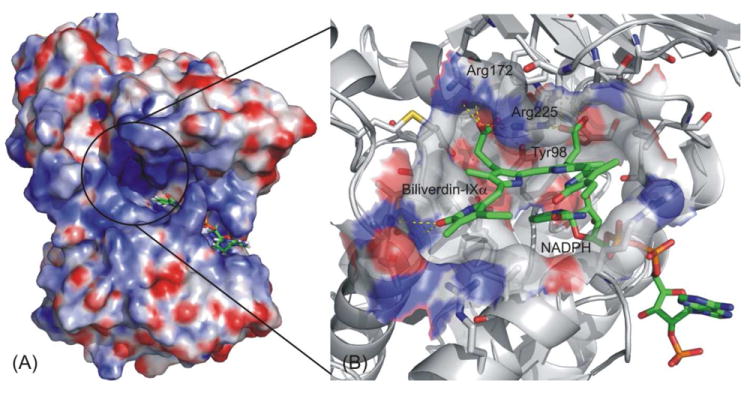
Induced fit docking study on hBVR-A binding mode. (A) The solid surface shows the electrostatic potential profile of the apo-enzyme, a binary complex of hBVRα and cofactor NADPH; Blue: electropositive area; Red: electronegative area. (B) Close-up of the ligand binding site. Substrate I and NADPH are represented by green (C), blue (N) and red (O), while the protein is represented by grey (C), blue (N) and red (O).

After we obtained the predicted binding mode for Substrate I in the protein, we employed the structure of the hBVR-A/NADPH/Substrate I complex for the docking of other analogs into the binding pocket using the same docking protocol (IFD) without any mutation. All the analogs could then be docked into the binding pocket and IFD generated only one reasonable binding mode for each analog. Furthermore, it should be noted that all of the analogs adopted a similar binding mode using this docking protocol. All substrates docked at the binding site cleft were partially stabilized by stacking interactions with the cofactor nicotinamide ring and by additional van der Waals contacts with active site residues. The electrostatic and hydrogen bonding interactions between the substrate propionate side chains and the basic arginine residues of the protein help to orient the substrate so that its reducible C10 in the γ-methylene bridge is located above the C4 of the cofactor nicotinamide moiety and poised for hydride transfer.

3.2 Stability of the ternary complex and flexibility of the substrates

To explore the dynamic stability of the five ternary complexes during the production phase, the root-mean-square displacement (rmsd) values for the backbone C_α atoms of hBVR-A were monitored relative to the starting structures. Figure 5 shows the rmsd of the five systems versus simulation time. For the simulations of the ternary complexes, there were no significant rmsd variations and the rmsd values of the five systems converged to 1.27, 1.22, 1.08, 1.29, and 1.22 Å, respectively. Since the rmsd values were stable during the 3.6 ns production run, the snapshots obtained in this period were used for the subsequent structural and energetic analysis. The hBVR-A structure remained Si-face stereospecific in accordance with the crystal structure. No rotation of the nicotinamide ring was observed during the simulations. The free rotation was prevented primarily by the stacking and hydrogen bond interactions between the cofactor and the substrates. Since during reduction the pro-S hydrogen (H_s) would be transferred from the C4 of the nicotinamide moiety of NADPH to the corresponding substrate reaction center, the distance between H_s from NADPH and C10 from the substrate was monitored during the simulation in order to evaluate the feasibility of direct hydride transfer (Figure 6). The small distances with average values of 2.88, 3.52, 2.80, 3.40, and 2.98 Å for the five systems indicate that the substrates are well positioned for direct hydride transfer, with I, III and V maintaining the closest proximity.

Figure 5.

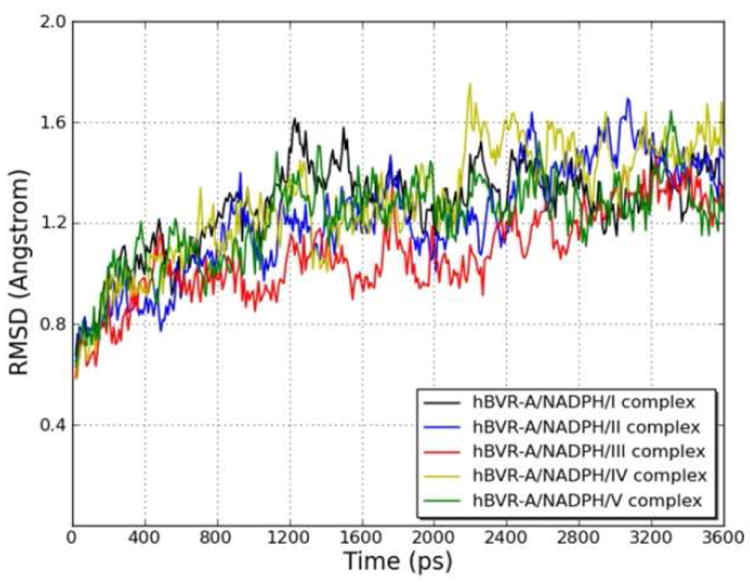
Root-mean-square displacement (rmsd) of the backbone C_α atoms of the hBVR-A/NADPH/substrate complexes with respect to the first snapshot, during the MD simulations as a function of time.

Figure 6.

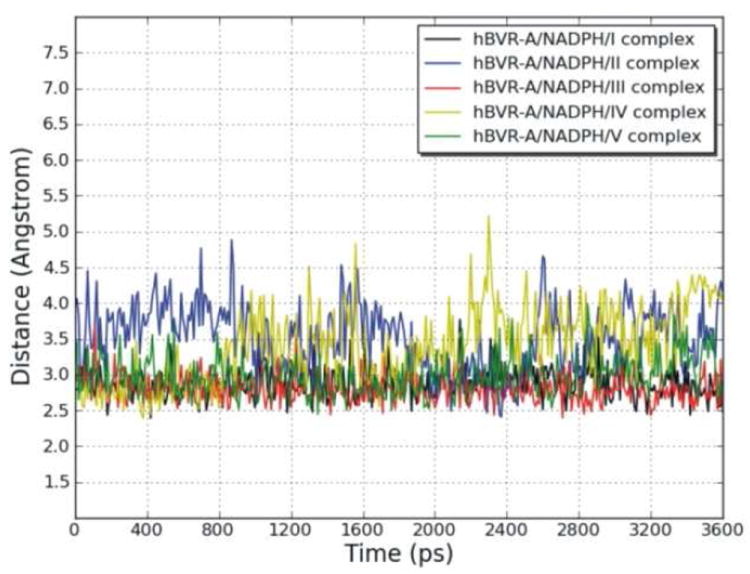
Variation of the distance between the reducible C10 in the γ-methylene bridge of the substrates and pro-S hydrogen (H_s) linked to the C4 of the cofactor nicotinamide during the MD simulations of the hBVR-A/NADPH/substrate complexes, as a function of time.

To assess the conformational flexibility of the open-chain tetrapyrrole backbone of each substrate, rotation around the exocyclic methylene bridges was investigated. Since the open-chain tetrapyrrole backbone is highly conjugated, and the extent of conjugation and location of double bonds was difficult to predict during the simulations, the rotational potentials for all the single bonds and double bonds of the exocyclic methylene bridges were investigated. The variation of the exocylic torsions, ϕ₁, ϕ₂, ϕ₃, ϕ₄, ϕ₅, and ϕ₆, in the five systems versus simulation time are plotted in Figure 7. The dihedral angle plots show that the two central pyrrole rings (C and D) which were buried in the protein binding pocket did not change their conformations significantly during the simulations, and the peripheral pyrrole ring A which is stacked on top of the nicotinamide moiety of NADPH also did not undergo significant conformational changes. However, there was a great degree of conformational change of the peripheral pyrrole ring B for four systems, the ones with I, II, III, and V. So except for the pyrrole ring B, the tetrapyrrole structures are considerably rigid. For the hBVR-A/NADPH/I complex, the dihedral angle ϕ₄ moved from −116° (average value during the first 1.6 ns of the simulation) to −18° (average value during the last 2.0 ns). For the hBVR-A/NADPH/II complex, the dihedral angle ϕ₃ moved from −130° (average value during the first 0.8 ns) to −32° (average value during the last 2.8 ns). For the hBVR-A/NADPH/III complex, both dihedral angles ϕ₃ and ϕ₄ fluctuated during the first 0.4 ns simulation, then stayed close to −22° and −7° (average value during the last 3.2 ns), respectively. For the hBVR-A/NADPH/V complex, both the dihedral angles ϕ₃ and ϕ₄ fluctuated during the first 2.0 ns of the simulation, then stayed close to 137° and 134° (average value during the last 1.6 ns), respectively. Thus, the flexibility of the peripheral pyrrole ring B is relatively high upon binding. Eventually, all the torsions reached stability in the production run. All the substrates adopted the typical helical porphyrin-like conformations after the simulations, similar to the active conformations found in previous studies.^2,22 Superimposition of the final trajectories of the substrates revealed that they all have the same orientation and similar binding mode in the ternary complexes (Figure 8). The figure shows that apart from contrasts in the side chain conformations, the major difference between them is that ring B of V obviously is significantly twisted out of the plane compared to the B rings of the other analogues.

Figure 7.

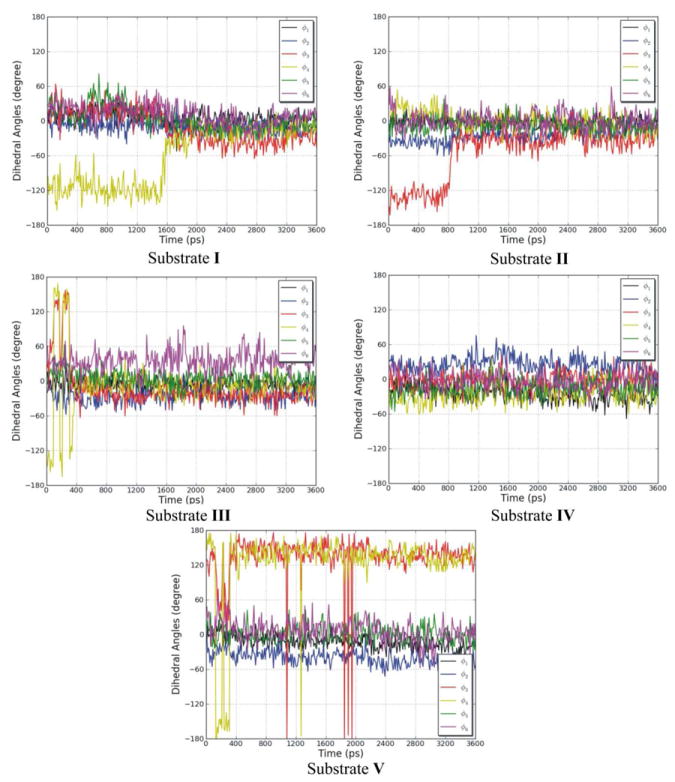
The variation of the exocylic torsions, ϕ₁, ϕ₂, ϕ₃, ϕ₄, ϕ₅, and ϕ₆, in the five systems, during the MD simulations as a function of time.

Figure 8.

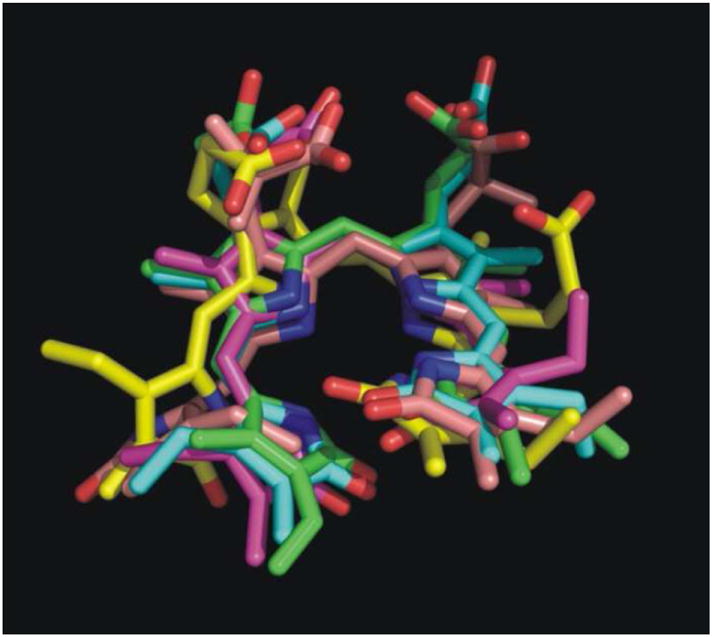
Superimposition of the final snapshots from the trajectories of the five biliverdin reductase substrates. Color code: green for substrate I; blue for substrate II; yellow for substrate III; magenta for substrate IV; pink for substrate V.

Detailed analysis of the MD trajectories of the five ternary complexes indicated that the orientation of the substrate in the binding pocket was maintained mainly by the strong hydrogen bonding and electrostatic interactions between the two bridging propionates from the substrates and an array of polar and charged residues from the proteins. These residues, including Arg172, Arg225, Arg227, Tyr98, Ser171, and Lys219, constitute the “carboxylate pocket” which was responsible for keeping the flexible substrates bound to the protein. The important hydrogen bonding interactions were monitored and are listed in Table 1. The three arginine residues contributed significantly to the binding in all five of the systems. Tyr98 contributed to the orientation of substrates I and V, Ser171 contributed to the binding of substrates I, III, IV, and V, and Lys219 contributed to the binding only of substrate II. Other important hydrogen bonding interactions were involved, including the interaction between the carbonyl group from the cofactor nicotinamide moiety and the amine or amide groups from the substrates.

Table 1.

Summary^a of Important Hydrogen Bonding Interactions (occupancies > 20%) Between Substrates and Functional Groups around Binding Pocket During the Production Phase of MD Simulations

Residue	Functional Group	Substrate Atom	Distance (Å) (SDb)	Angle (°) (SDb)	Occupancy (%)
Substrate I
Arg172	N1-H2	O4	2.785 (0.10)	161.33 (9.04)	99.72
Tyr98	O-H	O4	2.769 (0.15)	158.21 (11.20)	99.17
Arg225	N2-H1	O4	2.887 (0.17)	149.78 (12.31)	97.50
Arg225	N2-H2	O5	3.032 (0.21)	144.04 (11.26)	96.39
Arg225	N1-H2	O5	2.892 (0.16)	153.73 (10.79)	95.56
Arg225	N3-H	O6	2.919 (0.17)	152.15 (10.51)	95.00
Arg225	N2-H1	O6	3.043 (0.19)	141.83 (9.49)	93.33
Arg227	N2-H1	O1	2.887 (0.17)	145.58 (12.13)	92.78
Arg225	N2-H2	O1	3.000 (0.21)	155.81 (10.35)	89.72
Ser171	O-H	O1	2.764 (0.19)	149.60 (13.42)	88.06
Arg25	N2-H2	O2	2.920 (0.15)	154.23 (10.58)	43.06
Arg172	N1-H1	O1	3.177 (0.22)	134.00 (8.99)	40.00
Arg25	N1-H2	O2	3.030 (0.20)	145.46 (11.77)	38.06
Arg172	N2-H2	O4	3.265 (0.18)	134.77 (6.90)	28.06
NADPH	C=O	N3-H18	3.030 (0.20)	151.39 (11.93)	21.11
Substrate II
Arg172	N2-H2	O6	2.822 (0.12)	163.21 (8.99)	100.00
Arg172	N1-H2	O4	2.840 (0.13)	162.98 (8.88)	100.00
Arg172	N1-H1	O1	2.841 (0.14)	157.81 (10.95)	80.56
Arg172	N2-H2	O4	3.250 (0.17)	135.78 (6.39)	73.33
Arg225	N2-H2	O1	2.922 (0.19)	158.50 (12.83)	70.00
Arg225	N2-H2	O5	3.041 (0.23)	147.24 (15.28)	65.28
Lys219	N-H2	O6	2.838 (0.12)	160.43 (9.88)	65.00
Arg227	N2-H2	O5	2.895 (0.17)	152.87 (12.60)	63.61
Arg225	N2-H1	O4	2.980 (0.20)	155.82 (10.09)	60.28
Arg225	N1-H2	O5	2.911 (0.20)	157.09 (12.87)	59.17
Arg227	N1-H2	O1	2.939 (0.19)	156.60 (11.13)	53.89
Arg227	N1-H2	O5	3.001 (0.21)	146.49 (11.54)	38.33
Arg227	N2-H2	O1	3.066 (0.20)	142.22 (11.80)	34.72
NADPH	C=O	N2-H11	3.077 (0.20)	141.87 (12.85)	29.17
Arg172	N1-H2	O6	3.354 (0.11)	132.61 (5.88)	21.94
Lys219	N-H3	O6	2.847 (0.15)	156.03 (10.96)	21.39
Arg18	N1-H2	O2	2.923 (0.16)	148.16 (11.22)	20.28
Substrate III
Arg172	N1-H1	O1	2.842 (0.13)	157.52 (10.45)	100.00
Ser171	O-H	O1	2.666 (0.12)	163.99 (8.48)	99.72
NADPH	C=O	N2-H11	2.818 (0.11)	159.67 (9.81)	90.00
Arg225	N2-H1	O4	2.904 (0.18)	154.57 (12.38)	70.00
NADPH	C=O	N1-H2	3.109 (0.18)	138.69 (12.06)	52.78
Arg172	N1-H1	O4	3.137 (0.20)	131.08 (7.33)	43.33
Arg227	N1-H1	O4	2.853 (0.14)	152.08 (9.59)	34.72
Substrate IV
Arg172	N1-H2	O3	2.827 (0.11)	154.80 (11.63)	99.72
Arg225	N3-H	O3	2.887 (0.14)	152.00 (9.39)	99.17
Arg172	N2-H2	O4	2.904 (0.16)	160.33 (10.40)	98.89
Arg225	N2-H1	O3	2.890 (0.17)	146.28 (9.60)	96.67
Arg225	N2-H2	O5	2.888 (0.18)	152.59 (13.31)	93.06
Arg172	N1-H2	O4	3.212 (0.18)	140.74 (8.45)	81.39
Arg225	N1-H2	O5	3.094 (0.25)	140.55 (11.28)	62.50
Arg225	N1-H2	O6	2.955 (0.19)	160.62 (9.83)	44.72
Arg227	N1-H2	O6	2.982 (0.21)	149.06 (12.60)	43.89
Ser171	O-H	O5	2.693 (0.13)	164.38 (8.57)	39.72
Arg227	N2-H2	O6	2.961 (0.22)	151.93 (12.74)	21.39
Substrate V
Arg227	N2-H2	O5	2.882 (0.15)	160.44 (9.75)	98.89
Arg225	N1-H2	O1	2.876 (0.16)	153.18 (11.75)	96.94
Arg225	N2-H2	O1	3.011 (0.22)	141.82 (11.37)	92.50
Arg227	N1-H2	O1	2.947 (0.19)	151.41 (12.45)	90.00
Arg225	N2-H2	O5	2.935 (0.18)	158.80 (10.22)	88.33
Arg172	N1-H1	O5	3.030 (0.18)	146.31 (11.00)	80.56
Arg225	N2-H1	O4	2.918 (0.20)	151.73 (13.88)	80.56
Arg172	N1-H2	O6	2.932 (0.22)	153.12 (12.58)	75.00
Arg225	N2-H1	O6	2.930 (0.19)	149.78 (13.85)	69.72
Arg172	N1-H2	O4	2.940 (0.23)	153.01 (12.44)	68.06
Arg227	N1-H2	O5	3.154 (0.21)	138.93 (8.13)	63.89
Tyr98	O-H	O6	2.760 (0.17)	149.52 (12.90)	50.56
Tyr98	O-H	O4	2.766 (0.16)	149.20 (11.90)	41.39
Arg227	N2-H2	O1	3.243 (0.19)	135.22 (9.41)	40.28
Ser171	O-H	O5	2.904 (0.29)	151.45 (14.19)	26.11
Arg225	N3-H	O4	3.089 (0.23)	146.14 (10.08)	25.28
Arg225	N3-H	O6	3.097 (0.22)	143.63 (9.58)	22.50

^aThe order is ranked by the occupancies (from largest to smallest).

^bStandard Deviation.

3.3 Binding free energy analysis

The binding free energies were calculated and averaged over the MD trajectories of each complex. The total binding energies and the individual energy components are collected in Table 2. The significance of k_cat and K_M and the ratio between them in the enzyme mechanism of the reductase has been examined and it is believed that the similarity of all the first-order rate constants that characterize the general reductase kinetic mechanism makes K_M approximately equal to the true dissociation constant K_D. So a high K_M value indicates a high dissociation rate, which implies a low binding affinity of the substrate for the protein. The kinetic parameters (K_M) of hBVR-A are available from previous work.²⁵ The experimental binding free energies derived from the K_M values are −7.14, −6.87, −5.12, −5.71, and −6.14 kcal/mol for the five tetrapyrrole substrates, respectively (using ΔG_exp = −RT ln K_M). The theoretical (ΔG_bind) and experimental (ΔG_exp) binding free energies were compared and are plotted in Figure 9. The correlation coefficient of r² = 0.94 indicates that the predicted binding energies are in good proportion with the experimental activities. Notably, the calculations correctly predict the relative order of binding affinities of the five substrates which supports that the predicted binding mode of hBVR-A/NADPH/I ternary complex is reasonable.

Table 2.

Binding Free Energies of Biliverdin-IXα Reductase (BVR-A) Complexed with Biliverdin-IXα and the other Four Biliverdin Analogues ^a

Substrate	ΔGvdW	ΔGelec	ΔGsolv-pol	ΔGsolv-nonpol	ΔGbindb	ΔGexpc
I	−49.07	−114.81	103.19	−6.47	−67.16	−7.14
II	−45.14	−74.91	67.35	−6.83	−59.54	−6.87
III	−52.58	−71.42	97.42	−6.91	−33.50	−5.12
IV	−40.74	−134.25	133.81	−6.35	−47.53	−5.71
V	−43.29	−141.46	135.97	−6.64	−55.43	−6.14

^aAll energies are in kcal/mol.

^bBinding free energies do not include the contribution of conformational entropy.

^cThe ΔG_exp were calculated from the experimental data via ΔG_exp = −RT lnK at T = 303 K. The binding energies were calculated based on K_M.

Figure 9.

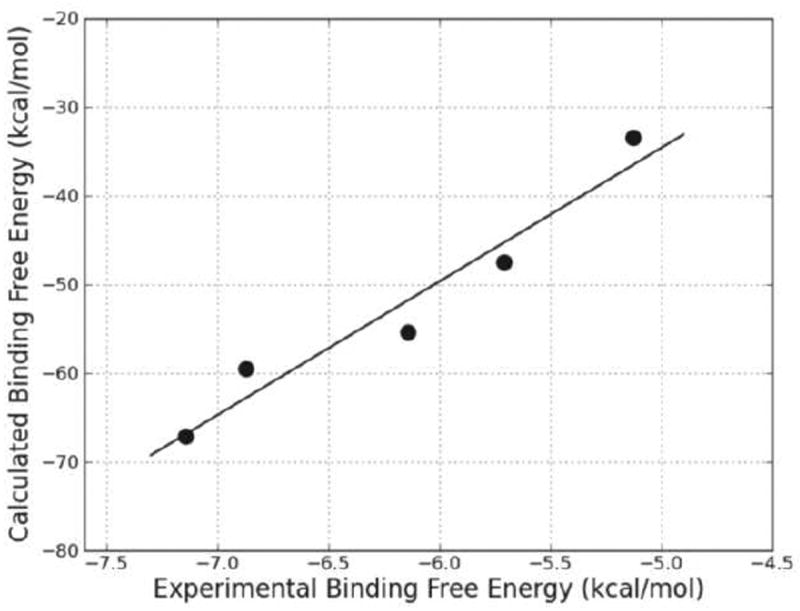
Calculated (ΔG_bind) versus experimental (ΔG_exp) binding free energy for the five ternary complexes.

A detailed analysis of the individual energy components showed that the major favorable contributors to substrate binding are van der Waals and electrostatic energies, and the electrostatic term is the most important driving force for substrate binding. This fact is consistent with the observations from hydrogen bonding analysis. The polar solvation term opposes binding, whereas the nonpolar solvation term, which corresponds to the burial of SASA upon binding, contributes slightly favorably to binding.

To obtain a detailed picture of the ligand-residue interaction, the binding free energies were decomposed into substrate-residue pairs as well as substrate-cofactor pairs, which are shown in Figure 10. The quantitative information is extremely useful for understanding the binding mechanism in the ternary complex and the contributions of each individual residue and cofactor to the binding free energy. A set of 13 residues plus cofactor at the binding site were selected for the decomposition analysis, using those residues for which the absolute value of the decomposed ΔG_bind was larger than 1.0 kcal/mol for at least one ternary complex. Energy contributions from 13 residues and cofactor are listed in Table 3. Overall, the interaction footprints of the five systems are quite similar. There is only one unfavorable residue, Glu217, which makes a slightly negative contribution to the substrate binding for four out of the five systems. The favorable residues can be classified into hydrophilic and hydrophobic categories. The hydrophilic residues containing polar or charged side chains can form strong hydrogen bonding and electrostatic interactions with the substrates. Most of these hydrophilic residues are centered on the “carboxylate pocket” to interact with the two bridging propionates, including Tyr98, Ser171, Arg172, Lys219, Arg225, Arg227. Since four residues (Tyr98, Arg172, Arg225, and Arg227) consistently made the most favorable contributions to the substrate binding, analysis of different components for each residue-based binding free energy was carried out (Table S1). The three positively charged residues (Arg172, Arg225, and Arg227) made the favorable contributions to binding free energy mainly through electrostatic interactions. It is noteworthy that Tyr98 in the ternary complex of hBVR-A/NADPH/Substrate I contributed favorably to the substrate binding mainly through polar contact using the side chain hydroxyl group. The observation can explain the mutagenesis result that the reduction of the catalytic activity by ~50% in the mutant Y97P of rat BVR-A was mainly attributed to the reduced binding potency due to the lack of polar contact.²³ The hydrophobic residues which make van der Waals interactions with the substrates contribute significantly to maintain the helical conformations of the substrates. As can be seen in Table 3, the energy contributions from different residues and the cofactor were substrate specific. For instance, Lys219 made a slightly negative contribution to the binding of substrate V which was opposite to its role in the binding of other substrates; the cofactor also made a positive contribution to the binding of substrate IV but a negative contribution to the binding of the other substrates; and Arg225 contributed significantly less to the binding of substrate III than to the binding of the other substrates.

Figure 10.

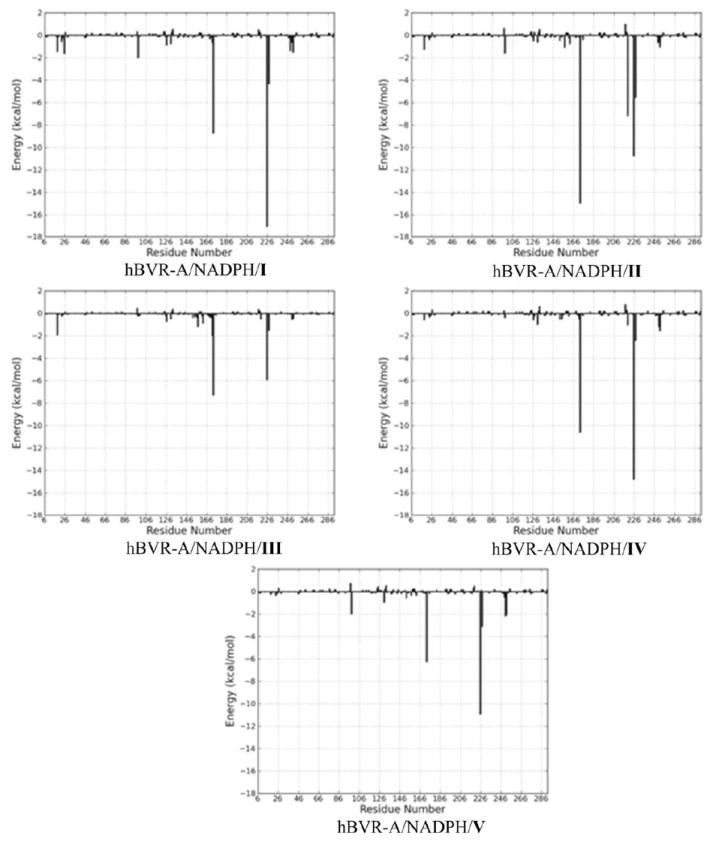
Interaction footprints for the substrate-residue pairs and substrate-cofactor pairs. The x-axis denotes the residue number (the cofactor, NADPH, is represented by the last residue number), and the y-axis denotes the energies of all pairwise contributions of each residue and cofactor.

Table 3.

Important Energy Contributions^a from Individual Residues and Cofactor to Substrate Binding in the Ternary Complexes

	Substrate I	Substrate II	Substrate III	Substrate IV	Substrate V
Arg18	−1.45	−1.23	−1.93	−0.57	−0.27
Arg25	−1.61	−0.16	−0.05	−0.19	−0.18
Tyr98	−2.02	−1.57	−0.27	−0.38	−2.02
Leu157	−0.05	−1.09	−1.16	−0.05	−0.32
Ser171	−0.68	−0.18	−1.96	−0.48	−0.18
Arg172	−8.70	−14.97	−7.31	−10.6	−6.27
Glu217	+0.49	+1.02	+0.39	+0.79	−0.16
Lys219	−0.26	−7.15	−0.48	−1.04	+0.52
Arg225	−17.03	−10.75	−5.92	−14.81	−10.90
Arg227	−4.33	−5.56	−1.51	−2.42	−3.12
Lys248	−1.38	−0.07	−0.07	−0.17	−0.17
Ile250	−0.68	−0.59	−0.53	−1.18	−2.15
Phe251	−1.51	−1.05	−0.45	−1.56	−2.04
NADPH	−1.20	−0.26	−1.90	+0.69	−1.30

^aAll energies are in kcal/mol.

3.4 QM/MM calculations on the catalytic mechanism

As detailed in Computational Methods, the last snapshot from the MD simulation for hBVR-A/NADPH/I complex was taken as the starting geometry for QM/MM calculations. During portions of the MD simulation, a water molecule was observed to be well conserved to occupy a position close to Substrate I and to participate in hydrogen bonding interactions with N2H11 from the B ring of I and the carboxyl group from the nicotinamide moiety of NADPH (Table S2). Upon minimization with the OPLS2005 force field, the H₂O molecule moved close enough to be hydrogen bonded to N4 of the substrate. For the QM/MM calculations, this water was manually protonated to form H₃O⁺. The pKa value of N4 was calculated by the Jaguar program⁶² to be 10.8 in dimethyl sulfoxide (DMSO), which means N4 is highly susceptible for protonation. In order for this H₃O⁺ to remain in the oxonium form, two of its O–H bonds had to be constrained. Otherwise, it automatically would transfer a proton to N4 of the substrate during geometry optimization and be converted to H₂O, which suggests that this is a spontaneous process. In our study, we fixed both O–H1 and O–H2 bonds at 1.0 Å. A similar approach was used earlier to study enzymatic reactions that involve H₃O^+.63 The optimized structure of the reactant complex (RC) for substrate I is shown in Figure 11. In RC, the H₃O⁺ forms a strong hydrogen bond (1.57 Å) with N4 of the heme. In addition, the distance between the H_s of NADPH and C10 of the substrate is 3.35 Å, which indicates that H_s is ready to be transferred to the substrate.

Figure 11.

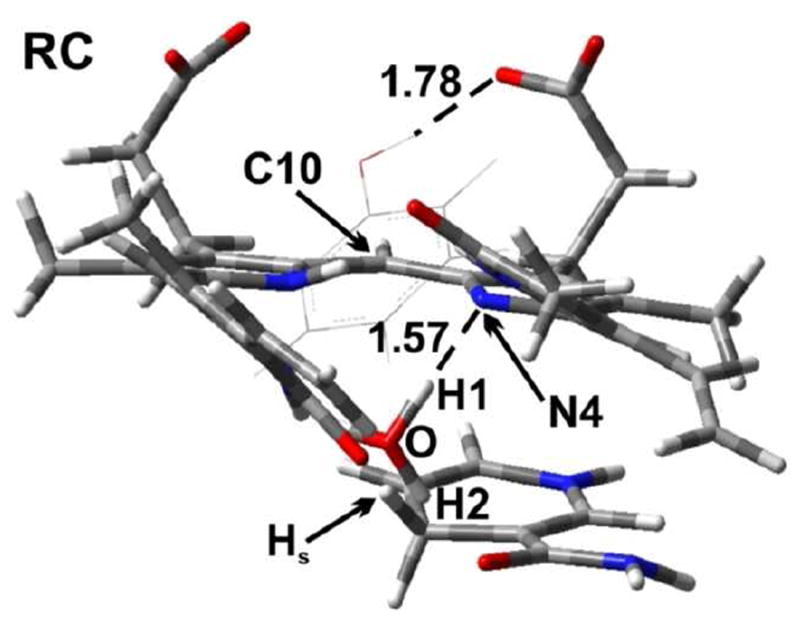
The optimized structure of the reactant complex (RC) (substrate I). A tyrosine residue Tyr97 is also shown. Distances are in angstrom (Å). Color key: C (gray); O (red); N (blue); and H (white).

In a previous experimental study,²³ it was proposed that a tyrosine residue Tyr97 is able to act as an acid to protonate N4 of the substrate. However, in RC Tyr97 forms a hydrogen bond (1.78 Å) with a carboxylic arm of the substrate. The distance Tyr-OH⋯N4 is 5.66 Å. Since this is such a long distance and considering the constraint on the −OH group of Tyr97 by the carboxylic group of the substrate, it not likely that this tyrosine residue is able to act as an acid to protonate the substrate. Therefore we did not consider this reaction pathway further.

In Mechanism 1, the reaction occurs in a stepwise manner. That is, H₃O⁺ first acts as an acid to protonate N4 of the substrate followed by a hydride transfer from NADPH to C10. The optimized structures and potential energy surface (PES) are shown in Figures 12 and 13, respectively.

Figure 12.

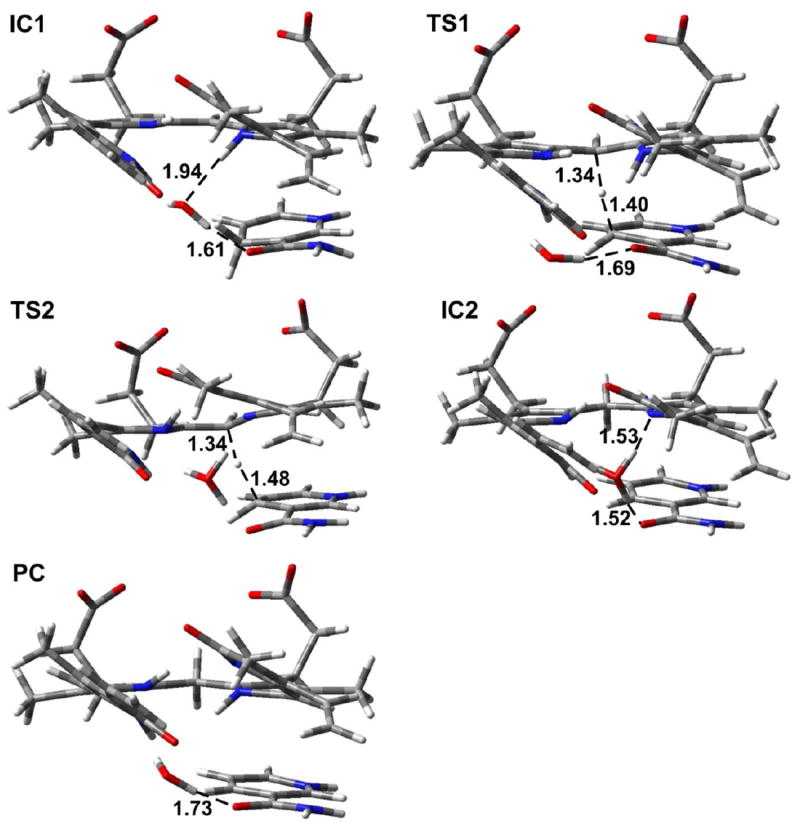
The optimized structures of the intermediates (IC1 and IC2), transition states (TS1 and TS2) and product complex (PC) for Mechanism 1 and Mechanism 2 (substrate I). Distances are in angstrom (Å). Color key: C (gray); O (red); N (blue); and H (white).

Figure 13.

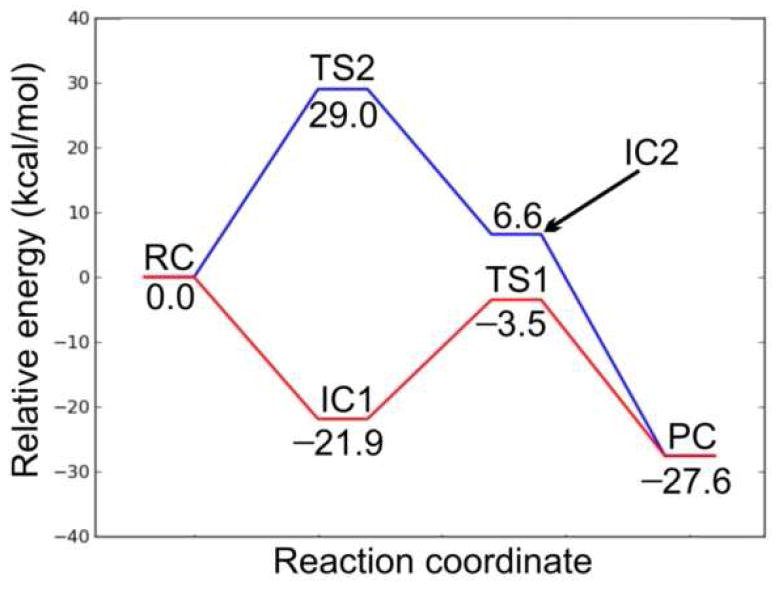
Potential energy surface diagrams showing the energetic barriers for Mechanisms 1 (red line) and 2 (blue line).

In order to study the protonation step, we performed a PES scan on the N4⋯H1. As can be seen from Figure 14, no transition state was located. Hence, this is a barrierless process. The resulting intermediate complex (IC1) lies 21.9 kcal/mol lower in energy than RC. In IC1, N4 of the substrate is protonated by H₃O⁺, which itself is converted to H₂O. The water molecule forms hydrogen bonds (1.94 and 1.61 Å) with N4–H of the substrate and the exocyclic amide oxygen of NADPH. In addition, the distance between H_s of NADPH and C10 of the substrate is shortened to 3.28 Å. In the next step, a hydride from NADPH transfers to C10 of the substrate. The transition structure (TS1) lies 3.5 kcal/mol lower in energy than RC. Hence, the hydride transfer step has a barrier of 18.4 kcal/mol. In TS1, the distances H_s⋯C_NADPH and C4⋯H_s are 1.34 and 1.40 Å, respectively. In addition, the hydrogen bond between N4 of the substrate and H₂O is broken. The N4–H⋯O_water distance is 3.36 Å. This is due in part to the fact that NADPH has to move closer to the substrate for the hydride transfer, which results in the formation of only one hydrogen bond between the water molecule and the exocyclic amide oxygen of NADPH at a distance of 1.69 Å. The collapse of TS1 leads to the product complex (PC), which lies 27.6 kcal/mol lower in energy than RC. In PC, the hydride has fully transferred to the substrate, which results in lengthening of the C10–C9 and C10–C11 bonds from 1.42 to 1.51 Å and 1.38 to 1.51 Å, respectively, compared with RC.

Figure 14.

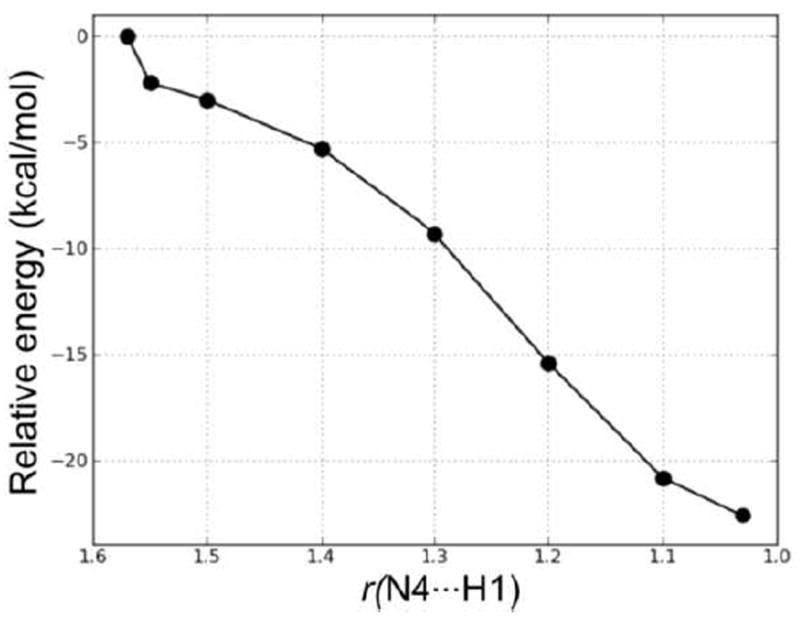
PES scan of the forming N4⋯H1 distance (in Å) in the proton transfer step of Mechanism 1.

In Mechanism 2, the reaction also occurs in a stepwise manner. However, the difference compared to Mechanism 1 is that the NADPH first transfers a hydride to C10 which is then followed by the protonation of N4 by H₃O⁺. The optimized structures and potential energy surface are shown in Figures 12 and 13, respectively.

In the first step, NADPH transfers a hydride to C10 of the substrate. This occurs via TS2, which lies 29.0 kcal/mol higher in energy than RC. This barrier is 10.6 kcal/mol higher in energy than the hydride transfer step in Mechanism 1. Thus, Mechanism 1, in which the proton transfer occurs prior to hydride transfer, is the preferred reaction pathway. In TS2, the distances H_s⋯C_NADPH and C4⋯H_s are 1.48 and 1.34 Å, respectively. The longer H_s⋯C_NADPH distance compared with TS1 is also consistent with the larger reaction barrier for the hydride transfer step in Mechanism 2. The collapse of TS2 results in the formation of the intermediate complex IC2, which lies 6.6 kcal mol^-1 higher in energy than RC. In IC2, H_s has transferred to C10 with the C10–C9 and C10–C11 bonds both 1.51 Å. The H₃O⁺ forms two hydrogen bonds (1.53 and 1.52 Å) in IC2, with N4 and the exocyclic amide oxygen of NADPH, respectively. In the next step, N4 of the substrate is protonated by H₃O⁺. We performed a PES scan (Figure 15) on the forming N4⋯H1 distance, which also suggested that the protonation step is a barrierless process. Finally, the protonation of N4 leads to the same product complex (PC) as Mechanism 1.

Figure 15.

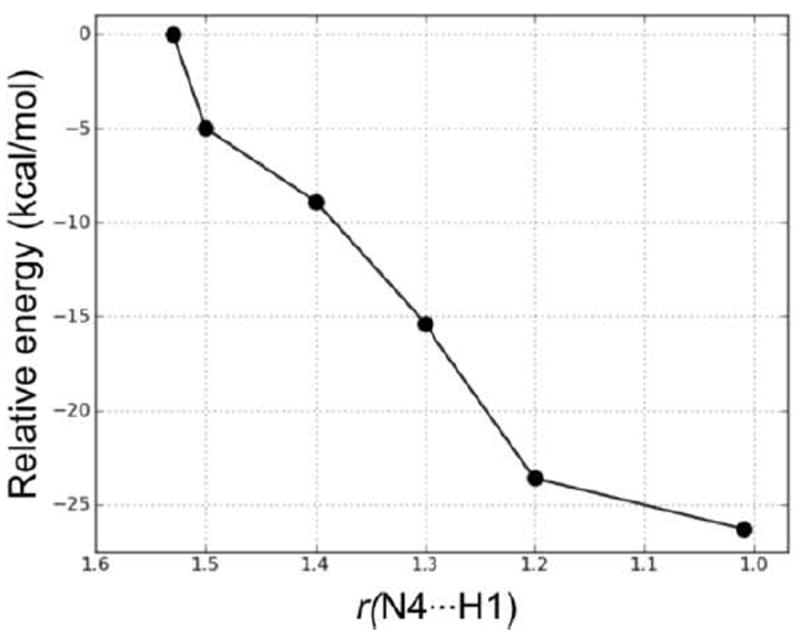
PES scan of the forming N4⋯H1 distance (in Å) in the proton transfer step in Mechanism 2.

Mechanism 3 is a concerted pathway with simultaneous proton and hydride transfers. However, we could not locate any transition state for this mechanism. A 3-dimensional PES scan (Figure 16) was performed on the forming H1⋯N4 and H_s⋯N10 distances. The scan clearly shows that the possible reaction pathways are stepwise. The concerted mechanism is not possible for this enzyme.

Figure 16.

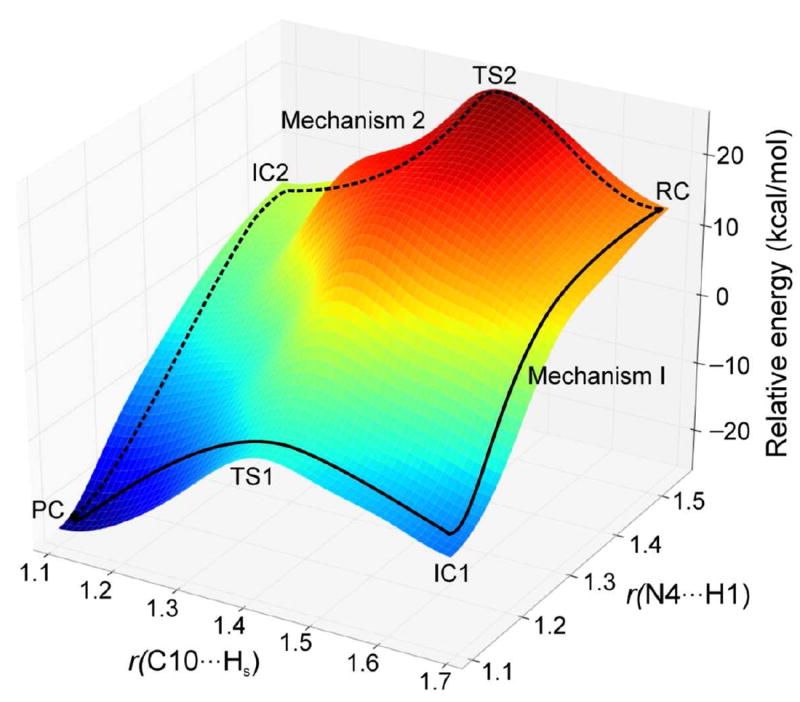
The 3-dimensional PES scan on the forming N⋯H and C⋯H distances (in Å). Mechanisms 1 and 2 are shown using solid and dotted lines, respectively.

4. Conclusions

To take into account conformational changes upon substrate binding, induced-fit docking (IFD) was employed to construct ternary complex structures consisting of hBVR-A, a substrate and cofactor NADPH. The large propionates on the substrates acting as anchors to stabilize the substrate binding through strong electrostatic interactions were accommodated by the “carboxylate pocket” comprised of three basic residues, Arg172, Arg225 and Arg227. During protein structure sampling included in IFD, Arg225 underwent significant conformational change which enlarged the binding cavity. The open-chain tetrapyrrole backbone of the substrate was forced to adopt a helical porphyrin-like conformation, and the two central pyrrole rings buried in the binding site cleft were stabilized by stacking interactions with the cofactor nicotinamide ring. The nicotinamide moiety of the cofactor NADPH extended into the active site cleft where the Si-face of the ring is accessible for hydride transfer.

The stability and reliability of the proposed binding modes were further examined by systematically sampling the conformational space using MD simulations in explicit solvent. The five ternary complex systems were proven to be stable during the 3.6 ns production runs, and the distances between H_s from the NADPH and C10 from the substrates were found to be short enough (<3.5 Å) to allow for direct hydride transfer. The conformational flexibility of the open-chain tetrapyrrole backbones of the substrates was also evaluated and except for pyrrole ring B, the rest of the parts of the tetrapyrrole structure were found to be considerably rigid during the simulations.

The commonly used MM-PBSA and MM-GBSA analyses were performed in order to obtain binding free energies and for energy decomposition analysis. The strong correlation (r² = 0.94) between the predicted binding free energies and the experimental activities provided solid evidence that the predicted binding modes are reasonable. A detailed decomposition analysis showed that the favorable van der Waals and electrostatic energies contributed by the residues located in the “carboxylate pocket” are the most important driving forces to stabilize the flexible substrate binding and maintain the helical conformations of the substrates.

The ternary complex structure of hBVR-A binding to biliverdin-IXα and NADPH obtained from the last snapshot of the MD simulations was exploited in QM/MM calculations to investigate the catalytic mechanism of this enzymatic reaction. Our calculations suggest that the concerted mechanism is not possible for this enzymatic reduction and instead the reaction should proceed via a stepwise mechanism involving proton and hydride transfers. The bulk solvent was demonstrated to be the proton source instead of Tyr98, which is too far away (5.66 Å) from the pyrrolic nitrogen. However, Tyr98 contributed favorably to the substrate binding through polar contact. So it is not surprising that the mutant Y97P of rat BVR-A which lacks such polar contact yielded a reduced catalytic activity. The oxonium ion can spontaneously protonate N4 of the substrate without any barrier. With the substrate protonated, the barrier of the subsequent hydride transfer step is 10.6 kcal/mol lower compared to the hydride transfer from NADPH to the neutral substrate. Therefore, the protonation is the driving force for catalysis and the lowest energy pathway proceeds through a positively charged pyrrole intermediate, which is subsequently subjected to hydride transfer. This new understanding of the reaction mechanism can facilitate the promotion of hBVR-A as a pharmacological target and assist the design of potential hBVR-A inhibitors.