Auditory Nerve Frequency Tuning Measured with Forward-Masked Compound Action Potentials

Abstract

Frequency selectivity is a fundamental cochlear property. Recent studies using otoacoustic emissions and psychophysical forward masking suggest that frequency selectivity is sharper in human than in common laboratory species. This has been disputed based on reports using compound action potentials (CAPs), which reflect activity in the auditory nerve and can be measured in humans. Comparative data of CAPs, obtained with a variety of simultaneous masking protocols, have been interpreted to indicate similarity of frequency tuning across mammals and even birds. Unfortunately, there are several issues with the available CAP measurements which hamper a straightforward comparison across species. We investigate sharpness of CAP tuning in cat and chinchilla using a forward masking notched-noise paradigm—which is less confounded by cochlear nonlinearities than simultaneous masking paradigms and similar to what was used in the psychophysical study reporting sharper tuning in humans. Our parametric study, using different probe frequencies and notch widths, shows relationships consistent with those of auditory nerve fibers (ANFs). The sharpness of tuning, quantified by Q₁₀ factors, is negatively correlated with probe level and increases with probe frequency, but the Q₁₀ values are generally lower than the average trend for ANFs. Like the single fiber data, tuning for CAPs is sharper in cat than in chinchilla, but the two species are similar in the dependence of tuning on probe frequency and in the relationship between tuning in ANFs and CAP. Growth-of-maskability functions show slopes <1 indicating that with increasing probe level the probe is more susceptible to cochlear compression than the masker. The results support the use of forward-masked CAPs as an alternative measure to estimate ANF tuning and to compare frequency tuning across species.

Introduction

Frequency tuning is a fundamental property of responses from the cochlea and higher level structures in the auditory system. Frequency tuning of the cochlea and auditory nerve fibers (ANFs) is most commonly studied by determining the stimulus intensity needed to achieve a criterion response (e.g., basilar membrane displacement or spike rate) over a range of pure tone frequencies. The resulting typically V-shaped curve is referred to as a frequency threshold curve, and from it the characteristic frequency (CF) and a measure for sharpness of tuning are obtained. By sharpness of tuning, we refer to the width of the V-shape relative to the CF, commonly expressed in terms of the so-called quality (Q) factor (see “Methods”).

In humans, sharpness of frequency tuning has been studied with a variety of behavioral and physiological methods but is unknown for single ANFs because their study requires invasive recordings. Despite the lack of single ANF measurements, it is generally thought that frequency tuning in humans is similar to that in commonly studied laboratory mammals (Ruggero and Temchin 2005). On the other hand, an increasing number of studies report sharper tuning in humans. An early study by Harrison et al. (1981) compared Q factors calculated from compound action potential (CAP) recordings in human patients to similar measurements obtained in guinea pig. The CAP is an evoked potential which reflects some properties of ANFs; it is the weighted summed extracellular response of synchronized ANFs at the onset of acoustic stimuli (Goldstein and Kiang 1958; Kiang et al. 1976; Antoli-Candela and Kiang 1978). Extrapolating from CAP measurements and from Q factors of single ANFs in guinea pigs, Harrison et al. (1981) concluded that frequency selectivity is higher in humans than in guinea pigs. More recently, based on behavioral (Oxenham and Shera 2003) and otoacoustic (Shera et al. 2010) measurements, it was concluded that frequency selectivity in humans is higher than previously thought, by a factor of more than two. Finally, cortical recordings in humans also reveal high frequency selectivity (Bitterman et al. 2008). It is controversial whether the high Q values reflect real species differences rather than differences in experimental paradigm (Ruggero and Temchin 2005; Eustaquio-Martin and Lopez-Poveda 2011). Comparison of tuning estimates from otoacoustic emissions and single ANF in macaque monkey supports the correspondence between the two methods and suggests that frequency tuning in Old World primates may be superior to that observed in more commonly studied species (Joris et al. 2011).

CAP recordings provide an electrophysiological means to compare tuning across species. In order to make predictions of the tuning at the single neuron level in humans, it is necessary to first assess the quantitative relationship between CAP and single unit measures in species where both can be measured or are available. To achieve this goal in the present study, we adopt a forward masking procedure (Oxenham and Shera 2003) to measure Q factors from CAP recordings in two species for which tuning in ANF is well characterized, but for which little data on CAP tuning are available (Ruggero and Temchin 2005).

Methods

Surgical preparation

The experiments were conducted using six adult cats and nine chinchillas of either sex. All procedures were approved by the KU Leuven Ethics Committee for Animal Experiments and were in accordance with the National Institutes of Health Guide for the Care and Use of Laboratory Animals. Animals were briefly examined for clear external and middle ears. Cats were anesthetized with a mixture of ketamine (20 mg/kg) and acepromazine (0.2 mg/kg) administered intramuscularly. A venous cannula was then placed to infuse lactated Ringer’s solution and sodium pentobarbital to maintain a deep state of anesthesia. A cannula was inserted into the trachea. Chinchillas were anesthetized with an intramuscular injection of ketamine (20 mg/kg), xylazine (3 mg/kg), and atropine (0.04 mg/kg). Supplementary doses of ketamine or intraperitoneal injection of pentobarbital were administered to maintain a surgical level of anesthesia.

The left pinna was surgically removed and the auditory bulla was exposed and opened. Through the opening in the bulla, a silver Teflon-insulated wire with ball electrode was inserted and placed at the round window. The electrode lead was glued to the bone and the bulla opening was closed again with ear impression compound (Microsonic). Two silver wire electrodes were placed in the skin: a reference electrode at the nape of the neck and a ground electrode near the contralateral bulla. During the measurements, the animals were kept warm with a homeothermic blanket (Harvard). The experiments were conducted in a double-walled soundproof and faradized room (Industrial Acoustics Company).

Stimulus generation

Stimuli were generated with custom software and a digital sound system (Tucker-Davis Technologies, system 2, sample rate 125 kHz/channel) consisting of a digital-to-analog converter (PD1), a digitally controlled attenuator (PA5), a headphone driver (HB7), and an electromagnetically shielded acoustic transducer (for chinchilla, Etymotic Research, ER1, 20 Hz–16 kHz; for cat a dynamic electro-acoustic transducer, Radio Shack, 20 Hz–50 kHz). The transducer was connected with plastic tubing to a custom earpiece coupler. In cat, the coupler was fit in the transversely cut ear canal; in chinchilla, the coupler was sealed with ear impression compound to the bony external auditory meatus. The acoustic system was calibrated in situ near the eardrum, through the custom coupler, with a calibrated probe microphone (Brüel & Kjær, type 4192, 1/2-in. condenser microphone and conditioning amplifier Nexus 2690).

Signal sampling

The cochlear responses were differentially measured (low noise differential preamplifier, Signal Recovery, Model 5115) between the signal electrode at the round window and the reference electrode in the nape of the neck. The ground of the differential preamplifier was connected to the electrode at the contralateral mastoid. The signal was filtered (100 Hz–10 kHz, cut-off slopes 12 dB/oct.) and amplified with another external amplifier (Stanford Research, SR560) to a total gain of × 10,000. All of the relevant signals including the filtered cochlear response, the stimulus waveform, and synchronization pulses at the start of every probe were visualized on an oscilloscope (LeCroy, WaveSurfer 24Xs), sampled and digitized with an ADC (TDT, RX8, ~100 kHz/channel, max. signal-to-noise ratio (SNR) 96 dB), and stored on disk for further analysis.

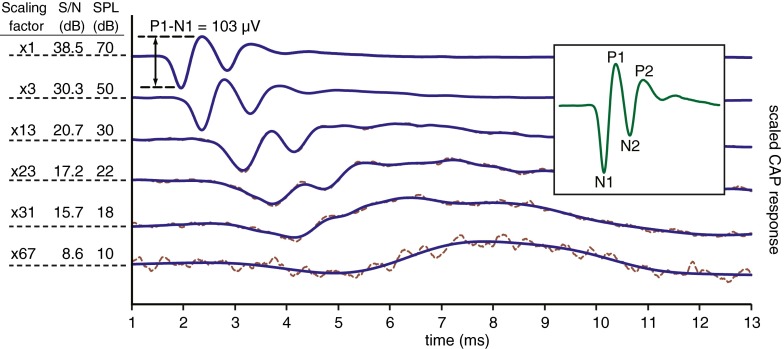
The amplitude of the CAP was measured between P1 (first positive peak) and N1 (first trough) as shown in the inset of Figure 4 (the remainder of that figure will be discussed later in the “Results” section). Whenever P1 was not clearly defined, the amplitude was measured between P2 and N1, and when P2 was not clearly visible, between the positive and negative maxima. Before the amplitude was measured, the CAP response was de-noised with a wavelet filter. At low probe frequencies (<2 kHz), an additional sharp notch FIR filter at twice the probe frequency was used to remove the neural phase-locked response. The measured responses contained significant background noise uncorrelated to the stimulus; at low stimulus intensities, the background noise exceeded the desired response signal. To increase the response SNR, we used signal averaging, typically 512 or 1,024 repetitions, depending on the background noise level.

FIG. 4.

CAP responses extracted from the alternated round window responses for different probe levels, dashed signals. The solid blue traces are the waveforms de-noised with a custom wavelet filter; the curves are offset and the amplitudes scaled. Table at the left indicates the scaling factors, the SNR (response and background in V_rms) and the probe levels. The probe frequency is 8 kHz and response amplitude for 70 dB is 103 μV_pp (peak to peak). Inset: the CAP response at 70 dB, with the different positive and negative peaks. The time axis is not compensated for the system delay, e.g., acoustical transmission tubes (0.3 ms).

Stimulus paradigm

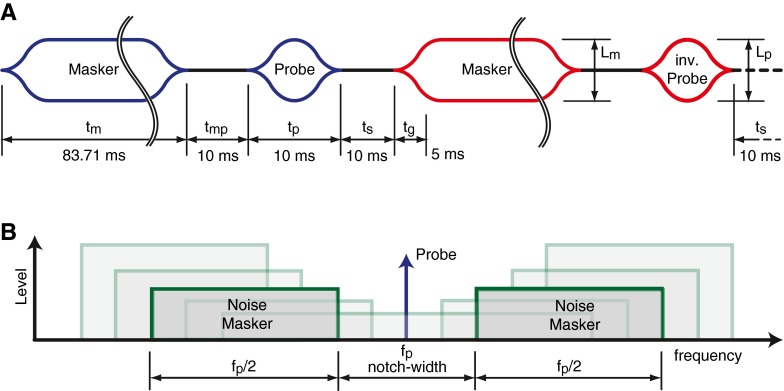
Schematic representations of the notched-noise forward masking (NNFM) paradigm in the time and frequency domain are shown in Figure 1. The general principle is as follows: A notched-noise masker of variable level was followed by a 10-ms tonal probe at a fixed level (Fig. 1A). We varied the notch width of the masker and searched for the masker level required to suppress the CAP response to the fixed probe tone by a given percentage, from hereon called the masking criterion. (A full description of the protocol is given in the next section). To reduce spectral splatter due to the on- and off-switching of the stimuli, probe and masker were gated with 5 ms raised-cosine ramps. The 10-ms probe thus never reached steady state; it smoothly ramped up and down. The polarity of the probe tone alternated in successive presentations. The cochlear microphonic follows the polarity of the stimulus and is largely symmetrical, so that it is almost completely removed by averaging the responses to stimuli with alternating polarity (Dallos 1973). In contrast, the CAP—the signal we want to measure—is mainly from neural origin and is largely preserved after averaging.

FIG. 1.

Representation of the stimulus in the time domain (A) and frequency (B) domain with the following parameters: masker duration, t _m; probe duration, t _p; masker–probe interval, t _mp; probe–masker interval, t _s; gating time, t _g; masker spectrum level, L _m; probe level, L _p; and probe frequency, f _p. A Each complete representation consists of two identical masker–probe sequences with alternating polarity between the first and second probe. B The notched-noise consists of two Gaussian noise bands with fixed bandwidth f _p/2. The notch width and masker level (L _m) are variable.

Figure 1B depicts the idealized frequency spectrum of the stimulus. The notched-noise masker consisted of two Gaussian noise bands generated in software in the complex frequency domain and designed with infinitely steep edges (brick-wall shape). The real and imaginary parts of the spectral components were generated with a Gaussian random generator (randn) in MATLAB, spectrally calibrated and converted to the time domain with a discrete fast Fourier transformation (FFT function in MATLAB). For convenience, the amplitudes for the masker and probe signals were calculated before signal gating and before calibration. Note that (a) the probe levels with gating are 4.3 dB lower than those without gating and (b) the masker level is expressed as an overall level (total noise band), and not as a “masker spectrum level” (intensity level within a 1-Hz band). The conversion factor between the overall level and masker spectrum level is −10log₁₀(BW), where BW = f_p in this study.

Spectrally, the noise bands had equal bandwidth and straddled the probe frequency (f_p), so as to create a notch symmetrically spaced on a linear frequency axis. The masker notch width and level were the main experimental variables. The duration of the masker was set to exceed the settling time of the adaptation in the masker response. In initial pilot experiments, we used 300 ms, but after validation, we shortened the duration to 83.71 ms to speed up data collection. For a few test cases (not included in the results), we shortened it further to 33.71 ms, which resulted in Q values that were not significantly different compared to longer masker durations. Masker and probe were separated by a silent interval t_mp, so as to reduce overlap between the responses from the masker and the probe. Successive presentations of probe–masker combinations were separated with the interval t_s. The values of the intervals t_mp and t_s were adjusted in initial experiments and were fixed at 10 ms for the remaining experiments.

Experimental protocol

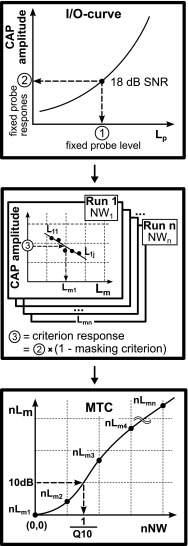
Masking tuning curves (MTCs) were constructed with a predetermined masking criterion by varying the notch width (NW) and masker level (L_m) while keeping the probe constant in level and frequency. Within a run, NW was held constant and L_m was varied in search for the probe response associated with the predetermined masking criterion, called the “criterion response.” The L_m values obtained at runs for different NW values resulted in one MTC.

The procedure to extract the MTC consisted of the steps schematically illustrated in Figure 2 (top panel). We obtained an input–output (I/O) curve in quiet, i.e., the probe level (L_p) was varied in level and the corresponding CAP amplitudes were measured without the masker. From these responses, a suitable probe level was determined. The choice of this level has to meet two conflicting demands. On the one hand, it should be low to obtain Q values as close as possible to CAP response threshold for better comparison with Q values from frequency threshold curves of single ANFs. On the other hand, it should be high enough to yield a reasonable SNR without requiring many measurement repetitions. For pragmatic reasons, we used the SNR of the CAP response (signal and noise in V_rms) as a figure of merit, and aimed at 18 dB SNR. To obtain a response with such SNR, a stimulus probe level was required of approximately 15 dB above the CAP threshold level, which is defined as the (averaged) probe level that produces a CAP response equal to the background noise (≡0 dB SNR). We refer to this probe level as the “fixed probe level” (① in Fig. 2) and to its response as the “fixed probe response” (② in Fig. 2). The fixed probe level is maintained throughout the different runs needed to collect data to construct a MTC. Note that the SNR value was chosen to have enough headroom to cover the smaller amplitudes of the masked responses, e.g., a masking criterion of 33 % reduces the SNR by approximately 3.5 dB.

FIG. 2.

Schematic representation of the procedure for constructing MTCs. From an I/O curve, a fixed probe level ①and corresponding response ② were chosen. Subsequently, a criterion response amplitude ③ is calculated by applying the masking criterion to the fixed probe response ②. Masked probe responses from a varying masker level (L ₁₁, L ₁₂, …, L _1j) are then obtained for consecutive runs with increasing notch widths. For every run, simple linear regression is applied on the masked probe responses to determine the masker levels (L _m1, L _m2, …, L _mn) resulting in the criterion response ③. Finally, the MTC is estimated with polynomial (linear) regression and Q ₁₀ is extracted.

Next (middle panel Fig. 2), we searched for the masker levels that suppressed the response amplitude at the fixed probe level with the masking criterion. In initial experiments, the masking criterion was chosen at 50 %, i.e., we determined L_m that reduced the response amplitude to the fixed probe by half. In later experiments, the masking criterion was refined to 33 % (see “Results”). In the first run (run 1), we presented a spectrally continuous masker (no-notch condition) and varied the masker level L_m in small steps to search for the level, e.g., L_m1, that resulted in the criterion response as estimated by simple linear regression. In the other subsequent runs, the masker levels (L_m2, L_m3, …, L_mn) were determined in the same way with the same probe and criterion conditions, but with increasing masker notch widths.

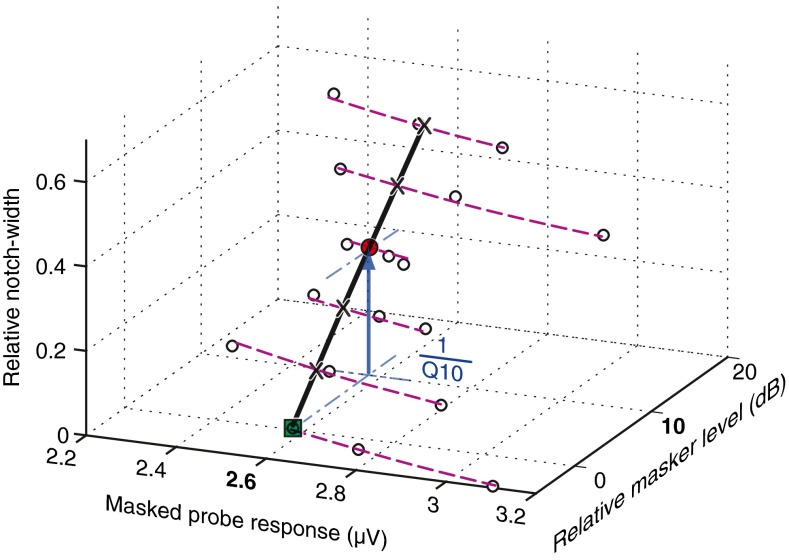
In the third and final step (bottom panel in Fig. 2), a plot of masker levels for different notch widths (L_m1, L_m2, …, L_mn) constitutes the MTC, from which the Q factor is obtained. To facilitate comparison across MTCs, we normalize both abscissa and ordinate. Masker levels at different notch widths are normalized by subtracting the masker level for the no-notch condition L_m1 and the notch widths are divided by the probe frequency (f_p). Thus, the first data point (NW₁, L_m1) with the no-notch condition is positioned at the origin of the normalized MTC. For clarity, the names of the normalized parameters are indicated with the letter “n” at the beginning of the corresponding label (e.g., nNW₂ = NW₂ / f_p and nL_m2 = L_m2 − L_m1). The MTC curve is estimated by second order polynomial regression. This is illustrated in Figure 3 where the data points from all runs, with different notch widths and masker levels, are plotted (open circles). For a better view, the axes are rotated relative to Figure 2 (bottom panel); the extra axis (x-axis) is the probe response. The dashed curves are fits, obtained with polynomial linear regression, through the responses of one run (i.e., one notch width). The intersections of these fits with the criterion response (here 2.6 μV) are indicated with crosses. The MTC is obtained as a fit through these crosses using polynomial linear regression (solid line in Fig. 3).

FIG. 3.

An example of a normalized MTC (thick line) with the masked probe response as extra dimension, here presented on the x-axis. The independent variables are relative notch width and relative masker level, presented on the y- and z-axes, respectively. The purple dashed curves were obtained by polynomial regression from masked probe responses (open dots); the parameter is the notch width. The (black) thick curve is the MTC obtained with a similar regression method, but from data points on the (purple) dashed curves at the response criterion (~2.6 μV; black crosses, red circle, and green square). The Q ₁₀ factor is graphically illustrated by the blue arrow (projection of the MTC between the red-filled dot and green-filled square on the axis of the relative notch width); it is the reciprocal of the normalized notch width at 10 dB relative masker level.

In this study, sharpness of tuning is quantified using two Q factors: the Q₁₀ and the Q_ERB. Since sharpness of tuning obtained with the notched-noise paradigm is compared with that from single nerve fibers obtained with tones, the Q factors were extracted in two ways: first, directly from the iso-response data, and secondly, from a calculated auditory filter (Patterson 1976), which is the representation of an equivalent filter for tonal maskers.

Direct extraction method

For this method, the Q₁₀ is defined as f_p/NW_{10 dB}, where f_p is the probe frequency in Hertz and NW_{10 dB} is the notch width at 10 dB above the nadir of the MTC. This notch width is graphically illustrated by the blue arrow in Figure 3. The Q_ERB is the ratio of the probe frequency to the MTC’s equivalent rectangular bandwidth (ERB). The ERB is an approximation of the bandwidth of the filter, modeled as a rectangular band-pass filter passing the same power. The Q_ERB is calculated as

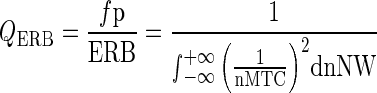1

where Q_ERB is the dimensionless Q factor, f_p is the probe frequency in Hz, ERB is the equivalent rectangular bandwidth in Hz, nNW is the dimensionless notch width normalized to the probe frequency, and nMTC is the normalized MTC in decibel. Because the exact MTC is not known and needs to be estimated, we use a numerical integration technique to approximate the definite integral in Eq. 1. The Q_ERB is calculated with the trapezium rule for non-uniform intervals. The following equation was used

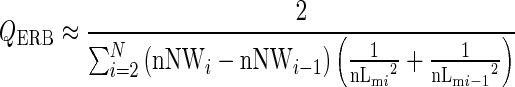2

where nNW_i are the dimensionless normalized discrete notch widths, nL_mi are the normalized discrete masker levels in decibel, and N is the number of runs. Due to time constraints, only the most relevant part at the region of the nadir was measured and used in the calculation of the Q_ERB.

When enough data points are available, the Q_ERB is a more robust measure for the sharpness of tuning than the Q₁₀. The Q_ERB is calculated from all available data points, whereas the Q₁₀ is derived from the data points at 10 dB above the nadir of the MTC. This makes the Q_ERB less prone to local variations and more informative regarding the curvature of the slopes. Nevertheless, to limit the total time span needed to obtain a single Q value, we optimized our measurements more towards Q₁₀ than to Q_ERB estimates. To achieve this, in some cases, a more direct method was used where NW_{10 dB}, the notch width at the corresponding masker level 10 dB above the nadir, was sought at the masking criterion; the Q₁₀ is then calculated as the reciprocal of the normalized NW_{10 dB}. We refer to this method as the “fast method.”

Extraction from an auditory filter

The Q factors were calculated in a similar manner as for the direct extraction method, but from estimated tonal auditory filters commonly used in psychophysical experiments. The auditory filter shapes were obtained with the same fitting procedure as used in a recent psychophysical study (Oxenham and Shera 2003), but without correction for the middle ear transfer function and off-frequency listening. This fitting procedure is based on the power spectrum model of masking (Patterson 1976) assuming a rounded exponential (ROEX) filter shape (Patterson et al. 1982; Glasberg et al. 1984). Here, a symmetrical ROEX(p,w,t) function (Equation 3 in Oxenham and Shera 2003) with three independent parameters was used, with two equal filter sides. The equation for one of the symmetric sides of this ROEX filter is equal to

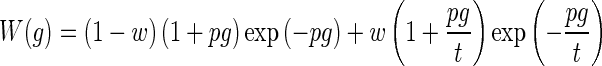3

where W(g) is the filter power weighting function, g is one half of the discrete normalized notch width (nNW_i/2), w is the weighting factor between the first and second term, p is a measure for the slope of the left term, and t is the ratio between the slopes of the left and right terms. From the power spectrum model, a fourth, dependent, parameter K (decibel) was extracted, which represents the masking “efficiency” corresponding to the predefined masking criteria, and is defined as the ratio of the powers of the probe and the amount of masker (spectral noise) passing the filter (W) necessary to comply with the masking criterion. For clarity, we indicate the sharpness of tuning obtained from these filters with the prefix ROEX.

In a few animals, we also studied the asymmetry of MTCs obtained with a single noise band positioned above or below the probe frequency. In those instances, the two MTCs obtained with single noise bands were merged and represented as a V-shaped MTC; we refer to these as single-sided MTCs (ss-MTC).

Results

In this study, we focus on the sharpness of tuning of CAP responses in cat and chinchilla. We calculate Q₁₀ and Q_ERB factors from iso-response tuning curves derived from masked CAP responses recorded at the round window using a NNFM paradigm. The most complete datasets were obtained in cat. The probe frequencies varied from 0.5 to 14 kHz for cat and from 1 to 12 kHz for chinchilla. The sequence of probe frequencies tested was arbitrary. In the course of an experiment, repeated measurements were occasionally made as a control: in those cases, average Q factors are calculated and reported. We strove to use probe levels as low as practical. In some measurements, the probe level was systematically increased to explore the dependence of Q₁₀ on level.

Fixed probe level

The first step was to determine a fixed probe level for the remainder of the procedure. Examples of typical CAP responses from cat to unmasked tone pips are depicted in Figure 4, for a probe frequency of 8 kHz. Traces for six different probe levels, increasing from bottom to top, are shown. The amplitudes are scaled: the table to the left gives the scaling factor, SNR and probe level for the corresponding responses. In this example, 22 dB SPL was chosen as the fixed probe level, based on the corresponding SNR of 17.2 dB, which is close to our predefined target value of 18 dB. Note that at high levels, P1 and N1 (as well as other components such as P2, N2) are clearly defined so that the CAP response can be simply defined as their amplitude difference. However, at low levels, a broad maximum rather than a distinct P1 component was often seen (lower traces in Fig. 4) and was used to quantify the response amplitude. In these cases, it is impossible to know whether this absolute maximum corresponds to P1, P2, or the summating potential or a mixture thereof. In practice, the exact choice of response metric is not critical because our paradigm uses iso-response conditions and the intrinsic shape of the CAP response does not change much with notch width and masker level.

Masking criterion

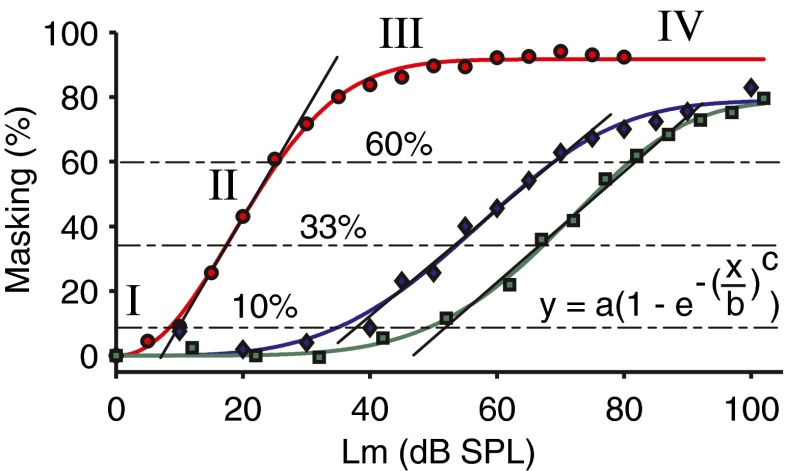
Earlier studies (Eggermont 1977; Harrison et al. 1981) used a variety of masking criteria. In our initial experiments, we used a masking criterion of 50 %, but subsequently settled on 33 % which we found to be optimal, as illustrated in Figure 5. This figure shows three masking intensity curves in cat for three different conditions (see caption Fig. 5). The normalized masking is plotted as a function of masker level. The curves show four distinct regions: region I: no masking; region II: steep linear growth of masking between ~10 and 60 % (upper and lower horizontal dashed dotted lines) on a semi-log scale; region III: transition region, with a slope significantly smaller than in region II; and region IV: saturation of masking, the region is only visible for the leftmost curve (red filled dots). Region II shows a linear relationship between level and masking in the three curves, which differ in frequency, notch width, and probe level. We therefore chose 33 % as the optimal level for our masking criterion (middle dashed dotted line) and used simple linear regression. There is a clear difference in slope between the two curves with higher probe levels (blue diamonds and green squares, slopes of 1.7 and 1.8 dB⁻¹, respectively) and the one with low probe level (red dots, 3.4 dB⁻¹). The masking intensity curves are similar to those for single fiber measurements (Harris and Dallos 1979); the red curve in our example with low probe level is almost identical with the same ascending slope to the normalized curve in their Figure 9.

FIG. 5.

Masking intensity curves, amount of masking as a function of masker level, for different conditions in two different cats. The masking curves are fits of cumulative Weibull distribution functions (formula included in the figure). The conditions for the curves are, from left to right: red-filled dots, L _p = 40 dB SPL, f _p = 10 kHz, nNW = 0, a = 91.68, b = 24.89, c = 2.129, animal 1; blue diamonds, L _p = 67 dB SPL, f _p = 2 kHz, nNW = 0.44, a = 78.89, b = 62.62, c = 3.668, animal 2; and green squares, L _p = 60 dB SPL, f _p = 6 kHz, nNW = 0.34, a = 78.72, b = 75.29, c = 5.031, animal 2. Four different regions can be identified: I, region with almost no masking; II, region with a steep linear growth (on semi-log plot, solid lines), i.e., between ~10 and 60 % masking (upper and lower horizontal dashed dotted lines); III, transition region with a much smaller growth; and IV a region clipped to maximal masking. The middle of region II is the best region for the masking criterion, chosen at ~33 % (middle horizontal dashed dotted line).

FIG. 9.

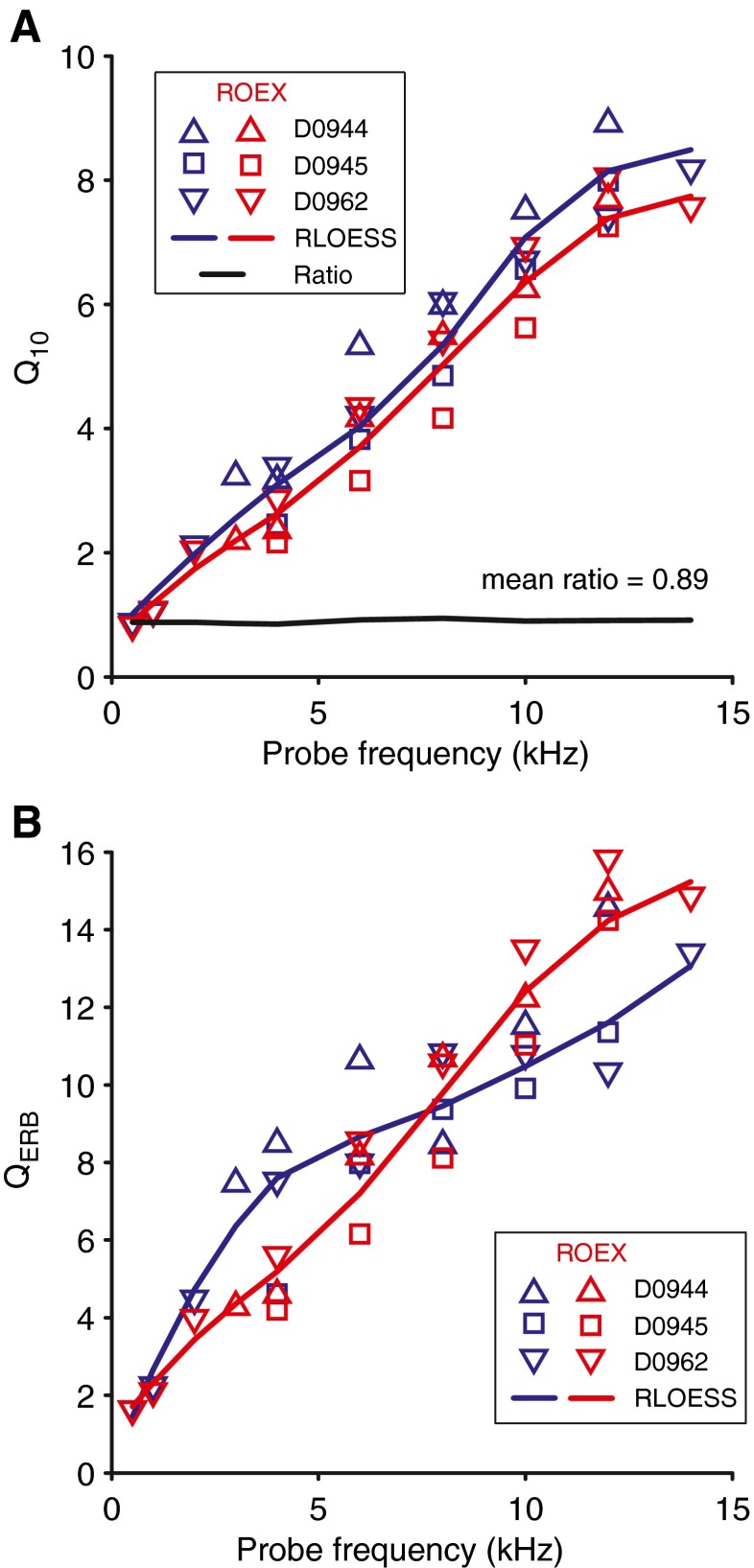
Comparison between directly obtained Q factors (Fig. 8) and Q factors from an estimated ROEX filter function using a power spectrum model for masking. A Q ₁₀ and B Q _ERB. Q values for three cats are plotted against probe frequencies ranging from 0.5 to 14 kHz. The blue symbols indicate Q values from CAP; the red symbols are extracted from the fitted ROEX filter function. The lines are trend lines calculated with a RLOESS function available in MATLAB. The black line in A is the relationship between the sharpness of the two trend lines (ROEX-Q ₁₀/direct-Q ₁₀).

Masking recovery

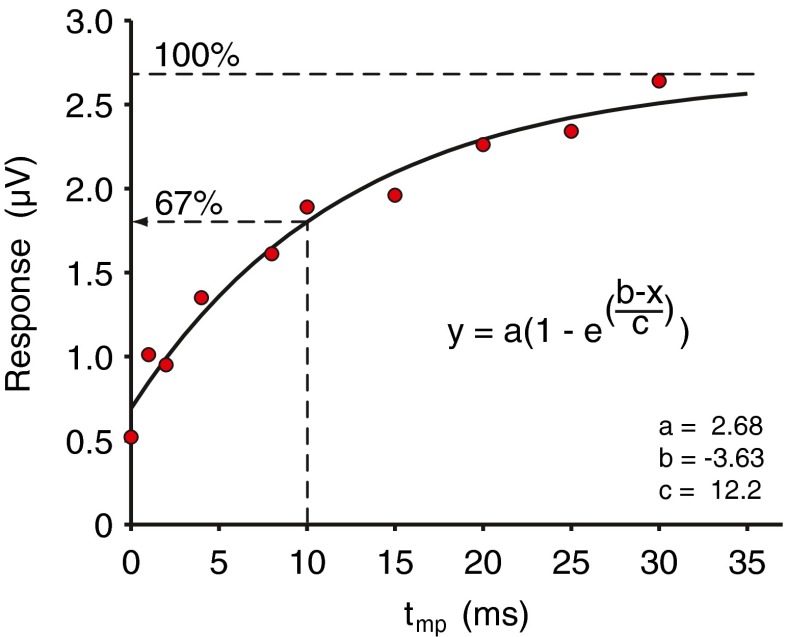
As a final check on the chosen parameter values in our NNFM paradigm, i.e., t_m, t_mp, and t_s, we verified the (fast) recovery from masking. Figure 6 illustrates the recovery of a 10-kHz, 10-ms, probe tone from a preceding no-notch noise masker with a duration of 83.71 ms (t_m); t_s was chosen to allow full (fast) recovery. The recovery function is measured in successive measurements where t_mp is increased from 0 to 30 ms in steps of approximately 5 ms while the masker to masker interval was held constant. The data points are well described by a recovery curve based on an exponential fast recovery model used for forward masking in single auditory nerve fibers (Harris and Dallos 1979). The exponential fast recovery model predicts that >99 % of the probe response would recover within the next probe to probe interval of 113.71 ms (t_p + t_s + t_m + t_mp), which validates the current chosen parameter values.

FIG. 6.

An example of a recovery curve derived with the NNFM paradigm. The amplitudes of the masked responses (red dots) are plotted as a function of ten different masker–probe intervals (t _mp) ranging from 0 to 30 ms. The conditions of the measurement were: nNW = 0, L _m = L _p = 40 dB SPL, f _p = 10 kHz. The solid curve is a fit through the data points using the formula in the figure with y the response and x the masker–probe interval. The parameters a, b, and c were determined using the Gauss–Newton method for nonlinear regression. The upper dashed line is the unmasked amplitude limit. The lower dashed line shows the fitted response value at t _mp = 10 ms, which is the value used in our standard paradigm.

MTCs, Q₁₀, and Q_ERB

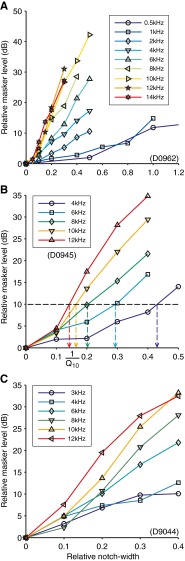
Figure 7 presents three sets of MTCs obtained in three different cats for various probe frequencies. The MTCs are reconstructed by straight lines between the data points. All MTCs show a monotonic increase with notch width and can have a slightly concave or convex curvature. In the three animals, there is a consistent increase in slope with increasing probe frequency which is a good indication that the CAP responses are generated by single units with CF close to the probe frequency.

FIG. 7.

Normalized MTCs for three different cats (A–C). The relative masker level is plotted as a function of relative notch width for a range of probe frequencies. The extraction of the estimated Q ₁₀ from the MTCs is illustrated in B; it is the reciprocal of the intersection of the dashed line at 10 dB relative masker level with the MTC. The masker reference levels (overall level in decibel) for the MTCs are presented in Table 1, indicated by “Ref L _m.”

The notched-noise paradigm yields one-sided masking tuning curves and, in its standard configuration with symmetrical notch, does not allow separate examination of the part of the filter above and below the probe frequency. One of the assumptions made, validated below in “Single-sided noise maskers,” is that the MTC, at low probe level, is symmetric around the nadir, i.e., both noise bands produce the same amount of masking for a given notch width. As illustrated in Figure 7B, the intersection of these one-sided tuning curves with a horizontal line at a relative masker level of 10 dB provides an estimate of the Q₁₀ for notched-noise maskers.

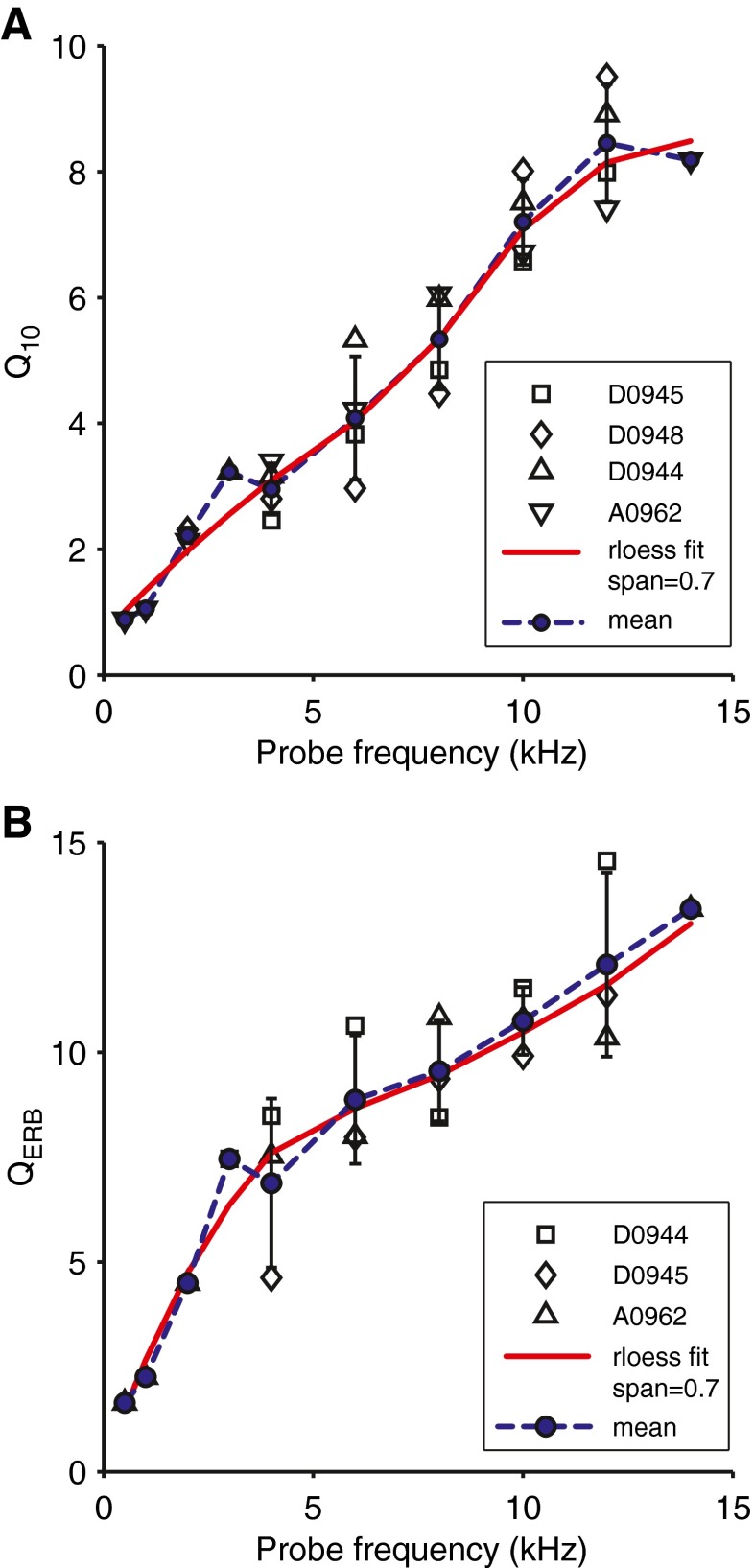
Figure 8 shows the two indicators of sharpness, Q₁₀ (Fig. 8A) and Q_ERB (Fig. 8B), plotted on a linear frequency axis for different cats (indicated with different symbols, see legend). In both figures, the filled dots, connected with dashed lines, are the average values across animals. The mean trend line of the Q₁₀ (Fig. 8A, dashed line) shows a fairly linear relation with probe frequency. For some probe frequencies, measurements are available for only a single animal and are thus statistically less reliable. For example, at 14 kHz, the mean trend line suggests a decreasing Q₁₀ factor beyond 12 kHz, but this is not supported by the within-animal trend (experiment A0962, … < Q_{10, 10 kHz} < Q_{10, 12 kHz} < Q_{10, 14 kHz}). A trend predictor more resistant to outliers, missing and scattered data points is the robust LOESS trend line (MATLAB routine smooth, method RLOESS, span 0.7), indicated in red in both plots. The LOESS trend lines show a, monotonically increasing, smoother course than the mean trend lines. The Q_ERB trend line (Fig. 8B) shows a clear bend at 4 kHz with a much steeper slope at the lower frequency side.

FIG. 8.

Dependence of Q factors on probe frequency in cats. A Q ₁₀ values for four cats are plotted against probe frequencies ranging from 0.5 to 14 kHz. The blue-filled dots connected with dashed lines are the mean values. The error bars indicate the standard errors of the mean; they are omitted for single data points. The red line is a trend line calculated with a RLOESS function (MATLAB). B Same as A, but for Q _ERB for three cats.

In this study, Q factors are obtained with notched-noise maskers whereas Q factors from single fibers are obtained with tones. To make a more appropriate comparison between the results from different maskers/exciters, i.e., noise maskers versus tones, the MTCs from three cats were converted to auditory filters as commonly used in psychophysical experiments (see “Extraction from an auditory filter” in “Methods”). The filter parameters and Q factors obtained from the ROEX filters are given in Table 1. It is clear from this table that for most of the obtained ROEX filter functions the second term in the ROEX(p,w,t) is negligible (w < −100 dB). Note that the masking “efficiency,” K, in the table depends on the specific probe level and masking criterion and that direct comparison between K factors with different conditions is meaningless.

TABLE 1.

Parameters, filter parameters, and results derived from the same data as in Figure 7

Frequency	L p	Ref L m	p	t	10 log(w)	K	Q 10	Q ERB
Cat 1: D0944 (masking criterion 50 %)
3,000	36	43	17.1	308.9	−335.7	−1.9	2.2	4.3
4,000	28	39	18.4	578.3	−342.7	−5.4	2.4	4.6
6,000	12	21	32.7	149.4	−439.2	−0.2	4.2	8.2
8,000	13	21	42.8	559.7	−402.9	4.3	5.5	10.7
10,000	15	23	48.9	239.9	−447.5	4.3	6.3	12.2
12,000	20	25	60.0	5.6	−34.6	7.4	7.7	15.0
Cat 2: D0945 (masking criterion 50 %)
4,000	50	51	16.8	394.0	−396.2	6.0	2.2	4.2
6,000	41	35	24.7	361.7	−365.8	14.4	3.2	6.2
8,000	34	34	32.5	124.2	−307.4	8.9	4.2	8.1
10,000	29	29	44.1	253.8	−390.6	11.3	5.6	11.0
12,000	33	31	57.0	713.4	−49.9	15.5	7.3	14.2
Cat 3: D0962 (masking criterion 33 %)
500	48	38	6.5	24.9	−355.4	14.4	0.8	1.6
1,000	47	37	8.4	336.5	−251.4	14.4	1.1	2.1
2,000	35	41	16.0	461.1	−383.2	6.9	2.1	4.0
4,000	35	40	22.5	419.1	−390.9	6.8	2.9	5.6
6,000	30	33	33.8	227.1	−193.3	10.9	4.4	8.5
8,000	22	27	42.3	158.1	−317.1	7.5	5.4	10.6
10,000	20	20	54.2	2.1	−25.3	14.4	6.9	13.5
12,000	20	23	63.3	295.3	−357.4	13.6	8.1	15.8
14,000	27	28	59.8	5.7	−29.7	13.1	7.6	14.9

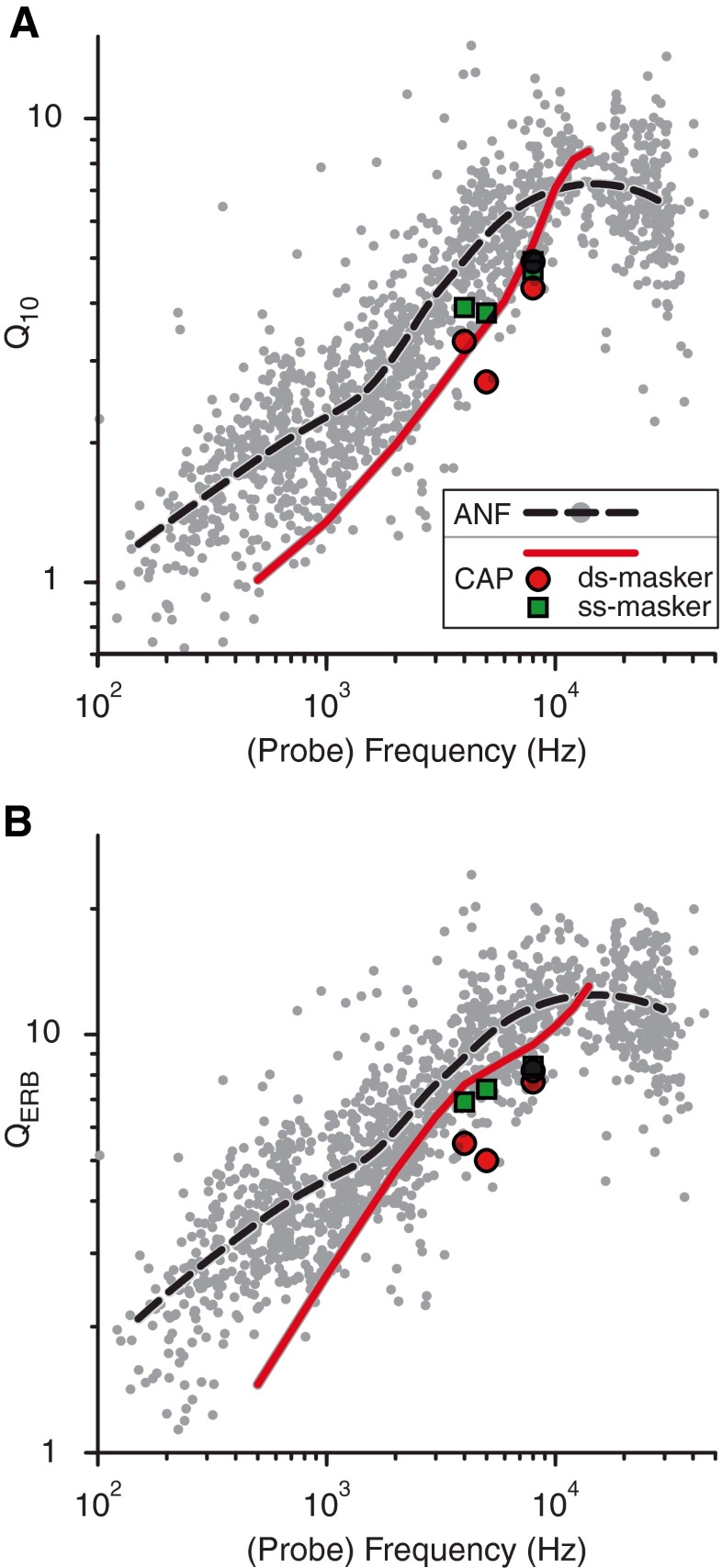
The Q₁₀ and Q_ERB factors from Table 1 are depicted as a function of frequency in Figure 9. The ROEX-Q₁₀ trend line in Figure 9A shows the same course as the directly obtained Q₁₀ trend line (replotted from Fig. 8A), but with slightly lower values. The relationship (ratio) between the ROEX-Q₁₀ and the directly obtained Q₁₀ trend lines is constant over the considered frequency range with a mean value of 0.89 (STD 0.09) and is depicted as the black line in Figure 9A. Since the ratio is small and because of the additional uncertainties in the ROEX-Q₁₀ arising from the assumptions (linearity and ROEX filter shape) in the derivation of the auditory filter, we consider the difference between the two curves too small to warrant use of the ROEX filter method. Therefore, in the remainder of this study, we only consider the Q₁₀ values directly obtained from the MTCs.

In panel B, the values for the ROEX-Q_ERB and for the directly obtained Q_ERB are shown for the same animals as in panel A. The trend line for the ROEX-Q_ERB is besides a proportionality factor identical to the trend line of the ROEX-Q₁₀ in panel A. The proportionality factor is equal to 1.95 and is biased by the dominant term in the ROEX(p,w,t) function at the tip of the symmetric auditory filter, i.e., W(g) = (1 + p|g|)exp(−p|g|). This value is almost equal to the theoretical value of ~1.945, which is calculated from the following derived equation

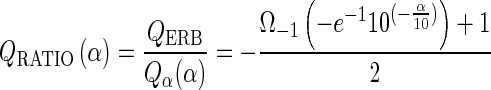4

where α means the relative level (decibel) associated to the type of the Q factor, e.g., α = 10 for Q₁₀; and where Ω₋₁ represents the omega function, which is the inverse relation of the function f(w) = we^w for the lower branch. The course of the directly obtained Q_ERB deviates significantly from the ROEX-Q_ERB; it is further discussed below in the part “Comparison with single auditory nerve fibers.”

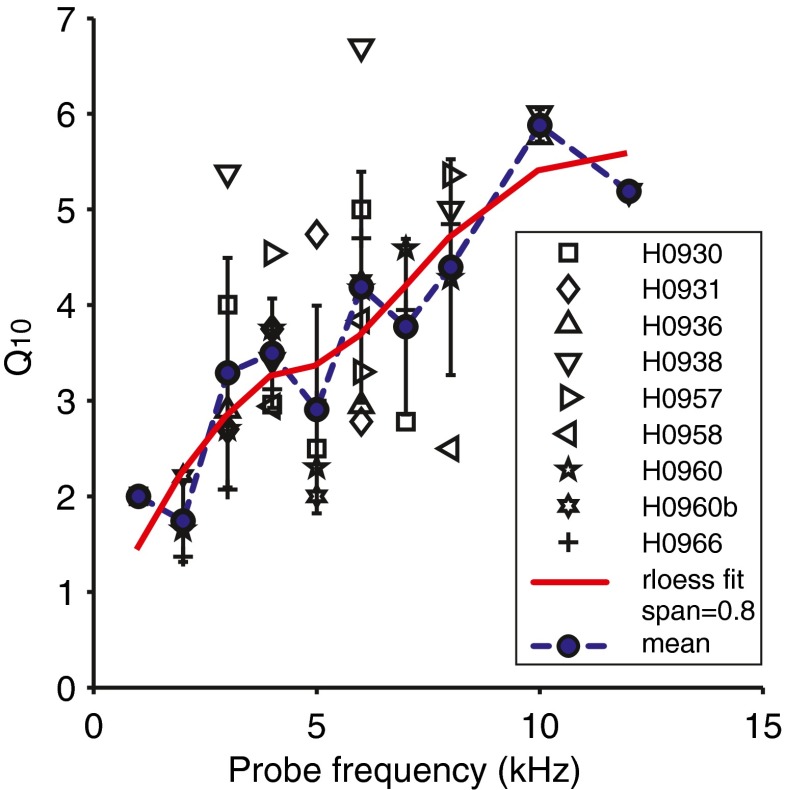
Figure 10 presents Q₁₀ factors as a function of probe frequency for nine chinchillas. The mean values have a similar increasing trend with probe frequency as in cat, but display much more variability. Despite the large variability, the trend (RLOESS) is very similar to the trend for cats. The trends for cat and chinchilla are further discussed below.

FIG. 10.

Q ₁₀ as a function of frequency for nine chinchillas, the probe frequency ranges from 1 to 12 kHz. The (blue) filled dots connected with dashed lines are the calculated mean values. The error bars indicate the standard errors of the mean; they are omitted for single measured data points. The red line is calculated with a RLOESS function (MATLAB).

Dependence on parameter choices

Most studies examining frequency tuning are conducted at threshold or at low probe levels, at which frequency selectivity is highest (Robles and Ruggero 2001). Due to the nature of the recorded signal and paradigm, compromises had to be made regarding SNR and number of repetitions. Probe levels were never at threshold, but at least 15 dB above CAP threshold and varied across the measured MTCs. So far, in the comparison between MTCs, we made abstraction of the probe level by normalizing the results. In this section, we examine the implication of some of our experimental parameter choices.

Probe level

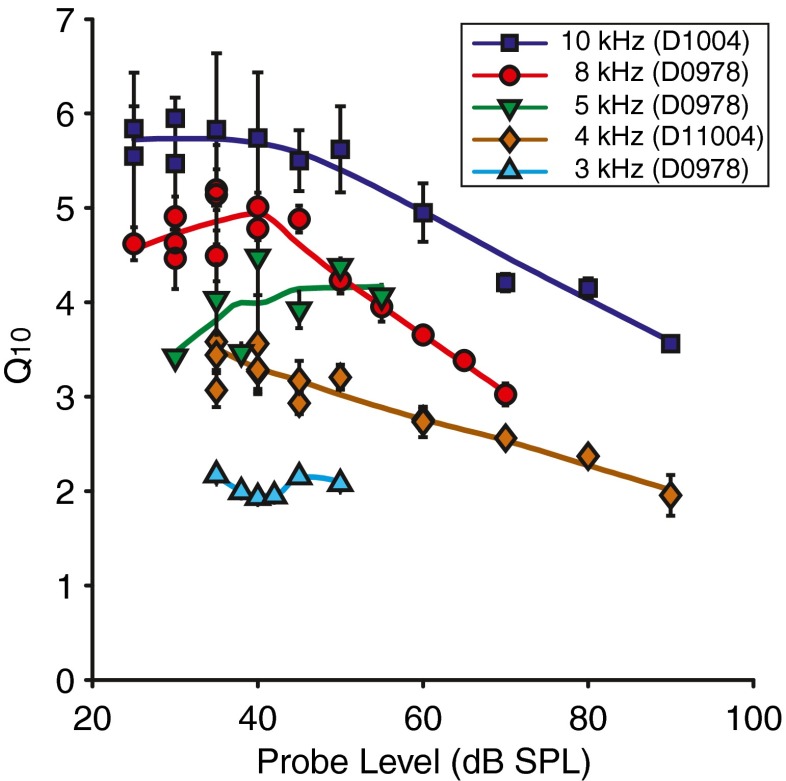
We examined the dependence of Q₁₀ on probe level. Cochlear frequency selectivity decreases with level: this is well documented for iso-input measurements although it may increase for iso-response measurements (Eustaquio-Martin and Lopez-Poveda 2011). Figure 11 presents Q₁₀ values as a function of probe level for probe frequencies ranging from 3 to 10 kHz, for three different cats. The trend lines for the most comprehensive data show a low-pass behavior with a cut-off level between approximately 40 and 50 dB SPL. Below the cut-off level, the Q₁₀ is roughly independent of the probe level. Some trends, i.e., for 5 and 8 kHz might suggest a local increasing or decreasing trend with frequency, but these are not significant, given the large standard error of the estimate for regression Above the cut-off level, the Q₁₀ declines monotonically with slopes of approximately −0.050, −0.067, and −0.046 dB/dB for 4, 8, and 10 kHz (curves with data points above 55 dB SPL). The probe levels that would typically be used (with the predefined SNR criterion of 18 dB) would be 45, 40, 35, 35, and 40 dB SPL for 3, 4, 5, 8, and 10 kHz, respectively. Thus, the Q₁₀ values obtained with our 18 dB SNR criterion represent the highest values that can be measured with this paradigm at all probe frequencies.

FIG. 11.

Dependence of Q ₁₀ factors on probe level for different probe frequencies in cat. Repeated measurements are shown separately; the error bars indicate the standard error of the estimate for regression (SEE). The lines are smoothed trend lines through the scattered data (the trend is obtained with a RLOWESS function and smoothed with a cubic spline interpolation (MATLAB)). All results were obtained with the fast method.

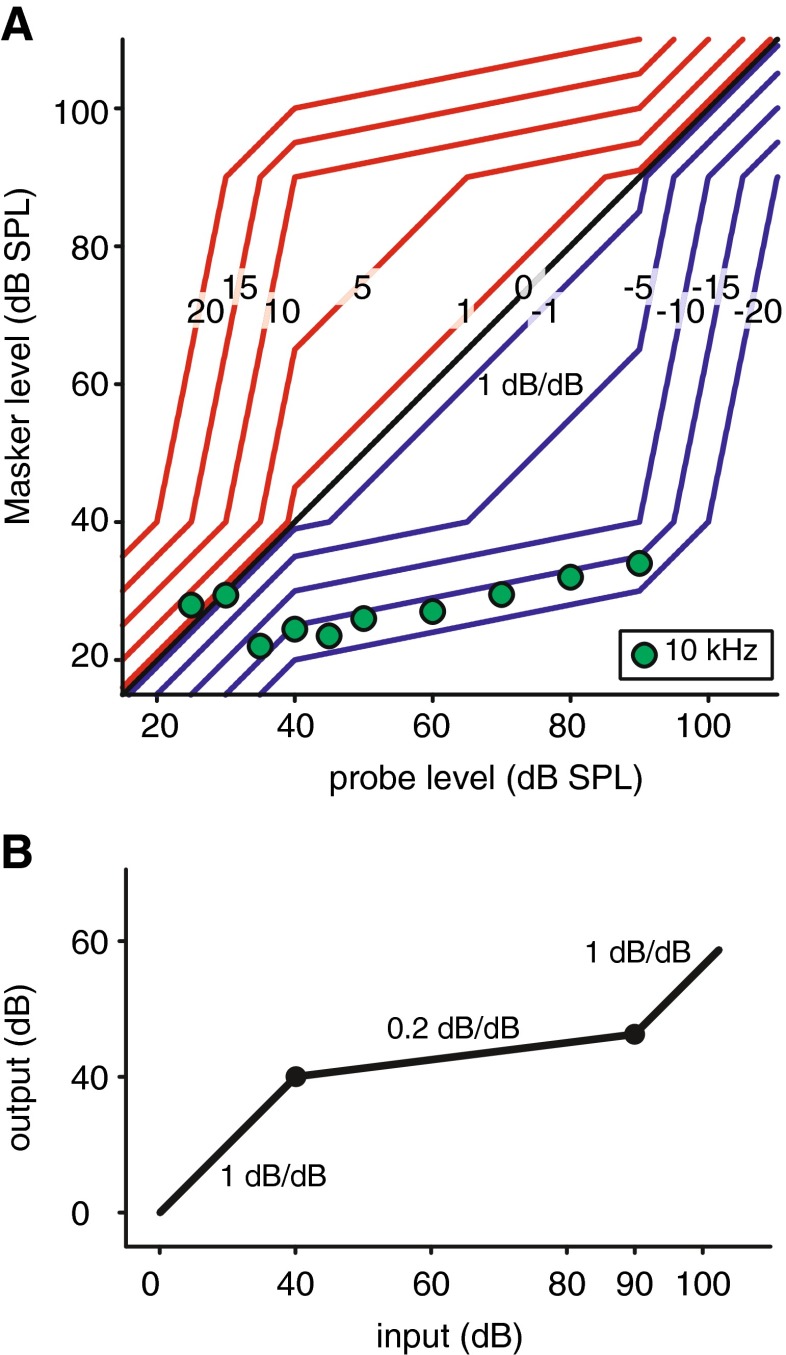
We interpret the decline of Q₁₀ beyond the cut-off level (Fig. 11) to reflect a change in operation mode (linear to compressive) of the probe. Mechanical measurements of basilar membrane motion to tones (Robles and Ruggero 2001) reveal an input–output (I/O) relationship consisting of three regimes (Fig. 13B): linear (1 dB/dB) regimes at the lowest and highest SPLs, connected by a compressive portion with shallower slope (taken at 0.2 dB/dB). At low probe levels, both probe and masker are in the linear regime and Q values are independent of SPL. With our masking criterion of 33 %, at higher probe levels, the probe can be in the compressive regime of the I/O curve while the masker is in the low SPL linear regime. In this situation, a change (reduction) in response due to a small increase in masker level is greater than a change (increase) in response to the same small increment in the probe level. The decline in Q₁₀ associated with the compression of the probe is not the result of the corresponding additional increase in probe level, but is related to the associated deformation (widening) of the probe’s excitation pattern. As a global effect, to keep the amount of masking constant, the notch width of the masker has to be widened, so the Q value decreases.

FIG. 13.

Illustration of the influence of cochlear compression on the GMB. A Simulated GMB curves for different masking conditions. The simplified model assumes that (1) the probe and masker input levels are subject to the same I/O curve (B); (2) masking is a linear operation; and (3) the masking criteria are proportional to the ratios of the excitation patterns (power) from masker and probe. These ratios, in decibel, are indicated on the curves in A. As comparison, the data points of the GMB in Figure 12 for a probe frequency of 10 kHz are included; the resemblance in absolute values is only a coincidence. B The BM I/O curve (log-log scale) used in the model. The compression coefficients (slopes) and cut-off points (40 and 90 dB) are chosen as suggested values.

Growth-of-maskability

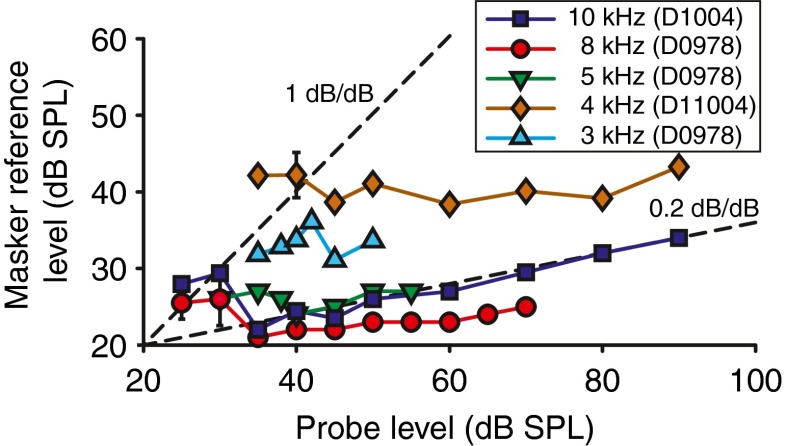
The interplay between probe level and masker level is traditionally measured with growth-of-masking (GOM) functions, which describe the dependence of masked threshold on masker level. We examined how the masker level required to generate a criterion response depends on probe level. Following the psychophysical literature (Nelson et al. 2001), we call the resulting functions (Oxenham and Plack 1997) growth-of-maskability (GMB) functions. According to the reasoning in the previous paragraph, we expect GMB functions to have a slope <1 dB/dB if the probe level is in a compressive regime while the masker level is in a linear regime. GMB functions for several probe frequencies are plotted in Figure 12 using a no-notch masker (masker reference level, i.e., L_m1 in Fig. 2). Masker (reference) levels for probe levels above roughly 40 dB SPL, associated to the cut-off level in Figure 11, show little dependence on probe level. The slopes are smaller than 1 dB/dB (cf. dashed line of equality) and closer to ~0.2 dB/dB (lower dashed line). These small slopes are consistent with our interpretation that the masker is operating in the linear region while the probe is operating in the compressive region, causing the decline in Q₁₀ with probe level (Fig. 11). At the lowest probe levels, the data points deviate significantly from the course of the other data points; the reason is unclear and is further briefly discussed below in the topic about the GMB model.

FIG. 12.

Growth-of-maskability (GMB) functions for the same data as in Figure 11. The data points are mean values measured at the masking criterion (33 %) and masker reference level conditions (no-notch, continuous noise spectrum). The dashed lines indicate a compression exponent of 0.2 and 1 dB/dB for equality. The error bars indicate standard error of the mean, when applicable.

For comparison with psychophysical data, it is useful to illustrate our reasoning with a very simple model. Figure 13A shows GMB curves for different masking conditions. For example, let us assume that for a given masking condition the effective “output” (e.g., the vibration pattern of the basilar membrane) in response to the probe stimulus has to be 15 dB higher than the response to the masker. At low stimulus intensities, in the linear regime, this requires a masker level 15 dB below the probe level. At high stimulus intensities, with the probe in the compressive regime, the masker level required is much lower than −15 dB relative to the probe level (e.g., for the I/O function in Fig. 13B, this would be a difference of −47 dB for a probe level of 80 dB SPL). The −15-dB blue line in Figure 13A shows all combinations of probe and masker levels that will generate at 15 dB difference between probe and masker output. If, on the other hand, the masking conditions would be such that the response to the probe stimulus has to be 15 dB lower than the response to the masker, the pattern is inverted so that the predicted GMB curves are mirror symmetric relative to the diagonal of equality (red vs. blue curves in Fig. 13).

The masking conditions (paradigm parameters such as masking criterion, masker–probe interval, masker length, etc.) determine the relative levels required between masker and probe to obtain masking and therefore the expected trajectory of the GMB curves. The black line in Figure 13A (diagonal of equality) represents the relation when the levels of probe and masker are equal. This situation can be obtained with tonal on-frequency maskers; for an example, see listener CP for 6 kHz in Fig. 2 (left) in Oxenham and Plack (1997). For all other curves, the compressive nature of the cochlea introduces regions with slopes deviating from unity. For an idealized I/O curve, the values of these slopes correspond to the compression exponent (e.g., 0.2 or 5 dB/dB). GMB or GOM curves obtained from studies using two-interval forced choice adaptive procedures or using “linear” off-frequency maskers to estimate compression exponents (Relkin and Turner 1988; Oxenham and Plack 1997; Plack and Oxenham 1998) typically have higher masker levels than probe levels and look similar to the red curves in Figure 13A. In the present paradigm, the masker level needed to achieve the masking criterion of 33 % is significantly lower than the probe level and therefore the shape of the curves is reciprocal (blue curves) to GMBs reported in the literature.

The slope of the GMB above the cut-off level (~40 dB SPL) for the 10-kHz data (green dots in Fig. 13A) is well predicted by the model. Below the cut-off level, some of the masker levels deviate from the prediction of the model, i.e., the lowest data points are off-set and do not show a clear predicted slope equal to 1 dB/dB. This observation is also valid for most of the other GMB curves in Figure 12 having different probe frequencies. Note that these data points were measured at unusually low probe levels, below our quality criterion.

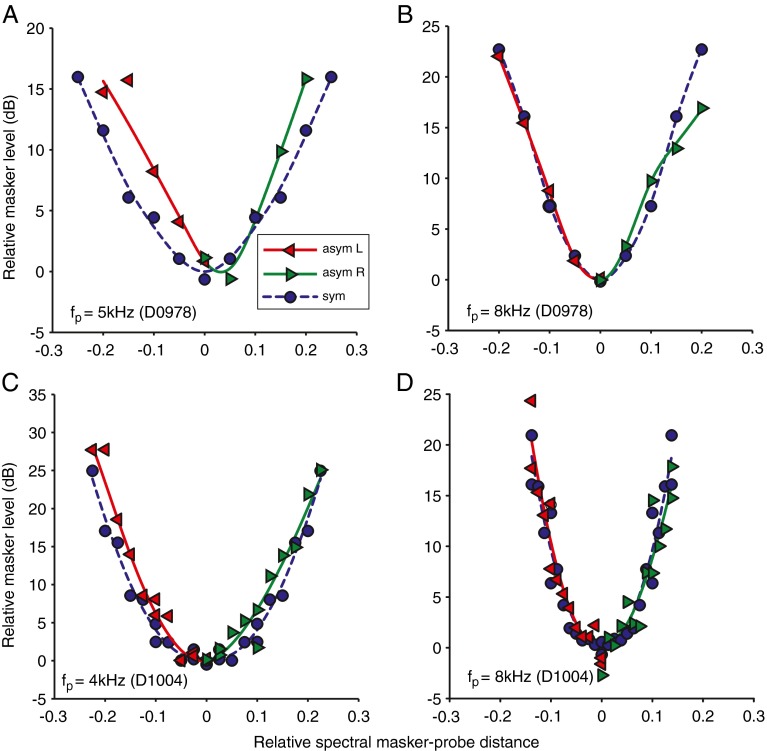
Single-sided noise maskers

All previous results were obtained with notched-noise maskers symmetrically positioned with respect to the probe frequency. The assumption here is that, at least at low probe levels, the slopes of the MTCs are symmetrical at both sides. To explore the validity of this assumption, we compared MTCs obtained using stimuli with single- and (symmetrical) double-sided noise maskers, hereafter named ss-MTCs and ds-MTCs, respectively. Figure 14 depicts four MTCs, with ss-MTCs and ds-MTCs at frequencies of 4, 5, and 8 kHz, obtained from two different cats. The abscissa shows the normalized spectral distance between the closest edge of the masker and the probe. The ss-MTCs are obtained by joining two independently measured MTCs obtained with a left and a right single-sided noise masker: negative relative masker–probe distances indicate a masker band below the probe frequency (f_m < f_P) while positive values indicate a masker band above the probe frequency (f_m > f_P). For the standard double-sided masker, we plot the MTC twice, mirror symmetrically. Note that in this case, the spectral distance equals half of the notch width. For visualization, left and right sides were fit by a trend line and vertically aligned at the origin. To minimize drift and variability between responses to single- and double-sided noise maskers, all measurements with the same notch widths were interleaved and recorded in one continuous measurement. The ds- and ss-MTCs do not show large differences. Particularly for single-sided maskers above the probe frequency, the trend line is very similar to that of the double-sided maskers. For single-sided maskers below the probe frequency, the data points are slightly elevated at the lowest probe frequencies (red curves in Fig. 14C and A, 4 and 5 kHz), but the slopes of the trend lines are similar.

FIG. 14.

Comparison between left/right single-sided and (symmetrical) double-sided noise masker MTCs. The measured probe frequencies are: A 5 kHz (L _p = 35 dB), B 8 kHz (L _p = 30 dB), C 4 kHz (L _p = 50 dB), and D 8 kHz (L _p = 40 dB). The trend lines are obtained with RLOESS and spline smoothing (MATLAB); the dashed blue line and blue circles denote the standard double-sided condition, the red line and left triangles denote the left single-sided masker condition, and the green line and right triangles denote the right single-sided masker condition. The masker reference levels are: A asym L = 31 dB, asym R = 32 dB, sym = 28 dB; B asym L = 26 dB, asym R = 28 dB, sym = 23 dB; C: asym L = 30 dB, asym R = 37 dB, sym = 30 dB; D asym L = 26 dB, asym R = 40 dB, sym = 31 dB.

Comparison with single auditory nerve fibers

The main goal of our study was to develop an electrophysiological method to estimate sharpness of tuning from mass cochlear potentials. In this section, we compare our estimates with those for single ANFs. The dots in Figure 15 show neural Q₁₀ values for ANFs available from previous studies in our laboratory. As observed in many previous studies, not only in ANFs but also behaviorally and in the CNS (Oxenham and Shera 2003; Shera and Guinan 2003; Sayles and Winter 2010), Q₁₀ increases approximately linearly with CF on a log-log scale. Interestingly, again in agreement with many previous ANF studies in different species (guinea pig [Evans 1972; Sayles and Winter 2010]; cat [Liberman 1978]; squirrel monkey [Rhode et al. 2010]; macaque monkey [Joris et al. 2011]), the distribution levels off or even bends over at its upper end, i.e., there is no further increase in Q₁₀ values at the highest CFs. To our knowledge, the mechanism(s) behind this saturating relationship have not been addressed.

FIG. 15.

Comparison between Q factors from CAP (red lines, same data as in Fig. 8 but on a log-log scale) and single ANFs (gray dots, 1,200 units, 28 cats; threshold level range −10 to 67 dB, spontaneous rate 0 to 136 s⁻¹, unpublished data) as a function of frequency for cat. A Q ₁₀ and B Q _ERB. For ease of comparison, smoothed AN trend lines (dashed lines, RLOWESS, MATLAB) are included in both panels. Additional Q ₁₀ factors from the accurate MTCs in Figure 14 with double-sided and single-sided maskers are included as the red circles and green squares.

Figure 15A compares the Q₁₀ CAP trend line (red, same as in Fig. 8A) with the trend of the ANFs (dashed black line). Note that the CAP trend line is located within the cluster of ANF data points. For low and middle probe frequencies, the CAP trend closely follows the lower boundary of the ANF data cluster, but at 10 kHz, the CAP trend intersects the ANF trend.

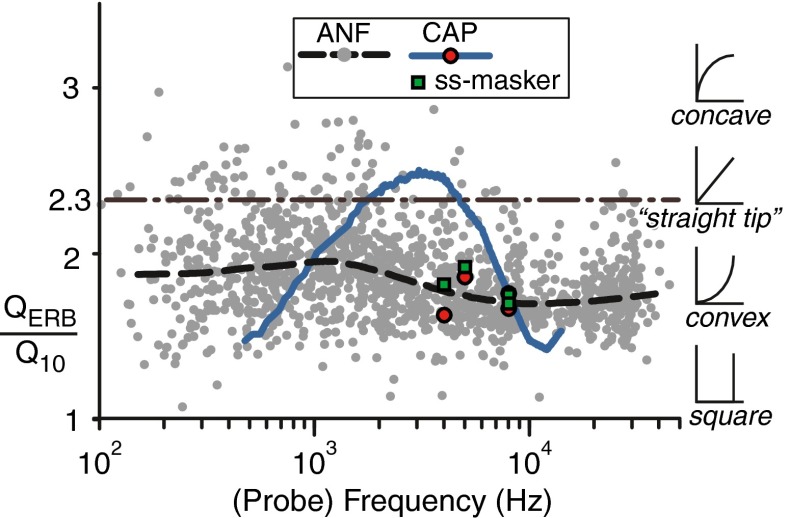
Many studies report Q_ERB rather than Q₁₀ values, the rationale being that the former provides a more robust measure because it incorporates all measurement points rather than only the points at the lowest threshold (CF) and 10 dB above. However, as pointed out in the “Methods” section, this is an advantage only when sufficient data points are available around the nadir of the tuning curve. Figure 15B compares the CAP-Q_ERB trend line (red, same curve as in Fig. 8B) with that from the ANF data. As in the case for the Q₁₀, the CAP-Q_ERB trend line is largely located within the cluster of ANF data points, but it is less congruent with the lower envelope of that distribution. This is in line with the earlier finding in Figure 9B, where the course of the CAP-Q_ERB clearly differed from that of the ROEX prediction. To understand this discrepancy, we studied the Q_ERB/Q₁₀ relationships in cat for ANF and CAP. For ANFs, the Q_ERB/Q₁₀ ratio is largely independent of species and CF ([Shera and Guinan 2003], footnote 6). Figure 16 shows the Q_ERB/Q₁₀ ratios derived from ANFs (gray dots and dashed line) and CAPs (blue line, data from Fig. 15) in cat. To illustrate the ratio for different tip curvatures, associated cartoons are shown at the right side of the figure. It is clear that the Q_ERB/Q₁₀ ratio of the CAPs has a much larger dependence on frequency than the trend of the ANFs, which is rather stable with a mean value of 1.82. Our interpretation is that due to a small number of data points near the nadir of the MTCs, the Q_ERB values for CAPs are unreliable. This is confirmed by the analysis of the MTCs from Figure 14 which have much finer spaced notch widths. The corresponding ratios of these double-sided and single-sided MTCs are included in Figure 15 as the red circles and green squares, respectively: these values straddle the lower boundary of the ANF distribution of Q_ERB values rather than the mean trend (red curve). The associated Q_ERB/Q₁₀ ratios depicted as the red circles and green squares in Figure 16 also show more consistency with the ratios of ANFs. In summary, the CAP-Q₁₀ values (Fig. 15A) are consistent between data obtained at high and at low resolution, while this is not the case for the Q_ERB values (Fig. 15B). This confirms our interpretation that Q_ERB factors are only reliable when enough data points are available around the nadir of the tuning curve. Because we do not have enough data with sufficient data points around the nadir, we restrict ourselves to Q₁₀ factors in the remaining analysis.

FIG. 16.

The Q ratio of the slopes near the nadir of the MTC as a function of probe frequency for cat, calculated as the ratios of Q _ERB and Q ₁₀ (blue solid line, data from trend lines in Fig. 8A, B). Ratios from AN fibers and a trend line are included as gray dots and the dashed line (trend obtained with RLOWESS function in MATLAB). The dashed dotted line indicates tuning curves with “straight” nadirs; above the line, the nadir is concave, below, convex (see tuning curve cartoons at the right side of the figure).

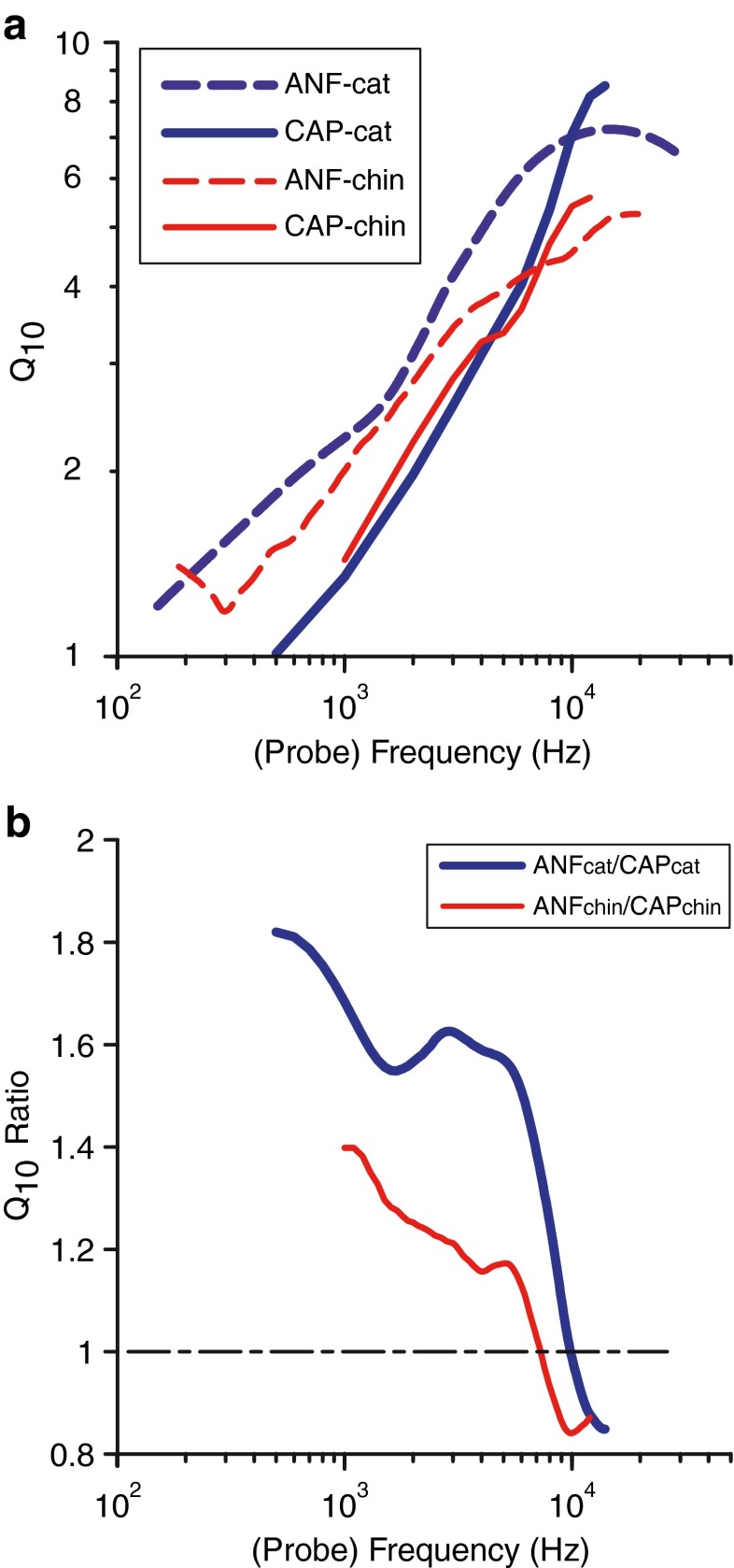
As has been pointed out in the “Introduction,” human sharpness of frequency tuning is unknown for single ANFs. CAP recordings provide an electrophysiological means to compare tuning across species, including humans. Moreover, CAP/ANF conversion functions of representative animals may allow us to estimate neural sharpness of tuning in animals or humans where no measurements of single units are available. In order to estimate ANF tuning from CAP tuning in other species and humans, we first have to assess the quantitative relationship between CAPs and single unit responses. In Figure 17A, the CAP-Q₁₀ of chinchilla (red line) and cat (blue line) are compared with the trends of ANFs (chinchilla: from (Ruggero and Temchin 2005); cat: own data from Fig. 15). As in cat (see earlier discussion in “Comparison with single auditory nerve fibers”), the CAP-Q₁₀ trend of chinchilla runs below the ANF trend, intersects it at 7.3 kHz, and is slightly larger above this frequency.

FIG. 17.

A Comparison between Q ₁₀ trend lines (trend obtained with RLOWESS function, MATLAB) from chinchilla and cat as a function of frequency. Cat—blue solid line: present CAP data, blue dashed line: ANF data (same data as in Fig. 15A); chinchilla—red solid line: present CAP data, red dashed line: ANF data as presented in Fig. 4 of Ruggero and Temchin (2005). B ANF-Q ₁₀/CAP-Q ₁₀ ratios from cat and chinchilla data in A.

The relationship between Q₁₀ ratios of ANF and CAP for cat (blue) and chinchilla (red) are shown in Figure 17B. Although the ratios in chinchilla are generally lower, the resemblance between the curves of the two animals is remarkable. Two regions can be distinguished that are separated by a deflection point at ~5 kHz. The first region, below the deflection point, shows a modest decrease with frequency. The second region has a much steeper declining slope and includes the intersection of the trend lines (cat—10 kHz, chinchilla—7.3 kHz), indicated by the dashed line.

Discussion

Whether frequency tuning is sharper in humans than in commonly studied laboratory animals is a matter of controversy (Ruggero et al. 1997; Shera et al. 2002; Oxenham and Simonson 2006; Lopez-Poveda et al. 2007; Eustaquio-Martin and Lopez-Poveda 2011; Joris et al. 2011). The aim of the present study was to examine whether the combination of forward masking and CAP recording provides a suitable means to investigate the basic frequency tuning of the neural input to the central nervous system. CAP recordings can be performed in humans in a minimally invasive way (Harrison et al. 1981) and may therefore provide comparative data across species. But the CAP is a mass potential, giving indirect information regarding tuning in single nerve fibers: “tricks” in stimuli and analyses are required to estimate frequency tuning. Behavioral studies also face this problem, and Oxenham and Shera (2003) argued that forward masking paradigms hold the greatest promise in this regard. However, from an extensive literature survey, Ruggero and Temchin (2005) concluded that “forward-masking psychophysical tuning curves […] greatly overestimate the sharpness of cochlear tuning in experimental animals and, hence, also probably in humans”. To investigate the validity of forward-masked CAP responses as a probe for frequency tuning, we adopted the masking paradigm of Oxenham and Shera (2003) and recorded from two species for which abundant single nerve fiber data are available: cat and chinchilla.

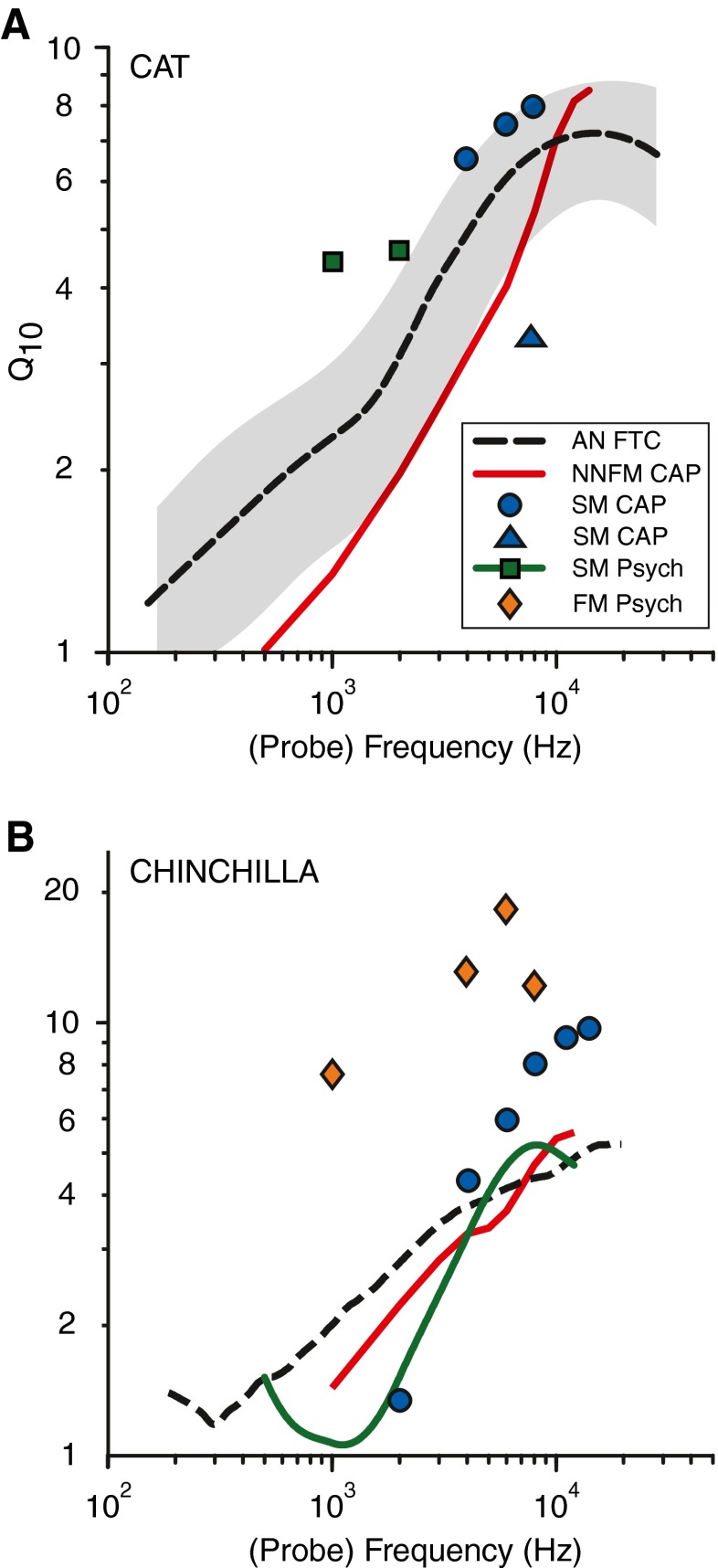
We find that masking of CAP responses behaves as expected from cochlear and nerve physiology in a number of respects. The masking intensity curve to broadband noise at low probe level (Fig. 5, red curve) is very similar to that of tonal maskers in single fibers (Harris and Dallos 1979). Also, recovery from masking as described by these authors applies in similar form to our data (Fig. 6). Masking tuning curves show a monotonic increase with notch width, and they become narrower with increasing probe frequency (Fig. 7). Tuning sharpness, as quantified by Q₁₀, decreases for probe levels above ~45 dB SPL (Fig. 11). The slope of the growth of maskability with probe level is as expected from cochlear compression (Figs. 12 and 13). Single-sided and double-sided maskers result in quite similar estimates for Q₁₀, which validates the assumption of symmetry around the nadir of the tuning curve (Figs. 14 and 15). Finally and most importantly, CAP-Q₁₀ values increase with probe frequency at a slope very similar to the trend in single ANFs (Figs. 15, 17, and 18), and the same basic relationship is found in the two species studied (cat and chinchilla), although the data in chinchilla showed more variability. We find that over most of the frequency range, the CAP-Q₁₀ closely follows the lower boundary of the distribution of neural Q₁₀ values (Fig. 18) and underestimates the trend rather than overestimating it as seen in some of the available masking studies (symbols in Fig. 18). Only at high frequencies does the CAP trend cross the trend for single fibers: in cat, this crossing point is near 9 kHz, and in chinchilla, it is near 7 kHz. Overall, the results show that the technique of notched-noise forward-masked CAP measurements provides a reliable estimate of the lower boundary of frequency tuning in the auditory nerve. Even if it would be the case that psychophysically the paradigm results in an overestimate of frequency tuning (Ruggero and Temchin 2005), this is not the case for the paradigm used in this study.

FIG. 18.

Comparison of sharpness between different paradigms and methods for cat (A) and chinchilla (B). The Q ₁₀ values from ANF and the NNFM paradigm for CAP are indicated by the dashed black and solid red lines, respectively; values from SM-CAP are indicated as blue circles and triangles. A Q ₁₀ values from psychophysical studies using simultaneous masking are indicated by filled green squares (Pickles 1979, Fig. 7); SM-CAP: blue circles (Carlier et al. 1979) and triangles (Van Heusden and Smoorenburg 1981); the gray area indicates the upper and lower border of the AN fiber’s standard deviation. B Q ₁₀ values from a psychophysical study using forward masking are indicated by yellow-filled diamonds (McGee et al. 1976); trend from values of psychophysical studies using simultaneous masking are indicated by the green line (Salvi et al. 1982; Niemiec et al. 1992); SM-CAP: blue circles (Spagnoli and Saunders 1987).

In the present paper, we explore the paradigm as an empirical tool to obtain Q measures from CAP recordings. To fully understand the relationship between single fiber and CAP responses, it is necessary to (1) characterize the population response of fibers to the stimuli used and (2) to characterize the “unit contribution” of each fiber at the round window. For example, the CAP response to click stimuli has been modeled convolving post-stimulus time histograms with spike-triggered averages of the round window potential for single fibers and summing across CF (Goldstein and Kiang 1958; Antoli-Candela and Kiang 1978; Wang 1979; Prijs 1986). Single fiber studies of forward masking are limited and restricted to probe frequencies at the CF of the fiber studied (Harris and Dallos 1979): population data are needed to allow prediction of forward-masked CAPs. In the absence of such data, auditory nerve models can be used to gain insight into the relationship between the notch-noise forward-masked CAP data and single fiber data. A full treatment of factors generating the patterns observed is deferred to a subsequent study and we here restrict ourselves to some general comments on potential mechanisms.

Synchronization across nerve fibers is essential to obtain a measurable CAP (Goldstein and Kiang 1958). Cochlear mechanisms cause a CF-dependent delay such that high CF fibers tend to be more synchronized to each other than low CF fibers. In Figure 17B, we show the ratio between neural and CAP-Q₁₀ values as a function of frequency, for cat (blue line) and chinchilla (red line). The trend is similar for the two species and shows two segments with different slopes. We surmise that the general decrease in the ratio from low to high probe frequencies, as well as the accelerating trend in this decrease, reflects an increase in across-fiber synchronization with increasing probe frequency. However, it is difficult to estimate the interaction of probe frequency, notch bandwidth, and probe and masker level on response variables such as response amplitude and synchronization without further empirical data or use of a detailed nerve model.

A factor which has to be taken into account is the (a)symmetry of the excitation patterns. One of the assumptions made in the paradigm is symmetry in the excitation patterns around the probe frequency. Preliminary modeling suggests that the presence of asymmetry around the nadir of the MTC predicts lower Q values measured with (symmetrical) double-sided maskers. We made a limited number of measurements with single-sided maskers (Fig. 14), which have the ability to reveal asymmetry in MTCs, and indeed, the Q factors yielded somewhat higher values than those obtained with double-sided maskers. This is illustrated in Figure 15A where the Q₁₀ values from the single-sided noise maskers (green squares) are consistently higher than the double-sided noise maskers (red circles).

Figure 18 shows Q values from several sources (compiled by Ruggero and Temchin 2005; for references, see legend). Behavioral studies used simultaneous masking (Fig. 18A: green squares, Fig. 18B: green line) or forward masking (orange diamonds); CAP studies also used simultaneous masking (blue circles) or forward masking (red trend line: this study). The trend lines for single fiber tuning are also shown. Surprisingly, nearly all values based on simultaneous masking are above our CAP trend line (red) and even above the trend line for the neural data (dashed). As pointed out by Ruggero and Temchin (2005), the behavioral data obtained with forward masking (chinchilla) yield extremely high Q values compared to either the single fiber nerve data or to our CAP data. Similar data and trends are shown for other species in Figs. 2 and 4 of Ruggero and Temchin (2005). The origin of the high Q values measured with behavioral forward masking in chinchilla (or in other species) is unclear. Ultimately, the behavioral data must reflect the interpretation by a central processor of activation patterns in the auditory nerve, and it is unclear which aspects of these patterns are critical (Relkin and Turner 1988; Relkin and Smith 1991). For example, “off-frequency listening” is mentioned by Ruggero and Temchin (2005) as a probable cause for the large difference between forward-masked behavioral and neural data. However, a possible peripheral factor leading to overestimation of sharpness is compression of the masker, also discussed by Eustaquio-Martin and Lopez-Poveda (2011). Note that compression can also occur in threshold tuning curves of auditory nerve fibers, especially for frequencies away from CF, which require higher signal levels to comply with the same response criterion. However, Q₁₀ values for auditory nerve fibers are unlikely to be affected by compression, because the corresponding SPL values (at the tuning curve nadir and the range 10 dB above) are too low to be in the compressive range. The schematic input–output function in Figure 13B shows two linear regions connected by a compressive region where larger masking levels are required to obtain the same effective masking as in the linear regions—an outcome which is phenomenologically similar to that of a high Q system. Growth-of-maskability functions in detection studies commonly show a slope ≥1 (Relkin and Turner 1988; Relkin and Smith 1991; Oxenham and Plack 1997; Plack and Oxenham 1998), as illustrated by the red lines (Fig. 13A). In contrast, in our data (Fig. 13A, green circles), these functions had a slope <1, suggesting that the probe was rather in the compressive region and the masker in the lower linear region and vice versa in detection studies like most psychophysical studies. The difference may stem from the masking criterion. We surmise that the effective masking criterion, and therefore masking, is high in detection studies, while it is typically low and predefined in physiological studies (e.g., 33 % here and in Dallos and Cheatham [1976], Fig. 6). Variables that increase masking (e.g., shortening of the masker–probe interval; increase in masker duration) can influence the masking criterion and thereby affect the estimated Q value. Most of our measurements were at low probe and masker levels: to the extent that the probe levels reached the compressive region of the input–output function, the Q values obtained with forward-masked CAPs would be underestimates of nerve fiber tuning.

In psychophysical studies, it is common practice to convert MTCs obtained with notched-noise maskers to tonal equivalent auditory filters using a power spectrum model of masking. In contrast to psychophysical studies, Q₁₀ values extracted from auditory filters (Fig. 9) were, although not importantly, smaller than those directly obtained from MTCs. This suggests that, for cochlear tuning, masking with notched-noise maskers is similar to masking with tonal maskers. The lack of off-frequency listening and central auditory processing could explain the difference with psychophysical studies.