Determining all parameters necessary to build Hill-type muscle models from experiments on single muscles

Abstract

Characterizing muscle requires measuring such properties as force–length, force–activation, and force–velocity curves. These characterizations require large numbers of data points because both what type of function (e.g., linear, exponential, hyperbolic) best represents each property, and the values of the parameters in the relevant equations, need to be determined. Only a few properties are therefore generally measured in experiments on any one muscle, and complete characterizations are obtained by averaging data across a large number of muscles. Such averaging approaches can work well for muscles that are similar across individuals. However, considerable evidence indicates that large inter-individual variation exists, at least for some muscles. This variation poses difficulties for across-animal averaging approaches. Methods to fully describe all muscle’s characteristics in experiments on individual muscles would therefore be useful. Prior work in stick insect extensor muscle has identified what functions describe each of this muscle’s properties and shown that these equations apply across animals. Characterizing these muscles on an individual-by-individual basis therefore requires determining only the values of the parameters in these equations, not equation form. We present here techniques that allow determining all these parameter values in experiments on single muscles. This technique will allow us to compare parameter variation across individuals and to model muscles individually. Similar experiments can likely be performed on single muscles in other systems. This approach may thus provide a widely applicable method for characterizing and modeling muscles from single experiments.

1 Introduction

A fundamental goal of neuroscience is explaining motor pattern generation. Given that muscles produce motor patterns, fulfilling this goal requires predicting muscle response to motor neuron input. Hill-type models (Hill 1938, 1950) are often used to make these predictions (Hannaford and Winters 1990; Winters 1990; Zahalak 1990; Zajac and Winters 1990). In most past work, the parameters in these models are determined by measuring the values of one or at most a few model parameters in one set of experiments, the values of another set of model parameters in another set of experiments, the values of yet another set of model parameters in yet another set of experiments, etc. The data obtained from each set of experiments are then averaged and these means are used to represent the population as a whole.

A potential problem with this approach is that many systems, including muscles, are characterized by multiple parameters, each of which could have large individual-to-individual variation, and which combine to create system activity. In such systems, individuals that have mean values for all these parameters may represent only a small minority, or none, of the population’s members, and models built using means calculated separately for each parameter may not re-create the mean activity present in the population. This property is well demonstrated by human beauty. The most beautiful faces are simply those in which all facial features (inter-eye distance, ear size, etc.) have the population mean (Langlois and Roggmann 1990). However, it is very rare for any individual human to have mean values for all of the many features that define a face. For instance, if humans assess beauty on the basis of eight such features, 50 % of the population has near the population mean for each feature, and the features assort independently, only 0.5⁸, or one in 250, humans have the ideal mean.

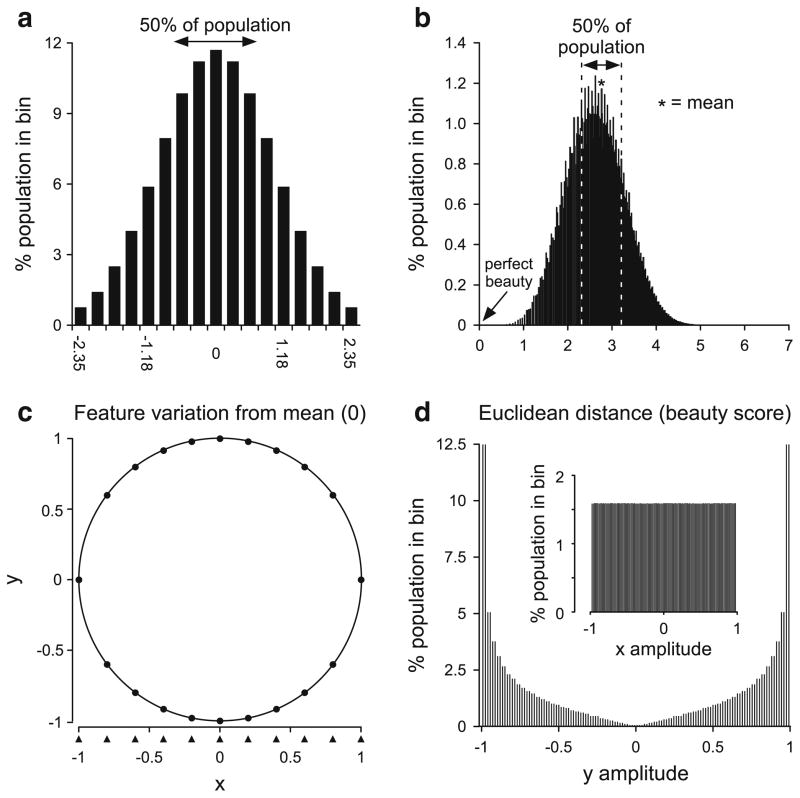
Using such means as models can pose two difficulties. To illustrate the first, consider the case in which each feature has a Gaussian distribution across the population centered on zero (Fig. 1a). In this case, the feature’s mean value is zero, and positive and negative values represent, for instance, noses that are smaller or larger than this mean. If the features assort independently, members of the population with a given value for one feature continue to have a Gaussian distribution in another. For instance, if Fig. 1a represents nose size, ear size follows a Gaussian distribution in each nose size class (each column in Fig. 1a). As such, of the 0.76 % of the population with very small noses (x axis value −2.35), 0.76 % also have very small ears, 11.84 % have ears with the population mean size, and 0.76 % have very large ears. One can thus calculate what percentage of the population has any given set of feature values. For example, the percentage of the population with very small noses (x axis value of nose size distribution, −2.35), moderately large ears (x axis value of ear size distribution, 1.18), and average eye separation (x axis value of eye size distribution, 0), is the product of their respective individual fractions (y axis value of each column divided by 100), 0.0076 × 0.0596 × 0.1184 × 100 = 0.536 %.

Fig. 1.

Explanation of potential difficulties of using the means of parameters measured in separate sets of experiments as population models. a Distribution of a single facial feature in a population. Zero is the mean of the feature. b Percentage of the population with a given Euclidean distance from the individual with the mean value for all features (zero distance, arrow) when each individual has eight facial features that assort independently. The overwhelming majority of the population is far from the individual with a mean value for all eight features, and the most representative model for the population would thus be one of the faces in the middle of the peak. c Plot of the function y² = 1− x². Note that calculating y values from evenly spaced x values (a flat distribution, arrowheads) gives primarily y values greater than 0.5 or less than −0.5. d Distribution of y when x has a flat distribution (inset). In the absence of a priori knowledge, there is no reason to believe the x and y are dependent. If, alternatively, the values of each (x, y) pair were known (that is, x and y were both measured for each individual of the population), then they could be plotted against each other as in (c) and the dependence is obvious

If one assumes that beauty depends on the sum of the values of the individual features, the shape of the beauty distribution across the population would differ from that of Fig. 1a, but would still have its peak at a beauty value of 0, the ideal mean. However, this mean would have two different sorts of individuals, a very small percentage (fⁿ, where f is the fraction in the center peak of each individual feature’s distribution and n is the number of features) that had mean values for each individual feature, and a much larger percentage that had a beauty score of zero because their individual features had both negative and positive variations from the mean, and thus their sum was zero. As such, even in this example in which the mean beauty value (zero) equals the sum of the means of each individual feature, the most representative member of the population is not the rare individual whose feature’s all have the mean value, but instead one of the many others whose individual features vary from the feature means, but whose positive and negative variations counterbalance each other.

This metric of beauty, however, is clearly incorrect, as having too small ears does not counterbalance having too large nose. Both deviations from the ideal mean instead add to decrease beauty. A metric which has this property is to set each individual’s beauty as the Euclidean distance from the mean, $\text{beauty}=\sqrt{{\sum }_i{({\overline{x}}_i-x_i)}^2}$, where the x_i are each facial feature and the x̄_i are each feature’s mean. A score of zero is thus perfect beauty and higher numbers indicate decreasing beauty. Assuming that the variations of each again follow the distribution in Fig. 1a and that the features assort independently, Fig. 1b shows the beauty distribution across the population if beauty were determined by eight facial features. Most of the population has faces of equal intermediate beauty with these faces differing from the ideal mean (arrow) in multiple ways. As such, any of these intermediate faces is much more representative of population beauty than is the ideal mean. In systems such as beauty in which an emergent property arises from combining multiple components, in general the best model is thus not the one built using each component’s mean, which may result in a very rare value (zero) of the emergent property (beauty). The best model is instead any of the (many) component combinations that result in the emergent property being at its mean value (in this case, about 2.6).

Modeling studies of rhythmically bursting neurons provide another example of how models built from component means can fail. Golowasch et al. (2002) constructed multiple model bursting neurons, each of which fired one action potential per burst. All the neurons contained the same types of membrane conductances, but different amounts of each. When the conductance amounts of these multiple single-spike bursters were averaged and a model neuron constructed using these means, this mean “single-spike” burster instead fired three spikes per burst. In this case using component-by-component means thus not only failed to represent the largest group in the population but also failed to represent any member of the population.

The above arguments concern features that assort independently. However, an analogous need to measure characteristics individual-by-individual also arises in dependent characteristics. For instance, consider two features, x and y, in which y² = 1 − x² (Fig. 1c) and x varies from −1 to 1 with a flat distribution across the population (inset, Fig. 1d). As a result of the quadratic, the flat distribution in x results in the y values alternatively clustering near ±1 (Fig. 1c, d; the arrowheads under the x axis in Fig. 1c shows ten equally spaced (flatly distributed) x points; the filled points on the circle show the associated y values). This example again shows the danger of reflexively using means, which in this case are x, y = 0, something true for each feature of only a vanishing small percentage of the population, and for both in no individual. More importantly for the issue at hand, if x and y are measured separately in different groups of animals, the only data available are the distributions in Fig. 1d. Although one can derive the quadratic from these distributions if one assumes x and y are related, one cannot from these distributions alone even show that x and y are correlated, much less causally related.

A clearly more appropriate approach is simply to measure both x and y in each individual and plot x versus y. This plot would reveal a circle and hence show both that x and y are correlated and the correlation’s form. Proving causation would require independently varying x and y to show that varying x caused y to vary but not vice versa. However, without evidence of the correlation, there would be no indication even to try these experiments.

The difficulty with following this approach in biological systems is that it is often difficult or impossible to measure all of the system’s defining characteristics in single animals. For instance, neurons typically contain multiple membrane conductances. Each conductance is defined by multiple characteristics—reversal potential, total conductance amount, the multiple parameters that define the voltage and time-dependent rates of conductance opening, closing, and inactivation, and the steady-state amount of opening, closing, and inactivation present at any given voltage. There are too many parameters in the equations that define these characteristics to measure them all, with present techniques, in single experiments on individual neurons. It is thus impossible to characterize completely any individual neuron’s complete conductance makeup. Different subsets of conductances are instead measured in many examples of “same” (e.g., cortical pyramidal) neurons to obtain mean values of these parameters for each conductance. However, as demonstrated in Fig. 1, the extent to which all these mean values are simultaneously present in any individual neuron, and to which different parameters co-vary (e.g., does the time constant of fast sodium current inactivation vary with the time constant of delayed rectifier current activation), cannot be discerned from such mean data.

Considerable recent work suggests that these concerns exist in real systems. As noted above, Golowasch et al. (2002) have shown that using separately obtained mean conductance values in building neuron models can be invalid. Marder and co-workers (2006) have simultaneously measured the amounts of a subset of the neuron’s conductances (which is possible with present techniques) in single neurons, and shown that these amounts show large and correlated across-animal changes. Stick insect (Carausius morosus) extensor muscles (Fig. 2; Hooper et al. 2006) and lobster (Panulirus interruptus) pyloric muscles (Thuma et al. 2003) also show great animal-to-animal variation. All the concerns noted above about using separately measured means to describe and model multi-component entities may thus apply to these biological systems. Resolving this issue requires being able to measure all of a system’s fundamental characteristics in single experiments on single exemplars of the system (single neurons, single muscles). In muscle, this requires measuring all the parameters that define the muscle’s passive steady-state force–length curve, parallel and series elasticities, force–length curves at all activations, and force–velocity curve.

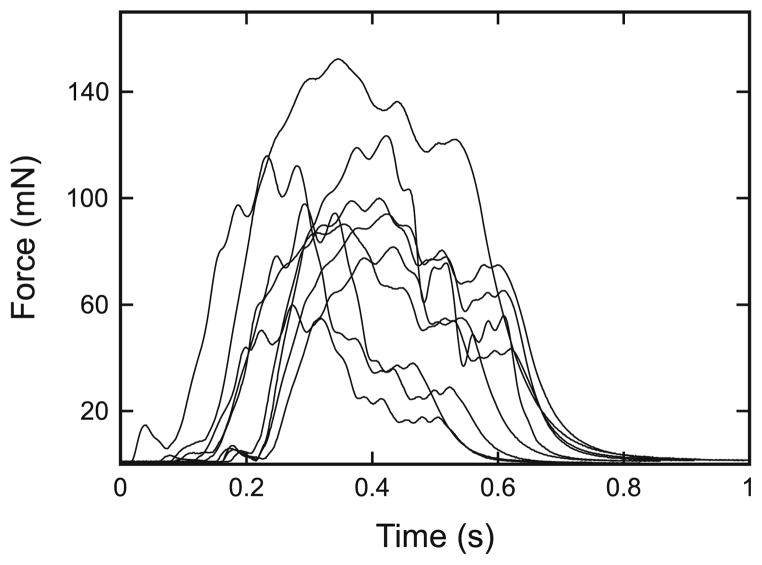
Fig. 2.

Individual muscles show large differences in force production in response to identical motor neuron stimulation. Isometric contractions of extensor muscles from nine different animals (muscles A–I here) induced by stimulation with a pulse train delivered with the same spike pattern as that previously (Hooper et al. 2006) recorded during a single stick insect sideways step. For a discussion on the variability of extensor muscle data, see Guschlbauer et al. (2007) and Hooper et al. (2006, 2007)

Methods that allow measuring all these parameters directly in single experiments in single muscles have not been described. Wagner et al. (2005) have described an alternative approach in which these parameters are not directly measured, but are instead derived by measuring force response to constant velocity length changes in individual muscles. A drawback of this approach is that it requires a well-defined large-scale model structure in which to perform parameter optimization. A more direct approach is to first measure muscle properties in sufficient detail to identify what types of equations describe the properties (e.g., that a Hill hyperbola describes force–velocity). These identifications often require considerable data, and thus the classic across-animal approach. If this work shows that the equation type of each property remains the same across animals, measuring equation parameter values generally takes many fewer measurements, perhaps few enough that every equation’s parameter values could be measured in single experiments on single muscles.

Prior work has defined what equation types describe all the properties required to construct C. morosus extensor muscle models, and that the same equations describe these properties across animals (Guschlbauer et al. 2007). We show here that the values of the parameters of all these equations can be measured in single experiments on single C. morosus extensor muscles. This approach allows individual stick insect muscles to be modeled, and thus overcomes the potential pitfalls associated with data averaging. In the second article of this series, we use this approach to show that these parameter values indicate large across-individual variation and that the changes in some of these parameters are correlated, and examine possible reasons for these correlations. In the third, we show that using individual muscle-specific parameter values markedly increases muscle simulation accuracy in response to tonic and physiological patterns of motor neuron activity. Taken together, these articles demonstrate that individual muscle-specific modeling is both possible and preferable in stick insect and likely other muscles.

2 Materials and methods

2.1 Dissection and experimental set-up

Experiments were performed at room temperature (20–25 °C) on adult female stick insects from the departmental colony during animal subjective day. Only animals that showed robust responses to handling were used. All legs except the right middle were amputated at midcoxa. The animal was then pinned dorsal side up on a balsa-wood platform and the coxa, trochanter, and femur embedded in dental cement (Pro-TempII, ESPE, Seefeld, Germany). The thorax was opened longitudinally, the gut lifted from the thorax and moved to one side, and the trachea and fat tissue were removed. The thoracic cavity was filled with C. morosus saline (Weidler and Diecke 1969) and the mesothoracic nerves dissected to gain access to nerve nl3, which contains all extensor tibiae motor axons: the fast and slow extensor tibiae axons and common inhibitor 1 (Bässler and Storrer 1980). The nl3 nerve was crushed near the ganglion, dried, lifted onto the hooks of a bipolar stimulation electrode, and isolated from the bath with white petroleum jelly (Engelhard Arzneimittel GmbH & CoKG, Niederdorfelden, Germany).

The femur was opened distally by cutting a small window in the dorsal cuticle taking care to damage as few extensor muscle fibers as possible. The femoral chordonotal organ was removed and tendon position at 90° femur-tibia angle (defined as rest length, Guschlbauer et al. 2007) was measured. The tendon was cut and connected to the lever of a dual-mode lever system Aurora 300 B (Aurora Scientific Inc., Ontario, Canada) with a hook-shaped insect pin. This is a high-accuracy force and length machine, with a force resolution of 0.3 mN and a length resolution of 1 μm, resolutions accurate enough for the measurements being made here (force changes from 0.4 to 247 mN, length changes from 2 to 150 μm). The muscle was reset to rest length until muscle property measurements were made. Saline was applied to the exposed muscle periodically throughout the experiment. The extensor is a simple unipinnate muscle (Bässler et al. 1996) with a maximum pinnation angle of 15.6° within the physiological working range (Guschlbauer et al. 2007). Assuming the muscle fibers are parallel to the muscle long axis therefore causes maximum muscle fiber length errors of less than 3.8 % (Guschlbauer et al. 2007). We therefore used this approximation here and in Blümel et al. (2012a,b), using a rest muscle fiber length of 1.41 mm (the mean reported in Guschlbauer et al. 2007) and muscle fiber length changing 1:1 with changes in total muscle length (e.g., when the muscle was stretched 1 mm, muscle fiber length was taken to be 2.41 mm).

Experiments were performed on a total of 10 extensor muscles, each from a different animal. We demonstrate here our method for measuring all Hill-type model parameters in single experiments showing in the figures data from only one muscle. We measure method accuracy by giving the mean R² values of the various fits and the R² standard deviations for all 10 muscles. We present in the companion articles across-muscle comparisons and parameter correlations (Blümel et al. 2012a) and the extent to which individual muscle-specific models improve model performance (Blümel et al. 2012b).

2.2 Nerve stimulation

Motor nerve stimulations were performed using a Spike2 (Cambridge Electronic Design) sequencer script. This output triggered a digital pulse generator to produce (typically) 0.5 or (experiments in which 0.5 ms pulses required too large a current amplitude) 1 ms square-wave current pulses that drove a stimulation isolation unit (both from the electronics workshop at the Zoologisches Institut, Köln) attached to the bipolar hook electrode noted above. The extensor muscle is innervated by a fast motor neuron (whose individual spikes produce 1:1 muscle force twitches), a slow motor neuron (whose individual spikes do not), and an inhibitory neuron (whose activation cannot be easily observed in recordings of muscle force). Ideally, we would have performed these experiments activating only the fast motor neuron, which has the lowest threshold. However, the necessity of stimulating at somewhat more than this threshold to be certain to achieve 1:1 fast motor neuron activation at high stimulation frequencies, and our inability to be certain that under some stimulation conditions therefore one or more of the other axons would not also be at least occasionally activated, prevented us from doing so (see Guschlbauer et al. 2007 for a detailed consideration of this issue).

We therefore used a stimulation current level that prior data on axon diameters indicate should reliably activate all three axons under all conditions (Bässler and Storrer 1980), and thus ensure that the muscle was receiving the same complement of motor neuron input under all stimulation conditions. To achieve this goal, using a 15 pulse train at 50 Hz, we first increased current amplitude until the elicited contraction amplitude no longer increased, and thus presumably both the fast and slow extensor tibiae motor axons were being activated (the common inhibitor has the highest threshold). We then set stimulation current amplitude at least 2.5 times this amplitude to ensure common inhibitor 1 activation as well.

After this setting procedure, single-pulse nerve stimulations and tonic stimulations for 1 s at 40, 60, 80, and 100 Hz were used in the parameter measurement protocols. In these same experiments, the muscles were also stimulated with three pulse trains delivered with spike patterns observed during stick insect sideways stepping (one of which is shown in Fig. 2 here; see also Fig. 8 in Blümel et al. 2012b, and Fig. 2A in Hooper et al. 2006).

2.3 Muscle protocols

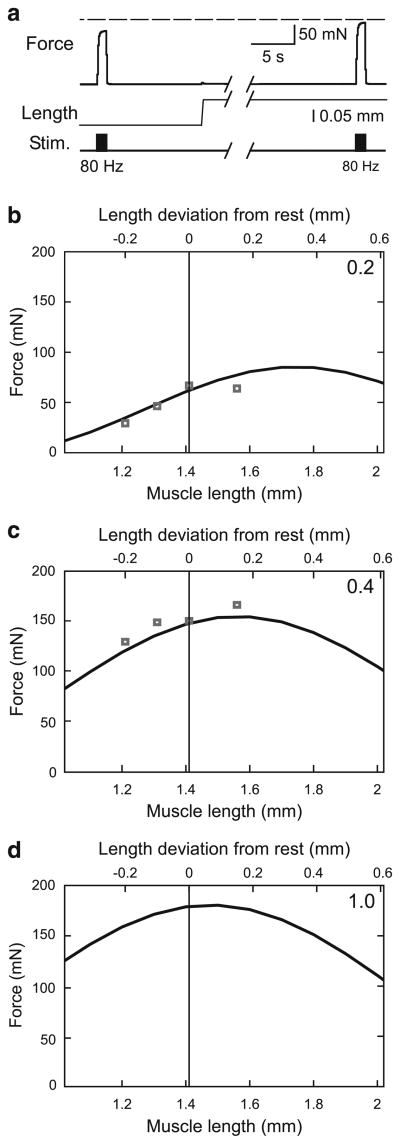
Three protocols were used: imposed length changes on unstimulated (passive) muscles to give passive force–length curves, motor nerve stimulations at multiple muscle lengths and nerve stimulation frequencies to give force–activation and active force–length curves, and quick release and quick stretch experiments to give force–velocity curves and measure series elasticity. All experiments were performed in the muscle’s physiological working range (Guschlbauer et al. 2007). Passive force–length experiments were performed with Spike2 sequencer-generated ramps (0.5–0.75 mm/s) from −0.2 to −0.1 mm to 0 to 0.15 mm (all relative to muscle rest length, 0 mm) with the motor nerve being stimulated with a brief high-frequency pulse to remove muscle slack (Proske et al. 1993) immediately after the muscle was set to −0.2 mm at the beginning of the protocol.

In response to passive stretches, the muscles showed a rapid force increase followed by an initially rapid and then ever-decreasing rate of force decrease (see Fig. 3a). Ideally, one would wait until this force decrease had ceased and measure the muscle force change induced by the imposed length change at this steady-state force value. However, as in other muscles (Malamud 1989), this late decrease in force continues very slowly for at least hours following stretch (data not shown). These late force decreases were, however, very small compared to those occurring in the first few seconds following the stretches (see Fig. 3a). To keep not only acceptable experimental durations but also ensure that the large majority of the force declines had occurred, we made passive force–length measurements at the following times (with the time increasing with increased muscle stretch to compensate for the increased forces that resulted): 40 s after the slack-removing stimulation at −0.2 mm, 60 s after the stretch to −0.1 mm, 80 s after the stretch to 0 mm, and 100 s after the stretch to the 0.15 mm.

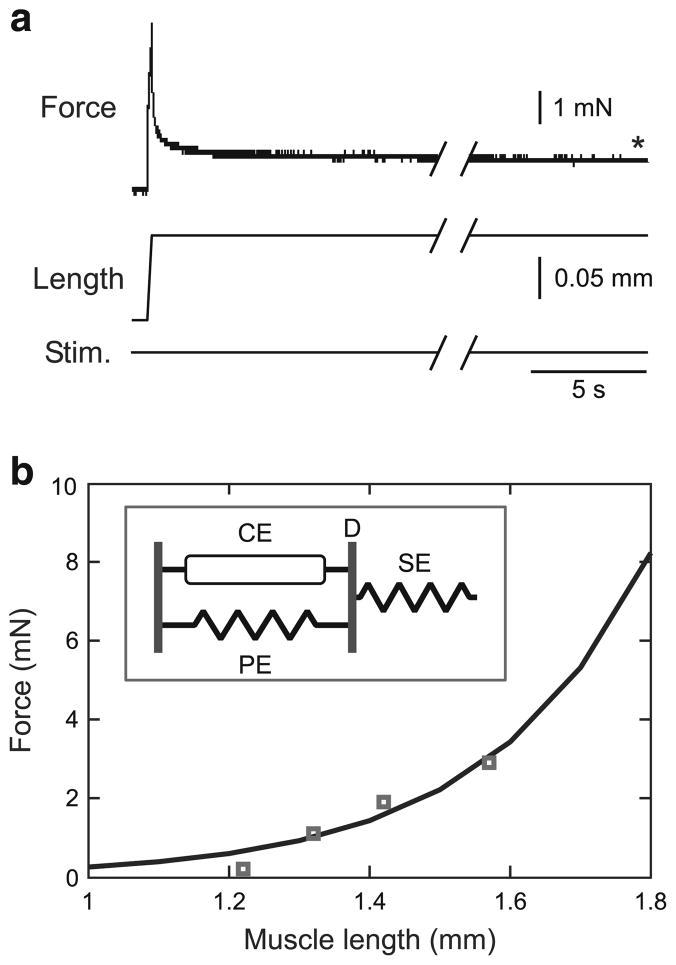
Fig. 3.

“Steady-state” passive force–length curve determination. a Muscle force after the end of the initial rapid force decrease (asterisk; see Sect. 2.3 for further explanation of extensor muscle passive relaxation characteristics) was measured at a series of muscle lengths. The “Stim.” trace is included to stress that in these measurements no motor nerve stimulation was used. Initial length was 1.3 mm; initial force was 1.1 mN. b Prior work (Guschlbauer et al. 2007) showed that the “steady-state” passive force length curve is an exponential function with two parameters (k₁, k₂). These parameters were fit with data from four measurements (squares). Inset A muscle model in which this equation would describe the (equal but pulling in opposite directions on the line marked D) passive (PE) and series (SE) “steady-state” elastic element forces as a function of muscle length. CE: contractile element

Immediately after the passive force–length measurements were made at each length (i.e., at 40, 60, 80, and 100 s), the motor nerve was stimulated (while keeping the muscle at the same length) at the frequencies noted above to induce muscle isometric contractions (see Figs. 5a, 8a) to construct the force–activation and active force–length curves.

Fig. 5.

Force–activation curve at rest length. a Data were obtained by holding the muscle at constant length and stimulating the muscle’s motor nerve at multiple spike frequencies. Initial length was 1.41 mm (rest length). b A Gompertz equation (Eq. 9, Sect. 3.4) well fit the data. The fit was constrained to go through (0,0). The first data point is the force produced by a single-motor nerve stimulation

Fig. 8.

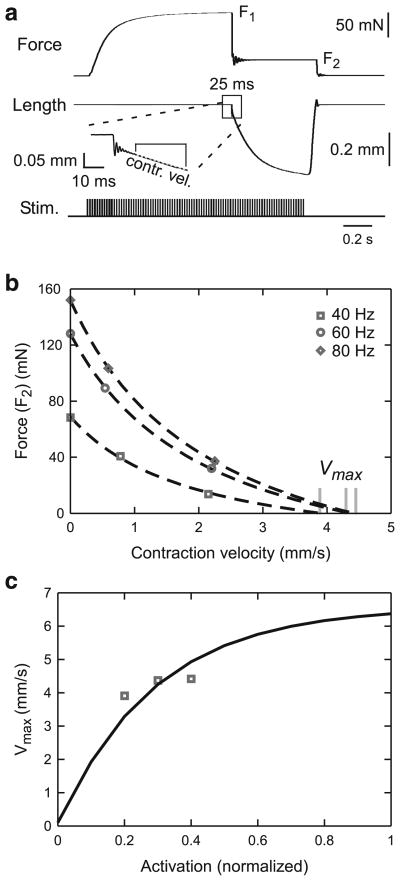
Determining ν_max as a function of muscle activation. a The same quick release and quick stretch experiments as in Fig. 4a were used but the velocity immediately after the slope discontinuity (see inset) was used. Initial length was 1.41 mm (rest length). b Force versus contraction velocity for two force steps at each of three activation levels (and the relevant rest length isometric tetanic force for the ν = 0 points) were plotted and fit with a modified Eq. 17 (see text) to determine ν_max at each activation level. c These ν_max values were used to fit the ν_max(act=1) term in Eq. 19

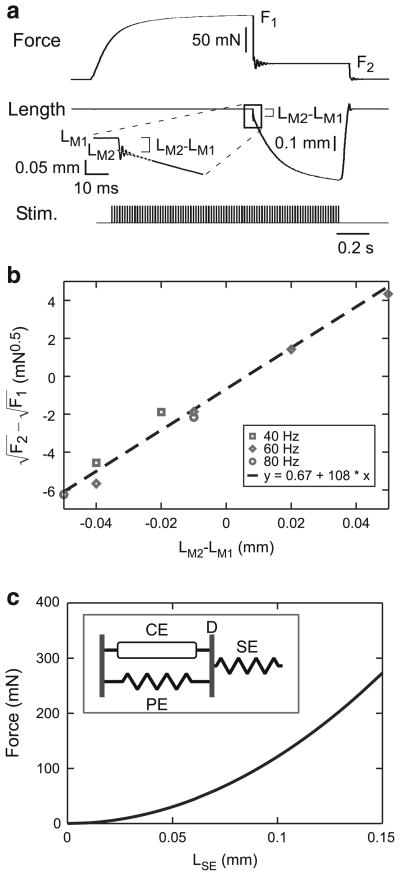
The quick release and quick stretch experiments (series elasticity, force velocity; see Figs. 4a, 8a) all began at muscle rest length. The motor nerve was first stimulated at the frequencies noted above and the muscle allowed to contract isometrically until force reached near steady-state values (F₁ in Fig. 4a). Muscle counter-force was then stepped to smaller and larger levels (in Fig. 4a, a smaller level, F₂) and the resulting change in muscle length observed. For steps to smaller forces, this change consisted of an extremely rapid change in muscle length followed by a brief period of oscillation (Edman 1988) and finally a slower and continually decreasing length change (see inset Fig. 4a). The slope of the initial 25 ms of the third portion of the length change was used to construct force–velocity curves (see inset Fig. 8a). The amplitude of the initial portion of the length change was measured by extrapolating the slope of the third portion through the oscillation to its intersection (L_M2) with the initial portion of the length change (see inset Fig. 4a), and used for determining muscle series elasticity.

Fig. 4.

Initial length responses of activated muscles to rapid force changes. a The muscle’s motor nerve was stimulated with the muscle held at constant length until force reached steady-state. Counter force was then rapidly changed and the initial rapid muscle length change measured. The inset shows the oscillation and slope discontinuity used as the boundary between the initial and late muscle lengthenings (see Sect. 2.3). Initial length was 1.41 mm (rest length) and initial force 1.9 mN (true for all subsequent figures in which the initial length was rest length). b A linear fit was applied to a plot of $\sqrt{F_2}-\sqrt{F_1}$ versus L_M2 − L_M1 (see text for definitions). The slope of the fit equaled $\sqrt{k_3}$, where k₃ is the proportionality constant relating muscle force and the length of the component of the muscle (L_SE) responsible for the rapid length change. c A plot of muscle force using the model in the inset (in which muscle force equals F_SE ), the quadratic series spring equation $F_{\text{SE}}=k_3·L_{\text{SE}}^2$, and the mean k3 calculated for this muscle

In most cases, exactly the same procedure could be followed for cases in which F₂ was larger than F₁. However, in two of these experiments, when F₂ was much greater than F₁, no slope discontinuity or oscillation was present. No L_SE could be associated with these counter-forces, and these experiments were therefore not used to calculate series elasticity. An effective contraction velocity for the force–velocity curves could, however, be calculated as follows. We first assumed that in these cases the first two portions of the length change had become too short to be observed, and thus all of the observed length changes were due the third component. An initial response would be to take simply the length change occurring over the initial 25 ms to calculate contraction velocity. However, in these contractions, contraction velocity slowed substantially over this 25 ms interval, and thus this procedure would have underestimated contraction velocity.

We therefore needed to define a briefer interval over which to measure the contraction velocity. We chose this interval on the basis of the measurements to the smallest F₂ values, which not only had the most rapid length changes of the force changes to smaller values but also had all three length change components. For these contractions, we measured the length change that occurred in the first 25 ms of the third component. We then determined, in the cases with the increased F₂ values, how long, starting from the beginning of the length change, it took for the muscle length to change by the same absolute magnitude. Contraction velocity was then calculated as this amplitude of muscle length change divided by this duration.

In most of the cases with F₂ values much greater than F₁, a discontinuity, sometimes associated with a subsequent brief oscillation, was present, but again contraction velocity slowed substantially over the nominal 25 ms measurement interval. Measuring velocity over the entire 25 ms interval would therefore have again underestimated contraction velocity. In these cases, velocity was measured with a procedure exactly analogous to that explained above, except that how long it took for the muscle to change its length by the appropriate amplitude (as determined above) was calculated using the discontinuity or the end of the oscillation (when present) of the lengthening as time zero.

With respect to how these changes in muscle force were achieved, the Aurora dual-mode level system is a servo mechanism in which the user sets both a muscle length and a threshold force. If muscle force at the set muscle length is less than the threshold, the Aurora delivers not the threshold force, but simply enough force to maintain the present (set) muscle length. Alternatively, if muscle force is greater than the threshold, muscle length decreases until the muscle force reaches the threshold. Therefore, decreasing load levels were induced by a Spike2 sequencer script that decreased the Aurora threshold level, which allowed the muscles to shorten. Muscle lengthening, however, could not be achieved by this method as increasing the Aurora threshold alone would not make the muscle lengthen. Muscle lengthening was therefore achieved by simultaneously increasing muscle set length (with a Spike2 sequencer script) and increasing the Aurora threshold force (with a digital pulse generator). The increase in set length was such that, if the new length had been actually achieved, the muscle would have produced a force greater than the new Aurora threshold force. However, the Aurora will not allow the muscle to have a length at which it would produce a force greater than the Aurora threshold force. These simultaneous changes in muscle set length and Aurora threshold force thus resulted in muscle length increasing exactly to the length at which the muscle produced the new Aurora threshold force setting.

To minimize muscle fatigue, isometric force experiments were performed first and isotonic force experiments involving large muscle length changes were performed at the end of the experiment. To help further to minimize muscle fatigue (apart from stimulations mimicking motor neuron activity during walking, data not shown here but presented in Blümel et al. 2012b), motor nerve stimulations were separated by at least 30 s. Muscle fatigue was tested by repeated measurements of rest length isometric tetanic force at 40, 60, and 80 Hz stimulation frequency throughout the experiment. Such data were obtained in the early isometric portion of the experiment while measuring the force–activation at rest length (Fig. 5) and force–length at all activations (Fig. 7) curves and in the late isotonic portion of the experiment in the quick release and quick stretch protocols of Sects. 3.3 and 3.6 (F₁ in Fig. 4a and the equivalent force in Fig. 8a). In the late tests, two isometric tetanic force values were obtained at each of the 40, 60, and 80 Hz stimulations in the release to smaller force experiments and two more at 60 Hz in the quick stretch to greater force experiments. These measurements thus gave in toto one 40, 60, and 80 Hz measurement early in the experiment and two measurements each at 40 and 80 Hz and four 60 Hz measurements late in the experiment. Only experiments in which each stimulation frequency’s rest length isometric tetanic force was in all cases at least 80 % of its greatest value were used. The mean of each stimulation frequency’s rest length isometric tetanic force was used in all relevant calculations (Figs. 4b, 5b, 7b, c, 8b, 9a–c).

Fig. 7.

Experimental and fitting procedures used to calculate curv_ω from reduced number of experiments. a Muscle active force was measured at four muscle lengths at each of two activation levels (40 and 80 Hz); data shown here are for two muscle lengths at the 80 Hz activation level. Initial length was 1.21 mm, initial force was 0.2 mN. To compensate for changes in passive force resulting from the changes in muscle length, active force was calculated by subtracting passive force immediately before stimulation beginning from force during motor nerve stimulation. b, c Active force–length curves calculated from four muscle lengths (squares in two panels) at the two activation levels (numbers in upper right corner of each panel). See text for detailed explanation. Data points at rest length (1.41 mm) are means of three individual measurements at this length, one using the protocol shown in panel a and two from the forces before the force change in the force–velocity protocol shown in Fig. 8a. d Predicted force–length curve for an activation of 1 (200 Hz)

Fig. 9.

Force–velocity curves at all muscle activation levels (the upper right numbers in each panel) calculated using parameter values from data in Fig. 8. Solid lines denote portions of the curves for which experimental data had been obtained (shortening contractions in a–c; lengthening contraction, b); dashed lines are extrapolations using Eqs. 17 and 18. Squares are shortening contractions; x’s (b) lengthening contractions

2.4 Parameter optimization

Calculations were performed in GnuOctave on Linux (Ubuntu 9.04, Kernel 2.6.28-15-generic, Intel Core2 T5600). Parameters were optimized using the leasqr routine of the optim package (version 1.0.12).

3 Results

3.1 General approach

We show below how we fit the parameters for the following curves: passive steady-state force–length, immediate force–length (“series elasticity”), force–activation at rest length, and force–length and force–velocity at all activations. In each section, we describe what type of curve previous work (Gus-chlbauer et al. 2007) has shown represents the relationship in question in extensor muscle and the experimental technique and data analysis used to determine equation parameters. This previous work also showed that the equation parameters did not vary, in a single muscle, across the physiological range. As such, in the present work, we had only find the values, for each muscle, of the parameters. In all cases either classic Hill (1938, 1950) muscle model equations, or direct extrapolations of them, were used (see also Discussion). In some cases, ad hoc functions, particularly functions with greater numbers of free parameters, might have led to better fits. However, this would have prevented us from making use of the previous work noted above (which was all interpreted in terms of Hill-based models), and introduced equation parameters that we would not have been able to interpret in terms of the widely used Hill muscle model. Hence, the latter was not an option for us. As a guide to the reader, the functions are plotted across the entire physiological range even though the experimental data used to obtain the parameter values typically covered a much smaller range. As is typically done in these descriptions, all measurements were made at steady-state force levels (how the dynamic components of the contractions were modeled is explained in Blümel et al. 2012b). In some cases, we have also used data from the literature to test whether our approach works well for other muscles.

3.2 Passive steady-state force–length curve

Passive steady-state force–length curves were measured by sequentially stretching unactivated muscles and measuring steady-state muscle force at each length (Fig. 3a). Prior work in stick insect extensor (Guschlbauer et al. 2007) and other muscles (Brown et al. 1999; Malamud 1989) has shown that these curves vary as an exponential function of muscle length. These data points were therefore fitted to

$$F_{\text{P}}=k_1·{\text{e}}^{k_2{L}_{\text{M}}},$$ (1)

where F_P is muscle passive force, L_M is muscle length (set equal to muscle fiber length, see Sect. 2.1 and Guschlbauer et al. 2007), and k₁ and k₂ are the parameters that must be fit. In the work reported here, we used four measurements (squares) to fit this curve (Fig. 3b). In Fig. 3b, the fits of these parameters had an R² value of 0.92; mean R² across the ten experiments used in this study was 0.94 ± 0.04. As described, this curve is simply a descriptor of muscle properties and does not depend on choice of muscle model. However, for a frequently used muscle model (inset, Fig. 3b), this curve would correspond to the forces on the parallel and series elastic elements, which at steady state are equal and pull in opposite directions on the line marked ‘D’.

3.3 Initial length responses of activated muscles to rapid force changes

When muscles were induced by motor nerve stimulation to contract isometrically until steady-state force levels were achieved and then a step change in counter force was made, muscle length responded with an initial rapid change followed by a slower and continually decreasing change (Fig. 4a). The inset shows the oscillation and slope discontinuity that marks the boundary between the two domains (see Sect. 2.3). Prior work in stick insect (Guschlbauer et al. 2007) and frog (Wilkie 1956; Jewell and Wilkie 1958) showed that these forces increase non-linearly with the change in muscle length. Guschlbauer et al. (2007) modeled this non-linear dependency with a quadratic relationship between final force (F₂) and the associated length change (L_M2 − L_M1). The Wilkie (1956) and Jewell and Wilkie (1958) data are also well fit with a R² values >0.987). Guschlbauer et al. (2007) interpreted these data as being consistent with a rapidly stretching elastic (SE) element in the muscle whose force varies as

$$F_{\text{SE}}=k_3·L_{\text{SE}}^2.$$ (2)

Because the data in Guschlbauer et al. 2007 are expressed in terms of final force versus change in total muscle length, the logic of this equation can initially be confusing. We therefore explain in detail the process of measuring k₃ using the model shown in the inset of Fig. 4c. Because of the placement of the series elastic element, in this model, muscle force equals F_SE. We assume that element length only slowly changes, and thus the initial rapid length changes induced by step changes in applied force result solely from changes in L_SE. Therefore, at F₁, where muscle length equals L_M1,

$$\sqrt{F_1}=\sqrt{F_{\text{SE}1}}=\sqrt{k_3}·L_{\text{SE}1},$$ (3)

and at F₂, where muscle length equals L_M2,

$$\sqrt{F_2}=\sqrt{F_{\text{SE}2}}=\sqrt{k_3}·L_{\text{SE}2}.$$ (4)

The change in applied muscle force thus changes L_SE by

$$\sqrt{F_2}-\sqrt{F_1}=\sqrt{k_3}·(L_{\text{SE}2}-L_{\text{SE}1}).$$ (5)

Because the change in total muscle length is due solely to the change in L_SE,

$$L_{\text{SE}2}-L_{\text{SE}1}=L_{\text{M}2}-L_{\text{M}1},$$ (6)

and thus

$$\sqrt{F_2}-\sqrt{F_1}=\sqrt{k_3}·(L_{\text{M}2}-L_{\text{M}1}).$$ (7)

Squares of the slopes of fits to plots of $\sqrt{F_2}-\sqrt{F_1}$ versus L_M2 − L_M1 therefore equal k₃ (Fig. 4b). Both these data (R² = 0.96) and those of the other nine muscles analyzed in this study (mean R² of all 10, 0.93 ± 0.09) showed linear relationships, suggesting that k₃ is a constant across the multiple activation levels and muscle forces used to obtain these data. We therefore used Eq. 7 to calculate a k₃ value for each of the multiple force steps that were applied to each muscle (e.g., the eight data points in Fig. 4b gave eight estimates of this muscle’s k₃), and the mean of these multiple determinations as each muscle’s k₃. Once k₃ is known, Eq. 2 can be used to calculate L_SE at each muscle force; Fig. 4c plots F_SE versus L_SE for the mean k₃ given by the data in Fig. 4b.

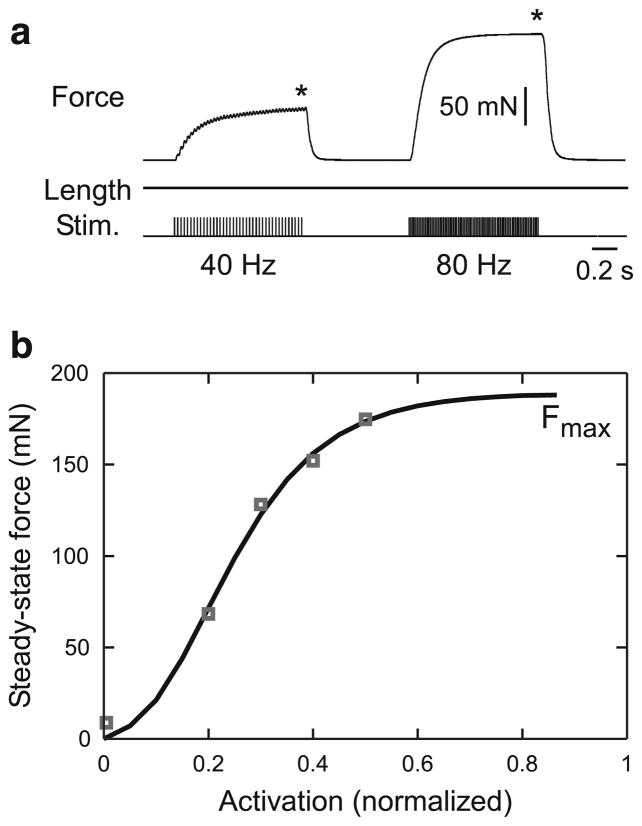
3.4 Rest length force–activation curve

Muscle models must predict not only passive force but also muscle response to motor neuron activity. To achieve this goal, we stimulated the muscle’s motor nerve at multiple spike frequencies while holding the muscle at rest length (isometric contractions, Fig. 5a) and measured muscle force at steady state (asterisks). Activation level (the x-axes in these plots, Fig. 5b) was normalized to 200 Hz, the stimulation frequency beyond which increases in force production are no longer observed (Guschlbauer et al. 2007).

Guschlbauer et al. (2007) fitted these data with an equation of the form

$$F_{\text{A}}=F_{max}·(1-{\text{e}}^{-\text{act}/\alpha }),$$ (8)

with both F_max and α being free parameters. F_max is thus the maximum isometric force the muscle can produce at rest length. We had sufficient data points to determine independently what function best fit the data, and found that a Gompertz equation,

$$F_{\text{A}}=F_{max}·{\text{e}}^{-{\text{e}}^{-A·(\text{act}-B)}},$$ (9)

where F_max, A, and B are all free parameters, gave better fits (Fig. 5b). This equation better fit the data than Eq. 8 when constrained to go (as the curve must) through (0, 0), and better than a sigmoid function because its positive (activation 0–0.3) and negative (activation 0.3–1) curvatures can have different values. In Fig. 5b, the fit had an R² value of 0.997; mean R² across the ten experiments used in this study was 0.999 ± 0.001. The Gompertz equation also fits the constant length force–activation curves of cat soleus muscle in Rack and Westbury (1969) very well (R values >0.99).

3.5 Force–length curves at all activations

Section 3.4 describes steady-state force versus muscle activation at muscle rest length. Extending this description to predict steady-state force versus activation at all muscle lengths is typically performed by plotting multiple curves, one for each activation level, on force–length plots. Figure 6a shows such plots using normalized force (force divided by F_max) data from Guschlbauer et al. (2007). The curves connecting the data points (dotted lines) smoothly varied and were single peaked, with peak amplitude decreasing, and the position of the peak shifting to greater muscle lengths, as activation (labels in “data” insets, Fig. 6a, d, normalized to 200 Hz stimulation frequency) decreased. Similar decreases in peak amplitude and shifts in peak position are typical of such data (e.g., Rack and Westbury 1969; Brown et al. 1999). The single-peaks and shape of these data curves suggested that they would be well fit by sine curves of the general form

Fig. 6.

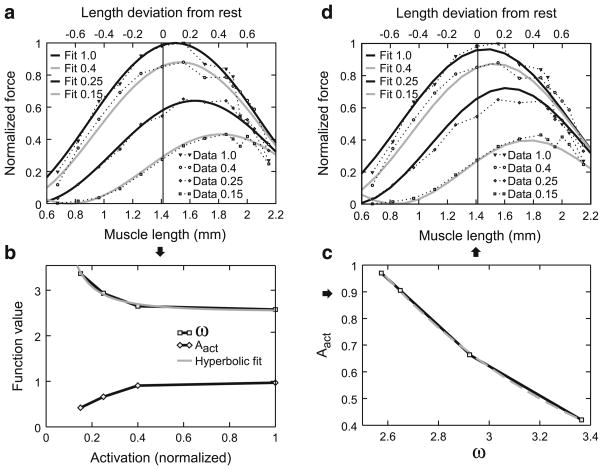
Explanation of how active force–length curve parameters were determined. a Data from Fig. 9a of Guschlbauer et al. (2007) replotted with force normalized to the maximum force (99 mN) this muscle produced at 200 Hz (act = 1), which occurred at a length 0.15 mm greater than rest length (see upper x-axis labels), and fit with Eq. 13, Sect. 3.5. b Plot of A_act and ω of Eq. 13 versus activation level. Note hyperbolic variation of both parameters (Eq. 15, Sect. 3.5 for ω) and the apparent co-variation of the two functions. c Plot of A_act versus ω and exponential fit to the data (Eq. 14, Sect. 3.5). d Curves obtained when the fit of ω in Fig. 6b is used to calculate ω the fit of A_act in (c) is used to calculate A_act from ω, and these terms are substituted into Eq. 13, Sect. 3.5, to calculate muscle active force. The insets in (a, d), and the x-axis label in b, refer to activation normalized to maximum activation (200 Hz motor nerve stimulation)

$$F=\text{amplitude}·[sin(\omega ·L_{\text{M}}+\varphi )],$$ (10)

where amplitude is curve maximum amplitude (unitless, since force is normalized); ω is cycle period (how many oscillations occur within one muscle length, with ω thus having units of mm⁻¹); ϕ is phase (unitless), specifying where in the cycle the oscillation is at L_M = 0; function is evaluated in radians. Fits in which amplitude, ω, and ϕ, were all allowed to vary independently gave very good fits (data not shown).

However, accurately fitting these three parameters independently requires a large number of data points. In the case at hand, where our goal is to measure all of a muscle’s defining characteristics in a single experiment, obtaining so many data points for this one aspect of muscle activity and also performing all the other measurements described here would be impossible. In working with the data in Fig. 6a, it became apparent that these three parameters could be expressed in terms of a single parameter, thus requiring many fewer data points to describe each muscle’s force–length curves at all activations. The first step in this process was noting that the descending arms of the fits to the data in Fig. 6a all reached zero normalized force at approximately the same muscle length, 2.7 mm. This length is presumably the length at which the thin and thick filaments no longer overlap (this length is well outside of the muscle’s physiological working range), and thus the muscle cannot produce force regardless of the level of activation. Sine curves with different wavelengths can be made to overlap with amplitude 0 at a single value (here, 2.7 mm) of the independent variable (L_M) by replacing the phase term in Eq. 10 with

$$-\left(\frac{\pi }{2}+2.7·\omega \right).$$ (11)

Equation 10 then becomes

$$F_{\text{L}}=\text{amplitude}·sin\left(\omega ·L_{\text{M}}-\left(\frac{\pi }{2}+2.7·\omega \right)\right),$$ (12)

which has amplitude 0 at L_M = 2.7 mm for all amplitudes and ωs. The sine portion of Eq. 12 will vary between −1 and 1, whereas normalized force varies between 0 and 1. Amplitude will ultimately (see below) be expressed as a function of muscle activation (stimulation spike frequency normalized to 200 Hz, and thus unitless), and will also vary between 0 and 1. It is therefore necessary to alter the sine portion of Eq. 12 so that it also varies between 0 and 1, which can be achieved by adding 1 to it and dividing the sum by 2, which gives

$$F_{\text{L}}=A_{\text{act}}·\left[\frac{1+sin\left(\omega ·L_{\text{M}}-\left(\frac{\pi }{2}+2.7·\omega \right)\right)}{2}\right],$$ (13)

where amplitude has been replaced with A_act, the function that relates muscle activation to maximum muscle normalized force.

Fits to the data using Eq. 13 and A_act and ω as fit parameters gave very good fits (solid lines, Fig. 6a). Plotting the A_act and ω values obtained in these fits versus activation showed both that A_act and ω varied as a function of muscle activation and appeared to co-vary (Fig. 6b). Figure 6c plots A_act versus ω. An initial impulse (and good fit, R² = 0.985) is to fit these data with a linear function. However, when ω is expressed in terms of muscle activation (see below), doing so leads to negative A_act values at low activation (high ω) values. We therefore fit these data instead with an exponential function

$$A_{\text{act}}=15·{\text{e}}^{-1.06·\omega },$$ (14)

(where the “−1.06” term has units of millimeter and the “15” term is unitless), which had an even better fit (R² = 0.998) and is positive for all ω. The final step was to express ω as a function of activation. This curve (upper curve in Fig. 6b) was well fit (R² = 0.99) with a hyperbolic function: 1

$$\omega =2.5+\frac{1}{{({\text{curv}}_{\omega }·(\text{act}+0.05))}^2},$$ (15)

with the fit giving a curv_ω value of 5.35 (units, mm^0.5; the “2.5” has units of mm⁻¹).

Equations 14 and 15 allow A_act and ω of Eq. 13, and hence normalized force, to be calculated from fits of only a single parameter (curv_ω). Figure 6d shows normalized muscle force following this procedure. Remarkably good fits are obtained (R² = 0.92, 0.94, 0.94, and 0.96 for activations of 1.0, 0.4, 0.25, and 0.15, respectively) for an equation with only one fit parameter. A final point to make about Eq. 13 is that it gives a rhythmically varying force (e.g., note the increasing force at L_M less than 0.8 for the 0.15 activation curves in Fig. 6a, d). This is of course incorrect; muscle force–length curves are single-peaked (i.e., once the curve reaches zero force at very short and very long lengths, it remains zero for all lengths less and greater than these lengths). In all the muscle examined here, the fits were such that, across the physiological range, this requirement was essentially met (i.e., the very small force increases at very short muscle lengths noted above were so small that they had negligible effects on model accuracy). For cases in which this is not the case, Eq. 13 would need to be modified with a logic statement so that only a single half-cycle of the sine curve was used, with forces outside this length range being set to zero.

The approaches used in Sects. 3.2–3.4 and 3.6 (see below) to characterize stick insect muscle properties are either relatively straightforward extensions (Sects. 3.2, 3.4) or exact recapitulations (Sects. 3.2, 3.6) of widely used approaches. The approach outlined above allowing a muscle’s force–activation curves at all muscle lengths to be modeled by fit-ting a single parameter is, alternatively, to our knowledge novel. Testing this section’s approach using data from another muscle was therefore particularly important. We chose to apply it to data from cat soleus muscle (Brown et al. 1999), which is a mammalian spiking muscle, and thus very different from stick insect muscles.

Brown et al. report data for activations of 1, 0.5, 0.33, 0.25, and 0.15. Repeats of the fits in Fig. 6a with amplitude, ω, and ϕ being fit independently gave very good fits (R² between 0.977 and 0.999, mean 0.99 ± 0.01). The data for the 0.15 activation level did not have points on the descending arm of the sine wave and therefore did not well specify the muscle length on the descending arm at which force equaled zero. The other four activation curves well specified a common descending arm zero force length (1.73 ± 0.03 mm), and the fits were therefore rerun with amplitude and ω being free parameters and the “2.7” term in Eq. 13 being 1.73 mm. All five activation curves were very well fit with this descending arm zero force muscle length (R² between 0.977 and 0.997, mean 0.987 ± 0.01). The curves in Fig. 6b were again well reproduced, with the hyperbolic fit of ω giving a curv_ω of 0.627 and an R² of 0.968. Figure 6c was well reproduced for activations of 1, 0.5, 0.33, and 0.25, but the A_act for activation level 0.15 did not fit on the exponential curve of the other four activations. It was therefore necessary to fit Eq. 14 twice, once for activations of 1.0, 0.5, 0.33, and 0.25, and again for activations of 0.25, 0.125, and 0 (assuming that A_act equals zero when act equals 0). Both of these fits had high R² values (0.999 and 0.998). Using these functions to reproduce Fig. 6d (it was immaterial which exponential function was used for act = 0.25) gave good fits, with R² ranging from 0.821 (act = 0.125) to 0.996 (act = 0.33) with a mean of 0.953 ± 0.07.

The technique described above thus also worked well to describe cat soleus muscle force–activation curves at all lengths. It is important to stress that the need in cat soleus muscle to use two versions of Eq. 14 does not affect the procedure described below to characterize curv_ω using small measurement numbers. In characterizing a muscle, the constants in Eqs. 14 and 15 would be determined from prior experiments similar to those shown in Fig. 6a. These constants would be used in the equations in the later experiments in which all of a muscle’s characteristics are described in single experiments, with only curv_ω being fit in these later experiments. As is shown below, fitting just curv_ω and substituting it into otherwise fixed Eqs. 14 and 15 gives very good final model outputs.

The data shown in Fig. 6 required 14 measurements at each of four activation levels for a total of 56 measurements, too many for our goal of measuring all Hill-type parameters in single experiments. We fulfilled this goal by assuming that all parameters in Eqs. 13–15 were constant across muscles except for the value of the curvature of the hyperbola (curv_ω) in Eq. 15. We then measured the active force–length curves at four lengths and two activation levels (Fig. 7a shows this determination for two muscle lengths at the 80 Hz—0.4—activation level) and normalized these data using the F_max value calculated in Fig. 5b. As ω is a constant at any given level of activation, Eq. 15 had only one free variable (curv_ω), which we determined as follows. We first fit Eq. 13 to each activation level’s four data points. This gave us two points (one for each activation level) of ω for the ω curve in Fig. 6b, which we used to determine the value of curv_ω in Eq. 15. Using this value in Eq. 15 then allowed calculating ω at each activation level. These ω values were then substituted into Eq. 14 to obtain A_act, and the ω and A_act values were then substituted into Eq. 13 to obtain normalized active muscle force at all lengths and activation levels. The normalized muscle forces were then multiplied by F_max to obtain absolute muscle force. Figure 7b, c shows the resulting curves for the activation levels (0.2 and 0.4 of 200 Hz) used to obtain the data for the fitting. Figure 7d shows the predicted curve at an activation level of 1.

This procedure resulted in good fits for the shown data (Fig. 7b, R² = 0.83; Fig. 7c, R² = 0.91) and when applied to all 10 muscles analyzed here (mean R² = 0.93 ± 0.07 for panel b, mean R² = 0.96 ± 0.03 for panel c). This goodness of fit could be because all muscles indeed have very similar values for the parameters held constant in the procedure, or because the sensitivity of the active force–length curves on these parameters is small compared to their sensitivity on curv_ω. Regardless, the consistent goodness of these fits convinced us that these experimental measurements and fit procedures were adequate to define individual muscle active force–length curves.

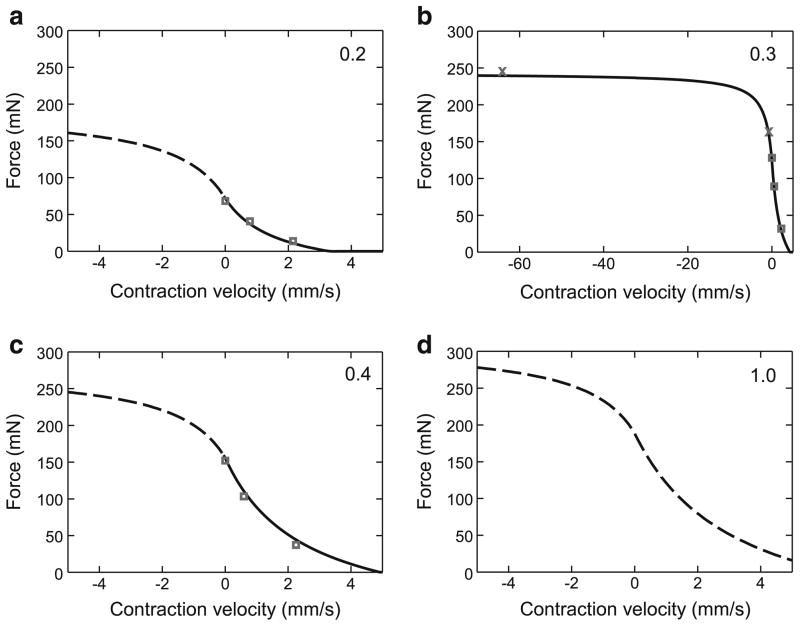
3.6 Force–velocity curve

We characterized stick insect force–velocity curves using completely standard techniques (Hill 1938; Edman 1988). This approach begins with the classic Hill hyperbola

$$F_{\text{V}}=\frac{c·(1+c)}{(\nu /{\nu }_{max})+c}-c,$$ (16)

where F_V is normalized to F_max (and is hence unitless), ν(mm/s) is the velocity of muscle length change, ν_max is the maximum rate of length change (at zero force), and c is a unitless constant that determines hyperbola curvature. A first difficulty to overcome with this equation is that different hyperbolas, with different curvatures and ν axis intersections, have to be used for shortening and lengthening contractions, with the negative ν portion of the lengthening contraction hyperbola used for lengthening (eccentric) contractions and the positive ν portion of the shortening contraction hyperbola used for shortening (concentric) contractions. It is therefore necessary to use different pairs of ν_max and c parameters, one for concentric and one for eccentric contractions, to model the entire range of muscle contractions. A consequence of using two equations is that they must meet at zero contraction velocity. Furthermore, this zero velocity contraction is by definition an isometric contraction, and its (normalized to F_max) amplitude is therefore given by the Gompertz equation e^{−e−A·(act−B)} described in Sect. 3.4. These two requirements are met by altering the classic Hill parabola as follows:

$$F_{\text{V}}={\text{e}}^{-{\text{e}}^{-A·(\text{act}-B)}}·\frac{c_{\text{pos}}·(1+c_{\text{pos}})}{(\nu /{\nu }_{max\text{pos}})+c_{\text{pos}}}-c_{\text{pos}}(\text{shortening}\text{contractions})$$ (17)

$$F_V=\frac{c_{\text{neg}}·(1+c_{\text{neg}})}{(\nu /{\nu }_{max\text{neg}})+c_{\text{neg}}}-c_{\text{neg}}-\left(1-{\text{e}}^{-{\text{e}}^{-A·(\text{act}-B)}}\right)(\text{lengthening}\text{contractions}),$$ (18)

where F_V is normalized to F_max. c_pos was set to 0.5 based on data from Guschlbauer et al. (2007). It is therefore necessary to determine only ν_{max pos}, ν_{max neg}, and c_neg.

ν_{max pos} was determined from the same quick release experiments that were used in Sect. 3.3 but using the initial slope of the second, slow length change (Fig. 8a, inset). These experiments were performed using two step changes in force (each of which induced muscle shortening) at each of three activation levels. In conjunction with the rest length isometric (at which ν equals 0) tetanic force values already obtained at each stimulation frequency, this gave three points per activation curve (Fig. 8b; in this figure, F_V has been multiplied by F_max to give absolute muscle force; note that this global scaling does not alter the ν_{max pos} values—where the curves cross the x axis). Since the A, B, act, and c_pos, terms in Eq. 17 are all known, we originally performed these fits with the Gompertz term in the equation. Although these fits had relatively high R² values, they often did not go through all three points, presumably due to the large dependence of the Gompertz portion of the equation on small variations in the A and B terms. We therefore replaced the Gompertz term with a variable that was allowed to freely scale the curves, which resulted in extremely good fits to the data (Fig. 8b). These ν_{max pos} values were then plotted versus activation (8c) and fitted to an equation from Guschlbauer et al. 2007

$${\nu }_{max\text{pos}}={\nu }_{max(\text{act}=1)}·\left(1-{\text{e}}^{-\text{act}/0.3}\right).$$ (19)

to determine ν_max(act=1), which is the ν_{max pos} at an activation of 1. The unitless “activation constant” of 0.3 (57.7 Hz) is from Guschlbauer et al. (2007) and was used for all muscles.

This step of our procedure (calculating the amplitude parameter of V_{max pos} dependence on activation, Eq. 19) depends on only three data points in the middle of the activation range. However, as we already know the exponential scaling factor (the “0.3”) of this equation, we are determining only its amplitude factor, for which three points are sufficient. It is also important to stress that we have a second check of the goodness of this estimation because this measurement is only an intermediate step in determining the equations of interest, the force–velocity curves themselves (Eqs. 17, 18). As is shown below, the ν_max(act=1) values obtained using the procedure shown in Fig. 8 resulted in excellent force–velocity curves. c_neg and ν_{max neg} were fit using two data points from lengthening contractions at an activation of 0.3 (x points in Fig. 9b).

These fitted values were then used in Eqs. 17 and 18 (including the Gompertz term) to construct continuous force–velocity curves (Fig. 9, again scaled to absolute force by multiplication by F_max) at different activation levels (the numbers in the upper right of the panels). In these plots, the solid lines are the portions of the curves for which we had experimental data (the data in Fig. 8); note the different x axis scale in Fig. 9b to incorporate the two lengthening contractions performed at this activation level. Figure 9d is the predicted force–velocity curve for an activation of 1. Because the lengthening data only had two data points, goodness of fit was only calculated for the shortening portions of the curves. In the data shown, the fits for these contractions (Figs. 9a–c) had R² values of 0.995, 0.99997, and 0.9998; across the 10 experiments, the mean R² values of the panels were 0.99 ± 0.007, 0.997 ± 0.007, and 0.998 ± 0.003.

4 Discussion

We have described here protocols that measure with good R² values all Hill-type parameters in experiments on single extensor muscles. A possible concern with this approach is that the measurements were made with only 2–11 data points per characteristic. The R² values of these measurements, however, were uniformly high across the ten muscles investigated, suggesting that these numbers of data points were sufficient to well constrain the fits. It is important to stress that this success depended on our extensive prior knowledge of the muscle (Guschlbauer et al. 2007), that pre-determined which functions were appropriate, in some cases fixed some function parameters, and in all cases allowed us to pre-determine which experiments should be performed to find the most useful data points for constraining the various curves. Although this need for prior curve-defining work is time consuming, the experiments to obtain these background data are standard, and for many systems these data are already available in the literature. For the cases in which we used non-standard equations, we also tested our approaches on published data from other muscles; in all cases, our approach worked well. As such, the approach detailed here is likely applicable to many other muscles, at least those of comparable robustness to stick insect muscles.

Wagner et al. (2005) provided an alternative method for determining muscle-defining parameter values in single experiments. These authors subjected muscles to iso-velocity length changes at multiple activation levels and then fitted the parameters of an existing muscle model so as to best reproduce muscle response to this input. This approach fundamentally differs from that used here in that no direct measurements of muscle Hill-type characteristics were attempted, but instead were inferred once optimization was accomplished. In as much as a given muscle has only one set of such characteristics, provided the model used in Wagner et al. is sufficiently accurate, both approaches should give equivalent results. The Wagner et al. approach has certain advantages, particularly the ability to measure muscle responses in vivo. It has the drawback that an accurate muscle model must be already available, and it is unclear how sensitive the results obtained from it are to model details. Although in some cases, we explain our data in terms of a muscle model (the insets in Figs. 3b, 4c), the data shown in these figures are model independent. As such, the approach detailed here may have advantages for investigating muscle properties in cases in which insufficient model detail, or computer resources to perform model optimizations, are available. The direct relationship between the measurements made here and well understood and widely used descriptors of muscle characteristics are also an advantage of our approach.

In summary, we describe here a methodology that describes the passive steady-state force–length curve, immediate force–length curve (“series elasticity”), rest length force–activation curve, and force–length and force–velocity curves at all activations, from a small enough number of measurements to perform in experiments on single muscles. This approach allows muscles to be modeled individually, and will be useful for investigating muscle variability across individual animals, correlation between muscle parameters, and how much muscle-specific modeling improves model performance. We examine these issues in the stick insect extensor muscle in the following articles (Blümel et al. 2012a,b).

List of symbols

α

Isometric force–activation constant (Eq. 8) (unitless)

A, B

Parameters in rest length force–activation curve (Eqs. 9, 17, 18) (unitless)

A_act

Maximum amplitude of force–length curves (Eqs. 13, 14) (unitless)

act

Muscle activation (Eqs. 8, 9, 15, 17–19) (normalized to 200 Hz, therefore unitless)

c, c_pos, c_neg

Curvatures of general Hill hyperbola and hyperbolas for shortening (Eq. 17) and lengthening (Eq. 18) contractions, respectively (unitless)

curv_ω

Curvature of hyperbola relating omega; and act (Eq.15) (mm^0.5)

F_A

Active force at rest length (Eqs. 8, 9) (mN)

F_L

Active force at different muscle lengths (force–length curve) (Eqs. 12, 13) (normalized to F_max, and therefore unitless)

F_P

Steady-state passive force (parallel spring) (Eq. 1) (mN)

F_SE, F_SE1, F_SE2

Series elastic spring force (Eqs. 2–4) (mN)

F_V

F_L at different contraction velocities (force–velocity curve (Eqs. 16–18) (normalized to F_max, and therefore unitless)

F_max

Maximum isometric force at rest length (Eqs. 8, 9) (mN)

k₁, k₂

Passive steady-state force–length curve constants (Eq. 1) (k₁, mN; k₂, mm⁻¹)

k₃

Proportionality constant in quadratic force equation (Eqs. 2–5, 7) (mN/mm²)

L_M, L_M1, L_M2

Muscle length (Eqs. 1, 6, 7, 10, 12, 13) (mm)

L_SE, L_SE1, L_SE2

Series elastic element length (Eqs. 2–6) (mm)

ν

Velocity of muscle length change (Eqs. 16–18) (mm/s)

ν_max, ν_{max pos}, ν_{max neg}

Maximum velocity of length change in general Hill hyperbola (Eq. 16) and hyperbolas for shortening (Eqs. 17, 19) and lengthening (Eq. 18) contractions, respectively (mm/s)

ν_max(act=1)

ν_{max pos} at an activation of 1 (Eq. 19) (mm/s)

ω

“Length” frequency of force–length curves (Eqs. 10–15) (mm⁻¹)