A note on the derivation of epidemic final sizes

Abstract

Final size relations are known for many epidemic models. The derivations are often tedious and difficult, involving indirect methods to solve a system of integro-differential equations. Often when the details of the disease or population change, the final size relation does not. An alternate approach to deriving final sizes has been suggested. This approach directly considers the underlying stochastic process of the epidemic rather than the approximating deterministic equations and gives insight into why the relations hold. It has not been widely used. We suspect that this is because it appears to be less rigorous. In this note we investigate this approach more fully and show that under very weak assumptions (which are satisfied in all conditions we are aware of for which final size relations exist) it can be made rigorous. In particular the assumptions must hold whenever integro-differential equations exist, but they may also hold in cases without such equations. Thus the use of integro-differential equations to find a final size relation is unnecessary and a simpler, more general method can be applied.

1 Introduction

One of the first applications of infectious disease modeling was a final size calculation for well-mixed populations [15]. We demonstrate this in a simplified case. We divide the population into susceptible, infected, and recovered fractions: S(t), I(t), and R(t) respectively. Assuming a large population, constant transmission and recovery rates, and mass action mixing, we have

$$\stackrel{.}{S}=-\beta IS,\stackrel{.}{I}=\beta IS-\gamma I,\stackrel{.}{R}=\gamma I$$ (1)

Using S + I + R = 1, eliminates R from the analysis. We have $\frac{\text{d}I}{\text{d}S}=-1+\frac{\gamma }{\beta S}$ which yields $I(t)=-S(t)+\frac{\gamma }{\beta }lnS(t)+C$. We can find C from initial conditions. Using I(∞) = 0 we can solve for S(∞). Assuming S(0) is asymptotically close to 1 gives the relation

$$S(\infty )=exp\left[-\frac{\beta }{\gamma }[1-S(\infty )]\right]$$

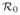If we let = β/γ, this becomes S(∞) = e^{− [1−S(∞)]}, or equivalently R(∞) = 1 − e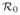^{− R(∞)} which is the well-known relation. If S(0) is not close to 1, these final steps are marginally modified resulting in a similar relation. Unfortunately this indirect derivation gives little insight into why this relation holds. We will show how to derive this and other final size relations more directly by considering the underlying stochastic process rather than the approximating deterministic equations.

The “reproductive number” is often defined to be the expected number of new infections caused by a single infected individual in an otherwise susceptible population. It is more properly defined to be the expected number of new infections caused by a typical infected individual early in the epidemic [10]. As the population becomes more complex this apparently subtle distinction becomes more important. The reproductive number is a threshold parameter in that if < 1, it is impossible for an epidemic to take off, while if > 1 an arbitrarily small initially infected proportion of the population can result in an outbreak that grows exponentially until limited by the finite population.

In recent years, a number of related calculations have been done for various modifications of the basic model (1) [16, 6, 3, 2, 1, 13]. Surprisingly, even when the population structure or the details of the underlying disease process change, the final size relation is remarkably consistent as shown by [16] across a range of population structures.

The usual framework used to derive a final size relation begins from a system of integro-differential equations and finds a relation between I and S. Given this relation and the fact that I(∞) = 0, we can find S(∞). However, finding this relationship is often an unpleasant calculation. An alternative, simpler method was suggested by Diekmann and Heesterbeek [9], who described it as “less formal but much more direct.” This method has not been widely used, perhaps because of the perception of being less formal. We will show that the method can be made rigorous. The resulting approach is indeed much more direct but also more easily generalized and more widely applicable. The derivation does not depend on the dynamics of the infection process, but just the final probability that one individual will transmit to another if infected. An immediate consequence of this fact is that only the ultimate transmission probability affects the final size, not the details of the timing of the transmission. This single observation explains most results of [16].

Throughout this paper, we focus on calculating the final proportion infected in susceptible-infected-recovered (SIR) epidemics in asymptotically large closed populations. Individuals begin susceptible and become infected due to interactions with infected individuals. Once infected, interactions with other infected individuals have no impact. Eventually an infected individual recovers, becoming immune. We use S(t), I(t), and R(t) to denote the susceptible, infected, and recovered proportions of the population at time t. We want to find S(∞) or equivalently R(∞) given S(0), I(0), and R(0). For most of this paper we make the simplifying assumption R(0) = 0, which can be relaxed.

We assume the epidemic is governed by a stochastic process spreading disease from one individual to another, so that each new infection has a single “parent” infection. We further assume that there is no behavior change during the epidemic. We note that in stochastic realizations the disease may die out at early time due to random chance. We assume that the initial number of infections is large enough to neglect stochastic fade-out (though we allow for the population size to be large enough that the initial proportion infected may be negligibly small).

This paper is structured as follows. In section 2 we introduce the concept of a test individual, discuss the fundamental assumption, and outline our methodology. In section 3 we apply the methodology to a number of populations, always assuming that the initial infections begin instantaneously at t = 0. We show that many existing results are trivial consequences of our observations. We begin by considering “well-mixed” populations: contacts between individuals occur as independent events. We look at the cases where all individuals are equally susceptible, where some are more susceptible than others, and where an individual’s susceptibility is related to its infectiousness. We then adapt the approach to some populations in which contacts are not independent: having a partnership with one individual reduces the probability of having a simultaneous partnership with another (as might be expected in many sexual networks). We note that the fact that our approach has a formal mathematical basis does not guarantee that we can find a relation in all cases. We give an example where an analytic differential equations model exists in the large population limit, but we have not been able to find a direct relation between the final size and the initial conditions, for reasons which we explain. Finally in section 4 we give some extensions to the method: showing how to use the approach to derive equations for the dynamics rather than just the final size and showing how to adapt the approach if the initial infections do not all occur instantaneously at t = 0 or if R(0) > 0.

2 The test individual

If it makes sense to discuss the final size of an epidemic, then the variation in the final sizes of an ensemble of epidemic realizations must be small compared to the final size. That is, if it we use a single number to represent the final size of any realization, we are implicitly stating that all realizations have the same size. Typically this requires that the population be asymptotically large and may place restrictions on how contact rates are distributed.

The assumption that all epidemic realizations have the same size leads to a somewhat surprising conclusion: if we consider a single randomly chosen individual u, the sizes of epidemics in which u is infected must be the same as epidemics in which u is not infected. That is, if it makes sense to define a final size, then no one individual can be important to the final size. So the infections caused by u have a negligible impact on the final size. This will become important later when we argue that by choosing a single random individual and preventing it from causing infection we do not change the size of the epidemic. This will be the key assumption that underlies our calculation.

We note that in cases where we use integro-differential equations, we are actually making a stronger assumption than is needed here: not only do all epidemics have the same final size, but at any intermediate time the size is the same. There are many scenarios where the final size may have very little variation even when there may be significant variation in the sizes at some intermediate time, and so it may make sense to talk about the final size even when the integro-differential equations are a poor approximation to the stochastic epidemics. Having an integro-differential equations system is sufficient (though not necessary) for our key assumption to hold.

We can now define the concept of a test individual. The test individual is randomly chosen from the population. We will calculate the probability the test individual is susceptible at the end of an epidemic. Because all epidemics have the same size, this probability will equal the proportion of the population that is susceptible at the end of an epidemic.

So the process of calculating the total proportion infected in an epidemic can be reduced to the equivalent problem of finding the probability a randomly chosen test individual u is infected during the epidemic. This is equal to one minus the probability that no other individual infects u. Calculating this can become problematic because whether an individual v transmits to u depends on whether v becomes infected, which could result from a chain of infections that passed through u before reaching v, and so the probability v transmits to u depends on whether u has been infected. This would require conditional probability considerations, which may become quite complex. However, we instead find another equivalent problem. We modify the test individual slightly by preventing it from causing infections to others. This will have no impact on the final size of an epidemic because of our assumption that the final size is not affected by u’s infection, and it also has no impact on the probability u is infected. This eliminates the need for conditional probability arguments.

So we calculate the probability π that u is infected over the course of the epidemic, given that u is prevented from causing infections. In the simplest cases this depends only on the proportion of the remaining population that is infected, also π. Thus we arrive at an implicit equation for π representing a consistency relation. As populations become more complicated this approach must be adapted, and may not always be successful (but when it fails, the usual method also fails).

3 Final Size Calculation

We begin our calculations with populations that mix fully. For these populations, we know that whether or not v transmits to the test individual u is independent of whether some other individual w transmits to u. In the final part of this section we address what happens when this is violated.

The formula we arrive at will be a consistency relation. The left hand side will be the proportion of the population infected. The right hand side represents the probability that the test individual u is infected given the proportion of the population infected. These must be equal. We note that if we assume that the initial proportion infected is effectively zero (such as occurs if we take the population size to infinity much faster than the number of initial infections), then there may be two solutions, one of which is π = 0. It is consistent to say that if no-one is infected, then u will not be infected. Below the epidemic threshold = 1, this is the only solution. Above the epidemic threshold, there will be an additional solution 0 < π ≤ 1. If this larger solution is unique, then it gives the final size assuming an epidemic happens. If the solution is not unique, then the final size will be one of the possible solutions, but more information is needed to choose the correct one. Usually it is unique.

3.1 Homogeneous Susceptibility

Consider a population in which every individual is equally likely to receive infection from a given infected individual. We allow for variation in infectiousness. Most of the cases presented in [16] fit this framework.

We begin with a susceptible proportion S(0), and an infected proportion I(0) = 1 − S(0); thus R(0) = 0 (though this assumption can be relaxed without significant difficulty). The expected number of transmissions a randomly chosen infected individual causes is (if infectiousness varies, this is the average value). A transmission successfully causes infection if it happens to a susceptible individual. Otherwise there is no effect.

We take u to be a test individual, preventing u from transmitting to others. We have two options to calculate the probability u remains susceptible, and we present both because both have advantages in different contexts later.

We begin by noting that the probability u begins susceptible is S(0). The probability a random infected individual transmits to u is /N. Thus the probability that u is susceptible at the end of the epidemic is S(0)(1 − /N )^πN where πN is the number infected in the remaining population. We assume π approaches a fixed value as N → ∞. The probability u is infected also approaches the same value. So in the large N limit,

$$\pi =\underset{N\to \infty }{lim}1-S(0){\left(1-\frac{{\mathcal{R}}_0}{N}\right)}^{\pi N}=1-S(0)e^{-{\mathcal{R}}_0\pi }$$

We arrive at

$$\pi =1-S(0)e^{-{\mathcal{R}}_0\pi }$$ (2)

In the limit of a negligible fraction infected,

$$\pi =1-e^{-{\mathcal{R}}_0\pi }$$ (3)

The second approach is based on concepts of Poisson processes. Each infected individual contributes a small amount to the expected number of transmissions that u receives. If a proportion π of the population is infected, then the expected number of transmissions u receives is π. Because each event is independent, an analogy with Poisson processes says u escapes transmission with probability e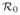^{− π}. Alternately, we can derive this formula directly, saying that f(ξ) is the probability none of the first M infected individuals transmits to u where ξ = M/N. Then f(π) is the probability u does not receive transmission. We find that f(ξ) − f(ξ + 1/N) is the probability that the first M do not transmit to u, but the M + 1st individual does.¹ This must equal f(ξ) /N, the probability the first M do not transmit times the probability the next one does. Taking N to ∞, we arrive at $\frac{\text{d}f}{\text{d}\xi }=-{\mathcal{R}}_{0}f(\xi )$, and so since f(0) = 1, we arrive at f(ξ) = e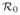^{− ξ}. Since the total proportion infected in the large N limit is π, we again conclude that u escapes transmission with probability e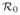^{− π}, and so u remains susceptible with probability S(0)e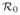^{− π}. This leads to equation (2).

For sections 3.2 and 3.3 it is simpler to use the second approach: observing that if the expected number of transmissions is ξ and each transmission event occurs independently and each event has negligibly small probability, then u escapes transmission with probability e^−ξ. Because of the assumption that a well-defined final size exists, we are able to assume that given an epidemic in a large population, the expected number of transmissions is close to ξ and approaches ξ as the population size increases. We will use this whenever the population is well-mixed such that all individuals have a chance to infect u independently. In cases where transmission events do not have negligible probability as N → ∞ (as in section 3.4), we will use an approach more like the first.

3.1.1 Examples

Although this result may seem trivial, there are a number of important examples where this calculation applies. We show that most of the cases investigated by [16] are immediate consequences of our result. To show that equation (2) holds, we need only show that the assumptions used in the derivation are satisfied.

The final size in the standard SIR model (section 2 of [16])

The standard Mass-Action SIR model (1) assumes that infected individuals transmit at rate β and recover at rate γ. The expected number of transmissions per individual is thus = β/γ. The assumptions are satisfied: any susceptible individual will be infected by an infected individual with probability /N (as N → ∞). So equation (2) holds.

Latency and multiple infectious stages (sections 3–5 of [16])

We can modify the standard Mass-Action SIR model so that there are multiple infected stages each with its own transmission rate β_i (which may be 0). We can assume that individuals leave stage i to enter stage i + 1 at rate γ_i. This allows us to write down a system of ordinary differential equations which has been used to find the final size relation by others. However, by the same argument as above it immediately follows that equation (2) holds (though the form of changes).

Arbitrarily distributed stage durations (sections 6 and 7 of [16], and [6])

In [16] the model was generalized further to allow for a finite number of infectious stages, each with its own fixed transmission rate, β_i, but with an arbitrary duration distribution. This was further generalized by [6] which allows the transmission and recovery rates to be arbitrary functions of time since infection. Again, in the large population limit, the probability that u receives transmission from any given infected individual is /N, and so equation (2) holds.

Super-spreaders (section 8 of [16])

Rather than having individuals pass through several stages, we could also have individuals take one of several paths once infected: for example, some could be highly infectious, while others are less infectious. This is similar to the observation that duration of infection can vary. The same argument applies. All that matters is that when an individual becomes infected, the a priori number of transmissions that it is expected to cause is . If we assume that those who are super-spreaders are no more or less susceptible than other individuals, then all individuals have equal probability of being infected and the a priori expected number of transmissions is , and so the probability of transmitting to a random susceptible individual is /N. So equation (2) holds.

Erdős–Rényi Networks

The simplest network disease models use Erdős–Rényi Networks, where each pair of individuals are in a partnership with probability 〈K〉/N, independent of all other partnerships. In the large N limit, the expected number of partnerships an individual has is 〈K〉.

We consider a disease spreading in which each individual has a probability T of receiving a transmission if a partner is infected. A newly infected individual has N − 2 potential partners other than itself and its infector who it can transmit to. The expected number of partners is 〈K〉(N − 2)/N and so the expected number of infections caused by an early infected individual is = 〈K〉 (N − 2)T/N. Taking N large, we have = 〈K〉 T.

We note that some individuals may be more infectious than others (e.g., their infectious period may be longer [18, 14]), but this does not affect the expected number of transmissions a test individual u receives. Each infected individual has a probability 〈K〉T/N = /N of both having an edge to u and transmitting to u. Again equation (2) holds.

3.2 Varying susceptibility

In this section we modify the homogeneous susceptibility assumption, but keep the well-mixed population assumption. We assume susceptibility varies from individual to individual, but an individual’s infectiousness and susceptibility are uncorrelated. This has recently been investigated by [13] and was investigated earlier by [4].

We distinguish individuals by their susceptibility x, defined so that x/N is the probability a random infected individual will transmit to an individual of type x. We define p(x) to be the probability density for a randomly chosen individual to be of type x and S(x, 0) to be the probability an individual of type x is susceptible at time 0. The probability an individual of type x is ultimately infected is defined to be π(x), with $\overline{\pi }={\int }_0^{\infty }\pi (x)p(x)\text{d}x$ giving the proportion of the entire population that is infected. The expected number of transmissions to a test individual u of type x is xπ̄. Thus the probability u remains susceptible is

$$1-\pi (x)=S(x,0)e^{-x\overline{\pi }}$$

So

$$\overline{\pi }=1-{\int }_0^{\infty }S(x,0)e^{-x\overline{\pi }}p(x)\text{d}x$$ (4)

Notice that the integral is in fact the Laplace transform of S(x, 0)p(x) evaluated at π̄. In the limit of a negligible initial proportion infected, we find

$$\overline{\pi }=1-{\int }_0^{\infty }p(x)e^{-x\overline{\pi }}\text{d}x$$

An equivalent relation was found by [13]. It was proven in [13] that above the epidemic threshold there is a unique solution for π̄ in (0, 1).

3.2.1 Example

Pre-existing immunity

This model is particularly appropriate when there is some form of pre-existing immunity to the disease. When a proportion of the population α is susceptible, but the rest immune, we define π to be the proportion of susceptible individuals that becomes infected and π̄ = απ the total proportion. In the absence of immunity, the probability a test individual would receive infection from a random infected individual is /N. For susceptible individuals this remains the same, so x/ . For the immune individuals x = 0. Then 1 − π = e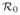^{− απ} = e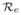^{− π} where 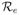= α is the effective reproductive number. Note that this formula is the same as in the homogeneous population, representing the fact that we can think of the disease as spreading just in the susceptible fraction of the population. If the pre-existing immunity is only partial, and all infected individuals have the same infectiousness then equation (4) applies but does not have an easy simplification.

3.3 Stratified Population

Still assuming a well-mixed population, we allow susceptibility and infectiousness to vary more generally. Assume that the population is such that the probability an individual becomes infected is related to its ability to infect others. For example, if an individual’s immune system is weak he or she may become infected with higher probability and shed virus at a higher rate. Alternately he or she may become sicker and therefore remain at home, reducing transmission rates. As another example, we may stratify the population by some characteristic, such as age, gender, or location, such that transmission within a stratum has different probability than between strata. Note that different strata may be represented at different levels at different times in the epidemic.

This problem has been considered by [1, 2, 3] in the special case of constant infection and recovery rates and a finite number of stratifications. However, the final size relation found is applicable even without constant rates as suggested in [9]. We now show the derivation of a more general result allowing for infinitely many stratifications.

We denote the types of individuals by x and y and let Λ_xy be such that Λ_xy/N gives the probability an infected type y individual would transmit to a given type x individual. We assume Λ_xy approaches a constant value as N → ∞. We define π(x) to be the probability a type x individual is eventually infected and p(x) to give the probability density for a random individual to be of type x. Then Nπ(x)p(x) measures the expected number of infected individuals of type x (with appropriate care for whether x is discretely or continuously distributed).

Consider now a test individual u of type x. The expected amount of transmission u receives is ${\int }_0^{\infty }\pi (y)p(y){\mathrm{\Lambda }}_{xy}\text{d}y$. So as N → ∞, u remains susceptible with probability

$$1-\pi (x)=S(x,0)e^{-{\int }_0^{\infty }\pi (y)p(y){\mathrm{\Lambda }}_{xy}\text{d}y}$$ (5)

We define $\overline{\pi }={\int }_0^{\infty }\pi (x)p(x)\text{d}x$ to be the probability a random individual is infected. In the limit of an infinitesimal initial proportion infected,

$$\pi (x)=1-e^{-{\int }_0^{\infty }\pi (y)p(y){\mathrm{\Lambda }}_{xy}\text{d}y}$$

If the population is divided into a finite number of stratifications, [2] proved there is a unique solution for (π₁, …, π_M ) in (0, 1)^M so long as the matrix of Λ_ij is non-negative and primitive (that is, infection starting in any one group can eventually reach all groups).

3.3.1 Examples

Patch Models (generalization of section 9 of [16], see also exercises 6.17 and 6.19 of [9])

Patch models are frequently used to introduce simple spatial dynamics to an epidemic model. Consider a population of M patches, each with its own population size having a total population of N. We will take N to ∞, keeping the relative sizes fixed. Let Λ_ij/N be the probability a randomly chosen infected individual of patch j transmits to a random individual of patch i. We assume each Λ_ij has a fixed limit as N → ∞. Let p_i denote the proportion of the population in patch i. Then if S(i, 0) is the initially susceptible proportion of patch i, equation (5) becomes

$${\pi }_i=1-S(i,0)exp\left[-\sum _{j=1}^M{\pi }_j{p}_j{\mathrm{\Lambda }}_{ij}\right]$$

Clearly if Σ_j p_jΛ_ij = Λ and S(i, 0) = S(0) are constant for all i, then π_i = π̄ for all i gives a solution. In this case, the formula derived in the homogeneous case would apply: π̄ = 1 − S(0)e^−Λπ̄, as observed in [16]. If ${\sum }_{j=1}^M{p}_j{\mathrm{\Lambda }}_{ij}$ or S(i, 0) depends on i, then no such simplification exists.

Mixed Poisson Networks (generalization of a result in [20])

One of the models introduced in [20] is an epidemic spreading in “Mixed Poisson Networks” (also called Chung-Lu Networks after [8]; these are a type of inhomogeneous random graphs [5, 12], and are almost identical to network classes introduced in [7, 23]). They are a special case of a stratified population, and a generalization of Erdős–Rényi Networks.

In a Mixed Poisson Network, each individual has an expected number of partnerships κ. The value of κ is assigned using the probability density ρ(κ). The probability that individuals v and w are in a partnership is κ_vκ_w/N 〈K〉 where $\langle K\rangle ={\int }_0^{\infty }\kappa \rho (\kappa )\text{d}\kappa$ is the average value of κ. Each pair of individuals is assigned to be in a partnership independently of any other partnerships. The number of partnerships an individual is in is referred to as its “degree”.

We assume that if one individual is infectious, infection will transmit along a partnership with probability T (infectiousness may vary, but we keep susceptibility constant). The probability an infected individual v transmits to the test individual u depends on whether v has a partnership with u and whether the partnership transmits. This does not alter whether an infected individual w transmits to u since the existence of partnerships are independent.

We assume that the initial condition is set by infecting a subset of the population instantaneously at t = 0, and we allow for the individuals to be infected with probability depending on their expected degrees, but not depending on properties of their (susceptible) partners. For the approach to work, the probability a neighbor of a susceptible individual is infected should not depend on properties of the susceptible individual.

This satisfies the assumptions we need. We note that infection is more likely to transmit to or from an individual with higher κ simply because there are more opportunities.

The probability an individual with given κ₂ infects an individual with κ₁ is given by the probability they share an edge (κ₁κ₂/N 〈K〉) times the probability the edge transmits (T ). So Λ_κ1κ2 = Tκ₁κ₂/〈K 〉. Thus,

$$\pi (\kappa )=1-S(\kappa ,0)e^{-\frac{\kappa }{\langle K\rangle }T{\int }_0^{\infty }\pi ({\kappa }^{\prime })\rho ({\kappa }^{\prime }){\kappa }^{\prime }\text{d}{\kappa }^{\prime }}$$

We define $\mathrm{\Theta }=1-[T/\langle K\rangle ]{\int }_0^{\infty }\pi (\kappa )\rho (\kappa )\kappa \text{d}\kappa$. So π(κ) = 1 − S(κ, 0)e^{−κ(1−Θ)} and

$$\begin{array}{l}\mathrm{\Theta }=1-\frac{T}{\langle K\rangle }{\int }_0^{\infty }[1-S(\kappa ,0)e^{-\kappa (1-\mathrm{\Theta })}]\rho (\kappa )\kappa \text{d}\kappa \\ =1-\frac{T}{\langle K\rangle }\left(\langle K\rangle -{\int }_0^{\infty }S(\kappa ,0)e^{-\kappa (1-\mathrm{\Theta })}\rho (\kappa )\kappa \text{d}\kappa \right)\\ =(1-T)+\frac{T{\mathrm{\Psi }}^{\prime }(\mathrm{\Theta })}{\langle K\rangle }\end{array}$$ (6)

where $\mathrm{\Psi }(x)={\int }_0^{\infty }S(\kappa ,0)e^{-\kappa (1-x)}\rho (\kappa )\text{d}\kappa$. Notice that Ψ is the Laplace transform of S(κ, 0)ρ(κ) evaluated at 1 − x. Also note that if S(κ, 0) = 1 for all κ, then 〈K〉 = Ψ′(1), and there is always a solution Θ = 1 corresponding to no infection. Above the epidemic threshold there is a second solution in (0, 1) which is unique since Ψ′(Θ) is convex. We have

$$\begin{array}{l}\overline{\pi }=1-{\int }_0^{\infty }S({\kappa }_2,0)e^{-{\int }_0^{\infty }\pi ({\kappa }_1)\rho ({\kappa }_1){\mathrm{\Lambda }}_{{\kappa }_2{\kappa }_1}\text{d}{\kappa }_1}\rho ({\kappa }_2)\text{d}{\kappa }_2\\ =1-{\int }_0^{\infty }S({\kappa }_2,0)e^{-{\kappa }_2\frac{T}{\langle K\rangle }{\int }_0^{\infty }\pi ({\kappa }_1)\rho ({\kappa }_1){\kappa }_1\text{d}{\kappa }_1}\rho ({\kappa }_2)\text{d}{\kappa }_2\\ =1-{\int }_0^{\infty }S({\kappa }_2,0)e^{-{\kappa }_2(1-\mathrm{\Theta })}\rho ({\kappa }_2)\text{d}{\kappa }_2\\ =1-\mathrm{\Psi }(\mathrm{\Theta })\end{array}$$ (7)

Thus we can solve for Θ implicitly using equation (6) and then find π̄ from Θ using equation (7). This generalizes a result of [20] where transmission and recovery are Poisson processes with rates β and γ [so T = β/(β+γ)] and the assumption was made that the initial proportion infected was negligible, so S(κ, 0) = 1 for all κ. In fact we can generalize further without altering the solution if we allow for infectiousness to vary as long as susceptibility (per partnership) is uniform, taking T to be the average per-partnership transmission probability.

In [20] this static network model was generalized to allow contacts to form and break independently of what contacts existed and what the infectious status of an individual is. Those individuals with higher expected degree form new partnerships at a higher rate. All existing partnerships break at the same rate. For these populations, it is possible to calculate the probability an infected individual of a given expected degree will transmit to a randomly chosen test individual. Whether or not a given partnership exists during an individual’s infectious period is independent of any other contacts in the population. Thus the assumptions hold and equation (5) can be adapted to find final sizes even in these dynamic populations.

3.4 Static Configuration Model Networks

In many reasonable scenarios, having a partnership with one individual reduces the probability of having a partnership with another. For example, a sexually transmitted disease cannot spread in a purely monogamous population. If v can infect u, then w cannot. For such cases we still use the same basic approach, but in our calculation of the probability that u is not infected, we cannot treat each potential infection as independent.

We use a network model commonly called the Configuration Model [22] in the physics literature, but also widely known as the Molloy-Reed model [21]. Consider a population in which the number of partnerships an individual has is denoted by k with k assigned independently to each individual from some probability distribution. Let P(k) denote the probability that an individual is assigned to have k partners. To create a sample network, we give each individual k “stubs” (or half-edges). We then select pairs of stubs and connect them to form edges until every stub is in an edge.² When a given stub of u is paired with another stub, the probability that the neighboring individual v has k partners is given by P_n(k) = kP (k)/〈K〉. This expression states that the probability a partnership is with a degree-k individual is proportional to k. This size bias effect is widely recognized [11, 20].

We again consider a test individual u which is prevented from transmitting to its neighbors, but apply the first approach of section 3.1. As before we assume that the initial infections occur instantaneously at t = 0, and individuals are infected without regard to properties of their susceptible neighbors. We set S(k, 0) to be the probability an individual with degree k is initially susceptible. Let θ denote the probability that a partner v of u does not transmit to u. Then given k the probability that u is eventually infected is π(k) = 1 − S(k, 0)θ^k. So the average is

$$\overline{\pi }=1-\sum _{k}P(k)S(k,0){\theta }^k=1-\psi (\theta )$$ (8)

where ψ(x) = Σ_k P(k)S(k, 0)x^k. To find θ, we note that the probability the partner v is never infected is given by Σ_k S(k, 0)P_n(k)θ^k−1 with the k − 1 in the exponent resulting from the fact that u is prevented from transmitting to v. It is straightforward to show that this is simply, ψ′(θ)/〈K〉. Then

$$\theta =1-T+T\frac{{\psi }^{\prime }(\theta )}{\langle K\rangle }$$ (9)

We can solve equation (9) for θ and then use equation (8) to find π. If S(k, 0) = 1 for all k, then ψ′(1) = 〈K〉. In this case, there is a solution to this with θ = 1, which corresponds to no infection. Above the epidemic threshold there is a second solution in (0, 1) which is unique since ψ′(θ) is convex. It was shown in [18] that heterogeneity in infectiousness has no impact on final size (though it alters epidemic probability), but heterogeneity in susceptibility does.

It is possible to generalize the Configuration Model to allow for individuals to change contacts. For example, an individual might have a given degree k, and as time progresses the individual breaks a partnership and forms another, preserving the degree. We lose the independence assumptions needed for this approach. If w is infected and u has a partnership with v, that provides some protection of u from w because it reduces the potential of u to have a partnership with w. This causes the approaches of sections 3.1–3.3 to fail. The approach of this section also fails because the amount of protection provided to u by the u–v partnership depends on how likely the partnership is to dissolve prior to w recovering. We have not been able to find a final size relation in this limit even though we have found a differential equations model for such an epidemic [20]. This is not a failure of the methodology: if we apply the usual method for calculating final sizes, the consistency relation we find does not have a unique solution so we cannot directly determine which solution is correct.

Configuration Model Networks are a special class of networks for which analytic calculation is relatively straightforward. Little is known about final size relations because some of the independence assumptions that go into our derivations fail. A few results are known about what conditions on the disease lead to larger epidemics [19, 17]. In particular, if all individuals are equally infectious and equally susceptible, this maximizes epidemic size for a given average transmission probability.

4 Extensions

4.1 Deriving dynamical equations

The approach we have introduced can be applied beyond just calculating the final size. For calculating the final size we needed to make the assumption that the final size did not vary between different epidemic realizations. If we make a slightly stronger assumption that the size at any intermediate time does not vary between different realizations, then this approach can be adapted to find equations that govern the dynamics.

This is effectively the approach used by [20] to derive equations governing the dynamics for epidemics in many different types of networks. Here we show how to apply the approach in the case of the standard SIR model. In the standard SIR model, infected individuals recover through a Poisson process with rate γ. They transmit infection through a Poisson process with rate β. When they transmit, the infection reaches a randomly chosen member of the population. If S is the proportion susceptible, the transmission successfully causes infection with probability S. If we assume the epidemic begins with only susceptible and infected individuals [i.e., R(0) = 0] and ξ(t) is the expected number of transmissions an individual has received by time t, then S(t) = S(0)e^−ξ(t). Since infected individuals recover at rate γ and transmit at rate β, for every transmission there are γ/β recoveries. We can conclude that R(t) = γξ(t)/β. We know that $\frac{\text{d}}{\text{d}t}\xi =\beta I$, and I = 1 − S − R = 1 − S(0)e^−ξ − γξ/β. So

$$\frac{\text{d}}{\text{d}t}\xi =\beta \left(1-S(0)e^{-\xi }-\frac{\gamma }{\beta }\xi \right),S=S(0)e^{-\xi },R=\frac{\gamma \xi }{\beta },I=1-S-R$$

with ξ(0) = 0. So we have a single differential equation for ξ plus auxiliary equations giving S, I, and R in terms of ξ. This is equivalent to the standard equations (1) assuming R(0) = 0. The final size relation can be derived quickly from setting $\frac{\text{d}}{\text{d}t}\xi =0$ (or equivalently I = 0) and substituting ξ = βR/γ = R into the resulting equation.

4.2 More general initial conditions

The derivations we have done have assumed that R(0) = 0 and that the initial infections occur instantaneously at t = 0. In general, this need not be the case. In particular, if we are introducing an intervention at some intermediate time and want to calculate its impact on the final size, we want to be able to apply the current initial conditions to the final size relation.

This is relatively straightforward. We will analyze those who are infected at or before t = 0 separately from those infected after t = 0. Note that if recovery and transmission are Poisson processes, then due to the memoryless property, we do not need to distinguish infections that occurred prior to t = 0 from those after t = 0. We show a few examples.

4.2.1 Well-mixed populations

We demonstrate this assuming homogeneous susceptibility but allowing for arbitrary infectious period distribution and allowing infectiousness to depend on time since infection.

Let Nξ₀ be the total number of transmissions that will occur after t = 0 coming from those who are infected at or before t = 0. Let Nξ₁ be the total number of transmissions by those infected later. Consider a test individual. With probability S(0) it is susceptible at t = 0. With probability S(0)e^{−ξ₀−ξ₁} it is susceptible at t = ∞. So the proportion of the population infected after t = 0 is π̂ = S(0)(1 − e^{−ξ₀−ξ₁}). Each of these infected individuals is expected to cause 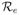transmissions where 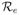is the number of new infections caused by an infected individual in the presence of whatever behavior change or intervention is in place. Since ξ₁ = 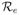π̂, we conclude

$$\widehat{\pi }=S(0)(1-e^{-{\xi }_0-{\mathcal{R}}_e\widehat{\pi }})$$

and the total proportion infected is π = R(0) + I(0) + π̂. This basic approach applies to the other generalizations.

4.2.2 Mixed Poisson Networks

Because epidemics on networks are less familiar to most researchers, we explicitly show how it proceeds in the network cases. The calculation proceeds largely in the same way in Mixed Poisson Networks. The main distinction is that depending on how the disease has been spreading prior to t = 0, the probability an infected individual’s partner is infected or recovered may be significantly different from that of a susceptible individual’s partner.

If Φ_S(0), Φ_I(0), and Φ_R(0) are the probabilities a partner of a susceptible individual is susceptible, infected, or recovered at t = 0, then we find

$$\begin{array}{l}\mathrm{\Theta }=1-{\mathrm{\Phi }}_I(0)\widehat{T}-{\mathrm{\Phi }}_S(0)\left(1-\frac{{\mathrm{\Psi }}^{\prime }(\mathrm{\Theta })}{{\mathrm{\Psi }}^{\prime }(1)}\right)T\\ \overline{\pi }=1-\mathrm{\Psi }(\mathrm{\Theta })\end{array}$$

where $\mathrm{\Psi }(x)={\int }_0^{\infty }S(\kappa ,0)e^{-\kappa (1-x)}\rho (\kappa )\text{d}\kappa$ and T̂ is the average probability an initially infected partner will transmit.³ The Ψ′(Θ)/Ψ′(1) term represents the probability an initially susceptible partner remains susceptible. The partner has a given κ with probability density $\kappa S(\kappa ,0)\rho (\kappa )/{\int }_0^{\infty }\kappa S(\kappa ,0)\rho (\kappa )\text{d}\kappa$, and given κ remains susceptible with probability e^{−κ(1−Θ)}. Combining this gives that a susceptible partner remains susceptible with probability Ψ′(Θ)/Ψ′(1). If the initial infections occur instantaneously at t = 0, then Φ_I(0) = 1 − Ψ′(1)/〈K〉, Φ_S(0) = Ψ′(1)/〈K〉, and T̂ = T. In this case this reduces to the previous system.

4.2.3 Configuration Model Networks

The modification for Configuration Model Networks is similar. We set φ_S(0), φ_I(0), and φ_R(0) to be the probability a partner of a susceptible individual is susceptible, infected, or recovered at t = 0. We set T̂ to be the probability one of the initially infected individuals (whose infection may have occurred prior to t = 0) will eventually transmit given that it has not by t = 0.

If the test individual is initially susceptible its partner v is initially susceptible with proba bility φ_S(0). If v is initially susceptible, the probability its degree is k is kP (k)S(k, 0)/Σ_k kP (k)S(k, 0). The probability v is susceptible at a later time is Σ_k kP (k)S(k, 0)θ^k−1/Σ_k kP (k)S(k, 0). We find

$$\begin{array}{l}\theta =1-{\phi }_I(0)\widehat{T}-\left(1-\frac{{\psi }^{\prime }(\theta )}{{\psi }^{\prime }(1)}\right)T\\ \overline{\pi }=1-\psi (\theta )\end{array}$$

where ψ(θ) = Σ_k P (k)S(k, 0)θ^k. Again if the initial infections occur instantaneously at t = 0 this reduces to the previous system.

5 Discussion

We have shown that a simple method can be used to find final size relations for SIR epidemics under a wide range of assumptions about the population and the disease. We have used this approach to reproduce a number of known relations, finding that these relations can be derived trivially with significantly less effort than used previously. The derivation gives more insight into why the particular relation should hold. It is important to observe that the population size required for the final size relation to hold is significantly smaller than required to use integro-differential equations to predict the dynamics.

The key observation needed for our approach is that if there is a well-defined single final size, no single individual has a macroscopic impact on the epidemic size. From this we can conclude that the probability a random test individual is infected must match the final size. From this starting point, we can use a mathematically rigorous argument to calculate the probability the test individual is infected in terms of the final size, and then we arrive at a consistency equation which gives the final size relation. We have not addressed the question of when a well-defined final size will exist. However when the model can be accurately represented by a system of integro-differential equations, then because the limit is deterministic, there is a well-defined final size in a large enough population. So this approach could be used instead whenever a final size relation has been derived through integro-differential equations. We have used this fact to reproduce the final size relations of [16, 6, 3, 2, 1, 13] more directly. We have also shown how to apply this approach to epidemics spreading in networks.