Comparison of electromyography and joint moment as indicators of co-contraction

Abstract

Antagonistic muscle activity can impair performance, increase metabolic cost, and increase joint stability. Excessive antagonist muscle activity may also cause an undesirable increase in joint contact forces in certain populations such as persons with knee osteoarthritis. Co-contraction of antagonistic muscles measured by electromyography (EMG) is a popular method used to infer muscle forces and subsequent joint forces. However, EMG alone cannot completely describe joint loads that are experienced. This study compares a co-contraction index from EMG to a co-contraction index calculated from simulated muscle moments during gait.

Co-contraction indices were calculated from nine healthy, able-bodied subjects during treadmill walking at self-selected speed. Musculoskeletal simulations that tracked experimental kinematics and kinetics were generated for each subject. Experimentally measured EMG was used to constrain the model’s muscle excitation for the vastus lateralis and semimembranosus muscles. Using the model’s excitations as constrained by EMG, muscle activation and muscle moments were calculated. A common co-contraction index (CCI) based on EMG was compared with co-contraction based on normalized modeled muscle moments (MCCI). While the overall patterns were similar, the co-contraction predicted by MCCI was significantly lower than CCI.

Because a simulation can account for passive muscle forces not detected with traditional EMG analysis, MCCI may better reflect physiological knee joint loads. Overall, the application of two co-contraction methods provides a more complete description of muscle co-contraction and joint loading than either method individually.

1. Introduction

Quantification of antagonistic muscle activity is a critical component of many in vivo analyses of human movement. Excessive antagonistic muscle contractions during dynamic activities can impair functional performance and increase the metabolic cost of performing the task (Frost et al., 1997). This phenomenon, known as co-contraction, also has the potential to increase the forces within the joint, as muscle forces are the greatest contributor to joint loads during weight-bearing activities (Richards and Higginson, 2010; Lu et al., 1998). Certain populations such as persons with knee osteoarthritis demonstrate abnormal muscle coordination strategies and in particular increased antagonist muscle activity around the knee joint (Zeni et al., 2010). The resultant excessive forces may lead to the initiation and progression of cartilage degeneration (Griffin and Guilak, 2005). Contrarily, coordinated antagonistic muscle activity may be a desired strategy to improve joint stability during rapid ballistic movements. These coordinated motor control patterns have the potential to protect ligaments from excessive forces during dynamic movements in which the bony segments undergo rapid acceleration or deceleration (O’Connor, 1993; Hirokawa et al., 1991). Therefore an accurate assessment of muscle-induced modifications in joint forces and moments is critical in understanding the biomechanical variables that may lead to injury or disease progression.

Although quantification of co-contraction is difficult, surface electromyography (EMG) has become a common experimental tool to evaluate the magnitude of antagonistic muscle activity. Using EMG, the summation of concomitant electrical activity from muscles that create opposing joint motions can provide a surrogate measure of antagonistic muscles forces acting across a joint. Although greater EMG magnitude is related to greater internal muscle force (Richards and Higginson, 2010; Griffin and Guilak, 2005), the relationship between EMG activity and force is not linear (Buchanan et al., 2004), particularly during high force levels. Additionally, accurate and detailed EMG-force models can be difficult and time-consuming to construct. Data collections associated with these models are complex and highly reliant on electrode placement (Rainoldi et al., 2004; Hogrel et al., 1998) and normalization procedures (Knutson et al., 1994), which may make them undesirable for certain applications. For these reasons, interpretation of muscle force and subsequent joint contact force based solely on surface EMG data is not ideal.

Recently, musculoskeletal simulations have provided a method for calculating realistic estimates of muscle forces during gait (Neptune, 2000; Thelen and Anderson, 2006; Anderson and Pandy, 2003; Richards and Higginson, 2010; Erdemir et al., 2007; Kim et al., 2009). The potential of musculoskeletal models to provide meaningful clinical interpretation has been highlighted, especially in cases where the relative forces of individual muscles are assessed (Erdemir et al., 2007). While accessibility to modeling software had been a previous limitation to this type of analysis, the recent emergence of the OpenSim software package (Delp et al., 2007) provides an open-source, user-friendly software package to perform these muscle force estimations from experimental kinetic and kinematic data. Musculoskeletal simulations also model the activation dynamics and force generating properties of muscle, and are able to estimate muscle force from excitation signals such as EMG (Buchanan et al., 2004). However, there are limitations to musculoskeletal modeling, such as applying generic muscle properties to a non-homogenous population and a limited ability to validate model results. In light of these limitations, appropriate use of simulations is paramount (Erdemir et al., 2007), and results must be evaluated before application to clinical scenarios. The purpose of this study was to compare a co-contraction index obtained from simulated muscle moments to a co-contraction index derived from experimentally measured muscle activity during gait.

2. Methods

2.1. Experiment

Nine healthy, able-bodied subjects without a history of neurological or orthopedic impairments (five males/four females, age 49.7 (13.8) years, mass 81.3 (9.5) kg, walking speed 1.28 (.12) m/s) were recruited as part of a study approved by the Human Subjects Review Board at the University of Delaware. EMG and motion data were collected while the subject walked at self-selected walking speed on an instrumented split-belt treadmill (Bertec Corp., Columbus, OH, USA). Self-selected walking speed was determined during an overground 20 m walk, of which the central 10 m was timed. The subjects were asked to walk at a comfortable, self-selected speed and the calculated walking speed was used during the treadmill data collection trials. Ground reaction forces, free moment, and center of pressure were obtained during a 30 s trial at self-selected speed on the treadmill. The three dimensional motion of retroreflective markers was captured at 60 Hz using a 6 camera system(Orthotrak, Motion Analysis Corp., Santa Rosa, CA, USA).Markers were placed on the bilateral lower extremities, pelvis and trunk using a modified Helen Hayes marker set. The subject’s skin was cleaned with rubbing alcohol prior to placement of the EMG electrodes on the skin surface above the vastus lateralis and semimembranosus. Accurate placement of the electrodes was validated by palpation of the muscle bellies and assurance of a clean EMG signal during manually resisted knee extension and flexion for the vastus lateralis and semimembranosus, respectively. EMG data were collected at 1080 Hz and then filtered in post-processing using a 20–400 Hz bandwidth filter. The EMG data were rectified then filtered with a 4th order zero-phase shift Butterworth filter with a cut-off frequency of 30 Hz. EMG data were selected for a representative stride and time-normalized to 100 points. The EMG data were then normalized to the peak EMG signal from the self-selected walking speed.

The co-contraction index (Rudolph et al., 2000) was chosen to describe the temporal and magnitude components of the EMG signals:

$$\text{CCI}=\frac{\mathit{\text{LEMG}}}{\mathit{\text{HEMG}}}(\mathit{\text{LEMG}}+\mathit{\text{HEMG}})$$ (1)

where LEMG is the normalized magnitude of the EMG signal for the less active muscle, HEMG is the normalized magnitude of EMG signal for the more highly active muscle. Therefore, for the self-selected walking speed the CCI at each time point can range from a value of zero (zero for both variables) to 2 (maximum normalized value for both variables). This CCI was calculated at each point of the gait cycle, providing a time series curve from which mean CCI was then calculated for each trial.

2.2. Modeling

The OpenSim software package was used to build a 3D, subject-specific, musculoskeletal model containing 92 actuators and 13 degrees of freedom for the walking trial from each subject (Delp et al., 2007). The model was scaled to the subjects’ height and mass. Inverse kinematics was used to calculate joint kinematics from the motion capture data. The residual reduction algorithm was then run to account for any discrepancies between experimentally measured kinetics and kinematics calculated by inverse kinematics (Delp et al., 2007) and resulted in minor adjustments to mass distribution and joint kinematics. Because EMG signals are representative of the neural input responsible for muscle activation, we used the EMG input to constrain the muscle excitation of our simulation. To do this, the magnitude and timing of muscle excitation for the vastus lateralis and semimembranosus were set equal to the experimentally measured EMG signals for the corresponding muscle. Next, computed muscle control (CMC) (Thelen and Anderson, 2006) was run to calculate the forces and resultant moments produced by these muscles while reproducing the experimental kinematics. The joint moments generated at the knee by the vastus lateralis and semimembranosus were normalized to the maximum muscle moment during the self-selected walking trial. Using the normalized muscle joint moments, the co-contraction index was modified:

$$\text{MCCI}=\frac{|\mathit{\text{LM}}|}{|\mathit{\text{HM}}|}(|\mathit{\text{LM}}|+|\mathit{\text{HM}}|)$$ (2)

where LM is the magnitude of the joint moment for the smaller muscle moment, and HM is the magnitude of the joint moment for the larger muscle moment at a given time.

CCI and MCCI were calculated for each point in the gait cycle. The mean values for normalized EMG, normalized moment, and CCI and MCCI were calculated and compared for the stance phase (first 65% of gait cycle), swing phase (terminal 35% of gait cycle) and weight acceptance phase (first 20% of gait cycle). Significant difference between the two methods for each phase was assessed using a paired t-test (p < 0.05). A descriptive comparison of the time series curves over the whole gait cycle was also performed for the CCI and MCCI.

3. Results

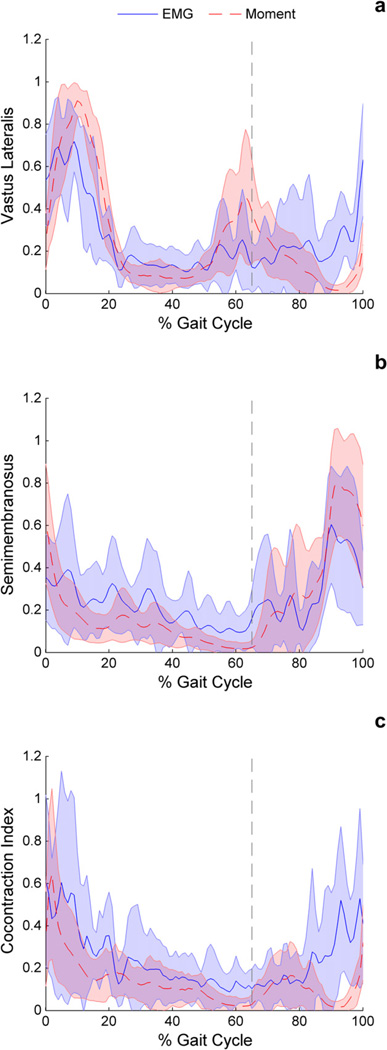
Data were collected for nine subjects. Overall, normalized vastus lateralis moment and normalized EMG activity followed a similar shape, with normalized muscle moment greater than normalized EMG during the loading (p = 0.001) and stance (p = 0.022) phase of gait (Fig. 1a, Table 1). Conversely, normalized EMG activity was greater than normalized muscle moment during swing (p = 0.003) for the vastus lateralis. The semimembranosus trended (p = 0.075) toward greater normalized muscle moment than normalized EMG activity in swing phase and showed lower normalized moment than normalized EMG activity during stance (Fig. 1b).

Fig. 1.

Comparison of the EMG and muscle moment techniques for (a) the vastus lateralis EMG activity versus simulated muscle moment, (b) the semimembranosus EMG activity versus simulated muscle moment, and (c) CCI versus MCCI. Vertical line indicates beginning of swing phase.

Table 1.

Mean values for the loading, stance, and swing phases of gait for the vastus lateralis, semimembranosus, and co-contraction indices. Grayed comparisons are not significant (p> 0.05).

Phase	Vastus Lateralis		Semimembranosus		Co-contraction
	EMG	Moment	EMG	Moment	CCI	MCCI
Loading	0.54 (0.09)	0.67 (0.07)	0.30 (0.18)	0.23 (0.12)	0.42 (0.27)	0.28 (0.17)
Stance	0.28 (0.06)	0.32 (0.04)	0.21 (0.11)	0.13 (0.06)	0.24 (0.14)	0.15 (0.09)
Swing	0.23 (0.13)	0.14 (0.08)	0.31 (0.09)	0.38 (0.12)	0.24 (0.16)	0.09 (0.06)

On average, the EMG based CCI was higher for all three phases of gait investigated in the study (loading p = 0.047, stance p = 0.02, swing p = 0.007) (Fig. 1c). The two methods showed similar shapes however, with CCI and MCCI greatest during the weight acceptance portion of the gait cycle when averaged across nine subjects. The largest difference between CCI and MCCI occurred during swing, with the mean MCCI less than 50% of the mean CCI.

4. Discussion

Co-contraction calculated from experimental EMG activity and modeled muscle moments of the vastus lateralis and semimembranosus were fairly similar with peak values occurring during early stance, which is consistent with previous reports of muscle activation (Perry and Burnfield, 2010). Overall, the co-contraction predicted by the MCCI technique was significantly lower than CCI. This is due to lower semimembranosus moment during stance and lower vastus lateralis moment during swing compared to EMG activity.

Discrepancies between EMG activity and muscle moments can be partially attributed to a combination of muscle properties (e.g. force-length and force-velocity) and mechanical properties (e.g. moment arm). These factors play an important role in the modulation of muscle force and are included in musculoskeletal joint models, but are not considered in traditional EMG co-contraction analyses. For example, muscle moment produced by the semimembranosus during the loading phase of gait is decreased due to the concentric behavior of the muscle as the knee flexes. In this case, loss in muscle moment due to shortening of the semimembranosus outweighs the small (~2 mm) increase in moment arm experienced by the semimembranosus over the knee flexion range during loading. Conversely, extension of the knee during terminal swing causes an eccentric contraction of the semimembranosus, enhancing the force and moment generated about the knee. The vastus lateralis has an eccentric contraction during loading, enhancing the moment production in stance, and a concentric contraction during terminal swing, decreasing moment production.

The apparent differences between the two approaches may reflect important non-neural factors that influence muscle forces. During dynamic activities, muscles can exert passive forces which are translated to the knee joint. Force–length and force–velocity properties in particular can heavily influence the force production of a muscle for a given activation level (Zajac et al., 2003). It is important to note that in our simulations, the excitation for each muscle was equal to the EMG signals. Therefore, the differences between the computed muscle moments and muscle EMG signals were attributable to the active and passive physiological properties of muscle that are considered within the simulation framework, but are not encompassed with traditional EMG analysis.

While using simulated muscle moments to calculate co-contraction may be advantageous, there are several limitations to this approach. Although there have been recent attempts to validate simulated muscle forces with the use of an instrumented knee implant (Kim et al., 2009), simulated muscles forces in general cannot be validated directly. In this study, generic muscle properties were used when modeling the muscle moment from EMG. While the normalization of muscle moment used to facilitate comparison between the EMG and muscle moment methods also removed the influence of maximum muscle force, other generically modeled muscle properties such as optimal fiber length may still affect the timing and magnitude of the simulated muscle moment. Although EMG provides an estimation of muscle activity, it is also subject to several limitations that make accurate assessment of co-contraction difficult. Assessment of electrical muscle activity from the same electrode within the same session, but at a different joint angle or during a different direction of contraction is an inherent limitation of EMG. Different joint angles will alter the tissue volume located beneath the muscle, which may also affect the magnitude and frequency characteristics of the EMG signal (Farina et al., 2002). The quality and repeatability of the EMG signal is dependent on the careful placement of electrodes (Hogrel et al., 1998; Rainoldi et al., 2004), but even with careful and repeatable electrode placement, EMG signals are subject to cross talk from other muscles (De Luca and Merletti, 1988) or may contain aberrant signals from electrical devices and motion artifact. Finally, all EMG processing is subject to a normalization process, and the selection of a normalization value (i.e. maximum within trial, global maximum) has an associated muscle state (i.e. velocity, length)which can affect the processed EMG values (Farina et al., 2002). Ideally, the muscle state during the maximal trial used for normalization would be comparable to the muscle state during the dynamic trial, however this is not always the case. Differences in normalization procedures can affect reported EMG magnitudes, as well as subsequent co-contraction indices. EMG magnitudes in this and other studies must be cautiously interpreted.

The combination of EMG and joint moment co-contraction analysis may give a more complete description of muscle activity and joint loads than either method can provide. Joint moment co-contraction analysis using modeling techniques accounts for additional factors that play a role in force production such as force–velocity and force–length properties. These properties may have substantial impact when considering abnormal gait patterns. In this study, only two muscles were compared between the experimental and simulated co-contractions. The muscles chosen in this paper represent the two muscles during the gait cycle that are likely to have overlapping on-times (Perry and Burnfield, 2010), produce the highest amount of muscle force (Delp, 1990), and are commonly attributed to abnormal antagonistic activity in patients with knee pathology (Rudolph et al., 2000; Zeni et al., 2010; Ramsey et al., 2007; Hubley-Kozey et al., 2009). Future studies evaluating co-contraction should consider using the MCCI with additional muscles as an alternate or supplement to EMG analysis.

Biographies

Brian A. Knarr received his B.S. in Mechanical Engineering from The College of New Jersey in 2006 and his M.S. in Mechanical Engineering from the University of Delaware in 2009. He is currently pursuing a Ph.D. in Biomechanics and Movement Science from the University of Delaware. His research interests include the development of new techniques involving computer based models to study and improve human biomechanical performance, particularly in populations with gait impairments.

Joseph Zeni, Jr. is an Assistant Professor in the Department of Physical Therapy at the University of Delaware. He graduated with his Masters of Physical Therapy in 2003 from Quinnipiac University and in 2008 he earned his Ph.D. in Biomechanics and Movement Science at the University of Delaware. He currently teaches the Anatomy and Biomechanics courses in the Physical Therapy Department. Dr. Zeni devotes his research time to the study of knee osteoarthritis and biomechanical factors relating to the progression of the disease. His clinical research is also focused on using novel rehabilitation paradigms to optimize patient outcomes after hip and knee arthroplasty.

Jill Higginson is an Associate Professor in Mechanical Engineering and Biomedical Engineering as well as Director of the Center for Biomedical Engineering Research at the University of Delaware. She trained at Cornell University (B.S. ’96), Penn State University (M.S. ’98) and Stanford University (Ph.D. ’05). Her research applies experimental and computational techniques to study muscle coordination during walking in healthy and impaired populations. As part of an interdisciplinary study funded by the National Institutes of Health, She has been studying the relationship between joint loading and cartilage geometry during the progression of knee osteoarthritis.